1. Introduction
In recent years, deep rock engineering has faced numerous challenges, including rock burst and large deformation of surrounding rock, which pose a serious threat to the safety of deep engineering. However, due to the difficulty in obtaining samples of deep rock mass, there have been limited studies on deep rock mass mechanics test, and the mechanical properties, deformation, and failure mechanism of deep rock mass remain unclear. Moreover, it has not been established that the mechanical theory of deep rock mass based on the deformation law and failure mechanism.
Many scholars have conducted experimental studies on rock-like materials to investigate the mechanical properties of rock mass, which have similar mechanical properties and failure mechanisms. These studies have enabled the deformation law and failure mechanism of different types of rock mass to be mastered, and corresponding theoretical models to be established.
Yang[
1] took barite powder and iron concentrate powder as aggregate, quartz sand as regulator, and quicklime and gypsum as cementing agents to and studied the effects of four factors on the mechanical properties of similar materials. Hu[
2] studied the effects of four factors on mechanical properties of rock-like specimens, which were water-binder ratio, ratio between binder components, ratio between aggregate components, and particle size of pottery sand. Gong[
3] investigated the mechanical properties of rock mass with different geological structures with rock-like material consisted of pulverized coal, sand, cement, water, gypsum, soil and sodium chloride. Zhang[
4], Liu[
5], Ning[
6], and Dai[
7] studied the influence of composition on the compressive strength, density, elastic modulus and permeability coefficient of rock-like materials. Wang[
8] studied the influence of sand-binder ratio, and residual water content on uniaxial compressive strength, elastic modulus and Poisson's ratio of rock-like specimens consisted of river sand and gypsum. Liu[
9] prepared rock-like specimens with gypsum, yellow sand, quartz and barite powder and investigated the effects of molding pressure, compaction rate and repeated stirring times on the mechanical properties of rock-like materials. Liu[
10] made rock-like material specimens with sand, cement, gypsum, diatomite, red clay and marl powder to studied mechanical properties of rocks with different weathering degrees.
Klammer[
11] Investigated the Influence of Grain-Scale Heterogeneity on Strainburst Proneness Using Rock-Like Material. Cao[
12] made a multi-scale model of plasticity and damage for rock-like materials with pores and inclusions。Ma [
13]investigated the behaviors and mechanism on rock-like specimen with two circular-holes under compression. Zhao[
14] investigated fracture mechanisms of intact rock-like materials under compression. Zhang[
15] investigated the Damage Characteristics and Fracture Behaviour of Rock-like Materials with Weak Interlayer Zones. Ding[
16] investigated the shear performance of anchored jointed rock-like mass under different corrosion levels. Fan[
17] carried out experimental and numerical investigation on crack mechanism of folded flawed rock-like material. Hou[
18] carried out excavation unloading response of cylindrical rock-like specimen with axial joints. Huang[
19] investigated the damage mechanisms under high pressure with plastic-damage model for rock-like materials. Jia[
20] investigated Crack Initiation and Propagation of Embedded Three-Dimensional Parallel Cracks in Transparent Rock-Like Material. Li[
21] investigated acoustic emission and mechanical characteristics of rock-like material containing single crack. Meng[
22] carried out experimental and numerical studies on the anisotropic mechanical characteristics of rock-like material. Pan[
23] established a damage constitutive model of rock-like materials under the action of chemical corrosion and uniaxial compression. Teng[
24] investigated the shear failure modes and acoustic emission characteristics of rock-like materials. Tian[
25] investigated the Multi-Angle Effects of Micron-Silica Fume on Micro-Pore Structure and Macroscopic Mechanical Properties of Rock-like Material. Wang[
26] investigated mechanical properties and failure mechanism of rock-like specimens. Wang[
27] investigated strength and failure characteristics of a Layered Composite Rock-Like Sample with a Single Hole. Wang[
28] made model with damage and cracking in heterogeneous rock-like materials by phase-field method. Yu[
29] made model with Mixed Cracks in Rock-Like Brittle Materials Under Compressive Stresses by a Double-Phase-Field Method. Zhao[
30] established a new discrete element model for rock-like materials.
However, most studies on rock-like materials focused on undamaged specimens, neglecting the impact of initial damage on the mechanical properties of rock mass. As there are random distributions of original defects in deep rock mass, such as holes, cracks, and joints, these defects cannot be ignored when conducting experimental research on the mechanical properties of deep rock mass. To address this issue, X-ray diffraction analysis was performed on deep rock mass to determine its main components. Based on the results of X-ray diffraction analysis, the author designed a set of orthogonal tests to confirm the component and ratio of rock-like materials applicable to deep damaged rock.
2. Experiment Design
2.1. Detection of deep rock composition
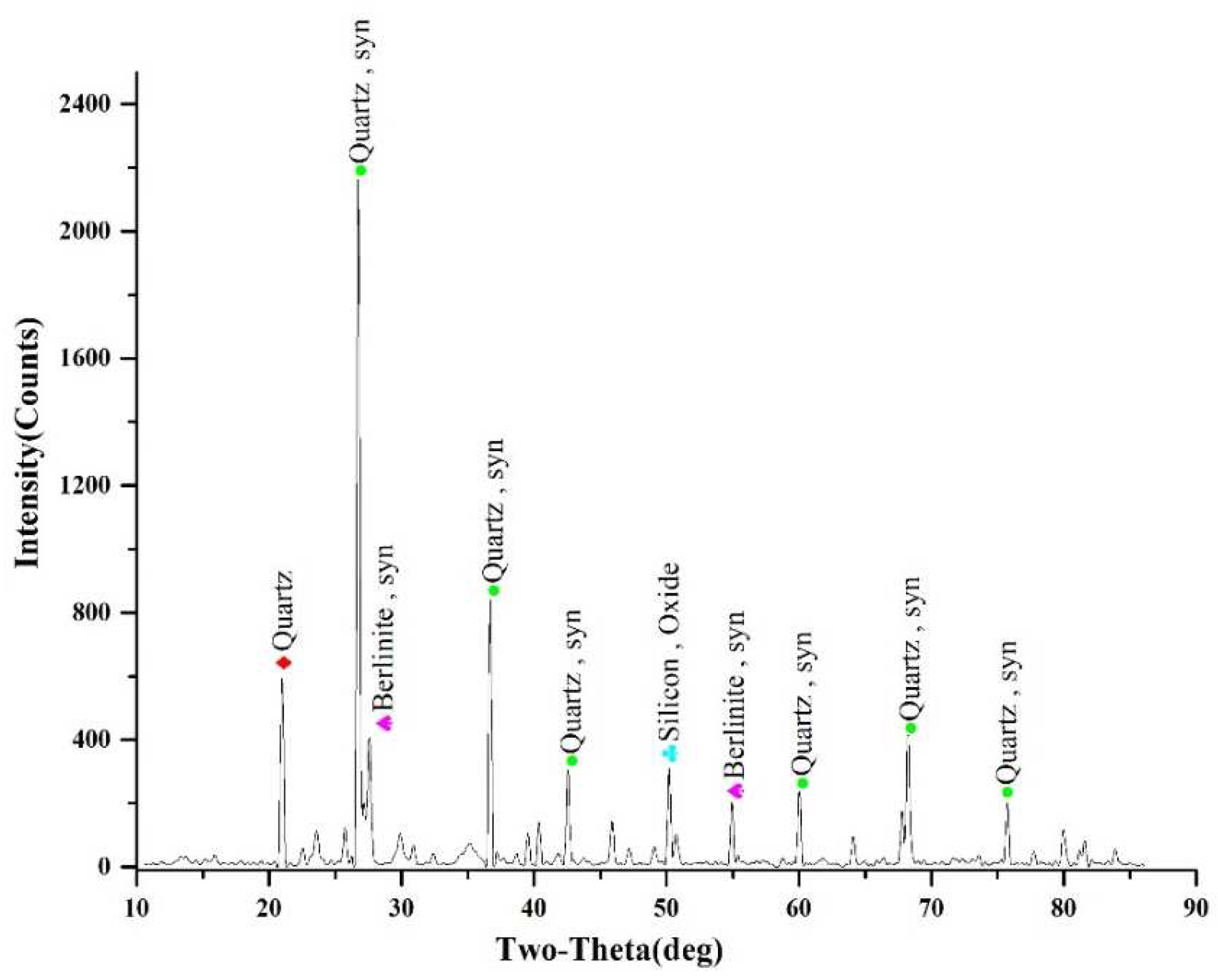
XRD diffraction analysis was conducted on rock samples from a deep environment to determine their composition. The analysis results, displayed in
Figure 1, indicated that the sandstone primarily consisted of quartz, silicon oxide, and berlinite.
2.2. Similarity Criterion
In accordance with the similarity criterion, a correlation between physical quantities of protolith (P) and rock-like material (M) has been established. To denote the similarity ratio between the two, the variable C has been assigned. The application of the following formula yields the required outcome.
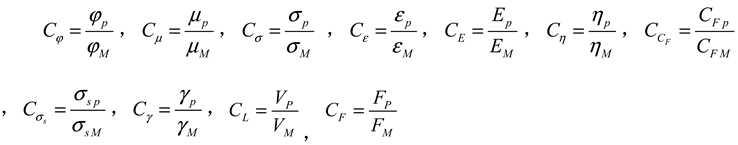
Where,
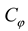
is the similarity constant of internal friction angle,

is the similarity constant of poisson's ratio,
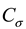
is the similarity constant of stress,
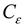
is the similarity constant of strain,
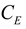
is the similarity constant of elasticity modulus,
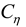
is the similarity constant of viscosity coefficient,
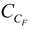
is the similarity constant of cohesion,
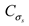
is the similarity constant of yield strength,
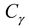
is the similarity constant of unit weight,
CL is the similarity constant of geometric,
CF is the similarity constant of force.
In accordance with the initial similarity criterion, which posits that comparable phenomena possess equivalent criteria of similarity and corresponding similarity indexes measuring 1, we can therefore establish the relationships between equivalent constants.

Given the differential scales between the engineering rock mass and the laboratory test rock specimen, a geometric similarity constant of 30 was established in order to ensure geometric equivalence. Consequently, it can be obtained by calculating the above formula that
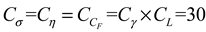
.
2.3. Orthogonal test of rock-like material
In order to ascertain the constitution of deep damaged rock in this document, two factors are considered. The first factor involves examining the composition of deep damaged rock and ensuring that rock-like material possess a comparable composition. The second factor involves assessing the physical and mechanical parameters of deep rock and ensuring that these parameters are within the same range for both rock-like material and deep damaged rock.
The aggregates chosen for this study is river sand with a diameter of 30-40 mesh, while the binder is Portland cement P.O42.5 and the regulator is gypsum powder, all aggregates are illustrated in
Figure 2. In order to replicate the effects of internal structural deterioration on the mechanical characteristics of rocks, researchers have employed the use of polystyrene foam, commonly known as EPS, to simulate the initial damage sustained by rocks located deep within the earth's surface. The polyethylene foam, which has a lower strength than rock mass, is approximately spherical in shape. The random filling technique is employed to replicate the irregular distribution of damage inside the rock.
An orthogonal experimental method was utilized to evaluate the impact of composition and ratio on the mechanical features of rock-like material. In order to determine the factors affecting the mechanical properties of deep damaged rock mass, four test factors were selected. Factor A denotes the proportion of binder relative to aggregate, whereas factor B signifies the proportion of polystyrene foam in the entire model. Moreover, factor C denotes the proportion of binder and regulator, and factor D is the size of polystyrene foam. Each factor was tested at three levels to explore their effect on the mechanical properties of rock-like material. The rock-like material ratio orthogonal test scheme is presented in
Table 1.
3. Specimen preparation and test process
3.1. Specimen preparation
This manuscript adhered to the directives delineated in the
Standard for Test Methods of Engineering Rock Mass (GB/T50266-2013) by utilizing a cylindrical sample with dimensions of Φ50×100mm.The non-parallelism error of the two end faces of the specimen was contained within a range of ±0.05mm, while the diameter error along the height of the specimen was controlled within a range of ±0.3mm. Additionally, the deviation between the end face and the axis of the specimen was limited to ±0.25°. To create the specimen, a cylindrical split mold, as depicted in
Figure 3, was employed.
Initially, weighed the aggregate, binder, and regulator followed the orthogonal test scheme, then mixed all components. Once the ingredients were mixed evenly, water was added and stirred in until a consistent mixture was achieved. The uniform mixture was then filled into a split mold, and the polystyrene foam (EPS) was equally divided and mixed in accordance with the predetermined proportion. In order to reduce the effects of stratification, a stratified compaction methodology was employed. Additionally, prior to packing, the surface of the specimen was intentionally scratched. In order to guarantee consistent density and strength across all specimens, the compaction pressure was set to 2kN. Once the specimens were assigned identification numbers, they underwent a drying process lasting 12 days in a well-ventilated environment, thus guaranteeing uniform drying throughout. A temperature and humidity chamber was used to dry all specimens at 80℃ to eliminate any moisture content differences that could affect the specimens' mechanical properties. The mass of the specimens was measured every two hours, and the drying process ceased once the mass difference was less than 0.1g for two consecutive measurements.
Figure 4 displays some of the test specimens.
3.2. Test process and results
Table 3 presents the results of the measurements carried out in accordance with the
Standard for test methods of engineering rock mass (GB/T 50266-2013) for the compressive strength, tensile strength, elastic modulus, axial strain, and Poisson's ratio of the specimens.
4. Sensitivity analysis of factors
The utilization of the range analysis method was implemented in the calculation of the range for each physical and mechanical parameter of rock-like material based on the measurements obtained from mechanical tests. The degree of influence of factors A to D on the aforementioned parameters was established through a comparison of the range size. A greater range signifies a stronger impact of the factor on the parameter, thereby indicating its higher sensitivity to the factor. Conversely, parameters with a smaller range are deemed less sensitive to the factor in question.
4.1. Sensitivity analysis of factors to elastic modulus
Based on the data presented in
Figure 5, it can be inferred that the elastic modulus of rock-like material experiences a gradual decrease with an increase in factor A. Similarly, factor A has a negative correlation with the elastic modulus of rock-like material. With an increase in the level of factor B, the elastic modulus experiences a decrease followed by an increase. The minimum elastic modulus value is observed at level 2 in the three groups of levels investigated. The elastic modulus of rock-like material first increases and subsequently decreases with an increase in factor C level, indicating significant changes in elastic modulus. On the other hand, the elastic modulus increases with an increase in factor D level. Factor D is positively correlated with the elastic modulus of rock-like material, and the greatest changes in elastic modulus are observed with an increase in factor D level. According to the elastic modulus range analysis, the sensitivity of rock-like material elastic modulus is ranked as D>C>B=A from strong to weak. Therefore, it can be inferred that factor D has the most significant impact on the elastic modulus of rock-like material, while factor B has the least effect. It is possible to adjust the elastic modulus of rock-like material by manipulating the size of the damage simulation material.
4.2. Sensitivity analysis of factors to Poisson's ratio
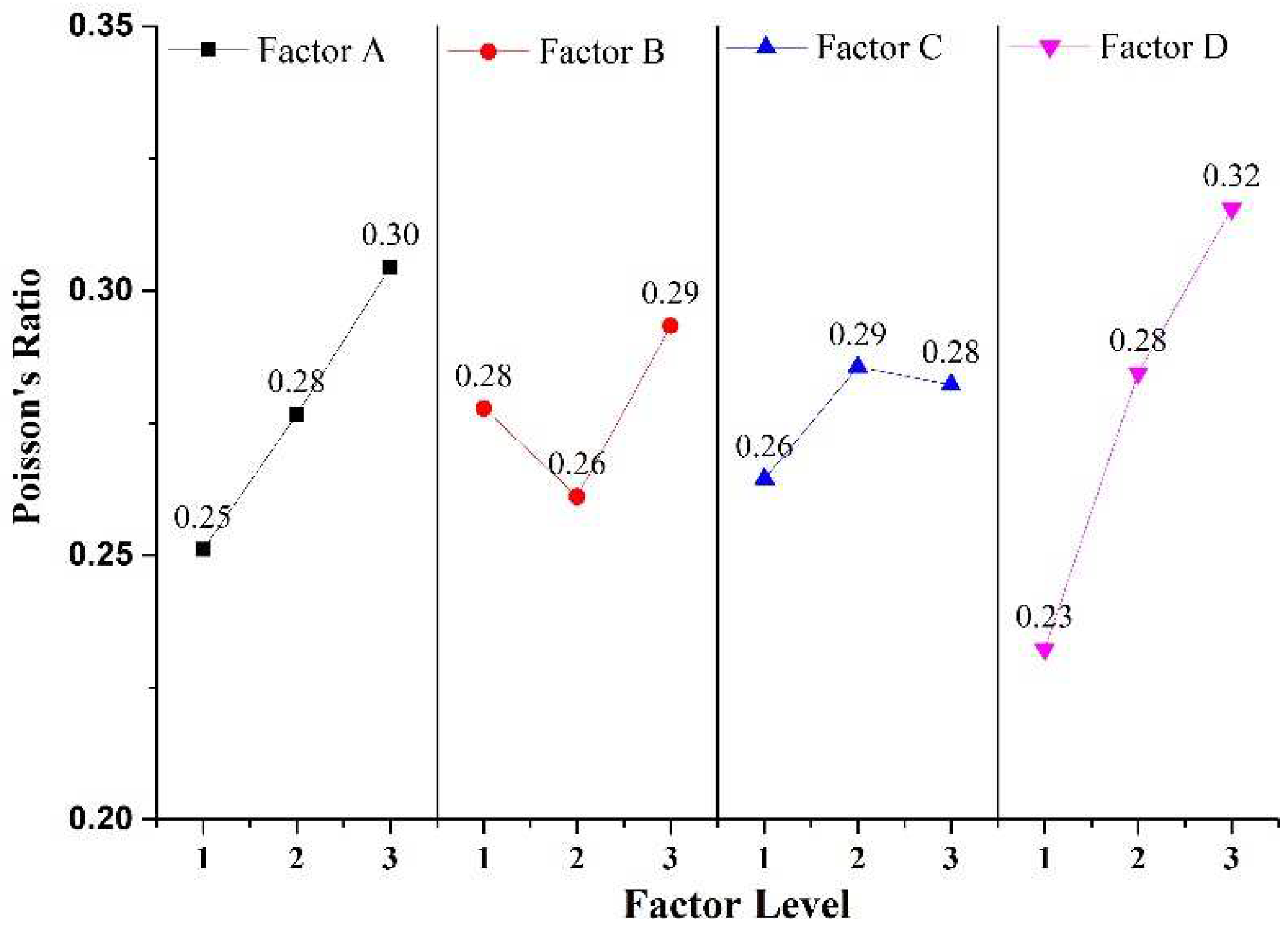
Based on the analysis of
Figure 6, it can be observed that the Poisson's ratio of rock-like material tends to increase gradually with the increase of factor A and factor D. The findings indicate a positive correlation between Poisson's ratio and these two factors, with factor D demonstrating a greater overall variation amplitude compared to factor A. Additionally, the study reveals that Poisson's ratio of rock-like material initially decreases and then increases with an increase in factor B level, and increases first and then decreases with an increase in factor C level. However, there is not a significant overall amplitude of Poisson's ratio of rock-like material change with these two factors. Based on the Poisson's ratio range analysis, it can be concluded that the sensitivity of Poisson's ratio to rock-like material is ranked from strong to weak as D>A>B=C. Thus, the findings suggest that factor D has the most significant impact on the Poisson's ratio of rock-like material. Conversely, factor A, factor B, and factor C have a minimal degree of influence on the Poisson's ratio of rock-like material. Consequently, by adjusting the size of damage simulation material of rock-like materials, it is possible to modify the Poisson's ratio of rock-like material.
4.3. Sensitivity analysis of factors to compressive strength
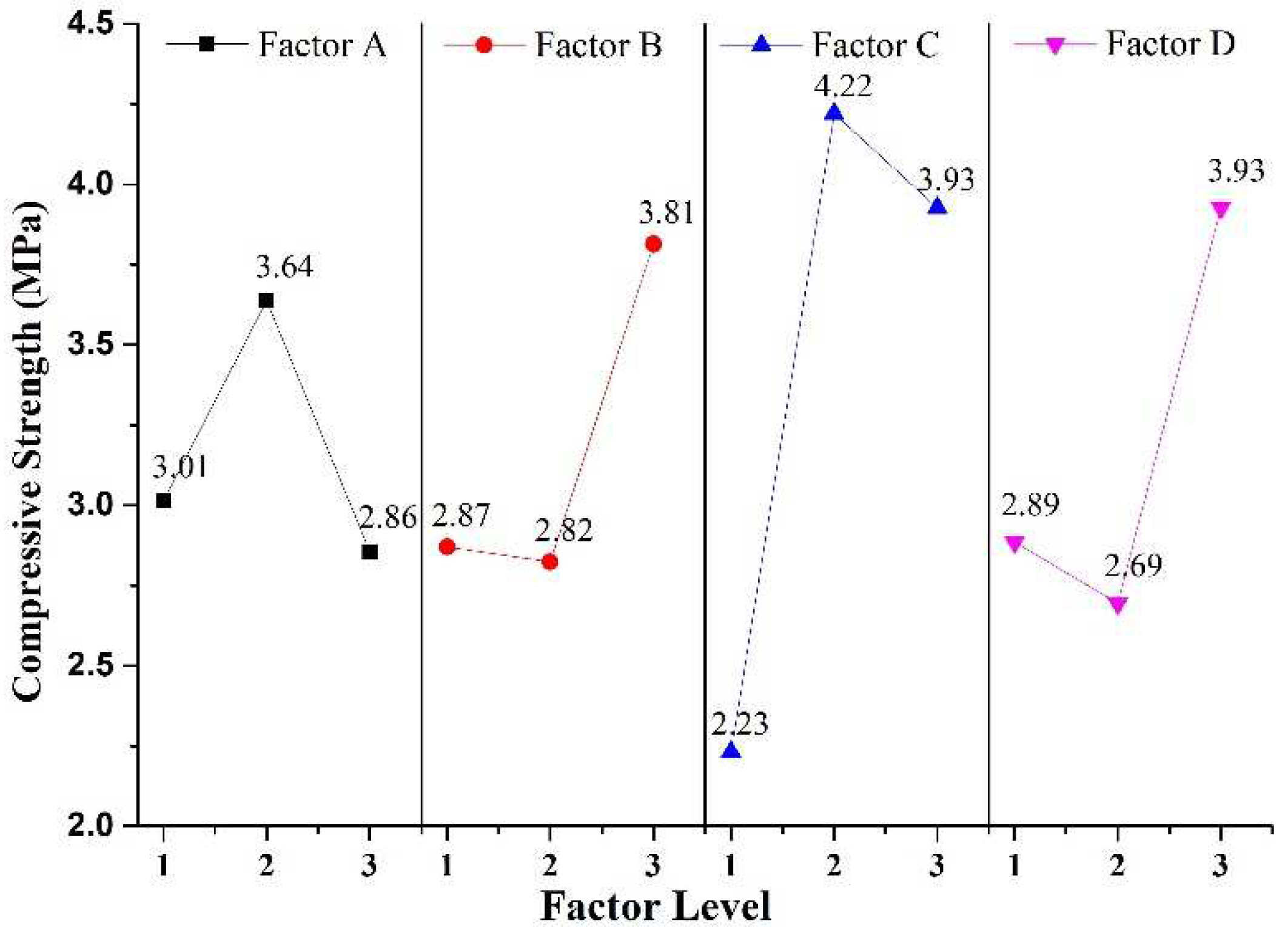
Based on the data presented in
Figure 7, it can be observed that the compressive strength of rock-like material follows a nonlinear trend with respect to factors A, B, C, and D. Factor C exerts a more significant influence on the compressive strength of rock-like material as compared to other factors. The compressive strength of the material initially increases and then decreases with the increase in factors A and C, whereas it initially decreases and then increases with the increase in factors B and D. Notably, the compressive strength of both factors increases significantly at the third level. A range analysis of compressive strength reveals that the response sensitivity of rock-like material to the four factors ranks from strong to weak as C>D>B>A. Factor C has the most substantial effect on the compressive strength of rock-like material, while factor A has the weakest effect on the compressive strength of rock-like material. Therefore, manipulating the binder-to-regulator ratio presents a viable approach for modifying the compressive strength of rock-mimicking substances.
4.4. Sensitivity analysis of factors to tensile strength
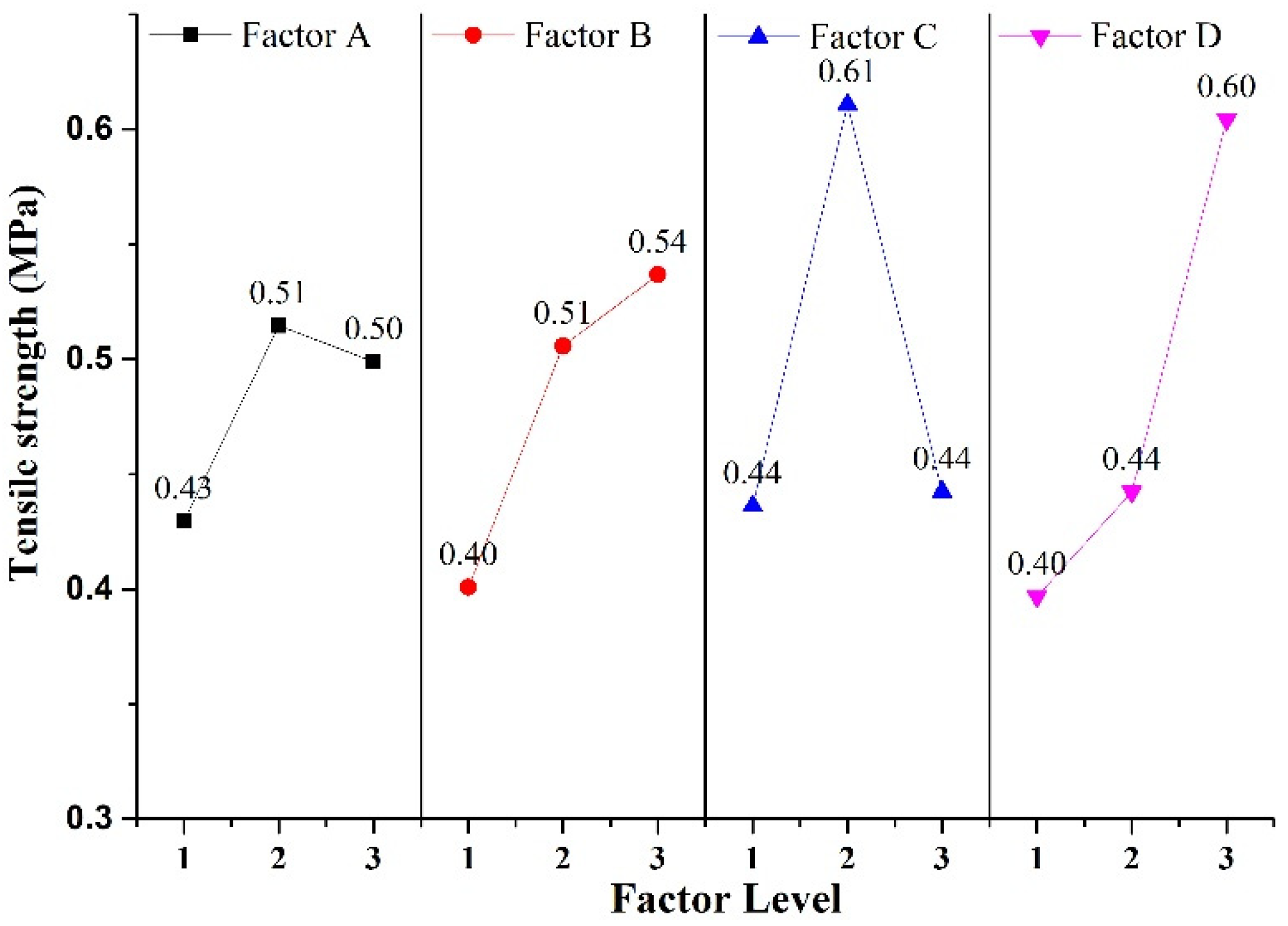
Based on the analysis of
Figure 8, it can be concluded that the tensile strength of rock-like material has a nonlinear relationship with factor A and factor C, where it first increases and then decreases. Additionally, the sensitivity of tensile strength to factor A is lower than that of factor C. On the other hand, the tensile strength of rock-like material increases with the levels of factor B and factor D, with a higher sensitivity to factor D. According to the range of tensile strength, the sensitivity to the four factors can be ranked from strong to weak as D>C>B>A. Therefore, the tensile strength can be regulated accordingly by altering the dimensions of the simulated rock-like substance.
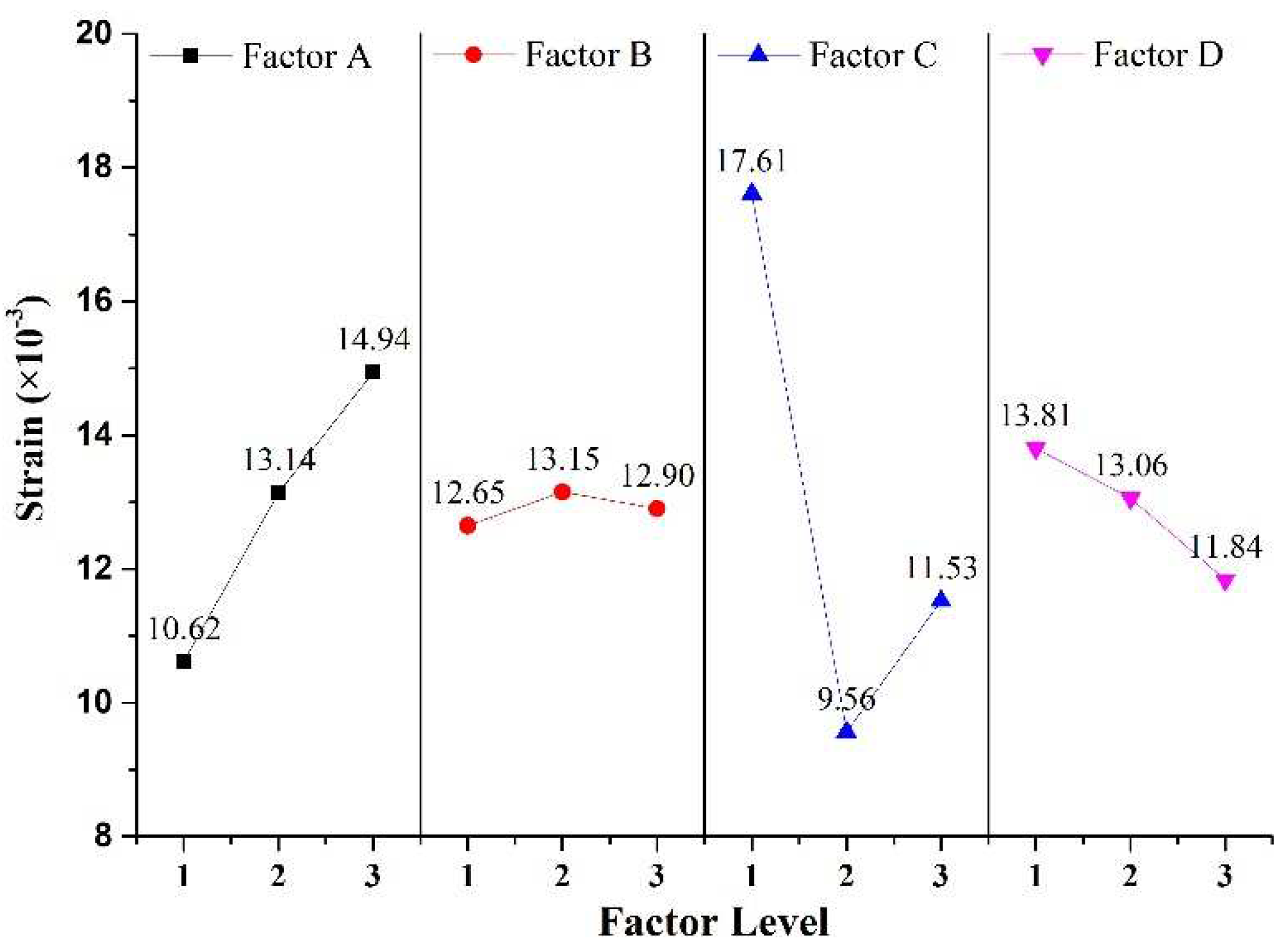
4.5. Sensitivity analysis of factors to axial strain
Based on the analysis of
Figure 9, it can be concluded that the strain of rock-like material increases gradually with an increase in factor A, while the axial strain exhibits negligible change in response to an increase in factor B. Factor C demonstrates a significant impact on the axial strain, which initially decreases and later increases over a wide range. Conversely, an increase in factor D leads to a gradual decrease in axial strain. The assessment of tensile strength range reveals that the sensitivity of strain to the four factors is ranked as C>A>D>B. Factor C has the most significant effect on the strain of rock-like material. Consequently, adjusting the ratio of binder to regulator can be instrumental in regulating the strain of rock-like material.
In essence, the size of damaged simulated materials has a significant impact on the elastic modulus, tensile strength, and Poisson's ratio of rock-like material. On the other hand, the ratio of binder and regulator in rock-like material has a more pronounced effect on the compressive strength and axial strain. Adjusting the size of damage simulation materials can alter the elastic modulus, tensile strength, and Poisson's ratio of rock-like material, whereas changing the ratio of binder and regulator can modify its axial strain and compressive strength.
5. Applicability of similar materials
The present study outlines a similarity criterion for determining the range of physical and mechanical parameters of rock-like material, which is presented in
Table 4. The mechanical parameters of rock-like materials, including compressive strength, tensile strength, elastic modulus and Poisson's ratio, can be modified by adjusting the component proportions, thereby enabling mechanical testing of various rock masses. Notably, the physical and mechanical parameters of the rock-like materials examined in this study are akin to those of well-known rocks such as granite, sandstone, shale, and limestone, rendering it possible to replicate these rocks for the purpose of exploring their diverse mechanical properties and modes of failure. The physical and mechanical parameters of both rocks and rock-like material are comprehensively listed in
Table 4.
6. Conclusions
This paper presents a method for simulating the mechanical properties of deep damaged rock utilizing river sand as aggregate, cement as cementing agents. Furthermore, in order to better simulate the influence of damage on mechanical parameters of deep rock masses, the authors suggest using polystyrene foam (EPS) as the damage simulation material.
The manipulation of damage simulation materials (EPS) size has been identified as a means of altering the compressive strength, tensile strength, elastic modulus, and Poisson's ratio of rock-like material. Furthermore, adjusting the ratio of binder and regulator has been observed to affect the axial strain and compressive strength of the said material.
The study introduces a type of rock-like material characterized by a diverse array of physical and mechanical attributes. The compressive strength estimates range from 37.2 to 310MPa, while the tensile strength values range from 3.9 to 25.5MPa, the elastic modulus values range from 4 to 53.6GPa, and the Poisson's ratio values range from 0.19 to 0.58. By altering the constituent proportions of the rock-like material, mechanical tests can be carried out to replicate the mechanical properties of various rock types, such as sandstone, shale, granite, and limestone, while adjusting the parameters within a customizable range.
Data Availability Statement
The data used to support the findings of this study are available from the corresponding author upon request.
Acknowledgments
This paper gets its funding from Project (2021BS24) supported by Scientific Research Foundation of Weifang University. The authors wish to acknowledge these supports. At the same time, authors are very grateful for the anonymous reviewers’ valuable comments.
Conflicts of Interest
The authors declare that there are no conflicts of interest regarding the publication of this paper.
References
- YANG. X., L.D. SU., B. ZHOU., et al. Experiment study on similarity ratio of similar material for model test on red-bed soft rock [J]. Rock and Soil Mechanics 2016, 37, 2231–2237.
- HU. M., X.M. YANG..X.D. LUO. Study on mixture ratio scheme of similar materials of red sandstone based on orthogonal experiment [J]. Jorunal of hefei university of technology(Natural Science), 2020, 43, 736–740.
- GONG. Y.F., G.W. ZHU., Y.P. JIANG., et al. Experimental study on the proportion of similar materials for different geological structures of coal seams [J]. Journal if Mining Science and Technology, 2022, 7, 267–274.
- ZHANG. Z.J., Q.Y. ZHANG., W. XIANG., et al. Development and application of new-style hydro-mechanical coupling similar materials in complex environment [J]. Journal of Central South University (Science and Technology), 2021, 52, 4168–4180.
- LIU. J.H., W.X. LI., Y.S. LIU., et al. A method for determining the ratio of similar material to simulate porous water-bearing stratum [J]. Rock and Soil Mechanics, 2018, 39, 657–664.
- NING. Y.B., H.M. TANG., B.C. ZHANG., et al. Investigation of the rock similar material proportion based on orthogonal design and its application in base friction physical model tests [J]. Rock and Soil Mechanics, 2020, 41, 2009–2020.
- DAI. S.H., H.R. WANG., R.J. HAN., et al. Properties of similar materials used in fluid-solid coupling model test [J]. Rock and Soil Mechanics 2020, 41, 1–8.
- WANG. P., C. SHU., SHI F., et al. Orthogonal experimental study of similar materials properties of different densities, sand-binder ratios and residual moisture contents [J]. Rock and Soil Mechanics, 2017, 38, 229–235.
- LI. C.J., Y.S. LIU., Y.C. LI., et al. Experimental study on influencing factors of mechanical properties for mudstone similar material [J]. Safety in Coal Mines, 2021, 52, 71–76.
- LIU. Y.L., W.Z. ZHOU., B. GUO., et al. Study on marl similar materials in similar simulation test [J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39, 2795–2803.
- KLAMMER, PEINTNER C., GOTTSBACHER L., et al. Investigation of the Influence of Grain-Scale Heterogeneity on Strainburst Proneness Using Rock-Like Material [J]. Rock Mechanics and Rock Engineering, 2023, 56, 407–425. [CrossRef]
- Y. J. CAO, SHEN W. Q., SHAO J. F., et al. A multi-scale model of plasticity and damage for rock-like materials with pores and inclusions [J]. International Journal of Rock Mechanics and Mining Sciences 2021, 138. [CrossRef]
- W. B. MA, CHEN Y. L., YI W., et al. Investigation on crack evolution behaviors and mechanism on rock-like specimen with two circular-holes under compression [J]. Theoretical and Applied Fracture Mechanics 2022, 118. [CrossRef]
- H. Y. ZHAO, ZHANG L. C., WU Z. H., et al. Fracture mechanisms of intact rock-like materials under compression [J]. Computers and Geotechnics 2022, 148. [CrossRef]
- L. ZHANG, JING H. W., MENG Y. Y., et al. Experimental Study on the Damage Characteristics and Fracture Behaviour of Rock-like Materials with Weak Interlayer Zones [J]. Ksce Journal of Civil Engineering, 2022, 26, 4157–4167. [CrossRef]
- W. T. DING, HUANG X. H., WANG Z. R., et al. Experimental study on the shear performance of a prestressed anchored jointed rock-like mass under different corrosion levels [J]. International Journal of Rock Mechanics and Mining Sciences 2022, 158. [CrossRef]
- W. C. FAN, YANG H., JIANG X. L., et al. Experimental and numerical investigation on crack mechanism of folded flawed rock-like material under uniaxial compression [J]. Engineering Geology 2021, 191. [CrossRef]
- G. Y. HOU, ZHOU Y. L., ZHAO T. L., et al. Excavation unloading response of cylindrical rock-like specimen with axial joints: laboratory experiment and numerical simulation [J]. Journal of Geophysics and Engineering 2023, 20, 21–37. [CrossRef]
- X. P. HUANG, KONG X. Z., CHEN Z. Y., et al. A plastic-damage model for rock-like materials focused on damage mechanisms under high pressure [J]. Computers and Geotechnics 2021, 137. [CrossRef]
- P. JIA, JI W. M., QIAN Y. J., et al. Crack Initiation and Propagation of Embedded Three-Dimensional Parallel Cracks in Transparent Rock-Like Material [J]. Journal of Testing and Evaluation 2022. [CrossRef]
- K. S. LI, ZHAO Z., MA D. P., et al. Acoustic Emission and Mechanical Characteristics of Rock-Like Material Containing Single Crack Under Uniaxial Compression [J]. Arabian Journal for Science and Engineering, 2022, 47, 4749–4761. [CrossRef]
- Y. Y. MENG, JING H. W., SUN S. H., et al. Experimental and Numerical Studies on the Anisotropic Mechanical Characteristics of Rock-Like Material with Bedding Planes and Voids [J]. Rock Mechanics and Rock Engineering, 2022, 55, 7171–7189. [CrossRef]
- J. L. PAN, CAI M. F., LI P., et al. A damage constitutive model of rock-like materials containing a single crack under the action of chemical corrosion and uniaxial compression [J]. Journal of Central South University, 2022, 29, 486–498. [CrossRef]
- M. Y. TENG, BI J., ZHAO Y., et al. Experimental study on shear failure modes and acoustic emission characteristics of rock-like materials containing embedded 3D flaw [J]. Theoretical and Applied Fracture Mechanics 2023, 124. [CrossRef]
- G. L. TIAN, DENG H. W., XIAO Y. G., et al. Experimental Study of Multi-Angle Effects of Micron-Silica Fume on Micro-Pore Structure and Macroscopic Mechanical Properties of Rock-like Material Based on NMR and SEM. Materials 2022, 15.
- WANG, LI Y., DAI F., et al. Experimental investigation on mechanical properties and failure mechanism of rock-like specimens containing an arc-shaped ice-filled flaw under uniaxial compression [J]. Theoretical and Applied Fracture Mechanics 2022, 119. [CrossRef]
- G. Z. WANG, WANG Y., SONG L., et al. Particle Flow Simulation of the Strength and Failure Characteristics of a Layered Composite Rock-Like Sample with a Single Hole [J]. Symmetry-Basel 2021, 13. [CrossRef]
- M. WANG, YU Z., JIN Y. D., et al. Modeling of damage and cracking in heterogeneous rock-like materials by phase-field method [J]. Mechanics Research Communications 2021, 114. [CrossRef]
- Z. YU, SUN Y., VU M. N., et al. Modeling of Mixed Cracks in Rock-Like Brittle Materials Under Compressive Stresses by a Double-Phase-Field Method [J]. Rock Mechanics and Rock Engineering 2022.
- H. Y. ZHAO, ZHANG L. C., WU Z. H., et al. A new discrete element model for rock-like materials [J]. Computers & Structures 2022, 261. [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
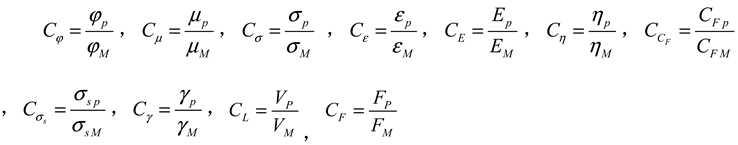
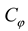 is the similarity constant of internal friction angle,
is the similarity constant of internal friction angle,  is the similarity constant of poisson's ratio,
is the similarity constant of poisson's ratio, 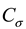 is the similarity constant of stress,
is the similarity constant of stress, 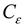 is the similarity constant of strain,
is the similarity constant of strain, 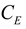 is the similarity constant of elasticity modulus,
is the similarity constant of elasticity modulus, 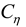 is the similarity constant of viscosity coefficient,
is the similarity constant of viscosity coefficient, 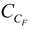 is the similarity constant of cohesion,
is the similarity constant of cohesion, 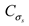 is the similarity constant of yield strength,
is the similarity constant of yield strength, 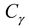 is the similarity constant of unit weight, CL is the similarity constant of geometric, CF is the similarity constant of force.
is the similarity constant of unit weight, CL is the similarity constant of geometric, CF is the similarity constant of force.

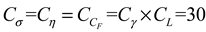 .
.