Investigation on the Power Consumption of Digital-Based Analog Amplifiers

1. Introduction

Ubiquitous electronic requires compact ultra-low power devices and fast prototypization. Technology scaling favors digital circuits thanks to their high speed and low power dissipation. In this context, it is rising the trend of implementing low-voltage inverter-based analog circuits. The elementary inverter-based amplifier is a couple of CMOS digital inverters that operates in an analog fashion due to the common-mode (CM) voltage that keeps both the NMOS and PMOS transistors in the saturation region. The resulting amplifiers have high differential gain, large transconductance, high output resistance, and high gain bandwidth (GBW). The gain of the simple inverter is the ratio of the small signal transconductances and output conductances: $A_v=(g_{mN}+g_{mP})/(g_{dsN}+g_{dsP})$, where $g_m$ is the transconductance and $g_{ds}$ the output conductance. Unfortunately, operating the inverter as an analog amplifier, leads to large variation with temperature and fabrication process of the DC gain and GBW. Furthermore, the higher is the voltage gain, the narrower is the range of the CM. To face these issues several techniques were proposed in the literature, mostly based on common mode feedback (CMFB) circuits, that sense the output CM to control the bias current of the inverter. Indeed, $g_{mN}$, $g_{mP}$, and $g_{dsN}$, $g_{dsP}$ depend on the drain and source voltages and, in turn, on the CM. Therefore, the DC gain can be regulated by changing the CM. In principle, only two resistors are required to extract the CM. The CMFB can be also implemented without resistors as in the Nauta operational transconductance amplifier and its most recent derivations [1]-[5]. Nevertheless, they remain analog circuits in which both the NMOS and PMOS are in saturation, the current flows continuously, and the static power consumption is large. Several approaches, based on current-starved topologies, were suggested in the literature to reduce the power consumption: they are fully differential circuits that need an output common mode voltage feedback to stabilize the small signal performances.

Another approach is to radically re-think analog functions in digital terms to use only digital circuits as, by the way of example, the class D amplifier [6]. VCO-based amplifiers [7], voltage to time converters [8], digital.-to-analog converters [9], hybrid analog-digital amplifiers [10] and digital-based amplifiers [11] - [19] are reported in the literature. In [11]-[19] a differential amplifier, composed of logic gates only, is shown. It has several appealing features: low power consumption, small area, easy design, and fast prototyping. It is an interesting approach and a deep understanding of the possible topologies, design, features, and limits is important for analog-background designers that, habitually, use different design methodologies. This paper is focused on the understanding of the DDA both from a circuital and mathematical standpoint with particular emphasis on the power consumption that is one of its main appealing features. In section II, the operating principles, the transistors operating conditions, and the main mathematical relations to design the DDA are devised. In section III, the full design of the amplifier in 180nm CMOS standard is shown, along with a comprehensive explanation of the operating regions and power consumption. In section IV, some conclusions are drawn.

2. Operating Principle of the DDA

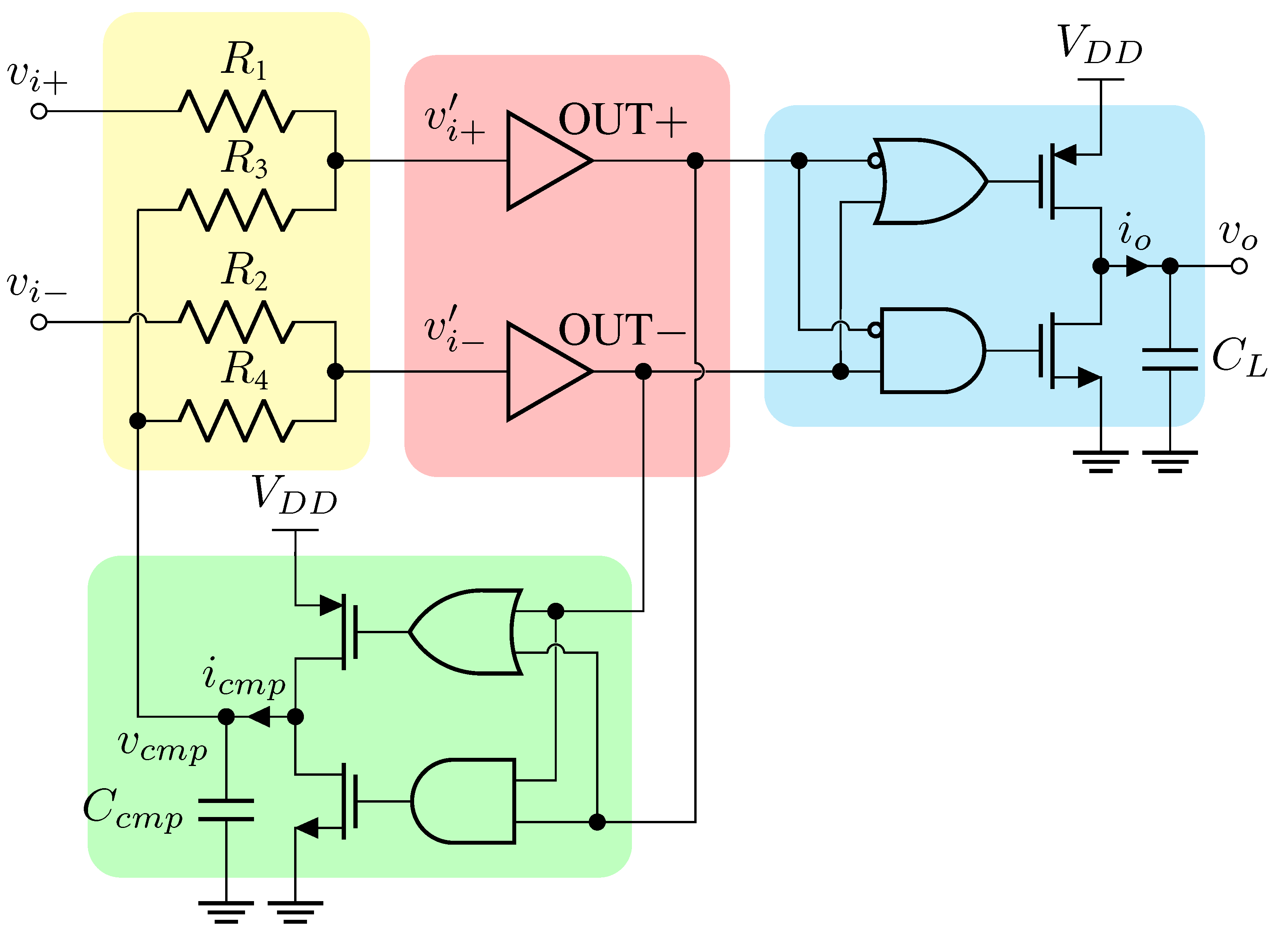
In Figure 1 the building blocks of the DDA are shown [11]. The output of the digital buffers ($OUT+$, $OUT-$) is high (H) when the input voltages $v_{i+}$, $v_{i-}$ are larger than the threshold voltage ($V_M$) and low (L) when are lower than $V_M$. The CMFB (green box) adjusts the CM voltage $v_{CM}$ in order to emulate the input stage of a differential amplifier. Hence, ($OUT+$, $OUT-$) are related to the differential voltage $v_D$ = $v_{i+}-v_{i-}$. A detailed description of the DDA, along with the basic mathematical relations, are reported in [11]. For the sake of clarity, here we recall: $v_{CM}=(v_{i+}+v_{i-})/2$, $v_{i\pm }=v_{CM}\pm v_D/2$ and, using a balanced resistor network, $v_{i\pm }^{\prime }=(v_{i\pm }+v_{CM})/2$.

Since the logic gates are assumed to switch much faster than the input signals of the DDA, the output and CMFB voltages $v_o$ e $v_{cmp}$ are well approximated by the following first order differential equations:

$$\frac{d{v}_o\left(t\right)}{dt}=\frac{i_o\left(t\right)}{C_L},\frac{d{v}_{cmp}\left(t\right)}{dt}=\frac{i_{cmp}\left(t\right)}{C_{cmp}}$$

(1)

where $i_o\left(t\right)=\{i_o^{pmos}$ if $[v_{i+}^{\prime }\left(t_1\right)>V_M]\wedge [v_{i-}^{\prime }\left(t_1\right)<V_M]$, $-i_o^{nmos}$ if $[v_{i+}^{\prime }\left(t_1\right)<V_M]\wedge [v_{i-}^{\prime }\left(t_1\right)>V_M]$, 0 elsewhere }, $i_{cmp}=\{i_{cmp}^{pmos}$ if $[v_{i+}^{\prime }\left(t_2\right)<V_M]\wedge [v_{i-}^{\prime }\left(t_2\right)<V_M]$, $-i_{cmp}^{nmos}$ if $[v_{i+}^{\prime }\left(t_2\right)>V_M]\wedge [v_{i-}^{\prime }\left(t_2\right)>V_M]$, 0 elsewhere }, $t_1=t-t_{D,o}$, $t_2=t-t_{D,cmp}$ and $t_{D,o}$ and $t_{D,cmp}$ represent the propagation time through the logic gates. Furthermore, for the sake of simplicity, the logic gates are assumed ideal with the same propagation time $t_D=t_{D,o}=t_{D,cmp}$, and $i_o^{pmos}=i_o^{nmos}=I_o$, $i_{cmp}^{pmos}=i_{cmp}^{nmos}=I_{cmp}$ constant and not depending on $v_o$ and $v_{cmp}$. Under those assumptions, in the following, the two possible operating conditions $v_D$ = 0 and $v_D\ne$ 0, will be discussed.

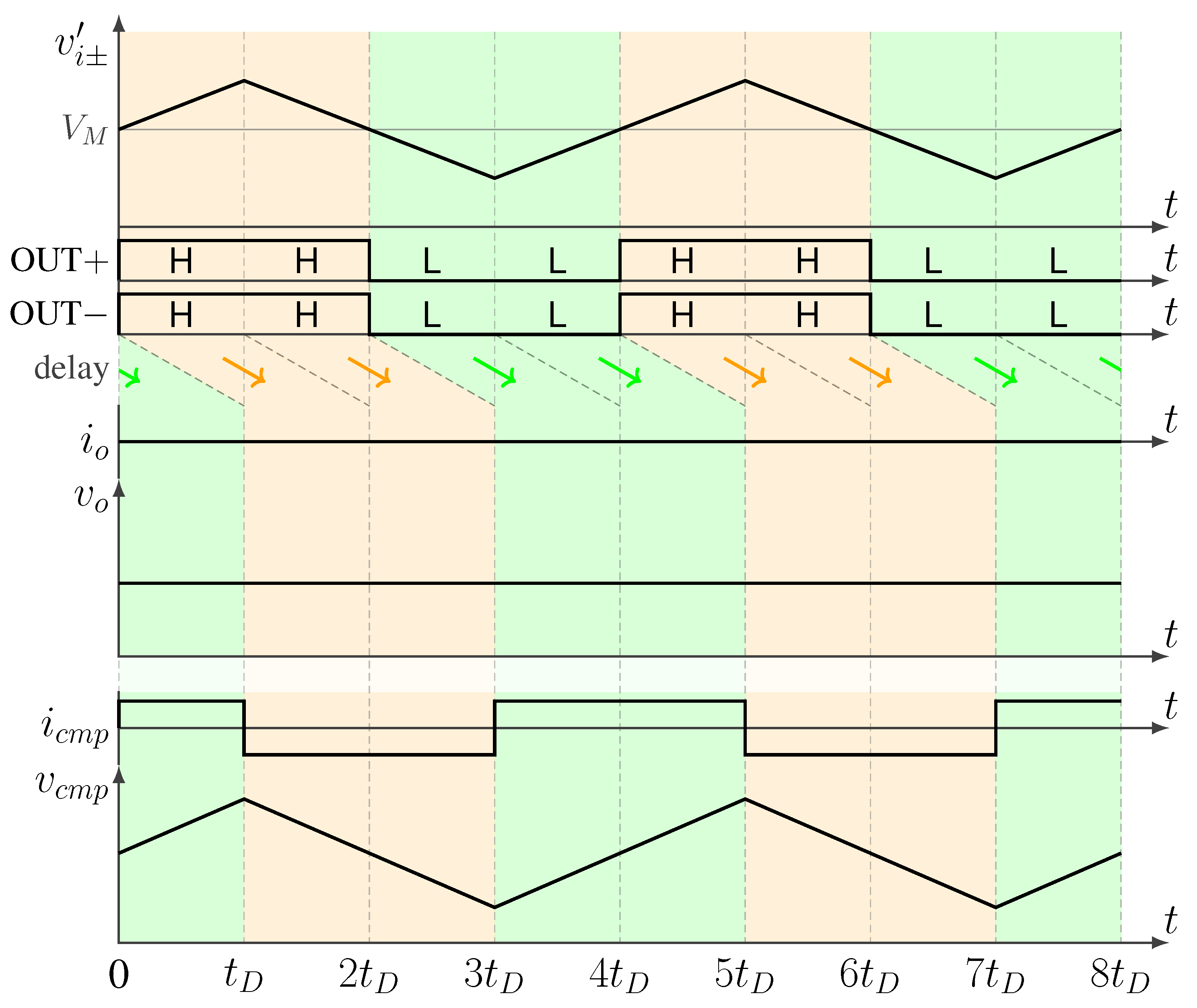
In Figure 2, the waveforms when $v_D$ = 0 are shown. When $v_D$ = 0, $OUT+$, $OUT-$ are the same, the output inverter is in high impedance, $v_o$ is constant and the load capacitor $C_L$ holds its charge. Nevertheless, the compensation voltage $v_{cmp}$ oscillates, in fact:

• At $t=0$ both $v_{i+}^{\prime }$ and $v_{i-}^{\prime }$ cross $V_M$, and $OUT+$, $OUT-$ switch from L to H. It takes a certain amount of time $t_D$ for the signal to propagate through the CMFB.
• Before $t_D$, although $OUT+$, $OUT-$ are high, the CM compensation inverter has not yet changed its state, and $C_{cmp}$ is still charging with $I_{cmp}$ as when $t=0$.
• At $t=t_D$, the CMFB changes its state: the pull-down switches on, and the capacitor $C_{cmp}$ is discharged with a constant current $-I_{cmp}$.
• From $t_D$ to $2t_D$, while $C_{cmp}$ is discharging, both $v_{i+}^{\prime }$ and $v_{i-}^{\prime }$ fall below the threshold $V_M$.
• At $2t_D$, $OUT+$, $OUT-$ switch from H to L;
• Before $3t_D$ the CM compensation inverter has not yet changed its state and $C_{cmp}$ is still discharging.
• At $3t_D$ the CM compensation inverter changes state, the pull-up switches on, and the capacitor $C_{cmp}$ is charged with the current $I_{cmp}$.
• This cycle is repeated every $T_{cmp}=4t_D$.

Hence, the delay introduced by the compensation network $t_D$ induces a triangular wave oscillation on $v_{cmp}$ of period $4t_D$ and peak-to-peak amplitude $v_{cmp,pp}=2t_D{I}_{cmp}/C_{cmp}$.

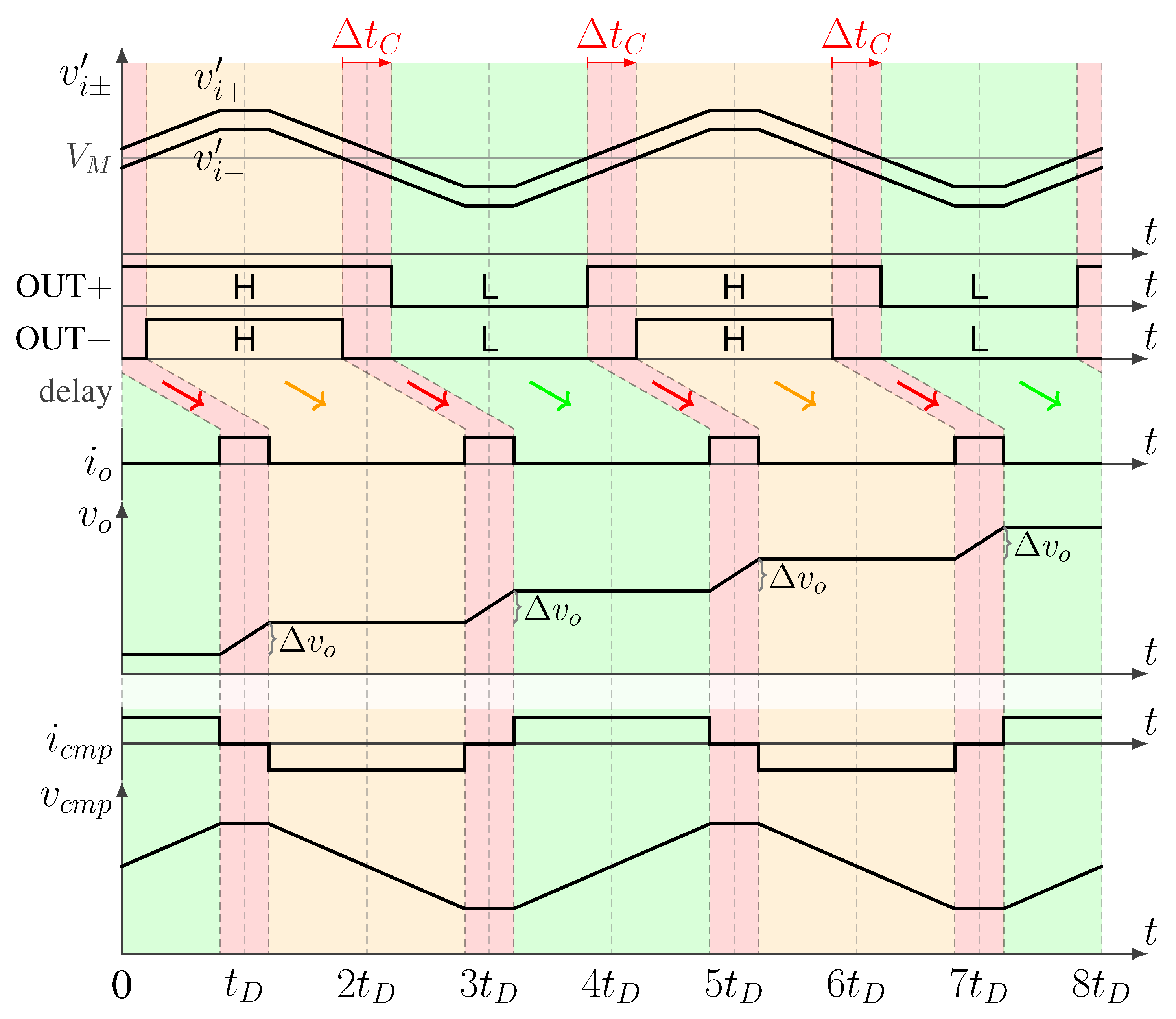
In Figure 3, the waveforms when $v_D>0$ are shown, similar considerations hold when $v_D<0$.

• The differential voltage $v_D$ corresponds to a small mismatch between $v_{i+}^{\prime }$ and $v_{i-}^{\prime }$ that, in turn, causes $v_{i-}^{\prime }$ to cross the threshold voltage $V_M$ with a small delay $\Delta t_C$; during $\Delta t_C$, the differential voltage is positive, $v_{i+}^{\prime }>v_{i-}^{\prime }$, and the outputs ($OUT+$, $OUT-$) = ($1,0$). After $2t_D$, it is $v_{i+}^{\prime }$, that crosses the threshold voltage $V_M$ with a small delay $\Delta t_C$ respect to $v_{i-}^{\prime }$.
• $v_{cmp}$ is a triangular wave with the same period $T_{cmp}=4t_D$, as in Figure 2 but, during the interval $\Delta t_C$, the voltage is clamped since the buffer is in the high impedance region.
• During the interval $\Delta t_C$, the output buffer charges $C_L$ and $v_o$ steps up of $I_o\Delta t_C$$/C_L$.
• The charge on $C_L$ is incremented by $I_o\Delta t_C$, twice every $T_{cmp}=4t_D$.

In other words, the DDA operates as a double conversion from voltage to time and back from time to voltage again. The first conversion is $v_D$ to $\Delta t_C$, thanks to the oscillation on $v_{cmp}$. Indeed, the mismatch on $v_{i+}^{\prime }$ and $v_{i-}^{\prime }$ is converted into a delay $\Delta t_C$, i.e. a time. Then, the output buffer converts the delay $\Delta t_C$ back into a voltage $\Delta v_o=I_o\Delta t_C$$/C_L$. The voltage gain of the DDA in the frequency domain, assuming only the capacitive load $C_L$, reads:

$$A_D\left(f\right)=\frac{G_D\left(f\right)}{j2\pi f{C}_L}=\frac{\alpha }{j2\pi f2t_D}{e}^{-j2\pi f{t}_D}$$

(2)

where $\alpha =I_o/C_L$,

$$G_D\left(f\right)=\frac{I_o\left(f\right)}{V_D\left(f\right)}\approx \frac{I_o}{2t_D}\frac{C_{cmp}}{I_{cmp}}{e}^{-j2\pi f{t}_D}$$

(3)

and $e^{-j2\pi f{t}_D}$ is the phase shift due to the propagation delay $t_D$. Furthermore, when $f\ll f_c/2$, eq. (2) can be simplified as $A_D\left(f\right)\approx \alpha /\left(j2\pi f2t_D\right)$. Thus, the transfer function is equivalent to an integrator with a unity gain frequency of $f_u=\alpha /\left(4\pi t_D\right)$. The digital-based analog amplifier can be used, almost as conventional analog amplifiers, in feedback loops. Nevertheless, the classical assumptions of infinite input impedance ($Z_i\to \infty$) and negligible output impedance ($Z_o\to 0$) are not properly verified. The transfer function can be approximated as:

$$G\left(f\right)=\frac{V_o\left(f\right)}{V_i\left(f\right)}=\frac{1/\beta }{1+j2\pi f/\left(\beta f_u\right)}$$

(4)

where $\beta$ is the gain of the feedback network set by the resistors’ ratio. In other words, the DDA operates as a first order system.

3. Design and Simulations of the DDA

The digital-based amplifier discussed in the previous section has been designed in the standard 180nm UMC (United Microelectronic Corporation) CMOS process and extensively simulated in different operating conditions. It is worth noting that the final schematic is slightly modified with respect to the base circuit of Figure 1 to equalize the propagation time of $OUT+$ and $OUT-$.The circuit is extremely simple, composed only of resistors and logic gates. The supply voltage is standard for this technology (1.8V) at the aim of investigate the DDA in normal operating conditions. Several simulations worked out at lower supply voltages show that the DDA operates correctly at supply as low as 400mV.

3.1. Sizing of the DDA in UMC 180 nm CMOS Process

The first step is to dimension the CMOS inverter with a logic threshold $V_M$ half of $V_{DD}$. Considering the different transistor’s threshold $V_{Tn,Tp}$ and mobility ${\mu }_{n,p}$, the ratio of the PMOS and NMOS, to maximize the symmetry of the inverter, results of 4.725. Minimum transistors are chosen to minimize the gate capacitance: $L_{n,p}=180$nm, $W_n=240$nm and $W_p=1134$nm. The NOR logic gate is composed of two PMOS connected in series and two NMOS in parallel. To have a symmetric behavior both the transistors of the pull-up and pull-down read: $L_{n,p}=180$nm, $W_n=240$nm and $W_p=2268$nm. Dual considerations hold for the NAND that comprises two PMOS in parallel and two NMOS in series: $L_{n,p}=180$nm, $W_n=480$nm and $W_p=1134$nm. The input resistors R1-R4, on the one hand, should be large to have a high input impedance, on the other hand should be not too large to limit the area consumption and the thermal noise. Although same resistances of 145k$\Omega$ were chosen to have an input differential impedance of 580k$\Omega$, in the layout $R_1-R_4$ were slightly modified to have true rail-to-rail common mode: $R_{1,2}$ = 140k$\Omega$ and $R_{3,4}$ = 150k$\Omega$. The output and the CMFB are dimensioned to balance the propagation delay between the logic gates. The dimensions of the output stage are: $L_{n,p}=180$nm, $W_n=5$$\mu$m and $W_p=10$$\mu$m. And for the inverter of the CMFB is: $L_{n,p}=180$nm, $W_n=240$nm and $W_p=720$nm. All the dimensions are in agreement to the technology minimum grid.

3.2. Simulation Results

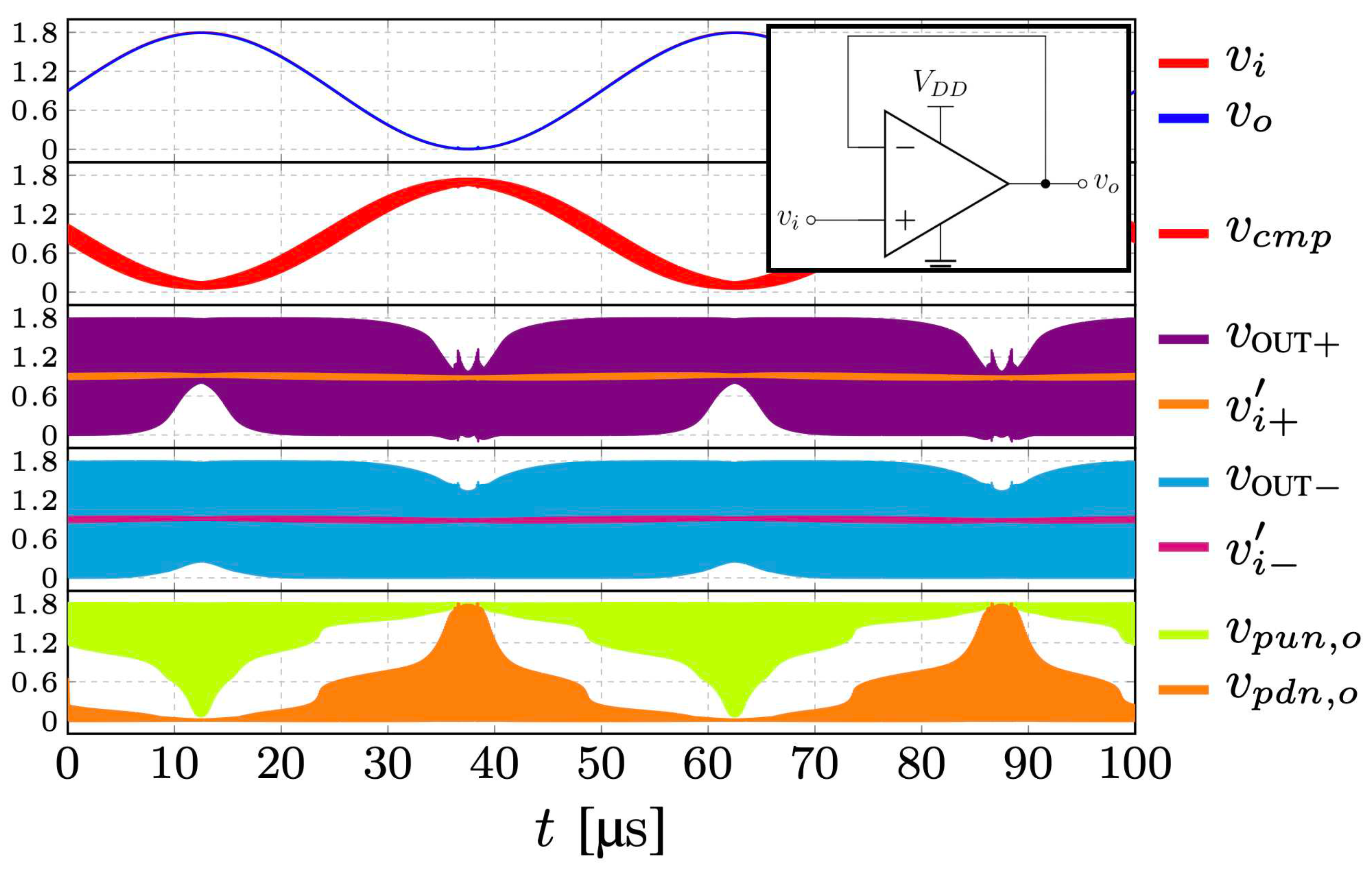
The DDA can hardly be simulated by means of the classical small-signal AC analysis tools since the core of its operating principle is digital and is related to the oscillation of $v_{cmp}$. Time-expensive transient analysis are required to design and characterize the amplifier. The DDA was simulated in two different configurations: open loop as a comparator, and closed loop as a feedback amplifier.

3.2.1. Open Loop

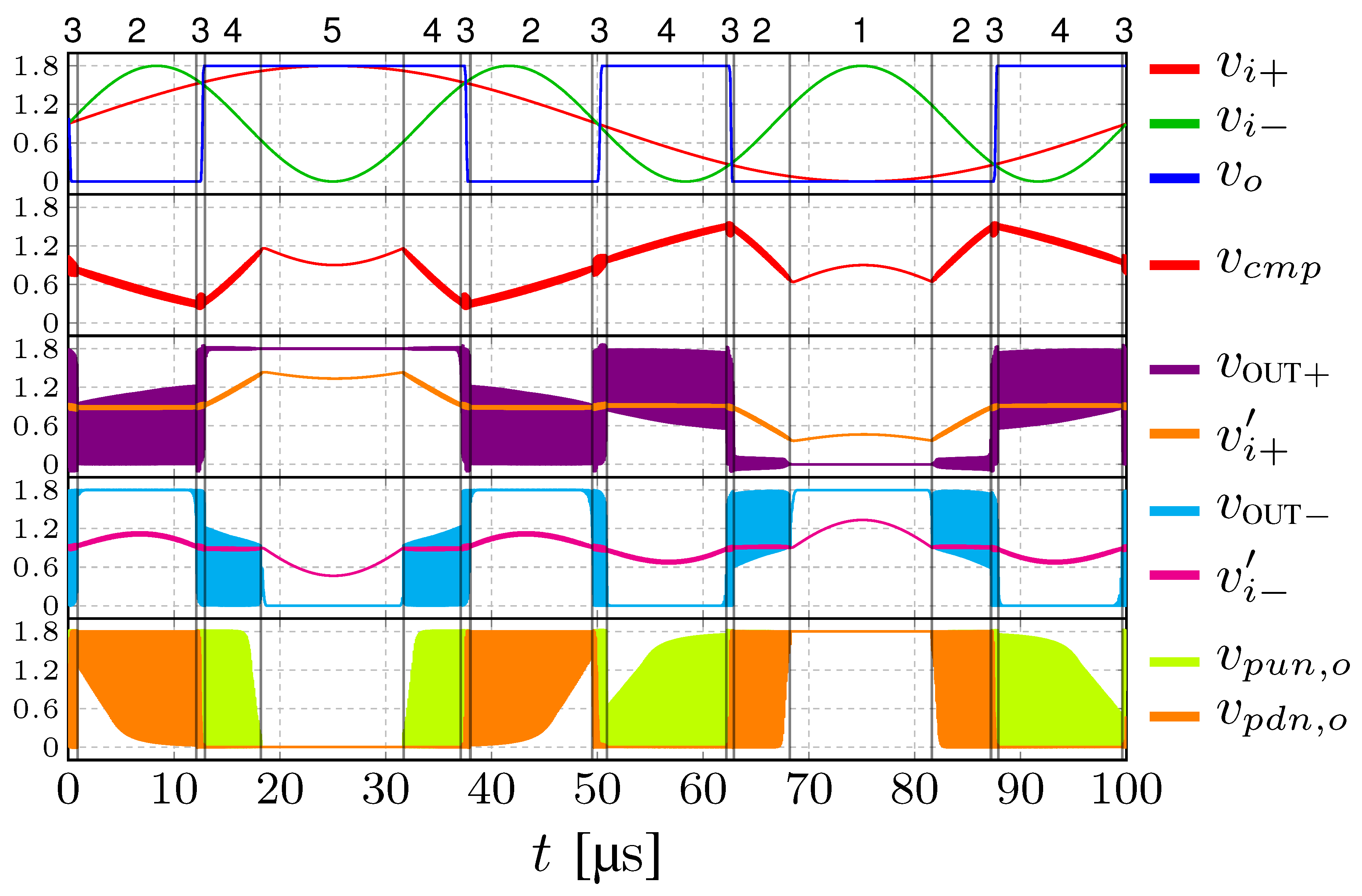
The amplifier is operated as a comparator. In the simulations, to generate a modulated differential voltage $v_D$ that emphasizes all the different operating regions of the amplifier, we used two input sinusoidal signals $v_{i+}$ and $v_{i-}$ of amplitude $V_{DD}$ with different frequencies: $v_{i+}$ 10kHz, $v_{i-}$ 30kHz. The transient simulation time is 100$\mu$s. 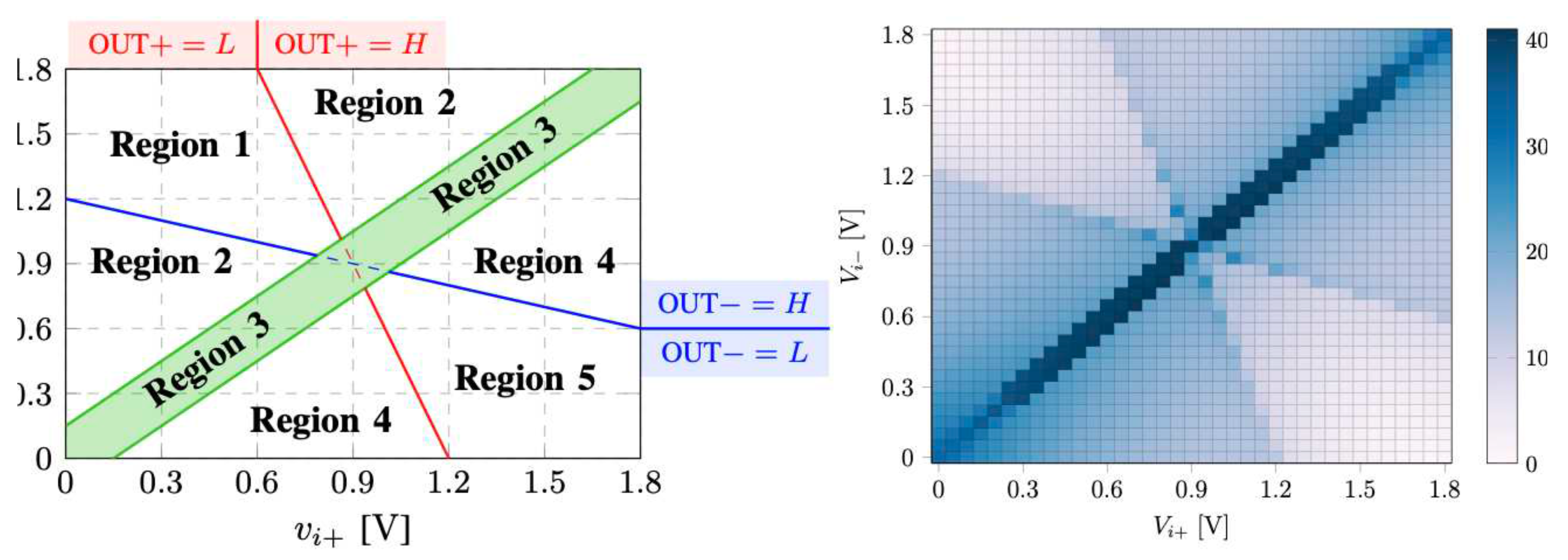The waveforms of the most relevant voltages of the internal nodes are shown in Figure 4: the bottom x-axis represents the simulation time, the top x-axis the operating regions, the y-axis the voltages at the nodes. In Figure 5, one can see that the DDA has five distinct behaviors and power consumption that we call operating regions 1-5:

• In the regions 1 and 5, the differential voltage $v_D$ is large, $v_{i\pm }$ are well separated and opposite with respect to the logic threshold $V_M$. In these regions the output voltage saturates to $V_{DD}$ or 0, the common-mode compensation network is not active and only the pull-up or the pull-down of output inverter turns on. In Figure 4, $v_{pun,o}$, $v_{pdn,o}$ are the gate voltages of the pull-up and pull-down respectively. In Figure 5, the regions 1 and 5 are limited by the equations $|v_{i+}^{\prime }|<V_M$ and $|v_{i-}^{\prime }|>V_M$:

  $$v_{i+}^{\prime }=\frac{v_{i+}{R}_3+v_{cmp}{R}_1}{R_1+R_3}$$

  (5)

  $$v_{i-}^{\prime }=\frac{v_{i-}{R}_4+v_{cmp}{R}_2}{R_2+R_4}$$

  (6)
  Furthermore, since the CMFB is not active $v_{cmp}=v_{CM}$, i.e. ($v_{i+}$ + $v_{i-}$)/2, the regions 1 and 5 reads:

  $$v_{i+}^{\prime }=\frac{v_{i+}+v_{CM}}{2}=\frac{3}{4}{v}_{i+}+\frac{1}{4}{v}_{i-}$$

  (7)

  $$v_{i-}^{\prime }=\frac{v_{i-}+v_{CM}}{2}=\frac{1}{4}{v}_{i+}+\frac{3}{4}{v}_{i-}$$

  (8)
• In the region 3, the differential voltage $v_D$ is small enough to activate the CMFB. The compensation voltage $v_{cmp}$ oscillates and the digital outputs $OUT+$ and $OUT-$ commute between L and H. Both the pull-up and the pull-down of the output inverter are active: if $v_D$ is positive, $v_o$ steps up, if $v_D$ is negative, $v_o$ steps down. This region is defined by the condition $\Delta t_C<t_D$ i.e. $v_D<I_{cmp}/C_{cmp}{t}_D$
• In the regions 2 and 4, the differential voltage $v_D$ is small, but not as small as in the region 3. In the region 2 $v_D<0$, $OUT+$ holds the low logic state, while $OUT-$ quickly commutes from H to L due to the CMFB. The pull-down of the output stage switches on. In the region 4 $v_D>0$, $OUT-$ holds the low logic state, while $OUT+$ quickly commutes from H to L due to the CMFB. The pull-up of the output stage switches on. Hence, the pull-up or the pull-down switches on, but are not always active as in region 1 and 5.

The power consumption of the DDA is mostly dynamic and is due to the switching of the gates ($P_{gates}$), to the charging and discharging of $C_{cmp}$ ($P_{cmp}$) and $C_L$ ($P_o$). It strongly depends on the operating regions of the amplifier as shown in Figure 5: the dissipated power, as a function of the differential voltage, is represented as a shade of blue from light (lower power consumption) to dark (higher power consumption). The x- and the y-axis are the input voltages $v_{i\pm }$, ranging from 0 to $V_{DD}$ in steps of 50mV. It is worth adding, that the simulations are worked out at 1.8V (standard for this technology): if the voltage supply is reduced, the power consumption gets remarkably smaller, [13]-[16]. This is due both to the dependence of the dynamic power on $V_{DD}$ and to the reduction of the switching frequencies of the CMFB and of the output stage. In the regions 1 and 5, the power dissipation is lower than in the region 2, 3, 4, since the common mode compensation network is always switched off, only the pull-up or pull-down is conducting, and the output voltage saturates to $V_{DD}$ or 0. In the regions 2 and 4 the power dissipation is higher since the CMFB is active. Finally in the region 3 the power consumption reaches its maximum since the differential voltage is small and $v_{cmp}$ oscillates continuously.

3.2.2. Closed Loop

The DDA can be used in feedback connection as an analog amplifier. In the simulations of the closed loop connection a sinusoidal rail-to-rail input signal of 20kHz is applied to the non-inverting input $v_{i+}$. The simulation time is 100$\mu$s. The Fast Fourier Transform (FFT) of the buffer connection with unitary loop gain (G) is 0.992, the phase delay ($\phi$) 0.08^o, and a total harmonic distortion (THD) 0.23%. Figure 6 show that, when the DDA is used as a buffer, the differential voltage $v_D$ is very small and always operates in the region 3. Hence, despite the rather good overall performances, the power consumption reaches its maximum.

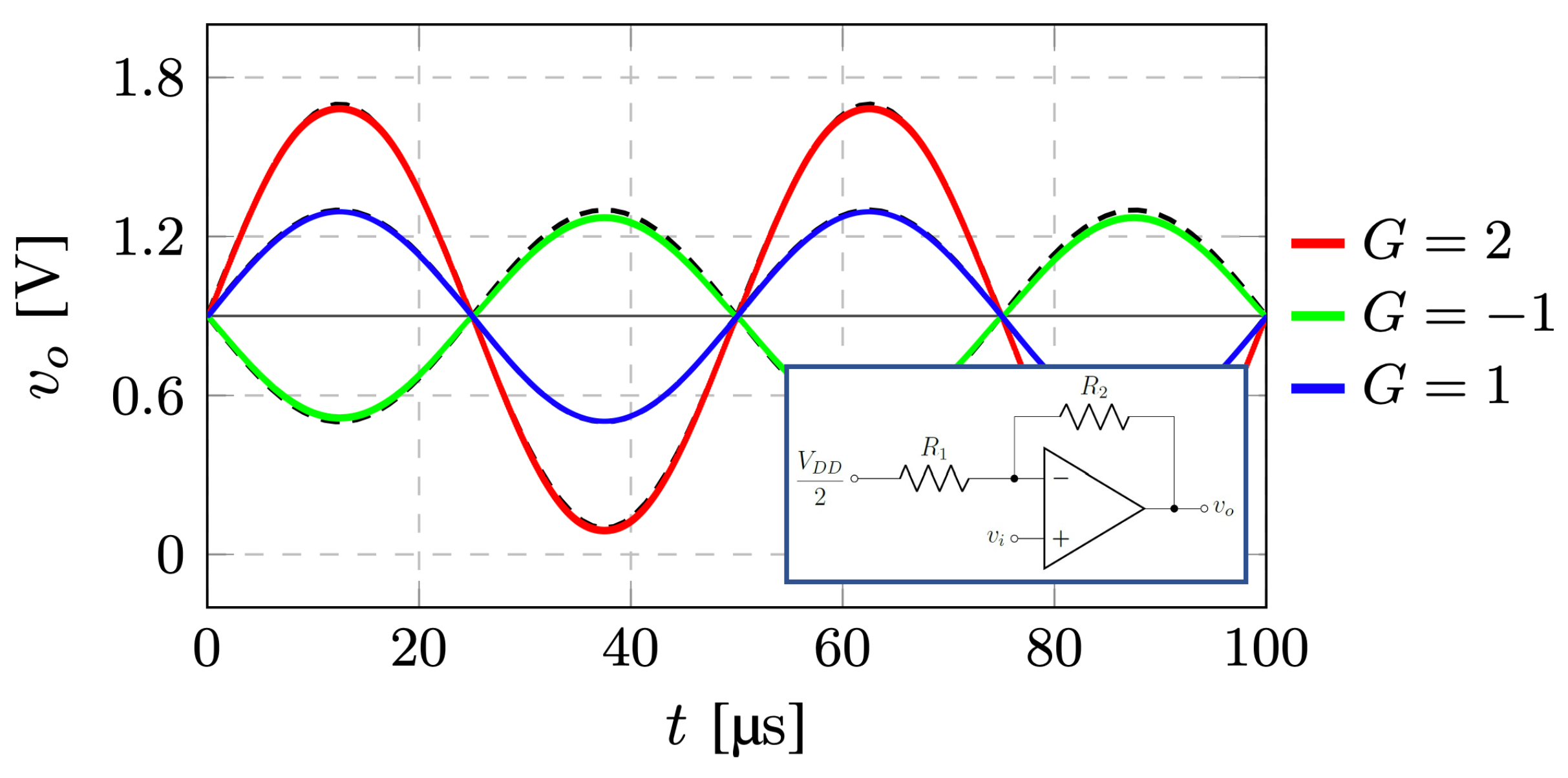
Furthermore, the closed loop configuration was simulated in several other configurations. Figure 7 shows the simulations in three different configurations: buffer (G=0.987, $\phi$=0.14^o, THD=0.31% ), inverter (G=-0.938, $\phi$=0.06^o, THD=1.58%), and gain two (G=2.007, $\phi$=0.06^o, THD=0.99%). The results are shown in Figure 7. Simulations are worked out with an input signal of 400mVp and a frequency of 20kHz. The voltage gain G and the output voltage $v_o$ are close to the ideal ones while the largest THD is smaller than 1.6%, the phase delay is below 0.14^o, and the larger offset 33.7 mV only.

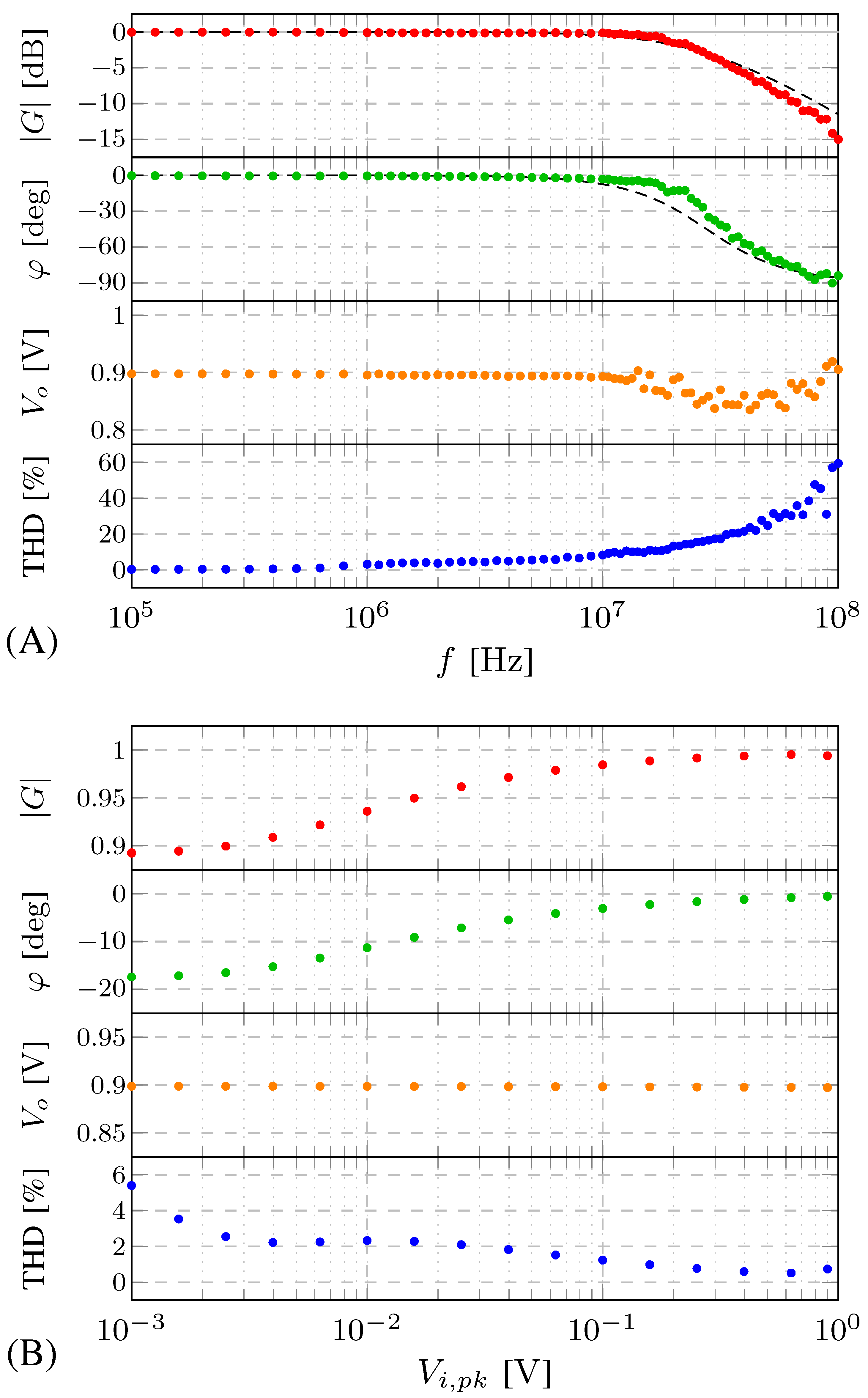
Finally, the closed loop amplifier is simulated with rail-to-rail input voltages at several frequencies. In Figure 8 (A) the FFT in the range of 100kHz-100MHz is shown.

The amplifier act as a single pole dominant system with a unity gain frequency of about 27.6MHz. The output voltage $v_o$ (gain and phase) is almost ideal up to 10MHz, while the THD starts rising at a lower frequency: about 1MHz. It is worth stressing that simulations are worked out at 1.8V. Nevertheless, one of the most appealing feature of the DDA is the small power consumption and lower $V_{DD}$ are often used: in that case, the overall performance degrades rather quickly. Finally, simulations were worked out by changing the amplitude of the input voltage at constant frequency (500kHz), i.e. within the bandwidth of the amplifier. The results are shown in Figure 8 (B), for an input signal ranging from 1mV up to 900mV. One can see that the DDA works very well when the amplitude of the input signal is large enough and slightly deteriorates as input voltage gets lower and lower. The resistive compensation network, in fact, limits the input impedance of the amplifier. In several applications, such as biomedical, wearable, IoT and sensoring, these limits do not represent a real drawback, and the DDA is a very promising architecture. High frequencies or low input signals represent the most important limit of the DDA that require some adjustments. To this aim, a more recent DDA architecture [16,19] with a new compensation network based on floating inverters, was reported. Thanks to this new common mode compensation circuit, the DDA in [16,19] can amplify low amplitude signals with very good overall performances.

4. Conclusions

The digital-based analog amplifier was designed and investigated along with its main mathematical relations. We have shown that the amplifier can operate in 5 different regions and that the power consumption peaks when $v_D$ is small. Several simulations were worked out both in the open and closed loop configuration. The simulations show that the amplifier represents a really attractive approach for the signal conditioning of the integrated circuits with advantages on power consumption and ease of design. The amplifier is better suited for low to medium frequency input signals with rather large amplitude. Nevertheless, it represent a very appealing architecture when the area on chip and the power dissipation are of paramount importance.