Identifying Bias in Social and Health Research: Measurement Invariance and Latent Mean Differences Using the Alignment Approach

Preprint

Article

Identifying Bias in Social and Health Research: Measurement Invariance and Latent Mean Differences Using the Alignment Approach

Altmetrics

Downloads

144

Views

Comments

A peer-reviewed article of this preprint also exists.

Ioannis Tsaousis^*,

And Fathima M. Jaffari

Ioannis Tsaousis^*,

And Fathima M. Jaffari

This version is not peer-reviewed

Submitted:

11 July 2023

Posted:

12 July 2023

You are already at the latest version

Alerts

Abstract

The scope of this study was twofold: first, to introduce a new method in examining measurement invariance, especially with large-scale studies where a large number of group comparisons are involved: the alignment approach, where only configural invariance is necessary to achieve measurement invariance. Second, to evaluate the psychometric robustness of this approach using real-life data. Particularly, we applied this approach to examine whether the factor structure of a cognitive ability test (PGAT) exhibits measurement invariance across the 26 universities of the Kingdom of Saudi Arabia. The sample consisted of 9,849 graduate students from 26 universities around the Kingdom. The results indicated a robust configural model suggesting that the P-GAT subscales were invariant across the 26 universities. Finally, the aligned factor mean values were estimated, and factor mean comparisons of every group’s mean with all other group means were conducted for both cognitive domains (Verbal and Quantitative). In both domains, King Saud University had the highest mean score among all universities. Moreover, its mean factor score was significantly higher than any other university besides Dammam University. On the other hand, several universities allocated at the northern and Southern borders of the country exhibited the lowest factor mean scores.

Keywords:

Subject: Social Sciences - Psychology

The purpose of any psychometric scale, test, or inventory is to produce a valid score that reflects the degree to which a person possesses a given attribute [1]. For scores to be useful, they should reveal differences among test takers in their attribute if they indeed vary on the attribute. Because an item is the building block of any instrument, the quality of items needs to be checked. That is, items of any assessment should function in the same matter for different groups of individuals (i.e., ethnicity, gender, school type, universities, etc.), assuming that the grouping condition is irrelevant to the attribute being measured. In the event that this is not the case, the item results in measurement error and has a bias toward a particular group of respondents [2].

To investigate whether or not an item is biased in relation to a grouping condition, the individuals belonging to varying groups should be matched first on the attribute of interest. Thus, a biased item produces differences in the probability of correct response despite equivalence in the attribute among the groups. The methods for investigating item bias are rooted in varying psychometric modeling theories, including classical test theory (CTT) and item response theory (IRT), in both of which the primary focus is on item-by-item analysis. One of the most prominent approaches to examining whether an item (or a scale) produces bias toward a group of participants is to test for measurement invariance. Measurement invariance implies that all items of an assessment function are the same matter across the grouping of individuals. If an item violates measurement invariance, systematic inaccuracy in measurement is introduced. Thus, the item is labeled as biased in relation to the grouping of individuals [3].

Measurement invariance is a key idea in many scientific fields, such as psychology, education, and sociology. When comparison among groups or populations is of major importance in a study, it is necessary to make sure that the measuring tool is measuring the same thing in the same way for all groups. If measurement invariance exists, this means that the construct under investigation is the same across the compared groups. On the other hand, lack of measurement invariance means that these comparisons are biased since respondents in one group provide systematically different responses than respondents from another group, although they share the same level of the latent trait. In such a case, the obtained differences among groups are not meaningful since they are the product of bias [4].

The most frequently used method to test measurement invariance across groups is the Multi-Group Confirmatory Factor Analysis (MGCFA) [5, 6]. Within this approach, various (nested) models are tested by constraining different parameters (e.g., factor loadings, intercepts, residual variances, etc.), and subsequent loss of fit is compared. The most frequently examined models are the configural model (i.e., whether the scale’s structure is conceptualized similarly across groups), the metric or weak model (i.e., whether each item contributes to the latent construct in the same manner and the same degree across groups); and the scalar or strong invariance (i.e., whether the same mean level in the latent construct is exhibited across groups [7]. It should be noted that, although additional constraints on certain parameters (e.g., item residuals, factor variances, and covariances) could be imposed, these additional forms of invariance are useful only when specific hypotheses regarding the relationship among the dimensions of the construct being measured may be of interest [8, 9].

Finally, to be able to compare group means at the latent level across different groups, scalar invariance must be supported since only then could one be confident that any statistically significant differences in group means are not due to idiosyncratic scale characteristics (e.g., poor quality items, low reliability, vague factor structure, etc.) but reflect true mean differences across groups [8, 9, 10). On the other hand, if scalar invariance fails, multigroup equivalence can’t be assumed, and as a result, no comparisons at the mean level can be undertaken.

The Alignment Approach

An important limitation of the MGCFA approach as a method of examining measurement invariance, especially with large-scale studies, is that it is extremely difficult to satisfy the assumption of scalar invariance when a large number of group comparisons are involved [11]. To overcome this problem and make group comparisons feasible, a new method for comparing latent variables across a large number of groups was introduced without requiring measurement invariance [12]. This method is called the alignment method and finds great application, especially in cross-cultural research where large-scale and widely diverse cultural groups are examined [e.g., 13, 14]. Interestingly, previous research has shown that measurement invariance with the alignment method can be possible even when the number of groups is large as 92 [15].

The alignment method involves estimating a configural model that assumes the same overall factor structure for all groups and aligning this model to the specific factor structures of each group. To do this, the alignment technique uses an alignment optimization function to look for invariant item loadings and intercepts, which in turn look for latent means and standard deviations. (e.g., a quadratic loss function). With this method, all groups may be compared at once, and latent means can be aligned and compared even if some loadings and intercepts are non-invariant. The function minimizes some non-invariances while leaving some of them large; its logic is similar to factor rotation. Once the groups have been aligned, the factor loadings can be compared directly to assess measurement invariance. Moreover, the resulting aligned model can be used to compare the factor means and variances across groups.

Mathematically, the goal of the alignment method is to align the factor loading matrices (e.g., λ₁ and λ₂ ₎ so that they are comparable across groups. To do this, the method attempts to align the groups on a common factor space using orthogonal Procrustes rotation. This involves finding a matrix that minimizes the difference between the factor loadings of the items in the different groups, while also preserving the overall structure of the factor space. This can be expressed as:

{| | λ_{1} - λ_{2}^{’} R | |}^{2},

(1)

subject to the constraint that R’R= I, where I is the identity matrix.

The degree of non-invariance in pattern coefficients between each pair of groups is estimated using a loss function, and Bayesian estimation is used to re-weight the estimates in the configural invariance model to minimize non-invariance in the aligned model. The equation || λ₁ - λ₂’ R ||² is part of the loss function and is used to measure the degree of non-invariance between two groups. Specifically, || λ₁ - λ₂’ R ||² measures the squared difference between the factor loading matrix for group 1 (λ₁) and the factor loading matrix for group 2 (λ₂) multiplied by the rotation matrix (R) that aligns the factor structures. The alignment method iteratively adjusts the rotation matrix to minimize the loss function and align the factor structures across all groups. Once we have found the Procrustes rotation matrix R, we can apply it to the factor loading matrix λ₂ to obtain the aligned factor loading matrix λ₂’:

λ₂’ = λ₂ R

(2)

We can then compare the factor loadings of the items between the two groups by testing whether the aligned factor loading matrix

λ_{2}

’ is equal to the factor loading matrix

λ_{1}

, or whether it differs by a constant factor. If the factor loading matrices are equal up to a constant factor, then the measurement instrument exhibits configural invariance. If the factor loadings are also equal in magnitude up to a constant factor, then the measurement instrument exhibits metric invariance. If the factor loadings are equal in magnitude and intercept up to a constant factor, then the measurement instrument exhibits scalar invariance.

Previous studies have introduced the alignment method as a powerful tool for analyzing measurement invariance across multiple groups, especially when the number of compared groups is large [e.g., 11, 12, 15]. In this perspective, the purpose of this study was to demonstrate the empirical usefulness of this method when a very large number of group comparisons are necessary. For that, we examined the measurement invariance of an instrument test measuring general cognitive ability across 36 universities in the Kingdom of Saudi Arabia. The findings from this study will help researchers to evaluate the psychometric robustness of the method in examining measurement invariance across multiple groups using real-life data. Additionally, it will help them in determining whether this strategy is useful in actual practice when meaningful comparisons between groups (e.g., universities) are important. The results of this study, for instance, may be a strong warrant for a better understanding of student’s academic performance and score differences among universities, helping policy educators and national governmental agencies in exploring possible factors that might have caused these gaps.

Method

Participants and Procedure

The sample consisted of 9,849 graduate students from all universities across the Kingdom. Of them, 4,682 (47.5%) were females, and 5,167 (52.5%) were males. The mean age of the participants was 25.78 (S.D. = 5.58). With regard to the region of residence, 169 (1.7%) came from the Albahah region, 163 (1.7%) from the Aljawf region, 812 (8.2%) from the Almadinah region, 491 (5.0%) from the Alqasim region, 2,515 (25.5%) from the Alriyadh region, 1,000 (10.2%) from the Asir region, 532 (5.4%) from the Eastern Province, 208 (2.1%) from the Hail region, 286 (2.9%) from the Jizan region, 3097 (31.5%) from the Makkah region, 92 (0.9%) from the Najran region, 122 (1.2%) from the Northern Borders region, and 359 (3.6%) from the Tabuk region. Three participants (0.01%) did not report their region of residence. Participants came from all 35 universities in the Kingdom. However, only universities with more than 59 participants were retained in the study to ensure adequate statistical power [11]. Therefore, nine universities with less than 60 participants (ranging from 3 to 27) were removed from the analysis. Table 1 presents the university code and its corresponding sample size.

Measure

The Post-Graduate General Aptitude Test (PGAT; Education & Training Evaluation Commission). The P-GAT is a psychometric tool measuring graduate students’ analytical and deductive skills. It consists of 104 dichotomous items covering ten different content areas organized into two broader cognitive domains: a) verbal (linguistic) and b) quantitative (numerical). The verbal domain comprises four sub-scales (i.e., analogy, sentence completion, context errors, and reading comprehension). The quantitative domain comprises six sub-scales (i.e., arithmetic, analysis, comparison, critical thinking, spatial, and logic). All PGAT items are in a multiple-choice format and scored as either correct (1) or wrong (0). The test has a 2.5-hour duration and is presented in Arabic.

Data Analysis Strategy

From a technical perspective, the alignment method allows for a pattern of approximate measurement invariance, in contrast to CFA, where full or partial measurement invariance (particularly at the scalar level) is a required criterion when group means are attempted to be compared. Particularly, the alignment method focuses only on the configural model and then automates the closeness of the factor loading estimates in establishing the most optimal measurement invariance pattern [12]. First, the factor loadings and intercepts of a configural invariance CFA model are estimated, and the alignment process uses these values as input. Then, the factor means and variances are freely estimated across the different groups, with the objective of choosing corresponding parameters that minimize the total amount of measurement non-invariance. The effect sizes of approximate invariance based on R² and the average correlation of aligned item characteristics among groups are also estimated. If the R² for factor loadings is close to 1 and the average correlation of aligned factor loadings is high, then all aligned item factor loadings are approximate invariant (metric invariance). If the R² for the intercepts is close to 1 and the average correlation of the aligned intercepts is high, then all aligned item intercepts are approximate invariant (scalar invariance).

During this process, the alignment estimation model identifies for each measurement parameter (e.g., factor loading, intercept, etc.) the largest invariant set of groups for which the specific parameter is not statistically significant from the mean value for that parameter across all groups. At the final stage, this minimization process results in many approximately noninvariant parameters and very few large noninvariant measurement parameters. On the other hand, no medium-sized non-invariance parameters are obtained. Interestingly, it has been argued that this approach is more sophisticated than the conventional MGCFA approach of measuring measurement invariance, where many medium-sized noninvariant measurement parameters could be used to support invariance [12].

In its simplest application (i.e., a one-factor model), the alignment method can be mathematically illustrated as follows [16]:

y_{i p g} = v_{p g} + λ_{p g} ŋ_{i g} + ε_{i p g}

(3)

Where

Y_{i p g}

is the pth observed variable for participant i in group g, the

v_{p g}

represents the intercept and the

λ_{p g}

the factor loading for the p-th observed variable in group g, the ε_ipg ~ N (0,

θ_{p g}

) represents the error term for individual i in group g, and

ŋ_{i g}

is the factor for individual i in group g. The alignment method estimates all the parameters, including

v_{p g}

λ_{p g}

α_{g}

ψ_{g}

, and

θ_{p g}

as group-specific parameters. This means that the method estimates the factor mean and variance separately for each group without assuming measurement invariance. In other words, the alignment method allows for each group to have its own unique factor structure rather than assuming that all groups.

The initial stage of the alignment method involves estimating the configural model, which assumes that all groups have the same overall structure. The configural model sets certain parameters in each group g to specific values (

α_{g} = 1, ψ_{g} = 1

) and estimates group-specific parameters for all other parameters. The configural factor model is represented as following:

ŋ_{i g} = α_{g} + \sqrt{ψ_{g}} ŋ_{i g, c o n f i g u r a l}

(4)

Since the aligned model has the same fit as the configural model, certain relationships must hold between these parameters.

v (y_{i p g}) = λ_{p g}^{2} ψ_{g} + θ_{p g} = λ_{p g, c o n f i g u r a l}^{2} + θ_{p g, c o n f i g u r a l}

(5)

E (y_{i p g}) = V_{p g} + λ_{p g} α_{g} = V_{p g, c o n f i g u r a l}

(6)

Where

v (y_{i p g})

and

E (y_{i p g})

are the

y_{i p g}

model estimated variance and mean.

By imposing equality restrain

θ_{p g} = θ_{p g, c o n f i g u r a l}

, equation (5) will be

λ_{p g}^{2} ψ_{g} = λ_{p g, c o n f i g u r a l}^{2}

λ_{p g}^{2} = \frac{λ_{p g, c o n f i g u r a l}^{2}}{ψ_{g}}

(7)

λ_{p g} = \frac{λ_{p g, c o n f i g u r a l}}{\sqrt{ψ_{g}}}

(8)

Putting the value of

λ_{p g} resulted from equation 7

in equation 6,

V_{p g} = V_{p g, c o n f i g u r a l} - α_{g} \frac{λ_{p g, c o n f i g u r a l}}{\sqrt{ψ_{g}}}

(9)

To make this more precise, the alignment function F will be minimized in terms of the α_g and ψ_g. This function takes into account all sources of non-invariance in the measurements.

F = \sum_{p} \sum_{g 1 < g 2} W_{g 1, g 2} f (λ_{p g 1} - λ_{p g 2}) + \sum_{p} \sum_{g 1 < g 2} W_{g 1, g 2} f (v_{p g 1} - v_{p g 2})

(10)

W_{g 1, g 2} = \sqrt (N_{1} N_{2})

(11)

where 𝑤: factor weight, N: sample size of the group_, and f is a component loss function:

f = \sqrt[4]{(x^{2}} + \in)

(12)

where

\in

represents a small value, typically around 0.0001. The alignment function F is designed to be approximately equal to the absolute value of x. To ensure that the function has a continuous first derivative, which makes optimization easier and more stable, we use a positive value for

\in

In terms of latent mean comparisons, the alignment method, via the optimization process, simplifies the invariance examination by taking the non-invariance of all factor loadings and intercepts parameters into account in the process of means estimation, thereby yielding mean values that are more trustworthy than those calculated without this strategy. This optimization process enables the estimation of trustworthy means despite the presence of some measurement non-invariance [12]. It should also be noted that the fixed alignment method was applied, in which the factor means and variances in the reference group were fixed to 0 and 1, respectively. We preferred this approach instead of the alternative of the free alignment method (for more information see [13] following the suggestion of the Mplus software after a warning message that the free alignment method (that we first attempted) was poorly identified. All analyses were conducted with the Mplus (8.5) software [17].

Results

Descriptive statistics, normality indices, and inter-correlations among the study variables are presented in Table 2. No violation of univariate normality of all variables was found (values <.2.0).

In terms of multivariate normality, the obtained results are presented in Table 3. As can be seen, both tests revealed that the data is not multivariate normal. For that, the Maximum likelihood with robust standard errors (MLR) estimation method was used since it is robust to non-normality and non-independence of observations. Finally, we used the Mahalanobis distance statistic (D²) to identify possible irrelevant response patterns [18]. The results revealed no outliers. No missing data were observed.

P-GAT Measurement Model

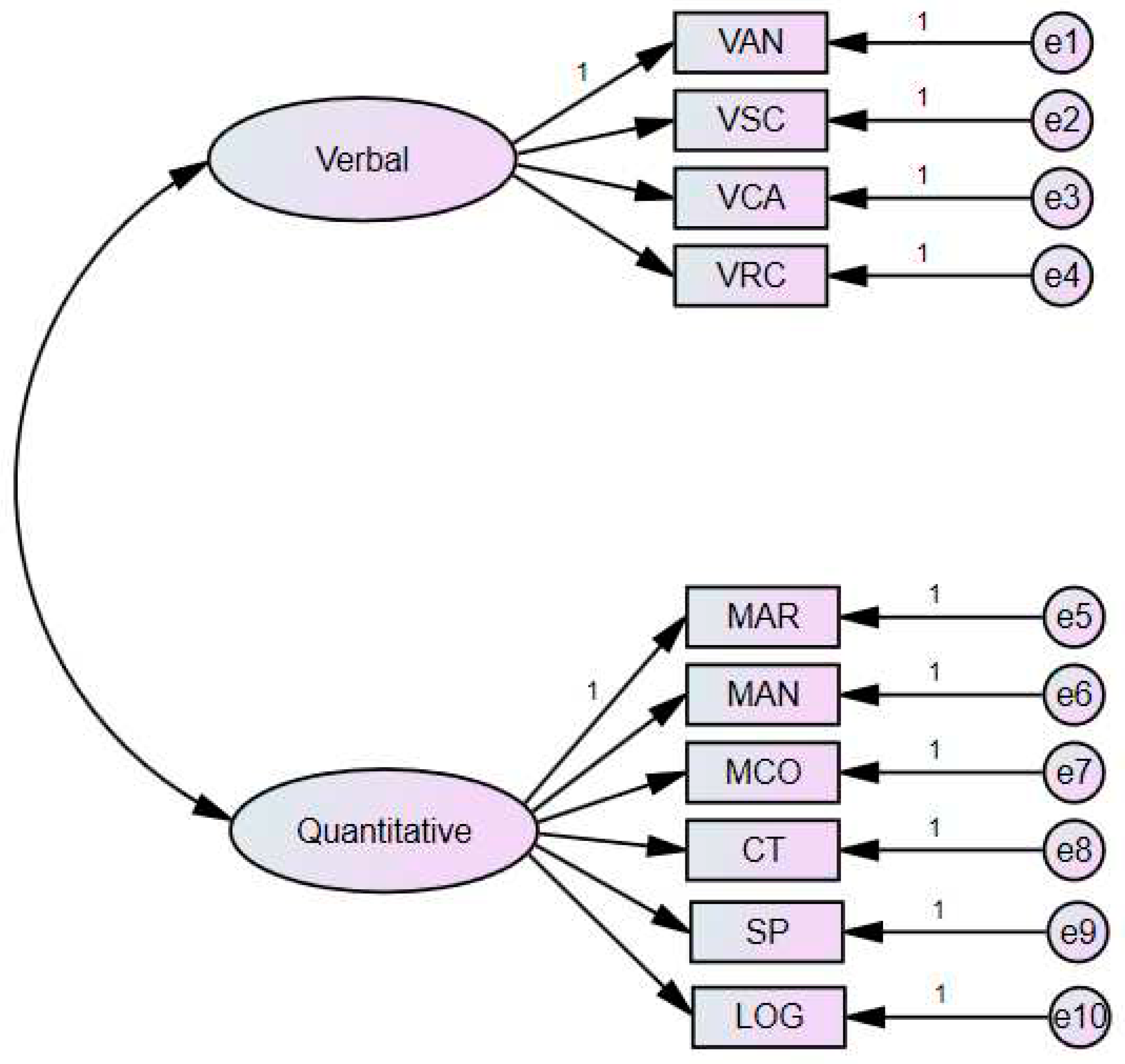
First, the P-GAT measurement model was tested via CFA. The CFA model of the P-GAT structure is shown schematically in Figure 1. As can be seen, the P-GAT is an instrument measuring ten analytical and deductive skills organized into two broader cognitive domains: a) verbal (linguistic) and b) quantitative (numerical). This is a higher-order conceptualization, where the ten cognitive variables (subscale scores) are treated as observed variables. It was hypothesized that this model would be a robust conceptualization for every university group. Previous findings have shown that this theoretical conceptualization provides an acceptable fit. The results from the analysis revealed that the P-GAT conceptual model exhibits an excellent fit [χ² = 1149.73 (34); CFI = .969, TLI = .959, RMSEA (90% CIs) = .058 (.055 - .061), SRMR = .035]. Therefore, we examine the test’s measurement invariance across universities.

P-GAT Measurement Invariance Results

Before applying the alignment method, MGCFA, the most commonly used approach to measuring invariance [19], was applied to examine whether configural, metric, and scalar invariance was supported. Table 4 shows the results of the analysis. As shown, it is clear that both the metric and the scalar invariance model were rejected, a finding that is not surprising due to the large number of contrasted groups (i.e., 26) and the large sample size (i.e., overpower).

Then, the alignment method was applied. The major advantage of this method is that metric and scalar invariance are not required. Only the configural model is necessary to be supported to compare group means meaningfully. A 26-group alignment analysis of the P-GAT subscales was performed across the 26 universities in Saudi Arabia. First, the results of the approximate measurement invariance (non-invariance) analysis for the intercept in each P-GAT subscale is shown in Table 5. The numbers in the parentheses represent the different universities and designate which item parameters (i.e., item threshold) are non-invariant in which groups. Universities that have a measurement parameter that is considered to be significantly noninvariant are shown in boldface within parentheses.

The results indicate that only in two groups (universities) the item intercepts of the VSC (Sentence Completion) and CT (Critical Thinking) were noninvariant. Particularly, the Sentence Completion subscale is significantly noninvariant at King Khalid University (i.e., 17), and the Critical Thinking subscale is at King Abdulaziz University. Next, the results of the approximate measurement invariance (noninvariance) analysis for the factor loadings in each P-GAT subscale is shown in Table 6. There were no noninvariant factor loadings at any P-GAT subscale across universities.

P-GAT Latent Mean Difference Results

Given that the configural invariance assumption was satisfied, the next step was to test for possible differences across universities at the latent mean level. The aligned factor mean values and factor mean comparisons of every group’s mean with all other group means for the Verbal and Quantitative domains are shown in Table 7 and Table 8. For ease of presentation, the factor means are arranged from high to low, and groups with significantly different factor means at the 5% level are presented in the last columns of the tables.

In terms of the Verbal domain, the results showed that King Saud University (Code No 19) had the highest mean score among all universities (0.454). More interestingly, almost all other universities (except Dammam University - code No 4) had P-GAT factor means significantly lower than King Saud’s factor mean. On the other hand, the Islamic University, the Jazan University, the Jouf University, the Northern Border University, and the Shaqra University had the lowest P-GAT mean scores among all universities. Moreover, their factor mean scores were not significantly higher than any other university’s factor means.

In terms of the Quantitative domain, the results showed again that King Saud University (Code No 19) had the highest mean score among all universities (0.578). Moreover, its factor mean was significantly higher than almost all other universities (except Dammam University - code No 4). On the other hand, the Jazan University, the Islamic University, the University of Bisha, the Shaqra University, the Jouf University, and the Northern Border University exhibited the lowest mean scores. Moreover, their factor mean scores were not significantly higher than any other university’s factor means.

Next, we examined the fit of the solution provided by the alignment analysis. Particularly, the alignment method provides some fitting statistics of both the factor loading and intercept for each observed variable to evaluate the robustness of the fitting function. The results are shown in Table 9. First, the fit information contribution (FIC) provides information values separately for the factor loading and the intercept of each observed variable, representing each parameter’s contribution to the final solution. As can be seen, the variable VCA (Contextual Errors) for the factor loading parameters and the variable VRC (Reading Comprehension) for the intercept parameters contributed the least to the fitting function (-114.00 and 112.20, respectively). Similarly, the total contribution function (TC) represents the total contribution of each variable to the fitting model (taking into account together the factor loadings and intercepts). Again, the results showed that the variable VRC (Reading Comprehension) contributed the least to the fitting function (-229.43). The above results can be interpreted as an indication that these variables exhibited the least amount of non-invariance.

Finally, the R² value indicates the degree of invariance of a given parameter. A value close to 1 designates a high degree of invariance, while a value close to 0 designates a low degree of invariance [12]. As seen in Table 4, in terms of the intercept parameter, all variables exhibited a high degree of invariance. This finding suggests that the latent means can be meaningfully compared across the universities. In terms of the factor loading parameter, however, this statistic shows that several variables exhibited a low degree of invariance (i.e., CT (Critical Thinking), SP (Spatial Thinking), and LOG (Logic). For the scope of this study, however, intercept invariance is considered more important since it is the prerequisite assumption before we conduct latent mean comparisons across universities. Therefore, from this perspective, the results from this analysis are considered acceptable.

Discussion

The scope of this study was twofold: first, to introduce a relatively new method in examining measurement invariance, especially with large-scale studies, where a large number of group comparisons are involved. In those situations, when traditional approaches for examining measurement invariance are applied (e.g., MGCFA), scalar invariance is rarely satisfied, and as a result, latent mean differences across groups can’t be examined. To overcome this problem and make group comparisons feasible, the alignment approach was introduced [12], where only configural invariance is necessary be satisfied. Second, to evaluate the psychometric robustness of this approach using real-life data. Particularly, we applied this approach to examine whether the factor structure of a cognitive ability test (PGAT) exhibits measurement invariance across the 26 universities of the Kingdom of Saudi Arabia.

The main advantage of this method is that metric and, most importantly, scalar invariance are not prerequisites for comparing group means meaningfully. Only the configural model must be established. The obtained result indicated a robust configural model. Particularly, all factor loadings of the P-GAT subscales were invariant across the 26 universities. Most importantly, almost all P-GAT intercepts were invariant across the 26 universities. Only two universities (i.e., King Khalid University and King Abdulaziz University) showed noninvariant intercepts for the Sentence Completion and Critical Thinking subscales, respectively. This means that from the 260 examined parameters (10 items x 26 universities), only two (0.8%) were found noninvariant. These findings are well below the recommended 25% cut-off rule of thumb for the minimum required noninvariant parameters to proceed with comparisons at the latent mean level [20].

Next, given that the configural invariance assumption was satisfied, P-GAT latent mean differences across universities were examined. The results showed that the five universities with the highest mean values in terms of Verbal P-GAT scores were: 1) the King Saud University (.454), the Dammam University (.333), the Prince Nourah Bin Abdulrahman University (.279), the Qassim University (.214), and the King Abdulaziz University (.174). On the other hand, the five universities with the lowest Verbal P-GAT scores were: 1) the Islamic University (-.306), 2) the Jazan University (-.308), 3) the Jouf University (-.401), 4) the Northern Border University (-.449), and 5) the Shaqra University (-.521).

Regarding the Quantitative P-GAT domain, at the top of the list appeared the same five universities, although some of them were at different positions: 1) the King Saud University (.578), 2) the King Abdulaziz University (.340), 3) the Dammam University (.324), 4) the Qassim University (.244), and the Prince Nourah Bin Abdulrahman University (.197). Finally, the six universities with the lowest mean scores in the Quantitative domain were: 1) the Jazan University (-.152), 2) the Islamic University (-.157), 3) the University of Bisha (-.168), 4) the Shaqra University (-.306), the Jouf University (-.312), 4), and the Northern Border University (-.342). Interestingly, King Saud University’s P-GAT factor means were found to be significantly higher than any other university apart from Dammam University in both domains (i.e., Verbal and Quantitative).

To sum up, the findings from this study showed that the alignment procedure is a valuable method to assess measurement invariance and latent mean differences when a large number of groups are involved. This technique provides refined scales, and unbiased statistical estimation of group means, with significance tests between pairs of groups that adjust both for sampling errors and missing data. Another important contribution of the current study is that it provided valuable information for policy makers and educators to examine the performance of each of the Kingdom’s universities in terms of P-GAT Verbal and Quantitative mean scores [15]. These findings may help experts to understand possible educational and socio-economic factors affecting individuals’ performance and design appropriate actions. For example, it seems that almost all universities exhibiting low mean scores are located at the borders of the country (north and south).

Author Contributions

Conceptualization, I.T.; Methodology, F.J.; Formal analysis, I.T.; Data curation, F.J.; Writing—original draft preparation, I.T.; Writing—review & editing, I.T., and F.J.; Supervision, I.T. Both authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Education & Training Evaluation Commission (ETEC).

Institutional Review Board Statement

The study was conducted in accordance with the Declaration of Helsinki, and approved by the Institutional Review Board (or Ethics Committee) of the Education & Training Evaluation Commission (ETEC).

Informed Consent Statement

Informed consent was obtained from all participants involved in the study.

Data Availability Statement

The data that support the findings of this study are available from the Education & Training Evaluation Commission (ETEC). Restrictions apply to the availability of these data, which were used under license for this study. Data are available from the authors upon reasonable request and with the permission of the ETEC.

Conflicts of Interest

The authors declare no conflict of interest.

References

Nunnally, J. C., & Bernstein, I. H. (1994). Psychometric theory (3rd ed.). McGraw-Hill, Inc.
Bandalos, D. L. (2018). Measurement theory and applications for the social sciences. The Guilford Press.
Millsap, R. E. (2011). Statistical approaches to measurement invariance. Routledge/Taylor & Francis Group. [CrossRef]
Van De Schoot, R., Schmidt, P., De Beuckelaer, A., Lek, K., & Zondervan-Zwijnenburg, M. (2015). Measurement invariance. Frontiers in Psychology, 6, 1064.
Vandenberg, R. J., & Lance, C. E. (2000). A review and synthesis of the measurement invariance literature: Suggestions, practices, and recommendations for organizational research. Organizational Research Methods, 3, 4-70. [CrossRef]
Milfont, T. L. & Fischer, R. (2010). Testing measurement invariance across groups: Applications in cross-cultural research. International Journal of Psychological Research, 3, 2011-2084. [CrossRef]
Putnick, D. L., & Bornstein, M. H. (2016). Measurement invariance conventions and reporting: The state of the art and future directions for psychological research. Developmental Review, 41, 71–90. [CrossRef]
Byrne, B. M. (2012). Structural equation modeling with Mplus: Basic concepts, applications, and programming. Routledge/Taylor & Francis Group.
Cheung, G., W., & Rensvold, R. B. (2002). Evaluating goodness of fit indexes for testing measurement invariance. Structural Equation Modeling: A Multidisciplinary Journal, 9, 233-255.
Chen, F. F. (2007). Sensitivity of goodness of fit indexes to lack of measurement invariance. Structural Equation Modeling, 14, 464-504. [CrossRef]
Byrne, B. M., & van de Vijver, F. J. R. (2010). Testing for measurement and structural equivalence in large-scale cross-cultural studies: Addressing the issue of nonequivalence. International Journal of Testing, 10, 107-132.
Asparouhov, T., & Muthén, B. (2014). Multiple-group factor analysis alignment. Structural Equation Modeling: A Multidisciplinary Journal, 21, 495–508.
Kim, E. S., Cao, C., Wang, Y., & Nguyen, D. T. (2017). Alignment optimization in multiple-group analysis of structural equation models. Structural Equation Modeling: A Multidisciplinary Journal, 24, 183-197.
Sirganci, G., Uyumaz, G., & Yandi, A. (2020). Measurement invariance testing with alignment method: Many groups comparison. International Journal of Assessment Tools in Education, 7, 657-673. [CrossRef]
Munck, I., Barber, C., & Torney-Purta, J. (2018). Measurement Invariance in Comparing Attitudes Toward Immigrants Among Youth Across Europe in 1999 and 2009: The Alignment Method Applied to IEA CIVED and ICCS. Sociological Methods & Research, 47(4), 687–728.
Asparouhov, T., & Muthén, B. (2023). Multiple group alignment for exploratory and structural equation models. Structural Equation Modeling: A Multidisciplinary Journal, 30, 169-191. [CrossRef]
Muthén, L.K. and Muthén, B.O. (1998-2017). Mplus User’s Guide. Eighth Edition. Muthén & Muthén.
Mahalanobis, P. C. (1936). On the generalized distance in statistics. Proceedings of National Institute of Science, 2, 49–55.
Davidov, E., Cieciuch, J., Meuleman, B., Schmidt, P., Algesheimer, R., & Hausherr, M. (2015). The Comparability of Measurements of Attitudes toward Immigration in the European Social Survey Exact versus Approximate Measurement Equivalence. Public Opinion Quarterly, 79, 244–266. [CrossRef]
Muthén, B., & Asparouhov, T. (2018). Recent methods for the study of measurement invariance with many groups: Alignment and random effects. Sociological Methods & Research, 47(4), 637–664.

Figure 1. The conceptual model of the P-GAT. Note. VAN=Analogy, VSC=Sentence Completion, VCA=Context Errors, VRC=Reading Comprehension, MAR=Arithmetic, MAN=Analysis, MCO=Comparisons, CT=Critical Thinking, SP=Spatial Thinking, LOG = Logic.

Table 1. Reference Code and sample size by university.

Code	University	N
1	Albaha University	223
3	Arab Open University	150
4	Dammam University	90
8	Hail University	182
9	Imam Mohammed Bin Saud Islamic University	1088
10	Islamic University	191
11	Jazan University	263
12	Jeddah University	202
13	Jouf University	180
14	King Abdulaziz University	1142
16	King Faisal University	237
17	King Khalid University	771
19	King Saud University	523
20	Majmaah University	173
21	Najran University	77
22	Northern Border University	102
24	Prince Sattam Bin Abdulaziz University	198
26	Prince Nourah Bin Abdulrahman University	295
27	Qassim University	496
29	Shaqra University	262
30	Tabouk University	358
31	Taiba University	574
32	Taif University	666
33	Umm Al-Qura University	1155
34	University of Bisha	192
35	University of Hafr Batin	59
Total		9849

Table 2. Descriptive Statistics and inter-correlations among the variables of the study (N=9,849).

Subscales	1	2	3	4	5	6	7	8	9	10
1. Analogy	-
2. Sentence Completion	.48	-
3. Context Errors	.54	.48	-
4. Reading Comprehension	.55	.49	.55	-
5. Arithmetic	.51	.36	.42	.46	-
6. Analysis	.41	.30	.35	.38	.57	-
7. Comparison	.42	.30	.35	.38	.53	.44	-
8. Critical Thinking	.42	.39	.39	.41	.35	.31	.30	-
9. Spatial	.44	.28	.36	.38	.54	.44	.44	.29	-
10. Logic	.46	.33	.42	.45	.56	.45	.42	.36	.49	-
Mean	9.77	3.99	6.14	11.04	6.75	3.37	2.95	5.84	4.86	4.37
SD	3.15	1.47	2.03	3.24	2.66	1.53	1.53	2.04	20.3	2.18
Skewness	-.64	-.51	-.44	-.29	-.06	-.09	.18	-.04	.001	.23
Kurtosis	-.18	-.41	-.58	-.38	-.74	-.73	-.66	-.30	-.65	-.59

Note: All correlation coefficients were significant at p <.001 level.

Table 3. Test for normality using Mardia’s test.

Test	Skewness	Kurtosis
Test Statistic	1.51	118.11
p-value	0.001	0.001

Table 4. Measurement invariance results (N=9,849).

Model	No par	Loglikelihood
Configural	806	-194,124.095
Metric	606	-194,247.290
Scalar	406	-194,476.274
Models Compared	χ²	df	p
Metric vs. Configural	262.051	200	.002
Scalar vs. Configural	725.901	400	.001
Scalar vs. Metric	457.782	200	.001

Table 5. Invariance results for aligned intercept parameters for P-GAT subscales (VAN – LOG).

Scales		University identification number
VAN	(1)	(3)	(4)	(8)	(9)	(10)	(11)	(12)	(13)	(14)	(16)	(17)	(19)
VAN	(20)	(21)	(22)	(24)	(26)	(27)	(29)	(30)	(31)	(32)	(33)	(34)	(35)
VSC	(1)	(3)	(4)	(8)	(9)	(10)	(11)	(12)	(13)	(14)	(16)	(17)	(19)
VSC	(20)	(21)	(22)	(24)	(26)	(27)	(29)	(30)	(31)	(32)	(33)	(34)	(35)
VCA	(1)	(3)	(4)	(8)	(9)	(10)	(11)	(12)	(13)	(14)	(16)	(17)	(19)
VCA	(20)	(21)	(22)	(24)	(26)	(27)	(29)	(30)	(31)	(32)	(33)	(34)	(35)
VRC	(1)	(3)	(4)	(8)	(9)	(10)	(11)	(12)	(13)	(14)	(16)	(17)	(19)
VRC	(20)	(21)	(22)	(24)	(26)	(27)	(29)	(30)	(31)	(32)	(33)	(34)	(35)
MAR	(1)	(3)	(4)	(8)	(9)	(10)	(11)	(12)	(13)	(14)	(16)	(17)	(19)
MAR	(20)	(21)	(22)	(24)	(26)	(27)	(29)	(30)	(31)	(32)	(33)	(34)	(35)
MAN	(1)	(3)	(4)	(8)	(9)	(10)	(11)	(12)	(13)	(14)	(16)	(17)	(19)
MAN	(20)	(21)	(22)	(24)	(26)	(27)	(29)	(30)	(31)	(32)	(33)	(34)	(35)
MCO	(1)	(3)	(4)	(8)	(9)	(10)	(11)	(12)	(13)	(14)	(16)	(17)	(19)
MCO	(20)	(21)	(22)	(24)	(26)	(27)	(29)	(30)	(31)	(32)	(33)	(34)	(35)
CT	(1)	(3)	(4)	(8)	(9)	(10)	(11)	(12)	(13)	(14)	(16)	(17)	(19)
CT	(20)	(21)	(22)	(24)	(26)	(27)	(29)	(30)	(31)	(32)	(33)	(34)	(35)
LOG	(1)	(3)	(4)	(8)	(9)	(10)	(11)	(12)	(13)	(14)	(16)	(17)	(19)
LOG	(20)	(21)	(22)	(24)	(26)	(27)	(29)	(30)	(31)	(32)	(33)	(34)	(35)

Note. VAN=Analogy, VSC=Sentence Completion, VCA=Context Errors, VRC=Reading Comprehension, MAR=Arithmetic, MAN=Analysis, MCO=Comparisons, CT=Critical Thinking, SP=Spatial Thinking, LOG = Logic.

Table 6. Invariance results for aligned factor loading parameters for P-GAT subscales (VAN – LOG).

Scales	University identification number
VAN	(1)	(3)	(4)	(8)	(9)	(10)	(11)	(12)	(13)	(14)	(16)	(17)	(19)
VAN	(20)	(21)	(22)	(24)	(26)	(27)	(29)	(30)	(31)	(32)	(33)	(34)	(35)
VSC	(1)	(3)	(4)	(8)	(9)	(10)	(11)	(12)	(13)	(14)	(16)	(17)	(19)
VSC	(20)	(21)	(22)	(24)	(26)	(27)	(29)	(30)	(31)	(32)	(33)	(34)	(35)
VCA	(1)	(3)	(4)	(8)	(9)	(10)	(11)	(12)	(13)	(14)	(16)	(17)	(19)
VCA	(20)	(21)	(22)	(24)	(26)	(27)	(29)	(30)	(31)	(32)	(33)	(34)	(35)
VRC	(1)	(3)	(4)	(8)	(9)	(10)	(11)	(12)	(13)	(14)	(16)	(17)	(19)
VRC	(20)	(21)	(22)	(24)	(26)	(27)	(29)	(30)	(31)	(32)	(33)	(34)	(35)
MAR	(1)	(3)	(4)	(8)	(9)	(10)	(11)	(12)	(13)	(14)	(16)	(17)	(19)
MAR	(20)	(21)	(22)	(24)	(26)	(27)	(29)	(30)	(31)	(32)	(33)	(34)	(35)
MAN	(1)	(3)	(4)	(8)	(9)	(10)	(11)	(12)	(13)	(14)	(16)	(17)	(19)
MAN	(20)	(21)	(22)	(24)	(26)	(27)	(29)	(30)	(31)	(32)	(33)	(34)	(35)
MCO	(1)	(3)	(4)	(8)	(9)	(10)	(11)	(12)	(13)	(14)	(16)	(17)	(19)
MCO	(20)	(21)	(22)	(24)	(26)	(27)	(29)	(30)	(31)	(32)	(33)	(34)	(35)
CT	(1)	(3)	(4)	(8)	(9)	(10)	(11)	(12)	(13)	(14)	(16)	(17)	(19)
CT	(20)	(21)	(22)	(24)	(26)	(27)	(29)	(30)	(31)	(32)	(33)	(34)	(35)
LOG	(1)	(3)	(4)	(8)	(9)	(10)	(11)	(12)	(13)	(14)	(16)	(17)	(19)
LOG	(20)	(21)	(22)	(24)	(26)	(27)	(29)	(30)	(31)	(32)	(33)	(34)	(35)

Note. VAN=Analogy, VSC=Sentence Completion, VCA=Context Errors, VRC=Reading Comprehension, MAR=Arithmetic, MAN=Analysis, MCO=Comparisons, CT=Critical Thinking, SP=Spatial Thinking, LOG = Logic.

Table 7. Factor means comparisons among the 26 universities at the 5% significance level for the Verbal domain.

Ranking	University Code	Factor mean	Universities with significantly smaller factor mean
1	19	.454	(26) (27) (14) (17) (31) (1) (21) (16) (35) (12) (9) (8) (32) (30) (3) (33) (20) (24) (34) (10) (11) (22) (13) (29)
2	4	.333	(17) (31) (1) (21) (16) (35) (12) (9) (8) (32) (30) (3) (33) (20) (24) (34) (10) (11) (22) (13) (29)
3	26	.279	(17) (31) (1) (21) (16) (35) (12) (9) (8) (32) (30) (3) (33) (20) (24) (34) (10) (11) (22) (13) (29)
4	27	.214	(17) (31) (1) (16) (35) (12) (9) (8) (32) (30) (3) (33) (20) (24) (34) (10) (11) (22) (13) (29)
5	14	.174	(17) (31) (1) (16) (12) (9) (8) (32) (30) (3) (33) (20) (24) (34) (10) (11) (22) (13) (29)
6	17	.064	(16) (12) (9) (32) (30) (3) (33) (20) (24) (34) (10) (11) (22) (13) (29)
7	31	.026	(9) (32) (30) (3) (33) (20) (24) (34) (10) (11) (22) (13) (29)
8	1	.000	(33) (20) (24) (34) (10) (11) (22) (13) (29)
9	21	-.078	(13) (29)
10	16	-.112	(22) (13) (29)
11	35	-.114	(29)
12	12	-.117	(13) (29)
13	9	-.119	(33) (11) (22) (13) (29)
14	8	-.120	(13) (29)
15	32	-.161	(13) (29)
16	30	-.173	(13) (29)
17	3	-.191	(29)
18	33	-.233	(13) (29)
19	20	-.238	(29)
20	24	-.272	(29)
21	34	-.282	(29)
22	10	-.306
23	11	-.308
24	22	-.401
25	13	-.449
26	29	-.521

Note. The numbers in parenthesis represent each university’s identification number (See Table 1).

Table 8. Factor means comparisons among the 26 universities at the 5% significance level for the Quantitative domain.

Ranking	University Code	Factor mean	Universities with significantly smaller factor mean
1	19	.578	(14) (27) (26) (35) (17) (31) (3) (12) (21) (8) (1) (24) (32) (16) (9) (20) (30) (33) (11) (10) (34) (29) (13) (22)
2	14	.340	(17) (31) (3) (12) (21) (8) (1) (24) (32) (16) (9) (20) (30) (33) (11) (10) (34) (29) (13) (22)
3	4	.324	(1) (24) (32) (16) (9) (20) (30) (33) (11) (10) (34) (29) (13) (22)
4	27	.244	(31) (12) (8) (1) (24) (32) (16) (9) (20) (30) (33) (11) (10) (34) (29) (13) (22)
5	26	.197	(1) (24) (32) (16) (9) (20) (30) (33) (11) (10) (34) (29) (13) (22)
6	35	.179	(29) (13) (22)
7	17	.146	(24) (32) (16) (9) (20) (30) (33) (11) (10) (34) (29) (13) (22)
8	31	.071	(9) (20) (30) (33) (11) (10) (34) (29) (13) (22)
9	3	.070	(29) (13) (22)
10	12	.049	(33) (29) (13) (22)
11	21	.028	(29) (13) (22)
12	8	.012	(29) (13) (22)
13	1	.000	(29) (13) (22)
14	24	-.026	(29) (13) (22)
15	32	-.043	(29) (13) (22)
16	16	-.058	(29) (13) (22)
17	9	-.075	(29) (13) (22)
18	20	-.093	(29)
19	30	-.102	(29)
20	33	-.123	(29)
21	11	-.152
22	10	-.157
23	34	-.168
24	29	-.306
25	13	-.312
26	22	-.342

Note. The numbers in parenthesis represent each university’s identification number (See Table 1).

Table 9. Alignment fit statistics for the P-GAT across universities.

	Factor loadings				Intercepts		Loadings+Intercepts
	Verbal		Quantitative
	FIC	R²	FIC	R²	FIC	R²	TC
VAN	-120.45	0.45			-121.13	0.91	-241.58
VSC	-114.07	0.57			-130.10	0.84	-244.08
VCA	-114.00	0.52			-119.02	0.85	-233.02
VRC	-117.24	0.45			-112.20	0.93	-229.43
MAR			-113.08	0.42	-119.17	0.72	-232.25
ΜAΝ			-125.33	0.36	-131.26	0.73	-256.59
MCO			-121.73	0.50	-127.04	0.88	-248.77
CT			-134.24	0.00	-149.18	0.75	-283.43
SP			-122.11	0.27	-118.40	0.88	-240.51
LOG			-112.62	0.29	-122.71	0.81	-235.33

Note: VAN=Analogy, VSC=Sentence Completion, VCA=Context Errors, VRC=Reading Comprehension, MAR=Arithmetic, MAN=Analysis, MCO=Comparisons, CT=Critical Thinking, SP=Spatial Thinking, LOG = Logic, FIC = Fit Information Contribution, TC = Total Contribution.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Identifying Bias in Social and Health Research: Measurement Invariance and Latent Mean Differences Using the Alignment Approach

Abstract

Method

Participants and Procedure

Measure

Data Analysis Strategy

Results

P-GAT Measurement Model

P-GAT Measurement Invariance Results

P-GAT Latent Mean Difference Results

Discussion

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe