1. Introduction
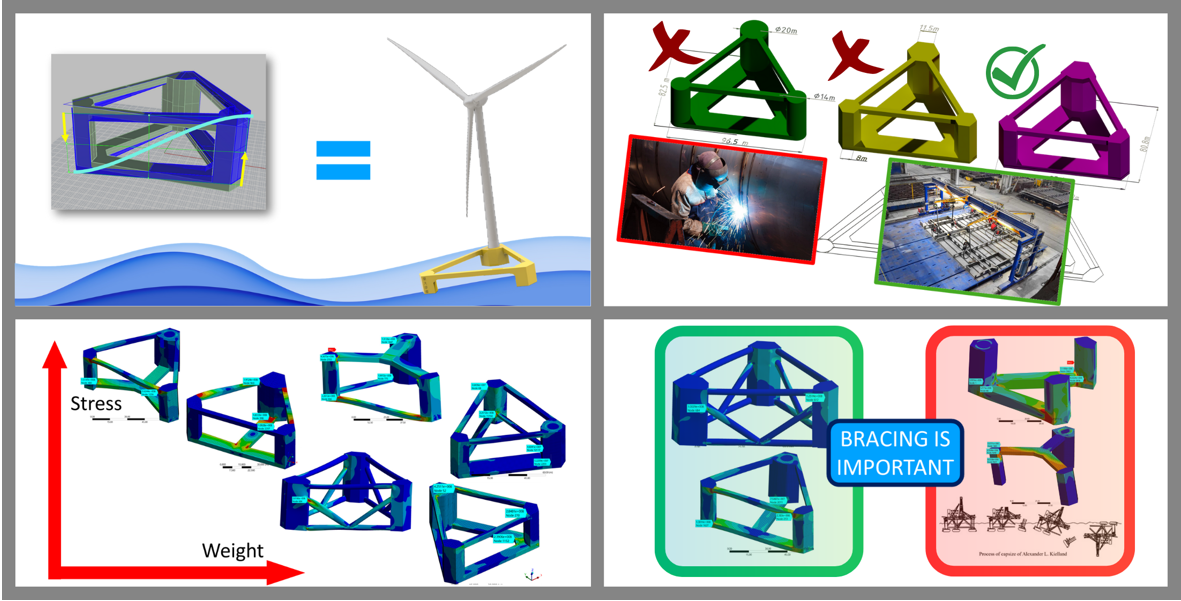
Recently, there are many different semi-submersible Floating Offshore Wind Turbines designs introduced to public attention [
1]. As with every new technology, it is uncertain which option is the best, only with time natural evolution will strike out the inefficient designs and standardize the invention to some extent. Regarding semi-sub FOWT, some configurations have already shown their superiority, such as tri-column design and off-center turbine placement, as proven by commercialized projects. However, other parts of the semi-sub design are still highly debated, such as how the pontoon should look and the optimal column shape.
Among current and planned projects by different companies and research teams (Figure 1.1), there are L-shape (Fukushima Shinpuu) [
2], T-shape (Bassoe T-floater) [
3], above water pontoons (Gusto Tri-Floater old version) [
4], tubular joints (WindFloat) [
5] and ship-like hull pontoons (DeltaFloat) [
6], platforms with and without above-water bracing (EOLFI floater [
7], Fukushima Shinpuu), platforms with bracing bigger than pontoon (SanXia YingLing Hao) [
8], and so on. It is evident, that every design team drafts their design with particular constraints and necessities in mind, however as most are made by for-profit companies, not much of their thought process is shared with the general public.
Figure 1.1.
Different designs of semi-submersible hulls for FOWT.
Figure 1.1.
Different designs of semi-submersible hulls for FOWT.
As researchers, we take the liberty to analyze and compare them without bias. With so many varieties, it is clear that some are to be outlived by the more efficient. The parts specifically looked at in this paper are the different pontoon, column and to a lesser extent, bracing configurations.
Pontoon and bracing have a practically similar purpose – to hold the columns together for them to make up a platform. In designs like Wind Float, they are practically the same, the only difference being pontoon is located underwater, while the bracing is above water. Bracing also provides a way for workers to walk between the columns.
The pontoon is filled with ballast and thus brings the platform’s center of gravity down, if its vertical footprint is big, it also acts as a heave-damping plate. Sometimes, it can also provide buoyancy as will be described later
2. Design Methodoligy
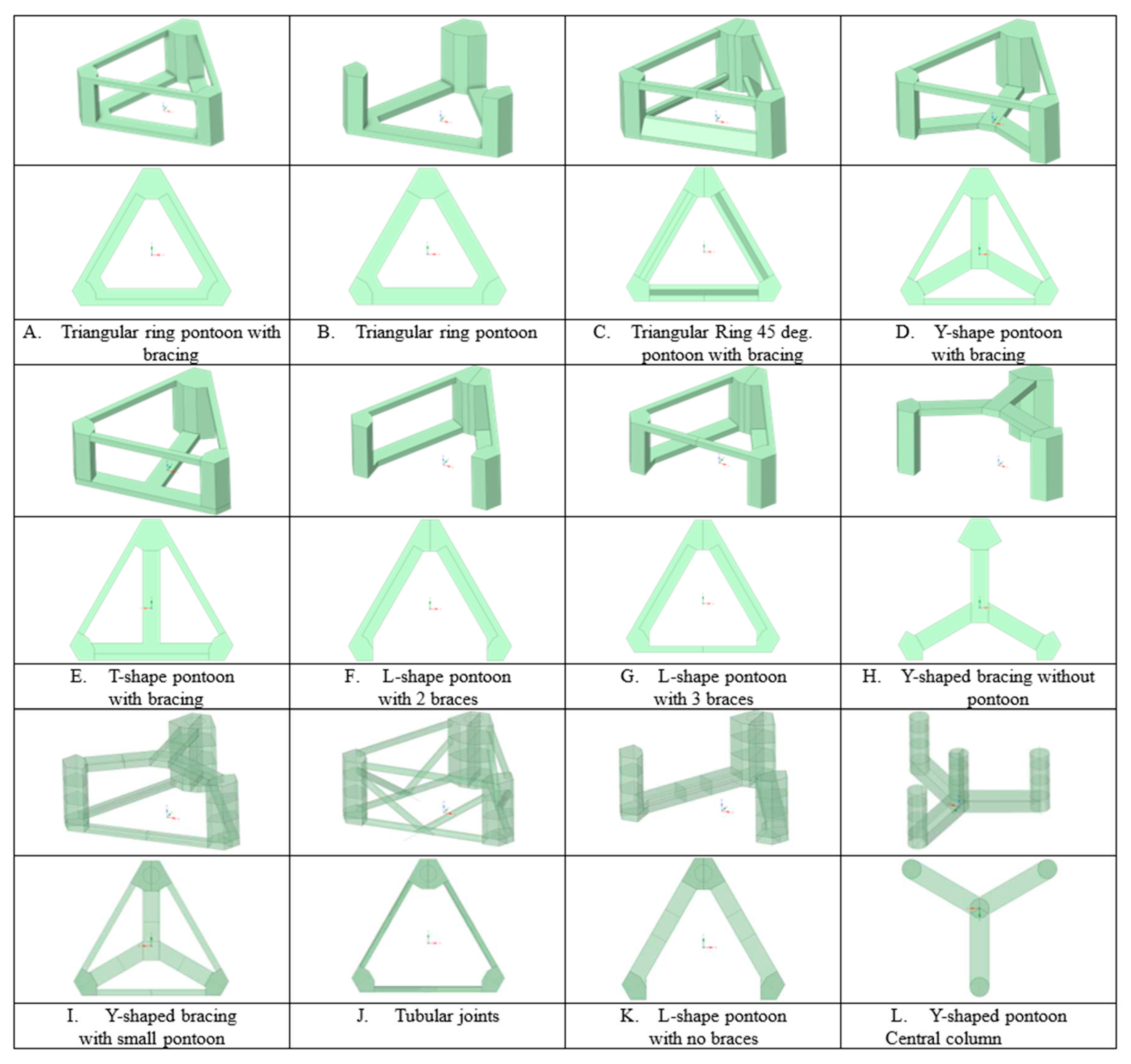
To compare different pontoons, eight (11) modifications of a base platform were created in ANSYS SpaceClaim, shown as the shapes A. to K. in Figure 1.2. The original triangular ring pontoon platform is an updated version of TaidaFloat [
9], a prototype platform to be used in Taiwan strait. While TaidaFloat pontoon can be fully functional (provide buoyancy) or partially functional (permanently ballasted), to remove the influence of wildly varying buoyancy between the different pontoons, they will be considered only partially functional. The other dimensions including all column dimensions, as well as overall length and width are the same among designs, shown in Table 2.1. The platform supports a 15 MW IEA turbine [
10,
11], with the following characteristics shown in Table 2.2. The platform also takes some ballast in columns for use in a dynamic stabilization system and to achieve the desired draught.
Figure 1.2.
Different pontoon and bracing arrangements.
Figure 1.2.
Different pontoon and bracing arrangements.
Table 2.1.
TaidaFloat’s principal characteristics.
Table 2.1.
TaidaFloat’s principal characteristics.
| Length |
81.6 m |
| Breadth |
94.2 m |
| Height |
35 m |
| Draught |
22 m |
| Total displacement |
±20 300 t |
| Hull weight |
4002 t |
| CG height |
17.35 m from BP |
| Coordinates Origin |
Pontoon centroid at base plane (BP) |
Table 2.2.
Wind turbine characteristics.
Table 2.2.
Wind turbine characteristics.
| Name |
IEA 15 MW |
Roter orientation,
Configuration |
Upwind,
3 Blades |
| Rotor Diameter |
240 m |
| Hub height |
150 m |
| Blade mass |
65.25 t |
| Tower mass |
1263 t |
| RNA mass |
991 t |
For every configuration, turbine, ballast and platform assembly weight characteristics including mass moments of inertia were calculated using ANSYS Mechanical, they are shown in Table 2.3.
Table 2.3.
Design cases mass characteristics.
Table 2.3.
Design cases mass characteristics.
| Case |
A |
B |
C |
D |
E |
F |
G |
H |
| System mass (t) |
19450 |
19450 |
20920 |
16410 |
16789 |
16750 |
16750 |
16612 |
| Center of mass, CM (m) (X,Y,Z) |
(0, 6.231, 18.803) |
(0, 6.276, 18.278) |
(0, 3.749, 19.358) |
(0, 8.5149, 22.061) |
(0, 6.629, 21.908) |
(0, 10.004, 21.173) |
(0, 10.017, 21.306) |
(0, 0.822, 24.620) |
| Principal inertias about CM (kg m2) |
Ixx
|
0.5335E+11 |
0.5330E+11 |
0.5301E+11 |
0.4868E+11 |
0.5218E+11 |
0.4696E+11 |
0.4702E+11 |
0.4950E+11 |
| Iyy
|
0.4931E+11 |
0.4923E+11 |
0.5037E+11 |
0.4438E+11 |
0.4460E+11 |
0.4647E+11 |
0.4632E+11 |
0.4984E+11 |
| Izz
|
0.2833E+11 |
0.2816E+11 |
0.3015E+11 |
0.2306E+11 |
0.2456E+11 |
0.2541E+11 |
0.2529E+11 |
0.3178E+11 |
| Ixy
|
-0.6734E+06 |
-0.6725E+06 |
-0.1504E+07 |
0.2873E+07 |
0.1138E+07 |
0.1171E+08 |
0.1172E+08 |
0.3347E+07 |
| Ixz
|
-0.3047E+07 |
-0.3057E+07 |
-0.3480E+07 |
0.1343E+08 |
-0.1606E+07 |
0.4037E+07 |
0.4086E+07 |
0.1330E+08 |
| Iyz
|
-0.9954E+10 |
-0.1003E+11 |
-0.1040E+11 |
-0.9048E+10 |
-0.1004E+11 |
-0.8096E+10 |
-0.8003E+10 |
-0.1068E+11 |
Every design case should be analyzed for the following results:
Strength
Stability
Costs
Exploitation
This paper focuses on strength and cost only. Stability and exploitation may be tackled in future research.
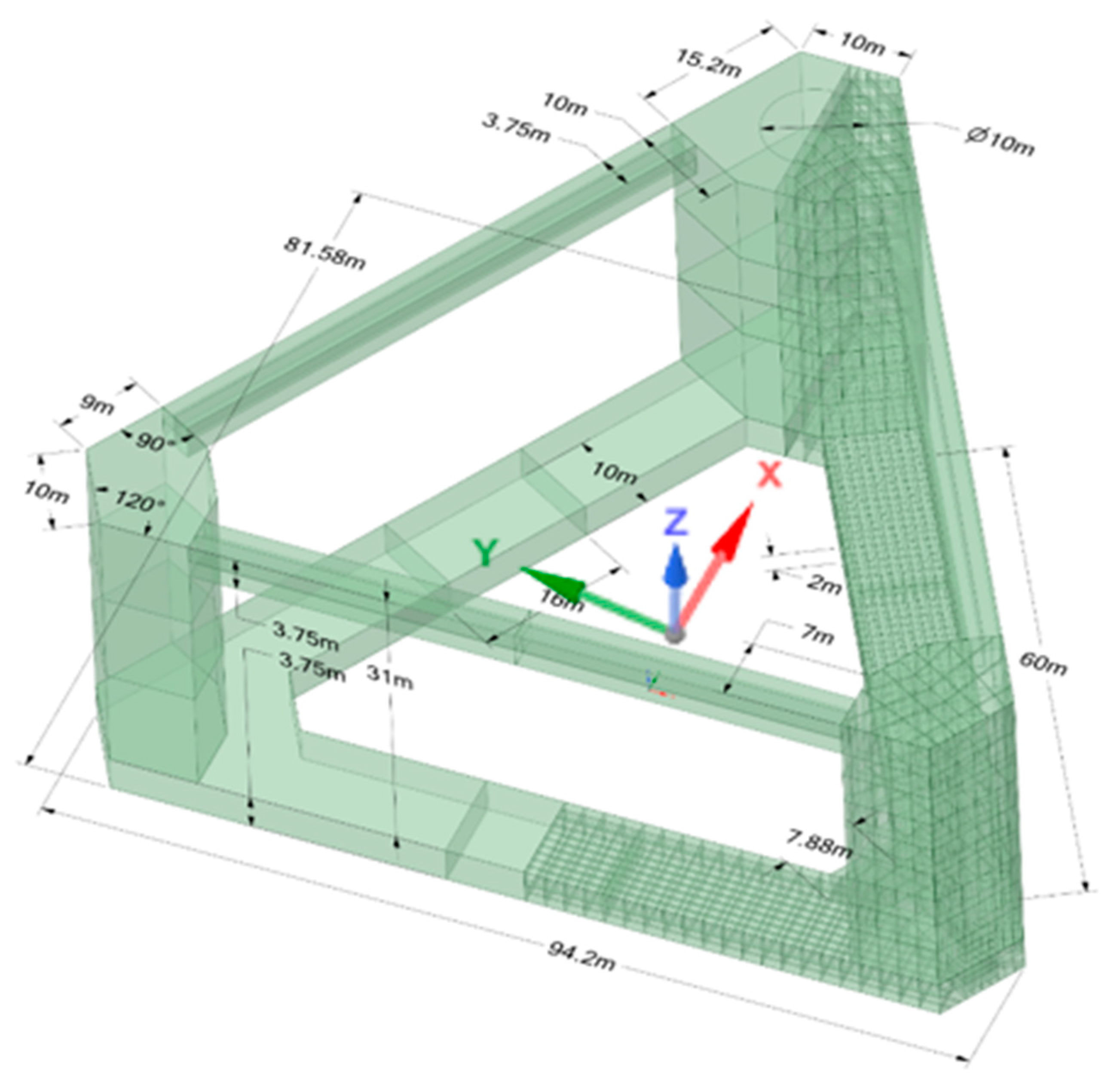
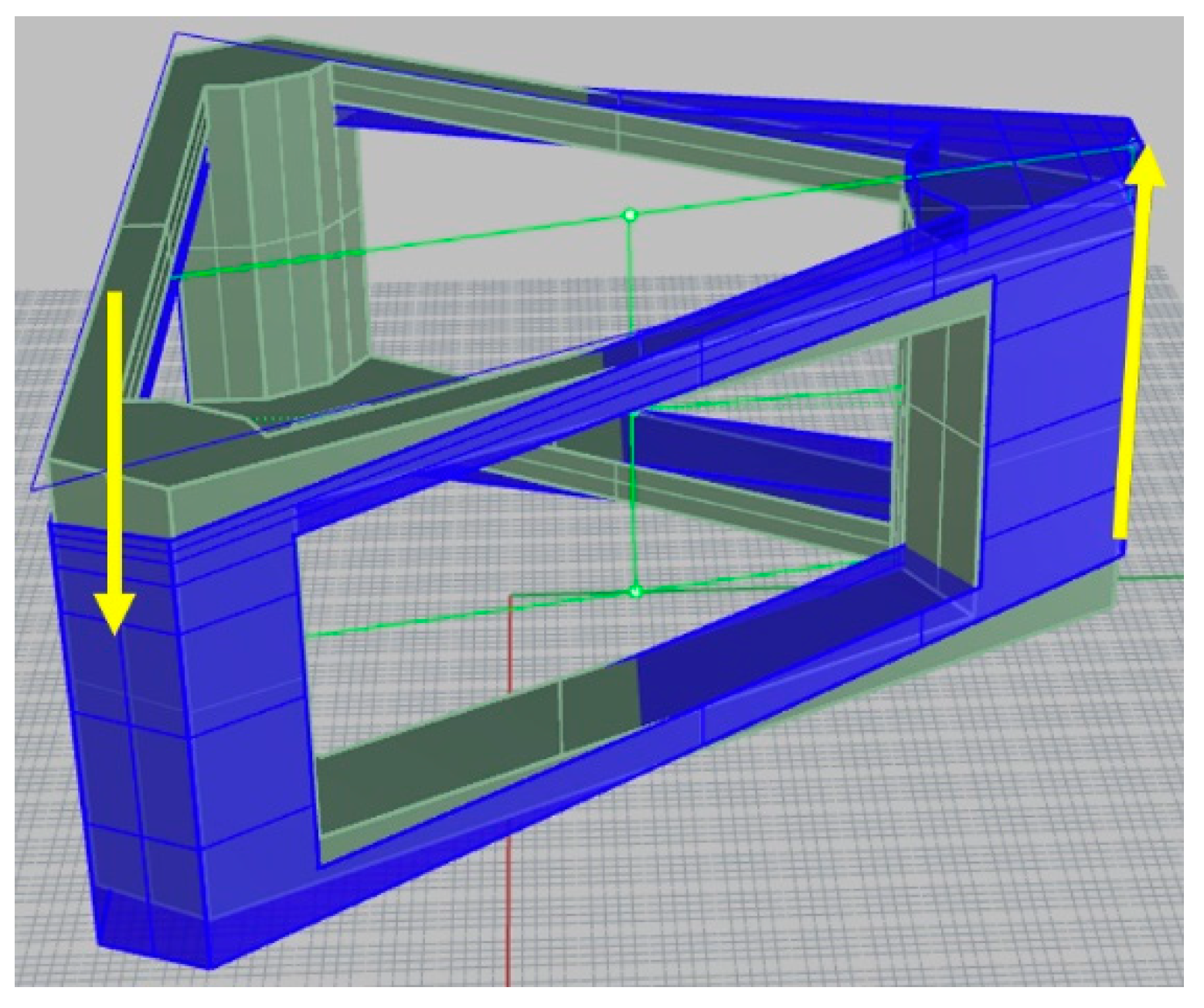
Nowadays, the common approach is to analyze the structural strength of a large number of designs with FEM. ANSYS Mechanical was used for this purpose here. Hull weight and mass moments of inertia were calculated with a framed, ship-like, inner structure. The inner structure is based on the original inner structure for configuration A, slightly modified to fit the shape in other cases. It is shown in Figure 2.1.
Figure 2.1.
TaidaFloat dimensions, structural arrangement and axes.
Figure 2.1.
TaidaFloat dimensions, structural arrangement and axes.
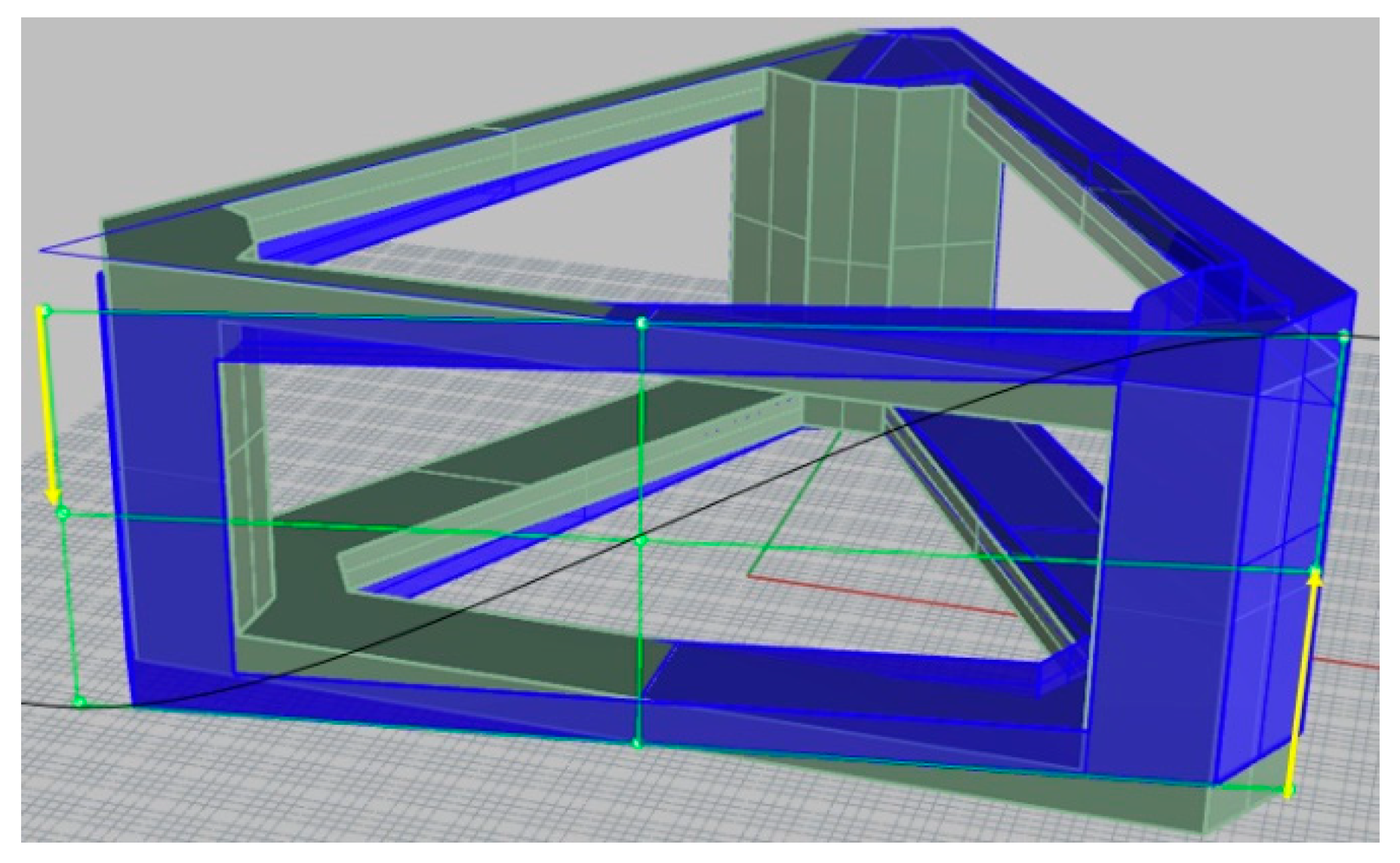
As the first step, all the configurations were subjected to static loads – gravity, water pressure (fully ballasted pontoon condition), turbine assembly weight and a 0.1G acceleration in x and y directions to approximately account for the wave loads.
It is not surprising, that every configuration successfully withstands these static loads, with no important difference between different designs. An example of the result is shown in Figure 2.2
Figure 2.2.
TaidaFloat static FEM analysis.
Figure 2.2.
TaidaFloat static FEM analysis.
The actual difference among the 12 pontoon designs can only be seen during its operation in the rough sea, with dynamic loads. According to ABS Rules [
12], and other major class societies’ rules [
13,
14,
15], offshore structures’ dynamic performance is to be analyzed with different DLP (Dominant Load Parameters) and DLC (Design Load Cases). They represent a comprehensive array of parameters such as wind, loading, waves applied together in the most unfavorable combinations (DLC), and their effect on particular structure parts and modes of deformation (DLP).
For a structure such as a FOWT floater, the matrix of DLP and DLC combinations reaches more than one hundred cases. For 8 pontoon configurations analyzed in this paper, that would be about a thousand cases to investigate. However, not all cases are equally important, here we use engineering judgement and compare 8 cases’ performance at critical DLPs and roughest wave load DLC.
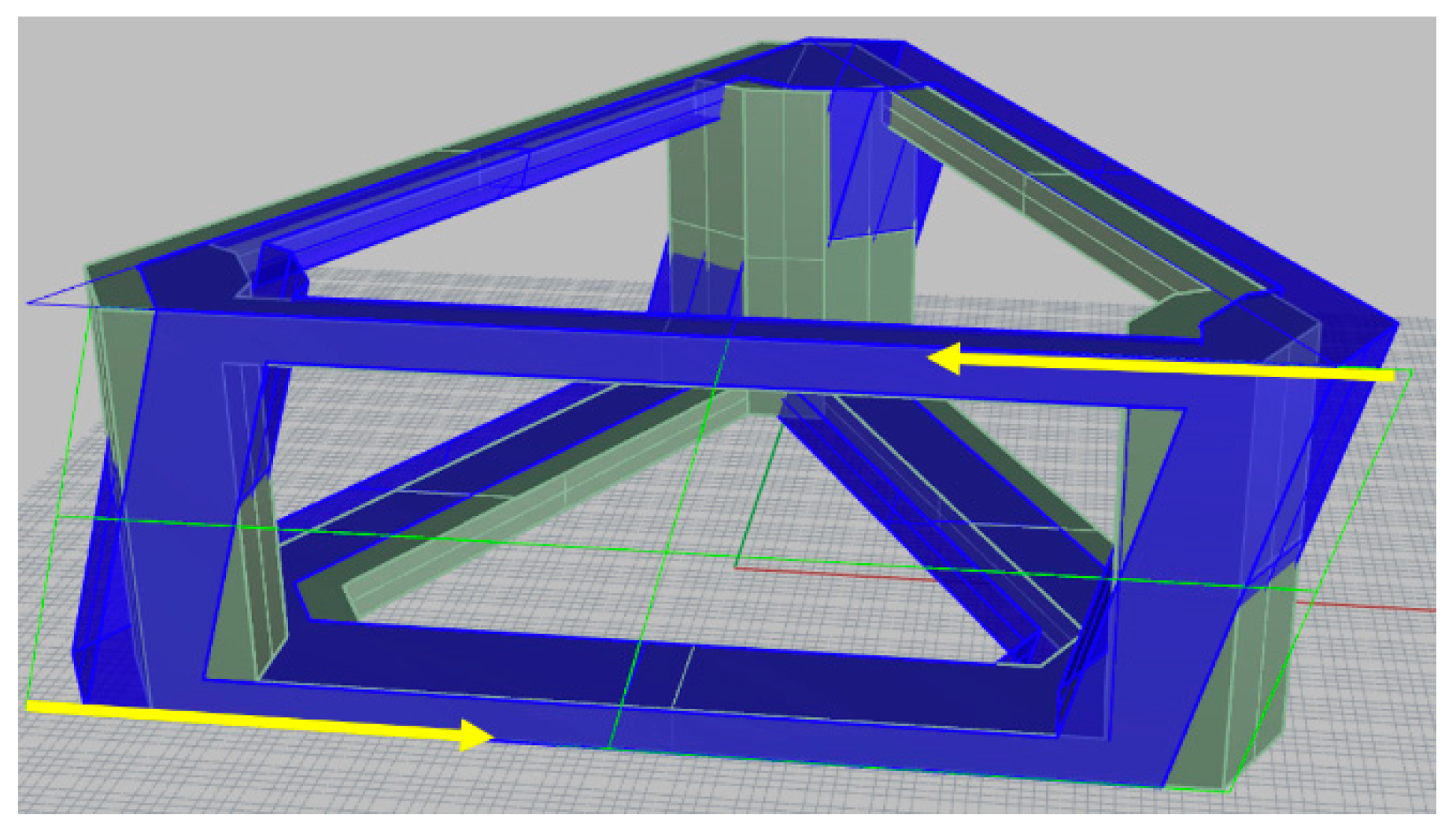
The most critical is arguably the DLP 1 when the wave front is along the platform’s X axis, then one side column is on the wave top, another side column in the crest, and the main column is at the middle height, as shown in Figure 2.3. Difference in buoyancy forces between the two columns produces a twisting moment on the pontoons linked with the main column, potentially breaking them.
Figure 2.3.
Wave-induced twist – DLP 1.
Figure 2.3.
Wave-induced twist – DLP 1.
DLP 2, shown in Figure 2.4., is when the wave front approaches along the Y axis, the main column on the wave top and both side columns in the crest, or vice versa.
Figure 2.4.
Wave-induced shear DLP 2.
Figure 2.4.
Wave-induced shear DLP 2.
DLP 3’s wave condition is similar to DLP 1, however here bending moment is considered not enough to break the platform and horizontal shear is analyzed instead.
3. Pontoon design
For this part of the study, simplified models were used, which had a uniform plate thickness of 30 mm and no reinforcement, except for bulkheads. The force application areas were kept rigid using coupled multi-point constraints. The adequacy of this simplification was demonstrated in a previous study. [
9]
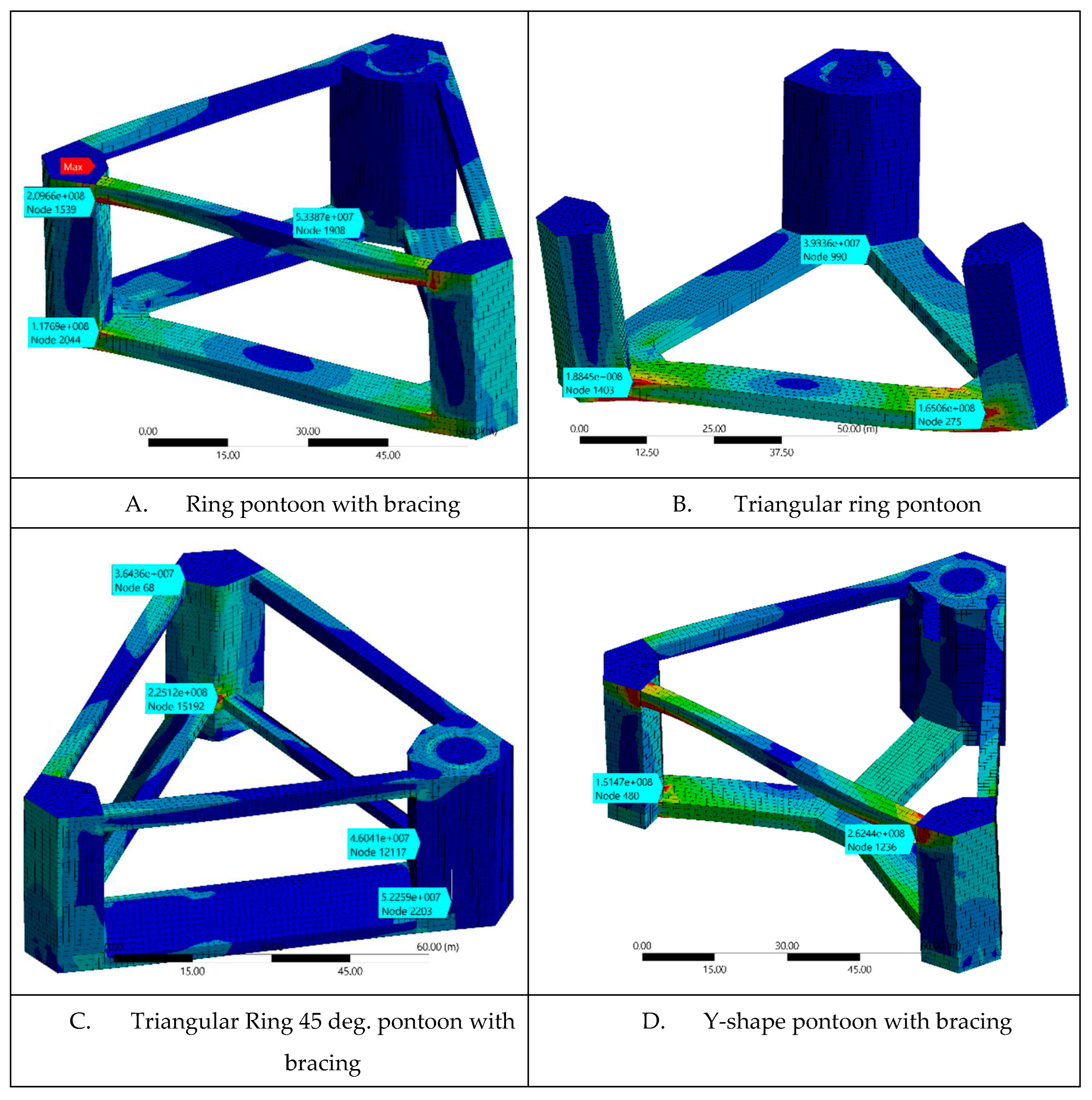
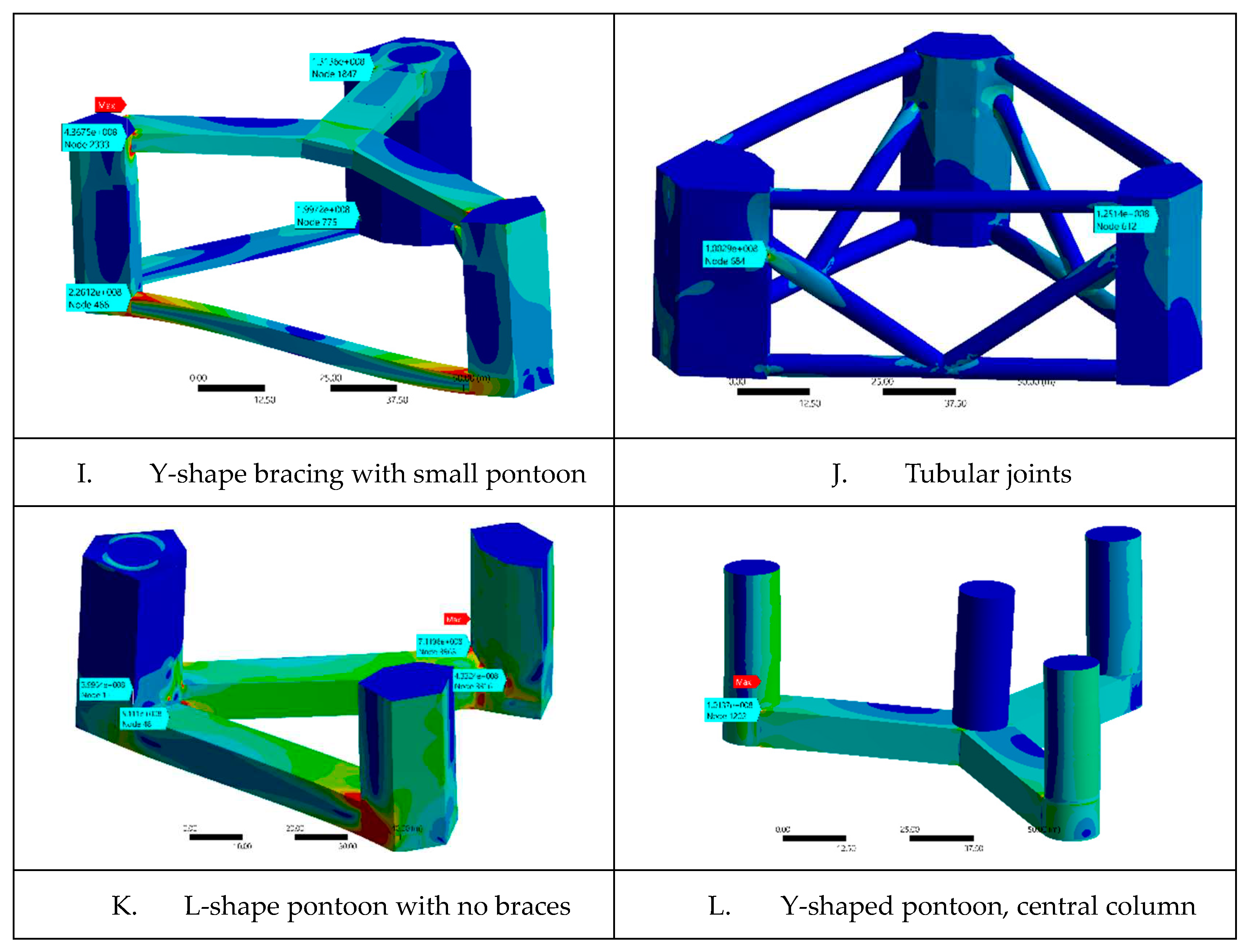
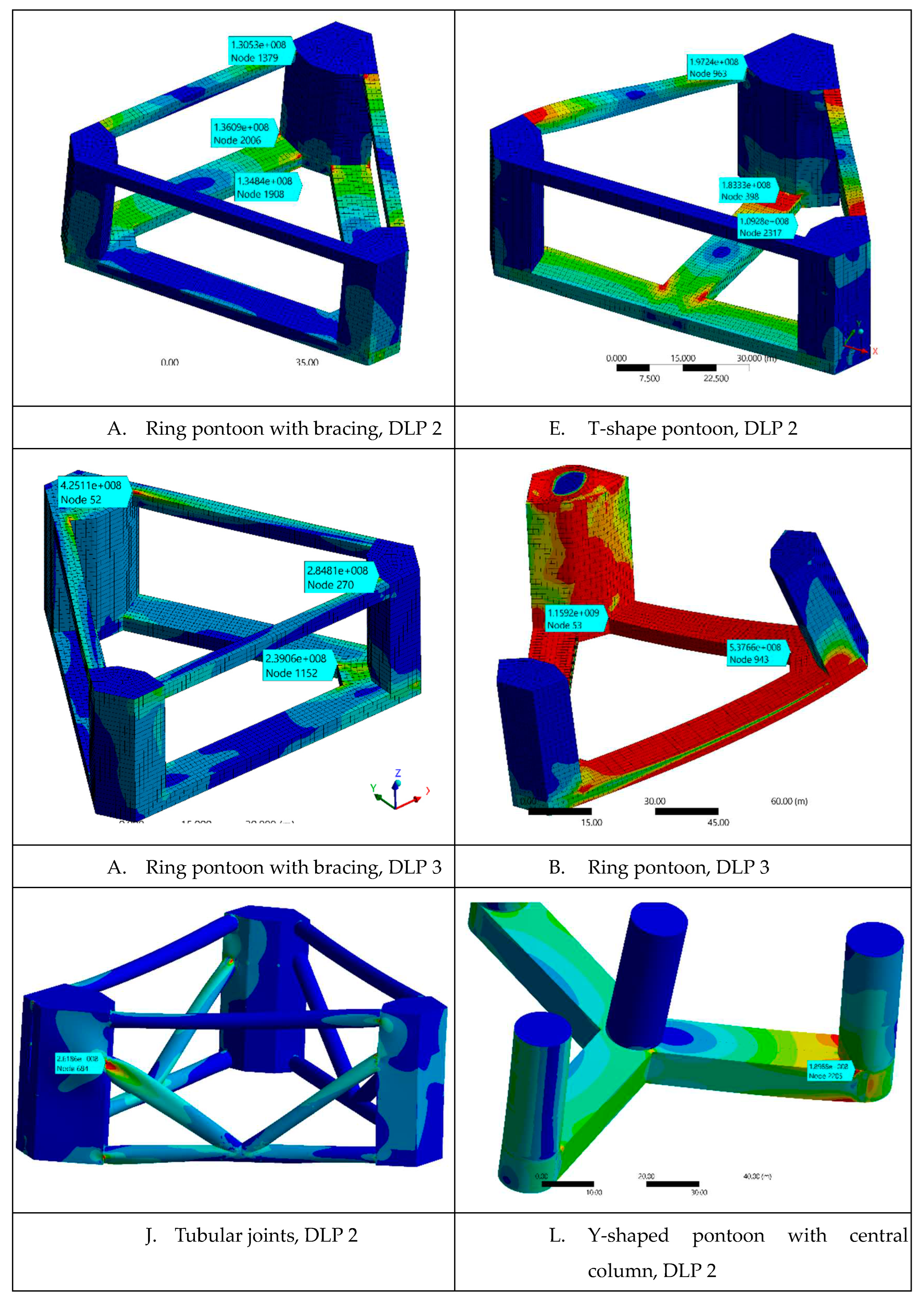
The eight configurations were analyzed according to DLP 1 conditions, and it was found that the configurations with a 3-part pontoon outperformed those without (L-G-H) by a large margin, as shown in Figures 3.1 - 3.3. Configuration A, with its firmly connected structural members, was found to be the most resistant to wave-induced torsion. Configuration C showed similar results, although there was some stress concentration on the inwards-facing side of the side column. Configuration B exhibited good resistance to torsion at the main column, but had large areas of stress concentration in the connection area between the pontoon and columns. Case F exhibited similar phenomena, which was common for all cases without full bracing. This confirms the necessity of bracing, which prevents column rotation relative to pontoons and distributes part of the pontoon's tension.
Figure 2.5.
Horizontal shear DLP 3.
Figure 2.5.
Horizontal shear DLP 3.
Figure 3.1.
Cases A-D DLP 1, stress plot.
Figure 3.1.
Cases A-D DLP 1, stress plot.
Figure 3.2.
Cases E-H FEA DLP 1, stress plot.
Figure 3.2.
Cases E-H FEA DLP 1, stress plot.
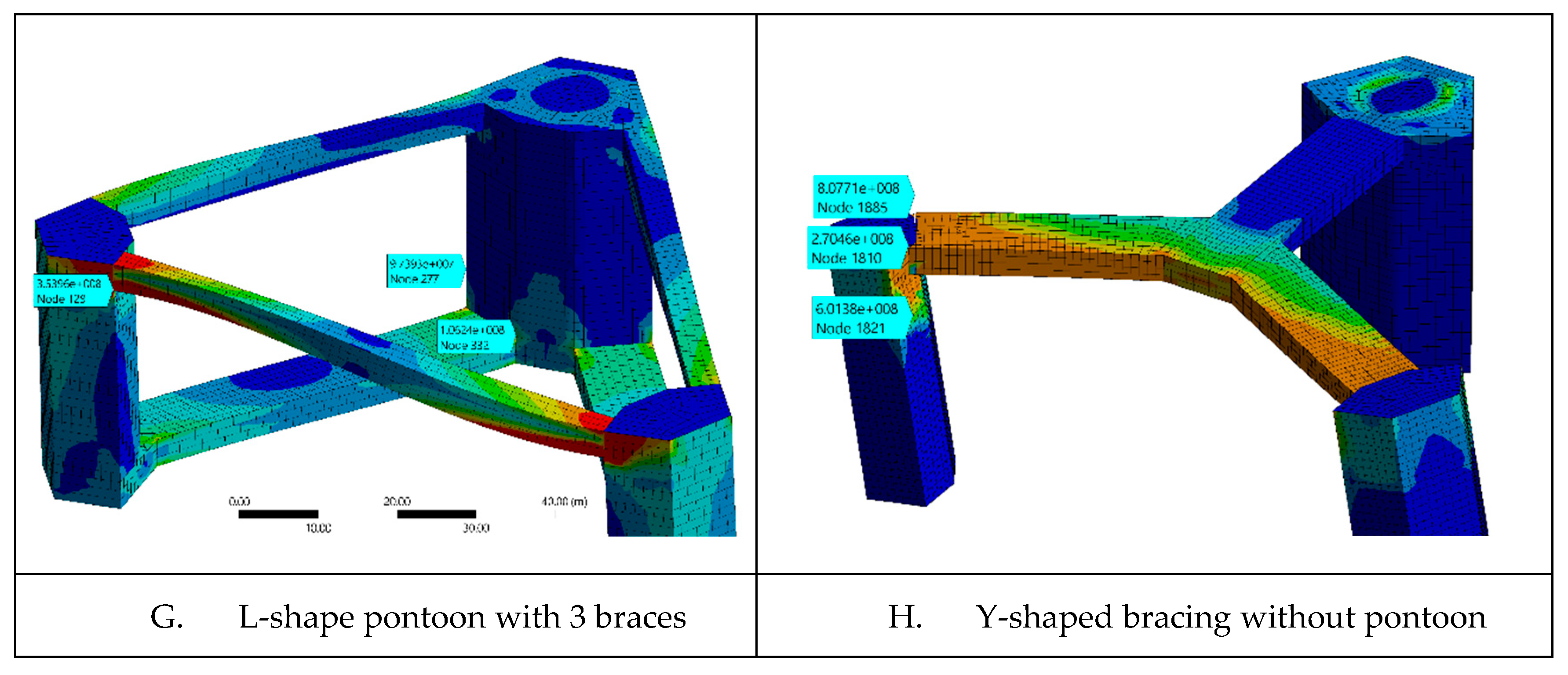
Figure 3.3.
Cases I-L FEA DLP 1, stress plot.
Figure 3.3.
Cases I-L FEA DLP 1, stress plot.
For configuration E, it was found that the T-shaped pontoon can resist torsion almost as well as ring-shaped pontoons, but with considerably less metal used. Cases A(C), B, and E that successfully resisted DLP 1 torsion were further analyzed under other loads.
The stress distribution for DLP 2 and DLP 3 FEA is shown in Figure 3.4. Although the T-shaped pontoon performed well in resisting DLP 1, it exhibited high-stress areas around its middle pontoon, bracing connections, and pontoon intersection corners under DLP 2 and DLP 3. This is because the load is mainly carried by the middle pontoon in a T-shape when the main column is on the wave peak, while in a ring shape, it is borne by two pontoons of the same dimensions. The need for bracing is further confirmed in case B under DLP 3, where a side pressure on the column resulted in a large deformation of the pontoon, causing stress concentrations five times higher than in the same pontoon with bracing (case A), where bracing prevented the rotation. Table 3.1 provides the average and maximum stresses and the relevant shape's hull weight for perspective.
Figure 3.4.
Cases A,B, E; DLP 2,3, stress plot.
Figure 3.4.
Cases A,B, E; DLP 2,3, stress plot.
Table 3.1.
Weight (detailed model) and stress (simplified model).
Table 3.1.
Weight (detailed model) and stress (simplified model).
| Case |
Hull weight, tones |
Average stress DLP 1, MPa |
Max. stress DLP 1, MPA |
Max. stress DLP 2, MPA |
Max. stress DLP 3, MPA |
| A |
4002 |
17 |
210 |
270 |
424 |
| B |
3674 |
20 |
260 |
- |
1159 |
| C |
4424 |
14 |
233 |
- |
- |
| D |
3493 |
20 |
391 |
- |
- |
| E |
3597 |
18 |
238 |
418 |
- |
| F |
3444 |
32 |
275 |
- |
- |
| G |
3561 |
22 |
355 |
- |
- |
| H |
3232 |
26 |
915 |
- |
- |
| I |
3694 |
20 |
446 |
- |
- |
| J |
3764 |
8 |
168 |
405 |
- |
| J2 |
6124 |
5 |
104 |
323 |
- |
| K |
3313 |
32 |
712 |
- |
- |
| L |
2733 |
20 |
101 |
953 |
- |
Table 3.1 in the paper shows that platforms with similar hull weights can have vastly different structural performances. Although their average stress is not significantly different, the maximum stress varies greatly under the same load (DLP 1), ranging from 72 to 915.
This indicates that some shapes have severe stress concentration areas compared to others.
The best and worst performers in each category are denoted by green and red colors, respectively. Interestingly, some platforms are the best in one category but the worst in another (cases H and L). Additionally, some platforms can withstand DLP 1 with lower stress than full bracing and pontoon configurations, but they may fail under other DLPs. The advantage of full configurations is that they perform sufficiently well under different DLPs, which is important since conditions at sea and during transportation can be unpredictable.
Note that the exact value of maximum stress may differ if a high-detail model were analyzed, but the table still provides a useful comparison of the structural performances of different platform shapes.
The strength of a structure can be measured by its average stress. A shape called J with tubular joints connecting columns is the strongest performer, with well-distributed loads. However, making tubular joints is complicated because they are round and need to connect to straight walls and each other. This causes high stress in connection regions, but this is not a problem if the columns, pontoon, and bracing intersect at right angles and their internal stiffeners align perfectly.
Although J is strong, it is heavier compared to other shapes with smaller pontoon and bracing configurations. The lightest shape is H with Y-shaped bracing and no pontoon, but it has high stress of almost 1000 MPa under DLP 1. This means it would need to be strengthened a lot, which negates its weight economy. A shape called L with a circular central column is excluded from the weight comparison because it's a different breed of structure. Interestingly, it performs exceptionally well at DLP 1 but fails the worst at DLP 2.
An experiment was done on J by increasing the hull thickness to 40 mm and the tubular joints to 60 mm, making a new shape called J2. Its maximum stress was closer to that of shape A at 323 MPa, which could be made equal to A's stress with connection reinforcement. However, J2 was heavier, weighing 6124 tons, which is 53% heavier than shape A.
4. Column design
In most of the cases presented above, the columns of the semi-submersible floater are hexahedral, while in others they are cylindrical. This raises a question about why the hexahedral shape was chosen. To understand this, it's important to know that the columns of a semi-submersible floater serve three main functions:
Changing any aspect of the column to improve its performance in one function will affect its performance in the other two functions as well. Therefore, a complex balancing process is required to optimize the design of the columns.
At the moment, the FOWT industry has two types of column designs, as shown in Figure 4.1 and Figure 4.2:
Round (e.g. WindFloat designed by Principal Power) [
5]
Square (e.g. Shinpuu designed by Fukushima Project) [
16]
Figure 4.1.
Round columns of WindFloat (Picture Courtesy of Principle Power Inc.).
Figure 4.1.
Round columns of WindFloat (Picture Courtesy of Principle Power Inc.).
Figure 4.2.
Square columns of Fukushima Shinpuu (Picture Courtesy of Fukushima Offshore Wind Consortium).
Figure 4.2.
Square columns of Fukushima Shinpuu (Picture Courtesy of Fukushima Offshore Wind Consortium).
Table 4.1 lists the advantages and disadvantages of circular and polygonal cross-section columns. Since they are two opposite shapes, it makes sense that the optimal design would be somewhere in between. To create a column that approximates the circular shape while only using straight plates, a polygonal cross-section column is used.
Table 4.1.
Comparison of cylindrical and square columns.
Table 4.1.
Comparison of cylindrical and square columns.
| |
Cylindrical columns |
Square columns |
| Pros |
1. Loads are spread evenly without stress concentrations.
2. Smaller wave impact and drag. [17] |
1. Flat plates are easy to put and weld together.
2. Column intersects with a pontoon at 90 degrees, making inner structure arrangement easy. |
| Cons |
1. Bending of plates adds time and cost to the construction.
2. It’s difficult to connect column girders with pontoon and bracings.
3. Increased sway and surge amplitudes [17] |
1. Potential stress concentration points in the corners.
2. Noticeably larger drag coefficient. |
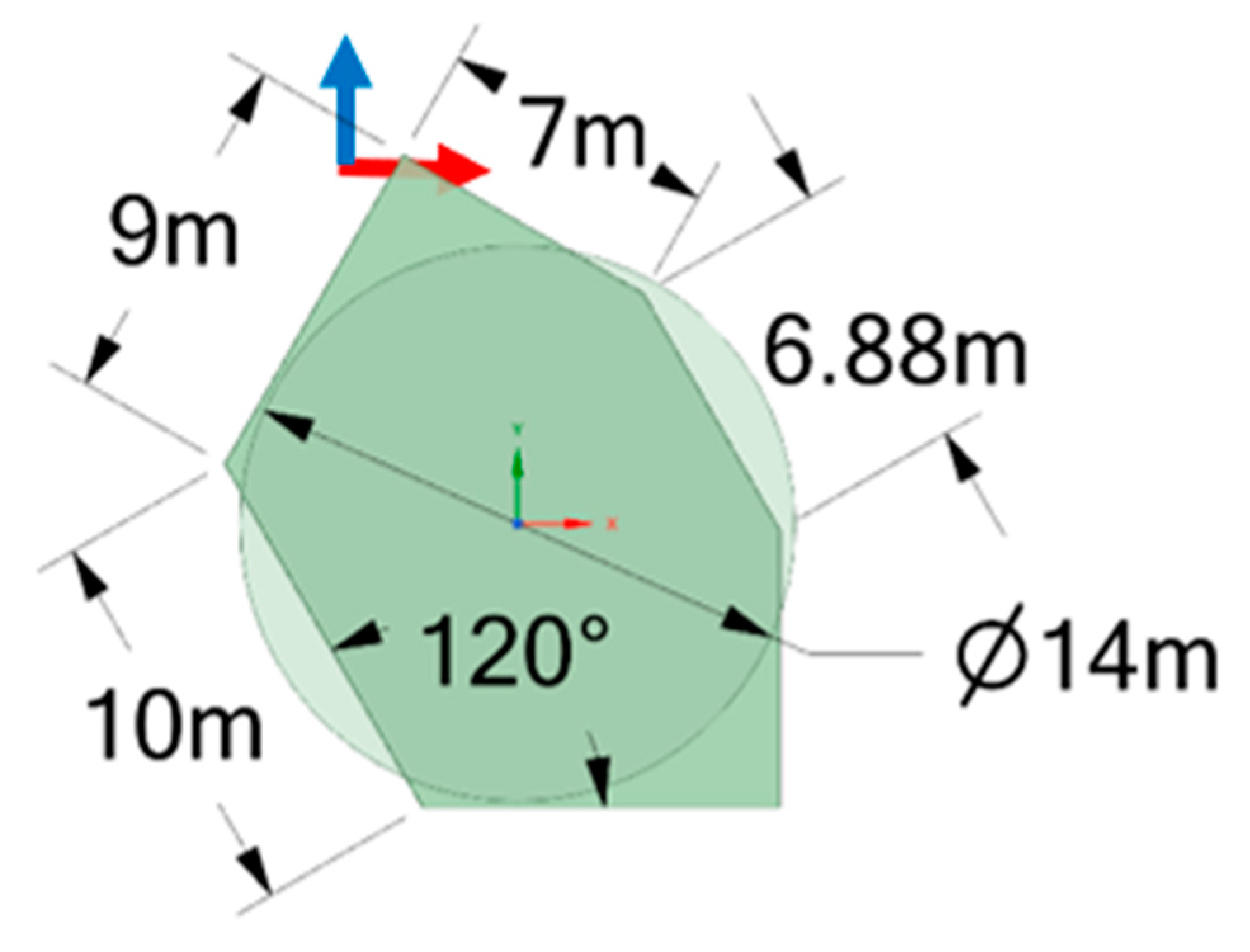
For TaidaFloat, which has three columns and three pontoons, one column needs to connect to two pontoons. After considering various options, a hexagonal shape is proposed as the most suitable design. To ensure that the stiffeners of the pontoons fit the stiffeners of the column perfectly, two of the column sides are made to be the same width as the pontoon. Other sides are chosen to be integers and dimensions are chosen so that the main column-to-side-column section area ratio is the same as for circular columns.
Table 4.2 and Figure 4.3 provide information about the column sections.
Table 4.2.
Section modulus and area of the columns.
Table 4.2.
Section modulus and area of the columns.
| |
|
Round |
Hex |
| Main column |
Area, m2
|
314.16 |
314.38 |
| min Wx, m3
|
785.4 |
802.05 |
| min Wy, m3
|
785.4 |
753.8 |
| Side column |
Area, m2
|
153.94 |
158.30 |
| min Wx, m3
|
269.4 |
275.89 |
| min Wy, m3
|
269.4 |
238.85 |
Figure 4.3.
Circular and hexagonal sections comparison. X-axis is in red, Y-axis is in blue.
Figure 4.3.
Circular and hexagonal sections comparison. X-axis is in red, Y-axis is in blue.
Both tetrahedral (square section) and hexahedral columns share the simplicity of manufacturing advantage. There is no equipment to make 14 m diameter pipes with one seam (at least in Taiwan), so cylindrical and polyhedral columns are all fabricated by welding numerous steel plates together. In the case of polyhedral columns, steel plates can be welded automatically into one wall-sections while lying flat, and then the sections are easily assembled together to form a column. In the case of cylindrical columns, every plate would have to be bent first, requiring equipment and processing time; moreover, plates could not be assembled into sections while lying flat because of their curvature, they would have to be placed vertically, supported by cranes, then welded manually or semi-manually, taking not only much more time, equipment and workers to complete the assembly, but also the quality of manual welding is inherently inferior to automatic welding; weld strength is particularly important for deeply submerged structures. All this equally applies to the internal stiffeners, which would also have to be bent and welded onto the shell. Finally, curved structures are more difficult to store and transport. Thus, it is evident, that with the same steel weight, cylindrical columns are definitely more expensive in manufacturing, thus the exact percentage of the cost difference is subject to local shipyard procedures and equipment.
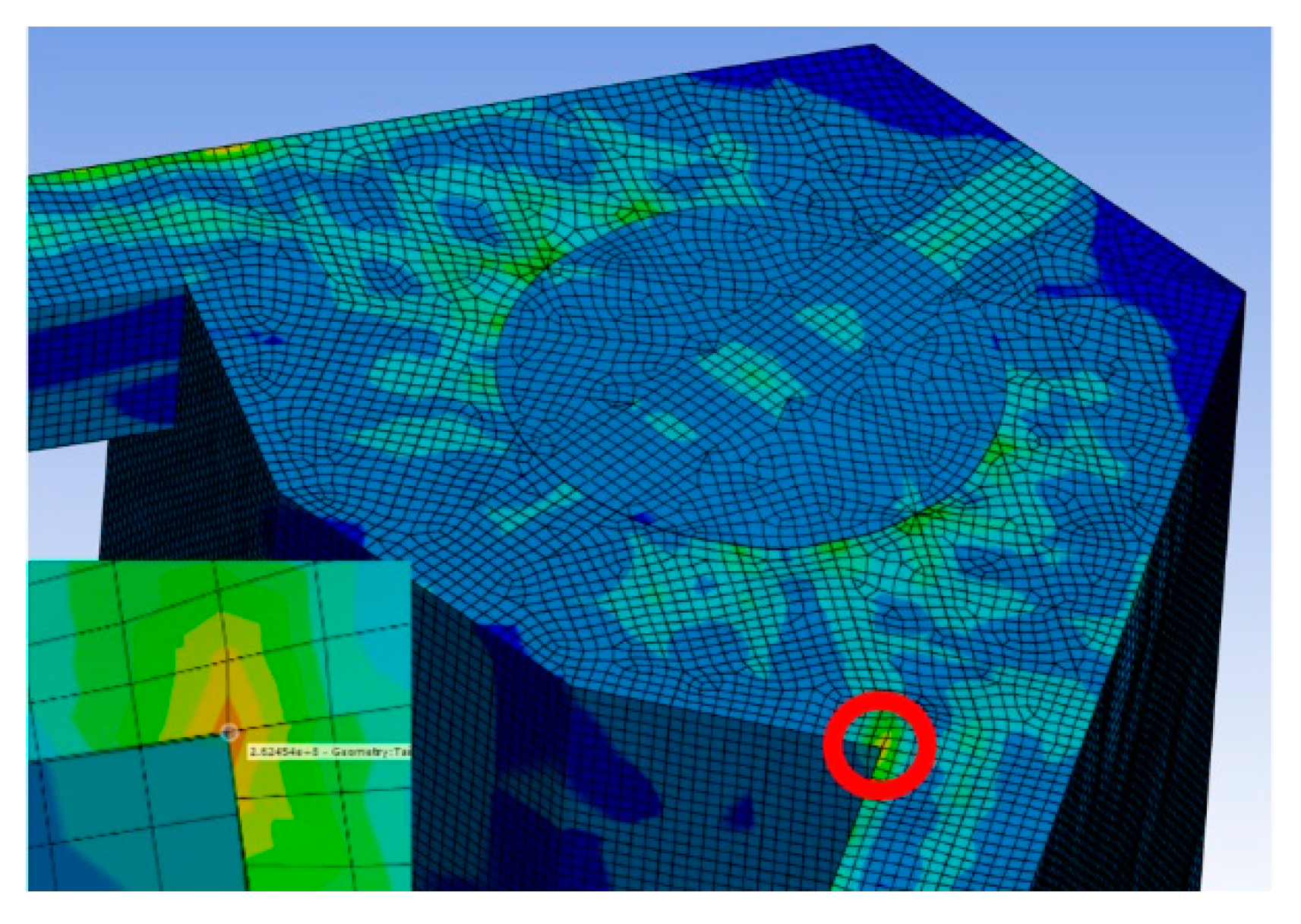
However, the easy-to-manufacture polyhedral shapes have another perceived weakness – stress concentrations. To check for them, finite elements analysis was conducted with turbine weight and gravity as loads. A stress concentration was indeed found in Fig. 4.4, but only in corners where the bracing and pontoon connect to the column’s inner side, and its value of 262 MPa is acceptable for the preliminary structure design stage. This corner can easily be reinforced during subsequent design.
Figure 4.4.
Stress distribution in the main column top.
Figure 4.4.
Stress distribution in the main column top.
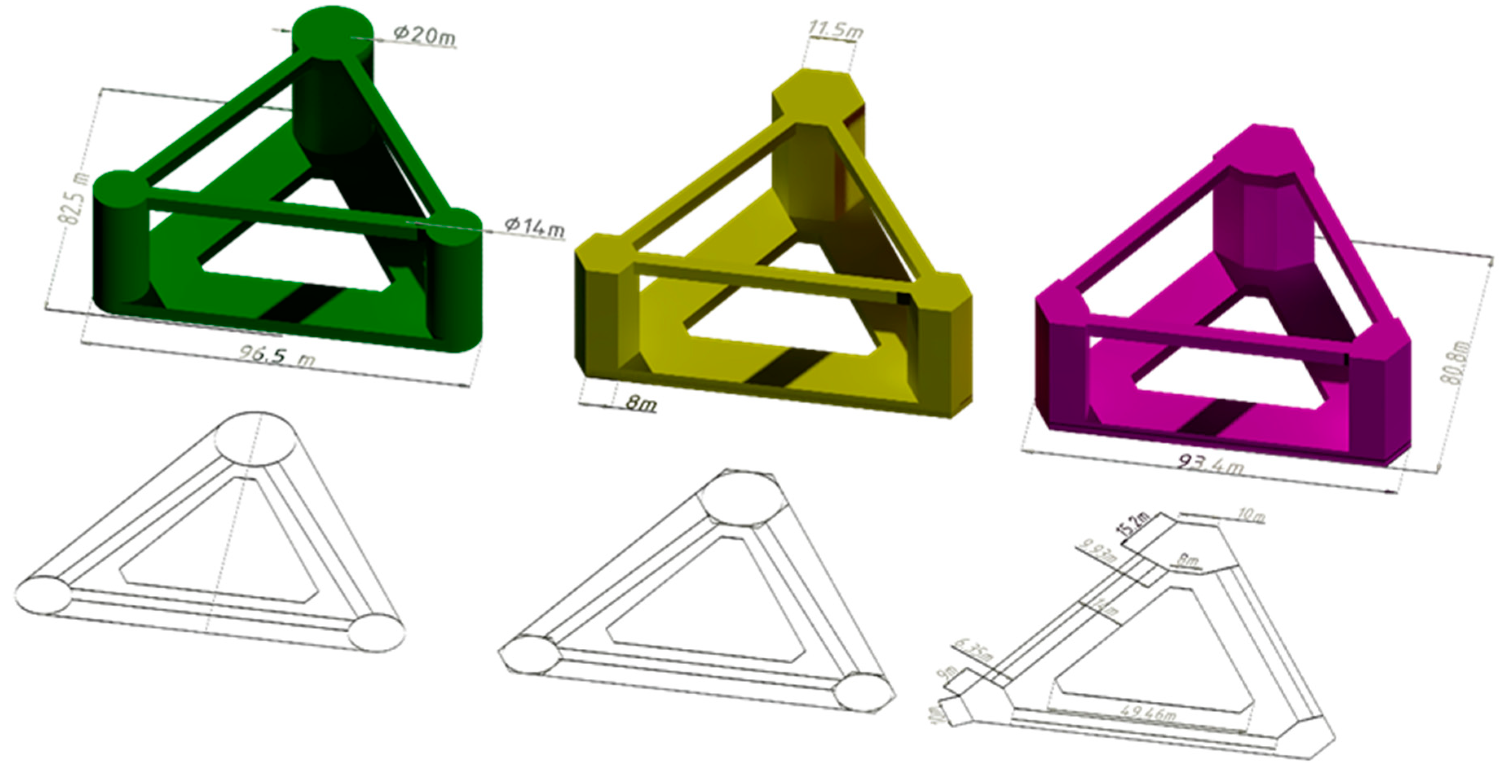
In Figure 4.5, the original TaidaFloat is shown along with two new hexagonal variants:
To determine the final shape, an international expert group consisting of twenty specialists from the industry and academia were asked to vote. Interestingly, half of the votes went to the original circular platform, and half went to the hexagonal platform concept.
Figure 4.5.
Three candidates of floater designs for TaidaFloat (dimensions before the change for manufacturing).
Figure 4.5.
Three candidates of floater designs for TaidaFloat (dimensions before the change for manufacturing).
After careful consideration, the purple hexagonal shape was chosen – as this platform is designed to be mass-manufactured, construction ease is more important than a slightly better wave response. As this platform is made with flat plates and the pontoon is perpendicular to the column side, it retains all the benefits of the square section column from Table 1, at the same time the cons are not as bad as for the full square shape, wave impact and drag are still less.
Following the principle of a close collaboration with the shipyard, the platform dimensions were changed to fit the shipyard’s steel plate dimensions and welding equipment sizes; e.g. pontoon and bracing height were reduced from 4 to 3.75 m to fit 3.8 m width steel plates produced by Taiwanese steel mills.
After all the modifications, the latest version TaidaFloat characteristics are as in Table 4.3.
Table 4.3.
TaidaFloat’s main characteristics.
Table 4.3.
TaidaFloat’s main characteristics.
| |
TaidaFloat
Version 3 |
TaidaFloat
Version 4 |
| Displacement (t) |
23000 |
20300 |
| Hull weight (t) |
4715 |
4000 |
| Pontoon ballast (t) |
13240 |
9829 |
| Column ballast (t) |
1850 |
3344 |
| GM (trim/heel) (m) |
21.6/ |
26.2/ |
| 13.2 |
16.8 |
| CG height (m) |
16.62 |
17.35 |
| Max. heel angle (°) |
8.08 |
6.64 |
5. Bracing design
In addition to the sea-incurred loads, it is important to consider the loads that the wind turbine will impose on the platform. During normal operation and even during typhoon conditions when the turbine blades still receive wind loads, the turbine will generate a significant bending moment on the supporting structure. This loading consists of three force components and three moment components, with the most prominent being the fore-aft bending moment and the vertical force that includes the weight of the turbine itself. Figure 5.1 shows the stress distribution in the platform, which highlights the importance of the bracing, especially in the connection parts, as they experience the highest stresses.
Figure 5.1.
Stress distribution with 6 components wind load applied. Green area is higher stress due to wind turbine moment.
Figure 5.1.
Stress distribution with 6 components wind load applied. Green area is higher stress due to wind turbine moment.
As first described by Jonkman [
18], the wind turbine installed on a FOWT can generate several times the moment on its support that the same turbine would generate on land. Thus, it is essential that the bracing is designed to withstand these loads to ensure the platform can fulfil its primary purpose of supporting the turbine. Fatigue life is also significantly reduced under these loads, further emphasizing the importance of robust bracing design. Future research will investigate the impact of wind turbine moments on bracing in more detail, and this will be the subject of an upcoming paper.
Note that bracing can be structurally critical. The worst structural failure in a semi-submersible may be the Alexander Kielland accident in 1980, which resulted in the capsizing of the floater [
19]. The disaster started from a fatigue crack in bracing. The damaged bracing caused the column to break off from the platform. Consequently, the semi-submersible capsized.
6. Discussion
In this section, we will discuss the findings of the study and highlight the key factors that need to be considered when designing a floating offshore wind turbine (FOWT) platform.
The study analyzed 13 different platform configurations, under three (3) different design load parameters (DLP). The objective was to identify the most cost-effective and structurally efficient platform design that can withstand the environmental loads and stresses exerted on the FOWT platform.
Based on the analysis, platform E with a T-shaped pontoon provides the most cost-effective solution under the assessed DLC and DLP. It is robust, relatively cheap, and easy to fabricate. However, considering that FOWT floaters are a relatively new type of structure with a history of failures, a safer platform configuration might be preferred for a new 15 MW platform. In this case, the material economy is not as important as the safety of the platform. Platforms A and C, both ring pontoons with full bracing, are considered the safest configurations. While they are structurally similar, they may have different hydrodynamic performance and RAO, which requires further investigation.
Additionally, it is important to consider the draft of the platform and its relation to the pontoon. Typically, pontoons are permanently filled with water before exploitation to counteract outside water pressure. However, in the case of a floating offshore wind turbine, the emptied pontoon provides floatation during the transportation and installation stages. The internal structure of the pontoon needs to be strong enough to support water pressure exceeding 200 kPa. However, the mass of all this reinforcement helps bring the pontoon’s center of gravity further down, improving stability. It is cheaper to add weight by increasing pontoon steel parts thickness than by pouring concrete inside when considering added operational costs. The added buoyancy is crucial when entering and exiting shallow ports, allowing platforms (Cases A-E) to be assembled and serviced closer to their deployment area, while cases G-K are limited to very deep ports or have to use temporary floatation modules.
Finally, the hexahedral column shape is chosen for TaidaFloat by the design team as it combines the best attributes of cylindrical and square shapes. The ease of construction with flat steel plates makes the square shape stand out.
One potential drawback of the hexahedral column shape chosen for TaidaFloat is that it may not be as efficient in terms of space utilization compared to other shapes. Future research could explore ways to optimize the design to maximize space utilization without compromising on other performance metrics.
Another area for future research is the long-term durability, fatigue life and maintenance requirements of these designs. As FOWT floaters are relatively new structures, there is still much to learn about their long-term behavior and performance in real-world conditions. Continued monitoring and research can help to identify any potential issues and optimize the design for improved durability and longevity.
7. Conclusion
In conclusion, designing an efficient and cost-effective floating offshore wind turbine platform requires consideration of various factors such as hydrodynamic performance, structural stability, and operational costs. Based on the research in this study, the design team chose the following for TaidaFloat:
A hexahedral column, as it combines the best attributes of cylindrical and square shapes, and uses flat steel plates making the construction much easier and faster.
A full-ring pontoon configuration for low stresses and the ability to control draught by ballasting.
The ring bracing configuration in order to prevent stress concentrations and fatigue damage at connection points and efficiently distribute the wind turbine’s force across the structure.
The findings of this study can provide valuable insights for future FOWT platform design and development. Further research is necessary to investigate other potential platform shapes and configurations and optimize their performance.
Acknowledgments
Anonimized.
References
- J. Zou and I. E. Udoh, "Driving Down Cost: A Case Study of Floating Substructure for A 10MW Wind," in Offshore Technology Conference, Houston, 2019.
- Fukushima Consortium, "Fukushima Experimental Offshore Floating Wind Farm Project," 22 06 2015. [Online]. Available: https://www.mhi.com/news/150622en.html. [Accessed 02 06 2022].
- BASSOE TECHNOLOGY, "BT FLOATER DESIGN," 2022. [Online]. Available: https://www.basstech.se/17/11/renewables/. [Accessed 02 07 2022].
- T. &. M. S. J. Hendriks, "Challenges in stability assessment of offshore floating structures," in IMAM 2017, Lisbon, Portugal, 2017.
- Principle Power Inc., "The WindFloat®," 2021. [Online]. Available: https://www.principlepower.com/windfloat/the-windfloat-advantage. [Accessed 02 06 2022].
- SOIC, "SOIC DeltaFloat FOWT platform," 2021. [Online]. Available: https://www.youtube.com/watch?v=qLmMU4hBvpk. [Accessed 02 07 2022].
- EOLFI, "EOLFI, PIONEER OF FLOATING WIND POWER," 2022. [Online]. Available: https://www.eolfi.com/en/expertises/marine-renewable-energy. [Accessed 02 07 2022].
- ChinaOffshoreWind, "National FOWT "San Xia Ying Ling" design and and analysis (In Chinese)," 17 03 2022. [Online]. Available: https://news.bjx.com.cn/html/20220317/1210998.shtml. [Accessed 02 07 2022].
- I.-J. Hsu and G. e. a. Ivanov, "Optimization of Semi-Submersible hull design for floating offshore wind turbines," in Proceedings of the ASME 2022 41st International Conference on Ocean, Offshore and Arctic Engineering, Hamburg, Germany, 2022.
- E. Gaertner, J. Rinker, L. Sethuraman and et. al, "Definition of the IEA 15-Megawatt Offshore Reference Wind," Golden, CO: National Renewable Energy Laboratory, 2020. [Online]. Available: https://www.nrel.gov/docs/fy20osti/75698.pdf. [Accessed 02 07 2022].
- C. Allen, A. Viselli, H. Dagher and et. al, "Definition of the UMaine VolturnUS-S Reference Platform Developed for the IEA Wind 15-Megawatt Offshore Reference Wind Turbine," Golden, CO: National Renewable Energy Laboratory, [Online]. Available: https://www.nrel.gov/docs/fy20osti/76773.pdf. [Accessed 02 07 2022].
- ABS, Guide for Building and Classing Floating Offshore Wind Turbines, American Bureau of Shipping, 2020.
- DNVGL, DNVGL-ST-0119. Floating Wind Turbine Structures, 2018.
- Class NK, Guidelines for Offshore Floating Wind Turbine Structures, 2012.
- BV, NI-572-R02-E, Classification and certification of Floating Offshore Wind Turbines, Bureau Veritas, 2015.
- M. Ohta, M. Komatsu, H. Ito and H. Kumamoto, "Development of a V-shaped Semi-Submersible Floating Structure for 7MW Offshore Wind Turbine.," in Proceedings of the International Symposium on Marine and Offshore Renewable Energy, Tokyo, Japan, 2013.
- W. Z. D. W. Siming Li, "Numerical Study of Column Rounded Corner Effects on Vortex-Induced Motions of Semi-Submersibles," in Proceedings of the Thirteenth (2018) Pacific-Asia Offshore Mechanics Symposium, Jeju, Korea, 2018.
- J. Jonkman, "Dynamics Modeling and Loads Analysis of an Offshore Floating Wind Turbine," National Renewable Energy Laboratory, Colorado, USA, 2007.
- T. Moan, The Alexander L. Kielland accident, NTNU, 2020.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).