Iterative List Patterned Reed-Muller Projection Detection-based Packetized Unsourced Massive Random Access

Preprint

Article

Iterative List Patterned Reed-Muller Projection Detection-based Packetized Unsourced Massive Random Access

Altmetrics

Downloads

116

Views

Comments

A peer-reviewed article of this preprint also exists.

Wenjiao Xie^*

,Runhe Tian,Huisheng Zhang

Wenjiao Xie^*

,Runhe Tian,Huisheng Zhang

This version is not peer-reviewed

Submitted:

09 July 2023

Posted:

10 July 2023

You are already at the latest version

Alerts

Abstract

We consider a coded compressed sensing protocol for unsourced massive random access (URA) that concatenates a shared Patterned Reed-Muller (PRM) inner codebook to an outer error-correction code. In this paper, an iterative list PRM projection algorithm is proposed to supplant the signal detector associated with the inner PRM sequences. In particular, we first propose an enhanced paths-saving algorithm called list PRM projection detection for the single-user scenario that keeps multiple candidates for the first few layers to remedy the risk of spreading errors. On this basis, we further propose an iterative list PRM projection algorithm for the multi-user scenario. The vectors for PRM codes and channel coefficients are jointly detected in an iterative manner, which offers significant improvements regarding the convergence rate for signal recovery. Furthermore, the performances of the proposed algorithms are analyzed mathematically, and we verified that the theoretical simulations are consistent with the numerical simulations. Finally, we concatenate the inner PRM codes that employ the iterative list detection to two practical error-correction outer codes. According to the simulation results, we conclude that the packetized URA with the proposed iterative list projection detection works better than benchmarks in terms of the number of active users it can support in each slot and the amount of energy needed per bit to meet an expected error probability.

Keywords:

Subject: Engineering - Telecommunications

1. Introduction

One of the most prominent use cases for 6G wireless networks will still be the massive machine-type communication’s (mMTC+) continuous evolution [1]. Indeed, mMTC+ services feature the presence of a large number of machines that sporadically link to the system while carrying short data packets. Besides, they are battery-limited and intended to achieve low transmission latency [2,3,4].

Grant-free transmission [5,6], in which packets are transmitted to the network without informing the base station in advance, is the approach that provides the most promise. The instance of "Sourced Random Access" [7] uses grant-free transmission and allocates distinct dictionaries to different users. Since there are so many users, employing various encoders would complicate reception since the decoder would first have to determine which encoders were being used. Therefore, using the same coding technique for all users is the most promising strategy. These systems are referred to as "Unsourced random access (URA)" [8]. In this way, the identification and decoding responsibilities are decoupled, and the URA receiver only needs to decode the messages without knowing who sent them. Additionally, all active users’ per-user probability of error (PUPE) is used to examine the access and transmission performance of the entire system.

The fundamental limits for the Gaussian multiple-access channel are described in [8], which formulates the URA problem from an information-theoretic perspective. Based on [8], an asymptotic improvement is presented in [9]. Both examine the scenario where the receiver has a fixed count of active users. These findings are expanded in [10] to the case where the receiver’s active user count is arbitrary and unknowable. For the Gaussian multiple-access channel, a range of low-complexity URA algorithms have been suggested. The main schemes are T-fold irregular repetition, which includes the T-fold irregular repetition slotted ALOHA protocol with collision detection [11,12], the sparse interleave division multiple access (IDMA) scheme [13], random spreading and correlation-based energy detection [14,15], as well as the coded compressed sensing (CCS) based URA scheme [16]. Coded compressed sensing is a divide-and-conquer strategy that concatenates the inner codes to outer A-channel codes, where a tree code is a specific instance of an outer A-channel code devised for this kind of application [17,18]. This makes it simple to accommodate novel channel models owing to the concatenated form’s adaptability for URA. Several later investigations on URA employed an outer A-channel code [19,20,21,22,23,24]. In paper [25], the study scope of a tree code behaving as the outer A-channel code is extended through the integration of the approximate message passing (AMP) mechanism with sparse regression codes [16]. The coded compressed sensing approach is further enhanced in [19] by enabling the inner AMP decoder and the outer tree decoder to communicate soft information through a common message-passing protocol. In order to simplify the high dimensional sparse signals’ joint detection pertaining to several bases, the research work in [26] suggests a coded demixing method.

Compressed sensing has made extensive use of codebook construction techniques related to second-order Reed-Muller (RM) sequences [27]. RM sequences are excellent options for massive access senario in continuous evolution of massive machine-type communication owing to the high capacity and capability for low-complexity random access [28]. In [29], the non-orthogonal Reed-Muller sequences are used as user identifiers (IDs) for active user identification in the grant-based access mechanism in mMTC+, which has low access potency and high expenses of signaling. In [30], a strategy for massive random access is proposed that makes use of the nested characteristics of RM codes. Besides, the coded compressed sensing scheme has made extensive use of inner codebook construction techniques related to second-order RM sequences [31,32], i.e., RM sequences are utilized as inner codes for the CCS protocol, and the outer tree codes are employed for coupling messages for slotted transmissions. In [33], a shared patterned Reed-Muller (PRM) codebook that embeds zero patterns in the second-order RM codes according to a binary vector space partition principle is employed as the inner codebook for the coded compressed sensing protocol.

This paper is inspired by a slot-controlled CCS protocol that concatenates outer error-correction codes to a common PRM inner codebook [33]. We replace the inner decoder related to PRM with a proposed iterative list PRM projection algorithm. We then deduce the theoretically successful detection probabilities of the proposed algorithm and validate its correctness via numerical simulations. We finally assess the performance of the slot-controlled URA system with the proposed iterative list algorithm as the inner code detector. According to simulation results, we demonstrate that the schemes using the proposed detection can help improve the overall system’s performance.

1.1. Contributions and Arrangement

Here is a summary of our contributions of this article:

A shared PRM codebook that embeds zero patterns in the second-order RM codes according to a binary vector space partition principle is employed as the inner codebook for the coded compressed sensing protocol. On this basis, we propose an enhanced algorithm called the "list PRM projection algorithm" that uses a list of candidates to hinder error spreading in each layer detection.
As for the multi-sequence scenario, an iterative list PRM projection algorithm is proposed. More specifically, except for the user’s information during the current loop, we consider all signals as interference. We remove the interference in priority and then employ the proposed list projection algorithm to recover the PRM sequence. The PRM estimations are then inserted into the channel estimator to enhance precision. After that, the modified channel estimations are utilized in the subsequent iteration to improve PRM detection further. As a result, the proposed iterative list PRM projection algorithm offers significant advantages regarding the convergence rate.
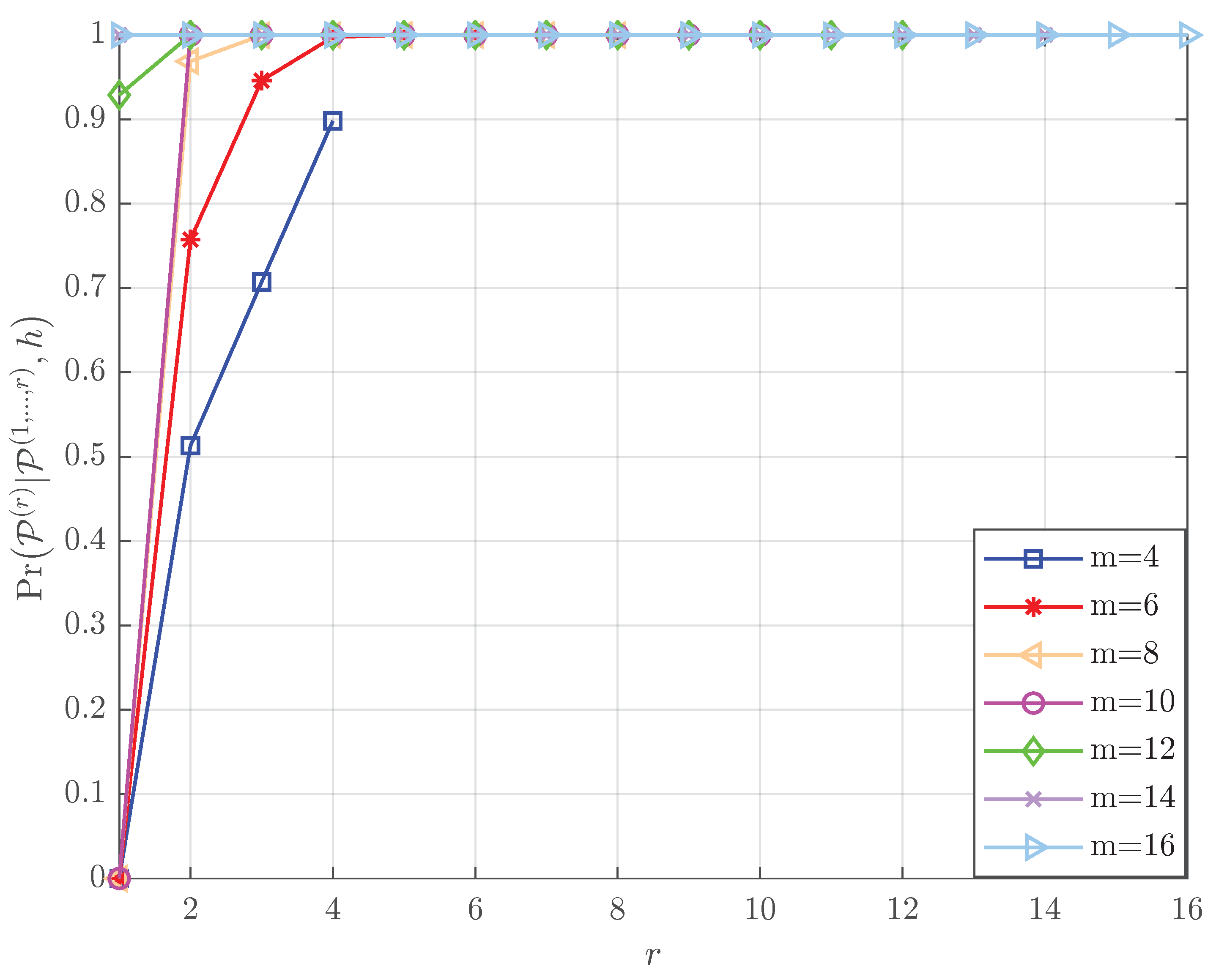
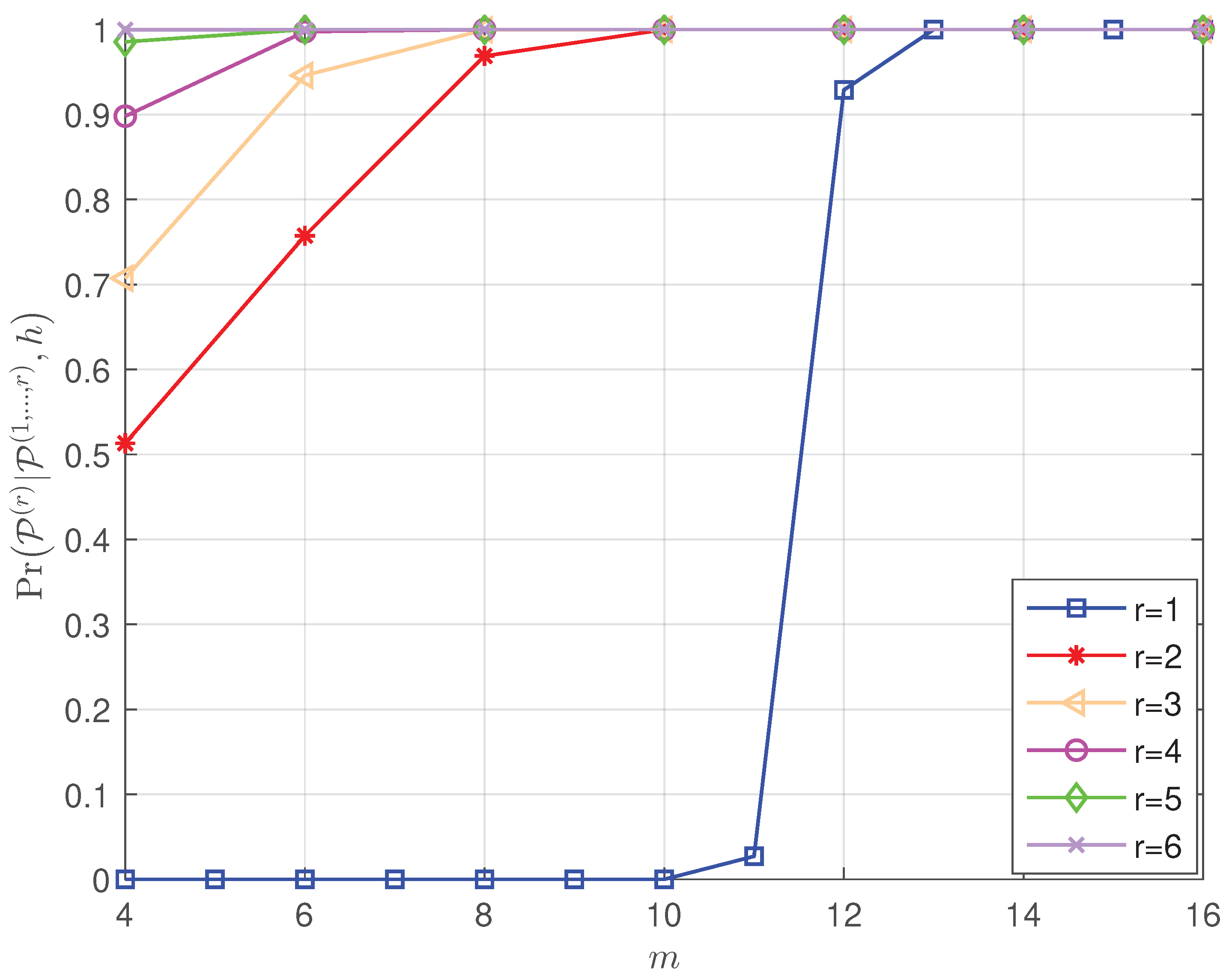
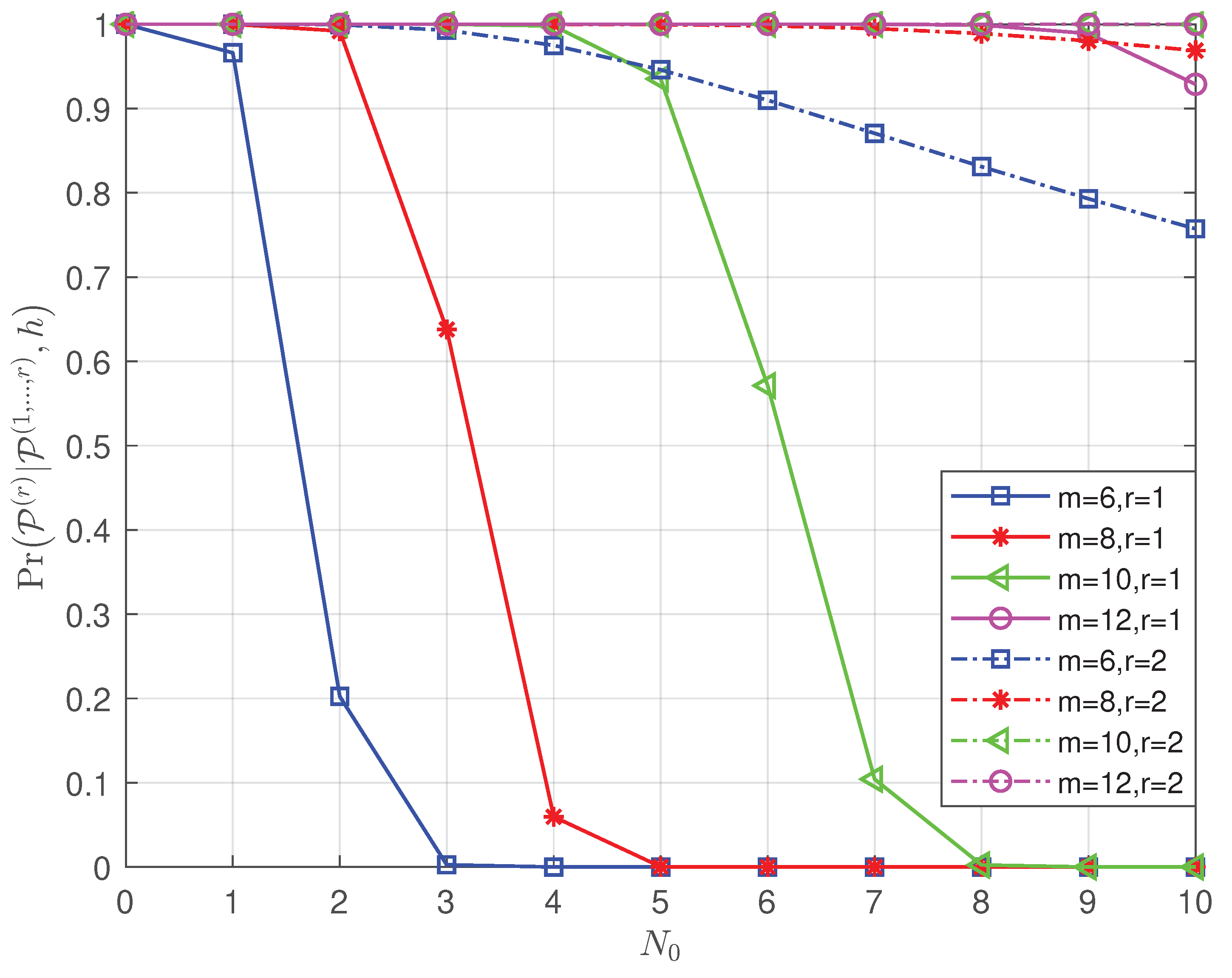
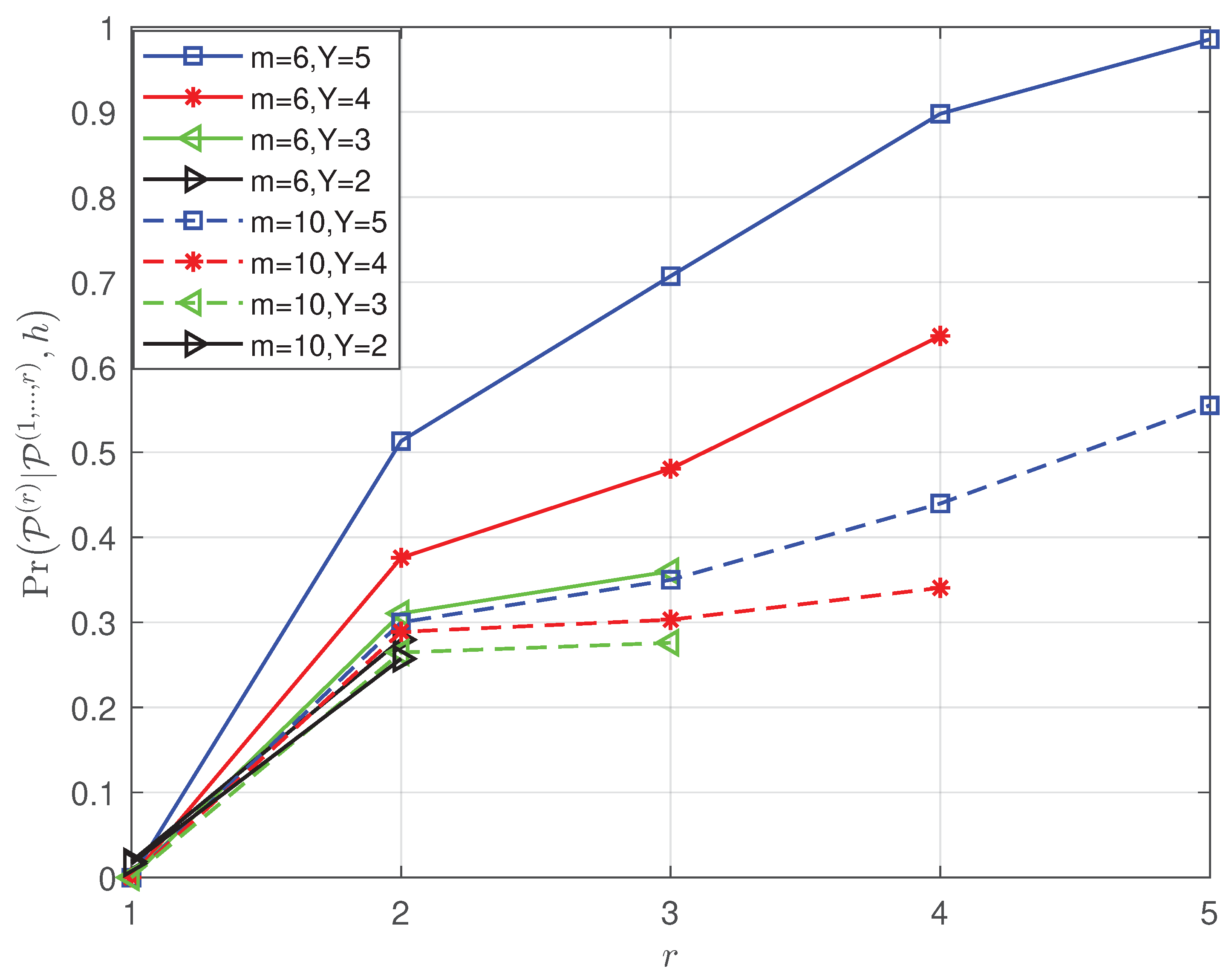
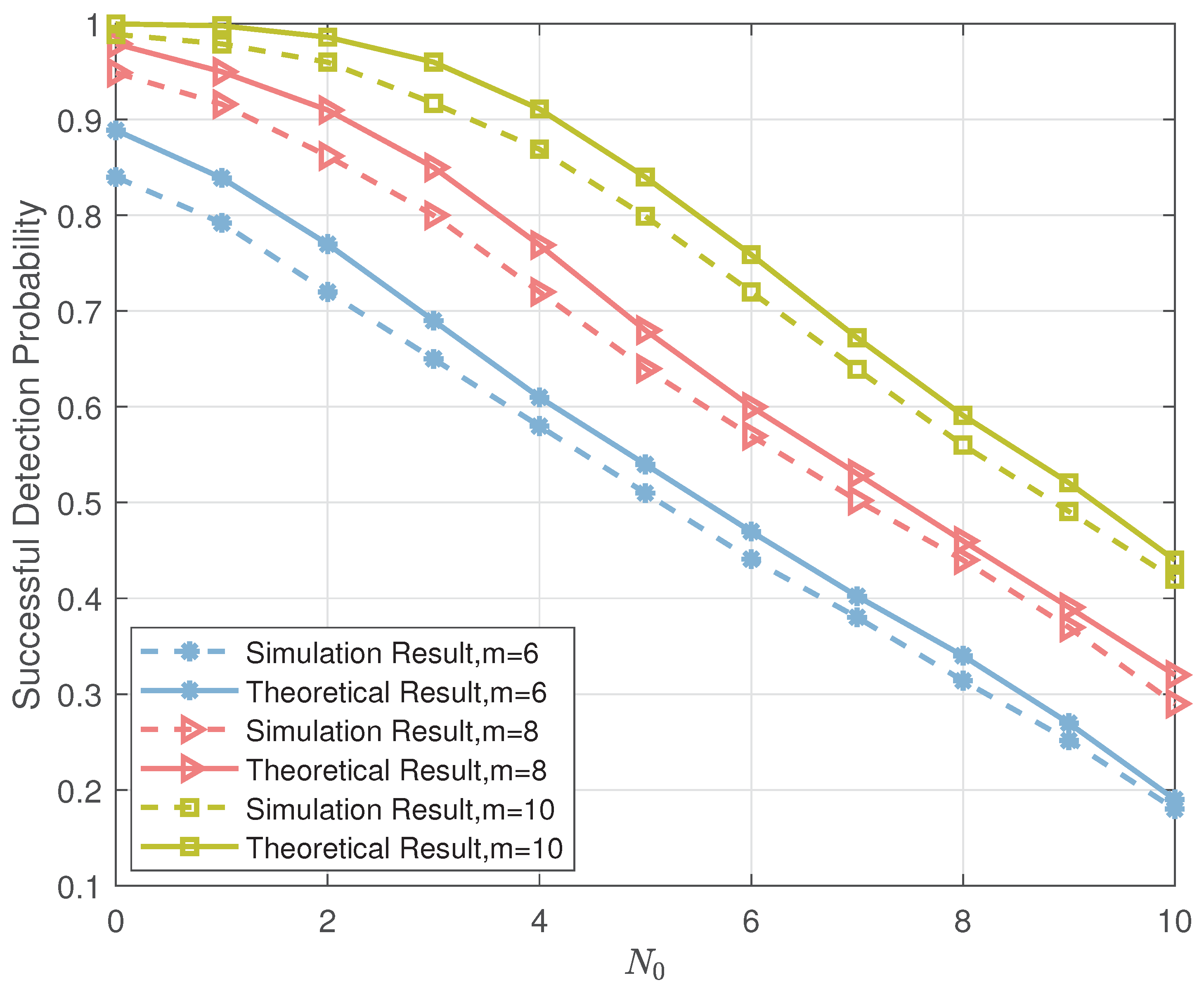
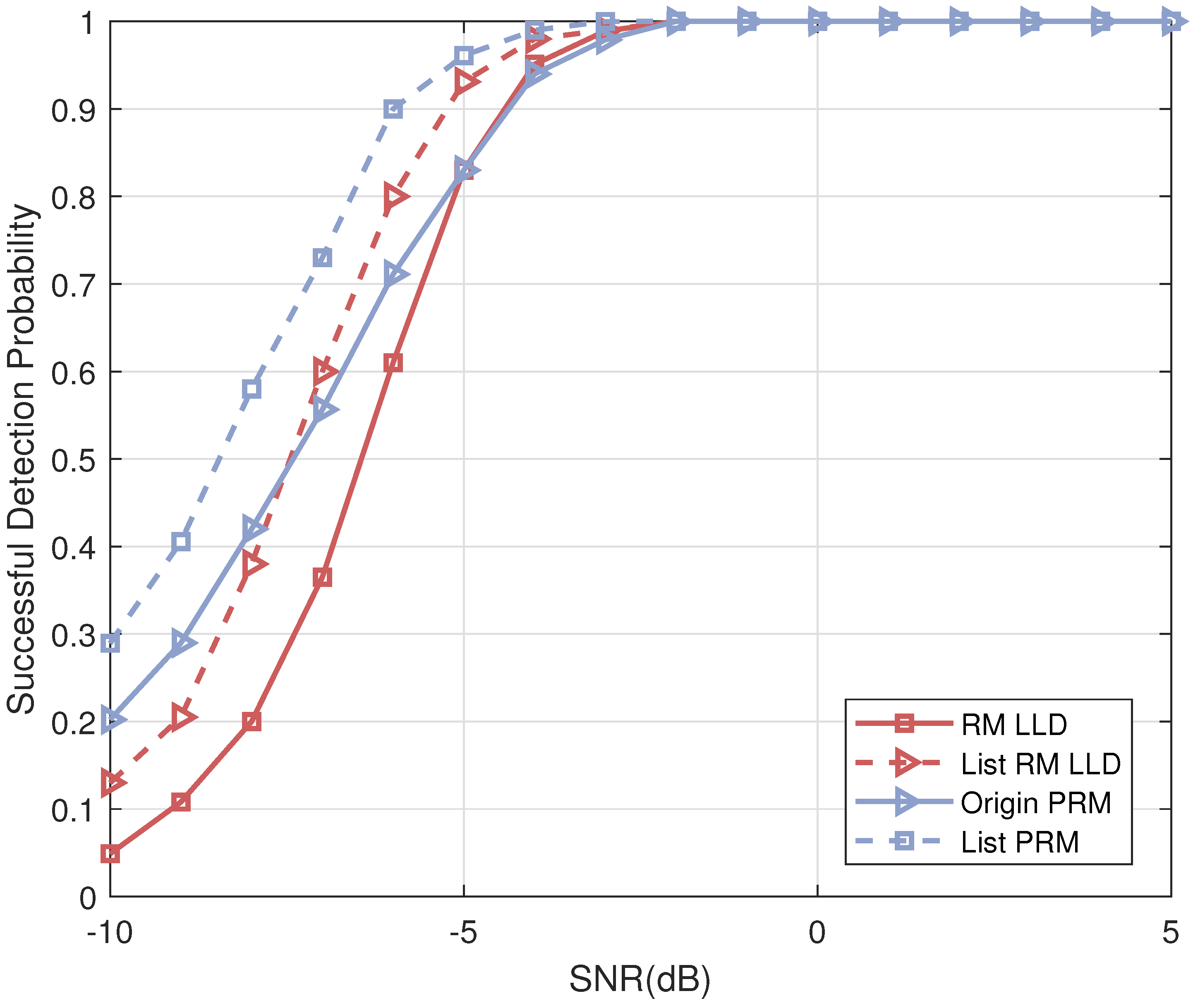
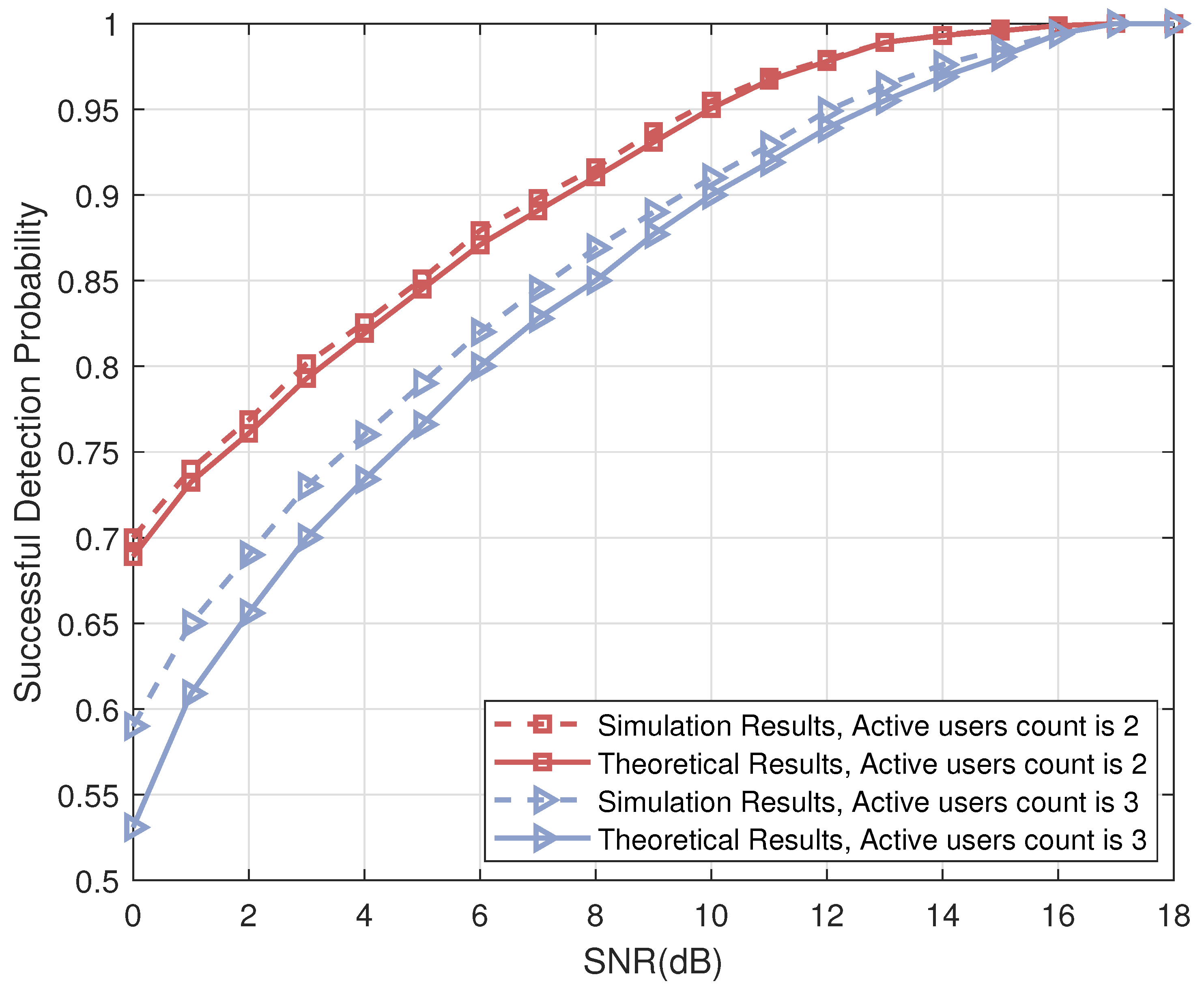
The theoretical successful detection probabilities of the proposed list projection and the iterative list projection algorithms are analyzed mathematically, and the results demonstrate that: (i) the factors that affect the efficiency of the list PRM projection algorithm are shown in the simulation results, which validate that the recovery reliability of the first few layers is crucial to the whole performance (see Figure 1); (ii) simulation results further explore the effect of the relation between rank $Υ$ and m for PRM sequence properties on the theoretical successful detection probability (see Figure 2, Figure 3 and Figure 4); (iii) we verified that the theoretical results are consistent with the simulation results (see Figure 5 and Figure 7).
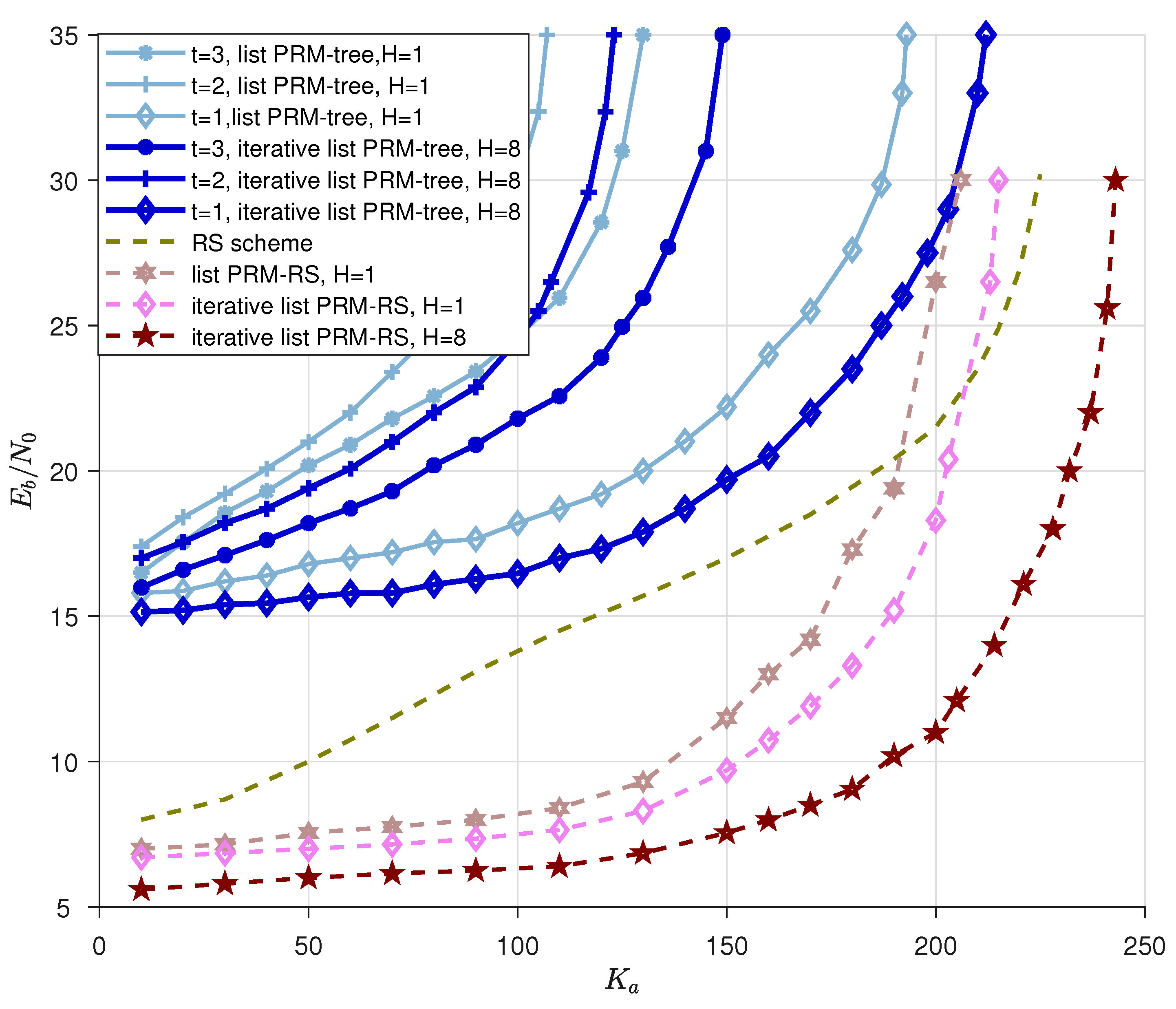
We substitute the inner decoder of the scheme [33] with the proposed iterative list PRM projection algorithm. Simulations of the quasi-static Rayleigh fading multiple-access channel (MAC) are performed numerically (see Figure 8), and we conclude the observations as follows: (i) the proposed scheme is superior to the OMP-based inner codes detection, i.e., the chance of successful recovery is significantly improved since the PRM detector and channel estimator share information, and the negative impacts can be further reduced by eliminating those sequences that are incorrectly detected in each operation; (ii) by increasing the count of candidates in the first few layers, we can boost the origin PRM projection algorithm’s performance, which further confirms the above proof of importance for ensuring the reliable recovery of the first few layers; (iii) the simulation results of the overall URA system confirm that the packetized URA with the proposed iterative list projection detection works better than benchmarks in terms of the number of active users it can support in each slot and the amount of energy needed per bit to meet an expected error probability.

Figure 1. Given m,

N_{0} = 10

and

Υ

, the variation of

\Pr (P^{(r)} | P^{(1, \dots, r - 1)}, h)

with

r

Figure 1. Given m,

N_{0} = 10

and

Υ

, the variation of

\Pr (P^{(r)} | P^{(1, \dots, r - 1)}, h)

with

r

Figure 2. Given

r

N_{0} = 10

and

Υ

, the variation of

\Pr (P^{(r)} | P^{(1, \dots, r - 1)}, h)

with m.

Figure 2. Given

r

N_{0} = 10

and

Υ

, the variation of

\Pr (P^{(r)} | P^{(1, \dots, r - 1)}, h)

with m.

Figure 3. Given

r

, m and

Υ

, the variation of

\Pr (P^{(r)} | P^{(1, \dots, r - 1)}, h)

with

N_{0}

Figure 3. Given

r

, m and

Υ

, the variation of

\Pr (P^{(r)} | P^{(1, \dots, r - 1)}, h)

with

N_{0}

Figure 4. Given

N_{0}

, m and

Υ

, the variation of

\Pr (P^{(r)} | P^{(1, \dots, r - 1)}, h)

with

r

Figure 4. Given

N_{0}

, m and

Υ

, the variation of

\Pr (P^{(r)} | P^{(1, \dots, r - 1)}, h)

with

r

Figure 5. The comparison of numerical simulation results and theoretical analysis results of list PRM projection algorithm.

Figure 6. The successful detection probability versus SNR for different schemes,

m = 8

Figure 6. The successful detection probability versus SNR for different schemes,

m = 8

Figure 7. The successful detection probability of Algorithm 1 versus SNR.

Figure 8. The simulations of energy efficiency are depicted. The simulations are listed as follows: list PRM-tree scheme for

t = 1, \dots, 3

from [33], iterative list PRM-tree scheme for

t = 1, \dots, 3

, Reed-Solomon scheme from [23], list PRM-RS scheme without iteration form [33], and iterative list PRM-RS schemes for

H = 1

and

H = 8

, respectively.

Figure 8. The simulations of energy efficiency are depicted. The simulations are listed as follows: list PRM-tree scheme for

t = 1, \dots, 3

from [33], iterative list PRM-tree scheme for

t = 1, \dots, 3

, Reed-Solomon scheme from [23], list PRM-RS scheme without iteration form [33], and iterative list PRM-RS schemes for

H = 1

and

H = 8

, respectively.

The rest of this paper is arranged as follows: in Section 2, we induce the system model and review the patterned Reed-Muller sequences as well as their projection algorithm. An enhanced list PRM projection algorithm and an iterative list PRM projection algorithm are proposed in Section 3. The theoretical probability of the algorithms proposed is derived in Section 4. The simulation results are presented in Section 5, and the conclusion of the paper is concluded in Section 6.

1.2. Conventions

It is stipulated that all vectors, whether complex or binary, will be column vectors. We employ

F_{2}^{m}

to present the finite (binary) field in this paper.

P_{m}

denotes the size of

m \times m

matrix.

P^{T}

stands for the transpose of matrix

P

and

P^{- T}

stands for the inverse transposed of matrix

P

. The superscript H stands for the conjugate transpose of a matrix. Vectors

0_{N}

and

1_{N}

are all-zero and all-one vectors of size

N \times 1

, respectively. We use

A = {[a_{i}]}_{i = 1}^{I}

to stand for the vector whose capacity is I, consisting of the components

a_{i}

(i = 1, \dots, I)

. The vectors

B_{1} \in C^{T_{1} \times 1}

and

B_{2} \in C^{T_{2} \times 1}

are added together to produce

B = [B_{1}; B_{2}] \in C^{(T_{1} + T_{2}) \times 1}

CN (0, I_{N})

stands for a complex standard normal random vector. The notation

x \sim N (μ, σ^{2})

stands for that x is a Gaussian random variable whose mean is

μ

and variance is

σ^{2}

, its probability density function (PDF) is written as

f_{N} (x; μ, σ^{2}) = \frac{1}{\sqrt{2 π σ^{2}}} exp (- \frac{{(x - μ)}^{2}}{2 σ^{2}}) .

while

x \sim CN (μ, σ^{2})

denotes that the random variable x follows circular symmetric complex Gaussian distribution with its PDF being

f_{C N} (x; μ, σ^{2}) = \frac{1}{π σ^{2}} exp (- \frac{{| x - μ |}^{2}}{σ^{2}}) .

2. System Model

Let us reconsider the system of CCS protocol. K prospective users exist in the URA model, and only

K_{a}

elements are engaged in accessing the system owing to the system’s occasional use. This case typically fulfills

K_{a} ≪ K

for the mMTC+ circumstance.

As for the transmitter of practical transmission, a B-bit message is carried by each active user as part of the set

{W_{1}, W_{2}, \dots, W_{K_{a}}}

for accessing the system. We let

N = 2^{B}

, and each message

W_{k}

(

1 \leq k \leq K_{a}

) is encoded into an

H_{N}

-length outer error-correction code, thus

W_{k} \in [N]

, where

[N] = \{1, \dots, N\}

. Furthermore, a length-

N = 2^{m}

sequence

C_{\hat{P}, B, I_{χ}}^{(k, n)}

represents an inner PRM code randomly picked from a shared codebook

Γ

that is sent by the k-th user within the n-th chunk, where

1 \leq n \leq H_{N}

. There is a one-to-one match between the sequence

C_{\hat{P}, B, I_{χ}}

and a partitioned message of length

B / H_{N}

. Using the slot-pattern-control rule from [33], we arrange

H_{N}

PRM sequences into

N_{T}

chunks, which leads to the system employing

T = N \cdot N_{T}

channel uses to operate a slotted-controlled transmission.

As for the receiver of the system, the outer decoder couples the divided information chunks after detecting codewords in each slot. The miss detection rate (MDR) and the false-alarm rate (FAR), which are denoted as

P_{e} ≜ \frac{1}{K_{a}} \sum_{k \in K_{a}} \Pr [W_{k} \notin \hat{D} (Y)]

and

P_{f} ≜ \Pr [\hat{D} (Y) {W_{k} | k \in K_{a}} \neq \emptyset]

(K_{a} = {1, \dots, K_{a}})

, respectively, are used as the main assessments for the performance evaluation from the standpoint of messages transmission.

The geometry properties of PRM codes and the decoder of the slot-controlled URA structure are presented roughly for the sake of clarity.

2.1. Patterned Reed-Muller Sequence

A new version of the Binary Subspace Chirp (BSSC) [34,35,36], which embeds zero patterns in the second-order RM codes according to the partition rule of the binary vector space, is proposed by reducing the subspace matrix

H_{χ}

I_{χ}

, where

χ \subseteq [m]

indicates all possible subsets of rank

Υ \in {1, 2, \dots, m}

under full dimension m.

The simplified sequence is denoted as patterned Reed-Muller (PRM) and can be writtern as follows

C_{\hat{P}, B, I_{χ}} (v) = \{\begin{matrix} \frac{1}{\sqrt{2^{Υ}}} i^{2 w^{T} {B |}_{1}^{Υ} + w^{T} \hat{P} w}, & if v = I_{χ} w + \tilde{I_{χ}} {B |}_{Υ + 1}^{m}, \\ 0, & otherwise, \end{matrix}

(1)

where

w \in F_{2}^{Υ}

, symmetric matrix

\hat{P}

and vector

B

are dominant parameters for RM

(Υ, 2)

, besides, sub-vector

{B |}_{Υ + 1}^{m}

indentifies the sequence of the last

(m - Υ)

-bit segment of the m-length vector

B

, and subspace

I_{χ}

is a matrix of size

(m \times Υ)

with column vectors

e_{χ (1)}, e_{χ (2)}, \dots, e_{χ (Υ)}

, where

e_{χ (r)}

is the unit vector with non-zero at the r-th position,

1 \leq r \leq Υ

. Similarly, matrix

\tilde{I_{χ}}

follows the same rule.

For the complex domain sequence, PRM codes have its geometry property : for any

z \in F_{2}^{m - Υ}

, the PRM sequence satisfies

E (I_{χ} e_{r}, \tilde{I_{χ}} z + I_{χ} {\hat{P}}_{r}) \cdot C_{\hat{P}, B, I_{χ}} = {(- 1)}^{B^{T} (e_{r}; 0^{m - Υ}) + {(B |_{Υ + 1}^{m})}^{T} z} \cdot C_{\hat{P}, B, I_{χ}},

(2)

where

{\hat{P}}_{r} = \hat{P} e_{r}

. According to (2), the PRM sequence has its specific projective property by letting

z = 0^{m - Υ}

λ_{P R M, ϖ}^{(r)} (0^{m - Υ}) \cdot C_{\hat{P}, B, I_{χ}} = \{\begin{matrix} C_{\hat{P}, B, I_{χ}}, & if ϖ = {(- 1)}^{B_{r};}, \\ 0, & if ϖ \neq {(- 1)}^{B_{r} .} \end{matrix}

(3)

where

λ_{P R M, ϖ}^{(r)} (0^{m - Υ}) = \frac{[I_{N} + ϖ \cdot E (I_{χ} e_{r}, I_{χ} {\hat{P}}_{r})]}{2},

(4)

is a projection operator for PRM sequences.

2.2. Detection Algorithm of Multi-PRM Sequence

The signal received in the receiver for the n-th slot is expressed as

y_{n} = \sum_{k = 1}^{K_{a}} h_{k, n} \cdot x_{k, n} + n_{n},

(5)

where

h_{k, n} \sim C N (0, 1)

represents a constant channel coefficient that is supposed to be stable for the duration of a user’s transmission between the active user k and the access point (AP) in n-th chunk. while,

n_{n} \sim C N (0, I_{N})

is the complex additive white Gaussian noise (AWGN). The detection algorithm suggested in [33] is carried out by the receiver. The efficiency of the method in [33] can be improved using a modified version based on list decoding, which will be described in the next part.

3. Iterative List PRM Projection Algorithm-based Inner-Code Detector

Our proposed detection scheme for inner codes is described in this section. In addition to the modified list PRM projection detection adopted for a single sequence, we propose an iterative list PRM projection algorithm implemented at the AP for multiple sequences.

3.1. List PRM Projection Algorithm

The received signal is

y = C_{\hat{P}, B, I_{χ}} + n

and the enhanced algorithm based on the detection proposed in [33] is executed for the single-user scenario. Specifically, in this single-user scenario, we propose a modified algorithm that utilizes a candidate-saving technique during each layer of detection to boost performance. The Algorithm 1’s particular processes are outlined in the following.

Three elements

\{I_{χ}, \hat{P}, B\}

of the PRM sequence need to be recovered, and the subspace matrix

I_{χ}

should be retrieved first. Since the rank is unknown, we go over every conceivable rank in

1 \leq Υ \leq m

and set aside L potential subspace matrices for each one (in Lines 3 and 4): after we calculate

F_{sum} (f_{χ_{(Υ)}}) = \sum_{j = 1}^{2^{(m - Υ)}} |y^{H} E (0, f_{χ_{(Υ)}}^{(j)}) y|

for every

f_{χ_{(Υ)}}^{(j)} \in F_{2}^{m}

, employ the relation of

{[f_{χ_{(Υ)}}^{(j)}]}_{j = 1}^{2^{(m - Υ)}} = span ({\tilde{I}}_{χ_{(Υ)}})

and seek the biggest

2^{(m - Υ)}

estimations of

F_{sum}

, the set

{[f_{χ_{(Υ)}}^{(j)}]}_{j = 1}^{2^{(m - Υ)}}

and the subspace matrix

{\tilde{I}}_{χ_{(Υ)}}

can be identified. We finally keep L candidates as

I_{χ_{(Υ)}} = \{{[{\tilde{I}}_{χ_{(Υ)}}^{(l)}]}_{l = 1}^{L}, Υ\}

The recovery of remaining elements

\{\hat{P}, B\}

depends on the subspaces in

I_{χ_{(Υ)}}

. In the following, we will decode the vector

\hat{P_{l}}

and bit

B_{l}

in a layer-by-layer manner. Furthermore, we will keep H parent candidates for the next layer at the end of each iteration. We initialize the corresponding parameters in Line 6: we denote the list of updated symmetric matrix and vector (under

{\tilde{I}}_{χ_{(Υ)}}^{(l)}

) as

H_{l}

during each layer, and update the list of search space as

{[F_{l, 1}^{(h)}]}_{h = 1}^{H}

using (6). During the iteration, as for each candidates derived from the previous layers, we get a list of H candidates for the current layer (in Lines 8-11): we first update the search space from the previous knowledge using (6) (in Lines 6 and 19). The detected layers notated as

R

(

R = 1, \dots, r - 1

) and utilize the recovered vector

{\hat{P}}_{r, l}^{(h)}

(

{\hat{P}}_{r, l}^{(h)}

is h-th candidates for

r

-th column vector of

\hat{P}

under subspace

I_{χ (Υ)}^{(l)}

) to fill out the symmetric matrix, thus, the matrix under the

r

-th layer can be represented as

{\underset{̲}{\hat{P}}}_{R}^{(h)}

. On this basis, the search space is limited to

F_{l, r}^{(h)} = \{f \in F_{2}^{m} ∣ f_{i} = {\underset{̲}{\hat{P}}}_{R}^{(h)} (i, r) for all i \in R\},

(6)

where the value of

{\underset{̲}{\hat{P}}}_{R}^{(h)} (i, r)

refers to the i-th row and

r

-th column of matrix

{\underset{̲}{\hat{P}}}_{R}^{(h)}

. Next, we derive H paths for each candidates of previous decoding (in Lines 9 and 10): for all vectors

f \in F_{l, r}^{(h)}

, we compute

F_{sum} (f) = \sum_{j = 1}^{2^{(m - Υ)}} |y^{H} E (I_{χ_{(Υ)}}^{(l)} \cdot e_{r}, f) y|

to search H largest

F_{sum}

, the corresponding H sets of

{[f_{j}]}_{j = 1}^{2^{(m - Υ)}}

is derived. Based on

{[f_{j}]}_{j = 1}^{2^{(m - Υ)}} = span ({\tilde{I}}_{χ_{(Υ)}}^{(l)}) + I_{χ_{(Υ)}}^{(l)} {\hat{P}}_{r, l} e_{r}

, vector

P_{r, l}^{(h)}

can be obtained. Once

2^{H}

iterations are complete, we finally get the

{[{\hat{P}}_{r, l}^{(h)}]}_{h = 1}^{H}

within

2^{H}

possibles.

As for the detection of

B_{l}^{(h)}

(in Lines 14-17), we make

z^{(m - Υ)} = 0^{m - Υ}

and compute

F_{r} (f) = y^{H} E (I_{χ_{(Υ)}}^{(l)} \cdot e_{r}, I_{χ_{(Υ)}}^{(l)} {\hat{P}}_{r, l} e_{r}) y

, then we obtain

sign (F_{r} (f)) = {(- 1)}^{B_{r, l}}

. In light of this,

B_{r}

can be obtained as follows

B_{r, l} = \{\begin{matrix} 1, & if sign (F_{r} (f)) = - 1; \\ 0, & if sign (F_{r} (f)) = 1 . \end{matrix}

(7)

Line 19 updates all parameters for the next layer detection. In Line 23, after conducting all iterations, we evaluate each rank’s

(L \times H)

results and retain the optimal results. The final results is selected at the end of the procedure for all ranks (in Line 25).

3.2. Iterative List PRM projection Algorithm

We consider a scenario where simultaneous presence of multiple active users in a system. As described below, we will detect multiple PRM sequences iteratively. We begin by introducing some notations in this section: it is possible to detect a maximum of

K_{0}

users. We denote the notation

{\hat{C}}_{\hat{P}, B, I_{χ}}^{(s, k)}

as the detected PRM sequence, and

{\hat{h}}_{k}^{(s)}

represents the channel estimation. Both notations indicate the case under the k-th user and during the i-th iteration (

1 \leq s \leq S_{m a x}

). The particular processes of Algorithm 2 are outlined in the following.

Firstly, the PRM sequence and the channel coefficient are initialized as

{\hat{C}}_{\hat{P}, B, I_{χ}}^{(0, k)} = 0^{N}

and

{\hat{h}}_{k}^{(0)} = 0

for

s = 0

, respectively (in Line 1). we then denote an interference for the user k during the s-th iteration as

Λ_{k}^{(s)} = \sum_{k^{'} = 1 a n d k^{'} \neq k}^{K_{0}} {\hat{h}}_{k^{'}}^{(s^{'})} \cdot {\hat{C}}_{\hat{P}, B, I_{χ}}^{(s^{'}, k^{'})},

(9)

where

\{\begin{matrix} s^{'} = s, & if 1 \leq k^{'} \leq k - 1, \\ s^{'} = s - 1, & if k + 1 \leq k^{'} \leq K_{0} . \end{matrix}

(10)

Then, in order to retrieve a PRM sequence

{\hat{C}}_{\hat{P}, B, I_{χ}}^{(s, k)}

, we feed the signal (

y - Λ_{k}^{(s)}

) into Algorithm 1.

Next, when detecting each user’s PRM sequence, the detected sequences are inserted into the linear least square channel estimator to improve their accuracy further, specified as (8) in Algorithm 2. Due to the exchange of information between the sequence detector and the channel estimator, the effectiveness gradually improves, and it terminates once the results have converged or the maximum number of iterations have been reached.

4. Performance Analysis

4.1. Successful Recovery Probability of the List PRM Projection Algorithm

For detecting a single PRM sequence, Algorithm 1 recovers the column vectors of the matrix

\hat{P}

layer by layer. In this section, we will derive the probability of successful recovery of each layer element

{\hat{P}}_{r}

for

1 \leq r \leq m

. The corresponding conclusions are summarized in Lemma 1 as well as Theorem 1.

Lemma 1.

Suppose that Algorithm 1’s the input signal is

y = h C_{\hat{P}, B, I_{χ}} + n

, where

h \sim C N (0, 1)

is the channel coefficient, and

n \sim C N (0, I_{N})

denotes the complex additive white Gaussian noise (AWGN). The notation

P^{(r)} (1 \leq r \leq m)

represents the event “the vector

{\hat{P}}_{r}

is recovered successful” and the notation

P^{(1, \dots, r - 1)}

denotes the event " the vectors

{\hat{P}}_{1}, \dots, {\hat{P}}_{r - 1}

are correctly recovered". On this basis, if h and

P^{(1, \dots, r - 1)}

is given, then for any

z \in F_{2}^{m - Υ}

\Pr (P^{(r)} | P^{(1, \dots, r - 1)}, h)

can be expressed as

\begin{matrix} \begin{matrix} \Pr (P^{(r)} | P^{(1, \dots, r - 1)}, h) \\ \geq & {[Q (- \frac{2^{Υ} {| h |}^{2} \cdot {(- 1)}^{B_{r} + {(B |_{Υ + 1}^{m})}^{T} z}}{\sqrt{2} σ_{F, r}}) \cdot Q (- \frac{2^{Υ} {| h |}^{2} \cdot {(- 1)}^{B_{r} + {(B |_{Υ + 1}^{m})}^{T} z}}{2 σ_{F, r}})]}^{2^{(Υ - r + 1)} - 1} . \end{matrix} \end{matrix}

(11)

In (11), function

Q (\cdot)

Q (x) = \int_{x}^{\infty} \frac{1}{\sqrt{2 π}} exp (- \frac{t^{2}}{2}) d t

, and the variance

σ_{F, r}^{2}

is defined as

σ_{F, r}^{2} = 2^{m - 1} [{2 | h |}^{2} \frac{N_{0}}{2^{r - 1}} + {(\frac{N_{0}}{2^{r - 1}})}^{2}] .

(12)

Theorem 1.

Taking into account the channel coefficients h and the results of (11), the average probability of successful detection for Algorithm 1 can be calculated as

P_{s u c c} = \int_{h} f_{CN} (h; 0, 1) \cdot \overset{ˇ}{P} (Υ, N_{0} | h) d h,

(13)

where

\overset{ˇ}{P} (Υ, N_{0} | h) = \prod_{r = 1}^{Υ} \Pr (P^{(r)} | P^{(1, \dots, r - 1)}, h)

and

f_{CN} (h; 0, 1) = \frac{1}{π} exp (- {| μ |}^{2})

Proof

(Proof). We assume that the subspace matrix

I_{χ}

is decoded correctly and

H = 1

. Define a concept

F_{S} (f_{r})

related to

f_{r} \in F_{2}^{m}

\begin{matrix} \begin{matrix} F_{S} (f_{r}) & = {(h C_{\hat{P}, B, I_{χ}} + n)}^{H} \cdot E (I_{χ} e_{r}, f_{r}) \cdot (h C_{\hat{P}, B, I_{χ}} + n) \\ = \underset{F_{A} (f_{r})}{\underset{︸}{{| h |}^{2} C_{\hat{P}, B, I_{χ}}^{H} E (I_{χ} e_{r}, f_{r}) C_{\hat{P}, B, I_{χ}}}} + \underset{Z_{1} (f_{r})}{\underset{︸}{n^{H} E (I_{χ} e_{r}, f_{r}) n}} + \underset{Z_{2} (f_{r})}{\underset{︸}{h [C_{\hat{P}, B, I_{χ}}^{H} E (I_{χ} e_{r}, f_{r}) n + n^{H} E (I_{χ} e_{r}, f_{r}) C_{\hat{P}, B, I_{χ}}]}}, \end{matrix} \end{matrix}

(14)

According to (14),

Z_{1} (f_{r})

and

Z_{2} (f_{r})

are the sources of interference, and we use

Z (f_{r}) = Z_{1} (f_{r}) + Z_{2} (f_{r})

to conclude all interferences. The following discussion will demonstrate Lemma 1 through mathematical induction.

(1)

when

r = 1

: according to Algorithm 1, the event

P^{(1)}

occurring is described as

\sum_{z \in F_{2}^{m - Υ}} |F (\tilde{I_{χ}} z + {\tilde{p}}_{χ, 1})| > \sum_{z \in F_{2}^{m - Υ}} |F (\tilde{I_{χ}} z + {\bar{\bar{p}}}_{χ, 1})|

(we omit the subscript

S

and record it as

F (\cdot)

in this section), where

{\tilde{p}}_{χ, 1} = I_{χ} \hat{P} e_{1}

, and symbol

{\bar{\bar{p}}}_{χ, 1}

denotes any possible vector that is different from

{\tilde{p}}_{χ, 1}

. It is known that the vector

{\bar{\bar{p}}}_{χ, 1}

has a total of

(2^{Υ} - 1)

possibilities, then we denote the probability of the event

P^{(1)}

as follows:

\begin{matrix} \begin{matrix} \Pr (P^{(1)} | h) & = \Pr (\sum_{z \in F_{2}^{m - Υ}} |F (\tilde{I_{χ}} z + {\tilde{p}}_{χ, 1})| > max \sum_{z \in F_{2}^{m - Υ}} |F (\tilde{I_{χ}} z + {\bar{\bar{p}}}_{χ, 1})|) \\ = \prod_{{[{\bar{\bar{p}}}_{χ, 1}^{(j)}]}_{j = 1}^{2^{Υ - 1}}} \Pr (\sum_{z \in F_{2}^{m - Υ}} |F (\tilde{I_{χ}} z + {\tilde{p}}_{χ, 1})| > \sum_{z \in F_{2}^{m - Υ}} |F (\tilde{I_{χ}} z + {\bar{\bar{p}}}_{χ, 1}^{(j)})|) . \end{matrix} \end{matrix}

(15)

In (15),

{[{\bar{\bar{p}}}_{χ, 1}^{(j)}]}_{j = 1}^{2^{Υ - 1}}

is the set of all possible vectors except

{\tilde{p}}_{χ, 1}

. Since each term within the summation function obeys the same distribution, calculating (15) is equivalent to compute its approximate probability as

\begin{matrix} \begin{matrix} \prod_{{[{\bar{\bar{p}}}_{χ, 1}^{(j)}]}_{j = 1}^{2^{Υ - 1}}} \Pr (|F (\tilde{I_{χ}} z + {\tilde{p}}_{χ, 1})| > |F (\tilde{I_{χ}} z + {\bar{\bar{p}}}_{χ, 1}^{(j)})|) . \end{matrix} \end{matrix}

(16)

For convenience, we let notation

{\tilde{Ξ}}_{χ, z}^{(1)} = \tilde{I_{χ}} z + {\tilde{p}}_{χ, 1}

and

{\bar{\bar{Ξ}}}_{χ, z}^{(1)} = \tilde{I_{χ}} z + {\bar{\bar{p}}}_{χ, 1}

. Since the

(2^{Υ} - 1)

events in (16) are independent of one another, we calculate the probability of one event first:

\begin{matrix} \begin{matrix} \Pr (|F (\tilde{I_{χ}} z + {\tilde{p}}_{χ, 1})| > |F (\tilde{I_{χ}} z + {\bar{\bar{p}}}_{χ, 1})|) \\ \overset{(a)}{=} & \Pr (|{| h |}^{2} C_{\hat{P}, B, I_{χ}}^{H} E (I_{χ} e_{1}, {\tilde{Ξ}}_{χ, z}^{(1)}) C_{\hat{P}, B, I_{χ}} + Z ({\tilde{Ξ}}_{χ, z}^{(1)})| > |Z ({\bar{\bar{Ξ}}}_{χ, z}^{(1)})|) \\ \overset{(b)}{=} & \Pr ({| h |}^{2} C_{\hat{P}, B, I_{χ}}^{H} E (I_{χ} e_{1}, {\tilde{Ξ}}_{χ, z}^{(1)}) C_{\hat{P}, B, I_{χ}} + Z ({\tilde{Ξ}}_{χ, z}^{(1)}) > |Z ({\bar{\bar{Ξ}}}_{χ, z}^{(1)})|) \\ \cdot \Pr ({| h |}^{2} C_{\hat{P}, B, I_{χ}}^{H} E (I_{χ} e_{1}, {\tilde{Ξ}}_{χ, z}^{(1)}) C_{\hat{P}, B, I_{χ}} + Z ({\tilde{Ξ}}_{χ, z}^{(1)}) > 0) \\ + \Pr (- {| h |}^{2} C_{\hat{P}, B, I_{χ}}^{H} E (I_{χ} e_{1}, {\tilde{Ξ}}_{χ, z}^{(1)}) C_{\hat{P}, B, I_{χ}} - Z ({\tilde{Ξ}}_{χ, z}^{(1)}) > |Z ({\bar{\bar{Ξ}}}_{χ, z}^{(1)})|) \\ \cdot \Pr ({| h |}^{2} C_{\hat{P}, B, I_{χ}}^{H} E (I_{χ} e_{1}, {\tilde{Ξ}}_{χ, z}^{(1)}) C_{\hat{P}, B, I_{χ}} + Z ({\tilde{Ξ}}_{χ, z}^{(1)}) < 0) \\ \overset{(c)}{\geq} & \Pr ({| h |}^{2} C_{\hat{P}, B, I_{χ}}^{H} E (I_{χ} e_{1}, {\tilde{Ξ}}_{χ, z}^{(1)}) C_{\hat{P}, B, I_{χ}} + Z ({\tilde{Ξ}}_{χ, z}^{(1)}) > |Z ({\bar{\bar{Ξ}}}_{χ, z}^{(1)})|) \\ \cdot \Pr ({| h |}^{2} C_{\hat{P}, B, I_{χ}}^{H} E (I_{χ} e_{1}, {\tilde{Ξ}}_{χ, z}^{(1)}) C_{\hat{P}, B, I_{χ}} + Z ({\tilde{Ξ}}_{χ, z}^{(1)}) > 0), \end{matrix} \end{matrix}

(17)

where the equal sign

(a)

is based on

C_{\hat{P}, B, I_{χ}}^{H} E (I_{χ} e_{1}, {\bar{\bar{Ξ}}}_{χ, z}^{(1)}) C_{\hat{P}, B, I_{χ}} = 0

(b)

and

(c)

are obtained according to the following equations:

\begin{matrix} \begin{matrix} \Pr (| A | \geq | B |) = & \Pr (A > | B |) \Pr (A > 0) + \Pr (- A > | B |) \Pr (A < 0) \\ \geq & \Pr (A > | B |) \Pr (A > 0), \end{matrix} \end{matrix}

(18)

and

| | A | - | B | | \leq | A \pm B | \leq | A | + | B |

To calculate the two probabilities of the result of (17), it is necessary to study the distribution of the variables

{| h |}^{2} C_{\hat{P}, B, I_{χ}}^{H} E (I_{χ} e_{1}, {\tilde{Ξ}}_{χ, z}^{(1)}) C_{\hat{P}, B, I_{χ}}

Z ({\tilde{Ξ}}_{χ, z}^{(1)})

and

Z ({\bar{\bar{Ξ}}}_{χ, z}^{(1)})

respectively. We prioritize the study of

{| h |}^{2} C_{\hat{P}, B, I_{χ}}^{H} E (I_{χ} e_{1}, {\tilde{Ξ}}_{χ, z}^{(1)}) C_{\hat{P}, B, I_{χ}}

: we omit the factor

1 / 2^{r}

for the representation of

C_{\hat{P}, B, I_{χ}}

and denote

F_{A} ({\tilde{Ξ}}_{χ, z}^{(1)})

as follows

\begin{matrix} \begin{matrix} F_{A} ({\tilde{Ξ}}_{χ, z}^{(1)}) & = {| h |}^{2} C_{\hat{P}, B, I_{χ}}^{H} E (I_{χ} e_{1}, {\tilde{Ξ}}_{χ, z}^{(1)}) C_{\hat{P}, B, I_{χ}} \\ = {| h |}^{2} \cdot i^{{(I_{χ} e_{1})}^{T} \cdot {\tilde{Ξ}}_{χ, z}^{(1)}} \sum_{w \in F_{2}^{m}} \bar{C_{\hat{P}, B, I_{χ}} (w + I_{χ} e_{1})} \cdot {(- 1)}^{w^{T} \cdot {\tilde{Ξ}}_{χ, z}^{(1)}} \cdot C_{\hat{P}, B, I_{χ}} (w) \\ = {| h |}^{2} \cdot \sum_{w \in F_{2}^{m}} i^{2 {({\hat{P}}_{1}; 0)}^{T} \cdot Q^{- 1} w + P_{1, 1} + 2 B^{T} (e_{1}; 0)} \cdot i^{{(I_{χ} e_{1})}^{T} \cdot {\tilde{Ξ}}_{χ, z}^{(1)}} \cdot {(- 1)}^{w^{T} \cdot {\tilde{Ξ}}_{χ, z}^{(1)}} \\ \cdot ϕ [B, Q^{- 1} w + (e_{1}; 0), Υ] \cdot ϕ [B, Q^{- 1} w, Υ] \\ = {| h |}^{2} \cdot i^{2 B^{T} (e_{1}; 0) + P_{1, 1}} \sum_{w \in F_{2}^{m}} i^{2 {({\hat{P}}_{1}; 0)}^{T} \cdot Q^{- 1} w + 2 w^{T} \cdot {\tilde{Ξ}}_{χ, z}^{(1)} + {(I_{χ} e_{1})}^{T} \cdot {\tilde{Ξ}}_{χ, z}^{(1)}} \\ \cdot ϕ [B, Q^{- 1} w + (e_{1}; 0), Υ] \cdot ϕ [B, Q^{- 1} w, Υ], \end{matrix} \end{matrix}

(19)

where

P_{1, 1} = e_{1}^{T} P e_{1} = e_{1}^{T} P_{1}

and

ϕ (B, Q^{- 1} w, Υ) = 1

in the case of

{B |}_{Υ + 1}^{m} = (Q^{- 1} w) |_{Υ + 1}^{m}

. We then substitute

{\tilde{Ξ}}_{χ, z}^{(1)} = \tilde{I_{χ}} z + {\tilde{p}}_{χ, 1}

in (19), and the equation expression becomes:

\begin{matrix} \begin{matrix} F_{A} ({\tilde{Ξ}}_{χ, z}^{(1)}) = & F_{A} (\tilde{I_{χ}} z + {\tilde{p}}_{χ, 1}) \\ = & {| h |}^{2} \cdot i^{2 B^{T} (e_{1}; 0) + 2 P_{1, 1}} \cdot \sum_{w \in F_{2}^{m}} i^{2 {(\tilde{I_{χ}} z)}^{T} w} \cdot ϕ [B, Q^{- 1} w + (e_{1}; 0), Υ] \cdot ϕ [B, Q^{- 1} w, Υ] \\ = & {| h |}^{2} \cdot i^{2 B^{T} (e_{1}; 0) + 2 P_{1, 1}} \cdot \sum_{w \in F_{2}^{m}} i^{2 {(B |_{Υ + 1}^{m})}^{T} z} \\ = & 2^{Υ} \cdot {| h |}^{2} {(- 1)}^{B_{1} + {(B |_{Υ + 1}^{m})}^{T} z}, \end{matrix} \end{matrix}

(20)

where

B_{1} = e_{1}^{T} B

and

z \in F_{2}^{m - Υ}

. To sum up,

F_{A} ({\tilde{Ξ}}_{χ, z}^{(1)})

takes the value of

2^{Υ} \cdot {| h |}^{2} \cdot {(- 1)}^{B_{1} + {(B |_{Υ + 1}^{m})}^{T} z}

if and only if

{\tilde{Ξ}}_{χ, z}^{(1)} = \tilde{I_{χ}} z + {\tilde{p}}_{χ, 1}

Next, we calculate the distribution of

Z ({\tilde{Ξ}}_{χ, z}^{(1)})

: we expand

Z ({\tilde{Ξ}}_{χ, z}^{(1)})

into two parts:

\begin{matrix} \begin{matrix} Z_{1} ({\tilde{Ξ}}_{χ, z}^{(1)}) & = n_{1}^{H} E (I_{χ} e_{1}, \tilde{I_{χ}} z + {\tilde{p}}_{χ, 1}) n_{1} \\ = i^{{(I_{χ} e_{1})}^{T} \cdot \sum_{z \in F_{2}^{m - r}} (\tilde{I_{χ}} z + I_{χ} {\hat{P}}_{1})} \sum_{w \in F_{2}^{m}} \bar{n_{1} (w + I_{χ} e_{1})} \cdot {(- 1)}^{w^{T} \cdot \sum_{z \in F_{2}^{m - r}} (\tilde{I_{χ}} z + I_{χ} {\hat{P}}_{1})} \cdot n (w) . \end{matrix} \end{matrix}

(21)

Therefore, the variance of

Z_{1} ({\tilde{Ξ}}_{χ, z}^{(1)})

2^{m} \cdot N_{0}^{2}

. Following the same rule,

Z_{2}

turns into

\begin{matrix} \begin{matrix} Z_{2} ({\tilde{Ξ}}_{χ, z}^{(1)}) = & h \cdot [C_{\hat{P}, B, I_{χ}}^{H} E (I_{χ} e_{1}, \tilde{I_{χ}} z + {\tilde{p}}_{χ, 1}) n + n^{H} E (I_{χ} e_{1}, \tilde{I_{χ}} z + {\tilde{p}}_{χ, 1}) C_{\hat{P}, B, I_{χ}}] \\ = & h \cdot i^{{(I_{χ} e_{1})}^{T} \cdot (\tilde{I_{χ}} z + I_{χ} {\hat{P}}_{1})} \sum_{w \in F_{2}^{m}} \bar{C_{\hat{P}, B, I_{χ}} (w + I_{χ} e_{1})} \cdot {(- 1)}^{w^{T} \cdot (\tilde{I_{χ}} z + I_{χ} {\hat{P}}_{1})} \cdot n (w) \\ + & h \cdot i^{{(I_{χ} e_{1})}^{T} \cdot (\tilde{I_{χ}} z + I_{χ} {\hat{P}}_{1})} \sum_{w \in F_{2}^{m}} \bar{n (w + I_{χ} e_{1})} \cdot {(- 1)}^{w^{T} \cdot (\tilde{I_{χ}} z + I_{χ} {\hat{P}}_{1})} \cdot C_{\hat{P}, B, I_{χ}} (w) . \end{matrix} \end{matrix}

(22)

According to (22), the mean of variable

Z_{2} ({\tilde{Ξ}}_{χ, z}^{(1)})

is 0 and the variance is

2 \cdot 2^{m} {| h |}^{2} N_{0}

. We denote the notation

σ_{F, 1}^{2} = 2^{m - 1} ({2 | h |}^{2} N_{0} + N_{0}^{2})

. Since the distribution of

Z ({\bar{\bar{Ξ}}}_{χ, z}^{(1)})

is the same with

Z ({\tilde{Ξ}}_{χ, z}^{(1)})

, we have

Z ({\tilde{Ξ}}_{χ, z}^{(1)}) \sim CN (0, 2 σ_{F, 1}^{2})

Z ({\bar{\bar{Ξ}}}_{χ, z}^{(1)}) \sim CN (0, 2 σ_{F, 1}^{2})

and

F_{A} ({\tilde{Ξ}}_{χ, z}^{(1)}) + Z ({\tilde{Ξ}}_{χ, z}^{(1)}) \sim CN (2^{Υ} \cdot {| h |}^{2} \cdot {(- 1)}^{B_{1} + {(B |_{Υ + 1}^{m})}^{T} z}, 2 σ_{F, 1}^{2})

Based on above distribution, the first term of the last equation in (17) can be approximated as:

\begin{matrix} \begin{matrix} \Pr ({| h |}^{2} C_{\hat{P}, B, I_{χ}}^{H} E (I_{χ} e_{1}, {\tilde{Ξ}}_{χ, z}^{(1)}) C_{\hat{P}, B, I_{χ}} + Z ({\tilde{Ξ}}_{χ, z}^{(1)}) > |Z ({\bar{\bar{Ξ}}}_{χ, z}^{(1)})|) \\ = & 1 - \Pr (Z_{1} ({\bar{\bar{Ξ}}}_{χ, z}^{(1)}) + Z_{2} ({\bar{\bar{Ξ}}}_{χ, z}^{(1)}) - Z ({\tilde{Ξ}}_{χ, z}^{(1)}) \geq {| h |}^{2} C_{\hat{P}, B, I_{χ}}^{H} E (I_{χ} e_{1}, {\tilde{Ξ}}_{χ, z}^{(1)}) C_{\hat{P}, B, I_{χ}}) \cdot \Pr (Z_{1} ({\bar{\bar{Ξ}}}_{χ, z}^{(1)}) + Z_{2} ({\bar{\bar{Ξ}}}_{χ, z}^{(1)}) > 0) \\ - \Pr (- Z_{1} ({\bar{\bar{Ξ}}}_{χ, z}^{(1)}) - Z_{2} ({\bar{\bar{Ξ}}}_{χ, z}^{(1)}) - Z ({\tilde{Ξ}}_{χ, z}^{(1)}) \geq {| h |}^{2} C_{\hat{P}, B, I_{χ}}^{H} E (I_{χ} e_{1}, {\tilde{Ξ}}_{χ, z}^{(1)}) C_{\hat{P}, B, I_{χ}}) \cdot \Pr (Z_{1} ({\bar{\bar{Ξ}}}_{χ, z}^{(1)}) + Z_{2} ({\bar{\bar{Ξ}}}_{χ, z}^{(1)}) < 0) \\ = & 1 - 2 \Pr (Z_{1} ({\bar{\bar{Ξ}}}_{χ, z}^{(1)}) + Z_{2} ({\bar{\bar{Ξ}}}_{χ, z}^{(1)}) - Z ({\tilde{Ξ}}_{χ, z}^{(1)}) \geq {| h |}^{2} C_{\hat{P}, B, I_{χ}}^{H} E (I_{χ} e_{1}, {\tilde{Ξ}}_{χ, z}^{(1)}) C_{\hat{P}, B, I_{χ}}) \cdot \Pr (Z_{1} ({\bar{\bar{Ξ}}}_{χ, z}^{(1)}) + Z_{2} ({\bar{\bar{Ξ}}}_{χ, z}^{(1)}) > 0) \\ \overset{(d)}{\geq} & 1 - Q (\frac{2^{Υ} {| h |}^{2} \cdot {(- 1)}^{B_{1} + {(B |_{Υ + 1}^{m})}^{T} z}}{2 σ_{F, 1}}), \end{matrix} \end{matrix}

(23)

where (d) depends on

Z_{1} ({\bar{\bar{Ξ}}}_{χ, z}^{(1)}) + Z_{2} ({\bar{\bar{Ξ}}}_{χ, z}^{(1)}) - Z ({\tilde{Ξ}}_{χ, z}^{(1)}) \sim N (0, 4 σ_{F, 1}^{2})

. We then compute the latter term of (17) as

\begin{matrix} \begin{matrix} \Pr ({| h |}^{2} C_{\hat{P}, B, I_{χ}}^{H} E (I_{χ} e_{1}, {\tilde{Ξ}}_{χ, z}^{(1)}) C_{\hat{P}, B, I_{χ}} + Z ({\tilde{Ξ}}_{χ, z}^{(1)}) > 0) \\ = & \Pr (Z ({\tilde{Ξ}}_{χ, z}^{(1)}) > - {| h |}^{2} C_{\hat{P}, B, I_{χ}}^{H} E (I_{χ} e_{1}, {\tilde{Ξ}}_{χ, z}^{(1)}) C_{\hat{P}, B, I_{χ}}) \\ = & \Pr (Z ({\tilde{Ξ}}_{χ, z}^{(1)}) > - 2^{Υ} {| h |}^{2} \cdot {(- 1)}^{B_{1} + {(B |_{Υ + 1}^{m})}^{T} z}) \\ = & Q (- \frac{2^{Υ} {| h |}^{2} \cdot {(- 1)}^{B_{1} + {(B |_{Υ + 1}^{m})}^{T} z}}{\sqrt{2} σ_{F, 1}}) . \end{matrix} \end{matrix}

(24)

By substituting (23) and (24) into (16), we finally get

\begin{matrix} \begin{matrix} \prod_{{[{\bar{\bar{p}}}_{χ, 1}^{(j)}]}_{j = 1}^{2^{Υ - 1}}} \Pr (|F (\tilde{I_{χ}} z + {\tilde{p}}_{χ, 1})| > |F (\tilde{I_{χ}} z + {\bar{\bar{p}}}_{χ, 1}^{(j)})|) \\ \geq & {[Q (- \frac{2^{Υ} {| h |}^{2} \cdot {(- 1)}^{B_{1} + {(B |_{Υ + 1}^{m})}^{T} z}}{\sqrt{2} σ_{F, 1}}) \cdot Q (- \frac{2^{Υ} {| h |}^{2} \cdot {(- 1)}^{B_{1} + {(B |_{Υ + 1}^{m})}^{T} z}}{2 σ_{F, 1}})]}^{2^{Υ} - 1} . \end{matrix} \end{matrix}

(25)

Equation (25) is consistent with (11) in Lemma 1, so Lemma 1 holds for

r = 1

. 4 (2) when

2 \leq r \leq Υ

: Algorithm 1’s input signal becomes

\begin{matrix} \begin{matrix} y_{r} & = λ_{P R M, ϖ}^{(r)} \cdot y_{r - 1} \\ = C_{\hat{P}, B, I_{χ}} + \prod_{i = 1}^{r - 1} λ_{P R M, ϖ}^{(i)} \cdot n \\ = C_{\hat{P}, B, I_{χ}} + \frac{1}{2^{i - 1}} \prod_{i = 1}^{r - 1} (I_{N} + ϖ_{i} \cdot E [I_{χ} e_{i}, I_{χ} {\hat{P}}_{i}]) \cdot n . \end{matrix} \end{matrix}

(26)

By substituting (26) into (14), we have

σ_{F, r}^{2} = 2^{m - 1} [{2 | h |}^{2} \frac{N_{0}}{2^{r - 1}} + {(\frac{N_{0}}{2^{r - 1}})}^{2}]

. Thus,

Z ({\tilde{Ξ}}_{χ, z}^{(r)}) \sim CN (0, 2 σ_{F, r}^{2})

, and

Z ({\bar{\bar{Ξ}}}_{χ, z}^{(r)}) \sim CN (0, 2 σ_{F, r}^{2})

. Furthermore, we get

F_{A} ({\tilde{Ξ}}_{χ, z}^{(r)}) + Z ({\tilde{Ξ}}_{χ, z}^{(r)}) \sim CN (2^{Υ} \cdot {| h |}^{2} {(- 1)}^{B_{r} + {(B |_{Υ + 1}^{m})}^{T} z}, 2 σ_{F, r}^{2})

. The derivation process is similar to

r = 1

and we omit it here. The result is comsistent with (11) and (12) in Lemma 1.

The PRM sequence is reconstructed successfully if the estimations for all layers are correct. Therefore, Algorithm 1 has the successful detection probability as follows:

\overset{ˇ}{P} (Υ, N_{0} | h) = \prod_{r = 1}^{Υ} \Pr (P^{(r)} | P^{(1, \dots, r - 1)}, h) .

(27)

Taking the channel coefficient h into account, we get the following equation

P_{s u c c} = \int_{h} f_{CN} (h; 0, 1) \cdot \overset{ˇ}{P} (Υ, N_{0} | h) d h,

(28)

thus, the proof of Theorem 1 is complete. □

The factors that affect the efficiency of layer-by-layer PRM projection algorithm are discussed below. According to Lemma 1, the conditional probability

\Pr (P^{(r)} | P^{(1, \dots, r - 1)}, h)

of the vector

{\hat{P}}_{r}

is related to three factors, namely

Υ

r

, m and

N_{0}

. Since it is challenging to mathematically express the relationship between them, we fix two elements and track the changes in the conditional probability as a result of changing the third factor. In accordance with the Figure 1– Figure 4, the following results are obtained:

Assume that the PRM code is of full rank with $Υ = m$ , when m and $N_{0}$ are given, as $r$ increases from 1 to m, the value of $\Pr (P^{(r)} | P^{(1, \dots, r - 1)}, h)$ increases (Figure 1). The results illustrate the properties of the projection algorithm: if the first few layers are error-free, the remaining layers are highly likely to be recovered correctly. Besides, a further conclusion can be drawn by observing the above proof that $n_{r} \sim CN (0, \frac{N_{0}}{2^{r - 1}})$ indicates that the noise power in each layer decreases exponentially as $r$ increases, leading to the successful recovery probability of the vector increasing layer by layer. Overall, the recovery reliability of the first few layers of the layer-by-layer PRM projection algorithm is crucial to its performance. This motivates us to increase the number of candidate paths in the first few layers to obtain better detections.
As shown in Figure 2, when $r$ , $Υ$ and $N_{0}$ are given, $\Pr (P^{(r)} | P^{(1, \dots, r - 1)}, h)$ increases as m increases, which shows that we can improve the performance of the PRM sequence detection algorithm by increasing the length of the PRM sequence.
Figure 3 gives the variation of $\Pr (P^{(r)} | P^{(1, \dots, r - 1)}, h)$ with $N_{0}$ for fixed $r$ , m and $Υ$ . It is clear that as $N_{0}$ increases, the Signal-to-Noise Ratio (SNR) decreases, resulting in $\Pr (P^{(r)} | P^{(1, \dots, r - 1)}, h)$ decreases consequently.
Figure 4 gives the variation of $\Pr (P^{(r)} | P^{(1, \dots, r - 1)}, h)$ with $r$ for fixed $N_{0}$ , m and $Υ$ : the larger $Υ$ indicates the better performance under the same m, and this result is consistent with the fact that a greater signal power will result in a greater signal-to-noise ratio. Furthermore, the larger the m, the worse the performance under the same layer $r$ , indicating that the closer $Υ$ to m, the better the performance will be.

4.2. Successful Recovery Probability of the Iterative List PRM Projection Algorithm

In this section, Lemma 2 and Theorem 2 analyze the performance of the iterative list PRM projection algorithm in the multi-user scenario.

Lemma 2.

Suppose that the input signal of Algorithm 2 contains a linear combination of all

K_{a}

active users’ sequences, We let these sequences be detected in the order of

(ρ_{1}, ρ_{2}, \dots, ρ_{K_{a}})

. We denote the event "the

ρ_{k}

-th recoverd sequence has been successfully detected" as

B_{ρ_{k}}

and the event "the sequences with order

(ρ_{1}, \dots, ρ_{k - 1})

have been successfully detected and have been subtracted from the received signal" as

B_{ρ_{1}, \dots, ρ_{k - 1}}

. Thus, given the channel parameters

\underset{̲}{h} = [h_{1}, \dots, h_{K_{a}}]

and the event

B_{ρ_{1}, \dots, ρ_{k - 1}}

, the chance of the event

B_{ρ_{1}, \dots, ρ_{k - 1}}

occurs in the first iteration of Algorithm 2 can be approximated as

\begin{matrix} \begin{matrix} \Pr (B_{ρ_{k}} | B_{ρ_{1}, \dots, ρ_{k - 1}}, h) = \Pr (P_{ρ_{k}}^{(1)} | \underset{̲}{h}) \cdot \overset{ˇ}{P} (Υ_{ρ_{k}} - 1, N_{0}^{(Υ_{ρ_{k}} - 1)} | \underset{̲}{h}) . \end{matrix} \end{matrix}

(29)

In (29),

\Pr (P_{ρ_{k}}^{(1)} | \underset{̲}{h})

refers to the probability of

{\hat{P}}_{ρ_{k}} e_{1}

being successfully recovered under the condition

\underset{̲}{h}

, which is expressed as

\begin{matrix} \begin{matrix} \Pr (P_{ρ_{k}}^{(1)} | \underset{̲}{h}) \\ = & \prod_{j = 1}^{2^{Υ_{ρ_{k}}} - 1} Q (- \frac{2^{Υ_{ρ_{k}}} {| h_{ρ_{k}} |}^{2} + \sum_{ρ_{k + 1} \leq i \leq ρ_{K_{a}}} (n_{ρ_{k}, i} \cdot 2^{Υ_{ρ_{i}}} | h_{i} |^{2} \cdot - n_{i, j} \cdot 2^{Υ_{ρ_{i}}} {| h_{i} |}^{2})}{\sqrt{2} σ_{Λ, 1}}) \\ \cdot Q {(- \frac{2^{Υ_{ρ_{k}}} {| h_{ρ_{k}} |}^{2}}{σ_{Λ, 1}})}^{2^{Υ_{ρ_{k}}} - 1}, \end{matrix} \end{matrix}

(30)

where the notation

n_{ρ_{k}, i}

indicates the number of intersections of positions corresponding to non-zero

F (\cdot)

for the i-th detected sequence and

ρ_{k}

-th detected sequence. The notation

n_{i, j}

represents the number of intersections of positions corresponding to non-zero

F (\cdot)

for the i-th detected sequence and the j-th coset of the set related to non-zero

F (\cdot)

for the first layer recovery of the

ρ_{k}

-th detected sequence. Besides, the variance in (30) is

σ_{Λ, 1}^{2} = \sum_{ρ = ρ_{k}}^{ρ_{K_{a}}} [\sum_{ρ^{'} = ρ_{k} a n d ρ^{'} \neq ρ}^{ρ_{K_{a}}} {| h_{ρ}^{H} \cdot h_{ρ^{'}} |}^{2} \cdot σ_{μ, 1}^{2} + 2^{m - 1} \cdot (\sum_{ρ = ρ_{k}}^{ρ_{K_{a}}} 2 {| h_{ρ} |}^{2} N_{0} + N_{0}^{2})],

(31)

in which μ is the inner product created by two PRM sequences of length-

2^{m}

and

σ_{μ, 1}^{2}

denotes the variance of the inner product. The second component

\overset{ˇ}{P} (Υ_{ρ_{1}} - 1, N_{0}^{(Υ_{ρ_{k}} - 1)} | h)

in the Equation (29) represents the matrix

{\hat{P}}^{Υ_{ρ_{k}} - 1}

’s likelihood of a successful recovery given

h

, where

{\hat{P}}^{Υ_{ρ_{k}} - 1}

denotes the submatrix of the symmetric matrix

{\hat{P}}_{ρ_{k}}

with rank

(Υ_{ρ_{k}} - 1)

for order

ρ_{k}

. Besides, the notation

N_{0}^{(Υ_{ρ_{k}} - 1)} = \frac{1}{2} (\sum_{ρ = ρ_{k + 1}}^{ρ_{K_{a}}} | h_{ρ} |^{2} + N_{0})

Theorem 2.

Suppose that the input signal of Algorithm 2 contains a linear combination of all

K_{a}

active users’ sequences, we denote each sequence by the specific notation k (

1 \leq k \leq K_{a}

) and let these sequences be detected in the order of

(ρ_{1}, ρ_{2}, \dots, ρ_{K_{a}})

. Then, given the channel parameter

\underset{̲}{h}

, the probability that Algorithm 2 can successfully detect the sequence ρ

(1 \leq ρ \leq K_{a})

in the first iteration is

\begin{matrix} \begin{matrix} {\overset{ˇ}{\overset{ˇ}{P}}}_{ρ} (K_{a}, m, N_{0} | \underset{̲}{h}) \\ = & \Pr (B_{ρ} | \underset{̲}{h}) + \sum_{k = 2}^{K_{a}} \{\sum_{(ρ_{1}, \dots, ρ_{k - 1}) \in N_{k}} [(\prod_{k^{'} = 1}^{k - 1} \Pr (B_{ρ_{k^{'}}} | B_{ρ_{1}, \dots, ρ_{k^{'} - 1}}, \underset{̲}{h})) \cdot \Pr (B_{ρ} | B_{ρ_{1}, \dots, ρ_{k - 1}}, \underset{̲}{h})]\}, \end{matrix} \end{matrix}

(32)

where the set

N_{k}

contains all permutations of

(k - 1)

indexes of order from the set

K_{a} ∖ ρ

. Furthermore, by taking the channel parameters into consideration, the average probability of successful detection for the first iteration of the iterative PRM sequence can be approximated as

\begin{matrix} \begin{matrix} {\overset{ˇ}{\overset{ˇ}{P}}}_{ave} (K_{a}, m, N_{0} | \underset{̲}{h}) = \frac{1}{K_{a}} \int_{\underset{̲}{h}} \{\prod_{ρ = 1}^{K_{a}} f_{CN} (h_{ρ}; 0, 1) \cdot \sum_{ρ = 1}^{K_{a}} {\overset{ˇ}{\overset{ˇ}{P}}}_{ρ} (K_{a}, m, N_{0} | \underset{̲}{h})\} . \end{matrix} \end{matrix}

(33)

Proof

(Proof). For convenience, two users are assumed to be active in the system. since users are not provided with IDs in the URA scenario, we can deduce the theoretical results of successful detection probabilities with the help of the detection order between sequences: we denote two sequences as a and b, respectively, and the detection order between them is represented by

ρ_{a}

and

ρ_{b}

. At this point, the input signal of the algorithm is rewritten as a linear superposition of the two users of form:

y = h_{a} C_{{\hat{P}}_{a}, B_{a}, I_{χ, a}} + h_{b} C_{{\hat{P}}_{b}, B_{b}, I_{χ, b}} + n .

The rank of PRM codes

C_{{\hat{P}}_{a}, B_{a}, I_{χ, a}}

and

C_{{\hat{P}}_{b}, B_{b}, I_{χ, b}}

are noted as

Υ_{a}

and

Υ_{b}

, respectively. According to the expansion of (14), the

F_{M}

can be expanded regarding the

r

-layer as

\begin{matrix} \begin{matrix} F_{M} (f_{r}) = & {(h_{a} C_{{\hat{P}}_{a}, B_{a}, I_{χ, a}} + h_{b} C_{{\hat{P}}_{b}, B_{b}, I_{χ, b}} + n)}^{H} \cdot E (I_{χ} e_{r}, f_{r}) \cdot (h_{a} C_{{\hat{P}}_{a}, B_{a}, I_{χ, a}} + h_{b} C_{{\hat{P}}_{b}, B_{b}, I_{χ, b}} + n) \\ = & \underset{F_{a} (f_{r})}{\underset{︸}{| h_{a} |^{2} C_{{\hat{P}}_{a}, B_{a}, I_{χ, a}}^{H} E (I_{χ} e_{r}, f_{r}) C_{{\hat{P}}_{a}, B_{a}, I_{χ, a}}}} + \underset{F_{b} (f_{r})}{\underset{︸}{| h_{b} |^{2} C_{{\hat{P}}_{b}, B_{b}, I_{χ, b}}^{H} E (I_{χ} e_{r}, f_{r}) C_{{\hat{P}}_{b}, B_{b}, I_{χ, b}}}} \\ + \underset{Z_{a b, 1} (f_{r})}{\underset{︸}{h_{a}^{H} \cdot h_{b} C_{{\hat{P}}_{a}, B_{a}, I_{χ, a}}^{H} E (I_{χ} e_{r}, f_{r}) C_{{\hat{P}}_{b}, B_{b}, I_{χ, b}}}} + \underset{Z_{a b, 2} (f_{r})}{\underset{︸}{h_{a} \cdot h_{b}^{H} C_{{\hat{P}}_{b}, B_{b}, I_{χ, b}}^{H} E (I_{χ} e_{r}, f_{r}) C_{{\hat{P}}_{a}, B_{a}, I_{χ, a}}}} \\ + \underset{X_{a, 1} (f_{r})}{\underset{︸}{h_{a} [C_{{\hat{P}}_{a}, B_{a}, I_{χ, a}}^{H} E (I_{χ} e_{r}, f_{r}) n + n^{H} E (I_{χ} e_{r}, f_{r}) C_{{\hat{P}}_{a}, B_{a}, I_{χ, a}}]}} \\ + \underset{X_{a, 2} (f_{r})}{\underset{︸}{h_{b} [C_{{\hat{P}}_{b}, B_{b}, I_{χ, b}}^{H} E (I_{χ} e_{r}, f_{r}) n + n^{H} E (I_{χ} e_{r}, f_{r}) C_{{\hat{P}}_{b}, B_{b}, I_{χ, b}}]}} + \underset{N (f_{r})}{\underset{︸}{n^{H} E (I_{χ} e_{r}, f_{r}) n}} . \end{matrix} \end{matrix}

(34)

For ease of use, we make

(Z_{a b, 1} + Z_{a b, 2} + X_{a, 1} + X_{a, 2} + N) (f_{r}) = Λ (f_{r})

We first assess the performance of the first-layer (

r = 1

) detection for

ρ_{a}

-th sequence: suppose in the first iteration of Algorithm 2, active users are detected successively according to the order

(ρ_{a}, ρ_{b})

. In the following, we write the probability of the event

P_{ρ_{a}}^{(1)}

as form

\begin{matrix} \begin{matrix} \Pr (P_{ρ_{a}}^{(1)} | h) & = \Pr (\sum_{z \in F_{2}^{m - Υ_{a}}} |F ({\tilde{I}}_{χ, a} z + {\tilde{p}}_{χ_{a}, 1})| > max \sum_{z \in F_{2}^{m - Υ_{a}}} |F ({\tilde{I}}_{χ, a} z + {\bar{\bar{p}}}_{χ_{a}, 1})|) \\ = \prod_{{[{\bar{\bar{p}}}_{χ_{a}, 1}^{(j)}]}_{j}^{2^{Υ_{a}} - 1}} \Pr (\sum_{z \in F_{2}^{m - Υ_{a}}} |F ({\tilde{I}}_{χ, a} z + {\tilde{p}}_{χ_{a}, 1})| > \sum_{z \in F_{2}^{m - Υ_{a}}} |F ({\tilde{I}}_{χ, a} z + {\bar{\bar{p}}}_{χ_{a}, 1}^{(j)})|) . \end{matrix} \end{matrix}

(35)

We omit the subscript

M

and record it as

F (\cdot)

in this section. As seen in (35), the present situation is more complicated than the single-user scenario. One of the problems is that the

2^{m - Υ_{a}}

jointly summed events are no longer independent and no longer obey the same distribution. In addition, for the property of the PRM sequence, the vector

({\tilde{I}}_{χ, a} z + {\tilde{p}}_{χ_{a}, 1})

in (35) is specific to the

ρ_{a}

-th detected sequences, and the

ρ_{b}

-th sequence utilizes a PRM whose rank

Υ_{b}

is not necessarily equivalent to

Υ_{a}

, therefore, the analysis requires a detailed consideration of the interference of the other user. For simplicity, we first approximate a single term in (35) as follows:

\begin{matrix} \begin{matrix} \Pr (\sum_{z \in F_{2}^{m - Υ_{a}}} (|(F_{a} + Λ) ({\tilde{Ξ}}_{χ_{a}, z}^{(1)})| + |F_{b} ({\tilde{Ξ}}_{χ_{a}, z}^{(1)})|) \geq \sum_{z \in F_{2}^{m - Υ_{a}}} (|F_{b} ({\bar{\bar{Ξ}}}_{χ_{a}, z}^{(j, 1)})| + |Λ ({\bar{\bar{Ξ}}}_{χ_{a}, z}^{(j, 1)})|)) \\ \overset{(e)}{=} & \Pr (|(F_{a} + Λ) ({\tilde{Ξ}}_{χ_{a}, z}^{(1)})| + \sum_{z \in F_{2}^{m - Υ_{a}}} |F_{b} ({\tilde{Ξ}}_{χ_{a}, z}^{(1)})| \geq |Λ ({\bar{\bar{Ξ}}}_{χ_{a}, z}^{(j, 1)})| + \sum_{z \in F_{2}^{m - Υ_{a}}} |F_{b} ({\bar{\bar{Ξ}}}_{χ_{a}, z}^{(j, 1)})|) \\ \overset{(f)}{\geq} & \Pr ((F_{a} + Λ) ({\tilde{Ξ}}_{χ_{a}, z}^{(1)}) + \sum_{z \in F_{2}^{m - Υ_{a}}} |F_{b} ({\tilde{Ξ}}_{χ_{a}, z}^{(1)})| \geq |Λ ({\bar{\bar{Ξ}}}_{χ_{a}, z}^{(j, 1)})| + \sum_{z \in F_{2}^{m - Υ_{a}}} |F_{b} ({\bar{\bar{Ξ}}}_{χ_{a}, z}^{(j, 1)})|) \cdot \Pr ((F_{a} + Λ) ({\tilde{Ξ}}_{χ_{a}, z}^{(1)}) > 0), \end{matrix} \end{matrix}

(36)

where

{\tilde{Ξ}}_{χ_{a}, z}^{(1)} = {\tilde{I}}_{χ, a} z + {\tilde{p}}_{χ_{a}, 1}

{\bar{\bar{Ξ}}}_{χ_{a}, z}^{(j, 1)} = {\tilde{I}}_{χ, a} z + {\bar{\bar{p}}}_{χ_{a}, 1}^{(j)}

(different from (17), the superscript "j" can not be removed from

{\bar{\bar{Ξ}}}_{χ_{a}, z}^{(j, 1)}

since the events in joint multiply from (35) are not independent anymore) and

{\bar{\bar{Ξ}}}_{χ_{a}, z}^{(j, 1)}

is the j-th coset of the set

{\tilde{Ξ}}_{χ_{a}, z}^{(1)}

(

1 \leq j \leq 2^{Υ_{a}} - 1

). it is known that

F_{a} ({\tilde{Ξ}}_{χ_{a}, z}^{(1)})

take non-zero values for the set

{\tilde{Ξ}}_{χ_{a}, z}^{(1)}

. Besides, the equal sign

(e)

in (36) retains one of the terms on both sides owing to the same distribution. The inequality sign

(f)

follows the formula (18). In the following, we will calculate each of the two probabilities of the result of (36).

We first solve the probability of the latter term. Since we know that

F_{a} ({\tilde{Ξ}}_{χ_{a}, z}^{(1)})

takes a fixed value, it is sufficient to obtain the distribution of

Λ ({\tilde{Ξ}}_{χ_{a}, z}^{(1)})

. Thus, the distribution of

Z_{a b, 1} ({\tilde{Ξ}}_{χ_{a}, z}^{(1)})

and

Z_{a b, 2} ({\tilde{Ξ}}_{χ_{a}, z}^{(1)})

Λ ({\tilde{Ξ}}_{χ_{a}, z}^{(1)})

can be extended as

\begin{matrix} \begin{matrix} Z_{a b, 1} ({\tilde{Ξ}}_{χ_{a}, z}^{(1)}) & = h_{a}^{H} \cdot h_{b} \cdot C_{{\hat{P}}_{a}, B_{a}, I_{χ, a}}^{H} E (I_{χ_{a}} e_{r}, {\tilde{Ξ}}_{χ_{a}, z}^{(1)}) C_{{\hat{P}}_{b}, B_{b}, I_{χ, b}} \\ = h_{a}^{H} \cdot h_{b} \cdot i^{{(I_{χ} e_{r})}^{T} {\tilde{Ξ}}_{χ_{a}, z}^{(1)}} \sum_{w \in F_{2}^{m}} \bar{C_{\hat{P_{a}}, B_{a}, I_{χ_{a}}} (w + I_{χ_{a}} e_{r})} \cdot {(- 1)}^{w^{T} \cdot {\tilde{Ξ}}_{χ_{a}, z}^{(1)}} \cdot C_{\hat{P_{b}}, B_{b}, I_{χ_{b}}} (w) \\ = h_{a}^{H} \cdot h_{b} \cdot i^{{(I_{χ} \cdot e_{r} + 2 w)}^{T} \cdot {\tilde{Ξ}}_{χ_{a}, z}^{(1)}} \cdot μ_{\bar{ρ_{a}}, ρ_{b}}^{(1)} \end{matrix} \end{matrix}

(37)

and

\begin{matrix} \begin{matrix} Z_{a b, 2} ({\tilde{Ξ}}_{χ_{a}, z}^{(1)}) & = h_{a} \cdot h_{b}^{H} \cdot C_{{\hat{P}}_{b}, B_{b}, I_{χ, b}}^{H} E (I_{χ_{a}} e_{r}, {\tilde{Ξ}}_{χ_{a}, z}^{(1)}) C_{{\hat{P}}_{a}, B_{a}, I_{χ, a}} \\ = h_{a} \cdot h_{b}^{H} \cdot i^{{(I_{χ} e_{r})}^{T} {\tilde{Ξ}}_{χ_{a}, z}^{(1)}} \sum_{w \in F_{2}^{m}} \bar{C_{\hat{P_{b}}, B_{b}, I_{χ_{b}}} (w + I_{χ_{a}} e_{r})} \cdot {(- 1)}^{w^{T} \cdot {\tilde{Ξ}}_{χ_{a}, z}^{(1)}} \cdot C_{\hat{P_{a}}, B_{a}, I_{χ_{a}}} (w) \\ = h_{a} \cdot h_{b}^{H} \cdot i^{{(I_{χ} \cdot e_{r} + 2 w)}^{T} \cdot {\tilde{Ξ}}_{χ_{a}, z}^{(1)}} \cdot μ_{ρ_{a}, \bar{ρ_{b}}}^{(1)}, \end{matrix} \end{matrix}

(38)

repectively, where

μ_{\bar{ρ_{a}}, ρ_{b}}^{(1)}

and

μ_{ρ_{a}, \bar{ρ_{b}}}^{(1)}

are inner product of two sequences. The inner product is related to the pattern form of the PRM. Since the distribution of the occupancy pattern have equal probability, the mean of the inner product is 0 and we denote its variance as

σ_{μ, 1}^{2}

. Thus we can obtain

Λ ({\tilde{Ξ}}_{χ_{a}, z}^{(1)})

obeys the distribution

N (0, σ_{Λ, 1}^{2})

, where the variance is

σ_{Λ, 1}^{2} = (| h_{a}^{H} \cdot h_{b} |^{2} + | h_{a} \cdot h_{b}^{H} |^{2}) \cdot σ_{μ, 1}^{2} + 2^{m - 1} [2 (| h_{a} |^{2} + | h_{b} |^{2}) N_{0} + N_{0}^{2}] .

In light of this, the latter term of (36) can be computed as

\begin{matrix} \begin{matrix} \Pr ((F_{a} + Λ) ({\tilde{Ξ}}_{χ_{a}, z}^{(1)}) > 0) \\ = & \Pr (Λ ({\tilde{Ξ}}_{χ_{a}, z}^{(1)}) > - F_{a} ({\tilde{Ξ}}_{χ_{a}, z}^{(1)})) \\ = & \Pr (Λ ({\tilde{Ξ}}_{χ_{a}, z}^{(1)}) > - 2^{Υ_{a}} {| h_{a} |}^{2} \cdot {(- 1)}^{B_{a, 1} + {(B_{a} |_{Υ + 1}^{m})}^{T} z}) \\ \overset{(g)}{=} & Q (- \frac{2^{Υ_{a}} {| h_{a} |}^{2}}{σ_{Λ, 1}}) . \end{matrix} \end{matrix}

(39)

In equal sign (g), we set

z = 0^{m - Υ}

, this setting is also extended in the following formulas.

We next solve the probability of the first term in (36), we suppose that the set corresponding to one-zero

F_{b} (\cdot)

is noted as

{\tilde{Ξ}}_{χ_{b}, z}^{(1)}

and we make

| {\tilde{Ξ}}_{χ_{a}, z}^{(1)} \cap {\tilde{Ξ}}_{χ_{b}, z}^{(1)} | = n_{a b}

, obviously,

| {\tilde{Ξ}}_{χ_{b}, z}^{(1)} | = 2^{m - Υ_{b}}

. We further denote

| {\bar{\bar{Ξ}}}_{χ_{a}, z}^{(j, 1)} \cap {\tilde{Ξ}}_{χ_{b}, z}^{(1)} | = n_{b, j}

and

n_{a b} + \sum_{j = 1}^{2^{Υ_{a}} - 1} n_{b, j} = 2^{m - Υ_{b}}

. On this basis, the first term of the results of (36) yeilds the following equation:

\begin{matrix} \begin{matrix} \Pr ((F_{a} + Λ) ({\tilde{Ξ}}_{χ_{a}, z}^{(1)}) + \sum_{z \in F_{2}^{m - Υ_{a}}} |F_{b} ({\tilde{Ξ}}_{χ_{a}, z}^{(1)})| \geq |Λ ({\bar{\bar{Ξ}}}_{χ_{a}, z}^{(j, 1)})| + \sum_{z \in F_{2}^{m - Υ_{a}}} |F_{b} ({\bar{\bar{Ξ}}}_{χ_{a}, z}^{(j, 1)})|) \\ = & \Pr ((F_{a} + Λ) ({\tilde{Ξ}}_{χ_{a}, z}^{(1)}) + n_{a b} \cdot 2^{Υ_{b}} | h_{b} |^{2} \geq |Λ ({\bar{\bar{Ξ}}}_{χ_{a}, z}^{(j, 1)})| + n_{b, j} \cdot 2^{Υ_{b}} {| h_{b} |}^{2} 2^{Υ_{b}}) \\ = & 1 - \Pr (Λ ({\bar{\bar{Ξ}}}_{χ_{a}, z}^{(j, 1)}) - Λ ({\tilde{Ξ}}_{χ_{a}, z}^{(1)}) \geq 2^{Υ_{a}} | h_{a} |^{2} + n_{a b} \cdot 2^{Υ_{b}} | h_{b} |^{2} - n_{b, j} \cdot 2^{Υ_{b}} {| h_{b} |}^{2}) \cdot \Pr (Λ ({\bar{\bar{Ξ}}}_{χ_{a}, z}^{(j, 1)}) > 0) \\ - \Pr (- Λ ({\bar{\bar{Ξ}}}_{χ_{a}, z}^{(j, 1)}) - Λ ({\tilde{Ξ}}_{χ_{a}, z}^{(1)}) \geq 2^{Υ_{a}} | h_{a} |^{2} + n_{a b} \cdot 2^{Υ_{b}} | h_{b} |^{2} - n_{b, j} \cdot 2^{Υ_{b}} {| h_{b} |}^{2}) \cdot \Pr (Λ ({\bar{\bar{Ξ}}}_{χ_{a}, z}^{(j, 1)}) < 0) \\ \geq & 1 - \Pr (Λ ({\bar{\bar{Ξ}}}_{χ_{a}, z}^{(j, 1)}) - Λ ({\tilde{Ξ}}_{χ_{a}, z}^{(1)}) \geq 2^{Υ_{a}} | h_{a} |^{2} + n_{a b} \cdot 2^{Υ_{b}} | h_{b} |^{2} - n_{b, j} \cdot 2^{Υ_{b}} {| h_{b} |}^{2}) \\ \overset{(h)}{=} & 1 - Q (\frac{2^{Υ_{a}} | h_{a} |^{2} + n_{a b} \cdot 2^{Υ_{b}} | h_{b} |^{2} - n_{b, j} \cdot 2^{Υ_{b}} {| h_{b} |}^{2}}{\sqrt{2} σ_{Λ, 1}}), \end{matrix} \end{matrix}

(40)

the equal sign (h) is based on

Λ ({\bar{\bar{Ξ}}}_{χ_{a}, z}^{(j, 1)}) - Λ ({\tilde{Ξ}}_{χ_{a}, z}^{(1)}) \sim N (0, 2 σ_{Λ, 1}^{2})

. On this basis, we return to (36) and get the final result

\begin{matrix} \begin{matrix} \prod_{j = 1}^{2^{Υ_{a}} - 1} \Pr ((F_{a} + Λ) ({\tilde{Ξ}}_{χ_{a}, z}^{(1)}) + \sum_{z \in F_{2}^{m - Υ_{a}}} |F_{b} ({\tilde{Ξ}}_{χ_{a}, z}^{(1)})| \geq |Λ ({\bar{\bar{Ξ}}}_{χ_{a}, z}^{(j, 1)})| + \sum_{z \in F_{2}^{m - Υ_{a}}} |F_{b} ({\bar{\bar{Ξ}}}_{χ_{a}, z}^{(j, 1)})|) \\ = & \prod_{j = 1}^{2^{Υ_{a}} - 1} (Q (- \frac{2^{Υ_{a}} | h_{a} |^{2} + n_{a b} \cdot 2^{Υ_{b}} | h_{b} |^{2} - n_{b, j} \cdot 2^{Υ_{b}} {| h_{b} |}^{2}}{\sqrt{2} σ_{Λ, 1}}) \cdot Q (- \frac{2^{Υ_{a}} {| h_{a} |}^{2}}{σ_{Λ, 1}})) . \end{matrix} \end{matrix}

(41)

This equation is consistent with (30) in Lemma 2.

Now we present a special example to provide a further explanation for the result of (41): we suppose that two users have the same submatrix

I_{χ}

and different vectors

{\hat{P}}_{1}

, thus (35) directly becomes

\begin{matrix} \begin{matrix} \prod_{j = 1}^{2^{Υ_{a}} - 1} \Pr (\sum_{z \in F_{2}^{m - Υ_{a}}} |(F_{a} + Λ) ({\tilde{Ξ}}_{χ_{a}, z}^{(1)})| > \sum_{z \in F_{2}^{m - Υ_{a}}} |(F_{b} + Λ) ({\bar{\bar{Ξ}}}_{χ_{a}, z}^{(j, 1)})|) \\ \geq & \prod_{j = 1}^{2^{Υ_{a}} - 1} (\Pr ((F_{a} + Λ) ({\tilde{Ξ}}_{χ_{a}, z}^{(1)}) > |F_{b} ({\bar{\bar{Ξ}}}_{χ_{a}, z}^{(j, 1)})| + |Λ ({\bar{\bar{Ξ}}}_{χ_{a}, z}^{(j, 1)})|) \cdot \Pr ((F_{a} + Λ) ({\tilde{Ξ}}_{χ_{a}, z}^{(1)}) > 0)) \\ = & {(Q (- \frac{2^{Υ_{a}} {| h_{a} |}^{2}}{σ_{Λ, 1}}))}^{2^{Υ_{a}} - 1} \cdot (\prod_{j = 1}^{2^{Υ_{a}} - 2} \underset{I}{\underset{︸}{\Pr ((F_{a} + Λ) ({\tilde{Ξ}}_{χ_{a}, z}^{(1)}) > |Λ ({\bar{\bar{Ξ}}}_{χ_{a}, z}^{(j, 1)})|)}}) \\ \cdot \underset{I I}{\underset{︸}{\Pr ((F_{a} + Λ) ({\tilde{Ξ}}_{χ_{a}, z}^{(1)}) > |F_{b} ({\bar{\bar{Ξ}}}_{χ_{a}, z}^{(j, 1)})| + |Λ ({\bar{\bar{Ξ}}}_{χ_{a}, z}^{(j, 1)})|)}} \\ = & {(Q (- \frac{2^{Υ_{a}} {| h_{a} |}^{2}}{σ_{Λ, 1}}))}^{2^{Υ_{a}} - 1} \cdot {(Q (- \frac{2^{Υ_{a}} {| h_{a} |}^{2}}{\sqrt{2} σ_{Λ, 1}}))}^{2^{Υ_{a}} - 2} \cdot Q (- \frac{2^{Υ_{a}} | h_{a} |^{2} - 2^{Υ_{b}} {| h_{b} |}^{2}}{\sqrt{2} σ_{Λ, 1}}) . \end{matrix} \end{matrix}

(42)

In this case, term I refers to interference imposed by the cosets other than set

{\tilde{Ξ}}_{χ_{a}, z}^{(1)}

on the

ρ_{a}

-th detected sequence. Since

| {\bar{\bar{Ξ}}}_{χ_{a}, z}^{(j, 1)} \cap {\tilde{Ξ}}_{χ_{b}, z}^{(1)} | = 2^{Υ_{b}}

for one particular j, we conclude that there is only one case in term

I I

. Besides, owing to

F_{b} ({\bar{\bar{Ξ}}}_{χ_{a}, z}^{(j, 1)}) = 0

for the remaining

(2^{Υ_{a}} - 2)

possible j, it allows

(2^{Υ_{a}} - 2)

possibles for the term I. The results of (42) satisfies (41) provided that

n_{a b} = 0

and

n_{b, j} = 1

for one j,

1 \leq j \leq 2^{Υ_{a}} - 1

. This equation is also consistent with (30) in Lemma 2.

Based on the above results, after recovering vector

{\hat{P}}_{ρ_{a}} e_{1}

, the

y_{2}

becomes

\begin{matrix} \begin{matrix} y_{2} & = λ_{P R M, ρ_{a}}^{(1)} \cdot y_{1} \\ = h_{ρ_{a}} C_{{\hat{P}}_{ρ_{a}}, B_{ρ_{a}}, I_{χ, ρ_{a}}} + λ_{P R M, ρ_{a}}^{(1)} \cdot (h_{ρ_{b}} C_{{\hat{P}}_{ρ_{b}}, B_{ρ_{b}}, I_{χ, ρ_{b}}} + n) \\ = h_{ρ_{a}} C_{{\hat{P}}_{ρ_{a}}, B_{ρ_{a}}, I_{χ, ρ_{a}}} + λ_{P R M, ρ_{a}}^{(1)} \cdot h_{ρ_{b}} C_{{\hat{P}}_{ρ_{b}}, B_{ρ_{b}}, I_{χ, ρ_{b}}} + λ_{P R M, ρ_{a}}^{(1)} \cdot n, \end{matrix} \end{matrix}

(43)

where

λ_{P R M, ρ_{a}}^{(1)}

is the first layer projection operator for the user whose detection order is

ρ_{a}

. We can approximate the noise as a Gaussian random variable whose mean is 0 and whose variance is set to be

N_{0}^{(Υ_{a} - 1)} = \frac{| h_{ρ_{b}} |^{2} + N_{0}}{2}

. In light of this, the following detection procedure in layer

2 \leq r \leq Υ_{a}

is equivalent to the recovery of symmetric matrix

{\hat{P}}_{ρ_{a}}^{Υ_{ρ_{a}} - 1}

in a single sequence scenario under the condition that the noise variance is

N_{0}^{(Υ_{a} - 1)}

. Since the

ρ_{a}

-th detected sequence can be successfully recovered if and only if both

{\hat{P}}_{ρ_{a}} e_{1}

and

{\hat{P}}_{ρ_{a}}^{Υ_{ρ_{a}} - 1}

are correct, the successful detection probability of event "the

ρ_{k}

-th recoverd sequence has been successfully detected" is

\begin{matrix} \begin{matrix} \Pr (B_{ρ_{a}} | \underset{̲}{h}) = \Pr (P_{ρ_{a}}^{(1)} | \underset{̲}{h}) \cdot \overset{ˇ}{P} (Υ_{ρ_{a}} - 1, N_{0}^{(Υ_{a} - 1)} | \underset{̲}{h}), \end{matrix} \end{matrix}

(44)

This result is consistent with (29) in Lemma 2.

Next, we assume that the sequence

C_{{\hat{P}}_{ρ_{a}}, B_{ρ_{a}}, I_{χ, ρ_{a}}}

is ideally eliminated from the signal

y

, the receiver proceeds to recover

C_{{\hat{P}}_{ρ_{b}}, B_{ρ_{b}}, I_{χ, ρ_{b}}}

, and we denote its probability of successful detection as

\Pr (B_{ρ_{b}} | B_{ρ_{a}}, \underset{̲}{h}) = \overset{ˇ}{P} (Υ_{ρ_{b}}, N_{0} | h_{ρ_{b}})

As a next step, we will calculate the average probability of two sequences a and b being detected successfully. In the following two scenarios, the sequences a can be recovered:

in the first instance, sequence a is detected successfully firstly, which has a chance of $\Pr (B_{a} | \underset{̲}{h})$ ;
in the second instance, sequence b is detected in priority with the probability of $\Pr (B_{b} | \underset{̲}{h})$ , followed by sequence a is detected from the substracted signal with the probability $\Pr (B_{a} | B_{b}, \underset{̲}{h})$ .

As a result, the probability that sequence a will be successfully detected equals

\overset{ˇ}{\overset{ˇ}{P}} (K_{a}, m, N_{0} | \underset{̲}{h}) = \Pr (B_{1} | \underset{̲}{h}) + \Pr (B_{2} | \underset{̲}{h}) \cdot \Pr (B_{1} | B_{2}, \underset{̲}{h}) .

The equation is consistent with (32) in Theorem 2. Finally, the average probability of successful detection equals

{\overset{ˇ}{\overset{ˇ}{P}}}_{ave} (K_{a}, m, N_{0} | \underset{̲}{h}) = \frac{1}{2} \int_{\underset{̲}{h}} \{\prod_{ρ = 1}^{2} f_{CN} (h_{ρ}; 0.1) \cdot ({\overset{ˇ}{\overset{ˇ}{P}}}_{1} (K_{a}, m, N_{0} | \underset{̲}{h}) + {\overset{ˇ}{\overset{ˇ}{P}}}_{2} (K_{a}, m, N_{0} | \underset{̲}{h}))\} .

The equation is consistent with (33) in Theorem 2. □

5. Simulation Results

In this section, we first examine the effectiveness of the proposed algorithms by evaluating the numerical simulation of the successful detection probability. The successful detection probability is the mean proportion of determined active users to the system’s overall number of active users. Additionally, a slot-controlled CCS scheme with the proposed iterative list projection algorithm in place of the origin inner decoder has been measured against several benchmarks.

5.1. Performances of the Algorithms 1 and 2

As for the performance of Algorithm 1: Figure 5 compares the numerical simulation results of the list PRM projection algorithm (Algorithm 1) with the theoretical analysis results based on (11) for different settings of m. We fix

Υ = m

H = 1

and the transmit power of an active user is normalized to one. This figure illustrates that the numerical simulation results and the theoretical analysis are closely matched, and it is clear that the difference between the two simulations is the result of some approximations in the theoretical analysis. Thus, this result confirms the correctness of the theoretical analysis in Lemma 1. In addition, comparing the successful detection probability for different m, we find that the performance of the list PRM projection algorithm improves as the sequence length increases, further validating the conclusion in Section 4.1.

Next, we will compare the performance of the list PRM projection algorithm with the existing decoding algorithm for RM sequences. The numerical simulation results are shown in Figure 6, where "Origin PRM" and "List PRM" represent the origin projection detection algorithm in [33] and its list version (Algorithm 1), respectively. "RM LLD" represents the RM sequence detection algorithm proposed in [29], which is based on the Shift-and-Multiply operation on the received signal, and "List RM LLD" represents its list version detection. For all algorithms, we set the sequence length to

N = 2^{8}

and the list size to

H = 8

. As can be seen from Figure 6, the successful detection probabilities of all algorithms are close to one when the signal-to-noise ratio (SNR) is larger than

- 2 dB

. However, the "RM LLD" algorithm suffers from severe performance degradation under low SNR conditions compared to the "Origin PRM", which shows strong robustness. In addition, since the enhanced list detection, the "List RM LLD" and the "List PRM" bring a more outstanding performance gain under lower SNR when compared with no candidate-saving algorithms.

As for the performance of Algorithm 2: in Figure 7, we compare the numerical simulation results of the iterative list PRM projection detection (Algorithm 2) with the theoretical analysis results derived from Lemma 2. We set the number of iterations in the numerical simulation 1. From the Figure 7, the theoretical analysis results can fit the numerical simulation results well, especially under high SNR conditions, thus verifying the correctness of Theorem 2. In addition, both simulation and theoretical results show that the detection capability of the algorithm decreases as the number of active users in the system increases.

5.2. Iterative List PRM Projection Algorithm-based Slot-controlled URA

In this section, we combine an inner code employing an iterative list PRM projection detector as the decoder with two types of practicable outer codes (t-tree and Reed-Solomon codes) to form a slot-pattern control-based CCS system (form [33]) and demonstrate the positive effects of the proposed algorithms on the overall system via simulation results. We consider a communication system in which each user transmits

B = 100

bits by employing a

H_{N}

length G-ary outer-code using

T = 2^{15}

channel uses. The

H_{N}

positions are carefully selected within

N_{T}

chunks. There are G codewords in the inner codebook, each of which has a length of

N = T / N_{T}

. We employ the PRM sequence under one rank

Υ

rather than all ranks in this section, and Algorithm 2 is used to decode the inner codes. Numerical results are presented in Figure 8. The energy efficiency of different schemes is plotted as: energy efficiency is the minimum

E_{b} / N_{0}

over the possible scheme-specific parameters in the URA scheme, besides,

P_{e} < 0.1

is the probability of error constraint for each user, and

P_{f} < 0.001

is the FAR constraint.

First of all, we concatenate the inner-code with iterative list PRM detection to an outer decoder that can correct up to t errors for various setups, i.e., the benchmarks called “

t = 3

, list PRM-tree,

H = 1

”, “

t = 2

, list PRM-tree,

H = 1

” and “

t = 1

, list PRM-tree,

H = 1

” are plotted in light blue in Figure 8, and we employ blue lines to illustrate the simulations for “

t = 3

, iterative list PRM-tree,

H = 8

”, “

t = 2

, iterative list,

H = 8

” and “

t = 1

, iterative list PRM-tree,

H = 8

”. Specifically, "list PRM-tree,

H = 1

" for different t directly drawn from [23] are regarded as benchmarks (it is named "PRM-RS" in [33]), and "iterative list PRM-tree,

H = 8

" for various t are the notations of substituting the origin detection with the proposed iterative list detection. Besides, a greedy information bit allocation method is applied to all list PRM-tree schemes, where each subsequent slot is assigned the maximum amount of information bits while maintaining the

E [| V_{l} |] \leq 2^{25}

constraint and finding the minimum

E_{b} / N_{0}

. The energy efficiency is the minimum power needed to serve

K_{a}

users with the per-user probality of error less than

0.1

, we depict the curves in the blue line in Figure 8 under the optimal setups.

Next, we denote the CCS scheme that concatenates the inner codes whose distribution is i.i.d. uniform on the power shell to an outer Reed-Solomon code as the "RS scheme” (it is named "Reed-Solomon scheme" in [23]), and use it as the first benchmark. The scheme called "list PRM-RS,

H = 1

" is directly drawn from [33] as the second benchmark (it is named "PRM-RS" in [33]). Besides, “iterative list PRM-RS,

H = 1

” is the scheme whose multi-user inner-code detector is substituted by Algorithm 2 without saving candidates while calling Algorithm 1, whereas “iterative list PRM-RS,

H = 8

” keeps

H = 8

candidates during each layer while conducting Algorithm 1. The energy efficiency is depicted in Figure 8.

From the simulations depicted in Figure 8, the following observations can be drawn:

as for all "List PRM-tree" schemes, since the outer-code length $H_{N} = 32$ is suitable for scheme $t = 1$ and $H_{N} = 64$ for $t = 2, 3$ cases, the former case ( $t = 1$ case) can accommodate more active users than $t = 2, 3$ owing to a smaller number of simultaneous appearances in each slot (the outer code length affects the probability of appearance over slots. See more setup details in [23]). Besides, a higher t for the outer code increases performance when the inner code has the same length. Therefore, $t = 3$ is superior to Furthermore, when comparing the curves of "list PRM-tree" and "iterative list PRM-tree", we conclude that the enhanced inner code with the proposed iterative list projection algorithm can help the entire system lower the energy-per-bit requirement to meet a target error probability as well as boost the ability to accommodate more users’ transmission.
Figure 8 illustrates how the "iterative list PRM-RS, $H = 1$ " curve outperforms the "list PRM-RS, $H = 1$ " curve regarding energy consumption when the number of active users is fixed. This observation is an unambiguous demonstration of the benefit of Algorithm 2, which carries out iterative detection.
when compared with different schemes of "iterative list PRM-RS, $H = 1$ " and "iterative list PRM-RS, $H = 8$ ", we demonstrate that the performance of the detection can be refined by raising the count of candidates in the first few layers, thereby confirming the significance of Algorithm 1, which guarantees the first few layers’ reliable recoveries.

6. Conclusions

In this paper, we address a packetized and slotted transmission CCS framework, which concatenates an inner PRM code to an outer error correction code. Firstly, we improve the decoder of the inner-code: we propose an enhanced algorithm that makes use of multiple candidates so as to remedy the venture of spreading errors. On this basis, an iterative list PRM projection algorithm is proposed for the multi-sequence scenario. We then deduce the theoretical probabilities of the list projection and iterative list projection detection methods. Via numerical simulations, we indicate the theoretical and the simulation results agreed. Finally, we implement the iterative list PRM projection algorithm in two practical error-correction codes. From the simulation results, we conclude that the packetized URA with the proposed iterative list projection detection works better than benchmarks in terms of the number of active users it can support in each slot and the amount of energy needed per bit to meet an expected error probability.

Additional interesting research avenues include: (i) the PRM-based system can be expanded to support multiple antennas, (ii) the decomposition of the Clifford matrix

G_{F}

associated with the patterned RM code can be considered as a transmitter’s information reconstruction, and the iterative approach is generalized at the receiver.

Author Contributions

Methodology, W.X. and H.Z.; software, W.X. and R.T.; validation, W.X.; formal analysis, W.X.and R.T.; investigation, W.X. and R.T.; resources, W.X.; data curation, W.X.; writing—original draft preparation, W.X.; writing—review and editing, W.X. and R.T.; visualization, W.X. and R.T.; supervision, H.Z.; project administration, H.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

Saad, W.; Bennis, M.; Chen, M. A vision of 6G wireless systems: Applications, trends, technologies, and open research problems. IEEE network 2019, 34(3), 134–142. [Google Scholar] [CrossRef]
Guo, F.; Yu, F. R.; Zhang, H.; Li, X.; Ji, H.; Leung, V. C. Enabling massive IoT toward 6G: A comprehensive survey. IEEE Internet of Things Journal 2021, 8(15), 11891–11915. [Google Scholar] [CrossRef]
Pan, C.; Mehrpouyan, H.; Liu, Y.; Elkashlan, M.; Arumugam, N. Joint pilot allocation and robust transmission design for ultra-dense user-centric TDD C-RAN with imperfect CSI. IEEE Wirel. Commun 2018, 17(3), 2038–2053. [Google Scholar] [CrossRef]
Chettri, L.; Bera, R. A comprehensive survey on Internet of Things (IoT) toward 5G wireless systems. IEEE Internet of Things Journal 2020, 7(1), 16–32. [Google Scholar] [CrossRef]
Masoudi, M.; Azari, A.; Yavuz, E. A.; Cavdar, C. Grant-free radio access IoT networks: Scalability analysis in coexistence scenarios. In Proceedings of the IEEE International Conference on Communications (ICC), Kansas City, MO, USA, 20-24 May 2018; pp. 1–7. [Google Scholar]
Shahab, M. B.; Abbas, R.; Shirvanimoghaddam, M.; Johnson, S. J. Grant-free non-orthogonal multiple access for IoT: A survey. IEEE Commun. Surv. Tut 2020, 22(3), 1805–1838. [Google Scholar] [CrossRef]
Chen, X.; Chen, T. Y.; Guo, D. Capacity of Gaussian many-access channels IEEE Trans. Inf. Theory 2017, 63(6), 3516–3539. [Google Scholar] [CrossRef]
Polyanskiy, Y. A perspective on massive random-access. In Proceedings of the IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, 25–30 June 2017; pp. 2523–2527. [Google Scholar]
Zadik, I.; Polyanskiy, Y.; Thrampoulidis, C. Improved bounds on Gaussian MAC and sparse regression via Gaussian inequalities. In Proceedings of the 2019 IEEE International Symposium on Information Theory (ISIT), Paris, France, 7-12 July 2019; pp. 430–434. [Google Scholar]
Ngo, K. H.; Lancho, A.; Durisi, G. Unsourced multiple access with random user activity. IEEE Trans. Inf. Theory 2023, 1–1. [Google Scholar] [CrossRef]
Ordentlich, O.; Polyanskiy, Y. Low complexity schemes for the random access Gaussian channel. In Proceedings of the 2017 IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, 25–30 June 2017; pp. 2528–2532. [Google Scholar]
Marshakov, E.; Balitskiy, G.; Andreev, K.; Frolov, A. A polar code based unsourced random access for the Gaussian MAC. In Proceedings of the 2019 IEEE 90th Vehicular Technology Conference (VTC2019-Fall), Honolulu, Hawaii, USA, 22–25 September 2019; pp. 1–5. [Google Scholar]
Pradhan, A. K.; Amalladinne, V. K.; Vem, A.; Narayanan, K. R.; Chamberland, J. F. Sparse IDMA: A Joint Graph-Based Coding Scheme for Unsourced Random Access. IEEE Trans. Commun. 2022, 70(11), 7124–7133. [Google Scholar] [CrossRef]
Ahmadi, M. J.; Duman, T. M. Random spreading for unsourced MAC with power diversity. IEEE Commun. Lett 2021, 25(12), 3995–3999. [Google Scholar] [CrossRef]
Pradhan, A.K.; Amalladinne, V.K.; Narayanan, K.R.; Chamberland, J.F. LDPC Codes with Soft Interference Cancellation for Uncoordinated Unsourced Multiple Access. In Proceedings of the IEEE International Conference on Communications (ICC), Montreal, QC, Canada, 14–23 June 2021; pp. 1–6. [Google Scholar]
Amalladinne, V.K.; Chamberland, J.F.; Narayanan, K.R. A Coded Compressed Sensing Scheme for Unsourced Multiple Access. IEEE Trans. Inf. Theory 2020, 66, 6509–6533. [Google Scholar] [CrossRef]
Amalladinne, V. K.; Vem, A.; Soma, D. K.; Narayanan, K. R.; Chamberland, J. F. A coupled compressive sensing scheme for unsourced multiple access. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, Alberta, Canada, April 15-20, 2018; pp. 6628–6632. [Google Scholar]
Lancho, A.; Fengler, A.; Polyanskiy, Y. Finite-blocklength results for the A-channel: Applications to unsourced random access and group testing. In Proceedings of the 2022 58th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, Illinois, September 28–30, 2022; pp. 1–8. [Google Scholar]
Amalladinne, V.K.; Pradhan, A.K.; Rush, C.; Chamberland, J.F.; Narayanan, K.R. Unsourced random access with coded compressed sensing: Integrating AMP and belief propagation. IEEE Trans. Inf. Theory 2022, 68, 2384–2409. [Google Scholar] [CrossRef]
Andreev, K.; Rybin, P.; Frolov, A. Reed-Solomon coded compressed sensing for the unsourced random access. In Proceedings of the 2021 17th International Symposium on Wireless Communication Systems (ISWCS), Berlin, Germany, 6–9 September 2021; pp. 1–5. [Google Scholar]
Che, J.; Zhang, Z.; Yang, Z.; Chen, X.; Zhong, C.; Ng, D.W.K. Unsourced random massive access with beam-space tree decoding. IEEE J. Sel. Areas Commun. 2021, 40, 1146–1161. [Google Scholar] [CrossRef]
Fengler, A.; Haghighatshoar, S.; Jung, P.; Caire, G. Non-Bayesian Activity Detection, Large-Scale Fading Coefficient Estimation, and Unsourced Random Access With a Massive MIMO Receiver. IEEE Trans. Inf. Theory 2021, 67, 2925–2951. [Google Scholar] [CrossRef]
Andreev, K.; Rybin, P.; Frolov, A. Coded Compressed Sensing with List Recoverable Codes for the Unsourced Random Access. IEEE Trans. Commun. 2022, 70, 7886–7898. [Google Scholar] [CrossRef]
Liang, Z.; Zheng, J.; Ni, J. Index modulation–aided mixed massive random access. Front. Commun. Networks 2021, 2, 694557. [Google Scholar] [CrossRef]
Fengler, A.; Jung, P.; Caire, G. SPARCs for unsourced random access. IEEE Trans. Inf. Theory 2021, 67, 6894–6915. [Google Scholar] [CrossRef]
Ebert, J.R.; Amalladinne, V.K.; Rini, S.; Chamberland, J.F.; Narayanan, K.R. Coded demixing for unsourced random access. IEEE Trans. Signal Process. 2022, 70, 2972–2984. [Google Scholar] [CrossRef]
Zhang, L.; Luo, J.; Guo, D. Neighbor discovery for wireless networks via compressed sensing. Perform. Eval. 2013, 70, 457–471. [Google Scholar] [CrossRef]
Zhang, H.; Li, R.; Wang, J.; Chen, Y.; Zhang, Z. Reed-Muller sequences for 5G grant-free massive access. In Proceedings of the GLOBECOM 2017 IEEE Global Communications Conference, Singapore, 4–8 December 2017; pp. 1–7. [Google Scholar]
Wang, J.; Zhang, Z.; Hanzo, L. Joint active user detection and channel estimation in massive access systems exploiting Reed–Muller sequences. IEEE J. Sel. Top. Signal Process 2019, 13, 739–752. [Google Scholar] [CrossRef]
Wang, J.; Zhang, Z.; Hanzo, L. Incremental massive random access exploiting the nested Reed-Muller sequences. IEEE Trans. Wirel. Commun. 2020, 20, 2917–2932. [Google Scholar] [CrossRef]
Calderbank, R.; Thompson, A. CHIRRUP: A practical algorithm for unsourced multiple access. Inform. Inference J. IMA 2020, 9, 875–897. [Google Scholar] [CrossRef]
Wang, J.; Zhang, Z.; Chen, X.; Zhong, C.; Hanzo, L. Unsourced massive random access scheme exploiting reed-muller sequences. IEEE Trans. Commun. 2020, 70, 1290–1303. [Google Scholar] [CrossRef]
Xie, W.; Zhang, H. Patterned Reed–Muller Sequences with Outer A-Channel Codes and Projective Decoding for Slot-Controlled Unsourced Random Access. Sensors 2023, 23(11), 5239. [Google Scholar] [CrossRef] [PubMed]
Pllaha, T.; Tirkkonen, O.; Calderbank, R. Binary subspace chirps. IEEE Trans. Inf. Theory 2022, 68, 7735–7752. [Google Scholar] [CrossRef]
Pllaha, T.; Tirkkonen, O.; Calderbank, R. Reconstruction of multi-user binary subspace chirps. In Proceedings of the 2020 IEEE International Symposium on Information Theory (ISIT), Los Angeles, CA, USA, 21–26 June 2020; pp. 531–536. [Google Scholar]
Tirkkonen, O.; Calderbank, R. Codebooks of complex lines based on binary subspace chirps. In Proceedings of the 2019 IEEE Information Theory Workshop (ITW), Visby, Sweden, 25–28 August 2019; pp. 1–5. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Iterative List Patterned Reed-Muller Projection Detection-based Packetized Unsourced Massive Random Access

Abstract

1. Introduction

1.1. Contributions and Arrangement

1.2. Conventions

2. System Model

2.1. Patterned Reed-Muller Sequence

2.2. Detection Algorithm of Multi-PRM Sequence

3. Iterative List PRM Projection Algorithm-based Inner-Code Detector

3.1. List PRM Projection Algorithm

3.2. Iterative List PRM projection Algorithm

4. Performance Analysis

4.1. Successful Recovery Probability of the List PRM Projection Algorithm

4.2. Successful Recovery Probability of the Iterative List PRM Projection Algorithm

5. Simulation Results

5.1. Performances of the Algorithms 1 and 2

5.2. Iterative List PRM Projection Algorithm-based Slot-controlled URA

6. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe