Combination Optimization Method of Grid Section Based on Deep Reinforcement Learning with Accelerated Convergence Speed

Preprint

Article

Combination Optimization Method of Grid Section Based on Deep Reinforcement Learning with Accelerated Convergence Speed

Altmetrics

Downloads

Views

Comments

Huashi Zhao,Zhichao Wu,Yubin He,Qiujia Fu,Shouyu Liang,Guang Ma,Wenchao Li,

Qun Yang^*

Huashi Zhao,Zhichao Wu,Yubin He,Qiujia Fu,Shouyu Liang,Guang Ma,Wenchao Li,

Qun Yang^*

This version is not peer-reviewed

Submitted:

02 July 2023

Posted:

06 July 2023

You are already at the latest version

Alerts

Abstract

Modern power system integrates more and more new energy and use a large number of power electronic equipment. This makes it face more challenges in online optimization and real-time control. Deep reinforcement learning(DRL) has the ability of processing big data and high-dimensional features, as well as the ability of independently learning and optimizing decision-making in complex environments. In this paper, we explore DRL based online combination optimization method of grid section for large complex power system. In our method, to improve the convergence speed of the model, we propose to discretize the output action of the unit and simplify the action space. We also design a reinforcement learning loss function with strong constraints to further improve the convergence speed of the model and facilitate the algorithm to obtain the stable solution. Moreover, to avoid the local optimal solution problem caused by the discretization of the output action, we propose to use the annealing optimization algorithm to make the granularity of the unit output finer. We verify our method on IEEE 118-bus system. The experimental results show that our model has fast convergence speed and better performance, and can obtain stable solutions.

Keywords:

Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning

1. Introduction

The fundamental issue of power systems is to ensure that the grid operates economically, reliably and stably. Nowadays, as new energy develops rapidly and its proportion in the total power supply continues to increases, the power system faces the new challenges in terms of real-time dispatch and stability control.

Most of the traditional power dispatching solutions are based on accurate modeling of the system, mainly using classical methods [1,2,3], meta-heuristic methods [4,5], and hybrid methods [6,7]. However, in modern power systems, the integration of renewable energy brings randomness into the energy output of unit commitment. It greatly increases the uncertainty of system operation. At the same time, as modern power systems use a large number of power electronic equipment, it reduces the system inertia, while decreasing the ability of resist faults. It also makes the fault form more complex and further increases the risk of chain reaction. Therefore, in modern power systems, the traditional power dispatching methods face the problems such as large action space, long decision-making steps, high computational complexity and poor performance. They also have to deal with uncertainty and sudden situations. In order to meet the high accuracy and real-time requirements of grid dispatching for the modern power system, it is of great practical significance to explore how to minimize the system power generation cost while maximizing the release of system regulation capacity under the premise of ensuring the safety and stability of the operation of the new power system, meanwhile, promote clean energy consumption and ensure the stable operation of the power grid.

Power dispatching is a multi-constraint, nonlinear, high-dimensional optimization decision problem. On the other hand, deep reinforcement learning combines the decision-making ability of reinforcement learning and the feature representation ability of deep learning, as well as the powerful approximation function of neural networks, so it has the ability to process large data and high-dimensional features. And, it can independently learn and optimize decision-making in complex environments. All these make the DRL very suitable for power dispatching. Actually, in recent years, DRL has gained momentum in the fields of power dispatching and system control.

The basic principle of reinforcement learning is that the agent performs a series of actions in an environment and obtains feedback from the environment to adjust its strategy, thus achieving optimal decision-making. [8] proposes an optimal power flow method based on Lagrangian deep reinforcement learning for real-time optimization of power grid control. [9] implements an online AC OPF by combining reinforcement learning and imitation learning. Imitation learning is a kind of supervised learning. It can improve the learning efficiency of agents in reinforcement learning by learning from expert experience. [10] uses DQN(Deep Q-network)-based reinforcement learning to model the reactive voltage optimization problem. It realizes the online optimization under the condition of new energy, load fluctuation and N-1 fault. Both [11] and [12] use the policy-based reinforcement learning algorithm PPO to realize autonomous dispatching of the power system. Different from [12], [11] combines graph neural network with reinforcement learning. Graph neural network is used to model the power grid structure and its topological changes, achieving autonomous dispatch of the power system with variable topology. [13] explores how to autonomously control of the power system under the influence of extreme weather. It proposes a DRL method based on imitation learning. Their method takes generation redispatch and load shedding, together with topology switching, into consideration. Imitation learning is used in their method to learn from domain knowledge, historical data, and expert experience. The imitation learning module interacts with agents during reinforcement learning, making the system to operate as much as possible in the original topology. Besides, imitation learning can also accelerate convergence speed of DRL model. [14] aims at the AC-OPF problem. It proposes a DRL base on the penalty convex process. In their method, a systematic control strategy is obtained through DRL, and the operation constraint is satisfied by using the convex safety layer.

All of the above works have investigated the application of deep reinforcement learning in power dispatching. In this paper, we explore the section control of the modern power system with which integrated new energy. We aim at online optimization for large-scale power system whose optimization goals are complex. In our method, we propose a DRL method with accelerated convergence speed to solve the problem of dimensional disaster that occurs when the problem scale and decision variables increase. We also addresses the problem that the dispatching algorithm is difficult to obtain a stable solution because the optimization targets are coupling and mutually constrained, moreover, each target is inconsistent sensitivity to the unit adjustment.

The contributions of this paper are as follows:

(1)

We propose a combination optimization method for grid dispatching based on deep reinforcement learning, in which we simplify the action space and improve the convergence speed of the model by discretizing the unit output action.

(2)

We also propose a reinforcement learning loss function with strong constraints to further improve the convergence speed of the model as well as achieve the stability of the algorithm solution.

(3)

We propose the annealing optimization algorithm to make the granularity of the unit output finer and avoid the problem of local optimal solutions caused by the discretization of the output actions.

Experimental results on IEEE 118-bus system show that our method is effective. By using our method, the converge speed of the DRL model is faster, and stable solutions can be achieved.

2. Mathematical model for combination optimization of grid sections

2.1. Objective function

With the objective of minimizing the total power generation costs of the hydro, thermal and wind power multi-energy complementary systems, and improving the system’s new energy consumption (see Equation (1) for details), a short-term optimal scheduling model for combination optimization of grid sections is established.

F_{c} = m i n \sum_{t = 1}^{T} (w_{1} \sum_{i \in I_{f}} C_{i, t} (p_{i, t}) + w_{2} \sum_{i \in I_{w}} C_{i, t} (p_{i, t}) + w_{3} \sum_{i \in I_{n} e} C_{i, t} (p_{i, t}) + w_{4} \sum_{i \in_{I_{n e}}} \frac{p_{i, t}}{p_{i}^{m a x}})

(1)

Where

C_{i, t} (p_{i, t})

is the operating cost of the i-th generator unit at interval t , it is a quadratic function related to the output range of each section of the generator unit and the corresponding energy price (see Equation (2) for details);

p_{i, t}

is the active power output of the i-th generator unit at interval t;

w_{1}

w_{2}

w_{3}

w_{4}

are combination coefficients;

I_{f}

is the hydroelectric generator sets;

I_{t}

is the thermal generator sets and

I_{w}

is the wind generator sets;

p_{i}^{m a x}

is the maximum active output of the i-th generator unit; T is the number of time slots in the scheduling cycle; N is the number of units participating in combination calculation.

C_{i, t} (p_{i, t}) = a * p_{i, t}^{2} + b * p_{i, t} + c

(2)

Where a , b and c are the coefficients for the quadratic, linear, and constant terms of the operating cost function, respectively.

2.2. Constraints

(1)

Load Balance Constraint

In the power system, the total output of the generator units should be equal to the system load at any time, which can be expressed as:

L_{t} - \sum_{i = 1}^{N} p_{i, t} = 0, \forall_{t}

(3)

Where

L_{t}

is the total load data of the power system at interval t.

(2)

Maximum and minimum output constraints of generator units

Considering the physical properties of the generator unit, the output of each generator unit in operation is adjustable within a certain range, which can be expressed as:

p_{i}^{m i n} \leq_{p_{i}} \leq p_{i}^{m a x}, \forall i

(4)

where

p_{i}^{m i n}

and

p_{i}^{m a x}

are the minimum and maximum output of the nth generator unit, respectively.

(3)

Cross-section power flow limit constraint In the power system, the active power flow of the grid section should be within a certain range at any time, which can be expressed as:

|P_{s} (a)| \leq |P_{s}^{m a x}|, \forall s \in S

(5)

where

P_{s} (a)

is the active power flow of the section s based on the current output p of the generator unit,

P_{s}^{m a x}

is the active power flow limit of the section s, and S represents the section set.

3. Combination optimization of grid section

3.1. Deep reinforcement learning

Reinforcement learning is an important method suitable for solving optimization problems. Its mathematical basis and modeling tool are Markov decision process (MDP). The components of an MDP include state space, action space, state transition function and reward function etc. Reinforcement learning implements MDP with agent, environment, state, reward and action.

Recently, deep reinforcement learning combines deep learning with reinforcement learning, and deep neural networks greatly improves the efficiency and performance of reinforcement learning. In DRL, deep learning models are used to learn the value function or the policy function so that agents can learn to make better decisions. Commonly used DRL algorithms include DQN (Deep Q-Network) [15], DDPG (Deep Deterministic Policy Gradient) [16] and Actor-Critic [17].

In this paper, we adopt the Actor-Critic(AC) algorithm and introduce two neural networks into it. One of the neural networks is the policy generation network. The other is the policy evaluation network.

The policy network

π (a | s; θ)

is equivalent to an actor. It can choose the corresponding action a based on the state s which is fed back by the environment. The policy network in the AC algorithm adopts a policy-gradient (PG) network to optimize the policy. The optimization method is that the agent learns to estimate the expected reward of each state, and use the learned knowledge to decide how to choose action.

The policy evaluation network plays the role of critic by using the value network

q (s; v)

. The value network evaluates the action a of the policy network, and feed back a temporal-difference (TD) [18] value to the policy network, evaluating whether the behavior of the policy network is good or bad.

The objective of policy network is to obtain a higher evaluation by adjusting action , where

θ

and v are the parameters to be trained in the policy network and value network respectively. In this paper, to reduce the network update error, we incorporate the TD error [19] method with baseline. We also use the asynchronous parallel computing method to maximize computing performance. We will give the detailed method In the following sections.

3.2. Environment setting for reinforcement learning

The basic elements of this reinforcement learning environment are as follows:

(1)

Environment. The environment mainly includes various grid section information, such as grid topology, system load, bus load, generator unit status and section data. Also, there are grid system constraints in the environment, including power flow constraints, load balance constraints and generator unit constraints.

(2)

Agents. It is sets of generator unit participating in combination optimization calculation of grid section.

(3)

State space. The state space in the grid section combination optimization problem includes current active power output of generator units, system load, bus load and branch load etc. The state transition function refers to the probability that the generator unit will take the next action in the current state.

(4)

Actions and action space. Actions represent current decisions made by the agent. Action space represents the set of all possible decisions. In the combination optimization problem of the grid section, action represents the active power output of the generator unit at the next moment. Action space is all possible values of the active power output of generators, which is constrained by the maximum and minimum value of the generators output.

In this paper, to improve the learning speed of the policy network, we simplify the action space from the absolute output of the generator unit to one of the three discrete values,

i . e .

1, 0, -1, which represent the next output of the generator unit is upward adjusted (represented as 1 in Table 1), downward adjusted (-1), or not adjusted(0), respectively. This optimization method transforms the multi-dimensional continuous action space into a multi-dimensional discrete action space, avoiding the curse of dimensionality and slow model convergence. Below, Table 1 gives the illustration.

Table 1. action space

generator	Traditional method action space	The action space of the proposed method
0	[0,30]	{-1,0,1}
1	[0,100]	{-1,0,1}
⋮	⋮	⋮
N	[0,80]	{-1,0,1}
action space	∞	$3^{N}$

(5)

Reward function. The reward function represents the reward value obtained by the agent after taking a certain action. The optimization goal is to obtain the maximum reward value. In view of the combination optimization problem of grid section, we design five types of rewards: 1) system cost rewards, 2) power flow limitation rewards, 3) load balancing rewards, 4) clean energy consumption rewards, 5) generator unit limitation rewards. The purpose of optimizing the reward function is to minimize the system cost and maximize the proportion of clean energy on the premise that the power flow does not exceed the boundary, the output of the generator unit does not exceed the boundary and the load is balanced in the grid system.

For each time step t, the evaluation score

R_{t}

of the system is as follows:

R_{t} = \sum_{i = 1}^{5} r_{i, t}

(6)

where

r_{i, t}

is the reward of i-th type at the time step t. For simplicity, the subscript in the following formulas is omitted. Specifically, each type of reward is calculated as follows:

1) system cost (positive reward), its value range is

A_{0}

*[0,100],

r_{0} = A_{0} * 100 * min (\frac{C_{min}}{\sum_{i = 1}^{N} C_{i}}, 1)

(7)

where

A_{0}

=1 is the score weight.

c_{i}

is the cost of the corresponding generator and the system has N generators in total.

C_{m i n}

is the normalization constant, which is the minimum cost of the system at a moment over a period of time. The lower the system cost is, the higher the reward score is.

2) power flow limit reward (positive reward), its value range is ,

r_{1} = A_{1} * max ((100 - \sum_{s = 1}^{S} r^{s}), 0))

(8)

where

A_{1}

=4 is the score weight. S is the total number of sections, and

r^{s}

is the reward value of the s-th section. It is calculated according to different situations (over-limit or normal). When over-limit (that is, exceeding the upper or lower limit of the predetermined value) severe penalties are imposed, whereas under normal circumstances, there is no penalty. The specific calculation method is as follows:

r^{s} = \{\begin{matrix} \frac{|P_{s} - P_{s}^{min}|}{10}, & if P_{s} < P_{s}^{min} \\ 0, & else \\ \frac{|P_{s} - P_{s}^{max}|}{10}, & if P_{s} > P_{s}^{max} \end{matrix}

(9)

where

P_{s}

is the power flow of section s,

P_{s}^{m a x}

is the upper limit of section s, and

P_{s}^{m i n}

is the lower limit of section s.

3) load balance reward (positive reward), its value range is ,

r_{2} = A_{2} * max (100 * (1 - \frac{|L - \sum_{i = 1}^{N} P_{i}|}{(0.1 * L)}), 0)

(10)

where

A_{2}

=3 is the score weight.L represents the total real load of system at time t and the denominator

0.1 * L

is a normalization parameter which is set according to the comprehensive consideration of ultra-short-term forecast deviation and score interval.

P_{i}

is the active power output of generator unit i and N is the total number of generator unit.

4) clean energy consumption reward (positive reward), its value range is ,

r_{3} = A_{3} * 100 * \frac{1}{M} \sum_{i = 1}^{M} m i n (1, \frac{P_{i}}{P_{i}^{m a x}})

(11)

where

A_{3}

is the score weight,

P_{i}

represents the active power output of the clean energy generator unit i and

P_{i}^{m a x}

represents the maximum output of the clean energy generator unit i. In order to avoid the denominator being 0 when calculating the score, when

P_{i}^{m a x}

appears 0, the score of generator unit i will be 0. There are totally M clean energy generators.

5) generator unit limit reward(positive reward), its value range is ,

r_{4} = A_{4} * m a x ((100 - \sum_{i = 1}^{N} r^{i}), 0)

(12)

where

A_{4}

=1 is the score weight, N is the total number of units and

r^{i}

is the reward value of the s-th generator. It is calculated according to different situations (over-limit or normal). When over-limit (that is, exceeding the upper or lower limit of the predetermined value) severe penalties are imposed, whereas under normal circumstances, there is no penalty. The specific calculation method is as follows:

r^{i} = \{\begin{matrix} \frac{|P_{i} - P_{i}^{min}|}{10}, & if P_{i} < P_{i}^{min} \\ 0, & else \\ \frac{|P_{i} - P_{i}^{max}|}{10}, & if P_{i} > P_{i}^{max} \end{matrix}

(13)

where

P_{i}

is the active output of generator i,

P_{i}^{m a x}

is the upper limit of active output of generator unit i, and

P_{i}^{m i n}

is the lower limit of active output of generator i.

3.3. Constrained reinforcement learning loss

In AC algorithm, the training of critic is to fit the reward. Its loss function is as follows:

L_{c r i t i c} = \frac{1}{N} \sum_{i}^{N} (G_{t} - V (s_{t} 0))

(14)

Where

G_{t}

R_{t + 1} + γ R_{t + 2} + \dots + γ^{n - 1} + γ^{n}

, and the training of actor is to find the optimal action a for the following minimization problem:

\begin{matrix} minimize L_{actor} & = w_{1} |L - \sum_{i \in I} a_{i}| + w_{2} \sum_{s \in S} |P_{s} (a) - P_{s}^{max}| \\ - & w_{3} \sum_{i \in I_{n e}} \frac{a_{i}}{a_{i}^{max}} + w_{4} \sum_{i \in I} c_{i} a_{i} \end{matrix}

(15)

Where

w_{1} - w_{4}

are the weight values of each item,L represents the total load of the grid system,

a_{i}

represents the active power output of the i-th generator, I represents the set of all generators; S represents the set of all grid sections,

P_{s} (a)

represents the power flow value of the section s, and a is the output of the generator unit.

P_{s}^{m a x}

is the maximum power flow of the section s,

I_{n e}

represents the clean energy generator set,

a_{i}^{m a x}

represents the maximum active output of the i-th clean energy generator,

c_{i}

represents the cost coefficient of the i-th generator.

However, in the above formula, the two strong constraints, namely load balance and power flow constraint, are relaxed as objective functions with weights, making the algorithm unable to obtain a stable solution in principle. Therefore, we proposes a constrained reinforcement learning loss as follows:

m i n i m i z e L_{a c t o r \underset{̲}{} c o n s t r a i n e d} = - W_{1} \sum_{i \in I} \frac{a_{i}}{a_{i}^{m a x}} + w_{2} \sum_{i \in I} c_{i} a_{i}

(16)

s . t . \{\begin{matrix} L - \sum_{i \in I} a_{i} = 0 \\ P_{s} (a) < = P_{s}^{max} \end{matrix}

While satisfying the load balance and power flow constraints, the objective function above can fits those actions that maximize clean energy consumption and minimize cost. It restores the essence of the grid section combination optimization problem, which is more conducive to the convergence of the reinforcement learning algorithm. We incorporate this loss into the training of the reinforcement learning algorithm by using Lagrangian constraints.

3.4. Training method and process

In this paper, we choose the Actor-Critic reinforcement learning algorithm. The implementation of DRL combined with Constrained RL Loss is shown in the Algorithm 1 below. The training process is as follows:

1) Firstly, generate the sample data by using the PYPOWER simulator. Then, clear the cache in the experience pool, set the initial state of the power system and reset the reward value.

2) Input the observed state

s_{t}

of the current grid section system into the policy network, and obtain the active power output

a_{t}

of the generator unit through the policy network.

3) Input the output

a_{t}

of the generator unit into the reinforcement learning environment, and obtain the grid state

s_{t + 1}

in the next stage, the reward value r corresponding to the current policy and the completion state

d o n e

4) Save the grid state

s_{t}

, the next moment’s state

s_{t +}

, the output policy

a_{t}

, the current reward value r and the completion state

d o n e

into the experience pool.

5) Judge whether the current experience pool has reached the upper limit of capacity. If the experience pool has not reached the limit, repeat step 3), otherwise go to step 6).

6) When the accumulated data in the experience pool reaches the batch size, it will be input into the policy network and value network as training data to train the network parameters, and return to step 1).

The detailed algorithm is described in Algorithm 1.

Algorithm 1 AC training based on constrained RL loss

Require: episode $e p$ , discount factor $γ$ , $L R_{a}$ , $L R_{c}$ , batch size b, $θ_{a}$ , $θ_{c}$ , $m a x s i z e$
while $i < e p$ do
reward=0; reset env; reset the experience pool
collect the trajectories information including $(S_{t}, A_{t}, R_{t}, S_{t + 1})$
if $p o o l s i z e < m a x s i z e$ then
$p o o l \leftarrow (S_{t}, A_{t}, R_{t}, S_{t + 1})$
end if
if $p o o l s i z e > b$ then
update $θ_{a}$ with $L_{a c t o r_{c} o n s t r a i n e d}$
update $θ_{c}$ with $L_{c r i t i c}$
end if
end while

4. Annealing optimization algorithm

In this paper, the action space is discretized, so the granularity of action output by the model is not fine enough, resulting in the obtained solution is still a distance from the optimal solution. In view of this problem, we use the annealing algorithm [20] after our DRL algorithm to optimize the output of generator unit. We call it the annealing optimization algorithm. It can further improve the above DRL method to find the optimal fine-grained solution.

Annealing algorithm is a global optimization method based on simulated physical annealing process. The basic idea of the algorithm is to start from an initial solution, continuously perturb the current solution randomly, and choose to accept the new solution or keep the current solution according to a certain probability. The function of this probability of accepting a new solution is called the "acceptance criterion". Acceptance criterion allows the algorithm to perform a random walk in the search space, and gradually reduce the temperature (that is, reduce the probability of accepting a new solution), until it reaches a stable state.

In annealing optimization algorithm, temperature parameter is usually used to control the variation of the acceptance criterion. At the beginning of the algorithm, the temperature is relatively high, so acceptance criterion is easy to accept new solutions. Therefore, a large-scale random search can be performed in the search space. As time goes by, the temperature gradually decreases, acceptance criterion becomes more and more difficult to accept the new solution, making the search process gradually stabilizes. Eventually, the algorithm arrives at a near-optimal solution.

Annealing optimization algorithms are often used to solve nonlinear optimization problems, especially those with a large number of local optima. The advantage of the algorithm is that it can avoid falling into a local optimal solution and can perform a global search in the search space. We use the output of the DRL model as the initial solution of the annealing optimization algorithm. The process of the annealing algorithm is as follows:

(1)

Initialize the temperature T and the initial solution x.

(2)

At the current temperature, a random perturbation of the current solution produces a new solution

x^{'}

(3)

Calculate the energy difference

Δ E

between the new solution and the current solution.

(4)

Δ E

< 0, accept the new solution as the current solution.

(5)

Δ E \geq 0

, accept the new solution as the current solution with probability

P = e x p (- Δ E / T)

(6)

Lower the temperature T.

(7)

Repeat steps 2-6 until the temperature drops to the end temperature or the maximum number of iterations is reached.

5. Case study

To verify the effectiveness of our method, this paper uses IEEE 118 calculation example. Power system IEEE 118 is a standard power system network example. It consists of 118 bus, 54 generators and 186 branches, representing a real power system network. In this paper, the generators Gen 1-Gen 20 are set as the new energy units.

The computing environment in this paper is based on PYPOWER. We set the scheduling cycle to 15min a day. According to the above description of the MDP process, AC algorithm has 20 dimensions of state space. The dimension of the action space is 54. The detailed setting of hyper-parameters is shown in Table 2.

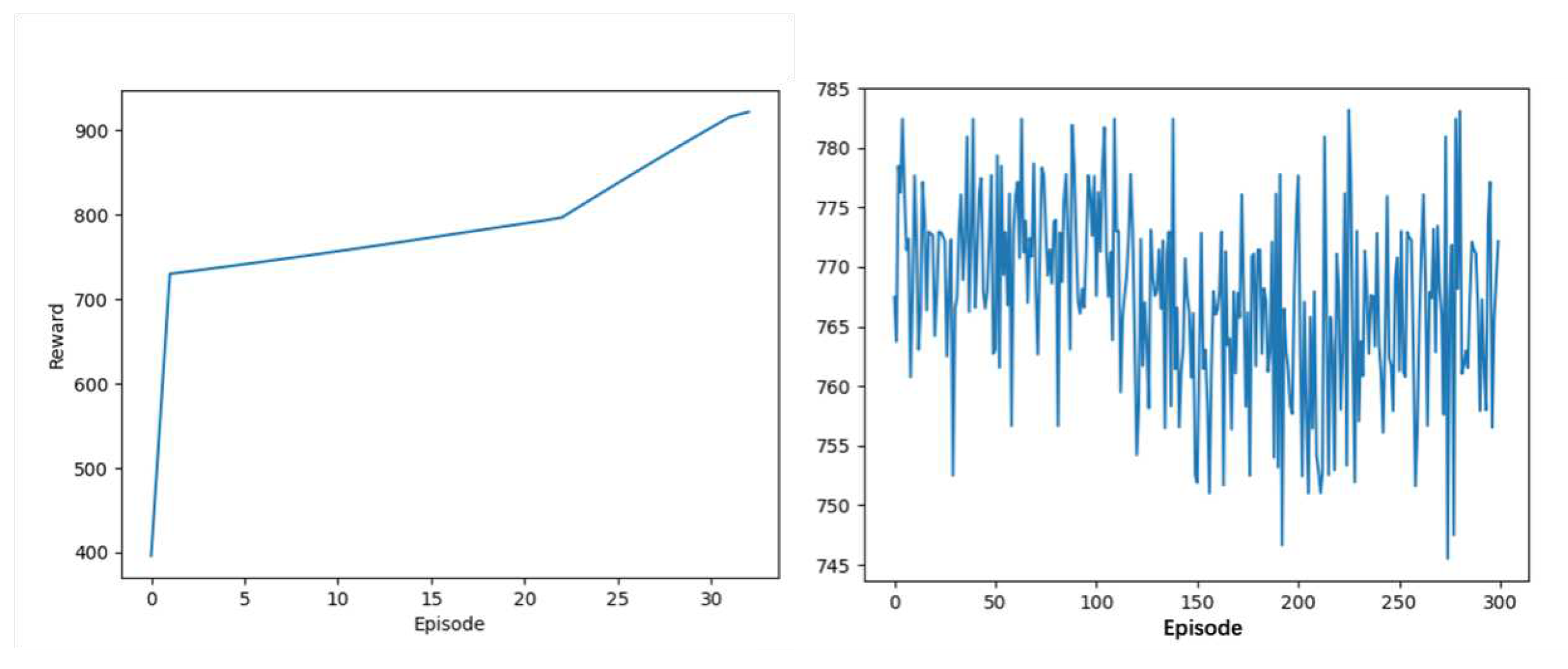
Using the environment in this paper and our AC algorithm based on the Constrained Reinforcement Learning Loss, the agent maximizes the reward by adjusting the active power generated by the generator unit, while minimizing the total cost and enhancing the new energy consumption. It can be seen from the Figure 1 that the AC algorithm based on Constrained Reinforcement Learning can converge and solve after 30 episodes. In contrast, it can be found that the traditional AC algorithm (Vanilla AC) cannot achieve convergence in the same episode, and it even cannot always reach the optimal solution. Table III shows that vanilla AC training takes much longer than 4 hours, but after using the Constrained Reinforcement Learning Loss we proposed, the model convergence time is reduced to 1 hour. By comparison, we can see that the proposed loss function plays a vital role in the stability of the solution and the convergence speed of model training.

Table 2. Setting of hyper-parameters

Hyper-parameter	Value
discount factor $δ$	0.95
BATCH SIZE	64
$A \underset{̲}{} L R$	0.0001
$C \underset{̲}{} L R$	0.001
w $_{1} i n L_{a c t o r \underset{̲}{} c o n s t a i n e d}$	1
w $_{2} i n L_{a c t o r \underset{̲}{} c o n s t a i n e d}$	1

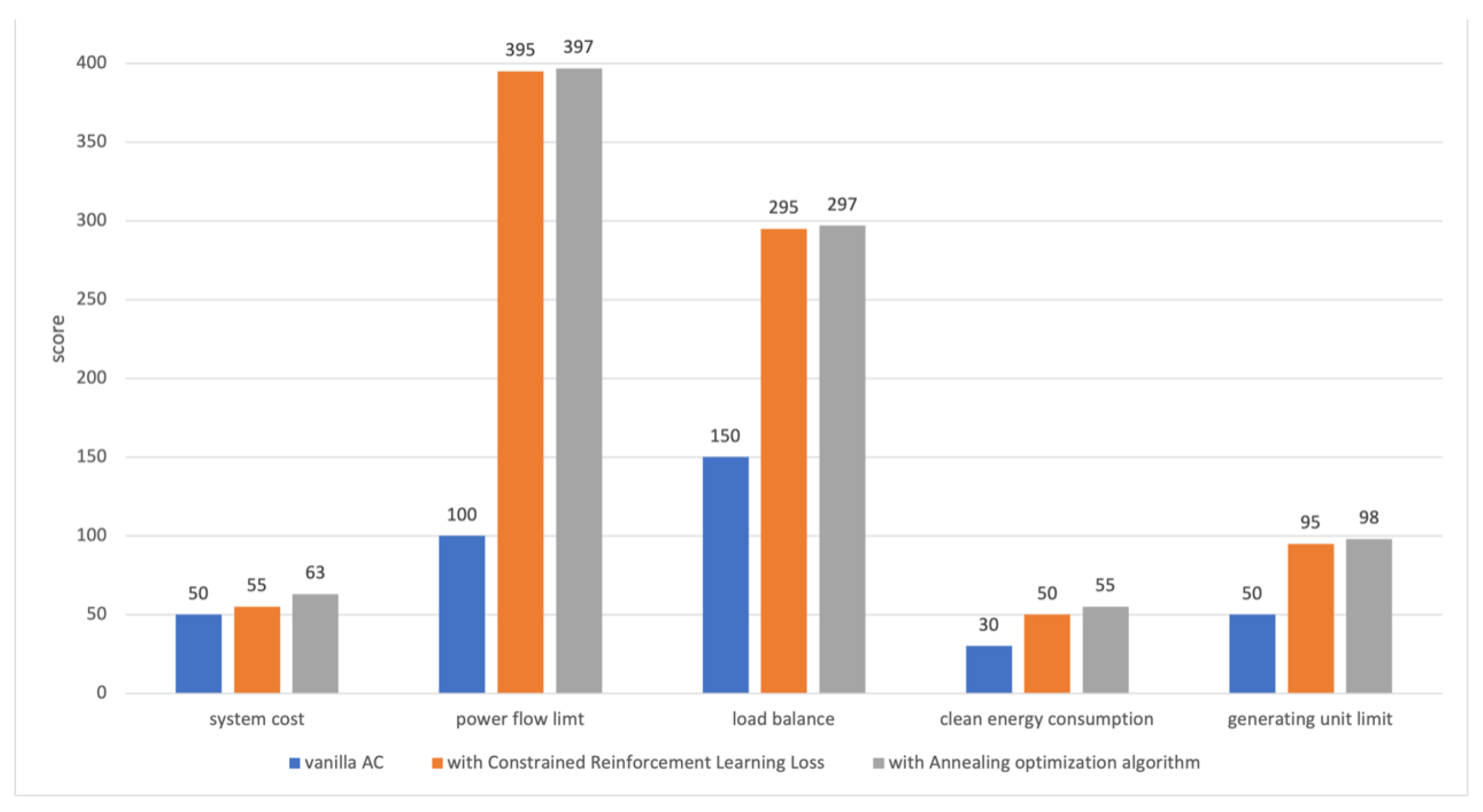
In Table 3, we compare experimental result of three methods: 1) Vanilla AC, 2) Vanilla AC plus Constrained Reinforcement Learning Loss, 3) Vanilla AC plus Constrained Reinforcement Learning Loss and annealing optimization algorithm. The score for all three methods is made up of five items. The full scores of system cost, power flow limit, load balance, clean energy consumption and generator unit limit are 100, 400, 300, 100 and 100, respectively. Among them, power flow limit, load balance and generator unit limit are strong constraints in the power grid section system. Our goal is to make these three items close to full marks.

As shown in Table 3, the scores of all indicators have been greatly improved due to the proposed loss function, meeting the safety requirements of power grid. The total reward score of the Vanilla AC is 380, while the AC algorithm with Constrained Reinforcement Learning Loss achieves a higher total reward score of 890.

Table 3. Control experiment to verify the effectiveness of the proposed method. CRLL:Constrained Reinforcement Learning Loss; AO:Annealing optimization algorithm

	model convergence time	system cost	power flow limt	load balance	clean energy consumption	generator unit limit	total reward score
Vanilla AC	>>4h	50	100	150	30	50	380
+ CRLL	1h	55	395	295	50	95	890
+ CRLL + AO	1h	63	397	287	55	98	910

Besides, by combing the DRL with the annealing optimization algorithm, it further improve the accuracy of the solution. In Table 3, the average reward score of the final model is 910, among which the reward of power flow limit, the reward of generator unit limit and the reward of load balance are all almost full scores. It indicates that the addition of the annealing optimization algorithm further improves the performance of the algorithm and obtains a fine-grained optimal solution.

We also present the results of the three methods in Figure 2 as a histogram. It intuitively demonstrate that the algorithm proposed in this paper is able to optimize the objective function under multiple strong constraints. So, we conclude that our method has good robustness and can meet the requirements of grid section dispatching.

6. Conclusion

In the face of high proportion of new energy generator unit and complex constrained environment, this paper uses deep reinforcement learning algorithm of simplified action space, together with Constrained Reinforcement Learning Loss, to search for the optimal active power output of generators. It also use annealing optimization algorithm to avoid the local optimal solution. The formulation and implementation process are introduced in detail. The test results on IEEE 118-bus system show that our method is effective and suitable for scheduling problems.

Author Contributions

Author 1 (Huashi Zhao):Conceptualization, Methodology of deep reinforment learning, Annealing optimization algorithm design and implementation, Writing - Original Draft; Author 2 (Zhichao Wu):Conceptualization, Methodology of section control, Mathematical model of grid dispatching, Formal analysis, Writing - Original Draft; Author 3(Yubin He): Validation, Writing - Original Draft; Author 4(Qiujia Fu): Data Curation; Author 5(Shouyu Liang): Resources, Supervision; Author 6(Guang Ma):Software, Validation; Author 7(Wenchao Li): Visualization; Author 8(Qun Yang): (Corresponding Author): Conceptualization, Funding Acquisition, Resources, Supervision, Writing - Review & Editing.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

Gherbi, F.; Lakdja, F. Environmentally constrained economic dispatch via quadratic programming. 2011 International Conference on Communications, Computing and Control Applications (CCCA). IEEE, 2011, pp. 1–5.
Irisarri, G.; Kimball, L.; Clements, K.; Bagchi, A.; Davis, P. Economic dispatch with network and ramping constraints via interior point methods. IEEE Transactions on Power Systems 1998, 13, 236–242. [Google Scholar] [CrossRef]
Zhan, J.; Wu, Q.; Guo, C.; Zhou, X. Fast λ-iteration method for economic dispatch with prohibited operating zones. IEEE Transactions on power systems 2013, 29, 990–991. [Google Scholar] [CrossRef]
Larouci, B.; Ayad, A.N.E.I.; Alharbi, H.; Alharbi, T.E.; Boudjella, H.; Tayeb, A.S.; Ghoneim, S.S.; Abdelwahab, S.A.M. Investigation on New Metaheuristic Algorithms for Solving Dynamic Combined Economic Environmental Dispatch Problems. Sustainability 2022, 14, 5554. [Google Scholar] [CrossRef]
Modiri-Delshad, M.; Kaboli, S.H.A.; Taslimi-Renani, E.; Abd Rahim, N. Backtracking search algorithm for solving economic dispatch problems with valve-point effects and multiple fuel options. Energy 2016, 116, 637–649. [Google Scholar] [CrossRef]
Aydın, D.; Özyön, S. Solution to non-convex economic dispatch problem with valve point effects by incremental artificial bee colony with local search. Applied Soft Computing 2013, 13, 2456–2466. [Google Scholar] [CrossRef]
Alshammari, M.E.; Ramli, M.A.; Mehedi, I.M. Hybrid Chaotic Maps-Based Artificial Bee Colony for Solving Wind Energy-Integrated Power Dispatch Problem. Energies 2022, 15, 4578. [Google Scholar] [CrossRef]
Yan, Z.; Xu, Y. Real-time optimal power flow: A lagrangian based deep reinforcement learning approach. IEEE Transactions on Power Systems 2020, 35, 3270–3273. [Google Scholar] [CrossRef]
Guo, L.; Guo, J.; Zhang, Y.; Guo, W.; Xue, Y.; Wang, L. Real-time Decision Making for Power System via Imitation Learning and Reinforcement Learning. 2022 IEEE/IAS Industrial and Commercial Power System Asia (I&CPS Asia). IEEE, 2022, pp. 744–748.
Jiang, L.; Wang, J.; Li, P.; Dai, X.; Cai, K.; Ren, J. Intelligent Optimization of Reactive Voltage for Power Grid With New Energy Based on Deep Reinforcement Learning. 2021 IEEE 5th Conference on Energy Internet and Energy System Integration (EI2). IEEE, 2021, pp. 2883–2889.
Zhao, Y.; Liu, J.; Liu, X.; Yuan, K.; Ren, K.; Yang, M. A Graph-based Deep Reinforcement Learning Framework for Autonomous Power Dispatch on Power Systems with Changing Topologies. 2022 IEEE Sustainable Power and Energy Conference (iSPEC). IEEE, 2022, pp. 1–5.
Zhou, Y.; Lee, W.J.; Diao, R.; Shi, D. Deep reinforcement learning based real-time AC optimal power flow considering uncertainties. Journal of Modern Power Systems and Clean Energy 2021, 10, 1098–1109. [Google Scholar] [CrossRef]
Liu, X.; Liu, J.; Zhao, Y.; Liu, J. A Deep Reinforcement Learning Framework for Automatic Operation Control of Power System Considering Extreme Weather Events. 2022 IEEE Power & Energy Society General Meeting (PESGM). IEEE, 2022, pp. 1–5.
Sayed, A.R.; Wang, C.; Anis, H.; Bi, T. Feasibility Constrained Online Calculation for Real-Time Optimal Power Flow: A Convex Constrained Deep Reinforcement Learning Approach. IEEE Transactions on Power Systems 2022. [Google Scholar] [CrossRef]
Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing atari with deep reinforcement learning. arXiv preprint, 2013; arXiv:1312.5602. [Google Scholar]
Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv preprint, 2015; arXiv:1509.02971. [Google Scholar]
Sutton, R.S.; McAllester, D.; Singh, S.; Mansour, Y. Policy gradient methods for reinforcement learning with function approximation. Advances in neural information processing systems 1999, 12. [Google Scholar]
Sutton, R.S. Learning to predict by the methods of temporal differences. Machine learning 1988, 3, 9–44. [Google Scholar] [CrossRef]
Silver, D.; Lever, G.; Heess, N.; Degris, T.; Wierstra, D.; Riedmiller, M. Deterministic policy gradient algorithms. International conference on machine learning. Pmlr, 2014, pp. 387–395.
Kirkpatrick, S.; Gelatt Jr, C.D.; Vecchi, M.P. Optimization by simulated annealing. science 1983, 220, 671–680. [Google Scholar] [CrossRef]

Figure 1. The scheduling results of the AC algorithm based on Constrained Reinforcement Learning Loss and the traditional AC algorithm.

Figure 2. Control experiment to verify the effectiveness of the proposed method.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Combination Optimization Method of Grid Section Based on Deep Reinforcement Learning with Accelerated Convergence Speed

Abstract

1. Introduction

2. Mathematical model for combination optimization of grid sections

2.1. Objective function

2.2. Constraints

3. Combination optimization of grid section

3.1. Deep reinforcement learning

3.2. Environment setting for reinforcement learning

3.3. Constrained reinforcement learning loss

3.4. Training method and process

4. Annealing optimization algorithm

5. Case study

6. Conclusion

Author Contributions

Funding

Institutional Review Board Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe