Event-Triggered Robust Fusion Estimation for Multi-Sensor Systems With State Delay and External Inputs

1. Introduction

In the last decade, multi-sensor systems have been extensively studied in path planning [1], environmental monitoring [2], and path tracking [3], and so on. In multi-sensor systems, the accuracy and stability of the system are improved due to the joint data collection by multiple sensors. However, the impact of sensor failures or network attacks in the channel may lead to data transmission time delay and random packet drop [4,5]. Therefore, the investigation of multi-sensor systems is of great importance.

Data processing in multi-sensor systems is performed in the form of fusion, and basic fusion methods include centralized [6,7] and distributed [8,9]. Centralized is ideally optimal, but when the number of sensors is large, fusion center data processing may be infeasible [10,11]. In contrast, the suboptimal distributed structure is more stable. As research goes further, adding an event-triggered policy to the system can reduce the energy consumption of sensors and decrease the communication burden. [12] proposed a distributed event-triggered policy in which the subsystem broadcasts state information to neighboring nodes only when the local state error exceeds a specified threshold. [13] proposed a data-driven transmission strategy based on the idea of minimizing the volume of the non-transmission area. [14] proposed a trigger decision based on the estimated variance, where a copy of the Kalman filter is run at the sensor node, and its measurement is transmitted only when the measurement prediction variance exceeds a certain threshold. The event-triggered policy in [15] is based on a threshold-based strategy, where the event generator transmits a state measurement only when a signal exceeds a threshold value. A stochastic-deterministic dynamic event-triggereed condition is proposed in [16].

At the same time, the treatment of time delay problems of systems has received much attention [17]. The linear matrix inequality (LMI) [18,19] and partial differential equation (PDE) [20,21] methods are also commonly used in the time delay treatment of systems . The state augmentation method in [22] converts time delay systems into non-time delay systems with nice results. The method in [22] was used in [23] for a multi-sensor system, but random packet drop was not considered.

In the process of system modelling, modelling errors are inevitable, so it is essential that the estimator performance has no sudden changes when the system parameters deviate from their nominal parameters in a reasonable manner [24]. Those with this property are called robust state estimators, and many research methods are available [25,26,27,28]. A framework based on regularized least squares (RLS) is proposed in [25], but the modelling errors are restricted to a specific form. A filter that compromises the nominal performance and uncertainty robustness is proposed in [26]. A robust state estimator based on sensitivity penalty is proposed in [27], which is not limited to structure-specific modelling errors. In addition, a robust state estimator based on the expectation minimization of estimation error is proposed in [28]. Therefore, it is of great significance to employ robust state estimators in multi-sensor systems.

In this paper, we investigated the problem of robust fusion estimation for multi-sensor systems with uncertainty, restricted communication, random packet drops, state delay, and deterministic control inputs. A robust state estimator based on state augmentation and sensitivity penalty is used at the local scale. An analytic expression for the robust fusion estimator is derived based on event-triggered and the pseudo-cross-covariance matrix of the fusion centers is updated. The consistent boundedness of the estimation error is proved. The effectiveness of the fusion estimator is verified by several simulations.

The rest of this paper is briefly described below. The problem description and a brief description of the event-triggered policy are given in Section 2. A robust fusion estimator for multi-sensor systems with state delays, deterministic control inputs, random packet drops, and communication constraints is derived in Section 3. The boundedness of the fusion estimator is studied in Section 4. Several sets of simulations are analyzed in Section 5. Section 6 concludes the paper.

[1in]

2. Problem formulation and some preliminaries

Consider the following discrete-time uncertain linear stochastic system with deterministic inputs and d-steps state delay

$$\left\{\begin{array}{cc}\hfill x_{k+1}& =A_{1,k}\left({\epsilon }_k\right)x_k+A_{2,k}\left({\epsilon }_k\right)x_{k-d}+B_{1,k}\left({\epsilon }_k\right)u_k+B_{2,k}\left({\epsilon }_k\right)w_k,\hfill \\ \hfill y_k^i& =C_k^i\left({\epsilon }_k\right)x_k+g_k^i,1\le i\le L,k\ge 0,\hfill \end{array}\right.$$

(1)

where k represents the discrete time and i represents the sensor label. Furthermore, $x_k$ is the state, $y_k^i$ is the measurement, $w_k$ represents the process noise, $u_k$ is the deterministic control input, and $g_k^i$ is the compound effect of measurement and communication errors.

To guarantee the fitness of the state estimation problem, the following assumptions need to be made.

(a) $w_k$ and $g_k^i$ are normally distributed with white noise, $x_0$, $w_k$, and $g_k^i$ are mutually independent random variables.

$$\begin{array}{c}\mathbf{E}\left(w_k\right)=0,\mathbf{E}\left(g_k^i\right)=0,\hfill \\ \mathbf{E}\left(\left[\begin{array}{c}{x}_0-\mathbf{E}\left(x_0\right)\\ w_k\\ g_k^i\end{array}\right]{(*)}^T\right)=\left[\begin{array}{ccc}{\Pi }_0\hfill & \hfill & \\ \hfill & Q_k{\delta }_{kj}\hfill & \\ \hfill & \hfill & R_k^i{\delta }_{kj}\hfill \end{array}\right],\hfill \end{array}$$

where ${\Pi }_0$ , $Q_k$, and $R_k^i$ are known positive definite matrices and ${\delta }_{kj}$ denotes the Kronecker symbolic function.

(b) The elements in the matrices $A_{1,k}\left({\epsilon }_k\right)$, $A_{2,k}\left({\epsilon }_k\right)$, $B_{1,k}\left({\epsilon }_k\right)$, $B_{2,k}\left({\epsilon }_k\right)$ and $C_k^i\left({\epsilon }_k\right)$ are known differentiable functions of the modelling errors, and the modelling errors ${\epsilon }_k$ consist of l mutually independent real-valued scalar bounded uncertainties ${\epsilon }_{k,j}$, $j=1,...,l$.

In the process of transmitting the measurement value Y from the sensor node to the fusion center, the channel may experience packet drops. A random variable r is defined to indicate the success failure of the communication between the sensor node and the fusion center, taking the value of 1 for the successful transmission and 0 when the communication channel fails.

The aim of this paper is to develop a fusion algorithm based on local estimates from each sensor node for multi-sensor systems with parameter uncertainty, state delay, random packet drops, and communication rate limitations. To balance communication cost and estimation performance, an event-triggered policy like in [13] is used in this paper.

Consider the following measurement channel

$$Y=H\varphi +g$$

where $Y\in {\mathbf{R}}^m$ is the measurement output, $h\in {\mathbf{R}}^{m\times n}$ is the measurement matrix of the system, $\varphi \in {\mathbf{R}}^n$ represents the state, and $g\in {\mathbf{R}}^m$ represents the measurement noise. A binary variable is denoted by t, and when $t=1$ indicates that the sensor node sends a measurement Y and the other way around. The specific form of the event-triggered policy is as follows

$$t_k^i=\left\{\begin{array}{c}0,Y-\tilde{Y}\in \Xi ,\\ 1,\mathrm{others},\end{array}\right.$$

in which $\tilde{Y}\in {\mathbf{R}}^m$ and $\Xi \in {\mathbf{R}}^m$ are measurable sets. Generally, the center of mass of $\Xi$ is at the origin, that is, ${\int }_{\Xi }\phi d\phi =0$. Note that the decision transmission in the event-triggered policy is actually when the difference between the measured value and the determined measured value is greater than a threshold value.

The transmission rate, $a^i\in \left(0,1\right)$, for each sensor is derived by ${lim}_{\tau \to \infty }\frac{1}{\tau }{\sum }_{k=1}^{\tau }E\left\{t_k^i\right\}=a^i$. In addition, for any given desired transmission rate $a^i$, a threshold $\Xi$ can be easily determined.

Based on Lemma 1 in [13], a virtual measure $Y=\tilde{Y}=H\epsilon +g-v$ is now defined, where is uniformly distributed over, and independent of X and g. Suppose, $f_{\varphi }\left(x\right)=N\left(x;\overline{x},{\Omega }_x\right)$, $f_G\left(g\right)=N\left(g;0,{\Omega }_g\right)$, $f_Y\left(y\right)=N\left(y;H\overline{x},{\Omega }_y\right)$ where ${\Omega }_y={\Omega }_g+H{\Omega }_x{H}^T$. Thus, the optimal transmission strategy is derived as

$$\parallel Y-H\overline{x}{\parallel }_{{\Omega }^{-1}}^2\ge \theta ,$$

where $\theta ={\gamma }_m^{-1}\left(1-a\right)$. The random variable $\parallel Y-H\overline{x}{\parallel }_{{\Omega }^{-1}}^2$ obeys chi-square distribution with degree of freedom m where ${\gamma }_m$ is the chi-square distribution function with degree of freedom m.

3. The robust fusion estimation procedure

Considering the effects of state delay and modelling errors on the estimation performance, a robust state estimation algorithm based on sensitivity penalty in [27] is used to obtain local estimates for multi-sensor systems. This robust state estimator is derived on the basis of the Kalman filter, based on a sensitivity penalty to the estimation error of the model uncertainty. A design parameter ${\gamma }_k^i$, $0<{\gamma }_k^i<1$, is defined to compromise between nominal estimation performance and performance deterioration due to modelling errors.

By introducing the augmentation matrix X and augmenting the original system (1) with states, the system becomes

$$\left\{\begin{array}{cc}\hfill X_{k+1}& ={\overline{A}}_k\left({\epsilon }_k\right)X_k+{\overline{B}}_{1,k}\left({\epsilon }_k\right)u_k+{\overline{B}}_{2,k}\left({\epsilon }_k\right)w_k,\hfill \\ \hfill y_k^i& ={\overline{C}}_k^i\left({\epsilon }_k\right)X_k+v_k^i,1\le i\le L,k\ge 0,\hfill \end{array}\right.$$

(2)

in which,

$$\begin{array}{c}{\overline{A}}_k\left({\epsilon }_k\right)=\left[\begin{array}{ccccc}{A}_{1,k}\left({\epsilon }_k\right)& 0_{n\times n}& \cdots & 0_{n\times n}& A_{2,k}\left({\epsilon }_k\right)\\ {\mathrm{I}}_n& & & & 0_{n\times n}\\ & {\mathrm{I}}_n& & & 0_{n\times n}\\ & & \ddots & & ⋮\\ & & & {\mathrm{I}}_n& 0_{n\times n}\end{array}\right],\\ {\overline{B}}_{1,k}\left({\epsilon }_k\right)={\left[\begin{array}{cc}{\left(B_{1,k}\left({\epsilon }_k\right)\right)}^T\hfill & 0_{n\times dn}^T\hfill \end{array}\right]}^T,\\ {\overline{B}}_{2,k}\left({\epsilon }_k\right)={\left[\begin{array}{cc}{\left(B_{2,k}\left({\epsilon }_k\right)\right)}^T\hfill & 0_{n\times dn}^T\hfill \end{array}\right]}^T,\\ {\overline{C}}_k^i\left({\epsilon }_k\right)=\left[\begin{array}{cc}{C}_k^i\left({\epsilon }_k\right)\hfill & 0_{n\times dn}\hfill \end{array}\right].\end{array}$$

As can be seen from the above transformation, the re-modeled system is a discrete linear uncertain system without state delay. Following the transformation of the system model from (1) to (2), it is evident that the system matrix dimension changes from n to $n\left(d+1\right)$.

To obtain the locally robust state estimate for the $i-$th sensor node, we first define several important matrices $S_k^i$, $T_{1,K}^i$, and $T_{2,K}^i$, which play a key role in the parameter modification process, as follows:

$$\begin{array}{c}\begin{array}{cc}\hfill & S_k^i={\left[{\left(S_{k,1}^i(0,0)\right)}^T,\cdots ,{\left(S_{k,l}^i(0,0)\right)}^T\right]}^T,\hfill \\ \hfill & T_{1,k}^i={\left[{\left(T_{1,k,1}^i(0,0)\right)}^T,\cdots ,{\left(T_{1,k,l}^i(0,0)\right)}^T\right]}^T,\hfill \\ \hfill & T_{2,k}^i={\left[{\left(T_{2,k,1}^i(0,0)\right)}^T,\cdots ,{\left(T_{2,k,l}^i(0,0)\right)}^T\right]}^T,\hfill \\ \hfill & S_{k,j}^i\left({\epsilon }_k,{\epsilon }_{k+1}\right)=\left[\begin{array}{c}\frac{\overline{\partial }{C}_{k+1}^i\left({\epsilon }_{k+1}\right)}{\partial {\epsilon }_{k+1,j}}{\overline{A}}_k\left({\epsilon }_k\right)\\ {\overline{C}}_{k+1}^i\left({\epsilon }_{k+1}\right)\frac{\partial {\overline{A}}_k\left({\epsilon }_k\right)}{\partial {\epsilon }_{k,j}}\end{array}\right],\hfill \\ \hfill & T_{1,k,j}^i\left({\epsilon }_k,{\epsilon }_{k+1}\right)=\left[\begin{array}{c}\frac{\partial {\overline{C}}_{k+1}^i\left({\epsilon }_{k+1}\right)}{\partial {\epsilon }_{k+1,j}}{\overline{B}}_{1,k}\left({\epsilon }_k\right)\\ {\overline{C}}_{k+1}^i\left({\epsilon }_{k+1}\right)\frac{\partial {\overline{B}}_{1,k}\left({\epsilon }_k\right)}{\partial {\epsilon }_{k,j}}\end{array}\right],\hfill \\ \hfill & T_{2,k,j}^i\left({\epsilon }_k,{\epsilon }_{k+1}\right)=\left[\begin{array}{c}\frac{\partial {\overline{C}}_{k+1}^i\left({\epsilon }_{k+1}\right)}{\partial {\epsilon }_{k+1,j}}{\overline{B}}_{2,k}\left({\epsilon }_k\right)\\ {\overline{C}}_{k+1}^i\left({\epsilon }_{k+1}\right)\frac{\partial {\overline{B}}_{2,k}\left({\epsilon }_k\right)}{\partial {\epsilon }_{k,j}}\end{array}\right],\hfill \\ \hfill & j=1,2,\cdots ,l\hfill \end{array}\end{array}$$

Let ${\mu }_k^i=\frac{1-{\gamma }_k^i}{{\gamma }_k^i}$. The detailed realization of the robust state estimation algorithm based on sensitivity penalty is given in Algorithm 1.

Here $P_{k|k}^i$ and ${\widehat{P}}_{k|k}^i$ are the pseudo-covariance matrices because ${\widehat{P}}_{k\mid k}^i\ne \mathbf{E}\left\{{\left(X_k-{\widehat{X}}_{k\mid k}^i\right)}^T\left(X_k-{\widehat{X}}_{k\mid k}^i\right)\right\}$ and $P_{k\mid k}^i\ne \mathbf{E}\left\{{\left(X_k-{\widehat{X}}_{k|k}^i\right)}^T\left(X_k-{\widehat{X}}_{k\mid k}^i\right)\right\}$.

Based on the event-triggered policy in the second part, whether each sensor node sends a local state estimate to the fusion center is determined by $t_k^i$. The transmission strategy mentioned above can be expressed as

$$t_k^i=\left\{\begin{array}{cc}\hfill & 0,{∥{\widehat{X}}_{k\mid k}^i-{\overline{X}}_{k\mid k}^i∥}_{{\Omega }_k^i}^2\le {\theta }^i,\hfill \\ \hfill & 1,\mathrm{others}.\hfill \end{array}\right.$$

(3)

In order to guarantee the transmission rate $a^i$, the vector ${\overline{X}}_{k|k}^i$, the positive definite weight coefficient matrix ${\Omega }_k^i$, and the positive real numbers ${\theta }^i$ must be chosen appropriately. ${\widehat{X}}_{k|k}^i$ is the local state estimate.

Notice that each local state estimate can be interpreted as a measurement $y_k^i$ of the true state $X_k$ collected through the virtual measurement channel defined as

$$Y_k^i={\widehat{X}}_{k|k}^i=X_k+\left({\widehat{X}}_{k|k}^i-X_k^{}\right),$$

(4)

where the estimation error ${\widehat{X}}_{k|k}^i-X_k^{}$ can be regarded as virtual measurement noise.

Now, considering only the event-triggered policy, (4) is corresponding to the measurements received by the fusion center from sensor node i, that is, $t_k^i=1$. When sensor data is not transmitted, (4) will be replaced by

$$Y_k^i={\tilde{X}}_{k|k}^i=X_k+\left({\widehat{X}}_{k|k}^i-X_k\right)-v_k^i.$$

(5)

Here $v_k^i$ is uniformly distributed within the ellipsoid mentioned in (3) and is not correlated with the estimation error ${\widehat{X}}_{k|k}^i-X_k^{}$.

According to the event-triggered policy, when there is packet drops in the communication channel from the estimator to the fusion center, the virtual measurement channel can be replaced with

$$\begin{array}{c}\hfill Y_k^i=\left\{\begin{array}{c}{\widehat{X}}_{k\mid k}^i,t_k^i=1,r_k^i=1,\hfill \\ {\widehat{X}}_{k\mid k-1}^i,t_k^i=1,r_k^i=0,\hfill \\ {\tilde{X}}_{k|k}^i,t_k^i=0,\hfill \end{array}\right.\end{array}$$

(6)

where $r_k^i$ is explicitly utilized in (6) to indicate whether packet drop occurs in sensor transmission to the fusion center and $r_k^i=\left\{0,1\right\}$. The state of the multi-sensor system is shown in Table 1. For simplicity, the event-triggered is abbreviated as ET and the success of the transmission is simplified as PD. The ${\widehat{X}}_{k|k-1}^i$ in (6) is the predicted values of the $i-$th sensor node for moment k. ${\eta }_k^i$ is the virtual measurement noise of the $i-$th virtual channel for moment k, which can be derived by

$$\begin{array}{c}{\widehat{X}}_{k|k-1}^i={\widehat{A}}_{k-1}^i{\widehat{X}}_{k-1|k-1}^i+{\widehat{B}}_{1,k-1}^i{u}_{k-1},\hfill \\ {\eta }_k^i=\left\{\begin{array}{cc}\hfill & {\widehat{X}}_{k\mid k}^i-X_k,t_k^i=1,r_k^i=1,\hfill \\ \hfill & {\widehat{X}}_{k\mid k-1}^i-X_k,t_k^i=1,r_k^i=0,\hfill \\ \hfill & {\widehat{X}}_{k\mid k}^i-X_k-g_k^i,t_k^i=0.\hfill \end{array}\right.\hfill \end{array}$$

(7)

The fusion estimation with both random packet drops and event-triggered polices is investigated and the following matrices are defined as

$$\begin{array}{cc}\hfill & Y_k=col\left\{t_k^i\left(r_k^i{\widehat{X}}_{k\mid k}^i+\left(1-r_k^i\right){\widehat{X}}_{k\mid k-1}^i\right)+{\left.\left(1-t_k^i\right){\tilde{X}}_{k|k}^i\right|}_{i=1}^l\right\},\hfill \\ \hfill & {\eta }_k=col\left\{{\left.\left(t_k^i{r}_k^i+\left(1-t_k^i\right)\right)\left({\widehat{X}}_{k|k}^i-X_k\right)\right|}_{i=1}^l\right\}\hfill \\ \hfill & +col\left\{{\left.t_k^i\left(1-r_k^i\right)\left({\widehat{X}}_{k\mid k-1}^i-X_k\right)\right|}_{i=1}^l\right\}+{\left.col\{\left(1-t_k^i\right)g_k^i\right|}_{i=1}^l\},\hfill \\ \hfill & H=col\left({\left.I^i\right|}_{i=1}^l\right).\hfill \end{array}$$

(8)

The information in the fusion center is obtained from the virtual measurement channel

$$Y_k=H{X}_k+{\eta }_k.$$

In accordance with the best linear unbiased criterion (BLUE) in [29], we can obtain the fusion estimate and its error covariance matrix.

$$\begin{array}{c}{\widehat{X}}_{k\mid k}={\left(H^T{\tilde{P}}_k^{-1}H\right)}^{-1}{H}^T{\tilde{P}}_k^{-1}{Y}_k,\\ P_k={\left(H^T{\tilde{P}}_k^{-1}H\right)}^{-1}.\end{array}$$

(9)

In (9), ${\tilde{P}}_k$ is the covariance matrix of the virtual measurement noise, which is the global error covariance matrix of the estimation error. From ${\eta }_k$ in (8), the expression of ${\tilde{P}}_k$ can be obtained as

$$\begin{array}{c}{\tilde{P}}_k={\Gamma }_k+diag\left\{\left({1-t}_k^i\right)\frac{{\theta }^i}{n+2}{\left({\Omega }_k^i\right)}^{-1}{|}_{i=1}^l\right\},\end{array}$$

(10)

in which ${\Gamma }_k={\Gamma }_{k,1}+{\Gamma }_{k,2}+{\Gamma }_{k,2}^T+{\Gamma }_{k,3}$. The matrices ${\Gamma }_{k,1}$, ${\Gamma }_{k,2}$ and ${\Gamma }_{k,3}$ in the formula are equal to

$$\begin{array}{cc}\hfill & {\Gamma }_{k,1}=\left[\begin{array}{ccc}{\left({\sigma }_{1,k}^1\right)}^2{P}_{k\mid k}^{1,1}& \cdots & {\sigma }_{1,k}^1{\sigma }_{1,k}^l{P}_{k\mid k}^{1,l}\\ ⋮& \ddots & ⋮\\ {\sigma }_{1,k}^l{\sigma }_{1,k}^1{P}_{k\mid k}^{l,1}& \cdots & {\left({\sigma }_{1,k}^l\right)}^2{P}_{k\mid k}^{l,l}\end{array}\right],\hfill \\ \hfill & {\Gamma }_{k,2}=\left[\begin{array}{ccc}0& \cdots & {\sigma }_{1,k}^1{\sigma }_{2,k}^l{\overline{P}}_{k\mid k-1}^{1,l}\\ ⋮& \ddots & ⋮\\ {\sigma }_{1,k}^l{\sigma }_{2,k}^1{\overline{P}}_{k\mid k-1}^{l,1}& \cdots & 0\end{array}\right],\hfill \\ \hfill & {\Gamma }_{k,3}=\left[\begin{array}{ccc}{\left({\sigma }_{2,k}^1\right)}^2{P}_{k\mid k-1}^{1,1}& \cdots & {\sigma }_{2,k}^1{\sigma }_{2,k}^l{P}_{k\mid k-1}^{1,l}\\ ⋮& \ddots & ⋮\\ {\sigma }_{2,k}^l{\sigma }_{2,k}^1{P}_{k\mid k-1}^{l,1}& \cdots & {\left({\sigma }_{2,k}^l\right)}^2{P}_{k\mid k-1}^{l,l}\end{array}\right],\hfill \\ \hfill & {\sigma }_{1,k}^i=\left(t_k^i{r}_k^i+\left(1-t_k^i\right)\right),{\sigma }_{2,k}^i=t_k^i\left(1-r_k^i\right).\hfill \end{array}$$

(11)

Then, we consider the state estimation errors of the following dynamic system.

$$\left\{\begin{array}{c}{X}_{k+1}={\widehat{A}}_k^i{X}_k+{\widehat{B}}_{1,k}^i{u}_k+{\widehat{B}}_{2,k}^i{w}_k,\\ y_k^i={\overline{C}}_k^i{X}_k+g_k^i,1\le i\le l.\end{array}\right.$$

(12)

The following relationships can be easily obtained

$$\begin{array}{cc}\hfill X_{k+1}-{\widehat{X}}_{k+1|k+1}^i=& {\left[I+P_{k+1|k}^i{\left({\overline{C}}_{k+1}^i\right)}^T{\left(R_{k+1}^i\right)}^{-1}{\overline{C}}_{k+1}^i\right]}^{-1}\hfill \\ \hfill \times & \left[{\widehat{A}}_k^i\left(X_k-{\widehat{X}}_{k|k}^i\right)+{\widehat{B}}_{2,k}^i{w}_k\right]\hfill \\ \hfill -& {\left[{\left(P_{k+1|k}^i\right)}^{-1}+{\left({\overline{C}}_{k+1}^i\right)}^T{\left(R_{k+1}^i\right)}^{-1}{\overline{C}}_{k+1}^i\right]}^{-1}\hfill \\ \hfill \times & {\left({\overline{C}}_{k+1}^i\right)}^T{\left(R_{k+1}^i\right)}^{-1}{v}_{k+1}^i,\hfill \\ \hfill X_{k+1}-{\widehat{X}}_{k+1|k}^i=& {\widehat{A}}_k^i\left(X_k-{\widehat{X}}_{k|k}^i\right)+{\widehat{B}}_{2,k}^i{w}_k.\hfill \end{array}$$

(13)

According to the above equation, the explicit expressions for the three pseudo mutual covariance matrices $P_{k+1\mid k+1}^{i,j}$, ${\overline{P}}_{k+1\mid k}^{i,j}$, and $P_{k+1\mid k}^{i,j}$ in (11) can be derived as follows

$$\begin{array}{cc}\hfill P_{k+1|k+1}^{i,j}=& \left[\begin{array}{c}I-P_{k+1\mid k}^i{\left({\overline{C}}_{k+1}^i\right)}^T\hfill \\ \times {\left({\overline{C}}_{k+1}^i{P}_{k+1\mid k}^i{\left({\overline{C}}_{k+1}^i\right)}^T+R_{k+1}^i\right)}^{-1}{\overline{C}}_{k+1}^i\hfill \end{array}\right]\hfill \\ \hfill \times & \left[{\widehat{A}}_k^i{P}_{k\mid k}^{i,j}{\left({\widehat{A}}_k^j\right)}^T+{\widehat{B}}_{2,k}^i{Q}_k{\left({\widehat{B}}_{2,k}^j\right)}^T\right]\hfill \\ \hfill \times & {\left[\begin{array}{c}I-P_{k+1\mid k}^j{\left({\overline{C}}_{k+1}^j\right)}^T\hfill \\ \times {\left({\overline{C}}_{k+1}^j{P}_{k+1\mid k}^j{\left({\overline{C}}_{k+1}^j\right)}^T+R_{k+1}^j\right)}^{-1}{\overline{C}}_{k+1}^j\hfill \end{array}\right]}^T,\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\overline{P}}_{k+1\mid k}^{i,j}=& {\left(I+P_{k+1\mid k}^i{\left({\overline{C}}_{k+1}^i\right)}^T{\left(R_{k+1}^i\right)}^{-1}{\overline{C}}_{k+1}^i\right)}^{-1}\hfill \\ \hfill \times & \left[{\widehat{A}}_k^i{P}_{k\mid k}^{i,j}{\left({\widehat{A}}_k^j\right)}^T+{\widehat{B}}_{2,k}^i{Q}_k{\left({\widehat{B}}_{2,k}^j\right)}^T\right],\hfill \end{array}$$

$$\begin{array}{cc}\hfill P_{k+1\mid k}^{i,j}=& {\widehat{A}}_k^i{P}_{k\mid k}^{i,j}{\left({\widehat{A}}_k^j\right)}^T+{\widehat{B}}_{2,k}^i{Q}_k{\left({\widehat{B}}_{2,k}^j\right)}^T,\hfill \end{array}$$

$$\begin{array}{cc}\hfill P_{k+1|k+1}^{i,i}=& \left[\begin{array}{c}I-P_{k+1|k}^i{\left({\overline{C}}_{k+1}^i\right)}^T\hfill \\ \times {\left({\overline{C}}_{k+1}^i{P}_{k+1|k}^i{\left({\overline{C}}_{k+1}^i\right)}^T+R_{k+1}^i\right)}^{-1}{\overline{C}}_{k+1}^i\hfill \end{array}\right]\hfill \\ \hfill \times & \left[{\widehat{A}}_k^i{P}_{k|k}^{i,i}{\left({\widehat{A}}_k^i\right)}^T+{\widehat{B}}_{2,k}^i{Q}_k{\left({\widehat{B}}_{2,k}^i\right)}^T\right]\hfill \\ \hfill \times & {\left[\begin{array}{c}I-P_{k+1\mid k}^i{\left({\overline{C}}_{k+1}^i\right)}^T\hfill \\ \times {\left({\overline{C}}_{k+1}^i{P}_{k+1\mid k}^i{\left({\overline{C}}_{k+1}^i\right)}^T+R_{k+1}^i\right)}^{-1}{\overline{C}}_{k+1}^i\hfill \end{array}\right]}^T\hfill \\ \hfill +& {\left(\begin{array}{c}{\left({\overline{C}}_{k+1}^i\right)}^T{\left(R_{k+1}^i\right)}^{-1}{\overline{C}}_{k+1}^i\hfill \\ +{\left(P_{k+1|k}^i\right)}^{-1}\hfill \end{array}\right)}^{-1}{\left({\overline{C}}_{k+1}^i\right)}^T{\left(R_{k+1}^i\right)}^{-1}\hfill \\ \hfill \times & {\overline{C}}_{k+1}^i{\left({\left(\begin{array}{c}{\left({\overline{C}}_{k+1}^i\right)}^T{\left(R_{k+1}^i\right)}^{-1}{\overline{C}}_{k+1}^i\hfill \\ +{\left(P_{k+1|k}^i\right)}^{-1}\hfill \end{array}\right)}^{-1}\right)}^T,\hfill \end{array}$$

in which $P_{k+1|k}^{i,i}=P_{k+1|k}^i$, $i,j=1,\cdots ,N$. $P_{k+1|k+1}^i$ is a pseudo-covariance matrix in robust state estimation. Thus, there is $P_{k+1|k+1}^{i,i}\ne P_{k+1|k+1}^i$.

4. Some properties of the fusion estimator

This section has the goal of investigating the steady-state properties of event-triggered robust fusion estimators for multi-sensor systems with deterministic inputs, random packet drops, and state delays. Assume that the modelling errors ${\epsilon }_{k,j}$ in this section are within the set $\mathcal{E}$, $\mathcal{E}=\left\{\epsilon \left|{\epsilon }_{k,j}\right|\le 1,j=1,2,\cdots ,l\right.\}$. The matrices $\left[\begin{array}{ccc}{\mathrm{A}}_{1,k}\left(0\right)& 0_{n\times n(d-1)}& {\mathrm{A}}_{2,k}\left(0\right)\\ & I_{nd}& 0_{nd\times n}\end{array}\right]$, $\left[\begin{array}{c}{B}_{2,k}\left(0\right)\\ 0_{n\times dn}\end{array}\right]$ and $\left[\begin{array}{cc}{C}_k^i\left(0\right)& 0_{m\times dn}\end{array}\right]$ are denoted as $M_k$, $F_k$ and $O_k^i$, respectively. In addition, the following assumptions need to be made.

(A)$A_{1,k}\left(0\right)$,$A_{2,k}\left(0\right)$, $B_{1,k}\left(0\right)$, $B_{2,k}\left(0\right)$, $C_k^i\left(0\right)$, $R_k^i$, $Q_k$, $S_k^i$, $T_{1,k}^i$, $T_{2,k}^i$, and ${\gamma }_k^i$ are time-invariant.

(B) The uncertain linear system of (1) is exponentially stable in the sense of Lyapunov and the matrices $A_{1,k}\left({\epsilon }_k\right)$, $A_{2,k}\left({\epsilon }_k\right)$, $B_{1,k}\left({\epsilon }_k\right)$, $B_{2,k}\left({\epsilon }_k\right)$, $C_k^i\left({\epsilon }_k\right)$, ${\Pi }_k$, $R_k^i$, $Q_k^{}$ are bounded whenever $k>0$ and ${\epsilon }_k\in \mathcal{E}$.

(C) For every sensor node, $\left(M_k,N_k^i\right)$ is detectable and the following matrix pair is detectable

$${\left(\begin{array}{c}{M}_k^T-{\lambda }_k^i{\left(S_k^i\right)}^T{\left(I_{n(d+1)}+{\lambda }_k^i{T}_{2,k}^i{Q}_k{\left(T_{2,k}^i\right)}^T\right)}^{-1}{T}_{2,k}^i{Q}_k{\left(F_k\right)}^T\\ {\left(I_{n(d+1)}+{\lambda }_k^i{Q}_k^{\frac{1}{2}}{\left(T_{2,k}^i\right)}^T{T}_{2,k}^i{Q}_k^{\frac{1}{2}}\right)}^{-\frac{1}{2}}{Q}_k^{\frac{1}{2}}{\left(F_k\right)}^T\end{array}\right)}^T,$$

where $N_k^i=\left[\begin{array}{c}{\left(R_k^i\right)}^{-\frac{1}{2}}{O}_k^i\\ \sqrt{{\lambda }_k^i}{S}_k^i\end{array}\right]$.

Theorem 1. 

Suppose that Assumptions (A), (B) and (C) hold and that each sensor transmits local estimate ${\widehat{X}}_{k|k}^i$ according to the event-triggered policy. If the weight matrix ${\Omega }_k^i$ of the sensor node satisfies the condition

$${\Omega }_k^i\ge {\omega }^{i}I$$

(14)

for some positive real number ${\omega }^i$, the estimation error $X_k{-\widehat{X}}_{k|k}$ is consistently bounded for any possible choice of $\left\{{\tilde{X}}_{k|k}^i,k\in Z_{+}\right\}$, which means

$$\underset{k\to \infty }{lim}supE\left\{{∥X_k{-\widehat{X}}_{k|k}∥}^2\right\}<+\infty .$$

Proof 

(Proof of Theorem 1). Let ${\overline{X}}_{k|k}$ be the estimate obtained at time k through ${\overline{Y}}_k$ instead of $Y_k$, ${\overline{Y}}_k=col\left\{{\sigma }_{1,k}^i{\widehat{X}}_{k\mid k}^i+{\left.{\sigma }_{2,k}^i{\widehat{X}}_{k\mid k-1}^i\right|}_{i=1}^l\right\}$, which gives

$${\widehat{X}}_{k|k}={\overline{X}}_{k|k}+{\left(H^T{\tilde{P}}_k^{-1}H\right)}^{-1}{H}^T{\tilde{P}}_k^{-1}\left(Y_k-{\overline{Y}}_k\right),$$

so we have

$$\begin{array}{c}E\left\{\parallel X_k-{\widehat{X}}_{k\mid k}{\parallel }^2\right\}\le 2E\left\{\parallel X_k-{\overline{X}}_{k\mid k}{\parallel }^2\right\}\\ +2\parallel {\left(H^T{\tilde{P}}_k^{-1}H\right)}^{-1}\stackrel{T}{H}{\tilde{P}}_k^{-1}{\parallel }^2\\ \times E\left\{\parallel Y_k-{\overline{Y}}_k{\parallel }^2\right\}.\end{array}$$

(15)

Taking into account the first term on the right-hand side in (15), since ${\overline{X}}_{k|k}$ is based on the vector ${\overline{y}}_k$, the following inequality can be obtained

$$E\left\{{∥X_k-{\overline{X}}_{k|k}∥}^2\right\}\le tr{\left(H^T{\tilde{P}}_k^{-1}H\right)}^{-1}.$$

(16)

According to Assumptions (A), (B), and (C), then $P_{k|k}^{i,i}$ is convergent, and ${\overline{P}}_{k|k-1}^{i,i}$ and $P_{k|k-1}^{i,i}$ are also convergent. The estimation error has a bounded covariance matrix at each k[30]. This indicates that ${\Gamma }_k$ is converged and the estimation error covariance matrix is bounded.

From the inequality condition in Theorem 1, and the remainder of ${\tilde{P}}_k$, we can obtain

$$\begin{array}{cc}\hfill tr\left(\left(1-t_k^i\right)\frac{{\theta }^i}{n+2}{\left({\Omega }_k^i\right)}^{-1}\right)& =\left(1-t_k^i\right)\frac{{\theta }^i}{n+2}tr\left({\left({\Omega }_k^i\right)}^{-1}\right)\hfill \\ \hfill & \le \left(1-t_k^i\right)\frac{{\theta }^i}{\left(n+2\right){\omega }^i}.\hfill \end{array}$$

(17)

Hence, the uniform boundedness of $E\left\{{∥X_k-{\overline{X}}_{k\mid k}∥}^2\right\}$ can be obtained by (16). Now it is only necessary to prove that the second part of the right-hand side of inequality (15) is uniform boundedness. Under the inequality condition in Theorem 1, it can be obtained as

$${∥{\widehat{X}}_{k\mid k}^i-{\overline{X}}_{k\mid k}^i∥}_{{\Omega }_k^i}^2\ge {\omega }^i{∥{\widehat{X}}_{k\mid k}^i-{\overline{X}}_{k\mid k}^i∥}^2.$$

(18)

When $t_k^i=0$, it means that there is ${\parallel {\widehat{X}}_{k|k}^i-{\overline{X}}_{k|k}^i\parallel }_{{\Omega }_k^i}^2\le {\theta }^i$. Furthermore, it can be obtained that ${\parallel {\widehat{X}}_{k|k}^i-{\overline{X}}_{k|k}^i\parallel }^2\le {\theta }^i/{\omega }^i$, then ${∥Y_k{-\overline{Y}}_k∥}^2\le {\Sigma }_{i=1}^l{\theta }^i/{\omega }^i$. The proof is done. □

To minimize the volume of the non-transported region, ${\overline{X}}_{k|k}^i$ and ${\Omega }_k^i$ can be appropriately denoted as

$$\begin{array}{c}{\overline{X}}_{k|k}^i={\widehat{X}}_{k|k-1}^i={\widehat{A}}_{k-1}^i{\widehat{X}}_{k-1|k-1}^i,\\ {\Omega }_k^i={\left(\frac{1}{\mathrm{tr}\left({\tilde{P}}_{k|k-1}^i\right)}{\tilde{P}}_{k|k-1}^i\right)}^{-1},\end{array}$$

(19)

in which ${\tilde{P}}_{k|k-1}^i={\overline{A}}_{k-1}\left[\begin{array}{c}{\sigma }_{1,k-1}^i{P}_{k-1\mid k-1}^{i,i}\hfill \\ +{\sigma }_{2,k-1}^i{P}_{k-1\mid k-2}^i\hfill \\ +\left(1-t_{k-1}^i\right)\frac{{\theta }^i}{n+2}{\left({\Omega }_{k-1}^i\right)}^{-1}\hfill \end{array}\right]{\left({\overline{A}}_{k-1}\right)}^T+{\widehat{B}}_{2,k-1}^i{\widehat{Q}}_{k-1}^i{\left({\widehat{B}}_{2,k-1}^i\right)}^T$. Two methods exist for determining the local prediction of $X_k$ as per (19). The first method, utilized in this paper, is local estimation based on sensor nodes. This fusion estimation method does not necessitate broadcasting but requires each sensor node to retain past information. The second method is based on the $k-1$ moment fusion estimation ${\widehat{X}}_{k-1|k-1}$.

5. Numerical simulations

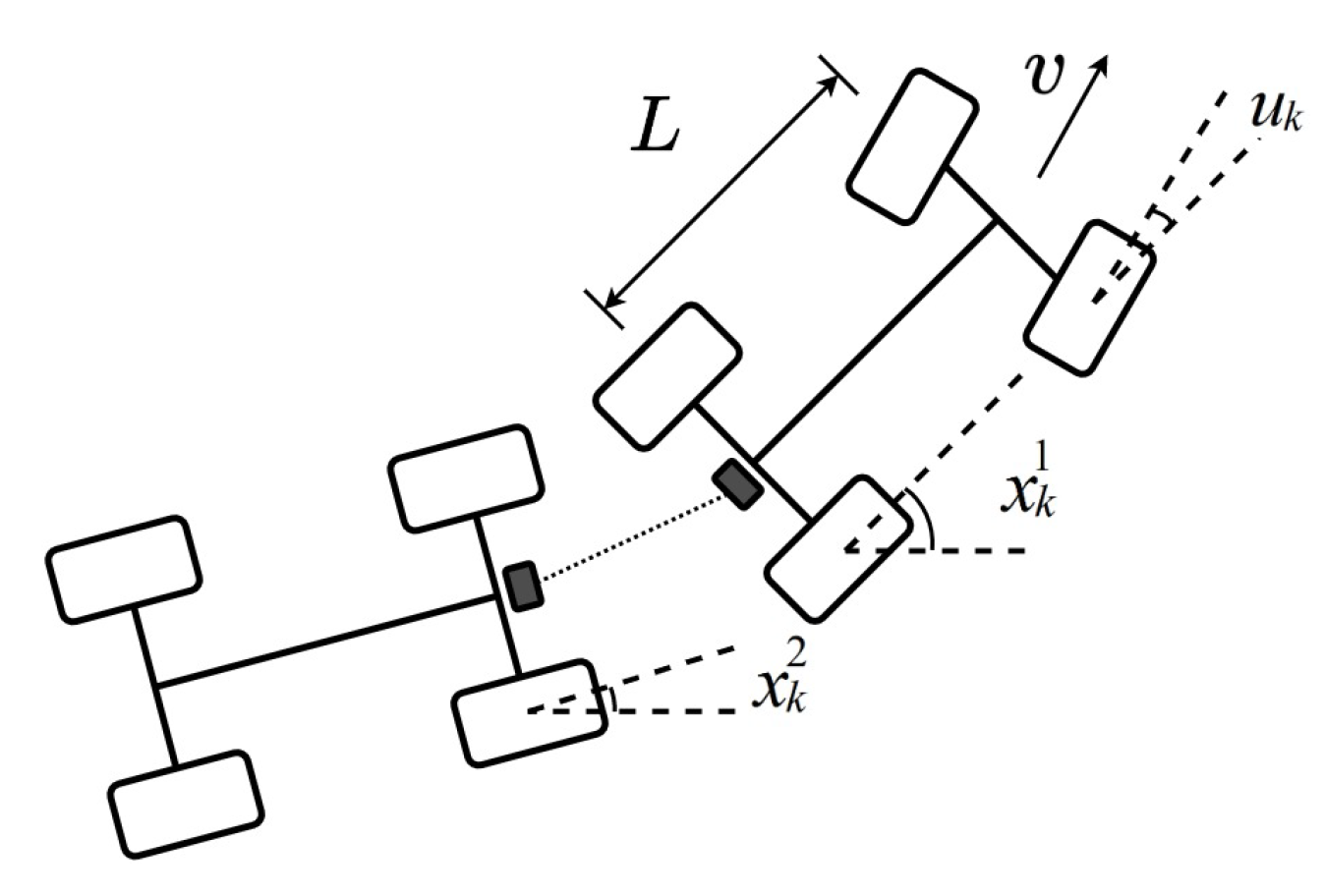
This section cites the tractor-car system detailed in [31], shown in Figure 1, and extends it to a multi-sensor systems for sample simulations. The performance of the derived robust fusion estimator is demonstrated through comparison with the Kalman filter based on actual and nominal parameters using the same fusion method across two distinct sets of numerical simulations with modelling errors(fixed or not), and varying transmission rates and packet drop rates. This numerical simulation consists of two sensors. For each set, 500-time experiments were conducted, with 200 moments designated for each set, generating 200 input-output data pairs. In the simulations, the overall average estimated error variance $E{∥X_k-{\widehat{X}}_{k\mid k}∥}^2\approx \frac{1}{500}{\sum }_{f=1}^{500}\parallel X_k-{\widehat{X}}_{k\mid k}^{\left(f\right)}{\parallel }^2$ is computed for each moment and the implementation of event -triggered and occurrence of packet drops are displayed.

Since the vehicle steering and directional angles in the tractor-car system of Figure 1 are nonlinear, it can be linearized and expressed as

$$\left\{\begin{array}{cc}\hfill x_{k+1}^1=& \left(1.0000-\frac{vk}{L}\right)x_k^1+\left(\frac{vk}{L}-0.2296\right)x_{k-d}^1+\left(0.1764+\frac{vk}{L}\right)x_k^2\hfill \\ \hfill & +\left(0.1764+\frac{vk}{L}\right)x_{k-d}^2+\left(0.9804+\frac{vk}{L}\right)w_k^1+\left(0.9804+\frac{vk}{L}\right)u_k^1,\hfill \\ \hfill x_{k+1}^2=& \left(1.0000-\frac{vk}{L}\right)x_k^2+\left(\frac{vk}{L}-0.2296\right)x_{k-d}^2+\left(0.9804+\frac{vk}{L}\right)w_k^2\hfill \\ \hfill & +\left(0.9804+\frac{vk}{L}\right)u_k^2,\hfill \end{array}\right.$$

(20)

in which $x_k^1$, $x_k^2$, $u_k$, $w_k$, $x_{k-d}^1$ and $x_{k-d}^2$ are the direction angle of the tractor, the direction angle of the car, the tractor steering angle, the process noise, d-step time delay for state 1, and d-step time delay for state 2, respectively. $x_k$ is the state vector, $x_k={\left[\begin{array}{cc}{x}_k^1\hfill & x_k^2\hfill \end{array}\right]}^T$. L, k, and v denote the length of the tractor, the sampling period, and the constant speed, respectively. Considering the system errors at linearization in the form of modelling errors ${\epsilon }_k$ substituted into the system model, the matrix parameters are obtained as

$$\begin{array}{c}{A}_{1,k}\left({\epsilon }_k\right)=\left[\begin{array}{cc}1.0000-\frac{vk}{L}& 0.1764+\frac{vk}{L}+{\epsilon }_k\\ 0.0000& 1.0000-\frac{vk}{L}\end{array}\right],\\ A_{2,k}\left({\epsilon }_k\right)=\left[\begin{array}{cc}\frac{vk}{L}-0.2296& 0.1764+\frac{vk}{L}+{\epsilon }_k\\ 0.0000& \frac{vk}{L}-0.2296\end{array}\right],\\ B_{1,k}\left({\epsilon }_k\right)=\left[\begin{array}{cc}0.9804+\frac{vk}{L}& 0.0000\\ 0.0000& 0.9804+\frac{vk}{L}\end{array}\right],\\ B_{2,k}\left({\epsilon }_k\right)=\left[\begin{array}{cc}0.9804+\frac{vk}{L}& 0.0000\\ 0.0000& 0.9804+\frac{vk}{L}\end{array}\right].\end{array}$$

(21)

In the numerical simulation, each parameter is taken as $L=500\mathrm{cm}$, $k=0.1s$, and $v=98\mathrm{cm}/\mathrm{s}$, and a two-step state delay system was used. The matrix parameters are as follows

$$\begin{array}{c}{A}_{1,k}\left({\epsilon }_k\right)=\left[\begin{array}{cc}0.9804& 0.196+1.99{\epsilon }_k\\ 0.0000& 0.9804\end{array}\right],A_{2,k}\left({\epsilon }_k\right)=\left[\begin{array}{cc}-0.2100& 0.196+1.99{\epsilon }_k\\ 0.0000& -0.2100\end{array}\right],\end{array}$$

$$B_{1,k}\left({\epsilon }_k\right)=\left[\begin{array}{cc}1.0000& 0.0000\\ 0.0000& 1.0000\end{array}\right],B_{2,k}\left({\epsilon }_k\right)=\left[\begin{array}{cc}1.0000& 0.0000\\ 0.0000& 1.0000\end{array}\right],$$

$$C_k^1\left({\epsilon }_k\right)=\left[\begin{array}{cc}1.0000& -1.0000\end{array}\right],\begin{array}{c}{C}_k^2\left({\epsilon }_k\right)=\left[\begin{array}{cc}0.4000& -0.5000\end{array}\right],\end{array}$$

$$\begin{array}{c}{R}_k^1=1.0000,R_k^2=1.0000,\end{array}$$

$$\begin{array}{c}{Q}_k=\left[\begin{array}{cc}1.9608& 0.0195\\ 0.0195& 1.9605\end{array}\right],{\Pi }_0=\left[\begin{array}{cc}1.0000& 0.0000\\ 0.0000& 1.0000\end{array}\right],u_k=\left[\begin{array}{c}1.0000\\ 0.1000\end{array}\right].\end{array}$$

The packet drop process $r_k^i$ is assumed to be a stationary Bernoulli process. A constant value of $0.7300$ is assigned to the filter design parameter ${\gamma }_k^i$.

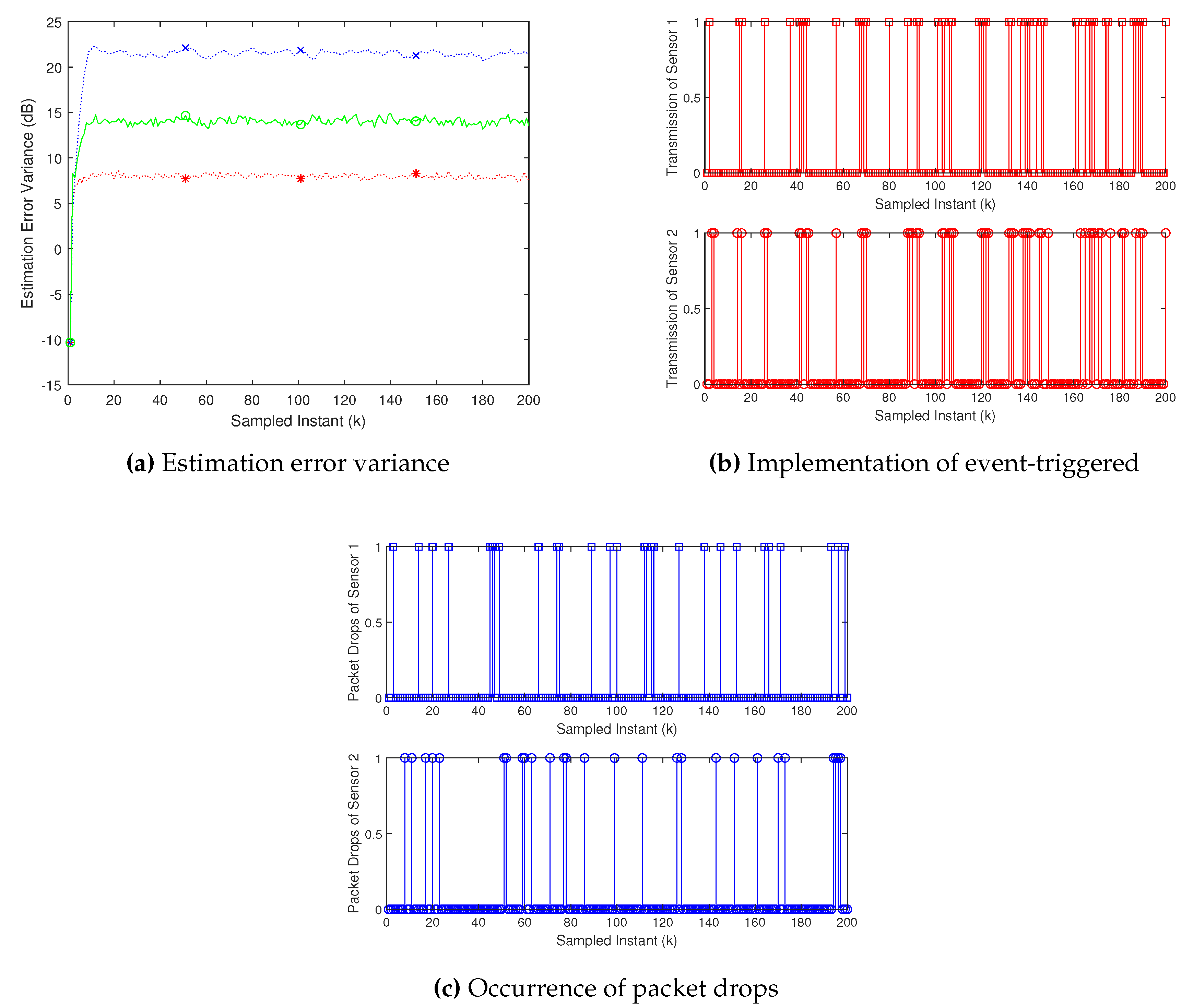
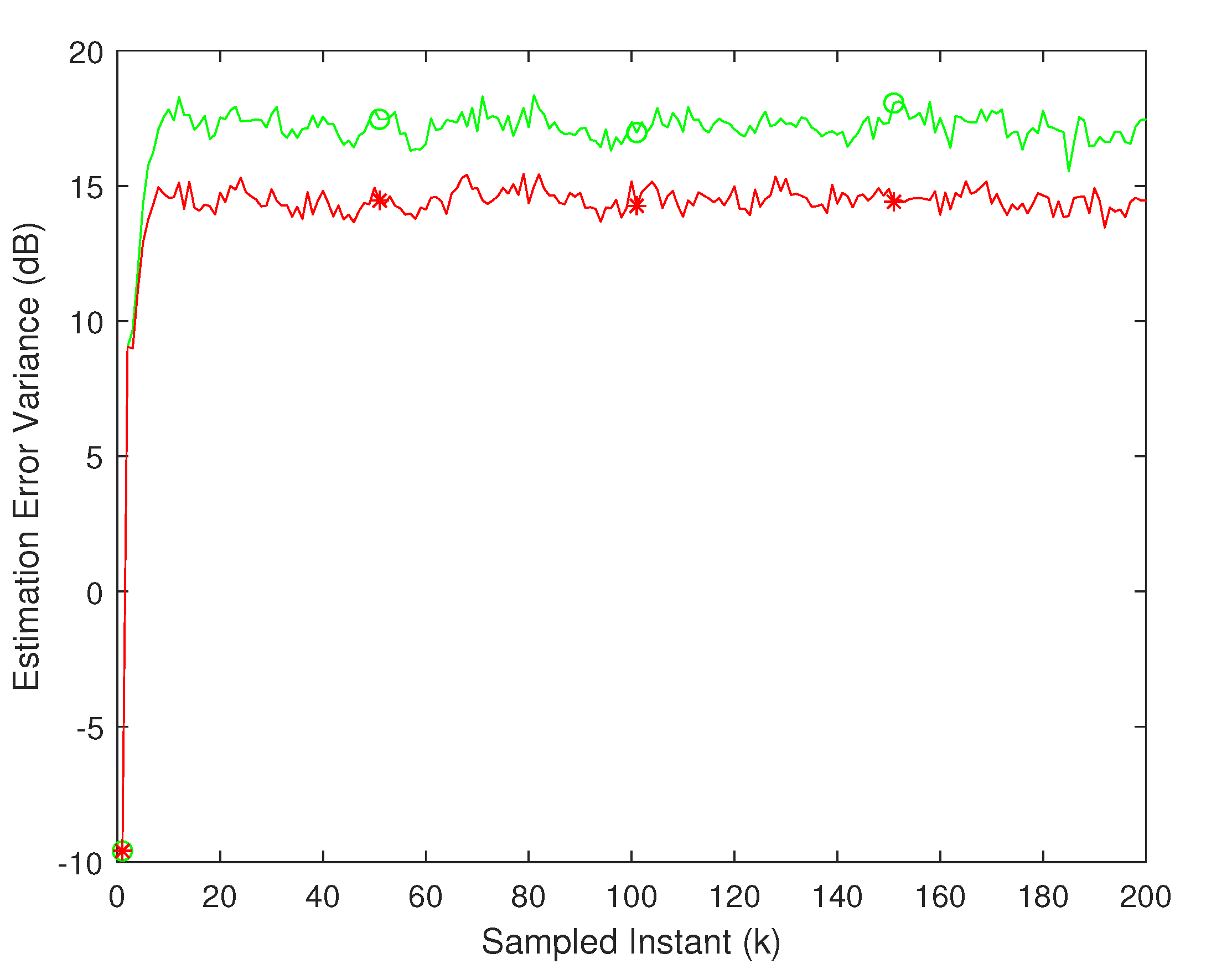
In Case 1, the modeling errors ${\epsilon }_k$ are assumed to be a fixed value of -0.8508. The transmission and packet drop rates for both sensors are set to 0.8 and 0.2, respectively. Figure 2a illustrates the fusion estimation error over time, demonstrating that the robust fusion estimator proposed in this study outperforms the Kalman filter based on nominal parameters by approximately 7.800 dB. Figure 2b,c depict the transmission of the two sensors and the packet drops of the communication channel, respectively. To clearly reflect the execution of the event-triggered, $t_k^i$ is inverted and $r_k^i$ is treated similarly.

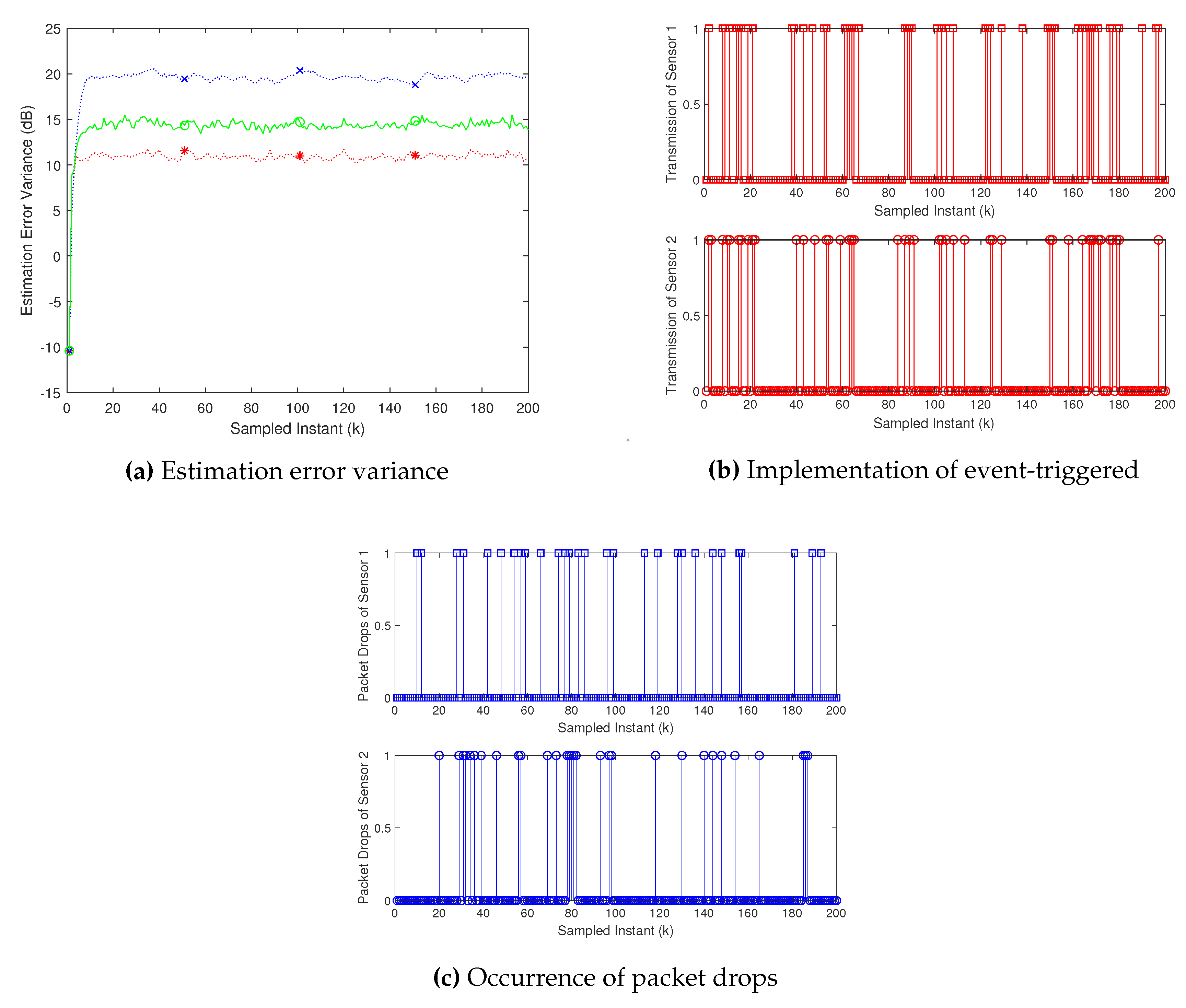
The modelling errors ${\epsilon }_k$ are generated randomly and independently, conforming to a normal distribution with a truncation. The mean, standard variance, and truncation values of the normal distribution are set to $0.0000$, $1.0000$, and $1.0000$, respectively. Figure 3a illustrates that the derived estimator surpasses the performance of the Kalman filter based on nominal parameters. The transmission of the sensor and channel packet drops are shown in Figure 3b,c, respectively.

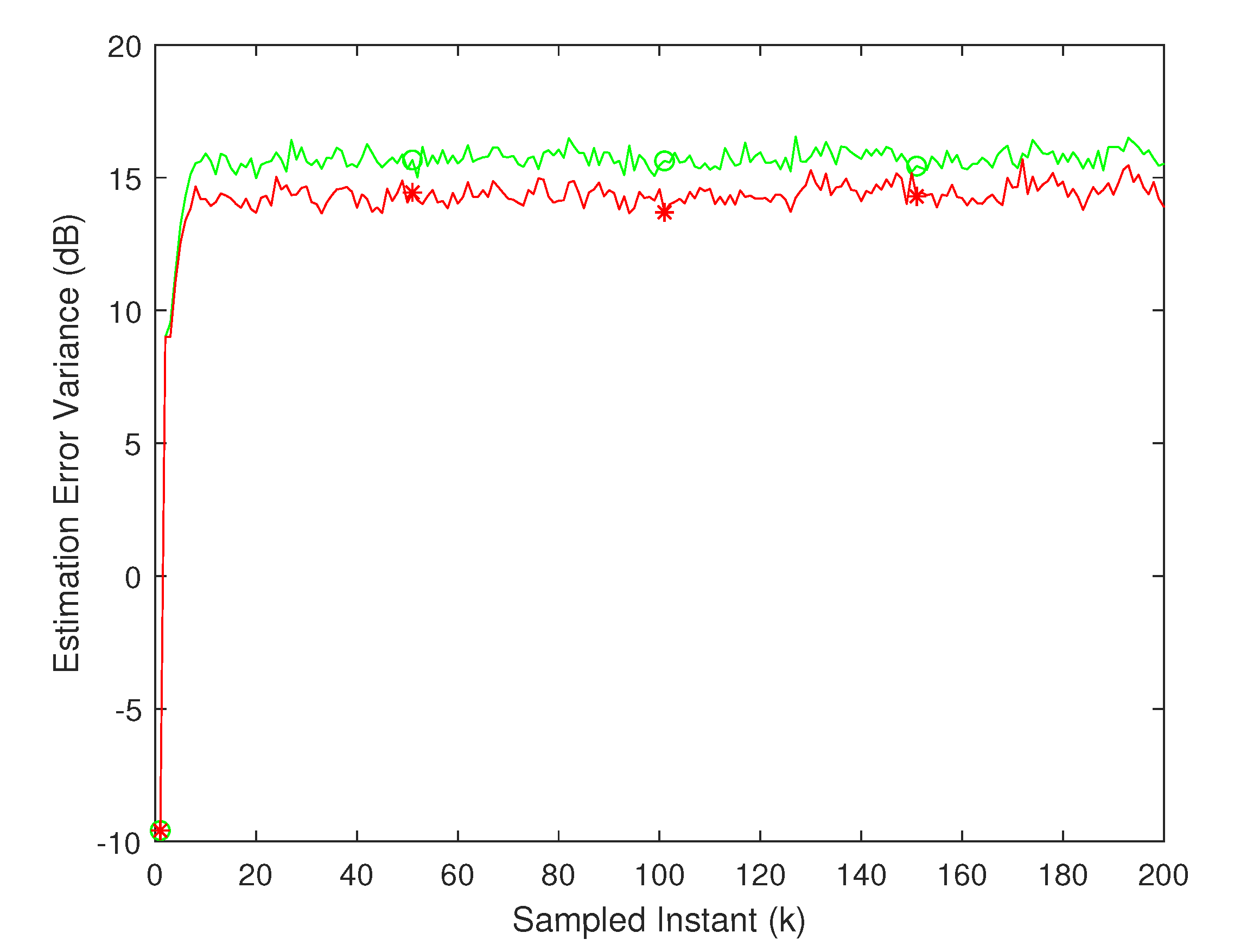
In Case 2, the derived robust fusion estimator is tested using different transmission rates and packet drop rates. The modelling errors are the same as in Case 1 with a truncated normal distribution. It can be seen in Figure 4 that a higher transmission rate gives a better performance of the estimator because a higher transmission rate gives more estimates received by the fusion center and more accurate results. It is reasonable to observe from Figure 5 that a higher packet drop rate results in worse estimation performance. The performance deterioration from lower transmission rates is lower than that from high packet drop rates.

As can be seen from the two sets of simulations, the proposed robust fusion estimator exhibits relatively better performance compared to the fusion estimator that ignores uncertainty. The derived robust fusion estimator is still applicable when the selection of modelling errors is not limited to the particular structure. The results show that the method is an effective multi-sensor fusion method in practical applications.

6. Conclusion

This paper takes into account the presence of deterministic inputs and state delay influences in the system based on the investigation of robust fusion estimators for multi-sensor systems with uncertainty, random packet drops, and transmission constraints. The model transformation is carried out for the state delay using the state augmentation method, and the pseudo-cross-covariance matrix is updated. It is demonstrated that the estimation error of the fusion estimation is uniform boundedness. Numerical simulations were performed using a tractor-car system to verify that the estimation performance of the updated estimator is better than the Kalman filter based on nominal parameters. Since the modelling errors are not restricted to a specific structure, the proposed fusion estimator has a wide range of applicability. In addition, follow-up work on the tractor-car system example is still in progress, and the further stage is to apply the algorithm designed in this investigation to a practical case.

References yes