Submitted:
27 June 2023
Posted:
27 June 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Brief History on Urban Runoff Modelling in Japan
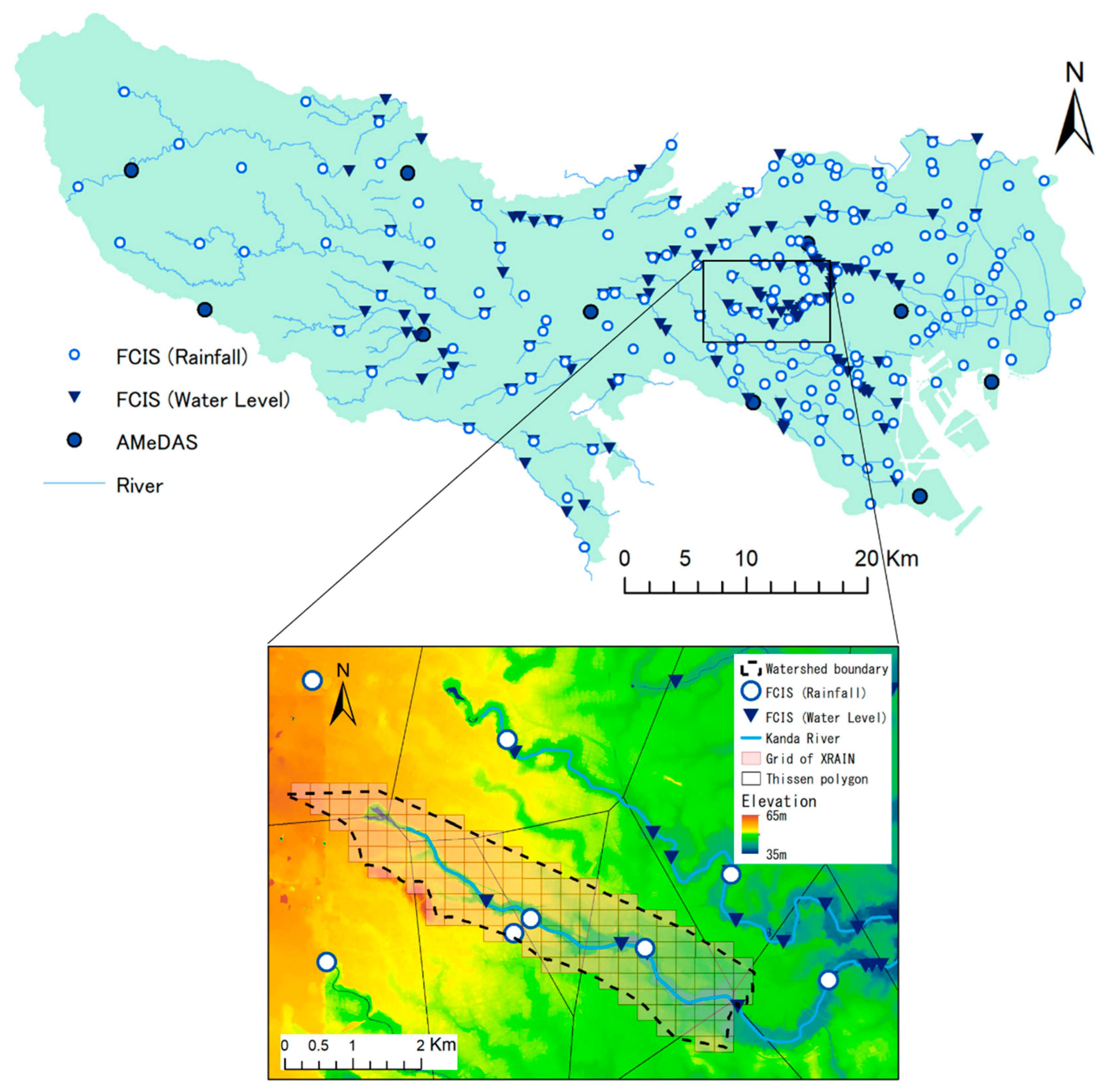
3. Rainfall and Water Level Observation System in Japan
4. Storage Function Model in Urban Watersheds
4.1. Conventional SF Models
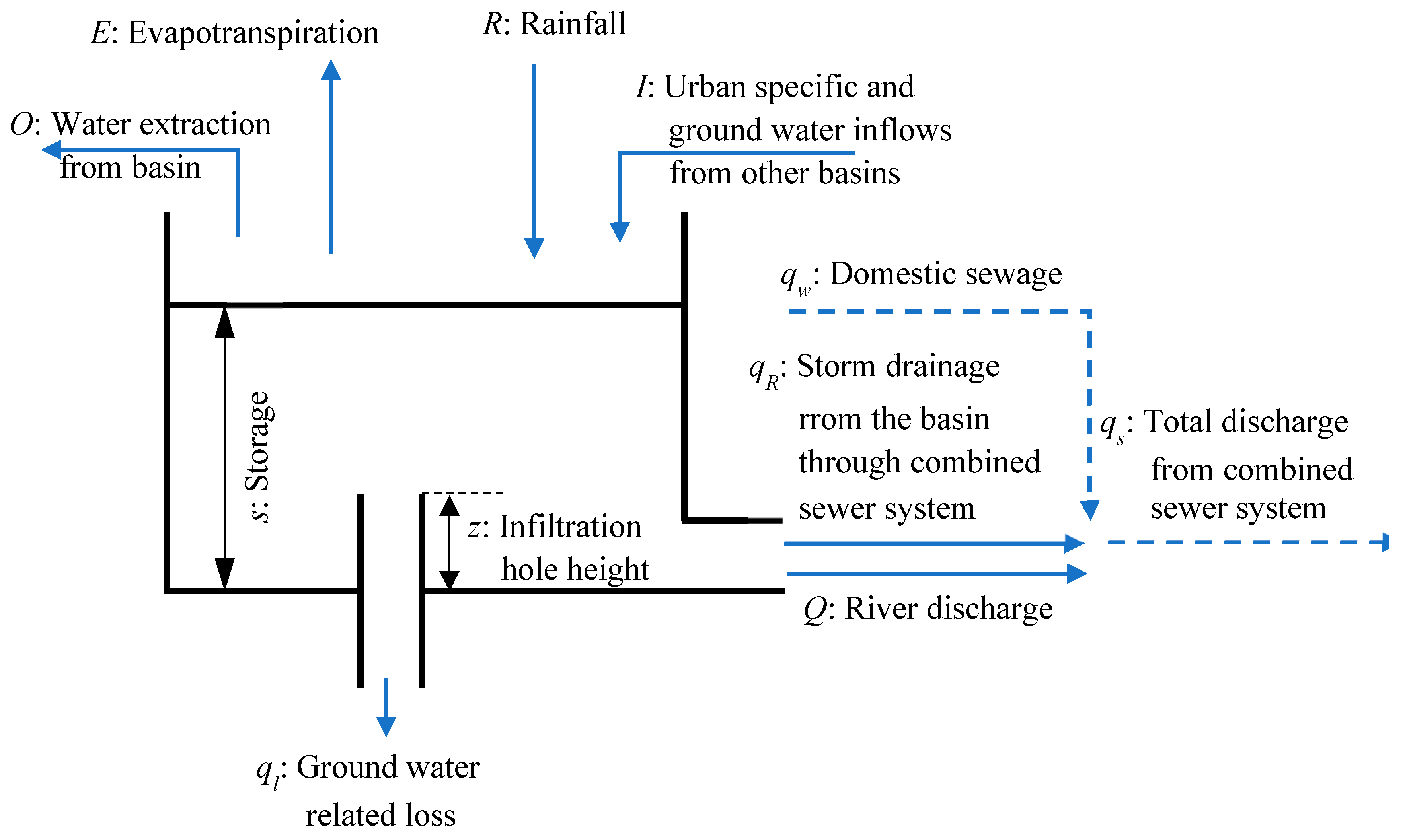
4.2. Urban Storage Function (USF) Model
4.3. Application of the USF Model in an Urban Watershed
4.4. Runoff Prediction by USF Using XRAIN Data in an Urban Watershed
4.5. AI-based Flood Runoff Modelling in Urban Watershed
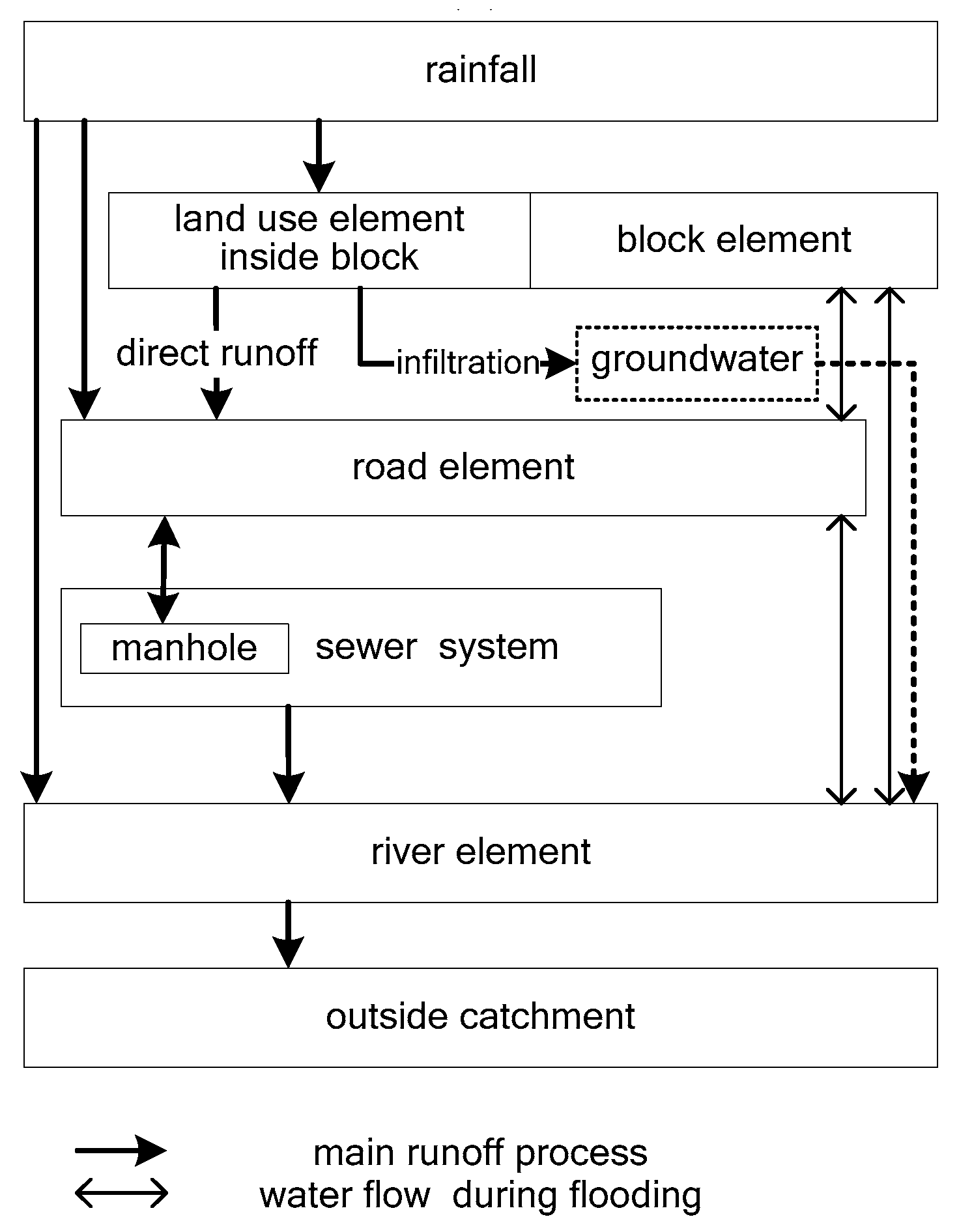
5. Distributed Physical Models in Urban Watersheds
5.1. Background
5.2. Representation of Uurban Structures in Distributed Physical Models
5.3. Structured Grid
5.4. Curvilinear Grid
5.5. Unstructured Grid
5.6. Road Network
5.7. Urban Landscape GIS Delineation
5.8. TSR Model
5.8.1. Outline of Tokyo Storm Runoff (TSR) Model
5.8.2. Model Application to Urban Watershed
6. Concluding Remarks and Future Prospects
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kinoshita, T. Runoff changes due to urbanization. Civil Eng. Tec. Mat. 1976, 9, 11–15. (in Japanese). [Google Scholar]
- Takahashi, Y.; Izumi, K.; Ando, Y.; Kanao, K. Change of flood runoff in hilly basins by urbanization. Pro. Hyd. Conf. Jpn. Soc. Civil Eng. 1982, 26, 261–266. (in Japanese). [Google Scholar]
- Yamada, T.; Ishii, F.; Yamazaki, K.; Iwatani, K. On relation between distribution of field moisture capacity and runoff characteristics in small basins. Pro. Hyd. Conf. of Jpn. Soc. Civil Eng. 1985, 29, 25–30. (in Japanese). [Google Scholar]
- Kadoya, M. A review of the study on runoff changes due to urbanization. Doboku Gakkai Ronbunshu 1985, 363, 23–34. (in Japanese). [Google Scholar] [CrossRef] [PubMed]
- Takahashi, Y. City and water, Iwanami Shinsho: Tokyo, Japan, 1988, 1-34. (in Japanese)
- Amaguchi, H.; Kawamura, A.; Olsson, J.; Takasaki, T. Development and testing of a distributed urban storm runoff event model with a vector-based catchment. J. Hydrol. 2012, 420–421, 205–215. [Google Scholar] [CrossRef]
- Tamai, N. River Engineering, Ohmsha: Tokyo, Japan, 1999, 55-95. (in Japanese)
- Ishihara, S.; Takasaki, T.; Kawamura, A.; Amaguchi, H. Background of new development plan and future development methods of urban rivers in Tokyo metropolis. Advances in River Eng. 2014, 20, 437–442. (in Japanese). [Google Scholar]
- Kanae, S. Characteristics of localized torrential rainfall (so-called guerrilla rainfall). J. of hydrol. Syst. 2009, 73, 11–16. (in Japanese). [Google Scholar]
- Nakakita, E.; Yamaguchi, K.; Yamabe, H. A study on detecting origin of localized torrential rainfall using volume scanning radar. DPRI Annuals 2008, 52, 547–562. (in Japanese). [Google Scholar]
- Ushiyama, M. A study of relationship between “Guerilla Heavy Rainfall” and disaster. J. Jpn Soc. Civil Eng. Ser.B1 (Hyd. Eng.) 2011, 67, I_505–I_510. (in Japanese). [Google Scholar] [CrossRef]
- Fujibe, F.; Togawa, H.; Sakata, M. Long-term change and spatial anomaly of warm season afternoon precipitation in Tokyo. SOLA, 2009, 5, 17–20. [Google Scholar] [CrossRef]
- Seino, N.; Aoyagi, T.; Tsuguti, H. Numerical Simulation of Urban Impact on Precipitation in Tokyo: How does Urban Temperature Rise Affect Precipitation? Urban Clim. 2018, 23, 8–35. [Google Scholar] [CrossRef]
- Kawamura, A. Urban flooding and its countermeasures, Urban Technology (Revised Edition). Edited by Graduate School of Urban Infrastructure and Environment, Tokyo Metropolitan University, Gihodo Pub. 2016, 235-249. (in Japanese)
- Singh, V.P. Watershed modeling. In Computer Models of Watershed Hydrology, Singh, V.P. Water Res. Pub.: Colorado, USA, 1995, 1-22.
- 16. JSCE Committee on Hydroscience and Hydraulic Engineering. Hydroscience Formulary. JSCE: Tokyo, Japan, 1999, 35-47. (in Japanese)
- Sugawara, M. Rainfall-runoff analysis. Kyoritsu pub: Tokyo, Japan, 1972, 257. (in Japanese)
- Kimura, T. Storage function model (1), Civil Eng. J., Public works research center: Tokyo, Japan, 1961, 3, 36–43. (in Japanese). [Google Scholar]
- Kawamura, A. Inverse problems in hydrology. In Introduction to Inverse Problems in Civil Engineering, Jpn. Soc. Civil Eng., Maruzen: Tokyo, Japan, 2000, 24-30. (in Japanese)
- Hino, M. What have hydrologists done and what should we do? What should we do from now on? J. Jpn Soc. Hydrol. Water Res. 1996, 9, 3–16. (in Japanese). [Google Scholar]
- Tanouchi, H.; Olsson, J.; Lindstrom, G.; Kawamura, A.; Amaguchi, H. Improving urban runoff contributions in multi-basin hydrological simulation by the HYPE model using EEA Urban Atlas. Hydrology, 2019, 6. [Google Scholar] [CrossRef]
- Baba, H.; Hoshi, K.; Hashimoto, N. Synthetic storage routing model coped with loss mechanisms, Pro. Hyd. Conf. Jpn. Soc. Civil Eng. 1999, 43, 1085–1090. (in Japanese). [Google Scholar]
- Takasaki, T.; Kawamura, A.; Amaguchi, H. ; Araki, K; Storage function model considering urban runoff process. Doboku Gakkai Ronbunshuu B. 2009, 65, 3, 217-230. (in Japanese)
- Shiiba, M.; Tachikawa, Y. ; IchikawaY. Hydrology and Hydraulic engineering planning studies. Kyoto University Press, 2013, 3-51.
- Hanaki, T.; Suharyanto, A.; Sugio, S. Investigation of flood control by rainwater infiltration facilities in urbanized watershed, Pro. Hyd. Conf. of Jpn. Soc. Civil Eng. 1999, 48, 37–42. (in Japanese). [Google Scholar]
- Jia, Y.; Ni, G.; Kinouchi, T.; Yoshitani, J.; Kawahara, Y.; Suetsugi, T. Study on effects of storm-water detention facilities in an urbanized watershed using distributed model. Jpn. Soc. Civil Eng. Hyd. Conf. 2001, 45, 109–114. (in Japanese). [Google Scholar] [CrossRef]
- Amaguchi, H.; Kawamura, A. A proposal of urban runoff model considering green infrastructures and its application. J. Jan. Soc. Civil Eng., Ser.G (Environ. Res.) 2020, 76, I_319–I_325. (in Japanese). [Google Scholar] [CrossRef]
- Sayama, T.; Ozawa, G.; Kawakami, T.; Nabesaka, S.; Fukami, K. Rainfall-runoff-inundation analysis of the 2010 Pakistan flood in the Kabul River basin. Hydrol. Sci. J. 2012, 57, 298–312. [Google Scholar] [CrossRef]
- Public Works Research Institute. RRI model. http://www.icharm.pwri.go.jp/research/rri/rri_top.html. (accessed on 18 November 2022).
- Beven, K.J.; Kirkby, M.J. A physically based variable contributing area model of basin hydrology. Hydrol. Sci. Bulletin 1979, 24, 43–69. [Google Scholar] [CrossRef]
- Zhoa, R.J. The Xinanjiang model applied in China. J. Hydrol. 1992, 135, 371–381. [Google Scholar]
- Ren, L.; Yuan, F. The Xinanjiang model on a digital basin platform. In Watershed Models, Singh, V.P.; Frevert. D.K. CRC Press: Boca Raton, USA, 2006; pp. 179–208. [Google Scholar]
- Bathurst, J.C.; Wicks, J.M.; O'Connell, P.E. The SHE/SHESED basin scale water flow and sediment transport modelling system. In Computer Models of Watershed Hydrology, Singh, V.P.; Water Res. Pub.: Colorado, USA, 1995; pp. 563–594. [Google Scholar]
- Calver, A.; Wood, W.L. The Institute of Hydrology Distributed Model. In Computer Models of Watershed Hydrology, Singh, V.P.; Water Res. Pub.: Colorado, USA, 1995; pp. 595–626. [Google Scholar]
- Bergström, S. The HBV Model. In Computer Models of Watershed Hydrology, Singh, V.P.; Water Res. Pub.: Colorado, USA, 1995; pp. 443–476. [Google Scholar]
- Lindström, G.; Pers, C.P.; Rosberg, R.; Strömqvist, J.; Arheimer, B. Development and test of the HYPE (Hydrological Predictions for the Environment) model - A water quality model for different spatial scales. Hydrol. Res. 2010, 41, 295–319. [Google Scholar] [CrossRef]
- SMHI, HYPE. Available online: https://www.smhi.se/en/research/research-departments/hydrology/hype-1.7994. (accessed on 18 November 2022).
- Koga, T.; Kawamura, A.; Amaguchi, H. Study on permeable area ratio of 10m-mesh land use classification using advanced GIS delineation in the upper Kanda River basin. J. of Jan. Soc. Civil Eng., Ser.B1 (Hyd. Eng.) 2012, 68, I_505–I_510. (in Japanese). [Google Scholar]
- Amaguchi, H.; Kawamura, A.; Takasaki, T. Physically based distributed flood runoff model for an urban catchment using polygon feature GIS data. Doboku Gakkai Ronbunshuu B 2007, 63, 206–223. (in Japanese). [Google Scholar] [CrossRef]
- Koga, T.; Kawamura, A.; Amaguchi, H.; Tanouchi, H. Assessing impervious area ratios of grid-based land-use classifications on an example of an urban watershed. Hydrol. Sci. J. 2016, 61, 1728–1739. [Google Scholar] [CrossRef]
- Sample, D. J.; Heaney, J.P.; Wright, L.; Koustas, R. Geographic information systems, decision support systems, and urban storm-water management, J. Water Plan. Man. 2001, 3, 155–161. [Google Scholar] [CrossRef]
- Rodriguez, F.; Andrieu, H.; Creutin, J.D. Surface runoff in urban catchments: morphological identification of unit hydrographs from urban databanks. J. of Hydrol. 2003, 283, 146–168. [Google Scholar] [CrossRef]
- Lee, J.G.; Nietch, C.T.; Panguluri, S. Drainage area characterization for evaluating green infrastructure using the storm water management model. Hydrol. Earth Syst. Sci. 2018, 22, 2615–2635. [Google Scholar] [CrossRef]
- Japan Society of Hydrology and Water Resources. Handbook of Hydrology and Water Resources; Asakura: Tokyo, Japan, 1997; p. 636. (in Japanese) [Google Scholar]
- JSCE Committee on Hydroscience and Hydraulic Engineering. Hydroscience Formulary, 1985 ed.; JSCE: Tokyo, Japan, 1985; p. 713. (in Japanese) [Google Scholar]
- JSCE Committee on Hydroscience and Hydraulic Engineering. Hydroscience Formulary, 1971 ed.; JSCE: Tokyo, Japan, 1971; p. 616. (in Japanese) [Google Scholar]
- JSCE Committee on Hydroscience and Hydraulic Engineering. Hydroscience Formulary, 1963 ed.; JSCE: Tokyo, Japan, 1963; p. 603. (in Japanese) [Google Scholar]
- Morita, S. Urban flood risk analysis. Forum 2014, 8, 3–75. (in Japanese). [Google Scholar]
- Matsubayashi, U. Runoff mechanism and characteristics in urban areas. Handbook of hydrology and water resources, J. Jpn Soc. Hydrol. Water Res. Asakura: Tokyo, Japan, 1997, 146-148. (in Japanese)
- Ishikawa, K.; Sato, K.; Izumi, K. Applicability of rational method to the urbanized channels in Tokyo. Pro. Hyd. Conf. of Jpn. Soc. Civil Eng. 1982, 26, 267–272. (in Japanese). [Google Scholar]
- Kadoya, M.; Fukushima, A. Concentration time of flood in small or medium river basin. DPRI Annuals 1976, 19B, 143–152. (in Japanese). [Google Scholar]
- Tanioka, Y.; Fukuoka, S.; Taniguchi, M.; Koyama, Y. Characteristics of floods in small urban rivers. Doboku Gakkai Ronbunshu 1998, 586, 1–12. (in Japanese). [Google Scholar] [CrossRef] [PubMed]
- Watanabe, A.; Sasada, T.; Watanabe, N.; Yamada, T. Theoretical derivation of synthesized rational formula. J. Jan. Soc. Civil Eng., Ser.B1 (Hyd. Eng.) 2012, 74, I_973–I_978. (in Japanese). [Google Scholar]
- Hashimoto, T.; Hasegawa, T. A runoff model to evaluate land use change. Civil Eng. J. 1977, 19, 221–226. (in Japanese). [Google Scholar]
- Yamaguchi, T.; Matsubara, S.; Yamamori, T. Second report of rainfall-runoff study in an urban area -Runoff estimation by modified R.R.L. method. Civil Eng. J. 1972, 14, 34–39. (in Japanese). [Google Scholar]
- Matsubayashi, U. Runoff model for urban watersheds. Handbook of hydrology and water resources. J. Jpn Soc. Hydrol. Water Res. 1997, 148-151. (in Japanese)
- Sukegawa, N.; Kitagawa, Y. A rainfall-runoff simulation model for assessing the effect of urbanization on flood runoff. Pro. of Jan. Soc. of Civil Eng. 1982, 325, 51–59. (in Japanese). [Google Scholar] [CrossRef]
- Iwagaki, Y.; Sueishi, T. On the unsteady flow in open channels with uniform lateral inflow – Hydraulic studies on the run-off phenomena or rain water, 1st report. Doboku Gakkai Ronbunshu 1954, 39, 575–583. (in Japanese). [Google Scholar]
- Sueishi, T. On the run-off analysis by the method of characteristics hydraulic studies on the run-off phenomena of rain water, 2nd report. Doboku Gakkai Ronbunshu 1955, 29, 74–87. (in Japanese). [Google Scholar] [CrossRef]
- 60. Lighthill MJ, Whitham GB. 1955. On kinematic waves: 1. Flood movement in long rivers. Pro. of Royal Soc. 1955, Series A 229: 281-316.
- Singh, V.P. ; Jain. S.K. Rainfall-Runoff Modeling. In Handbook of Applied Hydrology, Second Edition, Singh VP (ed.). Chap. 59, McGraw-Hill Educ.: New York, US, 2017, 59-1-59-8.
- Kimura, M.; Tanaka, T.; Azechi, I.; Nakatani, K.; Yamazaki, D. , Yoshioka, H. Interdisciplinary perspective of surface water flow numerical analysis, J. Jpn Soc. Hydrol. Water Res. 2017, 30, 307–334. (in Japanese). [Google Scholar] [CrossRef]
- Ando, Y.; Nabeyama, T.; Nishijima, S. Flood runoff analysis of urban watersheds. J. Urban Res. 1991, 41, 69–89. (in Japanese). [Google Scholar]
- Fujimura, K.; Ando, Y.; Maeda, M. A study on stormwater runoff model of urban lowland basin. Pro. Hyd. Conf. of Jpn. Soc. Civil Eng. 1995, 39, 61–66. (in Japanese). [Google Scholar] [CrossRef]
- Suzuki, T.; Terakawa, Y.; Matsuura, T. Development of physics-based distributed model for operational hydrological forecasting. Civil Eng. J. 1996, 38, 26–31. (in Japanese). [Google Scholar]
- Shahzad, A.; Gabriel, H.F.; Haider, S.; Mubeen, A.; Siddiqui, M. J. Development of a flood forecasting system using IFAS: a case study of scarcely gauged Jhelum and Chenab river basins. Arab J. Geosci. 2018, 11, 383. [Google Scholar] [CrossRef]
- Chikamori, H.; Oka, T.; Takara, K.; Okubo, G. Fundamental Study on Application of Geographic Information System to Construction of Rainfall-Runoff Model of Urbanized Area, DPRI Annuals 1997 B 40(B-2), 137-144. (in Japanese).
- Ministry of Land, Infrastructure, Transport and Tourism. In Investigation guidelines for river sand and gravel management technology standards, Research Edition. Chap. 3, Ministry of Land, Infrastructure, Transport and Tourism, Tokyo, 2016.
- Kawamura, A. Status quo and perspectives of flood runoff analysis for urban watersheds, J. Jpn Soc. Hydrol. Water Res. 2018, 31, 451–466. (in Japanese). [Google Scholar] [CrossRef]
- Shibuo, Y.; Furumai, H. Advances in Urban Stormwater Management in Japan: A Review. J. Disaster Res. 2021, 16, 310–320. [Google Scholar] [CrossRef]
- Water Management and Land Conservation Bureau. https://www5.river.go.jp/, (accessed on 27 Mar. 2023.
- Water Management and Land Conservation Bureau. River disaster prevention information, https://city.river.go.jp/kawabou/reference/index01.html, (accessed on 27 Mar. 2023.
- Japan Meteorological Agency. “Automated Meteorological Data Acquisition System 2020,” https://www.jma.go.jp/jma/en/Activities/amedas/amedas.html (accessed on 10 Nov. 2022.
- Ministry of Land, Infrastructure, Transport and Tourism. X-band MP Radar Network, Available online:. Available online: http://mp-radar.bosai.go.jp/mlit.htm, (accessed on 18 Nov. 18 2022).
- Schilling, W. Rainfall data for urban hydrology: what do we need? Atmospheric Research 1991, 27, 5–21. [Google Scholar] [CrossRef]
- Fabry, F.; Bellon, A.; Duncan, M. R.; Austin, G. L. High resolution rainfall measurements by radar for very small basins: the sampling problem reexamined. J. Hydro. 1994, 161, 415–428. [Google Scholar] [CrossRef]
- Koyama, N.; Sakai, M.; Yamada, T. Study on a Water-Level-Forecast Method Based on a Time Series Analysis of Urban River Basins—A Case Study of Shibuya River Basin in Tokyo. Water 2023, 15, 161. [Google Scholar] [CrossRef]
- Tokyo Metropolitan Government. - Flood Control Integrated Information System, Available online:. Available online: https://www.kasen-suibo.metro.tokyo.lg.jp/im/uryosuii/tsim0102g_en.html (accessed on 10 November 2022).
- Shiiba, M.; Tachikawa, Y.; IchikawaY. Hydrology and Hydraulic engineering planning studies. Kyoto University Press 2013, 3–51. [Google Scholar]
- JSCE Committee on Hydroscience and Hydraulic Engineering, Hydroscience Formulary, 1985 Edition, JSCE: Tokyo, Japan. 1985, 151-172. (in Japanese)
- Kadoya, M.; Nagai, A. Runoff analysis methods (Part 10) Storage method - flood runoff analysis by the storage function model -. J. of Jpn. Soc. of Agric. Civil Eng. 1980, 48, 43–50. [Google Scholar]
- Holmes, RRJr. Streamflow Ratings. In Handbook of Applied Hydrology, Second Edition, Singh VP (ed.). Chap. 6, McGraw-Hill Education: New York, USA, 2017, 6-1-6-14.
- Prasad, R. A nonlinear hydrologic system response model. J. Hyd. Div. 1967, 93, 201–222. [Google Scholar] [CrossRef]
- Hoshi, K.; Yamaoka, T. A relationship between kinematic wave and storage routing models. Pro. Hyd. Conf. of Jpn. Soc. Civil Eng. 1982, 26, 273–278. (in Japanese). [Google Scholar]
- Padiyedath, S.G.; Kawamura, A.; Amaguchi, H.; Azhikodan, G. Baseflow esti-mation for tropical wet and dry climate region using recursive digital filters. J. Jan. Soc. Civil Eng., Ser.G (Environ. Res.) 2017, 73, 9–16. [Google Scholar]
- Hoshi, K.; Baba, H.; Hashimoto, A. Development of a storage function method for tracking floods in watershed and channel systems. Advances in River Eng. 2000, 6, 297–302. (in Japanese). [Google Scholar]
- Takasao, T.; Takara, K. Evaluation of rainfall-runoff models from the stochastic viewpoint. J. Hydrol. 1988, 102, 381–406. [Google Scholar] [CrossRef]
- Takasaki, T.; Kawamura, A.; Amaguchi, H. Development of the storage function model for urban flood considering the outflow through combined wewer system. J. Jpn Soc. Hydrol. Water Res. 2008, 21, 228–241. (in Japanese). [Google Scholar] [CrossRef]
- Ministry of Land, Infrastructure, Transport and Tourism. History of the sewerage system, https://www.mlit.go.jp/crd/city/sewerage/data/basic/rekisi.html (accessed on 31 Jan 2023). (in Japanese)
- Padiyedath, S.G.; Kawamura, A.; Takasaki, T.; Amaguchi, H.; Azhikodan, G. An effective storage function model for an urban watershed in terms of hydrograph reproducibility and Akaike information criterion. J. Hydrol. 2018, 563, 657–668. [Google Scholar] [CrossRef]
- Kawamura, A.; Marabtene, T. Evolutionary computing: Genetic algorithms. In Handbook of applied hydrology, 2nd ed,; Singh, V.P., Ed.; McGraw-Hill Education: New York, USA, 2017; pp. 13-1–13-4. [Google Scholar]
- Duan, Q.; Sorooshian, S.; Gupta, V.K. Optimal use of the SCE-UA global optimization method for calibrating watershed models. J. Hydro. 1994, 158, 265–284. [Google Scholar] [CrossRef]
- Tanakamaru, H. Parameter estimation for the tank model using global optimization, Drainage and Reclamation Eng. 1995, 178, 503-512. 178.
- Matsubara, T.; Tsuchida, K.; Hibiya, M. Study on parameter identification of distributed runoffmodel using SCE-UA method. J. Jan. Soc. Civil Eng., Ser.B1 (Hyd. Eng.) 2015, 71, I_265–I_270. (in Japanese). [Google Scholar]
- Akaike, H. Likelihood of a model and information criteria. J. Econom., 1981, 16, 3–14. [Google Scholar] [CrossRef]
- Padiyedath, S.G.; Kawamura, A.; Takasaki, T.; Amaguchi, H.; Azhikodan, G. A bootstrap approach for the parameter uncertainty of an urban-specific rainfall runoff model. J. Hydrol. 2019, 579, 1–18. [Google Scholar] [CrossRef]
- Padiyedath, S.G.; Kawamura, A.; Takasaki, T.; Amaguchi, H.; Azhikodan, G. A generalized urban storage function model considering spatial rainfall distribution. J. Jan. Soc. Civil Eng., Ser.B1 (Hyd. Eng.) 2019, 75, I_223-I_228. [Google Scholar] [CrossRef] [PubMed]
- Padiyedath, S.G.; Kawamura, A.; Amaguchi, H.; Takasaki, T. and Azhikodan G. A generalized storage function model for the water level estimation using rating curve relationship. Water Res. Man. 2020, 34, 2603–2619. [Google Scholar]
- Takasaki, T.; Kawamura, A.; Amaguchi, H.; Ishihara, S. Real-time runoff forecasting characteristics of urban storage function model using particle filter. J. Jan. Soc. Civil Eng., Ser.B1 (Hyd. Eng.) 2012, 68, I_511–I_516. (in Japanese). [Google Scholar]
- Takasaki, T.; Kawamura, A.; Amaguchi, H.; Ishihara, S. Real-time runoff forecasting characteristics of Urban Storage Function Model using Kalman filter. J. Jan. Soc. Civil Eng., Ser.B1 (Hyd. Eng.) 2013, 69, I_457–I_480. (in Japanese). [Google Scholar]
- Yonese, Y.; Kawamura, A.; Tonotsuka, A.; Amaguchi, H. Runoff characteristics using XRAIN in a small urban watershed. J. Jan. Soc. Civil Eng., Ser.B1 (Hyd. Eng.) 2018, 74, I_97–I_102. (in Japanese). [Google Scholar]
- Yonese, Y.; Kawamura, A.; Amaguchi, H.; Tonotsuka, A. Precision evaluation of X-band MP radar rainfall in a small urban watershed by comparison to 1-minute ground observation rainfall data. J. Jan. Soc. Civil Eng., Ser.B1 (Hyd. Eng.) 2016, 72, I_217–I_222. (in Japanese). [Google Scholar]
- Yonese, Y.; Kawamura, A.; Amaguchi, H.; Tonotsuka, A. Study on the precision of 1-minute X-band MP radar rainfall data in a small urban watershed. Int. J. Sustainable Dev. and Planning 2018, 13, 614–625. [Google Scholar] [CrossRef]
- Yonese, Y.; Kawamura, A.; Amaguchi, H.; Tonotsuka, A. Spatiotemporal characteristic analysis of X-band MP radar rainfall in a small urban watershed on the movement of rainfall area. J. Jan. Soc. Civil Eng., Ser.B1 (Hyd. Eng.) 2017, 73, I_217–I_222. (in Japanese). [Google Scholar]
- Tonotsuka, A.; Kawamura, A.; Yonese, Y.; Amaguchi, H. Spatiotemporal correlation characteristics of X-band MP radar rainfall in a small urban watershed focused on torrential rainfall events at each ground observation point. J. Jan. Soc. Civil Eng., Ser.G (Environ. Res.), 2017, 73, I_261–I_268. (in Japanese). [Google Scholar]
- Hitokoto, M.; Sakuraba, M.; Sei, Y. Development of the real-time river stage prediction method using deep learning, J. Jan. Soc. Civil Eng., Ser.B1 (Hyd. Eng.) 2016, 72, I_187–I_192. (in Japanese). [Google Scholar] [CrossRef] [PubMed]
- Tamura, K.; Nanou, S.; Miura, S.; Yamawaki, M.; Kaneko, H. Application of deep learning to long-term prediction of dam inflow toward efficiency of the flood control operation. J. Jan. Soc. Civil Eng., Ser.B1 (Hyd. Eng.) 2018, 74, I_1327–I_1332. (in Japanese). [Google Scholar] [CrossRef] [PubMed]
- Hida, Y.; Chiha, H.; Asaoka, Y.; Nagabayashi, H. Real-time forecasting for water levels in sewer by machine learning and inundation simulation. J. Jan. Soc. Civil Eng., Ser.B1 (Hyd. Eng.) 2017, 73, I_649-I_654. [Google Scholar] [CrossRef] [PubMed]
- Fujizuka, S.; Kawamura, A.; Amaguchi, H.; Takasaki, T. Emulation of urban runoff model by deep learning for benchmark virtual hyeto and hydrograph. J. Jan. Soc. Civil Eng., Ser.G (Environ. Res.) 2019, 75, I_289–I_296. (in Japanese). [Google Scholar] [CrossRef] [PubMed]
- Fujizuka, S.; Kawamura, A.; Amaguchi, H.; Takasaki, T. Emulation performance evaluation of urban runoff model by neural network and deep learning. J. Jan. Soc. Civil Eng., Ser.B1 (Hyd. Eng.) 2019, 75, I_229–I_234. (in Japanese). [Google Scholar] [CrossRef] [PubMed]
- Fujizuka, S.; Kawamura, A.; Amaguchi, H.; Takasaki, T. Rainfall runoff benchmark test by deep learning model using urban medium and small river basin dataset. J. Jan. Soc. Civil Eng., Ser.B1 (Hyd. Eng.) 2020, 76, I_355–I_360. (in Japanese). [Google Scholar] [CrossRef]
- Hitokoto, M.; Sakuraba, M. Hybrid deep neural network and distributed rainfall-runoff model for the real-time river stage prediction. J. Jan. Soc. Civil Eng., Ser.B1 (Hyd. Eng.) 2017, 73, I_22–I_34. (in Japanese). [Google Scholar] [CrossRef]
- Iwasa, Y.; noue, K.; Mizutori, M. Hydraulic analysis of overland flood flows by means of numerical method, DPRI Annuals 1980, B, 23(B-2): 305-317 (in Japanese).
- Toda, K.; Inoue, K.; Murase, S.; Ichikawa, Y.; Yokoo, H. Inundation analysis due to heavy rainfall in urban area. Doboku Gakkai Ronbunshu 2000, 663, 1–10. (in Japanese). [Google Scholar] [CrossRef]
- Shibuo, Y.; Lee, S.; Sanuki, H.; Yoshimura, K.; Tajima, Y.; Sato, S.; Furumai, H. Development of couped river and sewer network model for improved water level prediction in urban rivers. J. Jan. Soc. Civil Eng., Ser.B1 (Hyd. Eng.) 2018, 74, I_1357–I_1362. (in Japanese). [Google Scholar]
- Rangari, V.A.; Umamahesh, N.V.; Bhatt, C.M. Assessment of inundation risk in urban floods using HEC RAS 2D. Mod. Earth Sys. and Env. 2019, 5, 1839–1851. [Google Scholar] [CrossRef]
- Mustafa A, Szydłowski M. Application of different building representation techniques in HEC-RAS 2-D for urban flood modeling using the Toce River experimental case. PeerJ. 2021, 2, 9:e11667. [Google Scholar]
- Rosenzweig, B.R.; Cantis, P.H.; Kim, Y.; Cohn, A.; Grove, K.; Brock, J.; Yesuf, P.; Mistry, P.; Welty, C. The value of urban flood modeling, Earth’s Future 2020, 9, e2020EF001739.
- Amaguchi, H.; Tsubaki, R. On the inundation prediction, present state and matters to be resolved. Advances in River Eng. 2015, 21, 425–430. (in Japanese). [Google Scholar]
- Miura, S.; Kawamura, I.; Kimura, I.; Miura, A. Study on inundation flow analysis method in densely populated urban area on alluvial fan. J. Jan. Soc. Civil Eng., Ser.B1 (Hyd. Eng.) 2011, 67, I_979–I_984. (in Japanese). [Google Scholar] [CrossRef] [PubMed]
- Nakamura, T.; Sasaki, Y.; Mizukusa, K. A guide of application for flood analysis models in the urban areas, Technical note of NILM 2004, No. 202.
- Inokawa, N.; Kobayashi, K. Analysis of flooding in underground space using 1m mesh elevation data and study of evacuation risk. J. Jan. Soc. Civil Eng., Ser.B1 (Hyd. Eng.) 2022, 78, I_1415–I_420. (in Japanese). [Google Scholar] [CrossRef]
- Kawaike, K.; Inoue, K.; Hayashi, H.; Toda, K. Development of inundation flow model in urban area. Doboku Gakkai Ronbunshu 2002, 698, 1–10. (in Japanese). [Google Scholar] [CrossRef]
- Fukuoka, S.; Kawashima, M.; Yokoyama, H.; Mizuguchi, M. The numerical simulation of flood-induced flows in urban residential area and the study of damage reduction. Doboku Gakkai Ronbunshu 1998, 600, 23–36. (in Japanese). [Google Scholar] [CrossRef]
- Akiyama, J.; Shigeeda, M.; Tanabe, T. Dynamic network model for free-surface-pressurized flows and its applicability to sewer network in the urban area. Advances in River Eng. 2008, 14, 425–430. (in Japanese). [Google Scholar]
- Akiyama, J.; Shigeeda, M.; Kozono, Y. Numerical model for rainfall-runoff and flood inundation processes and its application for Iizuka city. Pro. Hyd. Conf. of Jpn. Soc. Civil Eng. 2010, 54, 919–924. (in Japanese). [Google Scholar]
- Inoue, K.; Kawaike, K.; Hayashi, H. Inundation flow modeling in urban area. Pro. Hyd. Conf. of Jpn. Soc. Civil Eng. 1999, 43, 533–538. (in Japanese). [Google Scholar] [CrossRef]
- Sekine, M. Numerical analysis of inundation in the region of downtown Tokyo with residence area. J. Jan. Soc. Civil Eng., Ser.B1 (Hyd. Eng.) 2011, 67, 70–85. (in Japanese). [Google Scholar] [CrossRef]
- Sekine, M.; Kamata, T.; Hosono, Y.; Shibuya, Y. Inundation process in three cities of Musashino, Mitaka, and Chofu for the largest possible torrential rainfall. J. Jan. Soc. Civil Eng., Ser.B1 (Hyd. Eng.) 2022, 78, I_427–I_432. (in Japanese). [Google Scholar] [CrossRef] [PubMed]
- Araki, T.; Amaguchi, H.; Kawamura, A.; Takasaki, T. Development of a groundwater recharge model for an urban catchment using urban landscape GIS delineation and its simulation for actual catchment. J. of Jan. Soc. Civil Eng., Ser.B1 (Hyd. Eng.) 2012, 68, 109–124. (in Japanese). [Google Scholar]
- Tanouchi, H.; Amaguchi, H.; Kawamura, A.; Nakagawa, N. Development of an automated construction algorithm of advanced delineation GIS data using 1:2500 topological map. J. Jan. Soc. Civil Eng., Ser.B1 (Hyd. Eng.) 2013, 69, I_523–I_528. (in Japanese). [Google Scholar]
- Tanouchi, H.; Amaguchi, H.; Kawamura, A.; Nakagawa, N.; Koga, T. Study on an automated construction method of minute road segments aiming at urban storm runoff analysis. Theory and Applications of GIS 2014, 22, 25–34. (in Japanese). [Google Scholar] [CrossRef]
- Tanouchi, H.; Amaguchi, H.; Kawamura, A.; Koga, T.; Hagiwara, Y. Automated construction method of polygonal blocks for an urban watershed. J. Jpn Soc. Hydrol. Water Res. 2015, 26, 298–303. (in Japanese). [Google Scholar] [CrossRef]
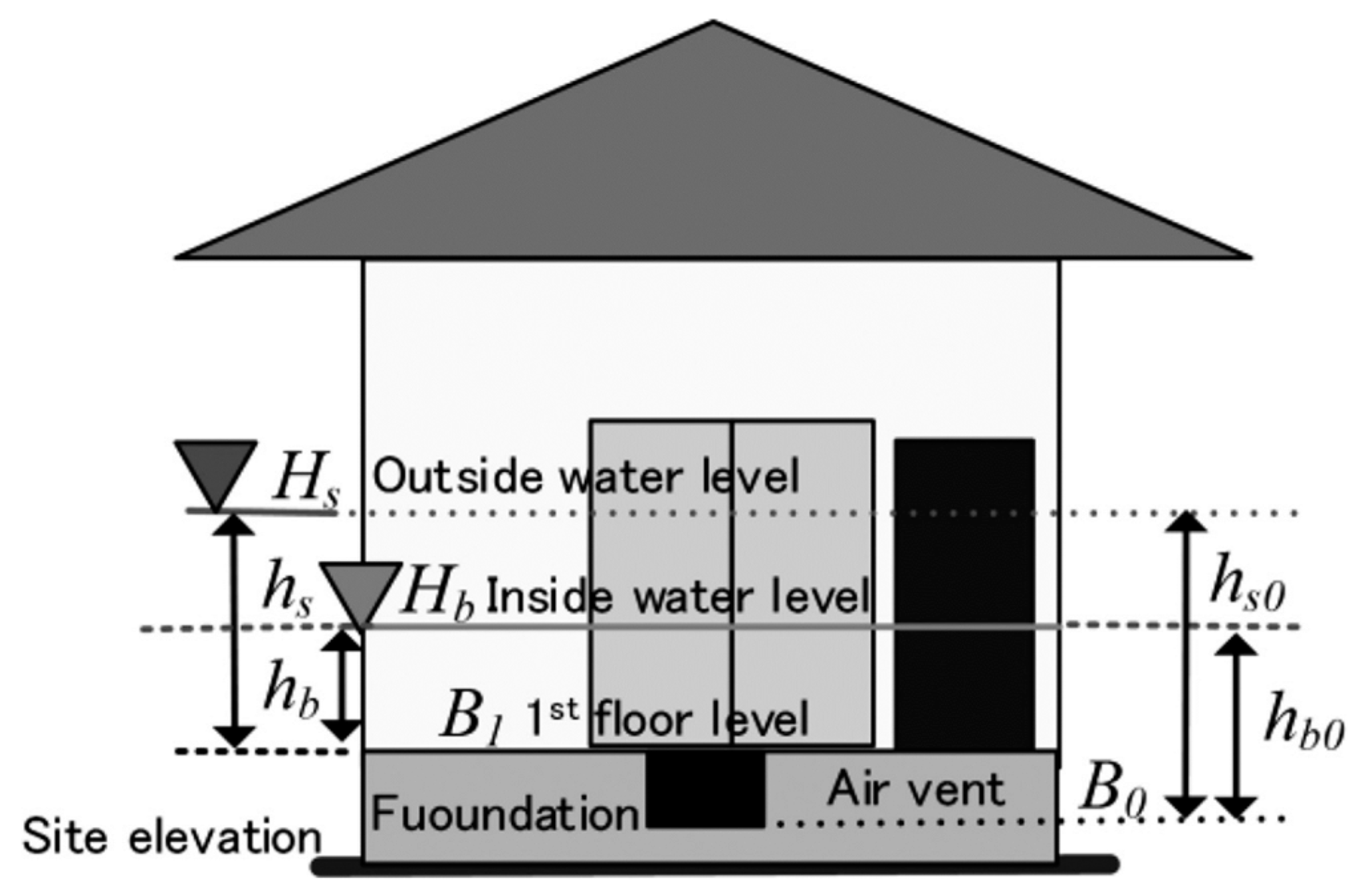
- Amaguchi, H.; Nagasaka, T.; Kawamura, A.; Takasaki, T.; Nakagawa, N. A proposal of storm runoff model considering process of building inundation for an urban catchment. Advances in River Eng. 2013, 19, 211–216. (in Japanese). [Google Scholar]
- Amaguchi, H.; Kawamura, A. Development of a storm runoff model considering process of individual building inundation. Int. J. Safety and Security Eng. 2016, 6, 570–581. [Google Scholar] [CrossRef]
| (PAR represents a parameter) | |||
| No. | Models | Storage equation | Continuity equation |
| 1 | Linear (3-PAR) |
||
| 2 | Kimura (4-PAR) |
||
| 3 | Prasad (5-PAR) |
||
| 4 | Hoshi (6-PAR) |
||
| 5 | USF (7-PAR) |
||
| Geometry | Image |
Characteristics (a) Objective, (b) Features, (c) Landuse, (d) Handling of buildings, (e) Surface flow equations |
| Structured Grid [120,121,122] |
 |
(a) Flood analysis. (b) Model data can be created and calculated efficiently. (c) Usually expressed as a percentage of impermeable area. If the resolution is sufficiently high below 10 m, land use information may be specified in the calculation grid. (d) The impact of building blockage effect is considered by building coverage ratio and conveyance reduction facters.If the resolution is fine enough, the height of the building may be set in the grid. (e) 2D diffusive wave model. |
| Curvilinear Grid [123,124] |
 |
(a) Flood analysis. (b) Capable of creating grids suitable for urban structures along road. Ideally, the road network in the targeted catchment should be like a grid. If the road network is complex, model data preparation becomes more difficult. (c) Usually expressed as a percentage of impermeable area. (d) Resistance is calculated separately for bottom friction, resistance due to plane vortices behind the house and hydrodynamic forces on the buildings. (e) 2D diffusive wave model. |
| Unstructured Grid [125] |
 |
(a) Flood analysis. (b) Represents complex terrain and boundaries on fewer grids. Manual processing, requires GIS data and a mesh generation software. (c) Usually expressed as a percentage of impermeable area. If the resolution is fine (less than 20 m), a Digital Surface Model (DSM) may be set for the elevation of the residential block. (d) Buildings of the same scale as the computational grid are subjected to a boundary-fitting process, while smaller buildings are subjected to a spatial averaging process, with the object group as drag. (e) 2D full shallow-water equations. |
| Road Network [127,128] |
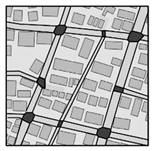 |
(a) Flood analysis. (b) Capability to represent complex road networks. The ground surface consists of roads and Residential grids. Relatively easy in a GIS enviironment. (c) Initially developed as a flood inundation model from rivers, rainfall-runoff processes and infiltration processes are not considered. Recently developed models set average building area percentages. (d) Roughness coefficients of large values are set against the flow between the road and the residentail block. (e) 1D Saint-Venant equations. |
| Urban Landscape Delineation [6] |
 |
(a) Flood runoff and inundation analysis. (b) Unlike other grids, polygon data is created for roads, buildings, permeable and impermeable ground, etc., classified according to permeability characteristics, with roads, for example, further divided into segments. It is possible to give detailed attributes to individually subdivided polygons (e.g. building structure, use, number of floors, presence of storage facilities, etc.). (c) Land use and grid geometry are consistent. (d) Parameters are set to take into account the building flooding process. (e) 1D Saint-Venant equations. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




