Submitted:
26 June 2023
Posted:
27 June 2023
You are already at the latest version
Abstract
Keywords:
MSC: 92D25; 35K57
1. Introduction
| Parameter | Description |
|---|---|
| The prey population occupies every node index i in the network | |
| The predator population occupies every node index i in the network | |
| The self-diffusion rate of prey population | |
| The self-diffusion rate of predator population | |
| The ratio of intrinsic growth rate to predator birth rate | |
| A | The weak Allee effect constant |
| The ratio of environmental capacity to half-saturation prey density | |
| e | The coefficients of light attenuation by water |
| The coefficients of light attenuation by self-shading | |
| The death rate of the predator population | |
| The elements in the network Laplacian matrix |
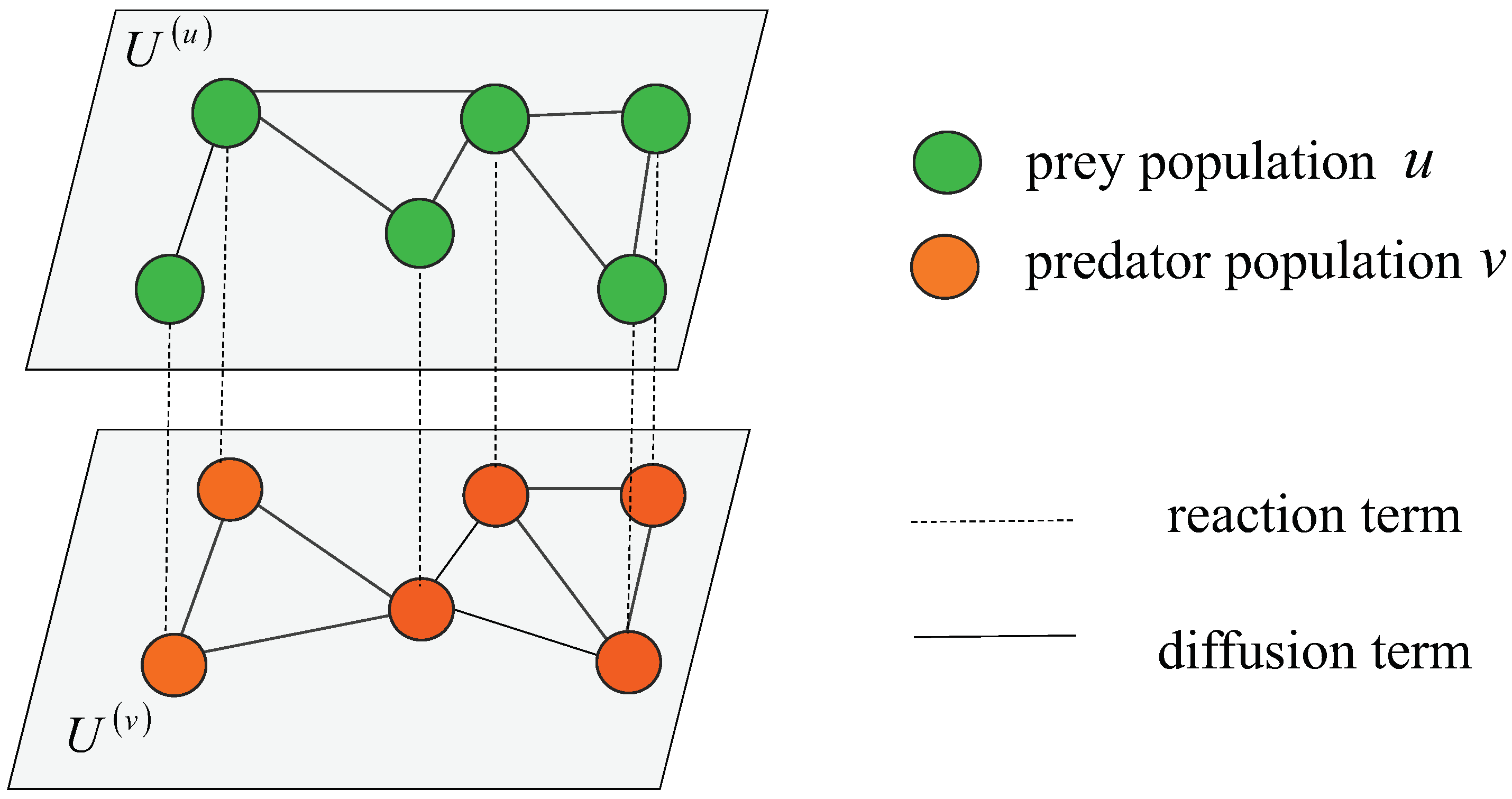
2. Turing instability on multiplex networks
- The positive equilibrium is always unstable which is a saddle.
- Let , which can be obtained . So we have the following conclusion: if , then is stable. If , then is unstable. Particularly, when Hopf bifurcation occurs since and
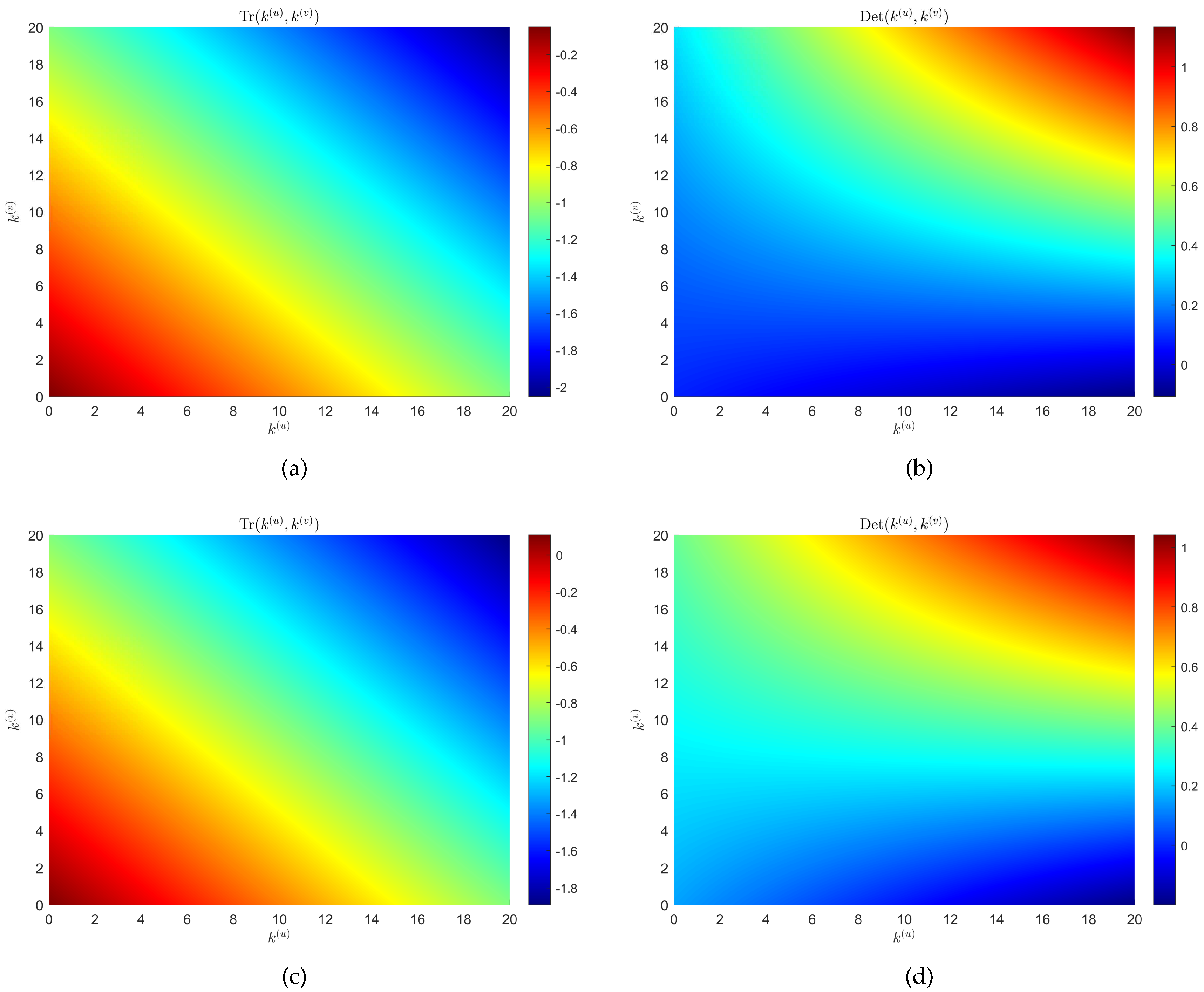
3. Turing pattern on networks
3.1. Diffusion rate induces Turing pattern on single-layer network
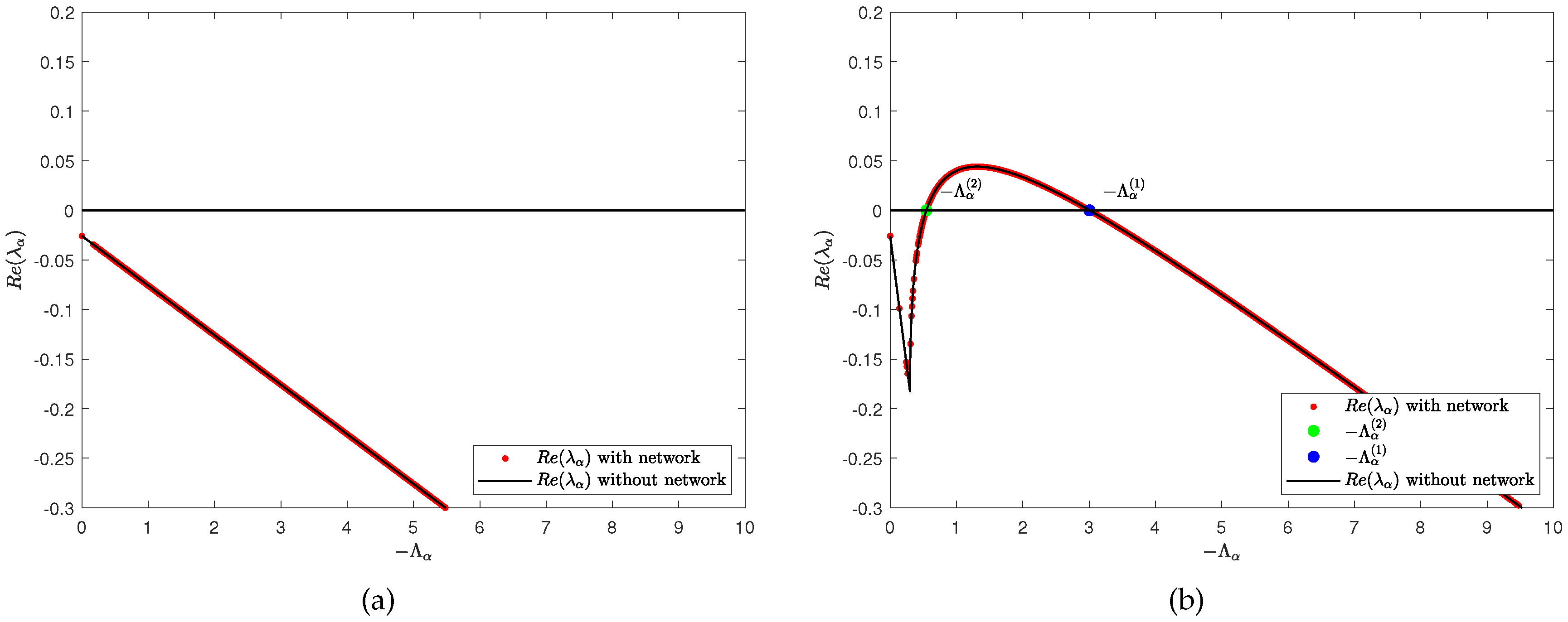
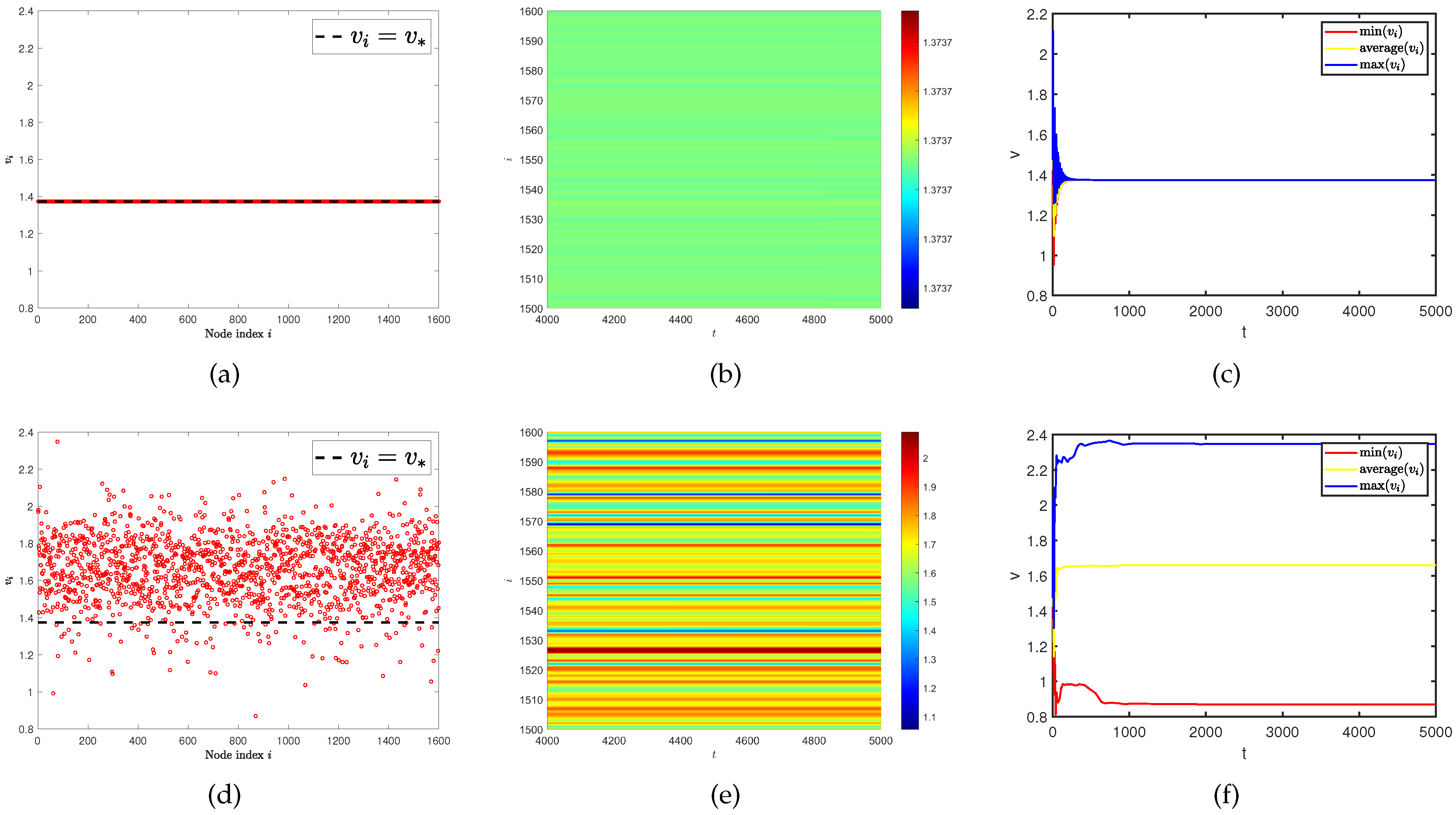
3.2. Network average degree induces Turing pattern on single-layer network
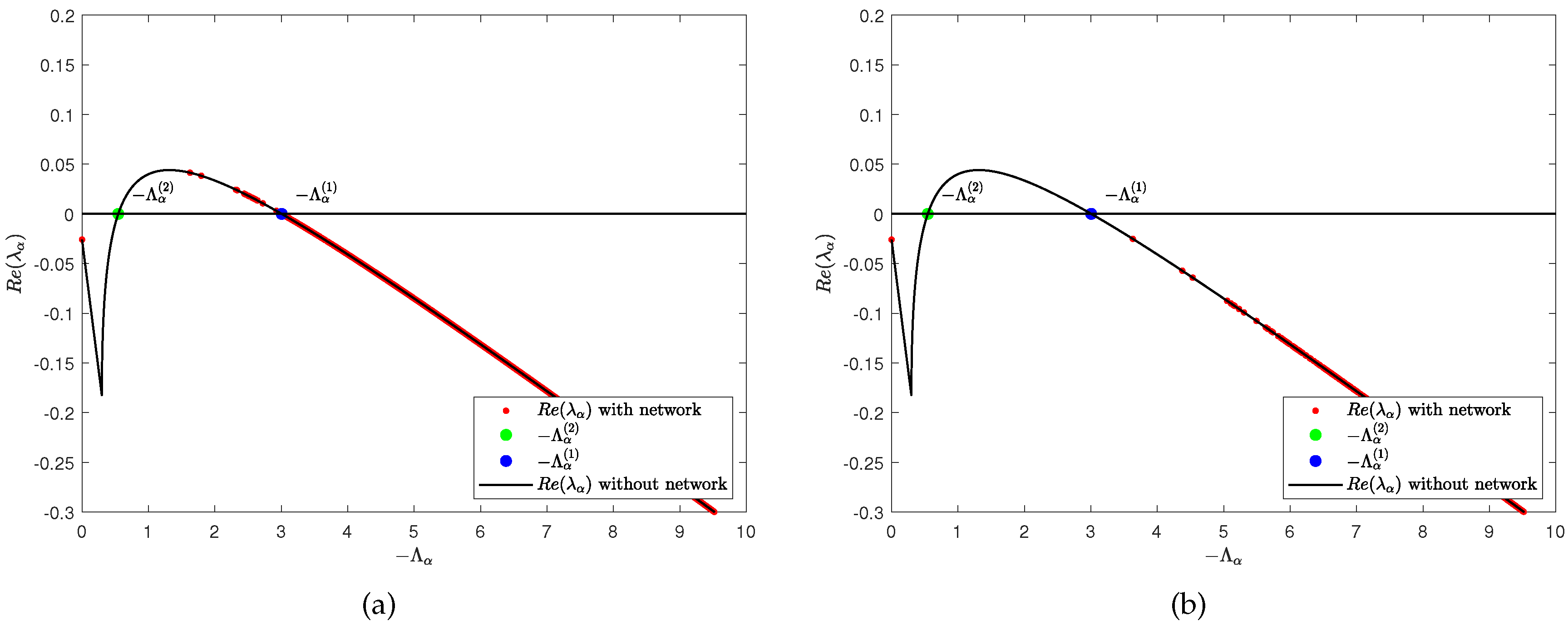
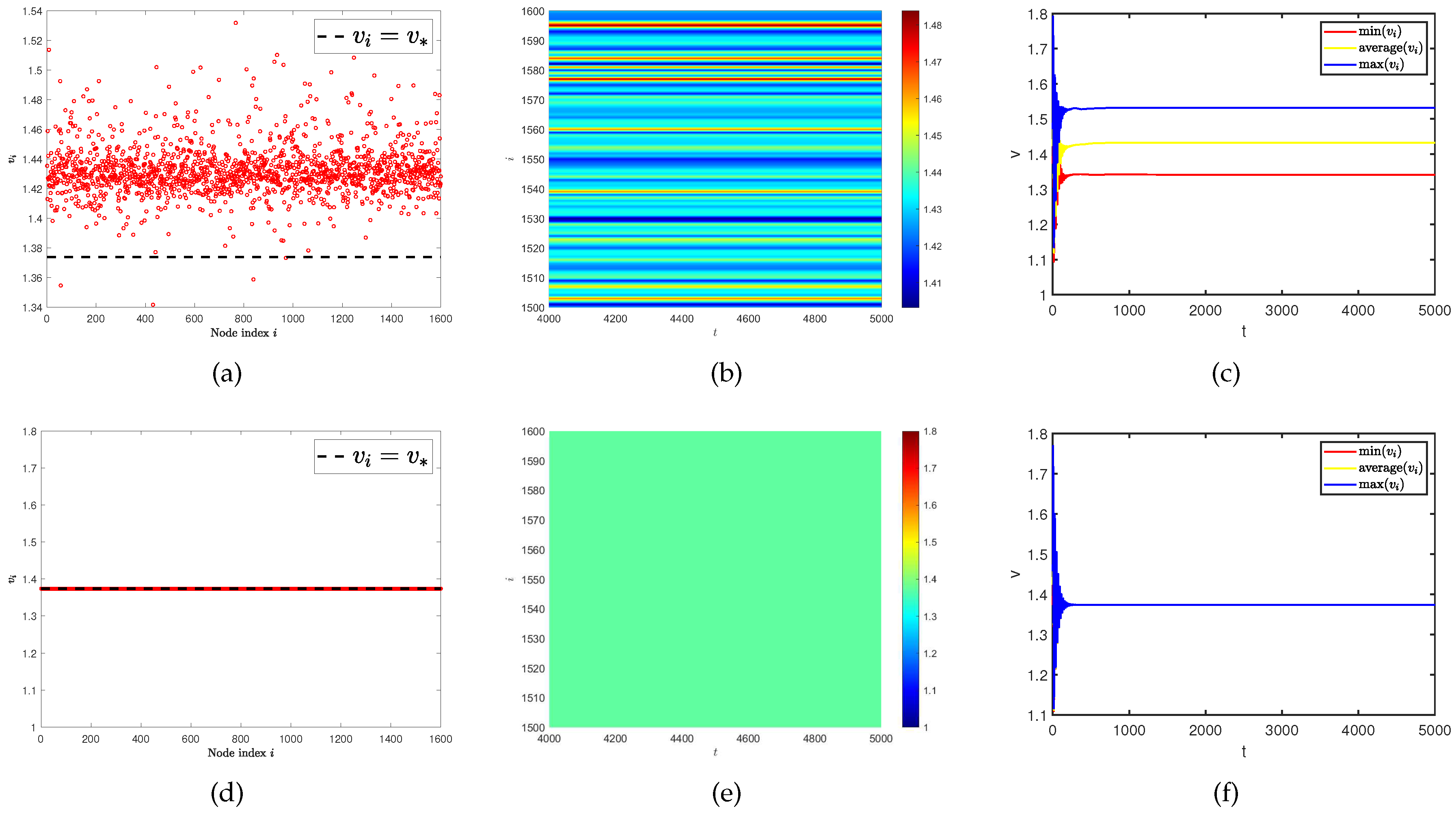
3.3. Ratio of network average degree induces Turing pattern on multiplex networks
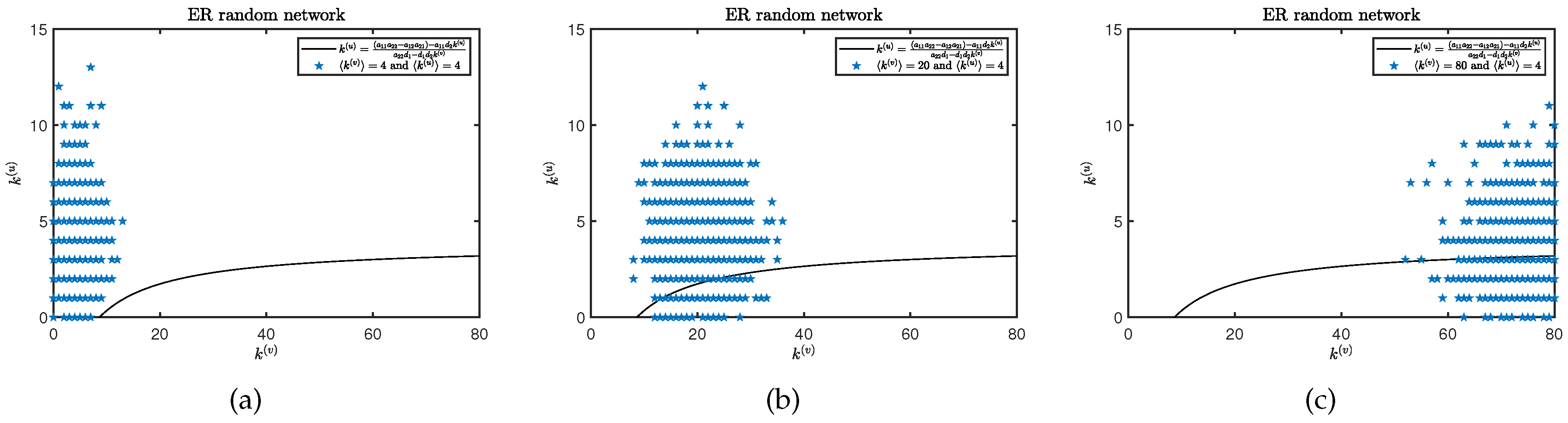
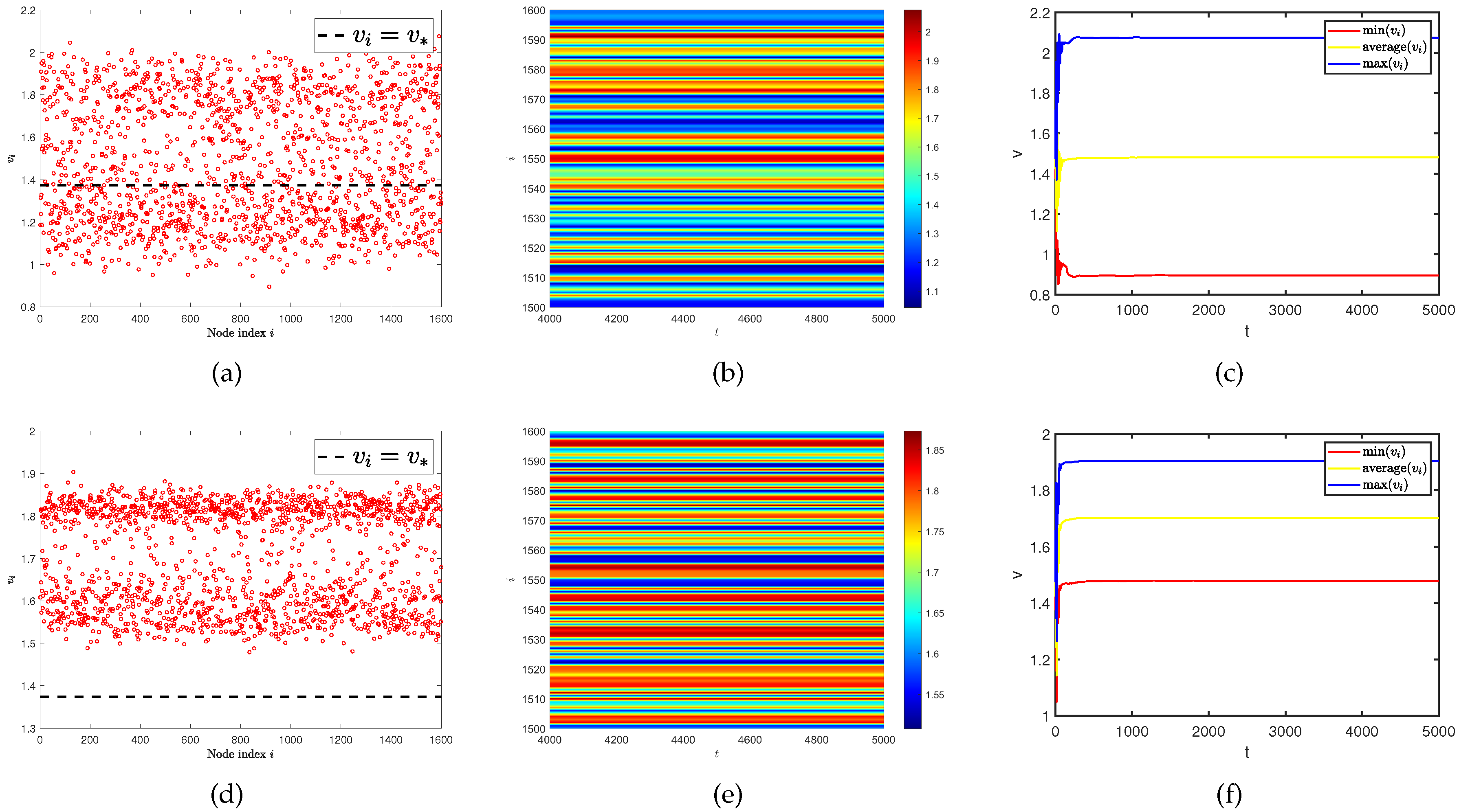
4. Spatiotemporal pattern on networks
4.1. Parameter induces spatiotemporal pattern on single-layer network
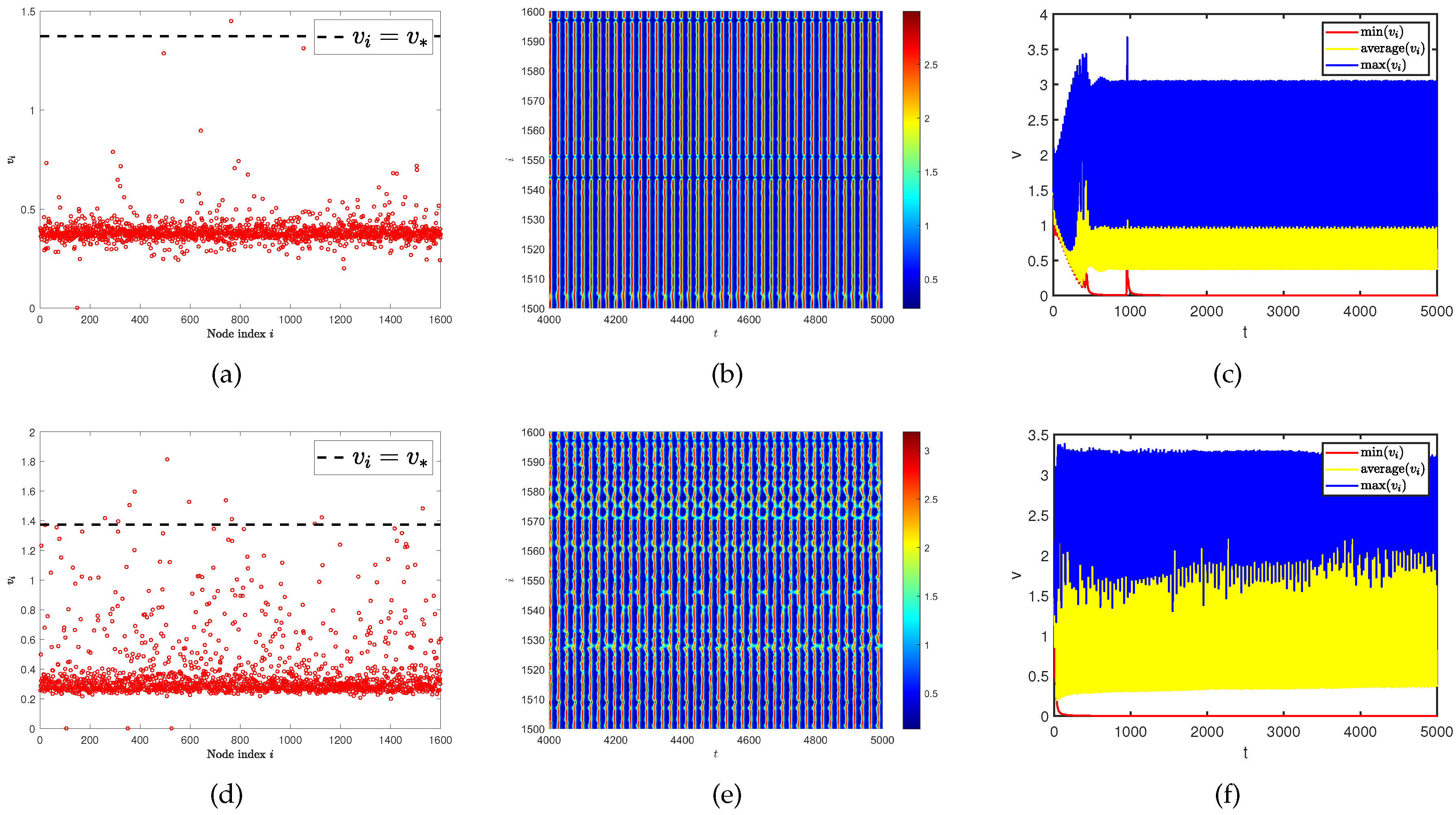
4.2. Network average degree induces spatiotemporal pattern on single-layer network and multiplex networks
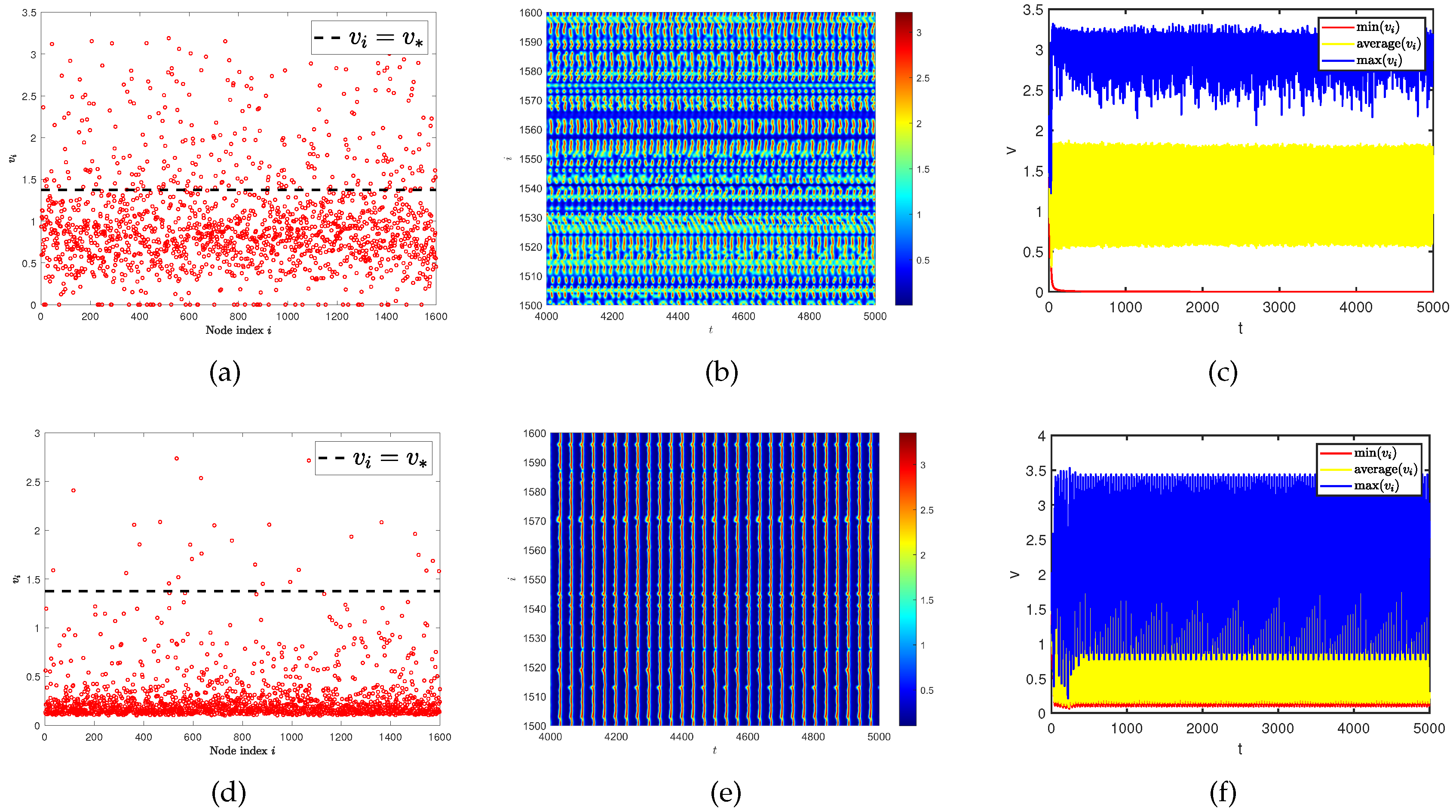
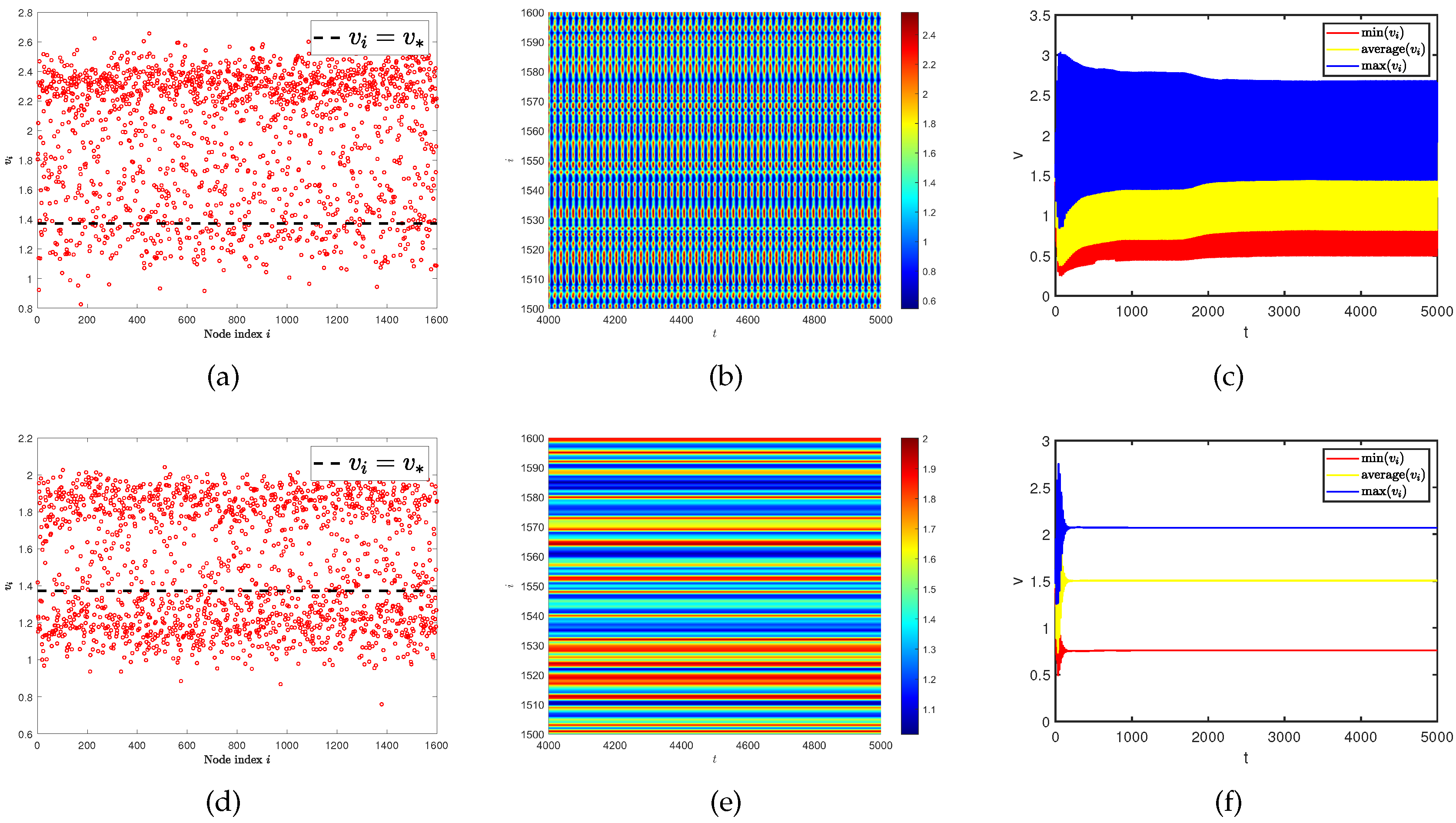
5. Conclusion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Murray, J.D. Mathematical biology: I. An introduction; Springer, 2002. [Google Scholar] [CrossRef]
- Nakao, H.; Mikhailov, A.S. Turing patterns in network-organized activator–inhibitor systems. Nature Physics 2010, 6, 544–550. [Google Scholar] [CrossRef]
- Nagano, S.; Maeda, Y. Phase transitions in predator-prey systems. Physical Review E 2012, 85, 011915. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Xing, Y.; Zang, H.; Han, M. Spatio-temporal dynamics of a reaction-diffusion system for a predator–prey model with hyperbolic mortality. Nonlinear Dynamics 2014, 78, 265–277. [Google Scholar] [CrossRef]
- Shi, L.; Liu, H.; Wei, Y.; Ma, M.; Ye, J. The permanence and periodic solution of a competitive system with infinite delay, feedback control, and Allee effect. Advances in Difference Equations 2018, 2018, 400. [Google Scholar] [CrossRef]
- Ye, Y.; Liu, H.; Wei, Y.; Zhang, K.; Ma, M.; Ye, J. Dynamic study of a predator-prey model with Allee effect and Holling type-I functional response. Advances in Difference Equations 2019, 2019, 1–15. [Google Scholar] [CrossRef]
- Liu, H.; Ye, Y.; Wei, Y.; Ma, W.; Ma, M.; Zhang, K. Pattern formation in a reaction-diffusion predator-prey model with weak Allee effect and delay. Complexity 2019, 2019, 6282958. [Google Scholar] [CrossRef]
- Ye, Y.; Liu, H.; Wei, Y.m.; Ma, M.; Zhang, K. Dynamic study of a predator-prey model with weak Allee effect and delay. Advances in Mathematical Physics 2019, 2019, 7296461. [Google Scholar] [CrossRef]
- Ye, Y.; Zhao, Y. Bifurcation analysis of a delay-induced predator–prey model with Allee effect and prey group defense. International Journal of Bifurcation and Chaos 2021, 31, 2150158. [Google Scholar] [CrossRef]
- Ye, Y.; Zhao, Y.; Zhou, J. Promotion of cooperation mechanism on the stability of delay-induced host-generalist parasitoid model. Chaos, Solitons & Fractals 2022, 165, 112882. [Google Scholar] [CrossRef]
- Li, D.; Liu, H.; Han, X.; Lin, X.; Wei, Y. Stability and Bifurcation Analysis of Bazykin’s Model with Holling I Functional Response and Allee Effect. International Journal of Bifurcation and Chaos 2022, 32, 2250248. [Google Scholar] [CrossRef]
- Li, D.; Liu, H.; Zhang, H.; Ma, M.; Ye, Y.; Wei, Y. Bifurcation Analysis in a Predator-Prey Model with an Allee Effect and a Delayed Mechanism. Acta Mathematica Scientia 2023, 43, 1415–1438. [Google Scholar] [CrossRef]
- Rosenzweig, M.L.; MacArthur, R.H. Graphical representation and stability conditions of predator-prey interactions. The American Naturalist 1963, 97, 209–223. [Google Scholar] [CrossRef]
- Zhang, T.; Zang, H. Delay-induced Turing instability in reaction-diffusion equations. Physical Review E 2014, 90, 052908. [Google Scholar] [CrossRef] [PubMed]
- Asllani, M.; Challenger, J.D.; Pavone, F.S.; Sacconi, L.; Fanelli, D. The theory of pattern formation on directed networks. Nature communications 2014, 5, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Asllani, M.; Busiello, D.M.; Carletti, T.; Fanelli, D.; Planchon, G. Turing patterns in multiplex networks. Physical Review E 2014, 90, 042814. [Google Scholar] [CrossRef]
- Kouvaris, N.E.; Hata, S.; Guilera, A.D. Pattern formation in multiplex networks. Scientific reports 2015, 5, 1–9. [Google Scholar] [CrossRef]
- Petit, J.; Asllani, M.; Fanelli, D.; Lauwens, B.; Carletti, T. Pattern formation in a two-component reaction–diffusion system with delayed processes on a network. Physica A: Statistical Mechanics and its Applications 2016, 462, 230–249. [Google Scholar] [CrossRef]
- Petit, J.; Lauwens, B.; Fanelli, D.; Carletti, T. Theory of Turing patterns on time varying networks. Physical review letters 2017, 119, 148301. [Google Scholar] [CrossRef]
- Tian, C.; Ruan, S. Pattern formation and synchronism in an allelopathic plankton model with delay in a network. SIAM Journal on Applied Dynamical Systems 2019, 18, 531–557. [Google Scholar] [CrossRef]
- Muolo, R.; Asllani, M.; Fanelli, D.; Maini, P.K.; Carletti, T. Patterns of non-normality in networked systems. Journal of theoretical biology 2019, 480, 81–91. [Google Scholar] [CrossRef]
- Liu, Z.; Tian, C. A weighted networked SIRS epidemic model. Journal of Differential Equations 2020, 269, 10995–11019. [Google Scholar] [CrossRef]
- Liu, Z.; Tian, C.; Ruan, S. On a network model of two competitors with applications to the invasion and competition of Aedes albopictus and Aedes aegypti mosquitoes in the United States. SIAM Journal on Applied Mathematics 2020, 80, 929–950. [Google Scholar] [CrossRef]
- Tian, C.; Liu, Z.; Ruan, S. Asymptotic and transient dynamics of SEIR epidemic models on weighted networks. European Journal of Applied Mathematics 2022, 1–24. [Google Scholar] [CrossRef]
- Muolo, R.; Gallo, L.; Latora, V.; Frasca, M.; Carletti, T. Turing patterns in systems with high-order interactions. Chaos, Solitons & Fractals 2023, 166, 112912. [Google Scholar] [CrossRef]
- Fernandes, L.D.; De Aguiar, M. Turing patterns and apparent competition in predator-prey food webs on networks. Physical Review E 2012, 86, 056203. [Google Scholar] [CrossRef] [PubMed]
- Chang, L.; Liu, C.; Sun, G.; Wang, Z.; Jin, Z. Delay-induced patterns in a predator–prey model on complex networks with diffusion. New Journal of Physics 2019, 21, 073035. [Google Scholar] [CrossRef]
- Gao, S.; Chang, L.; Wang, X.; Liu, C.; Li, X.; Wang, Z. Cross-diffusion on multiplex networks. New Journal of Physics 2020, 22, 053047. [Google Scholar] [CrossRef]
- Gan, W.; Zhu, P.; Liu, Z.; Tian, C. Delay-driven instability and ecological control in a food-limited population networked system. Nonlinear Dynamics 2020, 100, 4031–4044. [Google Scholar] [CrossRef]
- Chang, L.; Duan, M.; Sun, G.; Jin, Z. Cross-diffusion-induced patterns in an SIR epidemic model on complex networks. Chaos: An Interdisciplinary Journal of Nonlinear Science 2020, 30, 013147. [Google Scholar] [CrossRef]
- Liu, C.; Chang, L.; Huang, Y.; Wang, Z. Turing patterns in a predator–prey model on complex networks. Nonlinear Dynamics 2020, 99, 3313–3322. [Google Scholar] [CrossRef]
- Wang, X.; Song, Z.; Li, Z.; Chang, L.; Wang, Z. Delay-induced patterns in a reaction–diffusion system on complex networks. New Journal of Physics 2021, 23, 073022. [Google Scholar] [CrossRef]
- Chang, L.; Gao, S.; Wang, Z. Optimal control of pattern formations for an SIR reaction–diffusion epidemic model. Journal of Theoretical Biology 2022, 536, 111003. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Gao, S.; Song, M.; Bai, Y.; Chang, L.; Wang, Z. Optimal control of the reaction–diffusion process on directed networks. Chaos: An Interdisciplinary Journal of Nonlinear Science 2022, 32, 063115. [Google Scholar] [CrossRef] [PubMed]
- Gao, S.; Chang, L.; Romić, I.; Wang, Z.; Jusup, M.; Holme, P. Optimal control of networked reaction–diffusion systems. Journal of the Royal Society Interface 2022, 19, 20210739. [Google Scholar] [CrossRef]
- Hu, J.; Zhu, L. Turing pattern analysis of a reaction-diffusion rumor propagation system with time delay in both network and non-network environments. Chaos, Solitons & Fractals 2021, 153, 111542. [Google Scholar] [CrossRef]
- Zhou, J.; Zhao, Y.; Ye, Y.; Bao, Y. Bifurcation Analysis of a Fractional-Order Simplicial SIRS System Induced by Double Delays. International Journal of Bifurcation and Chaos 2022, 32, 2250068. [Google Scholar] [CrossRef]
- Zhou, J.; Zhao, Y.; Ye, Y. Complex dynamics and control strategies of SEIR heterogeneous network model with saturated treatment. Physica A: Statistical Mechanics and its Applications 2022, 608, 128287. [Google Scholar] [CrossRef]
- Zhu, L.; He, L. Pattern dynamics analysis and parameter identification of time delay-driven rumor propagation model based on complex networks. Nonlinear Dynamics 2022, 110, 1935–1957. [Google Scholar] [CrossRef]
- Zheng, Q.; Shen, J.; Xu, Y. Turing instability in the reaction-diffusion network. Physical Review E 2020, 102, 062215. [Google Scholar] [CrossRef]
- Zheng, Q.; Shen, J.; Zhao, Y.; Zhou, L.; Guan, L. Turing instability in the fractional-order system with random network. International Journal of Modern Physics B 2022, 36, 2250234. [Google Scholar] [CrossRef]
- Zheng, Q.; Shen, J.; Zhang, R.; Guan, L.; Xu, Y. Spatiotemporal Patterns in a General Networked Hindmarsh-Rose Model. Frontiers in Physiology 2022, 13, 936982. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Shen, S.; Zhu, L. Complex dynamic analysis of a reaction-diffusion network information propagation model with non-smooth control. Information Sciences 2023, 622, 1141–1161. [Google Scholar] [CrossRef]
- Xie, Y.; Wang, Z. Transmission dynamics, global stability and control strategies of a modified SIS epidemic model on complex networks with an infective medium. Mathematics and Computers in Simulation 2021, 188, 23–34. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Z. Bifurcation and propagation dynamics of a discrete pair SIS epidemic model on networks with correlation coefficient. Applied Mathematics and Computation 2022, 435, 127477. [Google Scholar] [CrossRef]
- Li, D.; Song, W.; Liu, J. Complex Network Evolution Model Based on Turing Pattern Dynamics. IEEE Transactions on Pattern Analysis and Machine Intelligence 2023, 45, 4229–4244. [Google Scholar] [CrossRef] [PubMed]
- Gao, S.; Chang, L.; Perc, M.; Wang, Z. Turing patterns in simplicial complexes. Physical Review E 2023, 107, 014216. [Google Scholar] [CrossRef] [PubMed]
- Song, M.; Gao, S.; Liu, C.; Bai, Y.; Zhang, L.; Xie, B.; Chang, L. Cross-diffusion induced Turing patterns on multiplex networks of a predator–prey model. Chaos, Solitons & Fractals 2023, 168, 113131. [Google Scholar] [CrossRef]
- Xue, L.; Zhang, K.; Wang, H. Long-Term Forecast of HIV/AIDS Epidemic in China with Fear Effect and 90-90-90 Strategies. Bulletin of Mathematical Biology 2022, 84, 132. [Google Scholar] [CrossRef]
- Erdos, P.; Rényi, A.; others. On the evolution of random graphs. Publ. Math. Inst. Hung. Acad. Sci 1960, 5, 17–60. [Google Scholar]
- Barabási, A.L.; Albert, R. Emergence of scaling in random networks. science 1999, 286, 509–512. [Google Scholar] [CrossRef]
- Ye, Y.; Zhou, J. Pattern formation in a predator-prey model with Allee effect and hyperbolic mortality on networked and non-networked environments 2023. 2023, arXiv:q-bio.PE/2306.11818]. [Google Scholar] [CrossRef]
- Othmer, H.G.; Scriven, L. Instability and dynamic pattern in cellular networks. Journal of theoretical biology 1971, 32, 507–537. [Google Scholar] [CrossRef] [PubMed]
- Ye, Y.; Zhou, J.; Zhao, Y. Pattern formation in reaction-diffusion information propagation model on multiplex simplicial complexes 2023. 2023. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




