Prerpints.org logo
Preprint
Review

Microscopic Flow of CO2 in Complex Pore Structures: A Recent 10-Year Review

Altmetrics

Downloads

215

Views

127

Comments

0

Submitted:

25 June 2023

Posted:

26 June 2023

You are already at the latest version

Alerts
Abstract
To prevent CO2 leakage and ensure the safety of long-term CO2 storage, it is essential to investigate the flow mechanism of CO2 in complex pore structures at the pore scale. This study focuses on reviewing the experimental, theoretical, and numerical simulation studies on the microscopic flow of CO2 in complex pore structures during the last decade. For example, advanced imaging techniques, such as X-ray computed tomography (CT) and nuclear magnetic resonance (NMR), are used to reconstruct the complex pore structures of rocks. Mathematical methods, such as Darcy's law, Young–Laplace’s law, and the Navier-Stokes equation, are used to describe the microscopic flow of CO2. Numerical methods, such as the lattice Boltzmann method (LBM) and pore network (PN) model, are used for numerical simulation. The application of these experimental and theoretical models and numerical simulation studies is discussed, considering the effect of complex pore structures. Finally, future research is suggested to focus on: (1) Conducting real-time CT scanning experiments of CO2 displacement combined with the developed real-time CT scanning clamping device to realize real-time visualization and provide quantitative description of the flow behavior of CO2 in complex pore structures; (2) The effect of pore structures change on the CO2 flow mechanism caused by the chemical reaction between CO2 and the pore surface, the flow theory of CO2 considering wettability and damage theory in a complex pore structures; (3) The flow mechanism of multi-phase CO2 in complex pore structures; (4) The flow mechanism of CO2 in the pore structures at multiscale and the scale upgrade from microscopic to mesoscopic to macroscopic. Generally, this study focuses on reviewing the research progress of CO2 flow mechanisms in complex pore structures at the pore scale and affords an overview of potential advanced developments to enhance the current understanding of CO2 microscopic flow mechanisms.
Keywords: 
Subject: Environmental and Earth Sciences  -   Environmental Science

1. Introduction

Because of the increasing greenhouse effect as well as acute global climate and environmental problems, countries worldwide have reached a consensus to actively respond to climate change and reduce greenhouse gas emissions [1,2,3,4,5]. As industrialization has continued since the industrial revolution, the use of fossil fuels has been increasing, and large amounts of CO2 gas have been directly discharged into the air, which is one of the main reasons for the intensification of the greenhouse effect [6,7,8,9]. CO2 emissions have caused a series of environmental problems, such as drought, glacier melting, and sea level rise, which have caused incalculable harm to the environment on which human beings depend [10]. At present, many technologies are available to control CO2 emissions, such as improving the efficiency of fossil energy combustion, efficient development and utilization of green and clean energy, and carbon capture and storage (CCS) [11]. CCS refers to the use of separation and purification technology to collect a large amount of CO2 from industrial waste gas and inject it into appropriate underground reservoirs for permanent storage [12,13], which is recognized as one of the effective methods to manage CO2 [14,15,16,17]. The main storage geological layers include abandoned mines, unrecoverable coal seams, depleted oil and gas fields, deep saline aquifers, and the ocean [18,19,20]. The storage depth is generally below 800 m. CO2 geological storage is the most important part of CCS, and the storage capacity and safety of geological storage bodies determine the effectiveness of CO2 emission control [21]. However, the complexity [22], heterogeneity, and wettability of the pores directly affect the flow behavior of CO2 in reservoirs. Therefore, investigating the CO2 flow law and revealing the CO2 microscopic flow mechanism have become key to evaluating the storage capacity and safety of geological storage bodies.
Numerous studies have been conducted on the flow of CO2 in geological storage bodies. Lassen et al. [23] injected gaseous CO2 into heterogeneous porous media at different rates, and the flow of CO2 was monitored by sensors. The results showed that large-scale heterogeneity controlled the overall migration of gaseous CO2 in porous media, whereas a smaller scale was important for gas saturation. The higher the injection rate, the larger the transverse diffusion of the gas phase. Zhang et al. [24] proposed that Darcy’s law can be used to describe two-phase fluid flow in porous media at the macroscopic scale. Saleem et al. [25] compared and verified the constructed two-phase flow model with field observation data, such as CO2 eruption time, changes in sediment pH, gas leakage rate, the flow process, fluid interaction, and CO2 dissolution in the CO2 plume. The results showed that the CO2 plume was formed and developed at a stable rate during the flow process, and the dissolution rate increased with an increase in the injection rate. These studies elucidated the flow of CO2 from a macroscopic perspective. However, the flow behavior of CO2 in a storage body is easily affected by its complex pore structures. In macroscale research, the complex pore structures of the storage body has not been accurately characterized. The research results are also based on macroscale flow and often ignore the effect of pore structure complexity. Therefore, an accurate description of the microscopic flow of CO2 is crucial for determining the storage capacity and long-term safety [26,27,28].
X-ray Computed Tomography (CT) and Nuclear Magnetic Resonance (NMR), as non-invasive, non-destructive advanced imaging technologies [29,30], have the advantage of being able to reconstruct the complex pore structures of cores [31,32] and obtain key parameters, such as porosity, permeability, contact angle, and capillary number. Visualization and quantitative characterization of the complex pore structures at the microscopic scale can be realized [11]. Berg and Dalton et al. [33,34] obtained an accurate complex pore structures of sandstone and investigated the effects of permeability and wettability on CO2 flow behavior. Liu et al. [35,36] first used a new reconstruction method to establish the fracture-controlled matrix unit then used the CT scanning technique to obtain the relevant parameters of the proposed fracture control matrix unit mass transfer model. The correctness of the model was verified by comparison with the experimental results of microscopic spontaneous imbibition. Liu et al. [37,38] studied the dynamic production process of a fractured reservoir and the influence of a complex pore structure on the imbibition recovery based on a fracture-controlled matrix unit. Liu et al. [39] performed microscopic spontaneous imbibition experiments, CT scans, and NMR tests on two mixed wetted core samples. The impact of mixed wettability on micro-spontaneous imbibition at the pore scale was investigated. The results showed that effective imbibition can be produced as long as water-wet walls are present in mixed wettability pores. Furthermore, a core-scale mixed wettability model was established by Liu et al. [40], and based on the phase-field theory, the influence of wettability on oil-water two-phase imbibition was studied. In addition, Liu and Song et al. [41,42] proposed two new modeling methods based on CT scanning: the finite volume element modeling method (Figure 1a) and the pore network model based on the maximum sphere algorithm (Figure 1b). The feasibility of the model was verified.
In addition, experts have conducted several theoretical and numerical simulations on the flow mechanism of CO2 at the macroscale. Krause et al. [43] carried out a numerical simulation study of CO2-brine two-phase flow using the modified Carman-Kozeny equation. The distribution of CO2-brine in the core was predicted. Theoretical studies and numerical simulations at the macroscale play a crucial role in revealing the flow mechanism of CO2. However, the complex pore structures have a very important effect on CO2 microscopic flow. The lack of mathematical and numerical models that consider the influence of pore structure complexity and may lead to bias in the conclusions.
Preprints 77551 g001
Figure 1. The new modeling method based on CT images: (a) Images of reconstructed porous samples in finite volume elements of pore space (b) EPNMs of rock samples [41,42].
Figure 1. The new modeling method based on CT images: (a) Images of reconstructed porous samples in finite volume elements of pore space (b) EPNMs of rock samples [41,42].
Preprints 77551 g001
To this end, we collated and analyzed relevant literature on the microscopic flow of CO2. In particular, the complex pore structures substantially affected the CO2 microscopic flow mechanism. At present, experimental methods, theoretical analysis, and numerical simulations are advanced owing to the pore structure complexity of geological storage bodies, which is difficult to accurately express in physical model reconstruction, mathematical model characterization, and numerical model construction. Therefore, it is challenging to clearly reveal the microscopic flow mechanism of CO2 in a complex pore structure. To solve this problem, this study systematically reviews recent advances in the microscopic flow of CO2 in complex pore structures in the last decade to provide some technical and theoretical support for CO2 geological storage. Overall, this review article focuses on the effects of complex pore structures on the microscopic flow behavior of CO2 through three aspects: experimental studies, theoretical studies, and numerical simulations. It aims to enhance the current understanding of the CO2 microscopic flow mechanism. Finally, potential challenges and new research directions for future work are identified and elucidated.

2. Flow experiments of CO2 in complex pore structures

A large number of experiments have been carried out to study the microscopic flow of CO2 in pore structures, and fruitful results have been achieved. This section introduces the research progress of the microscopic flow mechanism of CO2 from four different aspects through analysis of the relevant literature.

2.1. Traditional characterization of pore structures during CO2 microscopic flow

Mercury intrusion porosimetry (MIP) [44,45,46], scanning electron microscopy (SEM) [47,48], and gas adsorption [49,50,51] have been used to characterize the pore structures of the storage body and further explore the flow of CO2. Du et al.[52] used high-pressure mercury intrusion and permeation experiments to investigate the effect of CO2 injected into coal. The results showed that the reaction between CO2-water and coal led to an increase in pore space and greatly increased permeability, which increased the permeability area of CO2 and improved the CO2 storage capacity. Using SEM, Khather et al.[53] observed that the decrease in pH during CO2 injection caused the dissolution and migration of minerals, which resulted in an increase in rock permeability and the flow capacity of CO2. Pearce et al.[54] studied the physical properties of the reservoir after CO2 injection by SEM and found that the movement of fine particles may result in opening or blocking of the pores during CO2 injection, increasing or decreasing permeability, and affecting CO2 injection capacity. Brattekas and Haugen [55] used high-resolution micro-positron emission tomography (micro-PET) and radiotracers to achieve CO2 tracing during flow and capillary capture. The results showed that CO2 mainly flowed into the outer part of the core with high permeability.
However, these techniques have many limitations in accurately characterizing the pore structure complexity in rocks. For example, MIP can only obtain the total porosity of the sample and cannot characterize the complexity of the pore distribution within the sample. SEM is an effective technique for generating 2D images of microstructures. However, it cannot provide 3D images, which are important for evaluating the pore structure complexity [11]. More importantly, traditional characterization methods cannot visualize and quantitatively describe the microscopic flow of CO2. Therefore, to accurately reconstruct the 3D complex pore structures and visually and quantitatively study the microscopic flow mechanism of CO2 in the geological storage body, it is necessary to use advanced techniques, such as CT scanning and NMR, to conduct in-depth analysis using multidisciplinary intersection research ideas.

2.2. Effects of porosity and permeability characteristics on the microscopic flow mechanism of CO2

The influence of key parameters, including porosity and permeability, on CO2 flow in geological storage bodies is very important. By simulating 2D fluid flow experiments, Kitamura et al.[56] found that the flow behavior of CO2 is strongly influenced by the small-scale heterogeneity of the pore structures. However, the simulation results have some errors because the model is 2D and cannot fully describe the pore structure complexity. To investigate the effect of the reservoir laminar structures on the flow behavior of CO2, Krishnamuthy et al.[57] used the CT scanning technique to observe the flow path of CO2 by measuring the CO2 saturation variation in the rock. The results showed that CO2 would preferentially flow through the region with larger porosity and pass unevenly along the axial direction (Figure 2). However, seepage under in situ conditions was not considered, thus the pore distribution of reservoir cores under in situ conditions could not be obtained. To accurately study the CO2 microcosmic flow. Wang et al.[58] injected liquid CO2 into a brine-saturated core. Multiscale CT scanning of sandstone was conducted, and the distribution of porosity at different locations of the core under in situ flow conditions was obtained. The phenomenon of CO2 preferentially passing through the locations with higher porosity was observed from the images. Al-Bayati et al.[59] conducted a displacement experiment on stratified core samples using the CT scanning technique, and Figure 3 shows 2D images of fluid distribution in the XY direction of the stratified samples before and after CO2 displacement. As illustrated in the figure, CO2 first bypasses the low-permeability layer, leaving a large amount of oil to preferentially enter the high-permeability layer. Owing to the occurrence of the cross-flow phenomenon, CO2 is transferred from the high- to the low-permeability layer.
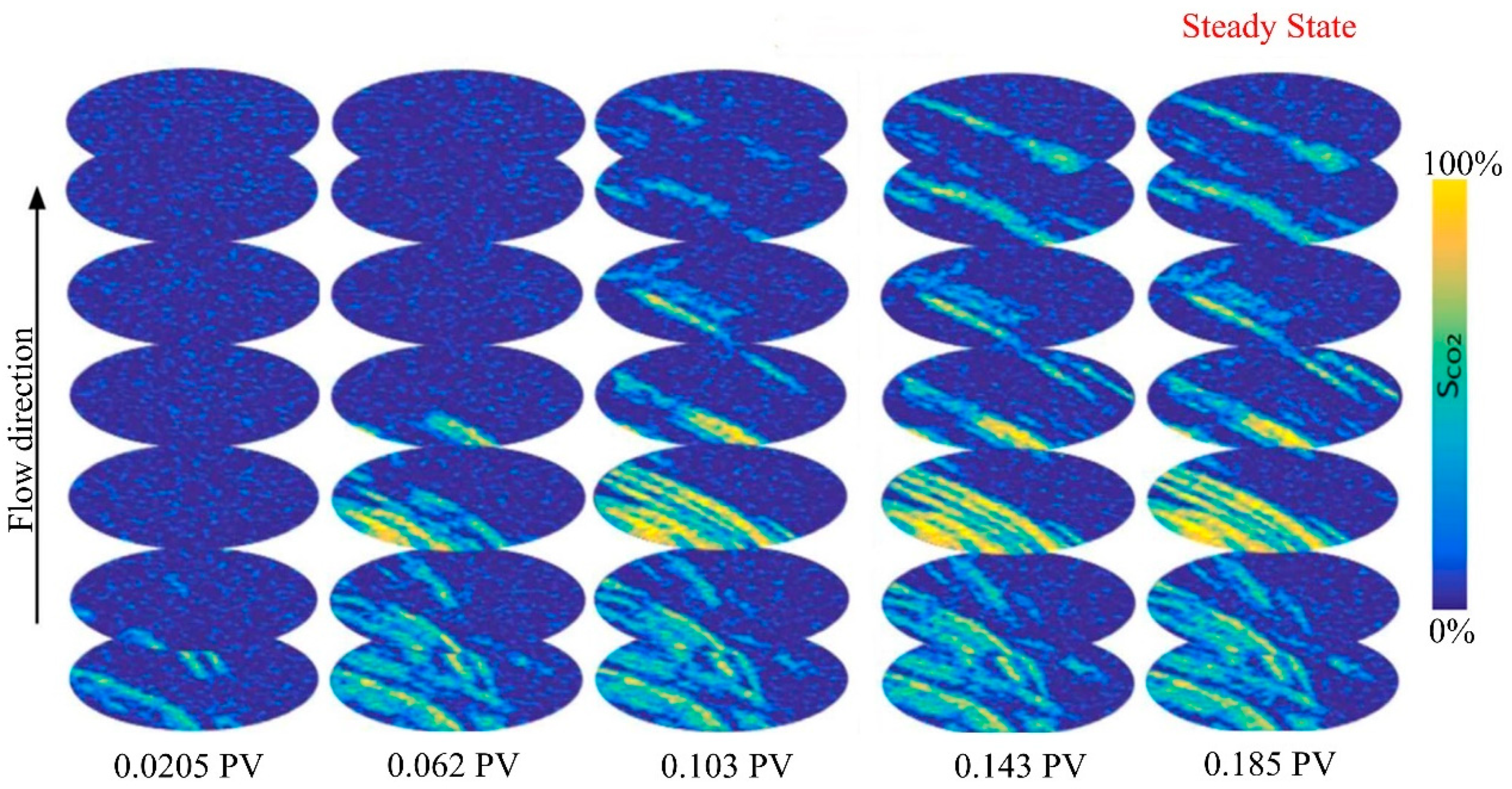
Preprints 77551 g002
Figure 2. Vertical stacked cross-section slices of CO2 saturation computed from CT data [57].
Figure 2. Vertical stacked cross-section slices of CO2 saturation computed from CT data [57].
Preprints 77551 g002
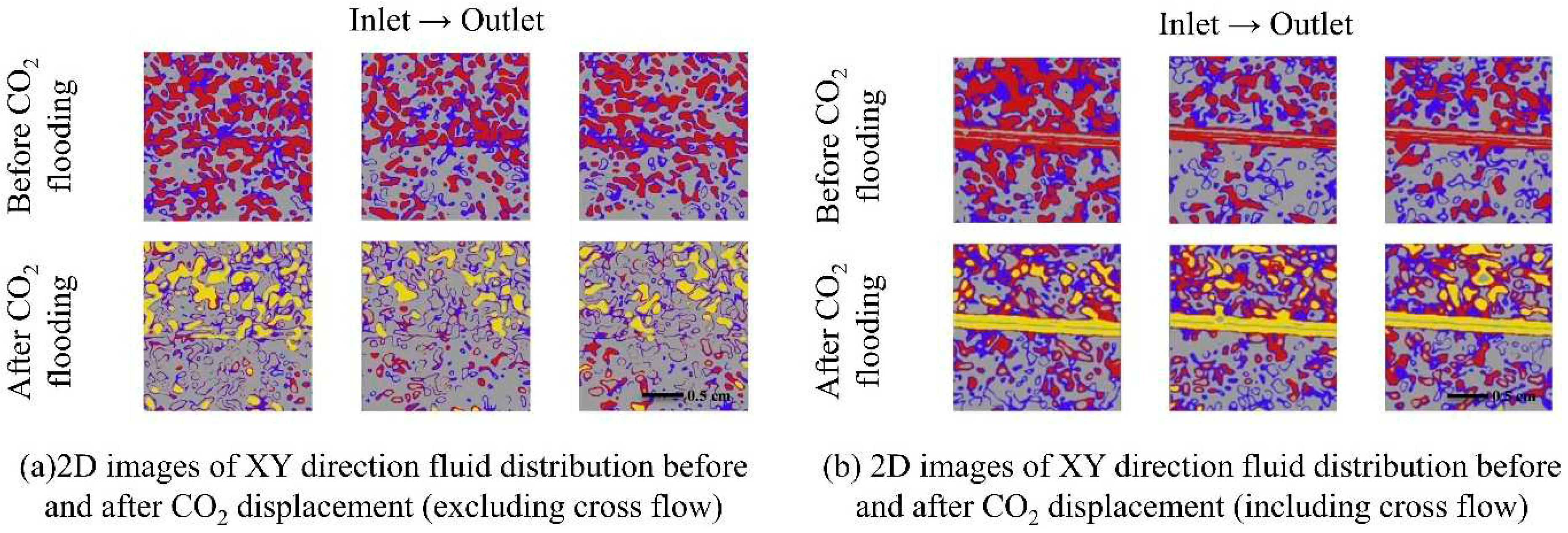
Preprints 77551 g003
Figure 3. 2D images in the XY direction of fluid distribution before and after CO2 flooding: (a) with cross-flow (b)without cross-flow [59].
Figure 3. 2D images in the XY direction of fluid distribution before and after CO2 flooding: (a) with cross-flow (b)without cross-flow [59].
Preprints 77551 g003
A clay interlayer, one of the typical representatives of a low-permeability layer, has an important influence on CO2 flow. Using CT scanning, Xu et al.[60] studied the flow characteristics of CO2 in a special sandstone containing multiple thin clay interlayers. The experiment demonstrated that the flow channel of CO2 was mainly established in the sandstone, and the clay interlayer hindered CO2 flow. However, the description of how the CO2 flow was hindered by the clay interlayer was too vague. Therefore, Xu et al.[61] further monitored the flow process of CO2 in the interior of the clay interlayer sample (Figure 4). When the injection direction was parallel to that of the clay interlayer, the clay interlayer separated the CO2 flow (Figure 4a). When the injection direction was perpendicular to that of the clay interlayer, the clay interlayer hindered the CO2 flow forward (Figure 4b).
Preprints 77551 g004
Figure 4. Image of CO2 distribution during sample drainage: (a) parallel injection (b) vertically injection [61].
Figure 4. Image of CO2 distribution during sample drainage: (a) parallel injection (b) vertically injection [61].
Preprints 77551 g004

2.3. Two-phase flow law in CO2 microscopic flow

When CO2 is injected into the deep brine layer, it enters the reservoir pore structures to displace the original fluid from the pore space, and the flow process is an immiscible two-phase flow [29]. However, it is difficult to observe the space-time variation of the two-phase interface between immiscible two-phase fluids in porous media. Therefore, immiscible two-phase flow must be understood from a pore-scale perspective, which is very important and extremely complex [62].
Using the CT scanning technique, Kogure et al.[63] injected CO2 into the Berea sandstone at different times in opposite directions, and the flow behavior of CO2 in the Berea sandstone was observed. The images show several narrow pore throats that allow CO2 flow. Despite injection from opposite directions, the distribution of CO2 is essentially the same in the final stage of injection (Figure 5). Liu et al.[64] injected CO2 into a glass bead bed in both the upward and downward directions, and a displacement saturated water experiment was conducted to investigate the distribution of CO2 in the core. As shown in Figure 6, the displacement effect of CO2 injected downward was substantially better than that of CO2 injected upwards (Figure 6b). This is attributed to the "gas channeling" phenomenon when CO2 is injected upward, but the cause of the "gas channeling" phenomenon was not discussed in depth. Lv et al.[65] combined the CT scanning technique and a micromodel to study the flow process of CO2-brine in the pore structures at different injection rates under static and transient conditions. The results showed that a higher injection rate gives rise to a higher displacement efficiency but a lower sweep efficiency. Further, using NMR technique, Teng et al.[66] found that the different viscosities and densities of CO2 and water caused the "gas channeling" phenomenon of CO2, which led to the premature breakthrough of CO2 and reduced the displacement efficiency. In addition, Zhang et al.[24] obtained the local porosity and saturation of Berea sandstone. The results showed that the forward movement of CO2 on the capillary pressure is the main reason for the formation of the pathway of CO2 flow. CO2 preferentially passes through the large-sized pores, and the seepage zone gradually expands whereas the CO2 saturation increases.
The influence of pore geometry on the microscopic flow mechanism of CO2 cannot be ignored. Zhang et al.[67] used CT scanning to scan the displacement process of CO2 and found that CO2 was unevenly distributed in sandstone samples. A larger flow patch was formed during the flow process. Herring et al.[68] adopted the Bentheimer sandstone core and used the CT scanning technique to observe the displacement process of CO2 at the pore scale. The images show that CO2 invaded the pore space in a capillary fingering regime (Figure 7). Liu et al.[69] visualized and quantitatively analyzed the dynamic diffusion process of CO2 in n-decane-saturated porous media. The results showed that the channels of the porous media hindered the diffusion of CO2. The local diffusion coefficient of CO2 gradually decreased with time along the diffusion path until it reached a steady state.
Preprints 77551 g005
Figure 5. X-ray CT images of distribution of scCO2 in Berea sandstone [63].
Figure 5. X-ray CT images of distribution of scCO2 in Berea sandstone [63].
Preprints 77551 g005
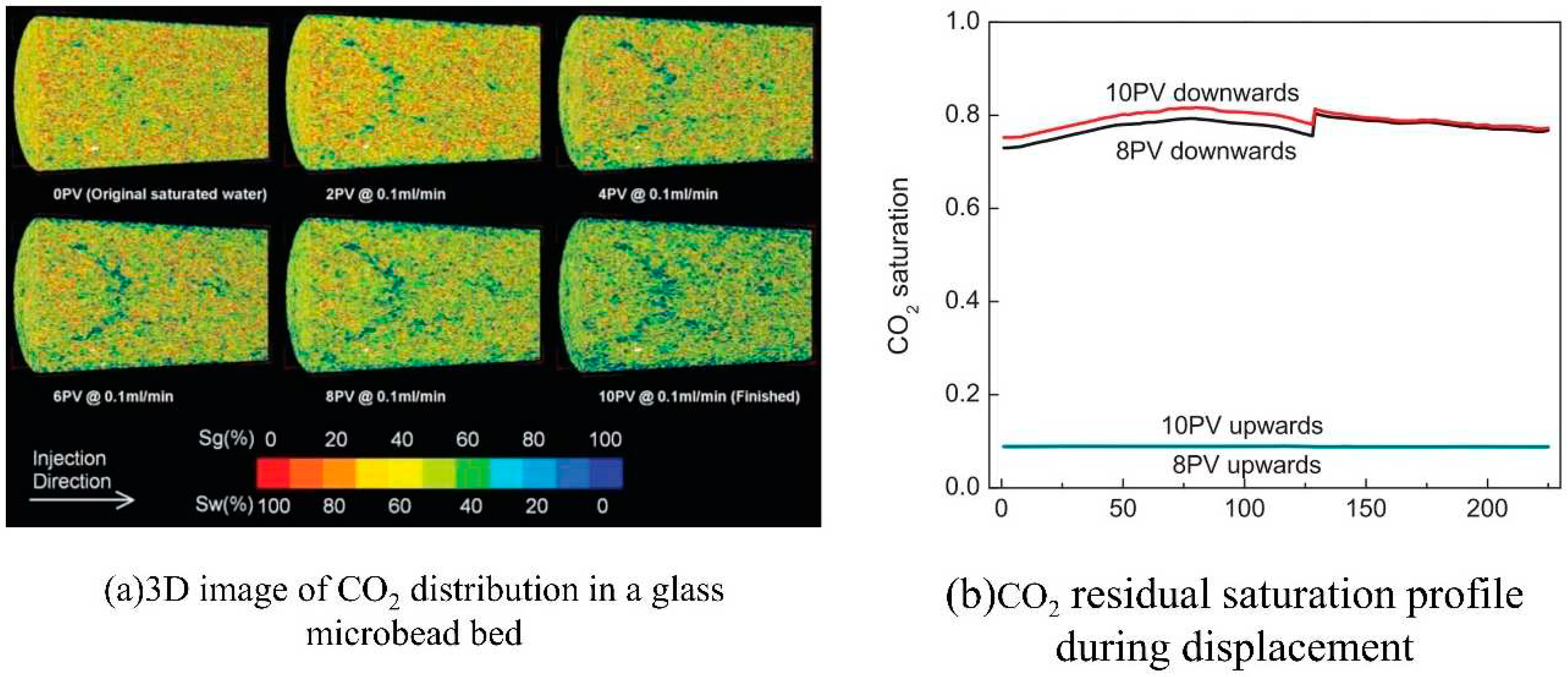
Preprints 77551 g006
Figure 6. 3D image of CO2 distribution in displacement process and analysis of up-and-down displacement efficiency [64].
Figure 6. 3D image of CO2 distribution in displacement process and analysis of up-and-down displacement efficiency [64].
Preprints 77551 g006
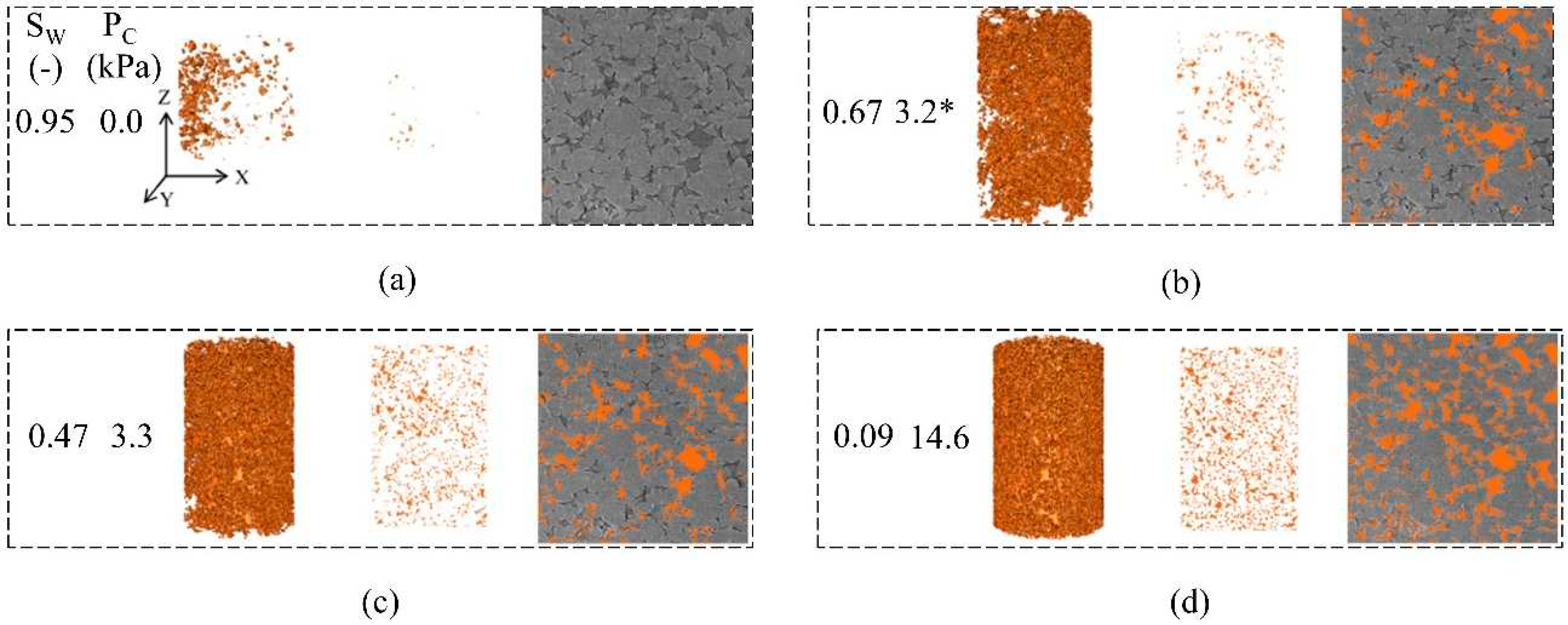
Preprints 77551 g007
Figure 7. 3D, 2D and 2D closer view overlain on the original grayscale image of CO2 within sandstone [68].
Figure 7. 3D, 2D and 2D closer view overlain on the original grayscale image of CO2 within sandstone [68].
Preprints 77551 g007

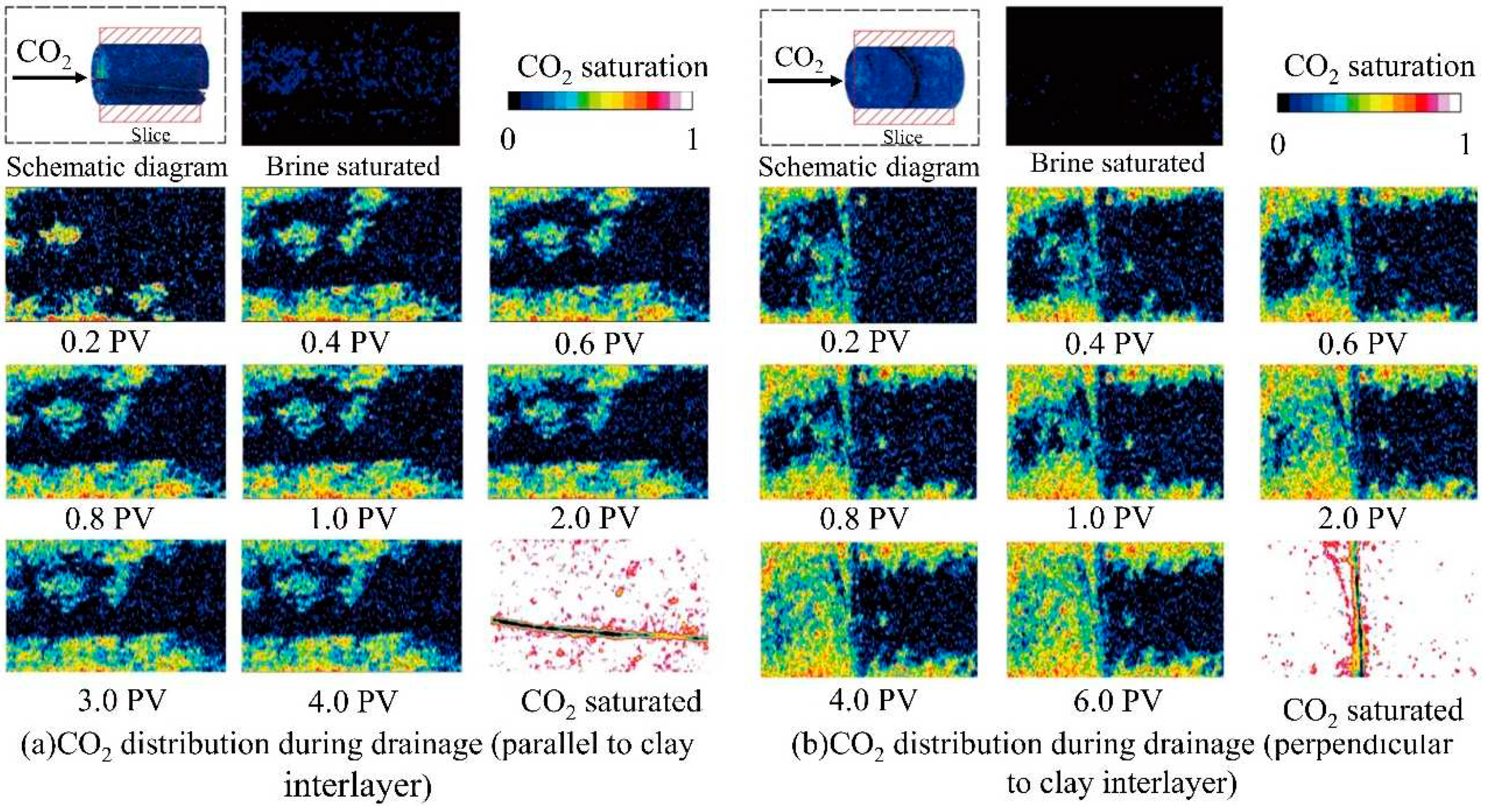
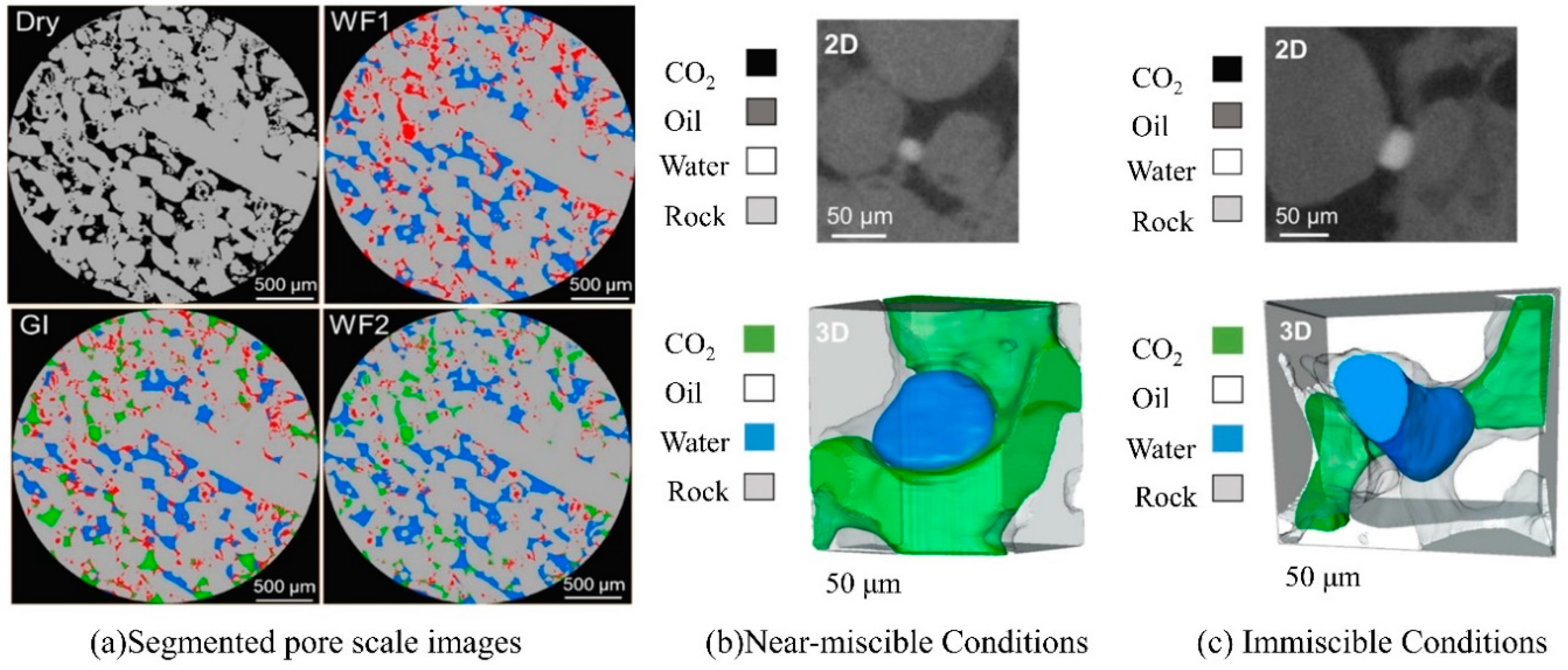
2.4. Microscopic flow of CO2 in different phase states

In geological storage, appropriate CO2 phase states, including gaseous, liquid, and supercritical, should be selected according to the specific conditions and requirements of the storage body for injection. The CT scanning technology has been used to conduct extensive research on the microscopic flow of CO2 in different phase states. CO2 bubbles, a typical representative of the gaseous state, have a stable state in porous media with a high resistance factor (i.e., good plugging capacity), which plays a very important role in the safety of long-term storage of CO2 [70,71,72]. Xue et al.[73] found that microbubble CO2 injection can minimize the content of free CO2 in the reservoir compared with that of conventional CO2 injection and can also efficiently utilize the pore space of the reservoir, which is conducive to the long-term safety of large-scale CO2 storage. Patmonoaji et al.[74] and Zhai et al.[75] conducted displacement experiments in sandstone and found that microbubble flow has a stronger sweeping efficiency than that of conventional flow, which can improve the displacement efficiency and storage capacity of CO2.
The experimental results proved that CO2 foam can not only improve oil and gas recovery compared with conventional CO2, but also improve pore space utilization and increase CO2 storage in the reservoir. Accordingly, Du et al.[76] further investigated the seepage characteristics of CO2 bubbles in porous media. However, the experimental object was self-made homogeneous porous media, whereas most of the actual reservoir is composed of heterogeneous rocks; thus, the experimental results have some limitations. For this reason, McLendon et al.[77] injected CO2 with and without a surfactant into real Berea sandstone under high-pressure conditions to observe in situ bubble generation. The results showed that CO2 tended to pass through the high-permeability reservoir without the addition of surfactant but resulted in a decrease in the sweep efficiency of CO2. Du et al.[78] studied the dynamic bubble flow behavior in the entrance region of porous media and obtained dynamic three-phase saturation distributions along the sample core. The results showed that the CO2 bubble could push most of the liquid phase into the latter part of the porous media, but the forepart was difficult to push, showing an obvious entrance effect.
The above studies investigated the microscopic flow of single-phase CO2. However, it is unusual that there is only CO2 in the actual storage body, and two or multiphase may be present. Therefore, it is essential to further study the microscopic flow of CO2 under the condition of polyphase coexistence (including miscible, near-miscible, and immiscible phases). Alhosani et al.[79] conducted an in situ study on immiscible-phase CO2 displacement in oil-wet reservoirs. The images show that in strongly oil-wet rocks, the largest pore space was occupied by water, the smallest pore space was occupied by oil, and the medium-sized pore space was occupied by CO2 (Figure 8a). CO2 was distributed in a connected layer under near-miscible phase conditions (Figure 8b) and existed as separated "ganglia" in medium-sized pores under immiscible phase conditions (Figure 8c). Qin et al.[80] conducted a study on the wettability and spatial distribution of near-miscible phase CO2 in oil-wet carbonate rocks under high temperature and pressure. The results showed that at the initial stage of injection, CO2 had good connectivity with the oil phase and poor connectivity with the brine phase. With the continuous injection of CO2, the wettability reversal process was triggered, resulting in a decrease in the oil wettability and an improvement in the CO2 connectivity with brine. Hao et al.[81] conducted multiphase and multiple injection experiments. It was found that under the immiscible phase condition, the porous media showed remarkable gas coverage and flow stratification owing to gas buoyancy. The miscible-phase CO2 injection eliminated the effect of buoyancy, thus expanding the storage area and flow range of CO2.
The reliability of CO2 geologic storage depends on the flow mechanism of CO2 in reservoirs. With the help of advanced imaging techniques, such as CT scanning and NMR, in experimental studies, it is beneficial to study the microscopic flow mechanism of CO2 in complex pore structures. However, few studies have used CT scanning and NMR technology to carry out real-time visualization and quantification research on the microscopic flow process of CO2. In addition, microscopic flow studies of CO2 in complex pore structures with multiphase are not sufficiently comprehensive, which is the focus of future research.
Preprints 77551 g008
Figure 8. 2D and 3D images of a trapped water ganglion in a single pore: (a) segmented pore scale images (b) immiscible condition (c)near-miscible condition [79].
Figure 8. 2D and 3D images of a trapped water ganglion in a single pore: (a) segmented pore scale images (b) immiscible condition (c)near-miscible condition [79].
Preprints 77551 g008

3. Theoretical model of CO2 flow in pore structures

Theory is the cornerstone of all experiments and numerical simulations, and continuous improvement of the theory is the premise of studying the microscopic flow mechanism of CO2. Darcy’s law [82] is one of the classical theories describing the macroscopic flow law of fluid in porous media, which is applicable to single- and multiphase fluid flow in loose sand columns, consolidated sandstone, and other dense porous media [83,84].
Zhang et al.[24] proposed Darcy’s law to describe two-phase fluid flow in porous media at the macroscopic scale:
q α = − k k r α μ ( ∇ P )
where q is the flow flux, m3/s; k is the absolute permeability, m2; kr is the relative permeability, μ is the viscosity of a fluid, Pa·s; ∇P is the pressure gradient, Pa; and α=1 and 2 are the two phases of a fluid.
Berg et al.[33] used Darcy’s law for two-phase flows to establish a mathematical model. The migration and mass transfer behaviors of saturated and unsaturated CO2-brine system in sandstone were studied. The governing equations are as follows:
φ ∂ S i ∂ t + ∇ ⋅ v i → = 0
v i → = − k r , i μ i K ( ∇ p i − ρ i g → )
Equation (2) describes the mass balance of CO2 and water. The saturation of the wetting phase (water or brine, i=w) and the non-wetting phase (CO2, i=nw) satisfies Sw+Snw=1. The flux of the phases v i → is described by Darcy’s law extending to two-phase flow, m/s; where φ is the porosity, K is the absolute permeability of the rock, m2; μi is the viscosity of the fluids, Pa·s; ρi is the density of the fluids, kg/m3; and g is the gravity constant, m/s2.
However, in the process of CO2 displacement, it is difficult to accurately capture the spatiotemporal variation of the interface of an immiscible two-phase fluid in the pore structures. For this reason, Porter et al.[85] redefined the simple expression of pressure in the absence of CO2 gas, considering the pressure drop caused by flow and heterogeneity, which can reliably predict the position of the single-phase to multiphase flow transition:
P c r = P s a t + μ q ( L − Z p ) k e f f
where Pcr is the critical pressure, Pa; Psat is the hydrostatic pressure, Pa; μ is the viscosity of water, Pa·s; q is the injection rate of CO2 saturated water, m/s; L is the location of the bottom of the porous media, mm; Zp is the location of the top of the porous media, mm; and keff is the vertical (harmonic) averaged effective permeability, m2.
So far, Darcy’s law has successfully solved many CO2 geological storage safety problems [86,87,88]. However, it also has some limitations; for example, in the case of high velocity flow, high Reynolds number (Re), and nonlinear flow, turbulent flow will occur in the complex pore structures, and Darcy’s law is no longer applicable. Therefore, many scholars have proposed the use of the extended form or combined with the actual situation to appropriately modify Darcy’s law to study single-phase CO2 flow, CO2-brine, or other miscible or immiscible flow behaviors at the pore scale.
Kogure et al.[63] proposed the extended Darcy’s law to calculate the relative permeability of porous sandstone in the CO2-water system at the sub-core scale, and the flow behavior of CO2 was studied:
Q i = k r i k a b s A μ i ( Δ P L − ρ i g )
where Qi is the flow rate of each fluid, m3/s; kri is the relative permeability, kabs is the absolute permeability, m2; A is the cross-sectional area of the sample, m2; L is the length of the sample, m; ΔP is the pressure difference of the sample, Pa; μi is the viscosity of the fluid, Pa·s; ρi is the density of the fluid, kg/m3; and g is the acceleration of gravity, m/s2.
However, the above scholars first determined the permeability of a complex pore structure based on Darcy’s law, then the flow behavior of CO2 in the complex pore structures was studied, a very complicated process. Therefore, Wang et al.[89] used the extended form of Darcy’s law to describe the flow behavior of CO2-water in the pore structures:
v α = − K k r α μ α ( ∇ p α − ρ α g )
where v denotes the Darcy velocity, m/s; K is the intrinsic permeability tensor, m2; kr is the relative permeability of the fluid phase, μ denotes the viscosity, Pa·s; ρ represents the density, kg/m3; P represents the pressure of the fluid phase, Pa; and g is the gravity vector, m/s2.
Besides Darcy’s law, the microscopic flow of CO2 can be effectively calculated based on the Young-Laplace law and Navier-Stokes equation. Chapman et al.[90] used the Young-Laplace law to calculate the displacement sequence in the node of the pore network model for predicting CO2 displacement. The governing equation is as follows:
P c = 2 γ cos θ ( 1 h + 1 w )
Pc is the capillary pressure, Pa; γ is the interfacial tension, N/m; θ is the contact angle, °; h is the height of the channel, mm; and w is the width of the channel, mm.
Ovaysi and Piri [91] simulated the microscopic flow of CO2 in a deep saline solution as follows:
D v D t = − 1 ρ ∇ P + μ ρ ∇ 2 v + g
∇ 2 = 0
where v is the velocity vector, m/s; μ is the viscosity, Pa·s; ρ is the density, kg/m3; g is the gravity vector, m/s2; and P is the pressure, Pa.
Although many theoretical models have been used to reveal the flow mechanism of CO2 in complex pore structures, some existing mathematical equations have weak universality. In particular, CO2 reacts with other fluid phases and pore surfaces during the flow process, resulting in pore structures damage and changes in the flow of CO2. In conclusion, theoretical models considering wettability and damage effects are rare; therefore, it is necessary to further study the flow theory of CO2 considering wettability and damage theory in complex pore structures.

4. Numerical simulation of CO2 flow in pore structures

Numerical simulation experiments on complex pore scales have become an effective tool for studying the flow of CO2 in pore structures, which can impose conditions that cannot be reached by experimental methods, provide insight into the main processes of multiphase fluid flow in the storage body, obtain complete parameters of the flow process, and conduct systematic and accurate analysis. By comparing the experimental results with theoretical analysis, more comprehensive and objective conclusions can be obtained. At present, a variety of pore-scale simulation methods have been developed for CO2 flow in porous media, including the Lattice Boltzmann Method (LBM) and Pore Network (PN) model [92].

4.1. Numerical simulation based on LBM

Computational Fluid Dynamics (CFD) [93], a traditional numerical simulation method for simulating fluid flow in porous media, has received considerable attention because of its simple algorithm, good conservation, and ability to handle complex geometric shape problems [94,95,96]. However, the traditional CFD method has some problems, including a large computational volume, low computational accuracy, difficulty in dealing with complex equations, and simple boundary conditions. To solve these problems, scholars [97,98,99] proposed adopting the LBM method to conduct CO2 microscopic flow numerical simulations. Compared with the traditional CFD method, the LBM method can be programmed on a computer system with parallel processing capability. It has the advantages of easy handling of complex boundaries, simple description of fluid interactions, high computational efficiency, and high numerical accuracy, making it suitable for simulating the CO2 flow in porous media at the pore scale. Therefore, gradually replacing the traditional CFD method is a promising research method.
Various types of multiphase multicomponent LBM models, including color models and phase field models, have been developed based on the description of different component interactions. Liu et al.[92] improved the LBM color fluid model to simulate the displacement of CO2 to water in a double-permeable pore network. It was found that the degree of directional flow and flow behavior of CO2 depend on the capillary number, as shown in Figure 9, which is consistent with the experimental results of Chang et al.[100]. To improve the accuracy of the simulation results, Jiang and Tsuji [31] introduced color function thresholds, velocity fields, and Neumann boundary conditions to construct a novel LBM numerical simulation method for pore-scale CO2 displacement simulations. The results showed that reducing the initial CO2 connectivity and sphericity index can reduce the CO2 mobility rate and improve the capillary trapping capacity of CO2.
Preprints 77551 g009
Figure 9. Final fluid distribution in a random heterogeneous system: (a) logCa=-4.36, (b) logCa=-4.16, (c) logCa=-4.06, (d) logCa=-3.59, (e) logCa=-3.36, (f) logCa=-3.06 [92].
Figure 9. Final fluid distribution in a random heterogeneous system: (a) logCa=-4.36, (b) logCa=-4.16, (c) logCa=-4.06, (d) logCa=-3.59, (e) logCa=-3.36, (f) logCa=-3.06 [92].
Preprints 77551 g009
However, the disadvantages of the color gradient model are also obvious, because it is not applicable to heterogeneous pore structures with real density and viscosity ratio of CO2-brine. Therefore, Fakhari et al. [101] developed a phase field-based LBM and verified that the model could accurately simulate the multiphase flow characteristics of heterogeneous porous media at the pore scale through experimental comparison. Bakhshian et al. [102] used a multiphase LBM model to simulate the flow of CO2-brine in Tuscaloosa sandstone rock. The results showed that heterogeneous CO2 wettability led to a more dispersed fluid distribution and more tortuous CO2 flow paths (Figure 10), and the residual trap of CO2 increased with the increase in CO2-wet regions. Guo et al. [103] studied the effect of the surface contact angle of Bentheimer sandstone on two-phase flow in porous media after the completion of CO2 displacement. The results showed that the heterogeneity of wettability has a substantial impact on the relative permeability of CO2. An immiscible phase displacement process in the CO2-water-rock system was simulated by Guo et al. [104] and Atia et al. [105]. The obvious local CO2 and water redistribution phenomena were caused by the heterogeneity of the pore-scale surface wettability under low water-wetting conditions while enhancing the aggregation or diffusion behavior of CO2.
In addition, Wang et al. [106] proposed the multi-relaxation time lattice Boltzmann method (MRT-LBM) to simulate the diffusion and miscible phase flow of a CO2-oil system in porous media at the pore scale. The results showed that CO2 could diffuse into the oil phase more easily from regions that are relatively attractive to CO2 and repulsive to oil in porous media.
Preprints 77551 g010
Figure 10. 3D distribution of CO2 in heterogeneous samples with different wettability [102].
Figure 10. 3D distribution of CO2 in heterogeneous samples with different wettability [102].
Preprints 77551 g010

4.2. Numerical simulation based on PN

The PN model [107,108] is designed to simplify the porous media model by connecting the pores with pore throats of the ideal geometry, which can improve computational efficiency. Benali et al.[109] developed a PN model with an extended visual field to study real-time bubble texture dynamics under high pressure. The results showed that continuous and rapid CO2 injection can bubble with a low surface viscosity. A large number of bubbles remained on the pore surface of the storage body, which improved the flow of CO2 in the pore structures. Liu et al.[110] developed a new two-phase steady-state model based on PN. The model considers the capillary and viscous forces in the pore structures and proved a stronger seepage effect of CO2 than that of brine. Cao et al.[111] used a high-pressure microscopic model and a PN model to simulate the displacement phenomenon during CO2 injection into a saturated brine reservoir. The results showed that CO2 has a better injection efficiency and capillary trap capability in regions with larger porosity.
Wettability, an important factor controlling the flow of multiphase fluids in porous media, has a remarkable influence on the microscopic flow of CO2 [112]. Hu et al.[112] used a PN model to study the effect of wettability on CO2-brine displacement. The results showed that CO2 has higher saturation, wider directivity, and a more compact displacement pattern under medium wetting conditions. In addition, the CO2-brine interface is smaller, which inhibits the mutual mass transfer. Basirat et al.[113] developed a numerical model based on the phase-field method to study the effect of different wettability on the two-phase flow of CO2 and brine at the pore scale. The results showed that the trapped wetting phase saturation and normalized interfacial area increase with decreasing contact angle. However, the wetting condition had no effect on the CO2 breakthrough time and saturation.
The numerical simulations of the microscopic flow of CO2 in complex pore structures have been extensively investigated. However, numerical simulation methods tend to simplify the pore structure complexity and wettability, which reflect the real in situ conditions of the geological storage body. Therefore, considering the pore structure complexity and complex mixed wettability conditions, the establishment of accurate numerical models of geological storage bodies, as well as the improvement of the numerical experimental computational rate and accuracy are the frontier issues in conducting CO2 numerical simulations of microscopic flow in complex pore structures.

5. Conclusions and outlook

CO2 flow is easily affected by reservoir complexity. The microscopic flow mechanism of CO2 is the key to revealing the flow mechanism of CO2 in the storage body, which is of great importance for evaluating the safety and effects of CO2 geological storage. This article thereby provides a systematic and comprehensive review for the last decade on the microscopic flow of CO2 in the complex pore structures by experimental research, theoretical research, and numerical simulation. Moreover, the understanding of the microscopic flow mechanism of CO2 in the complex pore structures was improved. It can be elucidated that pore structure complexity substantially impacts the microscopic flow process of CO2, and its influence on wettability and damage needs to be further explored.
By considering the real-time visualization technology, multiphase, multiscale, damage mechanism, and wettability, future research directions on the microscopic flow mechanism of CO2 may be anticipated:
(1) Future studies should carry out real-time CT scanning experiments for CO2 displacement in combination with the research and development of a CO2 microscopic flow real-time CT scanning clamping device to realize real-time visualization and quantitative description of CO2 flow behavior in complex pore structures.
(2) The flow mechanism of single-phase CO2 in complex pore structures has been extensively studied, but few studies investigated the micro-flow mechanism of multiphase CO2. It is suggested that more attention should be paid to the microscopic flow mechanism of multiphase CO2 in complex pore structures in the future.
(3) CO2 geological storage should meet the needs of long-term storage and wide range. It is suggested to explore the flow mechanism of CO2 in complex pore structures at multiscale to realize the upgrading from micro, mesoscopic to macro scales, which is of great importance for evaluating the long-term safety of CO2 geological storage.
(4) In the process of CO2 flow, chemical reactions occur with the pore surface, and the dissolution or precipitation of minerals changes the pore structures, which has a non-negligible impact on the microscopic flow mechanism of CO2. In the future, attention should be paid to the influence of changes in the pore structures caused by chemical reactions on the microscopic flow mechanism of CO2. The effects of wettability and damage are considered in the theoretical model study.
(5) The characteristics of the complex pore structures and wettability model are simplified, which cannot reflect the actual in situ conditions of the geological storage body. In the future, attention should be paid to the pore structure complexity and complex mixed wettability conditions. In addition, an accurate pore network numerical model of the geological storage body should be established for numerical simulation. The calculation rate and accuracy of the numerical experiment should also be improved.

Data Availability

The data and material that support the findings of this study are available from the corresponding author upon reasonable request, and the source code is not available publicly online but can be provided by the corresponding author for interested researchers.

Acknowledgments

We greatly appreciate the Autonomous Region Science and Technology Major Project of Inner Mongolia (Grant No. 2021ZD0034-2), and Liaoning Provincial Education Department Project (Grant No. LJKQZ20222325), and Project supported by discipline innovation team of Liaoning Technical University (Grant No. LNTU20TD-11).

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

  1. Conversano, A.; Porcu, A.; Mureddu, M.; et al. Bench-scale experimental tests and data analysis on CO2 capture with potassium prolinate solutions for combined cycle decarbonization. International Journal of Greenhouse Gas Control 2020, 93, 102881. [Google Scholar] [CrossRef]
  2. Varghese, A.M.; Karanikolos, G.N. CO2 capture adsorbents functionalized by amine – bearing polymers: A review. International Journal of Greenhouse Gas Control 2020, 96, 103005. [Google Scholar]
  3. Naghizadeh, A.; Larestani, A.; Nait Amar, M.; et al. Predicting viscosity of CO2–N2 gaseous mixtures using advanced intelligent schemes. Journal of Petroleum Science and Engineering 2022, 208, 109359. [Google Scholar] [CrossRef]
  4. Safaei-Farouji, M.; Vo Thanh, H.; Sheini Dashtgoli, D.; et al. Application of robust intelligent schemes for accurate modelling interfacial tension of CO2 brine systems: Implications for structural CO2 trapping. Fuel 2022, 319, 123821. [Google Scholar]
  5. Vitali, M.; Corvaro, F.; Marchetti, B.; et al. Thermodynamic challenges for CO2 pipelines design: A critical review on the effects of impurities, water content, and low temperature. International Journal of Greenhouse Gas Control 2022, 114, 103605. [Google Scholar]
  6. Soeder, D.J. Greenhouse gas sources and mitigation strategies from a geosciences perspective. Advances in Geo-Energy Research 2021, 5, 274–285. [Google Scholar] [CrossRef]
  7. Xu, Y.; Cui, G. Influence of spectral characteristics of the Earth’s surface radiation on the greenhouse effect: Principles and mechanisms. Atmospheric Environment 2021, 244, 117908. [Google Scholar]
  8. Yoro, K.O.; Daramola, M.O. Chapter 1 - CO2 emission sources, greenhouse gases, and the global warming effect. Advances in Carbon Capture 2020, 3–28. [Google Scholar]
  9. Park, J.H.; Yang, J.; Kim, D. Review of recent technologies for transforming carbon dioxide to carbon materials. Chemical engineering journal 2022, 427, 130980. [Google Scholar] [CrossRef]
  10. Wu, S.; Wang, L.; Cai, Q.; et al. Potential impact assessment for China’s dry and wet areas under global warming targets. Physics and Chemistry of the Earth Parts A/B/C 2020, 116, 102838. [Google Scholar] [CrossRef]
  11. Gan, M.; Zhang, L.; Miao, X.; et al. Application of computed tomography (CT) in geologic CO2 utilization and storage research: A critical review. Journal of Natural Gas Science and Engineering 2020, 83, 103591. [Google Scholar]
  12. Kumar, S.; Foroozesh, J.; Edlmann, K.; et al. A comprehensive review of value-added CO2 sequestration in subsurface saline aquifers. Journal of Natural Gas Science and Engineering 2020, 81, 103437. [Google Scholar] [CrossRef]
  13. Yanzhong, W.; Nianmin, Z.; Xu, C.; et al. Geologic CO2 storage in arkosic sandstones with CaCl2-rich formation water. Chemical Geology 2020, 558, 119867. [Google Scholar] [CrossRef]
  14. Cao, C.; Hou, Z.; Li, Z.; et al. Numerical modeling for CO2 storage with impurities associated with enhanced gas recovery in depleted gas reservoirs. Journal of Natural Gas Science and Engineering 2022, 102, 104554. [Google Scholar] [CrossRef]
  15. Romanak, K.; Dixon, T. CO2 storage guidelines and the science of monitoring: Achieving project success under the California Low Carbon Fuel Standard CCS Protocol and other global regulations. International Journal of Greenhouse Gas Control 2022, 113, 103523. [Google Scholar]
  16. Medina-Martos, E.; Gálvez-Martos, J.-L.; Almarza, J.; et al. Environmental and economic performance of carbon capture with sodium hydroxide. Journal of CO2 Utilization 2022, 60, 101991. [Google Scholar] [CrossRef]
  17. Alhosani, A.; Lin, Q.; Scanziani, A.; et al. Pore-scale characterization of carbon dioxide storage at immiscible and near-miscible conditions in altered-wettability reservoir rocks. International Journal of Greenhouse Gas Control 2021, 105, 103232. [Google Scholar] [CrossRef]
  18. Bui, M.; Adjiman, C.S.; Bardow, A.; et al. Carbon capture and storage (CCS): the way forward. Energy & Environmental Science 2018, 11, 1062–1176. [Google Scholar]
  19. Aminu, M.D.; Nabavi, S.A.; Rochelle, C.A.; et al. A review of developments in carbon dioxide storage. Applied Energy 2017, 208, 1389–1419. [Google Scholar] [CrossRef]
  20. Noy, D.J.; Holloway, S.; Chadwick, R.A.; et al. Modelling large-scale carbon dioxide injection into the Bunter Sandstone in the UK Southern North Sea. International Journal of Greenhouse Gas Control 2012, 9, 220–233. [Google Scholar] [CrossRef]
  21. Cao, C.; Liu, H.; Hou, Z.; et al. A Review of CO2 Storage in View of Safety and Cost-Effectiveness. Energies 2020, 13, 600. [Google Scholar] [CrossRef]
  22. Ragui, K.; Bennacer, R.; Chen, L. Pore-scale modeling on supercritical CO2 invasion in 3D micromodel with randomly arranged spherical cross-sections. Energy Reports 2021, 7, 33–42. [Google Scholar] [CrossRef]
  23. Lassen, R.N.; Plampin, M.R.; Sakaki, T.; et al. Effects of geologic heterogeneity on migration of gaseous CO2 using laboratory and modeling investigations. International Journal of Greenhouse Gas Control 2015, 43, 213–224. [Google Scholar] [CrossRef]
  24. Zhang, Y.; Kogure, T.; Nishizawa, O.; et al. Different flow behavior between 1-to-1 displacement and co-injection of CO2 and brine in Berea sandstone: Insights from laboratory experiments with X-ray CT imaging. International Journal of Greenhouse Gas Control 2017, 66, 76–84. [Google Scholar]
  25. Saleem, U.; Dewar, M.; Chaudhary, T.N.; et al. Numerical modelling of CO2 migration in heterogeneous sediments and leakage scenario for STEMM-CCS field experiments. International Journal of Greenhouse Gas Control 2021, 109, 103339. [Google Scholar] [CrossRef]
  26. Steefel, C.I.; Molins, S.; Trebotich, D. Pore Scale Processes Associated with Subsurface CO2 Injection and Sequestration. Reviews in Mineralogy and Geochemistry 2013, 77, 259–303. [Google Scholar] [CrossRef]
  27. Cheng, X.; Mei, K.; Li, Z.; et al. Research on the Interface Structure during Unidirectional Corrosion for Oil-Well Cement in H2S Based on Computed Tomography Technology. Industrial & Engineering Chemistry Research 2016, 55, 10889–10895. [Google Scholar]
  28. Zhang, L.; Ren, S.; Ren, B.; et al. Assessment of CO2 storage capacity in oil reservoirs associated with large lateral/underlying aquifers: Case studies from China. International Journal of Greenhouse Gas Control 2011, 5, 1016–1021. [Google Scholar]
  29. Xu, L.; Li, Q.; Myers, M.; et al. Application of nuclear magnetic resonance technology to carbon capture, utilization and storage: A review. Journal of Rock Mechanics and Geotechnical Engineering 2019, 11, 892–908. [Google Scholar]
  30. Kardjilov, N.; Manke, I.; Hilger, A.; et al. Neutron imaging in materials science. Materials Today 2011, 14, 248–256. [Google Scholar] [CrossRef]
  31. Jiang, F.; Tsuji, T. Numerical investigations on the effect of initial state CO2 topology on capillary trapping efficiency. International Journal of Greenhouse Gas Control 2016, 49, 179–191. [Google Scholar] [CrossRef]
  32. Hefny, M.; Qin, C.; Saar, M.O.; et al. Synchrotron-based pore-network modeling of two-phase flow in Nubian Sandstone and implications for capillary trapping of carbon dioxide. International Journal of Greenhouse Gas Control 2020, 103, 103164. [Google Scholar] [CrossRef]
  33. Berg, S.; Oedai, S.; Ott, H. Displacement and mass transfer between saturated and unsaturated CO2–brine systems in sandstone. International Journal of Greenhouse Gas Control 2013, 12, 478–492. [Google Scholar] [CrossRef]
  34. Dalton, L.E.; Klise, K.A.; Fuchs, S.; et al. Methods to measure contact angles in scCO2-brine-sandstone systems. Advances in Water Resources 2018, 122, 278–290. [Google Scholar] [CrossRef]
  35. Liu, Q.; Liu, J.; Pei, G.; et al. A New Method for Artificial Core Reconstruction of a Fracture-Control Matrix Unit. Advances in Civil Engineering 2020, 2020, 1–10. [Google Scholar]
  36. Liu, Q.; Song, R.; Liu, J.; et al. Mass transfer model of fracture-controlled matrix unit: Model derivation and experimental verification based on fractal theory and micro-CT scanning technology. Energy Reports 2020, 6, 3067–3079. [Google Scholar]
  37. Liu, Q.; Liang, B.; Liu, J.; et al. Imbibition oil recovery of single fracture-controlled matrix unit: Model construction and numerical simulation. Capillarity 2022, 5, 32–40. [Google Scholar]
  38. Liu, Q.; Liu, J.; Liang, B.; et al. The Influence of Pore Structure of the Core-Scale Fracture-Controlled Matrix Unit on Imbibition: Model Construction and Definition of the Fractal Coefficient. Lithosphere 2022, 2022, 6245345. [Google Scholar]
  39. Liu, Q.; Song, R.; Liu, J.; et al. Pore-scale visualization and quantitative analysis of the spontaneous imbibition based on experiments and micro-CT technology in low-permeability mixed-wettability rock. Energy Science & Engineering 2020, 8, 1840–1856. [Google Scholar]
  40. Liu, Q.; Li, J.; Liang, B.; et al. Complex wettability behavior triggering mechanism on imbibition: A model construction and comparative study based on analysis at multiple scales. Energy 2023, 275, 127434. [Google Scholar]
  41. Liu, J.-j.; Song, R.; Cui, M.-m. Improvement of predictions of petrophysical transport behavior using three-dimensional finite volume element model with micro-CT images. Journal of Hydrodynamics 2015, 27, 234–241. [Google Scholar]
  42. Song, R.; Liu, J.; Cui, M. Single- and two-phase flow simulation based on equivalent pore network extracted from micro-CT images of sandstone core. Springerplus 2016, 5, 817. [Google Scholar] [PubMed]
  43. Krause, M.; Perrin, J.-C.; Kuo, C.-W.; et al. Characterization of CO2 storage properties using core analysis techniques and thin section data. Energy Procedia 2009, 1, 2969–2974. [Google Scholar] [CrossRef]
  44. Abell, A.B.; Willis, K.L.; Lange, D.A. Mercury Intrusion Porosimetry and Image Analysis of Cement-Based Materials. Journal of Colloid and Interface Science 1999, 211, 39–44. [Google Scholar] [CrossRef] [PubMed]
  45. Zhang, N.; He, M.; Zhang, B.; et al. Pore structure characteristics and permeability of deep sedimentary rocks determined by mercury intrusion porosimetry. Journal of Earth Science 2016, 27, 670–676. [Google Scholar]
  46. Zou, X.Y.; Li, X.Q.; Zhang, J.Z.; et al. Characteristics of Pore Structure and Gas Content of the Lower Paleozoic Shale from the Upper Yangtze Plate, South China. Energies 2021, 14, 7603. [Google Scholar] [CrossRef]
  47. Chen, L.; Xu, J.; Chen, J. Applications of scanning electron microscopy in earth sciences. Science China Earth Sciences 2015, 58, 1768–1778. [Google Scholar]
  48. Xda, B.; Meng, W.; Cwa, B.; et al. Factors affecting shale microscopic pore structure variation during interaction with supercritical CO2. Journal of CO2 Utilization 2020, 38, 194–211. [Google Scholar]
  49. Loucks, R.G.; Reed, R.M.; Ruppel, S.C.; et al. Morphology, Genesis, and Distribution of Nanometer-Scale Pores in Siliceous Mudstones of the Mississippian Barnett Shale. Journal of Sedimentary Research 2009, 79, 848–861. [Google Scholar] [CrossRef]
  50. Clarkson, C.R.; Solano, N.; Bustin, R.M.; et al. Pore structure characterization of North American shale gas reservoirs using USANS/SANS, gas adsorption, and mercury intrusion. Fuel 2013, 103, 606–616. [Google Scholar]
  51. Ozotta, O.; Liu, K.; Gentzis, T.; et al. Pore Structure Alteration of Organic-Rich Shale with Sc-CO2 Exposure: the Bakken Formation. Energy & Fuels 2021, 35, 5074–5089. [Google Scholar]
  52. Du, Y.; Sang, S.; Pan, Z.; et al. Experimental study of supercritical CO2-H2O-coal interactions and the effect on coal permeability. Fuel 2019, 253, 369–382. [Google Scholar] [CrossRef]
  53. Khather, M.; Saeedi, A.; Rezaee, R.; et al. Experimental evaluation of carbonated brine-limestone interactions under reservoir conditions-emphasis on the effect of core scale heterogeneities. International Journal of Greenhouse Gas Control 2018, 68, 128–145. [Google Scholar] [CrossRef]
  54. Pearce, J.K.; Dawson, G.K.W.; Golab, A.; et al. A combined geochemical and μCT study on the CO2 reactivity of Surat Basin reservoir and cap-rock cores: Porosity changes, mineral dissolution and fines migration. International Journal of Greenhouse Gas Control 2019, 80, 10–24. [Google Scholar]
  55. Brattekås, B.; Haugen, M. Explicit tracking of CO2-flow at the core scale using micro-Positron Emission Tomography (μPET). Journal of Natural Gas Science and Engineering 2020, 77, 103268. [Google Scholar] [CrossRef]
  56. Kitamura, K.; Kogure, T.; Nishizawa, O.; et al. Experimental and Numerical Study of Residual CO2 Trapping in Porous Sandstone. Energy Procedia 2013, 37, 4093–4098. [Google Scholar] [CrossRef]
  57. Krishnamurthy, P.G.; Senthilnathan, S.; Yoon, H.; et al. Comparison of Darcy’s law and invasion percolation simulations with buoyancy-driven CO2-brine multiphase flow in a heterogeneous sandstone core. Journal of Petroleum Science and Engineering 2017, 155, 54–62. [Google Scholar]
  58. Yan, W.; Crandall, D.; Bruner, K.; et al. Core and Pore Scale Characterization of Liujiagou Outcrop Sandstone, Ordos basin, China for CO2 Aquifer Storage. Energy Procedia 2013, 37, 5055–5062. [Google Scholar] [CrossRef]
  59. Al-Bayati, D.; Saeedi, A.; Myers, M.; et al. Insights into immiscible supercritical CO2 EOR: An XCT scanner assisted flow behaviour in layered sandstone porous media. Journal of CO2 Utilization 2019, 32, 187–195. [Google Scholar]
  60. Xu, L.; Li, Q.; Myers, M.; et al. Experimental and numerical investigation of supercritical CO2 migration in sandstone with multiple clay interlayers. International Journal of Greenhouse Gas Control 2021, 104, 103194. [Google Scholar] [CrossRef]
  61. Xu, L.; Myers, M.; Li, Q.; et al. Migration and storage characteristics of supercritical CO2 in anisotropic sandstones with clay interlayers based on X-CT experiments. Journal of Hydrology 2020, 580, 124239. [Google Scholar]
  62. Zhu, Q.; Zhou, Q.; Li, X. Numerical simulation of displacement characteristics of CO2 injected in pore-scale porous media. Journal of Rock Mechanics and Geotechnical Engineering 2016, 8, 87–92. [Google Scholar]
  63. Kogure, T.; Nishizawa, O.; Chiyonobu, S.; et al. Effect of Sub-core Scale Heterogeneity on Relative Permeability Curves of Porous Sandstone in a Water-supercritical CO2 System. Energy Procedia 2013, 37, 4491–4498. [Google Scholar]
  64. Liu, Y.; Wang, H.; Shen, Z.; et al. Estimation of CO2 Storage Capacity in Porous Media by using X-ray Micro-CT. Energy Procedia 2013, 37, 5201–5208. [Google Scholar]
  65. Lv, P.; Liu, Y.; Yang, W. Investigation on CO2 permeation in water-saturated porous media with disordered pore sizes. Experimental Thermal and Fluid Science 2020, 119, 110207. [Google Scholar] [CrossRef]
  66. Teng, Y.; Liu, Y.; Lu, G.; et al. Experimental Evaluation of Injection Pressure and Flow Rate Effects on Geological CO2 Sequestration Using MRI. Energy Procedia 2017, 114, 4986–4993. [Google Scholar] [CrossRef]
  67. Zhang, Y.; Park, H.; Nishizawa, O.; et al. Fluid Distribution Effects on P-wave Velocity of CO2/brine Saturated Rocks: A Comparison Study and Implications for CO2 Storage Monitoring Using Seismic Method. Energy Procedia 2017, 114, 3786–3792. [Google Scholar]
  68. Herring, A.L.; Andersson, L.; Newell, D.L.; et al. Pore-scale observations of supercritical CO2 drainage in Bentheimer sandstone by synchrotron x-ray imaging. International Journal of Greenhouse Gas Control 2014, 25, 93–101. [Google Scholar]
  69. Liu, Y.; Teng, Y.; Lu, G.; et al. Experimental study on CO2 diffusion in bulk n-decane and n-decane saturated porous media using micro-CT. Fluid Phase Equilibria 2016, 417, 212–219. [Google Scholar] [CrossRef]
  70. Kim, J.S.; Yan, D.; Rossen, W.R. Steady-State Flow Behavior of CO2 Foam. SPE Journal 2013, 10, 405–415. [Google Scholar] [CrossRef]
  71. Khalil, M.; Liu, N.; Lee, R. Effect of particle hydrophobicity on CO2 foam generation and foam flow behavior in porous media. Fuel 2014, 126, 104–108. [Google Scholar]
  72. Fyen, T.; Bratteks, B.; Fern, M.A.; et al. Increased CO2 storage capacity using CO2-foam. International Journal of Greenhouse Gas Control 2020, 96, 103016. [Google Scholar] [CrossRef]
  73. Xue, Z.; Nishio, S.; Hagiwara, N.; et al. Microbubble Carbon Dioxide Injection for Enhanced Dissolution in Geological Sequestration and Improved Oil Recovery. Energy Procedia 2014, 63, 7939–7946. [Google Scholar] [CrossRef]
  74. Patmonoaji, A.; Zhang, Y.; Xue, Z.; et al. Experimental and numerical simulation of supercritical CO2 microbubble injection into a brine-saturated porous medium. International Journal of Greenhouse Gas Control 2019, 91, 102830. [Google Scholar] [CrossRef]
  75. Zhai, H.; Xue, Z.; Park, H.; et al. Migration characteristics of supercritical CO2 microbubble flow in the Berea sandstone revealed by voxel-based X-ray computed tomography imaging analysis. Journal of Natural Gas Science and Engineering 2020, 77, 103233. [Google Scholar]
  76. Du, D.; Wang, D.; Jia, N.; et al. Experiments on CO2 foam seepage characteristics in porous media. Petroleum Exploration and Development 2016, 43, 499–505. [Google Scholar]
  77. McLendon, W.J.; Koronaios, P.; Enick, R.M.; et al. Assessment of CO2-soluble non-ionic surfactants for mobility reduction using mobility measurements and CT imaging. Journal of Petroleum Science and Engineering 2014, 119, 196–209. [Google Scholar]
  78. Du, D.; Li, Y.; Zhang, D.; et al. Experimental study on the inlet behavior of CO2 foam three phase displacement processes in porous media. Experimental Thermal and Fluid Science 2019, 103, 247–261. [Google Scholar]
  79. Alhosani, A.; Lin, Q.; Scanziani, A.; et al. Pore-scale characterization of carbon dioxide storage at immiscible and near-miscible conditions in altered-wettability reservoir rocks. International Journal of Greenhouse Gas Control 2021, 105, 103232. [Google Scholar] [CrossRef]
  80. Qin, Z.; Arshadi, M.; Piri, M. Near-miscible supercritical CO2 injection in oil-wet carbonate: A pore-scale experimental investigation of wettability state and three-phase flow behavior. Advances in Water Resources 2021, 158, 104057. [Google Scholar]
  81. Hao, Y.; Li, Z.; Su, Y.; et al. Experimental investigation of CO2 storage and oil production of different CO2 injection methods at pore-scale and core-scale. Energy 2022, 254, 124349. [Google Scholar] [CrossRef]
  82. HortonGeorge, W. Darcy’s Law. American Journal of Physics 1964, 32, 569. [Google Scholar]
  83. Mathias, S.A.; Gluyas, J.G.; Bryant, S.L.; et al. On the importance of relative permeability data for estimating CO2 injectivity in brine aquifers. International Journal of Greenhouse Gas Control 2013, 12, 200–212. [Google Scholar] [CrossRef]
  84. Krishnamurthy, P.G.; Senthilnathan, S.; Yoon, H.; et al. Comparison of Darcy’s law and invasion percolation simulations with buoyancy-driven CO2-brine multiphase flow in a heterogeneous sandstone core. Journal of Petroleum Science & Engineering 2016, 155, 54–62. [Google Scholar]
  85. Porter, M.L.; Plampin, M.R.; Pawar, R.; et al. CO2 leakage in shallow aquifers: A benchmark modeling study of CO2 gas evolution in heterogeneous porous media. International Journal of Greenhouse Gas Control 2015, 39, 51–61. [Google Scholar]
  86. Islam, A.W.; Sharif, M.; Carlson, E.S. Numerical investigation of double diffusive natural convection of CO2 in a brine saturated geothermal reservoir. Geothermics 2013, 48, 101–111. [Google Scholar] [CrossRef]
  87. Mathias, S.A.; Gluyas, J.G.; Bryant, S.L.; et al. On relative permeability data uncertainty and CO2 injectivity estimation for brine aquifers. International Journal of Greenhouse Gas Control 2013, 12, 200–212. [Google Scholar] [CrossRef]
  88. Guanhong, Feng, Tianfu, et al. Three-phase non-isothermal flow behavior of CO2-brine leakage from wellbores. International Journal of Greenhouse Gas Control 2017, 64, 183–193. [Google Scholar] [CrossRef]
  89. Wang, D.; Zhao, M.; Song, Y.; et al. Influence of Capillary Pressure and Injection Rate as well as Heterogeneous and Anisotropic Permeability on CO2 Transport and Displacement Efficiency in Water-Saturated Porous Media. Energy Procedia 2013, 37, 3945–3951. [Google Scholar] [CrossRef]
  90. Chapman, E.M.; Yang, J.; Crawshaw, J.P.; et al. Pore Scale Models for Imbibition of CO2 Analogue Fluids in Etched Micro-model||junctions Using Micro-fluidic Experiments and Direct Flow Calculations. Energy Procedia 2013, 37, 3680–3686. [Google Scholar] [CrossRef]
  91. Ovaysi, S.; Piri, M. Pore-scale dissolution of CO2+SO2 in deep saline aquifers. International Journal of Greenhouse Gas Control 2013, 15, 119–133. [Google Scholar] [CrossRef]
  92. Liu, H.; Valocchi, A.J.; Werth, C.; et al. Pore-scale simulation of liquid CO2 displacement of water using a two-phase lattice Boltzmann model. Advances in Water Resources 2014, 73, 144–158. [Google Scholar] [CrossRef]
  93. Venkateswaran, S. Efficient Implementation of Turbulence Modeling for CFD. 363-367.
  94. Hang, S.C.; Park, H.C.; Huh, C.; et al. Numerical simulation of fluid flow and heat transfer of supercritical CO2 in micro-porous media. Energy Procedia 2011, 4, 3786–3793. [Google Scholar]
  95. Mazzoldi, A.; Colls, J.J.; Hill, T. Assessing the risk for CO2 transportation within CCS projects, CFD modeling. International Journal of Greenhouse Gas Control 2011, 5, 816–825. [Google Scholar] [CrossRef]
  96. Liu, X.; Godbole, A.; Lu, C.; et al. Investigation of the consequence of high-pressure CO2 pipeline failure through experimental and numerical studies. Applied Energy 2019, 250, 32–47. [Google Scholar] [CrossRef]
  97. Jiang, F.; Hu, C. Numerical simulation of a rising CO2 droplet in the initial accelerating stage by a multiphase lattice Boltzmann method. Applied Ocean Research 2014, 45, 1–9. [Google Scholar] [CrossRef]
  98. Wei, Chen, Shuyong, et al. Three-dimensional simulation of interfacial convection in CO2–ethanol system by hybrid lattice Boltzmann method with experimental validation. Chinese Journal of Chemical Engineering 2015, 23, 356–365. [CrossRef]
  99. Tang, M.; Zhan, H.; Lu, S.; et al. Pore Scale CO2 Displacement Simulation Based on Three Fluid Phase Lattice Boltzmann Method. Energy & Fuels 2019, 33, 10039–10055. [Google Scholar]
  100. Chang, C.; Kneafsey, T.J.; Zhou, Q.; et al. Scaling the impacts of pore-scale characteristics on unstable supercritical CO2-water drainage using a complete capillary number. International Journal of Greenhouse Gas Control 2019, 86, 11–21. [Google Scholar] [CrossRef]
  101. Fakhari, A.; Li, Y.; Bolster, D.; et al. A phase-field lattice Boltzmann model for simulating multiphase flows in porous media: Application and comparison to experiments of CO2 sequestration at pore scale. Advances in Water Resources 2018, 114, 119–134. [Google Scholar]
  102. Bakhshian, S.; Hosseini, S.A. Pore–scale analysis of supercritical CO2–brine immiscible displacement under fractional–wettability conditions. Advances in Water Resources 2019, 126, 96–107. [Google Scholar] [CrossRef]
  103. Guo, R.; Dalton, L.E.; Fan, M.; et al. The role of the spatial heterogeneity and correlation length of surface wettability on two-phase flow in a CO2-water-rock system. Advances in Water Resources 2020, 146, 103763. [Google Scholar] [CrossRef]
  104. Guo, R.; Dalton, L.; Crandall, D.; et al. Role of heterogeneous surface wettability on dynamic immiscible displacement, capillary pressure, and relative permeability in a CO2-water-rock system. Advances in Water Resources 2022, 165, 104226. [Google Scholar] [CrossRef]
  105. Atia, A.; Mohammedi, K. Pore-scale study based on lattice Boltzmann method of density driven natural convection during CO2 injection project. Chinese Journal of Chemical Engineering 2015, 23, 1593–1602. [Google Scholar] [CrossRef]
  106. Wang, H.; Su, Y.; Wang, W.; et al. CO2-oil diffusion, adsorption and miscible flow in nanoporous media from pore-scale perspectives. Chemical engineering journal 2022, 450, 137957. [Google Scholar] [CrossRef]
  107. Yiotis, A.G.; Stubos, A.K.; Boudouvis, A.G.; et al. A 2-D pore-network model of the drying of single-component liquids in porous media. Advances in Water Resources 2001, 24, 439–460. [Google Scholar] [CrossRef]
  108. Vogel, H.J.; Tlke, J.; Schulz, V.P.; et al. Comparison of a Lattice-Boltzmann Model, a Full-Morphology Model, and a Pore Network Model for Determining Capillary Pressure–Saturation Relationships. Vadose Zone Journal 2005, 4, 380–388. [Google Scholar] [CrossRef]
  109. Benali, B.; Føyen, T.L.; Alcorn, Z.P.; et al. Pore-scale bubble population dynamics of CO2-foam at reservoir pressure. International Journal of Greenhouse Gas Control 2022, 114, 103607. [Google Scholar] [CrossRef]
  110. Liu, B.; Suzuki, A.; Ito, T. Estimating the seepage effect of SC-CO2 and water fracturing with a steady-state flow model considering capillary and viscous forces at the pore scale. Journal of Petroleum Science and Engineering 2020, 184, 106483. [Google Scholar] [CrossRef]
  111. Cao, S.C.; Dai, S.; Jung, J. Supercritical CO2 and brine displacement in geological carbon sequestration: Micromodel and pore network simulation studies. International Journal of Greenhouse Gas Control 2016, 44, 104–114. [Google Scholar] [CrossRef]
  112. Hu, R.; Wan, J.; Kim, Y.; et al. Wettability effects on supercritical CO2–brine immiscible displacement during drainage: Pore-scale observation and 3D simulation. International Journal of Greenhouse Gas Control 2017, 60, 129–139. [Google Scholar]
  113. Basirat, F.; Yang, Z.; Niemi, A. Pore-scale modeling of wettability effects on CO2–brine displacement during geological storage. Advances in Water Resources 2017, 109, 181–195. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated