Prerpints.org logo
Preprint
Article

Measurements of J/ψ Production vs Event Multiplicity in the Forward Rapidity in p + p Collisions in the PHENIX Experiment

Altmetrics

Downloads

89

Views

24

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

12 June 2023

Posted:

13 June 2023

You are already at the latest version

Alerts
Abstract
J/ψ, a charmonium bound state made of a charm and an anti-charm quark, has been discovered in the 1970s and confirmed the quark model. Because the mass of charms quarks is significantly above the Quantum Chromodynamics (QCD) scale ΛQCD, charmonia are considered as excellent probes to test perturbative Quantum Chromodynamics (pQCD) calculations. Over the past decades, they have been studied extensively at different high energy colliders. However, their production mechanisms, which involves multiple scales, are still not very well understood. Recently, in high multiplicity p+p collisions at RHIC and at the LHC, a significant enhancement of J/ψ production yield has been observed, which suggests a strong contribution from the Multi-Parton Interaction (MPI). This is different from the traditional pQCD picture where charm quark pairs are produced from a single hard scattering between partons in p+p collisions. In this work, we will report the J/ψ normalized production yield as a function of normalized charged particle multiplicity over a board range of rapidity and event multiplicity in the J/ψ→μ+μ− channel with PHENIX Run 15 p+p data at \sqrt{s}=200 GeV. The results are compared with PYTHIA 8 simulations with the MPI option on and off. Finally, the outlooks of J/ψ in p+Au and Au+p collisions along with Color Glass Condensate (CGC) predictions and of multiplicity dependent ψ(2S)/J/ψ ratio in p+p data will be briefly discussed.
Keywords: 
Subject: Physical Sciences  -   Nuclear and High Energy Physics

1. Introduction

In 1974, J / ψ , a charmonium bound state made of charm and anti-charm quark ( c c ¯ ), has been discovered at Brookhaven National Laboratory [1] and Stanford National Linear Accelerator [2], which confirmed the existence of charm quarks [3] and validated the quark model. Since the charm quark mass is above the QCD scale Λ Q C D , the production of c c ¯ pair in high-energy collisions is perturbative, which makes J / ψ an excellent probe to test pQCD calculations.
The production of J / ψ at high energy hadronic colliders involves multiple stages across many different scales. Over the past decades, J / ψ has been studied extensively at different colliders [4,5,6]. Nonetheless, the description of J / ψ production is still not yet fully developed and cannot reach very high precision. However, thanks to the QCD factorization theorem [7], hard processes, which are perturbatively calculable, are factorized from soft processes, which are non-perturbative but can be modeled phenomenologically and constrained by experiments. This allows us to apply pQCD to calculate the production cross section of J / ψ . We can test QCD at high energy colliders through the comparison of the J / ψ production data with model calculations.
In hadronic collisions events, both elastic and inelastic scatterings may occur. Experimentally, we are interested in inelastic collision events. There are 2 types of events in inelastic hadronic collisions: diffractive and non-diffractive dissociations [8]. In this work, we focus on J / ψ produced in non-diffractive hadronic collisions events, which can be denoted as p p → J / ψ + X .
A simple sketch of J / ψ production in high-energy hadronic collision events can be summarized as below:
Initial Dynamics of Partons: According to the Parton Model. the structure of hadrons can be described by constituent partons [9]. The initial dynamics of partons are non-perturbative but can be parametrized by parton distribution function (PDF) [10]. They can be measured in deep inelastic scattering experiments at different colliders and related with each other via scaling [7]. Alternatively, phenomenological approaches [11], such as the String Percolation [12] and Color Glass Condensate [13], can be applied to model the incoming hadrons. These models have been compared with experimental data such as charged particle p T spectra and rapidity distribution d N c h / d η and demonstrate reasonably good agreement [14].
Initial State Interactions: They occur among energetic partons before hard scatterings. An example is the soft radiation of the partons [15], which is call the initial state radiation (ISR). ISR will influence the initial heavy-quark pair production [16]. Usually, the effect can widen c c ¯ azimuthal angle correlation [17] and broaden the p T spectra [18].
Hard Partonic Scattering: Energetic partons scatter off each other with large momentum transfers. In the traditional pQCD picture, it is simply described as a single hard scattering between two partons in each collision. They can be calculated analytically by pQCD with Feynman diagrams to very high precision [19]. At RHIC, the c c ¯ pair production is dominated by gluon-gluon fusion: g g → c c ¯ .
Multiple Parton Interaction (MPI): MPI is an elaborate paradigm to describe the partonic interaction stage at high energy colliders at the RHIC, Tevatron, and the LHC [20]. According to MPI, one hard scattering accompanied by several semi-hard interactions take place in each collisions. All of them need to be included in the partonic scattering amplitudes. This is different from the traditional pQCD picture. Nowadays, high energy hadronic colliders allow more phase space for MPI to happen. Many studies at the LHC suggest MPI should be included to better describe the data [21].
Hadronization: In the final state, the c c ¯ pairs will lose energy via radiation and evolve into the color-neutral J / ψ bound state. Because this process is also soft and non-perturbative, many phenomenological models have been developed to describe the c c ¯ → J / ψ process in different collision systems. Selected examples of theoretical models are listed below:
Non-Relativistic QCD (NRQCD): This is an effective field theory approach to describe the hadronization of c c ¯ pair thanks to their large mass compared to its internal kinetic energy, which results in a slow speed β [22] within the non-relativistic limit β < < 1 . NRQCD includes perturbative short distance and non-perturbative long distance effects for range of strong coupling α s . To the leading order (LO), there are two mechanisms describing charmonium production.
  • Color Singlet (CS): The c c ¯ pairs are in the color singlet state with the same quantum number as the c c ¯ bound state in J / ψ . When the c c ¯ pair kinematics reach the J / ψ mass, they will bind together [23].
  • Color Octet (CO): The c c ¯ pairs are in color octet state carrying net color changes and emit extra gluons [24] to reach color neutral state, which results in additional hadron production associated to the J / ψ observed in the J / ψ -hadron correlation studies [25].
NRQCD predicts sizable transverse polarization of J / ψ , which has also been observed experimentally [26]. There are other phenomenological models such as Color Evaporation Model [27], Statistical Hadronization Model [28] and Color String Reconnection Model [29] that describe the J / ψ hadronization. Currently, physicists are testing all these models with experimental data.
Final State Interaction (FSI): In the final state, the newly formed J / ψ mesons may still interact with comoving particles nearby [30]. In the elastic scenario, J / ψ kinematics will be modified. Ineslatically, J / ψ may possibly be broken up [31]. Hence, the final state comover effect may affect J / ψ production yield and will become more prominent at high multiplicity. Experimentally, the final state comover effect can be studied by J / ψ -hadron femtoscopic correlation measurements [31]. Theoretically, FSI has also been implemented in the EPOS event generator [32].
Experimental Observables: All the processes mentioned above will contribute to the final production of J / ψ that can be reconstructed from its decay particles with detectors in experiment. Experimental observables to study J / ψ production may be the p T spectrum and production yield as a function of event activity for fully reconstructed J / ψ . Experimentally, the event activity is quantified by charged particle multiplicity. The production yield as a function of event multiplicity can probe the processes in the partonic level and will shed light on the interplay between soft and hard particle production [33].
In particular, we can use a relative quantity: the normalized J / ψ yield R ≡ N J / ψ / 〈 N J / ψ 〉 as a function of normalized charged particle multiplicity N c h / 〈 N c h 〉 . In experiments, this observable has the advantage because it can cancel the luminosity and some efficiencies corrections, which ultimately reduces the systematic uncertainties. Theoretically, in the string percolation picture [12], there is a simple scaling of N J / ψ by the number of color strings N s in the partonic level, which is similar to N c o l l in heavy-ion collisions in the nucleonic level. Moreover, N c h is also scaled by N s , another analog to the N p a r t scaling for soft particle production in heavy-ion collisions. Therefore, this is also inspired from theoretical perspectives. The normalized J / ψ yield as a function of normalized charged particle multiplicity measurements have been extensively carried out by experiments at RHIC and the LHC over different kinematic regions.
Autocorrelation: The J / ψ itself can contribute to the charged particle multiplicity in many different ways listed below [34]:
  • The J / ψ decay daughters such as the dipion, dielectron, and dimuon pairs
  • The extra gluons emitted from the c c ¯ pair in the color octet state producing addition charged hadrons [25]
  • The J / ψ cluster collapsing into hadrons [35]
  • The feed down from b-hadron decays for non-prompt J / ψ
Generally speaking, the autocorrelation increases N c h in J / ψ events compared to minimum bias (MB) events. Removing the autocorrelation effects can improve in our study for dedicated physics processes.

2. Recent Developments

Today, with the advancement of technologies in detector instrumentation, high performance computing, and artificial intelligence, we are moving toward high precision QCD era. Many novel studies of J / ψ production have been conducted at RHIC and the LHC.
Recently, the ALICE Collaboration has reported the results on J / ψ production measured in dielectron channel with the LHC Run 2 p p data at s = 5, 7,13 TeV [36,37,38]. The measurements of J / ψ normalized yield are performed in both middle and forward rapidity regions over a wide range of normalized charged particle multiplicity [39] . The normalized J / ψ yield as function of N J / ψ / 〈 N J / ψ 〉 at mid-rapidity generally lie above the forward rapidity region. A significant enhancement of J / ψ production with respect to linear scaling is observed at high multiplicity for both middle and forward rapidities [38]. Several theoretical models incorporating both initial state effects and MPI attempt to explain the data [38].
At RHIC, the STAR experiment carried out the J / ψ studies also in the dielectron channel, which only shows up to about 3 units of average charged particle multiplicity at rapidity | y | < 1 [40]. The data is presented in different p T regions. However, the results also suggests hint of enhancement for J / ψ production and are comparable to ALICE at the LHC energy. The increase becomes steeper at higher p T and multiplicity region, albeit not significant due to large uncertainties and not at very high event multiplicity where the FSI is reduced and MPI effect is more prominent. The STAR result can be generally well described by CEM, CGC and NLO with NRQCD calculations at different p T regions. However, no conclusion regarding to MPI for J / ψ production at RHIC at mid-rapidity and near average charged particle multiplicity is drawn .
Phenomenologically, the MPI effect plays a significant role on charm-quark production [41]. In the MPI picture, the average number of heavy-quark pairs in p p collision increases compared to tradition pQCD picture of single hard scattering [42]. Along with the color reconnection model for J / ψ hadronization treatment, a significant enhancement of J / ψ production cross section [29] is predicted. Hence, the linear scaling assumed in traditional pQCD picture does not hold [43].
From the simulation side, the latest versions of PYTHIA 8 event generator has incorporated many physics processes including ISR, hadronization, and FSR in addition to MPI, to describe underlying events in high-energy p p collisions [44]. PYTHIA 8 simulations are able to reproduce the charged particle p T spectra and d N / d η with reasonably good agreement at RHIC with Detroit tune [45] and the LHC with Monash tune [46]. PYTHIA users can turn on and off MPI, use different underlying event tunes, and adjust the CSM and COM contribution in c c ¯ → J / ψ to compare with data.
The J / ψ produced from the recombination of c c ¯ pair described in the Introduction Section is traditionally considered as the dominating production mechanism of J / ψ [26] and will lead to a substantial amount of transverse polarization. However, recently, at the LHC, unpolarized J / ψ production from jets, an alternative production mechanism, in p p [47] and PbPb [48] collisions has been recently observed by the CMS experiment. Moreover, LHCb has shown that unpolarized J / ψ down to low p T is produced from jet fragmentation in p p collisions [49]. J / ψ are observed as hadrons within the jet cones radius. The J / ψ produced from jets will have different production processes described above.
Most J / ψ measurements are carried out in non-diffractive dissociation events at hadronic colliders. There are also some theoretical efforts to study novel QCD with J / ψ production in single diffractive p p collisions via Pomerons exchange ( p p → p X ) [50]. Measurements on single diffractive p p cross section have also been performed by the ALICE [51] and ATLAS experiments [52] at the LHC.
Therefore, all these latest developments motivate us to investigate J / ψ at high event multiplicity in the forward rapidity at RHIC. The PHENIX detector is desirable and capable for this physics [53]. Thanks to the excellent tracking, vertexing and muon performance of the PHENIX detector, we can perform charmonium studies in the forward region up to high multiplicity. Historically, the research on event multiplicity dependence of J / ψ production in small systems with PHENIX dates back to early 2013 in p + p collisions at s = 510 GeV [54]. We will report our latest studies on J / ψ using PHENIX Run 15 p + p data at s = 200 GeV.

3. Experimental Apparatus and Data Samples

The PHENIX experiment [53] is a general purpose detector at RHIC at Brookhaven National Laboratory for relativistic heavy-ion physics research [55]. It has broad ϕ and η acceptance coverage [56] and can collect large data samples to perform measurements at middle and forward rapidities. The tracking, particle identification, colorimeter, and muon systems of the PHENIX experiment apply various radiation detection techniques to maximize its physics capabilities.
The forward silicon tracker detector (FVTX) employs advanced silicon strip technologies and installed as 4 endcaps in the forward an backward regions covering 1.2 < | η | < 2.2 [57]. Its sensor contains two columns of mini-strips with 75 μ m pitches in radial direction and the lengths varying from 3.4 – 11.5 mm in the azimuthal direction. The FVTX is capable of performing excellent tracklet reconstruction and precise vertex determination. In addition to the FVTX, at mid-rapidity | η | < 1 , the Silicon Vertex Tracker (SVX) is a 4 layer barrel detector built to enhance the capabilities of the central arm spectrometers and provides excellent position resolution [58], which enables tracking at mid-rapidity .
Two muon arms are built in the forward and backward regions far away from the beam spot with a rapidity coverage of 1.2 < | η | < 2.4 [59]. A stack of absorber/low resolution tracking layers allow excellent muon detection and identification. Along with the three new resistive plate chambers, the rejection factor for muon from pions and kaons is on the order magnitude of 10 3 . Each muon arm is equipped with a radial field magnetic spectrometer to provide precision muon tracking. The muon momentum resolution is δ p / p ∼ 1.7 % , allowing excellent performance for quarkonia reconstruction and clean separation between J / ψ and ψ ′ [60].
The PHENIX Electromagnetic Calorimeter (EMCAL) uses Pb as the absorber material and a shashlik design with a block size 5.5 cm × 5.5 cm and wavelength shifting fibers to measure the energy of electromagnetic shower [61]. The EMCAL can provide excellent energy linearity and resolution for jet reconstruction.
The PHENIX experiment is also equipped with a ring image Cherenkov detector (RICH) to perform electron identification [62]. It can achieve great performance for electron selection from π , K, p separation at very high p T .
The beam-beam counters (BBC) are installed in both far north and south directions with advanced electronics to determine the event vertex and activity [63]. BBC uses coincidence of both sides along with a minimum ADC threshold to select MB events. The zero degree calorimeter (ZDC) is used as identical form for all 4 experiments at RHIC to characterize global event parameters in the very forward direction [64]. It can perform precise determination of event activity, luminosity, and forward neutron counting through the measurements of beam fragment energy deposition in the far forward direction.
With excellent detector hardware capabilities, PHENIX also designs and deploys dedicated Level 1 trigger to collect data samples for different physics topics [65] applying high performance computing and electronic readout technologies [66]. Many collisions occur at RHIC when the collider is running. However, only a small fraction of them is relevant for our physics studies. Thus, the MB trigger is developed for general physics studies. The MB trigger uses both BBC and ZDC to select non-diffractive dissociation processes and determine global event parameters such as the collision vertex, luminosity, and impact parameter. The overall efficiency of MB trigger is about 55 ± 5%.
For charmonium physics studies, we need high statistics J / ψ samples. The dimuon trigger samples enrich J / ψ by requiring MuID trigger identify muons and applying quality selections on the muon tracks (MuTr). The overall efficiency of the dimuon trigger is approximately 79 ± 2%.
The PHENIX detector is also equipped with beam clock trigger utilizing the Granule Timing Module with fast electronics [67]. It can operate at high frequency with excellent timing resolution to provide precise timing information for the raw data, which allows synchronization among subdetectors and event building. In addition, the EMCal/RICH trigger (ERT) is dedicated to sample hard scattering events for heavy flavor and jet physics studies .

4. Analysis

In 2015, PHENIX acquired p + p , p + A l , and p + A u collisions data with transversely polarized proton at s = 200 GeV. Based on the PHENIX p + p data, we can define the J / ψ normalized yield R ( J / ψ ) from quantities as follows:
R ( J / ψ ) = [ N S J / ψ N M B ϵ t r i g M B ϵ t r i g J / ψ ] / [ N S J / ψ ( t o t a l ) N M B ( t o t a l ) 〈 ϵ t r i g M B 〉 〈 ϵ t r i g J / ψ 〉 ] × f c o l l
The quantities are defined below:
  • N S J / ψ : the J / ψ signal raw yield extracted from dimuon invariant mass m μ μ distribution
  • N M B : the number of minimum biased events recorded
  • ϵ t r i g M B : minimum biased trigger efficiency
  • ϵ t r i g J / ψ : J / ψ trigger efficiency
  • f c o l l : correction factor for multiple collisions obtained from a data-model method
The quantities in bracket stand for the average value over the integral event multiplicity and the total in the parenthesis means the sum over all multiplicity bins. We reconstruct J / ψ from the dimuon decay channel: J / ψ → μ + μ − . It should be noted that we assume the luminosity, the branching ratio of J / ψ → μ + μ − , the acceptance, and the reconstruction efficiency cancel out in the normalization because they do not have significant event multiplicity dependence.
The normalized J / ψ yield R ( J / ψ ) is plotted as a function of normalized charged particle multiplicity N c h / 〈 N c h 〉 defined as the number of tracklets reconstructed by FVTX or SVX hits. Our results are presented in charged particle multiplicity bins of [0,1,2,3,4,6,7,8,10,19]. In our analysis, we use the MB data sample to obtain the N M B . The dimuon trigger sample is used to reconstruct J / ψ . Finally, the beam clock trigger sample is used for efficiency correction and systematic uncertainties studies in a data-driven manner.

4.1. Event, Track, and J / ψ Candidate Selections

In order to achieve the best analysis results, we need to apply selections to the data samples. We require the following to select events with good primary vertices:
  • The z-component of reconstructed event vertex is within 10 cm from the beam spot: | E v t _ v t x Z | < 10 cm
  • The z-component of the event vertex determined by BBC is within 20 cm from the beam spot: | E v t _ b b c Z | < 10 cm
  • The error on E v t _ v t x Z is within 0.2 cm: | σ ( E v t _ v t x Z ) | < 0.2 cm
  • Require | E v t _ v t x Z − E v t _ b b c Z | < 5 cm to reduce bad double collision events
We reconstruct the tracklets with the FVTX and SVX. To ensure the quality of our tracklets, we require the selections below:
  • 1.2 < | η | < 2.4 for FVTX and | η | < 1 for SVX tracklets
  • The transverse component of the distance of closest approach D C A r : D C A r < 0.2 cm for FVTX and D C A r < 0.21 cm for SVX tracklets
  • The fits χ 2 < 20 and at least 5% vertex probability
  • At least 2 hits on the silicon detectors
We also apply the following selections to the muons
  • Muon momentum is between 3 and 50 GeV/c
  • Good matching with the muon tracker and the muon identification trigger
  • Good muon χ 2 quality for both muon identification (MuID) and muon tracking (MuTr)
  • At least 4 hits on the MuID and 12 hits on the MuTr
Finally, we apply the following requirements to J / ψ candidates
  • Acceptance rapidity: 1.2 < | y J / ψ | < 2.2
  • Dimuon χ 2 fit within 5 to ensure the two muons coming from the same vertex

4.2. MB Event Multiplicity Determination

We use the MB sample to determine the N M B . We use the tight definition, | E v t _ b b c Z | < 15 cm, for N c h counting. With the N M B as a function of N c h , we can also obtain the N M B ( t o t a l ) by summing the distribution and 〈 N c h 〉 by taking the average on the distribution. We can then rescale the x-axis with to N c h / 〈 N c h 〉 and plot the N M B as a function of N c h / 〈 N c h 〉 .

4.3. J / ψ Signal Extraction

After applying all selections to the dimuon sample, we are able to observe a very clear J / ψ signal with good resolution and correct peak near the PDG value. The kinematics of the reconstructed J / ψ is p T < 5 GeV/c and 1.2 < | y | < 2.2 . To determine the J / ψ raw yield, we need to extract signal in the dimuon invariant mass in data. We develop a fitting model using a single Crystal ball function to describe the J / ψ signal component and an exponential decay function to describe background component in the data. The functional form of the signal component is given by
f S ( x ; α , n , μ , σ ) = N exp [ − ( x − μ ) 2 2 σ 2 ] , if ( x − μ σ > α ) N A ( B − x − μ σ ) − n if ( x − μ σ ≤ α )
where
A = n | α | n exp − | α | 2 2
and
B = n | α | − | α | .
The functional form of background component is given by
f B ( x ; D , λ ) = D e − λ x ,
Hence, the total fit function is given by
f = N S J / ψ · f s + N B · f B
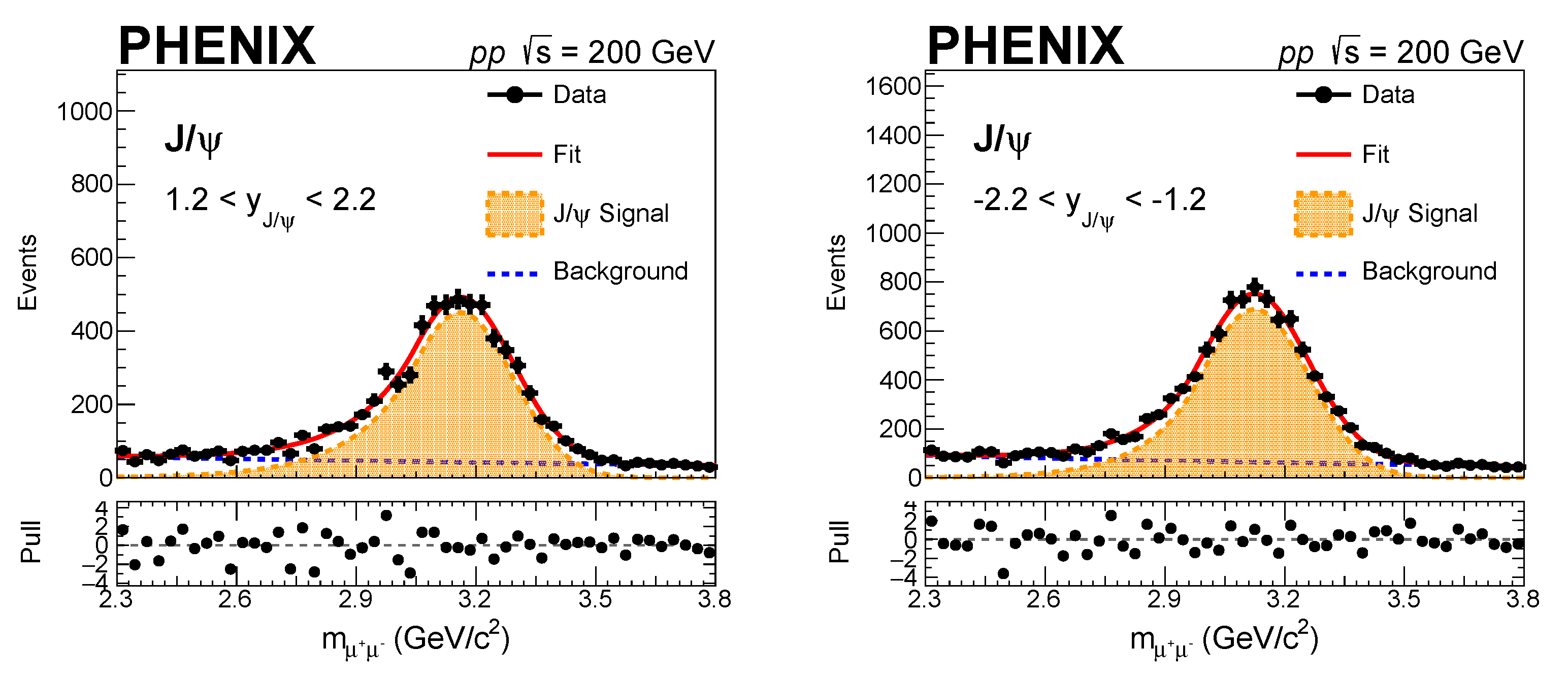
We then use the RooFit package [68] to fit the data points and obtain the J / ψ signal raw yield N S J / ψ . The invariant mass distribution of J / ψ from the north and south muon arms for inclusive event multiplicity along with the fits are shown below in Figure 1
The free parameters for the fits are NA, B, μ , σ , D, and λ . We fix A and N in the fit on the inclusive north and south muons arm sample to keep the overall shape to fit each N c h / 〈 N c h 〉 bin. Good statistics with reconstruction performance of J / ψ in the dimuon channel are observed in Figure 1. We sum N S J / ψ of all N c h / 〈 N c h 〉 bins to obtain N S J / ψ ( t o t a l ) .

4.4. Efficiency Correction

We quote the 〈 ϵ t r i g M B 〉 = 55 % and 〈 ϵ t r i g J / ψ 〉 = 79 % as mentioned in the description for the PHENIX detector. Then, we employ a data-drive method to correct the MB and J / ψ efficiencies.
To determine ϵ t r i g M B as a function of event multiplicity, we use the the RHIC beam clock trigger data. A collision is declared to have occurred if there is at least one tracklet in the FVTX or SVX. Hence, ϵ t r i g M B is the ratio of RHIC beam clock trigger sample with BBC local level 1 trigger also fired to the whole sample for BBC rate between 1000 – 1500 kHz. The systematic uncertainties σ ( ϵ t r i g M B ) are given by the deviation of ϵ t r i g M B at BBC rate from 600 – 800 kHz and 2000 – 2500 kHz from the nominal value 1000 – 1500 kHz as upper and lower bound respectfully.
To determine ϵ t r i g J / ψ as a function of event multiplicity, we use the ERT trigger sample. We calculate ϵ t r i g J / ψ using the multiplicity distribution of ERT sample with at least one track as the denominator and the multiplicity distribution of ERT sample with at least one track and a valid BBC vertex | E v t _ b b c Z | < 200 cm as the numerator. The statistical uncertainties of the first bin N c h = 1 is quoted as global systematic uncertainties σ ( ϵ t r i g J / ψ ) .

4.5. Multiple Collection Factor Correction

Multiple p + p collisions may occur at RHIC. Experimentally, each collision results in a primary vertex. The number of collisions in each event overall obey Poisson distribution. According to our studies, the double collision probability is in the level a few percent.
Because we focus on J / ψ produced in a single p + p collision, we need to correct multiple collisions effects in our data. We employ a data-model hybrid method to determine f c o l l . We use a model to calculate N M B as a function of N c h . We divide the normalized N M B distribution for south FVTX arm near BBC rate of 830 kHz, which consists of less than 2% of double collisions, by the single collision model and use the ratio as f c o l l . We quote the deviation from the model to the PHENIX data with BBC rate between 1000 - 1500 kHz as the systematic error on the multiple collision correction factor σ ( f c o l l ) , accounting for the disagreement between the model and the data.

4.6. Systematic Uncertainties Estimation

The systematic uncertainties on this measurement consist of the MB trigger efficiency, J / ψ trigger efficiency, multiple collision correction, and J / ψ reconstruction efficiency. The J / ψ reconstruction efficiency ϵ r e c o J / ψ has a weak dependence on N c h . It is treated as a constant but can be assigned with a global systematics of 5% from previous J / ψ measurements in the dimuon channel [69]. Finally, we treat individual uncertainties as uncorrelated and thus can estimate the total systematic uncertainties as follows:
σ ( t o t a l ) = σ ( ϵ t r i g M B ) ⊕ σ ( ϵ t r i g J / ψ ) ⊕ σ ( ϵ r e c o J / ψ ) ⊕ σ ( f c o l l )

5. Results

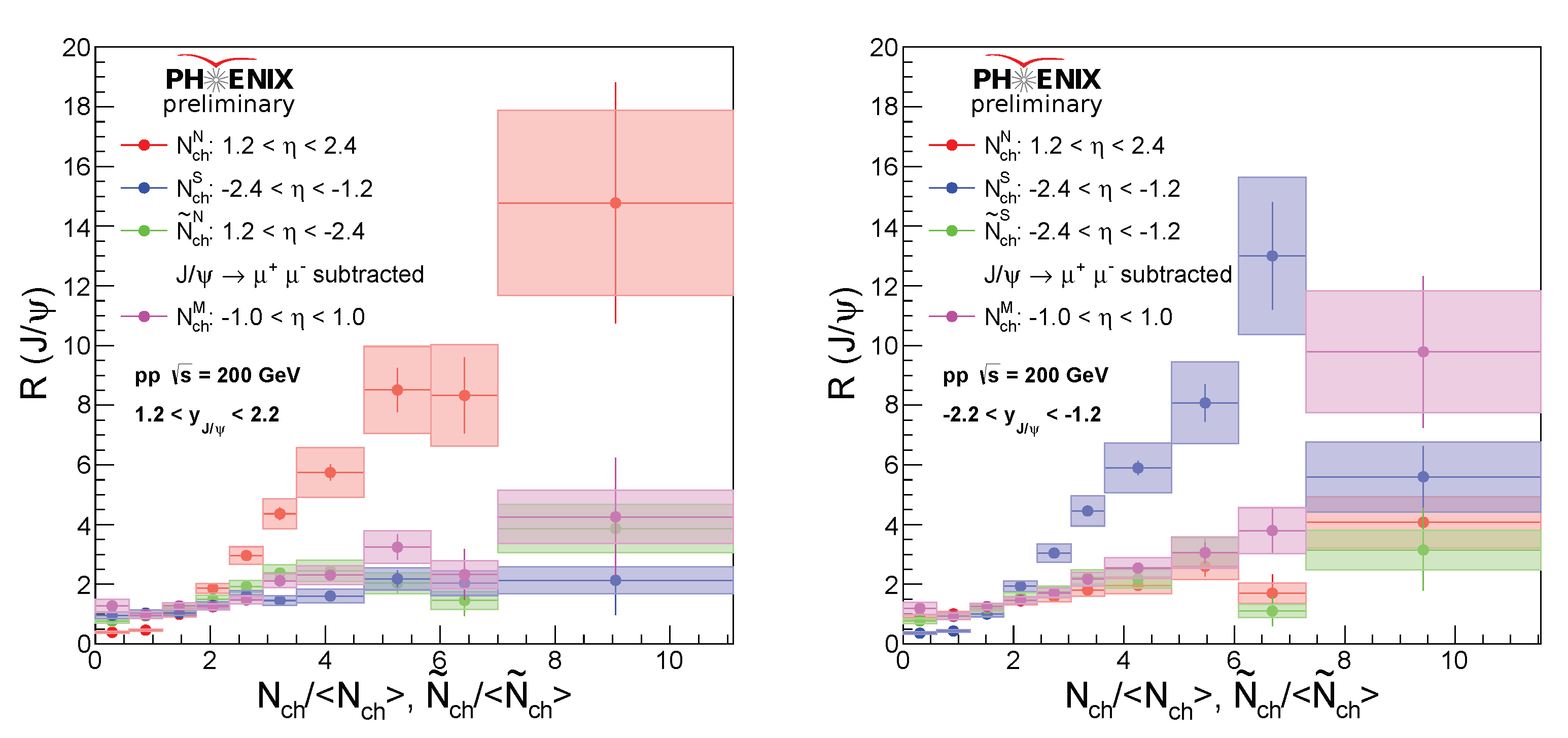
After finishing the data analysis, we have gather all ingredients to obtain the final results. Different underlying physics processes can be studied from different rapidity combinations of J / ψ and tracklet multiplicity measurements. Figure 2 illustrates the physics with different measurements
Phenomenologically, MPI always occurs regardless of the rapidity of the J / ψ and the charged particles. In the PHENIX experiment, when both the J / ψ and the tracklets are pointing to the same rapidity direction, we expect to have significant FSI contributions to J / ψ production due to the presence of particles nearby [32]. In the elastic scenario, J / ψ kinematics will be modified. Ineslatically, J / ψ may possibly be broken up [31]. As the J / ψ moves away from the charged particles, the comover effect in the final state is expected to diminish. This can be achieved by measuring the SVX and the opposite FVTX arm for the tracklet multiplicity with respect to the muon arms. Finally, muons can also contribute to the event multiplicity. For J / ψ → μ + μ − , the two muons on average increase the N c h by about 1.4. After removing this autocorrelation effect from the J / ψ decayed muons, the charged particle multiplicity will become N ˜ c h . We can also present the normalized J / ψ yield as a function of N ˜ c h / 〈 N ˜ c h 〉 by adjusting the x-axis in our measurement. These cases are all shown in Figure 2.
The final results of J / ψ reconstructed from the north muon arm located in the forward rapidity direction 1.2 < y J / ψ < 2.2 and the south muon arm located at the backward rapidity − 2.2 < y J / ψ < − 1.2 with respect to FVTX North and South and SVX measurements are shown below in Figure 3
The J / ψ yields up to about 10 units of average charged particle multiplicity are measured with good precisions. A stronger than linear rise is observed in the same rapidity direction between the J / ψ and the charged particles. The enhancement becomes more prominent at high multiplicity region. The slope decreases as the rapidity gap between the J / ψ and the charged particles increases when N c h / 〈 N c h 〉 > 1 . Finally, after subtracting the dimuon contributions in the same rapidity directions, the data points drop drastically and become consistent with the opposite rapidity measurements. These results imply that FSI effect does not have a substantial impact on J / ψ production in p + p collisions. However, MPI effects should be considered to explain the enhancement, particularly in the high multiplicity region.
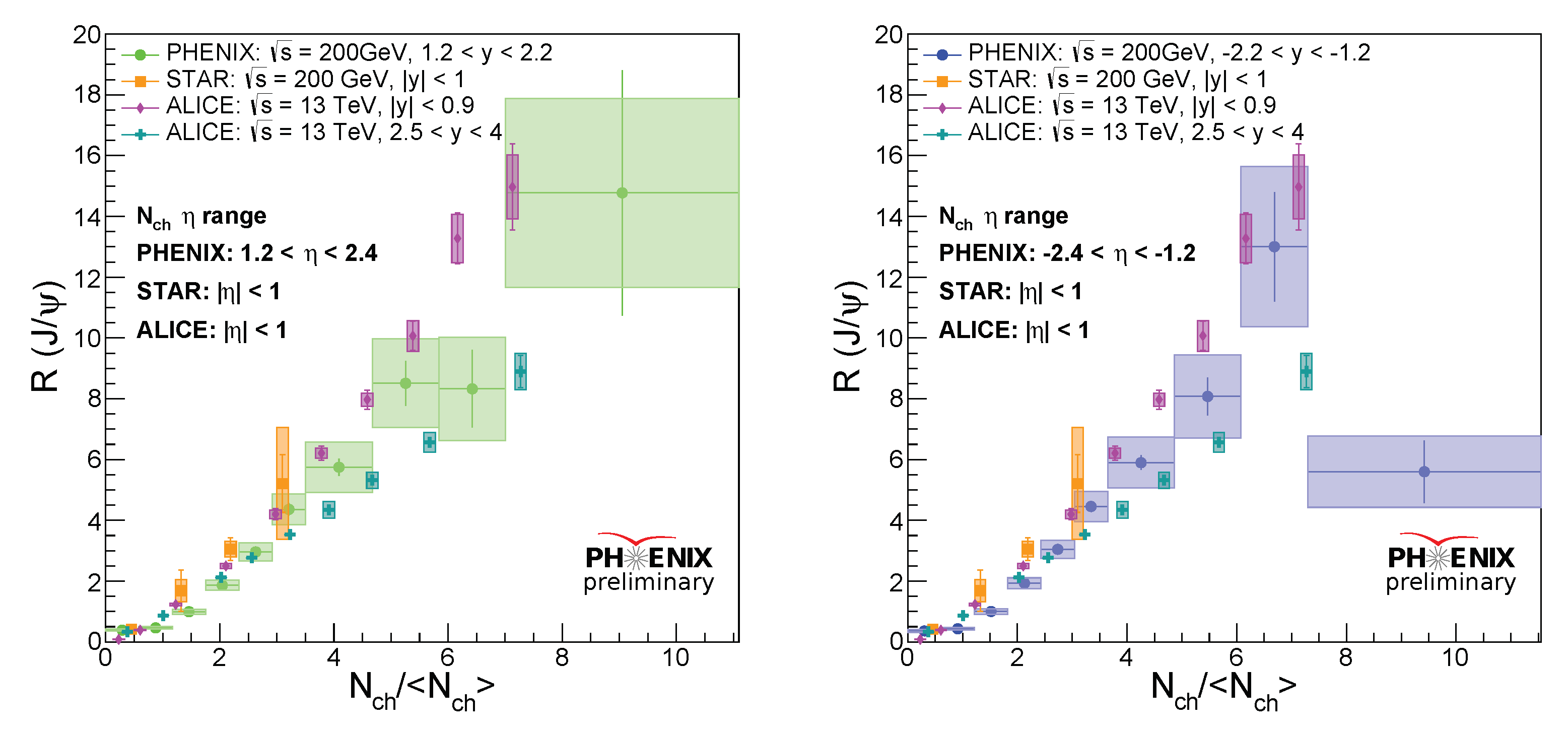
We also compare our data with recent measurements from STAR at RHIC [40] and ALICE at the LHC [38] shown below
In Figure 4, we can see that PHENIX has broader charged particle multiplicity measurements with better precision than STAR and comparable to ALICE. In low charged particle multiplicity, PHENIX data points are systematically below the STAR ones. In higher event multiplicity region, PHENIX data points ( 1.2 < | y | < 2.2 ) lie in between the ALICE middle ( | y | < 0.9 ) and forward rapidity ( 2.5 < y < 4 ) measurements, which fills the missing rapidity region from ALICE. All data points have slopes significantly above 1 when N c h / 〈 N c h 〉 > 1 . Hence, the comparisons suggest that J / ψ produced in the middle rapidity are generally above the forward rapidity at both RHIC and the LHC energies, which corresponds to the different phase space regions of x 1 , 2 of the partons during hard interaction.
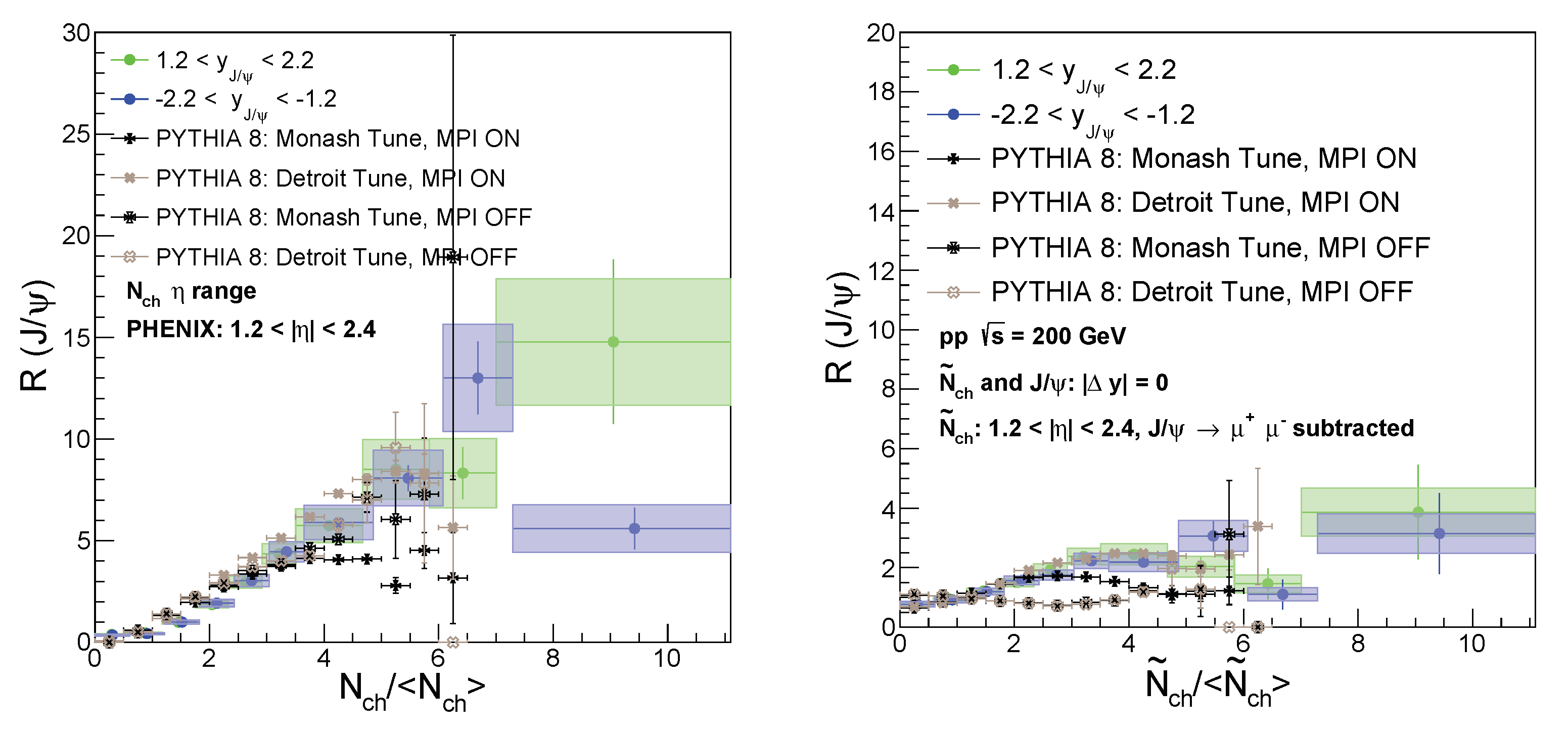
Finally, we compare our data with the PYTHIA 8 simulations with Monash and Detroit tunes including and not including MPI effect.
In PYTHIA 8 p + p simulations, we setup the c c ¯ event with large p ^ T for J / ψ production and use general inelastic hadronic collisions to model MB events. Because events with the high multiplicity has a relatively small probability, our simulation only covers up to N c h / 〈 N c h 〉 ≃ 6 and has large statistical uncertainties at high multiplicity. Nonetheless, PYTHIA 8 simulations with different setup diverge at high multiplicity. PYTHIA 8 using the Detroit Tune and turning on the MPI effect best describe the data. Hence, the MPI effect is significant for J / ψ production in p + p collisions at RHIC, particularly in the high multiplicity region.

6. Summary

We have reported the measurement of J / ψ normalized yield as a function of normal charged particle multiplicity with PHENIX Run 2015 p + p collisions at s = 200 GeV. The J / ψ is reconstructed from the dimuon channel with the PHENIX muon arms in the forward rapidity. The charged particle tracklets are reconstructed with FVTX and SVX detectors. Our results are presented in different combinations of J / ψ with p T < 5 GeV/c and 1.2 < | y | < 2.2 and charged particles at 1.2 < | y | < 2.4 for FVTX and | y | < 1 for SVX up to approximately 10 units of normalized event multiplicity. The J / ψ normalized yield beyond linear scaling is observed when the J / ψ and charged particles are both measured in the same rapidity. The enhancement of J / ψ production becomes more pronounced at high event multiplicity, which could possibly be explained by MPI. The J / ψ normalized yield decreases significantly as the rapidity gap between the J / ψ and the charged particles increases. After subtracting the dimuon contributions from the event multiplicity when the J / ψ and the charged particles point to the same rapidity directions, the results become consistent with the one where J / ψ and charged particles are produced in opposite rapidity directions, which hints the insignificance of the final-state comover effects for J / ψ production in p + p collisions.
Our forward J / ψ results lie systematically below the STAR measurement in middle rapidity and in between the ALICE data in the forward and middle rapidities. We notice that J / ψ produced in the middle rapidity generally is below forward rapidity within the same normalized charged particle multiplicity. This allows us to probe the partons distribution function in different phase space regions. Finally, through the comparison of our data with PYTHIA 8 simulation using the Detroit and Monash Tunes with MPI options on and off, we find that the Detroit Tune with MPI on best describes our data. Hence, the MPI contribution should be included in order to precisely describe J / ψ production in p + p collisions at RHIC, especially in high multiplicity events.
To investigate the possibility of J / ψ production from jet fragmentation, we plan to look at our results in different J / ψ p T regions. We expect J / ψ production from jet to be more likely at high p T . This study is currently ongoing. However, because of the limited statistics, particularly for p T > 3 GeV/c, we may not have sufficient precision to conclude the possible J / ψ production from jet fragmentation in p + p collisions at RHIC.
Currently, we also have discussions with the theoretical community to test the CGC model with J / ψ production in p + A u collisions. In addition, the ongoing measurement of ψ ( 2 S ) / J / ψ ratio in p + p collisions will help us understand charmonium hadronization. Many novel and exciting physics results about charmonium production in different collision systems with PHENIX data are coming in the near future.

Acknowledgments

We would like to thank Dr. Cesar da Silva and Dr. Ming Liu for their suggestions to improve the analysis and interpret the physics messages. We also appreciate the 2023 Zimányi Winter School organizers for their cordial reception and clarification of all questions related to conference registration and online presentations. Particularly, we are indebted to Professor Máté Csanád for the invitation to contribute this paper as part of the Zimányi School Special Issue.

References

  1. J. Aubert et al., “Experimental Observation of a Heavy Particle J”. Phys. Rev. Lett. 33 (23):(1974) 1404–1406.
  2. J. Augustin et al., “Discovery of a Narrow Resonance in e+e- Annihilation”. Phys. Rev. Lett. 33 (23): (1974) 1406–1408.
  3. S. L. Glashow, J. Iliopoulos, and L Maiani, “Weak Interactions with Lepton–Hadron Symmetry”. Phys. Rev. D. 2 (7) (1970) 1285–1292.
  4. M. Cacciari, M. Greco, M.L. Mangano, and A. Petrelli, “Charmonium Production at the Tevatron”, Phys. Lett. B 356 (1995) 553-560.
  5. X. Zhao and R. Ralf, “Forward and midrapidity charmonium production at RHIC”, Eur. Phys. J. C 62 (2009) 109-117.
  6. A. G. Stahl, Charmonium production in pp, pPb and PbPb collisions with CMS. Phys. Conf. Ser. 2017, 832, 012031.
  7. R.P. Feynman, “The behavior of hadron collisions at extreme energies”, Conf. Proc.C 690905 (1969) 237-258.
  8. D. E. Soper, “Parton distribution functions”, Nucl. Phys. B Proc. Suppl. 53 (1997) 69-80.
  9. J. C. Collins, D. E. Soper, and G. F. Sterman, “Factorization of Hard Processes in QCD”, Adv. Ser. Direct. High Energy Phys. 5 (1989) 1-91.
  10. J. Dias de Deus and C. Pajares. String Percolation and the Glasma. Phys. Lett. B 695 (2011) 211-213.
  11. N. Armesto, M. A. Braun, E. G. Ferreiro, and C. Pajares. “Percolation Approach to Quark-Gluon Plasma and J/ψ Suppression”, Phys. Rev. Lett. 3736; 77.
  12. C.Y.Wong, Introduction to high-energy heavy-ion collisions, Singapore, Singapore: World Scientific (1994) 516 p.
  13. F. Gelis; E. Iancu; J. Jalilian-Marian; R. Venugopalan. The Color Glass Condensate. Annual Review of Nuclear and Particle Science. 60: 463–489 (2010).
  14. M.A. Braun, F. Del Moral, and C. Pajares, Percolation of strings and the first RHIC data on multiplicity and transverse momentum distributions, Phys. Rev. C 65 024907 (2002).
  15. Y.-Q. Ma and R. Venugopalan, “Comprehensive Description of J/ψ Production in Proton-Proton Collisions at Collider Energies”, Phys. Rev. Lett. 113 19, 192301 (2014).
  16. H.S. Shao, “Initial state radiation effects in inclusive J/ψ production at B factories”, J. High Energ. Phys. 2014, 182 (2014).
  17. L. Buonocore, P. Nason, and F. Tramontano, “Heavy quark radiation in NLO+PS POWHEG generators”, Eur. Phys. J. C 78 (2018) 2, 151.
  18. S. Catani, M. Grazzini, and A. Torre, “Transverse-momentum resummation for heavy-quark hadroproduction”, Nucl. Phys. B 890 (2014) 518-538.
  19. E. L. Berger and R. Meng, “Transverse momentum distributions for heavy quark pairs”, Phys. Rev. D 49 (1994) 3248-3260.
  20. C. Anastasiou, L. Dixon, K. Melnikov, and F. Petriello, “High precision QCD at hadron colliders: Electroweak gauge boson rapidity distributions at NNLO”, Phys. Rev. D 69 (2004) 094008.
  21. B. Blok, Y. Dokshitser, L. Frankfurt, and M. Strikman, “pQCD physics of multiparton interactions”, Eur. Phys. J. C 72 1963 (2012).
  22. P. Bartalini et. al., “Multi-Parton Interactions at the LHC”, 10.48550/arXiv.1111.0469.
  23. J. Soto, “Overview of Non-Relativistic QCD”, Eur. Phys. J. A 31 (2007) 705-710.
  24. E. L. Berger and D. Jones, “Inelastic photoproduction of J/ψ and Υ by gluons”, Phys. Rev. D 23, 1521 (1981).
  25. R. Bain, L. Dai, A. Hornig, A. K. Leibovich, Y. Makris, and T. Mehen, “Analytic and Monte Carlo Studies of Jets with Heavy Mesons and Quarkonia”, JHEP 06 (2016) 121.
  26. P. L. Cho and A. K. Leibovich, “Color octet quarkonia production”, Phys. Rev. D 53, 150-162 (1996).
  27. M. Butenschoen and B. A. Kniehl, “J/ψ polarization at Tevatron and LHC: Nonrelativistic-QCD factorization at the crossroads”, Phys. Rev. Lett. 108 (2012) 172002.
  28. Y.-Q. Ma and R. Vogt, “Quarkonium production in an improved color evaporation model”, Phys. Rev. D 94, 114029 (2016).
  29. A. Andronic, P. Braun-Munzinger, M. K. Köhler, K. Redlich, J. Stachel, “Transverse momentum distributions of charmonium states with the statistical hadronization model”, Phys. Lett. B 797 (2019) 134836.
  30. P. Kotko, L. Motyka, and A. Stasto, “Color Reconnection Effects in J/ψ Hadroproduction”, Arxiv, e-Print: 2303.13128 [hep-ph].
  31. J. Crkovska, “Study of the J/ψ production in pp collisions at sNN = 5.02 TeV and of the J/ψ production multiplicity dependence in p-Pb collisions at sNN = 8.16 TeV with ALICE at the LHC”, High Energy Physics - Experiment [hep-ex]. Université Paris-Saclay, 2018. English. ⟨NNT : 2018SACLS343). (tel-01952850).
  32. M. Bahmani, D. Kikoła, and L. Kosarzewski, “A technique to study the elastic and inelastic interaction of quarkonium with hadrons using femtoscopic correlations”, Eur. Phys. J. C 81 (2021) 4, 305.
  33. K. Werner, B. Guiot, I. Karpenko, T. Pierog, Analysing radial flow features in p–Pb and pp collisions at several TeV by studying identified particle production in EPOS3. Phys. Rev. C89(6), 064903 (2014).
  34. Y. Bailung , “Measurement of D-meson production as a function of charged-particle multiplicity in proton–proton collisions at √s = 13 TeV with ALICE at the LHC”, PoS LHCP2021 (2021) 190.
  35. S. G. Weber, A. Dubla, A. Andronic, and A. Morsch, “Elucidating the multiplicity dependence of J/ψ production in proton–proton collisions with PYTHIA8”, Eur. Phys. J. C 79 (2019) 1, 36.
  36. E. Norrbin, T. Sjostrand, “Production mechanisms of charm hadrons in the string model”, Phys. Lett. B 442, 407-416 (1998).
  37. ALICE Collaboration, “Inclusive J/ψ production at mid-rapidity in pp collisions at √s=5.02 TeV”, JHEP 10 (2019) 084.
  38. ALICE Collaboration, “J/ψ polarization in pp collisions at s=7 TeV”, Phys. Rev. Lett. 108 (2012) 082001.
  39. ALICE Collaboration, “Multiplicity dependence of J/ψ production at midrapidity in pp collisions at s=13 TeV”, Phys. Lett. B 810 (2020) 135758.
  40. ALICE Collaboration, “Forward rapidity J/ψ production as a function of charged-particle multiplicity in pp collisions at √s= 5.02 and 13 TeV”, JHEP 06 (2022) 015.
  41. STAR Collaboration “J/ψ production cross section and its dependence on charged-particle multiplicity in p+p collisions at s=200 GeV”, Phys. Lett. B 786 (2018) 87-93.
  42. D. Thakur, S. De, R. Sahoo, and S. Dansana, “Role of multiparton interactions on J/ψ production in p+p collisions at LHC energies”, Phys.Rev.D 97 (2018) 9, 094002.
  43. U. Egede, T. U. Egede, T. Hadavizadeh, M. Singla, P. Skands, and M. Vesterinen, “The role of multi-parton interactions in doubly-heavy hadron production”, Eur. Phys. J. C 82 (2022).
  44. E. Gotsman and E. Levin, “High energy QCD: multiplicity dependence of quarkonia production”, Eur. Phys. J. C 81 (2021) 2, 99.
  45. M. R. Aguilar, Z. Chang, R. K. Elayavalli, R. Fatemi, Y. He, Y. Ji, D. Kalinkin, M. Kelsey, I. Mooney, and V. Verkest, “PYTHIA 8 underlying event tune For RHIC energies”, Phys. Rev. D 105 (2022) 1, 016011.
  46. P. Skands, S. Carrazza, and J. Rojo, “Tuning PYTHIA 8.1: the Monash 2013 Tune,” Eur. Phys. J. C74 no. 8, (2014) 3024.
  47. CMS Collaboration, “Study of J/ψ production inside jets in pp collisions at s= 8 TeV”, Phys. Lett. B 804 (2020) 135409.
  48. CMS Collaboration, “Fragmentation of jets containing a prompt J/ψ meson in PbPb and pp collisions at sNN = 5.02 TeV”, Phys. Lett. B 825 (2022) 136842.
  49. LHCb Collaboration, “Study of J/ψ Production in Jets”, Phys. Rev. Lett. 118 (2017) 19, 192001.
  50. F. Yuan, K.-T. Chao, “Diffractive J/y production as a probe of the gluon component in the Pomeron”, Phys. Rev. D 57 (1998) 5658-5662.
  51. ALICE Collaboration, “Measurement of inelastic, single- and double-diffraction cross sections in proton–proton collisions at the LHC with ALICE”, Eur.Phys.J.C 73 (2013) 6, 2456.
  52. ATLAS Collaboration, “Measurement of differential cross sections for single diffractive dissociation in √s = 8 TeV pp collisions using the ATLAS ALFA spectrometer”, JHEP 10 (2020) 182.
  53. K. Adcox et al. (PHENIX Collaboration), “PHENIX detector overview”, Nucl. Instrum. Methods Phys. Res., Sec. A 499, 469 (2003).
  54. PHENIX Collaboration, “Measurements of double-helicity asymmetries in inclusive J/ψ production in longitudinally polarized p+p collisions at s=510 GeV”, Phys. Rev. D 94 (2016) 11, 112008.
  55. K. Adcox et al. (PHENIX Collaboration), "Formation of dense partonic matter in relativistic nucleus–nucleus collisions at RHIC: Experimental evaluation by the PHENIX Collaboration", Nucl. Phys. A 757 (2005) 184-283.
  56. M. L. Brooks, “Physics Potential of and Status Report on the PHENIX Experiment”, Part of the Proceedings of ICPAQGP, Jaipur, India, March 17–21, 1997, 326-334.
  57. PHENIX Collaboration, “The PHENIX Forward Silicon Vertex Detector”, Nucl. Instrum. Meth. A 755 (2014) 44-61.
  58. Y. Akiba, “Proposal for a Silicon Vertex Tracker (VTX) for the PHENIX Experiment”, DOE Contact Number DE-AC02-98CH10886, United States: N. p., 2004. Web. doi:10.2172/15007383.
  59. PHENIX Collaboration, “PHENIX Muon Arms”, Nucl. Instrum. Meth. A 499.
  60. J. Newby, “Single and Dimuon Reconstruction Performance of the PHENIX South Muon Arm”, Poster for Quark Matter 2002, https://www.phenix.bnl.gov/WWW/publish/rjnewby/QM2002Poster.pdf.
  61. L. Aphecetche et. al. (PHENIX Collaboration), “PHENIX calorimeter”, Nucl. Instrum. Meth. A 499, 521-536 (2003).
  62. Y. Akiba, “Ring imaging Cherenkov detector of PHENIX experiment at RHIC”, Nucl. Instrum. Meth. 1999.
  63. PHENIX Collaboration “PHENIX inner detectors”, Nucl. Instrum. Meth. A470, 488 6499 (2001), arXiv:nucl-ex/0008005.
  64. C. Adler, A. C. Adler, A. Denisov, E. Garcia, M. J. Murray, H. Strobele, and S. N. White, “The RHIC zero degree calorimeter," Nucl. Instrum. Meth. A 433 (1999) 143-148.
  65. S. Belikov, J. S. Belikov, J. Hill, J. Lajoie, H. Skank, and G. Sleege, “PHENIX trigger system”, Nucl. Instrum. Meth. A 494 (2002) 541-547.
  66. J. G. Lajoie et al., “The PHENIX Level-1 trigger system”, 999 IEEE Conference on Real-Time Computer Applications in Nuclear Particle and Plasma Physics. 11th IEEE NPSS Real Time Conference. Conference Record (Cat. No.99EX295), Santa Fe, NM, USA, 1999, pp. 517.
  67. S.S Adler et al., “PHENIX on-line systems”, Nucl. Instrum. Meth. A 499 (2003) 560-592.
  68. T. Sjöstrand, S. Ask, J. R. Christiansen, R. Corke, N. Desai, P. Ilten, S. Mrenna, S. Prestel, C. O. Rasmussen, P. Z. Skands, “An Introduction to PYTHIA 8.2”, Comput. Phys. Commun. 191 (2015) 159–177.
  69. W. Verkerke and D. Kirkby, “The RooFit toolkit for data modeling”, in Statistical Problems in Particle Physics, Astrophysics and Cosmology, Oxford, UK, May 2006, pp. 186–189.
  70. PHENIX Collaboration, “J/ψ and ψ(2S) production at forward rapidity in p+p collisions at s=510 GeV”, Phys. Rev. D 101 (2020) 5, 052006.
Preprints 76427 g001
Figure 1. The dimuon invariant mass distributions of the J / ψ at 1.2 < y J / ψ < 2.2 (left) and − 2.2 < y J / ψ < − 1.2 (right) with the their fits are shown above.
Figure 1. The dimuon invariant mass distributions of the J / ψ at 1.2 < y J / ψ < 2.2 (left) and − 2.2 < y J / ψ < − 1.2 (right) with the their fits are shown above.
Preprints 76427 g001
Preprints 76427 g002
Figure 2. The definitions of four different rapidity measurements of the J / ψ with respect to the silicon tracklet measurements and the physics processes involved are illustrated above.
Figure 2. The definitions of four different rapidity measurements of the J / ψ with respect to the silicon tracklet measurements and the physics processes involved are illustrated above.
Preprints 76427 g002
Preprints 76427 g003
Figure 3. The J / ψ reconstructed from the north muon arm 1.2 < y J / ψ < 2.2 (left) and the south muon arm − 2.2 < y J / ψ < − 1.2 (right) are shown above. The J / ψ normalized signal yields R ( J / ψ ) from the dimuon channel are presented as function of normalized charged particle multiplicity N c h / 〈 N c h 〉 measured by FVTX and SVX. In addition, we show the results when J / ψ and the charged particles in the same directions with the dimuon contribution subtracted. In terms of color convention, the FVTX north data is in red, FVTX south data is in blue, SVX is in magenta, and the dimuon subtracted results are in magenta. These four sets data points are all overlaid with each other in the same figure.
Figure 3. The J / ψ reconstructed from the north muon arm 1.2 < y J / ψ < 2.2 (left) and the south muon arm − 2.2 < y J / ψ < − 1.2 (right) are shown above. The J / ψ normalized signal yields R ( J / ψ ) from the dimuon channel are presented as function of normalized charged particle multiplicity N c h / 〈 N c h 〉 measured by FVTX and SVX. In addition, we show the results when J / ψ and the charged particles in the same directions with the dimuon contribution subtracted. In terms of color convention, the FVTX north data is in red, FVTX south data is in blue, SVX is in magenta, and the dimuon subtracted results are in magenta. These four sets data points are all overlaid with each other in the same figure.
Preprints 76427 g003
Preprints 76427 g004
Figure 4. The J / ψ normalized yield as a function of normalized charged particle multiplicity of PHENIX, STAR [40], and ALICE [38] are all shown above. To make our results comparable with STAR and ALICE data, we present the measurements where J / ψ and tracklets are both in the north (green, left) and the south (blue, right). STAR uses the RHIC p + p data at s = 200 GeV to reconstruct J / ψ from dielectron channel and the charged particle multiplicity, both measured at mid-rapidity region | y | < 1 (orange). ALICE carries out both middle rapidity | y | < 0.9 with the SPD tracklets and forward rapidity 2.5 < y < 4 with the V0 tracklets from J / ψ → e + e − channel. All results above include daughter lepton tracks from J / ψ decay in the event multiplicity.
Figure 4. The J / ψ normalized yield as a function of normalized charged particle multiplicity of PHENIX, STAR [40], and ALICE [38] are all shown above. To make our results comparable with STAR and ALICE data, we present the measurements where J / ψ and tracklets are both in the north (green, left) and the south (blue, right). STAR uses the RHIC p + p data at s = 200 GeV to reconstruct J / ψ from dielectron channel and the charged particle multiplicity, both measured at mid-rapidity region | y | < 1 (orange). ALICE carries out both middle rapidity | y | < 0.9 with the SPD tracklets and forward rapidity 2.5 < y < 4 with the V0 tracklets from J / ψ → e + e − channel. All results above include daughter lepton tracks from J / ψ decay in the event multiplicity.
Preprints 76427 g004
Preprints 76427 g005
Figure 5. In the figure, same muon arms and FVTX directions are used for J / ψ and charged particle tracklet reconstructions. J / ψ in the forward (green) and backward (blue) rapidities and PYTHIA 8 simulations without d i m u o n subtraction (left) and with dimuon subtraction (right) are shown above. The PYTHIA 8 simulations present four different combinations, Monash Tune and Detroit Tune with MPI option on and off, to directly study MPI with the data.
Figure 5. In the figure, same muon arms and FVTX directions are used for J / ψ and charged particle tracklet reconstructions. J / ψ in the forward (green) and backward (blue) rapidities and PYTHIA 8 simulations without d i m u o n subtraction (left) and with dimuon subtraction (right) are shown above. The PYTHIA 8 simulations present four different combinations, Monash Tune and Detroit Tune with MPI option on and off, to directly study MPI with the data.
Preprints 76427 g005
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated