Dynamically Tunable Deflection of Radiation Based on Epsilon-Near-Zero Material

1. Materials and Methods

The proposed structure, consisting of three-dimensional (3D) ITO disk with height (H) of 400 nm and diameter (D) of 600 nm, as schematically shown in the inset of Figure 1a. The nonlinear material, composed of ITO, is illuminated by a plane wave with an electric field ${\mathbf{E}}_{\mathrm{inc}}\left(\mathbf{r},\omega \right)=(E_0/2)e^{i\left(\mathbf{k}·\mathbf{r}-\omega t\right)}{\mathbf{e}}_x+\mathrm{c}.\mathrm{c}.$, where $\left|\mathbf{k}\right|=2\pi /\lambda$ is the wavenumber, $\omega$ is the angular frequency, $E_0$ denotes the amplitude of incident field, and c.c. signifies the complex conjugate. $I_0=\frac{1}{2}c{\epsilon }_0{\left|E_0\right|}^2$ is the free-space intensity of the incident plane wave. The intensity-dependent refractive index of ITO, denoted as $n_{\mathrm{NL}}\left(\mathbf{r},\omega \right)$, is approximately equal to the square root of the nonlinear permittivity ${\epsilon }_{\mathrm{NL}}\left(\mathbf{r},\omega \right)$, where $n_{\mathrm{NL}}\left(\mathbf{r},\omega \right)$ is given by [18,19]

$$n_{\mathrm{NL}}\left(\mathbf{r},\omega \right)\approx \sqrt{{\epsilon }_{\mathrm{L}}+\stackrel{3}{\sum _{j=1}}{c}_{2j+1}{\chi }^{(2j+1)}\left(\omega \right){\left|\frac{\mathbf{E}\left(\mathbf{r},\omega \right)}{2}\right|}^{2j}},$$

(1)

Here, ${\chi }^{\left(3\right)}\left(\omega \right)$, ${\chi }^{\left(5\right)}\left(\omega \right)$, and ${\chi }^{\left(7\right)}\left(\omega \right)$ are the third-order, fifth-order, and seventh-order nonlinear susceptibilities (refer to Table 1 in Ref. [19]) of ITO, respectively. The degeneracy factors are given by $c_3=3,c_5=10,c_7=35$ [18]. The electric field inside the ITO is denoted by $\mathbf{E}\left(\mathbf{r},\omega \right)$. The real part of the dielectric constant $\epsilon$ of ITO is zero at 1240 nm that is the ENZ wavelength ${\lambda }_{ENZ}$ [14,19]. As per the relationship between refractive index and permittivity ($n=\sqrt{\epsilon }$), a change of $\Delta \epsilon$ in the permittivity $\epsilon$ leads to a change of $\Delta n$. Consequently, ITO exhibits strong nonlinear optical properties when the permittivity becomes small. 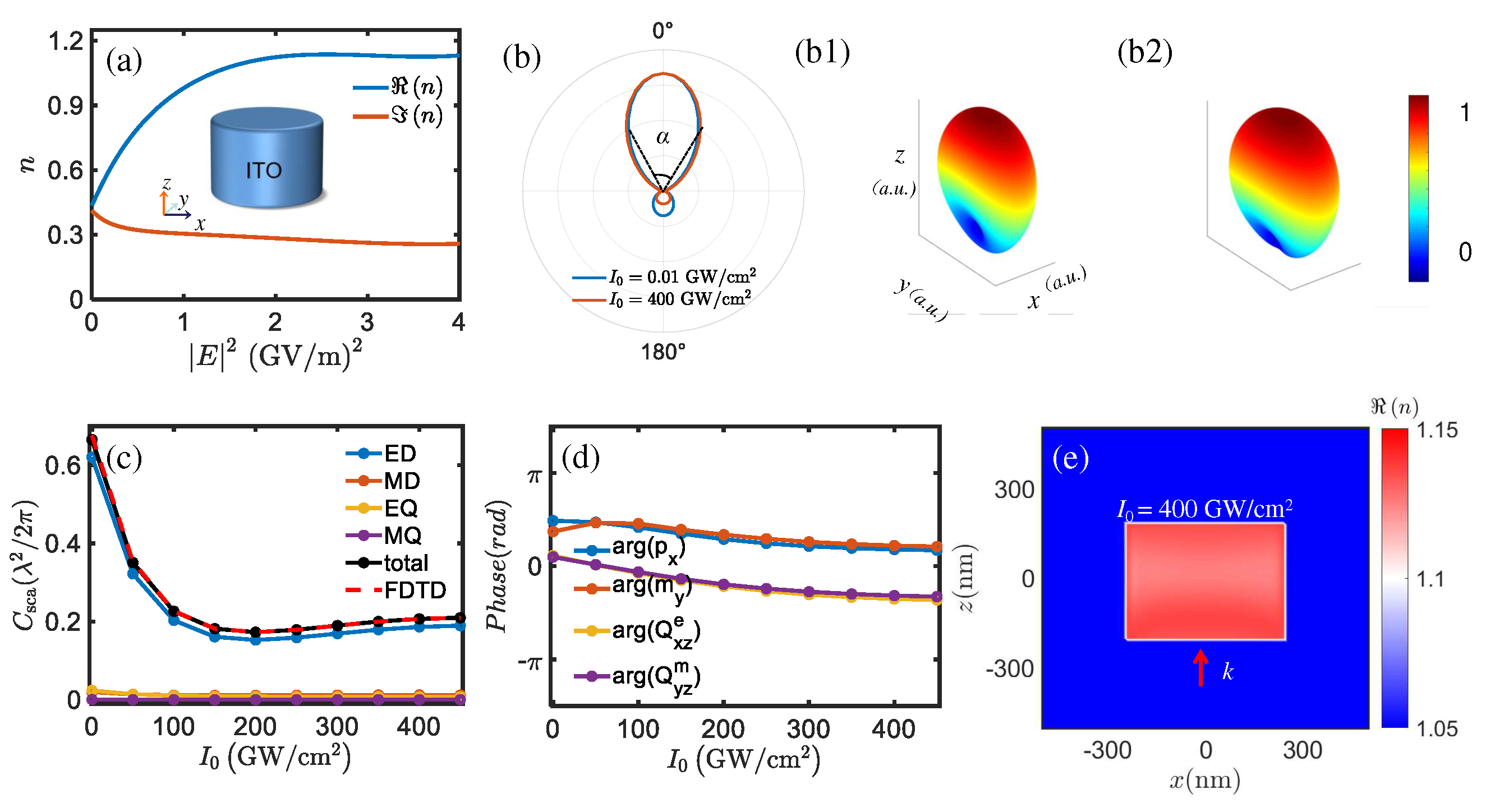Figure 1a illustrates the intensity-dependent refractive index of a single ITO at ${\lambda }_{ENZ}$ [14,19]. The change in the real part of the refractive index with intensity is approximately 0.72, while the linear refractive index is 0.4.

The optical response of radiation pattern can be described using the multipole expansion of the induced displacement current ${\mathbf{J}}_{NL}(r,\omega )=-i\omega \left[{ϵ}_{NL}(\mathbf{r},\omega )-{ϵ}_0\right]\mathbf{E}(\mathbf{r},\omega )$ [9,20]. The excited multipole can be obtained by the induced nonlinear displacement current ${\mathbf{J}}_{NL}$. The multipole expansion, introduced by [9,20], is given as follows:

$$\begin{array}{cc}\hfill p_{\alpha }& =-\frac{1}{i\omega }\left\{\int d^3\mathbf{r}{J}_{\alpha ,\mathrm{NL}}{j}_0\left(kr\right)\right.\hfill \\ \hfill & \left.+\frac{k^2}{2}\int d^3\mathbf{r}\left[3\left(\mathbf{r}·{\mathbf{J}}_{\mathrm{NL}}\right)r_{\alpha }-r^2{J}_{\alpha ,\mathrm{NL}}\right]\frac{j_2\left(kr\right)}{{\left(kr\right)}^2}\right\},\hfill \\ \hfill m_{\alpha }& =\frac{3}{2}\int d^3\mathbf{r}{\left(\mathbf{r}\times {\mathbf{J}}_{\mathrm{NL}}\right)}_{\alpha }\frac{j_1\left(kr\right)}{kr},\hfill \\ \hfill Q_{\alpha \beta }^{\mathrm{e}}& =-\frac{3}{i\omega }\left\{\int d^3\mathbf{r}\left[3\left(r_{\beta }{J}_{\alpha ,\mathrm{NL}}+r_{\alpha }{J}_{\beta ,\mathrm{NL}}\right)-2\left(\mathbf{r}·{\mathbf{J}}_{\mathrm{NL}}\right){\delta }_{\alpha \beta }\right]\right.\hfill \\ \hfill & \frac{j_1(kr}{kr}+2k^2\int d^3\mathbf{r}[5r_{\alpha }{r}_{\beta }(\mathbf{r}·{\mathbf{J}}_{\mathrm{NL}})-(r_{\alpha }{J}_{\beta ,\mathrm{NL}}+r_{\beta }{J}_{\alpha ,\mathrm{NL}})r^2\hfill \\ \hfill & -r^2(\mathbf{r}·{\mathbf{J}}_{\mathrm{NL}}){\delta }_{\alpha \beta }\left]\frac{j_3\left(kr\right)}{{\left(kr\right)}^3}\right\},\hfill \\ \hfill Q_{\alpha \beta }^m& =15\int d^3\mathbf{r}\left\{r_{\alpha }{\left(\mathbf{r}\times {\mathbf{J}}_{\mathrm{NL}}\right)}_{\beta }+r_{\beta }{\left(\mathbf{r}\times {\mathbf{J}}_{\mathrm{NL}}\right)}_{\alpha }\right\}\frac{j_2\left(kr\right)}{{\left(kr\right)}^2},\hfill \end{array}$$

(2)

where $\alpha ,\beta \in x,y,z$, $p_{\alpha }$, $m_{\alpha }$, $Q_{\alpha \beta }^e$, and $Q_{\alpha \beta }^m$ are the electric dipole (ED), magnetic dipole (MD), electric quadrupole (EQ), and magnetic quadrupole (MQ) multipole moments, respectively. $j_n\left(kr\right)$ is the nth spherical Bessel function. The total scattering cross section can be calculated using the following expression [9,20]

$$\begin{array}{ccc}\hfill C_{\mathrm{sca}}& =& \frac{k^4}{6\pi {\epsilon }_0^2{\left|E_0\right|}^2}\left[\sum _{\alpha }\left({\left|p_{\alpha }\right|}^2+{\left|\frac{m_{\alpha }}{c}\right|}^2\right)\right.\hfill \\ & & \left.+\frac{1}{120}\sum _{\alpha ,\beta }\left({\left|k{Q}_{\alpha \beta }^e\right|}^2+{\left|\frac{k{Q}_{\alpha \beta }^m}{c}\right|}^2\right)\right],\hfill \end{array}$$

(3)

which is the contribution of each multipole moment (marked ’total’ in Figure 1c and Figure 2c). The far field corresponding to the radiation pattern ($\propto {\left|\mathbf{E}\right|}^2$) in space is

$$\begin{array}{ccc}\hfill \mathbf{E}& \approx & \frac{k^2}{4\pi \epsilon }{p}_x\frac{e^{ikr}}{r}\left(-sin\phi \widehat{\phi }+cos\theta cos\phi \widehat{\theta }\right)\hfill \\ & -& \frac{k^2}{4\pi \epsilon }\frac{\sqrt{{\epsilon }_r}{m}_y}{c}\frac{e^{ikr}}{r}\left(sin\phi cos\theta \widehat{\phi }-cos\phi \widehat{\theta }\right)\hfill \\ & -& \frac{k^2}{4\pi \epsilon }\frac{ik{Q}_e}{6}\frac{e^{ikr}}{r}\left(-sin\phi cos\theta \widehat{\phi }+cos2\theta cos\phi \widehat{\theta }\right)\hfill \\ & -& \frac{k^2}{4\pi \epsilon }\frac{ik{Q}_m}{6c}\frac{e^{ikr}}{r}\left(-sin\phi cos2\theta \widehat{\phi }+cos\theta cos\phi \widehat{\theta }\right),\hfill \end{array}$$

(4)

Here, r, $\theta$, and $\phi$ represent the spherical coordinates. k is the wavenumber, c is the speed of light.

2. Results

We utilized the finite difference time domain (FDTD) to analyze the two-dimensional (2D) far-field radiation patterns at $I_0=0.01$$\mathrm{GW}/{\mathrm{cm}}^2$ and $I_0=400$$\mathrm{GW}/{\mathrm{cm}}^2$, respectively. For the simulations, periodic boundary conditions are employed along the x and y axes, while perfectly matched layer (PMLs) were used along the z axis. A single plane wave source at 1240 nm was employed for normal incidence. To ensure accurate results, the mesh size is optimized after conducting a converging test. The corresponding three-dimensional (3D) radiation pattern are presented in Figure 1(b1,b2). The changes observed in the scattering cross section in Figure 1c can be attributed to the contribution of different multipole moments, as described by Eq. (2). At an incident intensity of $I_0=400$$\mathrm{GW}/{\mathrm{cm}}^2$, the main lobe width of radiation pattern slightly increases compared to $I_0=0.01$$\mathrm{GW}/{\mathrm{cm}}^2$. This variation is due to the different electric field distributions associated with distinct local electromagnetic modes within the ITO structure, which can be calculated using an iteration method. The refractive index, $n=n(\mathbf{r}$) [see Figure 2d], has varying effects on each multipole moment. The enhanced forward scattering is achieved when the oscillating dipole and quadrupole modes are in phase [21]. Therefore, the induced ED, MD, and MQ moments (normalized to ${\lambda }^2/2\pi$) interfere constructively (destructively) in the forward direction. Consequently, the antenna exhibits a nearly unidirectional radiation pattern with small backscattering, known as generalized Kerker effect [21]. Hence, the observed slight differences in the backward radiation pattern are entirely due to the varying induced electric and magnetic multipole moments calculated by Eq. (2) [see Figure 1c]. Importantly, the scattering cross section calculated using FDTD demonstrate excellent agreement with the results obtained from the multipole expansion described in Eq. (3). The findings highlight the advantages capabilities of an ENZ-based antenna in controlling the radiation pattern($\propto {\left|\mathbf{E}\right|}^2$). Here, $\mathbf{E}$ is calculated by Eq. (4). When both electric/magnetic dipole and quadrupole coexist, the so-called generalized Kerker condition can be expressed as

$$\begin{array}{c}\hfill c{p}_x-m_y+\frac{ik}{6}c{Q}_{xz}^e-\frac{ik}{6}{Q}_{yz}^m\end{array}$$

(5)

The phase can be obtained using arg($p_x$), arg($m_y$), arg($Q_{ze}^x$ ) and arg($Q_{zm}^y$ ). When dipole and quadrupole oscillate in phase (i.e., “+”), they constructively interference with each other and the resulted scattering pattern will be strongly enhanced along the forward direction. As the intensity increases, ED and MD almost oscillate in phase (red solid line), which satisfy the Kerker effect. Likewise, EQ and MQ nearly meet the generalized Kerker effect. Since the phase difference between the dipole and the quadrupole modes (red dashed line) is about 0.4$\pi$ [see Figure 1d], the backscattering is maximally suppressed (see Figure 1(b1,b2)). Therefore, the far-field radiation of this nanoantenna exhibits almost unidirectionally forward scattering. Different local electromagnetic modes have different electric field distributions, and the distribution in the ITO is not uniform which can be calculated using $iteration$ method. The refractive index $n=n\left(\mathbf{r}\right)$[see Figure 1e] will eventually have different effects on each multipole.

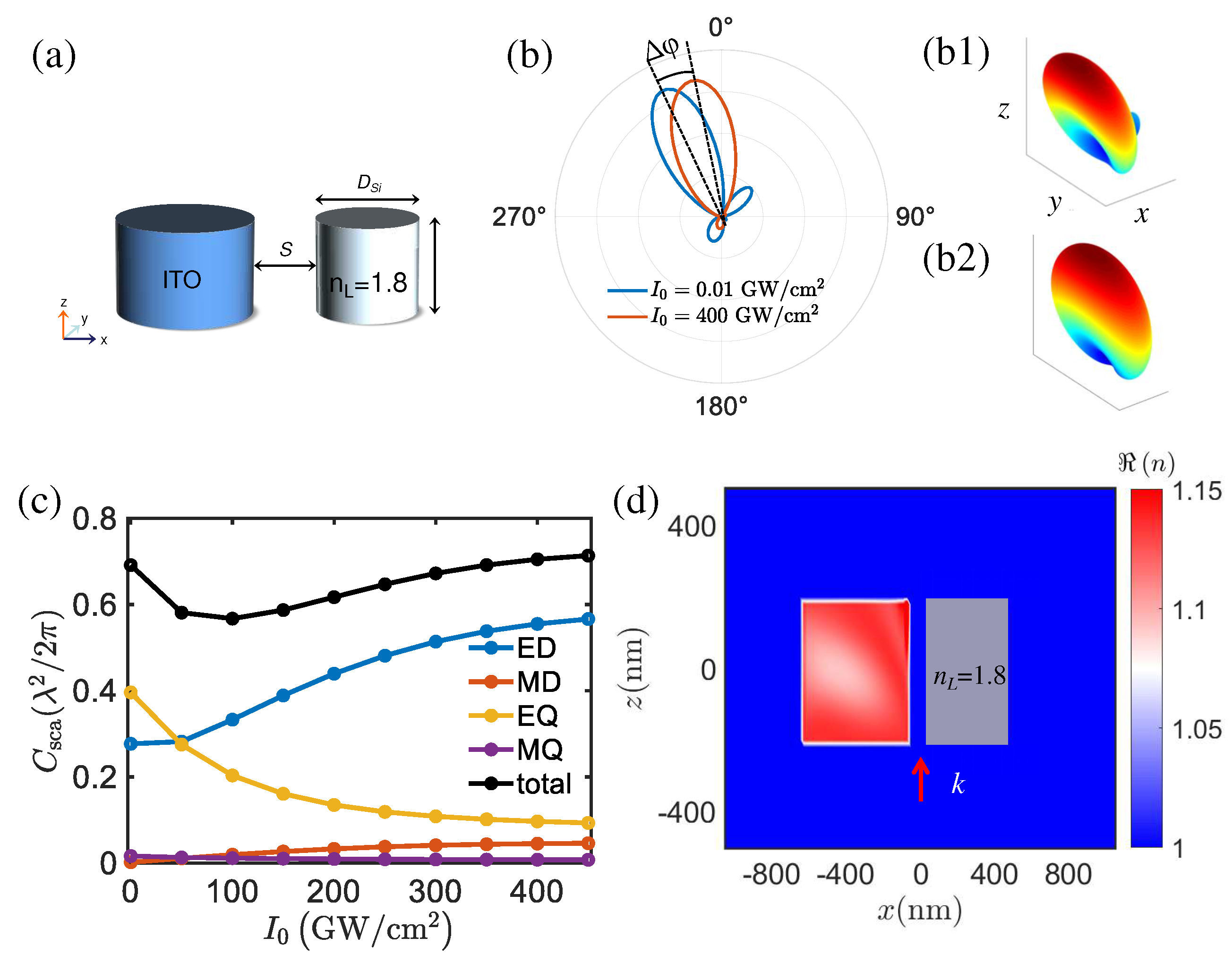
The utilization of high-refractive-index dielectric materials with low loss in antenna design results in a strong electromagnetic response and a significant large scattering cross section [11,22]. To further enhance control over the scattering properties of ITO antennas, we propose a nonlinear antenna composed of both ENZ and lossless dielectric materials. By incorporating a high-refractive-index material ($n_L$=1.8) and ITO nanodisks, a hybrid antenna is created to dynamically adjust the deflection and beamwidth angle of the radiation pattern. The optimized configuration consists of ITO ($D_{ITO}=600$ nm, $H_{ITO}=400$ nm) and dieletric material ($D_L=400$ nm, $H_L=400$ nm) with a separation distance of 100 nm, as depicted in Figure 2a. The dispersion angle in the $xz$ plane, denoted as $\Delta \phi$, is illustrated in Figure 2b. When the incident intensity gradually increases from $I_0=0.01$$\mathrm{GW}/{\mathrm{cm}}^2$ to $I_0=400$$\mathrm{GW}/{\mathrm{cm}}^2$, the radiation main lobe undergoes noticeable deflection, and the deflection angle $\Delta \varphi$ is ${16}^{\circ }$. The corresponding 3D radiation pattern calculated using Eq. (4) are presented in Figure 2(b1,b2). The varying intensities lead to difference in the multipole moments, resulting in intensity-dependent magneto-electric coupling [see Figure 2c]. Specifically, as the intensity increases, the contribution of the ED moment gradually increases, while the EQ moment decreases. The MD and MQ remain constant in the scattering cross section. The induced ED, MD, EQ and MQ moments interfere constructively (destructively), thereby, altering the radiation pattern, as observed in Figure 2b. In comparision with other methods of adjusting the angle size [23], our approach offers the advantage of achieving the deflection angle solely by changing the light intensity, with a maximum change of ${17}^{\circ }$ in the deflection angle. Additionally, in Figure 2d, we present the real part of the refractive index of the hybrid antenna in $xz$-plane when $I_0=400$$\mathrm{GW}/{\mathrm{cm}}^2$. The refractive index is position-dependent, influenced by the nonuniform electric field distribution within the antenna and the coupling effect between ITO and linear dielectric material.

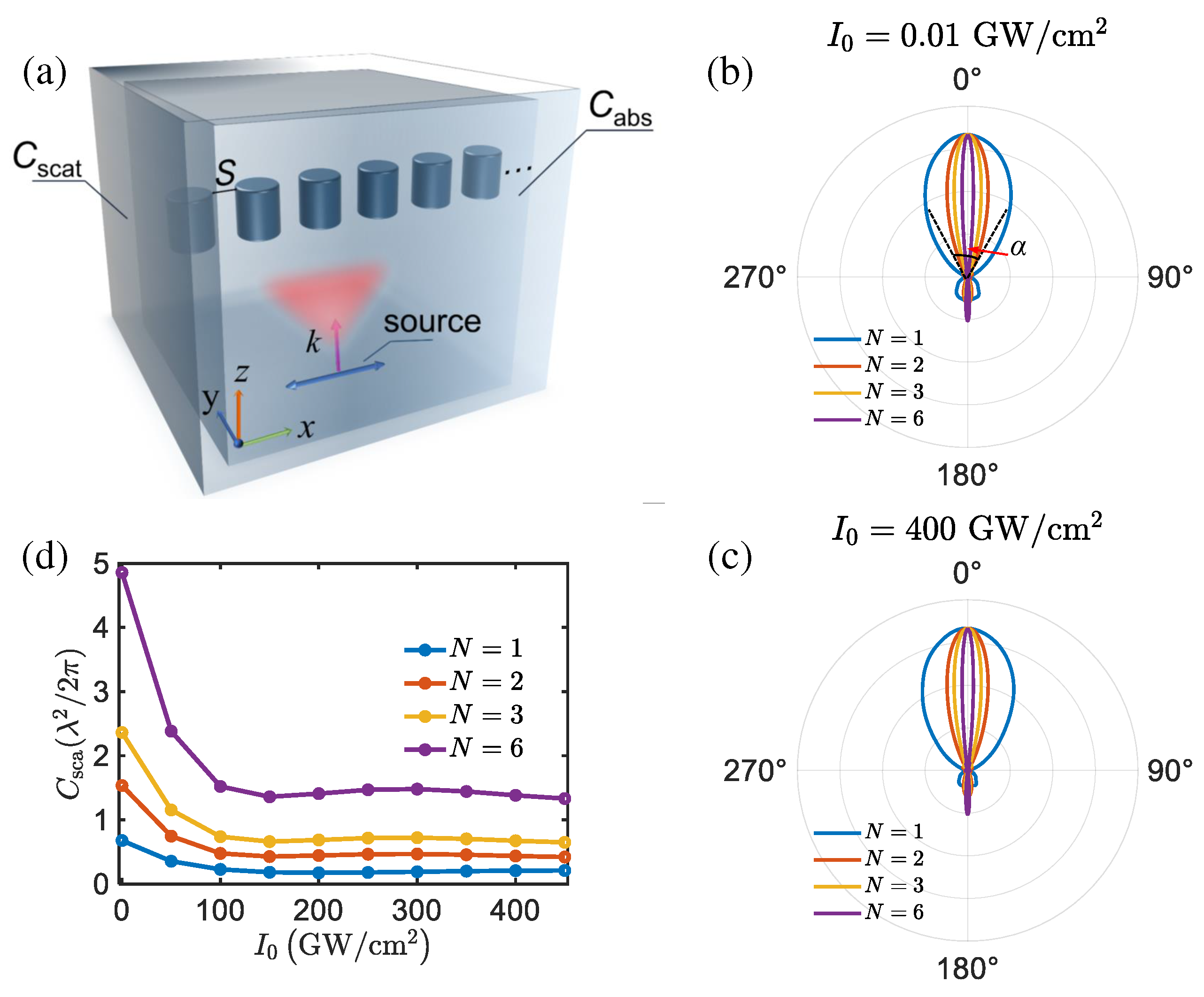
Figure 3a schematically illustrate a linear chain of ITO disks aligned along the x-axis. The normalized radiation pattern for different quantities of ITO disks are presented in Figure 3b,c at $I_0=0.01$$\mathrm{GW}/{\mathrm{cm}}^2$ and $I_0=400$$\mathrm{GW}/{\mathrm{cm}}^2$, respectively. As the number of ITO disks increases, the width of the main lobe in radiation decreases decreases. This trend is observed in both cases. Specifically, the angular beamwidth of the main lobe, denoted as $\alpha$, decrease from $61.{75}^{\circ }$ to $8^{\circ }$. This reduction indicates reduced energy leakage in the undesired directions, attributed to the constructive interference among dominant multipolar moments. The sharp angular beamwidth $\alpha$ of the main lobe signifies improved scattering directivity. Further increasing the number of ITO disks does not yield significant changes in the radiation pattern. The main lobe progressively achieves a high level of directivity, with ($\alpha$ approaching $3^{\circ }$) as more pairs of nanodisks are added. Consequently, the scattering cross section increases with the the number of ITO disks, as demonstrated in Figure 3d.

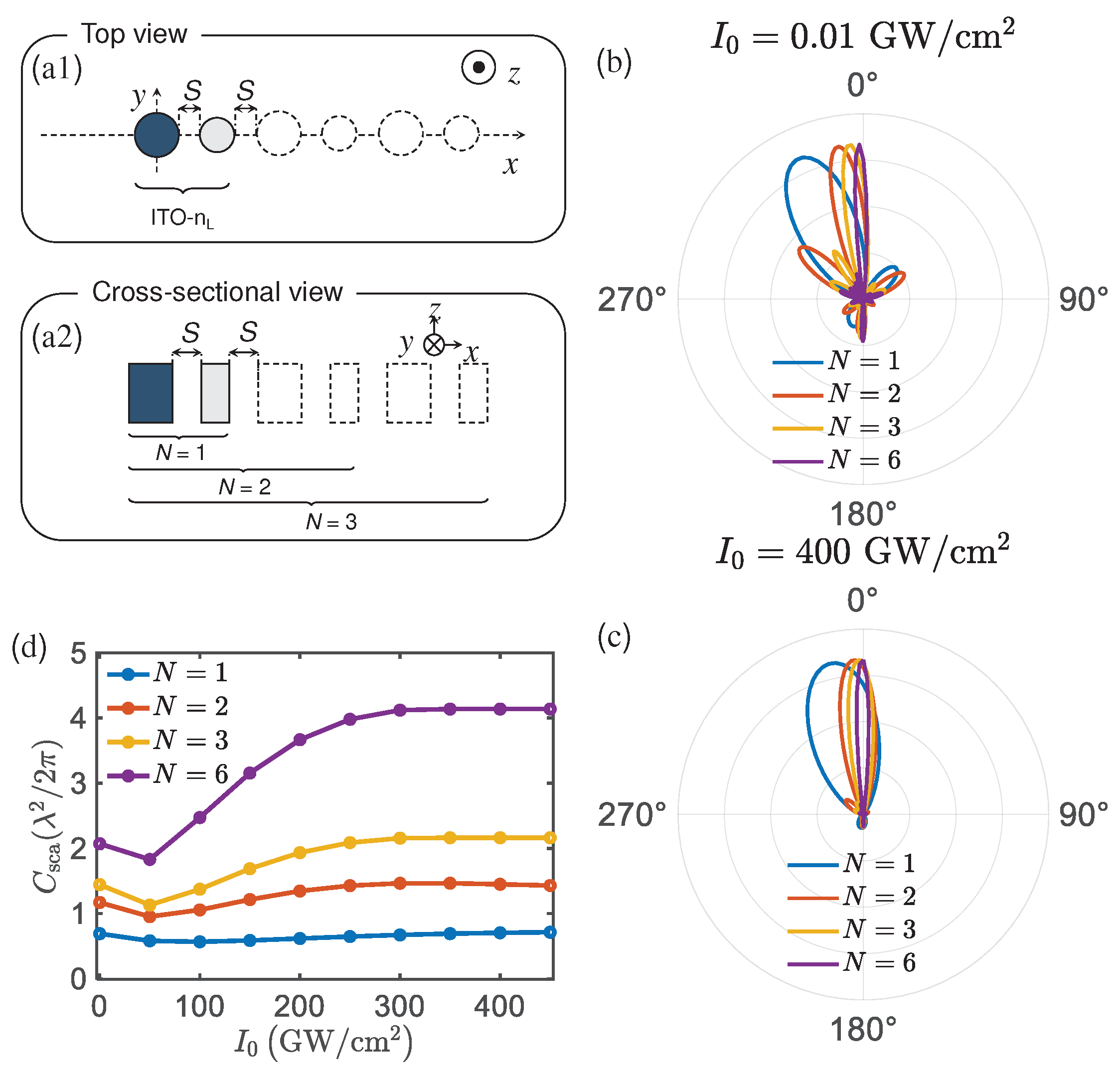
Finally, the influence of number of hybrid structure on radiation pattern is investigated, schematically illuminated in Figure 4(a1,a2). The radiation patterns are shown in Figure 4b,c at $I_0=0.01$$\mathrm{GW}/{\mathrm{cm}}^2$ and $I_0=400$$\mathrm{GW}/{\mathrm{cm}}^2$ in XZ plane, respectively. The deflection of 3D radiation patterns is prominent in XZ plane. A larger deflection is apparent for $I_0=0.01$$\mathrm{GW}/{\mathrm{cm}}^2$ when compared to $I_0=400$$\mathrm{GW}/{\mathrm{cm}}^2$. The deflection starts lowering for intensities larger than $0.01$$\mathrm{GW}/{\mathrm{cm}}^2$. Here, we only pay attention to the variation in XZ plane. For $N=1,2,3$ and 6, the deflection angle $\Delta \phi$ in $xz$ plane is ${16}^{\circ },6^{\circ }$, $4.5^{\circ }$ and $1.5^{\circ }$ from $I_0=0.01$$\mathrm{GW}/{\mathrm{cm}}^2$ to $I_0=400$$\mathrm{GW}/{\mathrm{cm}}^2$, respectively. The main lobe angular beamwidth $\alpha$ is significantly reduced as N increases. When $N\ge 2$, the influence on its deflection angle is reduced. To realize a practical application, at least 6 groups hybrids to be integrated into one design after simulation. Generally, the radiation pattern response, such as main lobe and deflection angle, of the finite structure will sustain in a comparable tunable response with that of ideal periodic structure. Therefore, it is possible to form micro-scale units with The proposed d design. Significantly, when added the hybrid group, the variation of the deflection angle gradually becomes smaller as the input intensity increases. The scattering cross section will increase as the the number of hybrid antenna increases as shown in Figure 4d. The 400 $\mathrm{GW}/{\mathrm{cm}}^2$ is very high and difficult to achieve practically. In fact, the refractive index does not change much after the intensity exceeds 100 $\mathrm{GW}/{\mathrm{cm}}^2$.

3. Conclusions

In conclusion, we have presented a novel approach for achieving an active control over the deflection angle of radiation patter using ENZ material. Initially, we investigated the influence of incident light intensity on the radiation pattern of a single ITO structure, leveraging its strong Kerr effect. By comparing the results with the single ITO case, we then proposed a structured hybrid nano-antenna that exhibits distinct radiation patterns, accompanied by a dispersion angle of ${17}^{\circ }$ as the light intensity increases. Furthermore, as the number of ITO or hybrid antenna groups is increased, the width of the radiation main lobe decrease, offering potential application in light beam directivity control. Notably, the addition of hybrid antenna groups leads to a reduction in the deflection angle as the intensity increases. These actively tunable nanoantennas introduce a new degree of freedom for controlling the far-field radiation pattern based on the significant Kerr effect of ENZ materials.