Prerpints.org logo
Preprint
Article

Item-Oriented Personalized LDP for Discrete Distribution Estimation

Altmetrics

Downloads

222

Views

52

Comments

1

This version is not peer-reviewed

Submitted:

05 June 2023

Posted:

08 June 2023

You are already at the latest version

Alerts
Abstract
Discrete distribution estimation is a fundamental statistical tool, which is widely used to perform data analysis tasks in various applications involving sensitive personal information. Due to privacy concerns, individuals may not always provide their raw information, which leads to unpredictable biases in the final results of estimated distribution. Local Differential Privacy (LDP) is an advanced technique for privacy protection of discrete distribution estimation. Currently, typical LDP mechanisms provide same protection for all items in the domain, which imposes unnecessary perturbation on less sensitive items and thus degrades the utility of final results. Although, several recent works try to alleviate this problem, the utility can be further improved. In this paper, we propose a novel notion called Item-Oriented Personalized LDP (IPLDP), which independently perturbs different items with different privacy budgets to achieve personalized privacy protection. Furthermore, to satisfy IPLDP, we propose the Item-Oriented Personalized Randomized Response (IPRR) based on the observation that the sensitivity of data shows an inverse relationship with the population size of respective individuals. Theoretical analysis and experimental results demonstrate that our method can provide fine-grained privacy protection and improve data utility simultaneously.
Keywords: 
Subject: Computer Science and Mathematics  -   Other

1. Introduction

Discrete distribution estimation is widely used as a fundamental statistics tool and has achieved significant performance in various data analysis tasks, including frequent pattern mining [1], histogram publication [2], and heavy hitter identification [3]. With the deepening and expansion of application scenarios, these data analysis tasks inevitably involve more and more sensitive personal data. Due to the privacy concerns, individuals may not always be willing to truthfully provide their personal information. When dealing with such data, however, discrete distribution estimation is difficult to play its due role. For instance, a health organization plans to make statistics about two epidemic diseases: HIV and Hepatitis, so they issued a questionnaire survey containing three options: HIV, Hepatitis, and None, to inquire whether the citizens suffer from these two diseases. Undoubtedly, this question is highly sensitive, especially for people who actually have these two diseases. As a result, they have a high probability to give false information when filling the the questionnaire, and this will eventually lead to unpredictable biases in the estimation of the distribution of diseases. Therefore, under the requirement of privacy protection, how to conduct discrete distribution estimation is increasingly drawn the attention of researchers.
Differential Privacy (DP) [4,5] is an advanced and promising technique for privacy protection. Benefiting from its rigorous mathematical definition and lightweight computation demand, DP has rapidly become one of the trend in the field of privacy protection. Generally, we can categorize DP into Centralized DP (CDP) [5,6,7,8,9] and Local DP (LDP) [10,11,12]. Compared with the former, the latter does not require a trusted server, and hence it is much more appropriate for privacy protection in the tasks of the discrete distribution estimation. Based on Randomized Response (RR) [13] mechanism, LDP provides different degrees of privacy protection through the assignment of different privacy budget. Currently, typical LDP mechanisms, such as K-ary RR (KRR) [14] and RAPPOR [15], perturb all items in the domain with the same privacy budget, thus providing uniform protection strength. However, in practical scenarios, each item’s sensitivity is different rather than fixed, and the number of individuals involved is also inversely proportional to their sensitivity level. For example, in the questionnaire mentioned above, HIV undoubtedly has a much higher sensitivity than Hepatitis, but a relatively less population of individuals with it than that of the latter. Additionally, None is a non-sensitive option, which naturally accounts for the largest population. Therefore, if we provide privacy protection for all items at the same level without considering their distinct sensitivity, unnecessary perturbation will be imposed on those less sensitive (and even non-sensitive) items that account for a much more population, which severely degrades the data utility of the final result.
Recently, several works proposed to improve the utility by providing different levels of protection according to various sensitivities of items. Murakami et al. introduced the Utility-Optimized LDP (ULDP) [16], which partitions personal data into sensitive and non-sensitive data and ensures privacy protection for the sensitive data only. While ULDP have better utility than KRR and RAPPOR by distinguishing sensitive data from non-sensitive data, it still protects all the sensitive data at the same level without considering the different sensitivities among them. After that, Gu et al. proposed the Input-Discriminative LDP (ID-LDP) [17], which further improved utility by providing fine-grained privacy protection for items with different privacy budgets of inputs. However, under ID-LDP, the strength of perturbation is severely restricted by the minimum privacy budget. As the minimum privacy budget decreases, the corresponding perturbations imposed on different items will approach the maximum level, which greatly weakens the improvement of utility brought by differentiating handling for each item with a independent privacy budget, thereby limiting the applicability of this method.
Therefore, the current methods of discrete distribution estimation in local privacy setting leave much room to improve the utility. In this paper, we propose a novel notion of LDP named Item-Oriented Personalized LDP (IPLDP). Unlike previous works, IPLDP independently perturbs different items with different privacy budgets to achieve personalized privacy protection and utility improvement simultaneously. Through independent perturbation, the strength of perturbation imposed on those less sensitive items will never be influenced by the sensitivity of others. To satisfy IPLDP, we propose a new mechanism called Item-Oriented Personalized RR (IPRR), and it uses the direct encoding method as in KRR to guarantee the equivalent protection for inputs and outputs simultaneously.
Our main contributions are:
1.
We propose a novel LDP named IPLDP, which independently perturbs different items with different privacy budgets to achieve personalized privacy protection and utility improvement simultaneously.
2.
We propose IPRR mechanism to provide equivalent protection for inputs and outputs simultaneously using the direct encoding method.
3.
By calculating the l 1 and l 2 losses through the unbiased estimator of the gound-truth distribution under IPRR, we theoretically prove that our method has tighter upper bounds than that of existing direct encoding mechanisms.
4.
We evaluate our IPRR on a synthetic and a real-world dataset with the comparison with the existing methods. The results demonstrate that our method has better performance than existing methods in data utility.
The remainder of this paper is organized as follows. Section 2 lists the related works. Section 3 provides an overview of several preliminary concepts. Section 4 presents the definition of IPLDP. Section 5 discusses the design of our RR mechanism and its empirical estimator. Section 6 analyzes the utility of the proposed RR method. Section 7 shows the experimental results. Finally, in Section 8, we draw the conclusions.

2. Related Work

Since DP was firstly proposed by Dwork [4], it has attracted much attention from researchers, and numerous variants of DP have been studied including d-privacy [18], Pufferfish privacy [8], dependent DP [19], Bayesian DP [20], mutual information DP [7], R´enyi DP [21], Concentrated DP [6], and distribution privacy [22]. However, all of these methods require a trusted central server. To address this issue, Duchi et al. [11] proposed LDP, which quickly became popular in a variety of application scenarios, such as frequent pattern mining [12,23,24], histogram publication [25], heavy-hitter identification [3,26], and graph applications [27,28,29]. Based on RR [13] mechanism, LDP provides different degrees of privacy protection through the assignment of privacy budget. Currently, typical RR mechanisms, such as KRR [14] and RAPPOR [15], perturb all items in the domain with the same privacy budget, thus providing uniform protection strength.
In recent years, several fine-grained privacy methods have been developed for both centralized and local settings. For example, in the centralized setting, Personalized DP [30,31], Heterogeneous DP [32], and One-sided DP [33] have been studied. In the local setting, Murakami et al. proposed ULDP [16], which partitions the value domain into sensitive and non-sensitive sub-domains. While ULDP optimizes utility by reducing perturbation on non-sensitive values, it does not fully consider the distinct privacy requirements of sensitive values. Gu et al. introduced ID-LDP [17], which protects privacy according to the distinct privacy requirements of different inputs. However, the perturbation of each value is influenced by the minimum privacy budget. As the minimum privacy budget decreases, the perturbations of different items approach the maximum, which degrades the improvement of utility.

3. Preliminaries

In this section, we formally describe our problem. Then, we describe the definitions of LDP and ID-LDP. Finally, we introduce the distribution estimation and utility evaluation methods.

3.1. Problem Statement

A data collector or a server desires to estimate the distribution of several discrete items from n users. The set of all personal items held by these users and its distribution are denoted as D and p ∈ S | D | , respectively, where S stands for a probability simplex and | · | is the cardinality of a set. For each x ∈ D , we use p x to denote its respective probability. We also have a set of random variables X n = { X 1 , . . . , X n } ∈ D held by n users, which are drawn i.i.d. according to p . Additionally, since the items may be sensitive or non-sensitive for users, we divide D into two disjoint partitions: D S , which contains sensitive items, and D N , which contains non-sensitive items.
Because of privacy issues, users perturb their items according to a privacy budget set E = { ε x } x ∈ D S , where ε x is the corresponding privacy budget of x ∈ D S . After perturbation, the data collector can only estimate p from users by observing Y n = { Y 1 , . . . , Y n } which is the perturbed version of X n through a mechanism Q , and the mechanism Q maps an input item x ∈ D to an output y ∈ D with probability Q ( y | x ) .
Our goals are: (1) to design Q that maps inputs ∀ x ∈ D to outputs ∀ y ∈ D according to the corresponding ε y ∈ E , and improves data utility as much as possible; (2) to estimate the distribution vector p from Y n .
We assume that the data collector or the server is untrusted, and users never report their data directly but randomly choose an item from D to send, where D is shared by both the server and users. E should be also public with D , so that users can calculate Q for perturbation, and the server can calibrate the result according to Q .

3.2. Local Differential Privacy

In LDP [11], each user perturbs its data randomly and then send the perturbed data to the server. The server can only access these perturbed results, which guarantees the privacy. In this section, we list two definitions of LDP notions, that is, the standard LDP and the ID-LDP [17].
Definition 1 
( ε -LDP). A randomized mechanism Q satisfies ϵ-LDP if, for any pair of inputs x , x ′ , and any output y:
e − ε ⩽ Q ( y | x ) Q ( y | x ′ ) ⩽ e ε ,
where ε ∈ R + is the privacy budget that controls the level of confidence an adversary can distinguish the output from any pair of inputs. Smaller ε means that an adversary feels less confidence for distinguishing y from x or x ′ , which naturally provides a stronger privacy protection.
Definition 2 
( E -ID-LDP). For a given privacy budget set E = { ε x } x ∈ D ∈ R + | D | , a randomized mechanism Q satisfies E -ID-LDP if, for any pair of inputs x , x ′ ∈ D , and any output y ∈ R a n g e ( Q ) :
e − r ( ε x , ε x ′ ) ⩽ Q ( y | x ) Q ( y | x ′ ) ⩽ e r ( ε x , ε x ′ ) ,
where r ( · , · ) is a system function of two privacy budgets.
Generally, we use E -MinID-LDP in practical scenarios, where r ( ε x , ε x ′ ) = min (
ε x , ε x ′ ) .

3.3. Distribution Estimation Method

The empirical estimation [34] and the maximum likelihood estimation [34,35] are two types of useful methods for estimating discrete distribution in local privacy setting. We use the former method in our theoretical analysis and use both in our experiments. Here, we explain the details of the empirical estimation.

3.3.1. Empirical estimation method

The empirical estimation method calculates the emprical estimate p ^ of p using the empirical estimate m ^ of the distribution m , where m is the distribution of the output of the mechanism Q . Since both p and m are | D | -dimensional vectors, Q can be viewed as a | D | × | D | conditional stochastic matrix. Then, the relationship between p and m can be given by m = p Q . Once the data collector obtains the observed estimation m ^ of m from Y n , the estimation of p can be solved by m ^ = p ^ Q . As n increases, m ^ remains unbiased for m , and hence p ^ converges to p as well. However, when the sample count n is small, some elements in p ^ can be negative. To address this problem, several normalization methods [35] can be utilized to truncate and normalize the result.

3.4. Utility Evaluation Method

In this paper, the l 2 and l 1 losses is utilized for our theoretical analysis of utility. Mathematically, they are defined as l 2 ( p , p ^ ) = ∑ x ∈ D ( p ^ x − p x ) 2 , and l 1 ( p , p ^ ) = ∑ x ∈ D p ^ x − p x . Both l 2 and l 1 losses evaluate the total distance between the estimate value and the ground-truth value. The shorter the distance, the better the data utility.

4. Item-Oriented Personalized LDP

In this section, we first introduce the definition of our proposed IPLDP. Then, we discuss the relationship between IPLDP and LDP. Finally, we compare IPLDP with MinID-LDP.

4.1. Privacy Definition

The standard LDP provides the same level of protection for all items using a uniform privacy budget, which can result in excessive perturbation for less sensitive items and lead to poor utility. To improve the utility, ID-LDP uses distinct privacy budgets for the perturbation of different inputs to provide fine-grained protection. Since all perturbations are influenced by the minimum privacy budget, the strength of all perturbations will be forced to approach the maximum value as the minimum privacy budget decreases. To avoid this problem, IPLDP uses different privacy budgets for outputs of the mechanism to provide independent protection for each item. However, using the output as the protection target may not provide equal protection for the input items. Therefore, in IPLDP, we force the input and output domains to be the same D . Formally, IPLDP is defined as follows.
Definition 3 
( ( D S , E ) -IPLDP). For a privacy budget set E = { ε 1 , ⋯ , ε | D S | } ∈ R + | D S | , a randomized mechanism Q satisfies ( D S , E ) -IPLDP if and only if it satisfies following conditions:
1.
for any x , x ′ ∈ D and for any x i ∈ D S ( i = 1 , ⋯ , | D S | ) ,
e − ε i ⩽ Q ( x i | x ) Q ( x i | x ′ ) ⩽ e ε i ,
2.
for any x ∈ D N and for any x ′ ∈ D ,
Q ( x | x ′ ) > 0 and Q ( x | x ′ ) = 0 for any x ≠ x ′
Since non-sensitive items need no protection, the corresponding privacy budget can be viewed as an infinity value. However, we cannot set the privacy budget to infinity in practice. Hence, inspired by ULDP, IPLDP handles D S and D N separately.
According to the definition, IPLDP guarantees that the adversary’s ability to distinguish any y ∈ D S whether it is from any pair of inputs x , x ′ ∈ D would not exceed the range determined by the respected ε y . That is to say, for ∀ x ∈ D S , it should satisfy ε x -LDP. For ∀ x ∈ D N , It can only be perturbed to any x ∈ D S or itself.

4.2. Relationship with LDP

We hereby assume D = D S . Then, the obvious difference between LDP and IPLDP is the number of the privacy budgets. A special case is that, when all the privacy budgets are identical, i.e. ε x = ε for all x ∈ D , then IPLDP becomes the general ε -LDP. Without loss of generality, on the one hand, if a mechanism that satisfies ε -LDP, it also satisfies ( D , E ) -IPLDP for all E with min { E } = ε . On the other hand, if a mechanism satisfies ( D , E ) -IPLDP, it also satisfies max { E } -LDP. Therefore, IPLDP can be viewed as a relaxed version of LDP. Noticeably, the relaxation does not mean that IPLDP is weaker than LDP in terms of the privacy protection, but LDP is too strong for items with different privacy needs. IPLDP has the ability to guarantee the personalized privacy for each item.

4.3. Comparison with MinID-LDP

According to the definition of notion, the main difference between IPLDP and MinID-LDP lies in the corresponding target of the privacy budget. Our IPLDP controls the distinguishability according to the output, while MinID-LDP focuses on the any pair of inputs. Both notions can be considered as a relaxed version of LDP. However, from Lemma 1 in [17], E -MinID-LDP relaxes LDP in ε = 2 min { E } at most, which means that the degree of relaxation is much lower than IPLDP with the same E . Therefore, as the minimum privacy budget of E decreases, the utility improvement under MinID-LDP is limited, and we will further experimentally verify this in Section 7.

5. Item-Oriented Personalized Mechanisms and Distribution Estimation

In this section, to provide personalized protection, we first propose our IPRR mechanism for the sensitive domain D S = D . We then extend the mechanism to be compatible with the non-sensitive domain D N . Finally, we present the unbiased estimator of IPRR using the empirical estimation method.

5.1. Item-Oriented Personalized Randomized Response

According to our definition of IPLDP, it focuses on the indistinguishability of the mechanism’s output. Then, the input and output domains should keep the same to ensure the equivalent protection for both inputs and outputs. Therefore, the only way to design the mechanism Q is to use the same direct encoding method as in KRR. To use such method, we need to calculate | D | 2 different probabilities for the | D | × | D | stochastic matrix of Q . However, it is impossible to directly calculate these probabilities which make Q invertible and satisfy IPLDP constraints simultaneously. To calculate all the probabilities of Q , a possible way is to find an optimal solution of minimizing the expectation of l 2 ( p ^ , p ) subject to the constraints of IPLDP, i.e.
min Q E Y n ∼ m ( Q ) l 2 ( p ^ , p ) s . t . ln Q ( y | x ) / Q ( y | x ′ ) ⩽ ε y , ( ∀ x , x ′ , y ∈ D ) .
Nevertheless, we still can not directly solve this optimization problem. Firstly, it is complicated to calculate a close-form of Q , since the objective function is likely to be non-convex and all constraints are non-linear inequalities. Secondly, even if we solve this problem numerically, the complexity of each iteration will become very large as the cardinality of the items increases, since we have to calculate an inverse matrix of Q to calculate the objective function in (5).
To address this problem, we reconsider the relationship between the privacy budget and the data utility. The privacy budget determines the indistinguishability of each item, i.e., y ∈ D , by controlling the bound of ln [ Q ( y | x ) / Q ( y | x ′ ) ] for any x , x ′ ∈ D . Among all inputs, the contribution to the data utility comes from the honest answers (when y = x ). Therefore, within the range controlled by the privacy budget, as long as the more honest answer can be distinguished from the dishonest ones, the more the utility can be improved. In other words, the ratio of Q ( x | x ) (denote as q x ) and Q ( x | x ′ ) (denote as q ¯ x ) should be as large as possible within the bound dominated by ε x . Hence, we can reduce the computation complexity of probabilities from | D | 2 to 2 | D | by making a tradeoff of forcing all q ¯ x to be identical for all x ′ ≠ x , and
q x = e ε x q ¯ x , x ∈ D .
Then, we can calculate each element p x of p through each element m x of m for all x ∈ D as follows:
m x = p x q x + ( 1 − p x ) q ¯ x = p x ( e ε x − 1 ) q ¯ x + q ¯ x .
Next, we use the estimate m ^ and p ^ with (7) to calculate our objective function in (5). Since n m ^ x follows the binomial distribution with parameters n and m x , its mean and variance are E ( n m ^ ) = n m x and Var ( n m ^ ) = n m x ( 1 − m x ) . We now can calculate the objective function in (5) according to (7):
E Y n ∼ m ( Q ) ℓ 2 ( p ^ , p ) = ∑ x ∈ D E ( p ^ x − p x ) 2 = ∑ x ∈ D 1 e ε x − 1 2 q ¯ x 2 m x − m x 2 n = ∑ x ∈ D p x e ε x − 1 + 1 n e ε x − 1 2 q ¯ x − ∑ x ∈ D p x e ε x − 1 + 1 2 n e ε x − 1 2 .
The second term and n in (8) can be viewed as constants since they are irrelevant to q ¯ x . Therefore, by omitting these two constants, our final optimization problem can be given as
min { q x , q ¯ x } x ∈ D ∑ x ∈ D p x e ε x − 1 + 1 e ε x − 1 2 q ¯ x s . t . q x + ∑ x ′ ∈ D ∖ { x } q ¯ x ′ = 1 , ∀ x ∈ D .
Since the objective is a convex function of q ¯ x for all x ∈ D and all the constraints are linear equations, we can efficiently calculate all the q x and q ¯ x for all x ∈ D via the Sherman-Morrison formula [36] at the intersection point of the hyper planes formed by the constraints in (9). After solving the linear equaltion groups, we can finally define our Item-Oriented Personalized RR (IPRR) mechanism as follows.
Definition 4 
(( D , E )-IPRR). Let D = { x 1 , ⋯ , x | D | } , E = { ε 1 , ⋯ , ε | D | } ∈ R + | D | , Then ( D , E )-IPRR is a mechanism that maps x ′ ∈ D to x ∈ D with the probability Q IPRR ( x | x ′ ) defined by
Q IPRR ( x | x ′ ) = q x if x = x ′ , q ¯ x otherwise ,
where q ¯ x = [ ( e ε x − 1 ) ( 1 + ∑ x ∈ D S ( e ε x − 1 ) − 1 ) ] − 1 and q x = e ε x q ¯ x .
In addition, the special case is that, when all the elements in E are identical, IPRR becomes KRR.
Theorem 1. 
( D , E )-IPRR satisfies ( D , E ) -IPLDP.

5.2. IPRR with Non-sensitive Items

We hereby present a full version of IPRR that incorporates the non-sensitive domain D N . For all x ∈ D N , privacy protection is not needed, which is equivalent to ε x → ∞ . Thus, to maximize the ratio of q x and q ¯ x , we set q ¯ x to zero. Then, inspired by URR, we define IPRR with the non-sensitive domain as follows.
Definition 5 
(( D S , D N , E )-IPRR). Let D S = { x 1 , ⋯ , x | D S | } , E = { ε 1 , ⋯ ,
ε | D S | } ∈ R + | D S | , then ( D S , D N , E )-IPRR is a mechanism that maps x ∈ D to x i ∈ D with the probability Q IPRR ( x | y ) defined by:
Q IPRR ( x | x ′ ) = q x if x ∈ D S ∧ x = x ′ , q ¯ x if x ∈ D S ∧ x ≠ x ′ , q ˜ if x ∈ D N ∧ x = x ′ , 0 otherwise ,
where q ˜ = 1 − ∑ x ∈ D S q ¯ x = ( 1 + ∑ x ∈ D S 1 e ε x − 1 ) − 1 .
In addition, the special case is that, when all the elements in E are identical (denoted as ε ), it is equivalent to the ( D S , ε ) -URR.
Theorem 2. 
( D S , D N , E ) -IPRR satisfies ( D S , E ) -IPLDP.
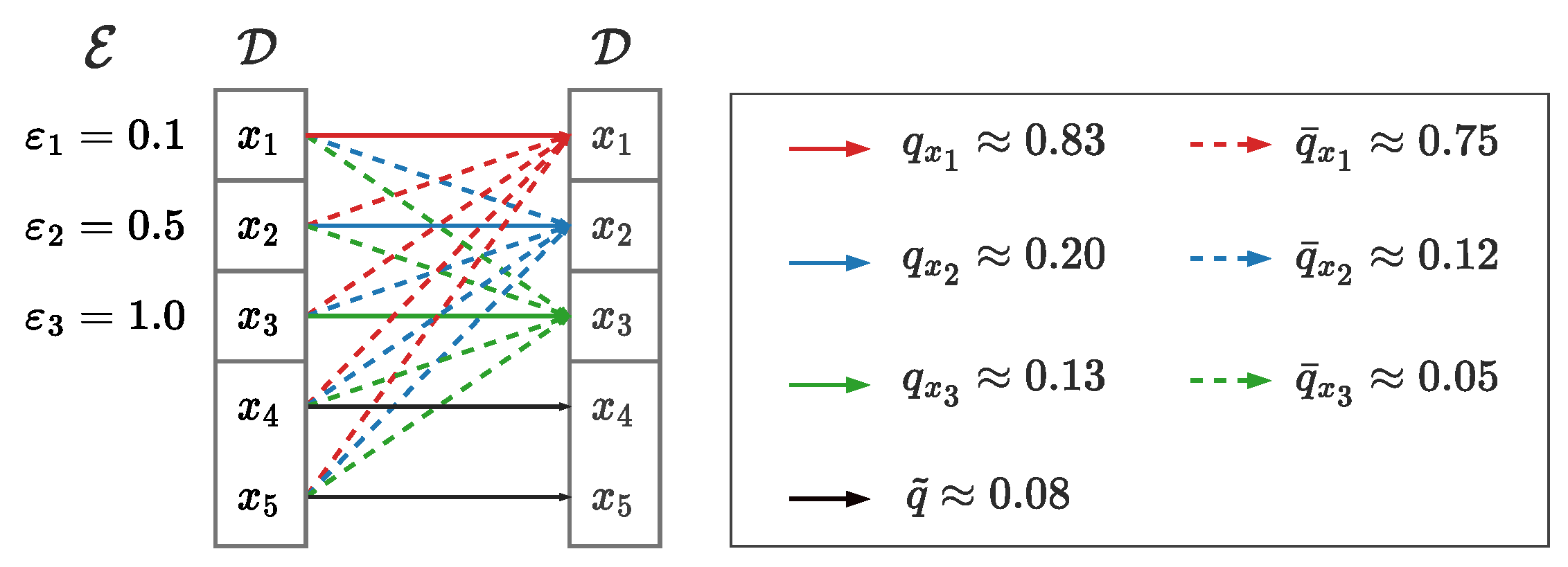
Figure 1 depicts an example of the ( D S , D N , E ) -IPRR, which illustrates the perturbation of our IPRR, and also shows detailed values of all involved probabilities under E = { 0.1 , 0.5 , 1.0 } . As shown in Figure 1, as the privacy budget decreases, users with sensitive items are more honest, which is different from the perturbation style of mainstream RR mechanisms. In those mechanisms, the probability of an honest answer will decrease as the privacy budget decreases. However, data utility is hard to be improved if we follow the mainstream methods to achieve independent personalized protection. Inspired by Mangat’s RR [37], data utility can be further improved through a different style of RR while guaranteeing the privacy as long as we obey the definition of LDP. Mangat’s RR requires users in the sensitive group always answer honestly and uses dishonest answers from other users to contribute to the perturbation. Then, the data collector still can not distinguish one response whether it is an honest answer or not. Furthermore, in practical scenerios, the sensitivity of data shows an inverse relationship with the population size of respective individuals. As a result, indistinguishability can be guaranteed by a large proportion of dishonest responses from less sensitive or non-sensitive groups, even if individuals in the sensitive group are honest. Therefore, in our privacy scheme, we can guarantees the privacy of the clients with improvement of utility as long as both server and clients reach an agreement on this protocol.

5.3. Empirical Estimation under IPRR

In this subsection, we show the details of the emprical estimate of p under our ( D S , D N , E ) -IPRR mechanism. To calculate the estimate, we define a vector r and a function S for convenience, which are given by
r x = 1 e ε x − 1 if x ∈ D S 0 if x ∈ D N , and S · = 1 ∑ x ∈ · r x + 1 ,
where r x is the corresponding element of r to x ∈ D , and “·” can be any domains, i.e., S D S = [ ∑ x ∈ D S r x + 1 ] − 1 . Then, for all x ∈ D S , we have q ¯ x = 1 ( e ε x − 1 ) · 1 ∑ i = 1 | E | ( e ε i − 1 ) − 1 + 1 = r x S D S , and, based on (7), we can calculate m and the estimate p ^ with each element m x and p ^ x for all x ∈ D as
m x = p x S D S + r x S D S ⇒ p ^ x = m ^ x / S D S − r x .
As the sample count n increases, m ^ remains unbiased for m , and hence p ^ converges to p as well.

6. Utility Analysis

In this section, we first evaluate the data utility of IPRR based on the l 2 and l 1 losses of the empirical estimate p ^ . Then, for each loss, we calculate its tight upper bound independent to the unknown distribution p . Finally, we discuss the upper bound in both high and low privacy regimes.
First, we evaluate the expectation of l 2 and l 1 losses under our IPRR mechanism.
Theorem 3. 
( l 2 and l 1 losses of ( D S , D N , E ) -IPRR) According to the Definition 5 and the empirical estimator given in (12), for all E , the expected l 2 and l 1 losses of the ( D S , D N , E ) -IPRR are given by
E [ l 2 ( p , p ^ ) ] = E ∑ x ∈ D ( p ^ x − p x ) 2 = 1 n ∑ x ∈ D ( p x + r x ) S D S − 1 − ( p x + r x ) ,
and for large n,
E [ l 1 ( p , p ^ ) ] = E ∑ x ∈ D p ^ x − p x ≈ 2 n π ∑ x ∈ D ( p x + r x ) ( S D S − 1 − ( p x + r x ) ) ,
where a n ≈ b n represents lim n → ∞ a n / b n = 1 .
According to (13) and (14), we can see that the two losses share the similar structure. Hence, to conveniently discuss the property of the losses, we define a general loss L as follows.
Definition 6 
(general loss of ( D S , D N , E ) -IPRR). The general loss L of ( D S , D N , E ) -IPRR is can be defined as
L ( E ; p , p ^ , D ) = C ∑ x ∈ D g ∘ f x ,
where f x = ( p x + r x ) S D S − 1 − ( p x + r x ) , g is any monotonically increasing concave function with g ( 0 ) = 0 , and C is a non-negative constant.
With this definition, we show that, for any distribution p , privacy budget set E , D S , and D N , both l 2 and l 1 losses of ( D S , D N , E ) -IPRR are lower than that of ( D S , min { E } ) -URR.
Through the assignment of fine-grained privacy budgets to each items in IPRR, the emprical estimator in Section 5.3 is a general version for mechanisms which use the direct encoding method. Due to the generality of our estimator, we can use it to calculate the empirical estimate of URR or KRR as long as all the privacy budgets are identical in E . Therefore, based on the general empirical estimator, (13) and (14) are also applicable to these two mechanisms, even other mechanisms that use direct encoding method. To show that the losses of IPRR are lower than that of URR, we first give a lemma below.
Lemma 1. 
Let · ˜ be a sorted version of any given set ·. For any two privacy budget sets E 1 and E 2 with same dimension k, L ( E 1 ; p , p ^ , D ) ⩽ L ( E 2 ; p , p ^ , D ) , if E 1 ⩽ E 2 , where A ⩽ B stands for that, for all a i ∈ A ˜ and b i ∈ B ˜ ( i = 1 , ⋯ k ) , we have a i ⩽ b i .
Based on Lemma 1, for any distribution p , privacy budget set E , D S , and D N , since E ⩾ { min { E } } ∈ R + | E | , the general loss L of ( D S , D N , E ) -IPRR are lower than that of ( D S , min { E } ) -URR. Since l 2 and l 1 losses are specific versions of L when g ( x ) = x and g ( x ) = x , r e s p e c t i v e l y , both two losses of IPRR also lower than that of URR in the same setting.
Next, we evaluate the worst case of the loss L. Observe that L is closely related to the original distribution p . However, since p is unknown for theoretical analysis, we need to calculate a tight upper bound of the loss that does not depend on the unknown p . Then, to obtain the tight upper bound, we need to find an optimal p that maximizes L. To address this issue, we convert this problem to an optimization problem subject to p being a probability simplex as
max p ∑ x ∈ D g ∘ f x s . t . p ∈ S | D | .
Then, the optimal solution can be given as the following lemma.
Lemma 2. 
Let D * be a subset of D . For all x ∈ D , if r x satisfies
( | D * | S D * ) − 1 − 1 < r x < ( | D * | S D * ) − 1 if x ∈ D * , r x ⩾ ( | D * | S D * ) − 1 otherwise ,
p * is the optimal solution that maximizes the objective function in (16), which is given by
p x * = ( | D * | S D * ) − 1 − r x if x ∈ D * , 0 otherwise .
According to Lemma 2, we can obtain the following general upper bounds of (13) and (14) as
Theorem 4 
(General upper bound of l 2 and l 1 losses of IPRR). Eq. (13) and (14) can be maximized by p * :
E [ l 2 ( p , p ^ ) ] ⩽ E [ l 2 ( p * , p ^ ) ] = 1 n 1 S D 2 − 1 | D * | S D * 2 − ∑ x ∈ D ∖ D * r x 2 ; E [ l 1 ( p , p ^ ) ] ≲ E [ l 1 ( p * , p ^ ) ]
= 2 n π ∑ x ∈ D ∖ D * r x ( S D − 1 − r x ) + S D * − 1 ( | D * | S D − 1 − S D * − 1 ) ,
where a n ≲ b n represents lim n → ∞ a n / b n ⩽ 1 .
Finally, we discuss the losses in the high and low privacy regimes based on the general upper bounds. Let ε min = min { E } and ε max = max { E } .
Theorem 5 
( l 2 and l 1 losses in high privacy regime). When ε max is close to 0, for all x ∈ D , we have e ε x − 1 ≈ ε x . Then, the worst case of l 2 and l 1 losses are:
E [ l 2 ( p , p ^ ) ] ⩽ E [ l 2 ( p * , p ^ ) ] ≈ 1 n ∑ x ∈ D S ∑ x ′ ∈ D S ∖ { x } 1 ε x ε x ′ ;
E [ l 1 ( p , p ^ ) ] ≲ E [ l 1 ( p * , p ^ ) ] ≈ 2 | D S | n π ∑ x ∈ D S ∑ x ′ ∈ D S ∖ { x } 1 ε x ε x ′ .
According to [16], in high privacy regime, the expectation of l 2 and l 1 losses of ( D S , ε min ) -URR are | D S | ( | D S | − 1 ) n ε min 2 and 2 n π · | D S | | D S | − 1 ε min , accordingly. Thus, the losses of our method is much smaller than that of URR in current setting.
Theorem 6 
( l 2 and l 1 losses in low privacy regime). When ε min > ln ( | D N |
+ 1 ) , for all x ∈ D , the worst case of l 2 and l 1 losses are:
E [ l 2 ( p , p ^ ) ] ⩽ E [ l 2 ( p * , p ^ ) ] = ∑ x ∈ D S | D S | + e ε x − 1 | D S | ( e ε x − 1 ) 2 1 − 1 | D | ;
E [ l 1 ( p , p ^ ) ] ≲ E [ l 1 ( p * , p ^ ) ] = 2 ( | D | − 1 ) n π · ∑ x ∈ D S | D S | + e ε x − 1 | D S | ( e ε x − 1 ) .
According to [16], in low privacy regime, the expectation of l 2 and l 1 losses of ( D S , ε min ) -URR are ( | D S | + e ε min − 1 ) 2 n ( e ε min − 1 ) 2 1 − 1 | D | and 2 ( | D | − 1 ) n π · | D S | + e ε min − 1 e ε min − 1 , accordingly. Thus, the losses of our method is much smaller than that of URR in current setting.

7. Evaluation

In this section, we evaluate the performance of our IPRR based on the emprical estimation method with the Norm-sub (NS) truncation method and maximum likelihood estimation (MLE) method, and compare it with the the KRR, URR, and Input-Discriminative Unary Encoding (IDUE) [17] satisfying ID-LDP.

7.1. Experimental Setup

7.1.1. Datasets

We conducted experiments over two datasets, and show their details in Table 1. The first dataset, Zipf, was generated by sampling from a Zipf distribution with an exponential parameter α = 2 , followed by filtering the results using a specific threshold to control the size of the item domain and the number of users. The second dataset, Kosarak, is one of the largest real-world datasets, which contains millions of records related to the click-stream of news portals from users (e.g. see [23,39,40]). For Kosarak dataset, we randomly selected an item for every user to serve as the item they hold, and then applied the same filtering process used for the Zipf dataset.

7.1.2. Metrics

We use Mean Squar Error (MSE) and Relative Error (RE) as the metrics of the performance, which are defined as
MSE = ∑ x ∈ D ( f x − f ^ x ) 2 n , ( ) ∑ x ∈ D | f x − f ^ x | f x ,
where f x (resp. f ^ x ) is the true (resp. estimated) frequency count of x. We take the sample mean of one hundred repeated experiments for analysis.

7.1.3. Settings

We conduct five experiments for both Zipf and Kosarak datasets, where the experiments #1∼#3 compare the utility of IPRR with that of KRR and URR under various privacy level groups with different sample ratios, the experiment #4 compares IPRR with URR under different | D N | , and the experiment #5 compares IPRR with IDUE under different sample ratios. We use S R (sample ratio) to calculate S R · | D | as the sample count n. In each experiment, we evaluate the utility under various privacy levels. Since the sensitivity of data shows an inverse relationship with the population size of respective individuals, we first sort the dataset based on the count of each item, and items with smaller counts are assigned to higher privacy levels. Then, we choose items with larger size as D N (others as D S ) by using N R (non-sensitive ratio), which controls the ratio of | D N | over | D | . For D S , we use ε min , ε max , L C (level count) to divide D S into different privacy levels, where L C divides D S and a range [ ε min , ε max ] evenly to assign the privacy level, accordingly. For example, assume we have D = { A , B , C , D , E , F } with sizes 6, 5, 4, 3, 2, and 1 for each item. Under ε min = 0.1 , ε max = 0.3 , L C = 3 , and N R = 0.5 , we can obtain D N = { A , B , C } , with privacy budgets of 0.3, 0.2, and 0.1 assigned to items D, E, and F, respectively. In practical scenarios, it is unnecessary to assign a unique privacy level to every item. Thus, we set L C = 4 for all experiments in our settings. Additionally, in all experiments, KRR and URR satisfy ε min -LDP and ( D S , D S , ε min ) -ULDP, respectively. Table 2 shows the details of the parameter settings for all experiments.

7.2. Experimental Results

7.2.1. Utility under various privacy level groups

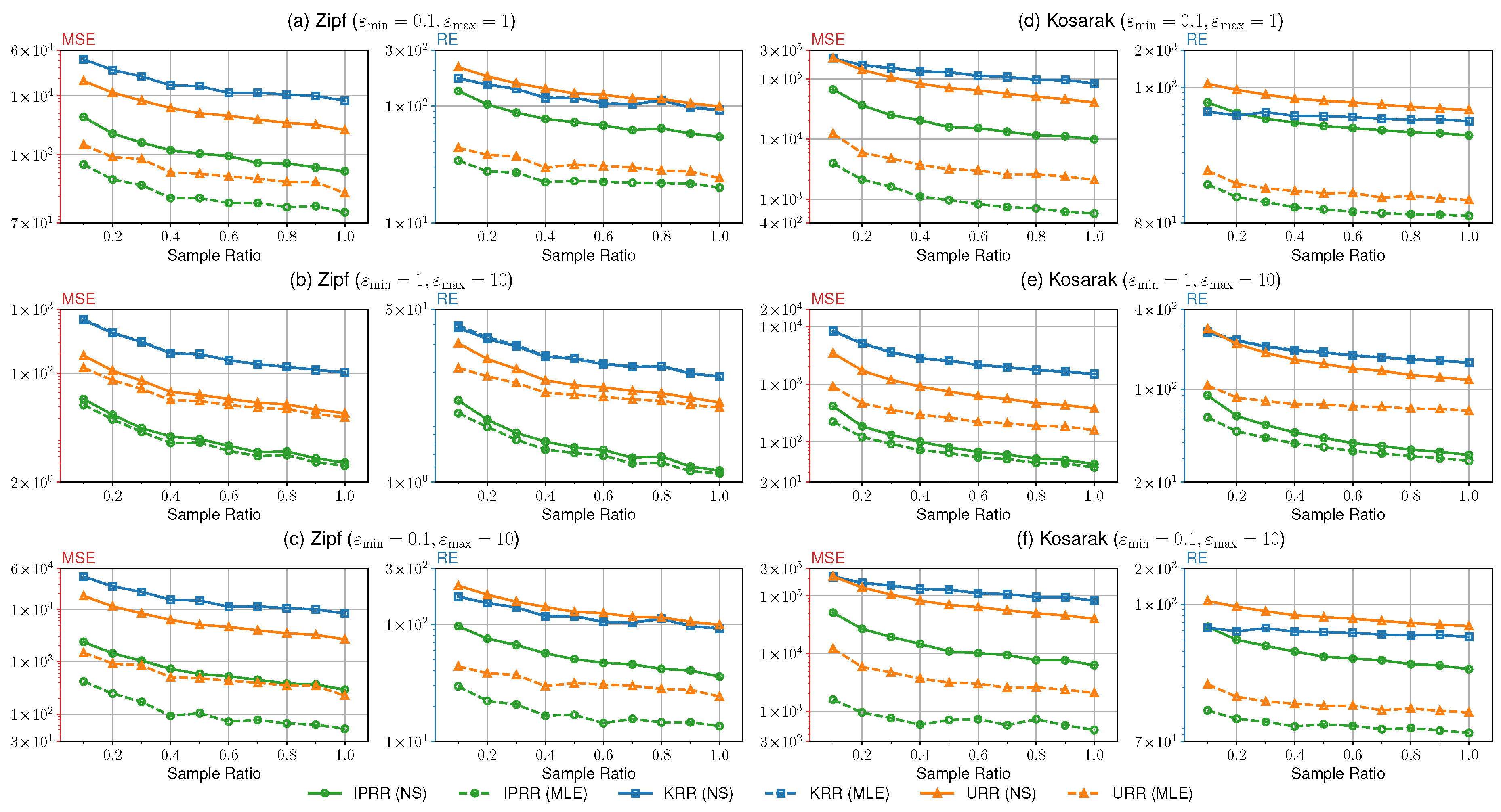
In Figure 2 we illustrate the results of the experiments #1∼#3. We conducted these experiments to compare the utility of our IPRR with other types of direct encoding mechanisms under various combinations of privacy budgets with fixed N R . Fristly, Figure 2(a) and (d) show the comparison of the utility in a high privacy regime among IPRR, URR and KRR on both datasets. As we can see in the high privacy regime, our method outperforms the others by approximate one order of magnitude. As the sample count n increases, the loss decreases as well. Noticeably, in the figure, the results of KRR under both the NS and MLE methods are almost indistinguishable, while our results of the latter method are improved significantly compared with that of the former method. The reason is that the former method may truncate the empirical estimate for lacking samples. Furthermore, the high privacy regime will also escalate the degree of truncation for the emprical estimate, which naturally introduces more errors than the latter method. Secondly, the results of Figure 2(b) and (e) present the comparison of the utility in a low privacy regime. It is clear that our method also has better performance than the others. Notably, in the current setting, the improvement of the MLE method over the NS method is less significant compared with that in the high privacy regime. We argue that a large privacy budget does not result in much truncation for the emprical estimate, so the results are close to each other. Finally, Figure 2(c) and (f) give the results of the hybrid high and low privacy regimes. The results are close to Figure 2(a) and (d), accordingly. Although the improvement is limited in this setting, it does not mean that all perturbations in our method are greatly influenced by the minimum privacy budget similar to IDUE.
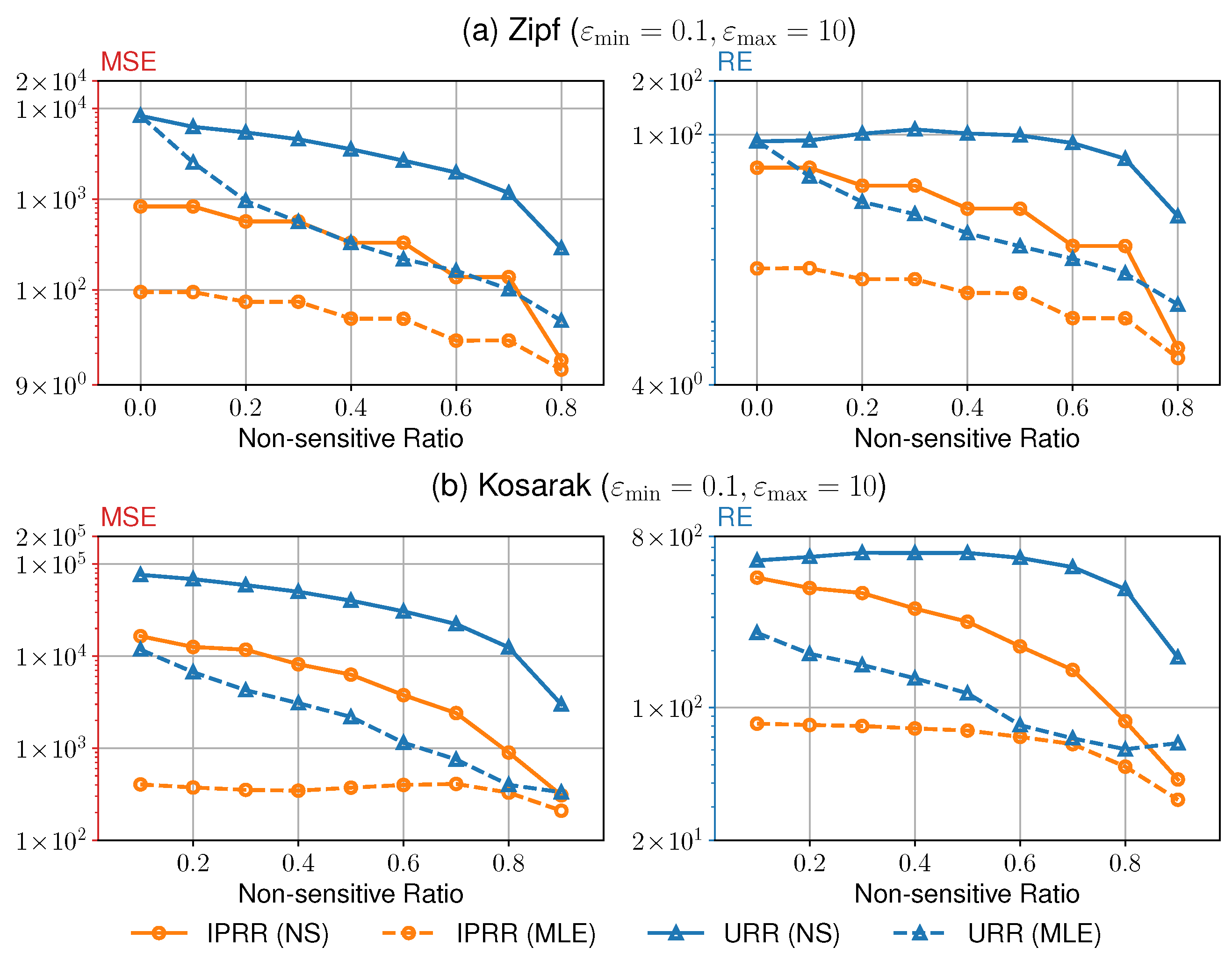
Figure 3 shows the results of the experiment #4. In this experiment, we compare the utility of our IPRR with URR in the same privacy budget set to check the influence of different | D N | . We only compare with URR because only these two mechanisms support non-sensitive items. We restricted the maximum value of N R to 80% for the Zipf dataset since | D S | will be less than L C = 4 if N R exceeds 0.8. As one can see, as | D N | increases, our method outperforms URR, and all metrics decrease.
After all, our IPRR shows better performance than URR and KRR on the two corresponding metrics in the two datasets, which verifies our theoretical analysis. Compared with KRR, URR reduces the perturbation for non-sensitive items by coarsely dividing the domain into sensitive and non-sensitive subsets, resulting in lower variance than that of KRR under the identical sample ratio. Thus, URR has better overall performance than KRR. Our method further divides the sensitive domain into finer-grained subsets with personalized perturbation for each item, which reduces the perturbation for less sensitive items. Therefore, with the same sample ratio, our method reduces much more total variance than URR, and thus our method performs better than other mechanisms.

7.2.2. Comparison with IDUE

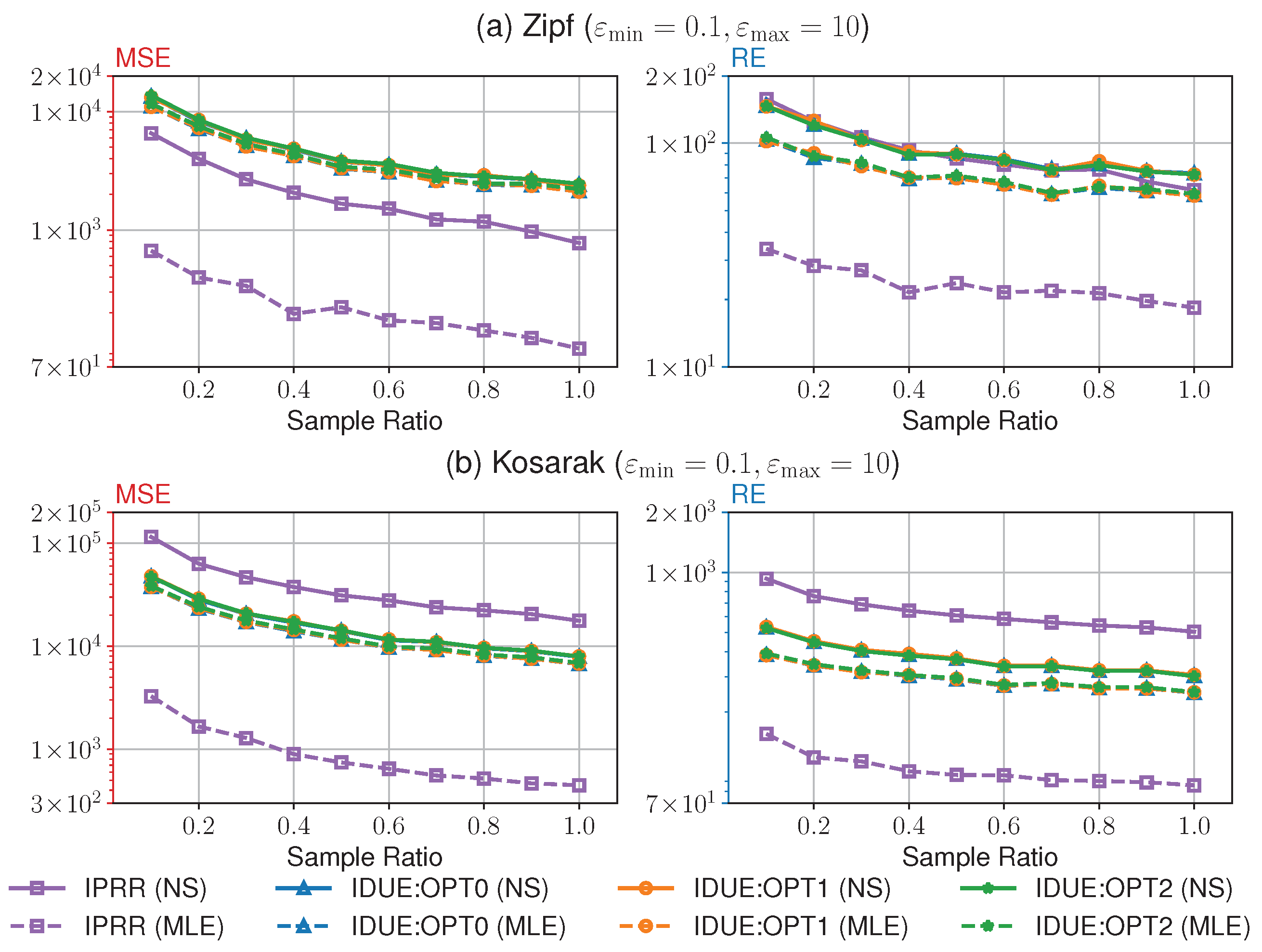
In Figure 4, we show the results of the experiment #5. Since IDUE does not support non-sensitive items, we conducted this separate experiment to compare the utility of our method with IDUE in the same privacy setting. It is clear that IPRR owns better performance than IDUE over Zipf with both NS and MLE methods, while IDUE outperforms IPRR over Kosarak with the NS method. The reason is that the unary encoding method used by IDUE has more advantages when processing an item domain with a larger size, and this may reduce the truncation for the empirical estimate. However, under the MLE method without the influence of truncation, IPRR outperforms IDUE even over Kosarak with the larger | D | . We think that our IPRR effectively reduces unnecessary perturbation for less sensitive items than IDUE since the strength of perturbation is highly affected by the minimum privacy budget. In the current setting of our experiment, the perturbation for items with the maximum privacy budget only needs to satisfy 10-LDP in our method, while IDUE can only relax their perturbation at most 0.2-LDP according to the Lemma 1 in [17].

8. Conclusions

In this paper, we first proposed a novel notion of LDP called IPLDP for discrete distribution estimation in local privacy setting. To improve utility, IPLDP perturbs items independently for personalized protection according to the outputs with different privacy budgets. Then, to satisfy IPLDP, we proposed a new mechanism called IPRR based on a common phenomenon that the sensitivity of data shows an inverse relationship with the population size of respective individuals. We prove that IPRR has tighter upper bound than that of existing direct encoding methods under both l 2 and l 1 losses of emprical estimate. Finally, we conducted related experiments on a synthetic and a real-world datasets. Both theoretical analysis and experimental results demonstrate that our scheme owns better performance than existing methods.

Appendix A. Item-Oriented Personalized LDP

Appendix A.1. Proof of Theorem 1

Proof. 
Since D N = ∅ , we only need to consider (3). Then, since q x / q ¯ x = e ε x , the inequality (4) holds.□ □

Appendix A.2. Proof of Theorem 2

Proof. 
For all x ∈ D S , since q x / q ¯ x = e ε x , the inequality (4) holds. Then, for all x ∈ D N , it follows from (3) that (4) also holds.□ □

Appendix B. Utility Analysis

Appendix B.1. Proof of Theorem 3

Proof. 
1. The l 2 loss of the estimate.
Since n m ^ x follows the binomial distribution with parameters n and m x , its mean and variance are E ( n m ^ ) = n m x and Var ( n m ^ ) = n m x ( 1 − m x ) . Then,
E Y n ∼ m ( Q ) [ l 2 ( p ^ , p ) ] = E ∑ x ∈ D ( p ^ x − p x ) 2 = ∑ x ∈ D E ( p ^ x − p x ) 2 = ∑ x ∈ D E ( m ^ x / S D S − m x / S D S ) 2 = 1 S D S 2 ∑ x ∈ D [ E ( m ^ 2 ) − m 2 ] = 1 S D S 2 ∑ x ∈ D m x − m x 2 n = 1 n S D S 2 ∑ x ∈ D p x S D S + r x S D S − ( p x S D S + r x S D S ) 2 = 1 n ∑ x ∈ D ( p x + r x ) S D S − 1 − ( p x + r x )
2. The l 1 loss of the estimate.
E Y n ∼ m ( Q ) [ l 1 ( p ^ , p ) ] = E ∑ x ∈ D | p ^ x − p x | = 1 S D S ∑ x ∈ D E [ | m ^ − m x | ] = 1 S D S ∑ x ∈ D Var ( n m ^ x ) n E n m ^ x − E ( n m ^ x ) Var ( n m ^ x ) .
It follows from the central limit theorem that n m ^ x − E ( n m ^ x ) Var ( n m ^ x ) converges to the normal distribution N ( 0 , 1 ) . Hence,
lim n → ∞ E Y n ∼ m ( Q ) n m ^ x − E ( n m ^ x ) Var ( n m ^ x ) = 2 n π
Therefore,
E Y n ∼ m ( Q ) [ l 1 ( p ^ , p ) ] ≈ 1 S D S 2 n π ∑ x ∈ D m x − m x 2 = 2 n π ∑ x ∈ D ( p x + r x ) S D S − 1 − ( p x + r x )
□□

Appendix B.2. Proof of Lemma 1

Proof. 
f x = ( p x + r x ) S D S − 1 − ( p x + r x ) = ( p x + r x ) ∑ x ∈ D ∖ { x } r x + 1 − p x .
Then,
∂ f x ∂ r x = ∑ x ∈ D ∖ { x } r x + 1 − p x > 0 , ∂ f x ∂ r x ′ = p x + r x > 0 if x ′ ∈ D ∖ { x } .
Apparently, f x is a monotonically increasing function of r x for all x ∈ D . Then,
∂ L ∂ r x = C g ′ ∘ f x · ∂ f x ∂ r x + C ∑ x ′ ∈ D ∖ { x } g ′ ∘ f x ′ · ∂ f x ′ ∂ r x > 0
Therefore, L is a monotonically increasing function of r x for all x ∈ D . Moreover, due to the loss L is non-negative and r x is a monotonically decreasing function of ε x for x ∈ D , the proposition holds. □ □

Appendix B.3. Proof of Lemma 2

Proof. 
To prove this lemma, we consider a more general optimization problem as
F ( w ) = max θ ∑ i = 1 K g [ ( θ i + c i ) ( C − ( θ i + c i ) ) ] s . t . θ ⊤ 1 = w , 0 ⩽ θ ⩽ 1 w ,
where θ and c are vectors with k-dimension, c is a constant vector, w ∈ ( 0 , 1 ) , and C is a large enough positive constant (e.g. C ≫ c ⊤ 1 + 1 ).
First, we find a proper constant vectors c to obtain the optimal θ without zero elements. Since g is any monotonically increasing concave function with g ( 0 ) = 0 , according to Jensen inequality, we have
∑ i = 1 K g [ ( θ i + c i ) ( C − ( θ i + c i ) ) ] ⩽ g K ∑ i = 1 K [ ( θ i + c i ) ( C − ( θ i + c i ) ) ] ,
where the equality holds iff θ 1 + c 1 = ⋯ = θ K + c K . Hence, to satisfy the equality condition, we have
∑ i = 1 K ( θ i + c i ) = w + ∑ i = 1 K c i ⇒ θ i = w + ∑ j = 1 K c j | k | − c i .
Then, since 0 < θ i < w ,
0 < w + ∑ j = 1 K c j K − c i < w .
Therefore, if all elements of c satisfy
w + ∑ j = 1 K c j K − w < c i < w + ∑ j = 1 K c j K ,
we can ensure that the optimal θ has no zero elements, and the maximum value is
F ( w ) = g K ∑ i = 1 K w + ∑ j = 1 K c j K C − w + ∑ j = 1 K c j K = g K 2 · w + ∑ i = 1 K c i K C − w + ∑ i = 1 K c i K = g w + ∑ i = 1 K c i K C − w + ∑ i = 1 K c i
Next, we consider the general case, where the optimal θ contains zero elements. Let
F ˜ ( w ) = ∑ t = 1 T F ˜ t ( w ) = ∑ t = 1 T g [ ( ( 1 − w ) ϕ t + c t ) ( C − ( ( 1 − w ) ϕ t + c t ) ) ] ,
where c t is a constant which satisfies c t ⩾ w + ∑ i = 1 K c i K , and ϕ t is a constant which satisfies ∑ t = 1 T ϕ t = 1 and 0 < ϕ t < 1 .
Let H ( w ) = F ( w ) + F ˜ ( w ) . Then,
H ′ = F ′ · K C − w + ∑ i = 1 K c i − w + ∑ i = 1 K c i + ∑ t = 1 T ϕ t F ˜ t ′ · [ ( ( 1 − w ) ϕ t + c t ) − ( C − ( ( 1 − w ) ϕ t + c t ) ) ] = K C − 2 w + ∑ i = 1 K c i 1 / F ′ + ∑ t = 1 T 2 [ ( 1 − w ) ϕ t + c t ] − C 1 / ϕ t F ˜ t ′ = ∑ t = 1 T C − 2 w + ∑ i = 1 K c i K T / K F ′ + 2 [ ( 1 − w ) ϕ t + c t ] − C 1 / ϕ t F ˜ t ′ ⩾ ∑ t = 1 T C − 2 w + ∑ i = 1 K c i K + 2 [ ( 1 − w ) ϕ t + c t ] − C max T / K F ′ , 1 / ϕ t F ˜ t ′ = 2 ∑ t = 1 T ( 1 − w ) ϕ t + c t − w + ∑ i = 1 K c i K max T / K F ′ , 1 / ϕ t F ˜ t ′ ⩾ 0 ,
where F ′ = g ′ w + ∑ i = 1 K c i K C − w + ∑ i = 1 K c i , and F ˜ t ′ = g ′ [ ( ( 1 − w ) ϕ t + c t ) ( C − ( ( 1 − w ) ϕ t + c t ) ) ] Since H ′ ⩾ 0 , H ( w ) reaches its maximum when w = 1 .
Finally, because any general case of the optimization problem in this lemma can be convert to the function H, the lemma holds. □ □

Appendix B.4. Proof of Theorem 4

Proof. 
For save the pages, we won’t give the details of the proof, since we just get the result by substituting p * of Lemma 2 into (13) and (14). □ □

Appendix B.5. Proof of Theorem 5

Proof. 
As ε max is close to 0, D * will become D N . Hence, according to Lemma 2, when D * = D N , min { r } = 1 e ε max − 1 > 1 | D N | ⇒ 0 < ε max < ln ( | D N | + 1 ) . In this case, p * = p u , where
p x u = 1 | D N | if x ∈ D N , 0 otherwise .
Therefore,
E Y n ∼ m ( Q ) [ l 2 ( p ^ , p ) ] ⩽ E Y n ∼ m ( Q ) [ l 2 ( p ^ , p u ) ] = 1 n ∑ x ∈ D S r x S D S − 1 − r x + ∑ x ∈ D N 1 | D N | S D S − 1 − 1 | D N | = 1 n ∑ x ∈ D S r x ∑ x ′ ∈ D r x ′ + 1 − r x + ∑ x ∈ D r x + 1 − 1 | D N | ≈ 1 n ∑ x ∈ D S 1 ε x ∑ x ′ ∈ D 1 ε x ′ + 1 − 1 ε x + ∑ x ∈ D 1 ε x + 1 − 1 | D N | = 1 n ∑ x ∈ D S 1 ε x 2 − ∑ x ∈ D S 1 ε x 2 + ∑ x ∈ D 2 ε x + 1 − 1 | D N | ≈ 1 n ∑ x ∈ D S 1 ε x 2 − ∑ x ∈ D S 1 ε x 2 = 1 n ∑ x ∈ D S ∑ x ′ ∈ D S ∖ { x } 1 ε x ε x ′ ,
and
E Y n ∼ Q [ l 1 ( p ^ , p ) ] ⩽ E Y n ∼ Q l 1 p ^ , p u = 2 n π ∑ x ∈ D S r x S D S − 1 − r x + | D N | S D S − 1 − 1 ⩽ 2 n π | D S | ∑ x ∈ D S r x S D S − 1 − r x + | D N | S D S − 1 − 1 ≈ 2 n π | D S | ∑ x ∈ D S 1 ε x ∑ x ′ ∈ D 1 ε x ′ + 1 − 1 ε x + | D N | ∑ x ∈ D 1 ε x + | D N | − 1 ≈ 2 n π | D S | ∑ x ∈ D S 1 ε x ∑ x ′ ∈ D 1 ε x ′ + 1 − 1 ε x = 2 n π | D S | ∑ x ∈ D S 1 ε x 2 + ∑ x ∈ D S 1 ε x − ∑ x ∈ D S 1 ε x 2
≈ 2 n π | D S | ∑ x ∈ D S 1 ε x 2 − ∑ x ∈ D S 1 ε x 2 = 2 n π | D S | ∑ x ∈ D S ∑ x ′ ∈ D S ∖ { x } 1 ε x ε x ′
□□

Appendix B.6. Proof of Theorem 6

Proof. 
According to Lemma 2, when ε min > ln ( | D N | + 1 ) , m is a uniform distribution. In this case, D * = D . Therefore,
E Y n ∼ m ( Q ) [ l 2 ( p ^ , p ) ] ⩽ E Y n ∼ m ( Q ) [ l 2 ( p ^ , p * ) ] = 1 n ∑ x ∈ D ( S D | D | ) − 1 S D S − 1 − ( S D | D | ) − 1 = 1 n | D | ( S D | D | ) − 1 S D S − 1 − ( S D | D | ) − 1 = 1 n S D − 1 S D S − 1 − ( S D | D | ) − 1 = 1 n S D S D S − 1 − ( S D | D | ) − 1 = 1 n S D S 2 1 − 1 | D | ,
and
E Y n ∼ Q [ l 1 ( p ^ , p ) ] ⩽ E Y n ∼ Q l 1 p ^ , p * = 2 n π ∑ x ∈ D ( S D | D | ) − 1 S D S − 1 − ( S D | D | ) − 1 = 2 n π | D | ( S D | D | ) − 1 S D S − 1 − ( S D | D | ) − 1 = 2 n π S D − 1 | D | S D S − 1 − S D − 1 = 2 n π S D − 2 ( | D | − 1 ) = 2 ( | D | − 1 ) n π S D − 1 .
□

References

  1. Han, J.; Pei, J.; Yin, Y. Mining Frequent Patterns without Candidate Generation. SIGMOD Conference. ACM, 2000, pp. 1–12.
  2. Xu, J.; Zhang, Z.; Xiao, X.; Yang, Y.; Yu, G. Differentially Private Histogram Publication. ICDE. IEEE Computer Society, 2012, pp. 32–43.
  3. Wang, T.; Li, N.; Jha, S. Locally Differentially Private Heavy Hitter Identification. IEEE Trans. Dependable Secur. Comput. 2021, 18, 982–993. [Google Scholar] [CrossRef]
  4. Dwork, C. Differential Privacy. ICALP (2). Springer, 2006, Vol. 4052, Lecture Notes in Computer Science, pp. 1–12.
  5. Dwork, C.; McSherry, F.; Nissim, K.; Smith, A.D. Calibrating Noise to Sensitivity in Private Data Analysis. TCC. Springer, 2006, Vol. 3876, Lecture Notes in Computer Science, pp. 265–284.
  6. Bun, M.; Steinke, T. Concentrated Differential Privacy: Simplifications, Extensions, and Lower Bounds. TCC (B1), 2016, Vol. 9985, Lecture Notes in Computer Science, pp. 635–658.
  7. Cuff, P.; Yu, L. Differential Privacy as a Mutual Information Constraint. CCS. ACM, 2016, pp. 43–54.
  8. Kifer, D.; Machanavajjhala, A. Pufferfish: A framework for mathematical privacy definitions. ACM Trans. Database Syst. 2014, 39, 3:1–3:36. [Google Scholar] [CrossRef]
  9. Lin, B.; Kifer, D. Information preservation in statistical privacy and bayesian estimation of unattributed histograms. SIGMOD Conference. ACM, 2013, pp. 677–688.
  10. Chen, R.; Li, H.; Qin, A.K.; Kasiviswanathan, S.P.; Jin, H. Private spatial data aggregation in the local setting. ICDE. IEEE Computer Society, 2016, pp. 289–300.
  11. Duchi, J.C.; Jordan, M.I.; Wainwright, M.J. Local Privacy and Statistical Minimax Rates. FOCS. IEEE Computer Society, 2013, pp. 429–438.
  12. Wang, T.; Li, N.; Jha, S. Locally Differentially Private Frequent Itemset Mining. IEEE Symposium on Security and Privacy. IEEE Computer Society, 2018, pp. 127–143.
  13. Warner, S.L. Randomized response: a survey technique for eliminating evasive answer bias. Publications of the American Statistical Association 1965, 60. [Google Scholar] [CrossRef]
  14. Kairouz, P.; Oh, S.; Viswanath, P. Extremal Mechanisms for Local Differential Privacy. NIPS, 2014, pp. 2879–2887.
  15. Erlingsson, Ú.; Pihur, V.; Korolova, A. RAPPOR: Randomized Aggregatable Privacy-Preserving Ordinal Response. CCS. ACM, 2014, pp. 1054–1067.
  16. Murakami, T.; Kawamoto, Y. Utility-Optimized Local Differential Privacy Mechanisms for Distribution Estimation. USENIX Security Symposium. USENIX Association, 2019, pp. 1877–1894.
  17. Gu, X.; Li, M.; Xiong, L.; Cao, Y. Providing Input-Discriminative Protection for Local Differential Privacy. ICDE. IEEE, 2020, pp. 505–516.
  18. Chatzikokolakis, K.; Andrés, M.E.; Bordenabe, N.E.; Palamidessi, C. Broadening the Scope of Differential Privacy Using Metrics. Privacy Enhancing Technologies. Springer, 2013, Vol. 7981, Lecture Notes in Computer Science, pp. 82–102.
  19. Liu, C.; Chakraborty, S.; Mittal, P. Dependence Makes You Vulnberable: Differential Privacy Under Dependent Tuples. NDSS. The Internet Society, 2016.
  20. Yang, B.; Sato, I.; Nakagawa, H. Bayesian Differential Privacy on Correlated Data. SIGMOD Conference. ACM, 2015, pp. 747–762.
  21. Mironov, I. Rényi Differential Privacy. CSF. IEEE Computer Society, 2017, pp. 263–275.
  22. Kawamoto, Y.; Murakami, T. Differentially Private Obfuscation Mechanisms for Hiding Probability Distributions. CoRR 2018, abs/1812.00939. [Google Scholar]
  23. Chen, Z.; Wang, J. LDP-FPMiner: FP-Tree Based Frequent Itemset Mining with Local Differential Privacy. CoRR 2022, abs/2209.01333. [Google Scholar]
  24. Wang, N.; Xiao, X.; Yang, Y.; Hoang, T.D.; Shin, H.; Shin, J.; Yu, G. PrivTrie: Effective Frequent Term Discovery under Local Differential Privacy. ICDE. IEEE Computer Society, 2018, pp. 821–832.
  25. Bassily, R.; Smith, A.D. Local, Private, Efficient Protocols for Succinct Histograms. STOC. ACM, 2015, pp. 127–135.
  26. Bassily, R.; Nissim, K.; Stemmer, U.; Thakurta, A.G. Practical Locally Private Heavy Hitters. NIPS, 2017, pp. 2288–2296.
  27. Lin, W.; Li, B.; Wang, C. Towards Private Learning on Decentralized Graphs With Local Differential Privacy. IEEE Trans. Inf. Forensics Secur. 2022, 17, 2936–2946. [Google Scholar] [CrossRef]
  28. Qin, Z.; Yu, T.; Yang, Y.; Khalil, I.; Xiao, X.; Ren, K. Generating Synthetic Decentralized Social Graphs with Local Differential Privacy. CCS. ACM, 2017, pp. 425–438.
  29. Wei, C.; Ji, S.; Liu, C.; Chen, W.; Wang, T. AsgLDP: Collecting and Generating Decentralized Attributed Graphs With Local Differential Privacy. IEEE Trans. Inf. Forensics Secur. 2020, 15, 3239–3254. [Google Scholar] [CrossRef]
  30. Jorgensen, Z.; Yu, T.; Cormode, G. Conservative or liberal? Personalized differential privacy. ICDE. IEEE Computer Society, 2015, pp. 1023–1034.
  31. Nie, Y.; Yang, W.; Huang, L.; Xie, X.; Zhao, Z.; Wang, S. A Utility-Optimized Framework for Personalized Private Histogram Estimation. IEEE Trans. Knowl. Data Eng. 2019, 31, 655–669. [Google Scholar] [CrossRef]
  32. Alaggan, M.; Gambs, S.; Kermarrec, A. Heterogeneous Differential Privacy. J. Priv. Confidentiality 2016, 7. [Google Scholar] [CrossRef]
  33. Kotsogiannis, I.; Doudalis, S.; Haney, S.; Machanavajjhala, A.; Mehrotra, S. One-sided Differential Privacy. ICDE. IEEE, 2020, pp. 493–504.
  34. Kairouz, P.; Bonawitz, K.A.; Ramage, D. Discrete Distribution Estimation under Local Privacy. ICML. JMLR.org, 2016, Vol. 48, JMLR Workshop and Conference Proceedings, pp. 2436–2444.
  35. Wang, T.; Lopuhaä-Zwakenberg, M.; Li, Z.; Skoric, B.; Li, N. Locally Differentially Private Frequency Estimation with Consistency. NDSS. The Internet Society, 2020.
  36. Abstracts of Papers. The Annals of Mathematical Statistics 1949, 20, 620–624. [CrossRef]
  37. Mangat, N.S. An Improved Randomized Response Strategy. Journal of the Royal Statistical Society. Series B (Methodological) 1994, 56, 93–95. [Google Scholar] [CrossRef]
  38. "Kosarak dataset".
  39. Wang, T.; Xu, M.; Ding, B.; Zhou, J.; Hong, C.; Huang, Z.; Li, N.; Jha, S. Improving Utility and Security of the Shuffler-based Differential Privacy. Proc. VLDB Endow. 2020, 13, 3545–3558. [Google Scholar] [CrossRef]
  40. Wang, Z.; Zhu, Y.; Wang, D.; Han, Z. FedFPM: A Unified Federated Analytics Framework for Collaborative Frequent Pattern Mining. INFOCOM. IEEE, 2022, pp. 61–70.
Preprints 75721 g001
Figure 1. Item-Oriented Personalized RR with D S = { x 1 , x 2 , x 3 } , D N = { x 4 , x 5 } , and E = { ε 1 , ε 2 , ε 3 } = { 0.1 , 0.5 , 1.0 } . For instance, x 1 = HIV , x 2 = Cancer , x 3 = Hepatitis , x 4 = Flu , and x 5 = None .
Figure 1. Item-Oriented Personalized RR with D S = { x 1 , x 2 , x 3 } , D N = { x 4 , x 5 } , and E = { ε 1 , ε 2 , ε 3 } = { 0.1 , 0.5 , 1.0 } . For instance, x 1 = HIV , x 2 = Cancer , x 3 = Hepatitis , x 4 = Flu , and x 5 = None .
Preprints 75721 g001
Preprints 75721 g002
Figure 2. Utility under Various Privacy Levels.
Figure 2. Utility under Various Privacy Levels.
Preprints 75721 g002
Preprints 75721 g003
Figure 3. Unility under Different N R .
Figure 3. Unility under Different N R .
Preprints 75721 g003
Preprints 75721 g004
Figure 4. Comparison between the IPRR and the IDUE (opt0, opt1, opt2).
Figure 4. Comparison between the IPRR and the IDUE (opt0, opt1, opt2).
Preprints 75721 g004
Table 1. Synthetic and Real-world Datasets.
Table 1. Synthetic and Real-world Datasets.
Datasets # Users # Items
Zipf 100000 20
Kosarak [38] 646510 100
Table 2. Parameter Settings.
Table 2. Parameter Settings.
# Mechanisms
to Compare		 ε min ε max L C N R S R
1 KRR,URR 0.1 1 4 0.5 0.2-1.0
2 KRR,URR 1 10 4 0.5 0.2-1.0
3 KRR,URR 0.1 10 4 0.5 0.2-1.0
4 URR 0.1 10 4 0.0-0.8 *
0.1-0.9 **		 1.0
5 IDUE 0.1 10 4 0 0.1-1.0
* is used on Zipf dataset and ** is used on Kosarak dataset.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated