1. Introduction

2. Method

3. FINDINGS AND COMMENTARY

3.1. Scale Development Studies of the Research

Scale development studies consist of five stages at the theory level. These are; literature review and item pooling, identifying field experts, receiving expert opinions and renewing the item pool, calculating the content validity rates of the revised item pool through the Lawshe technique and creating the original form of the scale (Lawshe, 1975:567; McGartland et al., 2003; Yurdugül, 2005). In this study, the following stages specified by many researchers were followed in order to develop the measurement tool for classroom teachers’ self-efficacy perceptions regarding mathematics learning difficulties (Karasar, 2018).

3.1.1. Substance Pool Process of the Research

The process of creating an item pool started with a large literature search. Domestic and international studies that measure the perception of self-efficacy regarding mathematics learning difficulties have been encountered very rarely, and mostly topics related to general self-efficacy perceptions for courses in schools have been studied. As a result of all these processes, scale items were created to measure the self-efficacy perceptions of classroom teachers about mathematics learning difficulties. In the process of creating the item pool, 3 classroom teachers, 3 mathematics teachers, 2 special education teachers, 1 psychologist working in the Guidance Research Center and 1 director of the Guidance Research Center, a total of 10 people who have previously worked in the field of mathematics learning difficulties or have master’s/doctorate subjects in this field, contributed. Participants were asked to write items related to self-efficacy perception related to mathematics learning disability. In line with the answers received from the participants, scale items were prepared by taking expert opinions from 1 academician in the field of mathematics learning difficulties, 1 in the field of special education, 1 in the field of scale development, and a total of 3 academicians. According to expert opinions in the scale, similar substances, inappropriate for the content and repeated substances were removed from the pool. As a result, 24 precursors were identified. A 5-point Likert type was prepared for the developed scale. Accordingly, the items in the scale were as follows: "Never (1 point) ", "Little (2 points)", "Medium (3 points) ", "Good (4 points)", "Always (5 points)".

3.1.2. Expert Opinion and Scope Validity Rates of the Research

While creating the item pool, the content validity of the items developed at the same time was tested. In this context, experts in their field were used to test. For this, the distribution of field experts formed from academicians and practitioners in the field is shown in Table 1 below.

A total of 24 items were created during the item pool process. The content validity test of these 24 items was performed. 21 field experts were studied on September 2022 (Table 1). Field experts consisted of two groups. The first group is a group of academicians consisting of 1 professor, 2 associate professors, 3 research assistants and a total of 8 people. In the selection of academicians, the criterion of publishing at least one scientific study was taken in mathematics learning difficulty and scale development research. The second group is a group of practitioners consisting of 5 classroom teachers, 4 counselors and psychological counselors, 2 Director/Assistant Director of the Guidance Research Center (RAM), 2 teachers receiving RAM, and a total of 13 people. Participants in the second study group were selected from among those who were trained in learning disability or math learning disability and experienced learning disability in their study areas. The study was conducted face-to-face. According to Lawshe (1975:567), the experts who received the suitability of item structures should be evaluated as "necessary", "corrected" and "unnecessary"; DeVellis (2014:100) stated that the expert group formed in scale development evaluated the originality and comprehensibility of the items. In light of these approaches, expert opinions on the scale items developed to determine the self-efficacy of the teachers participating in the study and content validity rates are given in Table 2 below.

Each item of the content validity rate (CVA) is calculated by the content validity index (CVA) $\frac{N_e-\frac{N}{2}}{\frac{N}{2}}$ formula (N_e: Required; N: Total number of experts; α=0.05) (Lawshe, 1975:567). According to the findings in Table 2, it can be said that the scale and its sub-items are statistically significant since the overall score of the scale is "KGO>0.703" (p<0.05). In addition, according to the Lawshe technique, the minimum value of 0.42, which corresponds to 21 field experts, was taken and the items 21 and 22, which are smaller than this value, were removed from the scale (CVI₂₁=-0.24<0.42; CVI₂₂=0.05<0.42). Based on all these findings, it was determined that the overall scale developed was statistically significant.

3.1.3. Preliminary Application Study of the Research

Pre-application is a very important stage in which the validity and reliability of the developed scale are questioned based on observational data. At this stage, care should be taken to ensure that the sample group to be pre-applied is compatible with the target audience of the research (Mertens, 1998; Büyüköztürk, 2012:143). In the scale development study, a preliminary application study was conducted with 44 teachers in November 2022 with the face-to-face interview technique in Sakarya province after expert opinions and content validity. There are two criteria in the selection of teachers. The first criterion is the presence of students with mathematics learning difficulties in their classes. The second criterion is that he/she has received in-service training on mathematics learning difficulties or has done postgraduate studies in this field. Accordingly, it was observed that teachers answered the developed scale questions in an average of 6 minutes and 41 seconds. They stated that the questions were understood and there was no expression that would challenge the misunderstanding. These results show that the analysis phase can be started without any question changes in the developed draft scale.

3.1.4. Accuracy Control of the Scale in the Study

In order not to affect the validity and reliability analysis results in the scale study, the averages, standard deviations and frequency distributions were investigated and the accuracy was checked. Material errors that may arise from reasons such as leaving questions unanswered, making mistakes in the entry of data, etc. have been checked. As a result of the controls, it was observed that there was no missing data, incorrect data and incorrect data entry-coding.

In the scale study, various parameters were examined to determine whether the data showed normal distribution. In this context, the skewness and kurtosis values and Kolmogorov-Smirnov values of the data were examined. Since our sample size was more than 30 individuals in the study, the Kolmogorov-Smirnov value was taken for the normality criterion. As seen in the findings in Table 5, the skewness and kurtosis values of the variables were in the range of ±2 (George and Mallery: 2010). In addition, as a result of the Kolmogorov-Smirnov test, the variables showed a significance value of less than 5% (p<0.05). According to these results, it was accepted that the data showed a normal distribution.

3.1.5. Construct Validity and Reliability in the Scale

Exploratory factor analysis was performed for the construct validity of the scale. Confirmatory factor analysis was tested according to the structures of the scale obtained with exploratory factor analysis results. In addition to these, the general validity of the scale was tested by conducting a criterion-based validity study with similarity and differentiation validity. In scale development studies, the validity test precedes the reliability test. The reason for this is that while validity is more about accuracy, reliability is more about stability and consistency (Alpar, 2012:412). Reliability is the consistency in measurement repetition or measurement repetition during measurement (Altunışık et al., 2010:122). Reliability is used for the consistency of the items that make up the scale among themselves.

3.1.6. Exploratory Factor Analyses of the Scale

Exploratory Factor Analysis (EFA) was performed to determine the construct validity of the scale and to reveal the factor structure. For this, basic components and direct oblique rotation methods were used. The reason for this is that the method of basic components is the most frequently and easily used method in practice, and the direct oblique rotation method is used when it is considered that there is a relationship between factors (Büyüköztürk, 2012:124-126).

First of all, the Kaiser-Meyer-Olkin (KMO) sample adequacy value was found to be 0.949 and the sample size was found to be sufficient for EFA. It is an index that compares the size of the partial coefficients with the size of the correlation coefficients observed. If the KMO index is less than 0.50, it is unacceptable, it is classified as weak between 0.50-0.59, moderate between 0.60-0.69, good between 0.70-0.79, very good between 0.80-0.89, and excellent between 0.90-1.00 (Büyüköztürk, 2012; Çokluk et al., 2012). The lowest KMO values calculated for each item were found to be 0.902 and confirmed that the sample was sufficient. However, Bartlett’s sphericity relationship test is another index data showing the appropriateness of explanatory factor analysis (Çokluk et al., 2012:208; Güvenç, 2022:71). As a result of the Barlett test, χ2= 2286.609 ~ df = 136, p=0.000<0.001, and this finding showed that the correlation between the items was large enough for EFA.

As seen in Table 4, the first of the horse dimensions consists of 11 items (items 1, 2, 3, 4, 5, 6, 7, 8, 9, 11 and 13) and the second consists of 6 items (items 14, 15, 16, 17, 18, 19). Tabachnick and Fidell (2007:490) stated that an item can be loaded on more than one item. In such cases, considering the difference between the scale items loaded on more than one factor, he states that it would be appropriate to exclude these items from the analysis if the difference takes a value of 0.10 or less. Accordingly, items 10 and 12 were attributed to more than one factor in the scale, and the difference between the factors on which these items were attributed was found to be less than 0.10. These two items were excluded from the analysis. In addition, Büyüköztürk (2012:136) stated that there may be items that do not give a factor load in any dimension. In such cases, he said, it would be appropriate to exclude the relevant items from the analysis. Accordingly, items 20, 21 and 22 in the scale were not attributed to any factor and these three items were excluded from the analysis.

The lowest item loads were determined as 0.508. Therefore, since factor loads of 0.40 and above are considered ideal (Field, 2009:666), it has been evaluated that the factors contribute significantly to the items. As a result of EFA, it was determined that the scale consisting of 17 items had a 2-dimensional (factor) structure and this factor explained 71.34% of the total variance. In addition, the factors were named as "Personal Teaching Competence" and "Instructional Support Competence", respectively.

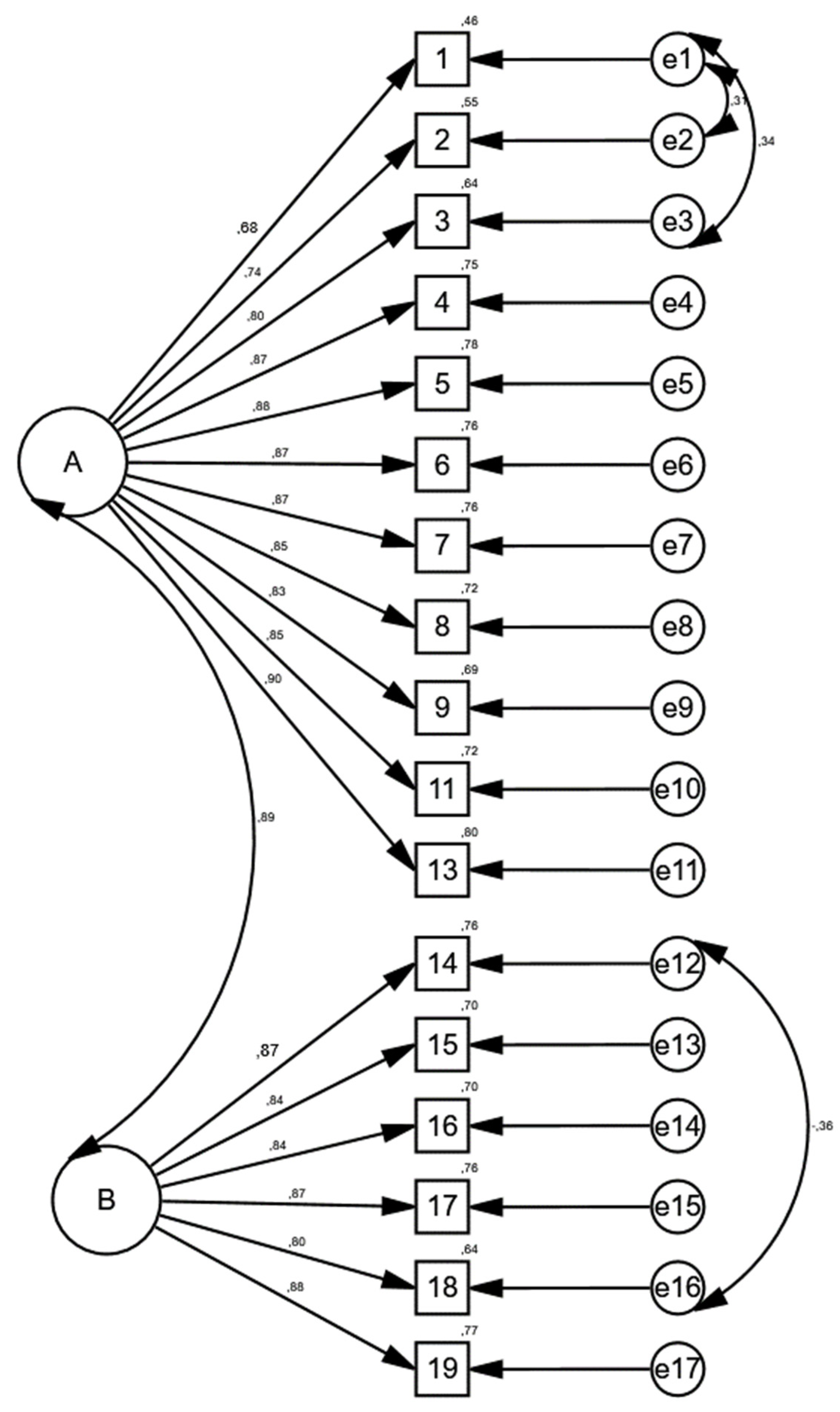
3.1.7. Confirmatory Factor Analyses of the Scale

The factor structure of the statements in the scale developed in the study was determined by exploratory factor analysis. Confirmatory factor analysis (CFA) will be performed at this stage in scale development. Thus, the structural accuracy of the scale can be tested. CFA is a type of structural equation model that determines the relationship between the hidden variables observed in the scale. In scale studies, the adaptation of the scale appears to be an important situation. For this reason, fit indices are used to measure the suitability of the research model with confirmatory factor analysis. Goodness of fit is the overlap value between the covariance matrix estimated in the developed scale and the matrix observed by the research (Raykov and Marcoulides, 2006:27). In the study, RMSEA (Kaya, 2014:36), Cmin/df (Tabachnick and Fidell, 2007:488), GFI (Çapık, 2014: 200), CFI (Elderlyoğlu, 2017: 81), NFI (Kaya, 2014: 36) and TLI (Gürbüz and Şahin, 2016:338) values were taken as criteria for the scale development goodness of fit test.

Table 5 summarizes the acceptable and perfectly acceptable fit indices of goodness of fit criteria values:.

Table 5. Goodness of Fit Metrics and Reference Values.

Table 5. Goodness of Fit Metrics and Reference Values.

Fit Indices	CFA Results	CFA Results	Conclusion	Acceptable fit indices	Excellent fit indices
CMIN/DF	1,904	1,568	Excellent	2 ≤ Cmin/DF ≤ 5	0 ≤ Cmin/DF ≤ 2
GFI	0.877	0.909	acceptable?	0,90 ≤ GFI ≤ 0,95	0,95 ≤ GFI ≤ 1,00
CFI	0.947	0,975	Excellent	0,90 ≤ CFI ≤ 0,95	0,95 ≤ CFI ≤ 1,00
NFI	0.904	0,934	acceptable?	0,90 ≤ GFI ≤ 0,95	0,95 ≤ GFI ≤ 1,00
TLI	0,936	0,966	Excellent	0,90 ≤ TLI ≤ 1,00	0,95 ≤ TLI ≤ 1,00
RMSEA	0,092	0.067	acceptable?	0.05 ≤ RMSEA ≤ 0.08	0,00 ≤ RMSEA ≤ 0,05
χ2=158.4; df=101;

Source: Schermelleh-Engel, Moosbrugger, & Müller, (2003).

According to the data in Table 5, the goodness of fit values of the confirmatory factor analysis are seen in the evaluation scale for managers’ performance program applications. Modifications were made to reach good fit values in confirmatory factor analysis. In this context, modifications were made between the error terms e1 and e2 and e1 and e3 in the items of the personal teaching competence factor, and between the error terms e12 and e16 in the items of the educational support competence factor. As a result of the modification analysis made from here, it was seen that the goodness of fit values of the model; GFI, NFI and RMSA values have acceptable good fit values, and Cmin/df, CFI and TLI and values have excellent acceptable good fit values (Schermelleh-Engel, Moosbrugger and Müller, 2003).

The CFA and goodness of fit test values of the criteria used to test the structural accuracy of the scale developed in the study are given in Figure 1 below (A: Personal teaching competence factor; B: Educational support competence factor).

In Figure 1C, Teacher Self-Efficacy Scale Confirmatory Factor Analysis in the Field of Learning Difficulty in Mathematics.

Figure 1 shows the confirmatory factor analysis and path graph of the teacher self-efficacy scale in the field of mathematics learning disability. Factor loadings of the confirmatory factor analysis of the teacher self-efficacy scale in the field of mathematics learning disability were found to be between 0.68 and 0.90 for the personal teaching competence factor. Here, the factor load of the first question of the Personal teaching competence factor is 0.68. The expected value is at least 0.70 or close to the factor load. However, considering other factor loads, 0.68 is considered to be negligible and acceptable (Schermelleh-Engel, Moosbrugger and Müller, 2003). It was determined that it varied between 0.80 and 0.88 for the educational support adequacy factor. In addition, the significance values of the regression weights obtained as a result of confirmatory factor analysis were less than 0.05. According to these results, we can say that the items are loaded correctly to the factors.

4. Conclusion and Recommendations

References

1. Akkoyunlu, B. , Orhan, F., & Umay, A. (2005). Computer teaching self-efficacy scale for computer teachers. Hacettepe University Journal of Education Faculty, 29, 1-8.
2. Allinder. R. M. (1995). An examination of the relativity between teacher effectiveness and curriculum based measurement and student achievement. Remedial & Special Education. 27.141-152.
3. Alpar, R. (2012). Applied Statistics and Validity-Reliability with Examples from Sports Health and Educational Sciences, Ankara: Detay Publishing.
4. Altunışık, R. , Coşkun, R., Bayraktaroğlu, S. and Yıldırım, E. (2010). |||UNTRANSLATED_CONTENT_START|||Sosyal Bilimlerde Araştırma Yöntemleri, SPSS Uygulamalı. |||UNTRANSLATED_CONTENT_END|||Sakarya: Sakarya Yayıncılık.
5. Arabacı, Ö. (2018). Examination of the Knowledge Levels and Opinions of Classroom Teacher Candidates on Special Learning Difficulties, Unpublished Master’s Thesis. Gaziantep University, Gaziantep.
6. Aydın, N. (2008). The effect of classroom level, seniority and value orientations on the self-efficacy beliefs of classroom teacher candidates and teachers towards environmental education. (Published master thesis) Aydın: Adnan Menderes University Institute of Social Sciences.
7. Balcı, E. (2019). Teachers’ opinions about dyslexia and the problems they face. Aegean Education Journal, 20(1), 162-179.
8. Bandura, A. (1993). Perceived self-efficacy in cognitive development and functioning. Educational psychologist, 28(2), 117-148.
9. Bandura, A. (1997). |||UNTRANSLATED_CONTENT_START|||Self-efficacy: The exercise of control. |||UNTRANSLATED_CONTENT_END|||New York: Freeman.
10. Bender, W. N. (2014). Individuals with learning disabilities and their education. In H. Sarı (Ed.), Changing definitions of special learning disability (M.Yılmaz, Trans.) (pp. 1-37). Ankara: Nobel.
11. Bıkmaz, F. H. (2002). Self-efficacy belief scale in science teaching. Educational Sciences and Practice, 1(2), 197-210.
12. Bıkmaz, F.H. (2004). Öz yeterlik inançları. In Raven, Y. and Deryakulu, D. (Ed.), Individual differences in education (pp. 289-315). Ankara: Nobel Yayın Dağıtım.
13. Büyüköztürk, Ş. (2012) Scientific Research Methods. Ankara: Pegem Akademi Yayınları.
14. Çapa, Y. , Çakırogğlu, J. and Sarıkaya, H. (2005). The development and validation of a turkish version of the teachers’ sense of efficacy scale. Education and Science, 30 (137), 74-81.
15. Çapık, C. (2014). Use of confirmatory factor analysis in validity and reliability studies. Anadolu Journal of Nursing and Health Sciences, 17(3), 196-205.
16. Davran, E. (2006). The Effect of Teaching Practice in Primary Education Institutions on Teacher Candidates’ Acquisition of Teaching Competencies (Van province example). Yüzüncü Yıl University Institute of Social Sciences, Master’s Thesis. Van.
17. Deniz, S. , & Hakan, S. (2021). Development of the teacher competence scale in the field of special learning disability. Trakya University Journal of Social Sciences, 23(1), 1-20. 1.
18. DeVellis, R. F. (2014). Scale development theories and applications. (3. Edition). Nobel Yayıncılık.
19. Diken, İ.H. (2004). Turkish adaptation of the teaching competence scale, validity and reliability study. Journal of Educational Research, 16, 102-112.
20. Dilmaç, B. and Izgar, H. (2008). Examination of self-efficacy perceptions and epistemological beliefs of prospective administrator teachers. Web: (Download Date: 10.02.2023). Available online: http://www.sosyalbil.selcuk.edu.tr/sos_mak/articles/2008/20/HIZGAR-DILMA C.PDF.
21. Dursun, F. and Saracaloğlu, A. S. (2017). Evaluation of Information Technology Teacher Competencies. |||UNTRANSLATED_CONTENT_START|||Turkish Studies International Periodical for the Languages, Literature and History of Turkish or Turkic, 12 (23), 89-120.|||UNTRANSLATED_CONTENT_END|||.
22. Ekici, G. (2005). Validity and reliability of the biology self-efficacy scale. Hacettepe University Journal of Education Faculty, 29, 85-94.
23. Exley, S. (2003). The effectiveness of teaching strategies for students with dyslexia based on their preferred learning styles. British Journal of Special Education, 30(4), 213-220. [CrossRef]
24. George, D. , & Mallery, P. (2016). SPSS For Windows, Step By Step: A Simple Guide And Reference. Boston, Ma: Allynand Bacon.
25. Gibson, S. & Dembo, M. H. (1984). Teacher efficacy: A construct validation. |||UNTRANSLATED_CONTENT_START|||Journal of Educational Psychology, 76(4), 569–582. |||UNTRANSLATED_CONTENT_END|||.
26. Girli, A. (2015). Education of children with learning disabilities. S. S. Yıldırım-Doğru, (Ed.), Learning Disabilities (p. 227-232). The Educational Book.
27. Gözütok, D. (1991). Evaluation of professional behaviors of teachers and students according to their perceptions. Ankara University Journal of Faculty of Educational Sciences, 24(2), 405-409.
28. Guskey, T. R. , & Passaro, P. D. (1994). Teacher effectiveness: A study of construct dimensions. American Educational Research Journal, 31, 627-643.
29. Gürbüz, S. & Şahin, F. (2016), Research Methods in Social Sciences; Philosophy-Method-Analysis (2. Ed.). Ankara: Seçkin Yayıncılık.
30. Güvenç, H. (2022). Factors affecting satisfaction with the purchased housing. Unpublished PhD Thesis, Hasan Kalyoncu University Graduate Education Institute, Gaziantep.
31. Karasar, N. (2018). Scientific research method (Thirty-third edition). |||UNTRANSLATED_CONTENT_START|||Ankara: Nobel Yayıncılık. |||UNTRANSLATED_CONTENT_END|||.
32. Kaya, Ş. (2014), Structural equation modeling: the relationship between dizziness, anxiety and exaggerating bodily sensations. Unpublished PhD Thesis, Uludağ University, Bursa.???
33. Korkut, A. , Keskin, I., & Can, S. (2016). Developing a scale of teacher competencies for students with learning disabilities. Journal of Amasya University Faculty of Education, 5(1), 133-155.
34. Lawshe, C. H. (1975). Quantitative aproach to content validity. FARUK ERSAN EVYAPAN be given Personnel Phychology, 28(4), 563-575.
35. Lerner, J. W. (1989). Educational interventions in learning disabilities. Journal of the American Academy of Child & Adolescent Psychiatry, 28(3), 326-331.
36. McGartland, R. D. , Berg-Weger, M., Tebb, S., Lee, E. S., & Rauch, S. (2003). “Objectifying content validity: Conducting a content validity study in social work research”. Social Work Research, 27(2), 94 – 104.
37. Mertens, D. (1998). Research methods in education and psycohology. New York: SAGE Pub.
38. Nunnally, J. C. (1978). An overview of psychological measurement. Clinical diagnosis of mental disorders: A handbook, 97-146.
39. Özyürek, M. (2006). Changing attitudes towards people with disabilities. Ankara: Kök Yayıncılık.
40. Raykov, T. & Marcoulides, G. A. (2006). A First Course in Structural Equation Modeling. Lawrence (2nd Ed.). Mahwah, New Jersey: Lawrence Erlbaum.
41. Official Gazette (2018). Special Education Services Regulation.
42. Saklofske, D. H. , Michayluk, J. O., & Randhawa, B. S. (1988). Teachers’ effectiveness and teaching behaviors. Psychological reports, 63(2), 407-414.
43. Saracaloğlu, A. S. and Yenice, N. (2009). Examination of science and classroom teachers’ self-efficacy beliefs in terms of some variables. Theory and Practice in Education. 5. (2). 244-260.
44. Schwarzer, R. , Schmitz, G. S., & Daytner, G. T. (1999). Teacher Self-Efficacy Scale. Directory of Survey Instruments.
45. Smith, T. E. (2005). IDEA 2004: Another round in the reauthorization process. Remedial and Special Education, 26(6), 314-319.
46. Tabachnick, B. G. & Fidell, L. S. (2007). Using Multivariate Statistics (5th ed.). New York: Allyn and Bacon.
47. Tezbaşaran, A. A. (1997). Likert-type scale development guide. Turkish Psychologists Association (TPD).
48. Tschannen-Moran, M. , & Hoy, A. W. (2001). Teacher competence: Catching a difficult structure. Teaching and teacher education, 17 (7), 783-805.
49. Üstüner, M. , Demirtaş, H., Cömert, M., & Özer, N. (2009). Secondary school teachers’ self-efficacy beliefs. Mehmet Akif Ersoy University Journal of Education Faculty, 9(17), 1-16.
50. Elderly, M. M. (2017). Factor analysis and validity in the social sciences: using exploratory and confirmatory factor analyses. Istanbul University Journal of Business Administration Faculty, 46(Special Issue), 74-85.
51. Yurdagül, H. (2005). Using content validity indices for content validity in scale development studies. XIV. National Educational Sciences Congress, 1,771-774.