Research on the Distributed Propeller Slipstream Effect of UAV Wing Based on the Actuator Disk Method

Distributed electric propulsion technology has great potential and advantage in the development of drones. In this paper, to study the slipstream effect of distributed propeller, the actuator disk method was used to verify a single propeller, and the calculated thrust was in good agreement with the test results. Then, based on the actuator disk method, the influence of different installation positions on the slipstream effect was studied, and the distributed propeller layout was optimized by genetic algorithm. The analysis results showed that lift of the wing will be larger when the propellers are higher than the wing. When the relative height between the propeller and the wing is zero, the drag is the lowest. The influence of disk diameter on the slipstream is that the larger the diameter is, the higher the lift force and the drag force are. The slipstream effect of the optimized propeller distribution improves the lift-drag ratio of the wing, by 108.5% in the initial lift-drag ratio.

Keywords:

Subject: Engineering - Aerospace Engineering

1. Introduction

With the increasing requirements of the international community for the environmental performance of aircraft (including noise pollution, air pollution caused by exhaust emissions, and the greenhouse effect) and the increasing demand for getting rid of or alleviating dependence on oil resources, electric propulsion and distributed propulsion technology have attracted much attention in the UAV(Unmanned Aerial Vehicle) field. Electric aircraft using motors to drive propellers, with ducted fans or other devices to generate forward power, are leading the direction of development of future aircraft with low emissions, low noise and high efficiency. The use of pure electric or hybrid propeller propulsion technology can improve the propulsion efficiency, and at the same time, can make full use of the slipstream effect of the propeller to achieve a more favorable aerodynamic layout, greatly improve the flight performance of the aircraft, and meet the needs of short-range and long-endurance flight[1].

In recent years, the National Aeronautic and Space Agency (NASA) has carried out a series of studies on distributed propeller electric propulsion technology[2,3,4,5,6], designed a hybrid electric integrated systems testbed (HEIST), applied leading edge asynchronous propeller technology (LEAPTech), and successfully completed a flight test of the X-57 distributed propeller electric propulsion demonstrator.

The improvement in the wing performance by the propeller depends on the location of the propeller along the chordwise direction of the wing. Propeller configurations are classified into three categories according to their positioning—tractor, pusher, and over-the-wing. The tractor propeller is placed in front of the wing. The dynamic pressure on the wing increases due to the contracted wake, which means the wing lift increases[7]. The pusher propeller is placed behind the wing. The separation of turbulent flow on the wing is delayed, which reduces the wing drag[8]. In the case of the over-the-wing propeller, which is positioned over the wing, the wing drag is reduced due to the suction along the leading edge of the wing[9]. The placement of propellers above a wing entails several benefits when compared to conventional tractor configurations. Firstly, it eliminates installation challenges in terms of ground clearance. Secondly, it can increase wing lift-to-drag ratio in both cruise[9] and high-lift[10] conditions. Thirdly, the array of propellers can be attached to the flap mechanism, providing a degree of thrust vectoring in low-speed conditions.

At present, a large number of literatures on distributed propeller electric propulsion technology are available for reference. Stoll et al.[11] used the actuator disk model to simulate the early LEAPTech concept aircraft with constant values. The results show that the lift coefficient of the aircraft can reach 5.2, which significantly improves the cruise lift-to-drag ratio. Patterson et al.[12] studied the performance of X-57 distributed high-lift propeller during takeoff and landing, and believed that distributed high-lift propeller could increase the lift generated at low speeds by accelerating the flow over the wing and stowing against the nacelle during higher-speed flight to reduce drag. Litherland et al.[13] analyzed the heat dissipation performance of a high lift and wingtip propeller system by a numerical simulation method for the X-57 distributed propeller scheme. Veldhuis et al.[14] studied the aerodynamic performance of a single propeller over the wing using numerical methods and wind tunnel validation, and found bilateral aerodynamic coupling between the propeller and wing. A configuration with the propeller attached to the flap showed wing lift increases of 8% and 3% in cruise and high-lift conditions, respectively. They also used wind tunnels to conduct an experimental study of aerodynamic interactions of distributed propellers during forward flight[15]. The velocities induced by the adjacent propeller slipstreams lead to local loading variations on the propeller disk of 5% – 10% of the average disk loading. Youngrock et al.[16] examined the aerodynamic performances of a wing and multiple propellers through a parametric analysis of wing–propeller interactions based on actuator disk method, and found that an increment in the number of propellers increased the wing lift and drag, in addition to the propeller thrust and power.

However, the comprehensive effect of propeller installation position on slipstream performance cannot be determined. Veldhuis et al. conducted a wind tunnel experiment wherein the propeller position was varied along the spanwise direction of the wing[17]. The results indicated that the improvement in the wing performance was maximum when the propeller was located close to the wing tip, due to the attenuation of the wing tip vortex by the propeller swirl. However, this experiment was conducted for one propeller. Thus, it is difficult to predict the effect of the spanwise location of multiple propellers on the performance.

The purpose of this study is to build upon the results of previous studies and study the parameters of propeller diameter, relative height between propeller and wing, and distance between propeller and wing leading edges. This enables maximizing the performance of the wing and propeller based on their interactions and provides relevant guidance on drones design.

Since wing–propeller interactions result in the development of complex flow fields, an accurate numerical method is required to simulate these interactions. Such simulations require considerable computational resources. To solve this problem, actuator disk method (ADM) [18,19,20] and actuator line method (ALM)[21] have been introduced; these methods enable efficient calculation by simulating the propeller through a source term or boundary condition instead of simulating it directly, which is known as full-CFD. Stokkermans et al. compared the results of using ADM, ALM, and full-CFD, and observed that ADM reduced the calculation time significantly while maintaining a high accuracy[22]. Considering that genetic algorithm is adopted in this paper to achieve multi-objective optimization of propeller parameters on the influence of slipstream effect, multiple iterations are required. If the unsteady solution is used, the process is complicated and time-consuming. Therefore, this paper adopts the steady method based on the actuator disk model to solve the problem.

2. Numerical Simulation Method

2.1. Actuator disk model

In the process of multi-objective optimization, it is necessary to perform multiple numerical simulations on the distributed propeller slipstream. If the unsteady slip grid method is used, many calculations will be generated, occupying extensive computing resources, and it will take a long time. To improve the computational efficiency and achieve the goal of rapid optimization, we used the actuator disk instead of the real propeller to perform steady-state solution to simulate the distributed propeller slipstream and achieve fast optimization.

The actuator disk method simplifies the rotating area of the blade into a disk without thickness and uses the time-averaged and steady-state approximation to treat the airflow flowing in and out from the upstream of the disk and maintain the airflow before and after the disk and the propeller. With the same parameters, the acceleration and swirl effect of the actuator disk on the airflow is similar to the effect of the propeller blade. When the propeller works, the corresponding pulling force and torque are generated by the air pressure increment and rotational momentum increment before and after the actuator disk, respectively. At radius r from the center of the propeller, the thrust force and torque of the unit of length dr at a certain time are expressed as:

\begin{array}{l} d T = \frac{1}{2} ρ W^{2} (C_{l} \cos ϕ - C_{d} \sin ϕ) c d r \\ d Q = \frac{1}{2} ρ W^{2} (C_{l} \sin ϕ + C_{d} \cos ϕ) c r d r \end{array}

(1)

where

C_{l}

C_{d}

and c are the lift coefficient, drag coefficient and chord length of the blade element at r, respectively; ρ, W and

ϕ

are the density of the local airflow, the resultant velocity of the relative blade and the induced angle of attack, respectively. The airflow velocity at a point before the propeller is (

\bar{u}

v_{θ}

v_{r}

), and ω is the rotational angular velocity of the propeller. Then, the resultant velocity is:

W = \sqrt{{\bar{u}}^{2} + (ω r - v_{θ})}

(2)

and the induced angle of attack is:

ϕ = \arctan (\frac{\bar{u}}{ω r - v_{θ}})

(3)

When the actuator disk model is used to solve the calculation, ρ,

\bar{u}

, and

v_{r}

remain unchanged before and after the disk. In this paper, the front of the actuator disk is set as the outflow boundary, and the back of the disk is set as the inflow boundary. At the same time, set parameters, such as the number of blades, radius, width, hub width, blade installation angle, torsion angle, rotational speed, etc., and read the lift-drag coefficient of the propeller blade at different angles of attack to use the actuator disk instead of the real disk.

2.2. Example Verification

To verify the accuracy of the numerical calculation of the actuator disk model, the calculation is compared with the test data for a propeller. The propeller test data are mentioned in the literature [18], and the detailed blade parameters are given in Table 1. The propeller is a two-bladed blade with a tip radius of 0.381m, while the hub radius is 0.2 of tip radius. And the blade profile is a Clark Y airfoil. Two cases were selected for verification. The velocity of the inflow in experiment is 30m/s. Rotation speed is 2420r/min for case 1 and 3200r/min for case 2. The comparison between the results calculated by the actuator disk model and the test data can be seen in Table 2.

As seen from Table 2, the actuator disk model is adopted in this paper to conduct numerical simulation of the propeller, and the deviations between the calculated thrust value and the test value are less than 4%, which means the accuracy of the actuator disk model.

Figure 1 shows the pressure cloud diagram before and after the actuator disk. The pressure in front of the disk decreases due to the contraction caused by the rotation of the propeller, while the pressure behind the disk suddenly jumps. The pressure in front and behind the disk of the propeller is discontinuous, which conforms to the rationality of momentum theory. The pressure behind the disk is greater than the pressure in front of the disk, resulting in forward thrust.

Figure 2 is the velocity vector diagram before and after the actuator disk. The flow in front of the disk is found to have no circumferential velocity, while the flow behind the disk generates circumferential velocity, that is, swirl flow, consistent with the actual situation.

The actuator disk method adopted in this paper can simulate the real aerodynamic effects of propellers and can be used for subsequent numerical simulation requirements of distributed propeller layout optimization design.

3. Analysis of factors affecting slipstream characteristics

For the propeller wake, when the propeller rotation rate is fixed, the diameter of the propeller will affect the area of the wake passing over the drone wing to affect the increase in lift of the wing. Considering that the axial induced velocity at the rear of the propeller disk is different in different radial positions, the height of the propeller relative to the wing also has an influence on the slipstream effect. According to classical momentum theory, the axial velocity of the wake after the propeller disk is a continuous acceleration process, so the distance between the propeller and the leading edge of the wing will affect the axial induced velocity when the slipstream reaches the wing[23]. In view of the above, we used the actuator disk method to preliminarily analyze the influence of propeller diameter, relative height and distance from the leading edge of the wing on the slipstream characteristics of the propeller.

3.1. Introduction of the propeller + wing model

The test object is a combined model of a flat wing and 4 propellers. The UAV wing employs NACA2412 airfoil with a span of 800 mm and a chord of 200 mm. And the four propellers are three-blade propellers with Clark Y airfoil. The actuator disk model is adopted, and the four propellers are represented by the disk without thickness. The propellers are perpendicular to the chord line of the wing, which means the propellers will have the same angle of attack as the wing. Taking the wing root as the starting point, the distribution distances of the four disk centers along the wing spanwise are 100 mm, 300 mm, 500 mm and 700 mm. The specific 3D model can be seen in Figure 3, and the inflow direction is the x-axis direction. Figure 4 shows the unstructured grid of this model, and the details of the grid can be found in Table 3.

The direction of incoming flow is the X-axis, that is, the chord direction of the wing is the X-direction. The Y-axis is the spanwise direction, and the Z-axis is perpendicular to the plane where the chord and spanwise direction of the wing are located, satisfying the right-hand rule. The simulation test conditions are as follows: the incoming flow speed is 20m/s; the rotation rate of the four propellers is 12000r/min; and the steering is clockwise rotation (viewed along the negative X-axis).

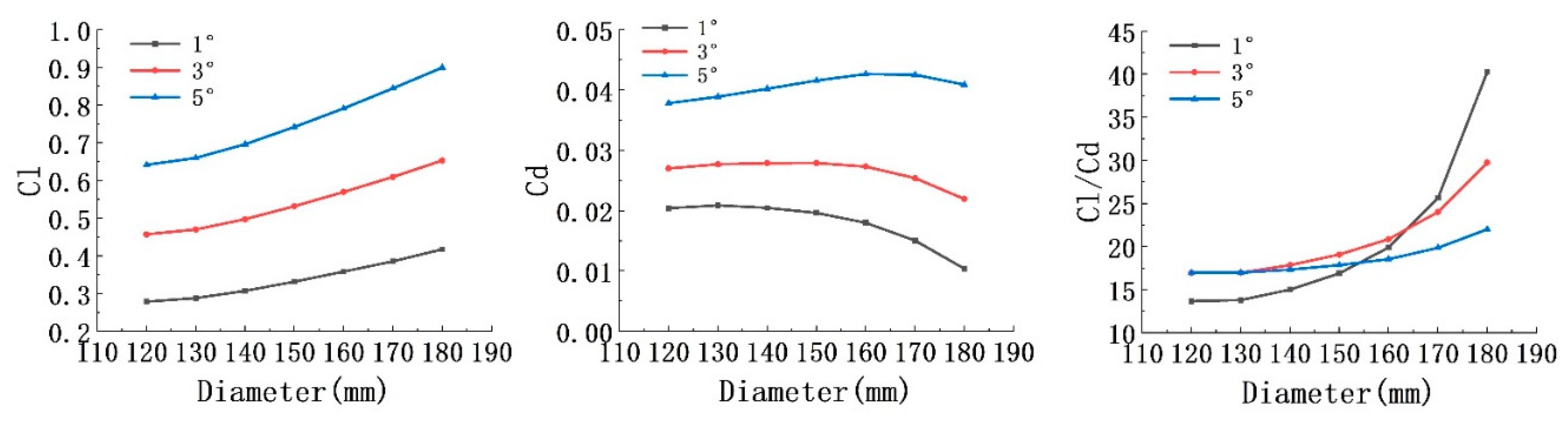
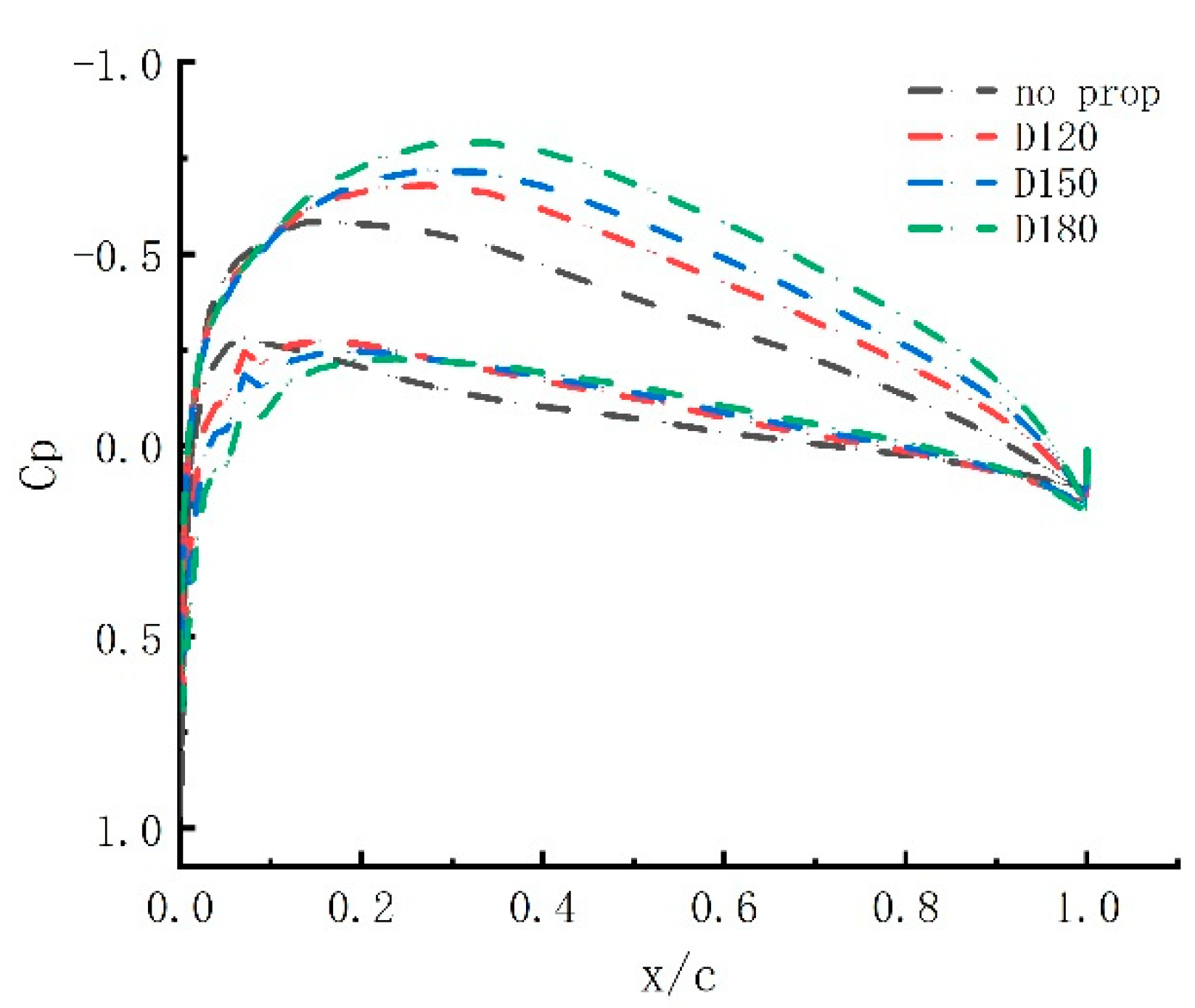
3.2. Propeller diameter

The lift coefficient, drag coefficient and lift-drag ratio of the UAV wing at angles of attack of 1°, 3° and 5° as a function of propeller diameter can be seen in Figure 5. With increasing propeller diameter, the lift coefficient of the wing increases gradually at different angles of attack. When the diameter is relatively small, the variation range of the drag coefficient is small, and when the diameter is large, the drag coefficient will show a downward trend. Therefore, as a whole, the lift-drag ratio of the wing increases with increasing diameter. When the propeller diameter is small, the lift-drag ratio is larger when the angle of attack is large, and when the propeller diameter is large, the lift-drag ratio is larger when the angle of attack is small.

When the angle of attack is 1°, the chordal surface at 500 mm (center of the third propeller disk) in the y-direction of the wing is intercepted, and the pressure coefficient data are extracted and drawn as shown in Figure 6. In the legend, “no prop” means no propellers; “D” stands for propeller diameter. The “c” in the X-axis means the wing chord. As the figure shows, the larger the propeller diameter is, the smaller the pressure coefficient on the upper surface of the wing; the larger the pressure difference between the upper and lower surfaces of the wing is, the greater the lift force of the wing.

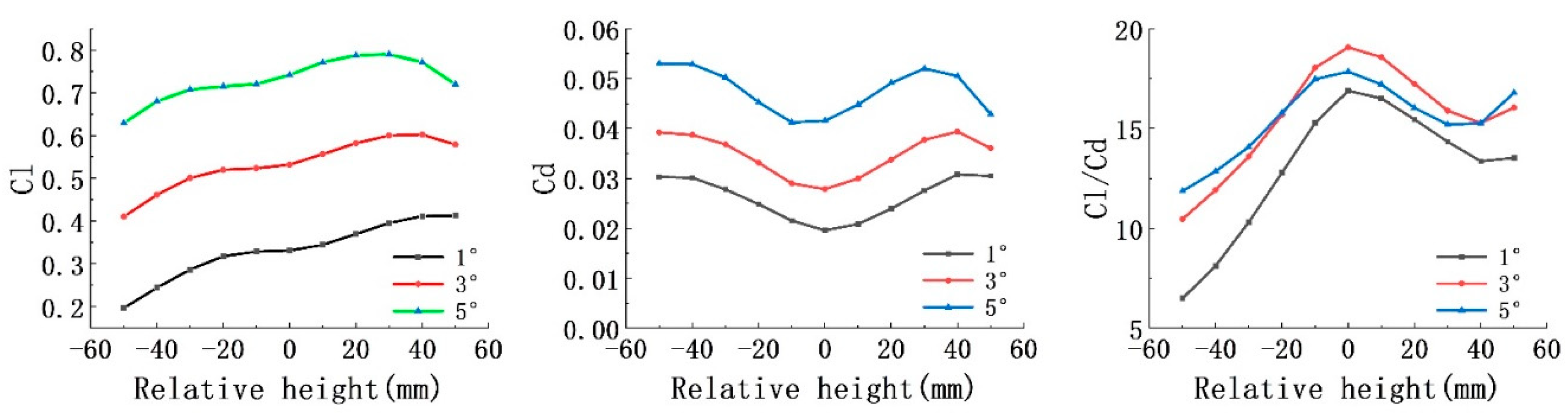
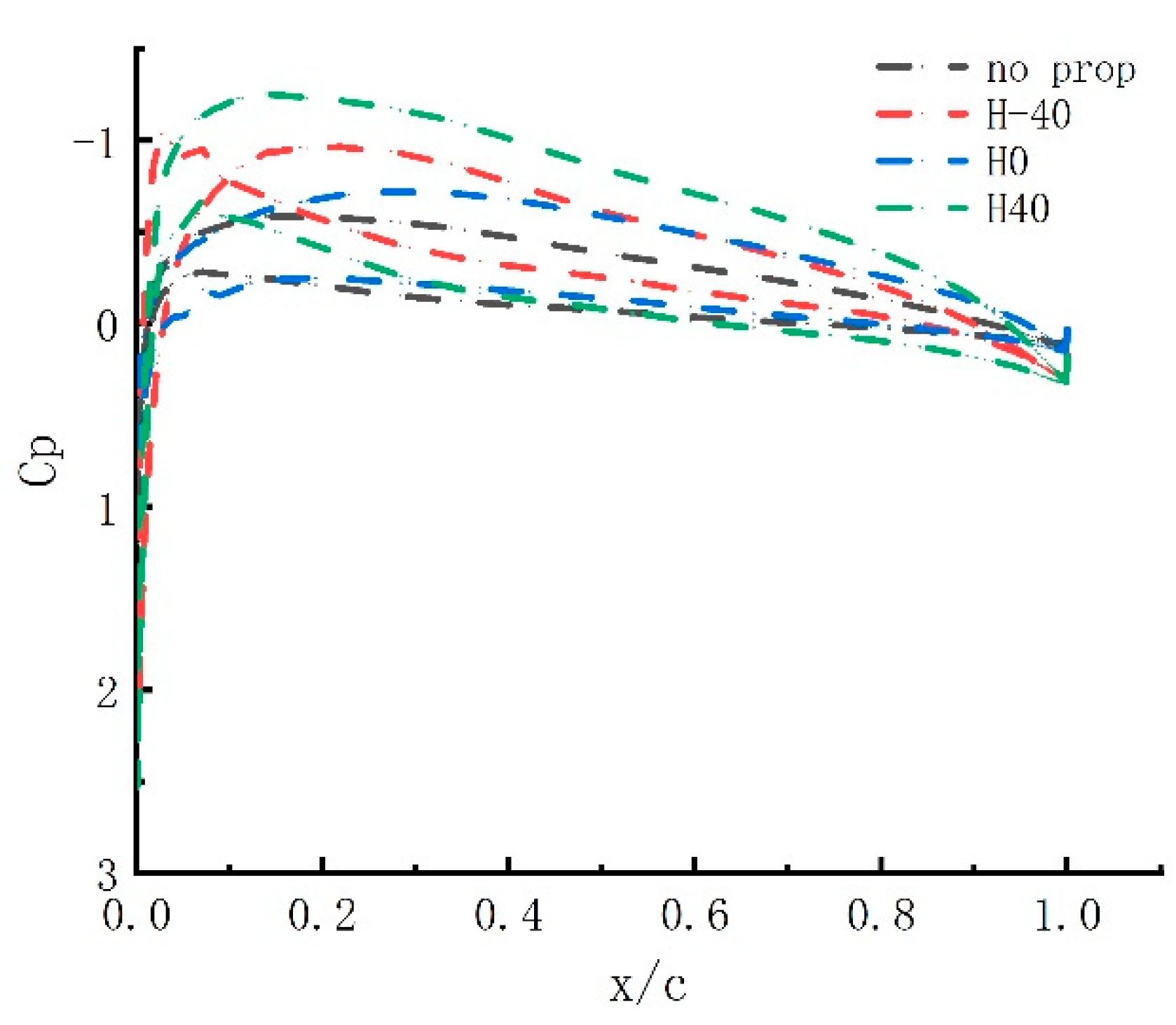
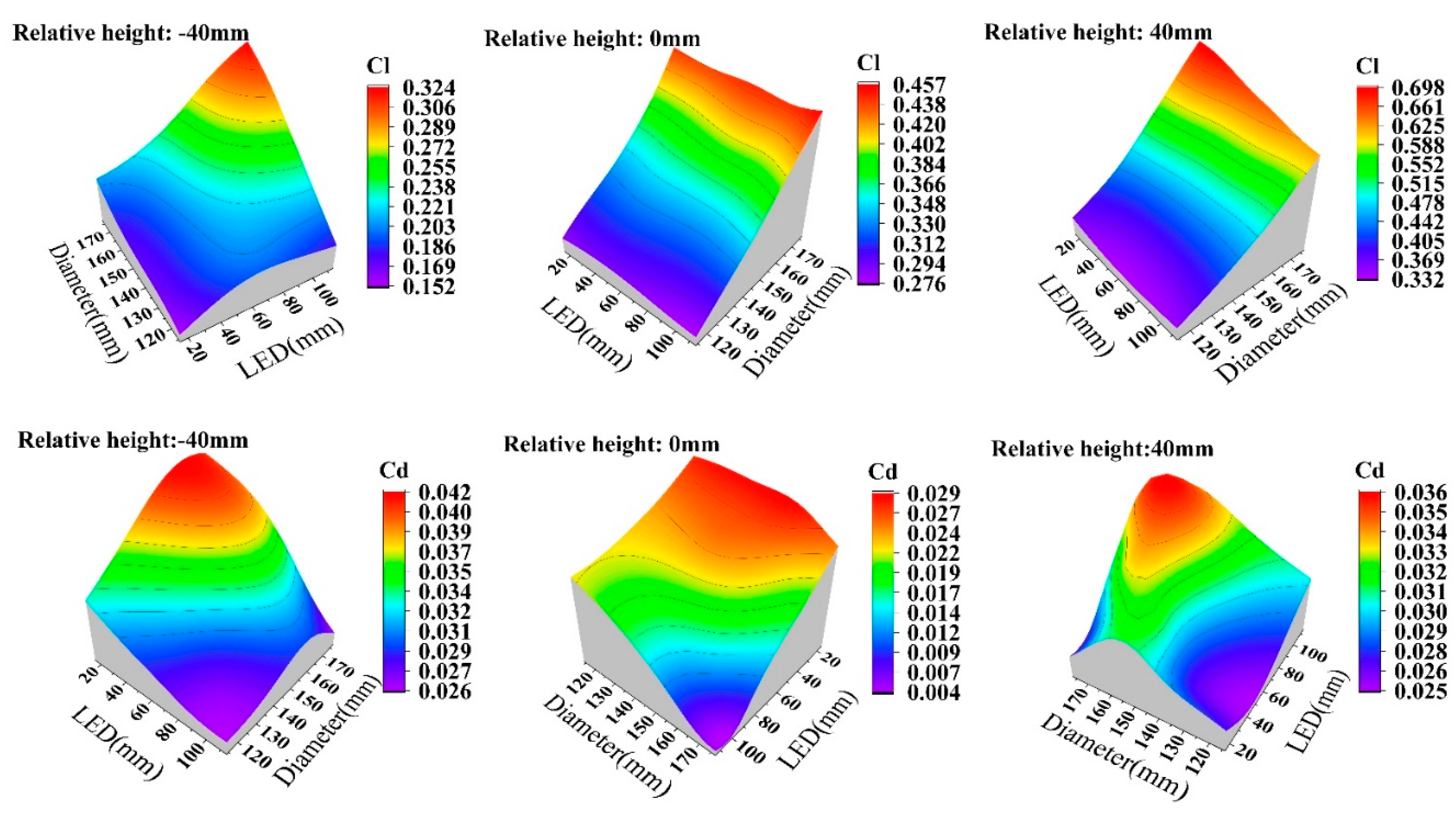
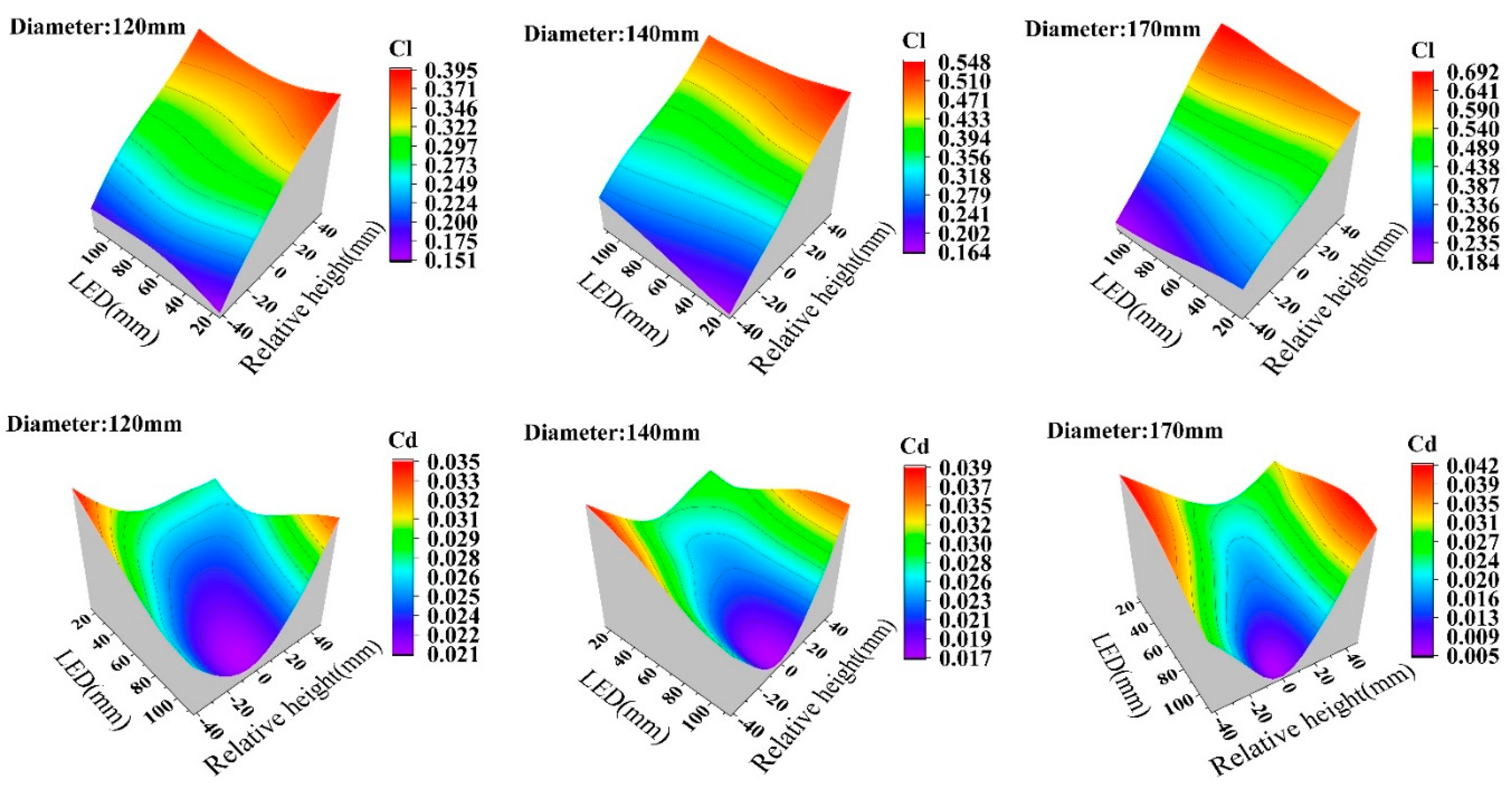
3.3. Relative height of propeller

Initially, the default position is zero when the center of the propeller disk is aligned with the chord line of the wing, that is, the height of the propeller relative to the wing is 0. If the propeller is higher than the wing, the direction is positive, and vice versa. At this time the diameter of the propeller is 150mm.

Figure 7 shows the lift coefficient, drag coefficient and lift-drag ratio of the UAV wing at angles of attack of 1°, 3° and 5° with the relative height of the propeller. The lift coefficient of the wing increases with increasing relative height of the propeller. The farther the propeller is from the wing, the drag coefficient is approximately larger, and the drag coefficient is the lowest when the relative height of the propeller from the wing is zero. Therefore, the farther the propeller is below the wing, the smaller the lift-drag ratio is, and the lift-drag ratio is the largest when the relative height of the propeller from the wing is zero.

When the angle of attack is 1°, the chordal surface at 500 mm (center of the third propeller disk) in the y-direction of the wing is intercepted to extract the pressure coefficient data and draw the data into Figure 8. In the legend, “H” stands for relative height of propeller. As the figure shows, when the relative height is -40 mm, that is, the propeller is under the wing, the pressure coefficient on the lower surface of the leading edge of the wing is smaller than the pressure coefficient on the top surface. As a whole, the pressure difference between the upper and lower surfaces of the wing is the smallest. When the relative height is positive, the pressure difference between the upper and lower surfaces of the wing is larger, and the wing can obtain greater lift. When designing a distributed propeller layout, the propeller can be properly mounted at a certain height above the wing.

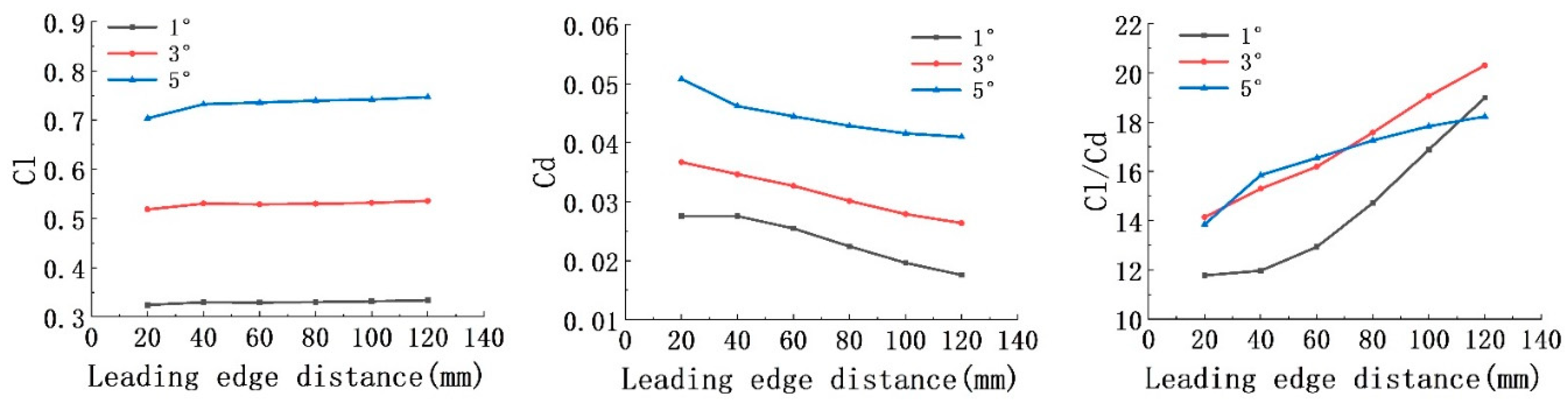
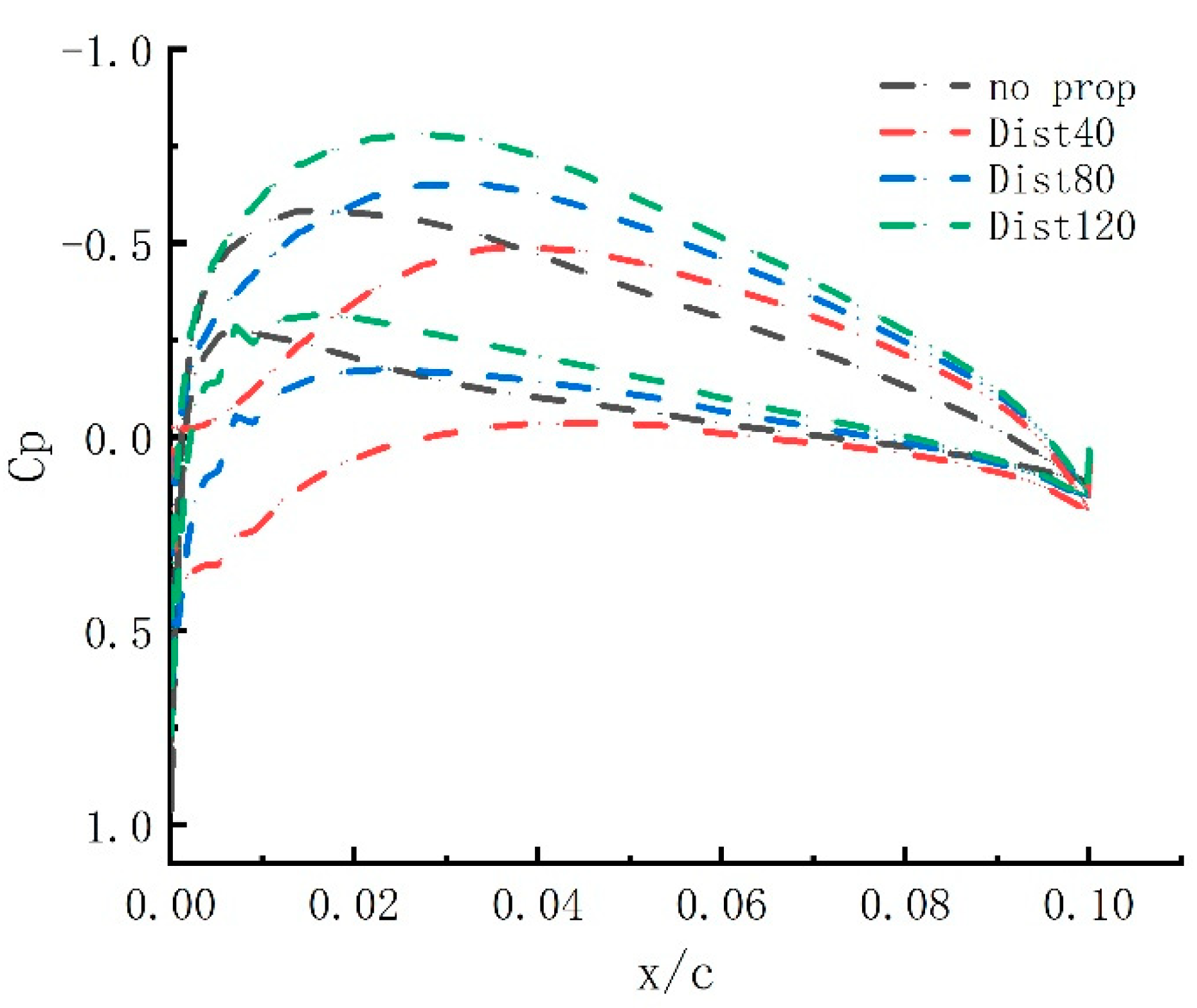
3.4. Distance between the propeller and wing leading edge

According to the momentum theory, when the propeller is far away from the leading edge of the wing, the incoming stream before the propellers will accelerate fully and the slipstream effect will be better. Figure 9 shows the lift coefficient, drag coefficient and lift-drag ratio of the UAV wing at angles of attack of 1°, 3° and 5° as a function of the distance between the propeller and the wing leading edge. The diameter of the propeller is maintained at 150mm and the relative height is 0mm. The lift coefficient of the wing increases slightly with increasing distance between the propeller and the wing leading edge, while the drag coefficient of the wing decreases with increasing distance between the propeller and the wing leading edge. As a whole, the lift-drag ratio of the wing increases with increasing leading edge distance.

When the angle of attack is 1°, the chordal surface at 500 mm (center of the third propeller disk) in the y-direction of the wing is intercepted, and the pressure coefficient data are extracted and drawn, as shown in Figure 10. In the legend, “Dist” stands for distance between the propeller and wing leading edge. When the distance between the propeller and the leading edge of the wing gradually increases, the wake velocity behind the propeller disk increases slightly, which makes the airflow velocity on the upper and lower surfaces of the wing relatively increase, and the pressure decreases. At the same time, the minimum pressure point on the upper and lower surfaces of the wing appears to move forward. However, as a whole, with the change in the leading edge distance, the pressure difference between the upper and lower surfaces of the wing is approximately unchanged, and the lift force has no significant change.

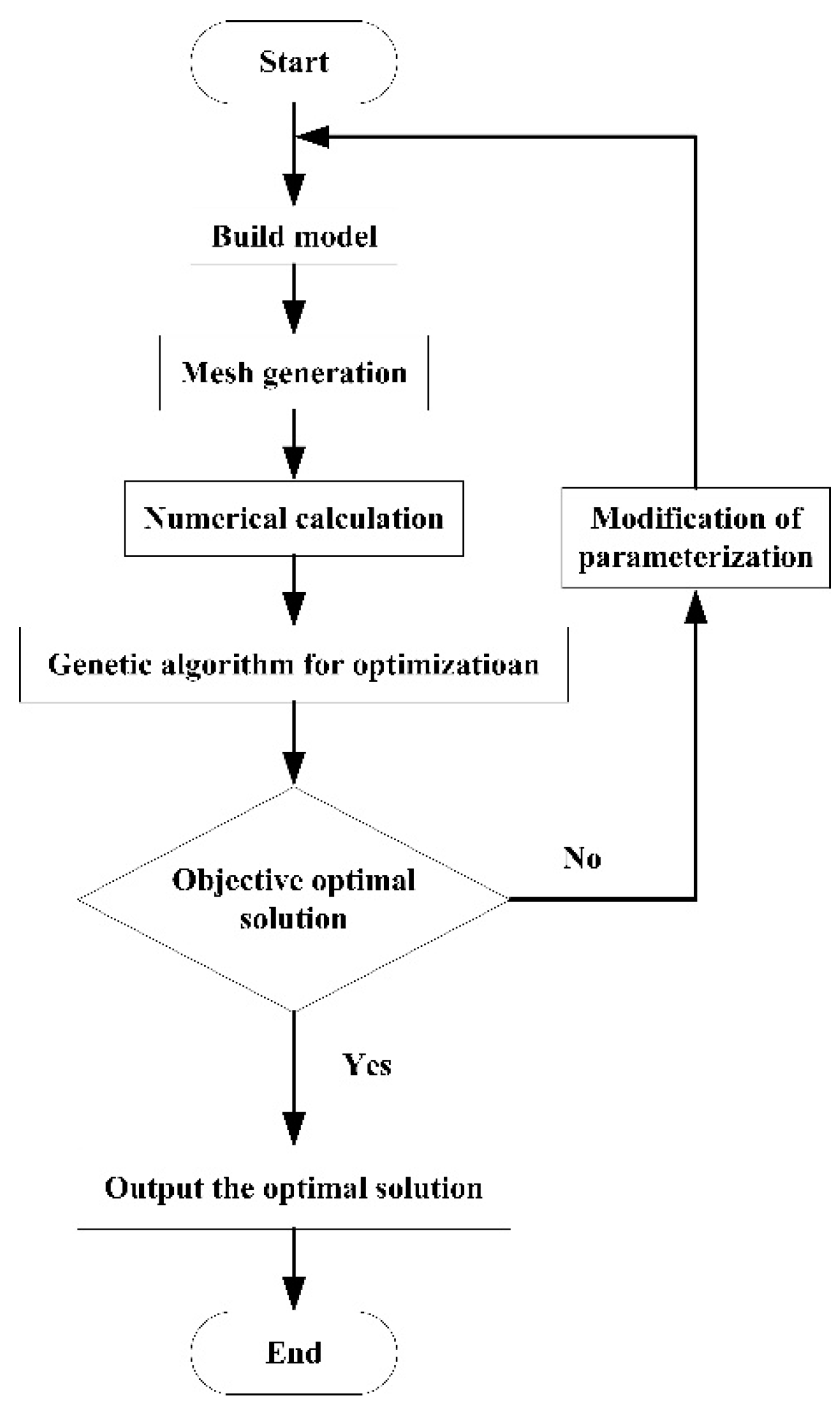
4. Genetic algorithm optimization

4.1. Optimization Introduction

The nondominated sorting genetic algorithm (NSGA) is a multi-objective algorithm based on a genetic algorithm. The main difference between NSGA and the basic genetic algorithm is that NSGA performs fast nondominated ranking on individuals before the selection operation, which increases the probability of excellent individuals being retained. Selection, crossover, mutation and other operations are the same as in the basic genetic algorithm. Through the research and testing of many scholars, the NSGA algorithm is found to be better than the traditional multi-objective genetic algorithm. However, the NSGA is found to still have some shortcomings in practical applications, and the NSGA-2 has made some improvements to make up for the defects of the NSGA.

Established considering the distributed propeller slipstream effect on airfoil aerodynamic characteristics of the distributed layout optimization design system diagram as shown in Figure 11, based on parametric modeling, T-rex unstructured meshing, equivalent plate model, stationary flow numerical simulation method, the "propeller + wing" combination of flow field is a quick, get the corresponding airfoil aerodynamic data. Combined with the NSGA-2 algorithm, the global optimal solution is found.

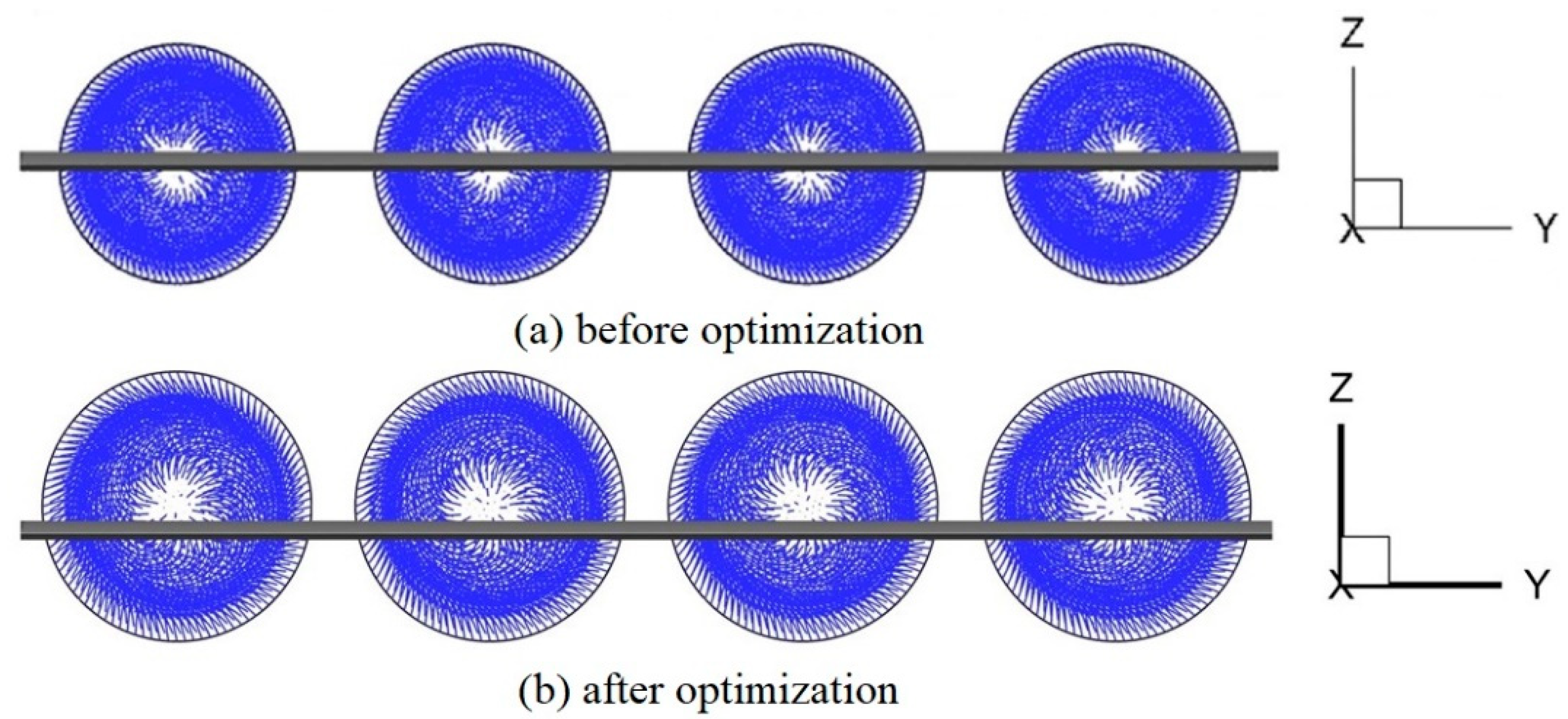
4.2. Analysis of optimization results

Distributed propellers improve lift mainly by increasing dynamic pressure on the wing surface through slipstream. Therefore, the distribution of propellers should cover the leading edge of the wing along the spanwise direction so that the slipstream of propellers can cover the wing span as much as possible. The configuration of the front edge distributed propeller wing is selected as the research object. The take-off speed is designed to be 30 m/s, and the angle of attack of the incoming stream is 1°. At the same time, the wing is a straight wing using the NACA2412 airfoil. The rotation rate of the four propellers is 12000r/min.

Considering the influence of the distributed propeller slipstream on the flow around the wing under takeoff conditions, the dynamic position layout of the distributed propeller aircraft was optimized. The actuator disk model was used to replace the real propeller, the y-coordinate position of the center of four actuator disks in the distributed propeller layout was determined, and the rotation direction of the propeller was clockwise (viewed along the -x direction). Combined with the above research, the relative height, leading edge distance and propeller diameter were designed as optimization variables, and the optimization objective was to find the maximum lift-drag ratio. The constraint conditions are:

\begin{array}{l} Objective function : \min (- Cl / Cd) \\ s . t . \{\begin{cases} - 50 \leq z \leq 50 \\ 10 \leq x \leq 120 \\ 100 \leq d \leq 180 \end{cases} \end{array}

where z, x and d represent the relative height, leading edge distance and propeller disk diameter, respectively, and the unit of values is mm.

According to the established optimization design system, the installation position of the distributed propeller under takeoff conditions was optimized, and the NSGA-2 algorithm was used for optimization calculation, in which the number of primary generation populations was 12, and the number of iterations was 10.

The optimized distributed propeller/wing configuration is shown in Figure 12, where the viewing angle is from the downstream direction to the positive upstream direction (-x-direction), and the blue disk represents the actuator disk. After optimization, the relative height of the propeller is higher than the relative height before optimization, and the diameter of the propeller disk is also increased. Refer to Table 4 for details.

By comparing the flow field calculation results before and after the optimization of the propeller installation position, the cloud images of the pressure coefficient on the upper surface of the wing of the two layout configurations correspond to Figure 13(a) and Figure 13(b), respectively. The whole spanwise direction of the leading edge of the wing is affected by slipstream to a certain extent, which is caused by the 3D effect of the wing. Second, the distributed propeller slipstream has a great influence on most areas between the leading edge and 2c/3 of the wing, and the negative pressure enhancement is relatively obvious, while the influence on the area between 2c/3 and trailing edge is relatively weak, and the negative pressure enhancement is not obvious. With different distributed propeller layouts, the area, area and strength of the slipstream on the wing changed significantly. Before optimization, the propeller was installed in front of the wing, and the wing was subjected to the downwash and upwash effects of the wake flow in the upper half plane of the propeller. The upwash area increased the local angle of attack of the current wing surface, and the negative pressure was larger. The downwash area will decrease the local angle of attack of the current wing surface, and the negative pressure is slightly weaker than the upwash area. The upwash, downwash and rotational effects of the slipstream deflect the area of maximum negative pressure in the positive direction of the y-axis downstream from the leading edge of the wing. After optimization, the propeller is above the wing, and the diameter of the propeller disk becomes larger, which enhances the upwash and downwash effects behind the disk. The negative pressure effect of the slipstream on the upper surface of the wing is significantly enhanced, and a large area of negative pressure enhancement appears on the upper surface of the wing.

From the point of view of aerodynamic data, as shown in Table 5. Compared with before optimization, the lift coefficient and lift-drag ratio of the optimized wing are significantly increased, and the drag coefficient is significantly decreased because of the change in the diameter of the propeller blade. The larger blade brings more induced velocity and accelerates the airflow velocity on the wing surface. As shown in Figure 14, the axial velocity at the rear of the disk is close to 60 m/s, approximately twice the velocity of the incoming flow, which greatly improves the lift force of the wing. Second, the change in propeller height affects the negative pressure effect of the wash and wash areas on the wing surface, increases the negative pressure increase and negative pressure area on the wing surface, and provides favorable support for the lift of the wing.

The comparison of spanwise pressure distribution coefficients at 1/4 C of the wing before and after distributed propeller layout optimization are given in Figure 15. The b in the X-axis means the wing span. Before the distributed propeller layout optimization, the slipstream made the upper and lower surfaces of the leading edge of the wing under obvious upwash and downwash, there are four negative pressure suction peaks on the upper and lower surfaces of the whole wing. The suction peak on the lower surface is on the right side of the propeller, and the suction peak on the upper surface is on the left side of the propeller. This is because the downwash flow on the right half plane of the propeller enhances the negative pressure on the lower surface of the wing, and the maximum negative pressure is located in the area around 0.6-0.7r on the right side of each propeller. The upwash flow on the left half plane of the propeller enhances the negative pressure on the upper surface of the wing, with the maximum negative pressure located around 0.6-0.7r to the left of each propeller. After optimization, the negative pressure effect of slipstream on the wing surface is greatly enhanced, and the position of suction peak remains unchanged. The negative pressure on the upper surface is enhanced along the spanwise direction, indicating that the slipstream has an effect on the spanwise direction of the whole wing. The enhancement of negative pressure on the lower surface is not conducive to lift, but the enhancement effect of negative pressure on the upper surface is significantly stronger than that on the lower surface, which is ultimately beneficial to lift.

By further comparing the pressure coefficients of the airfoil in the spanwise direction of the wing, the pressure coefficients of the sectional airfoil at the position of the right-most suction peak (y=662.5mm, center of the left side of the fourth propeller) on the upper surface of the wing were intercepted, and Figure 16 was drawn.

Figure 16 shows that, compared with before optimization, the negative pressure on the upper surface of the leading edge of the wing is significantly enhanced after the distributed propeller layout optimization due to the slipstream effect. Which makes the airflow velocity upstream of the wing faster and the dynamic pressure larger, and the airflow upwash and downwash are more obvious. This section is located in the upwash region, and the upwash flow increases the negative pressure on the upper surface of the wing and helps to increase the positive pressure on the lower surface, showing that the lift of the wing near the suction peak section with optimized is significantly improved.

When processing aerodynamic data in the process of optimization, the variation trends of the lift coefficient and drag coefficient at different relative heights are additionally compared, as shown in Figure 17. And Figure 18 gives that the variation trends of the lift coefficient and drag coefficient at different propeller disk diameters are also compared. In the legend, “LED” stands for distance between the propeller and wing leading edge.

Compared with Figure 17 and Figure 18, in general, the larger the relative height value between the propeller and the wing (negative below), the greater the lift, and the farther the distance between the propeller and the wing, the greater the drag. When the relative height between the propeller and the wing is zero, the drag is the lowest. The change in the leading edge distance has little influence on the lift of the wing, while it has some influence on the drag force. Roughly, the larger the distance is, the smaller the drag force. The influence of disk diameter on the slipstream is that the larger the diameter is, the higher the lift force and the higher the drag force.

5. Conclusion

In this paper, we used the actuator disk model to study the propeller slipstream effect of distributed electric propulsion UAV. Simulations of different relative heights, front distances and disk diameters on the effect of slipstream were performed. At the same time, the layout was optimized using a genetic algorithm for distributed propeller design. And the results showed the following:

1) The actuator disk can better replace the propeller for the numerical simulation of the slipstream flow field, which can meet the requirements of distributed propeller optimization design under the aerodynamic effect of the slipstream.

2) After the optimization of the distributed propeller layout, the lift coefficient of the UAV wing is greatly improved, and the drag coefficient is significantly reduced under the takeoff condition. The optimized distributed propeller aerodynamic layout is more reasonable, which can improve the lift-drag ratio of the wing during takeoff and is conducive to the skidding-off of the drones with a large load ratio or shorten the takeoff distance.

3) Theoretically, the change in the leading edge distance has little influence on the wing lift. But in fact, due to the presence of surrounding still air, the airflow velocity behind the disk is constantly attenuated, and the increase in the leading edge distance will attenuate the lift effect of the slipstream on the wing. From the perspective of the structure, an increase in the leading edge distance will improve the structural design requirements and add extra structural weight to the aircraft. We recommend that drones should be designed to reduce the distance between the propeller and the leading edge of the wing under takeoff.

Research on the slipstream effect of distributed propeller and layout optimization is of great significance to promote the development of the integrated design concept of distributed propeller UAV aerodynamic layouts.

Author Contributions

M.C. and K.L., designed research; M.C., K.L. and C.W., performed research; J.W., M.C. and Z.Q., analyzed and verified research; M.C. and J.W. wrote the paper. Our manuscript is original content and has not been submitted to other journals. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Natural Science Foundation of Shenzhen, China(2020N015).

Data Availability Statement

The supporting data of this study are available within the article.

Conflicts of Interest

The authors declare no conflict of interest.

References

Patterson, M. D. and German, B., "Conceptual design of electric aircraft with distributed propellers: multidisciplinary analysis needs and aerodynamic modeling development," 52nd Aerospace sciences meeting, 2014, pp. 0534.
Moore, M. D., "Misconceptions of electric aircraft and their emerging aviation markets," 52nd Aerospace Sciences Meeting, 2014, pp. 0535.
Borer, N. K., Patterson, M. D., Viken, J. K., Moore, M. D., Bevirt, J., Stoll, A. M. and Gibson, A. R., "Design and performance of the NASA SCEPTOR distributed electric propulsion flight demonstrator," 16th AIAA Aviation Technology, Integration, and Operations Conference, 2016, pp. 3920. [CrossRef]
Patterson, M. D., Derlaga, J. M. and Borer, N. K., "High-lift propeller system configuration selection for NASA's SCEPTOR distributed electric propulsion flight demonstrator," 16th AIAA Aviation Technology, Integration, and Operations Conference, 2016, pp. 3922.
Schnulo, S. L., Chin, J., Smith, A. and Paul-Dubois-Taine, A., "Steady state thermal analyses of SCEPTOR X-57 wingtip propulsion," 17th AIAA Aviation Technology, Integration, and Operations Conference, 2017, pp. 3783. [CrossRef]
Christie, R. J., Dubois, A. and Derlaga, J. M., "Cooling of electric motors used for propulsion on SCEPTOR," Vol. No. 2017, pp.
Moens, F. and Gardarein, P., "Numerical simulation of the propeller/wing interactions for transport aircraft," 19th AIAA applied aerodynamics conference, 2001, pp. 2404.
Catalano, F. and Stollery, J., "The effect of a high thrust pusher propeller on the flow over a straight wing," 11th Applied Aerodynamics Conference, 1993, pp. 3436.
JOHNSON, J., J and White, E., "Exploratory low-speed wind-tunnel investigation of advanced commuterconfigurations including an over-the-wing propeller design," Aircraft Design, Systems and Technology Meeting, 1983, pp. 2531.
Müller, L., Heinze, W., Kožulović, D., Hepperle, M. and Radespiel, R., "Aerodynamic installation effects of an over-the-wing propeller on a high-lift configuration," Journal of aircraft, Vol. 51, No. 2014, pp. 249-258. [CrossRef]
Stoll, A. M., Bevirt, J., Moore, M. D., Fredericks, W. J. and Borer, N. K., "Drag reduction through distributed electric propulsion," 14th AIAA aviation technology, integration, and operations conference, 2014, pp. 2851. [CrossRef]
Patterson, M. D. and Borer, N. K., "Approach considerations in aircraft with high-lift propeller systems," 17th AIAA Aviation Technology, Integration, and Operations Conference, 2017, pp. 3782.
Litherland, B. L., Patterson, M. D., Derlaga, J. M. and Borer, N. K., "A method for designing conforming folding propellers," 17th AIAA Aviation Technology, Integration, and Operations Conference, 2017, pp. 3781.
Marcus, E. A., de Vries, R., Raju Kulkarni, A. and Veldhuis, L. L., "Aerodynamic investigation of an over-the-wing propeller for distributed propulsion," 2018 AIAA Aerospace Sciences Meeting, 2018, pp. 2053. [CrossRef]
De Vries, R., van Arnhem, N., Sinnige, T., Vos, R. and Veldhuis, L. L., "Aerodynamic interaction between propellers of a distributed-propulsion system in forward flight," Aerospace Science and Technology, Vol. 118, No. 2021, pp. 107009. [CrossRef]
Seo, Y., Hong, Y. and Yee, K., "Numerical investigation of wing–multiple propeller aerodynamic interaction using actuator disk method," International Journal of Aeronautical and Space Sciences, Vol. 23, No. 2022, pp. 805-822. [CrossRef]
Sinnige, T., van Arnhem, N., Stokkermans, T. C., Eitelberg, G. and Veldhuis, L. L., "Wingtip-mounted propellers: Aerodynamic analysis of interaction effects and comparison with conventional layout," Journal of aircraft, Vol. 56, No. 2019, pp. 295-312. [CrossRef]
Li, B., Lu, H. and Deng, S., "Validation of an actuator disk model for numerical simulation of propeller," Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, Vol. 229, No. 2015, pp. 1454-1463. [CrossRef]
Barakos, G., Fitzgibbon, T., Kusyumov, A., Kusyumov, S. and Mikhailov, S., "CFD simulation of helicopter rotor flow based on unsteady actuator disk model," Chinese Journal of Aeronautics, Vol. 33, No. 2020, pp. 2313-2328. [CrossRef]
O'Brien, D. and Smith, M., "Analysis of rotor-fuselage interactions using various rotor models," 43rd AIAA Aerospace Sciences Meeting and Exhibit, 2005, pp. 468.
Troldborg, N., "Actuator line modeling of wind turbine wakes," Vol. No. 2009, pp.
Stokkermans, T. C., Van Arnhem, N., Sinnige, T. and Veldhuis, L. L., "Validation and comparison of RANS propeller modeling methods for tip-mounted applications," AIAA Journal, Vol. 57, No. 2019, pp. 566-580. [CrossRef]
Patterson, M. D., "Conceptual design of high-lift propeller systems for small electric aircraft," Vol. No. 2016, pp.

Figure 1. Pressure cloud diagram (a) before disk, (b) after disk.

Figure 2. Velocity vector diagram (a) before disk, (b) after disk.

Figure 3. Geometric model of propeller + wing.

Figure 4. Unstructured grid.

Figure 5. Curves of the lift coefficient, drag coefficient, lift-drag ratio and propeller diameter at different angles of attack.

Figure 6. Pressure coefficient of the wing surface under different propeller diameters (y=500 mm).

Figure 7. Curves of the lift coefficient, drag coefficient, lift-drag ratio and relative height at different angles of attack.

Figure 8. Pressure coefficient of the wing surface at different relative heights (y=500 mm).

Figure 9. Curves of the lift coefficient, drag coefficient, lift-drag ratio and leading edge distance at different angles of attack.

Figure 10. Pressure coefficient on the wing surface with different leading edge distances (y=500 mm).

Figure 11. Optimal design system diagram of the distributed propeller aerodynamic layout.

Figure 12. Distributed propeller/wing configuration before and after optimization.

Figure 13. Cloud image of the wing surface pressure coefficient before and after optimization.

Figure 14. Axial velocity cloud of the behind of the propeller disk (lateral view).

Figure 15. Comparison of the pressure coefficient distribution at the 1/4 chord length of the wing before and after optimization.

Figure 16. Distribution of the sectional pressure coefficient at the suction peak of the wing before and after optimization(y=662.5mm).

Figure 17. Variation in the lift and drag coefficient at different relative heights.

Figure 18. Variation in the lift and drag coefficient under different propeller disk diameters.

Table 1. Blade parameters of Clark Y airfoil twin-bladed blades[18].

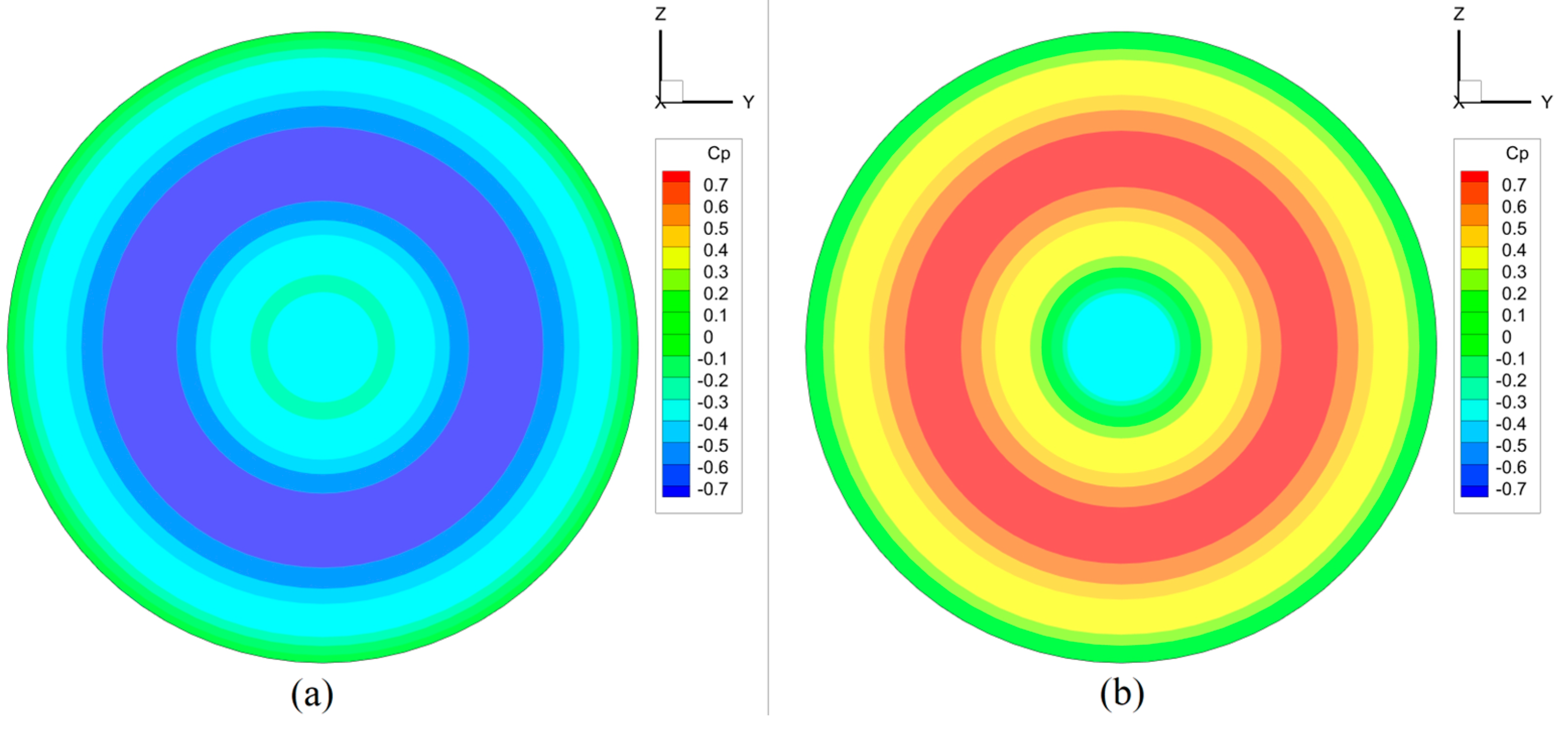
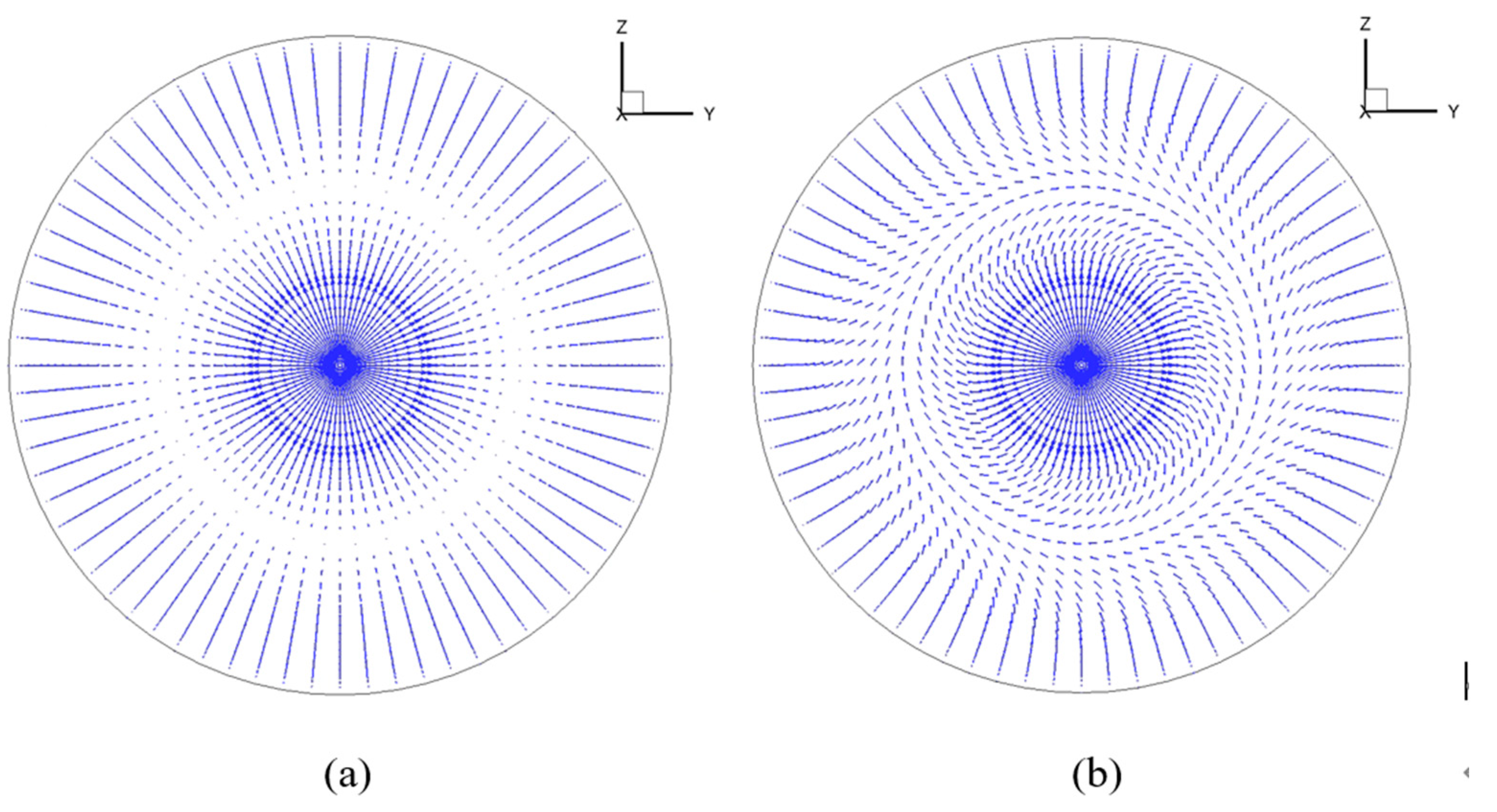
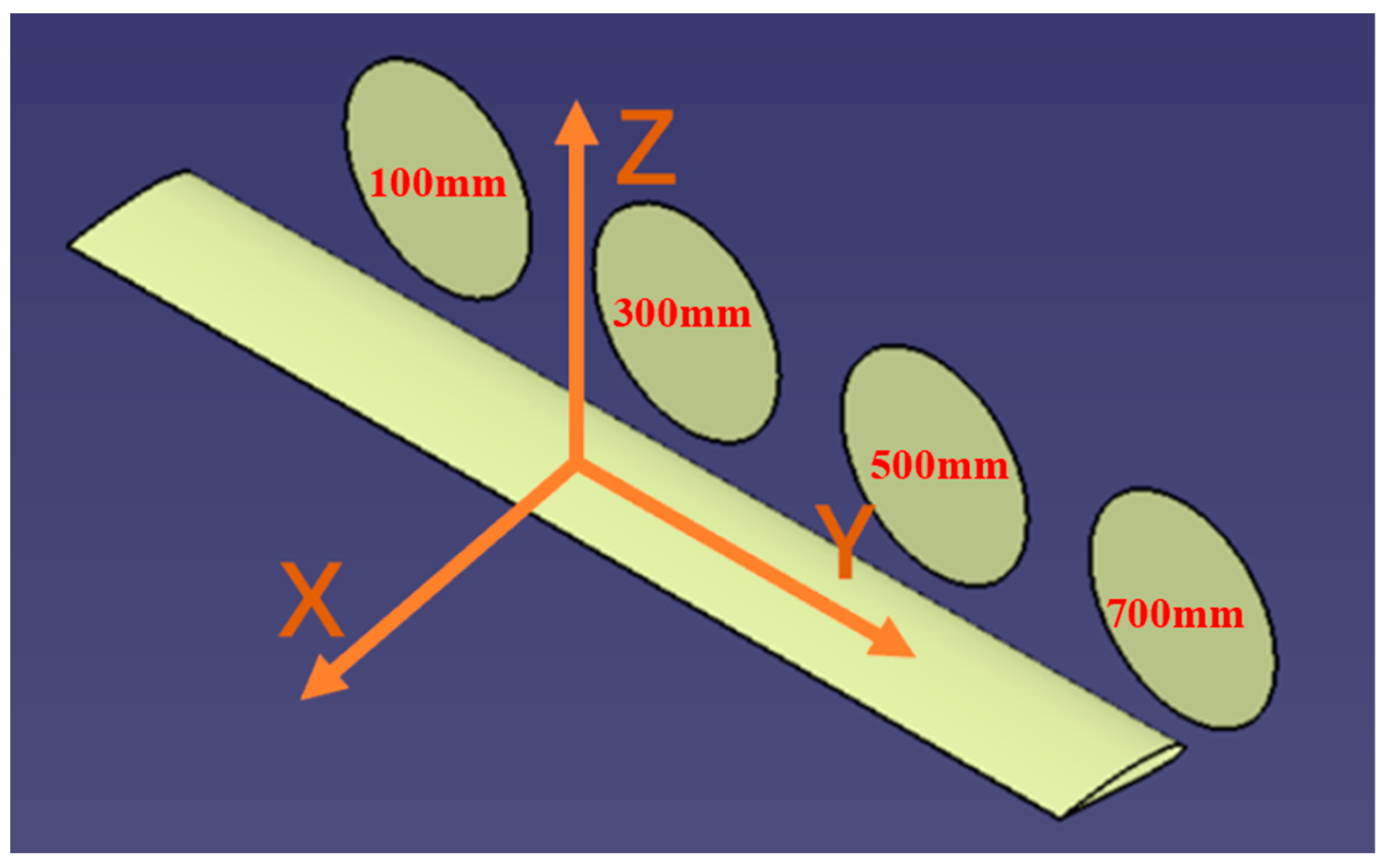
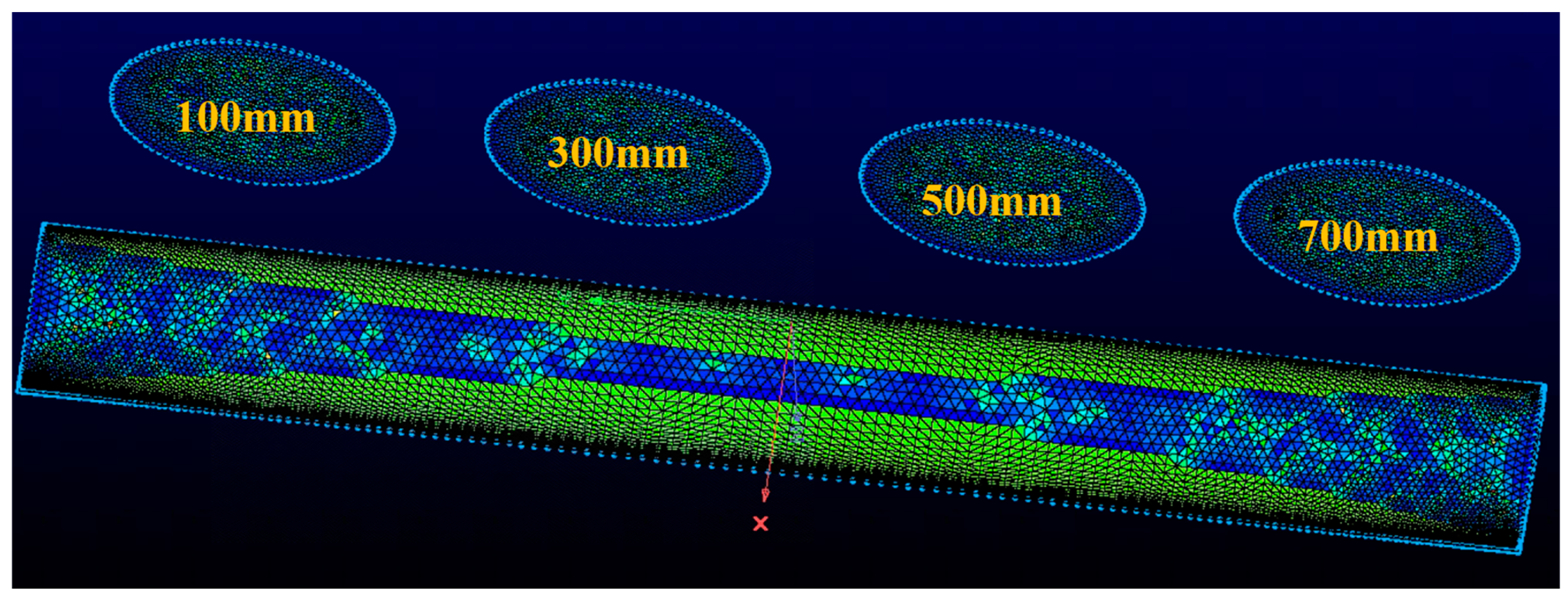
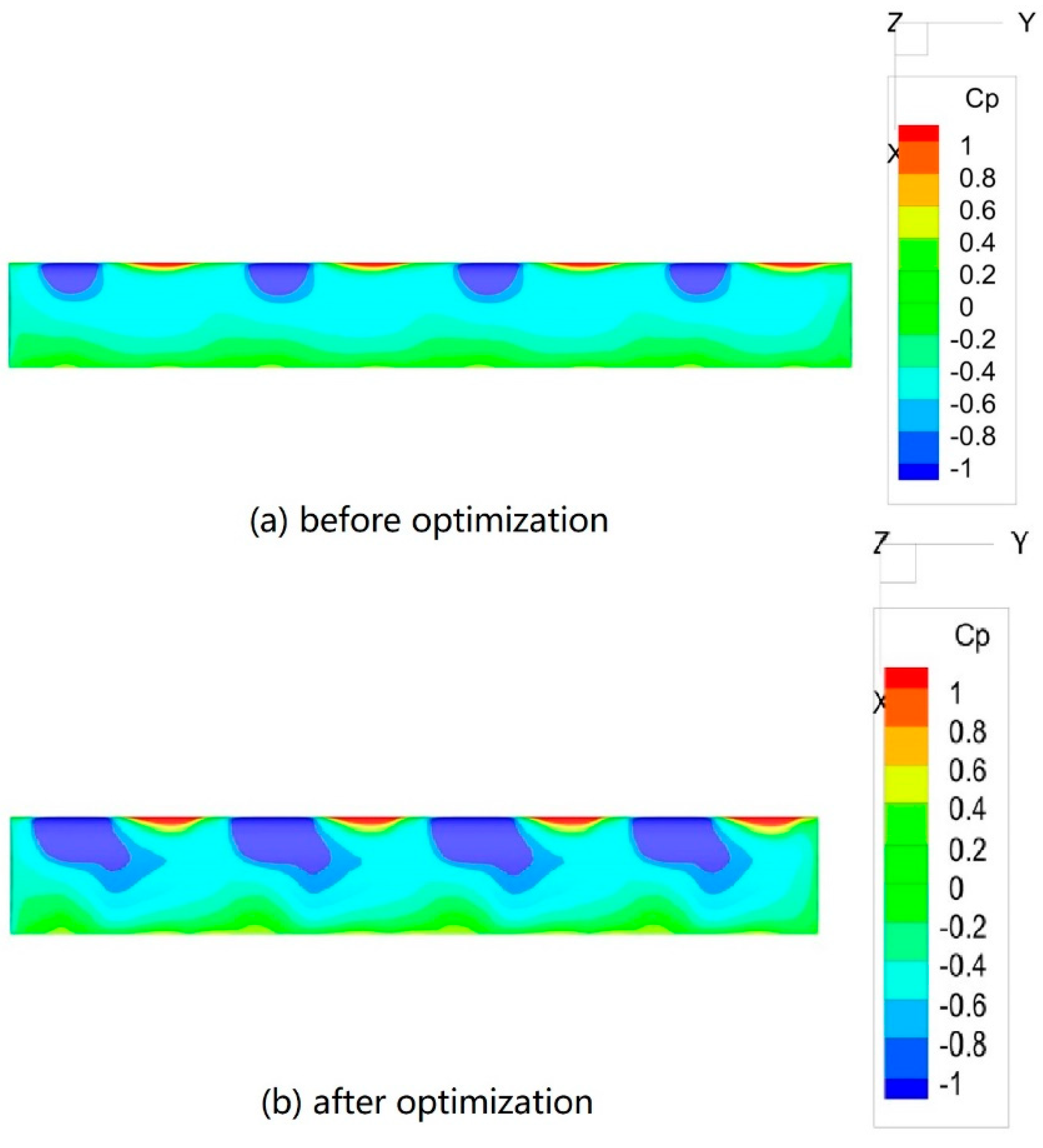
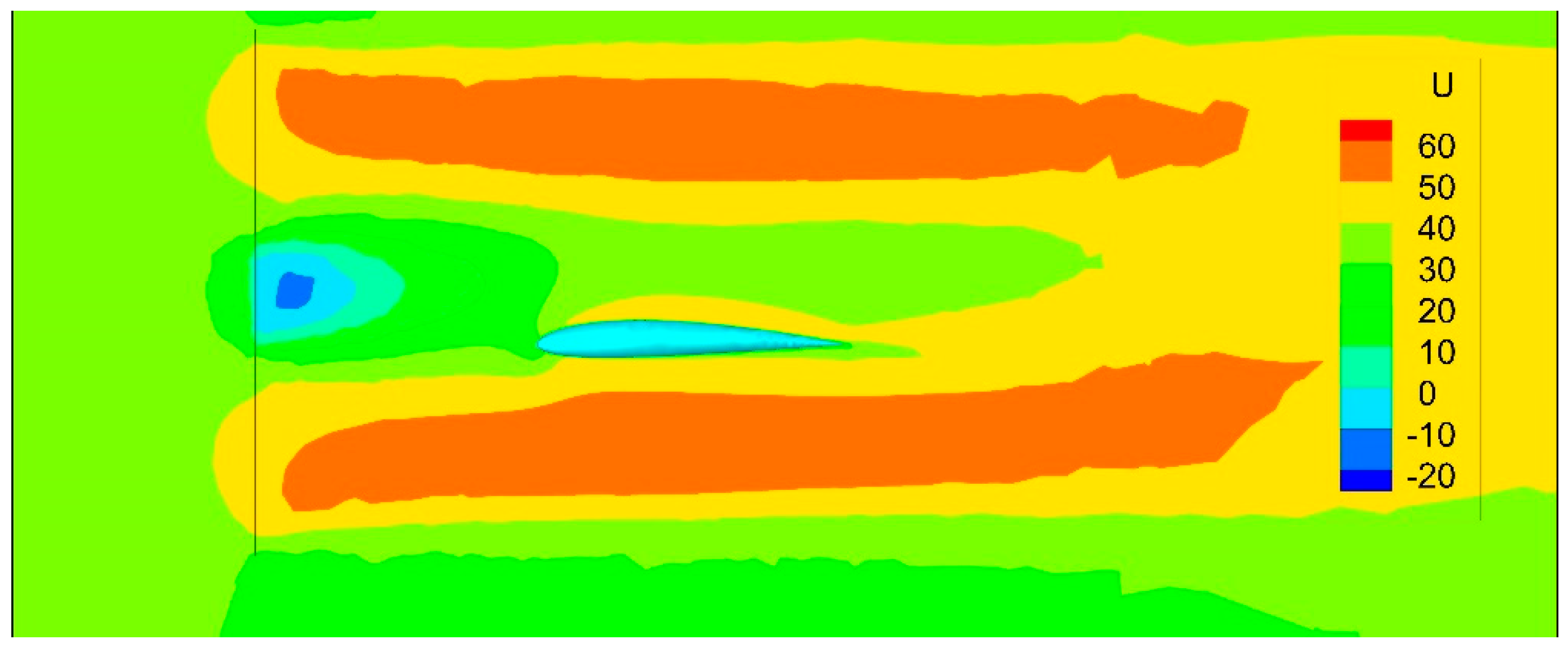
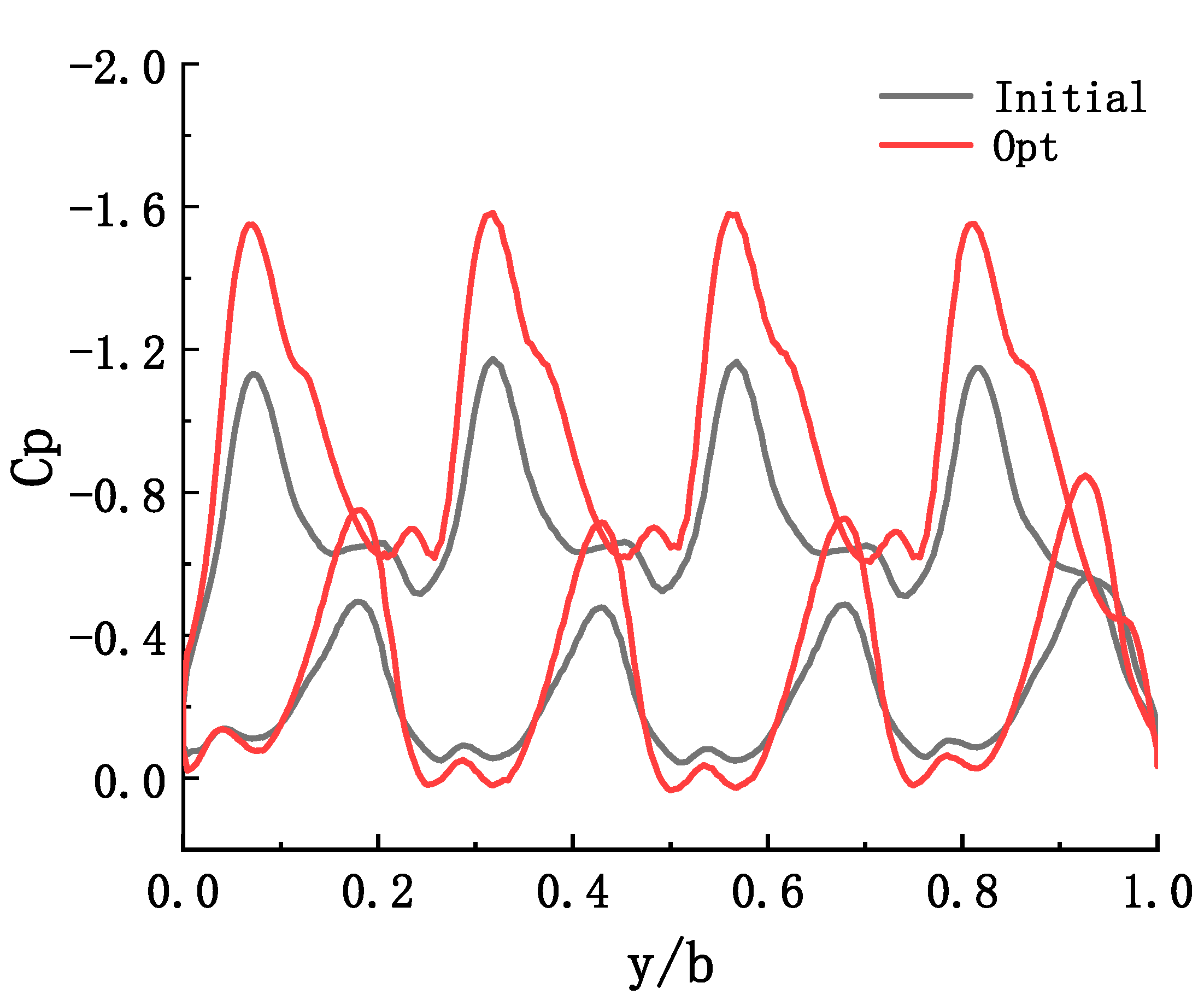
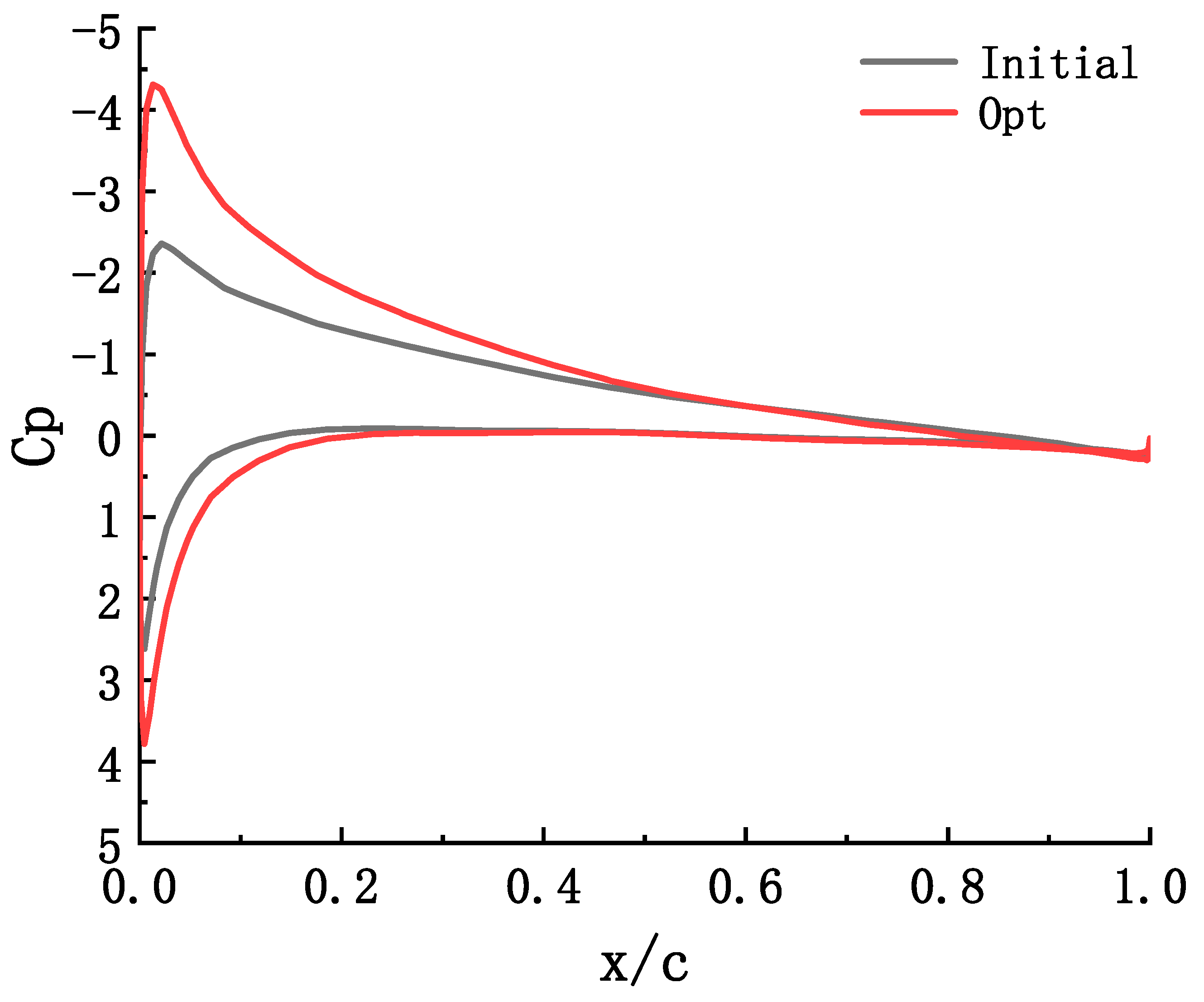
Relative radius	Local blade Angle	c/R	Relative thickness
0.2	39.88°	0.107	0.350
0.3	30.70°	0.144	0.274
0.4	26.60°	0.169	0.204
0.5	23.00°	0.178	0.171
0.6	19.80°	0.172	0.154
0.7	17.00°	0.159	0.146
0.8	14.65°	0.139	0.140
0.9	13.00°	0.117	0.135
1.0	12.00°	0.092	0.130

Table 2. The calculation results of propeller thrust are compared with the test data.

Case	$Experimental values C_{T}$	$Calculated value C_{T}$	Relative error, %
1	0.0655	0.0639	2.43
2	0.0560	0.0538	3.93

Table 3. Specific grid information.

Attribute	Setup
Grid type	Tetrahedral unstructured mesh
Minimum mesh size	0.13 mm
Grid number	2462861
Y+	1.0

Table 4. Propeller variable values before and after optimization.

	Diameter(mm)	Relative height(mm)	Leading edge distance(mm)
Before optimization	150	0	-100
The optimized	172	17	-92

Table 5. Comparison of aerodynamic characteristics of wings before and after optimization.

	Cl	Cd	Cl/Cd
The initial configuration	0.331655	0.019635	16.89101
The optimized	0.490959	0.013941	35.21773
Difference	48.03%	-29.00%	108.50%

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer