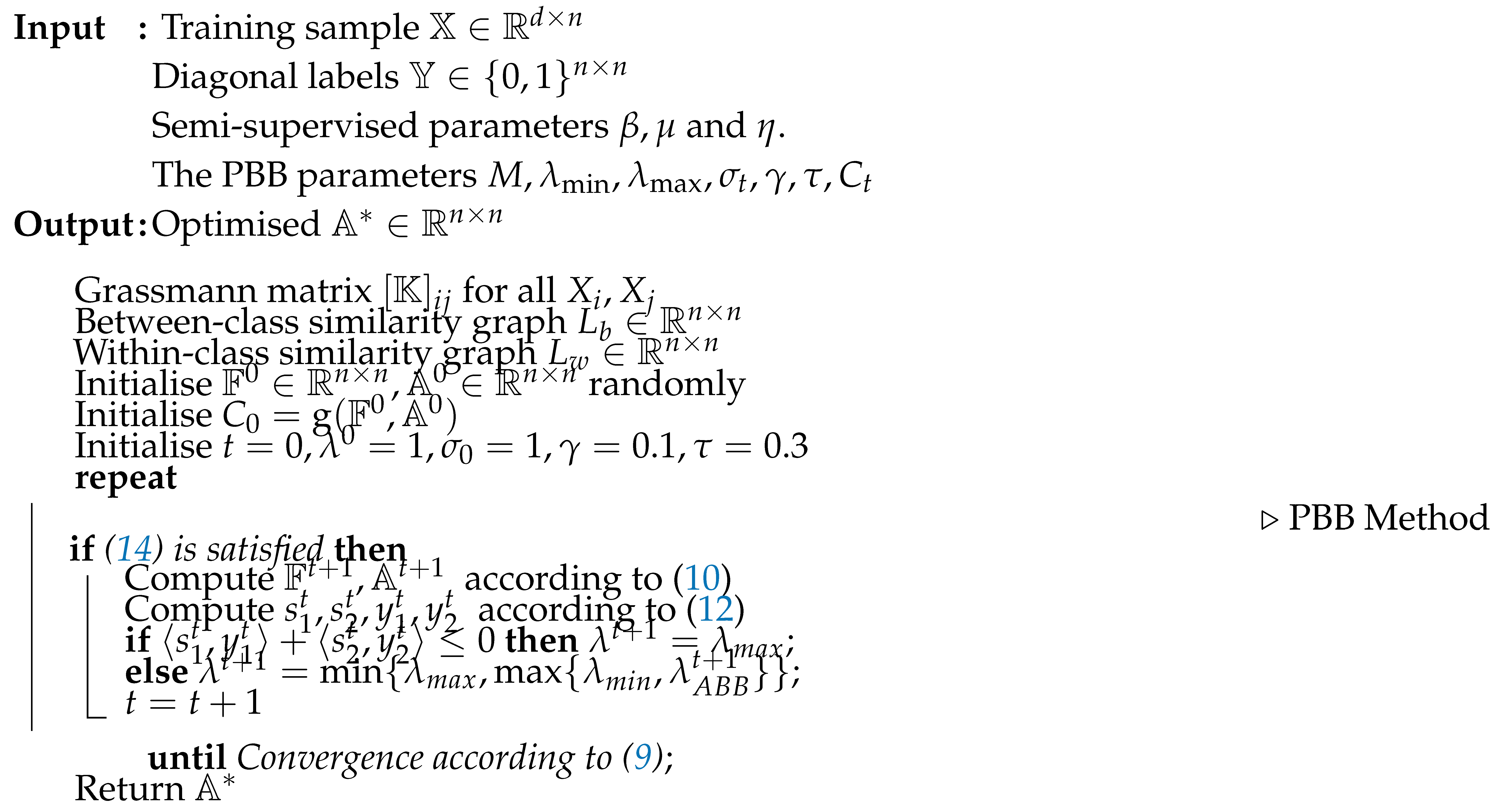Prerpints.org logo
Preprint
Article

Action Recognition via Adaptive Semi-Supervised Feature Analysis

Altmetrics

Downloads

122

Views

42

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

26 May 2023

Posted:

29 May 2023

You are already at the latest version

Alerts
Abstract
This paper presents a new algorithm for semi-supervised action recognition using adaptive feature analysis. We model the samples of the same action as the same manifold and those of different actions as different manifolds, and integrate feature correlation mining and visual similarity mining into a joint framework. By maximizing the separability between different classes based on the labeled data, the proposed algorithm learns multiple features from labeled data and utilizes the intrinsic geometric structure of the data distribution between labeled and unlabeled data to boost the recognition. We introduce Projected Barzilai-Borwein (PBB) to train a subspace projection matrix as classifier. Extensive experiments on three benchmark datasets demonstrate that our algorithm outperforms the existing semi-supervised action recognition algorithms when there are a few labeled training samples.
Keywords: 
Subject: Computer Science and Mathematics  -   Computer Vision and Graphics

1. Introduction

Effective feature representation of videos is key to action recognition. Spatiotemporal features [1,2], subspace features [3,4], and label information [5] have been investigated for action recognition. Correlations between multiple features may provide distinctive information; hence, feature correlation mining has been explored to improve the recognition results when labeled data are scarce [4,6]. However, these approaches may have limitations in learning discriminant features, they have limitations. First, although existing algorithms evaluate the common shared structures among different actions, they do not take inter-class separability into account. Second, current semi-supervised approaches solve the nonconvex optimisation problem by impressive derivation, but the global optimum may not be computed mathematically through alternating least squares (ALS) iterative method.
To overcome the limitations of using multiple features for training, we propose modelling intra-class compactness and inter-manifold separability simultaneously, then capturing high-level semantic patterns via Multiple feature analysis. Considering the optimisation process, we introduce the PBB algorithm because of its effectiveness in obtaining an optimal solution [7]. The PBB method is a non-monotone line-search technique considered for the minimisation of differentiable functions on closed convex sets [8].
Inspired by the research using multiple features [5,6], our framework was extended in a multiple-feature-based manner to improve recognition. We proposed the characterisation of high-level semantic patterns through low-level action features using multiple-feature analysis. Multiple features were extracted from different view of labeled and unlabeled action videos. Based on the constructed graph model, pseudo information of unlabeled videos can be generated by label propagation and feature correlations. For each type of feature, nearby samples preserve the consistency separately, while unlabeled training data perform the label prediction by jointly global consistency of multiple features. Thus, an adaptive semi-supervised action classifier was trained. The main contributions can be summarized as follows:
(1) This work first simultaneously consider manifold learning and Grassmannian kernels in semi-supervised action recognition, as we assume that action videos samples may be found in a Grassmannian manifold space. By modelling a embedding manifold subspace, both inter-class separability and intra-class compactness were considered.
(2) To solve the unconstrained minimisation problem, we incorporate PBB method to avoid matrix inversion, and apply globalisation strategy via adaptive step sizes to render the objective functions non-monotonic, leading to improved convergence and accuracy.
(3) Extensive experiments verified that our method is better than other approaches on three benchmarks in a semi-supervised setting. We believe that this study presents valuable insights in adaptive feature analysis for semi-supervised action recognition.

2. Related Work

We review the related researches on semisupervised action recognition, multiple feature analysis, and embedded subspace representation in this section.

2.1. Semisupervised Action Recognition

Unlabeled samples are valuable for learning data correlations in semi-supervised manner [3,4,9,10]. Although it tends to achieve remarkable performance even with very limited labeled data, there are still many issues in semi-supervised learning techniques, such as suboptimal due to without utilizing the temporal dynamics and inherent multimodal attributes, or obtained pseudo-labels using confident predictions from the model to teach itself [11,12].
Si et al.[13] tackle the challenge of semi-supervised 3D action recognition for effectively learning motion representations from unlabeled data. Singh et al.[14] maximize the similarity of same video at two different speeds, and recognize actions by training a two-pathway temporal contrastive model. Kumar and Rawat[15] detect action video ation via end-to-end semi-supervised learning, which develop a spatio-temporal consistency based approach with two regularization constraints: temporal coherency and gradient smoothness.

2.2. Multiple Feature Analysis

Because we can describe an object by different features which provide different discriminative information, multiple-feature analysis have gained increasing interest in many applications. In the early and late-fusion strategies, multistage fusion schemes have recently been investigated [4,16,17,18]. While the correlations of each feature type have not been considered in most late-fusion approaches.
Wang et al.[19] apply shared structural analysis to characterize discriminative information and preserve data distribution information from each type of feature. Chang and Yang [20] discover shared knowledge from related multi-tasks, take various correlations into account then select features in a batch mode. Huynh-The et al.[21] capture multiple high-level features at image-based representation by fine-tuning pre-trained network, transfer skeleton pose to encoded information and depict an action through spatial joint correlations and temporal pose dynamics.

2.3. Embedded Subspace Representation

Previous studies have shown that manifold subspace learning can mine geometric structure information by considering the space of probabilities as a manifold [22,23,24]. Recent researches focus on graph embedded subspace or distance metric learning to measure activities similarity [25,26,27,28,29].
Rahimi et al.[30] build neighborhood graphs with geodesic distance instead of euclidean distance, and project high-dimensional action to low-dimensional space by kernelized Grassmann manifold learning. Yu et al.[31] propose an action matching network to recognize open-set actions, construct an action dictionary and classifies an action via distance metric. Peng et al.[32] alleviate the over-smoothing issue of graph representation, when multiple GCN layers are stacked by flexible graph deconvolution technique.
The two aforementioned studies [3,4] are similar to ours. They assumed that the visual words in different actions shared a common structure in a specific subspace. A transformation matrix is introduced to characterise the shared structures. They solved the constrained nonconvex optimisation problem by ALS–like iterative approach and matrix derivation. Nevertheless, the deduced inverse matrix is poorly scaled during optimisation or close to singular, that may lead to inaccurate results.
To address these problems, we hypothesise that manifold mapping can preserve the local geometry and maximise discriminatory power. However, we did not aim to mine shared structures. Therefore, we ignored shared-structure regularisation and modelled the manifold by creating two graphs. As the optimisation solution in [3,4] may be mathematically imprecise, Karush-Kuhn-Tucker (KKT) conditions and PBB are introduced to improve algorithm convergence and avoid matrix inversion.
Different from another related research named semisupervised discriminant multimanifold analysis(SDMM) [10], we try to make modifications in two main aspects: multiple feature analysis through manifold subspace projection with combined Grassmannian kernels, unconstrained convex optimisation through non-monotone line search strategy with adaptive step sizes.

3. Proposed Approach

3.1. Formulation

To leverage the multiple feature correlation, n training sample points X = [ X 1 , . . . , X n ] ∈ R d × n are defined from the underlying Grassmannian manifold, where X i ∈ R d × 1 . We aim to uncover a new manifold while preserving the local geometry of data points, that is, α : X i → F i . Since we should demonstrate data distribution on manifold, a predicted label matrix F = [ F 1 , . . . , F n ] ∈ R n × n is defined, where the predicted vector of the i-th datum X i ∈ X is F i ∈ R n × 1 .
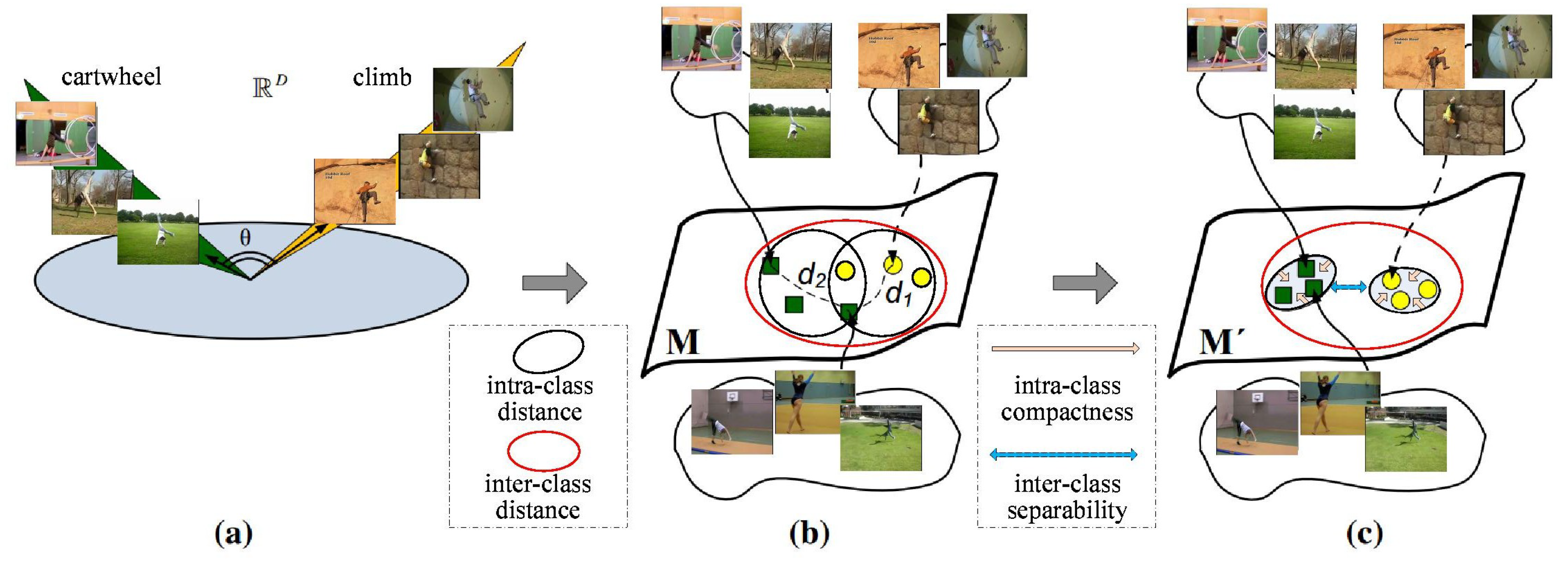
Preprints 74787 g001
Figure 1. An illustration of our method. (a) Video-sets can be represented in R D . We can use the principal angles between them, to compare two actions. (b) Data points on the Grassmannian manifold M can be described as linear subspaces in R D . When points on the manifold having a proper geodesic distance, the video-set matching problem may be converted to a points distance measurement problem. (c) By employing proper Grassmannian kernel, data points can be mapped into another Grassmannian manifold M ′ where same actions become closer while different actions are well separated.
Figure 1. An illustration of our method. (a) Video-sets can be represented in R D . We can use the principal angles between them, to compare two actions. (b) Data points on the Grassmannian manifold M can be described as linear subspaces in R D . When points on the manifold having a proper geodesic distance, the video-set matching problem may be converted to a points distance measurement problem. (c) By employing proper Grassmannian kernel, data points can be mapped into another Grassmannian manifold M ′ where same actions become closer while different actions are well separated.
Preprints 74787 g001
We assume that a similarity measurement of data points on manifold subspace is available through a Grassmannian kernel [22] k i , j = 〈 X i , X j 〉 . By confining the solution to a linear function, that is, α i = ∑ j = 1 n a i j X j , we define the prediction function f as f ( X i ) = F i = ( 〈 α 1 , X i 〉 , 〈 α 2 , X i 〉 , . . . , 〈 α r , X i 〉 ) T . By denoting A l = ( a l 1 , . . . , a l n ) T and K i = ( k i 1 , . . . , k i n ) T , it can be shown that 〈 α l , X i 〉 = A l T K i , and thus, f ( X ) = F = A T K ≈ Y , where A = [ A 1 | A 2 | . . . | A r ] and K = [ K 1 | K 2 | . . . | K n ] . As mentioned in [33], the performance of least square loss function is comparable to hinge loss or logistic loss. This is associated with its diagonal matrix Y = [ Y 1 , . . . , Y n ] ∈ { 0 , 1 } n × n , where Y i ∈ { 0 , 1 } n × 1 is the label matrix. We employed least squares regression to solve the following optimisation problem, then obtain the projection matrix A :
min A ∥ A T K − Y ∥ F 2 + η ∥ A T ∥ F 2 ,
where η is the regularisation parameter. ∥ · ∥ F 2 denotes Frobenius norm. ∥ A T ∥ F 2 controls the model complexity to prevent overfitting.

3.2. Manifold Learning

In contrast to [4], which utilises a graph model to estimate data distribution on manifold, we model the local geometrical structure by generating between-class similarity graph G b and within-class similarity graph G w , where G w ( i , j ) = 1 , if x i ∈ N w ( x j ) or x j ∈ N w ( x i ) , otherwise G w ( i , j ) = 0 . G b ( i , j ) applies the same method, although it selects x i ∈ N b ( x j ) or x j ∈ N b ( x i ) , where N b ( x i ) contains neighbours with different labels, N w ( x j ) is the set of neighbours x j sharing the same label as x i . Notably, the intra-class and inter-class distances be mapped on a manifold by similarity graphs [24].
Inspired by manifold learning [10,22,24], we maximised inter-class separability and minimised intra-class compactness simultaneously. An ideal transform pushes the connected points of A b to the extent possible while moveing the connected points of A w closer. The discriminative information can be represented as follows:
f = 1 2 ∑ i , j = 1 n ( F i − F j ) 2 G w ( i , j ) − 1 2 β ∑ i , j = 1 n ( F i − F j ) 2 G b ( i , j ) = t r ( F T ( L w − β L b ) F ) ,
where β is a regularisation parameter, which controls the trade-off between inter-class separability and intra-class compactness. t r ( · ) denotes the trace operator and L w = D w − G w denotes the Laplacian matrix. Furthermore, D b is a diagonal matrix with D b ( i , i ) = ∑ j = 1 n G b ( i , j ) , and D w is a diagonal matrix with D w ( i , i ) = ∑ j = 1 n G w ( i , j ) .

3.3. Multiple Feature Analysis

Multiple features imply combining kernelized embedding features, data-point manifold subspace learning (1st term in Eq.(4)), label propagation (2nd term in Eq.(4)) with low-level feature correlations (3rd term in Eq.(4)) for labeled and unlabeled data.
We modify the aforementioned function to leverage both labeled and unlabeled samples. First, the training dataset is redefined as X = [ X l T , X u T ] T , where X l = [ X 1 , . . . , X m ] T is the labeled data subset, and X u = [ X m + 1 , . . . , X n ] T is the unlabeled data subset. The label matrix Y = [ Y l T , Y u T ] T , where Y l = [ Y 1 , . . . , Y m ] T ∈ { 1 } m × m . The unlabeled matrix Y u = [ Y m + 1 , . . . , Y n ] T ∈ { 0 } ( n − m ) × ( n − m ) . According to [3,34], diagonal label matrix Y and the similarity graphs G w , G b should be consistent with the label prediction matrix F . We generalised the graph-embedded label consistency as follows:
min F t r ( F T ( L w − β L b ) F ) + ∥ F − Y ∥ F 2 ,
In contrast to previous shared-structure learning algorithms, we did not consider shared-structure learning within a semi-supervised learning framework. Alternatively, we proposed a novel joint framework that incorporates the multiple-feature analyses of multiple manifolds. As discussed in the problem formulation section, by employing the Frobenius norm regularised loss function, we can reformulate the objective:
min F , A t r ( F T ( L w − β L b ) F ) + ∥ F − Y ∥ F 2 + μ ∥ A T K − Y ∥ F 2 + η ∥ A T ∥ F 2 ,
where β > 0 , μ > 0 and η > 0 are regular parameters.
The presented function (4) is an unconstrained convex optimisation problem, hence, we can obtain the global optimum by performing ALS or the projected gradient method. Although the correlation matrix can only be singular under specific circumstances, the projected gradient method can handle the aforementioned issues without matrix inversion [7], and therefore leads to a better optimum than ALS. Notably, the convergence conditions in [3,4] merely depend on a monotone decrease, which may result in mathematically improper convergence; therefore KKT conditions is utilized to consider this problem.

3.4. Grassmannian Kernels

The similarity between two action sample points X i and X j ∈ R d × 1 can be measured by projective kernel combination:
k i , j [ p r o j ] = ‖ X i T X j ‖ F 2 .
One attempt to solve the point matching problem was the notion of principal angles [22]. Given X i and X j , we can define the canonical correlation kernel as
k i , j [ c c ] = max a p ∈ s p a n ( X i ) max b q ∈ s p a n ( X j ) a p T b q ,
subject to a p T a p = b p T b p = 1 and a p T a q = b p T b q = 0 , p ≠ q .
We create a combined Grassmannian kernel through existing Grassmannian kernels [22].
k [ A + B ] = δ [ A ] k [ A ] + δ [ B ] k [ B ] ,
where δ [ A ] , δ [ B ] ≥ 0 . Notably, k [ A ] + k [ B ] defines a new kernel based on the theory of reproducing kernel Hilbert space as described in [22].

3.5. Optimisation

According to [7,8], a general unconstrained minimisation problem can be solved by trace operator and PBB method. Hence, a new objective function g ( F , A ) instead of (4) is defined:
g ( F , A ) = t r ( F T ( L w − β L b ) F ) + t r ( F − Y ) T ( F − Y ) + μ t r ( A T K − Y ) T ( A T K − Y ) + μ η t r ( A A T ) .
If ( F * , A * ) is an approximate stationary point in (8), it must satisfy the KKT conditions in (8). Then, we have a iteration-stopping criterion
∥ ∇ g F ( F * , A * ) ∥ 2 + ∥ ∇ g A ( F * , A * ) ∥ 2 ≤ ε ,
where ε is a non-negative small constant.
Algorithm 1: Kernel Grassmann Manifold Analysis (KGMA)
Preprints 74787 i001

3.6. Projected Barzilai-Borwein

Similar to [7], a sequence of feasible points ( F t , A t ) are generated by the gradient method:
d F t = − λ t ∇ g F ( F t , A t ) , F t + 1 = F t + σ t d F t , d A t = − λ t ∇ g A ( F t , A t ) , A t + 1 = A t + σ t d A t ,
where σ t denotes the non-monotone line search step size and λ t = min { λ m a x , max { λ m i n , λ A B B t } } > 0 is another step size, that is determined through an appropriate selection rule. Following [8], we have two choices for step size
λ B B 1 t + 1 = 〈 s 1 t , s 1 t 〉 + 〈 s 2 t , s 2 t 〉 〈 s 1 t , y 1 t 〉 + 〈 s 2 t , y 2 t 〉 , λ B B 2 t + 1 = 〈 s 1 t , y 1 t 〉 + 〈 s 2 t , y 2 t 〉 〈 y 1 t , y 1 t 〉 + 〈 y 2 t , y 2 t 〉 ,
where
s 1 t = F t + 1 − F t , s 2 t = A t + 1 − A t , y 1 t = ∇ g F ( F t + 1 , A t + 1 ) − ∇ g F ( F t , A t ) , y 2 t = ∇ g A ( F t + 1 , A t + 1 ) − ∇ g A ( F t , A t ) ,
The characteristic of the adaptive step sizes (11) can render the objective functions non-monotonic; hence, g ( F t , A t ) may increase in some iterations. Alternatively, using (11) is better than merely using one of them [8]; the step size is expressed by
λ A B B t = λ B B 1 t , for odd number t λ B B 2 t , for even number t
To guarantee the convergence of ( F t , A t ) , a globalisation strategy based on the non-monotone line-search technique is described as [7]
g ( F t + 1 , A t + 1 ) ≤ C t + γ σ t { 〈 ∇ g F ( F t , A t ) , d F t 〉 + 〈 ∇ g A ( F t , A t ) , d A t 〉 }
where τ ∈ ( 0 , 1 ] , C t are the parameters of the Armoji line-search method [8]. Following [7], in order to overcome some drawbacks of non-monotone techniques, the traditional largest function value is converted by the weighted average function value:
C t = τ · min { t − 1 , M } C t − 1 + g ( F t , A t ) τ · min { t − 1 , M } + 1 ,

4. Experiments

The proposed method, called the Kernel Grassmann Manifold Analysis (KGMA), is summarised in Algorithm 1. The conventional method that uses SPG [10] and ALS method instead of PBB, called kernel spectral projected gradient analysis (KSPG) and kernel alternating least squares analysis (KALS), respectively, was also adopted to solve the objective function (8) for comparison in our experiments.
Features. For handcrafted features, we follow [10] to extracted improved dense trajectories (IDT) and Fisher vector (FV), as shown in Figure 2. For deep-learned features, we retrained the temporal segment network (TSN) [2] models of 15×c, and then extracted the global pool features of 15×c using pretrained TSN model, concatenating rgb+flow into 2048 dimensions with power L2-normalisation, as listed in Table 1.
We verified the proposed algorithm using three kernels: projection kernel k [ p r o j ] , canonical correlation kernel k [ C C ] , and combined kernel k [ p r o j + C C ] . In some cases, k [ p r o j ] is better than k [ C C ] , whereas vice versa, suggesting that the kernels combination is more suitable for different data distributions. For k [ p r o j + C C ] , the mixing coefficients δ [ p r o j ] and δ [ C C ] were fixed at one. We obtain better results by combining δ [ p r o j + C C ] two kernels.
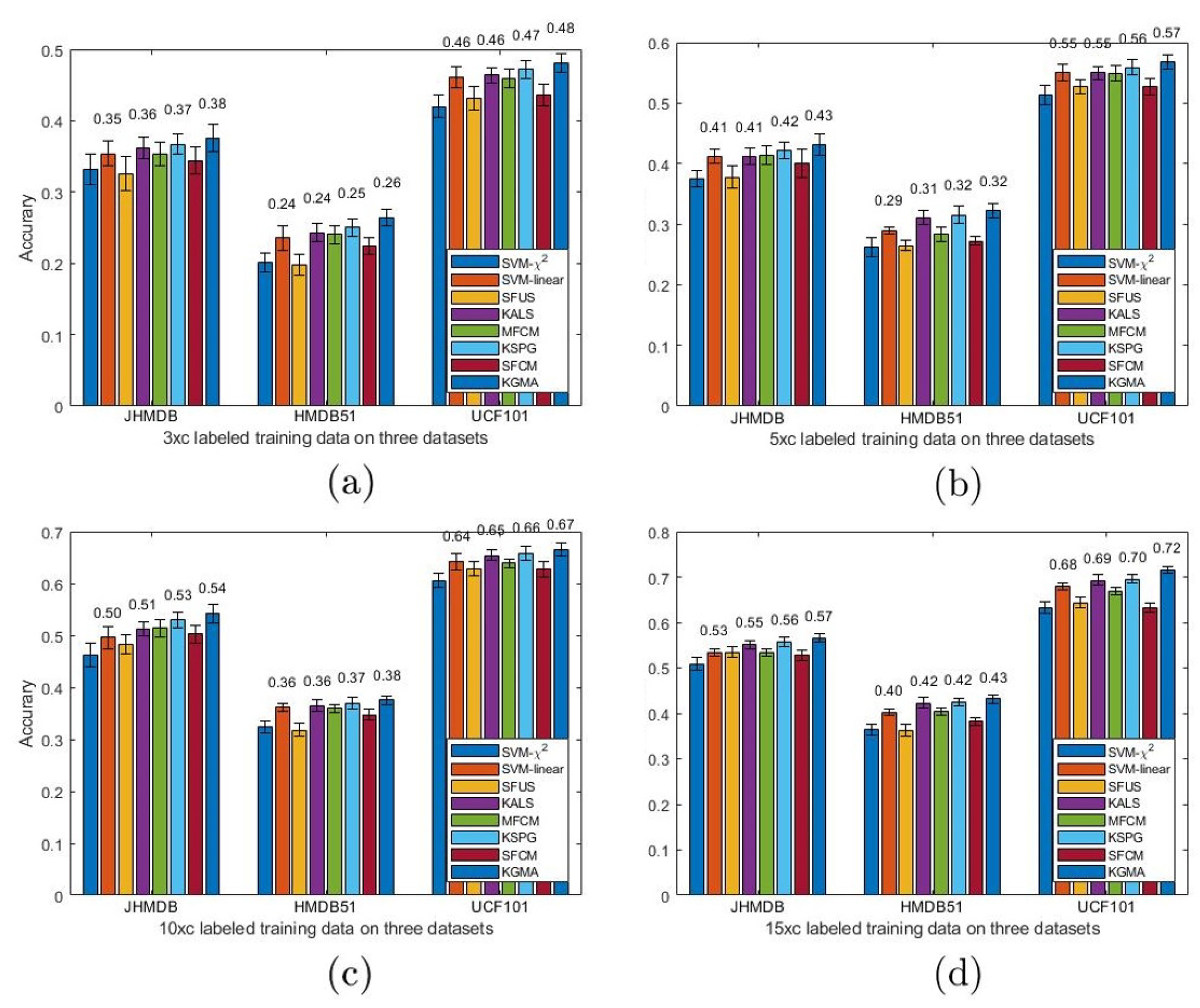
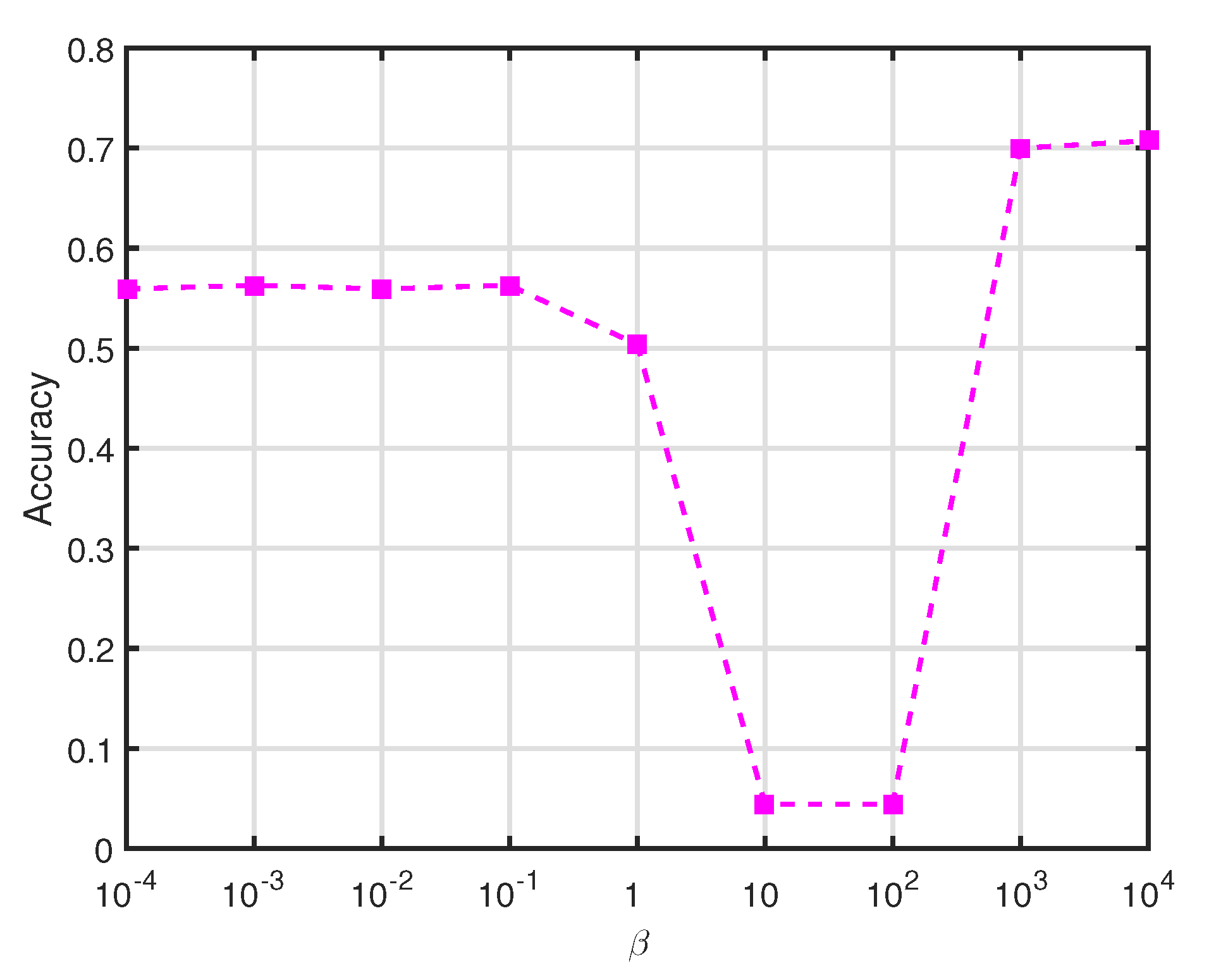
Datasets. Three datasets were used in the experiments: JHMDB, HMDB51, and UCF101 [1]. The JHMDB dataset has 21 action categories. The average recognition accuracies over three training–test splits are reported. The HMDB51 dataset records 51 action categories. We reported the MAP over three training–test splits. The UCF101 dataset includes 101 action categories, containing 13,320 video clips. The average accuracy of the first split was reported.
For the JHMDB dataset, we followed the standard data partitioning (three splits) provided by the authors. For other datasets, we used the first split provided by the authors, and applied the original testing sets for fair comparison. Because the semi-supervised training set contained unlabeled data, we performed the following procedure to reform the training set for each individual dataset. the class number c was denoted for each dataset (c = 21, 51, and 101 for JHMDB, HMDB51, and UCF101, respectively).
Using JHMDB as an example, we first randomly selected 30 training samples per category to form a training set ( 30 × c samples) in our experiment. From this training set, we randomly sampled m videos (m = 3, 5, 10, and 15) per category as labeled samples. Therefore, if m = 10 , 10 × c labeled samples will be available, leaving ( 30 × c − 10 × c ) videos as unlabeled samples for the semi-supervised training setting. We used a standard test set as the test set. Owing to the random selected training samples, the experiments were repeated 10 times to avoid bias.
To demonstrate the superiority of our approach (KGMA), we adopted 8 methods for comparison: SVM, SFUS [35], SFCM [3], MFCU [4], KSPG, and KALS. Notably, SFUS, SFCM, MFCU, KSPG, and KALS are semi-supervised action recognition approaches. Using the available codes, we can facilitate a fair comparison.
Table 1. Comparison with deep-learned features (average accuracy ± std) when 15 × c training videos are labeled
Table 1. Comparison with deep-learned features (average accuracy ± std) when 15 × c training videos are labeled
JHMDB HMDB51 UCF101
SFUS 0.6942 ± 0.0121 0.5217 ± 0.0114 0.7910 ± 0.0087
SFCM 0.7125 ± 0.0099 0.5394 ± 0.0108 0.8070 ± 0.0101
MFCU 0.7154 ± 0.0088 0.5556 ± 0.0098 0.8429 ± 0.0085
SVM- χ 2 0.6931 ± 0.0106 0.5190 ± 0.0095 0.8138 ± 0.0108
SVM-linear 0.7140 ± 0.0086 0.5385 ± 0.0077 0.8450 ± 0.0087
KSPG 0.7287 ± 0.0114 0.5697 ± 0.0833 0.8552 ± 0.0111
KALS 0.7218 ± 0.0087 0.5607 ± 0.0098 0.8411 ± 0.0095
KGMA 0.7361±0.0096 0.5762±0.1040 0.8673±0.0087
For the semi-supervised parameters η , β , μ for SFUS, SFCM, MFCU, KSPG, KALS, and KGMA, we follow the same settings utilised in [3,4], ranging from { 10 − 4 , 10 − 3 , 10 − 2 , 10 − 1 , 1 , 10 1 , 10 2 , 10 3 , 10 4 }. Because the PBB parameters were not sensitive to our algorithm, we initialised the parameters as in [7], as indicated in Algorithm 1. Notably, since KGMA applied PBB to solve the optimal value of objective function (8), it resulted in non-monotonic convergence with oscillating objective function values, as shown in Figure 3. Thus, using only the absolute error made it difficult to determine when to stop iterating, relative error of objective function values was better than absolute error, which may be mathematically improper convergence. We chose constant ε = 10 − 4 as the iteration-stopping criterion in (9).
Mathematical Comparisons. The recognition results with handcrafted features on three datasets were demonstrated in Figure 2. We compared our method with deep-learned features in Table 1.
Regarding the presented objective function 8, Figure 3 summarized the computational results of the three optimization methods. When we used the 2048-dimensional deep-learned features TSN on JHMDB dataset, the model was trained with only 15 labeled samples and 15 unlabeled samples per class, setup the same semi-supervised parameters η , β , μ , then the performance differences during the solving of the same objective function could be compared in terms of running time, number of iterations, absolute error, relative error, and objective function value. Figure 3 shown the convergence curves of three optimization methods. Since both SPG and PBB were non-monotonic optimization methods with relatively large fluctuations in objective function values, we omitted the first 29 iterations of SPG and PBB in Figure 3, and only displayed the data starting from the 30th iteration, so as to better illustrate the monotonic convergence process of ALS.
As shown in Table 2, for a randomly selected video data sample, ALS exhibited the fewest iterations, shortest running time and fastest computation speed of 0.1220 seconds after extracting the deep features by TSN. In contrast, PBB exhibited the most iterations, longest running time and slowest computation speed of 0.4212 seconds; while SPG’s performance were intermediate between ALS and PBB. Considering Figure 3 and Table 2, it is evident that despite using the PBB optimization method, our KGMA algorithm still achieves the highest accuracy on the kernelized Grassmann manifold space. Nevertheless, the equation 9 using SPG results in marginal improvement over ALS, which likely attributable to our novel kernelized Grassmann manifold space.
Performance on Action Recognition. A linear SVM was utilised as the baseline. Based on the comparisons, we observe the following:1) KGMA achieved the best performance, our semi-supervised algorithm was better than linear SVM which is widely-used supervised classifiers; 2) all methods achieved better performances using more labeled training data, as shown in Figure 2, or enlarging semi-supervised parameter (i.e., η , β , μ ) range such as Figure 4; 3) we averaged an accuracy of 3 × c , 5 × c , 10 × c , and 15 × c cases, and the recognition of KGMA on JHMDB, HMDB51, and UCF101 improved by 2.97%, 2.59%, and 2.40%, respectively. When using TSN features, the recognition of our KGMA on above-mentioned datasets improved by 2.21%, 3.77%, and 2.23%, respectively. Evidently, our semi-supervised method can improve recognition by leveraging unlabeled data compared to linear SVM with labeled data merely. Figure 2 illustrated that our algorithm benefits from the multiple-feature analysis, kernelized Grassman space and iterative skills of PBB method.
These results can be attributed to several factors. First, our method not only leverages semi-supervised approaches, but also leverages intra-class action variation and inter-class action ambiguity simultaneously. Therefore, ours gain more significant performance than other approaches when there are few labeled samples. Second, we uncover the action feature subspace on Grassmannian manifold by incorporating Grassmannian kernels, and solve the objective function optimisation by adaptive line-search strategy and PBB method mathematically. Hence, the proposed algorithm works well in few labeled case.
Convergence Study. According to the objective function (4), we conducted experiments with the TSN feature, fixed the semi-supervised parameters η , β , μ , and then executed both the ALS and PBB methods 10 times. The results of the study are listed in Table 2. Although no oscillation exists in the convergence of the ALS and it requires fewer iterations, the PBB method can outperform the ALS for three reasons. First, the PBB method uses a non-monotone line-search strategy to globalise the process [8], which can obtain the global optimal objective function value rather than being trapped in local optima using the monotone ALS method. Second, the character of adaptive step sizes is an essential characteristic that determines efficiency in the projected gradient methodology [8], whereas the iteration step skill has not been considered in ALS. Finally, the efficient convergence properties of the projected gradient method have been demonstrated because the PBB is well defined [8].
Computation Complexity. In the training stage, we computed the Laplacian matrix L, the complexity of which was O ( n 2 ) . To optimise the objective function, we computed the projected gradient and trace operators of several matrices. Therefore, the complexity of these operations was O ( n 3 ) .
Parameter Sensitivity Study. We verified that KGMA benefits from the intra-class and inter-class by manifold discriminant analysis, as shown in Figure 4. We analysis the impact of manifold learning on JHMDB and HMDB51, set η = 10 3 and μ = 10 − 1 at optimal values over split2, for 15 × c -labeled training data. As β varied from 10 − 4 to 10 4 , the accuracy oscillated significantly and reached a peak value when β = 10 4 . Since β controls the proportion of the intra-class local geometric structure and the inter-class global manifold structure, as shown in Figure 4. when the intra-class local geometric structure is treated as a constant 1, β 1 can be considered that the inter-class global manifold structure has a larger proportion in the objective function, and vice versa. When β = 0 , no inter-manifold structure is utilised; thus, if β → + ∞ , no intra-class structure is present. When the Grassmann manifold space leverages an adequate balance of intra-class action variation and inter-class action ambiguity, the proposed algorithm can further enhance the discriminatory power of the transformation matrix.

5. Conclusion

This study proposed a new approach to categorise human action videos. With Grassmannian kernels combination and multiple-feature analysis on multiple manifolds, our method can improve recognition by uncovering the intrinsic features relationships. We evaluated the presented approach on three benchmark datasets, and experiment results show ours outperformed all competing methods, particularly when there are few labeled samples.

References

  1. Wang, H.; Dan, O.; Verbeek, J.; Schmid, C. A Robust and Efficient Video Representation for Action Recognition. IJCV 2016, 119, 219–238. [Google Scholar] [CrossRef]
  2. Wang, L.; Xiong, Y.; Wang, Z.; Qiao, Y.; Lin, D.; Tang, X.; Van Gool, L. Temporal segment networks: towards good practices for deep action recognition. ECCV, 2016.
  3. Wang, S.; Yang, Y.; Ma, Z.; Li, X. Action recognition by exploring data distribution and feature correlation. CVPR, 2012, pp. 1370–1377.
  4. Wang, S.; Ma, Z.; Yang, Y.; Li, X.; Pang, C.; Hauptmann, A.G. Semi-Supervised Multiple Feature Analysis for Action Recognition. IEEE Transactions on Multimedia 2014, 16, 289–298. [Google Scholar]
  5. Luo, M.; Chang, X.; Nie, L.; Yang, Y.; Hauptmann, A.G.e.a. An Adaptive Semisupervised Feature Analysis for Video Semantic Recognition. IEEE Transactions on Cybernetics 2018, 48, 648–660. [Google Scholar] [CrossRef] [PubMed]
  6. Chang, X.; Yang, Y. Semisupervised Feature Analysis by Mining Correlations Among Multiple Tasks. IEEE TNNLS 2017, 28, 2294–2305. [Google Scholar] [CrossRef]
  7. Liu, H.; Li, X. Modified subspace Barzilai-Borwein gradient method for non-negative matrix factorization. Computational Optimization and Applications 2013, 55, 173–196. [Google Scholar]
  8. BARZILAI. ; JONATHAN.; BORWEIN.; Jonathan, M. Two-Point Step Size Gradient Methods. Journal of Numerical Analysis 1988, 8, 141–148. [Google Scholar] [CrossRef]
  9. Harandi, M.T.; Sanderson, C.; Shirazi, S.; Lovell, B.C. Kernel analysis on Grassmann manifolds for action recognition. Pattern Recognition Letters 2013, 34, 1906–1915. [Google Scholar]
  10. Xu, Z.; Hu, R.; Chen, J.; Chen, C.; Jiang, J.; Li, J.; Li, H. Semisupervised discriminant multimanifold analysis for action recognition. IEEE transactions on neural networks and learning systems 2019, 30, 2951–2962. [Google Scholar] [CrossRef] [PubMed]
  11. Xiao, J.; Jing, L.; Zhang, L.; He, J.; She, Q.; Zhou, Z.; Yuille, A.; Li, Y. Learning from temporal gradient for semi-supervised action recognition. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2022, pp. 3252–3262.
  12. Xu, Y.; Wei, F.; Sun, X.; Yang, C.; Shen, Y.; Dai, B.; Zhou, B.; Lin, S. Cross-model pseudo-labeling for semi-supervised action recognition. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2022, pp. 2959–2968.
  13. Si, C.; Nie, X.; Wang, W.; Wang, L.; Tan, T.; Feng, J. Adversarial self-supervised learning for semi-supervised 3d action recognition. Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, –28, 2020, Proceedings, Part VII 16. Springer, 2020, pp. 35–51. 23 August.
  14. Singh, A.; Chakraborty, O.; Varshney, A.; Panda, R.; Feris, R.; Saenko, K.; Das, A. Semi-supervised action recognition with temporal contrastive learning. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2021, pp. 10389–10399.
  15. Kumar, A.; Rawat, Y.S. End-to-end semi-supervised learning for video action detection. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2022, pp. 14700–14710.
  16. Bi, Y.; Bai, X.; Jin, T.; Guo, S. Multiple feature analysis for infrared small target detection. IEEE Geoscience and Remote Sensing Letters 2017, 14, 1333–1337. [Google Scholar]
  17. Shahroudy, A.; Ng, T.T.; Gong, Y.; Wang, G. Deep multimodal feature analysis for action recognition in rgb+ d videos. IEEE transactions on pattern analysis and machine intelligence 2017, 40, 1045–1058. [Google Scholar] [CrossRef] [PubMed]
  18. Khaire, U.M.; Dhanalakshmi, R. Stability of feature selection algorithm: A review. Journal of King Saud University-Computer and Information Sciences 2022, 34, 1060–1073. [Google Scholar] [CrossRef]
  19. Wang, S.; Ma, Z.; Yang, Y.; Li, X.; Pang, C.; Hauptmann, A.G. Semi-supervised multiple feature analysis for action recognition. IEEE transactions on multimedia 2013, 16, 289–298. [Google Scholar]
  20. Chang, X.; Yang, Y. Semisupervised feature analysis by mining correlations among multiple tasks. IEEE transactions on neural networks and learning systems 2016, 28, 2294–2305. [Google Scholar] [CrossRef]
  21. Huynh-The, T.; Hua, C.H.; Ngo, T.T.; Kim, D.S. Image representation of pose-transition feature for 3D skeleton-based action recognition. Information Sciences 2020, 513, 112–126. [Google Scholar] [CrossRef]
  22. Harandi, M.T.; Sanderson, C.; Shirazi, S.; Lovell, B.C. Graph embedding discriminant analysis on Grassmannian manifolds for improved image set matching. CVPR, 2011.
  23. Yan, Y.; Ricci, E.; Subramanian, R.; Liu, G.; Sebe, N. Multitask linear discriminant analysis for view invariant action recognition. IEEE Transactions on Image Processing 2014, 23, 5599. [Google Scholar]
  24. Jiang, J.; Hu, R.; Wang, Z.; Cai, Z. CDMMA: Coupled discriminant multi-manifold analysis for matching low-resolution face images. Signal Processing 2016, 124, 162–172. [Google Scholar] [CrossRef]
  25. Markovitz, A.; Sharir, G.; Friedman, I.; Zelnik-Manor, L.; Avidan, S. Graph embedded pose clustering for anomaly detection. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2020, pp. 10539–10547.
  26. Manessi, F.; Rozza, A.; Manzo, M. Dynamic graph convolutional networks. Pattern Recognition 2020, 97, 107000. [Google Scholar] [CrossRef]
  27. Cai, J.; Fan, J.; Guo, W.; Wang, S.; Zhang, Y.; Zhang, Z. Efficient deep embedded subspace clustering. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2022, pp. 1–10.
  28. Islam, A.; Radke, R. Weakly supervised temporal action localization using deep metric learning. Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, 2020, pp. 547–556.
  29. Ruan, Y.; Xiao, Y.; Hao, Z.; Liu, B. A nearest-neighbor search model for distance metric learning. Information Sciences 2021, 552, 261–277. [Google Scholar] [CrossRef]
  30. Rahimi, S.; Aghagolzadeh, A.; Ezoji, M. Human action recognition based on the Grassmann multi-graph embedding. Signal, Image and Video Processing 2019, 13, 271–279. [Google Scholar] [CrossRef]
  31. Yu, J.; Kim, D.Y.; Yoon, Y.; Jeon, M. Action matching network: open-set action recognition using spatio-temporal representation matching. The Visual Computer 2020, 36, 1457–1471. [Google Scholar]
  32. Peng, W.; Shi, J.; Zhao, G. Spatial temporal graph deconvolutional network for skeleton-based human action recognition. IEEE signal processing letters 2021, 28, 244–248. [Google Scholar] [CrossRef]
  33. Fung, G.M.; Mangasarian, O.L. Multicategory Proximal Support Vector Machine Classifiers. Machine Learning 2005, 59, 77–97. [Google Scholar] [CrossRef]
  34. Yang, Y.; Wu, F.; Nie, F.; Shen, H.T.; Zhuang, Y.; Hauptmann, A.G. Web and Personal Image Annotation by Mining Label Correlation With Relaxed Visual Graph Embedding. IEEE Transactions on Image Processing 2012, 21, 1339–1351. [Google Scholar] [CrossRef] [PubMed]
  35. Ma, Z.; Nie, F.; Yang, Y.; Uijlings, J.R.R.; Sebe, N. Web Image Annotation Via Subspace-Sparsity Collaborated Feature Selection. IEEE Transactions on Multimedia 2012, 14, 1021–1030. [Google Scholar] [CrossRef]
Preprints 74787 g002
Figure 2. Comparison (average accuracy±std) with IDT+FV when different number of training samples are labeled, gmmSize=16.
Figure 2. Comparison (average accuracy±std) with IDT+FV when different number of training samples are labeled, gmmSize=16.
Preprints 74787 g002
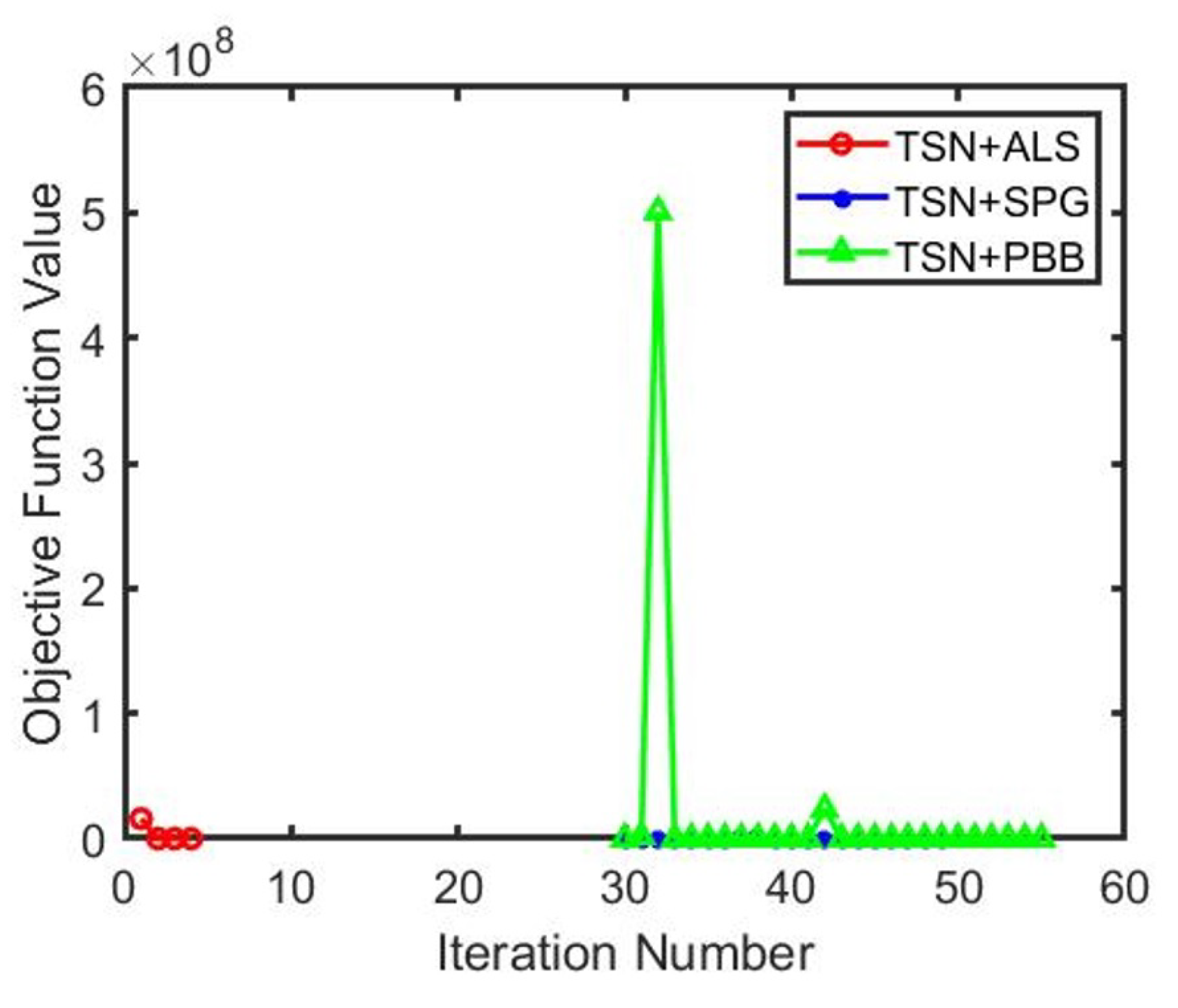
Preprints 74787 g003
Figure 3. The convergence curves of the three optimization methods on the JHMDB dataset, with the final convergence results shown in Table 2. Due to the larger oscillations of PBB, the data for the first 29 iterations of SPG and PBB have been omitted here in order to better illustrate the comparative convergence of ALS, SPG and PBB.
Figure 3. The convergence curves of the three optimization methods on the JHMDB dataset, with the final convergence results shown in Table 2. Due to the larger oscillations of PBB, the data for the first 29 iterations of SPG and PBB have been omitted here in order to better illustrate the comparative convergence of ALS, SPG and PBB.
Preprints 74787 g003
Preprints 74787 g004
Figure 4. Accuracy on JHMDB using TSN, w.r.t the parameter β with fixed η and μ .
Figure 4. Accuracy on JHMDB using TSN, w.r.t the parameter β with fixed η and μ .
Preprints 74787 g004
Table 2. Mathematical results on JHMDB using 15 × c labeled training samples, "Obj-Val" means objective function value.
Table 2. Mathematical results on JHMDB using 15 × c labeled training samples, "Obj-Val" means objective function value.
Methods Features(dim*nSample) Parameters Times(s) Iter. Error Relative Error Obj-Val
ALS TSN (2048*660) η = 0.001 , β = 0.01 , μ = 0.001 0.4880 4 0.5972 2.0691 × 10 − 4 2.0137
SPG TSN (2048*660) η = 0.001 , β = 0.01 , μ = 0.001 6.1992 49 0.4706 8.1024 × 10 − 4 32.0130
PBB TSN (2048*660) η = 0.001 , β = 0.01 , μ = 0.001 23.5855 56 0.6146 7.1873 × 10 − 4 10.0185
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated