Introduction
In recent years, formation tracking control of underactuated surface vessels (USVs) has gained compelling interests, as they can be widely used in ocean engineering fields [
1]. Compared with a single vessel, formation has many advantages. In the course of ocean exploration, the efficiency of a single vessel is low. Beyond that, formation can perform the complex tasks such as pursuing tasks that usually cannot accomplished by a single vessel. There are various formation control schemes include leader–follower approach [
2][
3], virtual structure [
4], graph-based mechanism [
5]. In particular, the leader-follower strategy is preferred in ocean engineering applications. The follower maintains a desired relative distance and angle with the leader, a reference trajectory can be defined by the leader. Therefore, the group behavior is directed by the leader, and the formation stability can be induced by the control law of single vessel.
There are two main challenges which are still worth mentioning. The first challenge is actuator saturation, it can severely degrade the closed-loop system performance [
6]. In practice, each actuator of vessel can only provide a limited force or torque. To reduce the risk of actuator saturation and enhance system performance, some methods are proposed in recent years. To avoid a poor tracking performance in formation control, generalized saturation functions combined with formation tracking errors are employed to handle the input saturation problem [
7]. To solve the input saturation and underactuated problems simultaneously, additional variables are induced to velocity errors in the body-fixed frame [
8] [
9]. Nonlinear saturation of actuator is approximated by a Gauss error function [
10], such that anti-saturation controller can be designed. An auxiliary dynamic system is constructed to solve the input saturation problem [
11]. The auxiliary dynamic system is designed as a second-order system, and it provides a conservative input signal. A first-order auxiliary system is designed [
12], it is employed to deal with input saturation of rudder. However, the limited acting frequency of actuator is not considered in the above articles.
High-frequency action may lead not only to mechanical abrasion but also to a short service life [
13]. Input saturation and actuator rate limits are considered in [
14], and a nonlinear controller is designed based on dynamic surface control and a backstepping technology. [
15] consider actuator saturation containing limited magnitude and rate, and design a sliding model controller. In [
14] and [
15], Zeno behavior is avoided because the acting frequency of actuator is bounded. A controller combined with an event-triggered condition is proposed in [
16], and the triggered condition is designed based on the flow time and error function. It still causes a large action times of actuator. [
17] propose an event-triggered control law, and an event-triggered mechanism is used to reduce the execution frequency of actuators. The event-triggered mechanism is designed in the controller-to-actuator channel, the execution rate of the actuator are reduced.
Table 1.
Notations and variables used in this paper.
Table 1.
Notations and variables used in this paper.
|
n dimensional Euclidean Space |
|
Absolute value of a variable |
|
Minimum eigenvalue of a matrix |
|
Minimum value of a set |
| inf
|
Supremum of a set |
|
Transpose of a matrix |
|
Euclidean norm of a vector |
|
Diagonal matrix |
|
dimensional identity matrix |
|
dimensional zero matrix. |
|
, , ,
|
Position and yaw of the ith USV and the leader j
|
|
, , , , ,
|
surge velocity, sway velocity and yaw rate of the ith USV and the leader j
|
|
, ,
|
inertia mass of the ith USV |
|
Hydrodynamic damping parameters and disturbances |
|
Input signals of the ith USV |
|
,
|
,
|
|
,
|
,
|
|
|
|
Rotation matrices of the ith USV |
|
calculated by the proposed controller |
|
The mismatch function between input
without saturation and with saturation |
|
,
|
Relative distance and
angle between the ith USV and the leader j
|
|
,
|
Desired distance and angle |
|
Estimate of variable x
|
|
Previous event-triggering time instant |
|
Transmitted signal between and
|
|
Event-triggered mechanism |
|
Estimation error of variable x
|
|
Formation tracking error vector |
|
Estimator used to estimate velocity of the leader |
|
Time constants of the first-order filters |
|
Yaw tracking error |
|
Virtual controls |
|
Auxiliary variables |
|
Errors caused by the first order filter |
|
,
|
Control laws at the kinetic level |
The second significant challenge is the uncertainties. Because of the working condition of surface vessel, the uncertainties contain model uncertainties and environmental disturbances. In [
18], the proposed controller is robust to the parameter uncertainties of the nonlinear terms and exogenous disturbances. Unknown plant parameters and environment disturbances are solved by using a parameter estimation and upper bound estimation in [
19]. In [
20], a robust adaptive control algorithm is proposed to solve uncertain parameters. Adaptive estimators are designed to estimate unknown time-varying functions of vessel model in [
21]. Considering the leader-follower formation tracking problem, a neural network is used to approximate the uncertainties, and the uncertainties are compensated by on line learning [
22]. A cooperative controller is proposed by using position–heading measurements only in [
23], where an extended state observer (ESO) is constructed to provide the estimations of velocity, yaw rate and the uncertainties. However, the existing observers presented in [
9,
11,
13,
17,
23,
24] rely on continuous sampling. In each execution cycle signals are transmitted, which means that many network resources and calculation resources are consumed. To remove unnecessary calculation and communication, an event-triggered extended state observer (ETESO) is proposed in [
25]. In [
26], an ETESO is proposed for a class of nonlinear networked control systems, and the state estimation problem is solved. As for USVs, when their working mode is tracking control, in most cases, yaw angle is unchanging. In the common continuous observer, the signals have to be transmitted during each execution cycle, which will consume many network resources and calculation resources. Therefore, it is rewarding to design a leader-follower tracking controller with light transmission load and less action times of actuator.
Based on the above research background, this paper investigates leader–follower formation tracking control of USVs subject to input saturation, model uncertainties and environmental disturbances. Inspired by the works in [
23] and [
16], an improved output feedback controller is proposed. Firstly, an ETESO is used to recover the velocity data, model uncertainties and disturbances. In each execution cycle, an event-triggered strategy is monitored to determine whether or not to transmit the position and head informations to the observer. Sensor-to-observer communication costs are drastically reduced. Secondly, an estimator is employed to estimate velocity of the leader and reduce the amount of data exchanged in formation. Thirdly, auxiliary variables provide a solution of input saturation and underactuated problem. Then, an event-triggered controller (ETC) is designed based on the ETESO, the estimator and auxiliary variables. Finally, the stability of closed-loop system is proved. Simulations demonstrate the proposed control strategy.
Two salient features of the proposed control are summarized as follows. First, an estimator is employed to estimate the velocity of the leader, the embedded processor of each follower does reading computations only use the position and yaw of the leader, the transmission loads between formation are saved. Second, an event-triggered mechanism is designed in the controller-to-actuator channel, action times of actuator are reduced.
Compared with the existing related results, the novelty of this paper is summarized as follows. First, different from the existing formation control approaches [
23] and [
17], velocity of the leader is estimated by an estimator, which reduce the amount of data exchanged between USVs. Second, compared with the observer proposed in [
23], the ETESO can reduce sensor-to-observer communication costs. Third, compared with the strategy proposed in [
16], the proposed control law can largely reduce the action times of actuator.
The rest sections are organized as follows. A table of notations containing some used variables in the paper is presented. Section II describes the preliminaries and problem formulation. Section III describes observer design, Section IV gives controller design and stability analysis. Simulation results are presented in Section V. Section VI concludes this paper.
1. Problem formulation
A group of USVs consists
N USVs, and the model of the
ith USV is given as [
27]
and
where
is the position, and
is the yaw angle.
is the surge velocity,
is the sway velocity,
is the yaw rate.
and
denote the inertia mass. The uncertainties
,
and
contain Coriolis parameters, hydrodynamic damping parameters and time-varying disturbances.
and
are input signals.
To facilitate observer design and analysis, the
ith USV model is written as
where
,
,
,
,
is the inertia mass.
,
The mismatch function between input without saturation and with saturation is described as , where with and are surge force and yaw moment calculated by the proposed controller, respectively. . Then, the saturated control is given by .
Assumption 1: The unknown function satisfies with is a positive constant.
a vector containing velocity, Coriolis parameters, hydrodynamic damping parameters and time-varying disturbances. It is natural to assume that their derivatives are bounded. Control inputs to drive USVs are bounded, Assumption 1 is reasonable.
Assumption 2: Velocity of the ith USV is bounded, such that , is a positive constant.
The control inputs to drive USVs are bounded, the energy of external disturbances is limited. Therefore, Assumption 2 is reasonable.
Assumption 3: The desired distance and angle are bounded.
Assumption 3 means that the desired value is reasonable.
The following definitions are made.
The subscript j is the index of the leader j. is used to denote the position and yaw of the leader j. is the velocity and yaw rate of the leader j.
The relative distance
and angle
between the
ith USV and the leader
j are expressed as
The differential equations of
and
are given by:
From
and
, then
The control objective is to design an event-trigged control law for USVs to track the leader with desired distance and angle .
Remark 1. In the controller design process, the ith USV track the the jth USV by using the informations , and . It means that the communication costs between the multiple USVs are not saved.
2. Event-triggered extended state observer
An ETESO is developed for estimating the uncertainties containing model uncertainties and time-varying disturbances, and an event-triggered condition is employed to avoid unnecessary communications. Inspired by [
25], an ETESO is designed as follow:
where
,
and
.
and
are the estimates of
and
, respectively.
is a positive constant and
is the transmitted signal given by
is the previous event-triggering time instant and
is an event-triggered mechanism designed as
is design threshold and
Remark 2. The continuous-time control scheme is emulated by computer with sampler and zero-order holder, and the control command is updated periodically. At each sampling instant, is monitored to determine whether or not to transmit the information to the observer. If , the event-triggering time instant is updated to the current time t, and is transmitted to the observer. Otherwise, only is available to the observer. The first event-triggering time is .
To facilitate controller design and stability analysis, define
, () can be written as
with
Define
,
,
,
,
,
,
Theorem 1. Consider the USVs model (
7) and (8), the ETESO (15), (16) and (17), and the event-triggering condition (19). If Assumptions 1 and 2 are satisfied, there exist
and
such that for any
,
Proof. Along with (18) and (19), the event-triggering mechanism can be described as
When
, the sample error
becomes
Using Assumption 2, it obtains that
There exists and , such that . Notes that , so it can draw a conclusion that .
Theorem 1 shows that Zeno behavior can be avoided by using the proposed observer. Next, the error dynamics of the proposed ETESO are investigated.
To facilitate the stability analysis, define
, and the error dynamics (30)-(32) can be expressed as
and
.
Using a transformation
with
, it follows that
where
,
, and
Theorem 3. The observer error dynamics are bounded, if there exist a positive definite matrix
P satisfying the inequalities used in stability analysis, the inequalities are defined as
where
is a positive constant,
is the upper bound of
.
Proof. Consider the Lyapunov function
Differentiating
with respect to time
Notes that
,
. It leads to
where
.
Then the state is bounded. Noticing and , the estimation error is bounded.
3. Controller Design
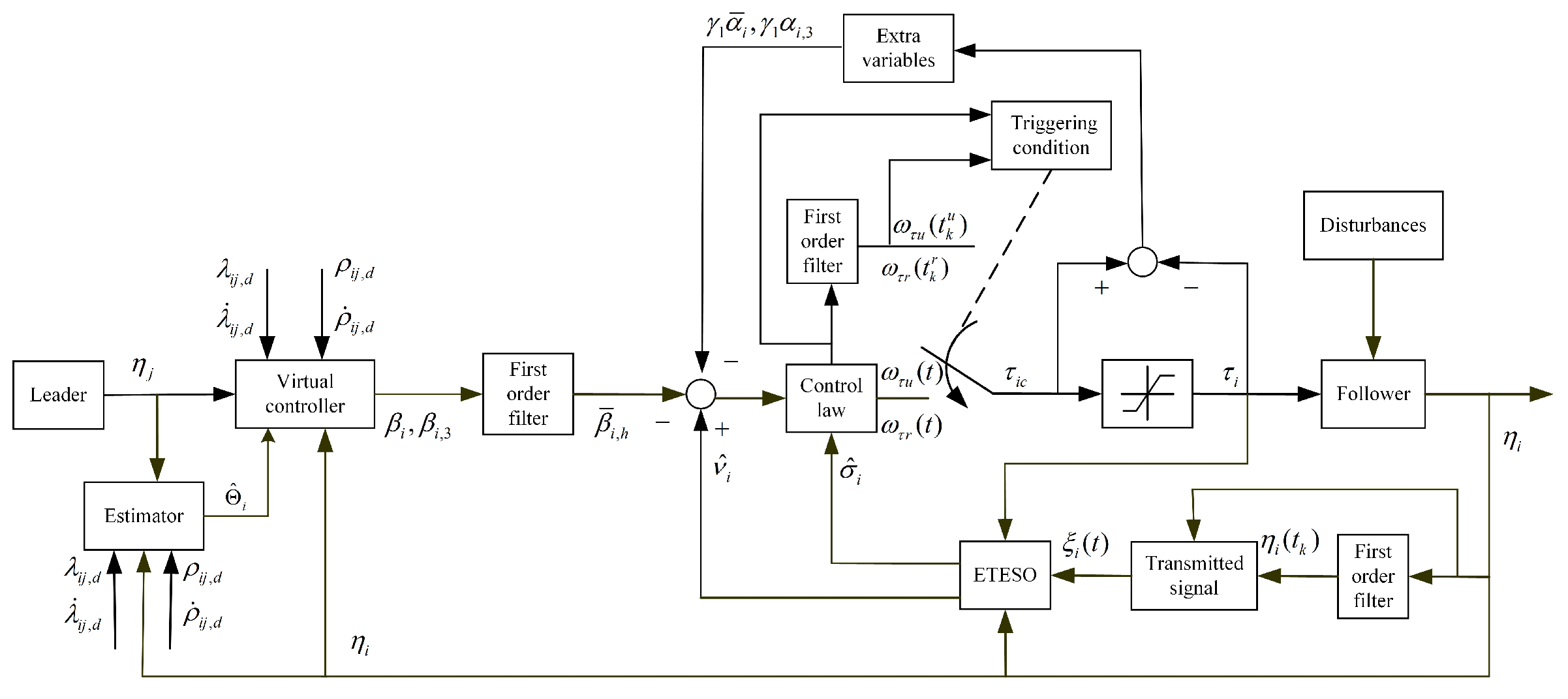
An output feedback controller combined with the ETESO is developed based on an event-triggered strategy. As shown in
Figure 1, the characteristic of the proposed controller is as follows. The estimator is used to provide the estimation of velocity of the leader; the ETESO is designed to provide the velocity, yaw rate and the uncertainties; the transmitted signal contains an event-trigged strategy which reduce sensor-to-observer communication costs; the triggering condition of controller can largely reduce the action times of actuator. The control law design process is divided into the following steps.
Step 1: Define the formation tracking error vector
where
,
.
Using (13) and (14), the time derivative of
is given as
where
,
, and .
Define , , is an unknown positive constant.
Remark 3: From the definition of , and , one notes that , and are bounded, so is reasonable.
Choosing
as a virtual controller,
is designed as:
where
,
is a positive definite matrix,
,
is a constant.
is the estimator of
,
, and it updates as
, is a positive definite matrix, and are positive constants.
Remark 4: The adaptive term
is employed to reduce the volume of data on the formation communication [
24], and estimate the information
.
can be estimated because
and
is bounded. It makes sure that formation tracking control is achieved without velocity of the leader, the amount of data exchange between USVs can be reduced. Unlike the controller presented in [
24], the proposed controller is designed without velocities of follower; the ETESO can reduce sensor-to-observer communication costs; the ETC can largely reduce the action times of actuator.
Step 2: Define a error as
with
where
is a positive constant.
Using the the USV’s dynamic, the time derivative of
is
The virtual control
is chosen as:
where
is a positive constant.
Step 3: Define error functions as follow:
where
,
,
is a positive constant.
,
is derived from the first order filter
,
is a constant.
,
,
is the auxiliary variable derived to deal with the underactuated problem and input saturation.
,
,
is the error caused by the first order filter.
The update laws of extra variables are given by
where
,
and
are positive constants.
Step 4: A control law at the kinetic level is designed as
where
and
are positive constants.
Remark 5: In the common continuous control schemes, the controller design has already been completed in Step 4. Here, an event-trigged controller is designed and the event-trigged condition will be established in the following step. During the flow period between two successive triggering instants, zero-order holder is used to keep input signals unchanged. The key to a successful ETC design is to choose an appropriate event-trigged strategy. In [
16], the triggered condition of time-varying threshold event-triggered controller (TTETC) is constructed based on flow time and Lyapunov function. Therefore, the action times of actuator is limited and Zeno behavior can be avoided. The signals calculated by controller should be closely related to the triggered condition, its size change determine whether or not to update the control inputs, and the change is used to design the proposed triggered condition. It is necessary to give the proof that Zeno behavior is avoided. The appropriate event-trigged strategy reduce the action times of actuator.
An event-trigged controller is chosen as
with
and are positive constants.
The following theorem is given to point out the stability of overall closed-loop system.
Theorem 3. Consider the system consisting of the USV dynamics (
7) and (8), the observer (15), (16) and (17), auxiliary variables (66), (67) and (68), the control law (71), with unknown environmental disturbances under Assumption 1-3. Then, the proposed control scheme guarantees: 1) All signals in the closed-loop system are bounded. 2) All USVs can track the leader with a bounded tracking error.
Proof. Choose a Lyapunov function candidate as follows :
where
.
Along with (50) and (60), the time derivative of
is given
By applying (21), (22), (23), (62) and (63) to (74), we obtain
Using (53), (54), (61), (66), (67) and (68) yields
where
,
,
,
.
According to (71) and (72), one has and . There exist time-varying functions , satisfying and . Then, and .
Notes that
and
Along with (69) and (70),
becomes
According to Young’s inequality,
with
.
According to [
28] and Young’s inequality,
The following inequalities are used to stability analysis, which are represented as
where
,
.
Then, the following inequality can be obtained:
where
,
.
Consider the total Lyapunov function as
Remark 5: The Lyapunov function include estimation errors , , . We cannot conclude that , and are positive constants. The Lyapunov function is constructed by inducing . In the time derivative of , the gain of estimation error is negative. We can conclude that . Then, it is proved that all signals of the closed-loop system are bounded.
Along with (48) and (92), the time derivative of
is
where
.
Define
,
and
. According to Young’s inequality,
. Then,
where
,
is a positive constant.
Define
,
,
is a positive constant. Choosing
with
is a constant. The follow can be attained:
Owing to
, the inequality (96) becomes
where
,
,
,
,
,
.
Theorem 4. The Zeno behavior can be avoided under the event-triggered mechanisms (71) and (72), and the implementation intervals and are lower bounded by a positive constant .
Proof. According to (72), one has that
The time derivatives of
and
are given
Theorem 3 shows that all signals in the closed-loop system are bounded. Then,
and
are bounded. According to the design of ETESO,
and
are bounded.
is bounded because
. Therefore, there are positive constants
and
satisfying
and
. Since
there exists the lower bound of implementation interval
and
. Hence, no Zeno phenomenon will occur by using the proposed control law.
4. Simulation Results
In this section, simulation results are proposed to prove the proposed event-triggered control method, and the ship parameters are chosen from [
29]. Four USVs are driven to track a leader at a desired distance and angle with the proposed control law in (69)-(72). The total duration of the simulation runs is 120s, the sampling time
for each time point is
s. The initial positions of followers are chosen as:
m,
m, 0 rad
,
m, 5 m, 0 rad
,
m,
m, 0 rad
,
m, 8 m, 0 rad
. The trajectory of leader is generated by:
m/s,
m/s and
rad/s for
s,
m/s,
m/s and
rad/s for 40 s
s,
m/s,
m/s and
rad/s for 60 s
s,
m/s,
m/s and
rad/s for 80 s
s,
m, 0 m, 0 rad
, The desired distance and relative angle are given by
m,
rad,
m,
rad,
m,
rad,
m,
rad.
The parameters of ETESO are chosen as: , . The parameters of the proposed control law are chosen as , , , , , , , , , , , . The parameters of trigger condition are .
Remark 6: According to inequality (97), we should keep as large as possible and as small as possible. The close-loop system can converge quickly with small errors. However, include the mismatch variables between input without saturation and with saturation and . Large gain factors , , , and corresponds to large mismatch variables. Therefore, we make gain factor as small as possible without violating the constraint . , and define the convergence rate of auxiliary variables, and they satisfy the inequalities and . determines the tracking speed of first order filter, which is related to sampling time of simulation. And too large value will make an unstable system, too small value will make a poor tracking performance. As a rule of thumb, the general recommended value of is between and . The parameters and define trigger condition of the proposed controller, larger and mean lower update frequency of input signals and a poor system performance. To find a balance between update frequency and system performance, and are defined as . define the estimation speed of ETESO, is the threshold of trigger condition of ETESO, and the process of parameter selection is similar to parameter selection in and .
For surface vessels, the effect of gravity can be neglected because gravity acting on USVs equals buoyancy acting on USVs. The USVs are subject to model uncertainties and environmental disturbances. Model uncertainties are induced by model errors and unknown system parameters. Therefore, only Centrifugal terms, damping parameters and environmental disturbances are considered. In this paper, the uncertainties , and are assumed to be unknown. Environmental disturbances contain wind, wave and current. The impacts on USVs of wind can be ignored due to small windward area. Therefore, environmental disturbances are designed as the sum of some sinusoidal signals, which are chosen as .
Simulation results are shown in
Figure 3,
Figure 4,
Figure 5,
Figure 6,
Figure 7 and
Figure 8.
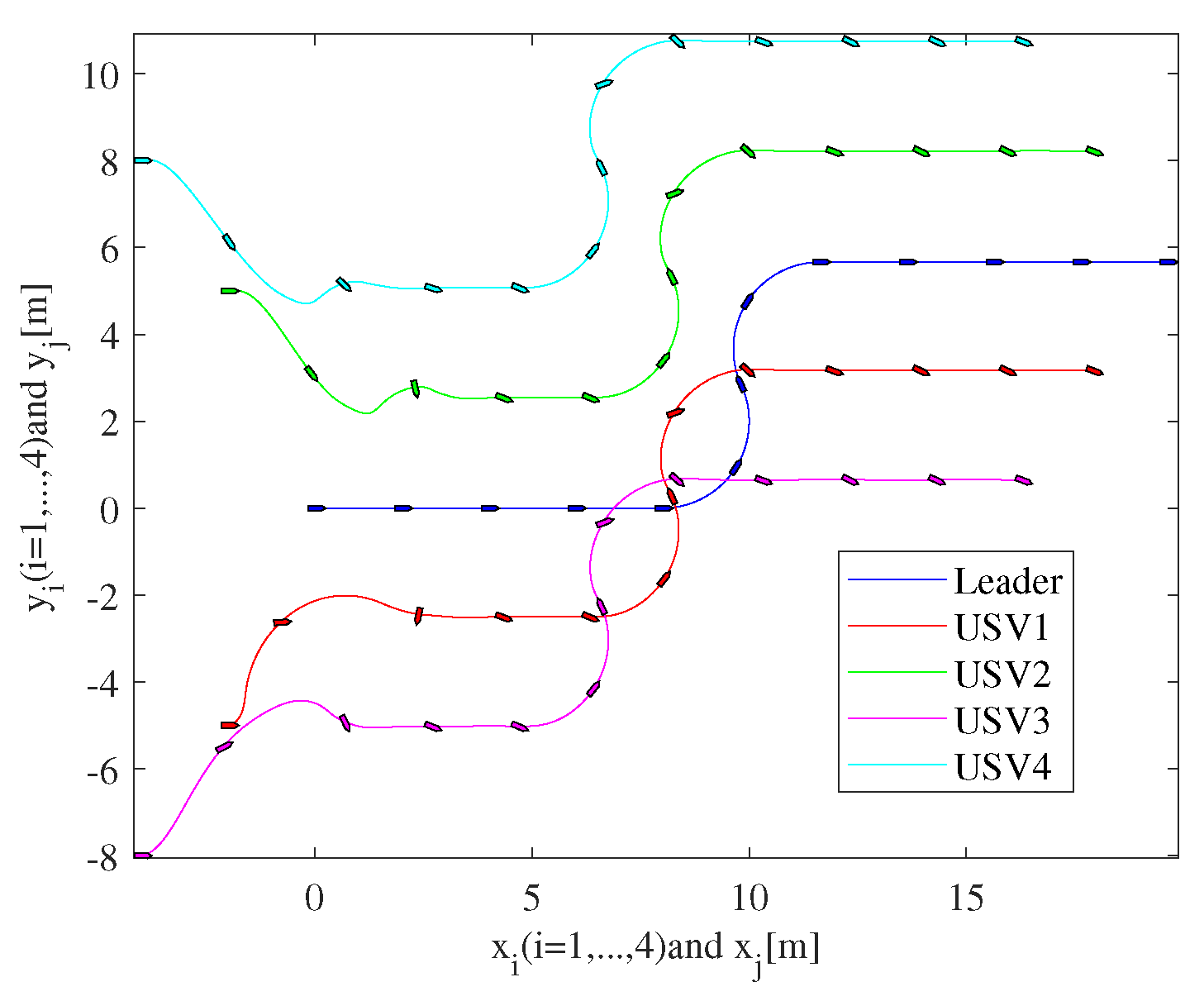
Figure 3 shows formation pattern shaped by the five vessels, and all followers can successfully track the leader.
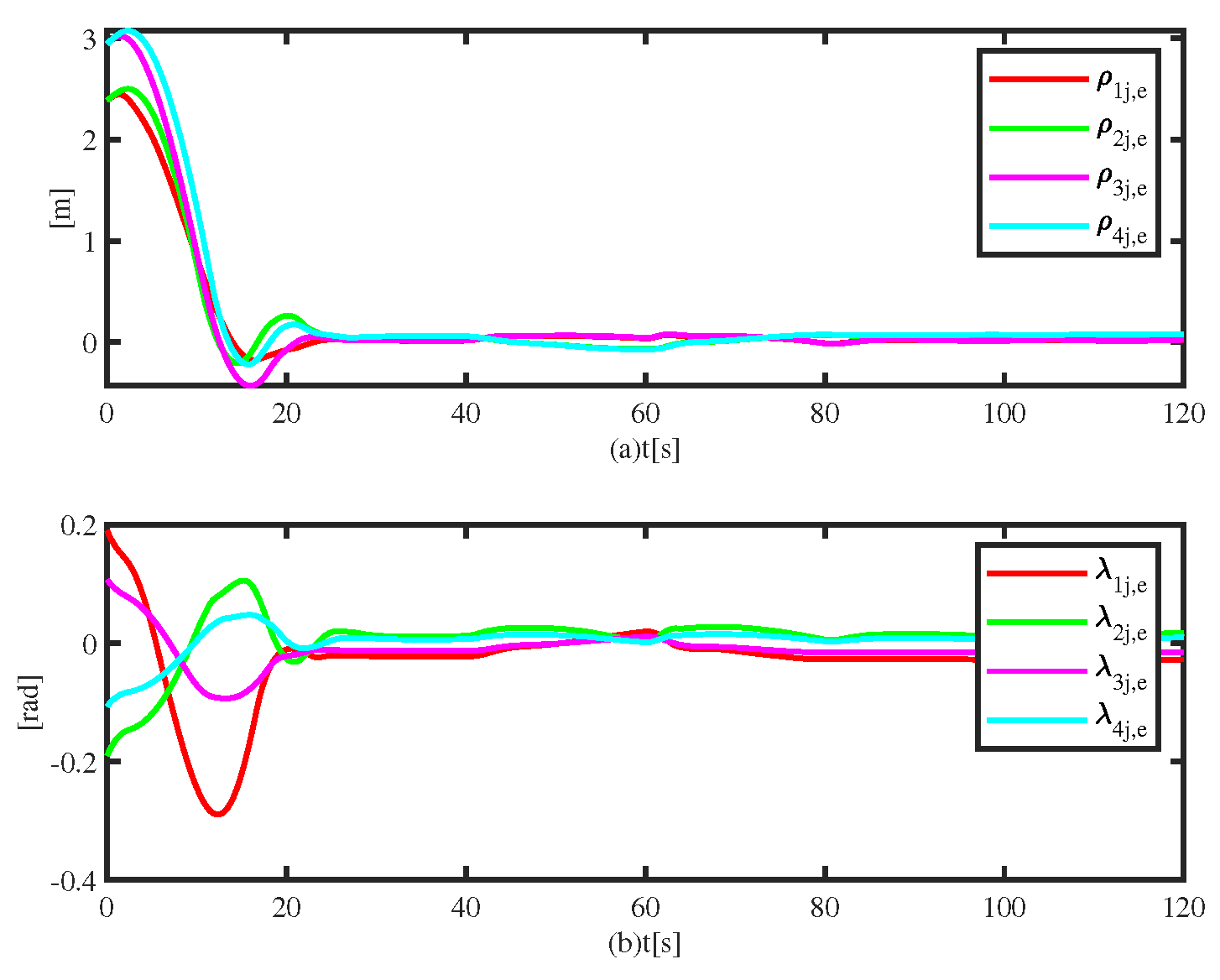
Figure 4 shows that the formation tracking errors approach zero regardless of model uncertainties and environmental disturbances.
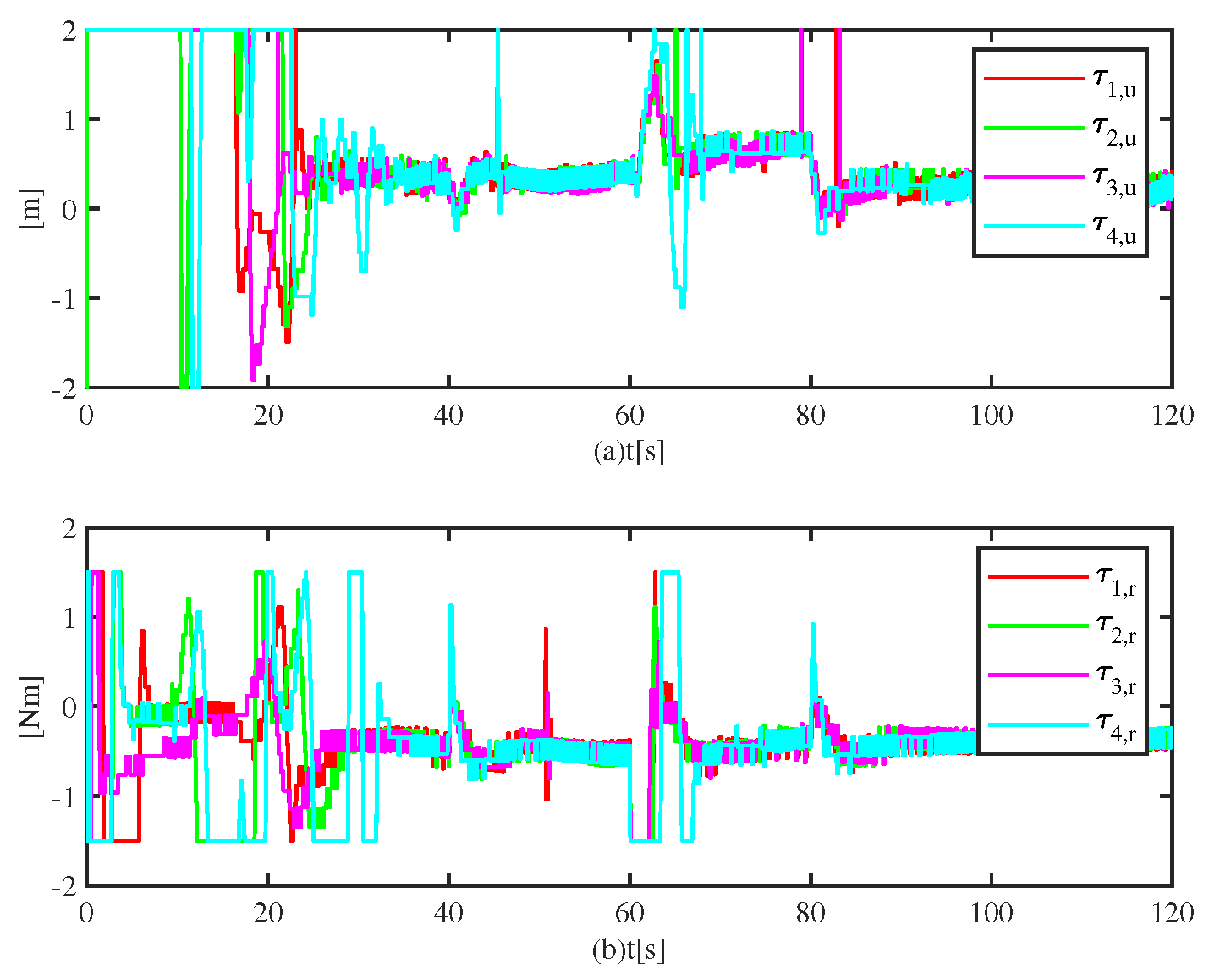
Figure 5 shows the input signals of four USVs. In the first 24s, since initial formation tracking errors are large, saturated control inputs suffer from sudden jumps. During 25s-40s, formation tracking errors approach zero, input signals convergences gradually. At 40s, 60s and 80s, the sudden changes of the control forces are caused by sudden change of the leader velocity.
The comparison of simulation results are shown in
Figure 6,
Figure 7 and
Figure 8, simulations are conducted using the TTETC proposed in [
16] and the ETC proposed in this paper. The two controllers have same control parameters, different parameters of trigger condition.
The TTETC is designed as follows:
with
, .
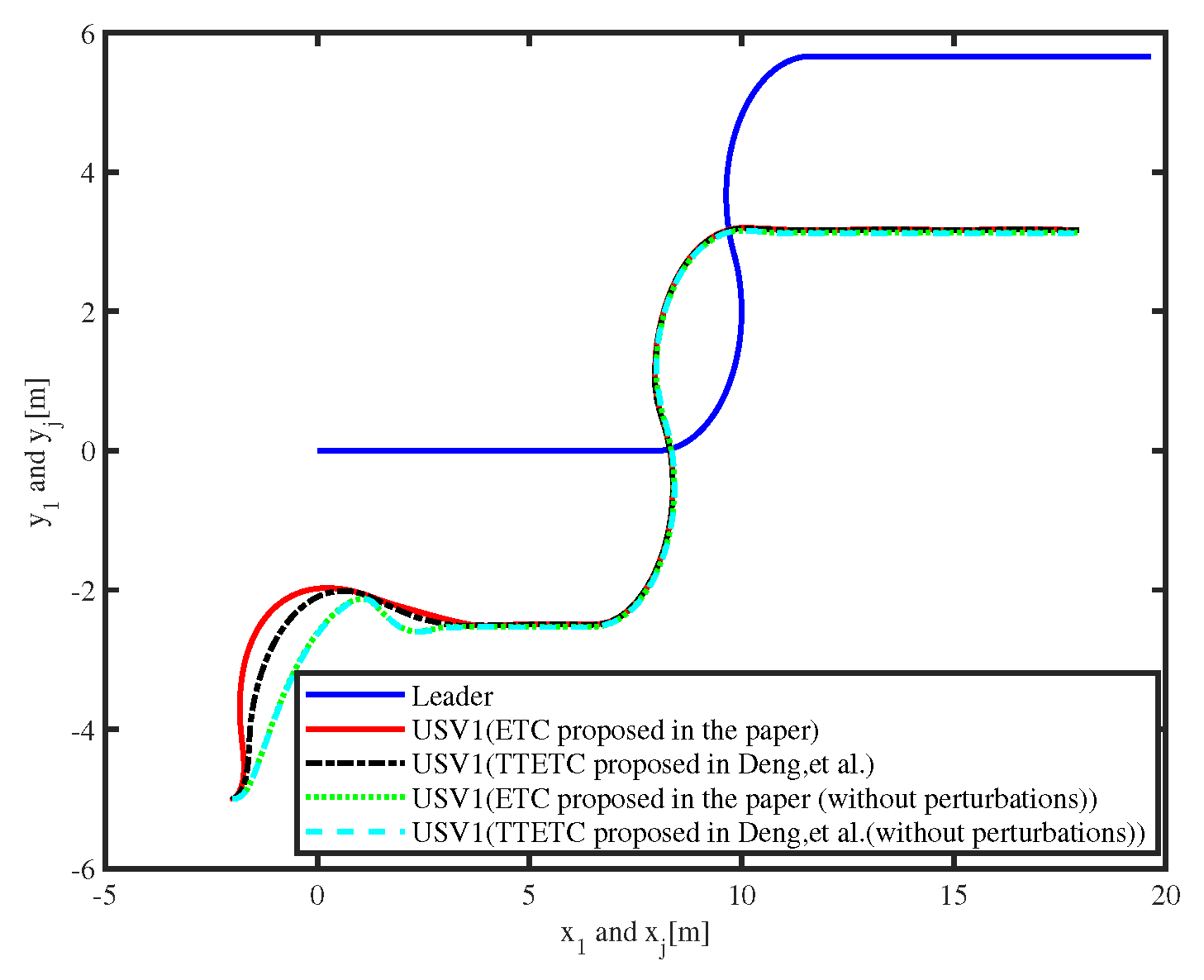
Figure 6 depicts formation pattern shaped by the
ith USV and the leader. The different controllers are applied to the system with and without perturbations, respectively. It reveals that the follower is able to track the leader successfully under four different conditions.
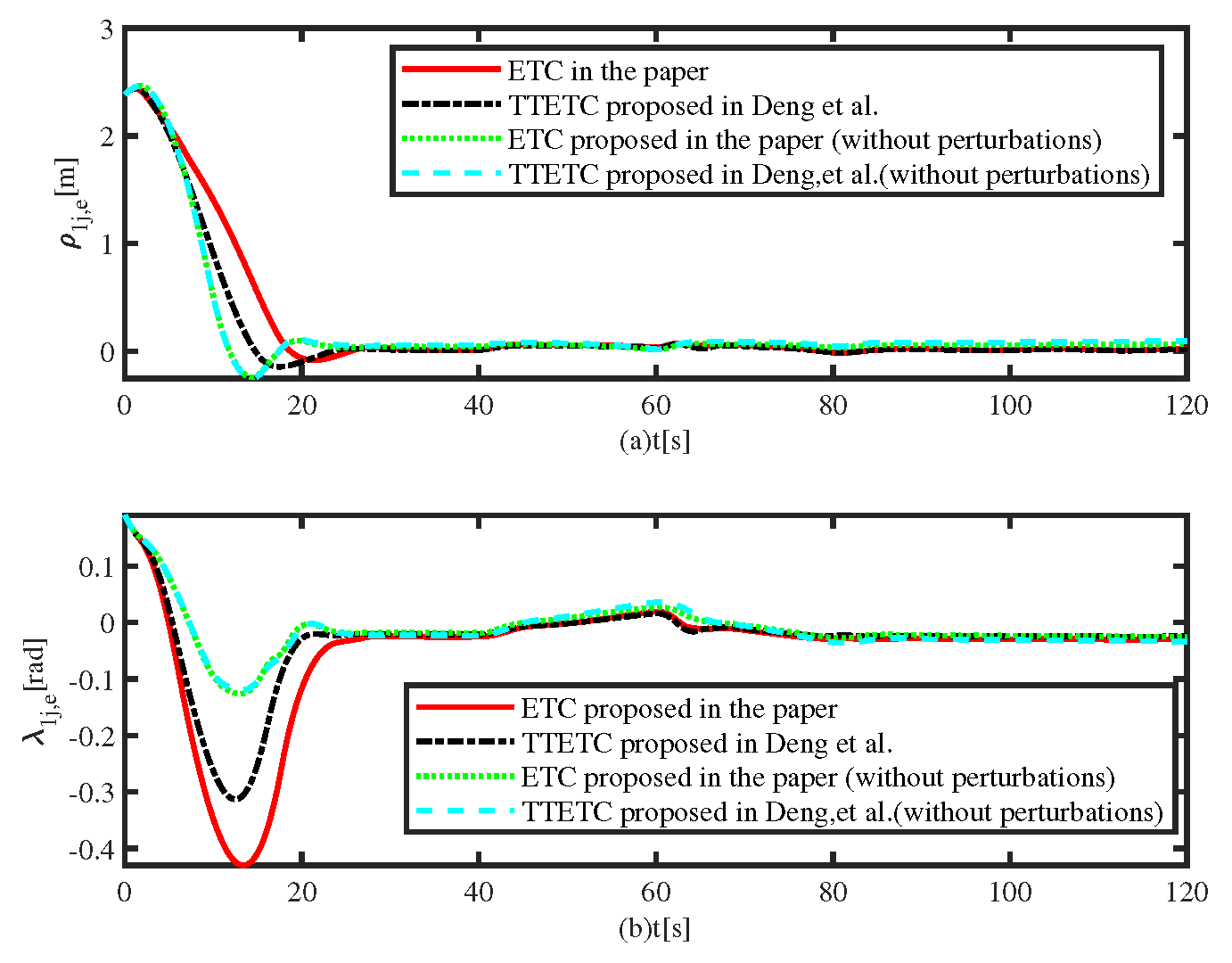
Figure 7 depicts the distance and angle tracking errors under four different conditions, and it shows the errors converge to a small neighborhood of the origin. Compared with the system with perturbations, the system without perturbations has faster convergent rate. In the system with perturbations, some control energy is used to reject disturbances including model uncertainties and environmental disturbances. Then, the energy that make the system convergent is reduced. Under the same condition, stability errors and convergence rates of TTETC and ETC are nearly the same. The two controllers have same structure but different event-triggered strategy. Therefore, they have same convergent rate but different action times of actuator.
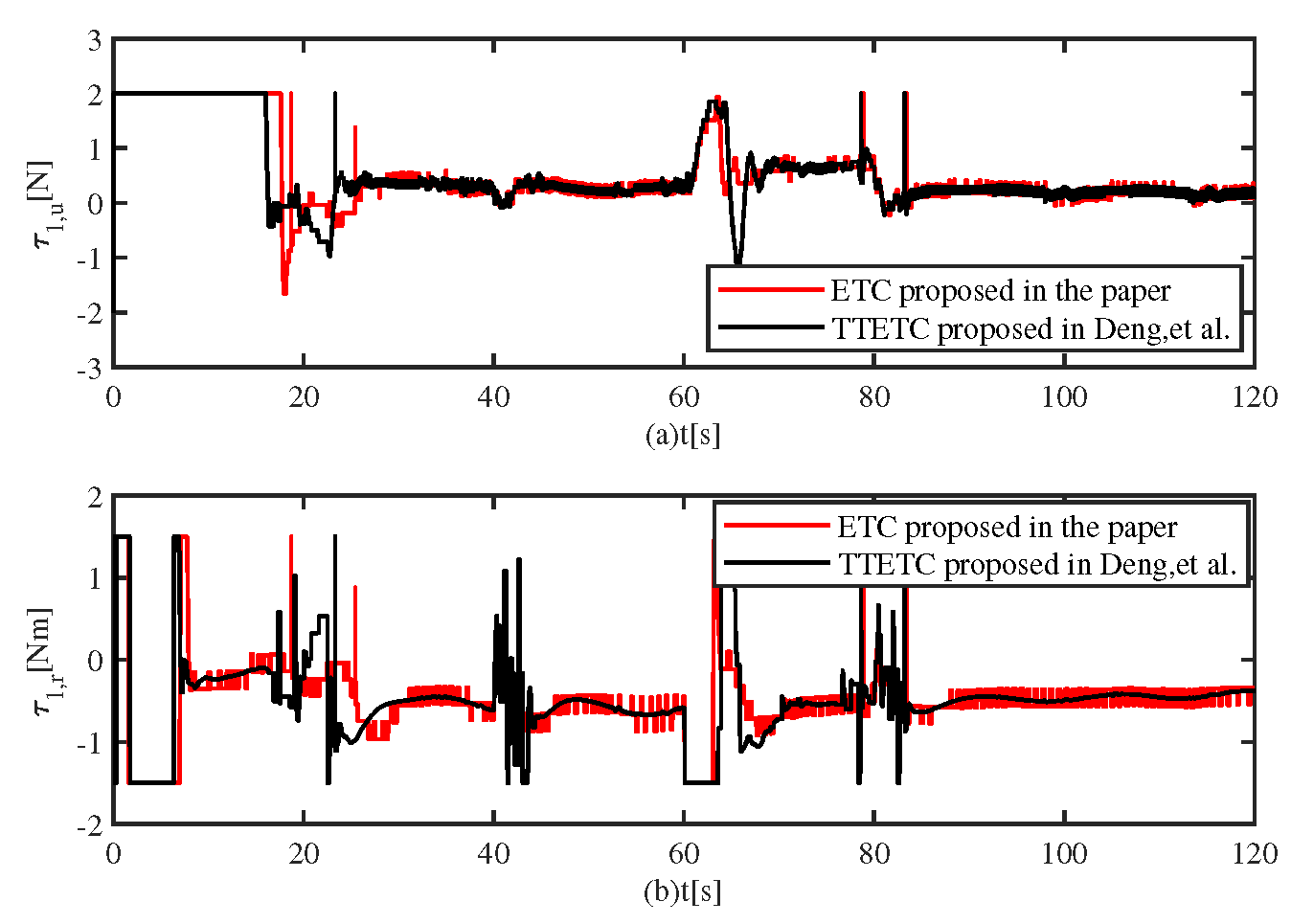
Figure 8 depicts the control signals generated by the two different controllers. By the effect of the proposed controller, the input signals are shaking in low frequencies, but the amplitudes are higher. At the beginning, due to large initial formation tracking error, the input signals are saturated. The input signals converge along with the convergence of formation tracking error. At 40s, 60s and 80s, the input signals are shaking due to change of the leader velocity.
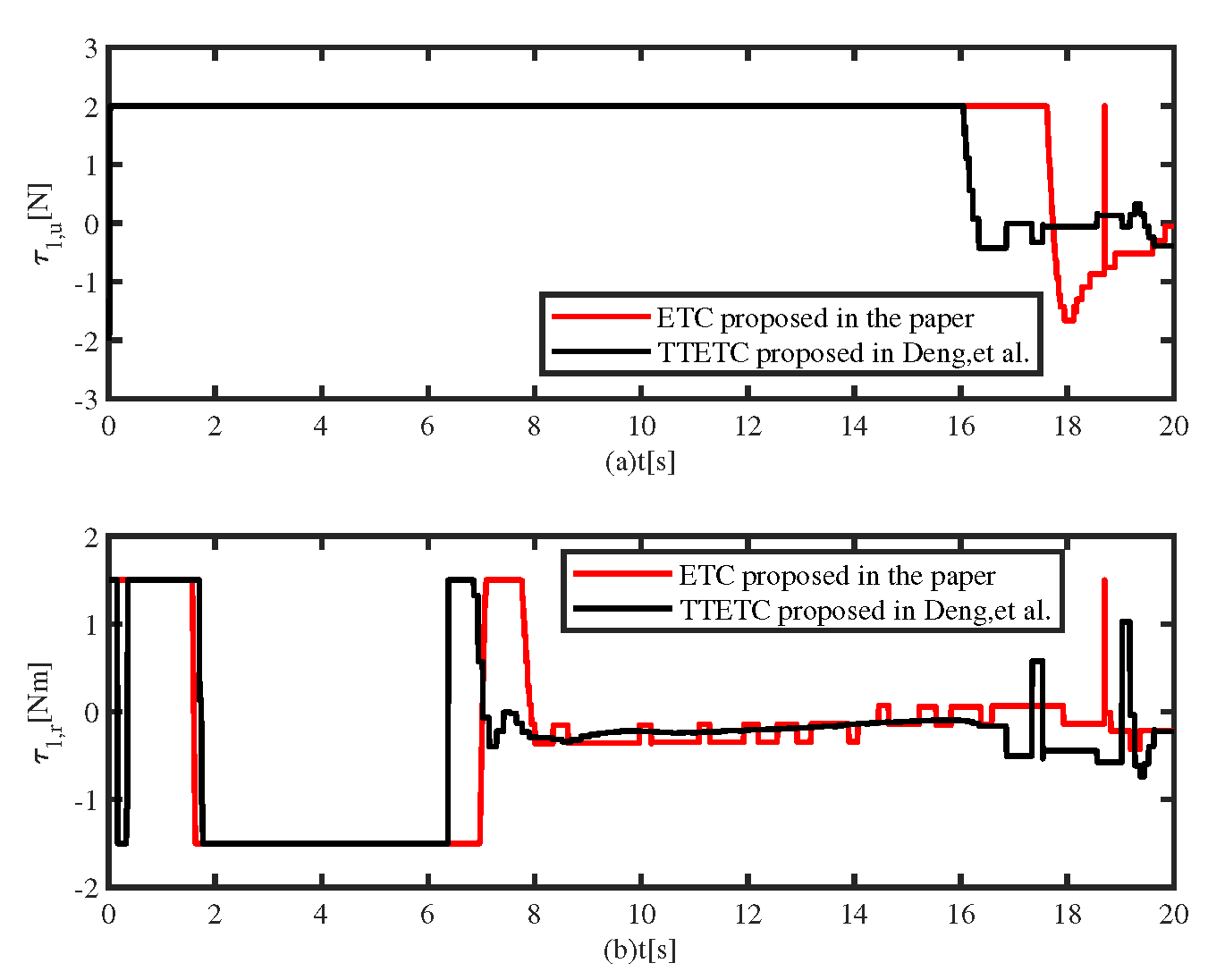
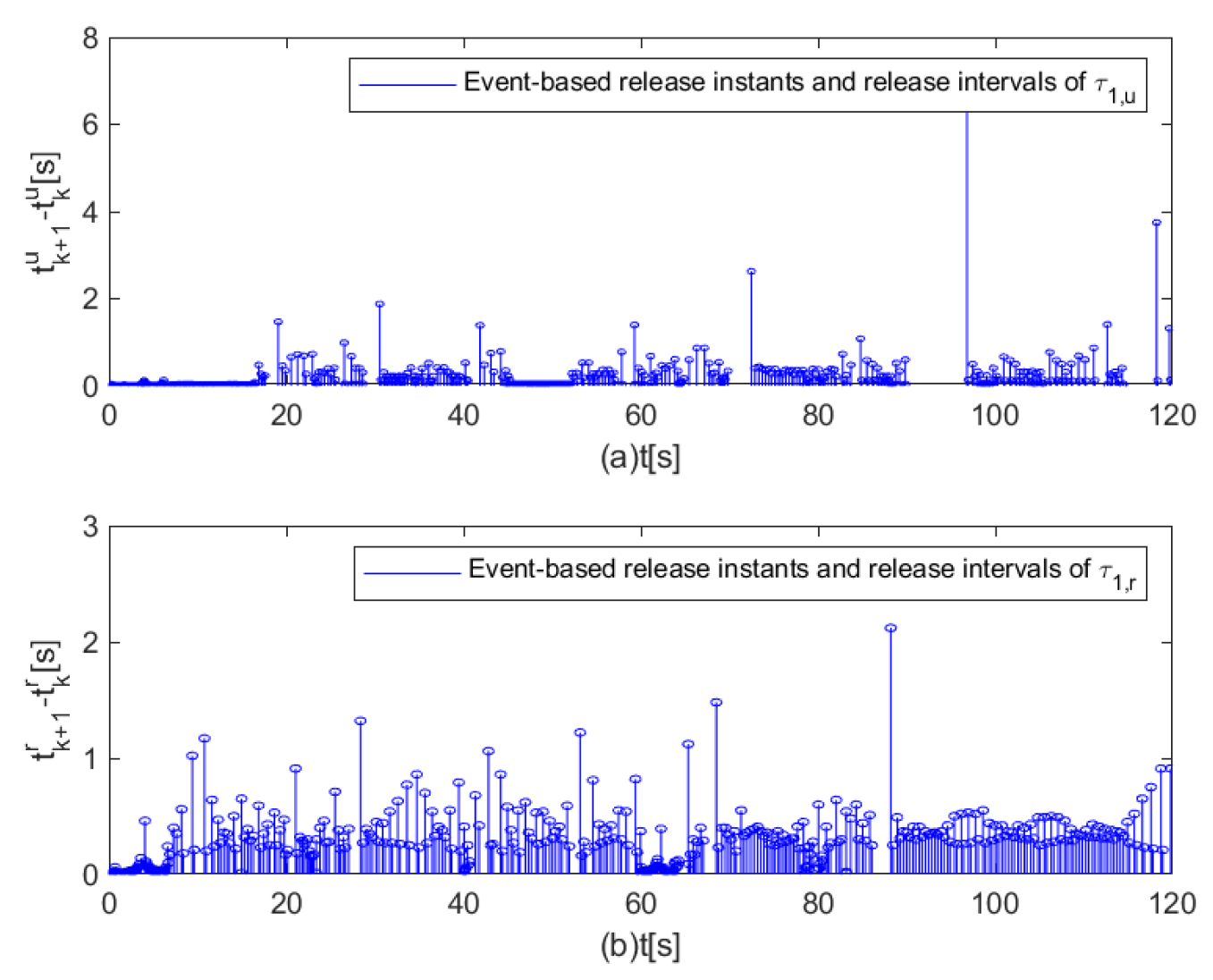
Figure 9 shows the control inputs at the first 20 seconds, and the update frequencies of control inputs are different due to different triggering strategies.
Figure 10 is the event-based release instants and release intervals of input signals under the proposed controller. As shown in
Table 2, compared with TTETC, the proposed ETC largely reduce the action times of actuator. The triggering condition of TTETC is designed based on the Lyapunov function
. In order to assure the performance of control systems, the threshold is set to a smaller value. The threshold of ETC is set to
, the action times of actuator can be largely reduced.
The ESO is proposed in [
23].
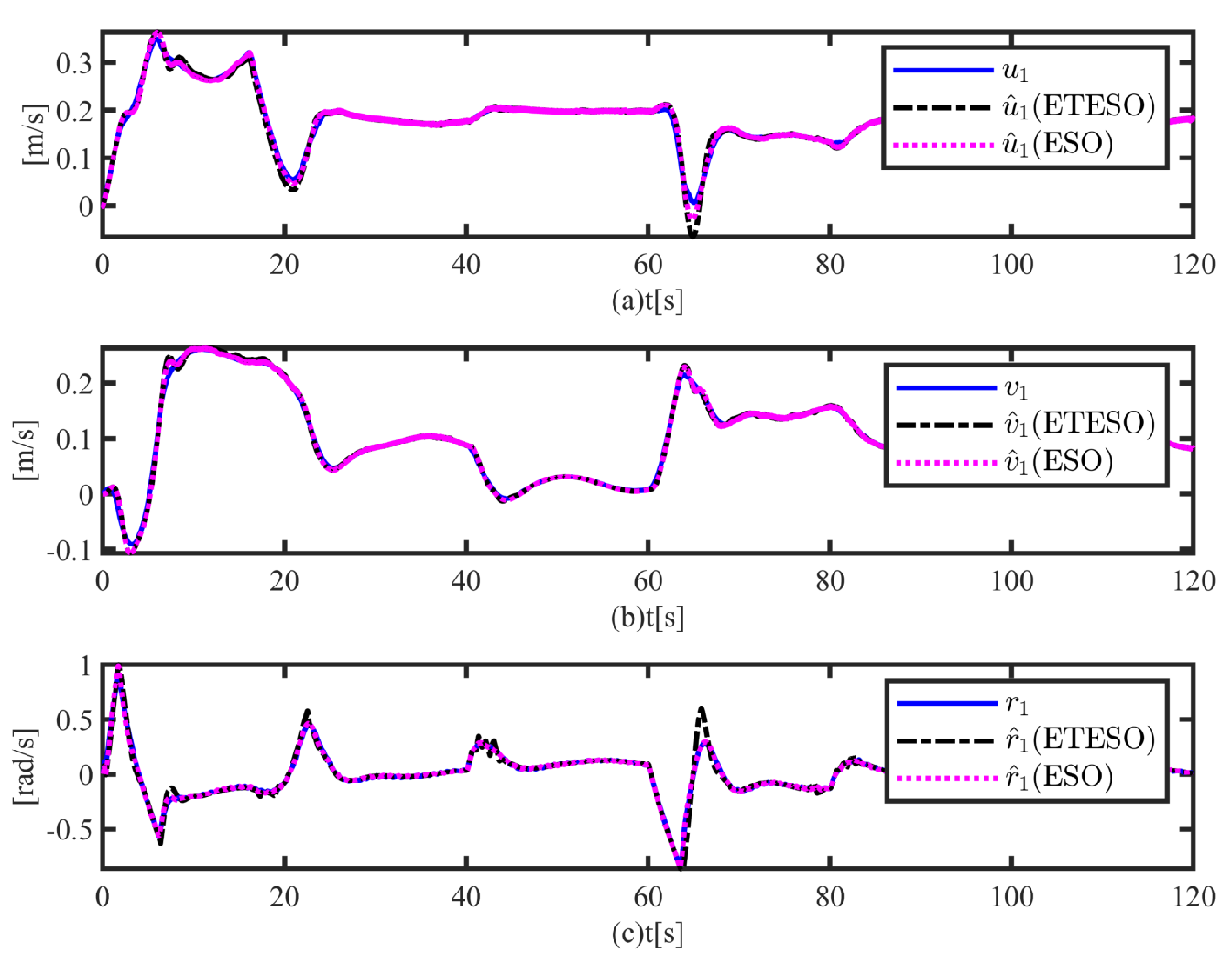
Figure 11 shows the estimated velocities and real velocities, illustrating that velocity estimate of ETESO is as good as that of ESO.
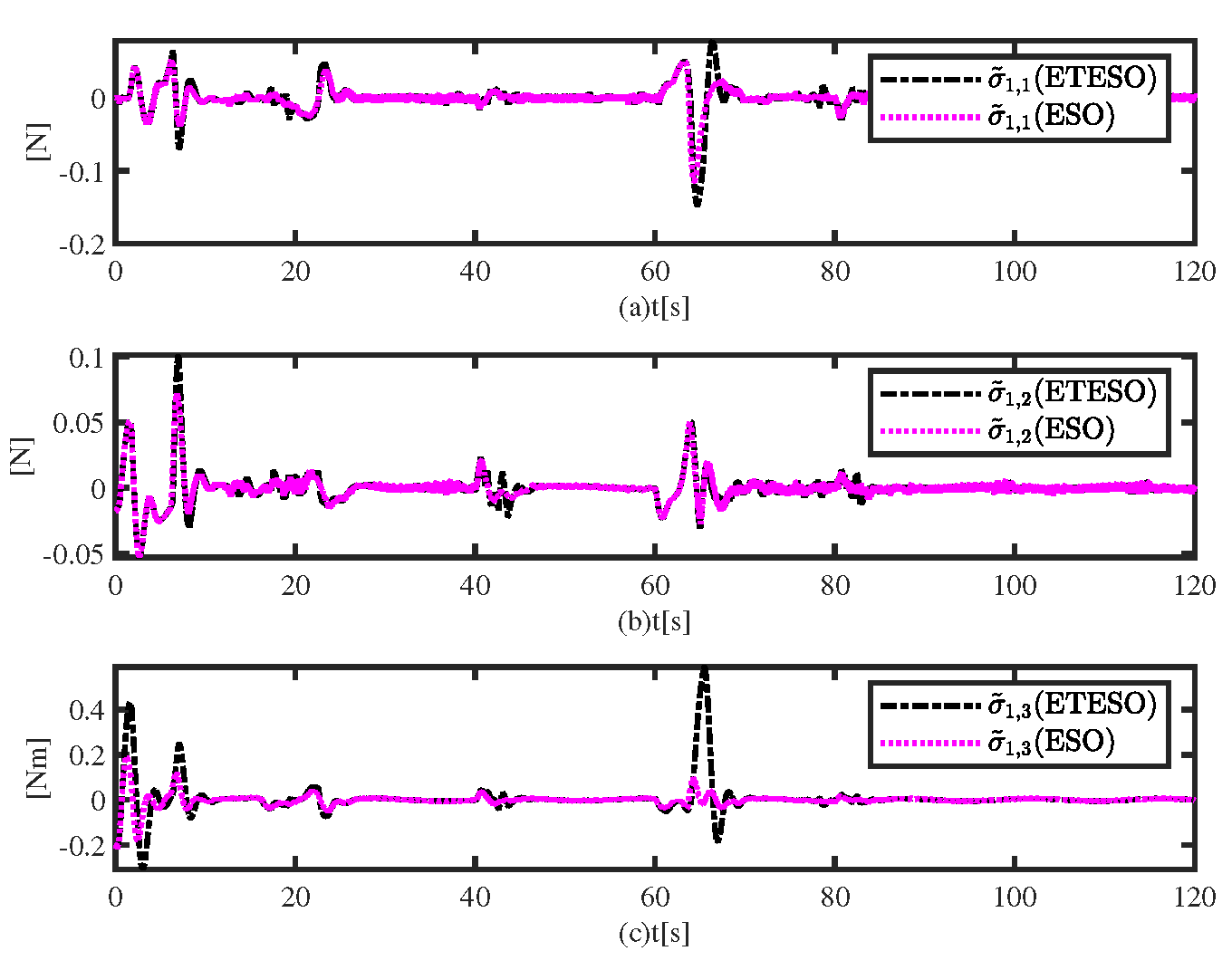
Figure 12 shows the uncertainties are effectively approximated by ESO and ETESO. Comparing to ESO, ETESO simultaneously get large steady error and large jitter.
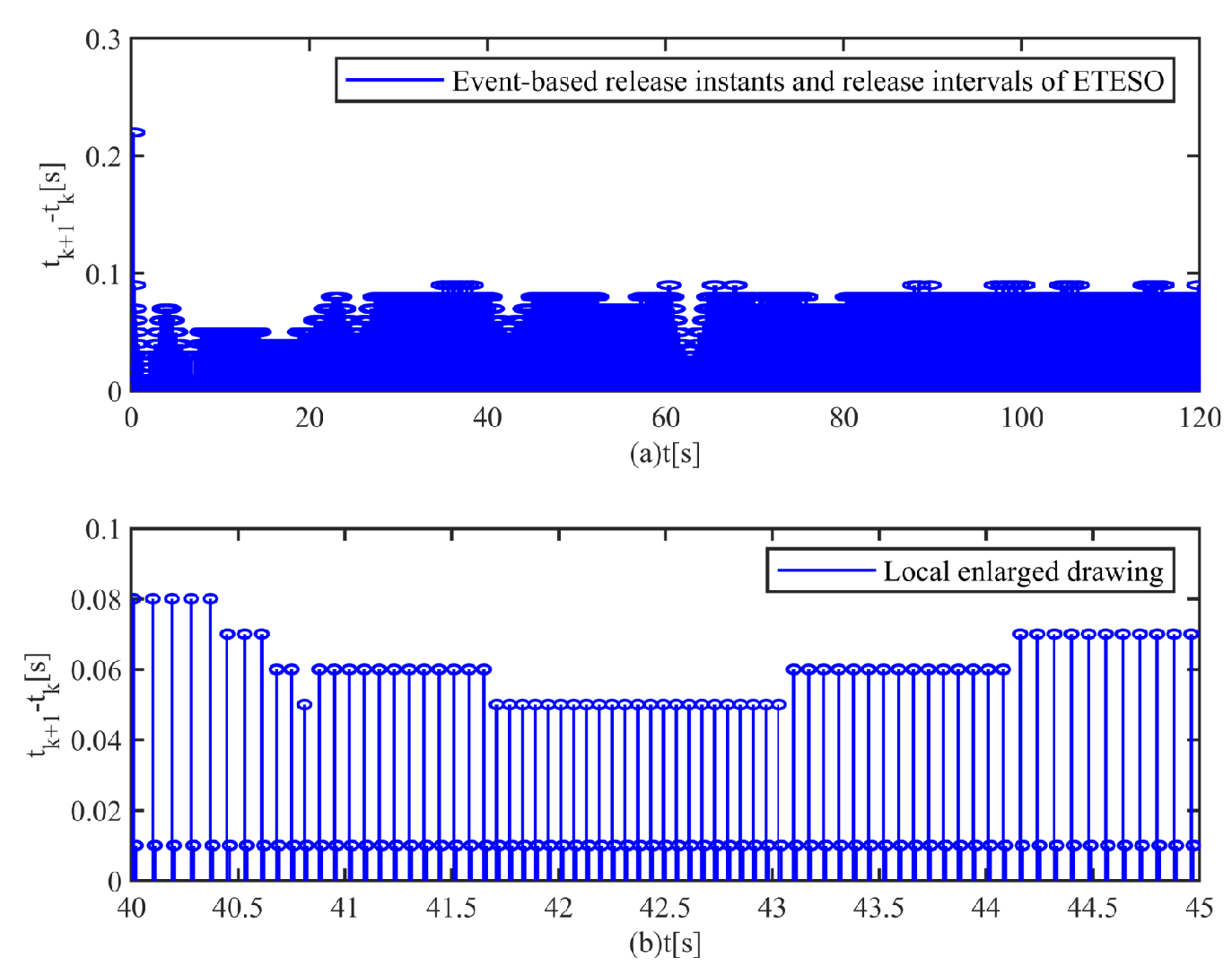
Figure 13 shows the event-based release instants and release intervals of ETESO, a local enlarged drawing is also given. During
s, the maximum release interval is
, and the minimum release interval is
. During
s, most of release intervals are greater than
. Therefore, some communication times are saved.
Table 3 shows communication times of two observers. A counter is added in simulation. When the event condition is met, the counter begin to count. After the application completes, the counter shows the total number of times the event has occurred. Communication times can be attained by multiplying the total number of times by the sampling time. Compared with ESO, the ETESO can reduce communication costs and communication time. The ETESO is applied to reduce communication costs in the cost of losing estimation accuracy.
5. Conclusion
This article suggests an output feedback controller for surface vessel with model uncertainties, unknown environmental disturbances, and input constraints. Static obstacles and unknown non-cooperative ships are also considered. An ESO is given, unknown model dynamics and velocity are simultaneously estimated. The controller is designed based on the ADS and MAPFs. Finally, the mathematic analysis is given to proved that all error signals of the system are bounded. Simulation experiments affirm the tracking performance of the proposed controller.
Author Contributions
Conceptualization, methodology, software, writing—review and editing, Xiaoming Xia; validation, Zhaodi Yang; writing—review and editing, Tianxiang Yang.
Funding
This work is supported by the Funded by the 7th Generation Ultra Deep Water Drilling unit Innovation Project.
Institutional Review Board Statement
This article does not contain any studies with human or animal subjects.
Data Availability Statement
The data of this paper is unavailable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Peng, Z.; Wang, J.; Wang, D.; Han, Q.L. An Overview of Recent Advances in Coordinated Control of Multiple Autonomous Surface Vehicles. IEEE Transactions on Industrial Informatics 2021, 17, 732–745. [Google Scholar] [CrossRef]
- Cui, R.; Ge, S.; How, B.; Choo, Y. Leader–Follower Formation Control of Underactuated Autonomous Underwater Vehicles. Ocean Engineering 2010, 37, 1491–1502. [Google Scholar] [CrossRef]
- Xia, G.; Xia, X.; Zhao, B.; Sun, C.; Sun, X. A Solution to Leader Following of Underactuated Surface Vessels with Actuator Magnitude and Rate Limits. International Journal of Adaptive Control and Signal Processing 2021, 35, 1860–1878. [Google Scholar] [CrossRef]
- Beard, R.; Lawton, J.; Hadaegh, F. A Coordination Architecture for Spacecraft Formation Control. IEEE Transactions on Control Systems Technology 2001, 9, 777–790. [Google Scholar] [CrossRef]
- Park, B.S.; Yoo, S.J. An Error Transformation Approach for Connectivity-Preserving and Collision-Avoiding Formation Tracking of Networked Uncertain Underactuated Surface Vessels. IEEE Transactions on Cybernetics 2019, 49, 2955–2966. [Google Scholar] [CrossRef]
- Chen, M.; Ge, S.S.; How, B.V.E.; Choo, Y.S. Robust Adaptive Position Mooring Control for Marine Vessels. IEEE Transactions on Control Systems Technology 2013, 21, 395–409. [Google Scholar] [CrossRef]
- Shojaei, K. Leader–Follower Formation Control of Underactuated Autonomous Marine Surface Vehicles with Limited Torque. Ocean Engineering 2015, 105, 196–205. [Google Scholar] [CrossRef]
- Park, B.S.; Kwon, J.W.; Kim, H. Neural Network-Based Output Feedback Control for Reference Tracking of Underactuated Surface Vessels. Automatica 2017, 77, 353–359. [Google Scholar] [CrossRef]
- Xia, G.; Xia, X.; Zhao, B.; Sun, C.; Sun, X. Distributed Tracking Control for Connectivity-Preserving and Collision-Avoiding Formation Tracking of Underactuated Surface Vessels with Input Saturation. Applied Sciences 2020, 10, 3372. [Google Scholar] [CrossRef]
- Deng, Y.; Zhang, X.; Im, N.; Zhang, G.; Zhang, Q. Adaptive Fuzzy Tracking Control for Underactuated Surface Vessels with Unmodeled Dynamics and Input Saturation. ISA Transactions 2020, 103, 52–62. [Google Scholar] [CrossRef]
- Xia, G.; Xia, X.; Sun, X. Formation Control with Collision Avoidance for Underactuated Surface Vehicles. Asian Journal of Control 2021, 24, 2244–2257. [Google Scholar] [CrossRef]
- Liu, C.; Chen, C.L.P.; Zou, Z.; Li, T. Adaptive NN-DSC Control Design for Path Following of Underactuated Surface Vessels with Input Saturation. Neurocomputing 2017, 267, 466–474. [Google Scholar] [CrossRef]
- Xia, G.; Xia, X.; Bo, Z.; Sun, X.; Sun, C. Event-Triggered Controller Design for Autopilot with Input Saturation. Mathematical Problems in Engineering 2020, 2020, e5362895. [Google Scholar] [CrossRef]
- von Ellenrieder, K.D. Dynamic Surface Control of Trajectory Tracking Marine Vehicles with Actuator Magnitude and Rate Limits. Automatica 2019, 105, 433–442. [Google Scholar] [CrossRef]
- Wang, S.; Gao, Y.; Liu, J.; Wu, L. Saturated Sliding Mode Control with Limited Magnitude and Rate. IET Control Theory & Applications 2018, 12, 1075–1085. [Google Scholar] [CrossRef]
- Deng, Y.; Zhang, X.; Im, N.; Zhang, G.; Zhang, Q. Event-Triggered Robust Fuzzy Path Following Control for Underactuated Ships with Input Saturation. Ocean Engineering 2019, 186, 106122. [Google Scholar] [CrossRef]
- Peng, Z.; Jiang, Y.; Wang, J. Event-Triggered Dynamic Surface Control of an Underactuated Autonomous Surface Vehicle for Target Enclosing. IEEE Transactions on Industrial Electronics 2021, 68, 3402–3412. [Google Scholar] [CrossRef]
- Ahmad, I.; Ouannas, A.; Shafiq, M.; Pham, V.T.; Baleanu, D. Finite-Time Stabilization of a Perturbed Chaotic Finance Model. Journal of Advanced Research 2021, 32, 1–14. [Google Scholar] [CrossRef]
- Sun, Z.; Zhang, G.; Lu, Y.; Zhang, W. Leader-Follower Formation Control of Underactuated Surface Vehicles Based on Sliding Mode Control and Parameter Estimation. ISA Transactions 2018, 72, 15–24. [Google Scholar] [CrossRef]
- Ahmad, I.; Shafiq, M. Oscillation Free Robust Adaptive Synchronization of Chaotic Systems with Parametric Uncertainties. Transactions of the Institute of Measurement and Control 2020, 42, 1977–1996. [Google Scholar] [CrossRef]
- Jin, X. Fault Tolerant Finite-Time Leader–Follower Formation Control for Autonomous Surface Vessels with LOS Range and Angle Constraints. Automatica 2016, 68, 228–236. [Google Scholar] [CrossRef]
- Peng, Z.h.; Wang, D.; Lan, W.y.; Sun, G. Robust Leader-Follower Formation Tracking Control of Multiple Underactuated Surface Vessels. China Ocean Engineering 2012, 26, 521–534. [Google Scholar] [CrossRef]
- Peng, Z.; Wang, D.; Li, T.; Han, M. Output-Feedback Cooperative Formation Maneuvering of Autonomous Surface Vehicles With Connectivity Preservation and Collision Avoidance. IEEE Transactions on Cybernetics 2020, 50, 2527–2535. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Zhang, G.; Qiao, L.; Zhang, W. Adaptive Output-Feedback Formation Control for Underactuated Surface Vessels. International Journal of Control 2020, 93, 400–409. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, W.; Wang, D.; Peng, Z. Event-Triggered Extended State Observers Design for Dynamic Positioning Vessels Subject to Unknown Sea Loads. Ocean Engineering 2020, 209, 107242. [Google Scholar] [CrossRef]
- Yu, Y.; Yuan, Y.; Yang, H.; Liu, H. A Novel Event-Triggered Extended State Observer for Networked Control Systems Subjected to External Disturbances. International Journal of Robust and Nonlinear Control 2019, 29, 2026–2040. [Google Scholar] [CrossRef]
- Do, K.; Jiang, Z.; Pan, J. Underactuated Ship Global Tracking under Relaxed Conditions. IEEE Transactions on Automatic Control 2002, 47, 1529–1536. [Google Scholar] [CrossRef]
- Polycarpou, M. Stable Adaptive Neural Control Scheme for Nonlinear Systems. IEEE Transactions on Automatic Control 1996, 41, 447–451. [Google Scholar] [CrossRef]
- Skjetne, R.; Fossen, T.I.; Kokotović, P.V. Adaptive Maneuvering, with Experiments, for a Model Ship in a Marine Control Laboratory. Automatica 2005, 41, 289–298. [Google Scholar] [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).