Submitted:
22 May 2023
Posted:
23 May 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Materials and Methods
2.1. The Study Area
2.2. Datasets
2.2.1. In Situ Rainfall Data
2.2.2. Satellite-Based Precipitation Products
2.2.3. The Tropical Rainfall Measuring Mission-Based Multi-Satellite Precipitation Analysis (TMPA)
2.2.4. African Rainfall Climatology Version 2
2.2.5. Climate Hazards Group Infrared Precipitation with Stations Data
2.2.6. GPM IMERG6 Satellite Rainfall Estimates
2.2.7. Precipitation Estimation from Remote Sensing Information using Artificial Neural Networks-Climate Data Record
2.2.8. The Tropical Applications of Meteorological Using SaTEllite and Ground-Based Observations (TAMSATv3.1)
2.3. Methods
2.3.1. Evaluation of Satellite Products
2.3.2. Model Evaluations
3.2.3. Assessment of the Rainfall Trends of Satellite Products
3. Results
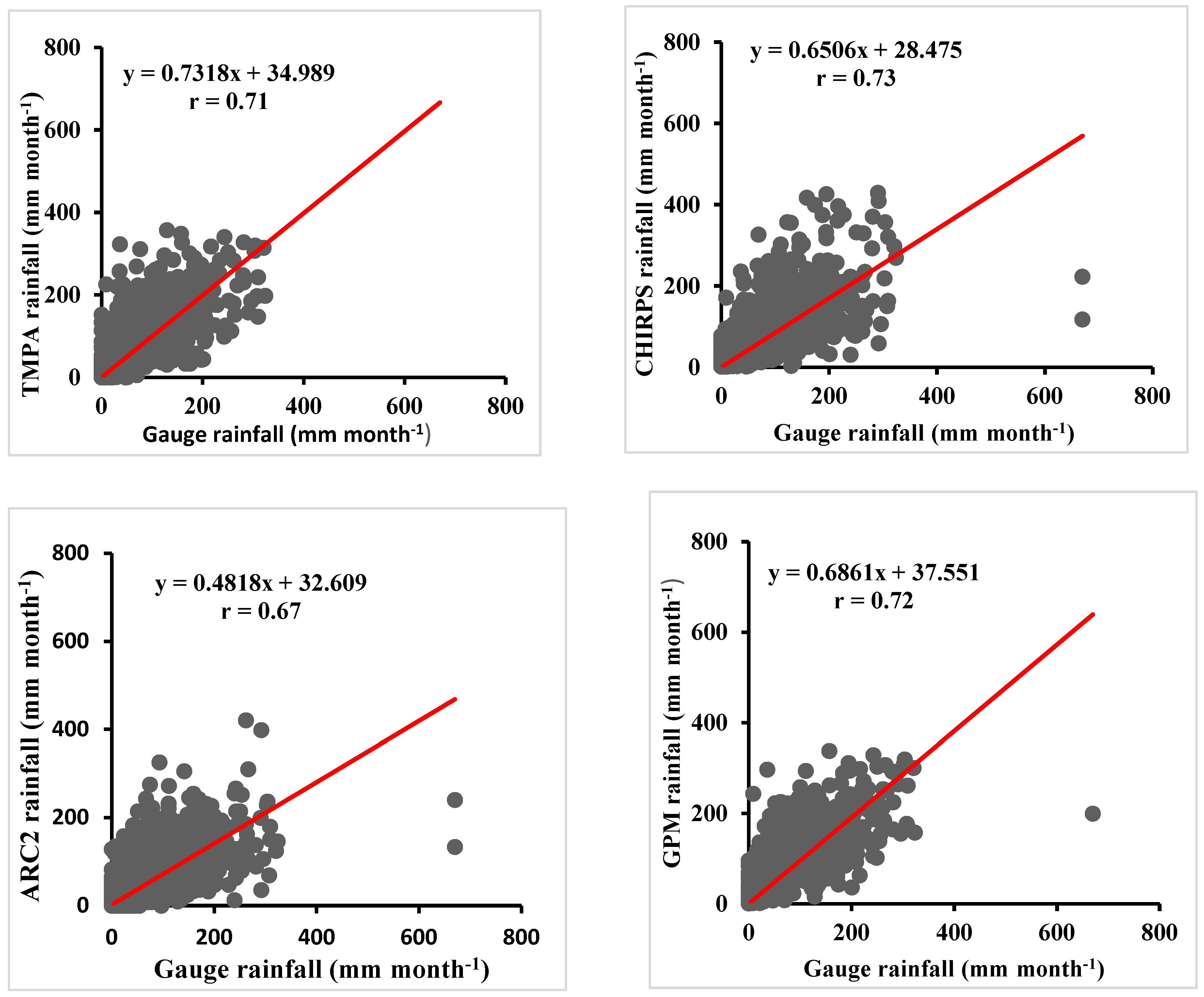
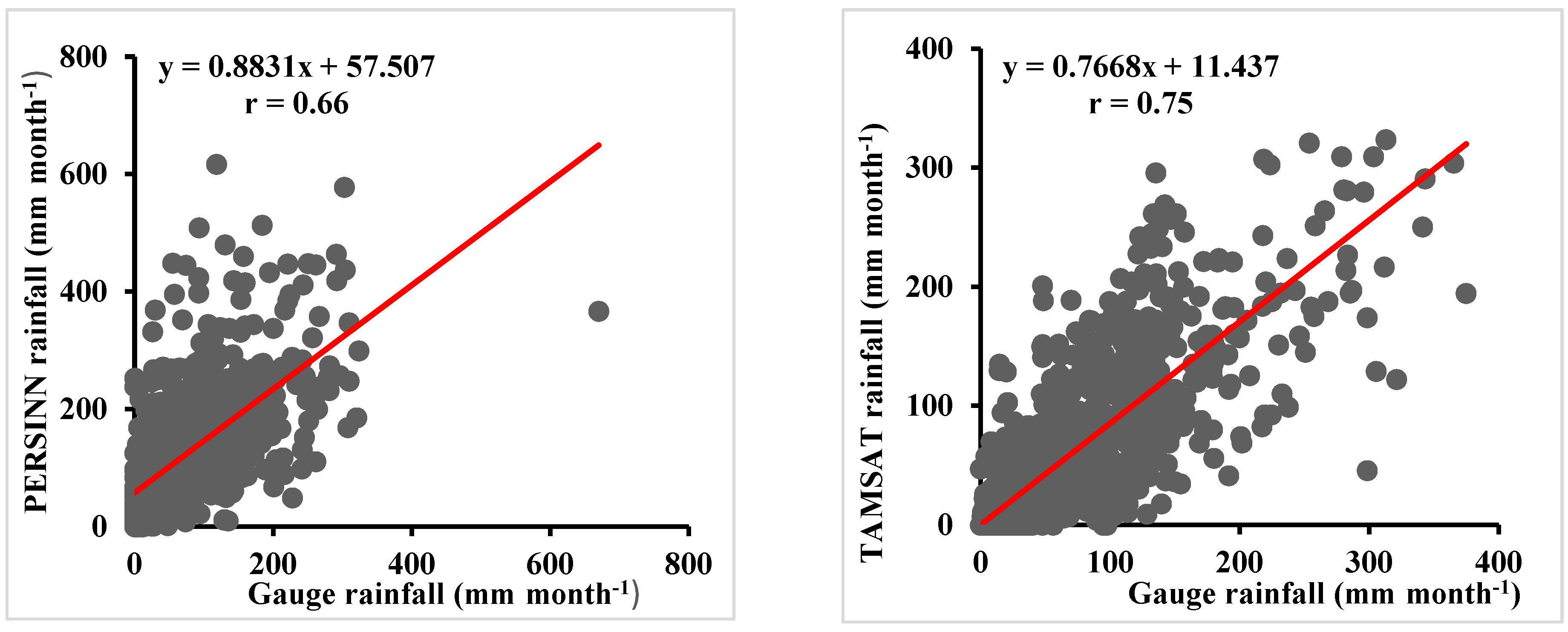
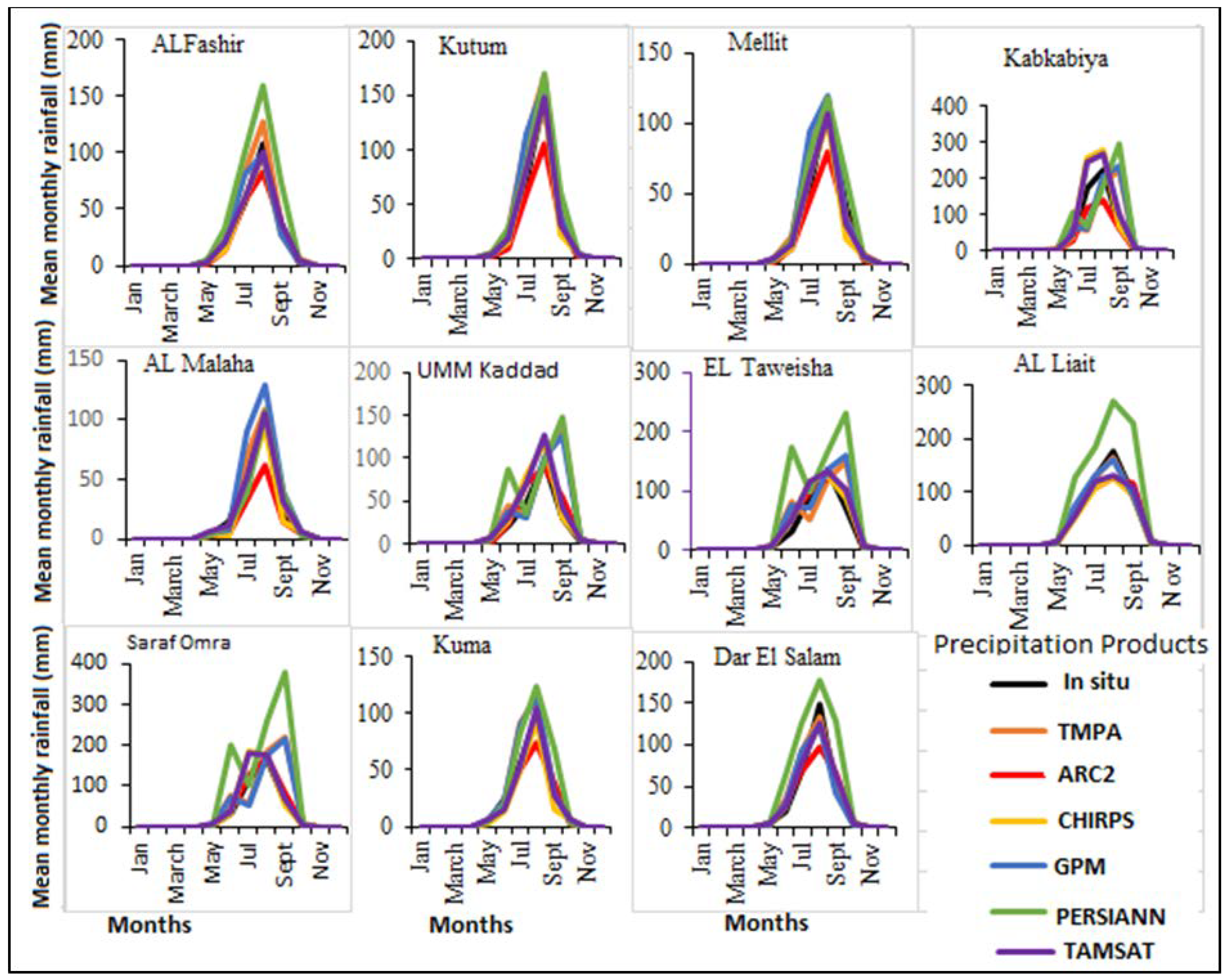
3.1. Monthly Comparisons of Rainfall Totals
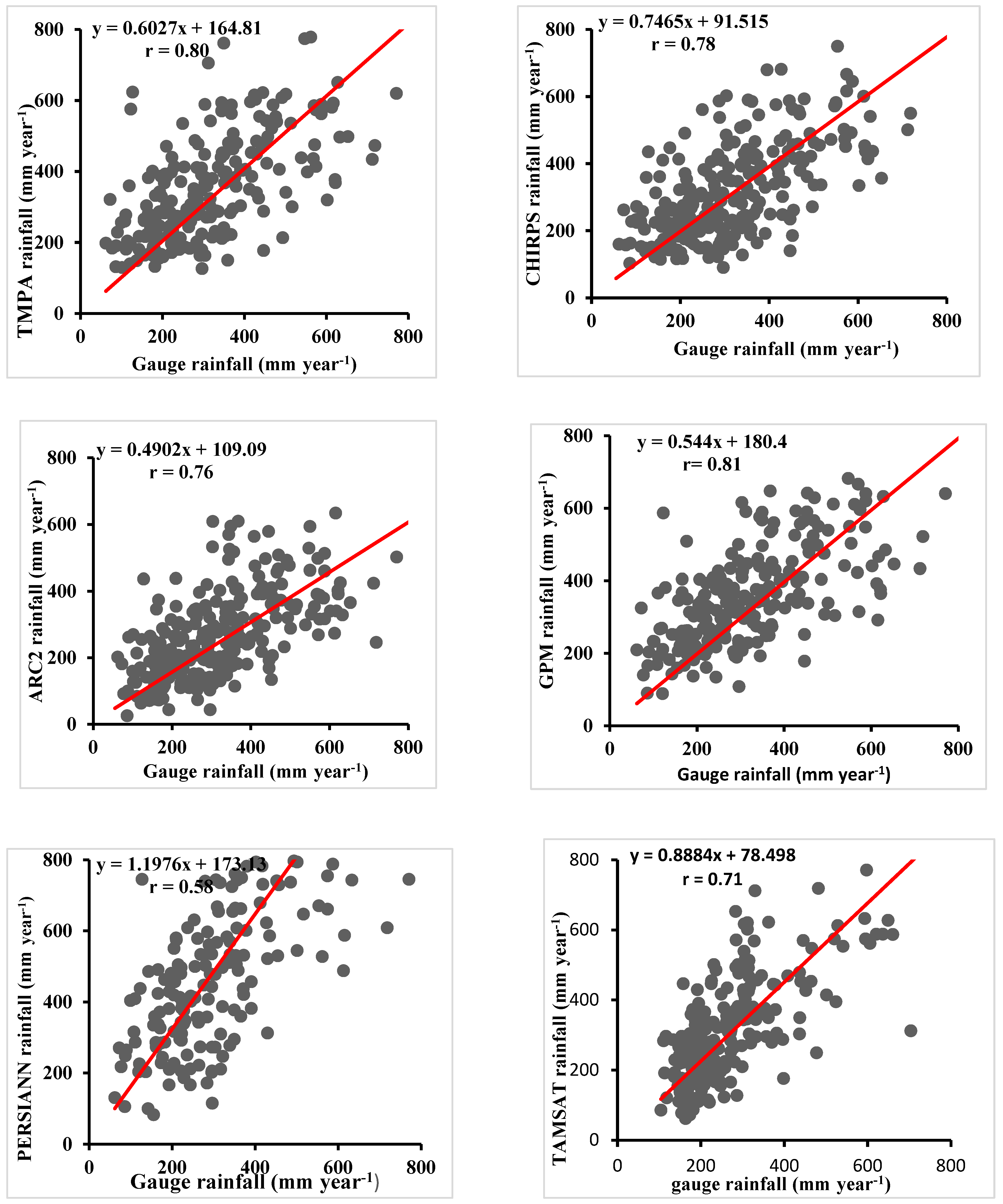
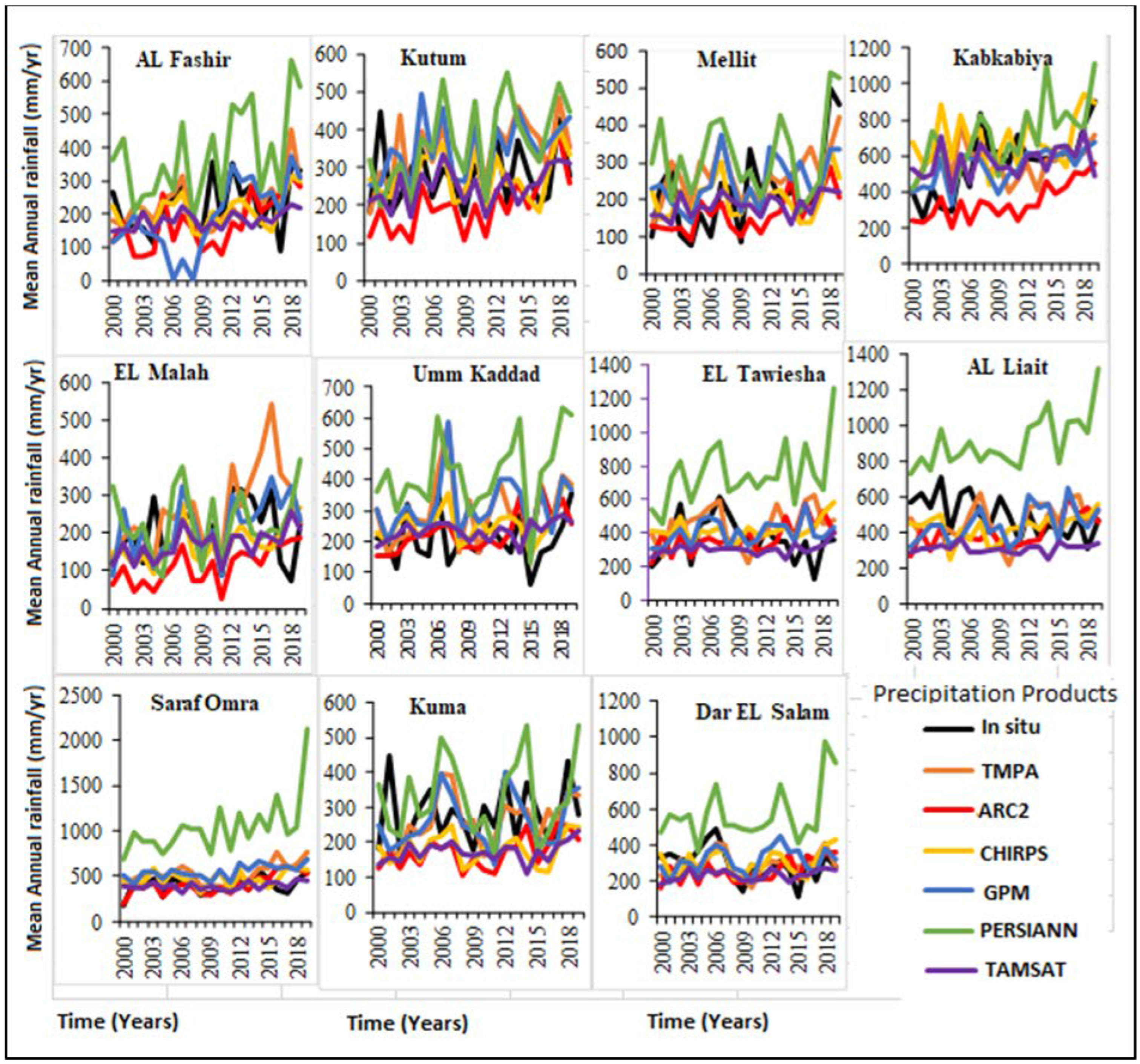
3.2. Annual Comparisons of Rainfall Totals
3.3. Mean Monthly Rainfall Trends
3.4. Mean Annual Rainfall Trends
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Stillman, S.; Ninneman, J.; Zeng, X.; Franz, T.; Scott, R.L.; Shuttleworth, W.J.; Cummins, K. Summer Soil Moisture Spatiotemporal Variability in Southeastern Arizona. J. Hydrometeorol. 2014, 15, 1473–1485. [Google Scholar] [CrossRef]
- Ayehu, G.T.; Tadesse, T.; Gessesse, B.; Dinku, T. Validation of new satellite rainfall products over the Upper Blue Nile Basin, Ethiopia. Atmospheric Meas. Tech. 2018, 11, 1921–1936. [Google Scholar] [CrossRef]
- Brocca, L.; Pellarin, T.; Crow, W.T.; Ciabatta, L.; Massari, C.; Ryu, D.; Su, C.; Rüdiger, C.; Kerr, Y. Rainfall estimation by inverting SMOS soil moisture estimates: A comparison of different methods over Australia. J. Geophys. Res. Atmos. 2016, 121. [Google Scholar] [CrossRef]
- Asfaw, A.; Simane, B.; Hassen, A.; Bantider, A. Variability and time series trend analysis of rainfall and temperature in northcentral Ethiopia: A case study in Woleka sub-basin. Weather. Clim. Extrem. 2018, 19, 29–41. [Google Scholar] [CrossRef]
- Zambrano-Bigiarini, M.; Nauditt, A.; Birkel, C.; Verbist, K.; Ribbe, L. Temporal and spatial evaluation of satellite-based rainfall estimates across the complex topographical and climatic gradients of Chile. Hydrol. Earth Syst. Sci. 2017, 21, 1295–1320. [Google Scholar] [CrossRef]
- Field, C.B.; Barros, V.R. Climate change 2014–Impacts, adaptation and vulnerability: Regional aspects; Cambridge University Press: 2014.
- Kevane, M.; Gray, L. Darfur: rainfall and conflict. Environmental Research Letters 2008, 3, 034006. [Google Scholar] [CrossRef]
- Ibrahim, F.N. Ecological imbalance in the Republic of the Sudan: with reference to desertification in Darfur. 1984.
- Maidment, R.I.; Grimes, D.; Black, E.; Tarnavsky, E.; Young, M.; Greatrex, H.; Allan, R.P.; Stein, T.; Nkonde, E.; Senkunda, S. A new, long-term daily satellite-based rainfall dataset for operational monitoring in Africa. Scientific data 2017, 4, 1–19. [Google Scholar]
- Trejo, F.J.P.; Barbosa, H.Á.; Peñaloza-Murillo, M.A.; Moreno, M.A.; Farias, A. Intercomparison of improved satellite rainfall estimation with CHIRPS gridded product and rain gauge data over Venezuela. Atmósfera 2016, 29, 323–342. [Google Scholar] [CrossRef]
- Ageet, S.; Fink, A.H.; Maranan, M.; Diem, J.E.; Hartter, J.; Ssali, A.L.; Ayabagabo, P. Validation of Satellite Rainfall Estimates over Equatorial East Africa. J. Hydrometeorol. 2022, 23, 129–151. [Google Scholar] [CrossRef]
- Kidd, C.; Huffman, G. Global precipitation measurement. Meteorological Applications 2011, 18, 334–353. [Google Scholar] [CrossRef]
- Toté, C.; Patricio, D.; Boogaard, H.; Van Der Wijngaart, R.; Tarnavsky, E.; Funk, C. Evaluation of Satellite Rainfall Estimates for Drought and Flood Monitoring in Mozambique. Remote Sens. 2015, 7, 1758–1776. [Google Scholar] [CrossRef]
- Gebremichael, M.; Krajewski, W.F.; Morrissey, M.L.; Huffman, G.J.; Adler, R.F. A Detailed Evaluation of GPCP 1° Daily Rainfall Estimates over the Mississippi River Basin. J. Appl. Meteorol. 2005, 44, 665–681. [Google Scholar] [CrossRef]
- Usman, M.; Nichol, J.E.; Ibrahim, A.T.; Buba, L.F. A spatio-temporal analysis of trends in rainfall from long term satellite rainfall products in the Sudano Sahelian zone of Nigeria. Agric. For. Meteorol. 2018, 260-261, 273–286. [Google Scholar] [CrossRef]
- Sanogo, S.; Fink, A.H.; Omotosho, J.A.; Ba, A.; Redl, R.; Ermert, V. Spatio-temporal characteristics of the recent rainfall recovery in West Africa. Int. J. Clim. 2015, 35, 4589–4605. [Google Scholar] [CrossRef]
- Dezfuli, A.K.; Ichoku, C.M.; Huffman, G.J.; Mohr, K.I.; Selker, J.S.; van de Giesen, N.; Hochreutener, R.; Annor, F.O. Validation of IMERG Precipitation in Africa. J. Hydrometeorol. 2017, 18, 2817–2825. [Google Scholar] [CrossRef] [PubMed]
- Dembélé, M.; Zwart, S.J. Evaluation and comparison of satellite-based rainfall products in Burkina Faso, West Africa. Int. J. Remote. Sens. 2016, 37, 3995–4014. [Google Scholar] [CrossRef]
- Bayissa, Y.; Tadesse, T.; Demisse, G.; Shiferaw, A. Evaluation of Satellite-Based Rainfall Estimates and Application to Monitor Meteorological Drought for the Upper Blue Nile Basin, Ethiopia. Remote Sens. 2017, 9, 669. [Google Scholar] [CrossRef]
- Babaousmail, H.; Hou, R.; Ayugi, B.; Gnitou, G.T. Evaluation of satellite-based precipitation estimates over Algeria during 1998–2016. J. Atmospheric Solar-Terrestrial Phys. 2019, 195, 105139. [Google Scholar] [CrossRef]
- Girma, D. Evaluation and Bias correction of Tropical Applications of Meteorology using SATellite (TAMSAT) daily rainfall estimates over the data-scarce region of Southern Ethiopia. 2021, 1–7. [CrossRef]
- Lu, X.; Wang, L.; Pan, M.; Kaseke, K.F.; Li, B. A multi-scale analysis of Namibian rainfall over the recent decade—comparing TMPA satellite estimates and ground observations. J. Hydrol. Reg. Stud. 2016, 8, 59–68. [Google Scholar] [CrossRef]
- Elhamid, A.M.; Eltahan, A.M.; Mohamed, L.M.; Hamouda, I.A. Assessment of the two satellite-based precipitation products TRMM and RFE rainfall records using ground based measurements. Alex. Eng. J. 2020, 59, 1049–1058. [Google Scholar] [CrossRef]
- Maidment, R.I.; Grimes, D.I.F.; Allan, R.P.; Greatrex, H.; Rojas, O.; Leo, O. Evaluation of satellite-based and model re-analysis rainfall estimates for Uganda. Meteorol. Appl. 2013, 20, 308–317. [Google Scholar] [CrossRef]
- Osman, A. Agricultural change, land and violence: An examination of the region of Darfur, Sudan. PhD Dissertation, Food Policy and Applied Nutrition, Gerald J. and Dorothy R …, 2012. [Google Scholar]
- Siddig, K.; Stepanyan, D.; Wiebelt, M.; Grethe, H.; Zhu, T. Climate change and agriculture in the Sudan: Impact pathways beyond changes in mean rainfall and temperature. Ecol. Econ. 2019, 169, 106566. [Google Scholar] [CrossRef]
- Brauch, H.G. Desertification–a new security challenge for the Mediterranean? Policy agenda for recognising and coping with fatal outcomes of global environmental change and potentially violent societal consequences. In Desertification in the Mediterranean Region. A Security Issue; Springer: 2006; pp. 11-85.
- Elagib, N.A.; Al Zayed, I.S.; Saad, S.A.; Mahmood, M.I.; Basheer, M.; Fink, A.H. Debilitating floods in the Sahel are becoming frequent. J. Hydrol. 2021, 599, 126362. [Google Scholar] [CrossRef]
- Mohmmed, A.; Zhang, K.; Kabenge, M.; Keesstra, S.; Cerdà, A.; Reuben, M.; Elbashier, M.M.; Dalson, T.; Ali, A.A. Analysis of drought and vulnerability in the North Darfur region of Sudan. Land Degrad. Dev. 2018, 29, 4424–4438. [Google Scholar] [CrossRef]
- Wedajo, G.K.; Muleta, M.K.; Awoke, B.G. Performance evaluation of multiple satellite rainfall products for Dhidhessa River Basin (DRB), Ethiopia. Atmospheric Meas. Tech. 2021, 14, 2299–2316. [Google Scholar] [CrossRef]
- Yong, B.; Chen, B.; Gourley, J.J.; Ren, L.; Hong, Y.; Chen, X.; Wang, W.; Chen, S.; Gong, L. Intercomparison of the Version-6 and Version-7 TMPA precipitation products over high and low latitudes basins with independent gauge networks: Is the newer version better in both real-time and post-real-time analysis for water resources and hydrologic extremes? Journal of Hydrology 2014, 508, 77–87. [Google Scholar]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Novella, N.S.; Thiaw, W.M. African Rainfall Climatology Version 2 for Famine Early Warning Systems. J. Appl. Meteorol. Clim. 2013, 52, 588–606. [Google Scholar] [CrossRef]
- Funk, C.; Verdin, A.; Michaelsen, J.; Peterson, P.; Pedreros, D.; Husak, G. A global satellite-assisted precipitation climatology. Earth Syst. Sci. Data 2015, 7, 275–287. [Google Scholar] [CrossRef]
- Sungmin, O.; Foelsche, U.; Kirchengast, G.; Fuchsberger, J.; Tan, J.; Petersen, W.A. Evaluation of GPM IMERG Early, Late, and Final rainfall estimates using WegenerNet gauge data in southeastern Austria. Hydrol. Earth Syst. Sci. 2017, 21, 6559–6572. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Xie, P.; Yoo, S.-H. NASA global precipitation measurement (GPM) integrated multi-satellite retrievals for GPM (IMERG). Algorithm Theoretical Basis Document (ATBD) Version 2015, 4.
- Ashouri, H.; Hsu, K.-L.; Sorooshian, S.; Braithwaite, D.K.; Knapp, K.R.; Cecil, L.D.; Nelson, B.R.; Prat, O.P. PERSIANN-CDR: Daily Precipitation Climate Data Record from Multisatellite Observations for Hydrological and Climate Studies. Bull. Am. Meteorol. Soc. 2015, 96, 69–83. [Google Scholar] [CrossRef]
- Hsu, K.-L.; Gao, X.; Sorooshian, S.; Gupta, H.V. Precipitation Estimation from Remotely Sensed Information Using Artificial Neural Networks. J. Appl. Meteorol. 1997, 36, 1176–1190. [Google Scholar] [CrossRef]
- Tarnavsky, E.; Grimes, D.; Maidment, R.; Black, E.; Allan, R.P.; Stringer, M.; Chadwick, R.; Kayitakire, F. Extension of the TAMSAT Satellite-Based Rainfall Monitoring over Africa and from 1983 to Present. J. Appl. Meteorol. Clim. 2014, 53, 2805–2822. [Google Scholar] [CrossRef]
- Maidment, R.I.; Grimes, D.; Allan, R.P.; Tarnavsky, E.; Stringer, M.; Hewison, T.; Roebeling, R.; Black, E. The 30 year TAMSAT African Rainfall Climatology And Time series (TARCAT) data set. J. Geophys. Res. Atmos. 2014, 119, 10–619. [Google Scholar] [CrossRef]
- Grimes, D.; Pardo-Igúzquiza, E.; Bonifacio, R. Optimal areal rainfall estimation using raingauges and satellite data. J. Hydrol. 1999, 222, 93–108. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. Journal of hydrology 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Diem, J.E.; Hartter, J.; Ryan, S.J.; Palace, M.W. Validation of Satellite Rainfall Products for Western Uganda. J. Hydrometeorol. 2014, 15, 2030–2038. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe Jr, G.J. Evaluating the use of “goodness-of-fit” measures in hydrologic and hydroclimatic model validation. Water resources research 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Katsanos, D.; Retalis, A.; Michaelides, S. Validation of a high-resolution precipitation database (CHIRPS) over Cyprus for a 30-year period. Atmos. Res. 2016, 169, 459–464. [Google Scholar] [CrossRef]
- Gebremicael, T.G.; Mohamed, Y.A.; van der Zaag, P.; Gebremedhin, A.; Gebremeskel, G.; Yazew, E.; Kifle, M. Evaluation of multiple satellite rainfall products over the rugged topography of the Tekeze-Atbara basin in Ethiopia. Int. J. Remote. Sens. 2019, 40, 4326–4345. [Google Scholar] [CrossRef]
- Fenta, A.A.; Yasuda, H.; Shimizu, K.; Ibaraki, Y.; Haregeweyn, N.; Kawai, T.; Belay, A.S.; Sultan, D.; Ebabu, K. Evaluation of satellite rainfall estimates over the Lake Tana basin at the source region of the Blue Nile River. Atmospheric Res. 2018, 212, 43–53. [Google Scholar] [CrossRef]
- Basheer, M.; Elagib, N.A. Performance of satellite-based and GPCC 7.0 rainfall products in an extremely data-scarce country in the Nile Basin. Atmospheric Res. 2018, 215, 128–140. [Google Scholar] [CrossRef]
- Dinku, T.; Funk, C.; Peterson, P.; Maidment, R.; Tadesse, T.; Gadain, H.; Ceccato, P. Validation of the CHIRPS satellite rainfall estimates over eastern Africa. Q. J. R. Meteorol. Soc. 2018, 144, 292–312. [Google Scholar] [CrossRef]
- Dinku, T.; Ceccato, P.; Grover-Kopec, E.; Lemma, M.; Connor, S.; Ropelewski, C. Validation of satellite rainfall products over East Africa’s complex topography. International Journal of Remote Sensing 2007, 28, 1503–1526. [Google Scholar] [CrossRef]
- Omonge, P.; Feigl, M.; Olang, L.; Schulz, K.; Herrnegger, M. Evaluation of satellite precipitation products for water allocation studies in the Sio-Malaba-Malakisi river basin of East Africa. J. Hydrol. Reg. Stud. 2021, 39, 100983. [Google Scholar] [CrossRef]
- Kimani, M.W.; Hoedjes, J.C.B.; Su, Z. An Assessment of Satellite-Derived Rainfall Products Relative to Ground Observations over East Africa. Remote. Sens. 2017, 9, 430. [Google Scholar] [CrossRef]
- Roushdi, M. Spatio-Temporal Assessment of Satellite Estimates and Gauge-Based Rainfall Products in Northern Part of Egypt. Climate 2022, 10, 134. [Google Scholar] [CrossRef]
- Liu, X.; Yang, T.; Hsu, K.; Liu, C.; Sorooshian, S. Evaluating the streamflow simulation capability of PERSIANN-CDR daily rainfall products in two river basins on the Tibetan Plateau. Hydrol. Earth Syst. Sci. 2017, 21, 169–181. [Google Scholar] [CrossRef]
- Zhang, Z.; Tian, J.; Huang, Y.; Chen, X.; Chen, S.; Duan, Z. Hydrologic Evaluation of TRMM and GPM IMERG Satellite-Based Precipitation in a Humid Basin of China. Remote. Sens. 2019, 11, 431. [Google Scholar] [CrossRef]
- Bitew, M.M.; Gebremichael, M. Assessment of satellite rainfall products for streamflow simulation in medium watersheds of the Ethiopian highlands. Hydrol. Earth Syst. Sci. 2011, 15, 1147–1155. [Google Scholar] [CrossRef]
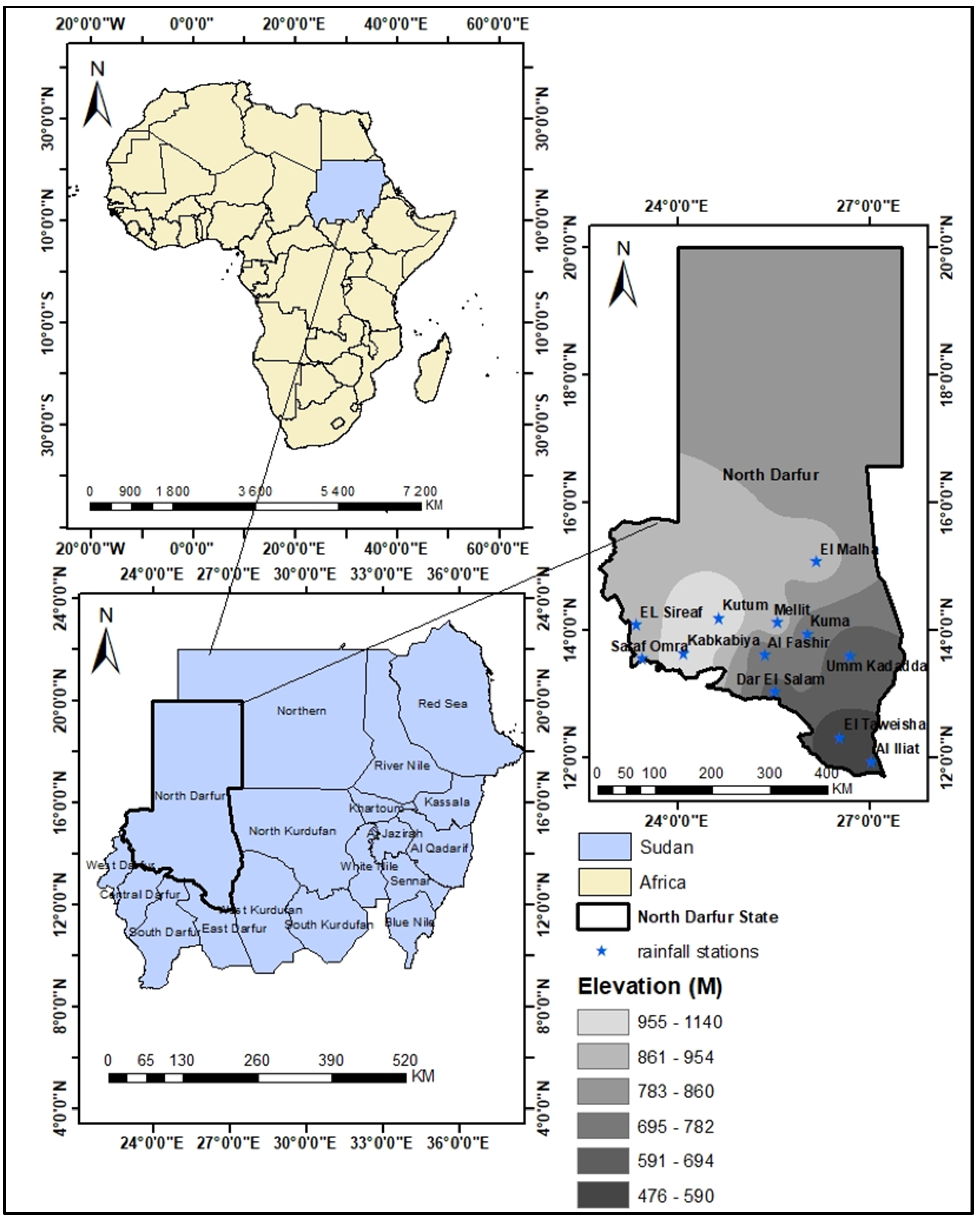
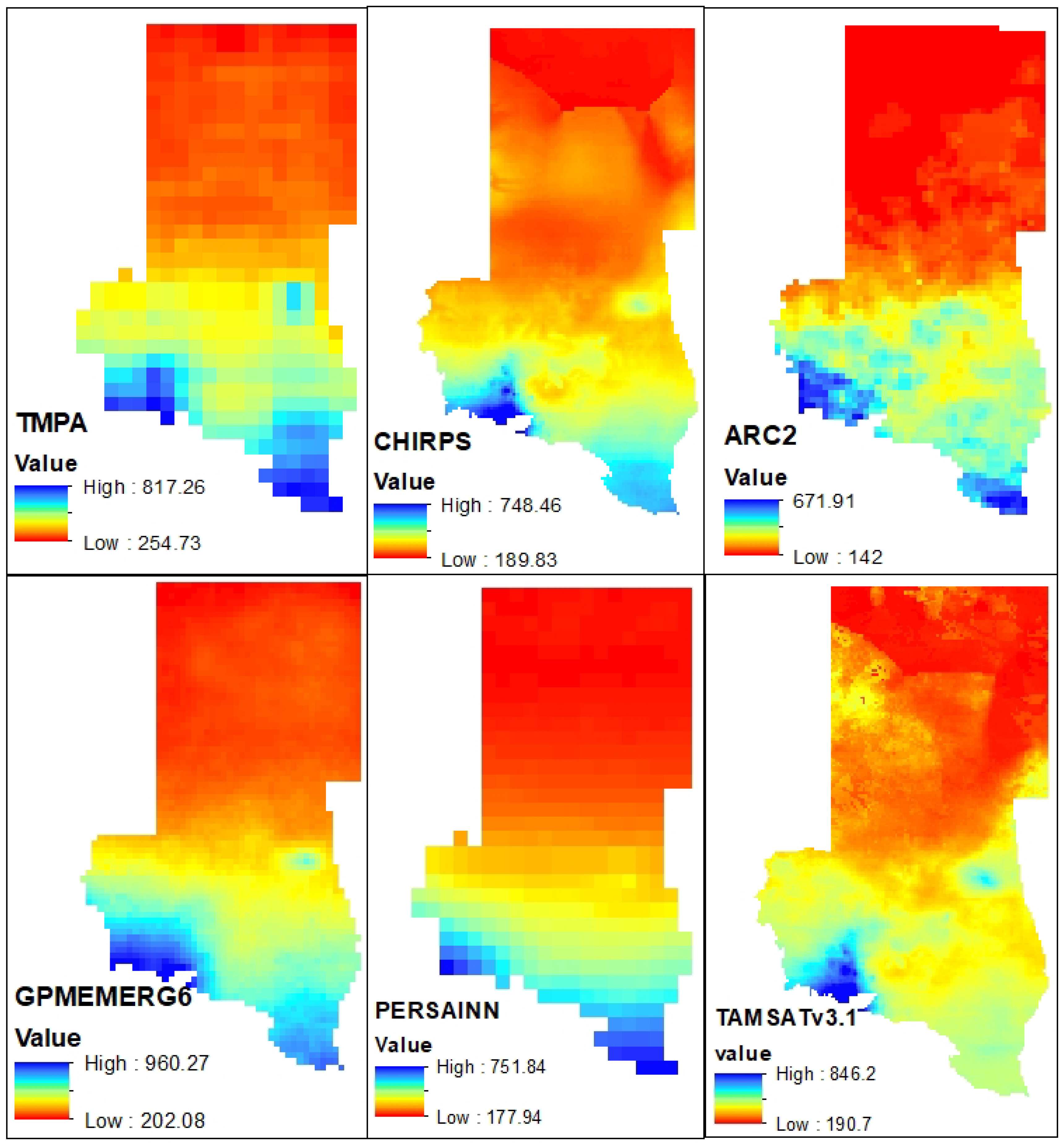
| No. | Rainfall station | Latitude (°N) | Longitude (°E) | Elevation (amsl) | Data availability | Mean annual rainfall |
| 1 | Al Fashir | 13° 38’ | 25° 20’ | 0740 | Monthly | 232.3 |
| 2 | Kutum | 14° 21’ | 24° 40’ | 1160 | Monthly | 279.8 |
| 3 | Mellit | 14° 13’ | 25° 55’ | 0900 | Monthly | 223.9 |
| 4 | Kabkabiya | 13° 39’ | 24° 5’ | 1120 | Monthly | 558.6 |
| 5 | EL Malha | 15° 09’ | 26° 15’ | 0900 | Monthly | 211.7 |
| 6 | Umm Kadadda | 13° 59’ | 26° 14’ | 0595 | Monthly | 227.2 |
| 7 | ELTawiesha | 12° 29’ | 26° 59’ | 591 | Monthly | 363.4 |
| 8 | AL Liait | 11° 57’ | 27° 04’ | 587 | Monthly | 517.1 |
| 9 | Saraf Omra | 13° 47’ | 23° 30’ | 1105 | Monthly | 404.3 |
| 10 | Kuma | 13° 39’ | 26° 01’ | 875 | Monthly | 220.2 |
| 11 | Dar EL Salam | 13° 05’ | 25° 53’ | 817 | Monthly | 302.2 |
| No. | Satellites-based rainfall products | Temporal coverage | Spatial coverage | Temporal resolution | Spatial resolution |
|---|---|---|---|---|---|
| 1 | TMPA-3B42v7.0 | 1998–2019 | Near global | Monthly | 0.25 ̊ × 0.25 ̊ |
| 2 | ARC Version 2.0 | 1983–present | Africa | Daily | 0.1 ̊ × 0.1 ̊ |
| 3 | CHIRPS Version 2.0 | 1981–present | Near global | Daily | 0.05 ̊ × 0.05 ̊ |
| 4 | GPM IMERG6 | 2000–2019 | Near global | Monthly | 0.1 ̊ × 0.1 ̊ |
| 5 | PERSIANN-CDR | 1982–2020 | Near global | Daily | 0.25 ̊ × 0.25 ̊ |
| 6 | TAMSATv3.1 | 1983–present | Africa | Daily | 0.0375 ̊ |
| Dataset | r | RMSE | Pbias | E |
|---|---|---|---|---|
| TMPA | 0.71 | 52.73 | 15.34 | 0.36 |
| CHIRPS2 | 0.73 | 50.64 | 1.49 | 0.41 |
| ARC2 | 0.67 | 51.19 | -20.25 | 0.40 |
| GPMIMERG6 | 0.72 | 51.49 | 18.01 | 0.39 |
| PERSIANN | 0.66 | 76.66 | 48.88 | -0.35 |
| TAMSAT | 0.75 | 47.1 | 10.29 | 0.49 |
| Dataset | r | RMSE | Pbias | E |
|---|---|---|---|---|
| TMPA | 0.80 | 110.2 | 21.33 | 0.50 |
| CHIRPS2.0 | 0.78 | 112.4 | 22.85 | 0.39 |
| ARC2.0 | 0.76 | 89.8 | -16.9 | 0.35 |
| GPMIMERG6 | 0.81 | 100.4 | 10.19 | 0.19 |
| PERSIANN | 0.58 | 235.2 | 82.69 | -0.57 |
| TAMSAT | 0.71 | 8.7 | 14.98 | 0.61 |
| stations | Statistic/ products | TMPA | CHIRPS2 | ARC2 | GPMIMERG6 | PERSIANN | TAMSAT |
|---|---|---|---|---|---|---|---|
| Al Fashir | r | 0.83 | 0.84 | 0.61 | 0.8 | 0.8 | 0.72 |
| Pbias | 24.91 | -10.23 | -19.72 | 5.56 | 67.57 | 3.62 | |
| Kutum | r | 0.77 | 0.79 | 0.79 | 0.7 | 0.67 | 0.67 |
| Pbias | 29.53 | -1.92 | -24.32 | 24.89 | 21.77 | 5.25 | |
| Mellit | r | 0.66 | 0.7 | 0.69 | 0.64 | 0.61 | 0.61 |
| Pbias | 14.59 | -10.77 | -24.68 | 21.38 | 25.45 | -1.94 | |
| Kabkabiya | r | 0.54 | 0.71 | 0.74 | 0.54 | 0.55 | 0.53 |
| Pbias | 0.55 | 23.57 | -34.98 | 5.67 | 16.10 | 28.46 | |
| EL Malha | r | 0.68 | 0.65 | 0.71 | 0.71 | 0.64 | 0.64 |
| Pbias | 4.19 | -20.84 | -43.36 | 28.49 | -4.58 | 7.50 | |
| Umm Kadadda | r | 0.61 | 0.41 | 0.44 | 0.55 | 0.57 | 0.6 |
| Pbias | 59.96 | 26.08 | 16.65 | 50.98 | 76.68 | 40.04 | |
| ELTawiesha | r | 0.47 | 0.65 | 0.43 | 0.53 | 0.53 | 0.66 |
| Pbias | 17.68 | 11.16 | 9.91 | 29.21 | 85.50 | 17.41 | |
| AL Liait | r | 0.48 | 0.41 | 0.25 | 0.42 | 0.2 | 0.48 |
| Pbias | -17.78 | -13.79 | 0.05 | 70.88 | -9.39 | -3.36 | |
| Saraf Omra | r | 0.5 | 0.7 | 0.68 | 0.39 | 0.46 | 0.72 |
| Pbias | 20.90 | 14.25 | 42.32 | 143.12 | 27.26 | 49.51 | |
| Kuma | r | 0.56 | 0.61 | 0.44 | 0.57 | 0.55 | 0.61 |
| Pbias | -15.65 | -14.13 | 27.71 | 37.49 | -2.47 | 29.27 | |
| Dar EL Salam | r | 0.61 | 0.62 | 0.56 | 0.59 | 0.45 | 0.72 |
| Pbias | 15.19 | 1.99 | -6.96 | 4.68 | 72.00 | 8.17 |
| stations | Statistic/ products | TMPA | CHIRPS2 | ARC2 | GPMIMERG6 | PERSIANN | TAMSAT |
|---|---|---|---|---|---|---|---|
| Al Fashir | r | 0.47 | 0.57 | 0.66 | 0.36 | 0.67 | 0.46 |
| Pbias | 0.79 | -24.26 | -9.45 | -16.26 | 65.96 | -20.22 | |
| Kutum | r | 0.50 | 0.57 | 0.56 | 0.61 | 0.72 | 0.74 |
| Pbias | 20.87 | -0.96 | -27.45 | 25.11 | 32.83 | 9.99 | |
| Mellit | r | 0.61 | 0.44 | 0.58 | 0.57 | 0.61 | 0.43 |
| Pbias | 19.08 | -8.07 | -26.94 | 11.15 | 42.91 | -16.70 | |
| Kabkabiya | r | 0.23 | 0.46 | 0.56 | 0.70 | 0.72 | 0.25 |
| Pbias | 23.25 | -38.37 | -3.59 | 25.58 | 1.12 | 1.30 | |
| EL Malha | r | 0.42 | 0.34 | 0.82 | 0.83 | 0.37 | 0.52 |
| Pbias | 29.50 | -15.47 | -44.78 | 6.97 | 12.97 | -15.97 | |
| Umm Kadadda | r | 0.25 | 0.63 | 0.38 | 0.44 | 0.46 | 0.21 |
| Pbias | 44.79 | 24.72 | 10.07 | 53.00 | 103.54 | 12.45 | |
| ELTawiesha | r | 0.41 | 0.22 | 0.43 | 0.42 | 0.64 | 0.36 |
| Pbias | 21.54 | 14.30 | 1.72 | 10.25 | 106.48 | -16.81 | |
| AL Liait | r | 0.22 | 0.38 | 0.46 | 0.55 | 0.66 | 0.34 |
| Pbias | -6.37 | -13.09 | -20.22 | -10.03 | 83.53 | -37.56 | |
| Saraf Omra | r | 0.51 | 0.40 | 0.51 | 0.62 | 0.63 | 0.28 |
| Pbias | 31.81 | 19.48 | 3.03 | 37.85 | 161.07 | -0.90 | |
| Kuma | r | 0.14 | 0.57 | 0.54 | 0.44 | 0.76 | 0.25 |
| Pbias | -7.25 | -35.51 | -38.05 | -6.63 | 18.67 | -37.98 | |
| Dar EL Salam | r | 0.43 | 0.51 | 0.39 | 0.17 | 0.47 | 0.46 |
| Pbias | -1.64 | 2.45 | -13.79 | 7.22 | 92.38 | -21.26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).





