Prerpints.org logo
Preprint
Article

New Wave Solutions for the Two-Mode Caudrey-Dodd-Gibbon Equation

This version is not peer-reviewed.

  ‡ These authors contributed equally to this work.

Submitted:

18 May 2023

Posted:

19 May 2023

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
In this paper, we exhibit new dynamical properties of the two-mode Caudrey-Dodd-Gibbon (TMCDG) equation. This model describes the motion of dual-waves in dispersive and nonlinear media, which mainly depends on the nonlinearity and dispersion parameters. The overlapping of such two-mode waves is affected by the phase-velocity parameter. The study takes a full advantages of the Kudryashov method and of the exponential-expansion method. For the first time, dual-wave solutions are obtained for arbitrary values of the nonlinearity and dispersive factors. The graphs of the novel solutions are also provided in order to depict the waves propagation, as well as to show the influence of the parameters.
Keywords: 
Subject: 
Physical Sciences  -   Mathematical Physics

1. Introduction

The two-mode nonlinear partial differential equations (NPDEs) represent extended form of the standard mode NPDEs. Both types of NPDEs, standard and two-modes, play a considerable role in explaining pragmatic phenomena in various fields [1].
The evolutionary standard NPDEs involve a first-order partial derivative in respect with time and describe the unidirectional motion of a single wave. The dual/two-mode equations are NPDEs of second order in time, and govern the propagation of two wave modes, in the same direction simultaneously, with the same dispersion relation but with different phase velocity, linear and nonlinear parameters. At present, investigations on the two-mode problems are mainly based on the Korsunsky proposed method [2]. It shows that for deriving the two-mode PDEs, it is necessary to collect, as two distinct components, the nonlinear terms N ( u , u x u , . . . ) and the linear terms L ( u n x , n ≥ 2 ) , other than u t . For more information and developments that have been achieved for two-mode PDEs, we recommend the following articles and the references therein [3,4,5,6]. The dynamics of the two-mode KdV equation associated to the standard mode third order KdV equation, was studied by various analytical methods: the reductive perturbation [7], the Hamiltonian system [8], or the Bell polynomials [9]. In [10], it was found that the two modes are solitons that separate without any change of their initial shapes and velocities except for the phase shifts after each collision. Also in [11] the bright, dark, periodic, and singular-periodic dual-wave solutions are constructed for the two-mode Sawada-Kotera equation arising in fluids by the modified Kudryashov and new auxiliary equation methods. A finite series in terms of tanh-sech functions is proposed as a suggested solution for dual-mode version of the nonlinear Schrödinger equation [12]. More exactly dual-mode dark and singular soliton solutions have been obtained. The innovative tanh-expansion method and Kudryashov technique are used in [13] to the dual-mode Kadomtsev-Petviashvili equation to find the necessary constraint conditions that guarantee the existence of soliton solutions. Multiple kink solutions are pointed out in [14] for the two-mode Sharma-Tasso-Olver equation, and for the two-mode fourth-order Burgers equation by using the Cole-Hopf transformation combined with the simplified Hirota’s method. Three different techniques including the tanh-expansion method, the rational sine–cosine method and the Kudryashov-expansion method have been applied in [15] in order to study the dynamic behaviours for a dual-mode generalized Hirota–Satsuma coupled KdV system.
The contributions of this work are two-fold. First, we find explicit dual-waves solutions for the dual/two-mode Caudrey-Dodd-Gibbon (TMCDG) equation for arbitrary nonlinearity and dispersion parameters, α and β . Previosly, only the case α = β = ± 1 was considered in [16], using the Hirota method. Second, we study the influence of the mentioned parameters as well as of s which stands for phase velocity, on the wave propagations, showing how the dual-wave propagation depends on them.
The paper is organized as it follows: After the Introduction, in section 2, an overview on the general form of the TMCDG equation is provided. In section 3 we present basic facts on the Kudryashov method [17,18] and the exponential expansion method [19]. The findings of our investigation, when the previous methods were applied to TMCDG equation, are pointed out in section 4. A general discussion and some graphical representations of the acquired solutions are presented in section 5. Section 6 is dedicated to some conclusions and final remarks.

2. Formulation of dual/two-mode equations

2.1. General form of the two-mode equation

The general form of the two-mode equation proposed by Korsunsky [2] is as follows:
u 2 t − s 2 u 2 x + ∂ ∂ t − α s ∂ ∂ x N ( u , u x u , . . . ) + ∂ ∂ t − β s ∂ ∂ x L ( u n x , n ≥ 2 ) = 0 .
Eq. (1) is established from the standard mode equation: u t + N ( u ,   u x u , . . . ) + L ( u n x , n ≥ 2 ) = 0 . In the dual/two-mode Eq. (1), u ( x , t ) is the unknown field-function, s > 0 is the interaction phase velocity, α ≤ 1 , β ≤ 1 represent the nonlinearity parameter and dispersion parameter, while N ( u , u x u , . . . ) and L ( u n x , n ≥ 2 ) indicate the nonlinear and respectively linear terms. It is important to note that the existence of the dispersion is essential for finding soliton solutions [20,21]. The way of generating a two-mode equation used here for CDG could be also applied to other NPDs, as for example the Eckhaus-Kundu Eq. [22] or the Kundu-Mukherjee-Naskar Eq. [23].

2.2. Two-mode Caudrey-Dodd-Gibbon (TMCDG) equation

In this paper we use a standard mode equation like as [24]:
G t + a G 2 G x + b G x G 2 x + m G G 3 x + G 5 x = 0 ,
where a , b , m are positive parameters [25], G 5 x is the linear term, while the nonlinear one is represented by a G 2 G x + b G x G 2 x + m G G 3 x . It is used to describe various phenomena in plasma physics, nonlinear optics, fluid dynamics, solid–state physics, mathematical biology, chemical kinetics, as well as quantum field theory [26]. It can for example shows how long waves flow in shallow water under gravity and in a one-dimensional nonlinear lattice. For a = 180 , b = m = 30 , the Eq. (2) becomes the Caudrey-Dodd-Gibbon (CDG) equation [27]:
G t + 180 G 2 G x + 30 G x G 2 x + 30 G G 3 x + G 5 x = 0 .
Many computational strategies have been successfully employed in order to develop various soliton solutions that provide a more hidden characterization of the shallow water [28,29,30].
Based on the Korsunsky proposal scheme, the two-mode equation associated to the Eq. (3) is under the form:
G 2 t − s 2 G 2 x + ∂ ∂ t − α s ∂ ∂ x ( 180 G 2 G x + 30 G x G 2 x + 30 G G 3 x ) + ∂ ∂ t − β s ∂ ∂ x G 5 x = 0 .
It is obvious that for s = 0 , after integrating regarding time t, the previous equation is reduced to the standard mode Eq. (2). It describes the propagation of two shallow waves under the influence of phase velocity s, nonlinearity α , and dispersion β factors. By expanding it, we arrive to the equivalent expression:
G 2 t − s 2 G 2 x + 30 [ 12 G G x G t + 6 G 2 G x t + G x t G 2 x + G x G ( 2 x ) t + G t G 3 x + G G ( 3 x ) t ] − 30 α s 12 G G x 2 + 6 G 2 G 2 x + 30 G 2 x 2 + 2 G x G 3 x + G G 4 x + G ( 5 x ) t − β s G 6 x = 0 .
In order to solve (5), we use the wave variable ξ = k x − c t and therefore we transform it into the travelling wave equation of the following form:
c 2 − k 2 s 2 G ′ ′ − 30 c [ 12 k G ( G ′ ) 2 + k G 2 G ′ ′ + k 3 ( G ′ ′ ) 2 + 2 k 3 G ′ G ( 3 ) + k 3 G G ( 4 ) ] − 30 α k 2 s [ 12 G ( G ′ ) 2 + G 2 G ′ ′ + k 2 ( G ′ ′ ) 2 + 2 k 2 G ′ G ( 3 ) + k 2 G G ( 4 ) ] − k 5 ( c + k β s ) G ( 6 ) = 0 .
In [16], one-soliton solution has been derived for (4) through the simplified Hirota method. It was obtain if and only if α = β . In the next section we will extend this result, showing how the equation can be solved for arbitrary nonlinearity and dispersion parameters, α and β . New dual-waves solutions of (4) will be reported for the first time, using two well-known solving methods: the Kudryashov and the exponential expansion methods. These are two of the methods for solving NPDEs based on the auxiliary equation techniques, but other alternative approaches, as for example the attached flow [31], the symmetry method [32,33], or the BRST technique [34] could be also considered.

3. Brief overview of the applied methods

In this section we will take a brief review of the two methods applied later to TMCDG equation. They are effective analytical methods for finding the travelling wave solutions of NPDEs with the generic form:
E ( u , u t , u x , u t t , u x x , . . . ) = 0 .
Here E is a polynomial function with respect to some specified independent variables x, t, and u = u ( x , t ) is the unknown function. When the wave transformation is applied:
u ( t , x ) = u ( ξ ) , ξ = k x − c t ,
where k , c are constants, the Eq. (7) becomes an ODE in u = u ( ξ ) and its derivatives in respect to β :
F ( u , u ′ , u ′ ′ , . . . ) = 0 .

3.1. Basics on the Kudryashov method (KM)

In this section a brief overview of the KM method [35,36] is presented. Let us assume that the solution of Eq. (9) can be expressed as follows:
u ( ξ ) = ∑ j = 0 N a j Q j ( ξ ) ,
where the arbitrary constants a j , j = 1 , N ¯ , a N ≠ 0 , are determined later and Q ( ξ ) is the solution of the equation [37]:
Q ′ ( ξ ) = Q 2 ( ξ ) − Q ( ξ ) .
The positive integer N can be found by taking into consideration the homogeneous balance between the highest order derivatives and the nonlinear terms which appear in the travelling wave Eq. (9). The general solution of the auxiliary Eq. (11) is:
Q ( ξ ) = 1 1 ± d e ξ , ∀ d = c o n s t . ≠ 0 .
By substituting Eqs. (10) and (11) into Eq. (9) yields to a polynomial R ( Q ( ξ ) ) . By setting all the coefficients of R ( Q ( ξ ) ) to zero, the parameters a j , k , c can be explicitly determined by solving the equations of their algebraic relations. Then, setting the obtained solutions in Eq. (10), one can finally generate new solitary wave solutions for the master Eq. (7).
’

3.2. Basics on the exponential expansion method (EEM)

In this section a brief overview of the EEM [38] is presented. In this case the solution of (9) is supposed to have the following form:
u ( ξ ) = ∑ j = 0 N ρ j e j f ( ξ ) ,
where ρ j , j = 1 , N ¯ are arbitrary constants to be calculated such that ρ N ≠ 0 and f ( ξ ) is the solution of the following auxiliary equation:
f ′ ( ξ ) = p e − 2 f ( ξ ) + r e 2 f ( ξ ) ,
where the parameters p , r appear.
The positive integer N can be determined by balancing the highest order derivatives and the nonlinear terms in Eq. (9). By inserting the expansion (13) with the value of N along with auxiliary Eq. (14), into Eq. (9) yield to a polynomial P ( e f ( ξ ) ) . By setting all the coefficients of P ( e f ( ξ ) ) to zero, the parameters ρ j , p , r , k , c can be explicitly found by solving the attained system of algebraic equations. Then, introducing the obtained parameters and the solution of Eq. (14) into exponential expansion (13), one can generate new solitary wave solutions for Eq. (7).

4. Construction of dual-wave solutions: mathematical analysis

In this section we will construct the dual-wave solutions to the TMCDG Eq. (4) via the methods described above.

4.1. Application of the Kudryashov method

Let us suppose that the solutions of Eq. (6) are expressed in accordance with (10)-(11). Taking into consideration the homogeneous balance between the most nonlinear term G 2 G ′ ′ and the higher order derivative G ( 6 ) , we conclude that N = 2 . Therefore, we will search for the travelling wave solutions under the form:
G ( ξ ) = a 0 + a 1 Q ( ξ ) + a 2 Q ( ξ ) 2 .
By substituting (15) and (11) into (6), the left-hand side of the underlying ODE becomes an eight degree polynomial in Q . Setting the coefficients of power Q j , j = 0 , 8 ¯ to zero yields an algebraic system for parameters a i , i = 0 , 2 , ¯ c , k , α ,   β . By using the Maple program, the following set of solutions are obtained:
Solution 1: ∀ k , ∀ s > 0 , ∀ α ≤ 1 , and
a 0 = − k 2 9 , a 1 = − a 2 = 4 k 2 3 , c 1 , 2 = ± k s , β = 1 + 10 α 9 , β ≤ 1 ;
Solution 2: ∀ k , ∀ s > 0 , ∀ α ≤ 1 , ∀ a 2 and
a 0 = a 2 12 , a 1 = − a 2 , c 3 , 4 = k 4 k 2 a 2 + 3 a 2 2 ± 16 k 4 a 2 2 + 24 k 2 a 2 3 + 9 a 2 4 + 64 k 2 a 2 s α + 64 s 2 + 48 a 2 2 s α 8 , β = ± E [ a 2 2 + 3 k 2 a 2 + 2 k 4 ] − 3 a 2 4 − 13 k 2 a 2 3 − 2 a 2 2 [ 9 k 4 + 4 s α ] − 8 k 2 a 2 [ k 4 + 3 s α ] 16 s k 4 ,
with
E = 9 a 2 4 + 24 k 2 a 2 3 + 16 a 2 2 ( k 4 + 3 s α ) + 64 k 2 a 2 s α + 64 s 2 , β ≤ 1 .
Plugging (16) and (17) along with the solution of the auxiliary Eq. (11) into Eq. (15), we obtain the following new dual-wave solutions:
G 1 , 2 ( x , t ) = k 2 3 1 3 + 4 1 1 + d e ( k x − c 1 , 2 t ) − 1 1 + d e ( k x − c 1 , 2 t ) 2 , ∀ d
G 3 , 4 ( x , t ) = a 2 1 12 − 1 1 + d e ( k x − c 3 , 4 t ) + 1 1 + d e ( k x − c 3 , 4 t ) 2 , ∀ d ,
where the waves’ velocities c 1 , 2 and c 3 , 4 are given by the expressions (16) and (17).

4.2. Application of the exponential expansion method (EEM)

In order to determine the dual-wave solutions of TMCDG equation through the EEM method, the finite expansion solution of Eq. (6) related to the homogeneous balance between dispersion and nonlinearity, is derived as follows:
G ( ξ ) = ρ 0 + ρ 1 e f ( ξ ) + ρ 2 e 2 f ( ξ ) .
By plugging Eq. (21) along with the auxiliary Eq. (14) into travelling wave Eq. (6) and equating the coefficients of various powers of exponential terms to zero, a set of algebraic equations involving ρ j , j = 0 , 2 ¯ , p , r , c , k is derived. Its solution is obtained with the help of Maple program, under the form:
∀ ρ 0 , ∀ ρ 2 , ∀ s > 0 , ∀ k , ∀ p , ∀ r , α = β = 1 , ρ 1 = 0 , c = ± s k .
Substituting the relations (22) into Eq. (21), we should look for other TMCDG solutions in the form:
G ( ξ ) = ρ 0 + ρ 2 e 2 f ( ξ ) .
For example, taking into account the solution of the auxiliary Eq. (14) and considering p r > 0 , the dual-wave solution is derived as a periodic one:
G 5 , 6 ( x , t ) = ρ 0 + ρ 2 p r tan 2 p r k ( x ± s t ) + q ,
with ρ 0 , ρ 2 , k , p , r , q , s > 0 arbitrary constants.

5. Disscussions on the dual-wave solutions

Let us now analyze the dual-wave solutions obtained in the previous section. We will give here their graphical representations that will help us to understand better the dynamical behaviour of the model.
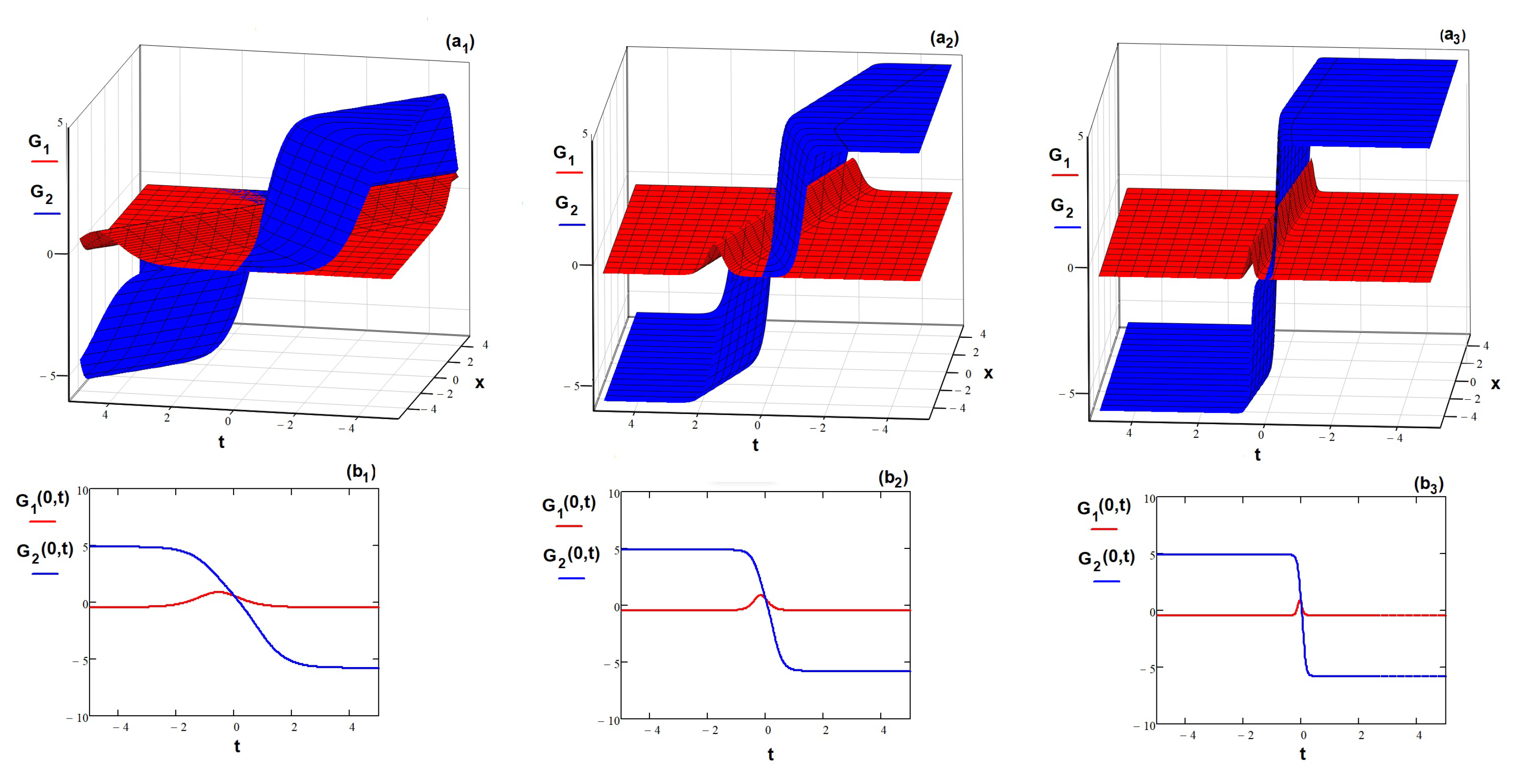
Let us start with the solutions (19). Their 3 D and 2 D graphics are presented in the Figure 1 by considering particular values of the free parameters as d = 3 , k = 2 , and α = 0 , 8 , β = 1 for different values of s. The subgraphs ( a 1 ) − ( a 3 ) present the spatio-temporal variation of these solutions for s = 1 , 3 , 10 , respectively. The subgraphs (b1)-(b3) show the cross-sectional 2 D plots of ( a 1 ) − ( a 3 ) when x = 0 .
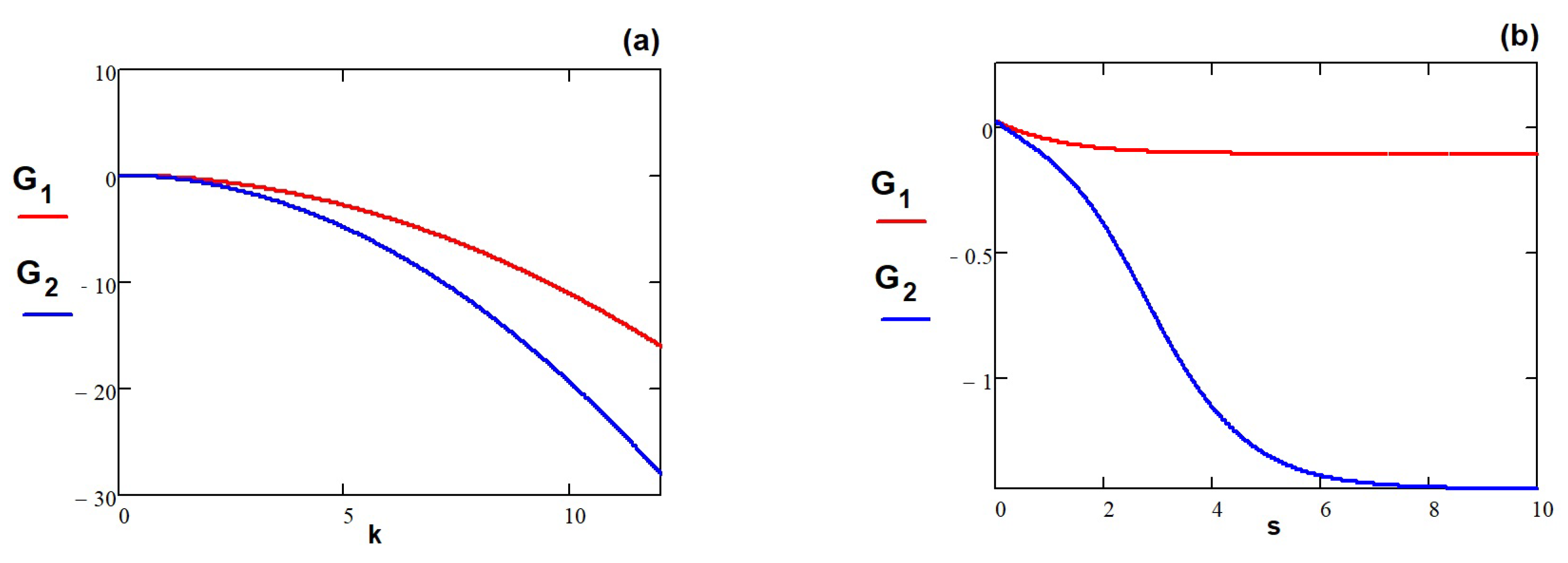
The two waves G 1 ( x , t ) and G 2 ( x , t ) interact with each other. Upon increasing the phase velocity, the width of each of the two waves is decreasing, but the amplitudes remain unchanged. The above behaviors are clearly displayed with the 2 D plots given by the subgraphs ( b 1 ) − ( b 3 ) . The impact of the wave number k and of the the interaction phase velocity s , on the motion of the waves (19) are shown respectively in the subgraphs ( a ) , ( b ) from the Figure 2 . It can be seen from the subgraph (a) that the profiles of G 1 and G 2 are stable for k ∈ [ 0 , 1 ] and then the profile of G 1 is higher than that of G 2 , when k increases from 1 to 5 . This happens under particular values x = 1 , t = 1 , s = 3 , d = 3 , α = 0 , 8 , β = 1 . On the other hand, the profile of G 2 is lower than that of G 1 and their profiles become stable for phase velocity s > 6 , when x = 1 , t = 1 , k = 1 , d = 3 , α = 0 , 8 , β = 1 are considered.
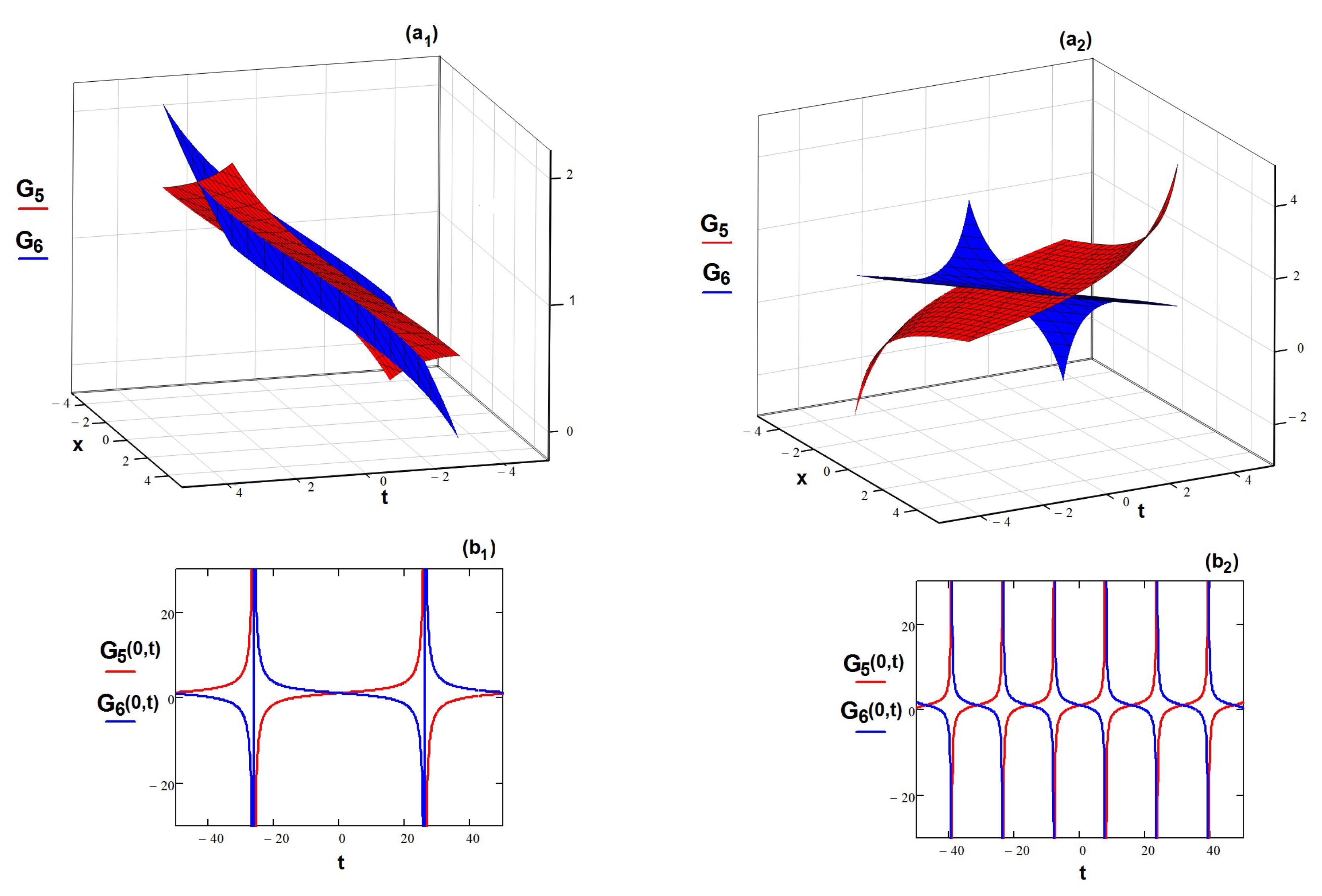
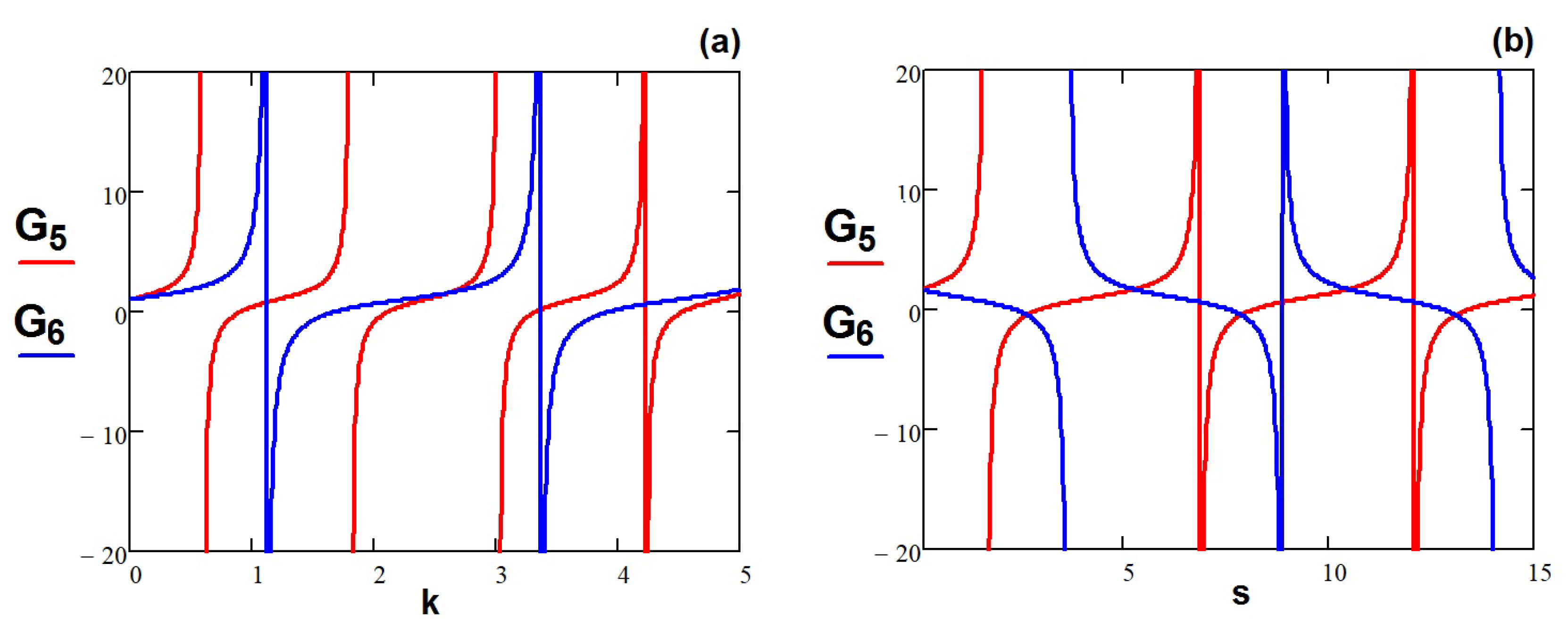
Moreover, in order to analyze the dynamical behaviour of the novel dual-mode solution (20), the 3 D and 2 D graphics are presented in the Figure 3, by considering particular values of the free parameters as a 2 = 0 , 1 , d = 3 , k = 2 , α = 0 , 2 , for various values of phase velocity s . The subgraphs ( a 1 ) − ( a 3 ) present the physical structure of the dual-waves G 3 ( x , t ) and G 4 ( x , t ) upon increasing s ( s = 1 , 3 , 5 ) which are respectively associated to the values of β = 0 , 881 , 0 , 971 ,   0 , 997 . The motion described by (20) looks as singular dual kink-waves, as it is clearly shown in the subgraphs ( b 1 ) − ( b 3 ) , representing the 2 D plots of ( a 1 ) − ( a 3 ) for x = 0 . The collision of the waves occurs for the phase velocity s = 5 . The influence of parameters k, s, and α on the motion of dual-waves (20) is illustrated in the subgraphs ( a ) − ( c ) from the Figure 4. When increasing both the wave number k within [ 1 ,   3 ] and the phase velocity s inside the interval of values s min = 6 , 8 and s max = 12 , we observe that the profiles of G 3 ( x , t ) and G 4 ( x , t ) increase and remain fixed for any values k > 3 , s > 12 .
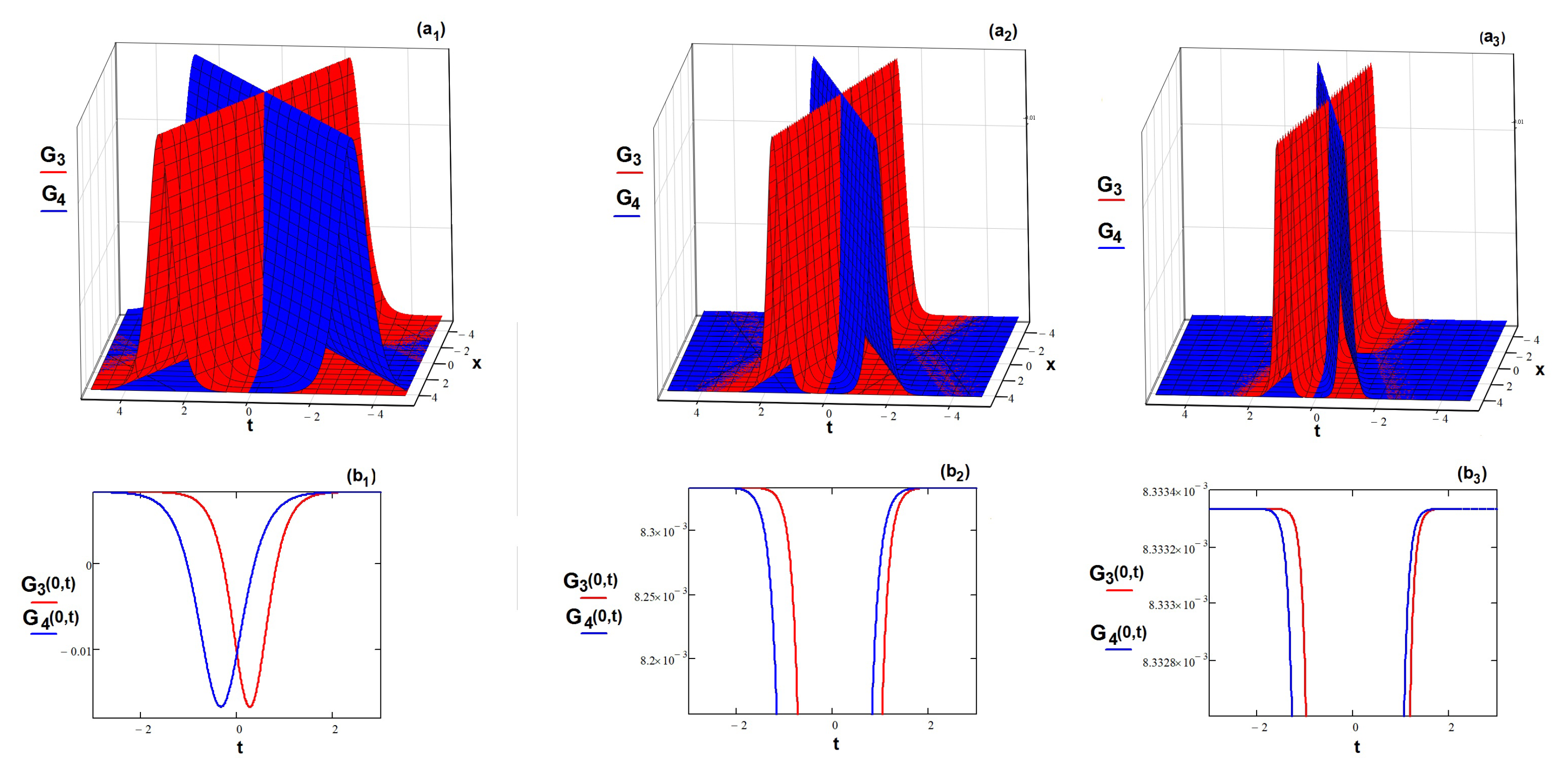
Next, we will analyze the remaining of the obtained solutions. The 3 D and 2 D graphical configurations of the dual-mode solutions (24), are presented in the Figure 5. The subgraphs ( a 1 ) , ( a 2 ) show the physical structure of the two-mode waves G 5 ( x , t ) and G 6 ( x , t ) upon increasing s ( s = 0 , 3 respectively s = 1 ), for the particular values of the free parameters ρ 0 = 1 , ρ 2 = 4 , k = 0 , 1 , p = 0 , 5 , r = 2 , q = 0 ,   α = β = 1 . Both waves have a periodic evolution, following t a n -shapes that collide with each other. For a fixed phase velocity parameter s, the periods of the dual-waves are the same. As s increases, one can observe from the 2 D plots which are shown in the subgraphs ( b 1 ) , ( b 2 ) , that the periodicity increases for G 5 ( x , t ) and G 6 ( x , t ) . 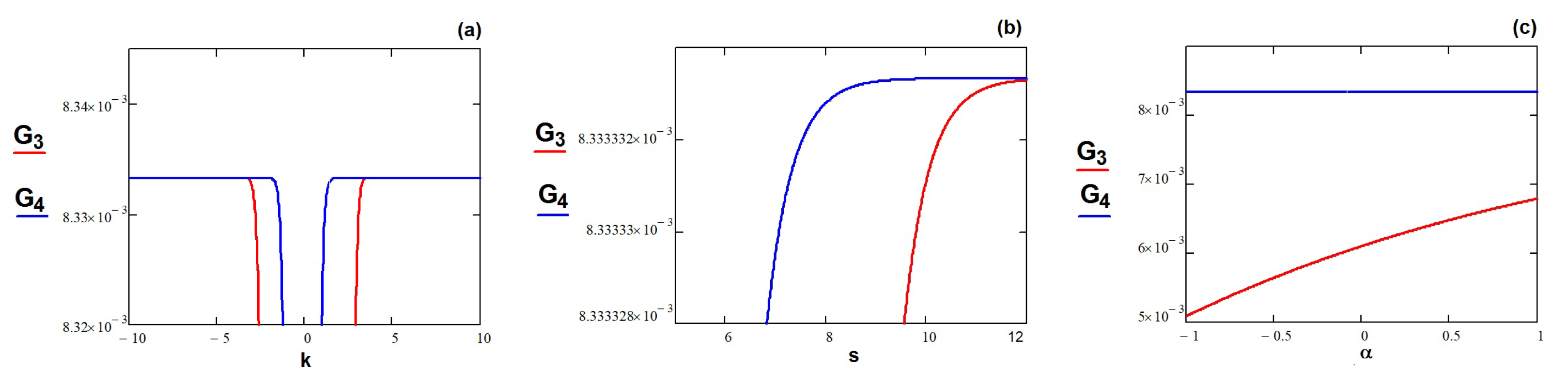The influence of the parameters k, s, on the motion of the two-mode waves (24), when x = 3 , t = 3 , ρ 0 = 1 , ρ 2 = 4 , p = 0 , 5 , r = 2 , q = 0 , α = β = 1 , are presented in the subgraphs (a)–(b) from the Figure 6.

6. Concluding remarks

In this work, we investigated the two-mode Caudrey-Dodd-Gibbon (TMCDG) equation that reads:
G 2 t − s 2 G 2 x + 30 ∂ ∂ t − α s ∂ ∂ x ( 6 G 2 G x + G x G 2 x + G G 3 x ) + ∂ ∂ t − β s ∂ ∂ x G 5 x = 0 .
Two eficient schemes namely, the Kudryashov-expansion and the exponential-expansion, are implemented in order to construct new dual-wave solutions. The previous studies [16] related to this model were all based on the unitary values of nonlinearity and dispersion parameters, α = β = ± 1 . In our article, novel dual-mode wave solutions given by (19), (20) and (24) are generated for arbitrary nonlinearity and dispersion parameters, α and β . For the best of our knowedge they are reported here for the first time. Some interesting properties of the dynamical behavior of the TMCDG model were pointed out using the graphical representations of the new aquired solutions. They can be summarized as it follows:
- The TMCDG equation admits all the classes of solutions, hyperbolic, harmonic and rational, as the unimodal Eq. (3). As examples, we have shown that, using the Kudryashov-expansion method, the TMCDG waves move in dual-mode, bright and kink-waves shapes, while by using the exponential-expansion method, the motion could appear as having a dual t a n -periodic pattern. Of course, these are not the only solutions that can be generated, other solutions appearing for different values of p and r.
- The influence of the main parameters (phase velocity s, wave number k and nonlinearity α ) is explained using the graphic representation of the solutions. Depending on their values, the parameters can increase or decrease the velocity of the dual-waves.
In conclusion, in this article novel dual-mode waves are fruitfully generated for arbitrary α and β . As it was mentioned earlier, previously the TMCDG model has been studied via the simplified Hirota method, and only one soliton solutions with the restricted condition on the nonlinearity and dispersion parameters, α = β = ± 1 were reported.
The approach used here can be applied to any evolutionary NPDE of interest in mathematical physics and engineerings, in order to achieve new dual-wave equations and their associated solutions. Ourselves, we will investigate in future works the possibility of extending the two-mode procedure to other higher-dimensional NPDEs, trying also to implement alternative techniques [39,40].

Author Contributions

The authors have equal contribution to this work, with a special involvement as it follows: conceptualization, Ro.C; methodology, Ro.C; formal analysis, Ra.C; writing—review and editing, Ra.C and Ro.C.

Funding

No special funding was used for this research.

Acknowledgments

The authors acknowledge the support offered by ICTP through the NT-03 Grant and by the University of Craiova.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Zwillinger, D. Handbook of differential equations; Academic Press: New York, 1992. [Google Scholar]
  2. Korsunsky, S.V. Soliton solutions for a second order KdV equation. Phys Lett A 1994, 185, 174–176. [Google Scholar] [CrossRef]
  3. Wazwaz, A.M. A study on a two-wave mode Kadomtsev–Petviashvili equation: conditions for multiple soliton solutions to exist. Math. Method Appl. Sci. 2017, 40, 4128–4133. [Google Scholar] [CrossRef]
  4. Wazwaz, A.M. Two wave mode higher-order modified KdV equations: Essential conditions for multiple soliton solutions to exist. Int. J. Numer. Method H. 2017, 27, 2223–2230. [Google Scholar] [CrossRef]
  5. Alquran, M.; Sulaiman, T.A.; Yusuf, A. Kink-soliton, singular-kink-soliton and singular-periodic solutions for a new two-mode version of the Burger-Huxley model: applications in nerve fibers and liquid crystals. Opt Quant Electron. 2021, 53, 227. [Google Scholar] [CrossRef]
  6. Jaradat, I.; Alquran, M. Geometric perspectives of the two-mode upgrade of a generalized Fisher–Burgers equation that governs the propagation of two simultaneously moving waves. J. Comput. Appl Math. 2022, 404, 113908. [Google Scholar] [CrossRef]
  7. Lee, C.T.; Liu, J.L. A Hamiltonian model and soliton phenomenon for a two-mode KdV equation. Rocky Mt. J. Math. 2011, 41, 1273–1289. [Google Scholar]
  8. Lee, C.T.; Lee, C.C. On wave solutions of a weakly nonlinear and weakly dispersive two-mode wave system. Wave Random Complex 2013, 23, 56–76. [Google Scholar] [CrossRef]
  9. Wazwaz, A.M. Multiple soliton solutions and other exact solutions for a two-mode KdV equation. Math. Method Appl. Sci. 2017, 40, 2277–2283. [Google Scholar] [CrossRef]
  10. Xiao, Z.J.; Tian, B.; Zhen, H. L; Chai, J.; Wu, X.Y. Multi-soliton solutions and Bcklund transformation for a two-mode KdV equation in a fluid. Wave Random Complex 2017, 27, 1–14. [Google Scholar] [CrossRef]
  11. Kumar, D.; Park, C.; Tamanna, N.; Paul, G. C.; Osman, M.S. Dynamics of two-mode Sawada-Kotera equation: Mathematical and graphical analysis of its dual-wave solutions. Results Phys. 2020, 19, 103581. [Google Scholar] [CrossRef]
  12. Jaradat, I.; Alquran, M.; Momani, S.; Biswas, A. Dark and singular optical solutions with dual-mode nonlinear Schrödinger’s equation and Kerr-law nonlinearity. Optik 2018, 172, 822–825. [Google Scholar] [CrossRef]
  13. Abu Irwaq, I.; Alquran, M.; Jaradat, I.; Baleanu, D. New dual-mode Kadomtsev–Petviashvili model with strong–weak surface tension: analysis and application. Adv. Differ. Equ. 2018, 2018, 1–7. [Google Scholar] [CrossRef]
  14. Wazwaz, A. M. Two-mode Sharma-Tasso-Olver equation and two-mode fourth-order Burgers equation: multiple kink solutions. Alex. Eng. J. 2018, 57, 1971–1976s. [Google Scholar] [CrossRef]
  15. Alquran, M.; Jaradat, I.; Baleanu, D. Shapes and dynamics of dual-mode Hirota–Satsuma coupled KdV equations: exact traveling wave solutions and analysis. Chinese J. Phys. 2019, 58, 49–56. [Google Scholar] [CrossRef]
  16. Wazwaz, A. M. Two-mode fifth-order KdV equations: necessary conditions for multiple-soliton solutions to exist. Nonlinear Dynam. 2017, 87, 1685–1691. [Google Scholar] [CrossRef]
  17. Alquran, M.; Alhami, R. Convex-periodic, kink-periodic, peakon-soliton and kink bidirectional wave-solutions to new established two-mode generalization of cahn-allen equation. Results Phys. 2022, 34, 105257. [Google Scholar] [CrossRef]
  18. Cimpoiasu, R.; Pauna, A.S. Complementary wave solutions for the long-short wave resonance model via the extended trial equation method and the generalized Kudryashov method. Open Phys. 2018, 16, 419–426. [Google Scholar] [CrossRef]
  19. Ferdous, F.; Hafez, M.G.; Akther, S. Oblique traveling wave closed-form solutions to space-time fractional coupled dispersive long wave equation through the generalized exponential expansion method. Int. J. Comput. Math. 2022, 8, 142. [Google Scholar] [CrossRef]
  20. Babalic, C.N. Complete integrability and complex solitons for generalized Volterra system with branched dispersion, Int. J. Mod. Phys. B 2020, 34(29), 2050274. [Google Scholar] [CrossRef]
  21. Babalic, C.N. , Integrable discretization of coupled Ablowitz-Ladik equations with branched dispersion, Rom. J. Phys. 2018, 63, 114. [Google Scholar]
  22. Cimpoiasu, R.; Constantinescu, R. , Invariant solutions of the Eckhaus-Kundu model with nonlinear dispersion and non-Kerr nonlinearities. Wave Random Complex 2021, 31(2), 331–341. [Google Scholar] [CrossRef]
  23. Cimpoiasu, R.; Rezazadeh, H.; Florian, D.A.; Ahmad, H.; Nonlaopon, K.; Altanji, M. Symmetry reductions and invariant-group solutions for a two-dimensional Kundu-Mukherjee-Naskar model. Results Phys. 2021, 28, 104583. [Google Scholar] [CrossRef]
  24. Zada, L.; Nawaz, R.; Alqudah, M.A.; Nisar, K.S. A new technique for approximate solution of fractional-order partial differential equations. Fractals 2022, 30, XX. [Google Scholar] [CrossRef]
  25. Polat, M.; Oruç, Ö.A. combination of Lie group-based high order geometric integrator and delta-shaped basis functions for solving Korteweg-de Vries (KdV) equation. Int. J. Geom. M. 2021, 18, 2150216. [Google Scholar] [CrossRef]
  26. A. Majeed, M.N. Rafiq, M. Kamran, M. Abbas, M. Inc, Analytical solutions of the fifth-order time fractional nonlinear evolution equations by the unified method. Mod. Phys. Lett. 2022, 36, 2150546.
  27. Majeed, A. M.; Rafiq, V.; Kamran, M.; Abbas, M.; Inc, M. Analytical solutions of the fifth-order time fractional nonlinear evolution equations by the unified method. Mod. Phys. Lett. B 2022, 36, 2150546. [Google Scholar] [CrossRef]
  28. Ghanbari, B. Employing Hirota’s bilinear form to find novel lump waves solutions to an important nonlinear model in fluid mechanics. Results Phys. 2021, 29, 104689. [Google Scholar] [CrossRef]
  29. Ma, H.; Wang, Y.; Deng, A. Soliton molecules and some novel mixed solutions for the extended Caudrey-Dodd-Gibbon equation, J. Geom. Phys. 2021, 168, 104309. [Google Scholar] [CrossRef]
  30. Rani, A.; Ashraf, M.; Ahmad, J. et al. Soliton solutions of the Caudrey–Dodd–Gibbon equation using three expansion methods and applications. Opt. Quant. Electron 2022, 54, 158. [Google Scholar] [CrossRef]
  31. Ionescu, C. The sp(3) BRST Hamiltonian formalism for the Yang-Mills fields. Mod. Phys. Lett. A 2008, 23(10), 737–775. [Google Scholar] [CrossRef]
  32. Cimpoiasu, R. Conservation Laws and associated Lie symmetries for 2D Ricci flow model. Rom. Journ. Phys. 2013, 58, 519–528. [Google Scholar]
  33. Cimpoiasu, R. Multiple invariant solutions of the 3 D potential Yu–Toda–Fukuyama equation via symmetry technique. Int. J. Mod. Phys. B 2020, 34(20), 2050188. [Google Scholar] [CrossRef]
  34. Ionescu, C.; Constantinescu, R. Solving Nonlinear Second-Order Differential Equations through the Attached Flow Method. Math. 2022, 10(15), 2811. [Google Scholar] [CrossRef]
  35. Alquran, M. Optical bidirectional wave-solutions to new two-mode extension of the coupled KdV–Schrodinger equations. Opt. Quant. Electron. 2021, 53, 588. [Google Scholar] [CrossRef]
  36. Jaradat, I.; Alquran, M. Construction of solitary two-wave solutions for a new two-mode version of the Zakharov-Kuznetsov equation. Math. 2020, 8, 1127. [Google Scholar] [CrossRef]
  37. Akbar, M.A.; Akinyemi, L.; Yao, S.W.; Jhangeer, A.; Rezazadeh, H.; Khater, M.M. .. & Inc, M. Soliton solutions to the Boussinesq equation through sine-Gordon method and Kudryashov method. Results Phys. 2021, 25, 104228. [Google Scholar]
  38. Akbar, M.A.; Ali, N.H. M,; Tanjim, T. Outset of multiple soliton solutions to the nonlinear Schrodinger equation and the coupled Burgers equation. J. Phys. Commun. 2019, 3, 095013. [Google Scholar] [CrossRef]
  39. Xu, G.Q.; Wazwaz, A.M. Bidirectional solitons and interaction solutions for a new integrable fifth-order nonlinear equation with temporal and spatial dispersion. Nonlinear Dynam. 2020, 101, 581–595. [Google Scholar] [CrossRef]
  40. Cimpoiasu, R.; Cimpoiasu, V.; Constantinescu, R. Nonlinear dynamical systems in various space-time dimensions. Rom. Journ. Phys. 2010, 55, 25–35. [Google Scholar]
Preprints 74044 g001
Figure 1. The 3 D plots of the dual-wave solutions G 1 ( x , t ) (red color) and G 2 (blue color) given by (19), for α = 0.8 , β = 1 , d = 3 , k = 2 , and the phase velocities: ( a 1 ) s = 1 , ( a 2 ) s = 3 , ( a 3 ) s = 10 . The 2 D cross-sectional of ( a 1 ) – ( a 3 ) at x = 0 are ploted in ( b 1 ) – ( b 3 ) .
Figure 1. The 3 D plots of the dual-wave solutions G 1 ( x , t ) (red color) and G 2 (blue color) given by (19), for α = 0.8 , β = 1 , d = 3 , k = 2 , and the phase velocities: ( a 1 ) s = 1 , ( a 2 ) s = 3 , ( a 3 ) s = 10 . The 2 D cross-sectional of ( a 1 ) – ( a 3 ) at x = 0 are ploted in ( b 1 ) – ( b 3 ) .
Preprints 74044 g001
Preprints 74044 g002
Figure 2. ( a ) The effect of the wave number k when s = 1 , d = 3 , α = 0 , 8 , β = 1 , ( b ) the effect of the phase velocity parameter s when k = 1 , d = 3 , α = 0 , 8 , β = 1 on the motion of the two-mode waves G 1 ( x , t ) (red color) and G 2 ( x , t ) (blue color) given by (19) for x = 1 , t = 1 .
Figure 2. ( a ) The effect of the wave number k when s = 1 , d = 3 , α = 0 , 8 , β = 1 , ( b ) the effect of the phase velocity parameter s when k = 1 , d = 3 , α = 0 , 8 , β = 1 on the motion of the two-mode waves G 1 ( x , t ) (red color) and G 2 ( x , t ) (blue color) given by (19) for x = 1 , t = 1 .
Preprints 74044 g002
Preprints 74044 g003
Figure 3. ( a ) The 3 D plots of the dual-wave solutions G 3 ( x , t ) (red color) and G 4 ( x , t ) (blue color) given by (20) for a 2 = 0 , 1 , d = 3 , k = 2 , α = 0 , 2 and variable s. Three phase velocities were considered: ( a 1 ) s = 1 , ( a 2 ) s = 3 , and ( a 3 ) s = 5 . The 2 D cross-sectional of ( a 1 ) − ( a 3 ) at x = 0 are plotted in ( b 1 ) − ( b 3 ) .
Figure 3. ( a ) The 3 D plots of the dual-wave solutions G 3 ( x , t ) (red color) and G 4 ( x , t ) (blue color) given by (20) for a 2 = 0 , 1 , d = 3 , k = 2 , α = 0 , 2 and variable s. Three phase velocities were considered: ( a 1 ) s = 1 , ( a 2 ) s = 3 , and ( a 3 ) s = 5 . The 2 D cross-sectional of ( a 1 ) − ( a 3 ) at x = 0 are plotted in ( b 1 ) − ( b 3 ) .
Preprints 74044 g003
Preprints 74044 g004
Figure 4. The effect on the motion of the two-mode waves G 3 ( x , t ) (red color) and G 4 ( x , t ) (blue color) given by (20), at x = 3 , t = 1 , of: ( a ) wave number k when s = 5 , α = 0 , 2 , a 2 = 0 , 1 , d = 3 , ( b ) phase velocity s when k = 2 , α = 0.2 , a 2 = 0 , 1 , d = 3 and ( c ) the nonlinearity parameter α when k = 2 , s = 5 , a 2 = 0 , 1 , d = 3 .
Figure 4. The effect on the motion of the two-mode waves G 3 ( x , t ) (red color) and G 4 ( x , t ) (blue color) given by (20), at x = 3 , t = 1 , of: ( a ) wave number k when s = 5 , α = 0 , 2 , a 2 = 0 , 1 , d = 3 , ( b ) phase velocity s when k = 2 , α = 0.2 , a 2 = 0 , 1 , d = 3 and ( c ) the nonlinearity parameter α when k = 2 , s = 5 , a 2 = 0 , 1 , d = 3 .
Preprints 74044 g004
Preprints 74044 g005
Figure 5. The 3 D plots of the dual-wave solutions G 5 ( x , t ) (red color) and G 6 (blue color) given by (24), with α = β = 1 , ρ 0 = 1 , ρ 2 = 4 , k = 0 , 1 , p = 0 , 5 , r = 2 , q = 0 , and the phase velocities: ( a 1 ) s = 0 , 3 , ( a 2 ) s = 1 . The 2 D cross-sectional plots of ( a 1 ) , ( a 2 ) at x = 0 are plotted in ( b 1 ) , ( b 2 ) .
Figure 5. The 3 D plots of the dual-wave solutions G 5 ( x , t ) (red color) and G 6 (blue color) given by (24), with α = β = 1 , ρ 0 = 1 , ρ 2 = 4 , k = 0 , 1 , p = 0 , 5 , r = 2 , q = 0 , and the phase velocities: ( a 1 ) s = 0 , 3 , ( a 2 ) s = 1 . The 2 D cross-sectional plots of ( a 1 ) , ( a 2 ) at x = 0 are plotted in ( b 1 ) , ( b 2 ) .
Preprints 74044 g005
Preprints 74044 g006
Figure 6. The effect on the motion of the two-mode waves G 5 ( x , t ) (red color) and G 6 ( x , t ) (blue color) given by (24) at x = 3 , t = 3 . of: ( a ) the wave number k when α = β = 1 , s = 0 , 3 , ρ 0 = 1 , ρ 2 = 4 , p = 0 , 5 , r = 2 , q = 0 , ( b ) the phase velocity parameter s when ρ 0 = 1 , ρ 2 = 4 , k = 0 , 1 , p = 0 , 5 , r = 2 , q = 0 .
Figure 6. The effect on the motion of the two-mode waves G 5 ( x , t ) (red color) and G 6 ( x , t ) (blue color) given by (24) at x = 3 , t = 3 . of: ( a ) the wave number k when α = β = 1 , s = 0 , 3 , ρ 0 = 1 , ρ 2 = 4 , p = 0 , 5 , r = 2 , q = 0 , ( b ) the phase velocity parameter s when ρ 0 = 1 , ρ 2 = 4 , k = 0 , 1 , p = 0 , 5 , r = 2 , q = 0 .
Preprints 74044 g006
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated