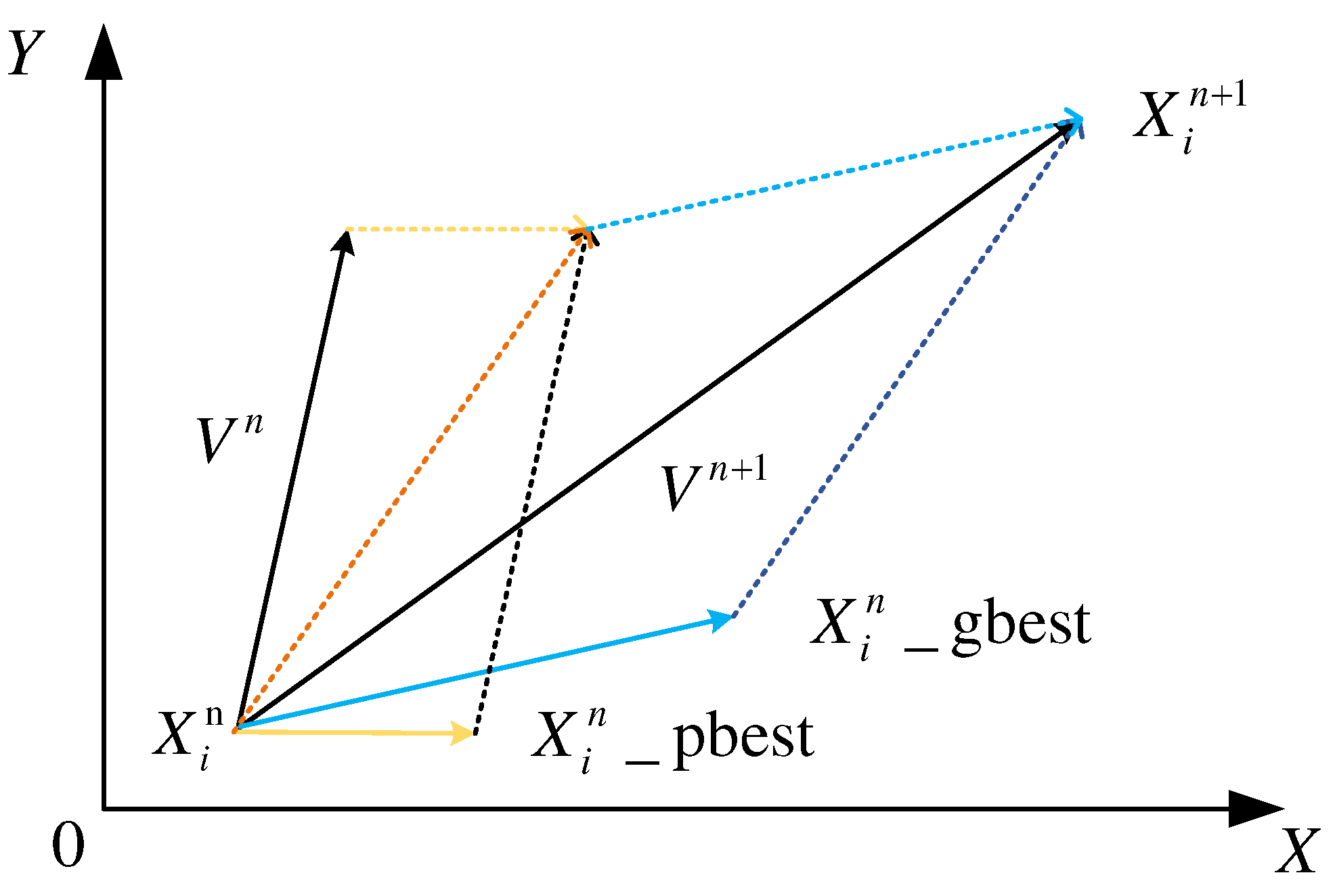1. Introduction

2. The Framework of the Inverse Finite Element Method

3. Coarse and Fine Two-Stage Calibration Method

3.2. Fine Calibration

3.2.1. The Nodal Degrees of Freedom Error Correction

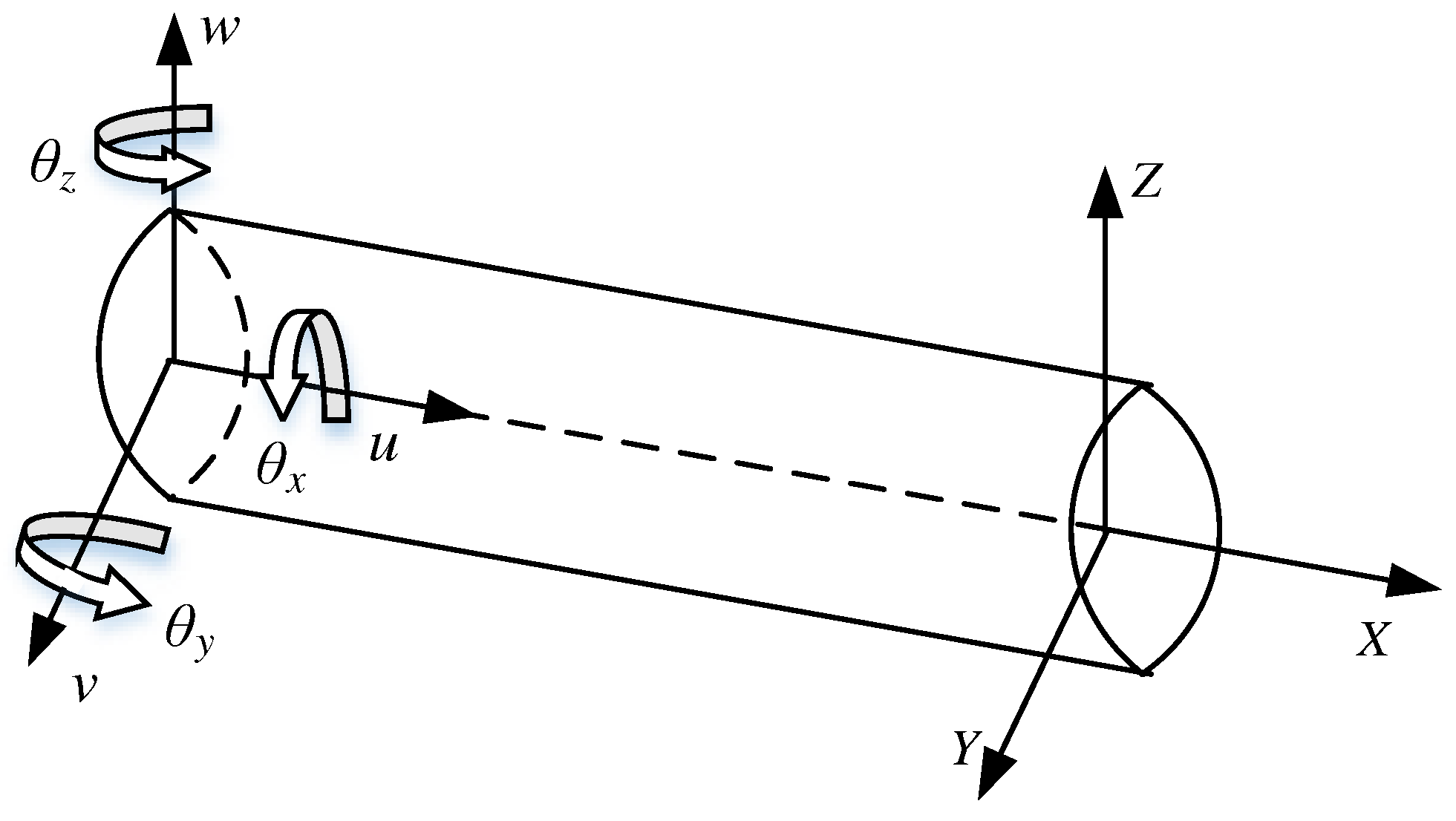
For the errors that still exist between the displacements reconstructed based on the iFEM and the actual displacements after the coarse calibration, the displacement-nodal degree of freedom error correction model is further proposed. As shown in Eq. (18), the theoretical displacement of the inverse finite element reconstruction is denoted as $d_i^t$, and the actual displacement is denoted as $d_i^a$

$$d_i^a=d_i^t+\Delta d_i$$

(18)

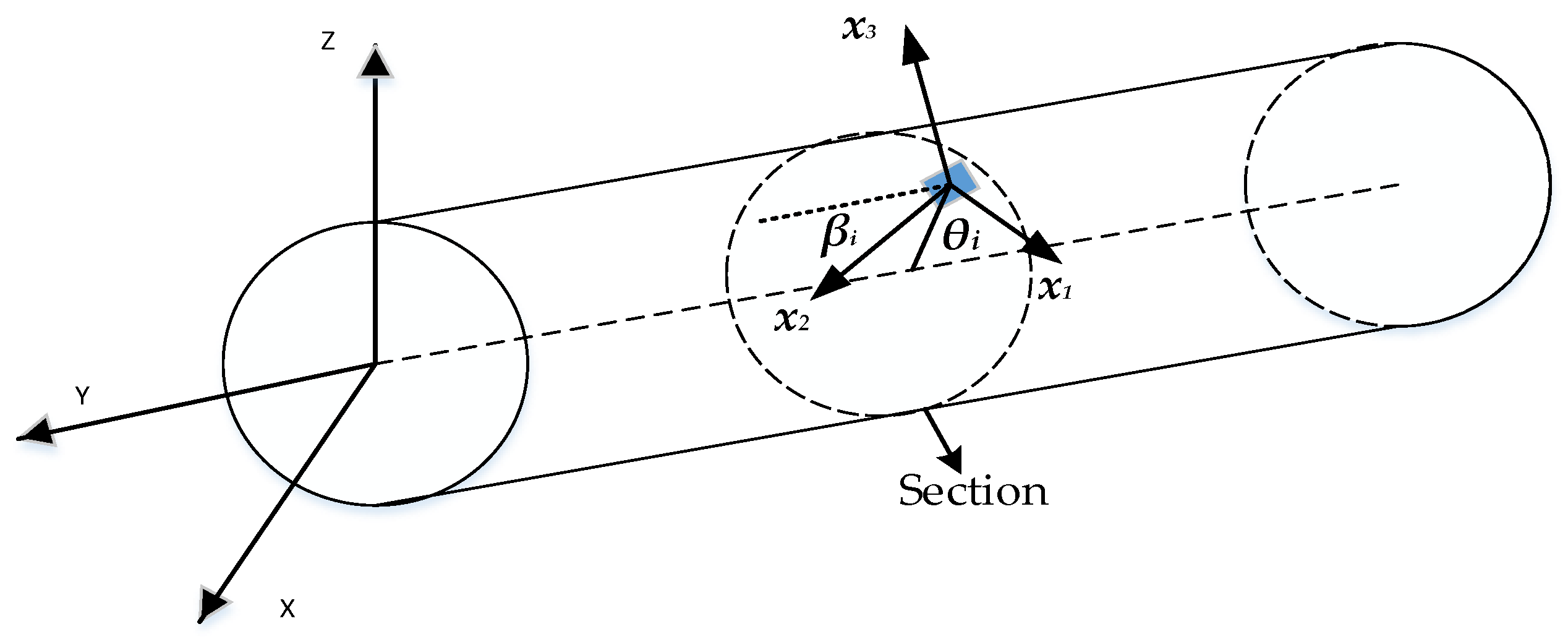
where i=1,... ,n denotes the ordinal number of observation points and Δd_i denotes the reconstruction error. Displacement at any position in the structure can be obtained from the shape function H(x) and the discrete nodal during the reconfiguration displacement. As a result, correcting the reconstruction error in the nodal DOF enables calibration of the entire displacement.

The relationship between displacement error and nodal DOF error can be expressed as Eq. (19).

$$\Delta d_i=\left[\begin{array}{c}\Delta d_i^x\\ \Delta d_i^y\\ \Delta d_i^z\end{array}\right]=G\times N_i\times \Delta u$$

(19)

where the number of nodal DOF is c. The displacement field error Δd_i of the inverse finite element reconstruction is derived by Eq. (19) to the nodal DOF error Δu_j(j= 1, ... , c), then the displacement-nodal DOF model can be expressed as Eq. (20)

$$\Delta d^z=H\cdot \Delta u+\beta$$

(20)

where Δd^z=[Δ$d_1^z$, Δ$d_2^z$, ... ,Δ$d_n^z$]^T, H=[H₁.H₂,... ,H_n], β is denoted as the residuals after displacement error correction and obeys Gaussian distribution. i.e.,$\beta ~N(0,{\sigma }^2)$, and $H_i=[H_{i1},H_{i2},\cdots ,H_{ic}]$ is the row vector of G*N_i for Δd^z.It follows that Δd^x and Δd^y can also be expressed analogously by Eq. (20).

The matrix H in Eq. (20) is the ill-conditioned matrix. The actual measured strain value of the sensor receives interference from random noise, which makes the estimated value Δu having error with the actual value, the error is reduced by Bayesian regularization algorithm using prior information. From Bayesian theory, p（Δu,σ²|Δd^x）is used to represent the joint posterior distribution of the unknown parameters, as defined as shown in Eq. (21)：

$$p(\Delta u,{\sigma }^2|\Delta d^x)\propto p(\Delta d^x|\Delta u,{\sigma }^2)\cdot p(\Delta u,{\sigma }^2)$$

(21)

where p(Δu,σ²) denotes the joint prior distribution, rewriting Eq. (21) into multiplicative form. where it is assumed that the residuals are independently Gaussian distributed, i.e.,$\beta =[∆d^x-H·∆u]\tilde{N}(0,{\sigma }^2)$, the non-informative prior of σ² is taken into account, i.e.,$p\left({\sigma }^2\right)\propto 1/{\sigma }^2$. Assuming that the prior distribution of Δu is Gaussian, i.e., $p(∆u)=N(0,{\tau }^2)$, the posterior distribution in logarithmic form $\mathit{ln}p=(∆u,{\sigma }^2|∆d^x)$ is represented

$$lnp(\Delta u,{\sigma }^2|\Delta d^z)\propto -{\displaystyle \sum _{i=1}^n[\Delta d_i^z-H_i\cdot \Delta u}{]}^2-\lambda {\displaystyle \sum _{j=1}^c{\Vert \Delta u_j\Vert }^2}$$

(22)

where $\lambda =\frac{{\sigma }^2}{{\tau }^2}$，The conditional posterior distribution of Δu in Eq. (23) is calculated using the conjugate distribution method as N(Δu_j,$∆s_j^2$) .

$$\begin{array}{l}\Delta u_j={({\displaystyle \sum _{i=1}^n{x}_{ij}^2+\lambda })}^{-1}{\displaystyle \sum _{i=1}^n{x}_{ij}}(\Delta d_i^z-{\displaystyle \sum _{j=1,j\ne j}^c{x}_{ij}\Delta u_j})\\ s_j^2={({\displaystyle \sum _{i=1}^n{x}_{ij}^2})}^{-1}{\sigma }^2+{\tau }^2\end{array}$$

(23)

For σ², the conditional posterior distribution is the inverse chi-square distribution, expressed as

$${\sigma }^2\text{~}\frac{1}{{\chi }^2}{{\displaystyle {\sum }_{i=1}^n(\Delta d_i^z-{\displaystyle {\sum }_{j=1}^c{x}_{ij}\Delta u_j})}}^2$$

(24)

Therefore, Markov Chain Monte Carlo samples are produced from the posterior p（Δu,σ²|Δd^x）via a Gibbs sampler for calibration amounts Δu ,the steps are as follows: (1) initialize Δu and σ²; (2) perform Gibbs sampling on Δu in Eq. (23); (3)The inverse chi-square distribution from Eq. (24) is selected σ². The specific process details are shown in Figure 4.

The calibration values of each kinematic variable in the nodal DOF error are derived from the Bayesian regularization algorithm and are combined with the actual measured strain values to form the sample data, defining in Eq. (25).

$$Q_j=\{{({\epsilon }_1,{\epsilon }_2,\mathrm{...},{\epsilon }_L)}_j,{(\Delta u_1\Delta u_2,\mathrm{...},\Delta u_m)}_j\}$$

(25)

where Q_j denotes the j th (j=1,2, ... , h) sample data under working conditions, ${\mathsf{\epsilon }}_{\mathrm{l}}$ denotes the l th (l=1,2,... ,L) strain value measured by the sensor. ∆u_i (i=1,2,...,m) denotes the error calibration value of the kinematic variable in the nodal DOF error.

3.2.2. Training Data Filtering and Sample Size Expansion

The error correction method has limitations: the nodal DOF errors can only be calibrated under specific working conditions. Therefore, in order to obtain the error calibration between strain values and nodal DOF under arbitrary working conditions, a self-constructed fuzzy network is used for calibration. The selection of appropriate training data affects the training effect of self-constructed fuzzy networks, and this paper employed the residual analysis to screen the sample data. In addition, the training effect of the self-constructed fuzzy network is also related to the number of training samples, so the number of training samples should be expanded before entering the training network.

The residual is the difference between the actual observed value and the fitted value of the sample. The reliability and reasonableness of the data is analyzed using the residual, defined as follows.

$$e=y-\widehat{y}$$

(26)

where y represents the actual observed value, $\widehat{y}$ represents the fitted value, and e represents the residual.

In this paper, considering that high-dimensional data can cause excessive computation, and the screening of sample data requires residual analysis for each kinematic variable in the calibration values of DOF to ensure the reasonableness of screening training data.

The new sample point is obtained by downscaling the original sample data Q_j in Eq. (25)

$$\{\begin{array}{l}{F}_1=\{{({\epsilon }_1,{\epsilon }_2,\cdots ,{\epsilon }_l)}_1,\Delta u_1\}\\ F_2=\{{({\epsilon }_1,{\epsilon }_2,\cdots ,{\epsilon }_l)}_2,\Delta u_2\}\\ \begin{array}{ccc}\begin{array}{cccc}& & & ⋮\end{array}& & \end{array}\\ F_m=\{{({\epsilon }_1,{\epsilon }_2,\cdots ,{\epsilon }_L)}_m,\Delta u_m\}\end{array}$$

(27)

Decompose each sample point is decomposed into F_i (i=1,2,... ,m) of the form, where each vector F_i consists of L measured strain values ${\epsilon }_L$ and 1 kinematic variable of nodal DOF error,and denote the kinematic variables as Δu_i (i=1,2,... ,m).

The sample fit values were obtained before the sample data were screened based on the magnitude of the residuals. In this paper,

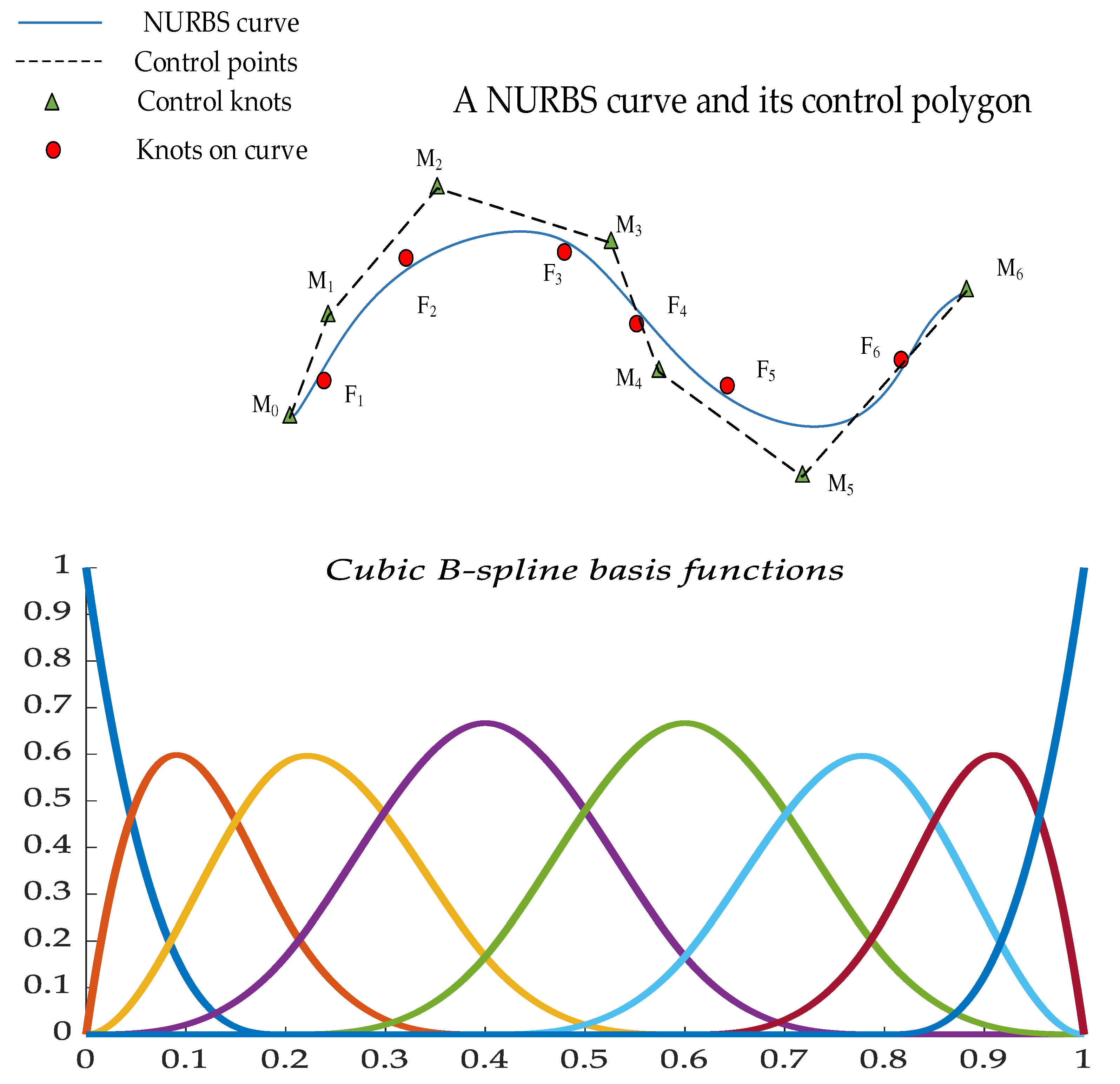
the Non Uniform Rational B-spline (NURBS) curve fitting method is used to fit the data F_i, as shown in Figure 4.

The NURBS curve of order c can be expressed as a segmented rational polynomial vector function, the mathematical definition is as follows.

$$p(t)=\frac{{\displaystyle {\sum }_{i=0}^h{k}_i{M}_i}{E}_{i,c}(t)}{{\displaystyle {\sum }_{i=0}^h{k}_i{E}_{i,c}(t)}}$$

(28)

where k_i (i=0,1,... ,h) denote the weight factors, respectively, associated with the control vertex M_i (i=0,1,...,h),due to the lack of expert experience, the weighting constants k_i=1 (i=0,1,... ,h). E_i,c(t) denotes the c-th order B-spline basis function, which is a non-decreasing sequence of parameter. T=[t₀,t₁,…,t_h+c+1] is the nodal vector and determined by the c-th order segmented polynomial.

The basis function can be recursively expressed by.

$$\begin{array}{l}{E}_{i,0}(t)=\{\begin{array}{c}1,t_i\le t\le t_{i+1}\\ 0,otherwise\end{array}\\ E_{i,c}(t)=\frac{t-t_i}{t_{i+c}-t_i}{E}_{i,c-1}(t)+\frac{t_{i+c+1}-t}{t_{i+c+1}-t_{i+1}}{E}_{i+1,c-1}(t)\end{array}$$

(29)

The parameterization of the data points reflects the nature of the curve constructed with the data points. Based on the nodal vector of basis functions and control points to construct the NURBS-fitted curves. A centripetal parameterization method is applied to the sample data as shown in Eq. (30).

$$\{\begin{array}{l}{\overline{t}}_0=0\\ {\overline{t}}_i={\overline{t}}_{i-1}+\frac{|F_i-F_{i-1}{|}^{\frac{1}{2}}}{{\displaystyle {\sum }_{i=1}^h|F_i-F_{i-1}{|}^{\frac{1}{2}}}}\\ {\overline{t}}_h=1\end{array}(i=1,2,\cdots ,h-1)$$

(30)

As required by the definition domain of the non-closed curve, multiple knot with repetition degree c+1 are taken at the two endpoints of the definition domain. According to the distribution of the sample and the method of centripetal parameterization, the non-uniform vector method is used for the construction, shown in Eq. (31).

$$\{\begin{array}{l}{t}_0=t_1=\cdots =t_c=0\\ t_{j+c}=\frac{1}{c}{\displaystyle {\sum }_{i=j}^{j+c-1}{\overline{t}}_i}(j=1,2,\cdots ,h-c)\\ t_{h+1}=t_{h+2}=\cdots =t_{h+c+1}=1\end{array}$$

(31)

The c-th order NURBS curve is constructed by m+1 sampling points F_i (i=0,1,... ,m). The approximation function is obtained by using the least squares method to approximate the parameter sequence $\overline{{\mathrm{t}}_{\mathrm{i}}}$(i=0,1,... ,m), shown in Eq. (32).

$$\delta (p,\overline{t})={{\displaystyle \sum _{i=1}^m\Vert F_i-p(\overline{t_i})\Vert }}^2$$

(32)

where the control points are set to A₀=F₀, A_m=F_h,then S_i=F_i-F₀E_0,c(${\overline{t}}_i$)-F_hE_p,c(${\overline{t}}_i$). and the partial derivatives of the control points in Eq. (32) are equal to 0.

The matrix form is expressed as.

$$M(E^{T}E)=S$$

(33)

where the E matrix is a matrix with h-1 rows and m-1 columns and E^T is the transpose matrix of E. The E, S, and M matrices are shown in Eq. (34).

$$\begin{gathered} E=\left[\begin{array}{cccc}{E}_{1,c}(\overline{t_1})& E_{2,c}(\overline{t_1})& \cdots & E_{h-1,c}(\overline{t_1})\\ E_{1,c}(\overline{t_2})& E_{2,c}(\overline{t_2})& \cdots & E_{h-1,c}(\overline{t_2})\\ ⋮& ⋮& \ddots & ⋮\\ E_{1,c}(\overline{t_{m-1}})& E_{2,c}(\overline{t_{m-1}})& \cdots & E_{h-1,c}(\overline{t_{m-1}})\end{array}\right] \\ S={\left[\begin{array}{cccc}{E}_{1,c}(\overline{t_1})& E_{2,c}(\overline{t_1})& \cdots & E_{h-1,c}(\overline{t_1})\\ E_{1,c}(\overline{t_2})& E_{2,c}(\overline{t_2})& \cdots & E_{h-1,c}(\overline{t_2})\\ ⋮& ⋮& \ddots & ⋮\\ E_{1,c}(\overline{t_{m-1}})& E_{2,c}(\overline{t_{m-1}})& \cdots & E_{h-1,c}(\overline{t_{m-1}})\end{array}\right]}^T\cdot \left[\begin{array}{c}{s}_1\\ s_2\\ ⋮\\ s_{m-1}\end{array}\right]M=\left[\begin{array}{c}{M}_1\\ M_2\\ ⋮\\ M_{h-1}\end{array}\right] \end{gathered}$$

(34)

The specific steps to obtain the sample fit values using NURBS curve fitting are as follows:

(1) the data are parameterized by Eq. (29) to obtain ${\overline{t}}_i$ (i=1,2,... ,m). and the basis function E_{i, c}(t).

(2) After obtaining ${\overline{t}}_i$, the nodal vector T is obtained by Eq. (30).

(3) The control point M_i (i=1,2,... ,h) is obtained according to Eq. (33).

(4) The constructed NURBS fitting curve is then derived from Eq. (28).

(5) When the NURBS fitted curve is obtained, the values of the sample data parameters are substituted into the curve Eq. of Eq. (28), and then the values on the fitted curve corresponding to the original sample data can be obtained.

Similarly, the fitted data $\widehat{F}$_i (i=1,2,... ,m) for the rest of the samples under a working condition can be obtained as shown below.

$$\{\begin{array}{l}{\widehat{F}}_1=\{{({\widehat{\epsilon }}_1,{\widehat{\epsilon }}_2,\cdots ,{\widehat{\epsilon }}_L)}_1,\Delta {\widehat{u}}_1\}\\ {\widehat{F}}_2=\{{({\widehat{\epsilon }}_1,{\widehat{\epsilon }}_2,\cdots ,{\widehat{\epsilon }}_L)}_2,\Delta {\widehat{u}}_2\}\\ \begin{array}{ccc}\begin{array}{cccc}& & & ⋮\end{array}& & \end{array}\\ {\widehat{F}}_m=\{{({\widehat{\epsilon }}_1,{\widehat{\epsilon }}_2,\cdots ,{\widehat{\epsilon }}_L)}_m,\Delta {\widehat{u}}_m\}\end{array}$$

(35)

When screening training data using residual analysis, the error in the kinematic variables Δu_i (i=1,2,...,m) varies considerably in order of magnitude due to the actual situation, which affects the residual analysis. The transformation matrix H in Eq. (2) is related to the observed coordinates of the position sensor (check point) and other factors, and the order of magnitude of each column of the transformation matrix H varies greatly. According to Eq. (19), Δd_i for the same working conditions is generally under the same order of magnitude, so it leads to kinematic variable errors Δu_i (i=1,2,...,m) obtained from the solution of different orders of magnitude.

According to the analysis described above, the main factor affecting the magnitude of the kinematic variable error is the column vector of transformation matrix H. Therefore, the weighting constants are calculated as shown in Eq. (36).

$$a_i=\frac{1}{v}{\displaystyle \sum _{k=1}^v{H}_{ki}}$$

(36)

where a_i (i=1, 2, ... ,m) denotes the weighting constants corresponding to the mth kinematic variable error, and H_ki denotes the k-th row and i-th column of the transformation matrix.

When the position of the position sensor is fixed, the matrix H is fixed under any working condition, so the weighting constants corresponding to the kinematic variable error are also unchanged. At this time, The integrated residual value e^t of sample under one working condition can be obtained from the Euclidean distance, which is calculated as shown in Eq. (37).

$$e^t=\sqrt{{{\displaystyle {\sum }_{i=1}^m(a_i\cdot (\Delta u_i-\Delta {\widehat{u}}_i))}}^2}$$

(37)

In summary, the integrated residuals of the samples $e_j^t$ (j=1,2,....,h) under the remaining working conditions can be obtained.

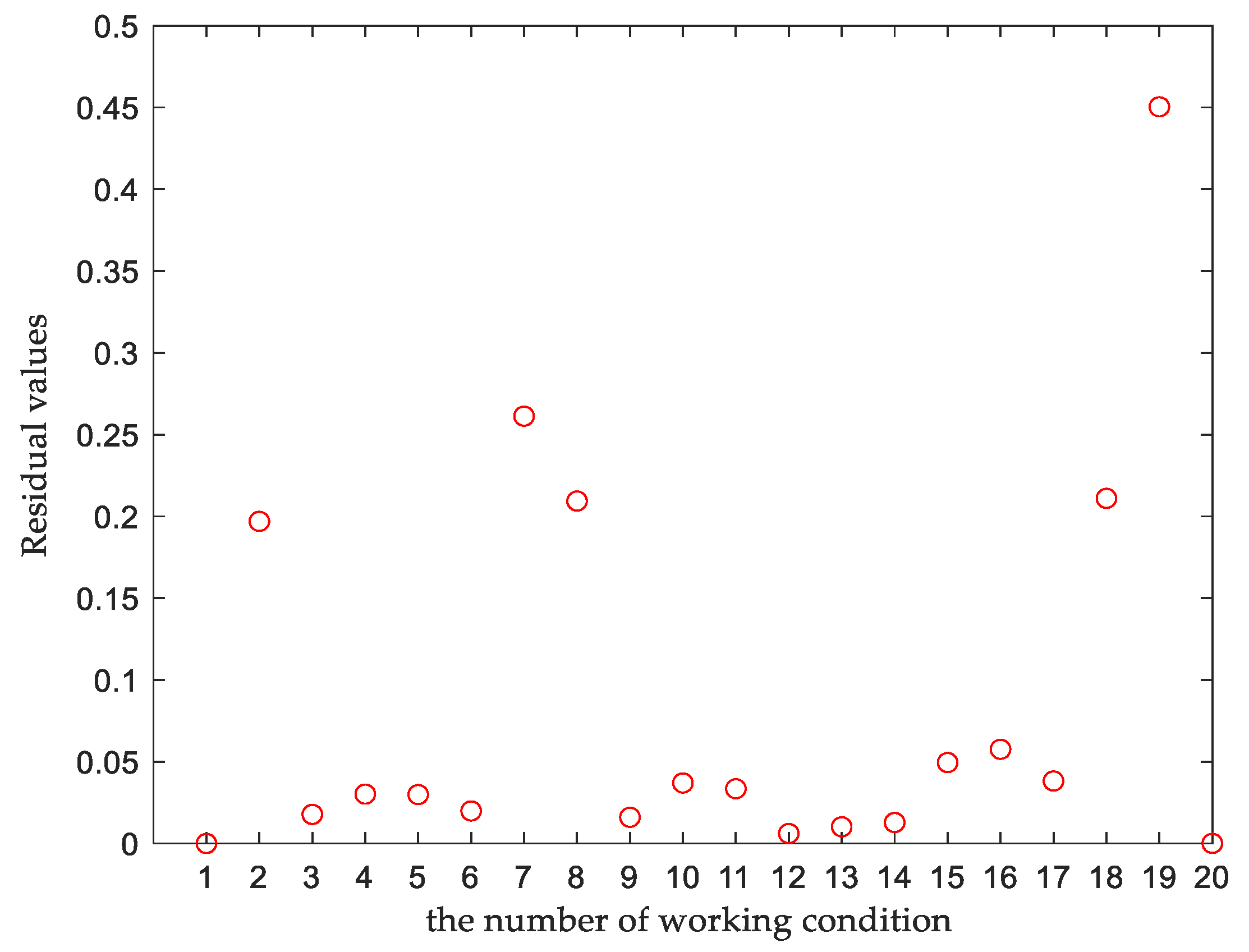
The screened training data consists of three parts: boundary samples, representative samples and normal samples after equidistant sampling. the boundary samples are the sample points where the structure is in the minimum and maximum load states in the experiment. After extensive experiments and summaries, it is concluded the normal sample points in the remaining sample points are all the values with small fluctuation range of residuals, And the residual values of representative sample points are more than twice the fluctuation range of the residual values of normal sample points.

The specific steps of the screening training data method are: (1) The NURBS curve fitting method is adopted to obtain the corresponding fitting data of sample points. (2) Subtracting the corresponding fitting data from the sample data to obtain the residual values of each sample point under different working conditions. (3) Selecting the boundary samples, representative samples, and normal samples obtained by equidistant sampling as the training samples for constructing the self-constructed fuzzy neural network.The training sample set F^sc are screened from all samples Q_j is denoted as:

$$F^{sc}=\{F_1^{sc},F_2^{sc},\cdots ,F_o^{sc}\}o\le j$$

(38)

Expanding the number of screened training samples $F_o^{sc}$ through the NURBS curve fitting method. After obtaining the fitting curve, a specific step is taken to extend the sample quantity by substituting values of ${\overline{\mathrm{t}}}_{\mathrm{i}}$ ranging from 0 to 1 into Eq. (28). Then, self-constructed fuzzy network is trained based on the extended samples.

3.2.3. Self-Constructed Fuzzy Network Calibration

Due to the nonlinearity and coupling relationship between the strain values in the sample data and the nodal DOF calibration values, it is difficult to establish a mathematical model. However, SCFN can effectively solve this nonlinearity problem. After screening all samples for suitable training samples and extending them, the SCFN is trained based on the extended samples. A strain-nodal DOF calibration model is established. The SCFN enhances the generalization ability of the strain-nodal DOF calibration value and improves the accuracy of the reconstructed displacement by calibrating the nodal DOF. SCFN is divided into two steps [31]: (1) Adding the affiliation function and generating the corresponding fuzzy rules. (2) Adaptively adjust the results of the fuzzy rules.

In this paper, because the triangular affiliation function has a simple structure, it is convenient to calculate the membership degree and efficient. Thus, SCFN chooses the triangular membership function and the 0th order T-S fuzzy model, which is represented by the fuzzy rule set as follows.

$$S^n:if{\epsilon }_{1}is{R}_1^{n}and{\epsilon }_{2}is{R}_2^n\cdots and{\epsilon }_{K}is{R}_K^{n}then{\widehat{p}}^n=w^n$$

(39)

where Sⁿ (n=1,2,...,N)denotes the nth fuzzy rule, ${\epsilon }_k$(k=1,2,... , K) is denoted as the input strain value, and $R_n^k$ denotes the membership degree corresponding to ${\epsilon }_k$in the nth rule. ${\widehat{p}}^n$denotes the output of the nth fuzzy rule and $w^n$ is the value corresponding to its fuzzy rule output.

The system output of SCFN ̂$\widehat{p}$ represents the nodal DOF error, and when a certain input activates m rules (n≥m), the system output is derived from the ${\widehat{p}}^n$ of these m outputs by weighted averaging, as shown in Eq. (33).

$$\widehat{Y}=\frac{{\displaystyle \sum _{n=1}^m{q}_n{\widehat{p}}^n}}{{\displaystyle \sum _{n=1}^m{q}_n}}=\frac{q_1{\widehat{p}}^1+q_2{\widehat{p}}^2+\cdots +q_m{\widehat{p}}^m}{q_1+q_2+\cdots +q_m}$$

(40)

The $q_n$ in Eq. (40) denotes the weighting constants of the rule, and the weighting constants are calculated by taking the smallest method, as shown in Eq. (41).

$$q_n=R_1^n\wedge R_2^n\wedge L\wedge R_K^n=\underset{k=1}{\overset{K}{\wedge }}{R}_k^n({\epsilon }_k)$$

(41)

The SCFN is initialized with one rule, and the membership functions and rule number are added or removed based on the error and completeness criteria. When the number of training samples is k+1, the error standard of SCFN is represented by root mean square error η_t, and the formula is shown below.

$$\widehat{U}(c){\eta }_t=\sqrt{\frac{{{\displaystyle \sum _{c=1}^k(\widehat{U}(c)-U(c))}}^2}{k}}$$

(42)

where denotes the actual output, U(c) denotes the desired output, η_a is denoted as a predetermined error threshold, and if η_t>η_a, it means that the system error does not meet the requirements and the membership function needs to be increased.

In SCFN, each input value at least corresponds to one membership function, if its membership degree $R_k^n$is greater than the completeness threshold α, the completeness of the membership function meets the requirements, if $R_k^n$ is less than α, it is necessary to increase the membership function and fuzzy rules. The completeness threshold is generally set to 0.5.

After adding the membership function and fuzzy rule, the fuzzy rule also needs to be adaptive adjustment to make it closer to the output value. The specific expression for adjusting the nth rule of the fuzzy controller at the ith moment is as follows.

$$a^n(i)=a^n(i-1)+V\cdot {\phi }^n(i-1)\cdot (U(k-1)-\widehat{U}(k))$$

(43)

where aⁿ(i) denotes the rule adjustment result at moment i, V is used to adjust the adaptive speed during rule adjustment, φⁿ(i-1) denotes the weighting constants of the nth rule at moment i-1, P(i-1) denotes the desired output of the nth rule at moment i-1, and (i) is the current system output.

$\widehat{p}$Each rule is added and adaptively adjusted according to the standard correspondence, and then used to train the SCFN. when η_t≤η_a, the training is stopped to jump out of the iteration and generate the fuzzy network, and the trained fuzzy rules are saved to obtain the calibrated nodal freedom results.

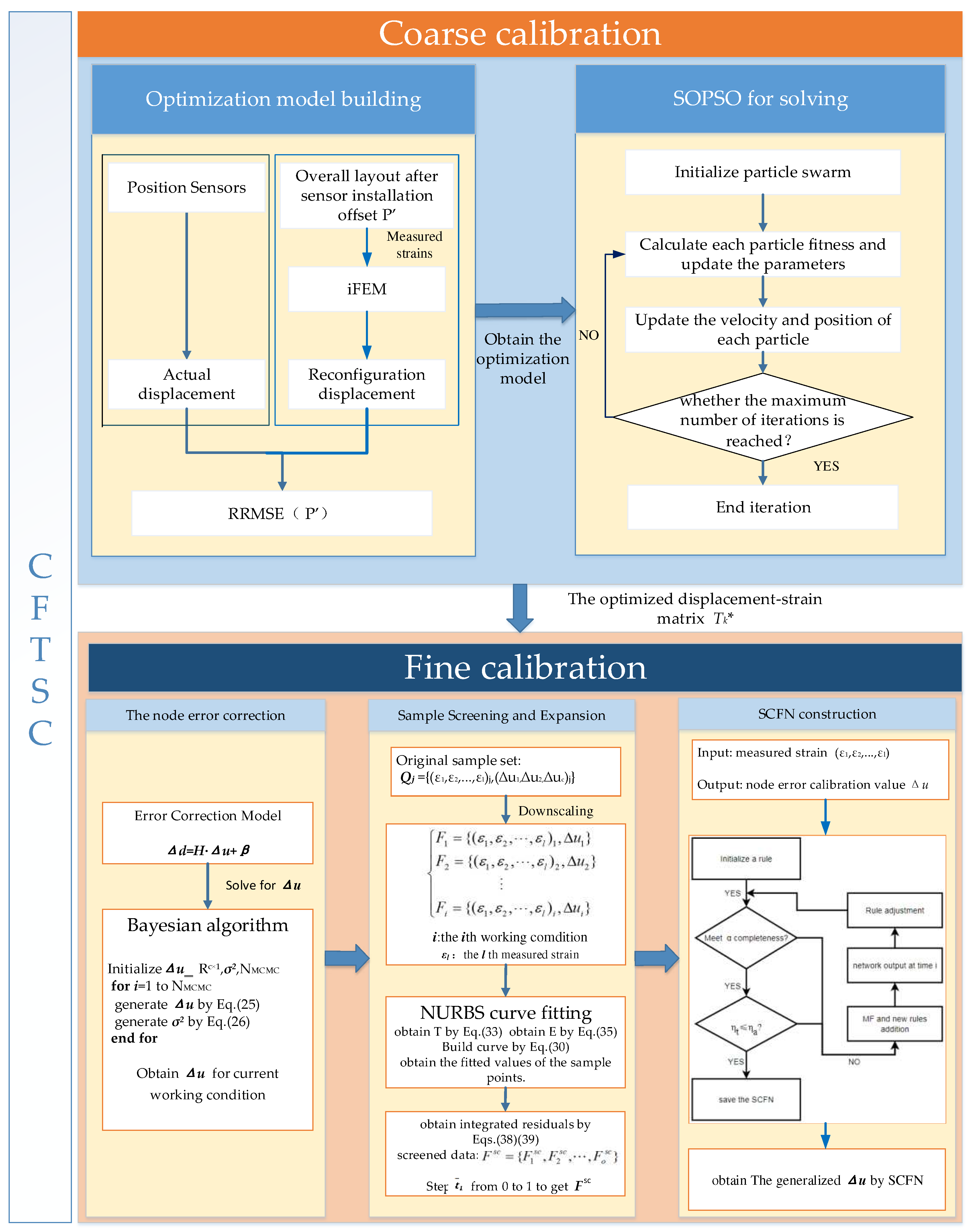
Summarize the above, The method flow framework for CFTSC method is shown in Figure 5.

Figure 5. Flow framework of CFTSC method.

Figure 5. Flow framework of CFTSC method.

4. Experimental Research

5. Conclusions

References

1. Tessler, A. Structural Analysis Methods for Structural Health Management of Future Aerospace Vehicles. Key Engineering Materials 2007, 74, 57–66. [Google Scholar] [CrossRef]
2. Zhao, F.F.; Xu, L.B.; Bao, H.; Du, J.L. Shape sensing of variable cross-section beam using the inverse finite element and isogeometric analysis. Measurement 2020, 158, 107656. [Google Scholar] [CrossRef]
3. Wang, L.P; Bi, S.L.; Lu, X. Deformation measurement of high-speed rotating drone blades based on digital image correlation combined with ring projection transform and orientation codes. Measurement 2019, 148, 106899. [Google Scholar] [CrossRef]
4. Agarwal, S.; Masotti, D.; Nikolaou, S.; Costanzo, A. Conformal Design of a High-Performance Antenna for Energy-Autonomous UWB Communication. Sensors 2021, 21, 5939. [Google Scholar] [CrossRef] [PubMed]
5. Zhang, S.; Zhang, G.Z.; Lu, C.Y.; Tian, H.L; Liu, J.B; Zhang, X.X. Flexible Planar Monopole Built-in GIS PD Sensor Based on Meandering Technology. Sensors 2022, 22, 4134. [Google Scholar] [CrossRef] [PubMed]
6. Zhang, J.; Huang, J.; Sun, P.; Meng, F.; Zhang, J.; Zhao, P.B. Analysis Method of Bending Effect on Transmission Characteristics of Ultra-Low-Profile Rectangular Microstrip Antenna. Sensors 2022, 22, 602. [Google Scholar] [CrossRef] [PubMed]
7. Zhao, Y.; Du, J.L.; Xu, Q.; Bao, H. Real-Time Monitoring of the Position and Orientation of a Radio Telescope Sub-Reflector with Fiber Bragg Grating Sensors. Sensors 2019, 19, 619. [Google Scholar] [CrossRef] [PubMed]
8. Carlo, M.; Aidana, B.; Aizhan, I.; Wilfried, B.; Daniele, T. 3D shape sensing of an epidural needle based on simultaneous spatial multiplexing of optical backscattering reflectometry. BiOS 2020, 11233, 1123318. [Google Scholar]
9. Li, X.J; Zheng, M.; Hou, D.; Wen, Q. Advantageous Strain Sensing Performances of FBG Strain Sensors Equipped with Planar UV-Curable Resin. Sensors 2022, 23, 110676. [Google Scholar] [CrossRef]
10. Cheng, X.; Zahra Sharif, K. Shape Sensing with Rayleigh Backscattering Fibre Optic Sensor. Sensors 2020, 20. [Google Scholar]
11. Souza, E.A.; Macedo, L.C.; Frizera, A.; Marques, C.; LealJunior, A. Fiber Bragg Grating Array for Shape Reconstruction in Structural Elements. Sensors 2022, 22, 6545. [Google Scholar] [CrossRef]
12. Ko, W.L.; Richards, W.L.; Fleischer, V.T. Displacement theories for in-flight deformed shape predictions of aerospace structures. NASA/TP 2007, 214612, 2007. [Google Scholar]
13. Ko, W.L.; Richards, W.L.; Fleischer, V.T. Applications of the Ko displacement theory to the deformed shape predictions of the Doubly-tapered Ikhana win. NASA/T 2009, 2009, 214652. [Google Scholar]
14. Foss, G.C.; Haugse, E.D. Using modal test results to develop strain to displacement transformations. In Proceedings of the 13th International Modal Analysis Conference, Nashville (1995). [Google Scholar]
15. Bogert, P.; Haugse, E.; Gehrki, R. Structural shape identification from experimental strains using a modal transformation technique. In Proceedings of the 44th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Norfolk (2003). [Google Scholar]
16. Tessler, A.; Spangler, J.L. A Variational Principal for Reconstruction of Elastic Deformation of Shear Deformable Plates and Shells. NASA/TM- 2003, 212445, 2003. [Google Scholar]
17. Tessler, A.; Spangler, J.L. A least-squares variational method for full-field reconstruction of elastic deformations in shear-deformable plates and shells. Computer methods in applied mechanics and engineering 2005, 194, 327–339. [Google Scholar] [CrossRef]
18. Kefal, A.; Oterkus, E. Displacement and stress monitoring of a Panamax containership using inverse finite element. Ocean Eng. 2016, 119, 16–29. [Google Scholar] [CrossRef]
19. Gherlone, M.; Cerracchio, P.; Mattone, M.; Sciuva, M.D.; Tessler, A. inverse finite element for beam shape sensing: theoretical framework and experimental validation. Smart Materials and Structures 2014, 23, 045027. [Google Scholar] [CrossRef]
20. Gherlone, M.; Cerracchio, P.; Mattone, M.; Sciuva, M.D.; Tessler, A. Shape sensing of 3D frame structures using an inverse finite element. International Journal of Solids and Structures 2012, 49, 3100–3112. [Google Scholar] [CrossRef]
21. Cerracchio, P.; Gherlone, M.; Sciuva, M.D. A novel approach for displacement and stress monitoring of sandwich structures based on the inverse finite element. Composite Structures 2015, 127, 69–76. [Google Scholar] [CrossRef]
22. Chen, K.Y.; Cao, K.T.; Gao, G.M.; Bao, H. Shape sensing of Timoshenko beam subjected to complex multi-nodal loads using isogeometric analysis. Measurement 2021, 184, 109958–109970. [Google Scholar] [CrossRef]
23. Niu, S.T.; Zhao, Y.; Bao, H. Shape sensing of plate structures through coupling inverse finite element and scaled boundary element analysis. Measurement 2022, 190, 110676. [Google Scholar] [CrossRef]
24. Zhao, Y.; Du, J.L.; Bao, H. Optimal Sensor Placement based on Eigenvalues Analysis for Sensing Deformation of Wing Frame Using iFEM. Sensors 2018, 18, 2424. [Google Scholar] [CrossRef]
25. Zhao, Y.; Du, J.L.; Bao, H. Optimal Sensor Placement for Inverse Finite Element Reconstruction of Three-Dimensional Frame Deformation. International Journal of Aerospace Engineering 2018, 2018, 1–10. [Google Scholar] [CrossRef]
26. Pan, X.; Bao, X. Zhang, The in-situ strain measurements modification based on Fuzzy nets for frame deformation reconstruction. Journal of Vibration, Measurement and Diagnosis 2018, 38, 360–364. [Google Scholar]
27. Fu, Z.; Zhao, Y.; Bao, H. Dynamic Deformation Reconstruction of Variable Section WING with Fiber Bragg Grating Sensors. Sensors 2019, 19, 3350. [Google Scholar] [CrossRef]
28. Xu, L.B.; Zhao, F.F.; Du, J.L. Two-Step Calibration Method for Inverse Finite Element with Small Sample Features. Sensors 2020, 20, 4602. [Google Scholar] [CrossRef]
29. Li, X.H.; Niu, S.T.; Bao, H.; Hu, N.G. Improved Adaptive Multi-Objective Particle Swarm Optimization of Sensor Layout for Shape Sensing with inverse finite element. Sensors 2022, 22, 5203. [Google Scholar] [CrossRef]
30. Li, Z.H.; Chen, K.Y.; Wang, Z.; Leng, G.J.; Bao, H. An effective calibration method based on fuzzy network for enhancing the accuracy of inverse finite element. Measurement 2022, 202. [Google Scholar] [CrossRef]
31. Cara, A.B.; Pomares, H.; Rojas, I. A new methodology for the online adaptation of fuzzy self-structuring controllers. IEEE Transactions on Fuzzy Systems 2011, 19, 449–464. [Google Scholar] [CrossRef]