Prerpints.org logo
Preprint
Article

Identification of Geometric Features of the Corrugated Board Using Images and Genetic Algorithm

Altmetrics

Downloads

172

Views

278

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

17 May 2023

Posted:

18 May 2023

You are already at the latest version

Alerts
Abstract
The corrugated board is a versatile and durable material that is widely used in the packaging industry. Its unique structure provides strength and cushioning, while its recyclability and bio-degradability make it an environmentally friendly option. The strength of corrugated board depends on many factors, including the type of individual papers on flat and corrugated layers, the geometry of the flute, temperature, humidity, etc. This paper presents a new approach to analysis geometric features of corrugated boards based on the images. It allows for precise determination of the geometry of the corrugated layer, as well as the thickness of individual papers in all cardboard layers. The experimental set used in the work and the created software are characterized by high reliability and precision of measurement thanks to the use of an identification procedure based on image analysis and evolutionary algorithms. This allows to quickly find the main geometric characteristics of the corrugated board, which in turn leads to the possibility of performing numerical analyzes taking into account the real model of the corrugated board. Calculations made on a real (correctly mapped geometrically) model allow, for example, a more reliable analysis of the composition of the cardboard, and thus also to obtain greater savings in the optimization process.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

Corrugated board is commonly used for shipping boxes, retail displays, and other packaging applications. It is lightweight, easy to handle, and can be printed with custom designs. Furthermore, corrugated board is recyclable and can be biodegradable, making it an eco-friendly choice for companies and consumers alike. It is a versatile and popular material used in the packaging industry [1,2]. It consists of a fluted sheet sandwiched between two flat linerboards, which provides strength and durability while also allowing for flexibility.
The fluted sheet in corrugated board is made by passing paper through a series of fluting rolls, which create the characteristic ridges and valleys that give corrugated its name. The flutes come in different sizes, with larger flutes providing more strength and cushioning, while smaller flutes provide a smoother surface for printing.
The linerboards that make up the outer layers of corrugated board are typically made from kraft paper, which is a type of paper made from wood pulp. Kraft paper is known for its strength, durability, and ability to resist tearing and puncturing, making it an ideal material for packaging.
There are several types of fluted sheets used in the production of corrugated board, each with its own characteristics and advantages. The most common types are:
  • A-flute: A-flute is the largest and thickest type of flute, with a height of approximately 5 mm. It provides excellent cushioning and is commonly used for packaging heavier items, such as appliances and furniture.
  • B-flute: B-flute has a height of approximately 3 mm and is the second most common type of flute. It is a versatile option that provides good cushioning and is often used for shipping boxes and retail displays.
  • C-flute: C-flute has a height of approximately 4 mm and is the most common type of flute. It provides good cushioning and is a popular choice for shipping boxes and re-tail displays.
  • E-flute: E-flute has a height of approximately 1.6 mm and is the thinnest type of flute. It provides a smooth surface for printing and is often used for retail displays and small boxes.
  • F-flute: F-flute has a height of approximately 0.8 mm and is the newest type of flute. It provides excellent printing quality and is ideal for small boxes and retail displays.
Each type of flute offers different benefits and is suitable for different types of pack-aging applications. Manufacturers can also combine different types of flutes to create custom corrugated board that meets specific requirements for strength, cushioning, and printing quality.
The corrugated board can be warped during the production as well as it can also be deformed after this process, during its storage, transportation and use. The causes of this phenomena are related to changes in temperature and humidity or mechanical loads. One can distinguish two types of imperfections of the corrugated board, which are global or local in nature. Beck and Ficherauer developed and described a model of systematic, large-scale deflections of the cardboard [3]. In this article, the authors paid more attention to local imperfections. The influence of imperfections size on the compressive strength of boxes made of the corrugated board was examined by Nordstrand in 1995 [4]. In 2004, the same author studied local imperfections by analyzing nonlinear buckling of Rhodes and Harvey orthotropic plated [5]. Mechanical properties of corrugated cardboards with imperfection during compression was analyzed by Lu et al. [6]. Analytical study of double-walled corrugated cardboard bending was performed by Garbowski and Knitter-Piątkowska [7]. A method for the analysis of single-walled corrugated cardboard with introducing initial imperfections was proposed by Mrówczyński et al. [8]. Cillie and Coetzee investigated corrugated cardboards with global and local imperfections under in-plane compression [9]. Recently Mrówczyński and Garbowski presented a simple method for calculation of the effective stiffness of corrugated board with geometrical imperfections using the finite element method and representative volumetric element [10].
The image processing is not so commonly used in the corrugated board analysis. However, the most common example is related to creating a system for automatic waste sorting. For instance, Liu et al. developed a new model for garbage classification based on transfer learning and model fusion [11]. Similarly, Rahman et al. developed a classificatory for recyclable waste paper sorting using the template matching [12]. The other application of image processing algorithm is counting of the corrugated board layers. Cebeci applied some typical image processing operations for automatic counting of the corrugated board [13]. Similarly, Suppitaksakul and Rattakorn applied a machine vision system and image processing techniques to count the corrugated board [14]. Later, Suppitaksakul and Suwannakit developed an algorithm for stitching corrugated board images [15].
In the literature, one can find analysis of cross-sections geometry and classification of various materials based on images. Caputo et al. applied the support vector machine to classify materials based on their images under various illumination and pose conditions [16]. Iqbal Hussain et al. applied the convolutional neural network, based on a pretrained network architecture ResNet-50, for recognition and classification of woven fabrics [17]. Wyder and Lipson examined convolutional neural networks for the identification of static and dynamic properties of cantilever beams based on their raw cross-section images [18]. Li et al. applied various deep learning techniques for analyzing geometric features of self-piercing riveting cross-section [19]. They showed that SOLOv2 and Unet architectures give best results. Ma et al. analyzed the geometrical features of crushed thin-walled carbon fiber-reinforced polymer tubes cross-sections [20].
Genetic algorithm is an optimization algorithm inspired by the process of natural selection and genetics [21]. They are used to solve complex problems by mimicking the principles of evolution, such as selection, crossover, and mutation. The basic idea behind genetic algorithms is to create a population of individuals that represent potential solutions to a given problem. Each individual is encoded as a set of parameters, often called chromosomes or genomes, which can be considered as the genetic material. These chromosomes are subject to operations like selection, crossover, and mutation, which emulate the genetic processes of reproduction and variation. The pioneer of genetic algorithms is John Henry Holland [22]. Genetic algorithms have been successfully applied to a wide range of problem, in the area of optimization, scheduling problems or artificial intelligence. They are particularly useful when dealing with complex, multi-dimensional search spaces, in which the traditional optimization algorithms may failed. The genetic algorithms have been also applied in some problems related to the corrugated boards. Recently, Shoukat applied the genetic algorithm in combination with mixed integer linear programming for the problem of minimizing cost and greenhouse gas emissions during papermaking processes [23]. Hidetaka and Masakazu used the genetic algorithm to solve the scheduling problem of corrugated board production [24]. However, the genetic algorithm has not been applied as yet to find the geometrical features of the corrugated board.
In this paper, the authors presented a new method for analysis of the corrugated board geometrical features. An equipment for the acquisition process of the corrugated board samples was designed and manufactured. Then an algorithm for analysis of the corrugated board geometrical features was proposed and implemented. The algorithm is based on image processing operations and application of the genetic algorithm for finding the geometrical features of the flute. The presented methodology can be a first step for automatic modelling of corrugated board geometry based on its cross-section image.

2. Materials and Methods

In this section, it is described the equipment designed and used for acquisition of the corrugated board samples as well as the algorithm proposed to identify geometrical parameters of the flute.

2.1. Device for the Acquition of Corrugated Board Cross-Section Images

In order to acquire the images of the corrugated board cross-section a dedicated device has been designed and manufactured. The device allows to record the images of the samples cross-section under uniform acquisition conditions. Figure 1a shows a visualization of the device with an example of the corrugated board section. The sample holder is placed on the door, the opening of which allows free mounting of the sample. Closing the door and limiting its uncontrolled opening is ensured by neodymium magnets placed in the door frame. The camera is mounted in the device frame in such a way that its optical axis is directed perpendicularly to the plane of the sample face (Figure 1b). Two LED strips with a power of 4.8 W/m, mounted on the dividing wall, provide uniform illumination of the photographed surface. Lighting is controlled manually by using a bistable key switch. Two wires are led out of the device: a power cable for the lighting module and a USB cable, which allows to acquire the image from the camera and save it on the computer. The construction of the device was manufactured using the 3D printing technology.
The system uses the ArduCam B0197 camera with the autofocus function and the Sony IMX179 (1/3.2") image sensor with a resolution of 8 MPx. The image from the camera was saved in JPEG format and a maximum resolution of 3264x2448 pixels.

2.2. Algorithm for the Geometrical Features Determination of the Corrugated Board

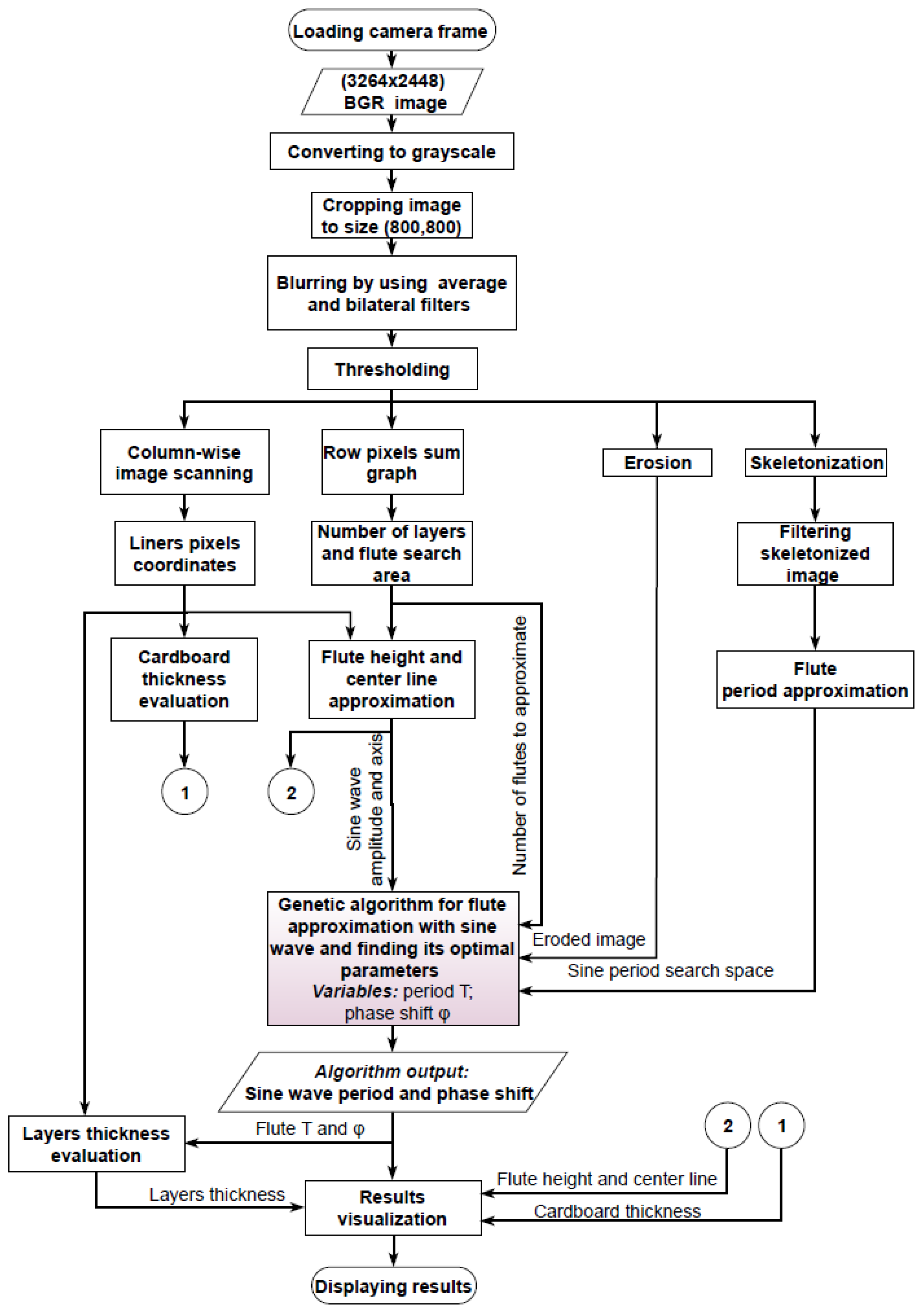
The flowchart of the proposed algorithm is presented in Figure 2. It consist of some preprocessing steps and parallel operations, in which the geometrical features of the corrugated board, including its height, flute period and phase shift, liners and flute thickness, are determined. The algorithm has been implemented in Python language using OpenCV library.

2.2.1. Preprocessing Stage

At the preprocessing stage, a single frame from the camera is acquired. It is an RGB image of 3264x2448 pixels. Then it is converted to a grayscale image in the range <0,255>. A fragment of the gray-scale image with dimensions of 800x800 pixels is cut out in the central acquisition area. An example of the results of these operations is shown in Figure 3a. In the next step, the image is blurred using two operations. At first, the averaging operation with normalized box filter with the kernel size of 3x3 is applied. Then the bilateral filter is used. The result of these operations is presented in Figure 3b. It allows to remove small noise (small fibers) in the image related to cutting the sample. One can notice that the larger fibers are still visible in the image. The last step in the preprocessing stage is lower threshold binarization. The threshold is equal to 75. All the parameters in the preprocessing stage were chosen empirically.

2.2.2. Corrugated Cardborad Thickness Estimation

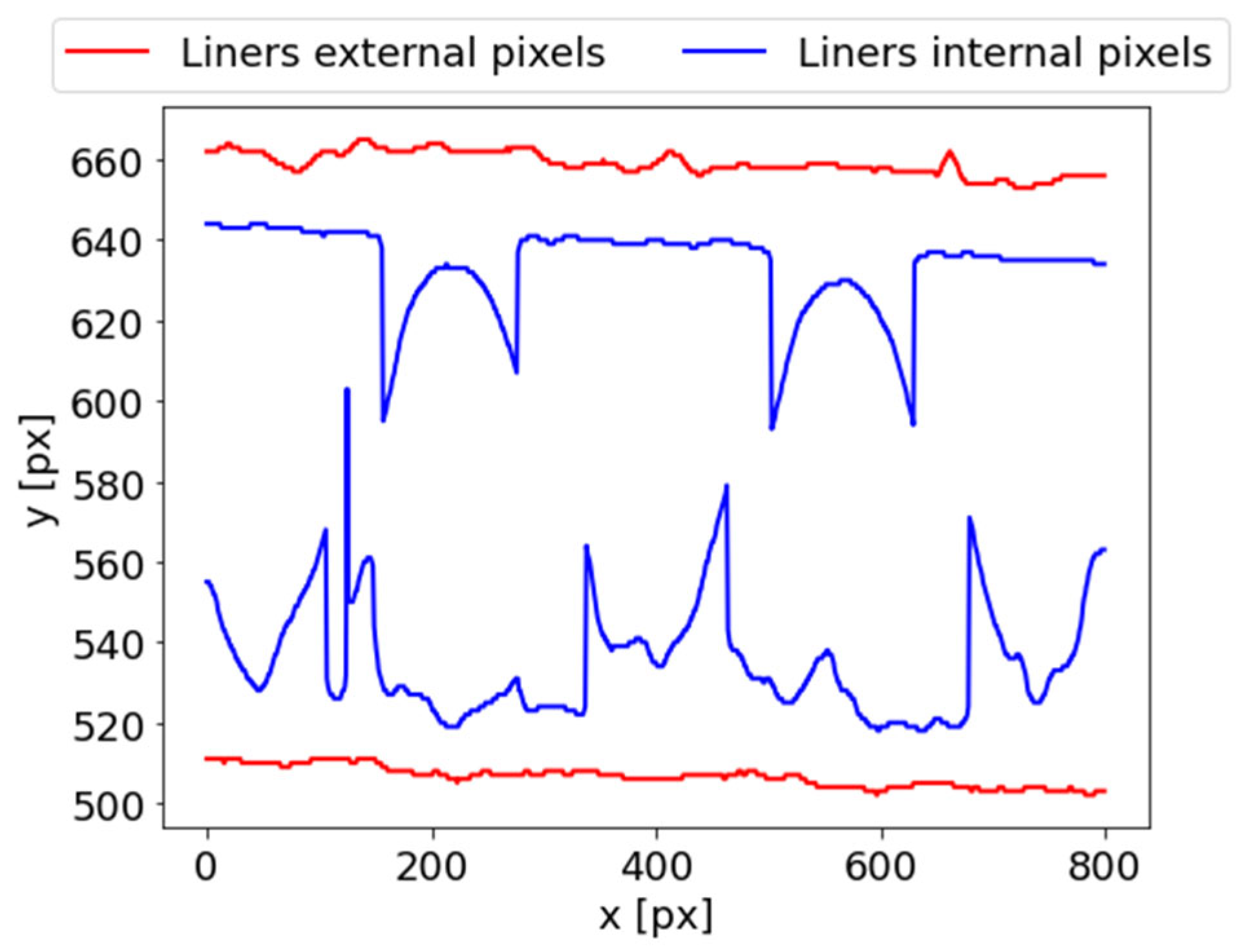
The purpose of the next stage is estimation of the corrugated cardboard thickness. It can be obtained by observing the boundary points of each corrugated cardboard layer in each column. This operation is called the column-wise image scanning. Furthermore, it is necessary to estimate the thickness of flute and liners in next stages of the proposed algorithm. In the column-wise image scanning operation, each column of the binary image (Figure 3c) is analyzed. Starting from the top towards the bottom of the image, the first white pixel is searched. The y coordinate of this pixel is written to the U L E P matrix, which contains the external points of the upper liner. In a given column, after finding the first white pixel, the first black pixel is searched. It describe the background in the flute area. The y coordinate of this pixel is written to the U L I P matrix, which contains the internal points of the upper liner. The similar procedure can be applied for the determination of lower liner points. The only difference is in the direction of searching. For the lower liner, it should be performed starting from the bottom towards the top of the image. As the results, the matrixes L L E P and L L I P are obtained, which denote the lower liner external points and lower liner internal points, respectively. The results of findings the internal and external points of the upper and lower liners are presented in Figure 4.
The corrugate cardboard height can be now obtained by calculating the average distance between the external points of upper and lower liners. Thus, it can be expressed as:
d = 1 N C ∑ x = 0 N C − 1 U L E P x − L L E P x
where x denotes the column index, N C is the total number of columns. Thus, in this case (for the cropped image), N C = 800 .
After the column-wise image scanning operation, the external boundaries of the liners can be determined using the matrixes U L E P and L L E P . Both boundaries can be approximated using linear functions based on these coordinates matrixes:
y U = a U x + b U ,
y L = a L x + b L ,
where a U and b U denote parameters of the upper liner approximation, while a L and b L are parameters the lower liner approximation.

2.2.3. Corrugated Cardborad Centre Line and Flute Height Estimations

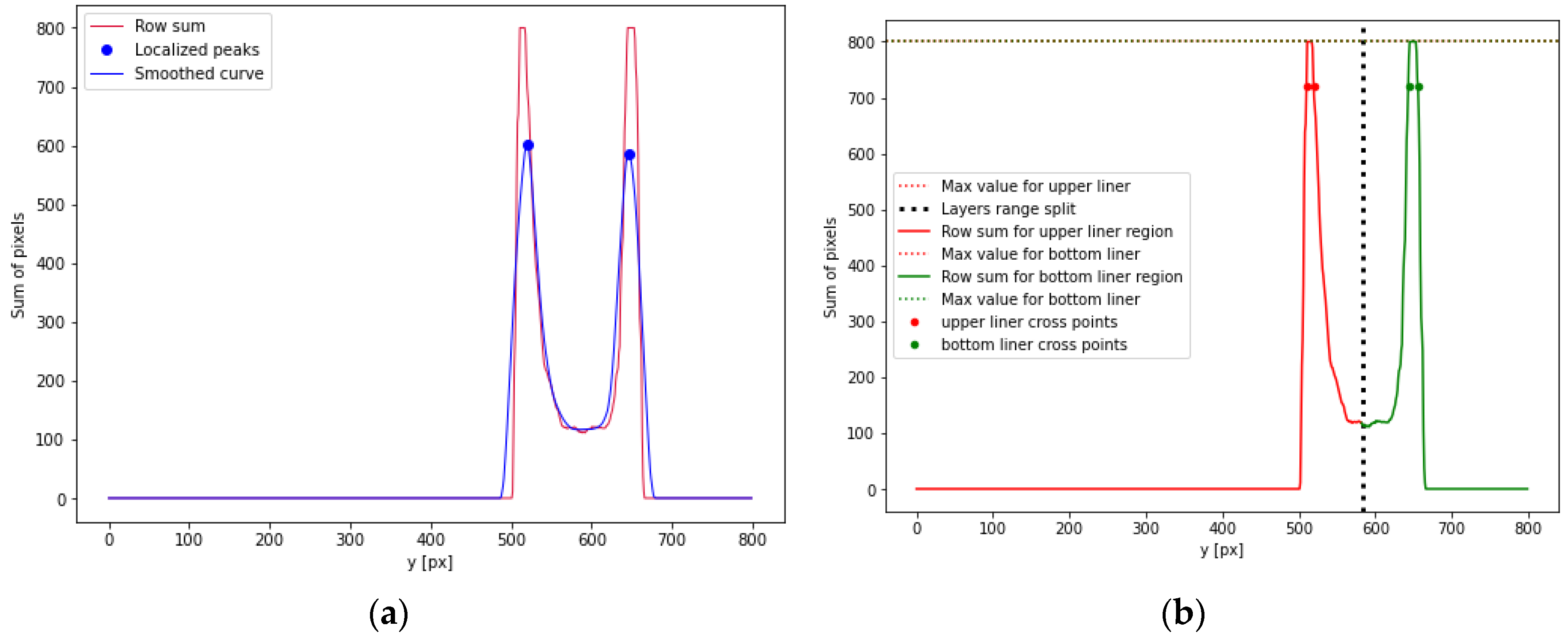
In the next stage, the corrugated cardboard centre line and flute height are estimated. The row sum curve of the binary image is determined in order to find the localization of liners. Now, the rows of the binary image are analyzed and the sum of white pixels at each row is calculated. The corrugated carboard sample is placed horizontally. Therefore, the maximums in the row sum curve are related with the liners localizations. Due to the flute and other disturbances, many local maximums can be observed in the row sum curve. Therefore, curve smoothing is applied using the Savitzky-Golay filter with 30 interpolation points and polynomial of degree 1. In such a way, the number of local minima is limited. Furthermore, to find the additional conditions were taken into account: the minimal distance between maximums, which was equal to 20, and the minimal value of the local maximum, which was equal to 0.4 of the global maximum value. The local minimums found in such a way are related to the vertical positions of liners (their y coordinates). This study is limited to 3-layered corrugated boards, which have always 2 liners and 1 flute. Thus, at this stage, two local maximums should be detected, as it is depicted in Figure 5a. It shows the row sum curve and the result of its smoothing using the Savitzky-Golay filter. It is also worth noting that for both the ideal samples and the creased samples, the layers of the corrugated carboard can have different thicknesses and be deformed in different ways, which affects the peak values and it is possible that they can differ significantly in the values of the local maximums.
Now, the original non-smoothed row sum curve can be analyzed, see Figure 5b. It is divided into two ranges. The split of them is determined as a middle point between the two local maximums (black bold dashed line). In Figure 5b, the upper liner range is marked in red, while the lower liner range is marked in green. Within each of these ranges, the following steps are performed:
  • The local maximum is determined.
  • All the points in the range, which has the values greater than 0.9 of the local maximum and the boundary points of them are chosen. It is depicted in Figure 5b. The boundary points of these points, which has the value greater than 0.9 of the local maximum value are marked by bold dots within each range.
  • The distances between the boundary points are calculated and denoted as b U S and b B S for the upper and bottom liners, respectively.
The boundary lines, which is used in the next steps for limitation of the searching range. Based on the external boundaries of the liners expressed in Eqs. (2) and (3), the boundary lines limiting the flute searching. They can be written in the following forms:
y U B L = a U x + b U + b U S ,
y L B L = a L x + b L − b L S .
These boundary lines are depicted in red in Figure 6a, while the external boundary lines, expressed in Eqs. (2) and (3), are presented in green. The center line is approximated as a central line between these two red lines and can be expressed as:
y c e n t e r = a c e n t e r x + b c e n t e r ,
where a c e n t e r , b c e n t e r are parameters of the center line.
The height of the flute, which is equal two times amplitude of the sinus function, can be approximated using the following formula:
H = 1 N C ∑ x = 0 N C − 1 y U B L x − y L B L x = 1 N C ∑ x = 0 N C − 1 a U − a L x + b U + b U S − b L + b L S .

2.2.4. Limitations for the Flute Period Searching

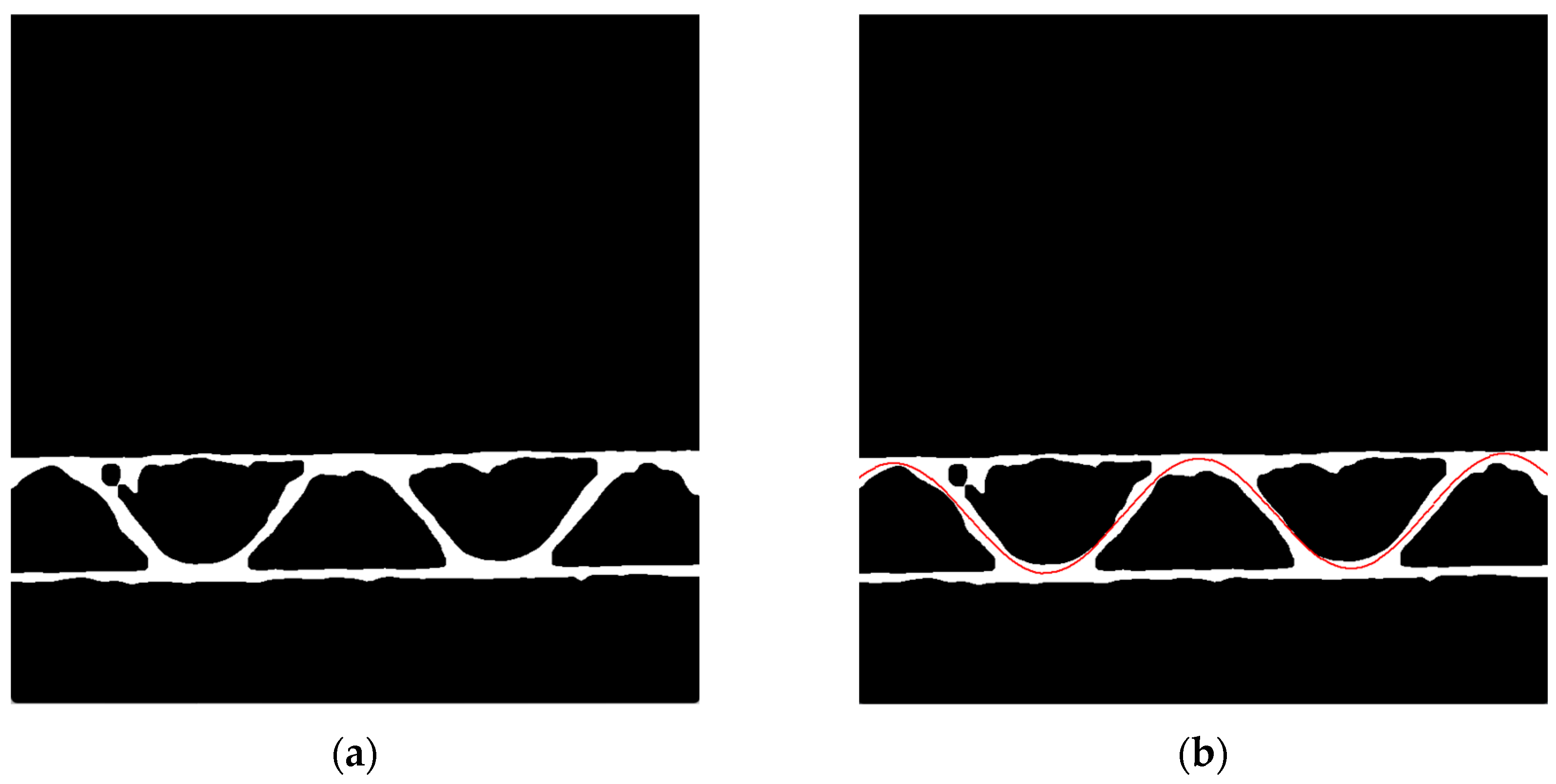
In next step, the skeleton of the binary image is determined, see Figure 7a. There are some disturbances in the skeleton related to existence of the fibers coming from the cutting process of the samples. Due to the presence of these unfavorable side branches, which are formed due to the skeletonization of the binary image, the skeleton is additionally subjected to a filtering process. It consists in removing side branches when their contour length is less than 50 pixels, see Figure 7b.
Limitation for the range of period searching determined by the values: T m i n and T m a x (the range of the period searching in pixels) is based on calculating of the distances between the intersection points of the skeleton contours with 3 parallel lines (parallel to the upper liner) drawn through the central flute area, see Figure 7c. Based on the averaged distances between successive intersection points and the maximum distance, the values T m i n = 0.5 d i a v , T m a x = 3 d i m a x are taken, where d i a v is the average distance between the intersections points for the 3 parallel lines and d i m a x denotes the maximal value of the distances between these intersections points. When the skeleton has to many disturbances and it makes it impossible to determine these values the period T for the genetic algorithm, e.g., due to the presence of long branches or critical deformation of the sample, the values T m i n = 50 , T m a x = 800 are adopted.

2.2.5. Sinus Function Parameters Searching using Genetic Algorithm

In the searching process for parameters of the flute, the following formula for its approximation was taken into account:
y f l u t e = a c e n t e r x + b c e n t e r − A sin ⁡ φ + 2 π T x ,
where the parameters a c e n t e r , b c e n t e r and amplitude A = H / 2 were determined in the previous stages of the proposed algorithm. The phase shift φ and the period T are to determine using the genetic algorithm.
As the input to the genetic algorithm, the eroded image of binary image is treated, presented in Figure 8a. Furthermore the searching for the phase shift φ and period T is limited by φ m i n = 0 , φ m a x = 2 π , T m i n , and T m a x . The objective function is the sum of the join pixels for the eroded image and the function expressed in Eq. (8) for the given φ and T .
The following parameters of the genetic algorithm were used:
  • maximal number of iterations: 500;
  • population size: 100;
  • mutation probability: 0.15;
  • elite group ratio: 0.01;
  • crossover probability: 0.2;
  • parents portion: 0.2;
  • crossover type: uniform.
An example of the genetic algorithm results is shown in Figure 8b.

2.2.5. Estimation of the Corrugated Cardborad Layers Thicknesses

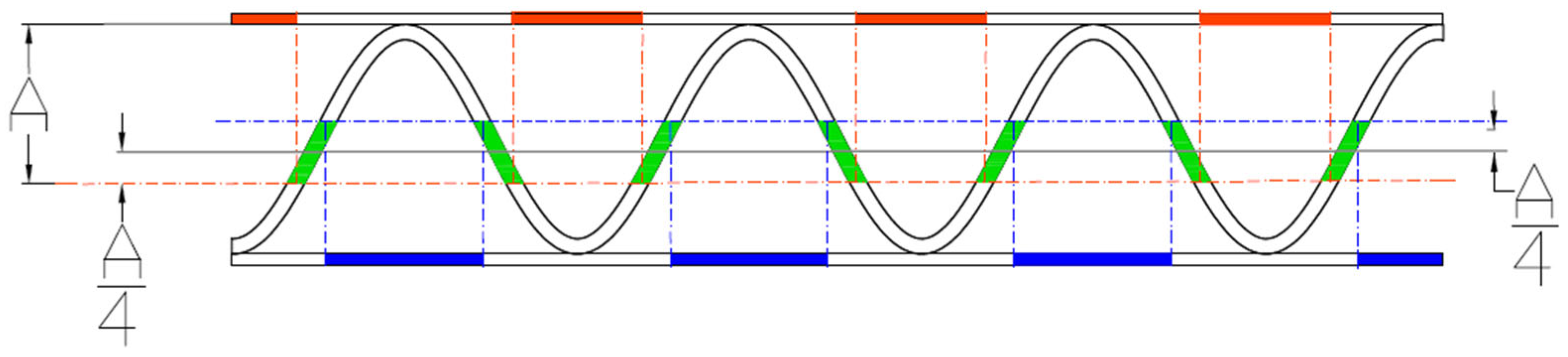
Estimation of the thicknesses is schematically shown in Figure 9. The estimated position of flute in the image, allows to choose the areas of liners and flute, in which the thickness of the papers can be measured. It allows to avoid the ranges of the gluing between the liner and flute. In these regions, there are also less number of disturbances related to the fibers coming from the sample cutting process. The area of the upper liner, where the thickness can be measured is marked in red. A similar area for the bottom liner is marked in blue. The green color indicates the area, in which the thickness of the fluting layer is determined.
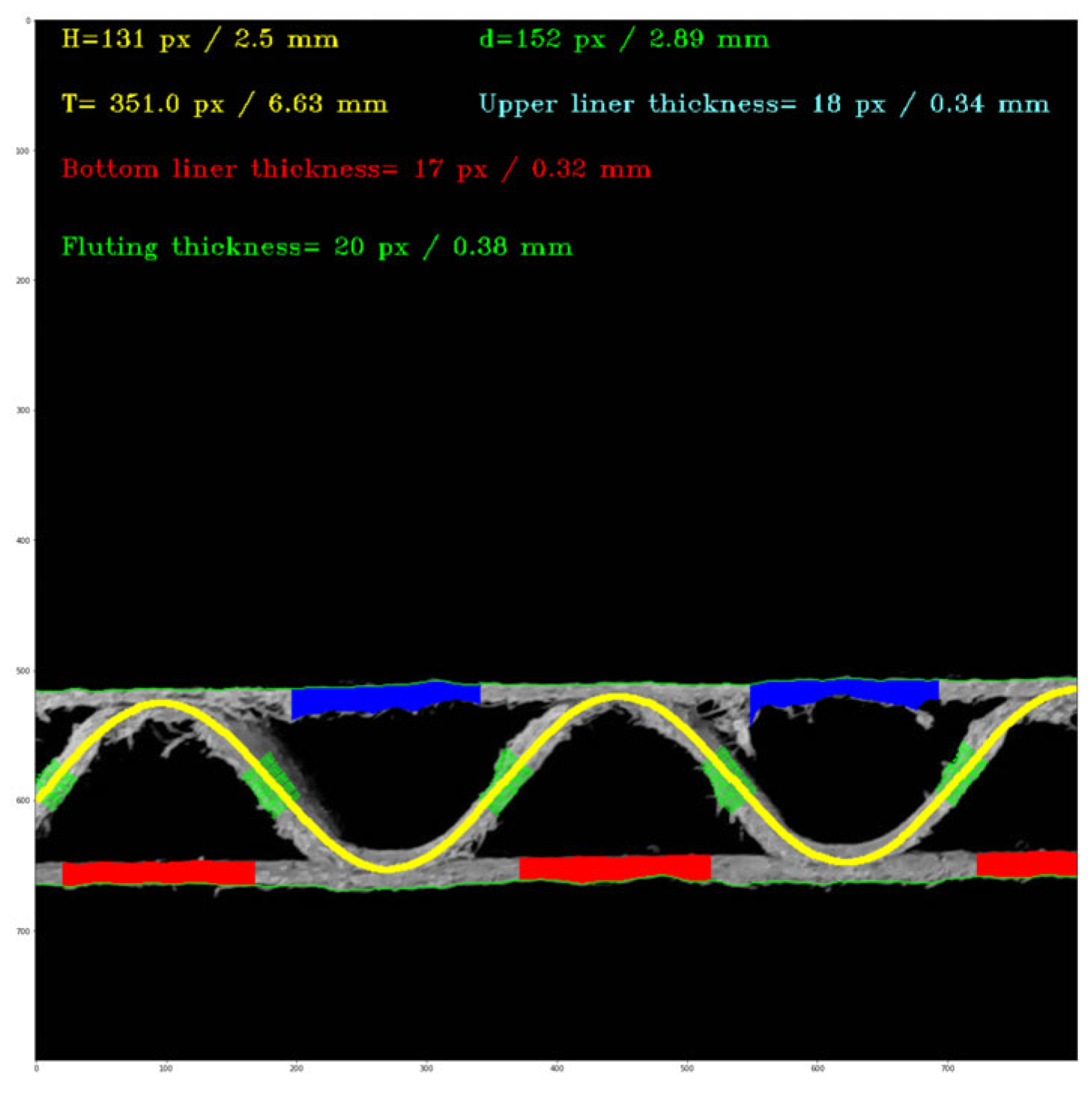
These three areas were determined based on the sine approximation determined in the previous step using the genetic algorithm. An example of the results is presented in Figure 10.

3. Results

The procedure presented above allows to identify the geometrical parameters of any single-wall corrugated board sample in a fully automatic manner. However, reliable results are obtained only for samples with relatively small cross-section crushing and cut in a way that does not damage the structure of individual layers.
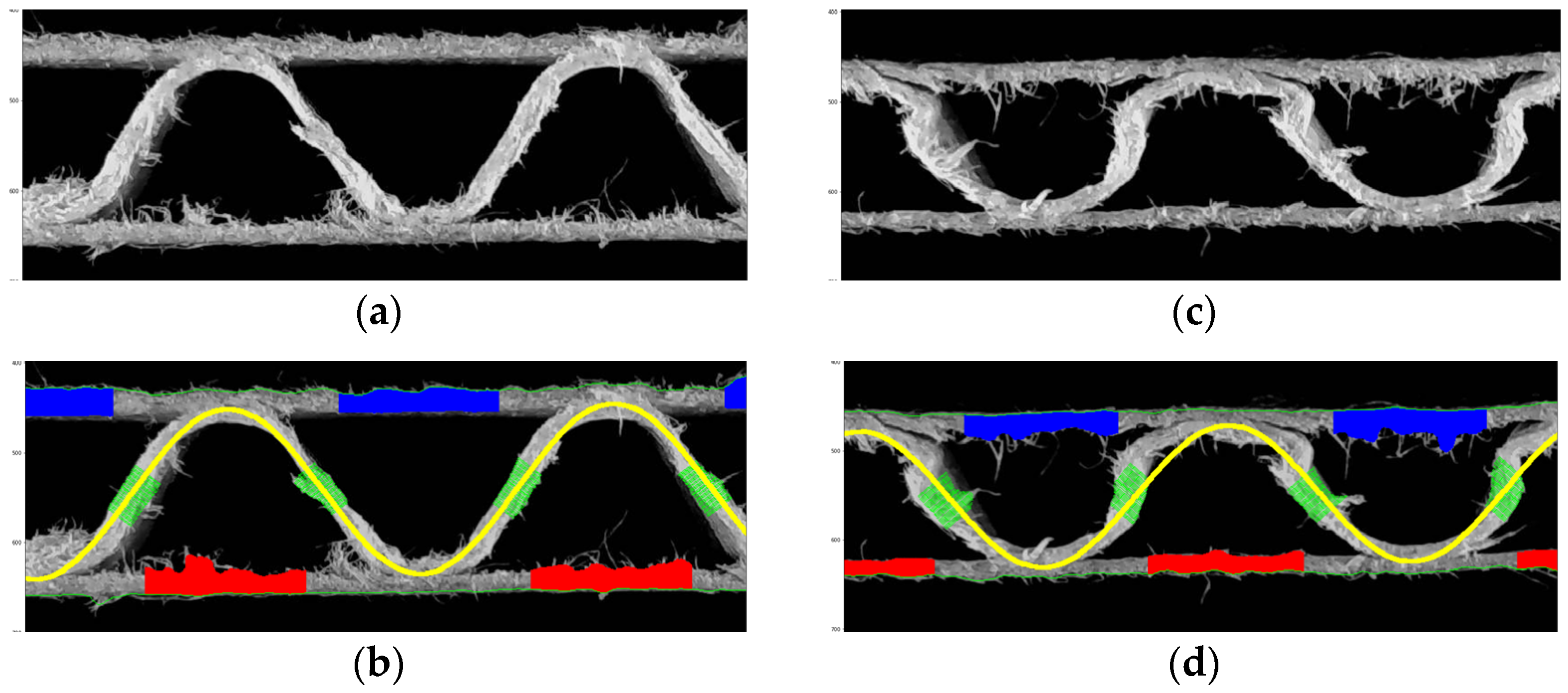
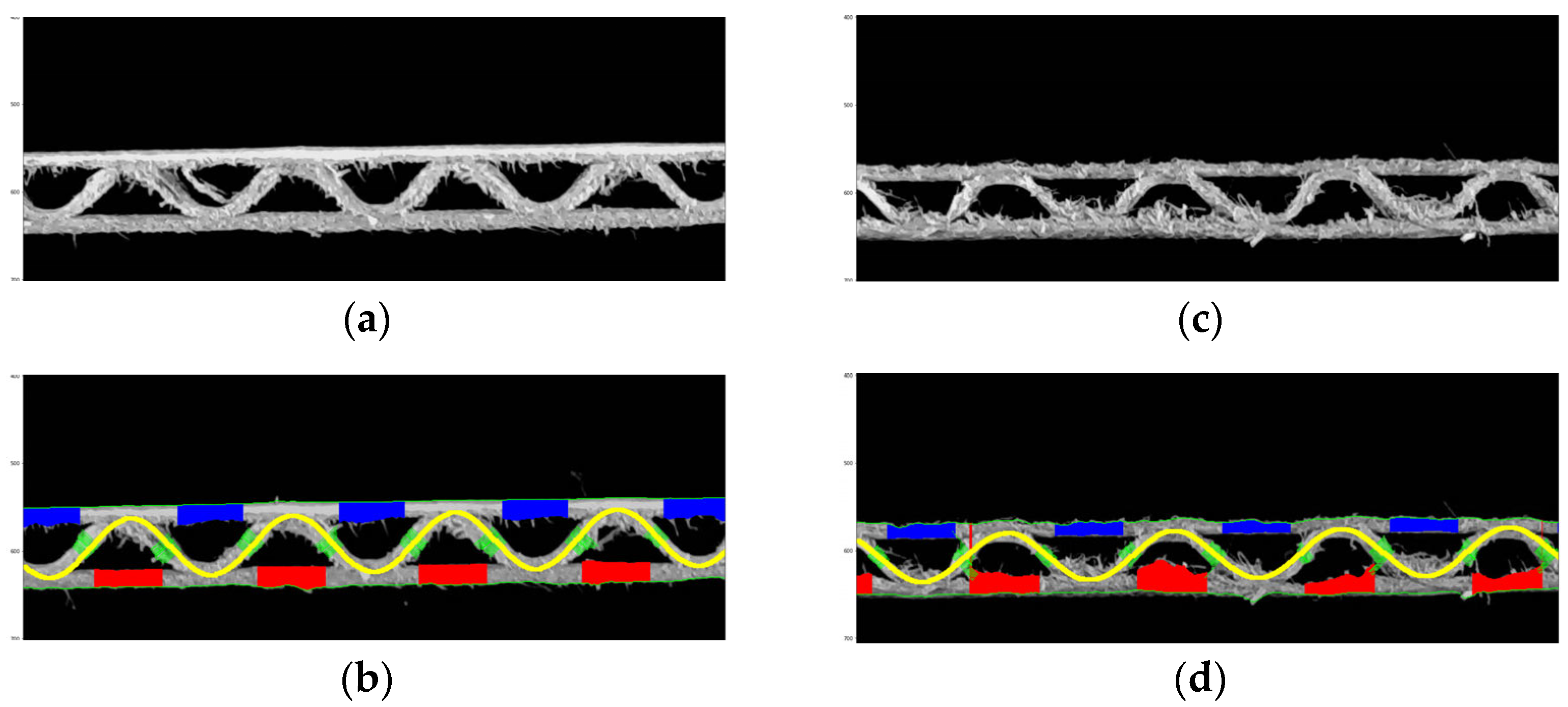
Figure 11 shows the visualization of the recognized fluting shapes of corrugated board and the thickness of individual layers for 3 samples, i.e. for flute C, B and E. All the geometrical features of the single-ply corrugated cardboard cross-section identified by the procedure presented in this paper are summarized in Table 1. The results are presented both in the form of measured pixels and millimeters converted in the calibration process.
Each measurement method has certain precision and limitations. In the case of the presented here procedure, the precision of the measurement and thus the identification of the geometrical parameters of the corrugated board is closely related to the quality of the provided sample. Any imperfections of the sample in the form of deformation of the corrugated layer as a result of crushing, shreds of fibers or inaccuracy of cutting directly affect the precision of the algorithms used for image analysis.
In Figure 12, it is easy to find out that the precision of identifying both the thickness of individual papers and the shape of the corrugated layer depends on the quality of the sample. If the sample has many jagged edges, it is difficult to identify the thickness, while when the sample is crushed (on the right) and the shape of the fluting changes, the sine function approximation is still possible but does not reflect its real shape. In such cases, the identified period and wave height can only be used as auxiliary indicators.
Table 2 shows the identification results for two samples of the same cardboard (flute C), one of which (on the left) is not damaged in any way by creasing, while the other is damaged stochastically. Both samples are cut on a plotter with an oscillating knife, which means that the cut edges are not regular and in both cases shreds of cellulose fibers were an additional difficulty in the identification process.
Figure 13 shows two samples of corrugated board with flute B. Again, two cases are presented here – cardboard without damage (left) and with damage in the form of a crushed flute (right).
Table 3 contains all identified geometrical features of both corrugated board samples with B-flute. It can be seen that in the case of cardboard with a lower flute, the identification of the shape of damaged cardboard is less error-prone, which makes the identified parameters of the corrugated layer more useful.
The last example is shown in Figure 14, where two samples of corrugated board with E flute are presented. This is the lowest flute of all the cases presented here, therefore the crease of such cardboard is less visible (example on the right). As the geometrical dimensions of the cross-section are reduced, the measurement noise, which arises as a result of jagged edges, becomes more important and thus it is more difficult to obtain reliable values of the thickness of individual papers.
Table 4 presents the results of the identification of parameters for both samples of corrugated board with E flute. Also in this case, damage to the board in the form of creases is not as spectacular as in the case of cardboard with C flute, which makes the identified parameters of the flute geometry more reliable.
The results presented in this section are only a small sample of all analyzed cases. The proposed identification procedure was tested on over 200 different cases. As already mentioned in the research campaign, both undamaged and damaged samples were used. All damages in the form of crushing of the corrugated layer were made by completely stochastic process with different forces and in different sample’s locations.

4. Discussion

The previous section presents representative examples of the operation of the algorithm for identifying the geometric parameters of cross-sections of various cardboard samples. Since, according to our knowledge, in the professional and scientific literature there are no similar attempts to identify the parameters describing the shape of the corrugated layer and the thickness of individual cross-section layers on real cardboard samples, this section focuses on a critical discussion of the results obtained, with particular emphasis on the limitations of the presented technique.
As already mentioned, the effectiveness of the method depends to a large extent on the quality of sample excision. Each attempt to cut the sample with the use of oscillating knives resulted in the formation of shreds of cellulose fibers at the edges of the sample. Their presence obviously interfered with the effectiveness of the algorithms, mainly in the part that is responsible for recognizing the thickness of individual layers of paper in corrugated board. The second negative effect, which significantly affected the accuracy of the created algorithms, was damage to the sample before or after cutting, by accidental crushing of the corrugated layer in stochastic locations of the cross-section.
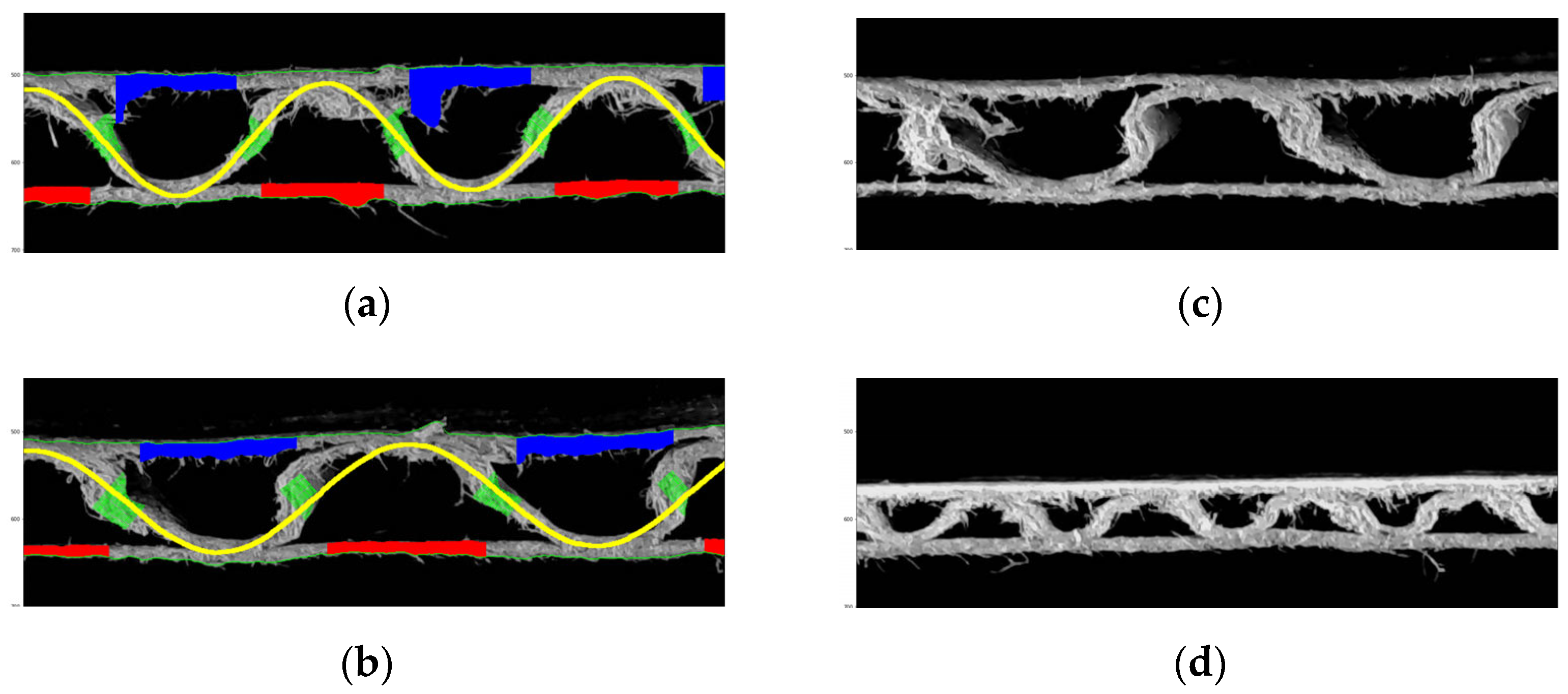
In the case of edge delamination of the paper or when an irregular edge was formed at the sample cut (example shown in Figure 15a,b), there was a clear difficulty in determining the correct thickness of the liners (flat layers) shown in Figure 15a or the thickness of the fluting (see Figure 15b). Damage to the corrugated board by crushing the corrugated layer obviously had the biggest impact on identifying the fluting period and amplitude (see examples shown in Figure 15c,d). Figure 15b also shows an inaccurate fit of the approximating function, which was assumed as a sine, to the shape of the crushed fluting. However, despite the inaccurate adjustment of the approximating function to the real shape of the distorted corrugated layer, the period of the wave in most of the analyzed cases was determined with a good approximation. The amplitude in such cases was treated only as an indicator determining the height of the cross-section after creasing.
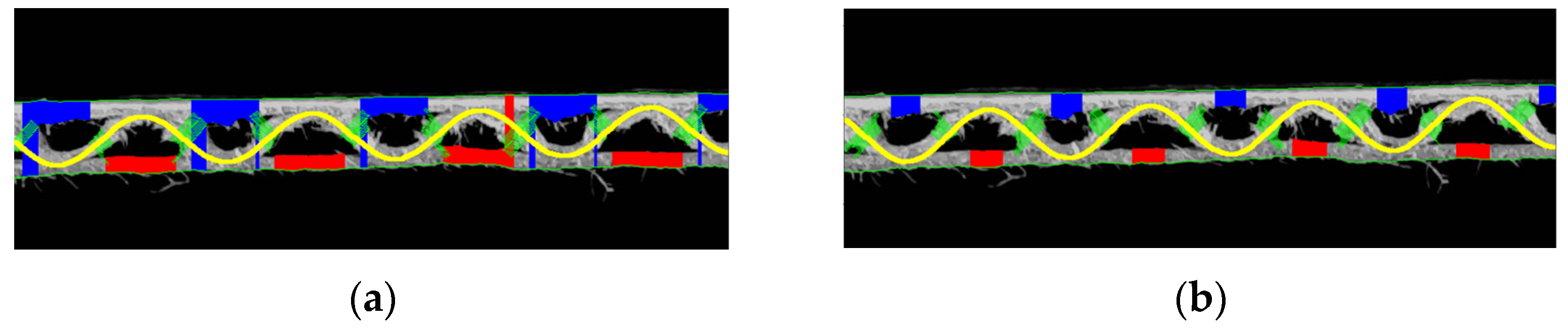
Unfortunately, almost all crushed microwave samples are only suitable for determining the wave period and amplitude (which are usually very well matched), while the problem is to determine the thickness of individual layers. This is due to too much interference (jagged fibers) in relation to the size of the area between the fluting walls. The solution that often allowed to improve the efficiency of the algorithm was to limit the area on which the thickness of the liners was measured. The original example (weak effect) and the operation on the same image after changing this area are shown in Figure 16a and Figure 16b, respectively.
In most cases, the source of errors and failures of the algorithm for identifying the geometric parameters of the cardboard cross-section are paper fibers. Due to the fact that all samples were cut on a plotter with an oscillating knife, the disadvantage of which is precisely leaving this type of disturbance on the cutting edge, the task of the created program was significantly difficult. It can be suspected that cutting samples on a laser plotter would significantly improve the reliability of the results and would ensure an increase in the efficiency of the developed algorithm. However, the known edge-burning effect of the laser could also introduce other types of interference into the identification process. For example, leaving black soot on the cut edge, which could visually reduce the thickness of the papers in the analyzed cardboard samples.

5. Conclusions

This article presents the procedure for identifying the geometric parameters of the cross-section of single-wall corrugated board. The procedure is based on a laboratory device developed for the purposes of these research which was used to take pictures of cardboard samples in constant and controlled conditions. The developed procedure uses a genetic algorithm, which is characterized by high efficiency and allows for very quick identification of geometrical parameters of the corrugated board cross-section. The use of local algorithms based on, for example, gradients is unfortunately not possible in this case due to the specific formulation of the optimization problem.
Unfortunately, the effectiveness of the procedure is strongly dependent on the quality of the excised sample. In most cases, it was possible to correctly determine the wave period of the corrugated layer approximated by the sine function. Determination of the amplitude and thus also the adjustment of the approximating function to the fluting shape depended to a large extent on the level of crushing of the cardboard cross-section. Fluting parameters in samples without damage were identified in almost 100 percent correctly.
Determining the thickness of individual layers was the most difficult in the case of samples with jagged edges. In the case of such samples, it was helpful to narrow down the measurement segments, however, it resulted in the loss of the automaticity of the identification process and the need to set individual algorithm settings. In the future, it is planned to improve the algorithm so that the parameters are selected automatically depending on the quality of the sample. The use of a different cutting technique may allow minimizing the delamination effect of the paper layers and thus also improving the effectiveness of the procedure in determining the thickness of the corrugated board layers.
The procedure in its current form is suitable for identifying geometric parameters of cardboard samples with relatively low crushing and without significant damage to the paper structure in the cutting process. The cutting process used in this article was intended to simulate real methods used in most laboratories. Changing the cutting technique to a laser plotter will allow minimizing damage to the sample in the cutting process, which will allow for even more effective determination of the actual geometry of the sample after production (which is different from the theoretical one) or after processing (which usually introduces crushing). The most important benefit of using the proposed procedure is the possibility of obtaining information on the actual geometry of the board sample, which is necessary for the correct modeling of structures made of cardboard.

Author Contributions

Conceptualization, T.G. and M.R.; methodology, M.R. and J.K.G.; software, M.R.; validation, M.R., J.K.G. and T.G.; formal analysis, M.R.; investigation, M.R. and J.K.G.; resources, M.R. and T.G.; data curation, M.R.; writing—original draft preparation, M.R., J.K.G. and T.G.; writing—review and editing, J.K.G. and T.G.; visualization, M.R.; supervision, J.K.G.; project administration, J.K.G. and T.G.; funding acquisition, J.K.G. and T.G. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Data available on request.

Acknowledgments

The authors would like to thank Kacper Andrzejak from the Werner Kenkel company and Monika Niziałek-Łukawska and Małgorzata Kuca from the Schumacher Packaging company for providing the research materials. We would also like to thank the Femat company for financial support in the conducted research and the possibility of using laboratory equipment as well as professional software.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Pereira, T.; Neves, A.S.L.; Silva, F.J.G.; Godina, R.; Morgado, L.; Pinto, G.F.L. Production Process Analysis and Improvement of Corrugated Cardboard Industry. Procedia Manuf. 2020, 51, 1395–1402. [Google Scholar] [CrossRef]
  2. Di Russo, F.M.; Desole, M.M.; Gisario, A.; Barletta, M. Evaluation of wave configurations in corrugated boards by experimental analysis (EA) and finite element modeling (FEM): the role of the micro-wave in packing design. Int. J. Adv. Manuf. Technol. 2023. [Google Scholar] [CrossRef] [PubMed]
  3. Beck, M.; Fischerauer, G. Modeling Warp in Corrugated Cardboard Based on Homogenization Techniques for In-Process Measurement Applications. Appl. Sci. 2022, 12, 1684. [Google Scholar] [CrossRef]
  4. Nordstrand, T.M. Parametric study of the post-buckling strength of structural core sandwich panels. Compos. Struct. 1995, 30, 441–451. [Google Scholar] [CrossRef]
  5. Nordstrand, T. Analysis and testing of corrugated board panels into the post-buckling regime. Compos. Struct. 2004, 63, 189–199. [Google Scholar] [CrossRef]
  6. Lu, T.J.; Chen, C.; Zhu, G. Compressive behaviour of corrugated board panels. J. Compos. Mater. 2001, 35, 2098–2126. [Google Scholar] [CrossRef]
  7. Garbowski, T.; Knitter-Piątkowska, A. Analytical Determination of the Bending Stiffness of a Five-Layer Corrugated Cardboard with Imperfections. Materials 2022, 15, 663. [Google Scholar] [CrossRef] [PubMed]
  8. Mrówczyński, D.; Knitter-Piątkowska, A.; Garbowski, T. Numerical Homogenization of Single-Walled Corrugated Board with Imperfections. Appl. Sci. 2022, 12, 9632. [Google Scholar] [CrossRef]
  9. Cillie, J.; Coetzee, C. Experimental and Numerical Investigation of the In-Plane Compression of Corrugated Paperboard Panels. Math. Comput. Appl. 2022, 27, 108. [Google Scholar] [CrossRef]
  10. Mrówczyński, D.; Garbowski, T. Influence of Imperfections on the Effective Stiffness of Multilayer Corrugated Board. Materials 2023, 16, 1295. [Google Scholar] [CrossRef] [PubMed]
  11. Liu, W.; Ouyang, H.; Liu, Q.; Cai, S.; Wang, C.; Xie, J.; Hu, W. Image recognition for garbage classification based on transfer learning and model fusion. Math. Probl. Eng. 2022, 2022, paper. [Google Scholar] [CrossRef]
  12. Rahman, M.O.; Hussain, A.; Scavino, E.; Hannan, M.A.; Basri, H. Recyclable waste paper sorting using template matching. In Visual Informatics: Bridging Research and Practice. First International Visual Informatics Conference, IVIC 2009 Kuala Lumpur, Malaysia, November 11-13, 2009 Proceedings; Zaman, H.B., Robinson, P., Petrou, M., Olivier, P., Schröder, H., Shih, T.K., Eds.; Springer-Verlag: Berlin Heidelberg, Germany, 2009; pp. 467–478. [Google Scholar] [CrossRef]
  13. Cebeci, U.; Aslan, F.; Çelik, M.; Aydın, H. Developing a new counting approach for the corrugated boards and its industrial application by using image processing algorithm. In Practical Applications of Intelligent Systems. Advances in Intelligent Systems and Computing 279; Wen, Z., Li, T., Eds.; Springer-Verlag: Berlin Heidelberg, Germany, 2014; pp. 1021–1040. [Google Scholar] [CrossRef]
  14. Suppitaksakul, C.; Rattakorn, M. Machine vision system for counting the number of corrugated cardboard. In Proceedings of the International Electrical Engineering Congress (iEECON), Chonburi, Thailand, 19-21 March 2014; pp. 1–4. [Google Scholar] [CrossRef]
  15. Suppitaksakul, C.; Suwannakit, W. A combination of corrugated cardboard images using image stitching technique. In Proceedings of the 15th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology, Chiang Rai, Thailand, 18-21 July 2018; pp. 262–265. [Google Scholar] [CrossRef]
  16. Caputo, B.; Hayman, E.; Fritz, M.; Eklundh, J.-O. Classifying materials in the real world. Image Vis. Comput. 2010, 28, 150–163. [Google Scholar] [CrossRef]
  17. Iqbal Hussain, M.A.; Khan, B.; Wang, Z.; Ding, S. Woven Fabric Pattern Recognition and Classification Based on Deep Convolutional Neural Networks. Electronics 2020, 9, 1048. [Google Scholar] [CrossRef]
  18. Wyder, P.M.; Lipson, H. Visual design intuition: predicting dynamic properties of beams from raw cross-section images. J. R. Soc. Interface 2021, 18, 20210571. [Google Scholar] [CrossRef] [PubMed]
  19. Li, M.; Liu, Z.; Huang, L.; Chen, Q.; Tong, C.; Fang, Y.; Han, W.; Zhu, P. Automatic identification framework of the geometric parameters on self-piercing riveting cross-section using deep learning. J. Manuf. Process. 2022, 83, 427–437. [Google Scholar] [CrossRef]
  20. Ma, Q.; Rejab, M.R.M.; Azeem, M.; Idris, M.S.; Rani, M.F.; Praveen Kumar, A. Axial and radial crushing behaviour of thin-walled carbon fiber-reinforced polymer tubes fabricated by the real-time winding angle measurement system. Forces Mech. 2023, 10, 100170. [Google Scholar] [CrossRef]
  21. Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning. Addison-Wesley Publishing Company, Inc., Reading, Massachusetts, USA, 1989.
  22. Holland, J.H. Adaptation in Natural and Artificial Systems, University of Michigan Press, USA, 1975.
  23. Shoukat, R. Green intermodal transportation and effluent treatment systems: application of the genetic algorithm and mixed integer linear programming. Process Integr. Optim. Sustain. 2023, 7, 329–341. [Google Scholar] [CrossRef]
  24. Hidetaka, M.; Masakazu, K. Multiple objective genetic algorithms approach to a cardboard box production scheduling problem. J. Jpn. Ind. Manag. Assoc. 2005, 56, 74–83. [Google Scholar]
Preprints 73963 g001
Figure 1. Device for corrugated board images acquisition: (a) Visualization of the device; (b) Layout diagram of the most important components of the device: 1 – corrugated board sample; 2 – camera; 3 – LED strip.
Figure 1. Device for corrugated board images acquisition: (a) Visualization of the device; (b) Layout diagram of the most important components of the device: 1 – corrugated board sample; 2 – camera; 3 – LED strip.
Preprints 73963 g001
Preprints 73963 g002
Figure 2. Flowchart of the proposed algorithm.
Figure 2. Flowchart of the proposed algorithm.
Preprints 73963 g002
Preprints 73963 g003
Figure 3. Results of the preprocessing stage: (a) a gray-scale cropped image of 800x800 pixels; (b) blurred image; (c) binary image.
Figure 3. Results of the preprocessing stage: (a) a gray-scale cropped image of 800x800 pixels; (b) blurred image; (c) binary image.
Preprints 73963 g003
Preprints 73963 g004
Figure 4. The results of the column-wise image scanning.
Figure 4. The results of the column-wise image scanning.
Preprints 73963 g004
Preprints 73963 g005
Figure 5. The row sum curve and localizations of the vertical positions of liners : (a) The row sum curve (red line) and the smoothed curve (blue line); (b) The upper (red) and lower (green) liners ranges.
Figure 5. The row sum curve and localizations of the vertical positions of liners : (a) The row sum curve (red line) and the smoothed curve (blue line); (b) The upper (red) and lower (green) liners ranges.
Preprints 73963 g005
Preprints 73963 g006
Figure 6. (a) The binary image with external boundaries of the liners (green lines), boundary lines for limiting the flute searching (red lines), and the central line (yellow line).
Figure 6. (a) The binary image with external boundaries of the liners (green lines), boundary lines for limiting the flute searching (red lines), and the central line (yellow line).
Preprints 73963 g006
Preprints 73963 g007
Figure 7. (a) Results of the skeletonization process; (b) results after skeletonization process and removing side branches; (c) 3 parallel lines for period limitations.
Figure 7. (a) Results of the skeletonization process; (b) results after skeletonization process and removing side branches; (c) 3 parallel lines for period limitations.
Preprints 73963 g007
Preprints 73963 g008
Figure 8. (a) The eroded image; (b) An example result of the optimization process using the genetic algorithm (red line).
Figure 8. (a) The eroded image; (b) An example result of the optimization process using the genetic algorithm (red line).
Preprints 73963 g008
Preprints 73963 g009
Figure 9. Schematic representation of the algorithm for determination of the liners and flute thicknesses.
Figure 9. Schematic representation of the algorithm for determination of the liners and flute thicknesses.
Preprints 73963 g009
Preprints 73963 g010
Figure 10. An example of the results obtained by applying the proposed algorithm.
Figure 10. An example of the results obtained by applying the proposed algorithm.
Preprints 73963 g010
Preprints 73963 g011
Figure 11. Visualization of the recognized fluting shapes of corrugated board: (a) Flute C sample; (b) Results obtained for the flute C sample; (c) Flute B sample; (d) Results obtained for the flute B sample; (e) Flute E sample; (f) Results obtained for the flute F sample.
Figure 11. Visualization of the recognized fluting shapes of corrugated board: (a) Flute C sample; (b) Results obtained for the flute C sample; (c) Flute B sample; (d) Results obtained for the flute B sample; (e) Flute E sample; (f) Results obtained for the flute F sample.
Preprints 73963 g011
Preprints 73963 g012
Figure 12. Figure 12. Examples of samples difficult to identify: (a) with many jagged edges; (b) results of identification the sample with many jagged edges; (c) crushed sample; (d) results of identification the crushed sample.
Figure 12. Figure 12. Examples of samples difficult to identify: (a) with many jagged edges; (b) results of identification the sample with many jagged edges; (c) crushed sample; (d) results of identification the crushed sample.
Preprints 73963 g012
Preprints 73963 g013
Figure 13. Flute B example: (a) cardboard without damage; (b) results of identification; (c) damaged sample; (d) results of identification.
Figure 13. Flute B example: (a) cardboard without damage; (b) results of identification; (c) damaged sample; (d) results of identification.
Preprints 73963 g013
Preprints 73963 g014
Figure 14. Flute E example: (a) cardboard without damage; (b) results of identification; (c) damaged sample; (d) results of identification.
Figure 14. Flute E example: (a) cardboard without damage; (b) results of identification; (c) damaged sample; (d) results of identification.
Preprints 73963 g014
Preprints 73963 g015
Figure 15. This is a figure. Schemes follow another format. If there are multiple panels, they should be listed as: (a) Description of what is contained in the first panel; (b) Description of what is contained in the second panel. Figures should be placed in the main text near to the first time they are cited.
Figure 15. This is a figure. Schemes follow another format. If there are multiple panels, they should be listed as: (a) Description of what is contained in the first panel; (b) Description of what is contained in the second panel. Figures should be placed in the main text near to the first time they are cited.
Preprints 73963 g015
Preprints 73963 g016
Figure 16. (a) The original example (weak effect) and (b) the operation on the same image after changing this area.
Figure 16. (a) The original example (weak effect) and (b) the operation on the same image after changing this area.
Preprints 73963 g016
Table 1. Identification results of the geometrical features for the corrugated boards with flutes C, B and E.
Table 1. Identification results of the geometrical features for the corrugated boards with flutes C, B and E.
Flute C Flute B Flute E
[px] [mm] [px] [mm] [px] [mm]
Flute height 187 3.60 140 2.70 67 1.30
Flute period 428 8.13 339 6.39 185 3.50
Board thickness 226 4.29 165 3.13 94 1.79
Upper liner thickness 27 0.51 24 0.46 21 0.40
Flute thickness 26 0.49 19 0.34 19 0.36
Bottom liner thickness 26 0.49 18 0.36 22 0.42
Table 2. Identification results of the geometrical features for the corrugated board with flute C (reference and crushed samples).
Table 2. Identification results of the geometrical features for the corrugated board with flute C (reference and crushed samples).
Flute C (reference) Flute C (crushed)
[px] [mm] [px] [mm]
Flute height 187 3.60 157 3.00
Flute period 428 8.13 414 7.82
Board thickness 226 4.29 182 3.46
Upper liner thickness 27 0.51 27 0.51
Flute thickness 26 0.49 30 0.57
Bottom liner thickness 26 0.49 18 0.34
Table 3. Identification results of the geometrical features for the corrugated board with flute B (reference and crushed samples).
Table 3. Identification results of the geometrical features for the corrugated board with flute B (reference and crushed samples).
Flute B (reference) Flute B (crushed)
[px] [mm] [px] [mm]
Flute height 140 2.70 118 2.20
Flute period 339 6.39 349 6.60
Board thickness 165 3.13 135 2.56
Upper liner thickness 24 0.46 23 0.44
Flute thickness 19 0.34 22 0.42
Bottom liner thickness 18 0.36 18 0.34
Table 4. Identification results of the geometrical features for the corrugated board with flute E (reference and crushed samples).
Table 4. Identification results of the geometrical features for the corrugated board with flute E (reference and crushed samples).
Flute E (reference) Flute E (crushed)
[px] [mm] [px] [mm]
Flute height 67 1.30 56 1.10
Flute period 185 3.50 191 3.61
Board thickness 94 1.79 82 1.56
Upper liner thickness 21 0.40 14 0.27
Flute thickness 19 0.36 22 0.30
Bottom liner thickness 22 0.42 16 0.42
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated