Prerpints.org logo
Preprint
Article

Spacetime as a Complex Network and the Cosmological Constant Problem

Altmetrics

Downloads

108

Views

36

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

09 May 2023

Posted:

10 May 2023

You are already at the latest version

Alerts
Abstract
We propose a promising model of discrete spacetime based on nonassociative geometry and complex networks. Our approach treats space as a simplicial 3-complex (or complex network), built from "atoms" of spacetime and entangled states forming n-dimensional simplices (n=1,2,3). At large scales, a highly connected network is a coarse, discrete representation of a smooth spacetime. We show that for high temperatures, the network describes disconnected discrete space. At the Planck temperature, the system experiences the phase transition, and for low temperatures, the space becomes a triangulated discrete space. We show that the cosmological constant depends on the universe’s topology. The "foamy" structure, analogous to Wheeler’s "spacetime foam," significantly contributes to the effective cosmological constant, which is determined by the Euler characteristic of the universe.
Keywords: 
Subject: Physical Sciences  -   Theoretical Physics

1. Introduction

In classical general relativity, the cosmological constant, Λ , added in the Einstein equations, governs the Universe’s accelerated expansion. However, the equivalence principle of general relativity requires that every form of energy gravitate similarly. Therefore, accordingly to this principle, the enormous energy of the quantum vacuum fluctuations must produce a large gravitational effect. Moreover, the virtual particles contributing to the vacuum energy density, ρ v a c , should alternate the value of the cosmological constant [1,2]. Although we do not know how to compute ρ v a c precisely, the quantum field theory (QFT) allows one to estimate its value. Unfortunately, the estimates disagree with observational data by 10 122 factor. It is the worst prediction of the theoretical physics, also known as the cosmological constant problem (For a review, see the references [3,4,5,6,7,8,9,10,11,12,13].). There is no generally recognized explanation for this discrepancy, although a lot of papers have been written on it.
In the middle of the last century, Pauli assumed that the vacuum energies of bosons and fermions might compensate for each other [14]. This assumption is based on the fact that the vacuum energy of fermion and bosons have opposite signs: the energy of bosons has a positive sign, while that of fermions has a negative one. Later Zeldovich developed this approach to link the vacuum energy to the cosmological constant. Instead of eliminating the divergences through a boson-fermion cancellation, he suggested a covariant Pauli-Villars regularization yielding the finite residual vacuum energy and negative pressure corresponding to a cosmological constant [1,2].
Recently the approach based on the Pauli-Zeldovich cancellation of the vacuum energy divergences has been revived to attack the cosmological constant problem by combining both ideas [15,16,17]. The Pauli suggestion was used for canceling all the ultraviolet divergences in the vacuum energy. Zeldovich’s approach was used to prove that the remaining finite part of the vacuum energy yields an effective cosmological constant. Several simple toy models, having particles with equal masses and spin 0 and 1 / 2 , illustrated the method, wherein interactions can be quite non-trivial. However, the problem is still far from its resolution.
The standard formulation of the cosmological constant problem is problematic since the spacetime and the vacuum energy density are highly inhomogeneous and wildly fluctuate at the Planck scales. The importance of quantum fluctuations in spacetime topology at small scales has been emphasized by many authors (See, for instance, [18,19,20,21,22,23,24].). Assuming that vacuum fluctuations at the Planck length scale might generate a cosmological constant requires quantum gravity [3,5,6,8,9,10,11,12]. The search for a quantum theory of gravity faces the challenge of comprehending and describing the quantum nature of space and time [25,26,27]. One can distinguish two general strategies to achieve these goals [28,29]. The first strategy consists in quantizing a classical structure that later is recovered as a limit of the quantum theory. The second strategy assumes that the classical structures are emergent from the other theory, the more fundamental theory from the beginning. In the second approach, a formulation of the quantum theory may require omitting the use of continuum concepts a priori. It means that at the Planck scale, the standard concept of spacetime must be replaced by some discrete structure (See, for instance, [28,30,31,32,33,34,35,36,37,38].).
In [39,40,41,42,43,44,45], we proposed a new unified algebraic approach, based on nonassociative geometry, for describing both continuum and discrete spacetimes. In our model of spacetime, time is quantized, and a random/stochastic process governs the evolution of spacetime geometry. As a result, we obtain a partially ordered set of events with spacetime geometry encoded in the nonassociative structure of spacetime [46]. Among advanced models that propose discreteness, two are related to our work: Causal Sets [47,48,49] and Causal Dynamical Triangulations [32,50,51,52,53,54,55,56]. These models are based on the hypothesis that spacetime is discrete and causality is a fundamental principle.
This paper addresses the cosmological constant derivation within the discrete spacetime model proposed in [45] by employing the Pauli-Zeldovich cancellation of vacuum bosonic and fermionic degrees of freedom. We treat 3-dimensional space as a simplicial 3-complex (complex network). Vertices (0-simplices) of the network are the atoms of spacetime, and it is assumed that they are fermions with the spin one half. Edges, or 1-simplices, are entangled particle states and have the spin 1. The 2-simplex is built from three vertices. Thus, the 2-simplex is formed as an entangled state with a total spin of 3/2. The 3-simplex is the entangled state of four atoms with a total spin 2. At large scales, a highly connected complex network is a coarse, discrete representation of a smooth spacetime.
The properties of spacetime are described by methods of statistical physics based on the information Shannon-Gibbs entropy [57,58,59]. For high temperatures, the space is presented by a simpilicial 0-complex (or a disconnected discrete space). With decreasing the temperature of the network, the process of triangulation begins with the formation of low dimensional complices and clusters. At the Planck temperature, T p , the system experiences the phase transition; for low temperatures, T ≪ T p , the network becomes a simplicial 3-complex (or a triangulated discrete space).
We show that the "foamy" structure, analogous to Wheeler’s "spacetime foam" [18], significantly contributes to the effective cosmological constant, Λ e f f . The latter is defined by the universe’s Euler characteristic, χ ; Λ e f f = − 8 π χ ℓ p / V , where ℓ p denotes the Planck length andV is the volume of the universe. It is our main result.
The paper is organized as follows. Sec. 2 discusses the statistical properties of complex undirected networks with a fixed number of vertices and a varying number of links, described by the grand canonical ensemble. As a particular application, we consider in detail simple (fermionic) graphs with only one edge allowed between any pair of vertices. In Sec. 3, we briefly introduce a discrete spacetime model based on nonassociative geometry. In Sec. 4, we introduce and explore in detail a spacetime model based on the fermionic network. In Sec. 5, we derive the cosmological constant and show that the Euler characteristic of the universe defines it. In Conclusion, we summarize our results and discuss possible generalizations of our approach.
Throughout the paper, we use the natural units, setting c = ℏ = k B = 1 .

2. Statistical Description of Complex Networks

The statistical description of complex networks (or graphs) is based on the informational Shannon-Gibbs entropy [57,58,59]:
S = − ∑ G ∈ G P ( G ) ln P ( G ) ,
where P ( G ) the probability of obtaining a graph G, belonging to ensemble of graphs, G . For an undirected network with a fixed number of vertices and a varying number of links, the probability of obtaining a graph G can be written as [57,60,61,62]
P ( G ) = 1 Z exp β ( μ L ( G ) − H ( G ) ) ,
where Z = ∑ G ∈ G exp β ( μ L ( G ) − H ( G ) ) , is the partition function, β = 1 / T is an inverse network temperature, μ is the chemical potential, and L ( G ) = ∑ i < j a i j is number of links in the graph G. An adjacency matrix, a i j , takes value 1 or 0 in the i , j entry for each existing or non-existing link between pairs of nodes ( i j ). The network connectivity is characterized by the connection probability p i j , i.e., the probability that a pair of nodes ( i j ) is connected. This probability is equivalent to the expected number of edges 〈 a i j 〉 between vertices i and j, namely, 〈 a i j 〉 = p i j .
To obtain the grand potential, Ω , which we will refer to as the Landau free energy, we use the relation Ω = − β − 1 ln Z . Next, one can recover the Helmholtz free energy F, internal energy E and entropy S, using the following relations:
F = Ω + μ L , E = F + T S ,
S = − ∂ Ω ∂ T | μ .
Having the Landau free energy, one can find the expected number of links as follows: L = − ∂ Ω / ∂ μ .
Let us assign the “energy" ε i j to each edge 〈 i , j 〉 . Then the graph Hamiltonian can be written as H ( G ) = ∑ i < j ε i j a i j , and the partition function is given by [61]
Z = ∑ G ∈ G ∏ i < j e β μ − ε i j a i j .
Using the partition function, one can obtain the connection probability of the existing link between nodes i and j as the derivative of the partition function [63,64,65,66]:
p i j = − ∂ ln Z ∂ ( β ε i j ) .

2.1. Fermionic graphs

Consider a set of undirected graphs with only one edge allowed between any pair of vertices (so-called fermionic graphs). The computation of the partition function yields
Z = ∏ 〈 i j 〉 1 + e β μ − ε i j ,
where the product is over the ordered pairs 〈 i j 〉 . Employing Eq. (6), we obtain the Fermi-Dirac distribution [57]:
p i j = 1 e β ε i j − μ + 1 ,
Using the relation Ω = − β − 1 ln Z , we obtain
Ω = − β − 1 ∑ i < j ln 1 + e β μ − ε i j .
Having the Landau free energy, one can find the expected number of links as follows: L = − ∂ Ω / ∂ μ . The computation yields
L = ∑ i < j 1 e β ε i j − μ + 1 .

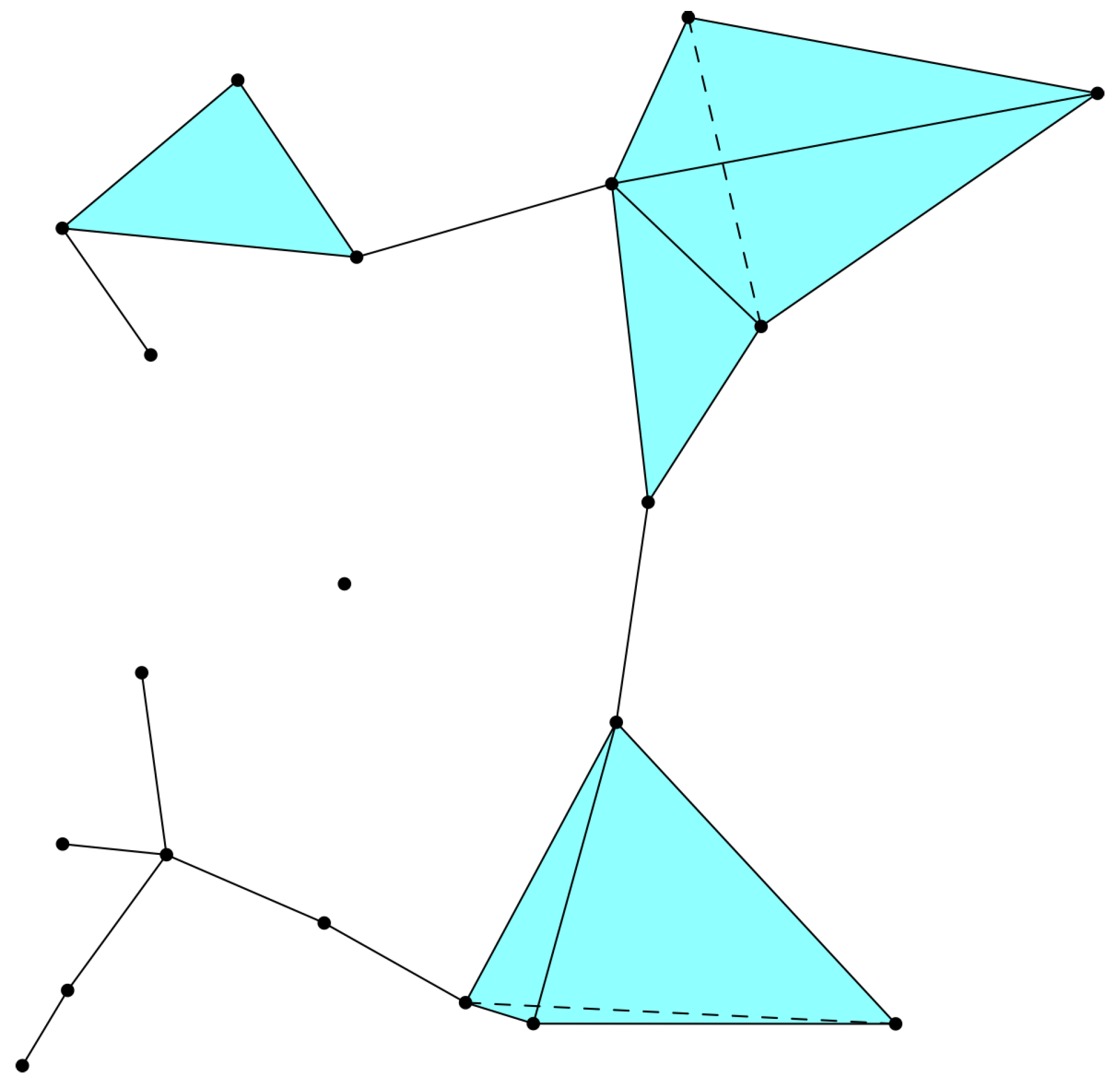
3. Building Discrete Spacetime

Our approach is based on the nonassociative geometry, statistical description of complex networks, and the following assumptions [41,45,46,67]:
  • Vertices or nodes of the network are "atoms" of spacetime.
  • The distance between two neighboring atoms can not be less than the fundamental length, ℓ p .
  • Spacetime geometry is encoded in the nonassociative structure of the network.
  • Interaction between atoms of spacetime, being nonlocal defines the spacetime geometry.
  • Time is quantized and the evolution of spacetime geometry is governed by a random/stochastic process.
  • The spacetime dimension is a dynamical variable.
We treat a discrete space as a simplicial 3-complex (see Figure 1). Vertices (0-simplices) of the network are the atoms of spacetime, and it is assumed that they are fermions with spin one half. Edges, or 1-simplices, are entangled particle states with the spin 1. We assign to the face of a 2-simplex a spin 1 / 2 , where spin up/down corresponds to the positive/negative curvature of a 2-simplex. The 2-simplex is built from three entangled atoms; its total spin is 3 / 2 . The 3-simplex has four atoms. It is considered as the entangled state with spin 2.
The curvature of 2-simplices is associated with their faces and described by an elementary holonomy. It contrasts the Regge model, where curvature resides at vertices [68,69,70]. The elementary holonomy of a 2-simplex can be written as h = 1 ± Δ S / R 2 , where Δ S is its area, 1 / R 2 is the curvature, and upper/lower sign corresponds to positive/negative curvature, respectively. The null curvature corresponds to the limit R → ∞ [67].
As an example, consider the homogeneous 2 D network with positive curvature. This network can be mapped onto the two-dimensional sphere with radius R, which we treat as a discrete toy model of the two-dimensional universe (see Figure 2): Left. The network is wholly disconnected, and the space is represented by the simplicial 0-complex. Middle. A partially triangulated space, described by a simplicial 2-complex. Together with isolated 0-simplices and 1-simplices, one can observe the formation of two-dimensional clusters connected by simplicial 1-complexes. Right. The network becomes completely connected, corresponding to the triangulated space.

4. Spacetime as a Complex Network

We consider the simplified version of the Hamiltonian proposed in [45]
H = − J ∑ 〈 i j k 〉 λ i j k a i j a j k a k i + ν ∑ 〈 i j 〉 a i j ,
where J is a coupling constant, λ i j k = 1 + ϵ 〈 i j k 〉 Δ S 〈 i j k 〉 / R 〈 i j k 〉 2 denotes the elementary holonomy of 2-simplex associated with the triplet of sites 〈 i , j , k 〉 forming a left triangle concerning the edge 〈 i j 〉 , and ϵ 〈 i j k 〉 = ± 1 . The first term in (11) describes the contribution of the quantum bosonic vacuum fluctuation and curvature, and the second one represents the quantum fermionic vacuum fluctuations. The summation is over 1- simplices and 2-simplices denoted as 〈 i j 〉 and 〈 i j k 〉 , respectively.
Within the mean field approximation, the Hamiltonian (11) is replaced by the effective Hamiltonian
H = 2 J ∑ 〈 i j k 〉 λ i j k p i j p j k p k i + ∑ 〈 i j 〉 ε i j a i j ,
where the effective energy is given by
ε i j = ν − 3 J ∑ k λ i j k p j k p k i .
The equilibrium state of the system is described by the generalized Fermi-Dirac distribution for the connection probability (8),
p i j = 1 e β ε i j − μ + 1 .
Employing Eq. (14), one can rewrite (13) in the equivalent form
p i j = 1 2 1 + tanh β 2 μ − ν + 3 J ∑ k λ i j k p j k p k i
We assume that the network is highly connected for low temperatures, and it has a low connectance for high temperatures:
p i j → 1 , if T → 0 0 , if T → ∞
It implies that the space is represented by a simplicial 0-complex for high temperatures (or a completely disconnected discrete space), and it becomes a simplicial 3-complex (or a triangulated space) for low temperatures.
In the limit of low/high temperatures, the energy of the system is given by
E = E 0 = N 1 ν − N 2 J λ , if T → 0 0 , if T → ∞
where N 1 = ∑ 〈 i j 〉 is the total number of edges (1-simplices) of the network, N 2 = ∑ 〈 i j k 〉 denotes the number of the 2-simplices in totally triangulated space, λ = 1 + ϵ Δ S / ℓ p 2 , and
ϵ = ℓ p 2 N 2 Δ S ∑ 〈 i j k 〉 ϵ 〈 i j k 〉 Δ S 〈 i j k 〉 R 〈 i j k 〉 2 .
Here Δ S is the average area of 2-simplices. The dimensionless parameter ϵ defines the average curvature of the network. In particular, ϵ = 0 describes the network with the null average spatial curvature. By employing Eq. (17), in the limit of low temperature, we obtain the vacuum energy density as
ρ 0 = E 0 V = 1 V ( N 1 ν − N 2 J λ ) ,
where V is the volume of the universe.

4.1. Toy Homogeneous Model

In what follows, we consider the case of a homogeneous network, assuming that a i j = a . With this assumption, the Hamiltonian (11) can be recast as follows:
H = − J λ ∑ 〈 i j k 〉 a 3 + ν ∑ 〈 i j 〉 a .
We assume that each 2-simplex is represented by an equilateral triangle with edges of length ℓ p so that Δ S = 3 ℓ p 2 / 4 . Using this relation, we obtain
λ = 1 + 3 4 ϵ .
Within the mean-field approximation, the Hamiltonian (20) is replaced by the effective Hamiltonian
H = 2 J λ ∑ 〈 i j k 〉 p 3 + ∑ 〈 i j 〉 ε a = N 1 ε a + 2 N 2 J λ p 3 ,
where N 1 is the total number of 1-simplices, N 2 is the total number of 2-simplices of the the network, and ε = ν − 3 J λ p 2 is the effective energy. The equilibrium state of the system is described by the Fermi-Dirac distribution,
p = 1 e β ε − μ + 1 .
Substituting ε = ν − 3 J λ p 2 , one can rewrite (23) as
p = 1 2 1 + tanh β 2 μ − ν + 3 J λ p 2 .
In the limit of low/high temperatures, the energy of the system is given by
E → E 0 = ν N 1 − J λ N 2 , if T → 0 0 , if T → ∞
Eq. (24) imposes the following constraints on the chemical potential:
μ ( T ) > 3 J λ − ν , if T → 0 μ ( T ) < ν , if T → ∞
Thus, for 0 < T < T 0 we obtain a triangulated spacetime and for T > T 0 the spacetimes becomes disconnected.
For illustrative purposes, we choose the dependence of the chemical potential on the temperature as μ ( T ) = μ 0 ( 1 − ( T / T p ) 2 ) . The typical behavior of the connection probability is shown in Figure 3. The graph is depicted for the choice of parameters: ϵ = 0 , μ 0 = 3 T p and J = ν = T P , where T P = 1.4 · 10 32 K is the Planck temperature. One can see that the system experiences a phase transition at the critical temperature T p forming the fermionic condensate with the maximally entangled states. This transition is speedy, and the universe becomes a wholly triangulated space at the temperature ∼ 10 31 K ≫ T G , where T G ∼ 10 29 K is the temperature of Grand unification epoch beginning.

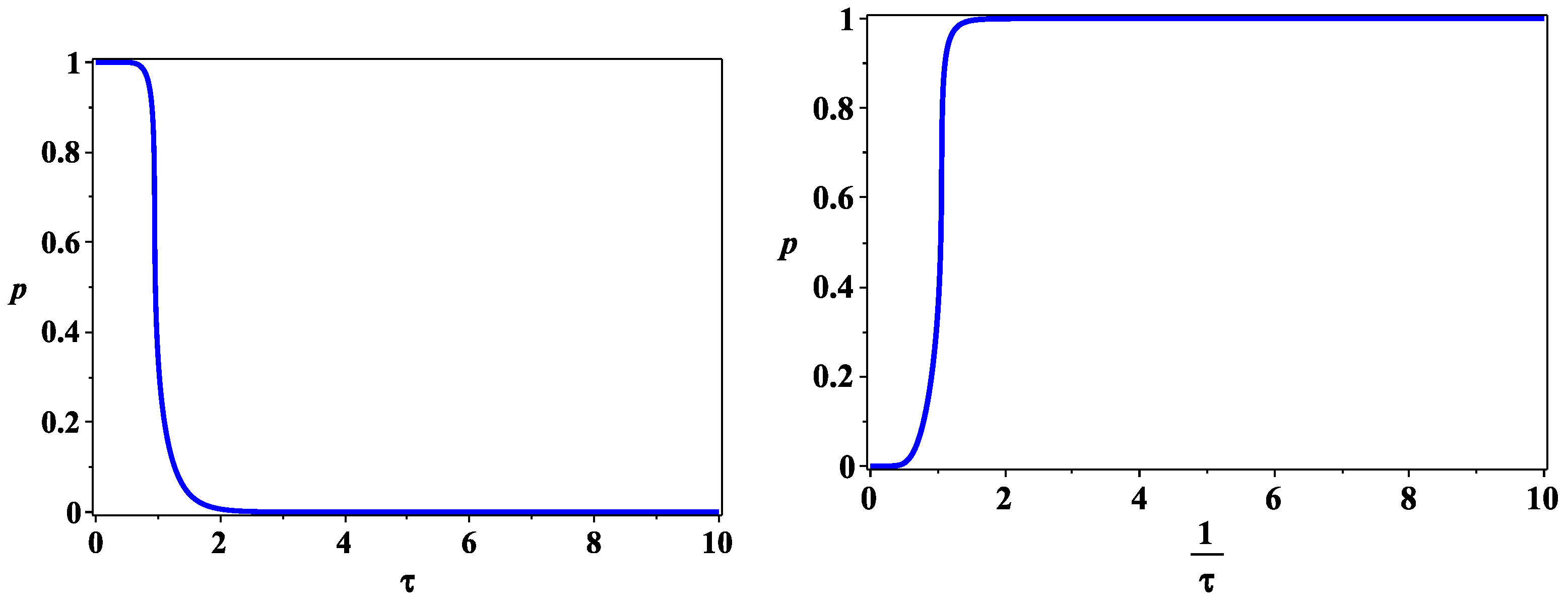
4.2. Spacetime Evolution

In our approach, space and time are quantized in the Planck units, and a random/stochastic process governs spacetime evolution. The cosmological scale factor, a n , is defined by a random walk with a reflecting barrier R 0 at n = 0 and a step ℓ p , where ℓ p is the Planck length. After n steps, the average cosmological scale factor grows as [46]
a n = a 0 + 2 n / π ,
where a 0 = R 0 / ℓ p is the scale factor related to the initial 3-simplex defining the minimal size of the universe. The initial singularity is absent, and the universe starts with the micro-universe formed by a 3-simplex.
Numerical simulations show that the probability p ≈ 1 of creating a 3-simplex corresponds to the temperature T i ∼ 10 31 K (see Figure 3). Therefore, considering T i as an initio of the universe’s evolution is reasonable. After ∼ 10 8 steps in Planck units of time, which corresponds to pre-inflationary time, t i ∼ 10 − 35 sec (time of the beginning of inflation) and temperature T p r ≈ 10 27 K , the cosmological scale factor would be a p r ∼ a 0 + 2 / π 10 4 . Comparison with the pre-inflationary universe’s scale factor, a p r ∼ 10 4 a 0 , estimated within the Λ CDM-model as a p r / a 0 ≈ T i / T p r , yields a good agreement with our prediction.

5. The Cosmological Constant Problem

Writing the Einstein equations as
R μ ν − 1 2 g μ ν R = 8 π G T μ ν − g μ ν Λ .
one can observe that space with non-zero cosmological constant produces the same gravitational field as the matter with mass density ρ Λ = Λ / 8 π G and pressure P Λ = − ρ Λ . Thus, one can speak about the energy density of the vacuum and its pressure.
According to the equivalence principle of general relativity, the energy of the quantum vacuum fluctuations must produce a gravitational field, and the semiclassical Einstein equations describe their contribution:
R μ ν − 1 2 g μ ν R = 8 π G 〈 T μ ν 〉 − g μ ν Λ ,
where 〈 T μ ν 〉 = 〈 0 | T μ ν | 0 〉 is the expectation value of the quantum vacuum energy-momentum tensor.
Lorentz invariance requires that 〈 T μ ν 〉 takes the form
〈 T μ ν 〉 = − ρ vac g μ ν ,
where ρ vac = 〈 0 | T 00 | 0 〉 is the expectation value of the energy density of the matter fields in the vacuum state. Employing (29), one can recast Eq.(27) as
R μ ν − 1 2 g μ ν R = 8 π G T μ ν − g μ ν Λ eff ,
where Λ eff = Λ + 8 π ρ vac ℓ p 2 is the effective (observable) cosmological constant.
In the standard QFT, the vacuum density energy is estimated as ρ vac ∼ m p 4 , where m p is the Planck energy. The current Hubble expansion rate H 0 yields an upper bound for λ eff [71],
Λ eff = 3 H 2 ≤ 3 H 0 2 ∼ 10 − 122 ℓ p − 2 ∼ 10 − 122 ρ vac ℓ p 2 ,
where H = a ˙ / a = Λ eff / 3 is the Hubble constant describing acceleration of the universe. Thus, one has a huge disagreement between the observed value of the cosmological constant and the theoretical prediction of its value resulting from the quantum field theory.
The general form of the vacuum energy density, including the contribution of different fermionic and bosonic fields, can be written as [72,73,74]
ρ = a 4 Λ u v 4 + a 2 Λ u v 2 M 2 + a 0 M 4 ln Λ u v 2 M 2 ,
where M is the mass of corresponding field, and Λ u v is the ultraviolet energy cut-off. In particular, if the vacuum is completely homogeneous and static, all the parameters vanish, corresponding to zero cosmological constant. In the presence of the interface between two different vacua, the energy density can depend not only on the mass M but also on the mass of the quantum field in the neighboring vacuum [74].
The standard computation of the cosmological constant assumes that the spacetime is homogeneous and isotropic, and the theory is Lorentz invariant. These assumptions are reasonable at a cosmological scale but questionable at a small (Planck) scale [71,75,76]. In addition, the QFT can not be applied on Planckian scales since spacetime is discrete. Instead of QFT, we use the statistical description of the spacetime, treating the latter as a complex network. Following the same approach as in the QFT, we define the effective cosmological constant as
Λ eff = 8 π ℓ p 2 ρ v a c ,
where ρ v a c is the energy density of the vacuum state defined by the contribution of all bosonic and fermionic fields of the simplicial manifold M . If we take into account the contributions from all pieces of the simplicial complex, we obtain
ρ v a c = − 1 V ∑ i = 0 3 ( − 1 ) i | E i | ,
where E i is the vacuum energy of i-simplex. In the limit of T → 0 and assuming ϵ = 0 , we get
ρ v a c = − m p V ∑ i = 0 3 ( − 1 ) i N i ,
where N i is the number of i-simplices in the network, and m p is the Planck mass defining the ultraviolet cut-off, Λ u v = m p . Employing Eq.(33), we obtain
Λ 0 ≡ Λ e f f ℓ p 2 = − 8 π ℓ p 3 V χ ( M ) ,
where χ ( M ) is the Euler characteristic of the simplicial complex M [77]. Thus, a non-vanishing cosmological constant implies a non-trivial topology of spacetime.
To estimate the Euler characteristic, χ ( M ) , we use Eq.(36) writing
χ ( M ) = − Λ 0 V 8 π ℓ p 3 .
The real size of the universe is unknown. For an estimate, we take V as the volume of the observable universe, V ≈ 3.566 × 10 86 cm 3 . This yields V / 8 π ℓ p 3 ∼ 10 183 . Taking Λ 0 ∼ 10 − 122 , we get | χ ( M ) | ∼ 10 61 . This huge number means that the topology of spacetime is highly non-trivial due to vacuum fluctuations. The fluctuations lead to forming the foamy structure, a version of Wheeler’s ”spacetime foam" [18].

6. Conclusion

We have shown how complex networks with hidden geometry lead to the emergence of discrete spacetime from entanglement. This phenomenon can be treated as a first-order phase transition from the free fermionic gas to the fermionic condensate formed by maximally entangled states of spacetime’s atoms. This transition and the formation of our universe occurred before the Grand Unification Epoch.
In our approach, spacetime is treated as evolving complex network, and a random/stochastic process governs its evolution. The irreversibility of evolution occurs due to information loss and the existence of the fundamental Planck length. In the pre-inflation epoch, the cosmological scale factor grows as a ( t ) ∝ t , which agrees with changing the cosmological scale factor for a radiation-dominated era.
We point out that the standard formulation of the cosmological constant problem is problematic since the spacetime and the vacuum energy density are highly inhomogeneous and wildly fluctuate at the Planck scales. We show that the "foamy" structure, analogous to Wheeler’s "spacetime foam" [18], significantly contributes to the effective cosmological constant defined by spacetime’s topology. Explicitly the effective cosmological constant, Λ e f f , is given by Λ e f f = − 8 π χ ( M ) ℓ p 3 / V , where χ ( M ) is the Euler characteristic of the simplicial complex M , and V is its volume. Taking V as the volume of the observable universe, we find that χ ∼ 10 61 . This enormous number implies that the topology of spacetime is highly non-trivial due to vacuum fluctuations. These fluctuations lead to forming the foamy structure that may be formed by micro-universes connected by the Einstein-Rosen bridges with wormhole topology.
Our approach opens the avenue to solving "The Worst Theoretical Prediction in the History of Physics”. The proposed solution may be considered a self-tuning solution to the cosmological problem, free from the fine-tuning problem associated with the cosmological constant.

Funding

This research received no external funding.

Acknowledgments

I would like to thank H.Mata Villafuerte for valuable discussions. The present work was supported by the CONACyT (Mexico).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Zel’dovich, Y.B. The cosmological constant and the theory of elementary particles. Soviet Physics Uspekhi 1968, 11, 381. [Google Scholar] [CrossRef]
  2. Zel’dovich, Y.B. The Cosmological Constant and Elementary Particles. JETP Letters 1967, 6, 316. [Google Scholar] [CrossRef]
  3. Weinberg, S. The cosmological constant problem. Rev. Mod. Phys. 1989, 61, 1–23. [Google Scholar] [CrossRef]
  4. Weinberg, S. The Cosmological Constant Problems (Talk given at Dark Matter 2000, February, 2000), 2000. arXiv:astro-ph/astro-ph/0005265.
  5. Carroll, S.M.; Press, W.H.; Turner, E.L. The Cosmological Constant. Annual Review of Astronomy and Astrophysics 1992, 30, 499–542. [Google Scholar] [CrossRef]
  6. Dolgov, A.D. The Problem of Vacuum Energy and Cosmology (A lecture presented at the 4th Colloque Cosmologie, Paris, June, 1997), 1997, [arXiv:astro-ph/astro-ph/9708045].
  7. Carroll, S.M. The Cosmological Constant. Living Reviews in Relativity 2001, 4, 1. [Google Scholar] [CrossRef] [PubMed]
  8. Peebles, P.J.E.; Ratra, B. The cosmological constant and dark energy. Rev. Mod. Phys. 2003, 75, 559–606. [Google Scholar] [CrossRef]
  9. Padmanabhan, T. Cosmological constant – the weight of the vacuum. Physics Reports 2003, 380, 235–320. [Google Scholar] [CrossRef]
  10. Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. International Journal of Modern Physics D 2006, 15, 1753–1935. [Google Scholar] [CrossRef]
  11. Rugh, S.; Zinkernagel, H. The quantum vacuum and the cosmological constant problem. Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics 2002, 33, 663–705. [Google Scholar] [CrossRef]
  12. O’Raifeartaigh, C.; O’Keeffe, M.; Nahm, W.; Mitton, S. One hundred years of the cosmological constant: from “superfluous stunt” to dark energy. The European Physical Journal H 2018, 43, 73–117. [Google Scholar] [CrossRef]
  13. Sahni, V.; Starobinsky, A. The Case for a Positive Cosmological Λ-term. International Journal of Modern Physics D 2000, 09, 373–443. [Google Scholar] [CrossRef]
  14. Pauli, W. Pauli Lectures on Physics, Volume VI: Selected Topics in Field Quantization; Pauli Lectures on Physics delivered in 1950–1951 at the Swiss Federal Institute of Technology, Dover Publications, 2000. [Google Scholar]
  15. Kamenshchik, A.Y.; Starobinsky, A.A.; Tronconi, A.; Vardanyan, T.; Venturi, G. Pauli–Zeldovich cancellation of the vacuum energy divergences, auxiliary fields and supersymmetry. The European Physical Journal C 2018, 78, 200. [Google Scholar] [CrossRef]
  16. Kamenshchik, A.Y.; Tronconi, A.; Vacca, G.P.; Venturi, G. Vacuum energy and spectral function sum rules. Phys. Rev. D 2007, 75, 083514. [Google Scholar] [CrossRef]
  17. Berkov, A.; Narozhny, N.; Okun, L. I Ya Pomeranchuk and Physics at the Turn of the Century; World Scientific, 2004. [Google Scholar] [CrossRef]
  18. DeWitt C.M., W.J.e. Superspace and the Nature of Quantum Geometrodynamics. In Battelle Rencontres: 1967 lectures in mathematics and physics; Benjamin, 1968. [Google Scholar]
  19. Hawking, S. Spacetime foam. Nuclear Physics B 1978, 144, 349–362. [Google Scholar] [CrossRef]
  20. Hawking, S.W. The Cosmological Constant [and Discussion]. Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences 1983, 310, 303–310. [Google Scholar] [CrossRef]
  21. Strominger, A. Vacuum Topology and Incoherence in Quantum Gravity. Phys. Rev. Lett. 1984, 52, 1733–1736. [Google Scholar] [CrossRef]
  22. Carlip, S. Spacetime Foam and the Cosmological Constant. Phys. Rev. Lett. 1997, 79, 4071–4074. [Google Scholar] [CrossRef]
  23. Carlip, S. Spacetime foam: a review. 2023, arXiv:gr-qc/2209.14282]. [Google Scholar] [CrossRef]
  24. Loll, R.; Silva, A. Measuring the Homogeneity (or Otherwise) of the Quantum Universe. 2023, arXiv:hep-th/2302.10256]. [Google Scholar]
  25. Ashtekar, A.; Stachel, J. Conceptual Problems of Quantum Gravity; Einstein Studies 2, Birkhüser, 1991. [Google Scholar]
  26. Gross D. et al, editors The Quantum Structure of Space and Time: Proceedings of the 23rd Solvay Conference on Physics Brussels, Belgium 1-3 December 2005; 3 December.
  27. Murugan, J.; Weltman, A.; Ellis, G.F.R.; editors. Foundations of Space and Time: Reflections on Quantum Gravity; Cambridge University Press, 2012. [Google Scholar]
  28. Butterfield, J.; Isham, C. Spacetime and the Philosophical Challenge of Quantum Gravity. In Physics meets Philosophy at the Planck Scale; Callender, C., Huggett, N., Eds.; Cambridge University Press: Cambridge, 2000. [Google Scholar]
  29. Oriti, D. (Ed.) Approaches to Quantum Gravity: Toward a New Understanding of Space, Time and Matter; Cambridge University Press: New York, 2009. [Google Scholar]
  30. Majid, S.; Polkinghorne, J.; Penrose, R.; Taylor, A.; Connes, A.; Heller, M. On Space and Time; Canto Classics, Cambridge University Press, 2012. [Google Scholar]
  31. Ambjørn, J. Discrete Quantum Gravity, In. In Approaches to Quantum Gravity: Toward a New Understanding of Space, Time and Matter; Oriti, D., Ed.; Cambridge University Press: New York, 2009. [Google Scholar]
  32. Loll, R. Discrete Approaches to Quantum Gravity in Four Dimensions. Living Reviews in Relativity 1998, 1, 13. [Google Scholar] [CrossRef]
  33. ’t Hooft, G. Quantum mechanics, statistics, standard model and gravity. General Relativity and Gravitation 2022, 54, 56. [Google Scholar] [CrossRef]
  34. Van Raamsdonk, M. Building up spacetime with quantum entanglement. General Relativity and Gravitation 2010, 42, 2323–2329. [Google Scholar] [CrossRef]
  35. Swingle, B. Spacetime from Entanglement. Annual Review of Condensed Matter Physics 2018, 9, 345–358. [Google Scholar] [CrossRef]
  36. Padmanabhan, T. Atoms of Spacetime and the Nature of Gravity. Journal of Physics: Conference Series 2016, 701, 012018. [Google Scholar] [CrossRef]
  37. Dowker, F. The birth of spacetime atoms as the passage of time. Annals of the New York Academy of Sciences 2014, 1326, 18–25. [Google Scholar] [CrossRef]
  38. Padmanabhan, T. Distribution Function of the Atoms of Spacetime and the Nature of Gravity. Entropy 2015, 17, 7420–7452. [Google Scholar] [CrossRef]
  39. Sabinin, L.V. Smooth quasigroups and loops; Kluwer Academic Publishers: Dordrecht, 1999. [Google Scholar]
  40. Nesterov, A.I.; Sabinin, L.V. Non-associative geometry and discrete structure of spacetime. Comment. Math. Univ. Carolin. 2000, 41,2, 347–358. [Google Scholar]
  41. Nesterov, A.I.; Sabinin, L.V. Nonassociative geometry: Towards discrete structure of spacetime. Phys. Rev. D 2000, 62, 081501. [Google Scholar] [CrossRef]
  42. Sabinin, L. Nonassociative Geometry and Discrete Space-Time. International Journal of Theoretical Physics 2001, 40, 351–358. [Google Scholar] [CrossRef]
  43. Nesterov, A.I.; Sabinin, L.V. Nonassociative Geometry: Friedmann-Robertson-Walker Spacetime. IJGMMP 2006, 3, 1481–1491. [Google Scholar] [CrossRef]
  44. Nesterov, A. Gravity within the Framework of Nonassociative Geometry. In Non-Associative Algebra and Its Applications; Lev Sabinin, Larissa Sbitneva, I.S., Ed.; Chapman and Hall/CRC, 2006; pp. 299–311. [Google Scholar]
  45. Nesterov, A.I.; Mata Villafuerte, P.H. Spacetime as a Complex Network with Hidden Geometry (unpublished).
  46. Nesterov, A.I.; Mata, H. How Nonassociative Geometry Describes a Discrete Spacetime. Frontiers in Physics 2019, 7, 32. [Google Scholar] [CrossRef]
  47. Dowker, F. Causal Sets and Discrete Spacetime. AIP Conference Proceedings 2006, 861, 79–88. [Google Scholar] [CrossRef]
  48. Bombelli, L.; Lee, J.; Meyer, D.; Sorkin, R.D. Space-time as a causal set. Phys. Rev. Lett. 1987, 59, 521–524. [Google Scholar] [CrossRef] [PubMed]
  49. Dowker, F.; Zalel, S. Evolution of universes in causal set cosmology. Comptes Rendus Physique 2017, 18, 246–253. Testing different approaches to quantum gravity with cosmology / Tester les théories de la gravitation quantique à l’aide de la cosmologie. [Google Scholar] [CrossRef]
  50. Ambjørn, J.; Carfora, M.; Marzuoli, A. The Geometry of Dynamical Triangulations; Springer Berlin Heidelberg, Berlin, 1997. [Google Scholar]
  51. Ambjørn, J.; Loll, R. Non-perturbative Lorentzian quantum gravity, causality and topology change. Nuclear Physics B 1998, 536, 407–434. [Google Scholar] [CrossRef]
  52. Loll, R. The emergence of spacetime or quantum gravity on your desktop. Classical and Quantum Gravity 2008, 25, 114006. [Google Scholar] [CrossRef]
  53. Ambjørn, J.; Jurkiewicz, J.; Loll, R. Reconstructing the Universe. Phys. Rev. D 2005, 72, 064014. [Google Scholar] [CrossRef]
  54. Ambjørn, J.; Jordan, S.; Jurkiewicz, J.; Loll, R. Quantum spacetime, from a practitioner’s point of view. AIP Conference Proceedings 2013, 1514, 60–66. [Google Scholar] [CrossRef]
  55. Glaser, L.; Loll, R. CDT and cosmology. Comptes Rendus Physique 2017, 18, 265–274. Testing different approaches to quantum gravity with cosmology / Tester les théories de la gravitation quantique à l’aide de la cosmologie. [Google Scholar] [CrossRef]
  56. Ambjørn, J.; Görlich, A.; Jurkiewicz, J.; Loll, R. Nonperturbative quantum gravity. Physics Reports 2012, 519, 127–210. [Google Scholar] [CrossRef]
  57. Park, J.; Newman, M.E.J. Statistical mechanics of networks. Phys. Rev. E 2004, 70, 066117. [Google Scholar] [CrossRef] [PubMed]
  58. Squartini, T.; Garlaschelli, D. Maximum-Entropy Networks: Pattern Detection, Network Reconstruction and Graph Combinatorics; Springer International Publishing: Cham, 2017. [Google Scholar]
  59. van der Hoorn, P.; Lippner, G.; Krioukov, D. Sparse Maximum-Entropy Random Graphs with a Given Power-Law Degree Distribution. Journal of Statistical Physics 2018, 173, 806–844. [Google Scholar] [CrossRef]
  60. Garlaschelli, D.; Loffredo, M.I. Maximum likelihood: Extracting unbiased information from complex networks. Phys. Rev. E 2008, 78, 015101. [Google Scholar] [CrossRef] [PubMed]
  61. Garlaschelli, D.; Ahnert, S.E.; Fink, T.M.A.; Caldarelli, G. Low-Temperature Behaviour of Social and Economic Networks. Entropy 2013, 15, 3148–3169. [Google Scholar] [CrossRef]
  62. Cimini, G.; Squartini, T.; Saracco, F.; Garlaschelli, D.; Gabrielli, A.; Caldarelli, G. The statistical physics of real-world networks. Nature Reviews Physics 2019, 1, 58–71. [Google Scholar] [CrossRef]
  63. Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
  64. Newman, M.E.J.; Strogatz, S.H.; Watts, D.J. Random graphs with arbitrary degree distributions and their applications. Phys. Rev. E 2001, 64, 026118. [Google Scholar] [CrossRef]
  65. Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D.U. Complex networks: Structure and dynamics. Physics Reports 2006, 424, 175–308. [Google Scholar] [CrossRef]
  66. Albert, R.; Barabási, A.L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47–97. [Google Scholar] [CrossRef]
  67. Nesterov, A.I.; Mata Villafuerte, P.H. Complex networks in the framework of nonassociative geometry. Phys. Rev. E 2020, 101, 032302. [Google Scholar] [CrossRef]
  68. Regge, T. General relativity without coordinates. Il Nuovo Cimento (1955-1965) 1961, 19, 558–571. [Google Scholar] [CrossRef]
  69. Williams, R.M.; Tuckey, P.A. Regge calculus: a brief review and bibliography. Classical and Quantum Gravity 1992, 9, 1409–1422. [Google Scholar] [CrossRef]
  70. Regge, T.; Williams, R.M. Discrete structures in gravity. Journal of Mathematical Physics 2000, 41, 3964–3984. [Google Scholar] [CrossRef]
  71. Wang, Q. Reformulation of the Cosmological Constant Problem. Phys. Rev. Lett. 2020, 125, 051301. [Google Scholar] [CrossRef] [PubMed]
  72. Ossola, G.; Sirlin, A. Considerations concerning the contributionsof fundamental particles to the vacuum energy density. The European Physical Journal C - Particles and Fields 2003, 31, 165–175. [Google Scholar] [CrossRef]
  73. Akhmedov, E.K. Vacuum energy and relativistic invariance. 2002, arXiv:hep-th/hep-th/0204048. [Google Scholar]
  74. Volovik, G.E. On Contributions of Fundamental Particles to the Vacuum Energy. In I Ya Pomeranchuk and Physics at the Turn of the Century; World Scientific, 2004; pp. 234–244. [Google Scholar] [CrossRef]
  75. Wang, Q.; Zhu, Z.; Unruh, W.G. How the huge energy of quantum vacuum gravitates to drive the slow accelerating expansion of the Universe. Phys. Rev. D 2017, 95, 103504. [Google Scholar] [CrossRef]
  76. Carlip, S. Hiding the Cosmological Constant. Phys. Rev. Lett. 2019, 123, 131302. [Google Scholar] [CrossRef]
  77. Klaus, S. On combinatorial Gauss-Bonnet Theorem for general Euclidean simplicial complexes. Frontiers of Mathematics in China 2016, 11, 1345. [Google Scholar] [CrossRef]
Preprints 73233 g001
Figure 1. A network presented as a simplicial 3-complex.
Figure 1. A network presented as a simplicial 3-complex.
Preprints 73233 g001
Preprints 73233 g002
Figure 2. Homogeneous discrete space with positive curvature. Left: a simplicial 0-complex (a non-triangulated, completely disconnected space). Middle: a simplicial 2-complex (a partially triangulated space). Right: a homogeneous simplicial 2-complex (a triangulated space).
Figure 2. Homogeneous discrete space with positive curvature. Left: a simplicial 0-complex (a non-triangulated, completely disconnected space). Middle: a simplicial 2-complex (a partially triangulated space). Right: a homogeneous simplicial 2-complex (a triangulated space).
Preprints 73233 g002
Preprints 73233 g003
Figure 3. Connection probability as a function of dimensionless temperature, τ = T / T p (left) and inverse dimensionless temperature (right).
Figure 3. Connection probability as a function of dimensionless temperature, τ = T / T p (left) and inverse dimensionless temperature (right).
Preprints 73233 g003
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated