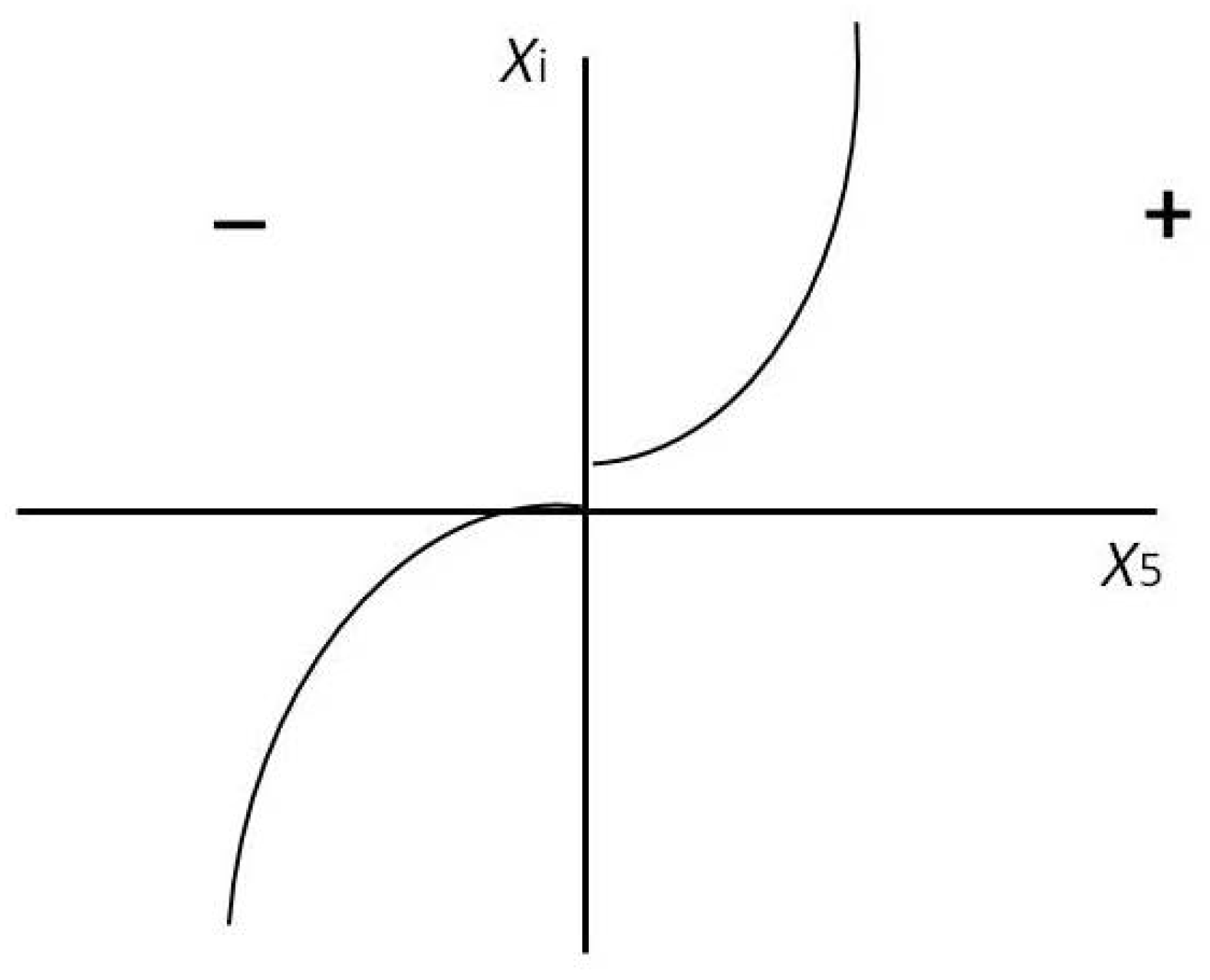Apart from the successful unification of the electric and the magnetic forces themselves, the-two fundamental interactions out of the remaining four attracting the most and most prolonged attention for unification attempts, are the gravitational and the electromagnetic ones. Pre-relativity phenomenology presented very little scope for such "attempts”, and only the description of gravitation by the Theory of General Relativity seemed to offer a promising basis: the geometric replacement of natural forces by manifold curvature. Thus, already rather soon after the introduction of General Relativity, first unification possibilities were explored. Einstein himself spent the main part of his later working life, searching for a real unification between gravitation and electromagnetism.
There is no need to go into detail with regard to the individual contributions to the unification at tempts between gravitation and electromagnetism (our main concern in this section). A variety of excellent reviews exists, being the result of or again a source for others [l,2]. One can distinguish basically two lines of approach: the affine connection method in four dimensions (space-time manifold) and the five dimensional manifold with its additional dimension being the ratio q/m (charge/mass).
The majority of present day theoreticians consider all past attempts as having been unsuccessful. This is certainly true for those yielding e.g., charged particle trajectories from the geodesic equations, which have no resemblance to reality (e.g., Einstein's affine connection theory). But other, more successful approaches are equally rejected on the grounds that either their unification emanates into already known physical structures and therefore renders itself meaningless (Weyl; his unified theory resulted in the established Maxwellian equations and therefore presented nothing excitingly new), or that the achieved unification was not a true one. Most of the five-dimensional theories are dismissed for the latter reason. It is argued, that a 5th dimension is physically unobservable. Another criterion is the non-total elimination of a characteristic electromag netic part of the stress energy tensor, which is practically true for any of the past attempts. However, the rejection arguments are nowadays open to debate again. Some authors [
3] argue that a true unification has already been achieved by the incorporation of electromagnetic terms into the stress energy tensor in Einstein's field equation; on the other hand the (4 +
n) -dimensionality concept sees a revival in gauge theoretical unification attempts of the "electroweak" with the strong force.
Initially, only classical phenomena are considered. The criteria to be met for a "true" unification are defined. By taking these criteria and an elevated "principle of equivalence" as theoretical basis and a V5-manifold with x5 = q/m as tool, one is lead to a qualitative, heuristic outline of the whole unification concept. After its presentation the formulated results are laid down in a separate paragraph with an interpretation of the new resulting field equation.
Heuristic Concept
The criteria for a true unification between gravitation and electromagnetism are the following:
(a) Both interactions have to be described by the same field equation, relating all field effects to the same source terms. If the unification is placed on a geometric basis, one and the same geometric structure must serve as a medium for the description of all these field effects.
(b) On a geometric basis all forces have to be replaced by a coupling of a single type main source term to geometry. No special remaining terms relating to one or the other non-unified descriptions are permitted.
(c) All dimensions of an n-dimensional manifold, presenting the geometrical framework, must be in some way physically observable. There are two principal lines of approach conceivable: a phenomenological one, based on geometry, and a more axiomatic one. Both lead to the same consequences. Let us first consider the phenomenological one.
The concept of force itself seems to be at the root of the present day split into four different types of interaction. Therefore to abandon it and place the description of physical effects on directly observable quantities, i.e. dimensions and energy, is a pre-condition for unification. This is exactly, what General Relativity does: the gravitational force is replaced by the coupling of curvature of a space-time manifold to an energy source term. It is therefore likely that only geometrical attempts for unification will be successful. As a consequence, the electromagnetic "force" as well has to be replaced by a cou pling of a manifold curvature to an energy source term. Both the manifold, in which the action takes place, and the source have to be common to gravi tational and electromagnetic events. This excludes immediately the V4-geometry of General Relativity as a unification basis and indicates for that at least a five-dimensional manifold. The common source has to be energy (related), bare of any specific terms with reference to one or the other interaction type.
The more axiomatic approach is outlined as follows: Let us postulate an "elevated principle of equivalence": "If an observer in a (special) inertial frame (i.e. a Faraday cage) is travelling in an 'accelerating' field, he can neither distinguish, whether he is moving in a gravitational or an electromagnetic or any other field, nor whether he is subjected to an apparent field (of any kind) due to acceleration of a reference frame."
This principle is a sufficient basis, to arrive with at the same conclusions, as the phenomenological approach did.
The following model in a V5-manifold offers itself: We have three space-like, one time-like dimension and x5 with (q/m) as affine parameter. Test-bodies and energy sources (masses, etc.) reside along x5 according to their (q/m)-value in four-dimensional slices V4 (x5 = const). Each V4 has its own space-time geometry. Let us for simplicity assume that a test-body or a source does never change position with respect to x5 (in V4(x5 0) only "neutral" test bodies move). For one and the same source term at a specific x5 the strength of the curvatures of the various V4's is normally different. Thus the V4's may appear "blown-up" or "contracted" with reference to each other and probed by the trajectories of test-particles, due to the gross curvature of the whole V5. Equally the gross curvature of the V5 changes, and thus the relative blow-up or contraction of the V4's to each other, when the source is positioned at a different x5. There is no real difference between a test-body and a source; their roles can be played by one and the same entity, and in mutual interactions of several test-bodies they are both at the same time. Thus we can postulate:
The curvature of the entire V5 geometry is dependent on the stress energy of a source and the position of the source along x5.
This is not quite all. As will be seen in the quanti tative results, curvature may also be coupled to the velocity of certain types of sources.
Table 1 gives possible combinations test-body/source.
For the Illustration of the above, let us pick the most general example, where both test-body and source are "charged". The source A resides at x5 = a. Thus the entire V5 is curved initially with respect to the strength and the position value a. If A would reside at x5 = b a the gross curvature of the V5 would be different. A test-body C moves in a V4(x5 = c). In general c a. The trajectory of C is dependent on the curvature of V4 (c). A test-body D at x5= dc (=a) would move in a different curved V4 and thus project a different trajectory.
In traditional language the above means: the trajectory of a test-body with mass mt1 and charge qt1 under the influence of a source with mass ms1 and charge qs1 changes, when the source is replaced by one with and ; or: the tra jectory of a test-body with mt1 and qt1 under the influence of a source with ms1 and qs1 is different from that of a test-body with and under the influence of the same source.
How does the general structure of a
V5 look like?
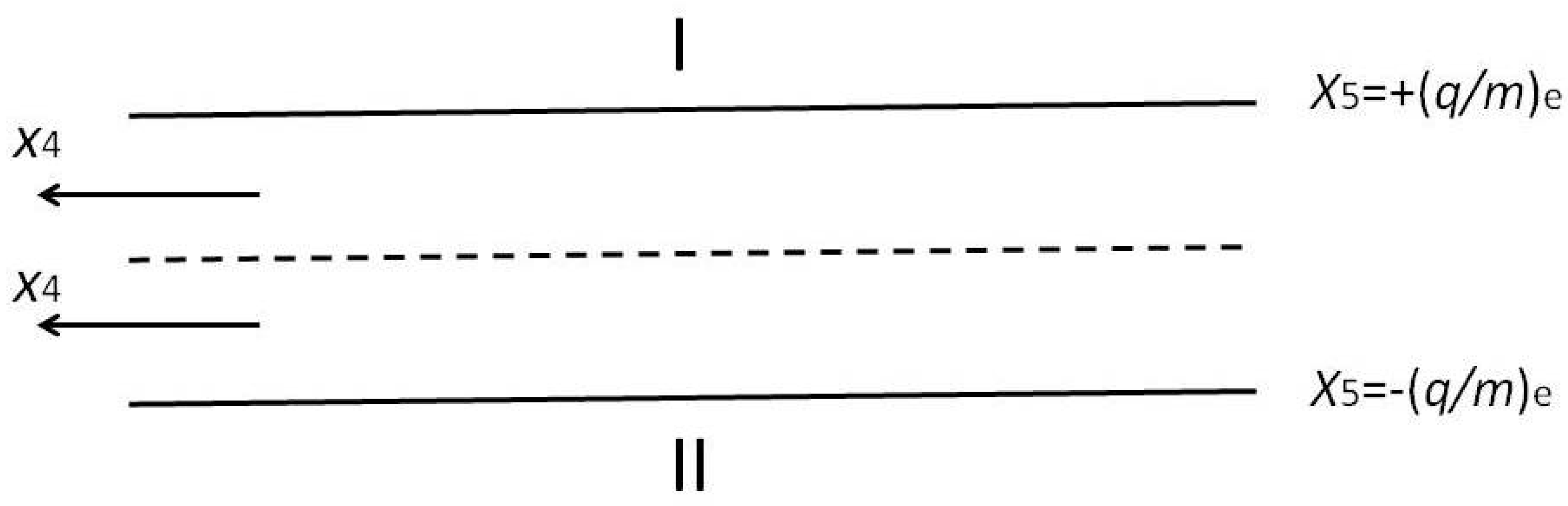
Figure 1 illustrates that a five-dimensional universe is a flat sheet, or rather an assembly of an infinite number of
V4 sheets piled onto each other. It is not infinite in the
x5-direction, since the maximum observed and for the time being theoretically possible value for
x5 is (
e/me)
, the ratio of the electron's charge over its mass. Therefore the regions I and II in Figure l are physically meaningless.
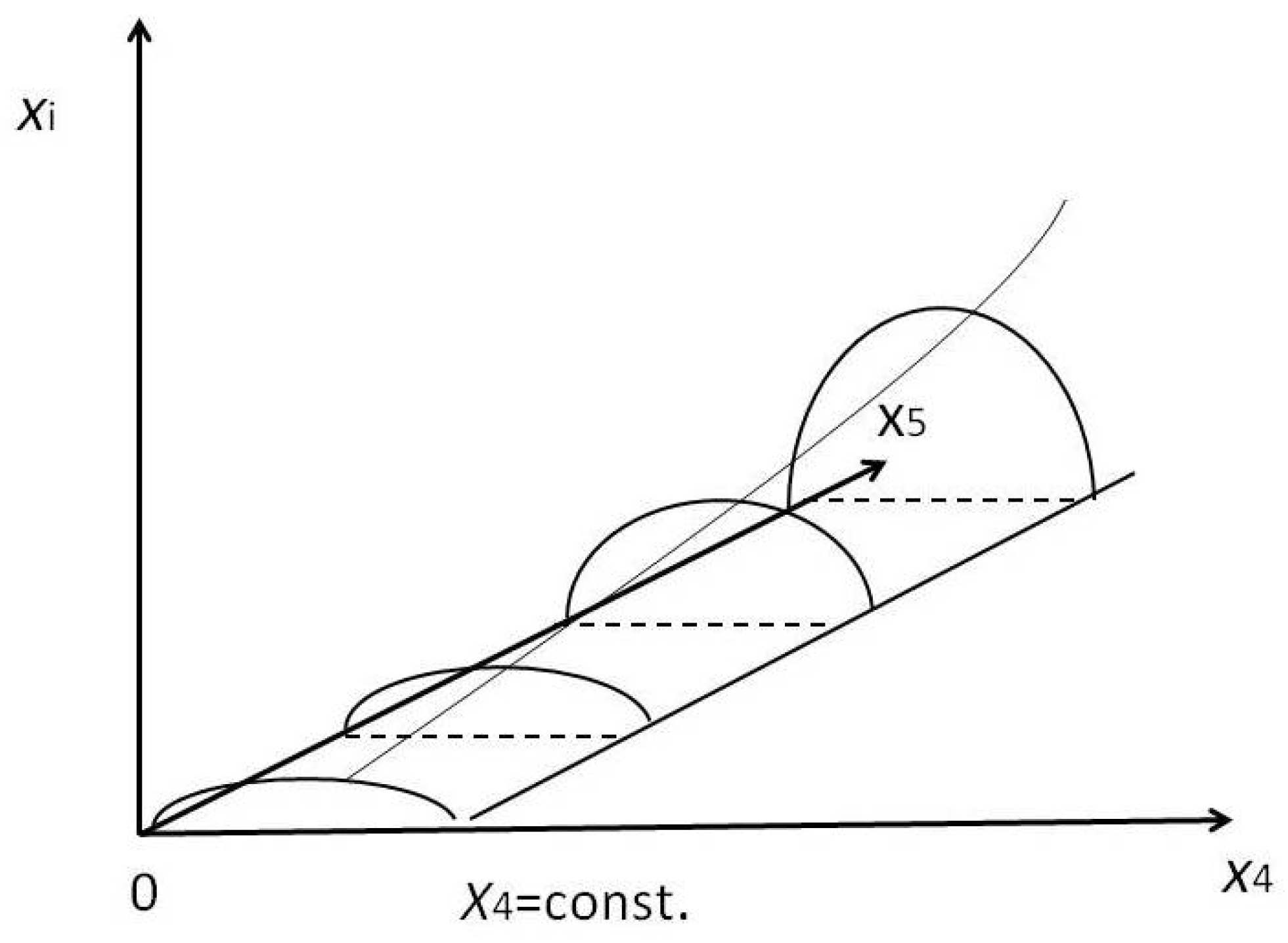
Figure 2 shows space-time curves (particle tra jectories e.g.) for constant time. The
V5, subjected to the influence of a source, somewhere situated along
x5, accommodates test-particles moving in various
V4 planes. The gross curvature of the
V5 determines the "blowing-up" of trajectories in the
V4's along
x5. Thus, each geometry is coupled to one and the same source exactly as in General Relativity, only the coupling constants and the weight of the
x5-position change along
x5.
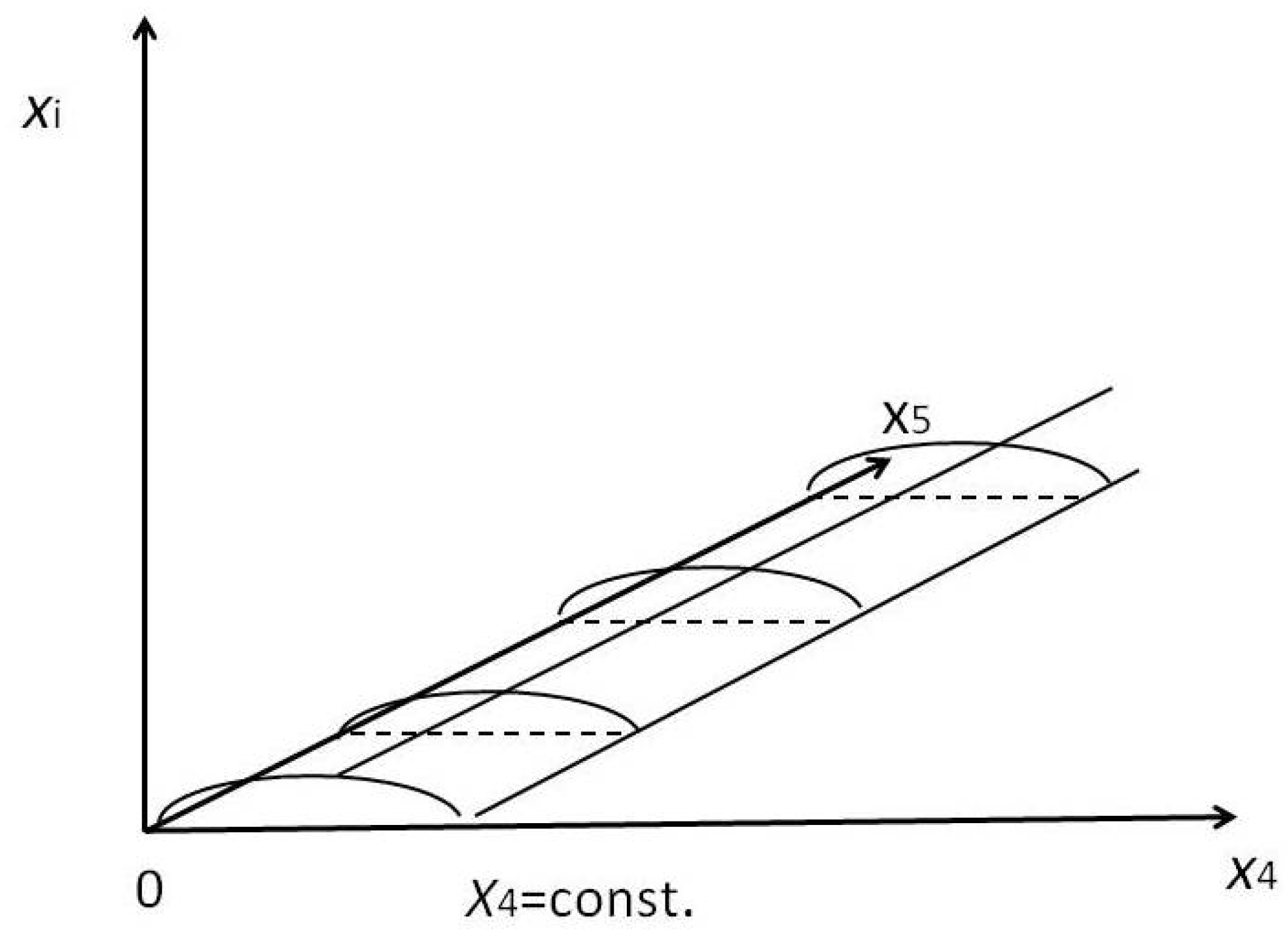
Figure 3 depicts the case
qs = 0. If a source is situated at
x5 = 0 the
V5 is flat and all
V4's are curv ed in parallel (only "gravitation"). If a test-body is placed at
x5 = 0 it will always move on a geodesic, entirely determined by the strength of the source alone, independent of the position of the source and almost negligible with respect to the adjacent ones along
x5 as "rest-curvature".
As was already obvious from Fig. l, the
V5-univers is divided into two sectors, a positive and a negative (with respect to
x5 assignment). If a source curves the positive sector a certain way, this curvature will be repeated inversely in the negative sector (repulsion and attraction) (s.
Figure 4).
What has been achieved so far? The model eliminates the concept of charge, by postulating that test-bodies and sources posses only mass or energy, positioned along a fifth dimension at various locations (charge eliminated by geometric concept). The electromagnetic force has been eliminated by coupling of the curvature of a five-dimensional manifold to "neutral" strength and position of such a source (always "neutral", only stress energy).
The unification criteria will be revisited after the quantitative presentation in the following.
Quantitative Results
The mathematically tedious construction of the new unified field equation shall not be outlined in detail here. Three main points have been observed:
(i) the quantitative presentation of the theory has to follow rigorously the heuristic expectations;
(ii) it has to result in Einstein's field equation for the case x5 = 0;
(iii) the "electromagnetic" part of the stress energy tensor had to be reduced to its "mechanical" parts only, by extracting the charge and incorporating it into x5 .
Thus the new unified field equation can be ex-pressed in the following way (without explicit indices):
T is the purely mechanical stress energy,
u the 4-velocity of a test body,
an interval of proper time,
with the various terms in
κ2 and
κ3 resulting from the old electromagnetic stress energy part.
G is the curvature tensor of the
V5 manifold. It can be constructed by the usual well known relations from General Relativity, i.e. the Riemannian tensor for
V5, the corresponding connection coefficients and the metric
with
x=xi and i = 1,2,3,4,5
x4 time-like, x5 "charge"-like (q/m),
15 metric coefficients gμν ..
For the construction of
G and the derivation of the geodesic equation one can either start from the global
V5 and end up at the various or particular
V4's or from the
V4'
s and build up the global
V5 geometry. Both approaches, which are complementary, may make use of a method, developed by Arnowitt, Deser and Misner [
5], briefly ADM-method, which connects a
Vn to a
Vn-1. For the Riemann tensor this looks like (with explicit indices):
K is called the extrinsic curvature operator,
n a normal vector, d
n would be the vectorial difference, generated by
K, after transporting
n parallel within a hyper-surface. Thus
K relates the intrinsic curvature in a
Vn-1 to the global extrinsic curvature of the
Vn itself;
e
μ being a basis.
We can interpret the unified field equation as follows: The curvature of a V5-manifold under the action of a unified gravitational/electromagnetic field depends on a mechanical stress energy tensor T, i.e. on its absolute value, its momentum with respect to x5 and the change of this momentum with proper time.
This is a somewhat unexpected result and differs entirely in shape from the purely gravitational Ein stein equation. However, some assumptions and simplifications have been introduced along the lines of the development of the equation and these are briefly recalled here.
T was assumed to be fixed along x5, therefore has to be applied to T, rendering the source part dependent on a stress energy flux, corresponding when multiplied by x5 to the classical magnetic forces arising from the movement of charges in traditional descriptions. If T is assumed to be changing along x5, one would always have to con-sider . This is e. g. important in ionization processes and mass conversion. In the first case the affine parameter in a geodesic equation is most likely x4, resulting in a trajectory of a test-body as a geodesic in a V4. In the second case x5 could be affine parameter as well, resulting in the trajectory of a test-body changing its charge or mass during the interval under consideration.
The other assumption was that κ2 and κ5 were to be considered uniform in any of the directions. This may be true for most cases; in general, however, they should be presented as indexed tensors, their components differing according to possible anisotropies within a specific coordinate frame.