Submitted:
09 May 2023
Posted:
10 May 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Materials and Methods
2.1. Force field
2.2. Simulation model and procedure
| Temperature/℃ | Ca2+ | NH4+ | Cl- | H2O | CO32- |
|---|---|---|---|---|---|
| 20 | 200 | 400 | 400 | 224 | 144 |
| 50 | 200 | 400 | 400 | 224 | 144 |
| 80 | 200 | 400 | 400 | 224 | 144 |
| 80 | 200 | 400 | 400 | 224 | 108 |
| 80 | 200 | 400 | 400 | 224 | 180 |
| Parameter | Force field | Summation method | Truncation radius | Number of iteration steps | Quality | Optimization method |
|---|---|---|---|---|---|---|
| Settings | Compass | Ewald | 12.5 Å | 1000 | Medium | Smart |
| Parameter | Force field | Ensemble | Temperature control method | Pressure control method | Step length | Analog time |
|---|---|---|---|---|---|---|
| Settings | Compass | NPT | Nose | Anderson | 1 fs | 1500 ps |
2.3. Properties analysis
3. Results and discussion
3.1. Effects of temperature
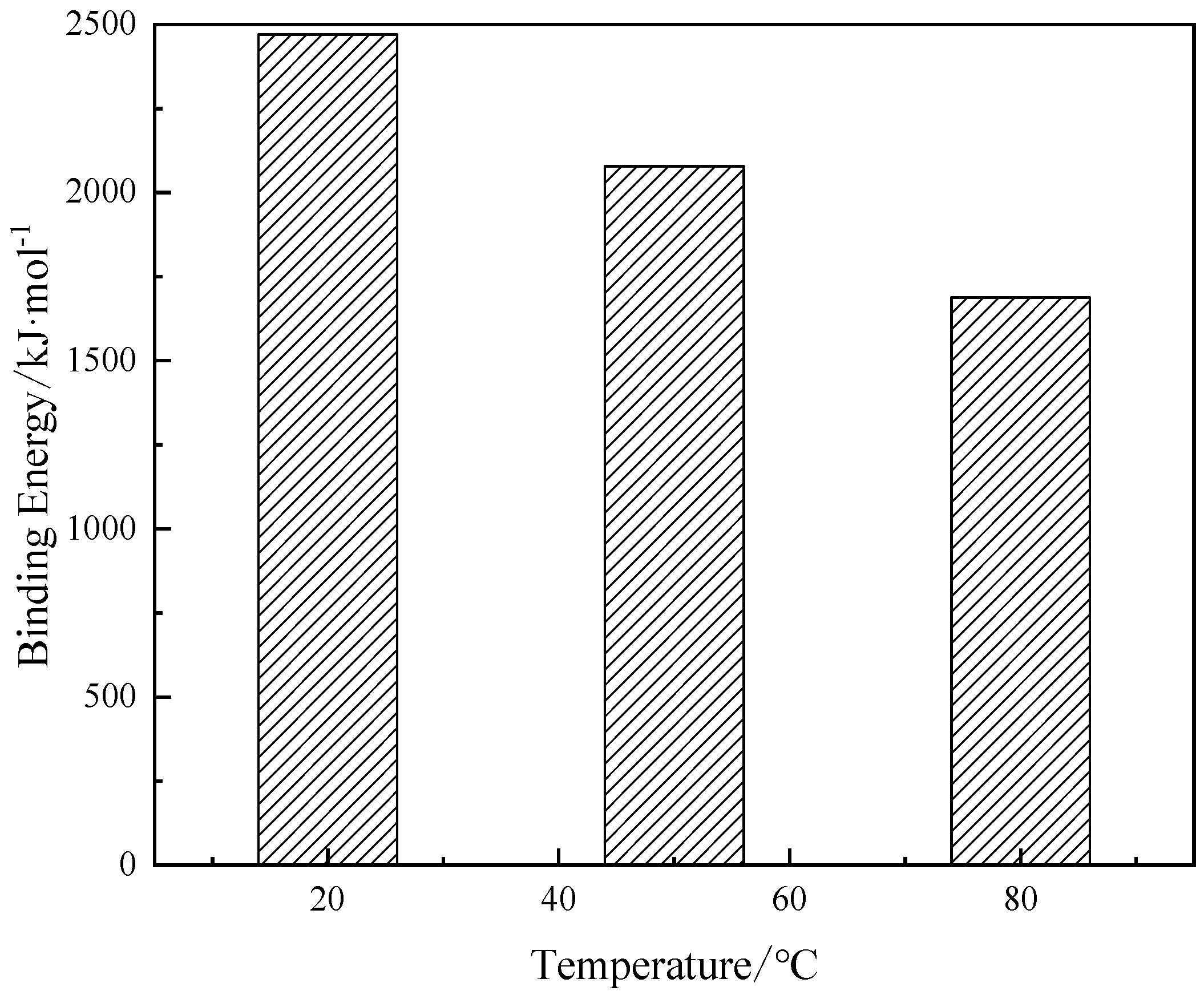
3.1.1. Binding energy
| Energy/kJ·mol-1 | 20 ℃ | 50 ℃ | 80 ℃ |
|---|---|---|---|
| -200885.32 | -199381.04 | -198523.37 | |
| -138188.01 | -137316.67 | -136352.72 | |
| -68686.58 | -67889.69 | -67311.95 | |
| -133390.83 | -132855.18 | -132724.31 | |
| -67266.41 | -66959.19 | -66086.94 | |
| -1349.42 | -1098.47 | -925.10 | |
| -197971.02 | -197657.37 | -196624.71 | |
| 2469.38 | 2078.09 | 1688.48 |
3.1.2. Microstructure of particles
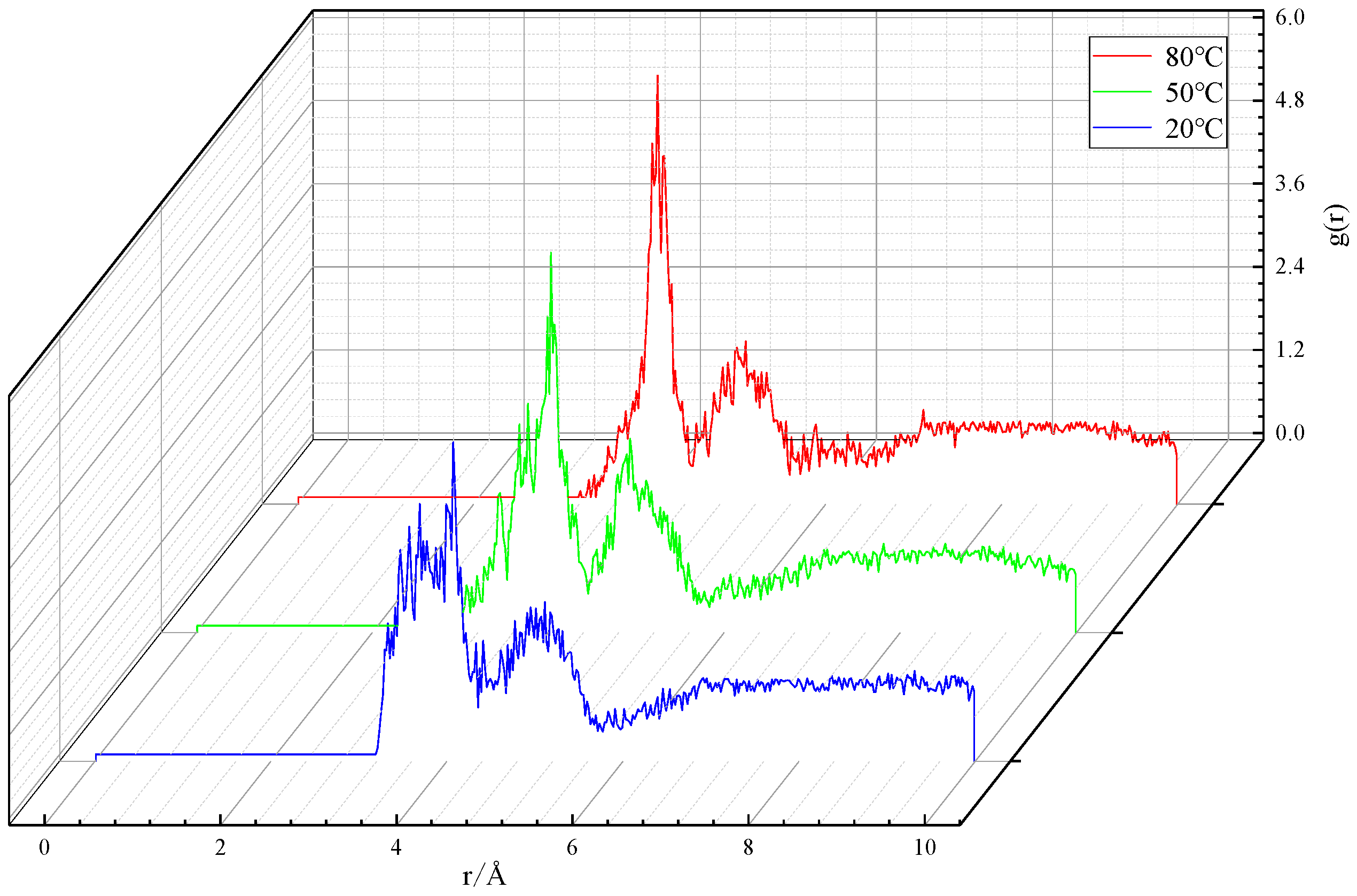
| Temperature/℃ | Peak position/Å | Peak value/ — |
|---|---|---|
| 20 | 4.07 | 4.51 |
| 50 | 4.03 | 5.39 |
| 80 | 4.09 | 6.11 |
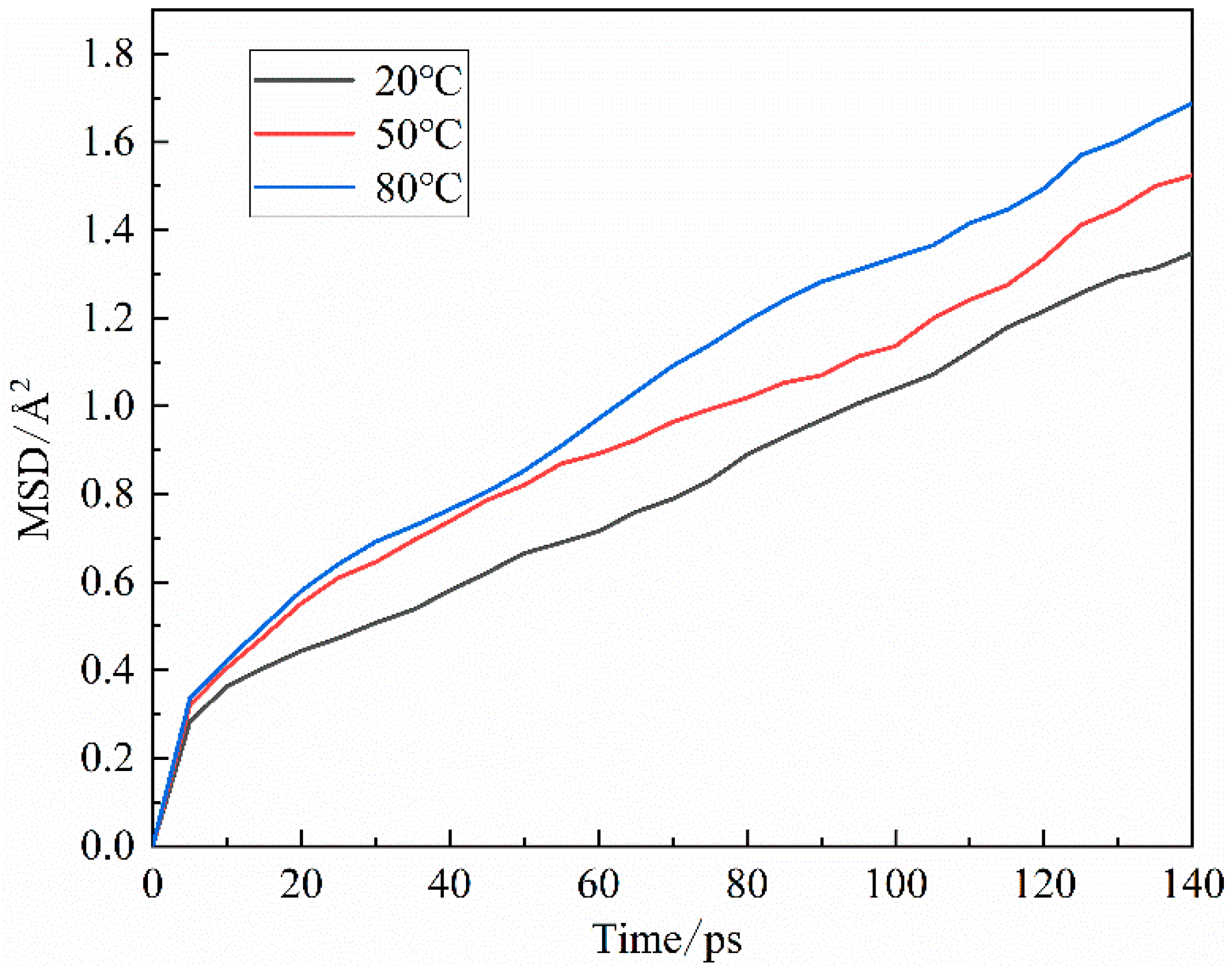
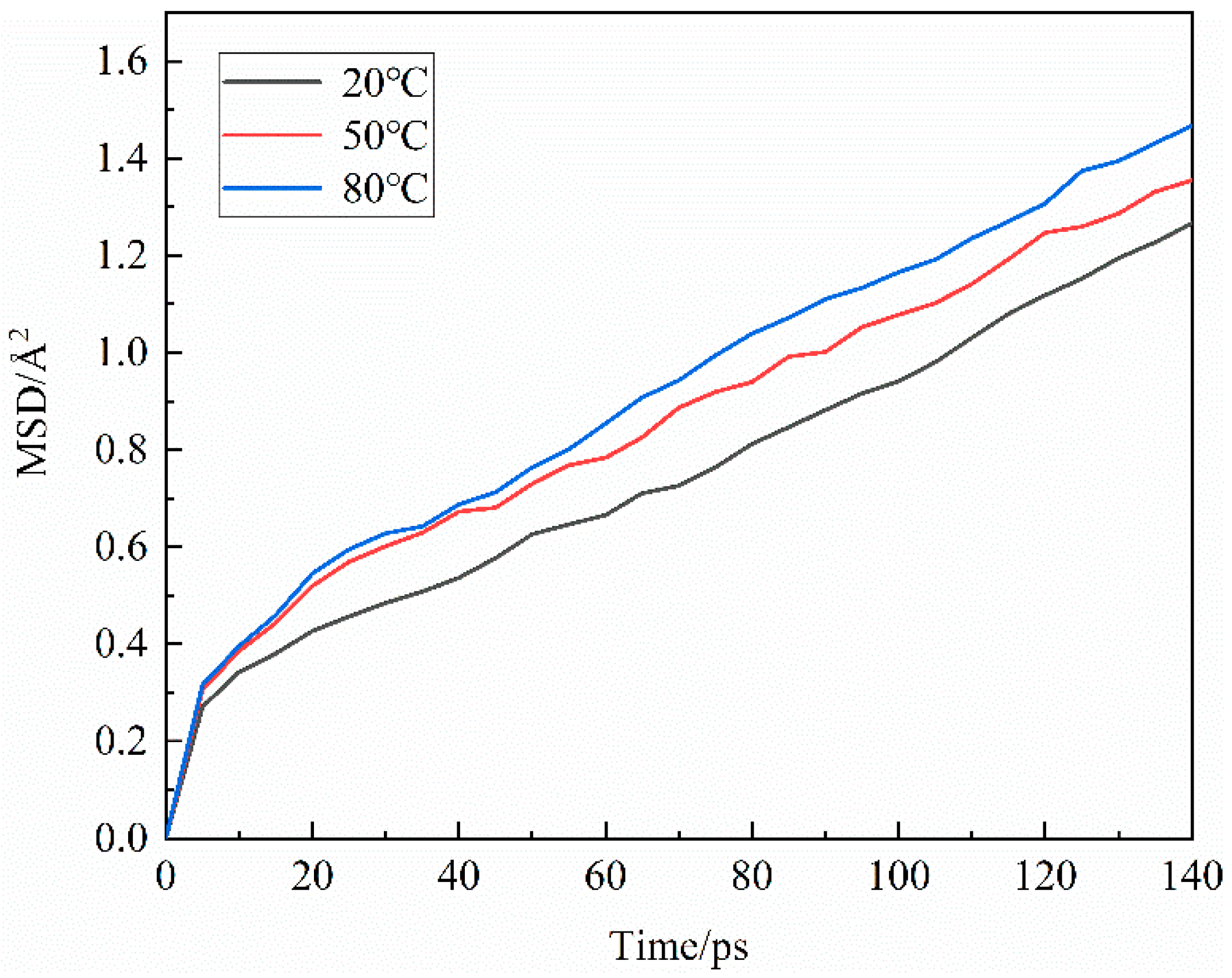
3.1.3. Agglomeration behavior

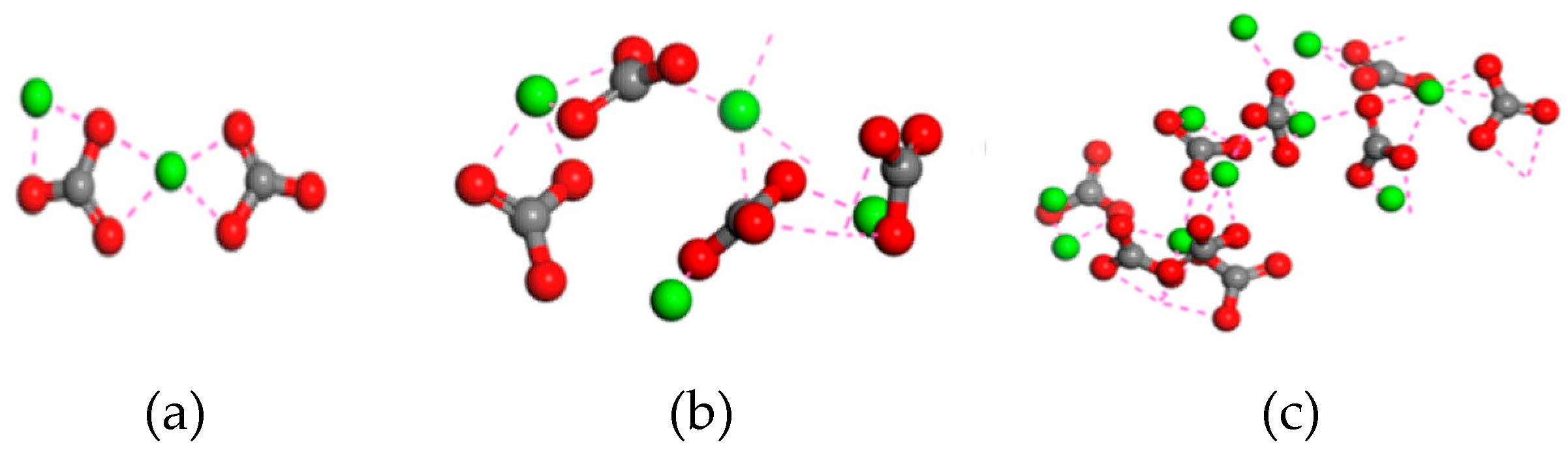
3.2. Effects of concentrations of CO32-
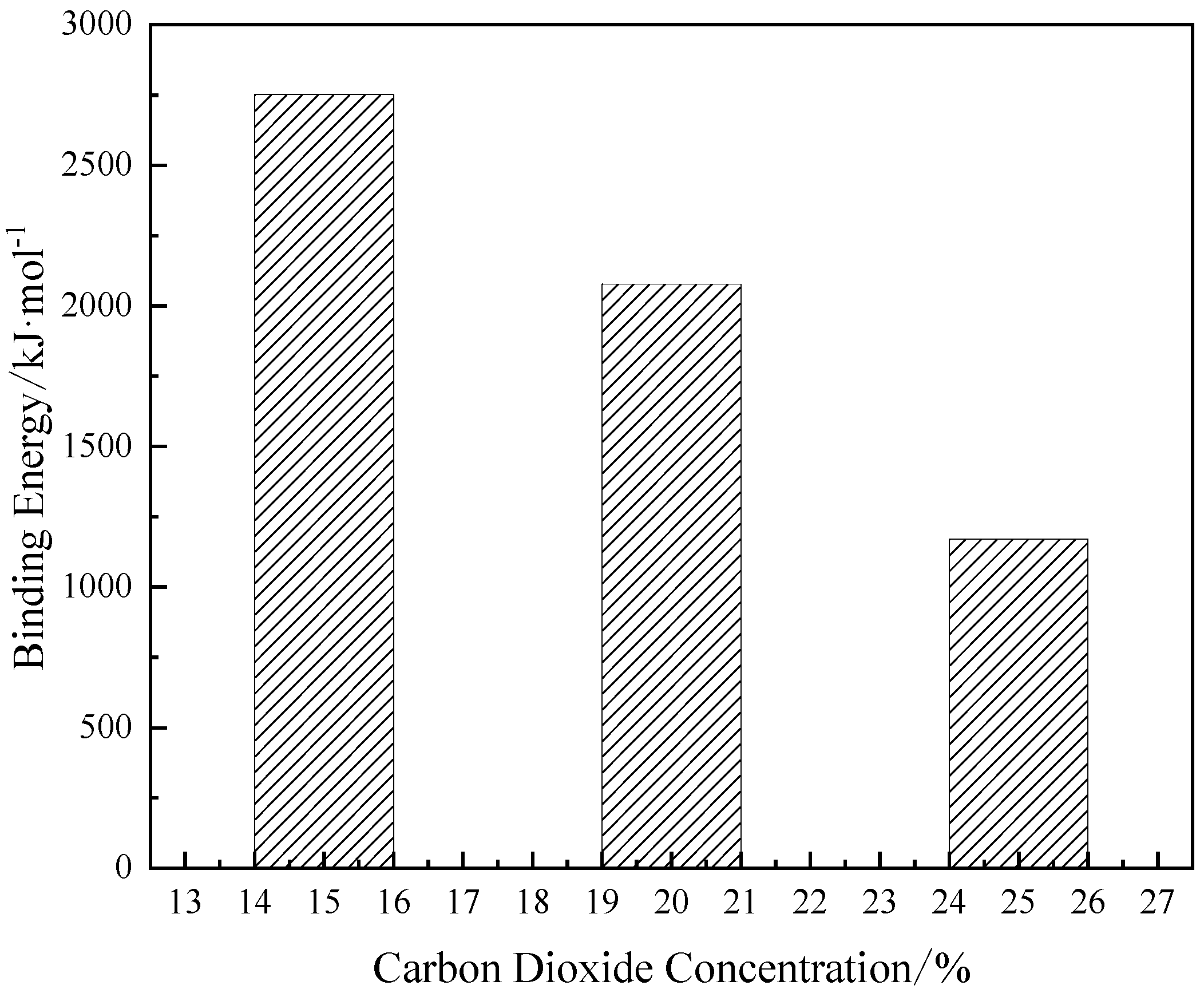
3.2.1. Binding energy
| Energy/kJ·mol-1 | 15 vol.% | 20 vol.% | 25 vol.% |
|---|---|---|---|
| -189592.61 | -199381.04 | -213739.43 | |
| -123302.42 | -137316.67 | -150464.40 | |
| -68686.58 | -67889.69 | -66684.57 | |
| -120190.84 | -132855.18 | -146846.78 | |
| -67266.41 | -66959.19 | -69376.41 | |
| -1349.42 | -1098.47 | -959.42 | |
| -184432.24 | -197657.37 | -212247.99 | |
| 2751.18 | 2078.09 | 1169.74 |
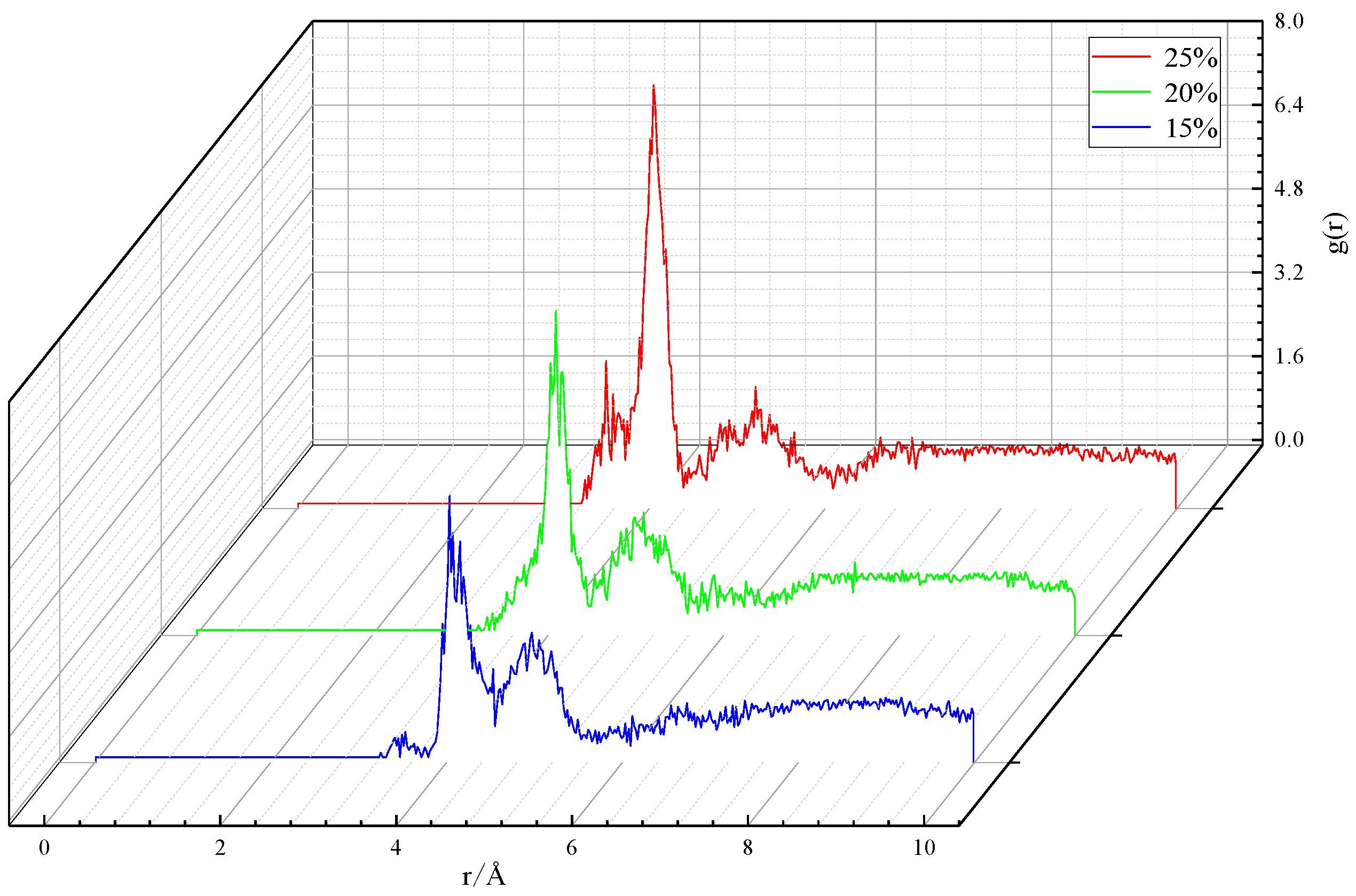
3.2.2. Microstructure of particles
| CO32- concentration/vol.% | Peak position/Å | Peak value/— |
|---|---|---|
| 15 | 4.03 | 5.01 |
| 20 | 4.09 | 6.11 |
| 25 | 4.05 | 8.00 |
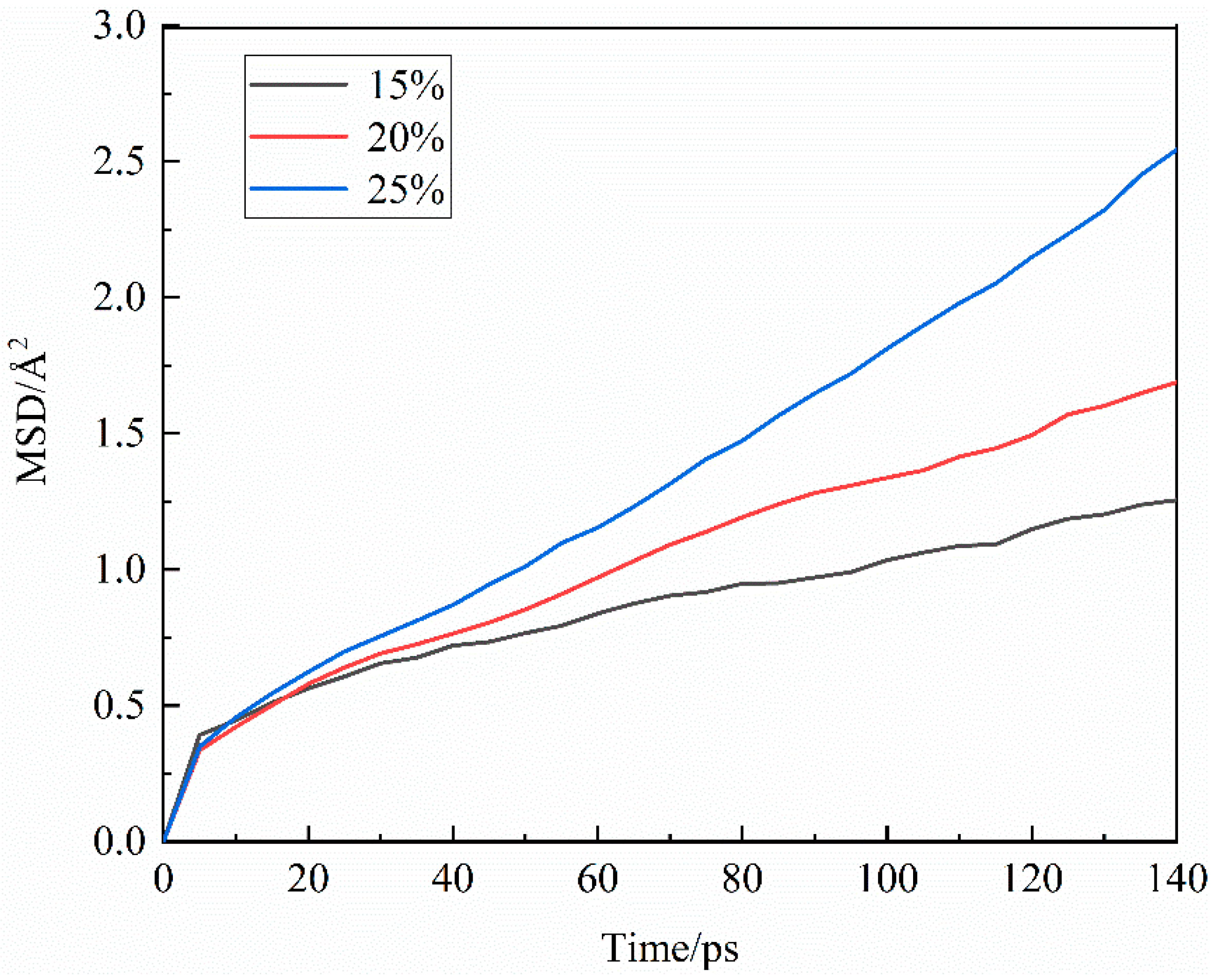
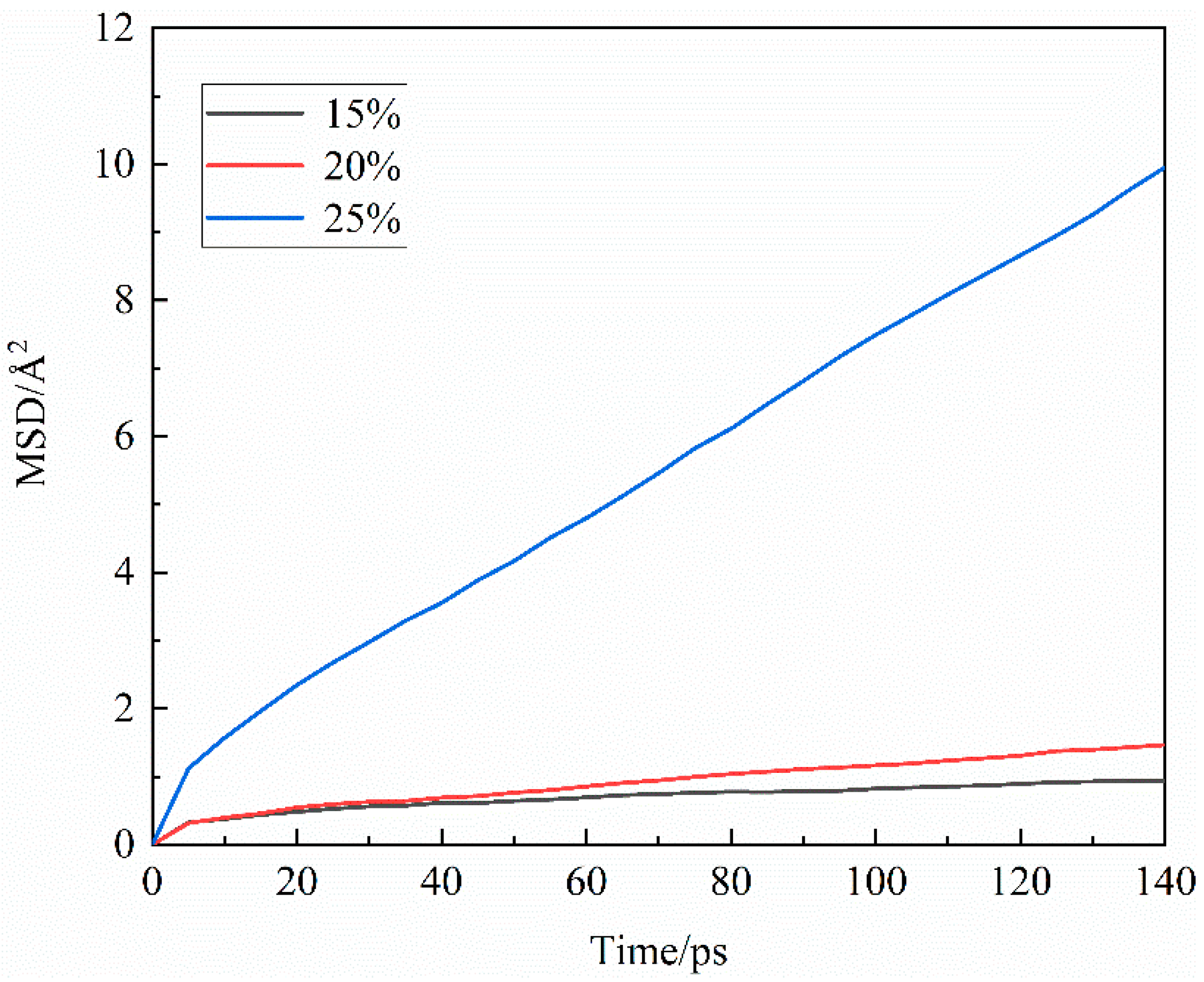
3.2.3. Agglomeration behavior
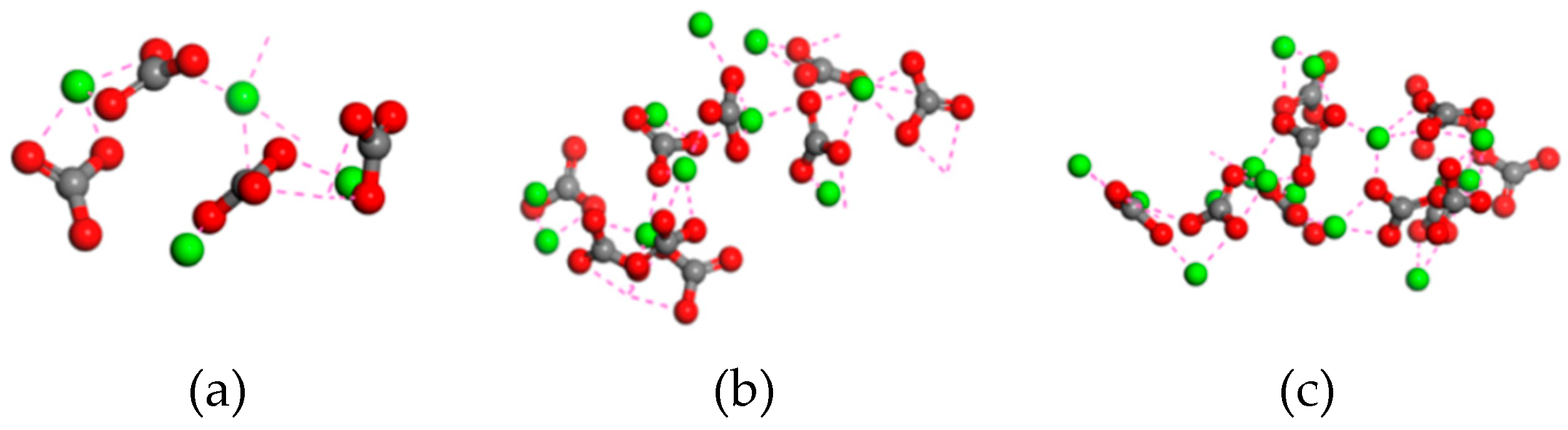
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chen, J; Xing, Y; Wang, Y; Zhang, W; Guo, Z; Su, W. Application of iron and steel slags in mitigating greenhouse gas emissions: A review. Science of The Total Environment 2022, 844, 157041. [CrossRef] [PubMed]
- Ali, N. S. Y; See, K. F. Revisiting an environmental efficiency analysis of global airlines: A parametric enhanced hyperbolic distance function. Journal of Cleaner Production 2023, 394, 135982. [Google Scholar]
- Wang, J. Y; Wang, Q; Sun, W. Q. Quantifying flexibility provisions of the ladle furnace refining process as cuttable loads in the iron and steel industry. Applied Energy 2023, 342, 121178. [Google Scholar] [CrossRef]
- Guo, J; Bao, Y; Wang, M. Steel slag in China: treatment, recycling, and management. Waste Manag 2018, 78, 318–330. [CrossRef] [PubMed]
- Zhao, Q; Liu, C; Mei, X. H; Saxén, H; Zevenhoven, R. Research progress of steel slag-based carbon sequestration. Fundamental Research 2022.
- Ostovari, H; Sternberg, A; Bardow, A. Rock ‘n’ use of CO2: carbon footprint of carbon capture and utilization by mineralization. Sustainable Energy & Fuels 2020.
- Zhao, Q; Liu, K; Sun, L. F; Liu, C. J; Jiang, M. F; Saxén, H; Zevenhoven, R. Towards carbon sequestration using stainless steel slag via phase modification and coextraction of calcium and magnesium. Process Saf Environ Prot 2020, 133, 73–81. [CrossRef]
- Zhang, Y. Y; Yu, L. H; Cui, K. K; Wang, H; Fu, T. Carbon capture and storage technology by steel-making slags: Recent progress and future challenges. Chemical Engineering Journal 2023, 455, 140552. [CrossRef]
- Teir, S. Fixation of carbon dioxide by producing carbonates from minerals and steelmaking slags. Helsinki University of Technology 2008. [Google Scholar]
- Eloneva, S. Reductiom of CO2 emissions by mineral carbonation: steelmaking slags as raw material with a pure calcium carbonate end product. Aalto University 2010. [Google Scholar]
- Bobicki, E; Liu, Q; Xu, Z; Zeng, H. Carbon capture and storage using alkaline industrial wastes. Progress in Energy and Combustion Science 2012, 38, 302–320. [CrossRef]
- Lee, S. W; Kim, J. W; Chao, S; Bang, J; Lee, S. W. CO2 sequestration technology through mineral carbonation: An extraction and carbonation of blast slag. Journal of CO2 Utilization 2016, 16, 336–345. [CrossRef]
- Mei, X. H; Zhao, Q; Min, Y; Liu, C. J; Saxén, H; Zevenhoven, R. Phase transition and dissolution behavior of Ca/Mg-bearing silicates of steel slag in acidic solutions for integration with carbon sequestration. Process Safety Environ Protect 2022, 159, 221–231. [CrossRef]
- Mei, X. H; Zhao, Q; Li, Y; Liu, C. J; Saxén, H; Zevenhoven, R. Phase transition and morphology evolution of precipitated calcium carbonate (PCC) in the CO2 mineralization process. Fuel 2022, 328, 125259. [CrossRef]
- Zappa, W. Pilot-scale experimental work on the production of precipitated calcium carbonate (PCC) from steel slag for CO2 fixation. Aalto University 2014. [Google Scholar]
- Kravchenko, E; Qin, C. H; Lin, Z. Z; Ng, C. Effect of polyvinyl alcohol on the CO2 uptake of carbonated steel slag. Construction and Building Materials 2023, 375, 130761. [CrossRef]
- Doucet, F. Effective CO2-specific sequestration capacity of steel slags and variability in their leaching behaviour in view of industrial mineral carbonation. Minerals Engineering 2010, 23(3), 262–269. [Google Scholar] [CrossRef]
- Wei, C; Dong, J. P; Hu, Z. H; Zhang, H; Wang, X; Tong, Z; Liao, C. CO2 sequestration exploration utilizing converter slag and cold-rolling waste water: The effect of carbonation parameters. In Process Safety and Environmental Protection; 2021; Volume 148, pp. 1233–1242.
- Sundermann, C. Production of calcium carbonate from steelmaking slag and captured CO2 optimisation of the carbonation process and product quality. Aalto University, Finland and Royal Institute of Technology 2016. [Google Scholar]
- Chang, R; Choi, D; Kim, M. H; Park, Y. Tuning crystal polymorphisms and structural investigation of precipitated calcium carbonates for CO2 mineralization. ACS Sustainable Chem 2017, 5, 1659–1667. [CrossRef]
- Clifford, Y; Chen, F. Polymorphism of CaCO3, precipitated in a constant-composition environment. AIChE. 1998, 44, 1790–1798. [CrossRef]
- Chang, R; Kim, S; Lee, S; Choi, S; Kim, M; Park, Y. Calcium carbonate precipitation for CO2 storage and utilization: A review of the carbonate crystallization and polymorphism. Energy Res 2017, 5, 17.
- Yang, P; Zeng, Q. H; Dong, K. J; Zhu, H. A quick method for developing interparticle force models of spherical gold nanoparticles from molecular dynamics simulation. Powder Technology 2020, 362, 501–506. [CrossRef]
- Gadikota, G; Matter, J; Kelemen, P; Brady, P; Park, A. Elucidating the differences in the carbon mineralization behaviors of calcium and magnesium bearing alumino-silicates and magnesium silicates for CO2 storage. Fuel 2020, 277, 117900. [CrossRef]
- Ma, Y; Sheng, J. J; Li, T. Y; Yang, C; Xiao, Q; Yang, R. Study on the optimal conditions of ultrasonic strengthening phosphogypsum storage and solidification of CO2. Sustainable Chemistry and Pharmacy 2023, 33, 101091. [CrossRef]
- Relmasira, K. J; Leonov, A. Y; Malenko, P. I. Application of molecular dynamics method for simulation of the process of increasing the diffusion mobility of atoms using vacancy diffusion mechanism. Procedia Engineering 2017, 206, 636–641. [Google Scholar] [CrossRef]
- Jing, X. W; Luo, Q; Cui, X. F; Wang, Q; Liu, Y; Fu, Z. Molecular dynamics simulation of CO2 hydrate growth in salt water. Journal of Molecular Liquids 2022, 366, 120237. [Google Scholar] [CrossRef]
- Zhang, W; Zhou, L; Yang, B; Yan, T. Molecular dynamics simulations of LiCl ion pairs in high temperature aqueous solutions by deep learning potential. Journal of Molecular Liquids 2022, 367, 120500. [CrossRef]
- Li, C. G; Zhang, C. P; Guo, X. Sintering mechanism of CaO during carbonation reaction in the presence of water vapor. Proceedings of the Combustion Institute 2022. [Google Scholar] [CrossRef]
- Yadav, S; Mehra, A. Experimental study of dissolution of minerals and CO2 sequestration in steel slag. Waste Management 2017, 64, 348–357. [CrossRef]
- Sun, Y; Yao, M. S; Zhang, J. P; Yang, G. Indirect CO2 mineral sequestration by steelmaking slag with NH4Cl as leaching solution. Chemical Engineering Journal 2011, 173(2), 437–445. [CrossRef]
- You, D; Wang, H; Sun, W. Understanding the effect of temperature, concentration, and substrate material on CaCO3 scaling: Molecular dynamics simulations and density functional theory. Computational Materials Science 2022, 209, 111352. [CrossRef]
- Nielsen, P; Boone, M. A; Horckmans, L; Snellings, R; Quaghebeur, M. Accelerated carbonation of steel slag monoliths at low CO2 pressure – microstructure and strength development. Journal of CO2 Utilization 2020, 36, 124–134. [CrossRef]
- Polettini, A; Pomi, R; Stramazzo, A. CO2 sequestration through aqueous accelerated carbonation of BOF slag: A factorial study of parameters effects. Journal of Environmental Management 2016, 167, 185–195. [CrossRef] [PubMed]
- Zhang, S. P; Ghouleh, Z; Liu, J. Y; Shao, Y. Converting ladle slag into high-strength cementing material by flue gas carbonation at different temperatures. Resources. Conservation and Recycling 2021, 174, 105819. [CrossRef]
- Hu, Q. C; Zhao, H. W; Li, H. X; Dong, Y; Liu, Z. Understanding the Raman spectroscopic quantification and dissolving behaviors of CO2 for the CO2–H2O system from water structure. Chemical Physics Letters 2019, 717, 47–52. [CrossRef]
- Pan, S. Y; Adhikari, R; Chen, Y. H; Li, P; Chiang, P. Integrated and innovative steel slag utilization for iron reclamation, green material production and CO2 fixation via accelerated carbonation. Journal of Cleaner Production 2016, 137, 617–631. [CrossRef]
- Li, J. L; Zhang, H. N; Xu, A. J; Cui, J; He, D; Tian, N. Theoretical and Experimental on Carbon Dioxide Sequestration Degree of Steel Slag. Journal of Iron and Steel Research, International 2012, 19(12), 29–32. [CrossRef]
- Mohamed, A. M. O; Gamal, M. M. E; Hameedi, S. M; Paleologos, E. Chapter 9 - Carbonation of steel slag. Sustainable Utilization of Carbon Dioxide in Waste Management 2023, 327–372. [Google Scholar]
- Huijgen, W. J. J; Witkamp, G. J; Comans, R. N. J. Mineral CO2 Sequestration by Steel Slag Carbonation. Environ Sci Technol 2005, 39(24), 9676–9682. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




