Submitted:
05 May 2023
Posted:
08 May 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Methods and Data
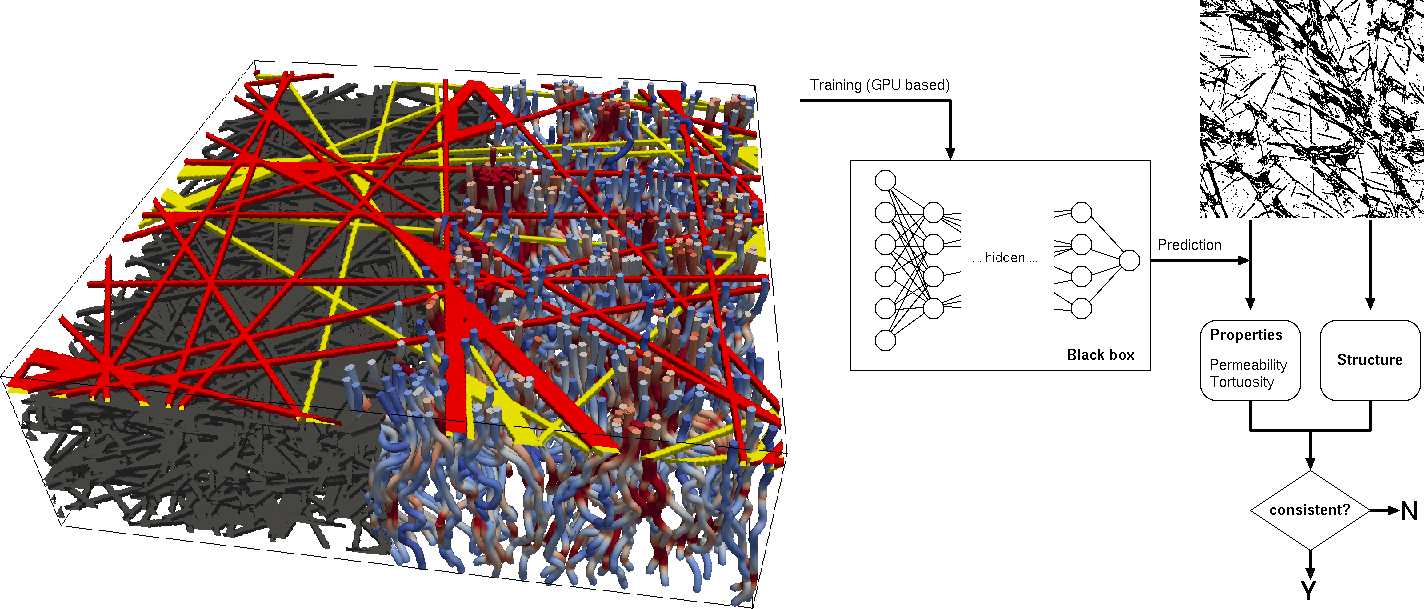
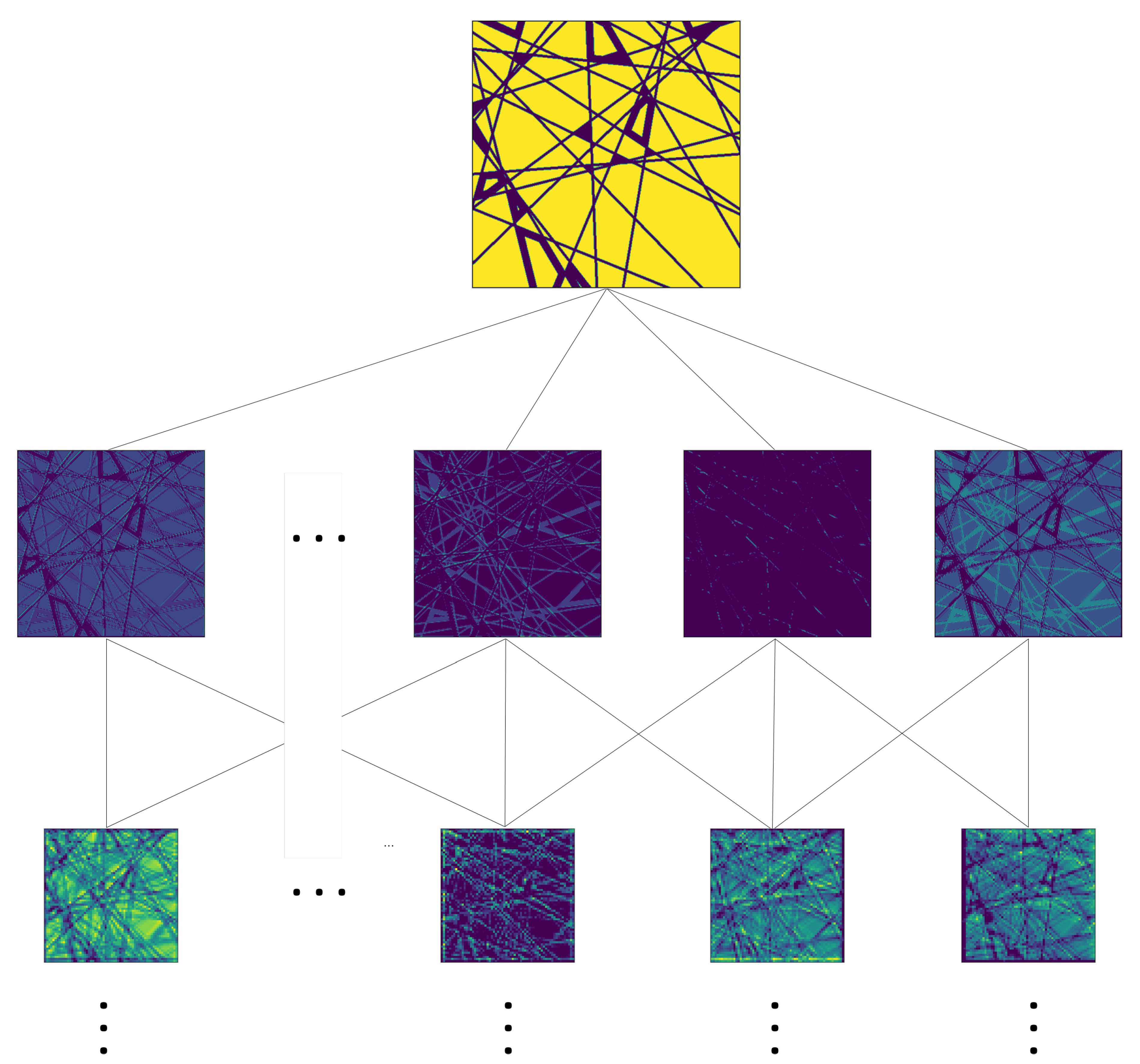
2.1. An Overview on the Machine Learning Model
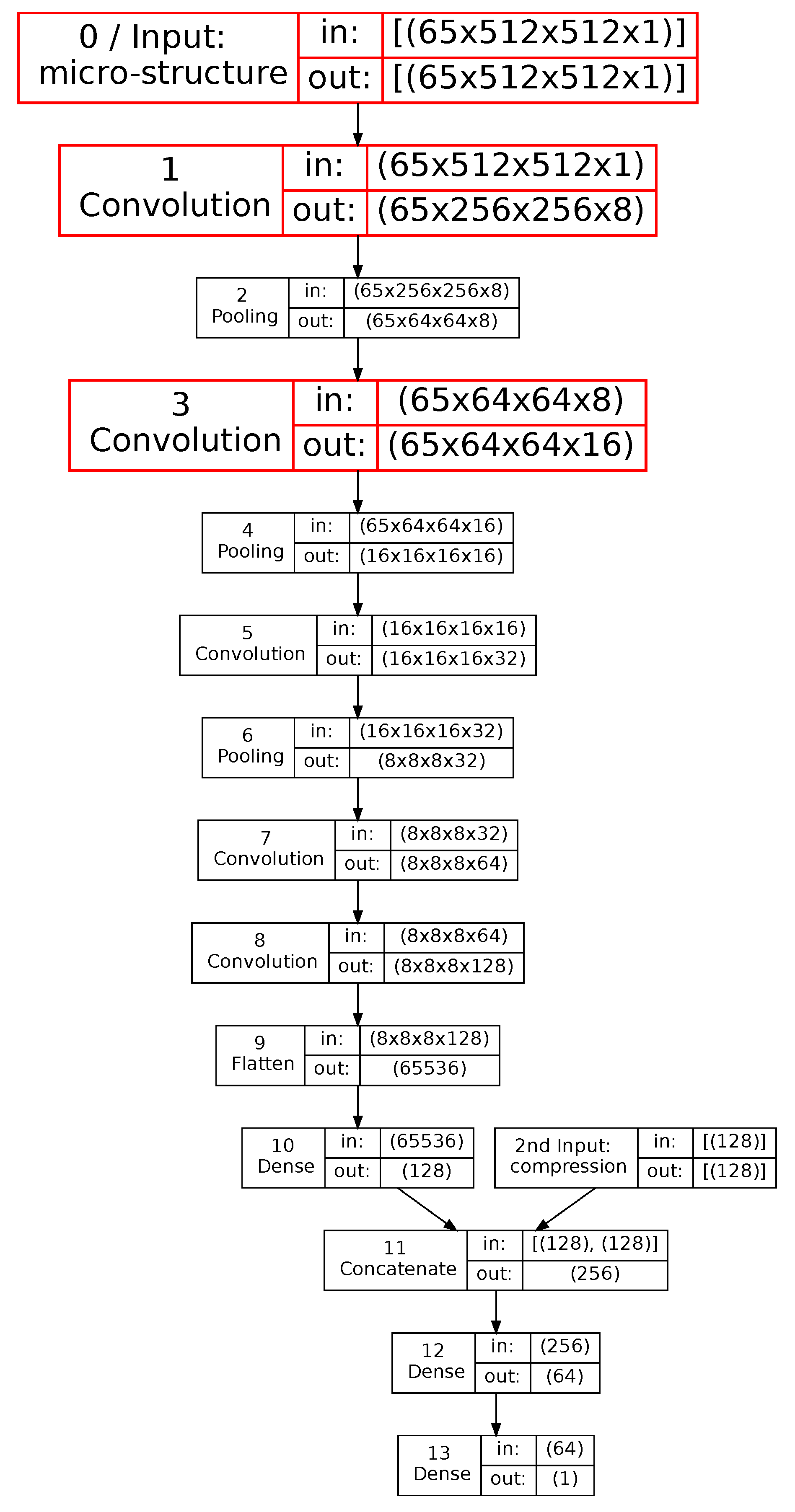
2.2. Convolutional Neural Network Model
2.3. Lattice–Boltzmann Simulations
2.4. Basic Data
- the number of the realizations of the fiber geometry: 25,
- the number of parameters used for different binder distributions: four,
- and the number of compression levels - six steps from 0% (uncompressed) to 50% – in steps of 10% – were used.
2.5. Real Data
- R1
- One image series of Toray GDL was reconstructed from the BESSY synchrotron, the image source from which the GDL model of Thiedmann et al. [30] was validated.
- R2
- Two image series were obtained from a Nano CT Zeiss Xradia Versa 420 at the IEK-14 at the Forschungszentrum Jülich, allowing a minimal voxel size of . Hoppe [33] investigated Toray TGP-H-060 GDL, one series with labels (Figure 5), and
- R3
- one without (Figure 6).
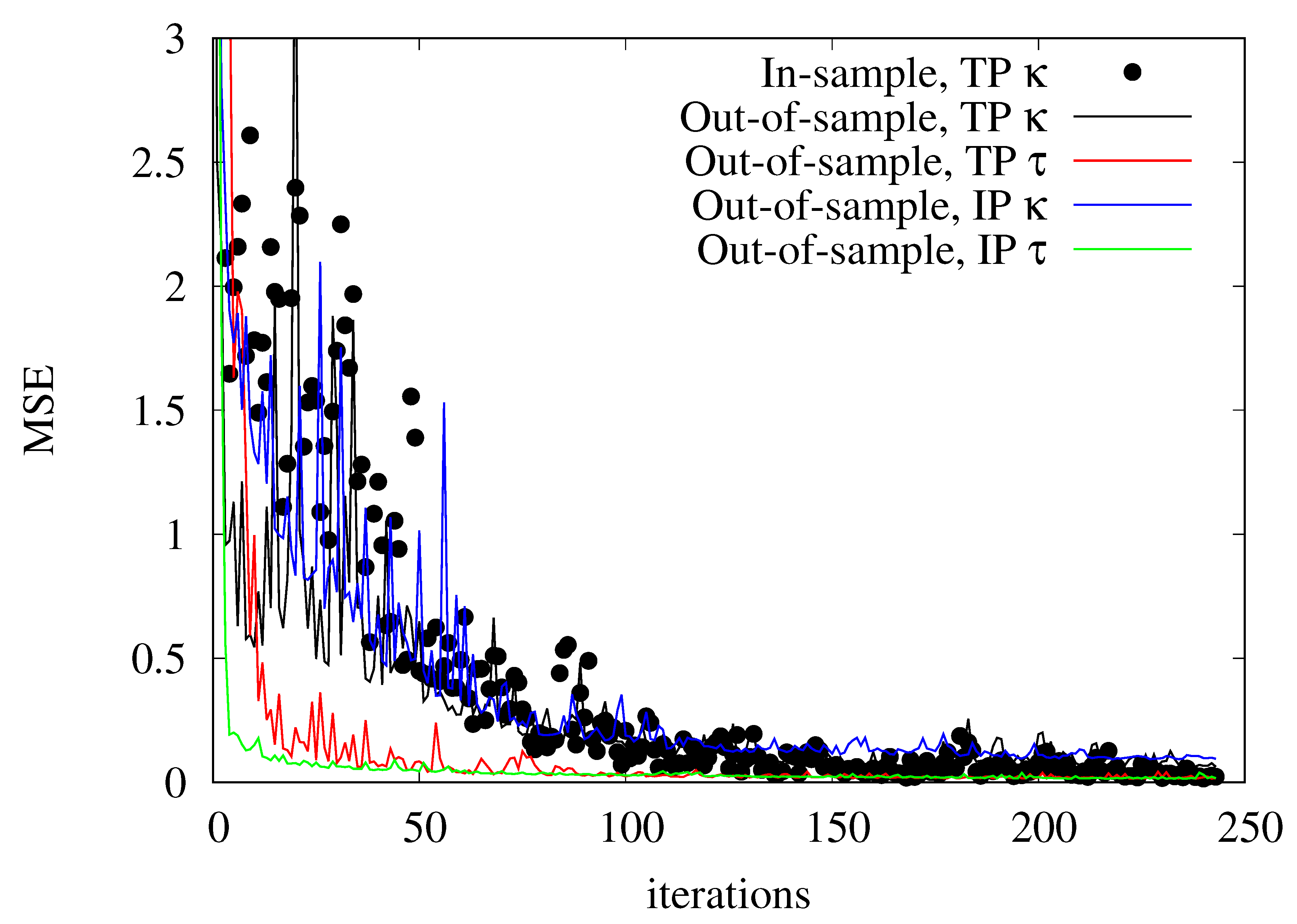
2.6. Evaluation of the Predictions
3. Data Preparation
3.1. Domain Size Normalization
3.2. Real Data
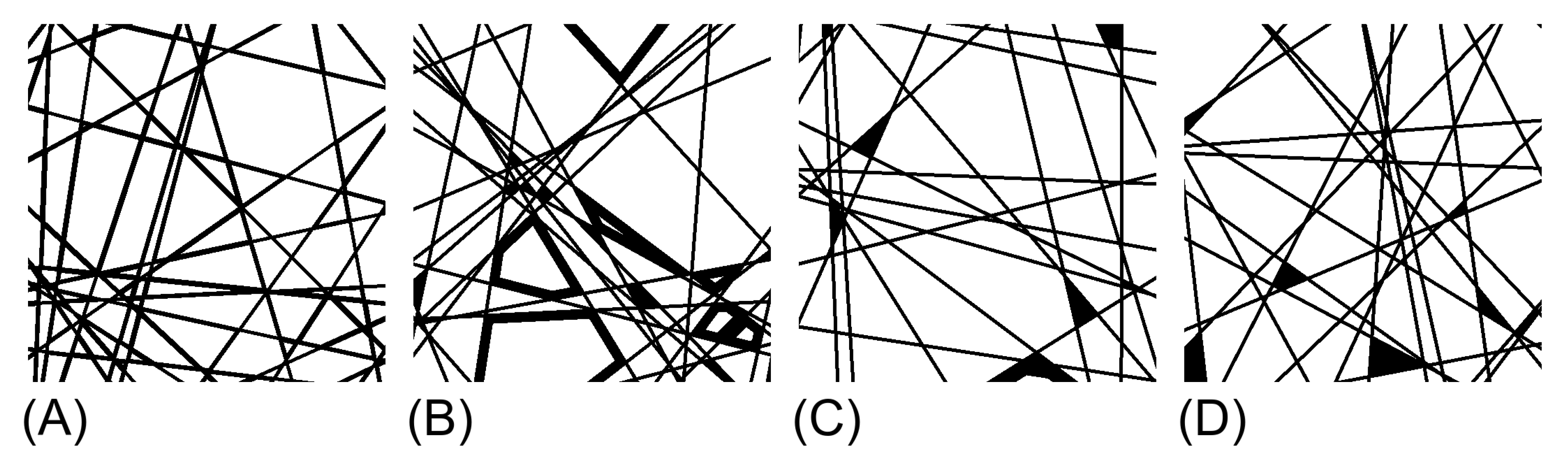
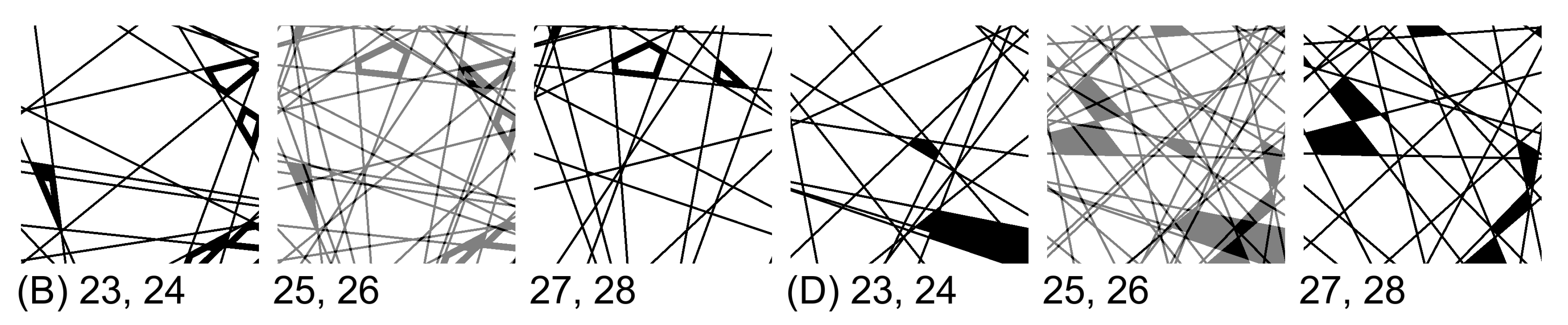
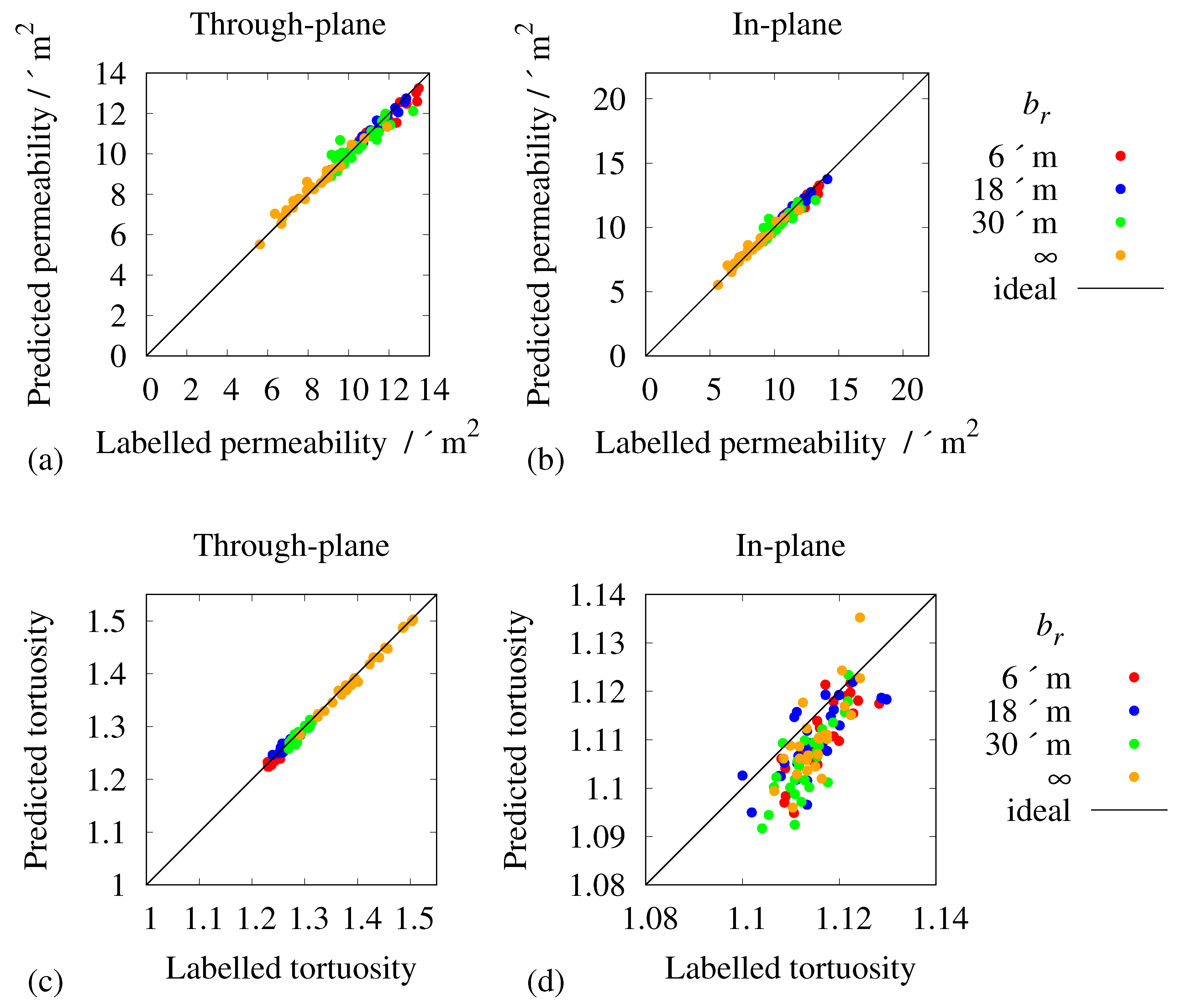
4. Validation
- A)
- permeability
- B)
- tortuosity
- C)
- permeability
- D)
- tortuosity
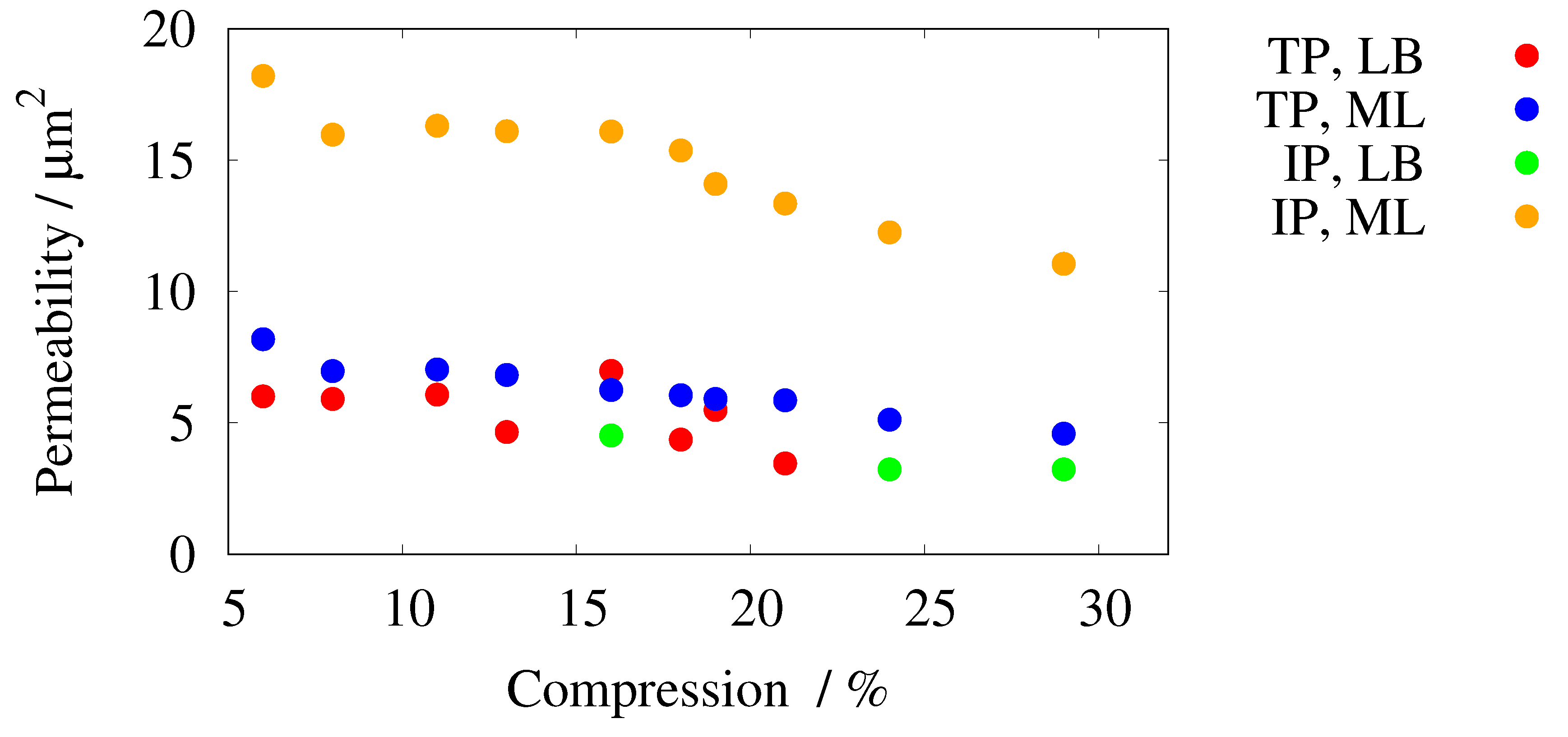
5. Results
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ye, D.H.; Gauthier, E.; Cheah, M.J.; Benziger, J.; Pan, M. The Effect of Gas Diffusion Layer Compression on Gas Bypass and Water Slug Motion in Parallel Gas Flow Channels. AIChE J. 2015, 61, 355–367. [Google Scholar] [CrossRef]
- Ryan, E.M.; Mukherjee, P.P. Mesoscale modeling in electrochemical devices—A critical perspective. Prog. Energy Combust. Sci. 2019, 71, 118–142. [Google Scholar] [CrossRef]
- Holzer, L.; Pecho, O.; Schumacher, J.; Marmet, P.; Stenzel, O.; Büchi, F.; Lamibrac, A.; Münch, B. Microstructure-property relationships in a gas diffusion layer (GDL) for Polymer Electrolyte Fuel Cells, Part I: Effect of compression and anisotropy of dry GDL. Electrochim. Acta 2017, 227, 419–434. [Google Scholar] [CrossRef]
- Zenyuk, I.V.; Parkinson, D.Y.; Connolly, L.G.; Weber, A.Z. Gas-diffusion-layer structural properties under compression via X-ray tomography. J. Power Sources 2016, 328, 364–376. [Google Scholar] [CrossRef]
- Bao, Z.; Li, Y.; Zhou, X.; Gao, F.; Du, Q.; Jiao, K. Transport properties of gas diffusion layer of proton exchange membrane fuel cells: Effects of compression. Int. J. Heat Mass Transf. 2021, 178, 121608. [Google Scholar] [CrossRef]
- Bosomoiu, M.; Tsotridis, G.; Bednarek, T. Study of effective transport properties of fresh and aged gas diffusion layers. J. Power Sources 2015, 285, 568–579. [Google Scholar] [CrossRef]
- Mukherjee, M.; Bonnet, C.; Lapique, F. Estimation of through-plane and in-plane gas permeability across gas diffusion layers (GDLs): Comparison with equivalent permeability in bipolar plates and relation to fuel cell performance. Int. J. Hydrog. Energy 2020, 45, 13428–13440. [Google Scholar] [CrossRef]
- Leonard, D.; Babu, S.K.; Baxter, J.; III, H.M.; Cullen, D.; Borup, R. Natural fiber-derived gas diffusion layers for high performance, lower cost PEM fuel cells. J. Power Sources 2023, 564, 232619. [Google Scholar] [CrossRef]
- Zhang, H.; Zhu, L.; Harandi, H.B.; Duan, K.; Zeis, R.; Sui, P.C.; Chuang, P.Y.A. Microstructure reconstruction of the gas diffusion layer and analyses of the anisotropic transport properties. Energy Convers. Manage. 2021, 241, 114293. [Google Scholar] [CrossRef]
- Ding, R.; Zhang, S.; Chen, Y.; Rui, Z.; Hua, K.; Wu, Y.; Li, X.; Duan, X.; Wang, X.; Li, J.; Liu, J. Application of Machine Learning in Optimizing Proton Exchange Membrane Fuel Cells: A Review. Energy AI 2022, 9, 100170. [Google Scholar] [CrossRef]
- Froning, D.; Wirtz, J.; Hoppe, E.; Lehnert, W. Flow Characteristics of Fibrous Gas Diffusion Layers Using Machine Learning Methods. Appl. Sci. 2022, 12, 12193. [Google Scholar] [CrossRef]
- Cawte, T.; Bazylak, A. A 3D convolutional neural network accurately predicts the permeability of gas diffusion layer materials directly from image data. Curr. Opin. Electrochem. 2022, 35, 101101. [Google Scholar] [CrossRef]
- Wang, Y.D.; Chung, T.; Armstrong, R.T.; Mostaghimi, P. ML-LBM: Predicting and Accelerating Steady State Flow Simulation in Porous Media with Convolutional Neural Networks. Transp. Porous Media 2021, 138, 49–75. [Google Scholar] [CrossRef]
- Pan, Y.; Wang, H.; Brandon, N.P. Gas diffusion layer degradation in proton exchange membrane fuel cells: Mechanisms, characterization techniques and modelling approaches. J. Power Sources 2021, 513, 230560. [Google Scholar] [CrossRef]
- Jafarizadeh, A.; Ahmadzadeh, M.; Mahmoudzadeh, S.; Panjepour, M. A New Approach for Predicting the Pressure Drop in Various Types of Metal Foams Using a Combination of CFD and Machine Learning Regression Models. Transp. Porous Media 2023, 147, 59–91. [Google Scholar] [CrossRef]
- Yeh, R.; Hasegawa-Johnson, M.; Do, M.N. Stable and symmetric filter convolutional neural network. 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE, 2016, pp. 2652–2656. [CrossRef]
- Li, H.W.; Liu, J.N.; Yang, Y.; Lu, G.L.; Qiao, B.X. Coupling flow channel optimization and Bagging neural network to achieve performance prediction for proton exchange membrane fuel cells with varying imitated water-drop block channel. Int. J. Hydrog. Energy 2022, 47, 39987–40007. [Google Scholar] [CrossRef]
- Shum, A.D.; Liu, C.P.; Lim, W.H.; Parkinson, D.Y.; Zenyuk, I.V. Using Machine Learning Algorithms for Water Segmentation in Gas Diffusion Layers of Polymer Electrolyte Fuel Cells. Transp. Porous Med. 2022, 144, 715–737. [Google Scholar] [CrossRef]
- Zhu, G.; Chen, W.; Lu, S.; Chen, X. Parameter study of high-temperature proton exchange membrane fuel cell using data-driven models. Int. J. Hydrog. Energy 2019, 44, 28958–28967. [Google Scholar] [CrossRef]
- Buchaniec, S.; Gnatowski, M.; Brus, G. Integration of Classical Mathematical Modeling with an Artificial Neural Network for the Problems with Limited Dataset. Energies 2021, 14, 5127. [Google Scholar] [CrossRef]
- Yasuda, T.; Ookawara, S.; Yoshikawa, S.; Matsumoto, H. Materials processing model-driven discovery framework for porous materials using machine learning and genetic algorithm: A focus on optimization of permeability and filtration efficiency. Chem. Eng. J. 2023, 453, 139540. [Google Scholar] [CrossRef]
- Arigbe, O.D.; Oyeneyin, M.B.; Arana, I.; Ghazi, M.D. Real-time relative permeability prediction using deep learning. J. Petrol. Explor. Prod. Technol. 2018, 9, 1271–1284. [Google Scholar] [CrossRef]
- Hurtz, S. Brettspiel Go: Hobbyspieler schlägt "übermenschliche" KI. https://www.sueddeutsche.de/wirtschaft/go-ki-kellin-pelrine-lee-sedol-alphago-hobbyspieler-1.5754972. Online: 2023-02-20 20:12.
- Froning, D.; Brinkmann, J.; Reimer, U.; Schmidt, V.; Lehnert, W.; Stolten, D. 3D analysis, modeling and simulation of transport processes in compressed fibrous microstructures, using the Lattice Boltzmann method. Electrochim. Acta 2013, 110, 325–334. [Google Scholar] [CrossRef]
- Galeone, P. Hands-On Neural Networks with TensorFlow 2.0; Packt Publishing: Birmingham, UK, 2019. [Google Scholar]
- Froning, D.; Gaiselmann, G.; Reimer, U.; Brinkmann, J.; Schmidt, V.; Lehnert, W. Stochastic Aspects of Mass Transport in Gas Diffusion Layers. Transp. Porous Media 2014, 103, 469–495. [Google Scholar] [CrossRef]
- Froning, D.; Yu, J.; Gaiselmann, G.; Reimer, U.; Manke, I.; Schmidt, V.; Lehnert, W. Impact of compression on gas transport in non-woven gas diffusion layers of high temperature polymer electrolyte fuel cells. J. Power Sources 2016, 318, 26–34. [Google Scholar] [CrossRef]
- Koponen, A.; Kataja, M.; Timonen, J. Tortuous flow in porous media. Phys. Rev. E 1996, 54, 406–410. [Google Scholar] [CrossRef] [PubMed]
- Krause, D.; Thörnig, P. JURECA: Modular supercomputer at Jülich Supercomputing Centre. J. Large-Scale Res. Facil. JLSRF 2018, 4. [Google Scholar] [CrossRef]
- Thiedmann, R.; Fleischer, F.; Hartnig, C.; Lehnert, W.; Schmidt, V. Stochastic 3D Modeling of the GDL Structure in PEMFCs Based on Thin Section Detection. J. Electrochem. Soc. 2008, 155, B391–B399. [Google Scholar] [CrossRef]
- Wang, Y.; Cho, S.; Thiedmann, R.; Schmidt, V.; Lehnert, W.; Feng, X. Stochastic modeling and direct simulation of the diffusion media for polymer electrolyte fuel cells. Int. J. Heat Mass Transf. 2010, 53, 1128–1138. [Google Scholar] [CrossRef]
- Lintermann, A.; Schröder, W. Lattice–Boltzmann simulations for complex geometries on high-performance computers. CEAS Aeronaut. J. 2020, 11, 745–766. [Google Scholar] [CrossRef]
- Hoppe, E. Kompressionseigenschaften der Gasdiffusionslage einer Hochtemperatur-Polymerelektrolyt-Brennstoffzelle. PhD thesis, RWTH Aachen University, 2021.
- Tomadakis, M.M.; Robertson, T.J. Viscous Permeability of Random Fiber Structures: Comparison of Electrical and Diffusional Estimates with Experimental and Analytical Results. J. Compos. Mater. 2005, 39, 163–188. [Google Scholar] [CrossRef]
- The ImageMagick Development Team. ImageMagick. https://imagemagick.org. Accessed: 2021-01-04.
- Nguyen, A.; Yosinski, J.; Clune, J. Understanding Neural Networks via Feature Visualization: A Survey. In Explainable AI: Interpreting, Explaining and Visualizing Deep Learning; Springer International Publishing, 2019; pp. 55–76. 76. [CrossRef]
- El-Amir, H.; Hamdy, M. Deep Learning Pipeline; Apress, Berkeley, CA, 2020. [CrossRef]
- Thiedmann, R.; Hartnig, C.; Manke, I.; Schmidt, V.; Lehnert, W. Local Structural Characteristics of Pore Space in GDLs of PEM Fuel Cells Based on Geometric 3D Graphs. J. Electrochem. Soc. 2009, 156, B1339. [Google Scholar] [CrossRef]
- Mangal, P.; Pant, L.M.; Carrigy, N.; Dumontier, M.; Zingan, V.; Mitra, S.; Secanell, M. Experimental study of mass transport in PEMFCs: Through plane permeability and molecular diffusivity in GDLs. Electrochim. Acta 2015, 167, 160–171. [Google Scholar] [CrossRef]
- Feser, J.; Prasad, A.; Advani, S. Experimental characterization of in-plane permeability of gas diffusion layers. J. Power Sources 2006, 162, 1226–1231. [Google Scholar] [CrossRef]
- Hoppe, E.; Janßen, H.; Müller, M.; Lehnert, W. The impact of flow field plate misalignment on the gas diffusion layer intrusion and performance of a high-temperature polymer electrolyte fuel cell. J. Power Sources 2021, 501, 230036. [Google Scholar] [CrossRef]




| Series | No. | Comp. | No. of | Dimensions |
| % | images | |||
| R1 | 1 | 0 | 200 | 1250x1250 |
| R2 | 1 | 6 | 40 | 694x670 |
| 2 | 8 | 22 | 671x688 | |
| 3 | 11 | 27 | 697x661 | |
| 4 | 13 | 40 | 684x673 | |
| 5 | 16 | 22 | 682x682 | |
| 6 | 18 | 40 | 673x687 | |
| 7 | 19 | 21 | 685x680 | |
| 8 | 21 | 40 | 688x677 | |
| 9 | 24 | 40 | 670x685 | |
| 10 | 29 | 40 | 670x685 | |
| R3 | 1 | 7 | 40 | 760x310 |
| 2 | 10 | 40 | 760x310 | |
| 3 | 11 | 40 | 760x310 | |
| 4 | 14 | 40 | 760x310 | |
| 5 | 18 | 40 | 760x310 | |
| 6 | 19 | 40 | 760x310 | |
| 7 | 24 | 40 | 760x310 | |
| 8 | 28 | 40 | 760x310 | |
| 9 | 30 | 40 | 760x310 | |
| 10 | 31 | 40 | 760x310 |
| TP | IP | |||||
| min | 8.89 | 1.17 | 11.73 | 17.44 | 1.07 | 19.23 |
| max | 11.94 | 1.36 | 15.18 | 19.82 | 1.14 | 22.02 |
| average | 10.54 | 1.27 | 13.43 | 18.83 | 1.10 | 20.80 |
| median | 10.54 | 1.28 | 18.85 | 1.10 | ||
| std. deviation | 0.62 | 0.038 | 0.75 | 0.56 | 0.014 | 0.69 |
| variance | 0.38 | 0.32 | ||||
| var. coeff. | ||||||
| average (B) in [24] | 11.18 | 1.27 | 17.98 | 1.11 | ||
| average (C) in [24] | 10.51 | 1.29 | 17.81 | 1.11 | ||
| favored: | C | B | B | B, C | ||
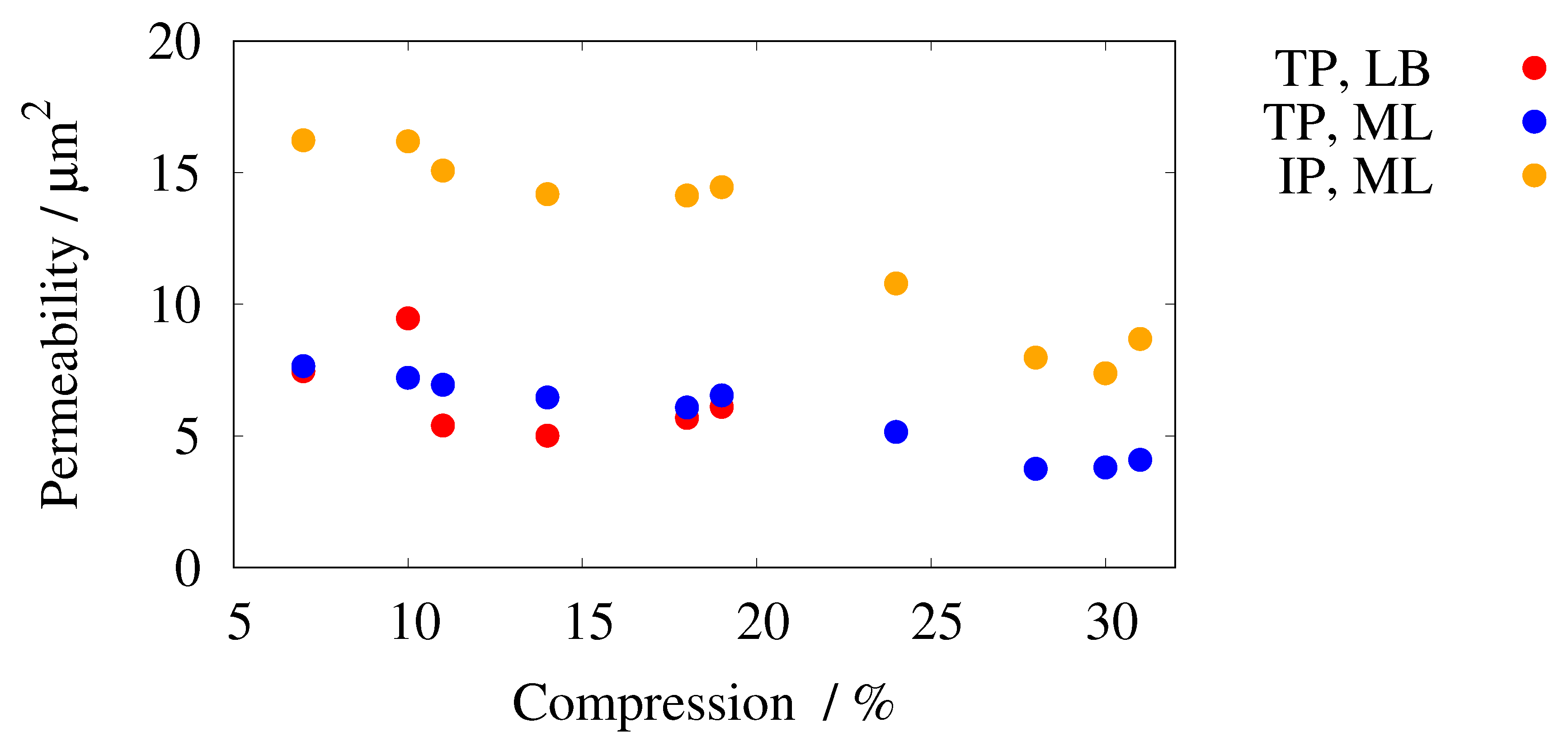
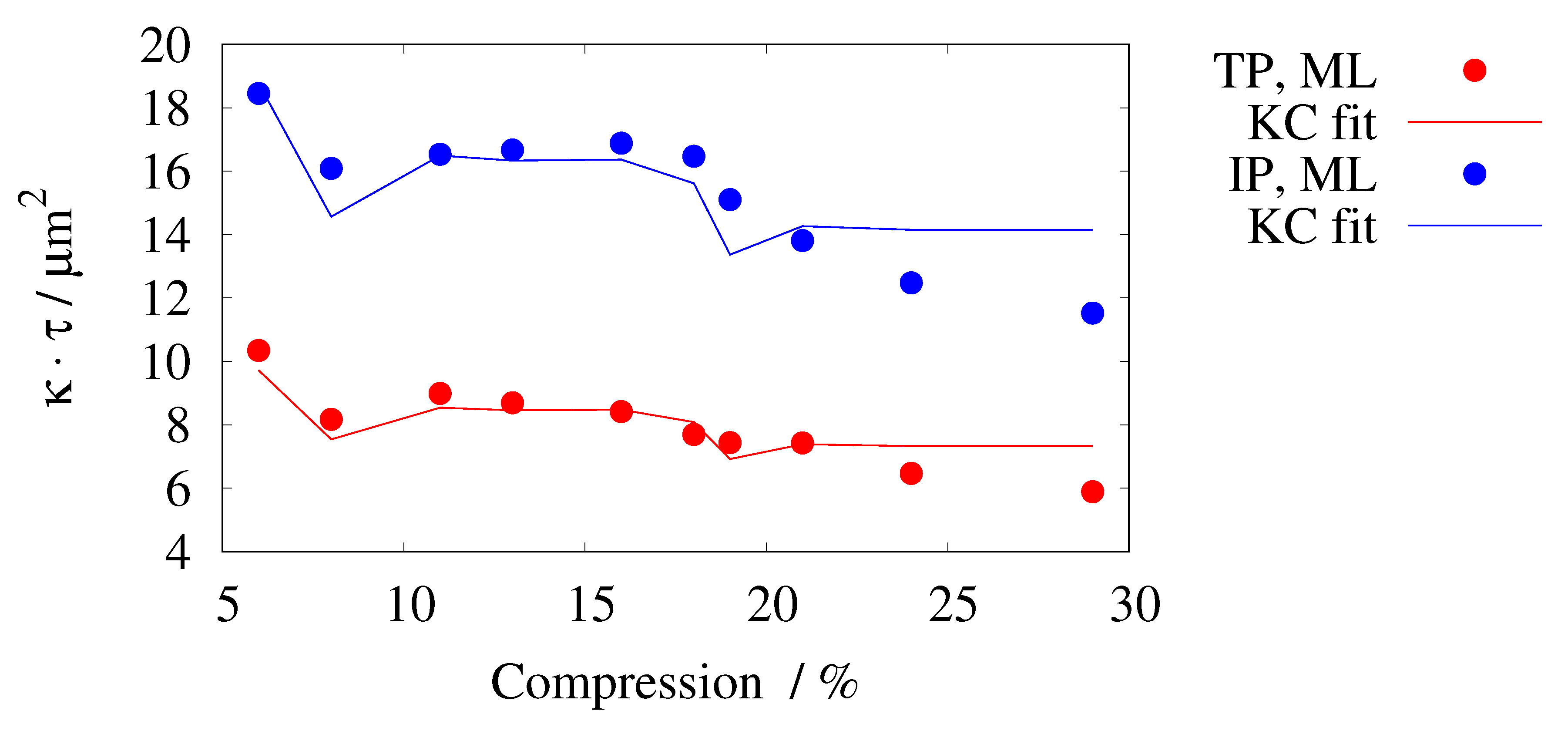
| Series | No. | Comp. | Porosity | TP | IP | |||||||
| % | ||||||||||||
| R2 | 1 | 6 | 0.688 | 7.12 | 1.22 | 1.26 | 6.01 | 8.18 | 1.01 | 18.20 | ||
| 2 | 8 | 0.666 | 6.38 | 1.13 | 1.17 | 5.91 | 6.97 | 1.01 | 15.97 | |||
| 3 | 11 | 0.678 | 6.72 | 1.15 | 1.28 | 6.07 | 7.03 | 1.01 | 16.31 | |||
| 4 | 13 | 0.669 | 6.74 | 1.23 | 1.27 | 4.65 | 6.82 | 1.04 | 16.10 | |||
| 5 | 16 | 0.669 | 6.74 | 1.11 | 1.35 | 6.98 | 6.25 | 1.05 | 16.09 | |||
| 6 | 18 | 0.669 | 6.59 | 1.25 | 1.27 | 4.36 | 6.05 | 1.07 | 15.37 | |||
| 7 | 19 | 0.680 | 6.05 | 1.12 | 1.26 | 5.49 | 5.91 | 1.07 | 14.09 | |||
| 8 | 21 | 0.644 | 6.42 | 1.26 | 1.27 | 3.46 | 5.86 | 1.03 | 13.35 | |||
| 9 | 24 | 0.640 | 6.41 | 1.27 | 1.27 | 3.23 | 5.12 | 1.02 | 12.25 | |||
| 10 | 29 | 0.640 | 6.41 | 1.27 | 1.28 | 3.23 | 4.59 | 1.04 | 11.05 | |||
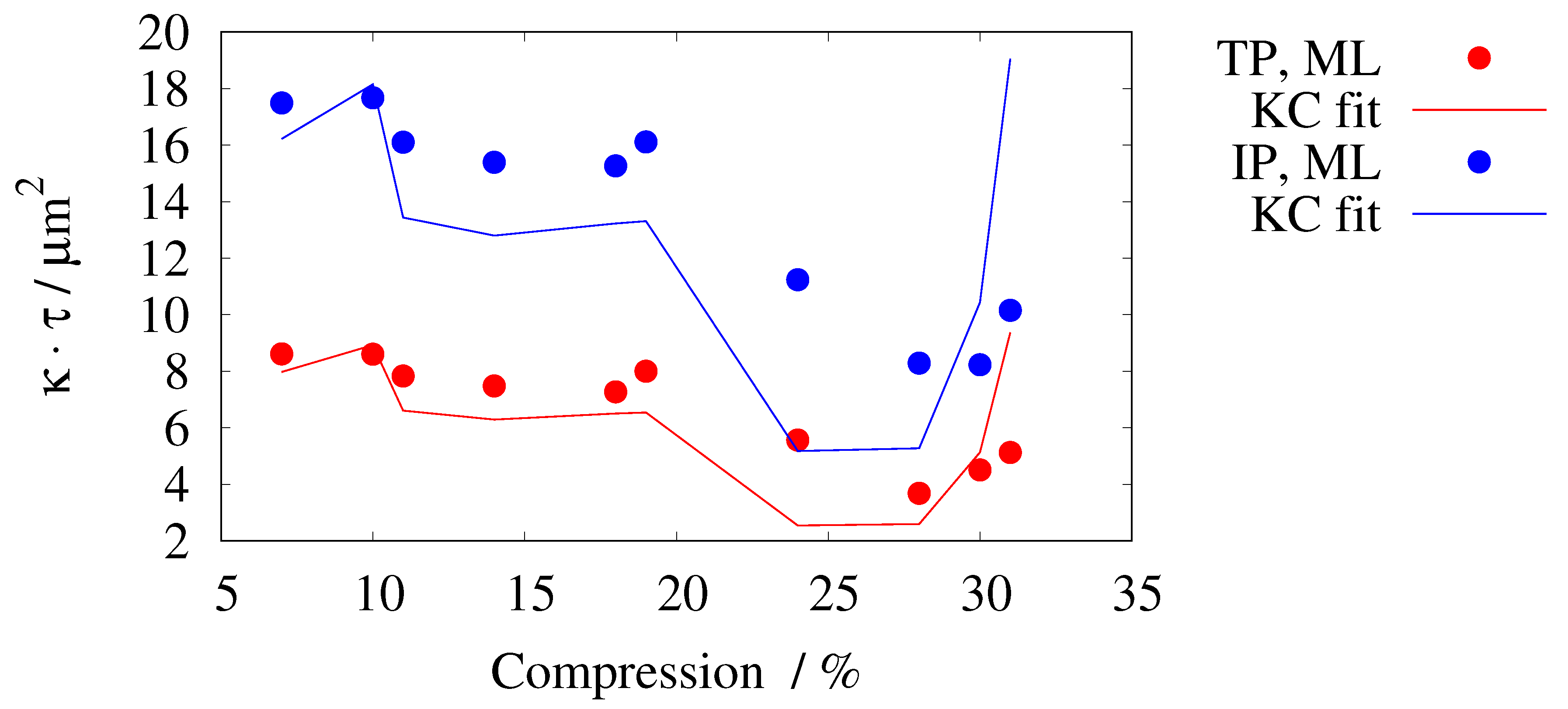
| R3 | 1 | 7 | 0.685 | 7.61 | 1.18 | 1.13 | 7.46 | 7.65 | 1.08 | 16.23 | ||
| 2 | 10 | 0.709 | 7.91 | 1.15 | 1.19 | 9.46 | 7.21 | 1.09 | 16.19 | |||
| 3 | 11 | 0.669 | 7.02 | 1.20 | 1.13 | 5.39 | 6.94 | 1.07 | 15.08 | |||
| 4 | 14 | 0.666 | 6.86 | 1.20 | 1.16 | 5.01 | 6.46 | 1.09 | 14.18 | |||
| 5 | 18 | 0.678 | 6.91 | 1.18 | 1.20 | 5.68 | 6.08 | 1.08 | 14.13 | |||
| 6 | 19 | 0.685 | 6.89 | 1.18 | 1.22 | 6.54 | 1.11 | 14.45 | ||||
| 7 | 24 | 0.597 | 4.61 | 1.08 | 5.15 | 1.04 | 10.79 | |||||
| 8 | 28 | 0.555 | 4.84 | 0.98 | 3.75 | 1.04 | 7.97 | |||||
| 9 | 30 | 0.570 | 6.69 | 1.19 | 3.80 | 1.12 | 7.38 | |||||
| 10 | 31 | 0.592 | 8.87 | 1.25 | 4.09 | 1.17 | 8.68 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





