Submitted:
23 April 2023
Posted:
26 April 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Problem formulation
2.1. Side Slope Problems
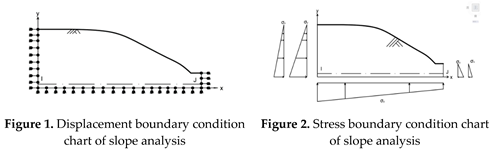
2.2. Retaining wall problem
3. Numerical theoretical solutions for side slopes and retaining walls
3.1. Basic Methods
3.2. Example of a two-dimensional slope retaining wall
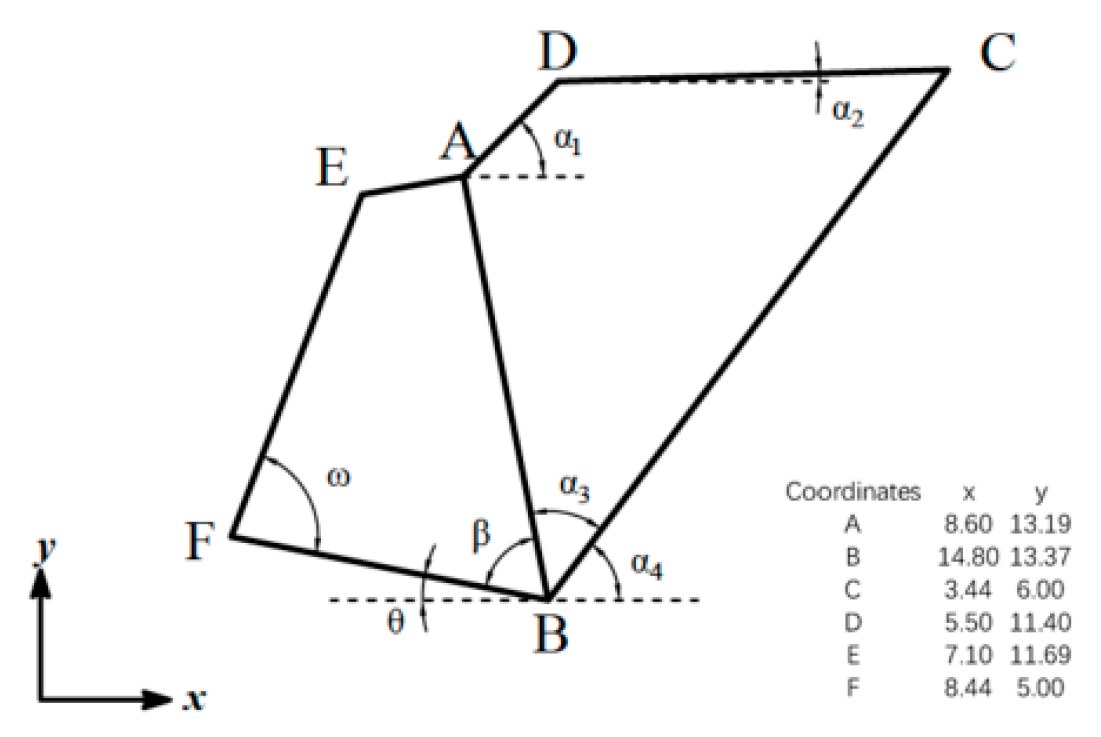
3.3 Examples
3.4 Computational Analysis
3.4.1 Example of a waste transfer station project
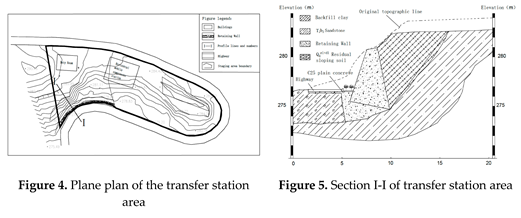
3.4.2. Calculating the Model Dimensions
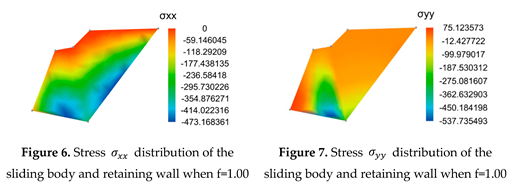
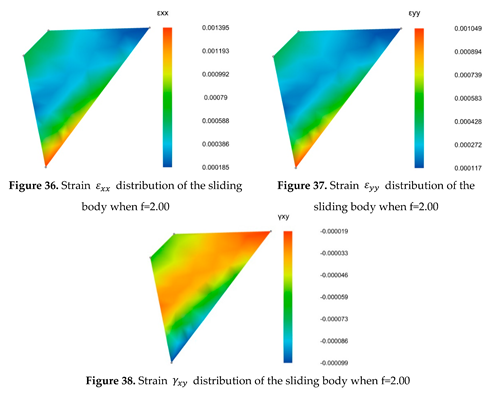
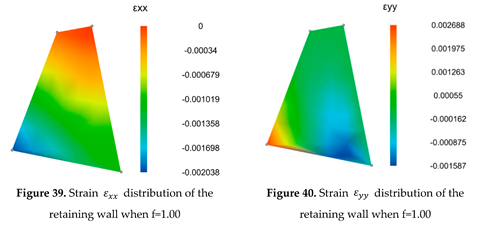
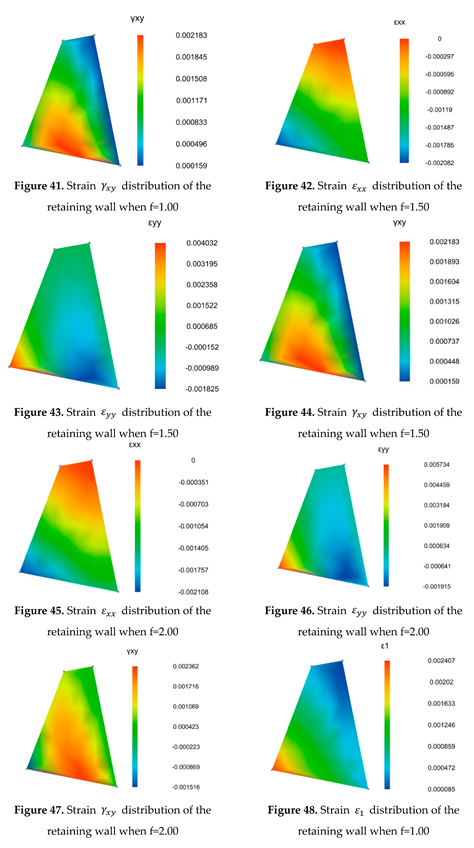
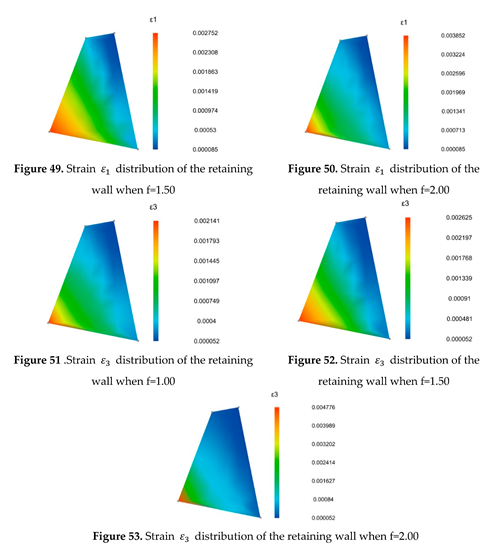
3.4.3. Analysis of the calculation results
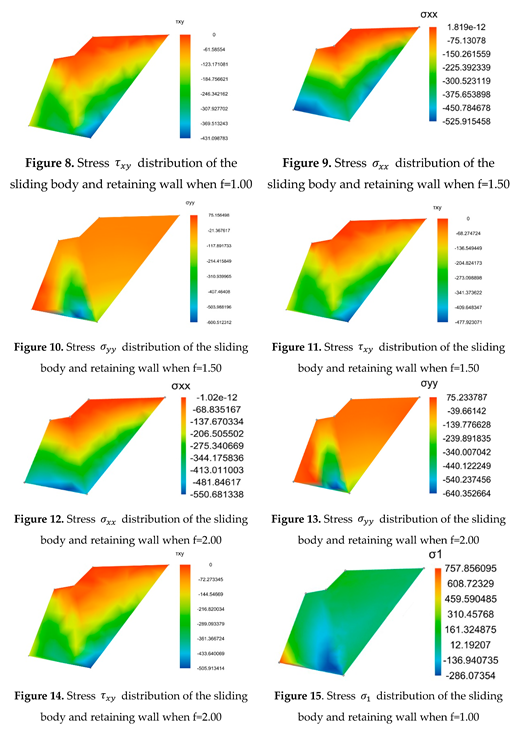
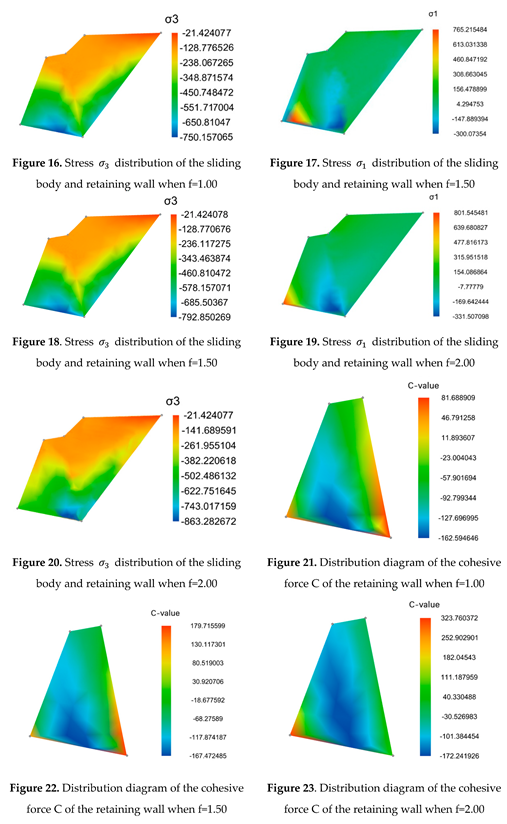
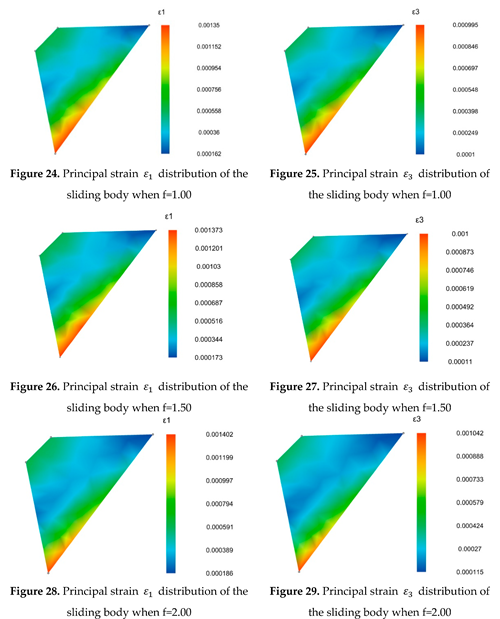
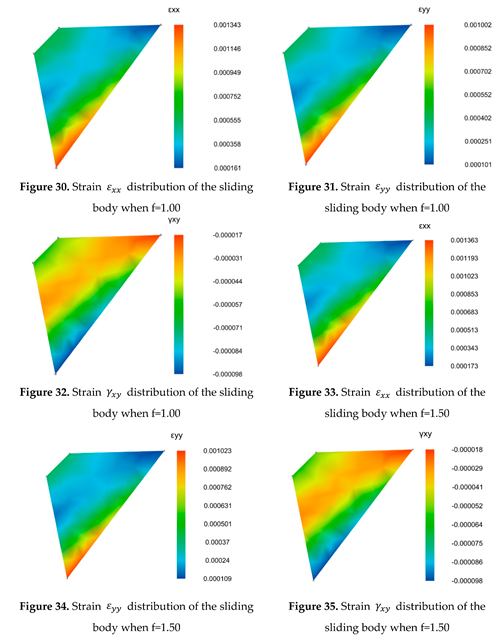
4. Conclusion
Funding
References
- Chen, Z. Design of highway retaining wall; People's Communications Press: Beijing, China, 1999. (In Chinese) [Google Scholar]
- Zhao, G. Study on the optimal design of balance weight retaining wall; China University of Geosciences: Beijing, China, 2006. (In Chinese) [Google Scholar]
- Li, R. Seepage field simulation and stability analysis of retaining wall with drainage pipe under rainfall infiltration; Zhengzhou University: Zhengzhou, China, 2014. (In Chinese) [Google Scholar]
- Xu, R. Model test of passive earth pressure on rigid retaining wall. Chinese Journal of Geotechnical Engineering 2002, 24, 569–575. (In Chinese) [Google Scholar]
- Dawson, E.M.; Roth, W.H.; Drescher, A. Slope stability analysis by strength reduction. Geotechnique 1999, 49, 835–840. [Google Scholar]
- Terzaghi, K. A fundamental fallacy in earth pressure computations. Journal of Boston Society of Civil Engineering 1936, 23, 71–88. [Google Scholar]
- MAO, Y. Two basic problems in the classical theory of earth pressure on retaining wall. Journal of Civil Engineering 1954, 3, 249–282. (In Chinese) [Google Scholar]
- Kezdi, A. Earth pressure on retaining wall tilting about the toe. Proceedings of the Brussels Conference on Earth Pressure Problems 1958, 1, 116–132. [Google Scholar]
- Handy, R.L. The arch in soil arching. Jourmal of Geotechnical Engineering 1985, 111, 302–318. [Google Scholar] [CrossRef]
- Wang, H.; Sun, D. Study on the sliding surface of soil behind retaining wall and the variational method of earth pressure. Chinese Journal of Geotechnical Engineering 1989, 11, 86–93. (In Chinese) [Google Scholar]
- Chen, L. Study on calculation method of active earth pressure of retaining wall under different displacement modes; Chongqing University: Chongqing, China, 2010. (In Chinese) [Google Scholar]
- HE, X. Improvement of active earth pressure analysis method and Research on relevant design standards of retaining wall; Sinohydro Research Institute: Beijing, China, 2015. (In Chinese) [Google Scholar]
- Zeng, G.; Zhou, Z. Design method of anti overturning stability of highway retaining wall. Journal of Central South University: Natural Science 2009, 40, 1154–1158. (In Chinese) [Google Scholar]
- Gan, S.; Peng, B. Discussion on the expression of the overturning stability equation of the retaining wall in the code for design of Highway Subgrade. Subgrade engineering 2012, 31–33. (In Chinese) [Google Scholar]
- Huang, R.; Xia, T.; et al. Study on safety factor of anti overturning stability of retaining wall under earthquake. Journal of rock mechanics and Engineering 2013, 2154–2159. (In Chinese) [Google Scholar]
- Huang, Y. Discussion on stability analysis of retaining wall against overturning. Journal of geotechnical engineering 2015, 37, 1158–1164. (In Chinese) [Google Scholar]
- Code for design of hydraulic retaining wall, SL379-2007, Ministry of Water Resources of the People's Republic of China, 2007. (In Chinese)
- LU, Y.-f. Deformation and Failure Mechanism of Slope in Three Dimensions. Journal of Rock Mechanics and Geo-technical Engineering 2015, 7, 109–119. [Google Scholar] [CrossRef]
- LU, Y.; SHI, J.; LIU, D. A Sliding surface boundary Method of Landslide Stability Analysis, Chinese Patent. NO. ZL 2014100250810 [P].
- LU Yingfa, LIU Defu, YAN Yuan, ZHan Lai, Stress solution based on force boundary and balance condition, Patent No:201611034900.3.
- LU, Y.-f.; DENG, G.-d.; YANG, L.-p.; et al. Study of Mechanical Behaviors of Key Block and Characteristics of Force Transmit and Stability Coefficient of Different State Stress of Landslides. Chinese Journal of Rock Mechanics and Engineering 2014, 33, 884–891. (In Chinese) [Google Scholar]
- LU, Y.-f. Deformation and Failure Mechanism of Slope in Three Dimensions. Journal of Rock Mechanics and Geo-technical Engineering 2015, 7, 109–119. [Google Scholar] [CrossRef]
- LU, Y.-f.; Huang, X.-b.; LIU, D.-f. Force -displacement Method of Slice Block Analysis of Slope Stability and Its Application. Rock and Soil Mechanics 2015, 36, 2780–2786. (In Chinese) [Google Scholar]
- LU, Y. Mechanism and Stability Analyses of Progressive Failure of Pull-type Landslide. Proceedings of the third Academic Conference of Geology Resource Management and Sustainable Development 2015, 2, 2812–91. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).



