Prerpints.org logo
Preprint
Article

Evaluation of Spiral Pneumatic Rubber Actuator using Finite Element Analysis for Radial Transportation

Altmetrics

Downloads

156

Views

42

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

21 April 2023

Posted:

21 April 2023

You are already at the latest version

Alerts
Abstract
Emerging soft actuators with various soft materials and traveling-wave motion have been frequently discussed. Various configurations and the resulting performances have been proposed, and it is very challenging for soft actuators in realizing large strokes. This study presents an experimentally validated nonlinear finite element model to predict the deformation produced by a spiral pneumatic rubber actuator to generate traveling-wave motion. The actuator consists of a membrane mounted on a rubber substrate with three air chambers in a spiral configuration, simplifying the actuator's structure. The sequential deformations of the successive chambers interact with each other and produce radial traveling-waves on the membrane surface, driving the objects placed on the actuator. Finite element analysis using ANSYS computer software analyzed the elastic movement by considering the influence of different initial structural types. The structure with three different length ratios was introduced using the four parameters: membrane thickness, chamber width, chamber depth, and wall thickness. The simulation results indicated an optimal structure with specific ratios. A reasonable correlation was obtained during experimental validation; the predicted displacement values were approximately 17% smaller than the experimental values. Finally, the transportation performance of the prototype was tested and a velocity of 2.28 mm/s in the desired direction was achieved. We expect that our demonstration will expand the range of applications of the spiral pneumatic rubber actuator to include conveying or worm-like robots.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

Pneumatic actuators are extensively used in soft robotics owing to their simple design, structure, and driving principles. Due to the compliant bodies and flexible transformation, pneumatic soft actuators move effectively in complex environments and are expected to be able to accomplish tasks in difficult terrain or safely interact with humans [1]. Besides, pneumatic rubber actuators are able to function in both dry and wet environments.
Emerging actuators with various soft materials and traveling wave motion have been frequently discussed. Traveling wave operation of mechanical actuation is a typical biomimetic motion. Their applications include conveyance devices [2], microrobots [3], peristaltic pumps [4], annelid robots [5], and piezoceramics [6]. This actuator configuration has been extensively used in piezoceramic devices as conventional ultrasonic motors. However, producing large traveling waves for locomotion applications is challenging. Poole et al. [7] presented a crawling actuator using multi-stack dielectric elastomers to generate locomotion based on the sequential actuation of their segments; however, the maximum attainable velocity was 2.1 mm/min, which is commercially insufficient. These actuators have multiple active regions in a single controllable device; thus, the peristaltic motion is manifested by cycling the active regions.
It is very challenging for soft actuators in realizing a fast crawling. Soft actuators driven pneumatic pressure have further advantages of a large deformation and high output-to-weight ratio. Thus, a variety of actuators have been developed and tested for traveling wave motions [8] [9]. The internal deformable hollow chambers indicate the desired output motion. Suzumori [10] presented a pneumatic rubber actuator comprising a rubber slab with interior chambers to produce linear motion on its surface. A walking speed of 4.7 mm/s was obtained from the prototype tests. However, their structure has multiple fins on the surface to generate traveling wave motion; thus, limitations are occurred for the structure of objects that can be transported. A pneumatic rubber actuator-based cylindrical actuator [11] was developed with four independent segments in a spiral configuration. The prototype produced a traveling wave motion on its outer surface for the pipeline interior inspection and testing.
Traveling wave-related motion has been applied to various configurations. The desired motion is achieved by predefining the layout and actuation patterns. The output comes from two processes: the production of traveling waves on the surface and the transfer process at the contact interface. A multi-stack dielectric elastomer actuator can travel between two planar surfaces by cycling active stacks [7]. The parallelly arranged stacks are expanded in the planar direction and shrunk in the perpendicular direction, thereby repeating locomotion and gripping the friction surface. Qi et al. [12] proposed a pneumatic soft snake robot to move in complex, constrained environments using traveling wave motion. Connolly et al. [13] developed a soft fluidic actuator with a segmented structure for crawling. In addition, in [14], a fluidic pump consisting of helical electrodes embedded within the walls of a polyurethane tube was designed to generate continuous fluid flow. Ran et al. [15] developed a miniature piezoelectric actuator without a tooth structure on the stator surface to drive actuation.
Traveling wave motion can simultaneously provide large strokes and high forces with appropriate materials and perfectly configured actuation systems. In the present study, a spiral pneumatic rubber actuator is proposed, which utilizes the Archimedean spiral configuration [16] to develop the finite element analysis model. The sequential deformations of the successive chambers interact with each other and produce radial traveling waves on the membrane surface, driving the objects placed on the actuator. The goal is to establish a simulation structural model, estimate the displacement, and optimize the design parameters to generate radial transportation with large strokes. The simulation model is designed using only three equidistantly placed active segments with several parameters: membrane thickness, chamber width, chamber depth, and wall thickness. In addition, the effects of structural parameters on actuation are investigated using 2D and 3D finite element models, then verified experimentally based on observations.
The remainder of this paper is organized as follows: Section 2 presents an overview of the proposed actuator's design, operating principles, and fabrication. Section 3 explains the theoretical models and methods used for finite element analysis. Section 4 presents the prototype testing to assess its performance characteristics and confirm the theoretical model's validity. Finally, Section 5 concludes this study.

2. Design and Fabrication

2.1. Structural Design

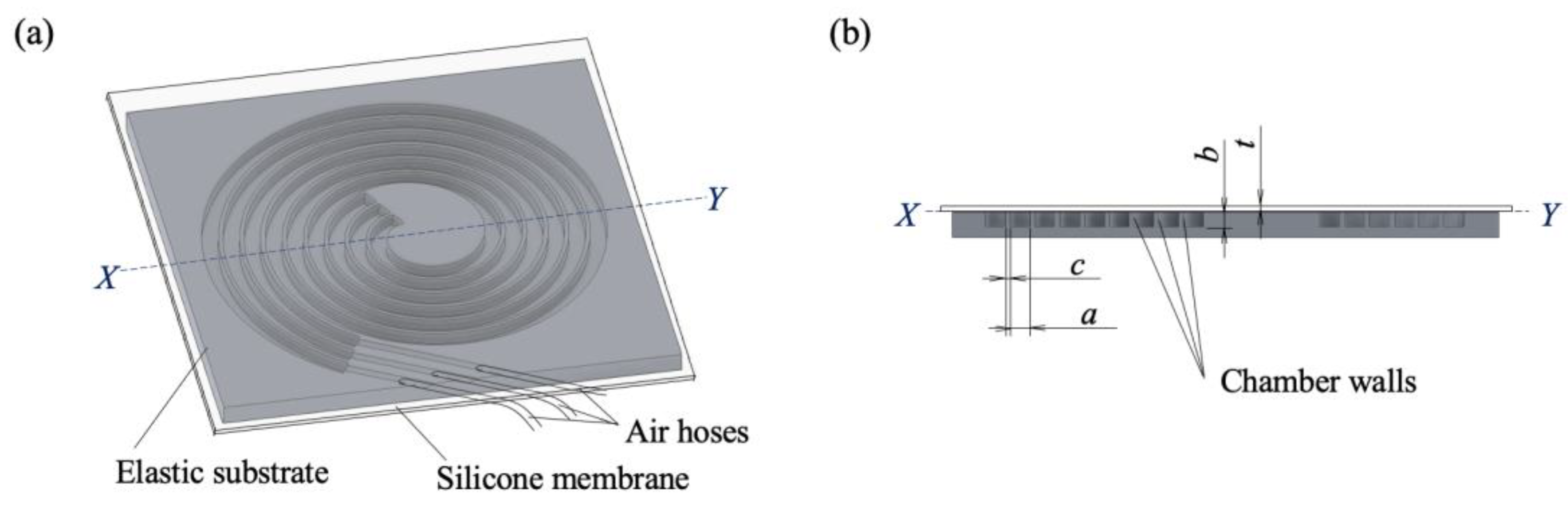
The spiral actuator, shown in Figure 1, comprises a silicone membrane mounted on an elastic substrate. Internal walls divide the inside of the actuator into three chambers, producing three inflatable air chambers. The Archimedean spiral configuration is introduced to generate an inflatable shape at the same distance from the surface during actuation. The rectangular cross-section allows the input air pressure to act on the membrane surface and internal free walls of the chambers. In Figure 1(b), a and b represent the width and depth of the chamber. Parameters c and t describe the wall and membrane thicknesses, respectively.

2.2. Actuator Principle

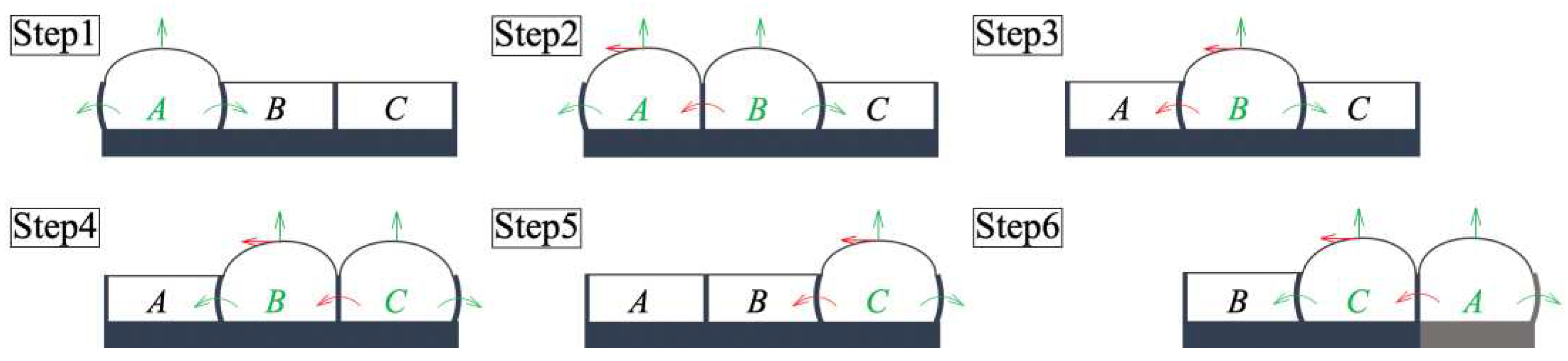
The relatively thin internal walls deform freely owing to the internal pressure difference in the air chambers. In addition, there is a shift in the center position of the pressurized membrane because of the elastic force caused by the bending motion of the walls and the initial pressure; thus, x- and y-axis displacements were generated. A schematic of the actuator used to induce traveling wave motion is shown in Figure 2. The green arrows indicate the deformation caused by the applied air pressure, and the red arrows indicate the deformations contributing to the transportation of the object.
In state Step1, chamber A is pressurized, causing the membrane to inflate and the walls of the substrate to bend outward. When air pressure is applied to adjacent chamber B in state Step2, the wall between A and B returns to the original position, and the elastic force pushes the membrane of chamber A to the left. 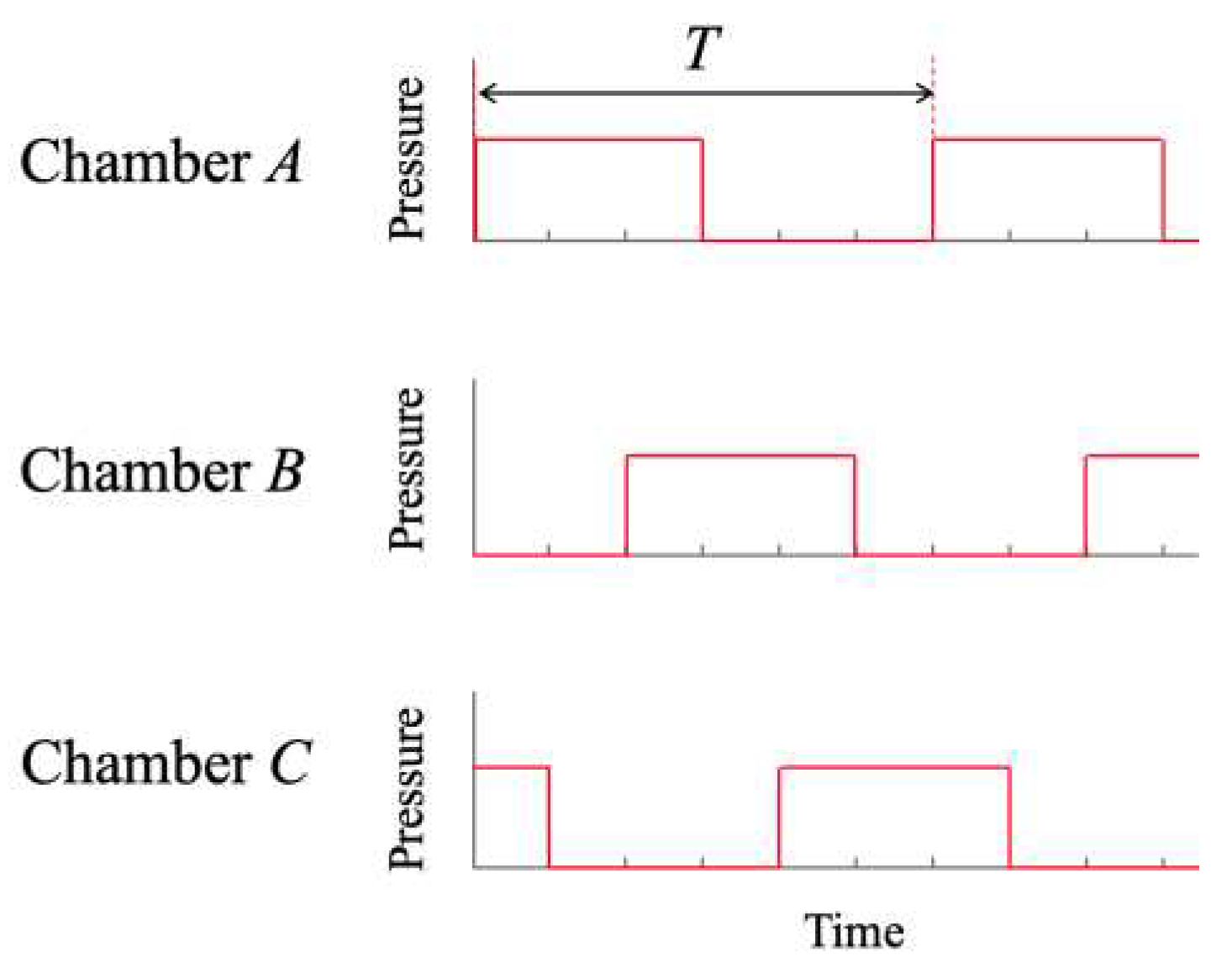In state Step3, chamber A, which inhibited the deformation of chamber B, becomes inactive, and the chamber B membrane is pushed to its center. Next, Step4 goes from Step5 to Step6 to Step1 through the same process. By repeating these steps, the actuator continues to deform and realize transportation. The periodic pressure signals applied to each chamber are shown in Figure 3. The operating frequency (1/T) was obtained from time per cycle.

2.3. Fabrication

Figure 4 shows the four main steps in the fabrication process: (a) preparation of the silicone membrane, (b) 3D printing of the mold, (c) rubber molding, and (d) direct bonding through atmospheric plasma treatment. A high-precision silicone membrane (ELASTOSIL® Film 2030, Wacker Chemie AG) was cut into sufficiently large pieces to cover the substrate while keeping the surface clean.
The rubber substrate part was made by pouring a liquid silicone (KE/CAT–1600, Shin-Etsu Silicones Corp.) into a mold. The mold was produced with specific dimensions using a polyjet 3D printer (Stratasys Objet260 Connex3, Stratasys). The material used was Vero White photosensitive resin. The two-component liquid silicone was mixed at the specified proportion in a mass ratio of 1:1 and thoroughly agitated using a mixer (ARV-310P, Thinky). There were two stages of mixing: 30 s at 2000 rpm and 45 s at 2,200 rpm. After the de-aeration process in a vacuum chamber, the rubber was cured at a room temperature of 18 °C for 24 h to maintain the flexibility properties constant.
A plasma treatment equipment (CIONE, Femto Science, Inc.) was used for direct bonding. While maintaining the air flow rate at 10 sccm (standard cubic centimeters per minute), plasma was obtained at a predetermined pressure of 7.6×102 Torr with a radio frequency power of 100 W. The base pressure was maintained at less than 5.0×10-2 Torr, and the plasma exposure time was set to 30 s.
The above process resulted in an actuator made entirely of soft material, with three chambers inside. Each chamber was connected by an air hose and had independent movement.

3. Finite Element Simulations

3.1. Finite Element Analysis Model of Spiral Actuator

Finite element analysis (FEA) of the designed actuator was performed using ANSYS 2023R1 software. Optimization aims to determine the structural parameters of the spiral actuator that maximize its output deformation. The displacement trajectories were analyzed through static structural analysis using ANSYS Workbench. The material properties were modelled as hyper elastic, incompressible materials using YEOH’s strain energy functions [17]:
W = C 10 I 1 − 3 + C 20 I 1 − 3 2 + C 30 I 1 − 3 3
where, W is the strain energy density, C10, C20, and C30 are the material properties, and I1 is the first invariant of the left CAUCHY-GREE deformation tensor.
For silicone membranes, material constants of C10, C20, and C30 are 0.1811, -0.01598, 0.00629 MPa, respectively [18]. The rubber substrate was assumed with the physical properties of a density of 1.27 g/cm3, Durometer (Type A) 45, and tensile strength of 6.5 MPa.
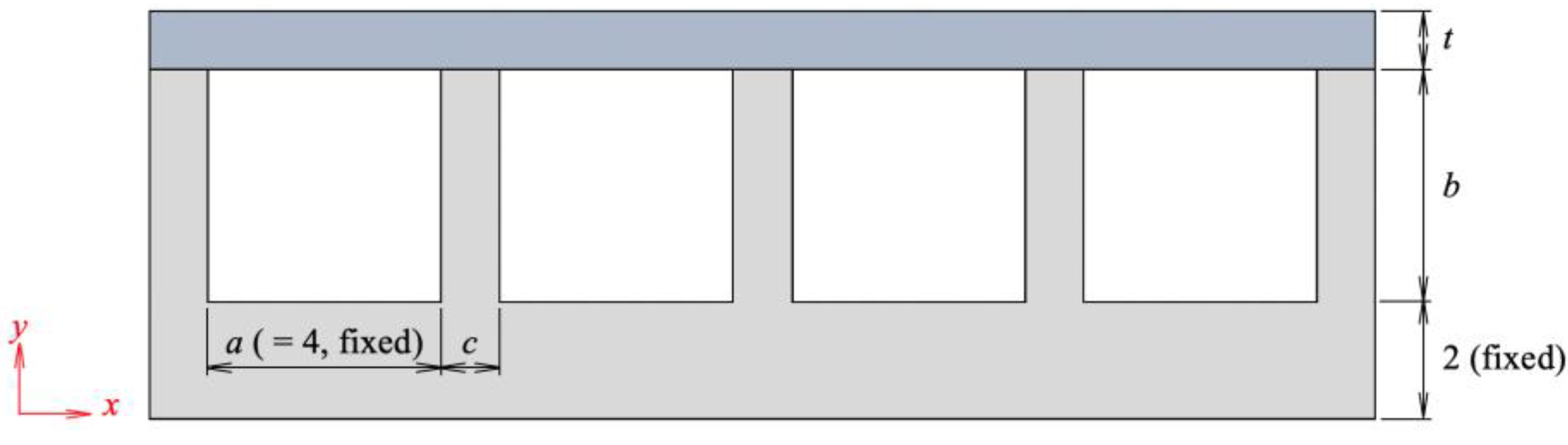
The Archimedean spiral structure has a large longitudinal dimension, which makes it suitable for use in the 2D plane strain model in the present study, as shown in Figure 5. Several structural parameters were defined, as listed in Table 1, to investigate the influence of initial structural type on actuation. The air chamber width a kept constant so that other candidate parameters in the optimization model could be expressed in terms of membrane thickness and length dimensions at several ratios: t/a, b/a, and c/a. The distance between the bottom of the rubber and chamber was fixed at 2 mm. The bottom of the rubber substrate was fixed, and the other surfaces were set to the free boundary condition. All the simulations were performed under an input air pressure of 80 kPa.
To evaluate the spiral actuator's deformation behavior and driving performance, we developed a procedure using two FEA simulations. The first simulation predicted the directional displacement along the y-axis for a pressurized membrane at the center point. The second simulation predicted the x-axis displacement produced by elastic deformation when adjacent segments were simultaneously pressurized. Displacement along the x-axis is important because it contributes to the transpiration performance of the object.

3.2. Effect of Structural Parameters

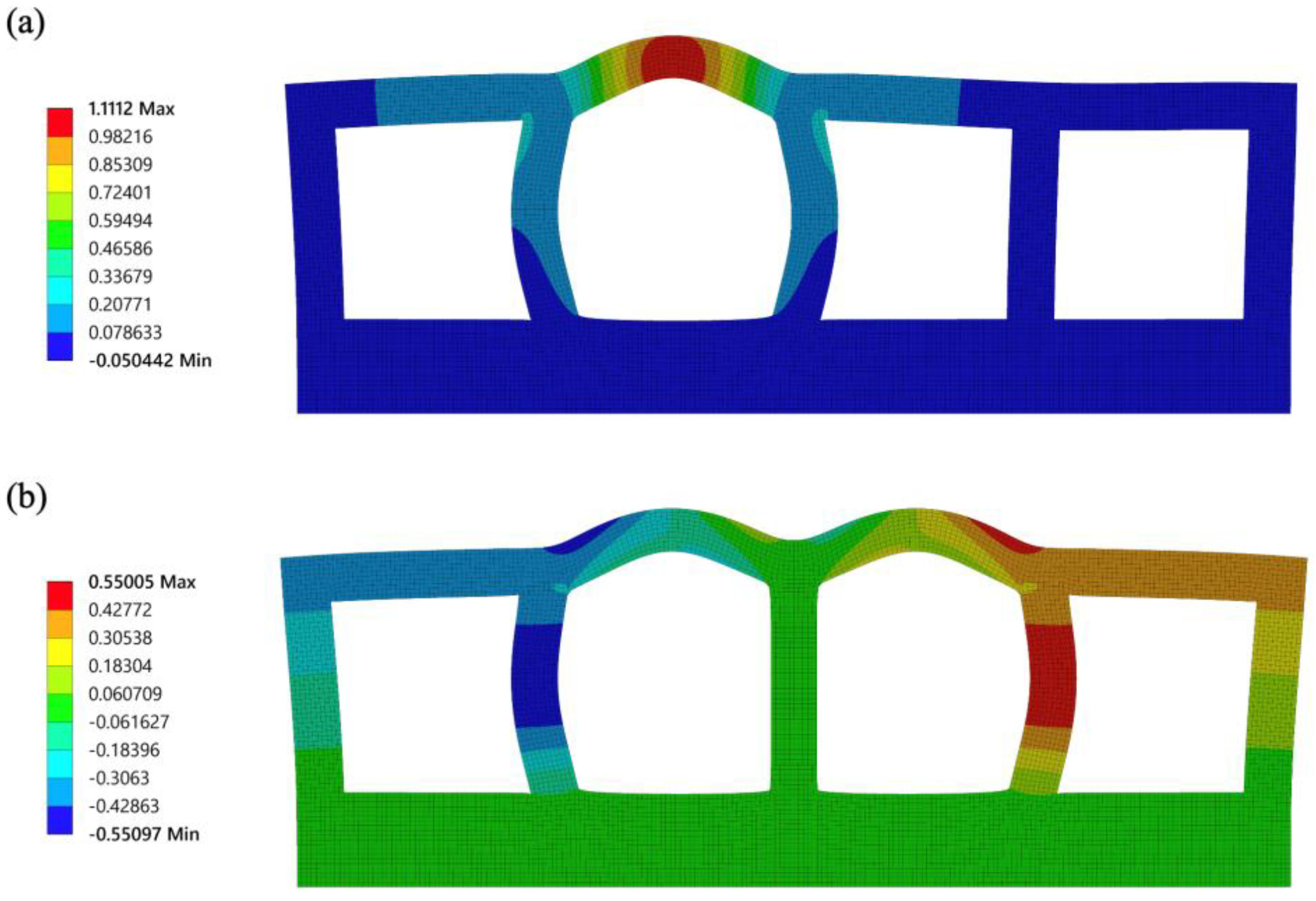
An example of the FEA simulation results is shown in Figure 6 for t = 1, b = 4, and c = 1. The predicted deformations with respect to the ratio parameter t/a are shown in Figure 7. As t/a increases, the deformation decreases. A smaller membrane thickness reduces the bending stiffness improving the actuator swell in a pressurized state. However, when the thickness is considerably reduced, the y-axis displacement exceeds the size of the actuator, but the effect on x-axis displacement is small.
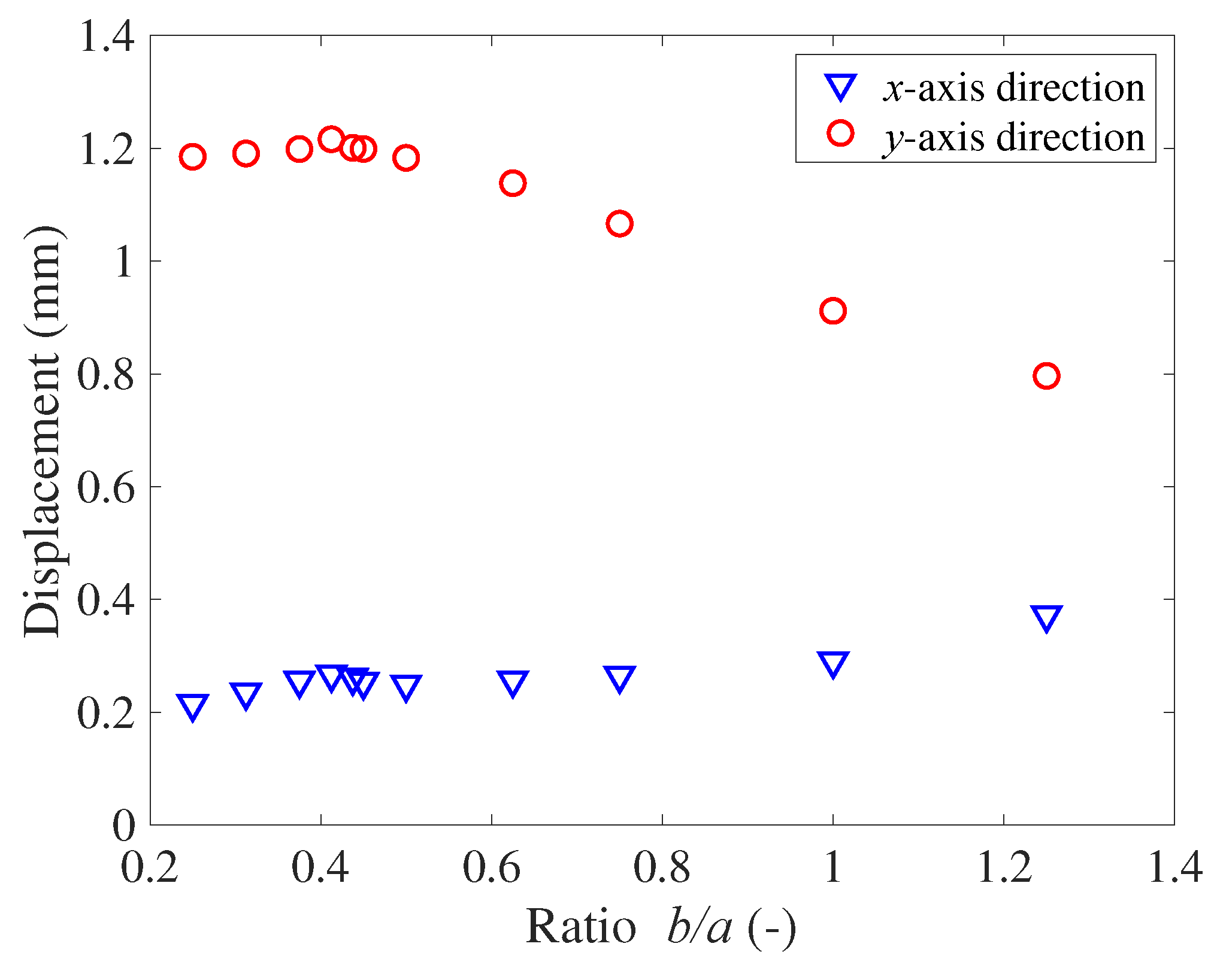
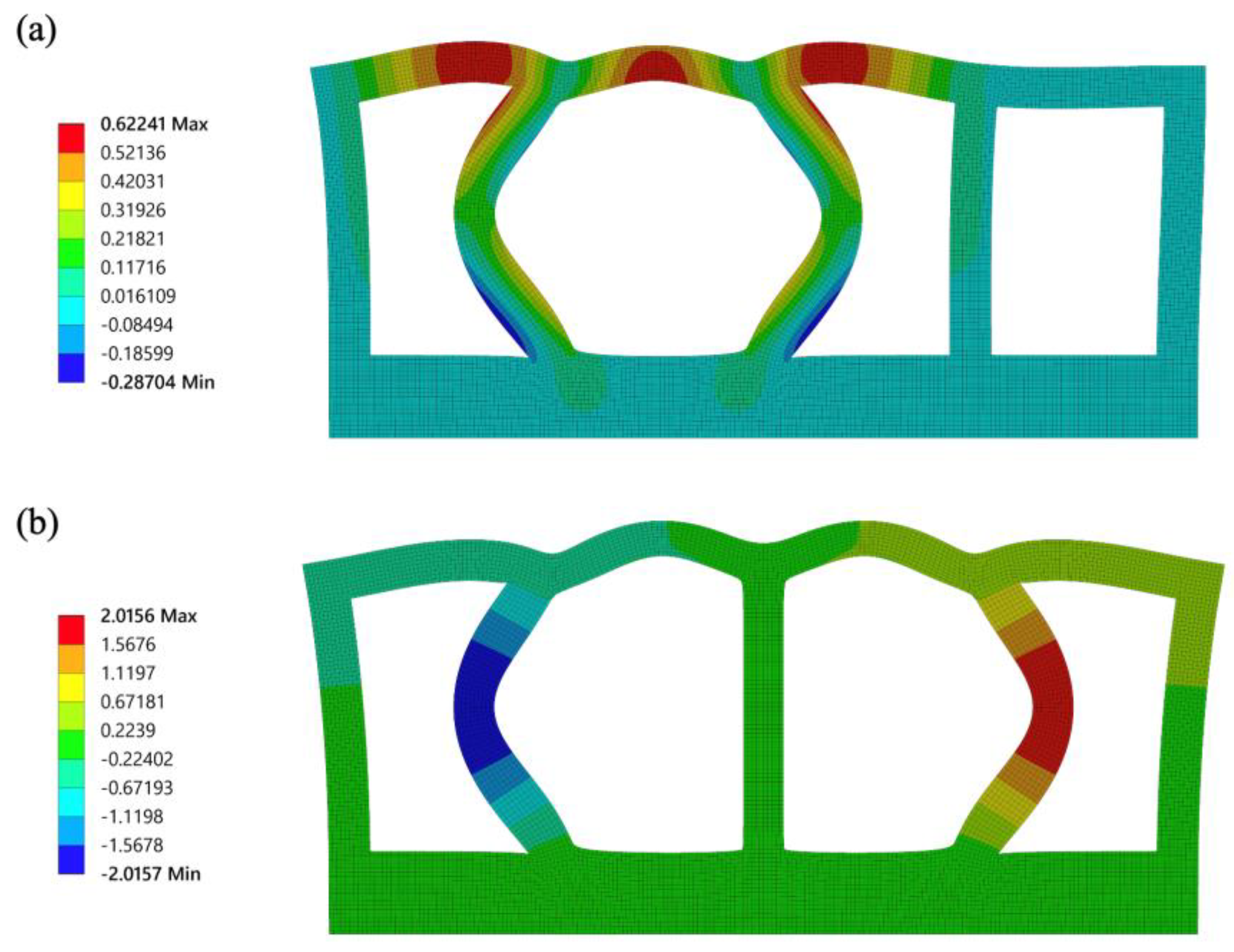
Displacements with respect to the ratio b/a are shown in Figure 8. For b/a up to 0.4, an increase in the air chamber depth increases the deformation, thus producing larger displacements under both operating conditions. When b/a exceeds 0.4, the bending of the walls increases, increasing the x-axis displacement and lowering the membrane position along the y-axis. This is the optimal condition for activating transportation. However, there is an optimal value for the chamber. For large values of b, it was observed that the center position of the membrane in a highly pressurized chamber became lower than the center position of the membrane in the other unpressurized chambers owing to excessive bending of the walls and the actuator fails to transport the object placed on its membrane surface. An example of this type of failure occurring in an FEA simulation is shown in Figure 9.
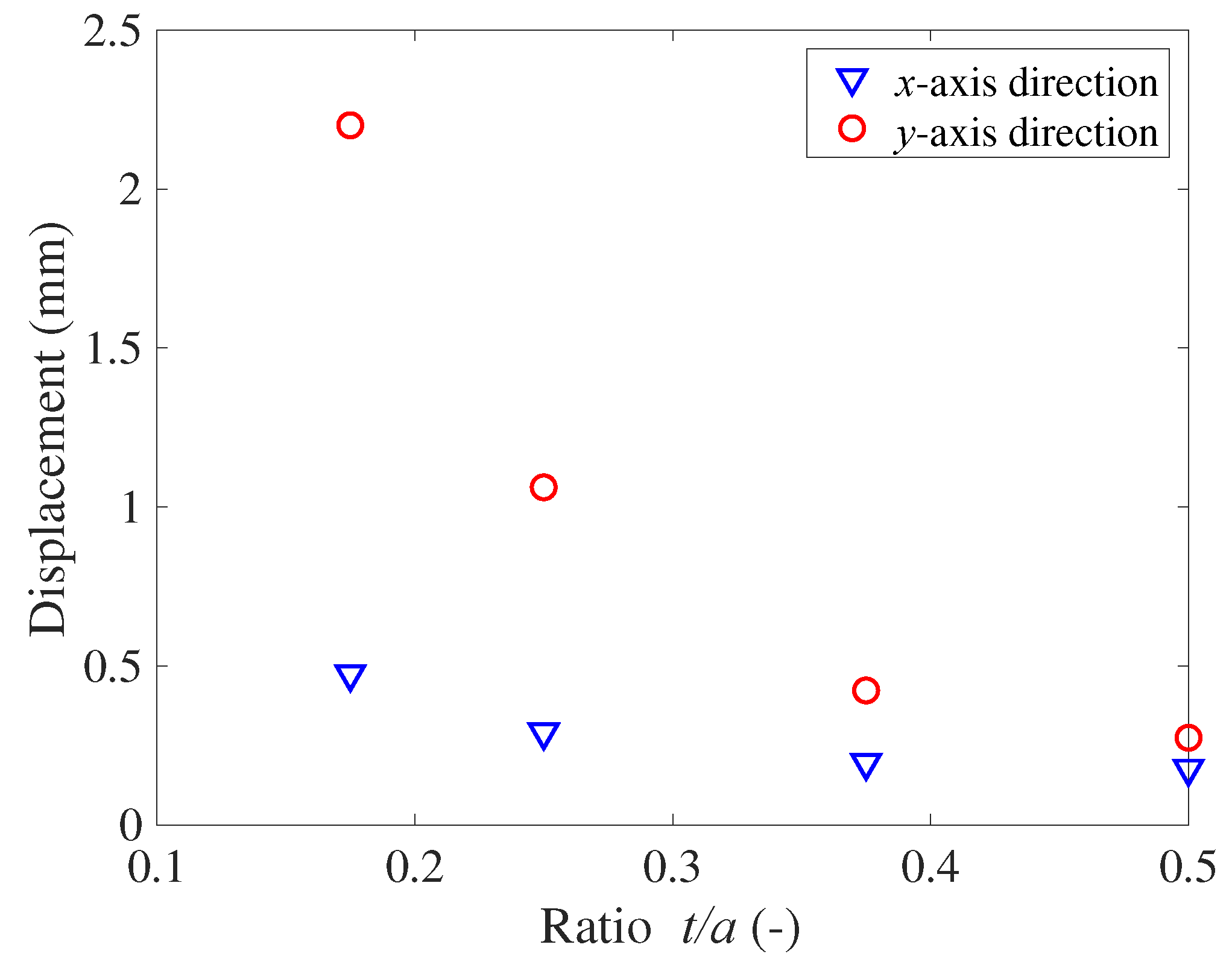
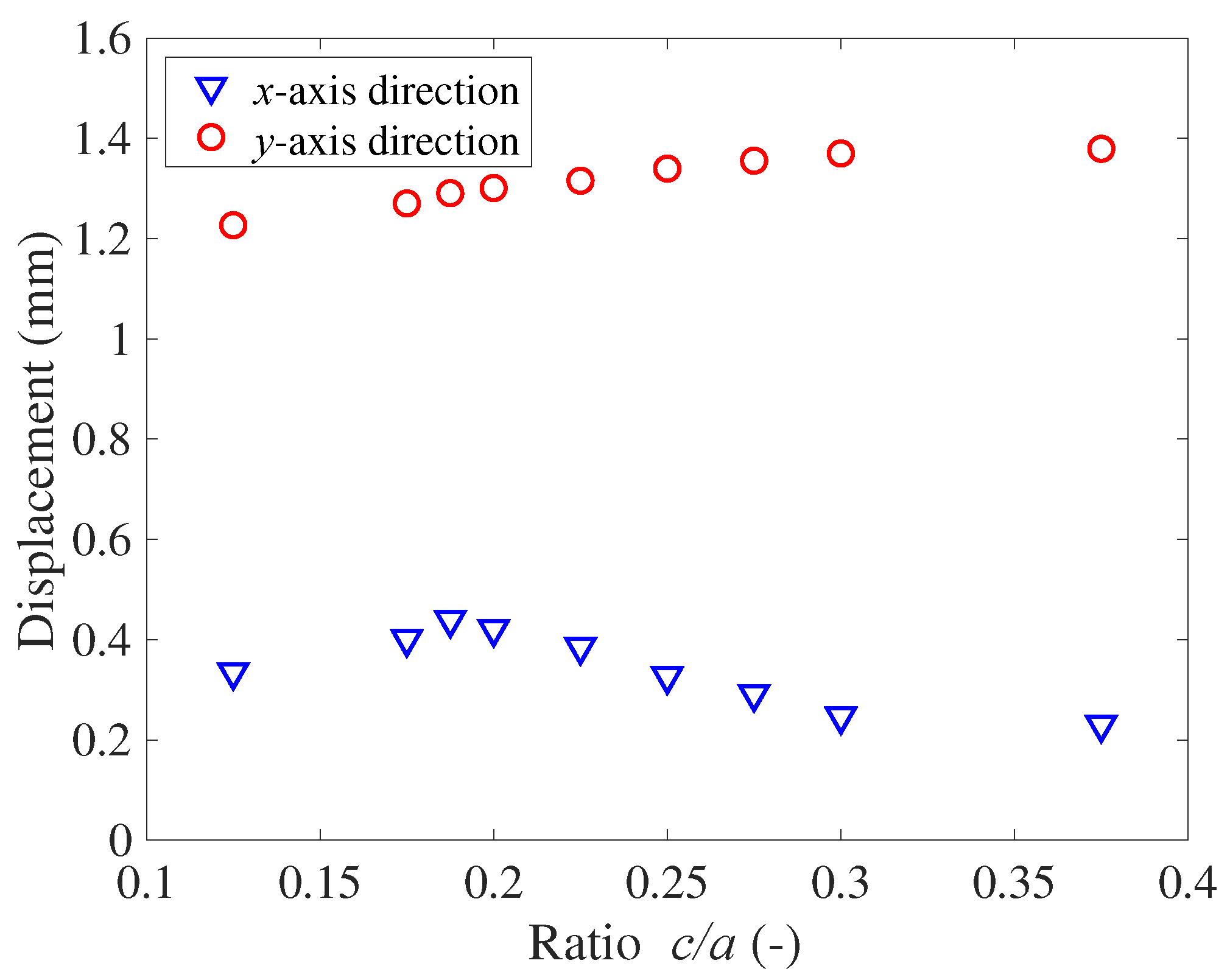
The effect of the ratio c/a on displacement is shown in Figure 10. As c/a increases, the y-axis displacement has a relatively small increment. However, for the x-axis displacement, the peak value is obtained at approximately c/a = 0.19, which is the optimal condition for object transportation. That is, an optimal structure exists to obtain a large displacement in the x-axis direction for realizing effective transportation.

4. Experiments and Discussions

4.1. Experimental Apparatus and Method

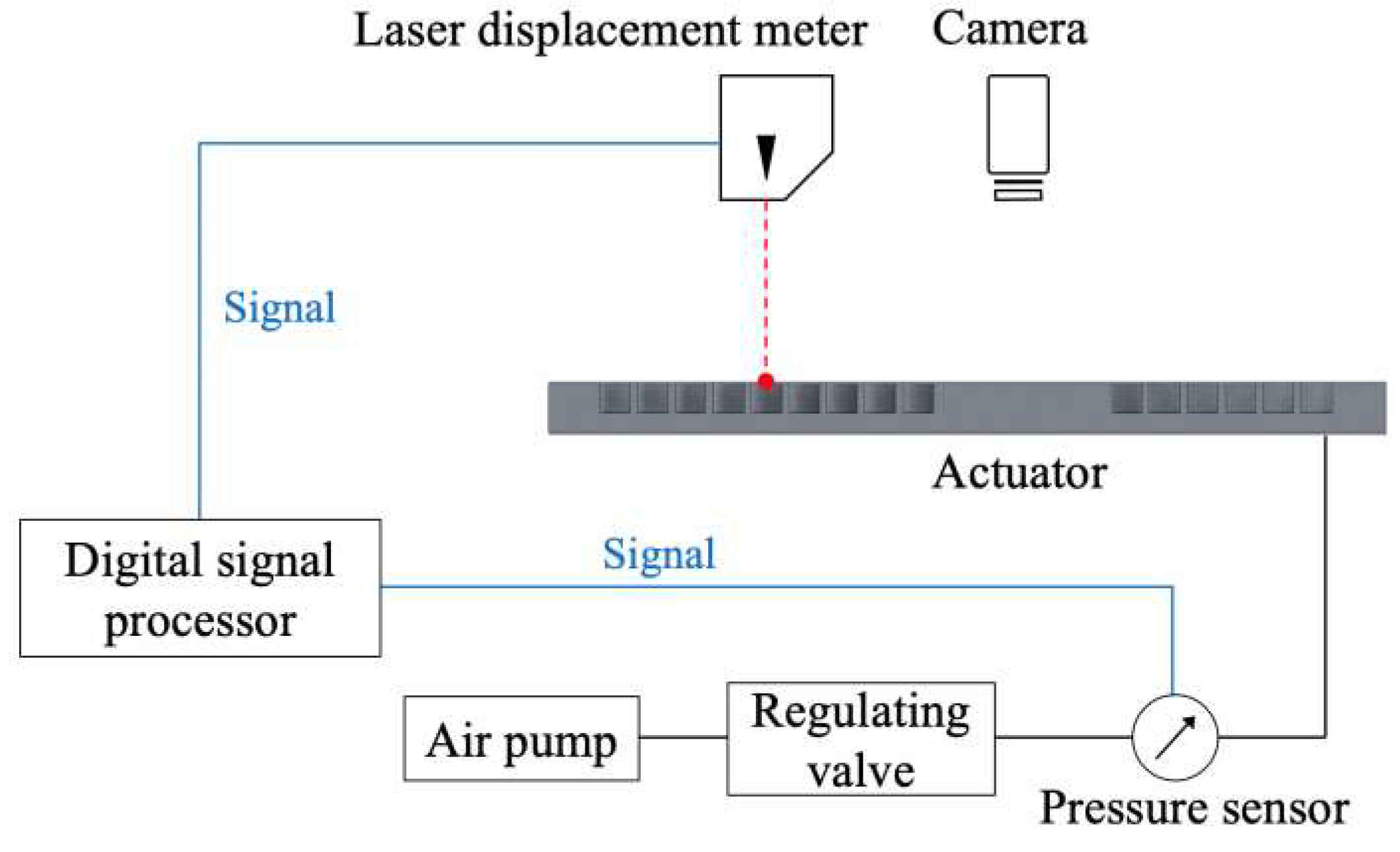
Following FEA simulations, a prototype actuator was prepared for experimental validation. The experimental setup is illustrated in Figure 11. Air pressure is supplied to expand each chamber and maintain the pressure constant; the pressure was measured using a pressure sensor (AP-C33, Keyence). The operating frequency is changed manually during the experiment and is obtained from the pressure signals recorded using an oscilloscope. The laser displacement meter (LK-G32, Keyence) displaces a point on the actuator; the resulting deformation is immediately recorded using a video camera.

4.2. Experimental Validation

Deformation tests were performed using a prototype with a, t, b, and c of 4, 1, 4, and 1 mm, respectively. The deformations were predicted using 2D and 3D finite element models and compared with the experimental results.
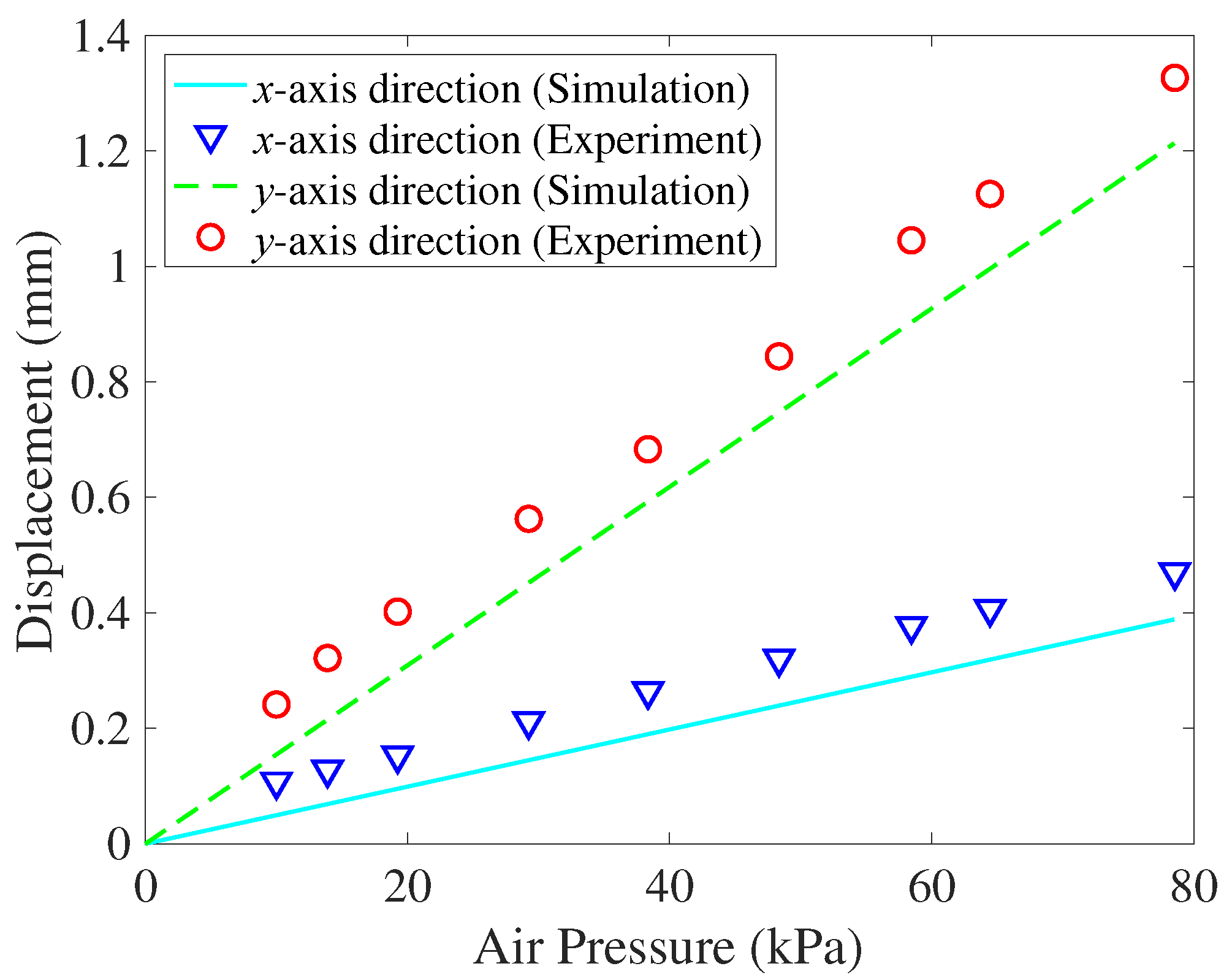
The results are presented in Figure 12 under the operation frequency of 0.32 Hz for the 2D finite element model. The deformations of the actuator increase linearly with air pressure, and the y-axis displacements are much larger than the x-axis displacements. These results provide a reasonable correlation, indicating the validity of the modeling method. The simulation and experimental results show the x-axis deformation of 0.39 and 0.47 mm, respectively, under an air pressure of 78.5 kPa. The y-axis displacement was 1.21 and 1.32 mm in the simulation and experimental results, respectively. Although the growth tendency is similar, the values of the predicted deformation were smaller probably because of the assumption of uniform wall thickness and errors in the stiffness of the simulated actuator. However, the fabrication processes or errors in the material properties can cause changes in wall thickness or stiffness coefficients.
The deformation results obtained from the simulation using the 3D finite element model are shown in Figure 13. When one chamber is pressurized, the displacement is concentrated at the center of the membrane. When the two successive chambers are pressurized, the deformation is concentrated in and around the center of the membrane. This indicates that the deformations in the two adjacent chambers affect each other and contribute to the transportation of the object, as shown in the 2D model evaluation.

4.3. Transportation Experiments

A transportation test of the spiral actuator was performed to evaluate its ability to perform spiral transportation and its velocity. The sequential deformation of successive chambers generated traveling waves on the surface, facilitating the transportation of objects. The maximum velocity obtained was 2.28 mm/s at an air pressure of 78.5 kPa at 10 Hz. Figure 14 shows objects on the actuator moving in the desired direction.
However, when comparing the results of transportation experiments with objects of different sizes and weights, it was indicated that a minimum size exists for conveying. This suggests that an object must be in effective contact with at least two consecutive chambers in order to be transported according to the actuation principle proposed. In practice, relatively large washers and paper covering two or more chambers were repeatedly transported. However, for smaller size objects such as a ball bearing and nuts, there was little or no movement. The weight of objects does not appear to have a significant impact.

5. Conclusions

A spiral pneumatic actuator consisting of a thin film and an elastic substrate with an Archimedean spiral configuration was developed to generate traveling wave motion for radial transportation. FEA simulations and experimental studies determined the deformation performance with different structural parameters for various predictable structures. The simulation model was designed using only three equidistantly placed active segments with several parameters: membrane thickness, chamber width, chamber depth, and wall thickness. A reasonable correlation is obtained between the simulation and experimental results, which can be transformed into 3D structures. The maximum deformation of the actuator was obtained considering three structural ratios: t/a, b/a, and c/a. The simulation results predicted the x, y-axis displacement for each structure and suggested the optimal structure condition to obtain a large stroke. While spiral configuration was introduced for ease of production, we propose a structure that can be applied to a variety of traveling wave actuators and evaluate their displacements. This concept can serve as a platform for other applications, such as conveying devices and crawling robots.
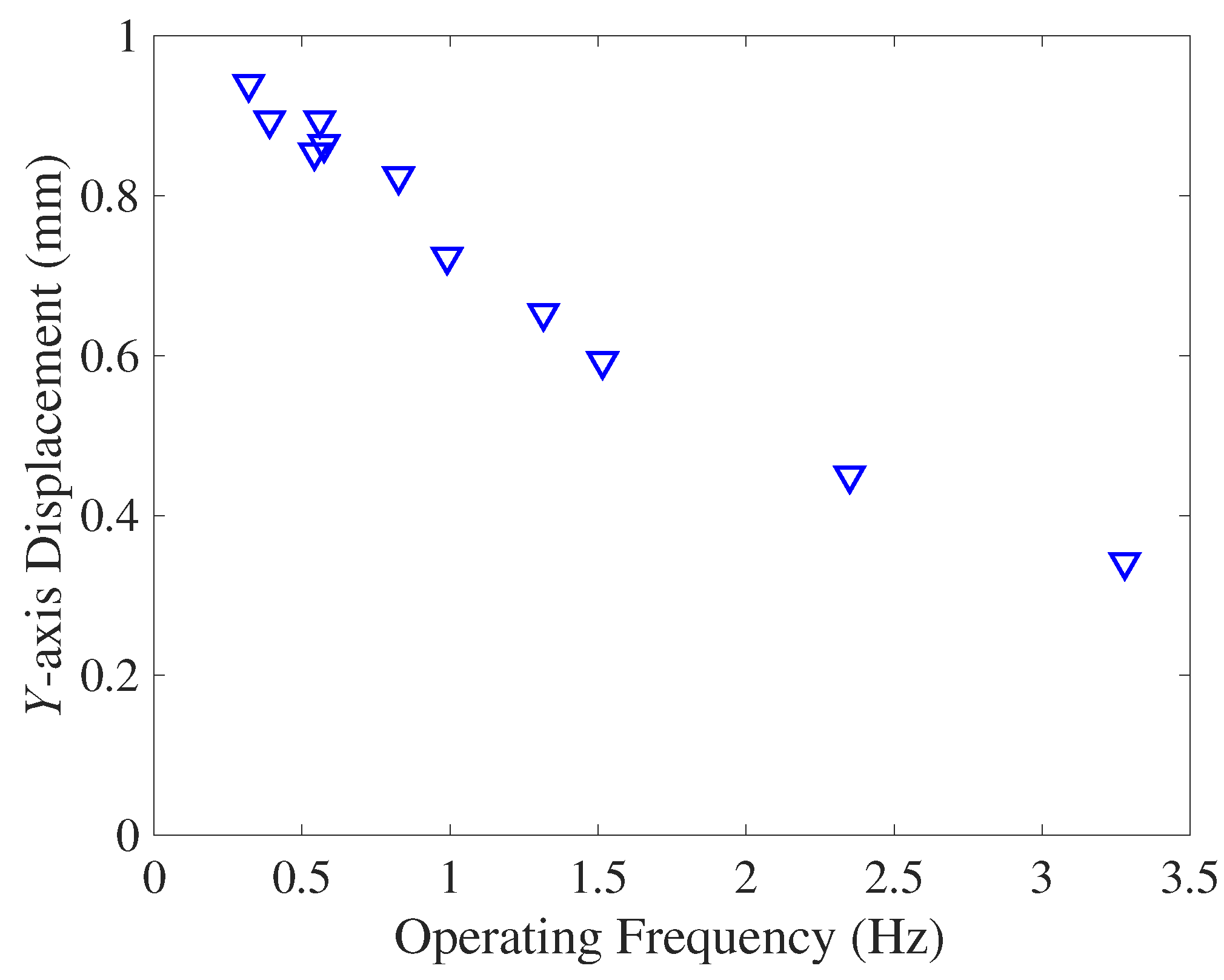
This actuator still has room for improvement in terms of operating frequency, which is currently fixed at 10 Hz. Due to the responsiveness of pneumatics, it is necessary to evaluate the effect of operating frequency on strokes and resulting transportation speed. Figure 15 shows a comparison of the y-axis displacements with respect to the operating frequency. Based on the experimental data, the displacement decreased almost linearly with operating frequency. Larger transport velocities can be expected to be obtained at lower operating frequencies, but it is important to evaluate the effect of frequency on operation. In addition, when considering contact with and transportation of objects, examination of the limits on their size should be examined. Future work will focus on robotic applications of the traveling wave actuator and discuss its usefulness.

Author Contributions

Conceptualization, K.S.; methodology, Y.J., H.N. and K.S.; validation, Y.J.; formal analysis, Y.J.; investigation, Y.J.; resources, Y.J.; writing—original draft preparation, Y.J.; writing—review and editing, H.N and K.S.; visualization, Y.J.; supervision, K.S.; project administration, K.S.; funding acquisition, K.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by JSPS KAKENHI, grant number JP18H05470.

Data Availability Statement

The datasets generated during and/or analyzed during the current study are available from the corresponding author upon reasonable request.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. Nurzaman, S.G.; Iida, F.; Margheri, L.; Laschi, C. Soft robotics on the move: Scientific networks, activities, and future challenges. Soft Robot. 2014, 1, 154–158. [Google Scholar] [CrossRef]
  2. Suzumori, K.; Asaad, S. A Novel Pneumatic Rubber Actuator for Mobile Robot Bases. In Proc. of IEEE/RSJ Int’l Conf. Intelligent Robots and Systems, 1996.
  3. Jung, K.; Koo, J.C.; Nam, J.; Lee, Y.K.; Choi, H.Y. Artificial annelid robot driven by soft actuators. Bioinsp. Biomim. 2007, 2, S42. [Google Scholar] [CrossRef] [PubMed]
  4. Lotz, P.; Matysek, M.; Schlaak, H.F. Peristaltic pump made of dielectric elastomer actuators. In Proc. Electroactive Polymer Actuators and Devices (EAPAD) Conf., 2009.
  5. Xu, L.; Chen, H.Q.; Zou, J.; Dong, W.T.; Gu, G.Y.; Zhu, L.M.; Zhu, X.Y. Bio-inspired annelid robot: A dielectric elastomer actuated soft robot, Bioinspir. Biomim. 2017, 12, 025003. [Google Scholar] [CrossRef] [PubMed]
  6. Suleman, A.; Burns, S.; Waechter, D. Design and modeling of an electrostrictive inchworm actuator. Mechatron. 2004, 14, 567–586. [Google Scholar] [CrossRef]
  7. Poole, A.D.; Booker, J.D.; Wishart, C.L.; McNeill, N.; Mellor, P.H. Performance of a Prototype Traveling wave Actuator Made From a Dielectric Elastomer. IEEE ASME Trans. Mechatron. 2012, 17, 525–533. [Google Scholar] [CrossRef]
  8. Qi, X.; Shi, H.; Pinto, T.; Tan, X. A Novel Pneumatic Soft Snake Robot Using Traveling wave Locomotion in Constrained Environments, IEEE Robot. Autom. Lett. 2020, 5, 1610–1617. [Google Scholar]
  9. Jang, Y.; Nabae, H.; Endo, G.; Suzumori, K. Analysis of the multi-balloon dielectric elastomer actuator for traveling wave motion. Sens. Actuator A Phys. 2022, 333, 113243. [Google Scholar] [CrossRef]
  10. Suzumori, K. Pneumatic Rubber Actuator Driven by Elastic Traveling Waves. JSME Int. J. C-Mech. Syst. 1999, 42, 398–403. [Google Scholar] [CrossRef]
  11. Suzumori, K.; Sekiguchi, S. Pneumatic Rubber Actuator Driven by Surface Traveling Waves, In 14th Annual Conference of the Robotics Society of Japan, 1996.
  12. Qi, X.; Shi, H.; Pinto, T.; Tan, X. A Novel Pneumatic Soft Snake Robot Using Traveling wave Locomotion in Constrained Environments. IEEE Robot. Autom. Lett. 2020, 5, 1610–1617. [Google Scholar] [CrossRef]
  13. Connolly, F.; Polygerinos, P.; Walsh, C.; Bertoldi, K. Mechanical Programming of Soft Actuators by Varying Fiber Angle. Soft Robot. 2015, 2, 26–32. [Google Scholar] [CrossRef]
  14. Smith, M.; Cacucciolo, V.; Shea, H. Fiber pumps for wearable fluidic systems. Science 2023, 379, 1327–1332. [Google Scholar] [CrossRef] [PubMed]
  15. Ran, L.; Zhou, W.; He, J.; Zhan, L.; Chen, Q.; Yu, H.; Peng, B. A novel three-dimensional contact model of piezoelectric traveling wave ultrasonic micromotor. Smart Mater. Struct. 2020, 29, 075016. [Google Scholar] [CrossRef]
  16. Holland, H. The Archimedes Spiral. Nature 1957, 179, 432–433. [Google Scholar] [CrossRef]
  17. Henke, E.-F.M.; Wilson, K.; Anderson, I. Entirely soft dielectric elastomer robots. Proc. SPIE 10163, Electroactive Polymer Actuators and Devices (EAPAD), 2017, 101631N.
  18. Holzapfel, G.A. Nonlinear solid mechanics: A continuum approach for engineering, Wiley, Chichester, Weinheim, 2010.
Preprints 71536 g001
Figure 1. Design of the spiral actuator (a) Designs of the silicone membrane, elastic substrate, and air hoses. (b) Cross-sectional view.
Figure 1. Design of the spiral actuator (a) Designs of the silicone membrane, elastic substrate, and air hoses. (b) Cross-sectional view.
Preprints 71536 g001
Preprints 71536 g002
Figure 2. Principle of operation of the actuator used to induce traveling wave motion. The expansion of the membrane and the bending motion of the thin walls, which varies with the difference in air pressure in each chamber, allows the object to be transported.
Figure 2. Principle of operation of the actuator used to induce traveling wave motion. The expansion of the membrane and the bending motion of the thin walls, which varies with the difference in air pressure in each chamber, allows the object to be transported.
Preprints 71536 g002
Preprints 71536 g003
Figure 3. Periodic pressure signal applied to each chamber. The time at which the chamber is pressurized is obtained, and the operating frequency is calculated from the time per cycle.
Figure 3. Periodic pressure signal applied to each chamber. The time at which the chamber is pressurized is obtained, and the operating frequency is calculated from the time per cycle.
Preprints 71536 g003
Preprints 71536 g004
Figure 4. Fabrication process (a) Preparation of silicone membrane (b) 3D printing of the mold (c) Rubber molding (d) Direct bonding through atmospheric plasma treatment.
Figure 4. Fabrication process (a) Preparation of silicone membrane (b) 3D printing of the mold (c) Rubber molding (d) Direct bonding through atmospheric plasma treatment.
Preprints 71536 g004
Preprints 71536 g005
Figure 5. 2D plane strain model for FEM simulation. Alli dimension units are in mm.
Figure 5. 2D plane strain model for FEM simulation. Alli dimension units are in mm.
Preprints 71536 g005
Preprints 71536 g006
Figure 6. Directional deformation obtained from FEA simulation at an air pressure of 80 kPa (a) y-axis (b) x-axis.
Figure 6. Directional deformation obtained from FEA simulation at an air pressure of 80 kPa (a) y-axis (b) x-axis.
Preprints 71536 g006
Preprints 71536 g007
Figure 7. Displacement with respect to t/a.
Figure 7. Displacement with respect to t/a.
Preprints 71536 g007
Preprints 71536 g008
Figure 8. Displacement with respect to b/a.
Figure 8. Displacement with respect to b/a.
Preprints 71536 g008
Preprints 71536 g009
Figure 9. FEA simulation for failure condition with b/a = 1.5. Direction displacement in the (a) y-axis and (b) x-axis.
Figure 9. FEA simulation for failure condition with b/a = 1.5. Direction displacement in the (a) y-axis and (b) x-axis.
Preprints 71536 g009
Preprints 71536 g010
Figure 10. Displacement with respect to c/a.
Figure 10. Displacement with respect to c/a.
Preprints 71536 g010
Preprints 71536 g011
Figure 11. Experimental apparatus.
Figure 11. Experimental apparatus.
Preprints 71536 g011
Preprints 71536 g012
Figure 12. Deformation values generated from FEA simulations and experiments.
Figure 12. Deformation values generated from FEA simulations and experiments.
Preprints 71536 g012
Preprints 71536 g013
Figure 13. Total transformation results obtained from 3D finite element model. Pressurized state of (a) one chamber and (b) two successive chambers.
Figure 13. Total transformation results obtained from 3D finite element model. Pressurized state of (a) one chamber and (b) two successive chambers.
Preprints 71536 g013
Preprints 71536 g014
Figure 14. Snapshots of the objects transported by the spiral actuator at a pressure of 78.5 kPa, 10 Hz: (a) Press from inside to outside segments; (b) press from outside to inside segments.
Figure 14. Snapshots of the objects transported by the spiral actuator at a pressure of 78.5 kPa, 10 Hz: (a) Press from inside to outside segments; (b) press from outside to inside segments.
Preprints 71536 g014
Preprints 71536 g015
Figure 15. Y-axis displacement with respect to operating frequency at a pressure of 52 kPa.
Figure 15. Y-axis displacement with respect to operating frequency at a pressure of 52 kPa.
Preprints 71536 g015
Table 1. Initial structural parameters for FEM simulation
Table 1. Initial structural parameters for FEM simulation
Parameter Value (mm)
Air chamber width, a 4.0
Membrane thickness, t 0.5-2.0
Air chamber depth, b 1.0-5.0
Wall thickness, c 0.5-2.0
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated