Study on Pricing of High Dimensional Financial Derivatives Based on Deep Learning

1. Introduction

High-dimensional (dimension ≥ 3) nonlinear partial differential equations (PDEs) are one of the topics that attract much attention and have been widely used in many fields. Many practical problems require the use of high-dimensional PDE, for example: the Schrodinger equation of the quantum many-body problem, whose PDE dimension is about three times that of the electron or quantum (particle) in the system; Black Scholes equation used to price financial derivatives, where the dimension of PDE is the number of relevant financial assets under consideration; Hamilton-Jacobi-Bellman equation in dynamic programming. Although high-dimensional nonlinear partial differential equations have strong practicability, there are few explicit solutions, or the analytical expressions are too complex, so they often need to be solved by some numerical methods. However, in practical applications, high-dimensional nonlinear partial differential equations are usually very difficult to solve, which is still one of the challenging topics in the academic community. The difficulty is that, due to the " curse of dimensionality " [1], the time complexity of traditional numerical solutions will increase exponentially with the increase of dimensions, thus requiring a lot of computing resources. However, because these equations can solve many practical problems, we urgently need to approximate the numerical solution of this high-dimensional nonlinear partial differential equation.

In recent years, deep learning algorithms have gradually emerged and achieved success in many application fields. Therefore, many scientists try to apply deep learning algorithms to solve high-dimensional PDE problems, and have achieved good results. In 2017, E W. Han et al. [2,3] proposed the deep BSDE method and systematically applied the deep learning to general high-dimensional PDE for the first time. After that, Han et al. (2018) [4] further extended the deep BSDE method to the field of random games, and also achieved good results. Beck et al. (2019) [5] extended the method to the case of 2BSDE and the corresponding fully nonlinear PDE. Raissi et al.(2017)[6] use the latest development of probabilistic machine learning to infer the control equation represented by a parametric linear operator, and modifies the prior value of the Gaussian process according to the special form of such operator, which is then used to infer the parameters of the linear equation from the scarce and possibly noisy observations. Sirignano et al. (2018) [7] proposed to use a deep neural network approach to approximate the solution of high-dimensional PDE. In a batch of randomly sampled time and space, the network was trained to meet differential operators, initial conditions and boundary conditions. The above series of achievements show that it is feasible to solve high-dimensional PDE with deep learning-based method.

In this paper, we mainly apply the deep learning algorithm to a special class of high-dimensional nonlinear partial differential equations with jumps, and obtain a numerical solution of the equation. Specifically, through mathematical derivation and equivalent formula expression of high-dimensional PDE and backward stochastic differential equation, the problem of solving partial differential equation is equivalent to the problem of solving BSDE, and then it is transformed into a stochastic control problem. Then, a deep neural network framework is designed to fit the problem. Therefore, this method can be used to solve high-dimensional PDE and corresponding backward stochastic differential equations simultaneously.

The method introduced in this paper to solve a kind of high-dimensional PDE with jump by using deep learning is mainly applied in the financial field, and has important applications in financial derivatives pricing, insurance investment decision-making, small and micro enterprise financing, risk measurement mechanism and other issues.

2. Background Knowledge

2.1. A class of PDE

The Materials and Methods should be described with sufficient details to allow others to replicate and build on the published results. Please note that the publication of your manuscript implicates that you must make all materials, data, computer code, and protocols associated with the publication available to readers. Please disclose at the submission stage any restrictions on the availability of materials or information. New methods and protocols should be described in detail while well-established methods can be briefly described and appropriately cited.

We consider a class of semilinear parabolic PDE with jump term in the following form:

Let $T\in \left(0,\infty \right)$, $d\in \mathbb{N}$, and $f:\mathbb{R}\times {\mathbb{R}}^d\to \mathbb{R}$ and $g:{\mathbb{R}}^d\to \mathbb{R}$ be continuous functions. For all $t\in \left[0,T\right]$, $x\in {\mathbb{R}}^d$, function to be solved $u=u\left(t,x\right)\in C^{\mathrm{1,2}}\left(\left[0,T\right]\times {\mathbb{R}}^d,\mathbb{R}\right)$has a terminal value condition $u\left(T,x\right)=g\left(x\right)$ and satisfies:

$$\frac{\partial u}{\partial t}\left(t,x\right)-Lu\left(t,x\right)-f\left(t,x,u\left(t,x\right),{{\sigma }^T\left(t,x\right)\nabla }_{x}u\left(t,x\right),Bu\left(t,x\right)\right)=0$$

(2.1)

Where we introduce two operators:

$$Lu\left(t,x\right)={\nabla }_{x}u\left(t,x\right)\left[\mu \left(x\right)-\lambda \beta \left(x\right)\right]+\frac{1}{2}Tr\left({\sigma \sigma }^T\left(t,x\right)\left({Hess}_{x}u\right)\left(t,x\right)\right)+\lambda \left\{u\left(t,x+\beta \left(x\right)\right)-u\left(t,x\right)\right\}$$

(2.2)

$$Bu\left(t,x\right)=u\left(t,x+\beta \left(x\right)\right)-u\left(t,x\right)$$

(2.3)

Here $t$ is the time variable, $x$ is the $d$-dimensional space variable, $f$ is the nonlinear part of the equation, ${\nabla }_{x}u$ represents the gradient of $u$ with respect to $x$, ${Hess}_{x}u$ represents the Hessian matrix of $u$ with respect to $x$. In particular, this equation can be regarded as a special case of partial integro-differential equation. What we are interested in is the solution at $t=0$, $x=\xi \in {\mathbb{R}}^d$, which is $u\left(0,\xi \right)$.

2.2. Backward Stochastic Differential Equations with Jumps

Let $\left(\mathsf{\Omega },\mathcal{F},P\right)$ be a complete probability space, $W:\left[0,T\right]\times \mathsf{\Omega }\to {\mathbb{R}}^d$ be the d-dimensional standard Brownian motion in this probability space, ${\left\{{\mathcal{F}}_t\right\}}_{t\in \left[0,T\right]}$ be the normal filtration generated by $W$ in space $\left(\mathsf{\Omega },\mathcal{F},P\right)$. ${\left\{X_t\right\}}_{0\le t\le T}$, ${\left\{Y_t\right\}}_{0\le t\le T}$, ${\left\{Z_t\right\}}_{0\le t\le T}$, ${\left\{U_t\right\}}_{0\le t\le T}$are integrable $\mathbb{F}$-adapted stochastic processes. For a class of forward backward stochastic differential equations with jump terms, it has the following form:

$$\left\{\begin{array}{c}{X}_t=X_0+{\int }_0^t\mu \left(s,X_s\right)ds+{\int }_0^t\sigma \left(s,X_s\right)d{W}_t+{\int }_0^t\beta \left({s,X}_s\right)d{\tilde{N}}_s\\ Y_t=g\left(X_T\right)+{\int }_t^{T}f\left(s,X_s,Y_s,Z_s,U_s\right)ds-{\int }_t^T{Z}_{s}d{W}_s-{\int }_t^T{U}_{s}d{\tilde{N}}_s\end{array}\right.$$

(2.4)

Where ${d\tilde{N}}_t$ is the compensated Poisson measure, ${\tilde{N}}_t$ is a centralized Poisson process with the compensator intensity $\lambda t$ such that ${\tilde{N}}_t=N_t-\lambda t$, $N_t$ is the Poisson process in the probability space $\left(\mathsf{\Omega },\mathcal{F},P\right)$ such that $E\left(N_t\right)=\lambda t$.

Under the standard Lipschitz assumptions on the coefficients $\mu$, $\sigma$, $\beta$, $f$, $g$, the existence and uniqueness of the solution have been proved. [8]

2.3. The Generalized Nonlinear Feynman-Kac Formula

Under the appropriate regularization assumption, and $u\left(t,x\right)\in C\left([0,T]\times R^d\right)$ satisfies equation (1) and linear growth condition $\left|u\left(t,x\right)\right|\le K\left(1+\left|x\right|\right)$, $\left|{\nabla }_{x}u\left(t,x\right)\right|\le K\left(1+\left|x\right|\right)$, $\left(t,x\right)\in C\left([0,T]\times R^d\right)$, the following relationships are established almost everywhere:

$$Y_t=u\left(t,x\right)\in R$$

(2.5)

$$Z_t={\nabla }_{x}u\left(t,x\right)\sigma \left(t,x\right)\in R^d$$

(2.6)

$$U_t=u\left(t,x+\beta \left(x,·\right)\right)-u\left(t,x\right)\in R$$

(2.7)

$\left(Y_t,Z_t,U_t\right)$ is the only solution of BSDE. [9,10]

2.4. Improvement of Neural Network Parameter Optimization Algorithm

Adam (Adaptive Moment Estimation) algorithm is an algorithm that combines RMSProp algorithm with classical momentum in physics. It dynamically adjusts the learning rate of each parameter by using the first-order moment estimation and second-order moment estimation of gradient. Adam optimizer is one of the most popular classical optimizers in deep learning, and it also shows excellent performance in practice. [11]

Although Adam combines RMSprop with momentum, the adaptive moment estimation with Nesterov acceleration is often better than momentum. Therefore, we consider introducing Nesterov acceleration effect [12] into Adam algorithm, that is, using Nadam (Nesterov-accelerated Adaptive Moment Estimation) optimization algorithm. The calculation formula is as follows:

$${\widehat{g}}_t=\frac{g_t}{1-{\prod }_{i=1}^t{\mu }_i}$$

(2.8)

$$m_t=\mu \mathrm{*}{m}_{t-1}+\left(1-\mu \right)\mathrm{*}{g}_t$$

(2.9)

$${\widehat{m}}_t=\frac{m_t}{1-{\prod }_{i=1}^{t+1}{\mu }_i}$$

(2.10)

$$n_t=\nu \mathrm{*}{n}_{t-1}+\left(1-\nu \right)\mathrm{*}{g}_t^2$$

(2.11)

$${\widehat{n}}_t=\frac{n_t}{1-{\nu }^t}$$

(2.12)

$${\overline{m}}_t=\left(1-{\mu }_t\right){\widehat{g}}_t+{\mu }_{t+1}{\widehat{m}}_t$$

(2.13)

$${\theta }_t={\theta }_{t-1}-\eta \frac{{\overline{m}}_t}{\sqrt{{\widehat{n}}_t}+\epsilon }$$

(2.14)

For parameters of neural network ${\theta }_t$ , $g_t$ is the gradient of ${\theta }_t$.Besides, $m_t$ and $n_t$ are the first order moment estimate and the second order moment estimate of the gradient respectively, which can be regarded as the estimation of the expectation $E\left|g_t\right|$ and $E\left|g_t^2\right|$, here $\mu$ and $\nu$ are their attenuation rates respectively. Moreover, ${\widehat{m}}_t$ and ${\widehat{n}}_t$ are the correction for $m_t$ and $n_t$, which can be approximated as an unbiased estimate of the expectation. It can be seen that Nadam has a stronger constraint on the learning rate, and has a more direct impact on the update of the gradient. Therefore, we try to apply the new optimization algorithm to our method and compare the results with the traditional Adam algorithm.

3. Main Theorem

3.1. Basic Ideas

In this paper we propose a deep learning-based PDE numerical solution for nonlinear PDE with jump terms in the form of Equation (2.1). The basic idea of the algorithm are as follows:

By using the generalized nonlinear Feynman-Kac formula, the PDEs to be solved can be equivalently constructed using BSDEs with jumps.

Taking the gradient operator and the jump term of the solution of the function to be solved as policy functions, the problem of solving the numerical solution of BSDEs can be considered as a stochastic control problem, which can be further considered as a reinforcement learning problem.

Two different depth neural networks are used to approximate this pair of high-dimensional strategy functions, and the neural networks are trained by deep learning method to obtain the numerical solution of the original equation.

3.2. Transforming the Nonlinear PDE Numerical Solution Problem into a Stochastic Control Problem

It is well known that PDE and BSDE can be linked by the generalized nonlinear Feynman-Kac formula under appropriate assumptions. Thus, the solution $Y_t\left(x\right)$ of the above equation is equivalent to the viscous solution $u\left(t,x\right)$ of the semilinear parabolic PDE partial differential equation with jump term in (2.1). [13,14] Because the numerical solution of the traditional partial differential equation does not perform well in high dimensions, we can estimate the solution $u\left(t,x\right)$ of equation (2.1) by estimating the solution of equation (2.4).

For the stochastic control problem related to equation (2.4), under the appropriate regularity assumption, for the nonlinear function $f$, it holds that a group of solution functions composed of $u\left(0,\xi \right)\in \mathbb{R}$, ${\nabla }_{x}u\left(t,x\right)\in \mathcal{A}$ and $u\left(t,x+\beta \left(x\right)\right)-u\left(t,x\right)\in \mathbb{R}$ is the unique global minimum of the following functions $\left(y,Z,U\right)\in \mathbb{R}\times \mathcal{A}\times \mathbb{R}$:

$$\left(y,Z,U\right)⟼\mathbb{E}\left[{\left|Y_T^{y,Z,U}-g\left(X_T\right)\right|}^2\right]\in \left[0,\mathrm{\infty }\right]$$

(3.1)

We regard $Z$ and $U$ as the policy function of deep learning problem, and use DNN to approximate $Z$ and $U$. In this way, the stochastic process $u\left(t,x\right)$ corresponds to the solution function of the stochastic control problem and can be solved by using the strategy functions $Z$ and $U$, and thus we can transform the nonlinear partial differential equation into a stochastic control problem.

3.3. Forward Discretization of the Backward Stochastic Differential Equations with Jumps

For the following BSDE:

$$\left\{\begin{array}{c}{X}_t=x+{\int }_0^t\mu \left(s,X_s\right)ds+{\int }_0^t\sigma \left(s,X_s\right)d{W}_t+{\int }_0^t\beta \left({s,X}_s\right)d{\tilde{N}}_s\\ Y_t=g\left(X_T\right)+{\int }_t^{T}f\left(s,X_s,Y_s,Z_s\right)ds-{\int }_t^T{Z}_{s}d{W}_s-{\int }_t^T{U}_{s}d{\tilde{N}}_s\end{array}\right.$$

(3.2)

We will discretize it in the time dimension and divide the time interval $[0,T]$ into N partitions, so that $t_0,t_1,\dots ,t_N\in [0,T]$ and $0=t_0<t_1<\dots <t_N=T$, assuming $t_i-t_{i-1}=h$, we use Euler scheme for discretization:

$$X_{t_{n+1}}-X_{t_n}=\mu \left(t_n,X_{t_n}\right)∆t_n+\sigma \left(t_n,X_{t_n}\right)∆W_{t_n}+\beta \left(t_n,X_{t_n}\right)∆{\tilde{N}}_{t_n}$$

(3.3)

$$Y_{t_{n+1}}=Y_{t_n}-f\left(t_n,X_{t_n},Y_{t_n},\left(\nabla u\sigma \right)\left(t_n,X_{t_n}\right)\right)∆t_n+〈\left(\nabla u\sigma \right)\left(t_n,X_{t_n}\right),W_{t_{n+1}}-W_{t_n}〉+〈U\left(t_n,X_{t_n}\right),{\tilde{N}}_{t_{n+1}}-{\tilde{N}}_{t_n}〉$$

(3.4)

Where $∆t_n=t_{n+1}-t_n$, $∆W_{t_n}=W_{t_{n+1}}-W_{t_n}$, $∆{\tilde{N}}_{t_n}={\tilde{N}}_{t_{n+1}}-{\tilde{N}}_{t_n}$.

In this way we can start from the initial value $X_0$ of (3.2) and finally obtain the approximation of the Euler format of (3.2) at N partitions.

3.4. General Framework for Neural Networks

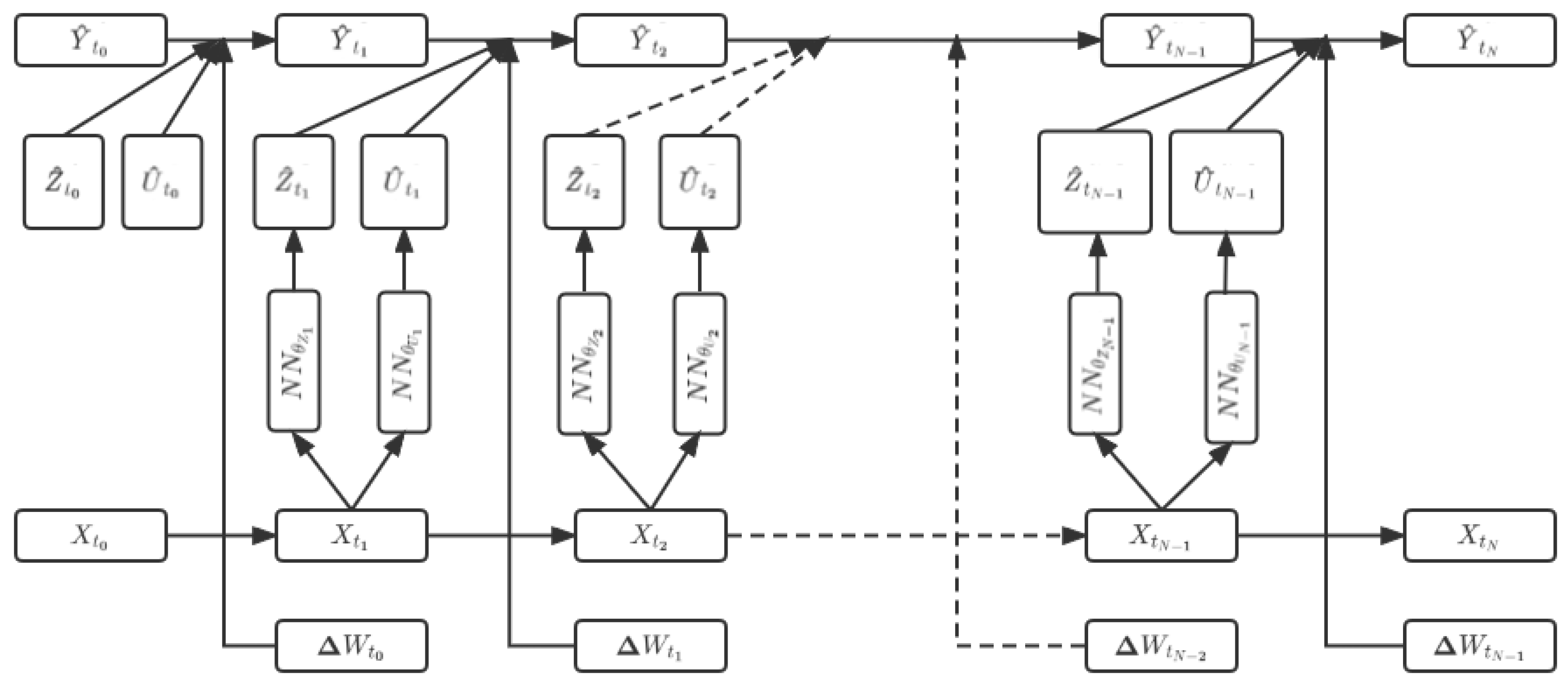
Two feedforward neural networks are established at each time step $t=t_n$ in (3.3) and (3.4). One is to approximate the gradient of the unknown solution, which means to approximate the function $X_{t_n}\to Z_{t_n}:{\nabla }_{x}u\left(t,x\right)\sigma \left(t,x\right)$, and this neural network is recorded as ${\mathrm{N}\mathrm{N}}_{{\mathsf{\theta }}_{{\mathrm{z}}_{\mathrm{n}}}}\left(\mathrm{x}\right)$, such that ${\mathsf{\theta }}_{{\mathrm{z}}_{\mathrm{n}}}$ represents all parameters of this neural network and $Z_{\mathrm{n}}$ indicates that this neural network is used to approximate $Z_{t_n}$ at time $t_n$. Another is to approximate the jump process of the unknown solution, which means to approximate the function $X_{t_n}\to U_{t_n}:u\left(t,x+\beta \left(x,·\right)\right)-u\left(t,x\right)$ and this neural network is recorded as ${\mathrm{N}\mathrm{N}}_{{\mathsf{\theta }}_{{\mathrm{U}}_{\mathrm{n}}}}\left(\mathrm{x}\right)$, such that ${\mathsf{\theta }}_{{\mathrm{U}}_{\mathrm{n}}}$ represents all parameters of this neural network, and ${\mathrm{U}}_{\mathrm{n}}$ indicates that this network is used to approximate $U_{t_n}$ at time $t_n$. For the convenience of expression, we can suppose ${\mathsf{\theta }}_Z=\left\{{\mathsf{\theta }}_{{\mathrm{Z}}_1},{\dots ,\mathsf{\theta }}_{{\mathrm{Z}}_{\mathrm{N}-1}}\right\}$,${\mathsf{\theta }}_U=\left\{{\mathsf{\theta }}_{{\mathrm{U}}_1},{\dots ,\mathsf{\theta }}_{{\mathrm{U}}_{\mathrm{N}-1}}\right\}$, $\theta =\left\{{\mathsf{\theta }}_Z,{\mathsf{\theta }}_{\mathrm{U}}\right\}$. As shown in Figure 1, all sub neural networks are stacked together to form a complete neural network.

$X_{t_0}=\xi \in {\mathbb{R}}^d$ in the initial layer is a random variable. $u\left(t_0,X_{t_0}\right)$, ${\nabla }_{x}u\left(t_0,X_{t_0}\right)$ and $u\left(t_0,X_{t_0}+\beta \left(X_{t_0},·\right)\right)-u\left(t_0,X_{t_0}\right)$ in the initial layer is unknown, and we treat it as parameters of the neural network. And $u\left(t_0,X_{t_0}\right)$, ${\nabla }_{x}u\left(t_0,X_{t_0}\right)$ and $u\left(t_0,X_{t_0}+\beta \left(X_{t_0},·\right)\right)-u\left(t_0,X_{t_0}\right)$ corresponds to the value of the BSDE with jumps as follows:

$$Y_0=u\left(0,\xi \right)$$

(3.5)

$$Z_0={\nabla }_{x}u\left(t_0,\xi \right)$$

(3.6)

And

$$U_0=u\left(t_0,\xi +\beta \left(\xi ,·\right)\right)-u\left(t_0,\xi \right)$$

(3.7)

In this neural network, the $X_{t_n}$ of the current layer is related to the $X_{t_{n-1}}$ of the previous layer, and at the same time the $u\left(t_n,X_{t_n}\right)$ of the current layer is related to the $X_{t_{n-1}}$, $u\left(t_{n-1},X_{t_{n-1}}\right)$, ${\nabla }_{x}u\left(t_{n-1},X_{t_{n-1}}\right)$ and $u\left(t_{n-1},X_{t_{n-1}}+\beta \left(X_{t_{n-1}},·\right)\right)-u\left(t_{n-1},X_{t_{n-1}}\right)$ of the previous layer. However, there are no ${\nabla }_{x}u\left(t_{n-1},X_{t_{n-1}}\right)$ and $u\left(t_{n-1},X_{t_{n-1}}+\beta \left(X_{t_{n-1}},·\right)\right)-u\left(t_{n-1},X_{t_{n-1}}\right)$ in the current layer. Therefore, as shown in the Figure 1, our solution is to start from the $X_{t_n}$ of the current layer to build two sub neural networks to represent these two values. In addition, the construction of the final loss function can be obtained from a given terminal value condition $u\left(T,x\right)$, that is, $u\left(t_N,X_{t_N}\right)$ in the neural network, which also corresponds to $g\left(X_T\right)$ in the nonlinear Feynman-Kac formula.

Specifically, for $n=\left\{\mathrm{0,1},\dots ,N-1\right\}$, we can set ${\widehat{Y}}_0$ , ${\widehat{Z}}_0$ as parameters to obtain the appropriate Euler approximation $\widehat{Y}$ of the process forward:

$${\widehat{Y}}_{t_{n+1}}={\widehat{Y}}_{t_n}-f\left(t_n,X_{t_n},{\widehat{Y}}_{t_n},{\widehat{Z}}_{t_n}\right)∆t_n+〈{\widehat{Z}}_{t_n},∆W_{t_n}〉+〈{\widehat{U}}_{t_n},∆{\tilde{N}}_{t_n}〉$$

(3.8)

For all appropriate ${\mathsf{\theta }}_{{\mathrm{z}}_{\mathrm{n}}}$ , we have ${\widehat{Z}}_{t_n}={\mathrm{N}\mathrm{N}}_{{\mathsf{\theta }}_{{\mathrm{z}}_{\mathrm{n}}}}\left(X_{t_n}\right)\approx \left(\nabla u\sigma \right)\left(t_n,X_{t_n}\right)$. For all appropriate ${\mathsf{\theta }}_{{\mathrm{U}}_{\mathrm{n}}}$ , we have ${\widehat{U}}_{t_n}={\mathrm{N}\mathrm{N}}_{{\mathsf{\theta }}_{{\mathrm{U}}_{\mathrm{n}}}}\left(X_{t_n}\right)\approx u\left(t_n,X_{t_n}+\beta \left(X_{t_n},·\right)\right)-u\left(t_n,X_{t_n}\right)$. Then we can get a suitable approximation of $u\left(0,\xi \right)$:

$${\widehat{Y}}_0\approx u\left(0,\xi \right)$$

(3.9)

The mean square error between the final output ${\widehat{Y}}_{t_N}$ of neural network and the true value $g\left(X_{t_N}\right)$ at the terminal time is selected as the loss function:

$$\theta ⟼loss\left(\theta \right)=\mathbb{E}\left[{\left|{\widehat{Y}}_{t_N}-g\left(X_{t_N}\right)\right|}^2\right]\in \left[0,\mathrm{\infty }\right]$$

(3.10)

$\theta$ is the set of all training parameters of the above system, such that $\theta =\left\{{\widehat{Y}}_0,{\widehat{Z}}_0,{{\widehat{U}}_0,\mathsf{\theta }}_{{\mathrm{z}}_1},\dots {\mathsf{\theta }}_{{\mathrm{z}}_{\mathrm{N}-1}},{\mathsf{\theta }}_{{\mathrm{U}}_1},\dots ,{\mathsf{\theta }}_{{\mathrm{U}}_{\mathrm{N}-1}}\right\}$. This loss function is used since $Y_T=g\left(X_T\right)$. And the expectation in the loss function in (3.10) is the expectation for all sample paths, but due to the infinite number of sample paths, it is not possible to traverse the entire training set. Therefore, we adopt an optimization method based on stochastic gradient descent. In each iteration of gradient descent, only a portion of samples are selected to estimate the loss function, thereby obtaining the gradient of the loss function over all parameters, and obtaining a one-step neural network parameter update.

Like this, the back propagation of this neural network uses optimizer to update the parameters layer by layer. When DNN is trained, ${\widehat{Y}}_0$ is fixed as the parameter value. Take this parameter value out and it is the required value.

3.5. Details of the Algorithms

The detailed steps of our proposed algorithm based on deep learning to numerically solve the BSDE with jumps is presented as follows.

According to our algorithm, which uses a deep learning-based neural network solver, the BSDE with jumps in the form of equation (2.4) can be numerically solved in the following ways:

• Simulate sample paths using standard Monte Carlo methods
• Use a deep neural network (DNN) to approximate $Z={\nabla }_{x}u\left(t,x\right)\sigma \left(t,x\right)$and$U=u\left(t,x+\beta \left(x,·\right)\right)-u\left(t,x\right)$, and then plug them into the BSDE with jumps to perform a forward iterative operation in time

For simplicity, here we use the one-dimensional case as an example, and the high-dimensional case is similar. We divide the time interval $[0,T]$ into N partitions, so that $t_0,t_1,\dots ,t_N\in [0,T]$ and $0=t_0<t_1<\dots <t_N=T$, assuming $h_i=t_{i+1}-t_i$, ${dW}_i=W_{i+1}-W_i$ and $d{\tilde{N}}_i={\tilde{N}}_{i+1}-{\tilde{N}}_i$. The detailed steps are as follows:

(1)

N Monte Carlo paths of the diffusion process $\left\{X_i^{\left(j\right)}:i=\mathrm{0,1},\dots ,N;j=\mathrm{1,2},\dots ,M;X_0^{\left(j\right)}\equiv X_0\right\}$ are sampled by Euler scheme:

$$X_{i+1}^{\left(j\right)}=X_i^{\left(j\right)}+\mu \left(t_i,X_i^{\left(j\right)}\right)h_i+\sigma \left(t_i,X_i^{\left(j\right)}\right)d{W}_i^{\left(j\right)}+\beta \left(t_i,X_i^{\left(j\right)}\right)d{{\tilde{N}}_i}^{\left(j\right)}$$

(3.11)

This step is the same as the standard Monte Carlo method. Other discretization schemes can also be used, such as logarithmic Euler discretization or Milstein discretization.

(2)

At $t_0=0$, the initial value $Y_0$, $Z_0=\frac{\partial Y}{\partial X}\left(0,X_0\right)\sigma \left(0,X_0\right)$ and $U_0=u\left(0,X_0+\beta \left(X_0,·\right)\right)-u\left(0,X_0\right)$ is randomly selected as parts of the neural network parameters, and $Y_0$, $Z_0$ and $U_0$ are all constant random numbers selected from an empirical range.

(3)

At each time step $t_i$, given $\left\{X_i^{\left(j\right)}:j=\mathrm{1,2},\dots ,M\right\}$, $\left\{Z_i^{\left(j\right)}:j=\mathrm{1,2},\dots ,M\right\}$ and $\left\{U_i^{\left(j\right)}:j=\mathrm{1,2},\dots ,M\right\}$ are approximated using deep neural networks, respectively. Note that every time ${t=t}_i$, two sub neural networks are used for all Monte Carlo paths. In our one-dimensional case, as described in Section 3.4, we introduce two sub deep neural networks: ${\mathsf{\theta }}_{{\mathrm{z}}_{\mathrm{i}}}:\mathbb{R}\to \mathbb{R}$, such that $\left\{Z_i^{\left(j\right)}={\mathsf{\theta }}_{{\mathrm{Z}}_{\mathrm{i}}}\left(X_i^{\left(j\right)}\right):j=\mathrm{1,2},\dots ,M\right\}$ and ${\mathsf{\theta }}_{{\mathrm{U}}_{\mathrm{i}}}:\mathbb{R}\to \mathbb{R}$, such that $\left\{U_i^{\left(j\right)}={\mathsf{\theta }}_{{\mathrm{U}}_{\mathrm{i}}}\left(X_i^{\left(j\right)}\right):j=\mathrm{1,2},\dots ,M\right\}$. And ${\mathsf{\theta }}_Z=\left\{{\mathsf{\theta }}_{{\mathrm{Z}}_1},{\dots ,\mathsf{\theta }}_{{\mathrm{Z}}_{\mathrm{N}-1}}\right\}$, ${\mathsf{\theta }}_U=\left\{{\mathsf{\theta }}_{{\mathrm{U}}_1},{\dots ,\mathsf{\theta }}_{{\mathrm{U}}_{\mathrm{N}-1}}\right\}$, $\theta =\left\{{\mathsf{\theta }}_Z,{\mathsf{\theta }}_{\mathrm{U}}\right\}$.

(4)

For $t_i\in [0,T]$ , we have

$$Y_{i+1}^{\left(j\right)}=Y_i^{\left(j\right)}-f\left(t_i,X_i^{\left(j\right)},Y_i^{\left(j\right)},Z_i^{\left(j\right)},U_i^{\left(j\right)}\right)h_i+〈Z_i^{\left(j\right)},d{W}_i^{\left(j\right)}〉+〈U_i^{\left(j\right)},d{{\tilde{N}}_i}^{\left(j\right)}〉$$

(3.12)

According to this formula, we can directly calculate the $Y_{i+1}^{\left(j\right)}$ at the next time step. This process does not require any parameters to be optimized. In this way, the BSDE with jumps propagates forward in time direction from $t_i$ to $t_{i+1}$. Along each Monte Carlo path, as the BSDE with jumps propagating forward in time from 0 to T, $Y_N^{\left(j\right)}$ is estimated as $Y_N^{\left(j\right)}\left(Y_0,Z_0,U_0,{\theta }^{\text{'}}\right)$, where ${\theta }^{\text{'}}=\left({\theta }_Z,{\theta }_U\right)$ is all the hyper-parameters for the N-1 layers neural networks.

(5)

Calculate the following loss function:

$$L_{Forward}=\frac{1}{M}\sum _{j=1}^M{\left(Y_N^{\left(j\right)}\left(Y_0,Z_0,U_0,\theta \right)-g\left(X_N^{\left(j\right)}\right)\right)}^2$$

(3.13)

Where g is the terminal function.

(6)

Use stochastic optimization algorithms to minimize the loss function:

$$\left(\widetilde{Y_0},\widetilde{z_0},\tilde{\theta }\right)=\underset{\left(Y_0,z_0,\theta \right)}{\mathrm{argmin}}\frac{1}{M}\sum _{j=1}^M{\left(Y_N^{\left(j\right)}\left(Y_0,z_0,\theta \right)-g\left(X_N^{\left(j\right)}\right)\right)}^2$$

(3.14)

The estimated value $\widetilde{Y_0}$ is the desired initial value at time t=0.

4. Numerical Results

In this section, we will use the depth neural network to code the theoretical framework of the proposed algorithm. In this paper, three classical high-dimensional PDEs with important applications in finance-related fields are selected for numerical simulation, they are: financial derivative pricing under jump-diffusion model, Bond pricing under Vasicek model with jump, Hamilton-Jacobi-Bellman equation.

The numerical experiments in this paper uses a 64-bit Windows 10 operating system, based on the PyTorch deep learning framework in Python. All examples in this section are calculated based on 1000 sample paths, each chosen for a time partition of N = 100. We ran each example 10 times independently to calculate the average result. All neural network parameters will be initialized by uniform distribution. Each sub neural network of each time node contains 4 layers: one d-dimensional input layer, two (d+10)-dimensional hidden layers, one d-dimensional output layer. We use the rectifier function (ReLU) as the activation function. Batch Normalization (BN) techniques are used after each linear transformation and before activation.

4.1. Pricing of Financial Derivatives under Jump Diffusion Model

In this section, we will apply the proposed method to the pricing of derivatives related to a 100-dimensional jump diffusion model. In this model, the stock price $X_t$ satisfies the following jump diffusion model [15]:

$d{X}_t=\left(r-\lambda k\right)X_{t}dt+\sigma X_{t}d{W}_t$	if an asset price does not jump
$=\left(r-\lambda k\right)X_{t}dt+\sigma X_{t}d{W}_t+\left(V-1\right)X_t$	if an asset price jumps

Where $r$ is the constant discount rate, $\lambda$ is the average number of jumps per unit time of the stock price, $\sigma$ is the constant volatility. $V$ represents the jump magnitude. Assuming that the jump amplitude is fixed and V is constant, we can let $k=V-1$ and $k>-1$. This equation can be written as $d{X}_t=r{X}_{t}dt+\sigma X_{t}d{W}_t+k{X}_{t}d{\tilde{N}}_t$.

It is known that the European call option with the stock as the underlying asset satisfies the following partial differential equation:

$$\frac{\partial u}{\partial t}\left(t,x\right)+{\frac{1}{2}{\sigma }^2{x}^2∆}_{x}u\left(t,x\right)+\left(r-\lambda k\right)x{\nabla }_{x}u\left(t,x\right)+\lambda \left[u\left(t,xV\right)-u\left(t,x\right)\right]-ru\left(t,x\right)=0$$

$$u\left(T,x\right)={\left(x-K\right)}^{+}$$

(4.1)

For all $t\in \left[0,T\right]$, $x,\omega \in {\mathbb{R}}^d$, $y\in \mathbb{R}$, $z\in {\mathbb{R}}^{1\times d}$. Suppose $d=100$, $T=1$, $N=100$, $\lambda =1$, $X_0=\left(1,\dots ,1\right)$, $\mu \left(t,x\right)=r{X}_t$, $\sigma \left(t,x\right)=\sigma X_t$, $\beta \left(t,x\right)=\left(V-1\right)X_t=k{X}_t$, $f\left(t,x,y,z\right)=-rY$, $g\left(x\right)={\left(\underset{1\le i\le 100}{\max }{x}_i-5\right)}^{+}$, here $r^i$, ${\sigma }^i$, $k^i$ are randomly selected in $\left[\mathrm{0,1}\right]$, $i=1,\dots 100$.

After calculation, Table 1 and Table 2 show the important numerical results of solving the related derivative pricing problem of the 100-dimensional jump diffusion model with Adam and NAdam optimizers respectively, including that with the change of iteration steps, mean and standard deviation of loss function $Y_0$, mean and standard deviation of loss function, and running time. Only the numerical results of iteration steps $n\in \left\{\mathrm{1000,2000,3000,4000}\right\}$ are selected as typical examples for display.

It can be seen from Table 1 and Table 2 that when the iteration steps are the same, the calculation time required for using the two optimizers is not very different. As the iteration progresses, the loss function value of the Nadam optimizer is smaller than that of the Adam optimizer at the same iteration steps, and the final loss function value is also smaller.

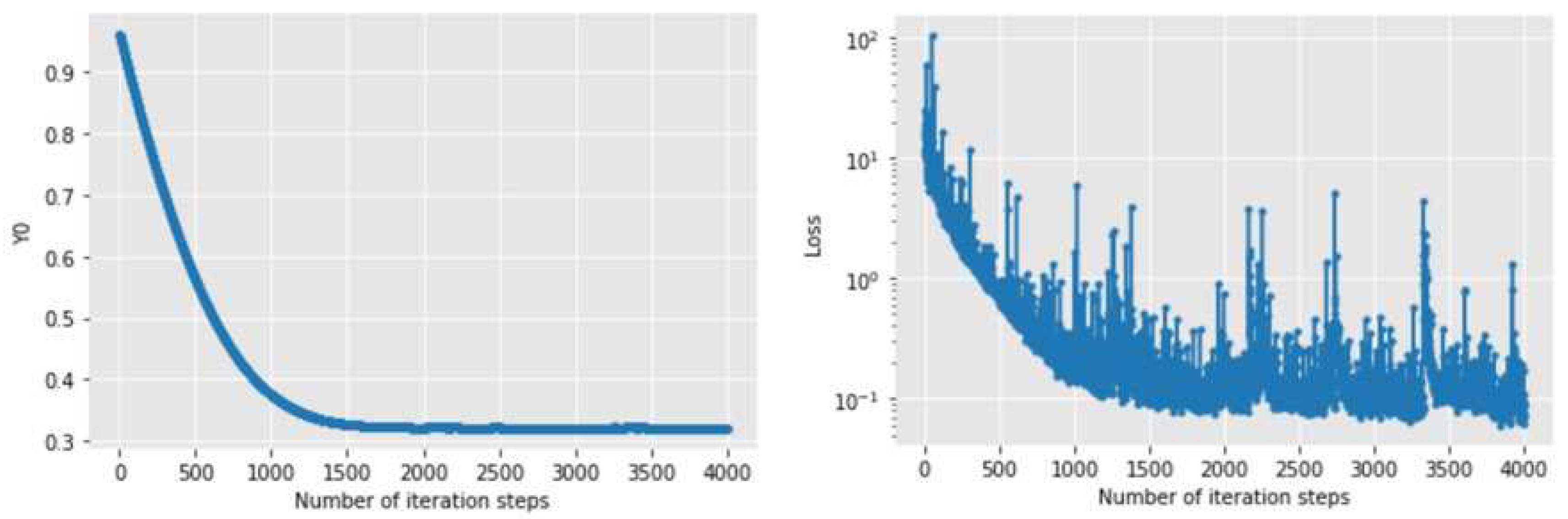
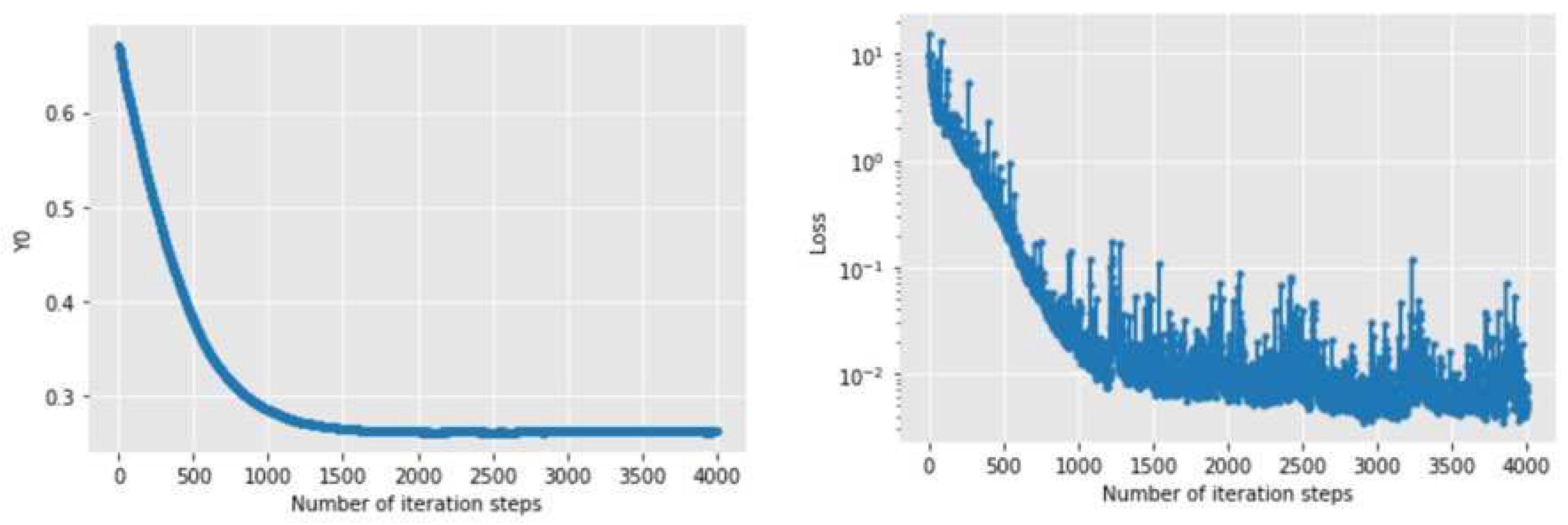
Figure 2 and Figure 3 show the changes of the initial value estimate and loss function with the number of iteration steps when Adam and NAdam optimizers are used for solving. It can be seen that the initial value estimates and loss functions of the numerical solutions of the two methods converge rapidly. However, the convergence speed of the latter is obviously faster than that of the former, whether it is the initial value estimate or the loss function. Among them, the former tends to converge after about 1500 iterations, while the latter tends to converge after about 700 iterations. When the iteration is 4000 times, the numerical solution obtained by Adam algorithm is 0.32143775, while the numerical solution obtained by NAdam algorithm is 0.32273737, which is similar.

4.2. Bond Pricing under the Jumping Vasicek Model

In this section, we use the proposed method to solve the pricing problem of a class of bonds with interest rates subject to the Vasicek model with jumps. [16,17] In this model, short-term interest rate $X_t$ obeys the following stochastic differential equations:

$$d{X}_t=a\left(b-X_t\right)dt+\sigma d{W}_t+kd{\tilde{N}}_t$$

(4.2)

i.e., each part of $X_t$ follows:

$$d{X}_t^i=a^i\left(b^i-X_t^i\right)dt+{\sigma }^{i}d{W}_t+k^{i}d{\tilde{N}}_t$$

(4.3)

For all $t\in \left[0,T\right]$, $x,\omega \in {\mathbb{R}}^d$, $y\in \mathbb{R}$, $z\in {\mathbb{R}}^{1\times d}$. Suppose $d=100$, $T=1$, $N=100$, $\lambda =1$, $X_0=\left(1,\dots ,1\right)$, $\mu \left(t,x\right)=\left({\mu }^1,\dots ,{\mu }^i,{\dots ,\mu }^d\right)$, ${\mu }^i=a^i\left(b^i-x^i\right)$, $\sigma \left(t,x\right)=\left({\sigma }^1,\dots ,{\sigma }^i,{\dots ,\sigma }^d\right)$, $\beta \left(t,x\right)=\left({\beta }^1,\dots ,{\beta }^i,{\dots ,\beta }^d\right)$, ${a^i,b}^i,{\sigma }^i,$ ${\beta }^i$are randomly selected in$\left[\mathrm{0,1}\right]$, $f\left(t,x,y,z\right)=-\left(\underset{1\le i\le n}{\max }{X}^i\right)Y$, $g\left(x\right)=1$. Then, for the zero-coupon bond price $u$ paying 1 at maturity T under the above jump Vasicek model, it satisfies that $u\left(T,x\right)=1$for all $t\in \left[0,T\right]$, $x\in {\mathbb{R}}^d$, and the following partial differential equation holds:

$$\frac{\partial u}{\partial t}\left(t,x\right)+\sum _{i=1}^n\left[a^i\left(b^i-x^i\right)-{\beta }^i\right]\frac{\partial u}{\partial x^i}+\frac{1}{2}\sum _{1\le i,j\le n}{\sigma }^i{\sigma }^j\sqrt{x^i{x}^j}\frac{{\partial }^{2}u}{\partial x^i\partial x^j}+u\left(t,x+\beta \left(x\right)\right)-u\left(t,x\right)-\left(\underset{1\le i\le n}{\max }{X}^i\right)u=0$$

(4.4)

After calculation, Table 3 and Table 4 show the important numerical results of solving a class of bond pricing problems with interest rates subject to the Vasicek model with jumps using Adam and NAdam optimizers respectively, including that with the change of iteration steps, mean and standard deviation of loss function $Y_0$, mean and standard deviation of loss function, and running time. Only the numerical results of iteration steps $n\in \left\{\mathrm{1000,2000,3000,4000}\right\}$ are selected as typical examples for display.

It can be seen from Table 3 and Table 4 that with the iteration, the loss function value of the NAdam optimizer is smaller than that of the Adam optimizer at the same iteration steps, and the final loss function value is smaller, but the cost is that the operation time becomes longer.

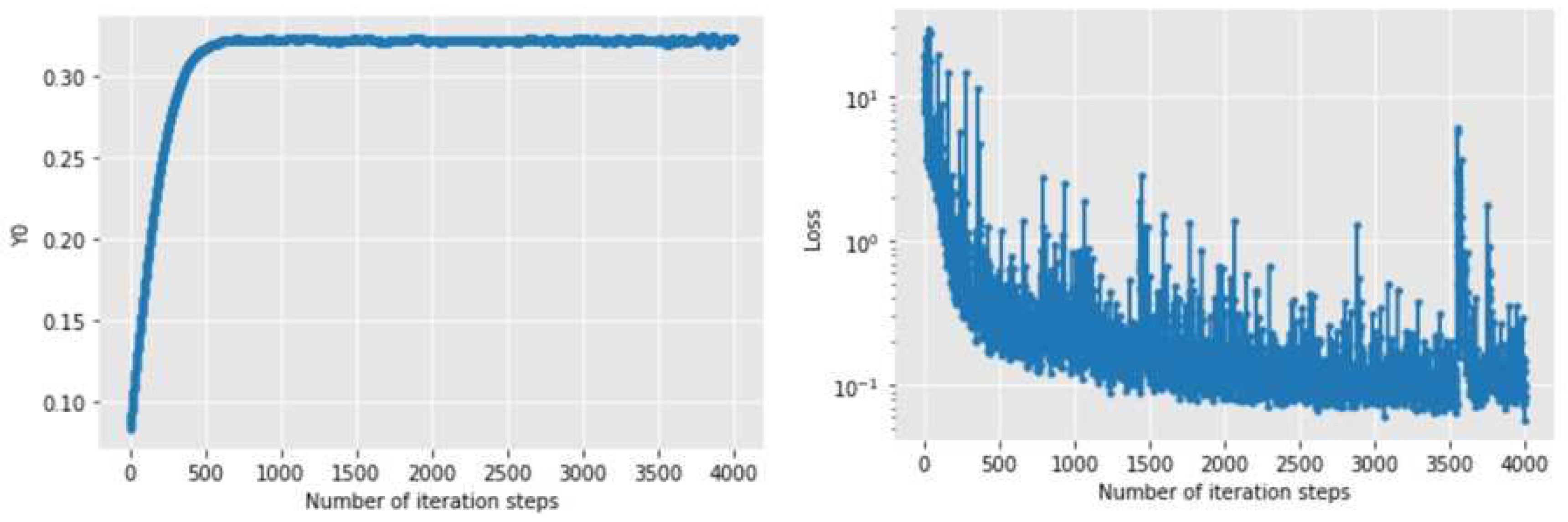
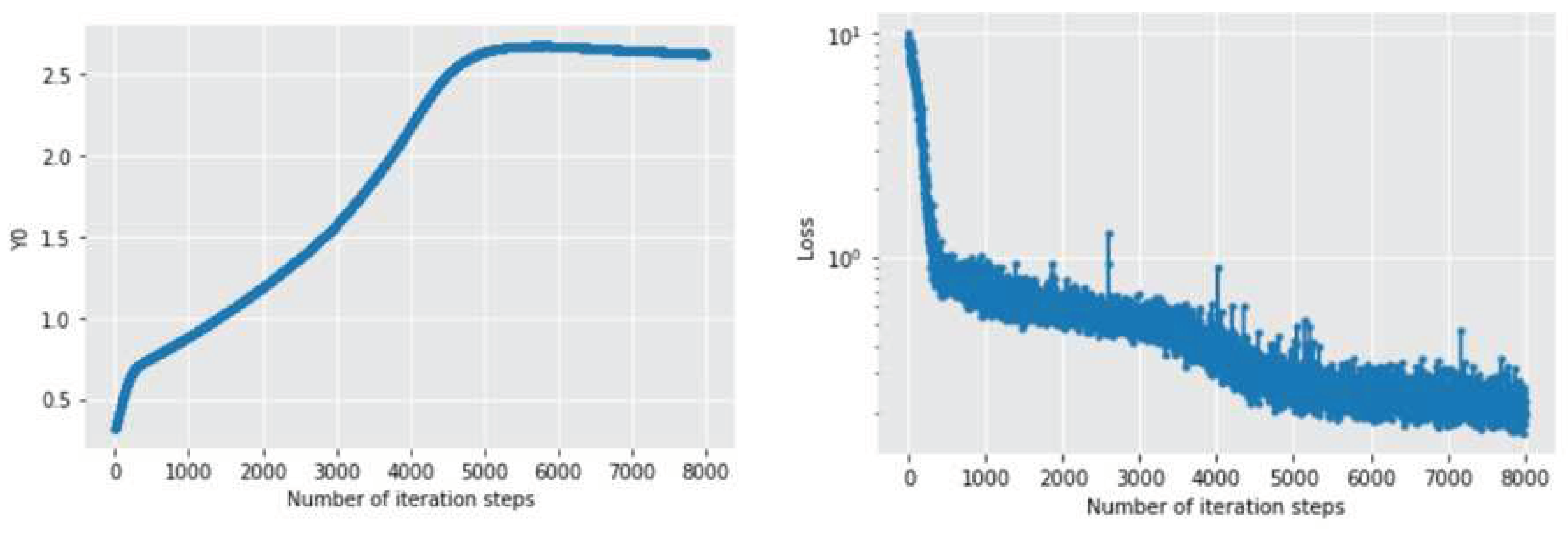
Figure 4 and Figure 5 show the changes of the initial value estimate and loss function with the number of iteration steps when Adam and NAdam optimizers are used for solving. It can be seen that the initial value estimates and loss functions of the numerical solutions of the two methods converge rapidly. However, the convergence speed of the latter is obviously faster and more stable than the former, whether it is the initial value estimate or the loss function. When the iteration is 4000 times, the numerical solution obtained by Adam algorithm is 0.25530547, while the numerical solution obtained by NAdam algorithm is 0.27403888. The difference is not significant.

4.3. Hamilton-Jacobi-Bellman (HJB) Equation

In fields such as finance, investment, and risk management, optimization and control problems are often involved, and these problems are often represented by stochastic optimal control models. One way to solve this kind of control problem is to obtain and solve the Hamilton-Jacobi-Bellman equation (HJB equation for short) of the corresponding control problem according to the principle of dynamic programming. In this section, we use the proposed method to solve a class of 100-dimensional HJB equations [9]:

For all $t\in \left[0,T\right]$, $x,\omega \in {\mathbb{R}}^d$, $y\in \mathbb{R}$, $z\in {\mathbb{R}}^{1\times d}$. Suppose $d=100$, $T=1$, $N=100$, $\lambda =1$, $X_0=\left(1,\dots ,1\right)$, $\mu \left(t,x\right)=0$, $\sigma \left(t,x\right)=\sqrt{2}$, $\beta \left(t,x\right)={\beta }^{T}x$, where${\beta }^T=\left({\beta }^1,\dots ,{\beta }^i,{\dots ,\beta }^d\right)$，${\beta }^i$are randomly selected in $\left[\mathrm{0,1}\right]$, $f\left(t,x,y,z\right)=-{‖z‖}_{{\mathbb{R}}^{1\times d}}^2$, $g\left(x\right)=ln\left(\left(1+{‖x‖}^2\right)/2\right)$, it satisfies that $u\left(T,x\right)=ln\left(\left(1+{‖x‖}^2\right)/2\right)$for all $t\in \left[0,T\right]$, $x\in {\mathbb{R}}^d$, and the following partial differential equation holds:

$$\frac{\partial u}{\partial t}\left(t,x\right)+{∆}_{x}u\left(t,x\right)+u\left(t,x+\beta \left(x\right)\right)-u\left(t,x\right)-{\nabla }_{x}u\left(t,x\right)\beta \left(x\right)={‖{\nabla }_{x}u\left(t,x\right)‖}^2$$

(4.5)

After calculation, the important numerical results of solving a class of HJB equations with Adam and NADam optimizers are shown in Table 5 and Table 6 respectively, including that with the change of iteration steps, mean and standard deviation of loss function $Y_0$, mean and standard deviation of loss function, and running time. Only the numerical results of iteration steps $n\in \left\{\mathrm{2000,4000,6000,8000}\right\}$ are selected as typical examples for display.

It can be seen from Table 5 and Table 6 that with the iteration, the loss function value of the NAdam optimizer is smaller than that of the Adam optimizer at the same iteration steps, and the final loss function value is smaller, but the operation time is longer.

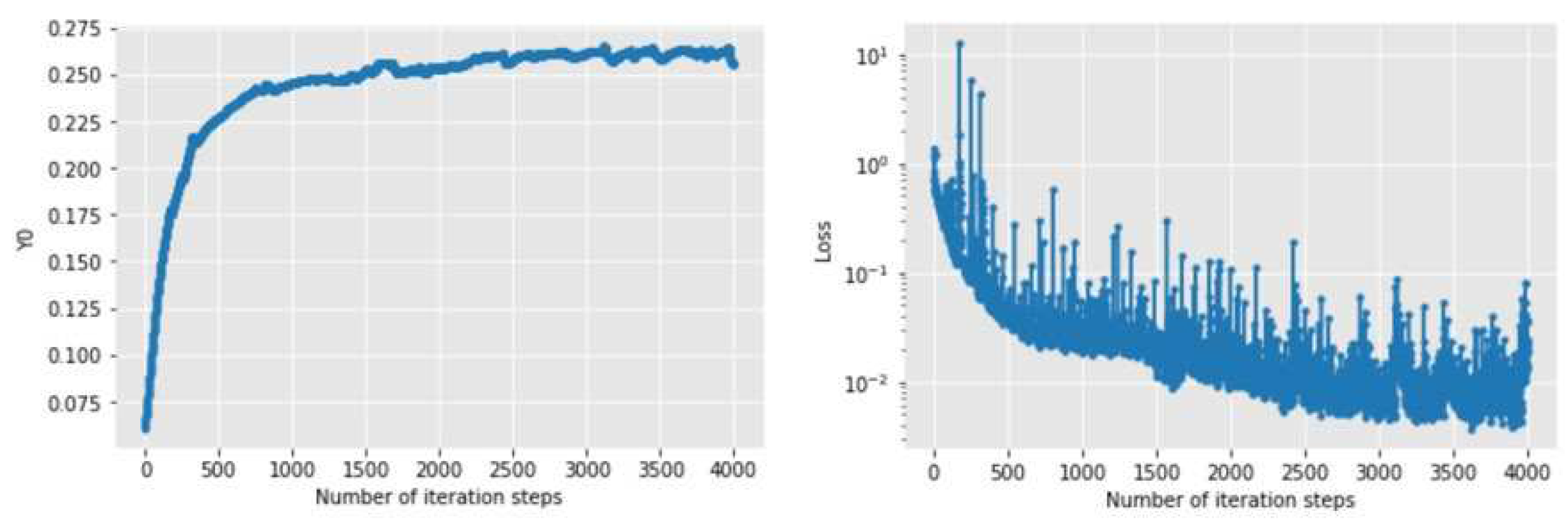
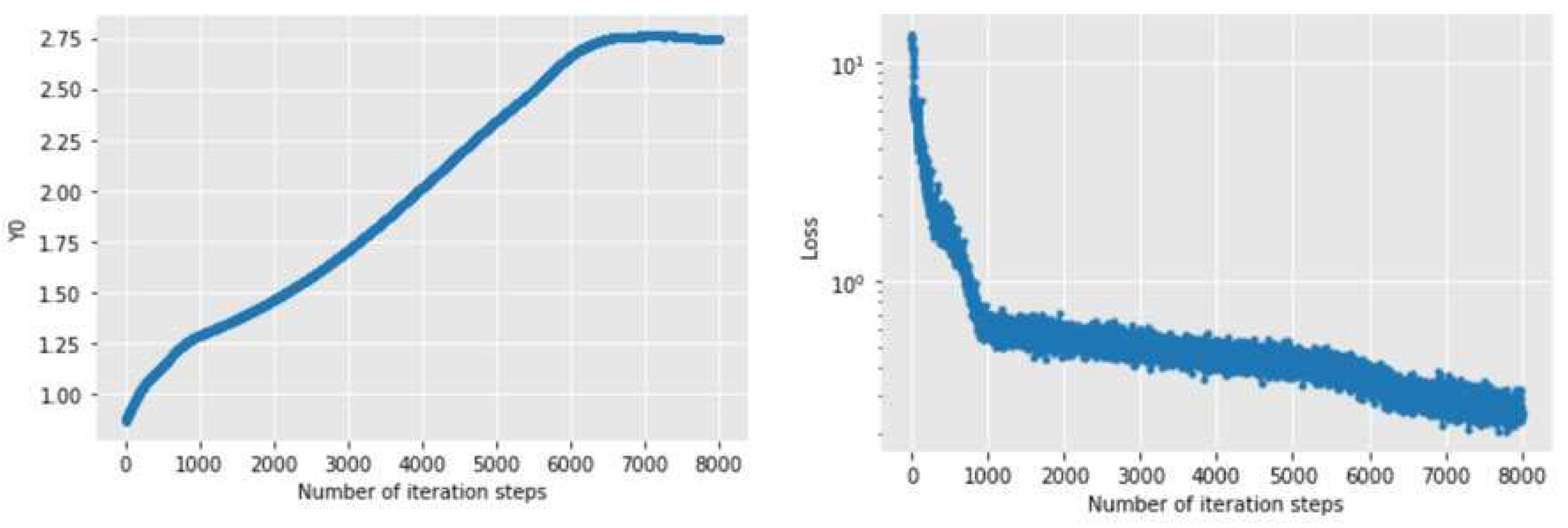
Figure 6 and Figure 7 show the changes of the initial value estimate and loss function with the number of iteration steps when Adam and NAdam optimizers are used for solving. It can be seen that the convergence speed of the latter is obviously faster than that of the former, whether it is the initial value estimate or the loss function. Among them, the former tends to converge after about 7000 iterations, while the latter tends to converge after about 5500 iterations. After 8000 iterations, the numerical solution obtained by Adam algorithm is 2.73136686, while the numerical solution obtained by NAdam algorithm is 2.6456454, with little difference between the two.

5. Conclusions

In this paper, we propose an algorithm that can be used to solve a class of partial differential equations with jump terms and their corresponding backward stochastic differential equations. Through the nonlinear Feynman-Kac formula, the above-mentioned high-dimensional nonlinear PDE with jumps and its corresponding BSDE can be expressed equivalently, and the numerical solution problem can be regarded as a stochastic control problem. Next, we treat the gradient and jump process of the unknown solution separately as policy functions, and use two neural networks at each time division to approximate the gradient and jump process of the unknown solution respectively. In this way, we can use deep learning to solve the " curse of dimensionality " caused by high-dimensional PDE with jumps and obtain numerical solutions.

Among them, jump process can depict the sudden impact of the outside world in its process, so that it can accurately depict a class of uncertain things, and this situation is most common in financial markets. In this way, we extend the numerical solution problem of high-dimensional PDE to the case of jump diffusion. Furthermore, we can use this algorithm to solve a series of problems in finance, insurance, actuarial modeling and other fields, such as the pricing problem of some special path dependent financial derivatives, and the bond pricing problem under the jump diffusion model of interest rates.

In addition, we attempt to replace the traditional Adam algorithm with the new stochastic optimization approximation algorithm and apply it to our algorithm. Next, focusing on the financial field, we applied our algorithm to solve three common high-dimensional problems in finance-related fields and then compared the results. We concluded that our algorithm performs well in numerical simulation. It is also concluded that after applying the new optimizer to the deep learning algorithm, the convergence speed of the model is mostly faster, and the generalization ability is significantly improved, at the cost of the operation time may be longer.