Preprint

Article

Development of Flood Early Warning Frameworks for the Small Streams in Korea

Altmetrics

Downloads

138

Views

Comments

A peer-reviewed article of this preprint also exists.

Tae-Sung Cheong,Changwon Choi,Sung-Je Yei,Jihye Shin,Seojun Kim,

Kang-Min Koo^*

Tae-Sung Cheong,Changwon Choi,Sung-Je Yei,Jihye Shin,Seojun Kim,

Kang-Min Koo^*

This version is not peer-reviewed

Submitted:

06 April 2023

Posted:

07 April 2023

You are already at the latest version

Alerts

Abstract

Currently, Korea is experiencing localized extreme rainfall, which accounts for more than 80% of flood-related disasters, and is increasing in small river basins, where more than 60% of flood-related casualties occur. These events are caused by climate change and geological factors and their impact is becoming more severe. As a result, an effective measurement system is required to mitigate their impact, particularly in small stream basins that are especially vulnerable due to their steep slopes, small catchment areas, and lack of maintenance and management capacity. In addition, a Flood Early Warning Framework (FEWF) that forecasts discharge and depth during flood events is crucial for reducing casualties. Therefore, this research is focused on developing the FEWF using the nomograph and rating curve methods, which are established by the robust constrained nonlinear equation solver and are suitable for small streams. The FEWF is evaluated using real-time data observed over 7-years period from the Closed-circuit Television-based Automatic Discharge Measurement Technology (CADMT), and the results show that the FEWF is effective in forecasting discharge and depth during flood events. The use of CADMT technology for real-time data can develop an accurate and reliable FEWF, which can help mitigate the impacts of extreme rainfall events and reduce the number of flood-related casualties in small stream basins.

Keywords:

Subject: Engineering - Civil Engineering

1. Introduction

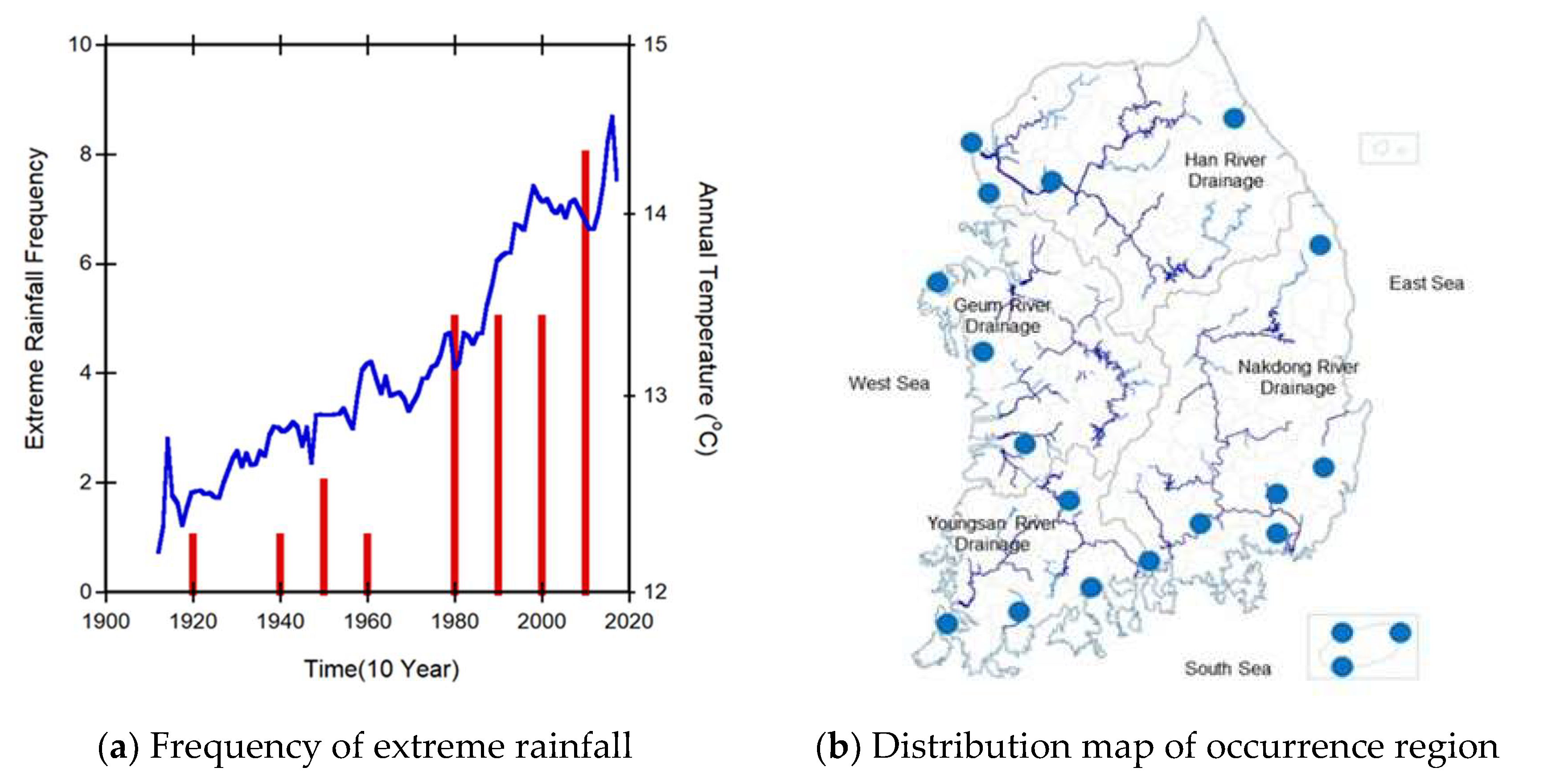
Localized extreme rainfall is one of the most severe hazards in Asia and globally, with immeasurable impacts due to increasing intensity and frequency attributed to climate change [1,2]. Over the past 93 years, from 1927 to 2019, the frequency of extreme rainfall exceeding 100

m m

per hour in Korea has steadily increased with the increase in average temperature, as shown by the blue line in Figure 1 a. The area of occurrence is also expanding throughout Korea. Extreme rainfall that occurred once in the 1920s increased to five times in the 1980s, then to eight times in the 2010s, and continued to increase gradually.

Flood disasters linked to these extreme rainfall events cause the largest socioeconomic losses over the Asian domain [3,4,5]. In Korea, more than 80% of flood disasters occur in river basins [6,7]. As extreme rainfall events occur suddenly and locally, such as in a flash flood, the flood damage caused by extreme rainfall events in small streams is on the rise. Disasters in the last 10 years, from 2010 to 2019, show that about 42.3% of the total damage of $68.5 million was caused in the small stream basins [8]. The floods bring more serious impacts on the small stream basin than the large river basin, as the small stream has fast flow characteristics within a one-hour flow duration time with a steep channel slope [6]. In particular, more than 60% of casualties have occurred in the small stream because it is located near the community and is easy to access, but it is not easy to escape when the water level suddenly rises.

1.1. Research necessity

Flood early warning can dramatically reduce human casualties by alerting people who live or leisure around the small streams to escape from risk areas before floods reach them [9]. However, the numerical model-based flood early warning system, which forecasts depth or discharge, is not suitable for ensuring the emergency response time needed to reduce human casualties because small streams have a short duration time due to the steep channel slope and the small basin area. Thus, a statistical-based flood early warning system is more useful for considering small stream characteristics. Furthermore, data analysis methods that consider the unique characteristics of small streams, such as steep slopes and rapid response times, are necessary to ensure the accuracy and reliability of flood early warning systems.

Additionally, accurate and real-time measurements of flow depth, velocity, and discharge in the small streams are needed to improve the accuracy of flood early warning systems. Besides technological advances, improved data collection and analysis for small streams is also necessary. Therefore, cost-effective and reliable data collection methods for small streams, such as the use of remote sensing technology, are needed. Community involvement and awareness are also essential for the success of flood early warning systems. The availability of easily accessible communication channels, such as mobile phone messaging and social media, can enhance the effectiveness of the flood early warning system by reaching a broader audience. Overall, a comprehensive approach that combines technological advances, statistical analysis, and community involvement is essential to improve flood early warning systems for small streams.

1.2. Challenges

Accurately forecasting flow depth and discharge using the FEWF requires direct measurement of water depth, discharge, and rainfall in the small stream basins. However, existing technologies, such as velocimetry and water surface level gauges, face challenges in measuring fast flow velocities due to steep channel slopes, finding safe measurement locations, risk of breakage due to suspended solids and bed load, high cost, and image resolution issues.

Accurate and reliable data on rainfall, water depth, and discharge are essential for developing effective flood early warning systems. However, many small streams lack adequate monitoring equipment, and data collection can be costly and challenging. As an alternative, Surface Image Velocimetry (SIV) has been researched in recent years for small streams [10,11,12,13]. Furthermore, the implementation of these technologies in small streams may also face challenges related to cost-effectiveness, maintenance, and the need for trained personnel to operate and maintain the technology.

Another challenge is the limited capacity of local governments to measure the large number of small streams in Korea during the flood season. The development and evaluation of key forecasting methods, such as rainfall-discharge nomographs and rating curves, for unmeasured small streams is critical. Estimated data from numerical models and measured data from other small streams can be used to develop and evaluate the FEWF for unmeasured small streams. However, similarities in watershed characteristics and flow patterns, as well as spatial and geographic correlations between measured and unmeasured small streams, must be demonstrated. Further research will be conducted to address these issues.

Additionally, the accuracy and reliability of the FEWFs may be affected by uncertainties in the rainfall forecast, especially during extreme weather events. The accuracy of the FEWFs also depends on the quality and frequency of data collection, the calibration of the models, and the availability of real-time data. Therefore, continuous monitoring and updating of the FEWFs based on the latest data and technology is necessary to improve their accuracy and effectiveness. The development of a robust data management system is also critical to the efficient and effective operation and maintenance of the FEWF.

1.3. Opportunities

One potential opportunity is to improve the accuracy of flood forecasting and disaster risk reduction in small streams through the use of CADMT and FEWF. Recent advances in ICT-based remote sensing technology, information technology, statistical analysis technology, and social media provide opportunities for flood early warning systems to gain additional capabilities [14]. These technologies provide an opportunity to overcome the technical limitations faced by flood early warning systems [15,16]. Statistical analysis technology can be an alternative to classical hydrological and hydraulic models and can be used for forecasting in small stream basins.

The National Disaster Management Institute (NDMI) in Korea developed the Closed-circuit television-based Automatic Discharge Measurement Technology (CADMT) using SIV technology in 2016 and evaluated it through field and hydraulic experiments [6]. The CADMT allows for real-time measurement of flow depth, velocity distribution, and discharge under extreme flow conditions without requiring direct measurement, recording, or data collection and analysis.

Since 2016, The Ministry of Interior and Safety (MOIS) in Korea has been installing the CADMT in small streams to collect real-time measurement data. The FEWF can be expanded to these small streams, and MOIS plans to install the CADMT in 10% of the 22,330 small streams in Korea by 2025. The selection of the 10% of small streams was based on flood risk assessments and local government demand surveys, reflecting the knowledge of local communities. The development and implementation of the CADMT is an excellent opportunity to improve flood forecasting and disaster risk reduction in small streams.

Additionally, the installation of CADMT in small streams can provide valuable data for further research and development of the FEWF, improving their effectiveness in the future. The approach of using local knowledge and flood risk assessments to prioritize the installation of CADMT in small streams also highlights the potential for community engagement and participation in flood management and risk reduction efforts. This technology and approach can provide real-time measurement and prediction of flow discharges and depth, allowing for early warning and effective response to flood events in small streams.

To develop the FEWFs, the research proposes a nomograph and rating curve for small stream flood warning. The rainfall-discharge nomograph forecasts discharge with expected rainfall data using the McGill Algorithm for Precipitation nowcasting by Lagrangian Extrapolation (MAPLE) developed by the Korea Meteorological Administration (KMA), and the rating curve forecasts flow depth for flood early warning. The FEWF can be further enhanced by incorporating remote sensing technology, such as the CADMT, which allows for real-time measurement of flow depth, velocity distribution, and discharge under extreme flow conditions without requiring direct measurement, recording, or data collection and analysis. Additionally, information technologies, such as social media, can be used to alert people in risk areas quickly and efficiently.

2. Materials and Methods

2.1. Determination of Measurement Sites

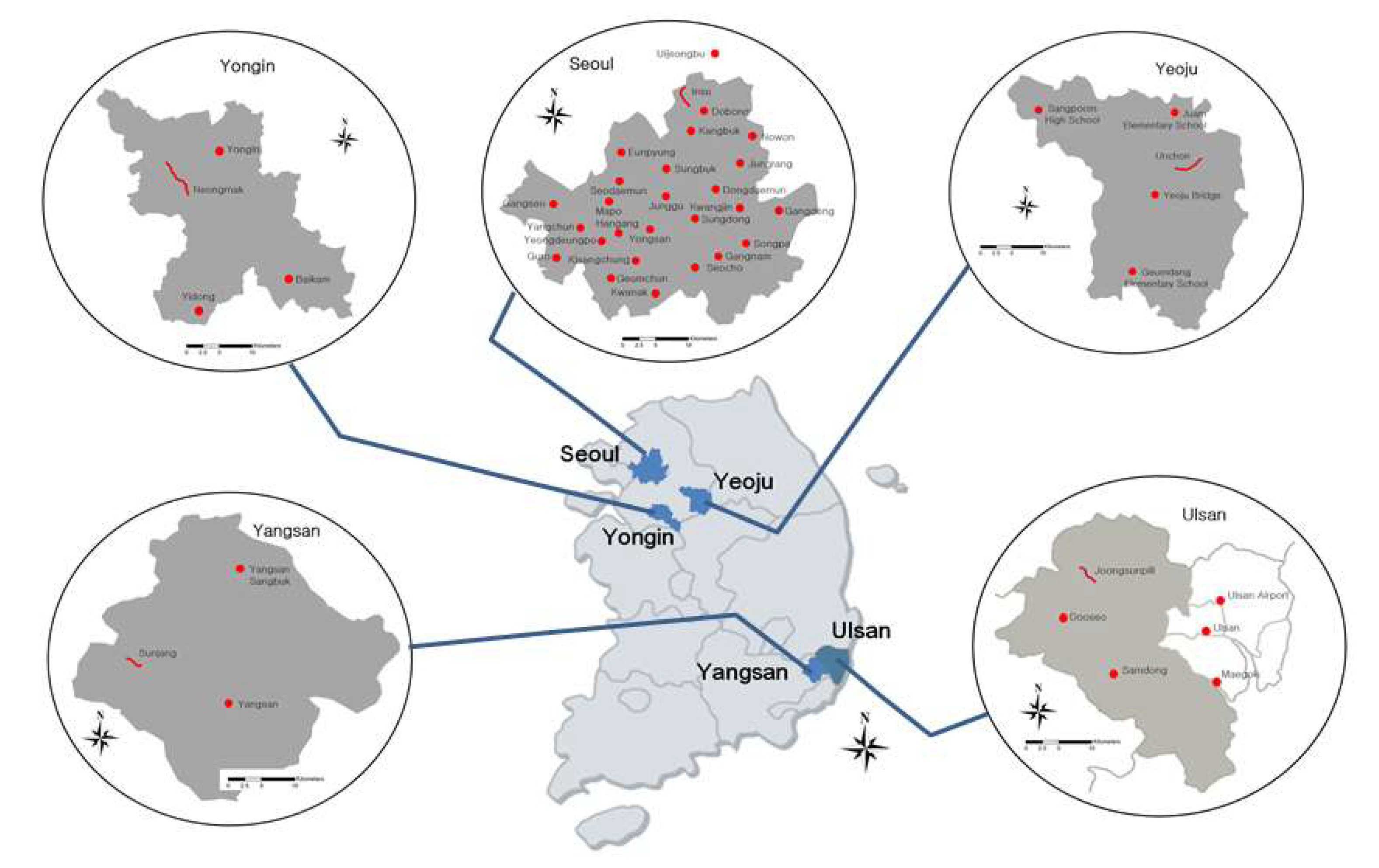
In order to develop and evaluate the FEWFs, the research selected five small streams with CADMT installed: Jungsunpill, Sunjang, Unchon, Neungmac, and Insu streams, as test beds. The selection of these streams took into account various factors, such as geographic location, basin characteristics, and real-time data collected over 6-year period from 2016 to 2021, which included measurements of rainfall, depth, velocity, and discharge Table 1 shows the characteristics of 5 small stream watersheds, in which

A_{b}

is the basin area;

W_{b}

is the mean basin width;

C_{b}

is the basin form coefficient (

= A_{b} / L_{c}^{2}

);

S_{c}

is the mean channel slope;

L_{c}

is the channel length; and

W_{c}

is the channel width. The Jungsunpill and Sunjang streams are relatively steep and are located in the mountainous areas of Ulsan and Yangsan cities, respectively, in Korea. The Unchon and Neungmac streams, on the other hand, are relatively flat and are located in the urban areas of Yeoju and Yongin cities, respectively. The Insu stream, located in Seoul, Korea, has the smallest channel slope among the test beds. All five small streams have a leaf-shaped watershed.

2.2. Selection of Rainfall Gauging Stations

To ensure that the rainfall gauging stations accurately represent the rainfall-runoff characteristics of each small stream, the research compared the distance between the gauging station and the stream, as well as the correlation between rainfall and runoff. This was done using measured discharge and rainfall data from all gauging stations, as shown in Figure 2. The total annual rainfall averages, as shown in Table 3, varied depending on local meteorological and geological conditions such as wind, rainfall direction, and mountain effects.

In order to collect both measured and estimated rainfall data per minute, we selected the nearest rainfall gauging stations using an adaptive analysis of distance and historical rainfall-runoff characteristics, except for the Insu stream located in Seoul. For this stream, the research selected the Uijeongbu gauging station as its rainfall characteristics reflect the runoff processes of the Insu small stream basin well. This is due to the high mountain (Bukhan) with a height of 727

m

, which is located between the Insu stream and the nearest gauging station (Dobong). The locations and reference information of the selected rainfall gauging stations are summarized in Table 2.

2.3. Measurement of Flow Velocity and Depth

Flow velocities, which are essential elements in the discharge measurement by using the CADMT, were measured by using the cross-correlation method applied and verified by [17] and [18]. In the CADMT, the interrogation area is determined in the first image and correlation area with large correlation coefficient,

C_{R}

is found in second image, and the flow velocity is calculated by dividing the moving distance between these areas by the time interval between both images. The correlation coefficient is calculated by following equation as:

C_{R} = \frac{(\sum_{i = 1}^{M X} \sum_{j = 1}^{N Y} (E_{a} E_{b}))}{{(\sum_{i = 1}^{M X} (\sum_{j = 1}^{N Y} E_{a}^{2} \sum_{i = 1}^{M X} \sum_{j = 1}^{N Y} E_{b}^{2}))}^{0.5}},

(1)

in which

M X

and

N Y

are the pixel size of the correlation area,

E_{a}

and

E_{b}

are residual values of the correlation area and the interrogation area. The residual values are calculated by

a_{i j} - \bar{a_{i j}}

and

b_{i j} - \bar{b_{i j}}

respectively in which

\bar{a_{i j}}

and

\bar{b_{i j}}

are average of contrast values in a range. Finally, the surface velocity,

u_{s}

is calculated by following equation as:

u_{s} = \frac{1}{N} \sum_{i = 1}^{N} \bar{{u_{s t}}_{i}},

(2)

in which

\bar{{u_{s t}}_{i}}

is the average time-velocity calculated at node

i

of the grid in the search area and

N

is the total number of nodes in the grid. To measure the surface velocity distributions, the research used densely designed grids spaced 20

c m

apart on cross control cross-sections and captured images at 20 frames per second from the CCTV, which has the capacity to capture images at 30 frames per second. The surface velocity distributions were measured from each image and then averaged over time to reduce sudden fluctuations. The flow velocity measurement interval was determined to be 2 minutes based on the verification results of the fields and the hydraulic model experiments [6]. While using more images for averaging can significantly reduce fluctuation ranges, it may distort the measurement results and increase the measurement interval due to the increase in calculation time.

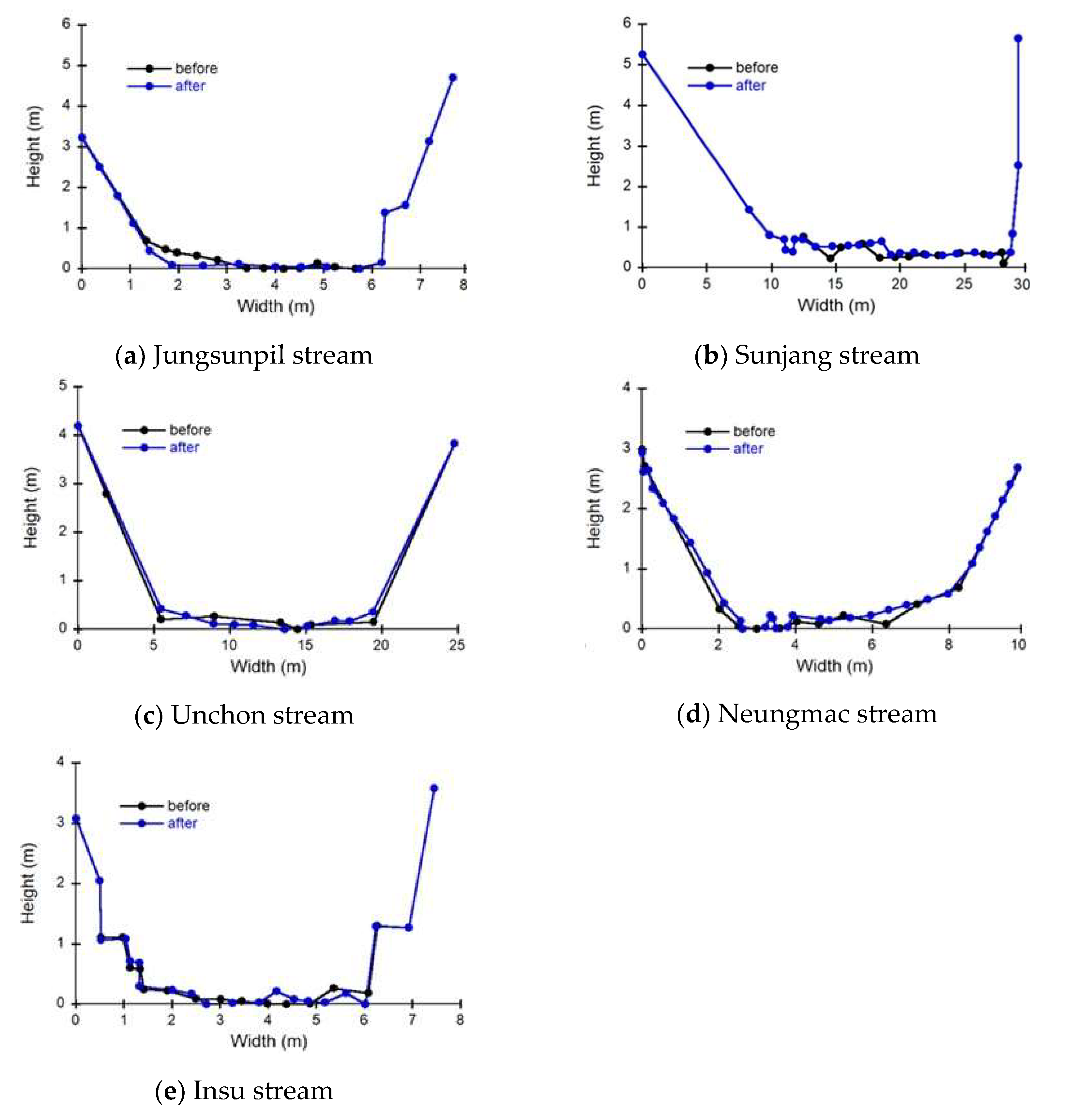
Real-time surface elevations were also measured using the ultrasonic water level gauge installed in the CADMT, and then converted into depth distributions on the same dense designed grid used for velocity measurements. To ensure accurate conversion to depth, the channel bed at the cross-section of each of the five small streams was measured before and after the flood season every year. Figure 3 shows the comparison results of the cross-sectional changes before and after the flood season in the year with the greatest changes among all measured data for each of 5 small streams. The Jungsunpil stream had the largest cross-sectional change, measuring 47.5

c m

on the cross-section in 2020, followed by the Sunjang stream with 41.3

c m

on the cross-section measured in 2020, the Neungmac stream with 23.2

c m

on the cross-section measured in 2018, the Unchon stream with 22.1

c m

on the cross-section measured in 2018, and the Insu stream with 21.0

c m

on the cross-section measured in 2020.

2.4. Discharge Measurements

For measuring discharge, the study used the mid-section method, which is commonly employed for calculating discharges. This method calculates the mean velocity in a subsection using the mean velocity on the vertical. The measured discharge (

Q_{m}

) and the measured area (

A_{m}

) were calculated using equations (3) and (4) respectively,

Q_{m} = \sum_{i = 1}^{N} \bar{u_{i}} (\frac{b_{i - 1} + b_{i + 1}}{2}) d_{i},

(3)

A_{m} = \sum_{i = 1}^{N} (\frac{b_{i - 1} + b_{i + 1}}{2}) d_{i},

(4)

in which

\bar{u_{i}}

is mean velocity at vertical

i

;

b_{i}

is the distance from the initial point to vertical

i

;

d_{i}

is the depth of flow at vertical

i

. The subsection area extends laterally from half the distances from the preceding vertical to half the distance to the next subsection. The mean velocity

u_{m}

was then calculated by using equation (5):

u_{m} = \frac{Q_{m}}{A_{m}},

(5)

{q_{s}}_{i} = {u_{s}}_{i} (\frac{b_{i - 1} + b_{i + 1}}{2}) d_{i},

(6)

in which

{u_{s}}_{i}

is the surface velocity at vertical

i

. If the cross-section of a small stream is rectangular or close to a rectangle, and the intervals between the verticals are equal, then the area of each subsection will be equal to the area of a subsection (a), and the discharge calculated using surface velocity is given by equation (7):

Q_{m} = {α Q}_{s},

(7)

in which

α

is the conversion coefficient. The conversion coefficient was estimated using equation (8), where the ratio of the mean cross-sectional velocity and mean surface velocity was straight line going through the origin.

α = \frac{Q_{m}}{Q_{s}} = \frac{\bar{u_{m}} A_{m}}{\bar{u_{s}} A_{m}} = \frac{\bar{u_{m}}}{\bar{u_{s}}},

(8)

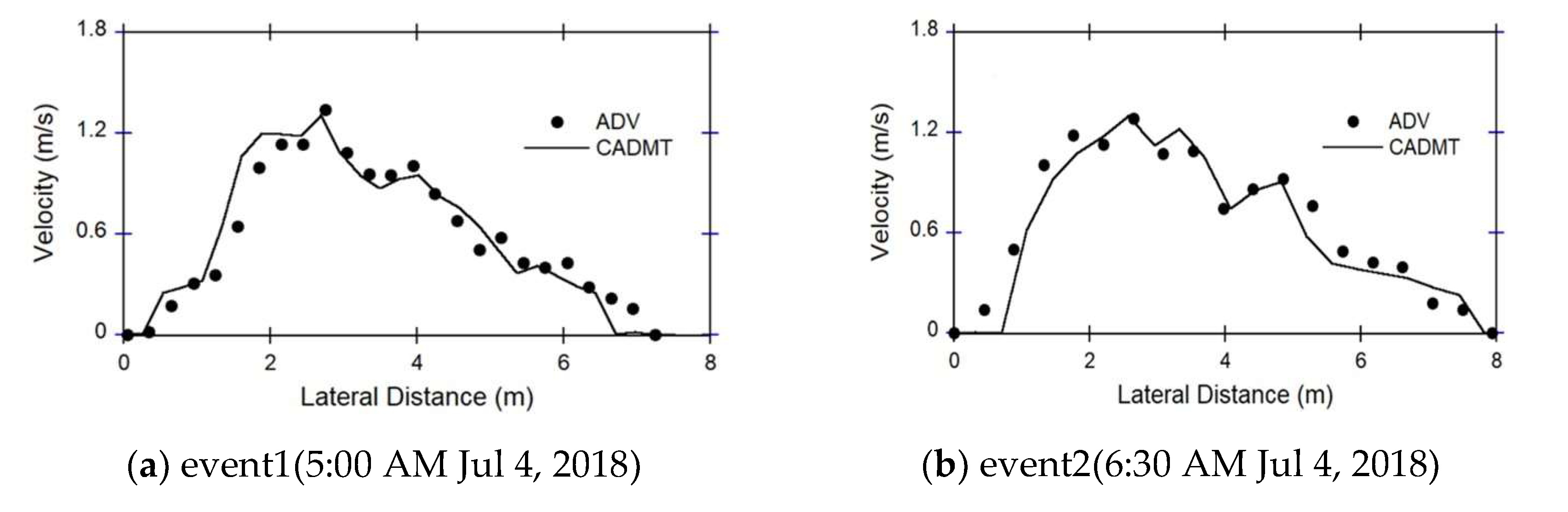
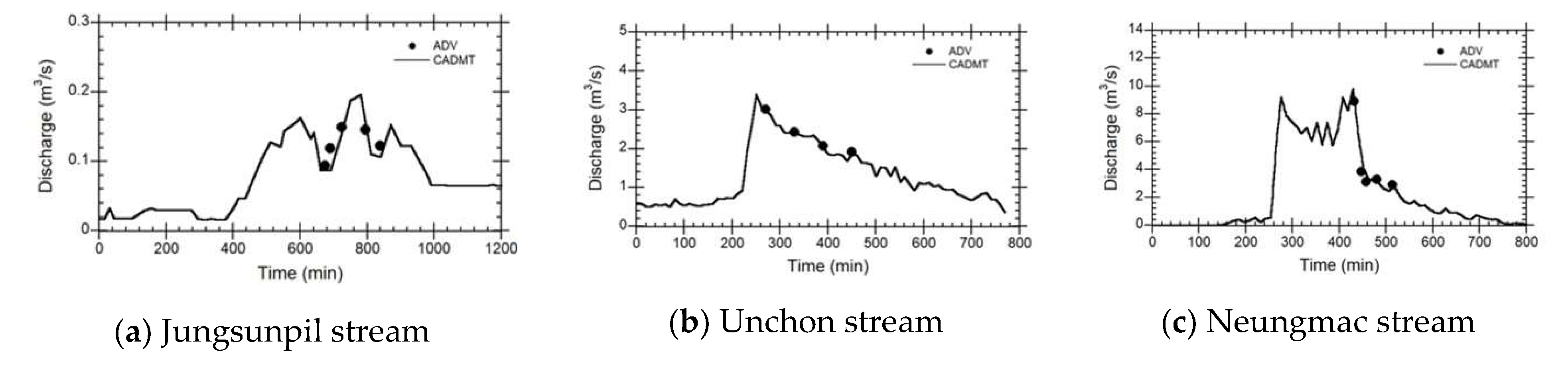
The average velocity distribution was measured by Aquatic Doppler Velocimetry (ADV) and the surface velocity was measured by CADMT in the same cross-controlled cross-section of 5 small streams. For compare mean velocity distribution, the research used 0.85 for the conversion coefficient recommended by USGS for all small streams. Figure 4 show that mean velocities measured by the CADMT were well represented the ADV data.

To quantitatively assess the difference between CADMT and ADV values, the research calculated Root Mean Square Errors (RMSE). The results indicate that the RMSE between the mean velocities of CADMT and ADV measured at 5:00 AM and 6:30 AM were 0.101

m / s

and 0.159

m / s

, respectively. Based on the error analysis, it can be inferred that the velocity data obtained by CADMT has the potential to be used for developing the FEWF. In order to determine the accuracy of flow discharges measured by the CADMT, the research conducted a comparison with ADV velocities for major floods in all small streams. The results are shown in Figure 5, which presents a comparison of time-discharges measured on September 11, 2017, August 24, 2017, and October 6, 2017. The comparison indicated that the discharges measured by the CADMT were well-represented by the ADV data.

The intercomparison analysis showed that the CADMT results measured at specific time intervals in the Jungsunpil, Unchon, and Neungmac small streams matched the ADV discharges very accurately with small errors ranging from 0.007

m^{3} / s

to 0.065

m^{3} / s

, depending on the time and location of the measurement, as shown in in Figure 5 a-c. The coefficient of determination,

R^{2}

, was 0.90 for the Jungsunpil stream and 0.99 for the Unchon and Neungmac streams. Compared to the ADV, measuring flow discharges using the CADMT offers several advantages, including a shorter measurement time interval of at least 2 minutes, allowing for the measurement of peak discharges. In contrast, the ADV requires 20 to 30 minutes to measure the entire cross-section of the Jungsunpil stream, and its measurements may have large variations in time-discharge curves. Overall, the CADMT has the potential to be a useful tool for developing flood early warning systems.

3. Development of the Flood Early Warning Framework

3.1. Development of a framework

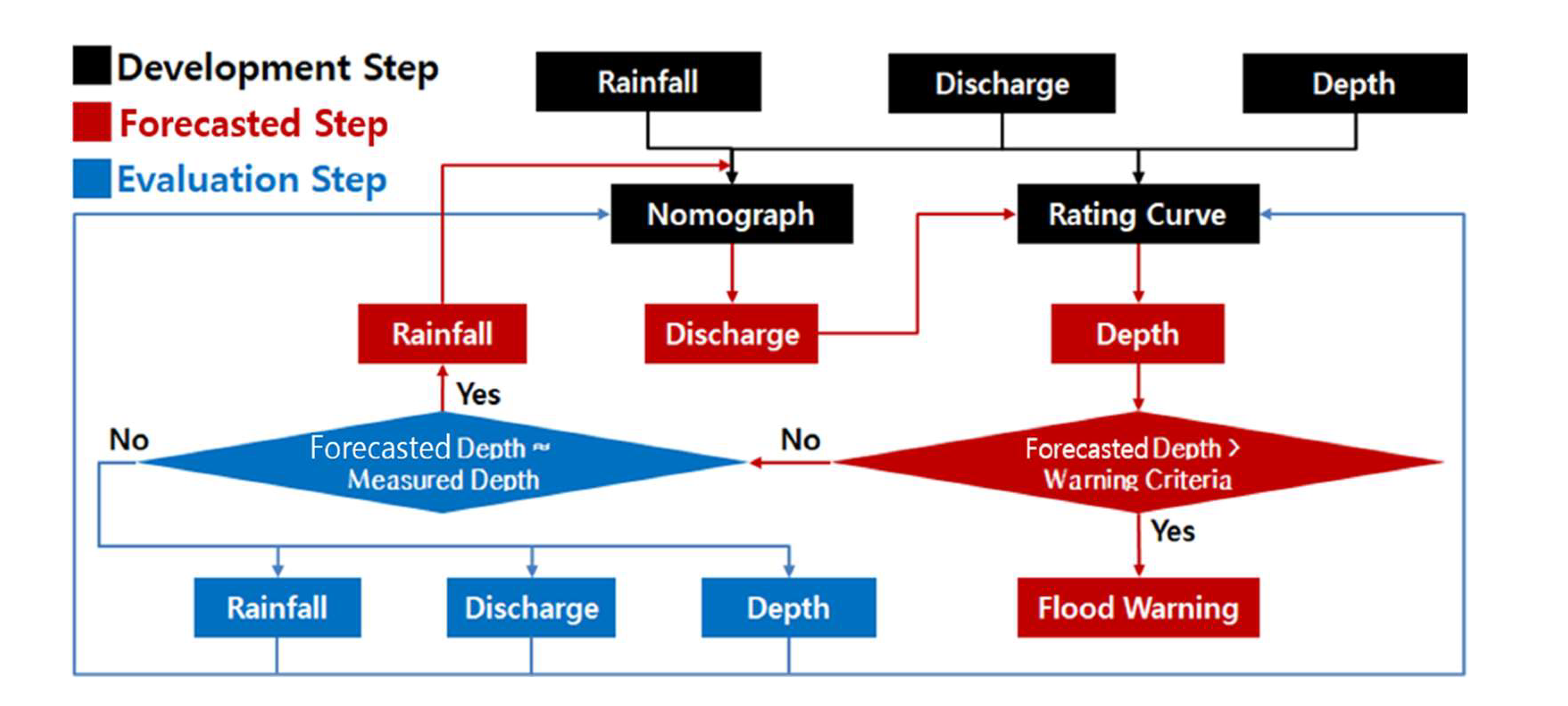
The research presents a framework for the FEWF, which consists of three major steps: development, forecasting, and evaluation, as illustrated in Figure 6. The first step, development, involves developing the rainfall-discharge nomograph and the rating curve using existing data collected in small stream basins. If measured rainfall, discharge, and depth data are available, the nomograph and rating curve are developed using this data. Otherwise, simulated data from simulation models such as the Unit Hydrograph and the Manning formula are used to develop the nomograph and rating curve.

In the second step, forecasting, involves using the developed rainfall-discharge and rating curves to forecast discharge and depth, respectively. In this step, forecasted rainfall is used to forecast discharges from the rainfall-discharge nomograph. The research utilizes MAPLE for forecasting rainfall. The forecasted flood discharge is then used to forecast depth by using the developed rating curve until the forecasted depth exceeds the warning criteria. If the forecasted depth exceeds the warning criteria, a flood warning is issued to evacuate people from hazardous areas, including small streams.

If the forecasted depth does not exceed the warning criteria, it is evaluated with newly measured depth in the evaluation step to determine whether to enhance the rainfall-discharge nomograph and rating curve with newly measured values of rainfall, discharge, and depth. If the residual between the forecasted and measured values meets the convergence criteria, the forecasting is repeated to forecast the next time discharge with forecasted rainfall and depth. If it does not meet the criteria, the rainfall-discharge nomograph and rating curve can be updated with newly measured discharge, rainfall, and depth data. The research utilizes the Robust Constrained Nonlinear Equation Solver (RCNES) to improve the rainfall-discharge nomograph and rating curve by minimizing the root mean square error (RMSE) between the forecasted and measured sets of normalized data.

The RCNES is a solver that minimizes a sum of less rapidly increasing functions of the residuals, rather than minimizing a sum of squared errors [19]. To solve for the correction vector (

Θ

), the following equation is used:

[μ Ι + Ρ {(\frac{r}{s})}^{T} Ρ (\frac{r}{s})] Θ = - Ρ {(\frac{r}{s})}^{T} s Ρ (\frac{r}{s}),

(9)

in which

Ι

is the unit matrix;

Ρ (∙)

is the Jacobian matrix of the residual function;

r

is the residual matrix;

s

is a known or previously estimated scale parameter; and

μ

is a non-negative parameter. The value of

μ

is chosen such that it is large enough to eliminate the singularity of the Jacobian matrix but not so large as to make moving away from the near singular region impossible. To solve for

Θ

, preliminary estimates of

Θ^{k}

are assumed and then computed by

Θ^{k + 1} = Θ^{k} + ψ Θ^{k}

in which

ψ

is the scalar step length. At this stage, absolute constraints may be imposed such that

(Θ) \geq 0

. The value of

ψ

is calculated by

ψ = m i n |α Θ^{k} / Θ^{k}|

, where

α

is determined to be 0.99 as proposed by [20]. The value of

μ

is calculated by

μ = m a x | Ρ (r / s) |

, in which

Ρ (r / s) = r

|r|

is smaller than the square root of the 0.975 quantile of residuals and

Ρ (r / s) = a s i n (r)

|r|

is larger than the square root of the 0.975 quantile of residuals [19]. The scale parameter is calculated by

s = 1.48 m e d |r - m e d (r)|

, in which the factor of 1.48 makes the scale parameter an approximately unbiased estimate of scale when the residual function is Gaussian [21].

The iterative procedure is carried out until the residual between the forecasted and measured values satisfies the convergence criteria. The identification of the solver is performed through a procedure that involves the repeated evaluation of various statistical measures for different parameters, ultimately selecting the best identified solvers that satisfy the criteria. The identification statistics recommended by the research are the RMSE criterion and the coefficient of determination criterion, given by

R^{2} = 1 - (σ_{r}^{2} / σ_{o}^{2})

in which

σ_{r}^{2}

is the variance of the model residuals and

σ_{o}^{2}

is the variance of the output. If the solver explains the measured data well and is not over-parameterized, both values of

R^{2}

approach unity, and the RMSE criterion becomes the smallest value.

3.2. Determination of a warning criteria

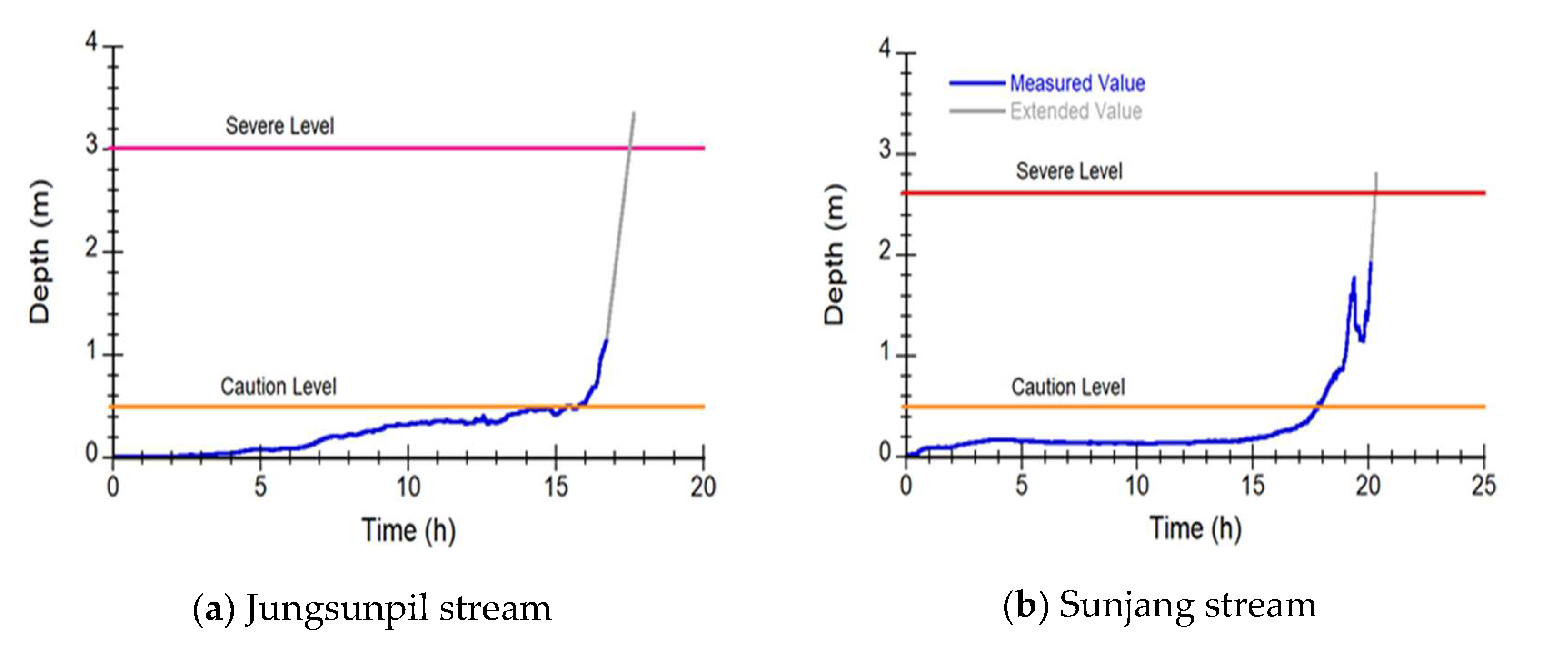
The small stream flood warning system in Korea includes two levels of warning criteria: the caution level and the severe level, as illustrated in Figure 7. The caution level warning is issued when the forecasted depth exceeds 0.5 m, as this depth is considered hazardous for people to access small streams due to the risk of being swept away by fast-flowing water. The caution level was determined based on stability conditions derived from experiments conducted by various researchers, which considered the correlation between depths, velocities, and human physical strength [22,23,24,25,26,27,28,29].

The severe level warning is issued when the forecasted depth reaches the design flood depth, in order to evacuate people from the hazard area. As shown in Figure 7, the depth increased rapidly after reaching the caution level in both small streams, and the severe level warning was issued within 2 or 3 hours. The depth increase in Jungsunpil stream was much steeper, which may be attributed to the stream's narrower channel width and steeper channel slope compared to the Sunjang stream.

3.3. Development of a rainfall-discharge nomograph

Real-time rainfall data from the rainfall gauging station listed in Table 2 and depth and discharge data collected using the CADMT in 5 small stream basins were utilized over a 6-year period from 2016 to 2021 to develop and evaluate the FEWFs. Specifically, rainfall, depth, and discharge data collected from 2016 to 2020 were used for developing the FEWFs, while data from 2021 were used for their evaluation. Table 3 summarizes the measured rainfall, depth, and discharge data from all five small stream basins over 6 years.

Table 3. Measured data ranges from all 5 small stream basins over 6 years (2016-2021), including rainfall, depth, and discharge. (Data from 2016 to 2020 were used to develop the FEWFs, while data from 2021 were used to evaluate them.).

Division	Small Streams	$Rainfalls (m m$ )			$Depths (m$ )			$Discharges (m^{3} / s$ )
Division	Small Streams	Min.	Mean	Max.	Min.	Mean	Max.	Min.	Mean	Max.
Development (2016~2020)	Jungsunpil	0.00	0.16	80.00	0.10	0.29	1.98	0.06	1.53	28.78
	Sunjang	0.00	0.19	95.80	0.13	0.36	2.45	0.20	1.32	210.3
	Unchon	0.00	0.14	50.50	0.10	0.19	1.01	0.01	0.25	6.860
	Neungmac	0.00	0.17	55.50	0.12	0.20	1.65	0.00	0.23	14.13
	Insu	0.00	0.20	51.50	0.01	0.21	1.39	0.00	0.14	21.39
Evaluation (2021)	Jungsunpil	0.00	0.15	61.00	0.15	0.19	1.29	0.00	1.43	26.00
	Sunjang	0.00	0.19	65.80	0.29	0.44	2.20	0.00	1.33	164.7
	Unchon	0.00	0.11	32.00	0.01	0.28	0.82	0.00	0.13	2.690
	Neungmac	0.00	0.12	40.00	0.00	0.16	1.11	0.00	0.07	4.740
	Insu	0.00	0.13	28.50	0.16	0.25	0.60	0.00	0.04	1.202

This research utilized the well-known rainfall-discharge nomograph, which forecasts discharge by employing a correlation equation between past rainfall and past discharge data [30,31,32,33]. To develop the rainfall-discharge nomograph for the measured small stream, the research utilized non-linear regression to establish an exponential function which includes optimal parameters estimated through the use of the RCNES, as follows:

Q_{p} = m_{1} e^{m_{2} R_{c}},

(10)

in which

Q_{p}

is the discharge;

R_{c}

is rainfall accumulated for one hour; and

m_{1}

and

m_{2}

are optimum parameters. To develop this nomograph, rainfall data measured at the rainfall gauging station listed in Table 2 and flood discharge data measured using the CADMT over 5 years (2016-2020) and summarized in Table 3 were used. The annual rainfalls measured in the small streams ranged from 1,180.10

m m

to 1,588.2

m m

, with most rainfall concentrated in the summer season from June to September. For the un-measured small streams, the rainfall-discharge nomograph was developed using measured rainfall data and simulated flood discharges obtained using hydrology and hydraulics models [34,35,36].

To forecast discharges accurately, the research incorporated Antecedent Moisture Condition (AMC) [37,38], which takes into account the initial water content and 5-day antecedent rainfall. AMC leads to three classes of soil moisture (AMC I, II, and III) shown in Table 4 by dividing a year into dormant and growing seasons. In this case, the growing season was defined as the flood season specified in the water resources design practice [39,40], from June 21st to September 20th, when flood damages were likely to occur in Korea.

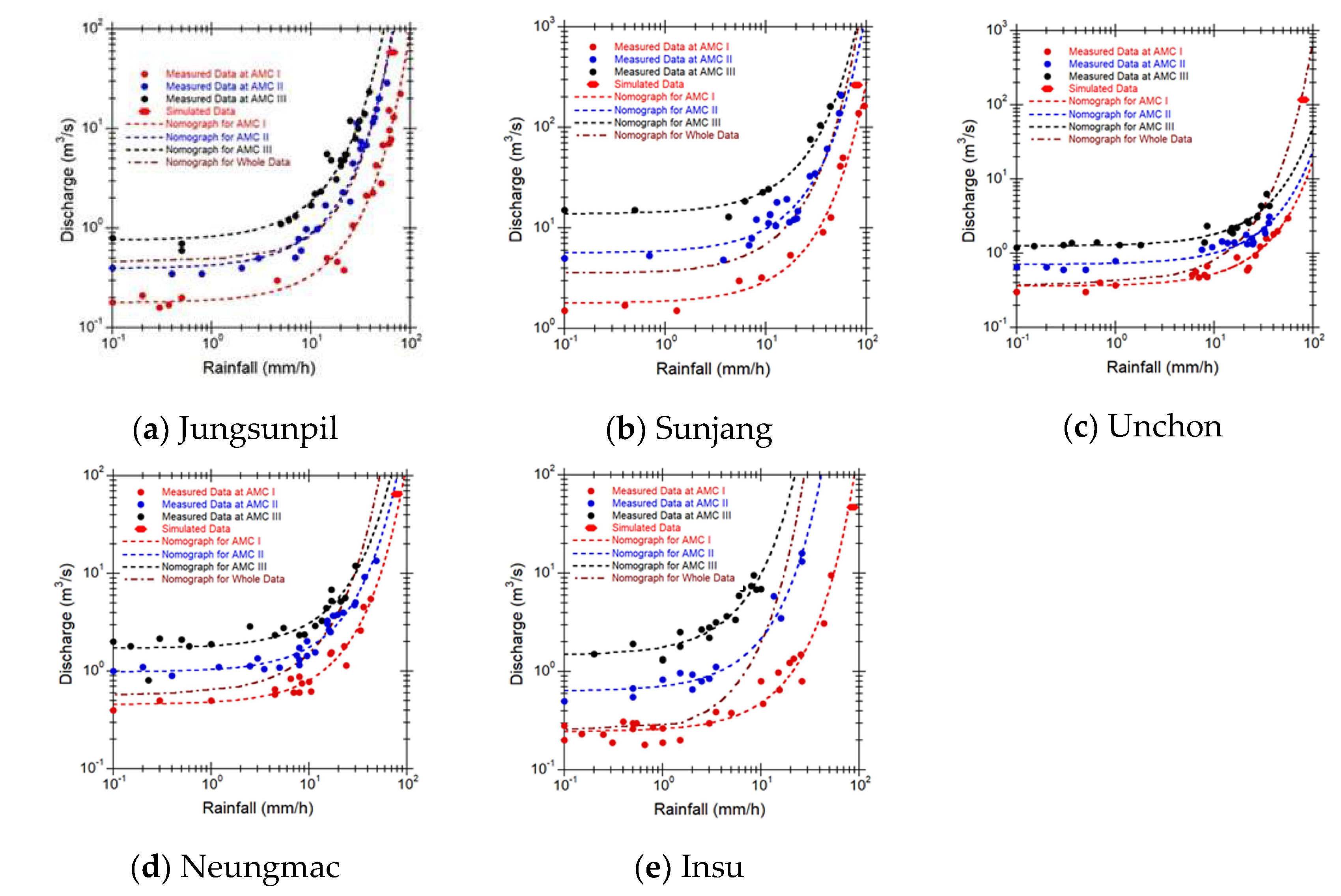
In this research, the measured rainfall and discharge in 5 small stream basins were subdivided into three subsets, each corresponding to a distinct Antecedent Moisture Condition (AMC) class, to consider the different initial soil moisture conditions. The corresponding rainfall and discharge time series were sorted into the relevant AMC classes based on the corresponding AMC values. Three types of rainfall-discharge nomographs were developed using three grouped rainfall events and discharges in each corresponding to a different AMC class. A total of 166 rainfall-discharge events were collected over 6 years, from 2016 to 2021, with 84 events in the AMC I class, 59 events in the AMC II class, and 23 events in the AMC III class. The largest rainfall-discharge events data were gathered in the Neungmac stream with 49, followed by the Sunjang stream with 39, the Jungsunpil stream with 29, the Unchon stream with 27, and the Insu stream with 22.

To develop the rainfall-discharge nomograph, the parameters shown in Equation 10 were estimated using the RCNES. The determined optimal values were summarized in Table 5, which showed that the coefficients of determination ranged from 0.899 to 0.966 for AMC I, 0.756 to 0.974 for AMC II, and 0.815 to 0.933 for AMC III. Table 5 also demonstrated that the coefficients of determination ranged from 0.286 for Insu stream to 0.523 for both Sunjang and Unchon streams for the entire data column, indicating that the whole data were utilized for developing the rainfall-discharge nomograph.

Table 6 summarized the event numbers and ranges of the discharge and rainfall used to develop the rainfall-discharge nomographs for each small stream. The research used a total of 67, 43, 59, 55, and 60 separate rainfall-discharge data sets obtained from the total 166 rainfall events for Jungsunpil, Sunjang, Unchon, Neungmac, and Insu streams, respectively.

To compare the accuracy of the rainfall-discharge nomographs, scatter plots were created using the measured data from 5 small streams, as shown in Figure 8. In addition, design flood discharge data was simulated using the Clark Unit Hydrograph model and measured rainfall data. This simulated data was also plotted to evaluate the effectiveness of the developed rainfall-discharge nomograph in unmeasured small streams. The results of the simulated design flood discharge that caused flooding in each small stream basin were as follows: 66.1

m^{3} / s

for Jungsunpil stream, 274

m^{3} / s

for Sunjang stream, 117.0

m^{3} / s

for Unchon stream, 78.7

m^{3} / s

for Neungmac stream, and 85.9

m^{3} / s

for Insu stream, respectively. Comparison of the forecasted discharge values using the nomographs with both the CADMT and simulated flood discharge values showed that the nomographs accurately matched the measured and simulated data. These results suggest that the rainfall-discharge nomograph can effectively forecast discharge in both measured and unmeasured small streams.

3.4. Development of a rating curve

A rating curve using the Manning equation was developed in this research, which is commonly used to establish the relationship between depth and discharge at a cross-section [41]. The Manning equation reflects the relationship among the average river velocity, riverbed roughness coefficient, and channel geometry, such as channel slope, cross-section, and sinuosity, which are collected from rivers and streams [42,43,44]. To account for variations in flow velocities in a compound cross-section, the section is generally divided into selected subsections, and the area values of the cross-section, wetted perimeter, and hydraulic radius of each subsection are measured. The equation for calculating the gauging section depends on the assumption that the hydraulic gradient of each subsection is the same [43], as follows:

Q = S_{c}^{\frac{1}{2}} \sum_{i = 1}^{n} \frac{A_{i} R_{i}^{2 / 3}}{n_{i}},

(11)

in which

A_{i}

is the area of the

i

th subsection;

R_{i}

is the hydraulic radius of the

i

th subsection; and

n_{i}

is the coefficient of roughness of the

i

th cross-section. The rating curve is then plotted to represent the relationship between depth and discharge at the gauging section. The Manning equation has the advantage of being applicable even to unmeasured streams without measured hydraulic data.

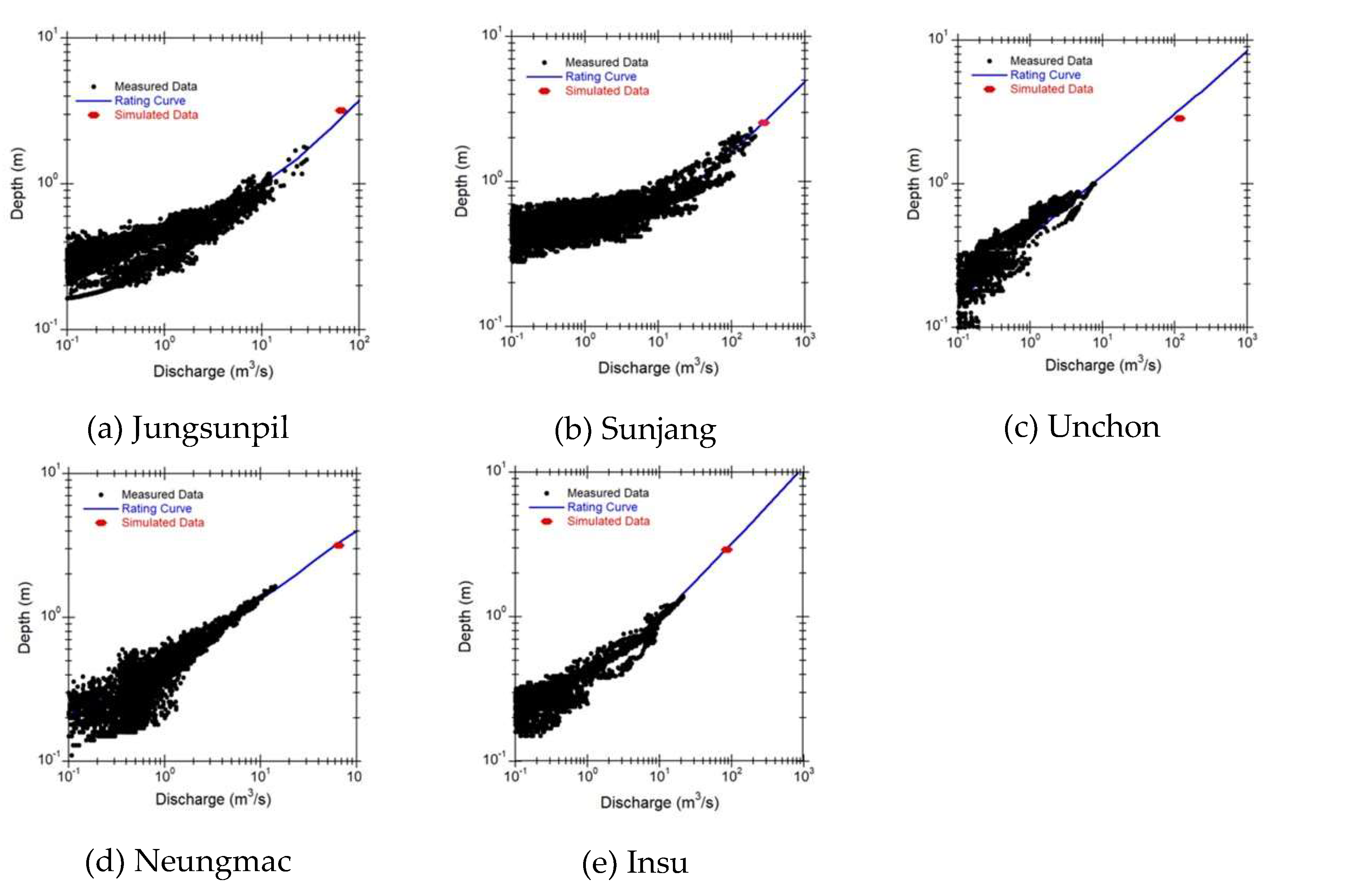
The developed rating curve was plotted to compare with the measured scatter data in Figure 9. The study used measured data collected from all five small streams listed in Table 3 to compare rating curves developed using the Manning equation. Additionally, the design flood depth was calculated using Equation 11 with the simulated design flood discharge as an input value for the Manning equation and plotted in Figure 9. The results of the calculated design flood depths were 3.18

m

for Jungsunpil stream, 2.55 m for Sunjang stream, 2.86

m

for Unchon stream, 2.93

m

for Neungmac stream, and 3.03

m

for Insu stream, respectively.

Figure 9 showed that the rating curve developed using the Manning equation accurately represents the measured and simulated data from 5 small streams. Therefore, this rating curve can be effectively used to forecast depth with discharge in both measured and unmeasured small streams. The comparison results demonstrated that the depth forecasted by the rating curves closely matched the CADMT values. The coefficient of determination values for the Jungsunpil stream, the Sunjang stream, the Unchon stream, the Neungmac stream, and the Insu stream were 0.88, 0.83, 0.83, 0.92, and 0.95, respectively. Among the rating curves analyzed, the coefficient of determination for the Insu stream was the highest.

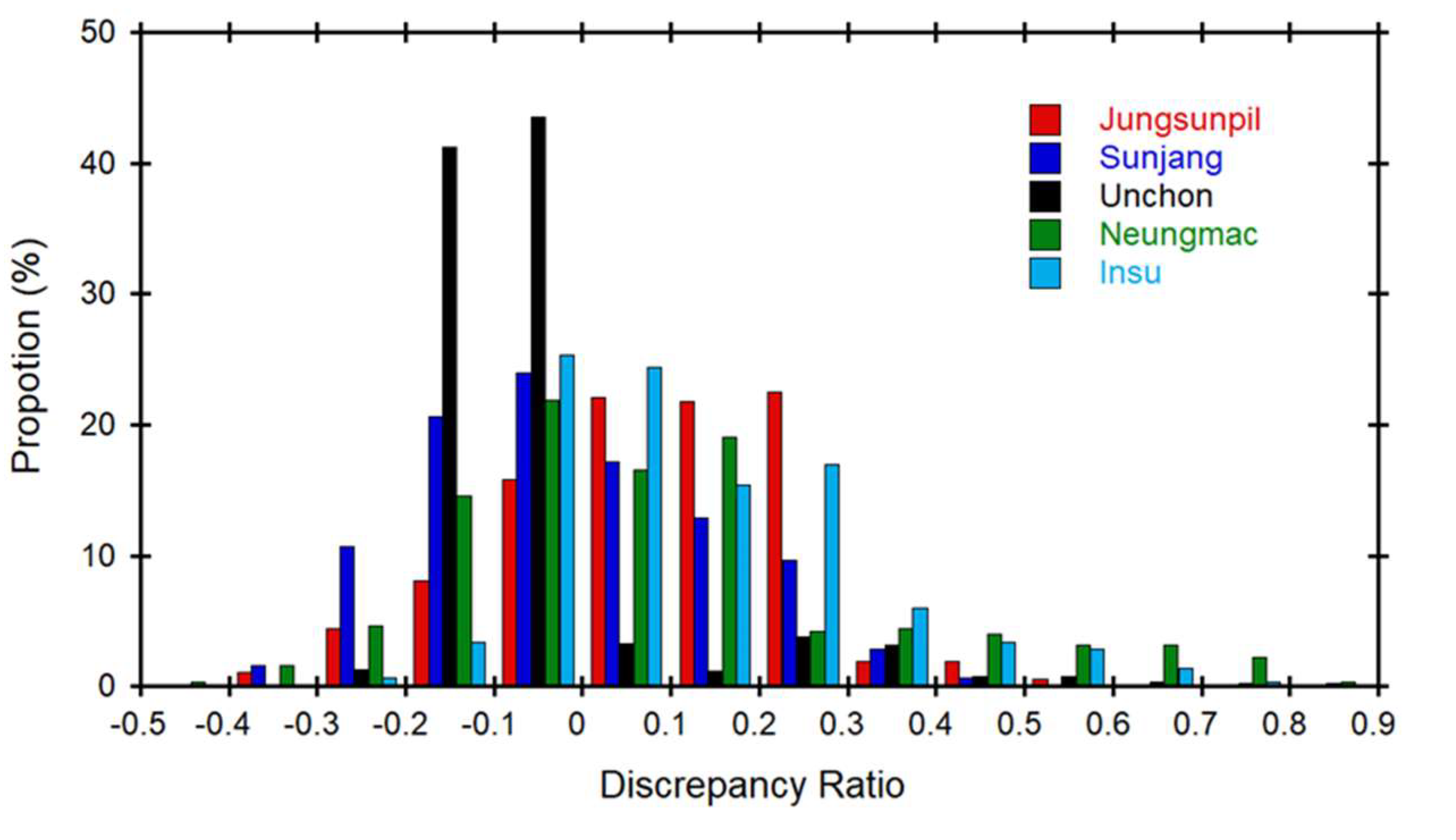
To quantitatively evaluate the differences between the measured and forecasted values, the research used the discrepancy ratio,

D_{r} = l n (H_{p} / H_{m})

as defined by [45] in which

H_{p}

is the predicted values of depth and

H_{m}

is the measured values of depth. A discrepancy ratio of zero indicates that the forecasted values were identical to the measured values. A positive discrepancy ratio indicates that the forecasted values overestimate the measured values, while a negative ratio indicates that the forecasted values underestimate them. Additionally, the research utilized the accuracy, defined as the proportion for which the discrepancy ratio fell between -0.2 and 0.2, to the total amount of data.

The Neungmac, Sunjang, Unchon, Insu, and Jungsunpil small streams were evaluated using rating curves to estimate their measured values. The rating curve for Jungsunpil overestimated the measured values while the rating curves for Neungmac, Sunjang, Unchon, and Insu underestimated the measured values. The distribution of discrepancy ratio for Jungsunpil showed that the majority of the values were distributed between -0.1 and 0.3. The discrepancy ratio distribution for Unchon had a bell-shaped curve, indicating that the majority of the values were distributed in the range between -0.2 and 0.2. The accuracy of the rating curves for Jungsunpil, Sunjang, Unchon, Neungmac, and Insu were found to be 90.29%, 84.29%, 92.98%, 76.24%, and 85.35%, respectively. Among the rating curves examined, the curve developed for the Unchon small stream showed the highest accuracy, while the curve for the Sunjang small stream showed the lowest accuracy.

4. Evaluation of the Flood Early Warning Framework

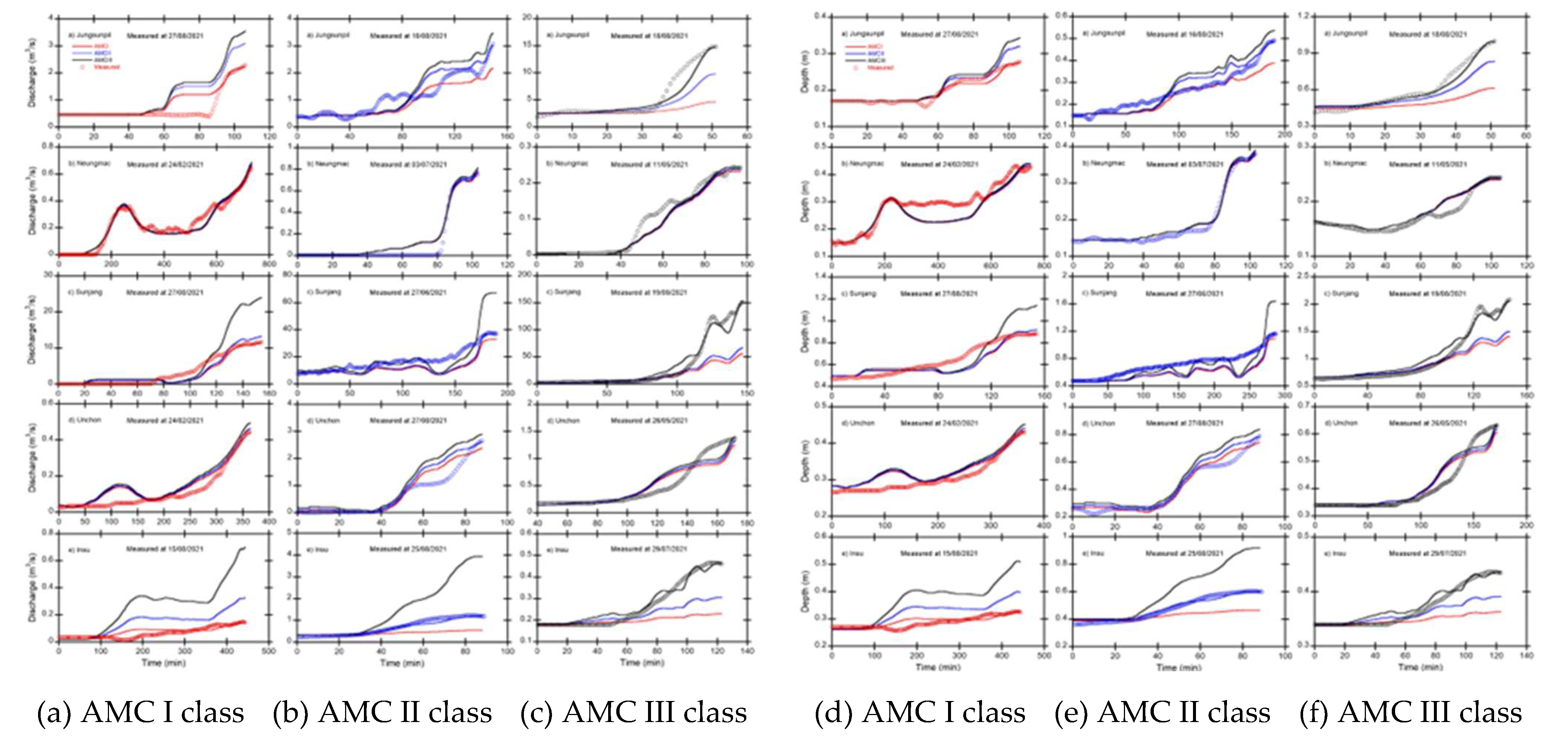
To evaluate the FEWF, the time-discharge and time-depth distributions predicted by the rainfall-discharge nomographs and rating curves were compared, respectively, with measured discharge and depth data in 2021 for 5 small streams that were not used in the development of the nomographs and rating curves.

Figure 11 showed the event verifications for each AMC class of the forecasted time-discharge and depth distributions compared to the measured data. Most of the rainfall events used for the evaluations occurred during the flood season from June 21st to September 20th. However, in the case of the Neungmac and Unchon streams, rainfall events occurred in February for the AMC I class and in May for the AMC III class. The rising curve to the peak of the time-discharge and depth distributions was considered for verification because the rising parts, especially the peaks, are relevant for issuing flood early warnings.

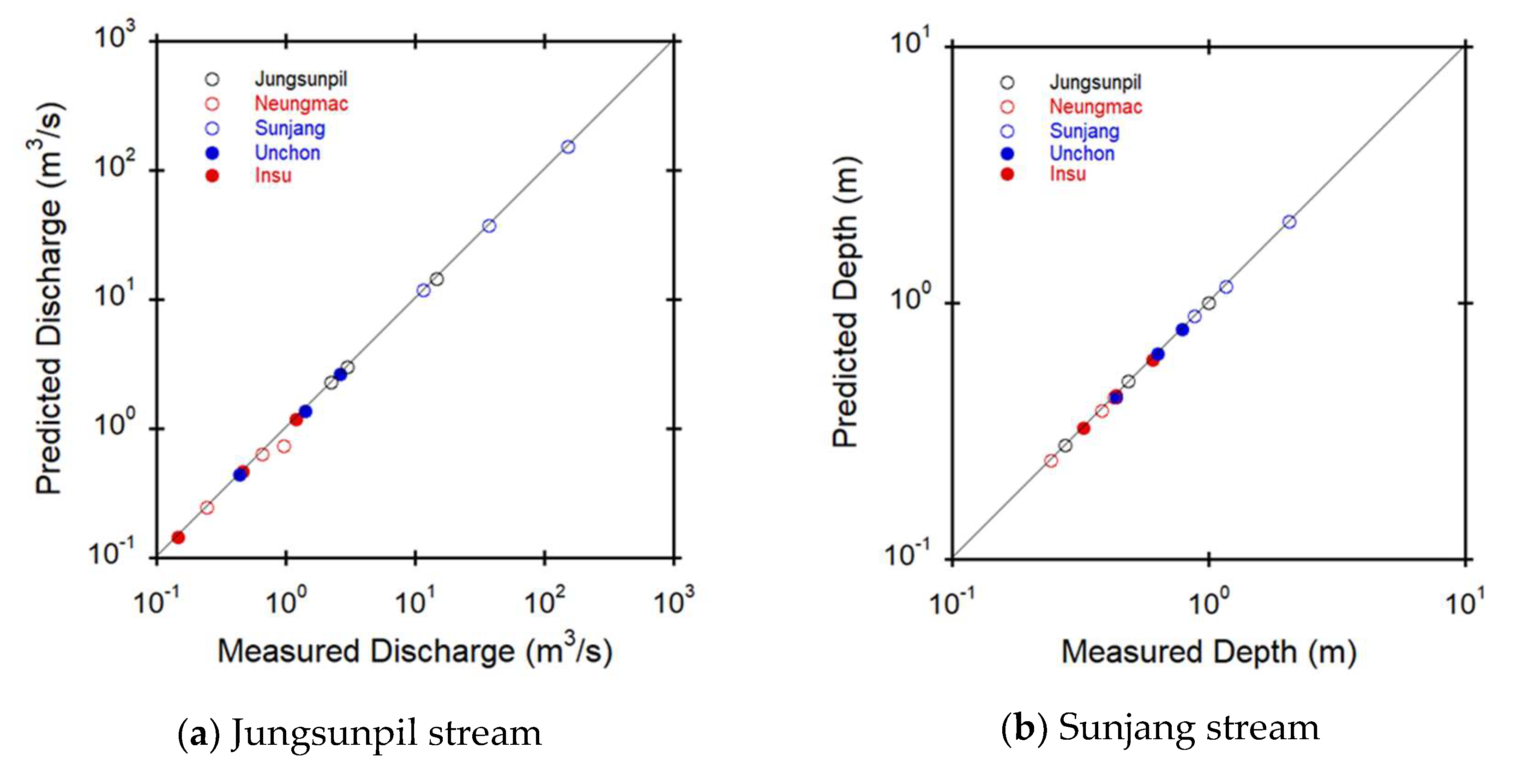
A quantitative evaluation of the forecasted peak discharge and depth values from the FEWF by comparing to the measured data, was conducted as shown in Figure 12. The results showed that the peak discharge and depth forecasted using the proposed rainfall-discharge nomograph and rating curve accurately represented the observed values for 5 small streams. However, the forecasted depth values matched the measured values better than the forecasted discharge values. The high accuracy of the depth forecasting increased the reliability of the FEWF because flood early warning is issued based on forecasting depth values.

The coefficient of determination,

R^{2}

was utilized to further evaluate the results, as shown in Table 7. The forecasted discharge results revealed that the Jungsunpill, Neungmac, and Unchon streams had the highest

R^{2}

in the AMC I, AMC II, and AMC III classes, respectively. On the other hand, the depth forecasting results showed that the Jungsunpil and Unchon streams had the highest

R^{2}

in the AMC I class, the Neungmac small stream had the highest

R^{2}

in the AMC II class, and the Sunjang and Insu small streams had the highest

R^{2}

in the AMC III class, respectively. The inter-comparison results indicated that the depth results predicted by the rating curves more accurately matched than the discharge results predicted by the rainfall-discharge nomograph.

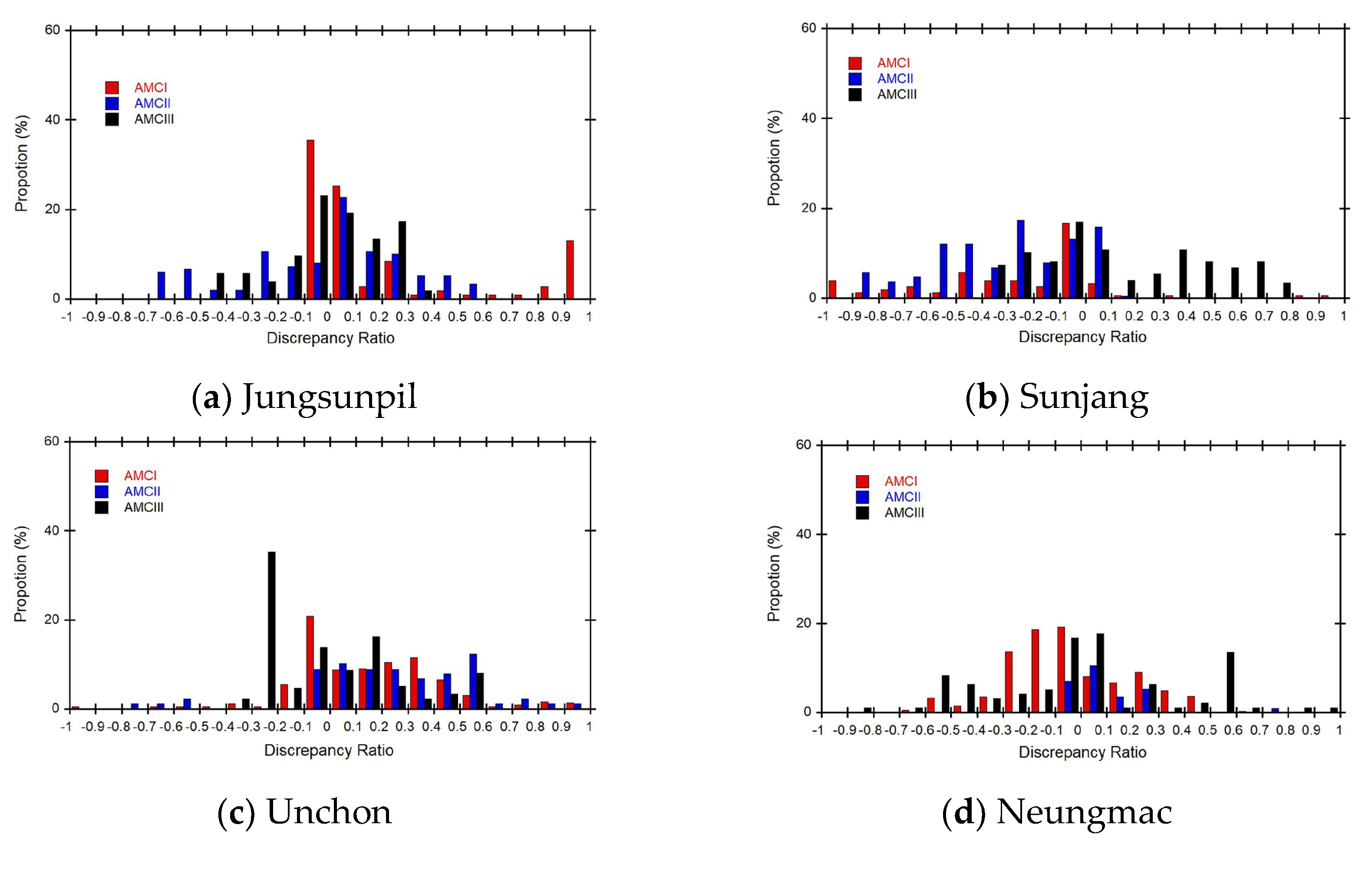
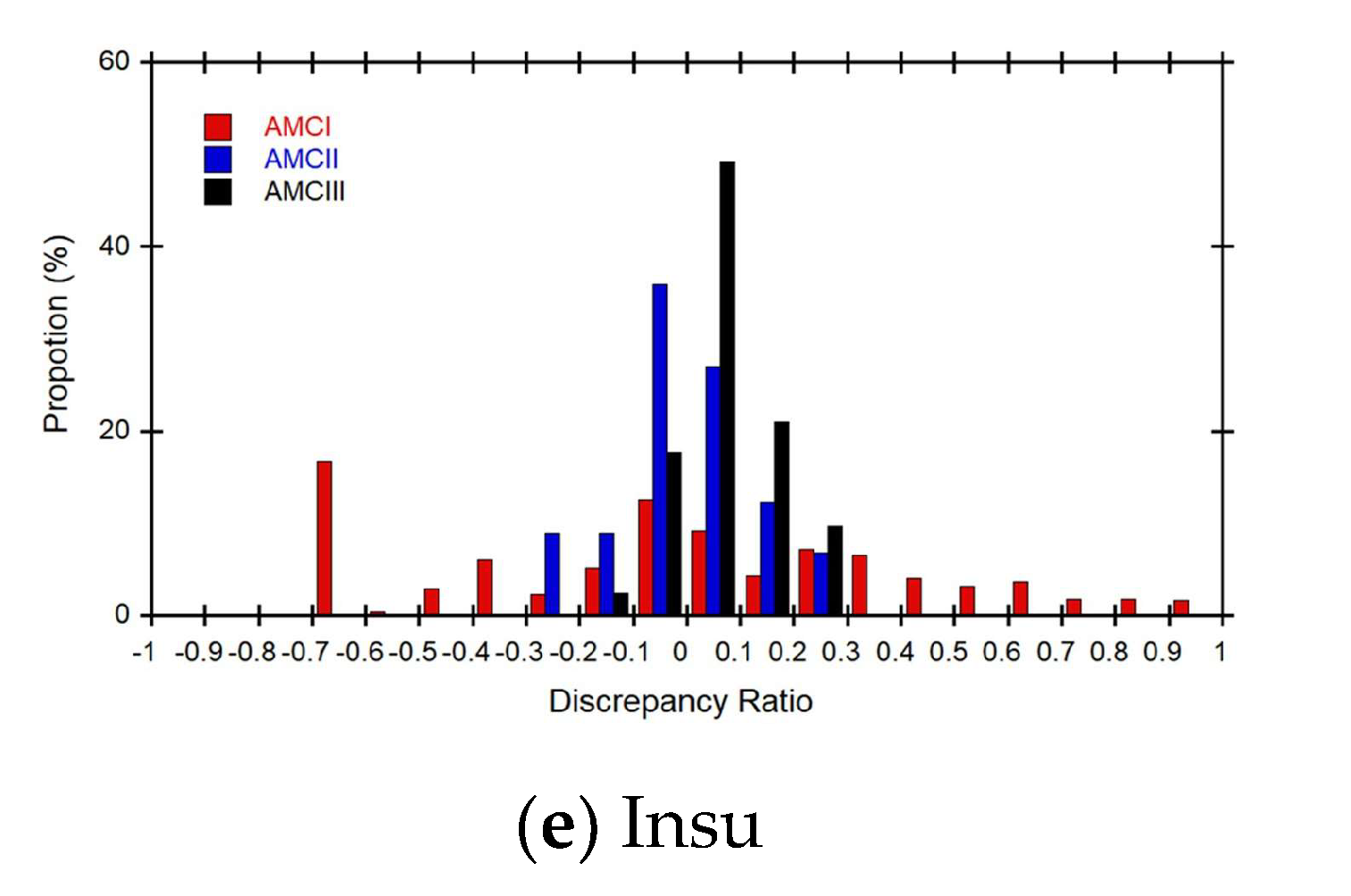
To quantitatively evaluate the difference between measured and forecasted discharge and depth values, we used the discrepancy ratio. Figure 13 shows the discrepancy ratio histograms of discharges forecasted by using the rainfall-discharge nomograph for each small stream. For the AMC I class, the rainfall-discharge nomograph of the Jungsunpil, Neungmac, Sunjang, and Unchon streams underestimated the measured values, while it overestimated the measured values of the Insu stream. For the AMC II class, the rainfall-discharge nomograph of the Jungsunpil, Neungmac, and Unchon streams overestimated the measured values, while it underestimated the measured values of the Sunjang and Insu streams. For the AMC III class, the rainfall-discharge nomograph of the Neungmac, Sunjang, and Insu streams overestimated the measured values, while it underestimated the measured values of the Jungsunpil and Unchon streams.

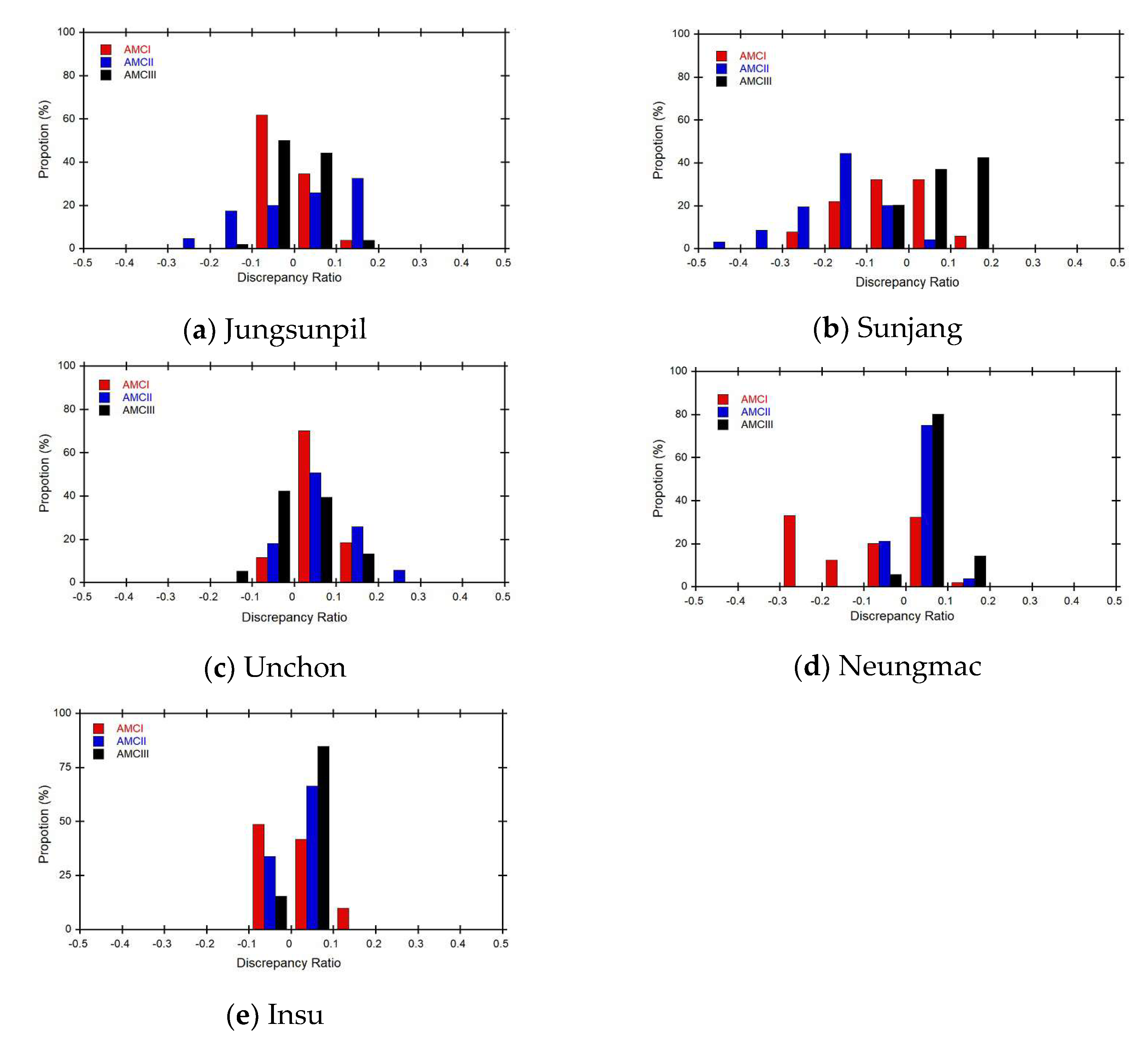
Figure 14 showed that the discrepancy ratio histograms of depth forecasts generated by the rating curves for each of 5 small streams. In the case of the AMC I class, the rating curves of Jungsunpil, Neungmac, Sunjang, and Insu streams underestimated the measured values, while that of the Unchon stream overestimated them. Conversely, for the AMC II class, the rainfall-discharge nomograph of the Jungsunpil, Neungmac, Unchon, and Insu streams overestimated the measured values, while that of the Sunjang stream underestimated them. Finally, for the AMC III class, the rainfall-discharge nomographs of the Neungmac, Sunjang, and Insu streams overestimated the measured values, while those of the Jungsunpil and Unchon streams underestimated them.

The accuracy of the rainfall-discharge nomographs and rating curves for each small stream, based on the forecasted discharge and depth as shown in Table 8. For the AMC I class, the accuracy of the rainfall-discharge nomographs was 93.92%, 28.09%, 93.26%, 44.66%, and 33.56% for the Jungsunpil, Sunjang, Unchon, Neungmac, and Insu streams, respectively. The accuracy of the rating curves for the same streams was 100.0%, 94.38%, 100.0%, 100.0%, and 100.0%, respectively. For the AMC II and AMC III classes, both methods had 100.0% accuracy for all streams. Notably, the rating curves developed for the Sunjang stream had the lowest accuracy. These results indicate that the rating curves were more accurate in forecasting depth compared to the rainfall-discharge nomograph in forecasting discharge.

The development of the FEWF used measured and predicted data from rainfall events that did not exceed the design flood depth. However, if future rainfall intensities increase due to climate change, the accuracy of the forecast may decrease. It is therefore crucial to secure long-term and high-quality measurement data to make more accurate predictions. In addition, the incorporation of planned flood simulation results could improve the accuracy of the FEWF to compensate for any deficiencies in the measured data. The FEWF can also be used to develop a forecast for unmeasured small streams.

5. Conclusions

Small streams are often exposed to flood risks, resulting in casualties and property damage to network services and public facilities. Responding to these risks is challenging due to the deficient flood arrival time and insufficient management capacity of local governments. More than 60% of casualties have occurred in small streams, making it crucial to establish an appropriate FEWF suitable for small streams to minimize flood-related damages.

In this research, the FEWF was developed as an early warning system for forecasting discharge and depth before reaching flood in both measured and unmeasured small streams. The FEWF uses the rainfall-discharge nomograph to forecast discharge with the forecasted rainfall as input values. These forecasted flood discharges are then used to forecast depths by using the rating curve to issue flood warnings. The flood warning is issued when the depth reaches the warning criteria. If the forecasted depth does not exceed the warning criteria, it is evaluated with new measured depth in the evaluation step to ensure that the residual meets the convergence criteria. If the forecasted depth does not meet the convergence criteria, the RCNES can be used to update the rainfall-discharge nomograph and the rating curve with newly measured discharge, rainfall, and depth data.

To develop the rainfall-discharge nomographs and rating curves, optimization techniques and the Manning equation with measured data were used to collect data for 5 years from 2016 to 2020 in 5 small streams as test beds. The intercomparison results showed that both developed nomographs and rating curves represented the measured values well. The forecasted values were evaluated using the developed nomographs and rating curves with discharge and depth values measured in 2021 in five small streams. The evaluation results showed that the rainfall-discharge nomographs and rating curves proposed herein forecasted the rising curve to the peak of the time-discharge and depth distributions quite well, respectively.

The research used the determinant coefficient, the discrepancy ratio, and accuracy to evaluate the difference between measured and forecasted discharge and depth values more quantitatively. Overall, the forecasted depth values matched the measured values better than the forecasted discharge values. It was found that the high accuracy of the depth forecasting increased the reliability of the FEWF because the flood early warning would be issued with forecasted depth values. The Jungsunpil stream had the highest accuracy for the AMC I class, and the Unchon stream had the highest accuracy for the AMC II and III classes, respectively. The accuracy of the rating curves for the Jungsunpil, Unchon, Neungmac, and Insu streams were 100.0% for the AMC I class, and for the AMC II and III classes, the accuracy was 100.0% in the 5 small streams.

The methods and procedures used to develop and evaluate the rainfall-discharge nomograph and rating curve are suitable for forecasting discharges and depths with forecasted rainfall data for small stream flood warning. Moreover, these methods could potentially help develop treatment methods or technology to solve problems related to the establishment of the flood early warning system. Nonetheless, continuous application and evaluation research is necessary to increase the forecasting accuracy of the FEWF using measured data collected from various characterized small streams. Both the measured data method and the estimated data method have unique benefits and drawbacks when developing a flood early warning framework for small streams. The measured data method is more precise as it uses real-time data and considers the current state of the stream. However, implementing this method requires a specific level of monitoring infrastructure, which may not be feasible in certain small stream basins. On the other hand, the estimated data method can be used in cases where no monitoring infrastructure is available. Nevertheless, this method is less accurate than measured data as it relies on assumptions and model inputs that may not accurately represent the true conditions of the stream. Combining both methods can enhance the accuracy of the FEWF, and it should be noted that both methods have their unique applications in the development of the framework.

Author Contributions

Conceptualization, T.-S.C. and S.K.; Methodology, T.-S.C., C.C., S.-J.Y., S.K. and K.-M.K.; Software, T.-S.C. and K.-M.K..; Validation, T.-S.C.; Formal Analysis, C.C. and J.S.; Investigation, S.-J.Y. and S.K.; Resources, T.-S.C. and S.K.; Data curation, T.-S.C., C.C.,S.-J.Y. and S.K.; Writing-original draft, T.-S.C., K.-M.K.; Writing-review & editing, T.-S.C., C.C., S.-J.Y., J.S., S.K. and K.-M.K.; Visualization, T.-S.C.; Supervision, T.-S.C. and S.K.; Project administration, T.-S.C. and S.K.; Funding acquisition, T.-S.C. and S.K. All authors have read and agreed to the published version of the manuscript.

Funding

Deep thanks and gratitude to the Research Project (NDMI-PR-2022-07-04), the National Disaster Management Institute, Ulsan, Korea for funding the research article.

Data Availability Statement

Datasets that are restricted and not publicly available.

Acknowledgments

We are thankful to the National Disaster Management Institute of Korea for providing necessary data used in this study.

Conflicts of Interest

The authors declare that there are no known competing financial interest or personal relationship that could have appeared to influence the work reported in this article.

References

Pörtner, H.-O.; Roberts, D.C.; Adams, H.; Adler, C.; Aldunce, P.; Ali, E.; Begum, R.A.; Betts, R.; Kerr, R.B.; Biesbroek, R. Climate change 2022: Impacts, adaptation and vulnerability; IPCC Geneva, Switzerland:: 2022.
Organization, W.M. WMO statement on the state of the global climate in 2019; 2020.
Rajeevan, M.; Bhate, J.; Jaswal, A.K. Analysis of variability and trends of extreme rainfall events over India using 104 years of gridded daily rainfall data. Geophysical research letters 2008, 35. [Google Scholar] [CrossRef]
Goswami, B.N.; Venugopal, V.; Sengupta, D.; Madhusoodanan, M.; Xavier, P.K. Increasing trend of extreme rain events over India in a warming environment. Science 2006, 314, 1442–1445. [Google Scholar] [CrossRef]
Vellore, R.K.; Krishnan, R.; Pendharkar, J.; Choudhury, A.D.; Sabin, T. On the anomalous precipitation enhancement over the Himalayan foothills during monsoon breaks. Climate dynamics 2014, 43, 2009–2031. [Google Scholar] [CrossRef]
Cheong, T.S.; Joo, J.; Choi, H.; Kim, S. Development and evaluation of automatic discharges measurement technology for small stream monitoring. Journal of the Korean Society of Hazard Mitigation 2018, 18, 347–355. [Google Scholar] [CrossRef]
Cheong, T.S.; Ko, T.; Choi, H.; Kim, S. Development of large scale particle image velocimetry prototype for the small stream discharge monitoring. Journal of Disaster Management 2017, 2, 19–28. [Google Scholar]
Cheong, T.S.; Joo, J.S.; Byun, H. Advancement of automatic discharge measurement technology to enhance disaster-safety codes for small stream (In Korean); NDMI-PR(ER)-2019-06-01; Ulsan, 2019.
Lee, J.; Lee, Y.; Kim, E.; Ha, J.; Jang, D. A study on the dynamical characteristics associated with heavy rainfall case of July 14, 2009. In Proceedings of the Proc. Autumn Meeting of Korea Meteor. Soc; 2010; pp. 244–245. [Google Scholar]
Muste, M.; Hauet, A.; Fujita, I.; Legout, C.; Ho, H.-C. Capabilities of large-scale particle image velocimetry to characterize shallow free-surface flows. Advances in water resources 2014, 70, 160–171. [Google Scholar] [CrossRef]
Bechle, A.J.; Wu, C.H. An entropy-based surface velocity method for estuarine discharge measurement. Water Resources Research 2014, 50, 6106–6128. [Google Scholar] [CrossRef]
Fujita, I.; Muste, M.; Kruger, A. Large-scale particle image velocimetry for flow analysis in hydraulic engineering applications. Journal of hydraulic Research 1998, 36, 397–414. [Google Scholar] [CrossRef]
Yang, D.; Shi, X.; Marsh, P. Variability and extreme of Mackenzie River daily discharge during 1973–2011. Quaternary International 2015, 380, 159–168. [Google Scholar] [CrossRef]
Perera, D.; Seidou, O.; Agnihotri, J.; Mehmood, H.; Rasmy, M. Flood impact mitigation and resilience enhancement; Intech Open) Challenges and Technical Advances in Flood Early Warning …: 2020.
Kumar, N.; Kharkwal, N.; Kohli, R.; Choudhary, S. Ethical aspects and future of artificial intelligence. In Proceedings of the 2016 International Conference on Innovation and Challenges in Cyber Security (ICICCS-INBUSH); 2016; pp. 111–114. [Google Scholar]
Kaplan, A.; Haenlein, M. Siri, Siri, in my hand: Who’s the fairest in the land? On the interpretations, illustrations, and implications of artificial intelligence. Business horizons 2019, 62, 15–25. [Google Scholar] [CrossRef]
Raffel, M.; Willert, C.E.; Kompenhans, J. Particle image velocimetry: a practical guide; Springer: 2018.
Kim, S.; Yu, K.; Yoon, B. Error analysis of image velocimetry according to the variation of the interrogation area. Journal of Korea Water Resources Association 2013, 46, 821–831. [Google Scholar] [CrossRef]
Huber, P.J.; Ronchetti, E.M. Robust Statistics; Wiley: 2011.
Gui, Q.; Zhang, J. Robust biased estimation and its applications in geodetic adjustments. Journal of Geodesy 1998, 72, 430–435. [Google Scholar] [CrossRef]
Holland, P.W.; Welsch, R.E. Robust regression using iteratively reweighted least-squares. Communications in Statistics-theory and Methods 1977, 6, 813–827. [Google Scholar] [CrossRef]
Abt, S.; Wittier, R.; Taylor, A.; Love, D. Human stability in a high flood hazard zone. JAWRA Journal of the American Water Resources Association 1989, 25, 881–890. [Google Scholar] [CrossRef]
Jonkman, S.; Penning-Rowsell, E. Human instability in flood flows. JAWRA Journal of the American Water Resources Association 2008, 44, 1208–1218. [Google Scholar] [CrossRef]
Jonkman, S.N. Global perspectives on loss of human life caused by floods. Natural hazards 2005, 34, 151–175. [Google Scholar] [CrossRef]
Jonkman, S.N.; Vrijling, J.K. Loss of life due to floods. Journal of Flood Risk Management 2008, 1, 43–56. [Google Scholar] [CrossRef]
Karvonen, R.; Hepojoki, A.; Huhta, H.; Louhio, A. The use of physical models in dam-break analysis. RESCDAM Final Report. Helsinki University of Technology, Helsinki, Finland, 2000. [Google Scholar]
Shand, D.; Smith, G.; Blacka, M. Appropriate criteria for the safety and stability of people in stormwater design. In Proceedings of the Proceedings of National Conference of the Stormwater Industry Association, Sydney, Australia, 2010; pp. 9–12.
Xia, J.; Falconer, R.A.; Wang, Y.; Xiao, X. New criterion for the stability of a human body in floodwaters. Journal of Hydraulic Research 2014, 52, 93–104. [Google Scholar] [CrossRef]
Yee, M. Human stability in floodways. University of New South Wales, Sydney, Australia, 2003.
Bae, D.-H.; Shim, J.B.; Yoon, S.-S. Development and assessment of flow nomograph for the real-time flood forecasting in Cheonggye stream. Journal of Korea Water Resources Association 2012, 45, 1107–1119. [Google Scholar] [CrossRef]
Jang, C.H.; Kim, H.J. Development of flood runoff characteristics nomograph for small catchment using R-programming. In Proceedings of the Proceedings of the Korea Water Resources Association Conference, 2015; pp. 590–590.
Neely, B.L. Flood frequency and storm runoff of urban areas of Memphis and Shelby County, Tennessee; US Geological Survey: 1984.
Safety, M.o.I.a. The integration model of flood forecasting for medium and small streams. 2016.
Chow, V.T.; Maidment, D.R.; Larry, W. Applied Hydrology. International edition, MacGraw-Hill, Inc 1988, 149. [Google Scholar]
Straub, T.D.; Melching, C.S.; Kocher, K.E. Equations for estimating Clark unit-hydrograph parameters for small rural watersheds in Illinois; US Department of the Interior, US Geological Survey: 2000.
Clark, C.O. Storage and the unit hydrograph. Transactions of the American Society of Civil Engineers 1945, 110, 1419–1446. [Google Scholar] [CrossRef]
Gray, D.M. Handbook on the principles of hydrology; Water Information Center, Incorporated: 1970.
Ponce, V.M.; Hawkins, R.H. Runoff curve number: Has it reached maturity? Journal of hydrologic engineering 1996, 1, 11–19. [Google Scholar] [CrossRef]
Institute, N.D.M. Establishment of the CCTV based automatic discharge measurement technology application system for enhancing the disaster safety codes of the small streams. 2020.
Jeong, J.; Yoon, H. Water resources design practice. 2020.
Lamb, R.; Zaidman, M.; Archer, D.; Marsh, T.; Lees, M. River Gauging Station Data Quality Classification (GSDQ); R&D Technical Report W6-058/TR: 2003.
Chow, V.T. Open channel hydraulics. 1959.
Li, Z.; Zhang, H.; Singh, V.P.; Yu, R.; Zhang, S. A simple early warning system for flash floods in an ungauged catchment and application in the Loess Plateau, China. Water 2019, 11, 426. [Google Scholar] [CrossRef]
Song, S.; Schmalz, B.; Zhang, J.; Li, G.; Fohrer, N. Application of modified Manning formula in the determination of vertical profile velocity in natural rivers. Hydrology Research 2016, 48, 133–146. [Google Scholar] [CrossRef]
White, W.; Mill, H.; Crabbe, A. Sediment transport: an appraisal of available methods: volume 1: summary of existing theories: volume 2: performance of theoretical methods when applied to flume and field data; 1972.

Figure 1. The frequency of the extreme rainfall and the distribution map of occurrence regions of Korea over the past 93 years from 1927 to 2019.

Figure 2. Location map of the small streams and the rainfall gauging stations, in which ━: the small streams and ●: the rainfall gauging stations.

Figure 3. The comparison results in the largest cross-sectional change among the measured data in each of 5 small streams.

Figure 4. Comparisons of the velocities measured in Jungsunpil stream, Korea.

Figure 5. Comparisons of the time-discharges measured (a) on September 11, 2017, (b) on August 24, 2017, and (c) on October 6, 2017.

Figure 2. The concept diagram of the FEWF for warning of the depth, the discharge, and the velocity.

Figure 7. The warning criteria examples of the FEWF, where the time-distributed depth of Jungsunpil and Sunjang small streams were measured on September 28, 2019 and August 29, 2020, respectively.

Figure 8. Comparison of rainfall-discharge nomographs forecasted by using the RCNES with measured data collected from 5 small streams.

Figure 9. Comparison of rating curves estimated by using the Manning equation with measured data collected from 5 small streams.

Figure 10. The histogram of discrepancy ratios of each small stream.

Figure 11. The event verifications as rainfall-discharge nomographs and depth for forecasting time-discharge (a, b, c) and depth distributions (d, e, f), respectively (The measurement date of rainfall events was indicated on the upper of each figure).

Figure 12. Comparison of peak discharge and depth forecasted by rainfall-discharge nomographs and rating curves with measured data in 5 small streams.

Figure 13. Comparison of discrepancy ratio to evaluate difference between measured and forecasted values of the rainfall-discharge nomographs for 5 small streams.

Figure 14. Comparison of discrepancy ratio to evaluate difference between measured and forecasted values of the rating curves for 5 small streams.

Table 1. Comparisons of the location and characteristics of small stream basins.

Small Streams	Latitude	Longitude	$A_{b}$ (km)	$W_{b}$ (km)	$C_{b}$	$S_{c}$	$L_{c}$ (km)	$W_{c}$
Jungsunpil	35.65.17	129.13.17	5.09	1.60	0.50	0.096	3.18	14.00
Sunjang	35.24.04	128.55.49	13.63	2.17	0.34	0.093	2.14	33.50
Unchon	37.33.15	127.70.96	6.98	2.01	0.58	0.054	2.88	21.50
Neungmac	37.24.31	127.16.81	2.41	0.78	0.25	0.054	3.09	9.450
Insu	37.40.20	127.00.20	3.66	1.17	0.38	0.025	3.12	17.06

Table 2. The reference information of selected rainfall gauging stations in each small stream basin.

Small Streams	Rainfall Gauging Station	Latitude	Longitude	Distance $(k m$ )	Average Annual Rainfall $(m m$ )	$Elevation (E L . m$ )	Started Observation
Jungsunpil	Dooseo	35.62.03	129.14.35	4.23	1,274.10	123.0	1991
Sunjang	Yangsan	35.30.74	129.02.01	9.86	1,588.20	6.290	2008
Unchon	Yeoju	37.17.43	127.38.53	6.58	1,180.10	51.50	1962
Neungmac	Yongin	37.27.01	127.22.18	5.83	1,293.50	83.00	2005
Insu	Uijungbu	37.73.50	127.07.50	10.4	1,544.50	72.00	2001

Table 4. The definition of AMC classes according to the SCS approach.

AMC Class	5-day Antecedent Rainfall (mm)		Soil Moisture (%)
AMC Class	Dormant season	Growing season	Soil Moisture (%)
AMC I (dry)	P5 < 12.70	P5 < 35.56	10
AMC II (medium)	12.70 ≤ P5 ≤ 27.94	35.56 ≤ P5 ≤ 53.34	50
AMC III (wet)	P5 > 27.94	P5 > 53.34	90

Table 5. The determined optimum values by using the RCNES.

AMC Class		Small Streams
AMC Class		Jungsunpil	Sunjang	Unchon	Neungmac	Insu
AMC I	$m_{1}$	0.179	1.788	0.362	0.458	0.246
	$m_{2}$	0.063	0.051	0.039	0.057	0.067
	$R^{2}$	0.899	0.929	0.966	0.949	0.939
AMC II	$m_{1}$	0.394	4.983	0.713	0.987	0.632
	$m_{2}$	0.081	0.066	0.035	0.058	0.124
	$R^{2}$	0.899	0.756	0.85	0.962	0.974
AMC III	$m_{1}$	0.756	13.838	1.262	1.723	1.471
	$m_{2}$	0.09	0.053	0.037	0.059	0.191
	$R^{2}$	0.933	0.929	0.865	0.894	0.815
Whole Data	$m_{1}$	0.29	3.506	0.385	0.579	0.213
	$m_{2}$	0.088	0.068	0.076	0.098	0.223
	$R^{2}$	0.412	0.523	0.407	0.523	0.286

Table 6. The event numbers and ranges of the discharge and rainfall used to develop the rainfall-discharge nomographs.

AMC Class		Small Streams
AMC Class		Jungsunpil	Sunjang	Unchon	Neungmac	Insu
AMC I	Events	21	12	19	19	27
	$Q$ range	0.16-22.88	1.50-164.4	0.30-2.970	0.40-5.520	0.18-3.090
	$R$ range	0.10-80.00	0.10-95.80	0.10-50.50	0.10-55.50	0.10-51.50
AMC II	Events	23	10	19	26	15
	$Q$ range	0.35-28.780	12.85-207.7	0.60-3.1400	1.00-13.590	0.50-16.000
	$R$ range	0.10-58.50	0.10-56.02	0.10-36.12	0.10-48.53	0.10-21.39
AMC III	Events	23	21	21	20	18
	$Q$ range	0.60-23.45	4.83-210.3	1.20-6.860	0.81-14.13	1.30-9.500
	$R$ range	0.10-38.61	0.10-45.80	0.10-36.00	0.10-30.11	0.20-10.04

Table 7. The determination of coefficient results for the discharges and depths predicted by using the rainfall-discharge nomographs and rating curves respectively in all five small streams.

Small Streams	Discharges by the rainfall-discharge nomograph			Depths by the rating curve
Small Streams	AMC I	AMC II	AMC III	AMC I	AMC II	AMC III
Jungsunpil	0.969	0.856	0.910	0.954	0.928	0.822
Sunjang	0.928	0.932	0.966	0.974	0.822	0.978
Unchon	0.964	0.706	0.969	0.977	0.958	0.928
Neungmac	0.896	0.918	0.778	0.890	0.973	0.802
Insu	0.521	0.859	0.967	0.517	0.889	0.991

Table 8. Accuracy of forecasted discharge and depth by using the rainfall-discharge nomographs and rating curves respectively in 5 small streams.

Small Streams	Discharges by the rainfall-discharge nomograph			Depths by the rating curve
Small Streams	AMC I	AMC II	AMC III	AMC I	AMC II	AMC III
Jungsunpil	90.32	59.33	27.09	100.0	100.0	100.0
Sunjang	28.09	66.17	50.00	94.38	100.0	100.0
Unchon	93.26	63.55	44.79	100.0	100.0	100.0
Neungmac	44.66	69.23	54.74	100.0	100.0	100.0
Insu	33.56	78.61	21.05	100.0	100.0	100.0

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Development of Flood Early Warning Frameworks for the Small Streams in Korea

Abstract

1. Introduction

1.1. Research necessity

1.2. Challenges

1.3. Opportunities

2. Materials and Methods

2.1. Determination of Measurement Sites

2.2. Selection of Rainfall Gauging Stations

2.3. Measurement of Flow Velocity and Depth

2.4. Discharge Measurements

3. Development of the Flood Early Warning Framework

3.1. Development of a framework

3.2. Determination of a warning criteria

3.3. Development of a rainfall-discharge nomograph

3.4. Development of a rating curve

4. Evaluation of the Flood Early Warning Framework

5. Conclusions

Author Contributions

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe