Resolution of the 3n+1 Problem Using Inequality Relation Between Indices of 2 and 3

1. Introduction

Collatz conjecture, or the $3n+1$ problem, is a simple arithmetic function applied to positive integers. If the integer is odd, triple it and add one. It is called the odd step. If the integer is even, it is divided by two and is denoted as the even step. It is conjectured that every integer will eventually reach the number 1. Much work has been done to prove or disprove this conjecture [1,2,3,4].

The problem is easy to understand, and since it has attracted much attention from the general public and experts alike, the literature is endless. Still, the efforts made to tackle the $3n+1$ problem can generally be categorized under the following headings:

• Experimental or computational method: This method uses computational optimizations to verify Collatz conjecture by checking numbers for convergence [5,6,7]. Numbers as large as ${10}^{20}$ have shown no divergence from the conjecture.
• Arguments based on probability: It is suggested that, on average, the sequence of numbers tends to shrink in size so that divergence do not occur. On average, each odd number is $3/4$ of the previous odd integer [8].
• Evaluation of stopping times: Many researchers seem to work on the $3n+1$ problem from this approach [9,10,11,12,13]. In essence, it is sought to prove that the Collatz conjecture yields a number smaller than the starting number.
• Mathematical induction: It is perhaps the most common method to “prove" the Collatz conjecture. The literature involving this particular method seems endless [14,15].

The issue is that the Collatz conjecture is a straightforward arithmetic operation, while the methods used are not. The mismatch is created because the problem has attracted the attention of brilliant people in mathematics who are used to dealing with complex issues with equally complex tools. Therefore, an elementary analysis of the problem might be lacking.

This article takes a rudimentary approach to the Collatz conjecture and treats it as a problem of inequality between indices of 2 and 3. The inequality relation will be turned into equality using variables. The values of these variables will be investigated, and it will be shown that the Collatz conjecture does not need complex analysis.

2. Prerequisite

Consider that n is an odd integer, and the following Collatz function f is applied to it

$$f\left(n\right)=\left\{\begin{array}{cc}3n+1,\hfill & \mathrm{if}\mathrm{n}\mathrm{is}\mathrm{odd}\hfill \\ \frac{n}{2}\hfill & \mathrm{if}\mathrm{n}\mathrm{is}\mathrm{even}\hfill \end{array}\right.$$

A sequence is formed by performing this operation repeatedly, taking the result at each step as the input for the next. Collatz conjecture states that, for all n, $f^k\left(n\right)=1$ for some non-negative integer k, where the function is applied to n exactly k times. Let the sequence of integers obtained be:

1^st odd, $z_1$ evens, 2^nd odd, $z_2$ evens, ⋯, $k^{th}$ odd.

After the $k^{th}$ odd term, the odd step is applied to obtain an even integer. This even integer is computed in terms of the function $f^k\left(n\right)$:

$$\begin{array}{cc}\hfill f^k\left(n\right)& =3\left\{\frac{\left\{3\frac{\left\{3\frac{\left\{\frac{3n+1}{2^{z_1}}+1\right\}}{2^{z^2}}+1\right\}}{2^{z_3}}+1\right\}}{⋮}\right\}+1\hfill \\ \hfill f^k\left(n\right)& =\frac{3^{k}n+3^{k-1}+3^{k-2}{2}^{z_1}+\cdots +3^1{2}^{z_1+z_2+\cdots +z_{a-1}}+2^{z_1+z_2+\cdots +z_{a-1}+z_a}}{2^{z_1+z_2+\cdots +z_{a-1}+z_a}}\hfill \\ \hfill f^k\left(n\right)& =\frac{3^{k}n+C}{2^z}\hfill \end{array}$$

(1)

where $z=z_1+z_2+\cdots +z_{a-1}+z_a$ and

$$C=3^{k-1}+3^{k-2}{2}^{z_1}+\cdots +3^1{2}^z+2^z$$

(2)

It is noted that $(z,C)>0$.

3. Methodology

One of the significant results of the Collatz conjecture is that “almost all orbits of the Collatz map attain almost bounded values [9,10]." In simpler words, suppose the Collatz conjecture is valid up to the integer $n-1$. To test if the integer n complies with the Collatz conjecture, it is enough to show that the Collatz function attains a value smaller than the integer n.

Secondly, for the integer n to repeat, an integer of the form $2^{i}n$ must appear in the sequence where $i\ge 1$. Let $f^k\left(n\right)=2^{i}n$ in Equation (1).

$$\begin{array}{cc}\hfill 2^{i}n& =\frac{3^{k}n+C}{2^z}\hfill \\ \hfill n& ={\left(1-\frac{3^k}{2^z{2}^i}\right)}^{-1}\frac{C}{2^z{2}^i}\hfill \end{array}$$

(3)

Equation (3) tells that the maximum n that can repeat depends on two factors: (1) The minimum value of $1-3^k/2^z{2}^i$ and (2) The maximum value of $C/2^z{2}^i$.

Therefore, a basic strategy towards resolving the $3n+1$ problem can be outlined as follow:

• Establish the conditions that prevent the Collatz sequence from falling below the starting integer and also allows for the starting integer to re-appear.
• Obtain an upper bound on $C/2^z{2}^i$.
• Obtain a lower bound on $1-3^k/2^z{2}^i$.

4. Conditions for an unbounded Collatz orbit & repeating integers

Let the Collatz function fall below the starting integer n in Equation (1).

$$\begin{array}{cc}\hfill n& >f^k\left(n\right)\hfill \\ \hfill n& >\frac{3^k}{2^z}n+\frac{C}{2^z}\hfill \\ \hfill n& >\frac{3^k}{2^z}n\hfill \\ \hfill 1& >\frac{3^k}{2^z}\hfill \end{array}$$

If the above inequality is valid for a bounded Collatz orbit, the opposite must be correct for an unbounded Collatz orbit.

Similarly, the following relation should be true for n to be a positive integer in Equation (3):

$$\frac{3^k}{2^z{2}^i}<1$$

Therefore, the conditions that allow for an unbounded Collatz orbit and repeating integers are

$$\begin{array}{cc}\hfill \frac{3^k}{2^z}& >1\hfill \\ \hfill \frac{3^k}{2^z{2}^i}& <1\hfill \end{array}$$

(4)

5. Maximum value of $\frac{C}{2^z{2}^i}$

Equation (2) is re-written as

$$\begin{array}{c}\hfill \frac{C}{2^z{2}^i}=\underset{\mathrm{First}\mathrm{term}}{\underbrace{\frac{3^{k-1}}{2^z{2}^i}}}+\underset{\mathrm{Sec}\mathrm{ond}\mathrm{term}}{\underbrace{\frac{3^{k-2}{2}^{z_1}}{2^z{2}^i}}}+\cdots +\underset{\mathrm{Last}\mathrm{term}}{\underbrace{\frac{2^z}{2^z{2}^i}}}\end{array}$$

(5)

Analysis of each term starts with the second inequality in Equation (4).

First term

$$\begin{array}{cc}\hfill \frac{3^k}{2^z{2}^i}& <1\hfill \\ \hfill \frac{3^{k-1}}{2^z{2}^i}& <\frac{1}{3}\hfill \end{array}$$

Second term

$$\begin{array}{cc}\hfill \frac{3^k}{2^z{2}^i}& <1\hfill \\ \hfill \frac{3^{k-2}{2}^{z_1}}{2^z{2}^i}& <\frac{2^{z_1}}{9}\hfill \end{array}$$

The index $z_1$ is decided in the first even step when the Collatz function looks like

$$f^1\left(n\right)=\frac{3n+1}{2^{z_1}}$$

To ensure that the first inequality in Equation (4) is upheld so that the Collatz orbit remains unbounded until $2^{i}n$ is obtained, it is imperative that $z_1\le 1$. Therefore, the maximum value of the second term is obtained by substituting the maximum value of $z_1$.

$$\frac{3^{k-2}{2}^{z_1}}{2^z}<\frac{2}{9}$$

Third term

$$\begin{array}{cc}\hfill \frac{3^k}{2^z{2}^i}& <1\hfill \\ \hfill \frac{3^{k-3}{2}^{z_1+z_2}}{2^z}& <\frac{2^{z_1+z_2}}{27}\hfill \end{array}$$

The index $z_2$ is decided in the second even step when the Collatz function looks like

$$f^2\left(n\right)=\frac{3^{2}n+3+2^{z_1}}{2^{z_1+z_2}}$$

To ensure that the first inequality in Equation (4) is upheld so that the Collatz orbit remains unbounded until $2^{i}n$ is obtained, it is imperative that $z_2\le 2$, as $z_1=1$. Substitute the maximum value of $z_2$ to obtain the maximum value of the third term.

$$\frac{3^{k-2}{2}^{z_1+z_2}}{2^z}<\frac{8}{27}$$

General term

It is shown that $z_1=1$ and $z_2=2$. When higher order indexes are calculated, values are observed to alternate between 1 and 2. Therefore, the series of terms are replaced by a geometric series with the average common ratio of $\frac{\sqrt{8}}{3}$. The sequence of terms looks like

$$\frac{1}{3},\frac{\sqrt{8}}{9},\frac{8}{27},\frac{8\sqrt{8}}{81},\frac{64}{243}\cdots$$

The last term is less than 1. Therefore, the maximum value of Equation (5) is

$$\begin{array}{cc}\hfill \frac{C}{2^z{2}^i}& <\left\{\frac{1}{3}+\frac{\sqrt{8}}{9}+\frac{8}{27}+\frac{8\sqrt{8}}{81}+\frac{64}{243}+\cdots \right\}+1\hfill \\ \hfill \frac{C}{2^z{2}^i}& <\left\{\frac{\frac{1}{3}}{1-\frac{\sqrt{8}}{3}}\right\}+1\hfill \\ \hfill \frac{C}{2^z{2}^i}& <7\hfill \end{array}$$

(6)

6. Minimum value of $1-\frac{3^k}{2^z{2}^i}$

The second inequality in Equation (4) gives the necessary condition for an integer of the form $2^{i}n$ to appear in the Collatz sequence. The minimum value of $2^z{2}^i$ for the inequality $2^z{2}^i>3^k$ to be true is $3^k+3$ because

• $|2^z{2}^i-3^k|=1$ is valid only for $(k,z+i)=(1,1),(1,2),(2,3)$.
• $2^z{2}^i\ne 3^k+2$ as $3^k+2$ is odd.

Therefore,

$$\begin{array}{cc}\hfill 2^z{2}^i& =3^k+3\hfill \\ \hfill 2^z& =\frac{3^k+3}{2^i}\hfill \\ \hfill 3^k-2^z& =3^k-\frac{3^k+3}{2^i}\hfill \\ \hfill \frac{3^k}{2^z}-1& =\frac{3^k}{2^z}-\frac{3^k+3}{2^z{2}^i}\hfill \\ \hfill \frac{3^k}{2^z}& =1+\frac{3^k}{2^z}-\frac{3^k+3}{2^z{2}^i}\hfill \\ \hfill \frac{3^k}{2^z{2}^i}& =\frac{1}{2^i}+\frac{3^k}{2^z{2}^i}-\frac{3^k+3}{2^z{2}^i{2}^i}\hfill \\ \hfill 1-\frac{3^k}{2^z{2}^i}& =1-\frac{1}{2^i}-\frac{3^k}{2^z{2}^i}+\frac{3^k+3}{2^z{2}^i{2}^i}\hfill \\ \hfill 1-\frac{3^k}{2^z{2}^i}& =1-\frac{1}{2^i}-\frac{3^k}{2^z{2}^i}\left\{1-\frac{1}{2^i}\right\}+\frac{3}{2^z{2}^i{2}^i}\hfill \\ \hfill 1-\frac{3^k}{2^z{2}^i}& >1-\frac{1}{2^i}-\frac{3^k}{2^z{2}^i}\left\{1-\frac{1}{2^i}\right\}\hfill \end{array}$$

(7)

Substitute $\frac{3^k}{2^z{2}^i}=1-q$ in the RHS where $0\le q<1$.

$$\begin{array}{cc}\hfill 1-\frac{3^k}{2^z{2}^i}& >1-\frac{1}{2^i}-(1-q)\left\{1-\frac{1}{2^i}\right\}\hfill \\ \hfill 1-\frac{3^k}{2^z{2}^i}& >q\left\{1-\frac{1}{2^i}\right\}\hfill \\ \hfill 1-\frac{3^k}{2^z{2}^i}& >1-\frac{1}{2^i}\hfill \end{array}$$

(8)

Alternatively, starting from Equation (7),

$$\begin{array}{cc}\hfill 1-\frac{3^k}{2^z{2}^i}& =-\frac{3^k}{2^z{2}^i}\left\{1-\frac{1}{2^i}\right\}+\left\{1-\frac{1}{2^i}+\frac{3}{2^z{2}^i{2}^i}\right\}\hfill \\ \hfill 1-\frac{3^k}{2^z{2}^i}& >-\frac{3^k}{2^z{2}^i}\left\{1-\frac{1}{2^i}\right\}\hfill \\ \hfill 1& >\frac{3^k}{2^z{2}^i{2}^i}\hfill \\ \hfill 2^i& >\frac{3^k}{2^z{2}^i}\hfill \\ \hfill 1-\frac{3^k}{2^z{2}^i}& >1-2^i\hfill \end{array}$$

(9)

7. Resolution to the $3n+1$ problem

Substitute Equations (8), (9) and (6) in Equation (3) and take union to obtain the range of integers that repeat in the Collatz sequence

$$\begin{array}{c}\hfill n<7{\left(1-\frac{1}{2^i}\right)}^{-1}\bigcup n<7{\left(1-2^i\right)}^{-1}\end{array}$$

A few values of n for i are given in the Table 1. The integers that repeat in the Collatz sequence lie in the $(-\infty ,7]$ range. It is unnecessary to check the Collatz conjecture beyond the integer 7. The Collatz sequence is never violated till 7; therefore, it will not be broken for any integer greater than 7. But it does violate for negative integers.

8. Do all positive integers reach 1?

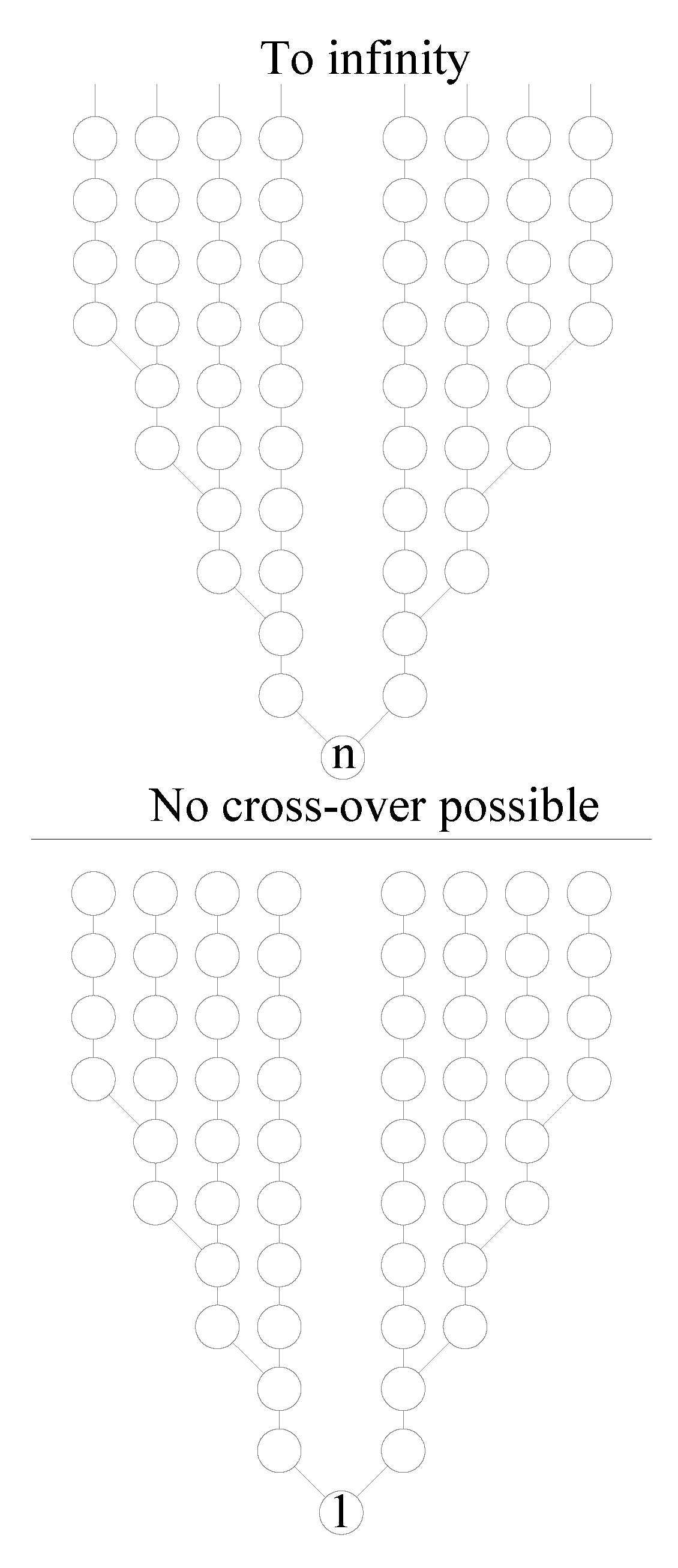
Let there exist a number chain that does not converge to 1. Since the only closed chain in the $3n+1$ series is $1,4,2,1$, this n-chain is an open chain. The n-chain converges to n from infinity and then diverges to infinity.

The n-chain contains all terms of the form $2^{i}n$ where $i\ge 0$. Further, terms arising from the arithmetic function $3n+1$ are also part of this chain. Every even integer x in the n-chain is connected to a precursor even number and a precursor odd number (iff $3m+1=x$ is possible for some m). Similarly, every odd integer is connected to a precursor even number. The branches that arise out of the n-chain are infinite. In short, the n-chain contains every integer greater than n up to infinity.

However, there should exist no linkage between the n-chain and the 1-chain. Because, if there were some linkage, all the integers in the n-chain would converge to 1 using the said linkage.

It is absurd, as shown in Figure 1, as this means the 1-chain ends abruptly below n. It implies that there exists no integer $2x$ in the n-chain such that $x<n$. Conversely, there exists no x in the 1-chain such that $3x+1>n$.

It is concluded that a n-chain that does not converge to 1 is impossible.

9. A comment on Collatz-like series

9.1. 3n - 1 series

The $3n-1$ series is akin to using a negative integer in the $3n+1$ series. The range of integers that repeat in the $3n+1$ series is $(-\infty ,7]$. Since negative integers repeat for the $3n+1$ series, the integers that repeat for the $3n-1$ series will lie in the range $(-7,\infty )$.

9.2. 5n + 1 series

This series is defined as follows

$$f\left(n\right)=\left\{\begin{array}{cc}5n+1,\hfill & \mathrm{if}\mathrm{n}\mathrm{is}\mathrm{odd}\hfill \\ \frac{n}{2}\hfill & \mathrm{if}\mathrm{n}\mathrm{is}\mathrm{even}\hfill \end{array}\right.$$

The value of $\frac{C}{2^z{2}^i}$ is

$$\begin{array}{cc}\hfill \frac{C}{2^z{2}^i}& <\frac{1}{5}+\frac{2^4}{5^2}+\frac{2^4{2}^2}{5^3}+\frac{2^4{2}^2{2}^2}{5^4}+\frac{2^4{2}^2{2}^2{2}^3}{5^5}+\cdots +1\hfill \end{array}$$

It is seen that the common ratio is less than 1 for some terms while it is greater than 1 for other terms. The value of the above sum is uncertain - it can be bounded or unbounded. Thus, the series might have many closed-chain solutions or a tendency to diverge to infinity.

9.3. 7n + 1 series

This series is defined as follows

$$f\left(n\right)=\left\{\begin{array}{cc}7n+1,\hfill & \mathrm{if}\mathrm{n}\mathrm{is}\mathrm{odd}\hfill \\ \frac{n}{2}\hfill & \mathrm{if}\mathrm{n}\mathrm{is}\mathrm{even}\hfill \end{array}\right.$$

The value of $\frac{C}{2^z{2}^i}$ is

$$\begin{array}{cc}\hfill \frac{C}{2^z{2}^i}& <\frac{1}{7}+\frac{2^5}{7^2}+\frac{2^5{2}^3}{7^3}+\frac{2^5{2}^3{2}^3}{7^4}+\cdots +1\hfill \end{array}$$

The common ratio is greater than 1 for every term, and the above sum is unbounded. Therefore, this series will diverge to infinity. No comment can be made on the number of closed-chain solutions.

10. Conclusion

This article re-writes the Collatz sequence in the form $n={\left(1-\frac{3^k}{2^z{2}^i}\right)}^{-1}\frac{C}{2^z{2}^i}$, where $\frac{C}{2^z{2}^i}=\frac{3^{k-1}}{2^z{2}^i}+\frac{3^{k-2}{2}^{z_1}}{2^z{2}^i}+\cdots +\frac{2^z}{2^z{2}^i}$. Further, conditions for an unbounded Collatz orbit and repeating integers are discovered. It helps in placing bounds on the value of $1-\frac{3^k}{2^z{2}^i}$ and $\frac{C}{2^z{2}^i}$. Correspondingly, it is possible to place a bound on the value of n that repeats in the $3n+1$ sequence. It is found that the methodology adopted in this article helps analyze other related sequences like $3n-1$, $5n+1$, and $7n+1$, which proves the validity of the proposed modus-operandi.