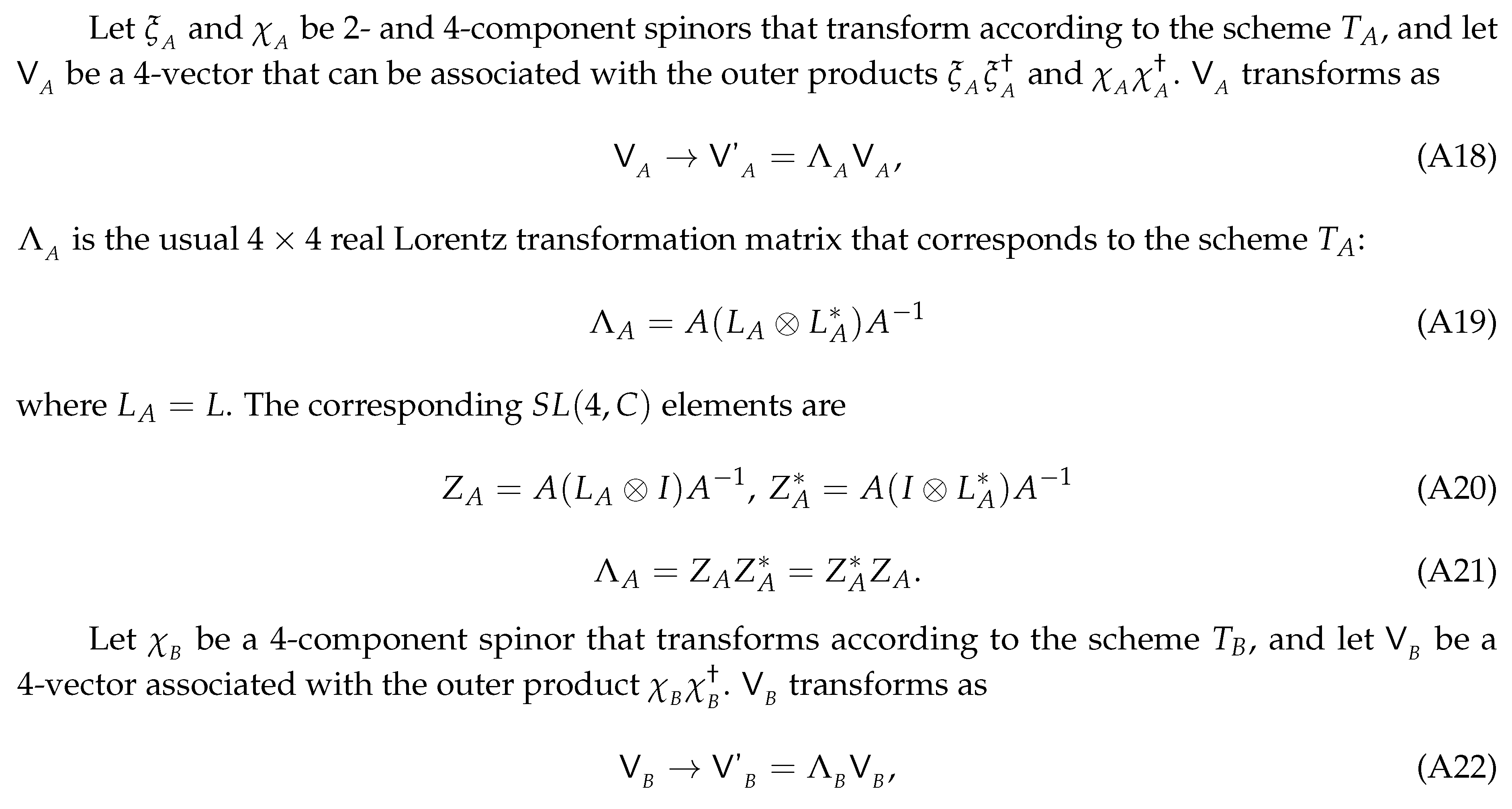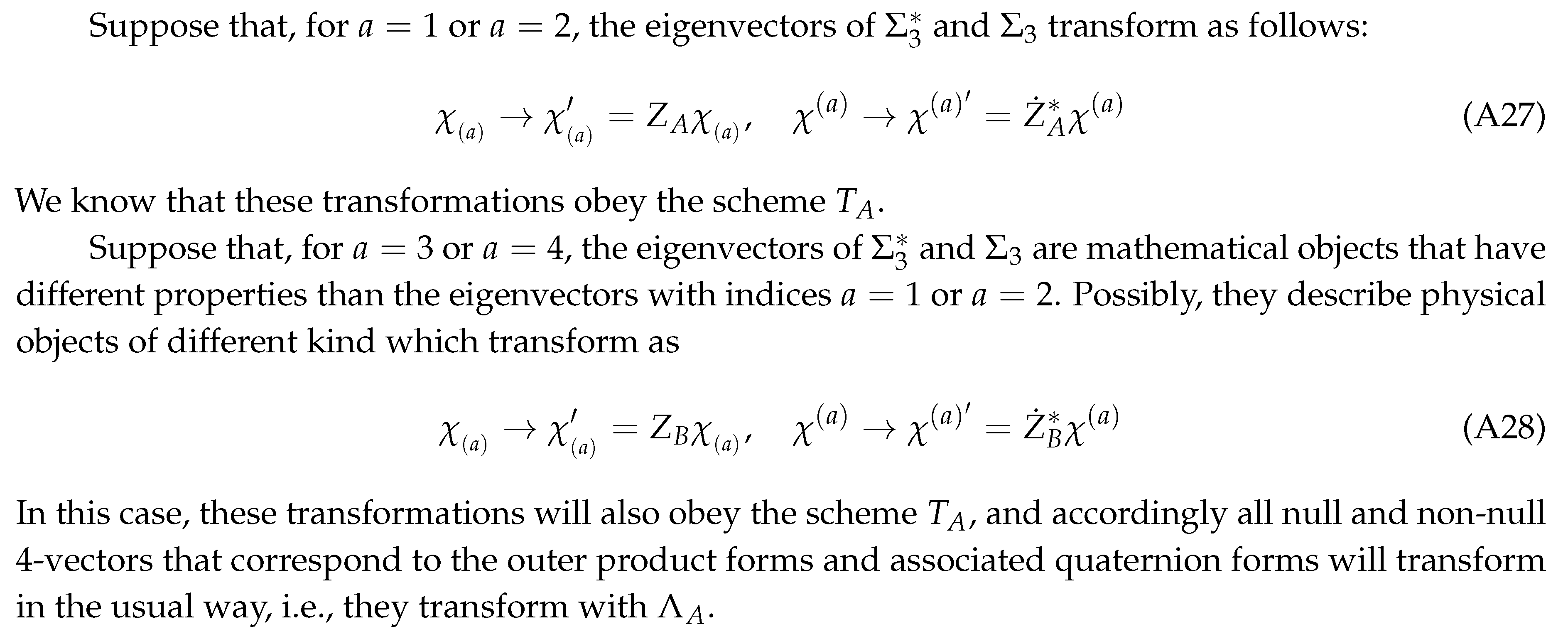Let $L_A$ be an element of $SL(2,C)$. In an exponential form with parameters $\theta$ and $\eta$: $\overrightarrow{\sigma }$ is the Pauli vector with ${\sigma }_1={\sigma }_x,{\sigma }_2={\sigma }_y,{\sigma }_3={\sigma }_z$. The subscript ${ }_A$ is introduced in order to distinguish the other forms of L that will be introduced subsequently.

We rewrite $L_A$ and its complex conjugate in the following compact forms: ${\left({\pi }_A\right)}_i={\theta }_i+i{\eta }_i$ and ${ }^{*}$ denotes complex conjugation. $L_A$ corresponds to the Lorentz transformation with ${\theta }_i$ and ${\eta }_i$ being the rotation and boost parameters, respectively.

It is well known that the complex version of the $4\times 4$ Lorentz transformation matrix can be written as a matrix direct product of $L_A$ and $L_A^{*}$: In order to obtain the familiar real matrix form of the Lorentz transformation matrix it is enough to change the basis: where

Now, it is straightforward to show that $SO(3,1)$ can be written as a commutative product of $SL(4,C)$ and $SL{(4,C)}^{*}$ by simply rewriting Eq.(4) in a factorized form:

$Z_A$ and $Z_A^{*}$ are the $4\times 4$ versions of $L_A$ and $L_A^{*}$ matrices. They can be expressed in terms of ${\Sigma }_i$ matrices: $\overrightarrow{\Sigma }=({\Sigma }_1,{\Sigma }_2,{\Sigma }_3)$ and ${\Sigma }_i$ are $4\times 4$ versions of Pauli matrices: These are traceless Hermitian matrices and they satisfy the same commutation relations as ${\sigma }_i$ matrices By definition, ${\Sigma }_{\mu }=A({\sigma }_{\mu }\otimes I)A^{-1}$, $(\mu =0,1,2,3)$, ${\Sigma }_0$ is the $4\times 4$ identity. ${\Sigma }_{\mu }$ basis do not form a complete set for $4\times 4$ matrices, but the set of ${\Sigma }_{\mu }{\Sigma }_{\nu }^{*}$ does.

From the Eq.(7), $Z_A$ can be found in terms of the elements of $L_A$: where ${\alpha }_0=\frac{1}{2}(L_{11}+L_{22})$,${\alpha }_1=\frac{1}{2}(L_{12}+L_{21})$,${\alpha }_2=\frac{i}{2}(L_{12}-L_{21})$, and ${\alpha }_3=\frac{1}{2}(L_{11}-L_{22})$. Hence, $L_A$ can be written in terms of ${\alpha }_{\mu }$ as We can write $L_A$ and $Z_A$ in terms of ${\sigma }_{\mu }$ and ${\Sigma }_{\mu }$ matrices: Or, simply

We also define the spinor metric g for $SL(4,C)$ that corresponds to the spinor metric $ϵ$ of $SL(2,C)$: $\eta$ is the mostly minus Minkowski metric1.

$Z_A$ preserves the Minkowski metric: Since $\eta$ is real, $Z_A^{T}g{Z}_A=g$ directly entails ${\Lambda }^{T}g\Lambda =g$. In an analogy with $ϵ{\sigma }_i{ϵ}^{-1}=-{\sigma }_i^{*}$, we have the following very useful relation:

In this note we will show that there are eight generalized eigenvectors of ${\Sigma }_3^{*}$ matrix that can be interpreted as 4-component covariant spinors. The generalized eigenvectors can be pairwise grouped into four categories. The first pair transforms in the usual way, but the other three transform in different ways.

In the following we will study the first and the second pairs in detail, and we will introduce the remaining two in the last section.

Let $L_A=exp(-\frac{i}{2}{\overrightarrow{\pi }}_A·\overrightarrow{\sigma })$ be the $(\frac{1}{2},0)$ representation of the Lorentz group that acts on the 2-component left-chiral spinor ${\xi }_{{ }_L}$: where In terms of the components $u,v$ of ${\xi }_{{ }_L}$: Let us call this transformation scheme $T_A$.

Let ${\dot{L}}_A=exp(-\frac{i}{2}{\overrightarrow{\pi }}_A^{*}·\overrightarrow{\sigma })$ be the dotted version corresponding to the $(0,\frac{1}{2})$ representation of the Lorentz group. ${\dot{L}}_A={\left(L_A^{-1}\right)}^{†}$. Let ${\xi }_{{ }_R}$ be the 2-component right-chiral spinor. ${\xi }_{{ }_R}=ϵ{\xi }_{{ }_L}^{*}$, where ${\xi }_{{ }_R}$ transforms as In terms of the components $u,v$, Eq.(24) is equivalent to the scheme $T_A$ given in Eq.(22).

What happens when $L_A$ acts on $ϵ{\xi }_{{ }_L}$? In this case, in terms of the components Let us call this transformation scheme $T_B$. We can write $T_B$ in a matrix form: Let us name this transformation matrix as $L_B$. Note that, $L_B={\left({\dot{L}}_A\right)}^{*}$, and Eq.(26) is nothing but the transformation of ${\xi }_{{ }_L}$ under the action of $L_B$, which is a type $T_B$ transformation.

Now, let $Z_A=exp(-\frac{i}{2}{\overrightarrow{\pi }}_A·\overrightarrow{\Sigma })$ be the $(\frac{1}{2},0)$ representation of $SL(4,C)$ that acts on the first pair of the 4-component undotted covariant spinors: where ${\chi }_{{ }_{\left(1\right)}}$ and ${\chi }_{{ }_{\left(2\right)}}$ are the generalized eigenvectors of ${\Sigma }_3^{*}$ 2: Indices in the parentheses are simply labels for 4-component spinors.

Now consider the second pair of the generalized eigenvectors of ${\Sigma }_3^{*}$: Transformation scheme of ${\chi }_{{ }_{\left(3\right)}}$ and ${\chi }_{{ }_{\left(4\right)}}$ is different from that of ${\chi }_{{ }_{\left(1\right)}}$ and ${\chi }_{{ }_{\left(2\right)}}$. Under the action of $Z_A$, ${\chi }_{{ }_{\left(1\right)}}$ and ${\chi }_{{ }_{\left(2\right)}}$ transform according to the scheme $T_A$, but ${\chi }_{{ }_{\left(3\right)}}$ and ${\chi }_{{ }_{\left(4\right)}}$ transform according to the scheme $T_B$. However, we may think in an alternative way: ${\chi }_{{ }_{\left(3\right)}}$ and ${\chi }_{{ }_{\left(3\right)}}$ are different kind of objects with different transformation properties, such that another transformation matrix, $Z_B$, acts on them and under the action of $Z_B$ they transform according to the scheme $T_A$: By definition $Z_B=A(L_B\otimes I)A^{-1}$: Or, simply

Now let ${\dot{Z}}_A=exp(-\frac{i}{2}{\overrightarrow{\pi }}_A^{*}·\overrightarrow{\Sigma })$ be the $(0,\frac{1}{2})$ representation. ${\dot{Z}}_A={\left(Z_A^{-1}\right)}^{†}$. We regard the generalized eigenvectors of ${\Sigma }_3$ as 4-component undotted contravariant spinors and we define the first pair as follows: Under the action of ${\dot{Z}}_A$, dotted versions of ${\chi }^{{ }^{\left(1\right)}}$ and ${\chi }^{{ }^{\left(1\right)}}$ transform according to the scheme $T_A$.

The second pair of the generalized eigenvectors of ${\Sigma }_3$ is defined as Under the action of ${\dot{Z}}_A$, the dotted versions of ${\chi }^{{ }^{\left(3\right)}}$ and ${\chi }^{{ }^{\left(4\right)}}$ transform according to the scheme $T_B$. But, they transform according to the scheme $T_A$ under the action of ${\dot{Z}}_B$: where ${\dot{Z}}_B={\left(Z_B^{-1}\right)}^{†}$ by definition. ${\chi }^{{ }^{\left(a\right)}}$ is related to ${\chi }_{{ }_{\left(a\right)}}$ by the $SL(4,C)$ metric, ${\chi }^{\left(a\right)}=g{\chi }_{{ }_{\left(a\right)}}$, and its dotted version is defined as 3.

We write various forms of Z and L matrices in compact notation to manifest the parallelism between them:

Let us define the outer product $W_{{ }_L}={\xi }_{{ }_L}{\xi }_{{ }_L}^{†}$ which transforms as In terms of the components of $u,v$ of ${\xi }_{{ }_L}$ This is a type $T_A$ transformation with $u\to u^{\prime }=L_{11}u+L_{12}v$ and $v\to v^{\prime }=L_{21}u+L_{22}v$:

Determinant of $W_{{ }_L}$ is zero, hence $W_{{ }_L}$ can be associated with a null 4-vector through the substitutions, $t=\frac{1}{2}(u\dot{u}+v\dot{v}),x=\frac{1}{2}(u\dot{v}+v\dot{u}),y=\frac{i}{2}(u\dot{v}-v\dot{u}),z=\frac{1}{2}(u\dot{u}-v\dot{v})$:

We also define the outer product $W_{{ }_R}={\xi }_{{ }_R}{\xi }_{{ }_R}^{†}$ which transforms as This is also a type $T_A$ transformation. Determinant of $W_{{ }_R}$ is zero and $W_{{ }_R}$ can be associated with a null 4-vector: Note that $W_{{ }_R}$ can be obtained from $W_{{ }_L}$ by parity inversion.

There are outer product forms of 4-component spinors that can be associated with null 4-vectors. ${\mathcal{W}}_{{ }_{\left(11\right)}}={\chi }_{{ }_{\left(1\right)}}{\chi }_{{ }_{\left(1\right)}}^{†}$ and ${\mathcal{W}}_{{ }_{\left(22\right)}}={\chi }_{{ }_{\left(2\right)}}{\chi }_{{ }_{\left(2\right)}}^{†}$ transform in a similar way with $W_{{ }_L}$: For $a=1$ and $a=2$, ${\mathcal{W}}_{{ }_{\left(aa\right)}}$ transform according to the scheme $T_A$ as

On the other hand, ${\dot{\mathcal{W}}}^{{ }^{\left(11\right)}}={\dot{\chi }}^{{ }^{\left(1\right)}}{\dot{\chi }}^{{ }^{\left(1\right)†}}$ and ${\dot{\mathcal{W}}}^{{ }^{\left(22\right)}}={\dot{\chi }}^{{ }^{\left(2\right)}}{\dot{\chi }}^{{ }^{\left(2\right)†}}$ transform in a similar way with $W_{{ }_R}$: For $a=1$ and $a=2$, ${\dot{\mathcal{W}}}^{{ }^{\left(aa\right)}}$ transform according to the scheme $T_A$ as ${\mathcal{W}}_{{ }_{\left(aa\right)}}$ and ${\dot{\mathcal{W}}}^{{ }^{\left(aa\right)}}$ are Hermitian and zero determinant matrices, hence they correspond to null 4-vectors.

We also have outer products of 4-component spinors of the other kind. For $a=3$ and $a=4$, ${\mathcal{W}}_{{ }_{\left(aa\right)}}$ and ${\dot{\mathcal{W}}}^{{ }^{\left(aa\right)}}$ transform according to the scheme $T_A$ under the action of $Z_B$ and ${\dot{Z}}_B$: These are also Hermitian and zero determinant matrices and they correspond to null 4-vectors.

In general, we can treat $t,x,y$ and z as variables that do not depend on u and v. Then, we can associate the following matrices $X_{{ }_L}$ and $X_{{ }_R}$ with 4-vectors, which are not necessarily null: det$X_{{ }_L}=$det$X_{{ }_R}=t^2-x^2-y^2-z^2$ and in general not zero. $X_{{ }_L}$ and $X_{{ }_R}$ transform as These are matrix representations of quaternions, because $-i{\sigma }_1,-i{\sigma }_2,-i{\sigma }_3$ matrices have the same properties as the Hamilton’s quaternion basis, $\mathbf{i},\mathbf{j},\mathbf{k}$: Similarly,

In order to make the analogy with $SL(4,C)$ we consider the following two column objects that are pairwise combinations of 4-component spinors: where ${\chi }_{{ }_{\left(12\right)}}=({\chi }_{{ }_{\left(1\right)}},{\chi }_{{ }_{\left(2\right)}})$, ${\chi }_{{ }_{\left(34\right)}}=({\chi }_{{ }_{\left(3\right)}},{\chi }_{{ }_{\left(4\right)}})$, ${\chi }^{{ }^{\left(12\right)}}=({\chi }^{{ }^{\left(1\right)}},{\chi }^{{ }^{\left(2\right)}})$, ${\chi }^{{ }^{\left(34\right)}}=({\chi }^{{ }^{\left(3\right)}},{\chi }^{{ }^{\left(4\right)}})$.

We define outer products of 4-component spinor pairs in the forms ${\mathcal{W}}_{{ }_{\left(ab\right)}}={\chi }_{{ }_{\left(ab\right)}}{\chi }_{{ }_{\left(ab\right)}}^{†}$ and ${\dot{\mathcal{W}}}^{{ }^{\left(ab\right)}}={\dot{\chi }}^{{ }^{\left(ab\right)}}{\dot{\chi }}^{{ }^{\left(ab\right)†}}$. First we let $a=1$ and $b=2$. The outer product ${\mathcal{W}}_{{ }_{\left(12\right)}}={\chi }_{{ }_{\left(12\right)}}{\chi }_{{ }_{\left(12\right)}}^{†}$ is formally a quaternion: ${\mathcal{W}}_{{ }_{\left(12\right)}}$ can be written as a sum of two basic forms: ${\mathcal{W}}_{{ }_{\left(12\right)}}={\mathcal{W}}_{{ }_{\left(11\right)}}+{\mathcal{W}}_{{ }_{\left(22\right)}}$. In its present form det${\mathcal{W}}_{{ }_{\left(12\right)}}=0$ and ${\mathcal{W}}_{{ }_{\left(12\right)}}$ corresponds to a null 4-vector, but we can associate ${\mathcal{W}}_{{ }_{\left(12\right)}}$ with an arbitrary 4-vector in terms of the variables $t,x,y$ and z: ${\mathcal{Q}}_{{ }_{\left(12\right)}}={(++++)}_{\Sigma }$ and it is the $4\times 4$ version of $X_{{ }_L}$: On the other hand, ${\dot{\mathcal{W}}}^{{ }^{\left(12\right)}}$ has a different form: In terms of the variables $t,x,y$ and z: ${\dot{\mathcal{Q}}}^{{ }^{\left(12\right)}}={(+---)}_{\Sigma }$ and it is the $4\times 4$ version of $X_{{ }_R}$: ${\dot{\mathcal{Q}}}^{{ }^{\left(12\right)}}$ can be obtained from ${\mathcal{Q}}_{{ }_{\left(12\right)}}$ by parity inversion and they transform as These are type $T_A$ transformations, hence these forms correspond to 4-vectors.

Now let $a=3$ and $b=4$. The outer product ${\mathcal{W}}_{{ }_{\left(34\right)}}={\chi }_{{ }_{\left(34\right)}}{\chi }_{{ }_{\left(34\right)}}^{†}$ is also a quaternion: In terms of variables $t,x,y$ and z: ${\mathcal{W}}_{{ }_{\left(34\right)}}={(+-+-)}_{\Sigma }$. We also write ${\dot{\mathcal{W}}}^{{ }^{\left(34\right)}}$: ${\dot{\mathcal{Q}}}^{{ }^{\left(34\right)}}={(++-+)}_{\Sigma }$ and it can be obtained from ${\mathcal{Q}}_{{ }_{\left(34\right)}}$ by parity inversion. ${\mathcal{Q}}_{{ }_{\left(34\right)}}$ and ${\dot{\mathcal{Q}}}^{{ }^{\left(34\right)}}$ transform with $Z_B$ and ${\dot{Z}}_B$: These transformations obey the scheme $T_A$ also, hence they correspond to 4-vectors.