The M-basis Functions and Their Application

1. Introducing M-basis functions

The M-basis functions of the n^th-order are defined as the arguments for optimizing the following objective function:

(1)

Subject to knowing the boundary conditions, i.e., the values of θ and up to the (n-1)^th derivative of θ at t = 0 and t = t_f, we will show that the solution to (1) is a linear combination of 2n basis functions that we call M-basis functions. First, the third-order (n = 3) is discussed because (1) results in minimum jerk patterns [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16].

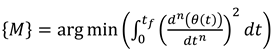
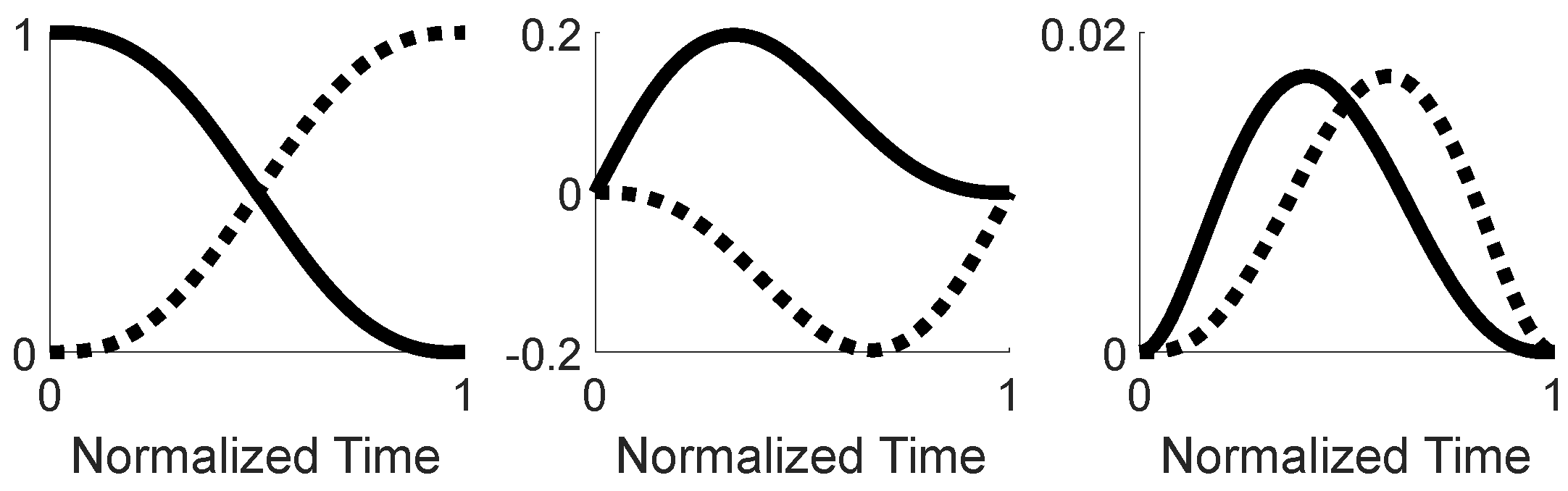
1.1. The third-order M-basis functions (minimum jerk)

As shown in [2], the solution of this problem is a quintic spline, or 5^th-order polynomial, which can be described as (2).

(2)

where, t is the time variable, and A and X are the following vectors.

(3)

(4)

A vector defined by (5) shows the boundary conditions at the initial (t = 0) and final (t = t_f) moments.

(5)

where, t_f represents the total time duration, B describes the boundary conditions, and the dot on top of θ indicates the first derivative of θ with respect to time. We can change (5) to (6) using (2).

(6)

We can write (7) using (2) and (6).

(7)

(8)

Using (3) and (7), we can write (8).

(9)

It is possible to convert (9) to (10).

(10)

where, T and M are defined as follows:

(11)

(12)

where, t_n is the normalized time variable, i.e., t_n = t/t_f. Each row of the M describes one of the M-basis functions. The M-basis functions are normalized in terms of time and can be calculated simply by using (12). Third-order M-basis functions are illustrated in Figure 1.

Finally, we can write (13) from (5), (11), and (12).

(13)

Equation (13) shows that the solution of (1) is a linear combination of the M-basis functions scaled by the time duration (T) and boundary conditions (B).

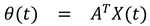
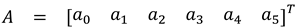
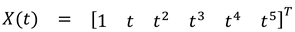
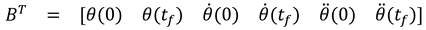
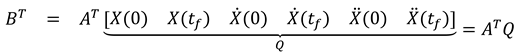
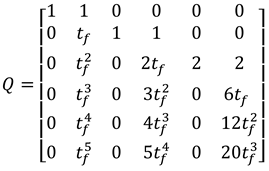
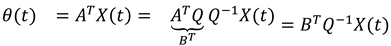
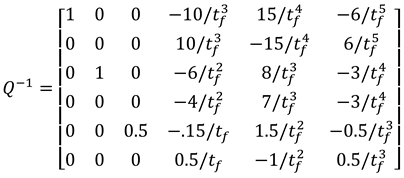
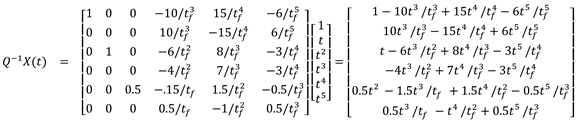
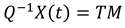
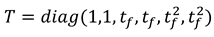
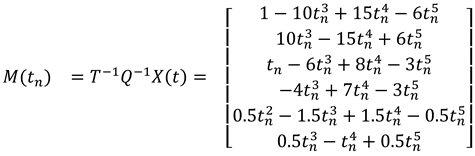
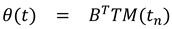
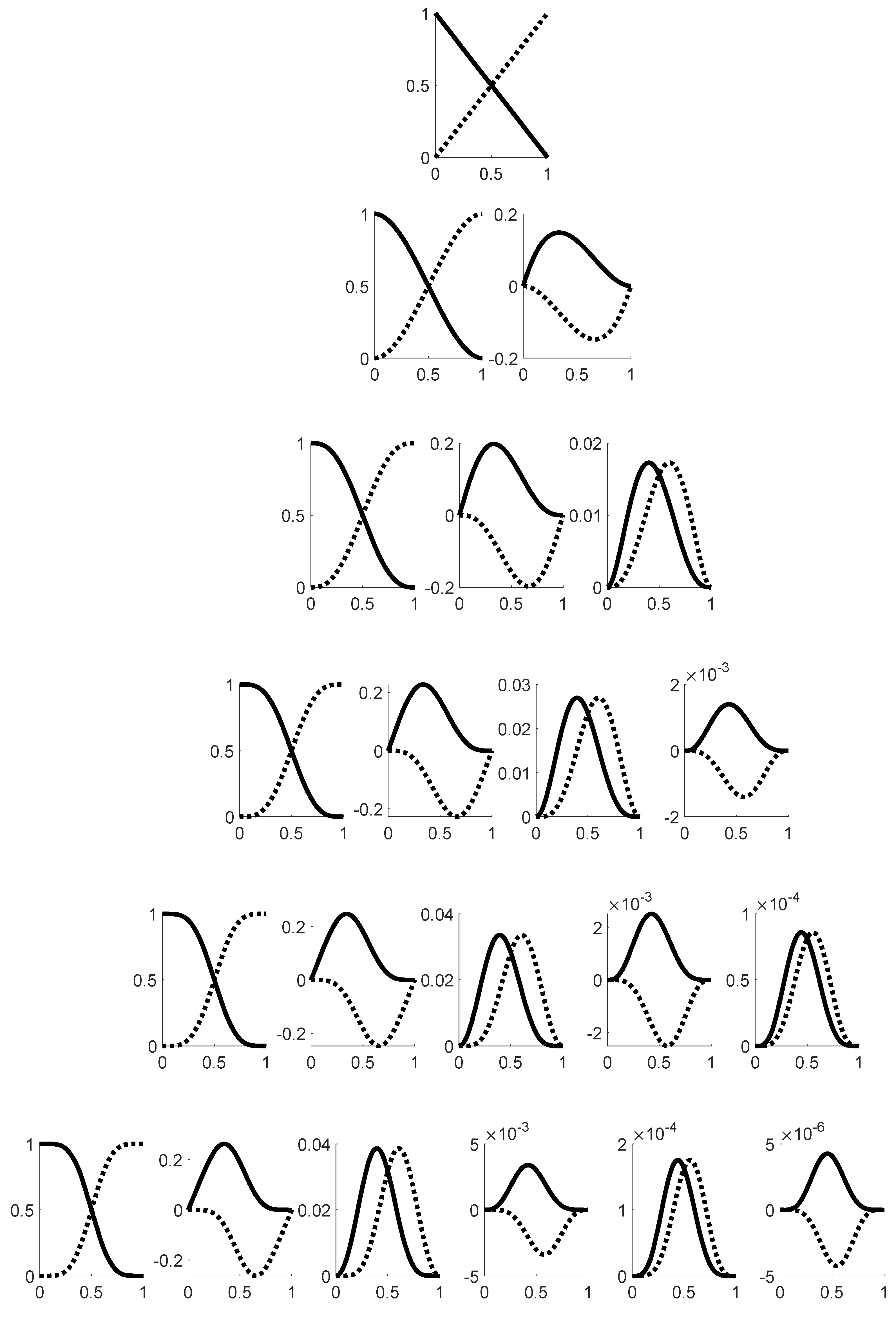
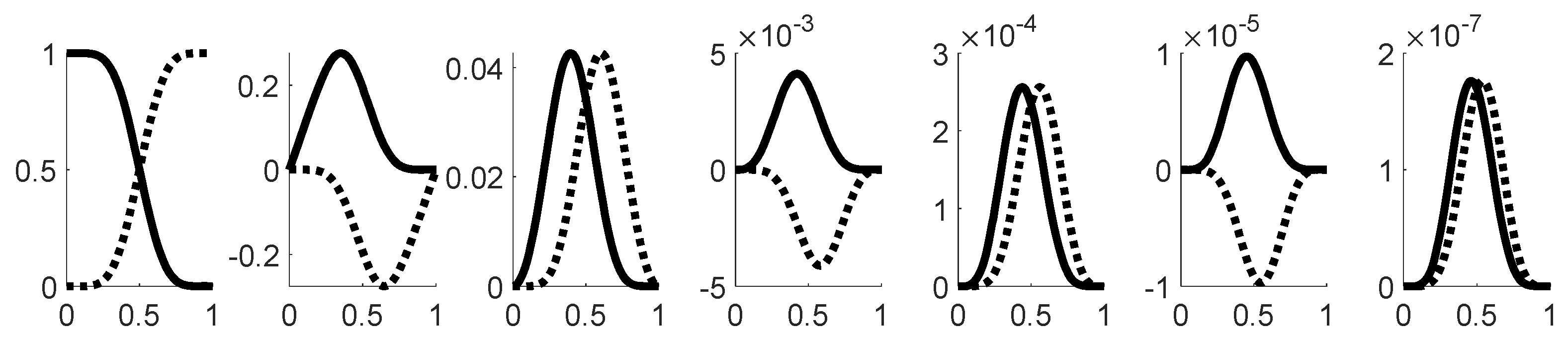
1.2. The n^th-order M-basis functions

Similar to [2], it is easy to prove that the solution to (1) is a (2n-1)^th-order polynomial. Therefore, inspired by what is written above, it is possible to show that the solution of (1) can be described simply by (13) for any order of n.

In this case, X, B, T, and M are as follows:

(14)

(15)

(16)

(17)

It should be mentioned that the Q matrix can be created using (18).

(18)

Finally, having $Q^{-1}$ makes it easy to calculate M using (19).

(19)

Finally, θ can be calculated using (13) with the help of (15), (16), and (17).

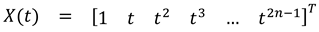
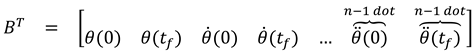
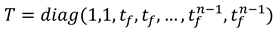
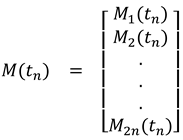
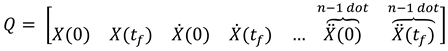
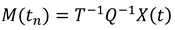
1.3. The 4^th-order M-basis (minimum snap)

In this case, X, B, T, and M are as follows:

(20)

(21)

(22)

The $Q$and $Q^{-1}$ can be written as (23) and (24) respectively.

(23)

(24)

Finally, using (20), (22), and (24) as shown below, the M-basis functions can be derived from (19).

(25)

where, t_n is the normalized time variable, i.e., t_n = t/t_f. In the end, similarly, θ can be computed by (13) using (21), (22), and (25). Each row of the M describes one of the fourth-order M-basis functions. The M-basis functions from the first to seventh-order are illustrated in Figure 2. The application of the third-order M-basis functions has already been investigated in human movement [1,3,4,5,6,7,8].

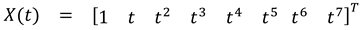
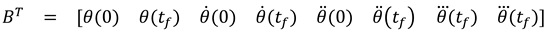
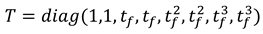
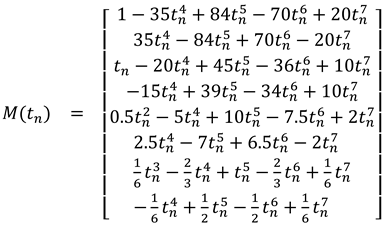
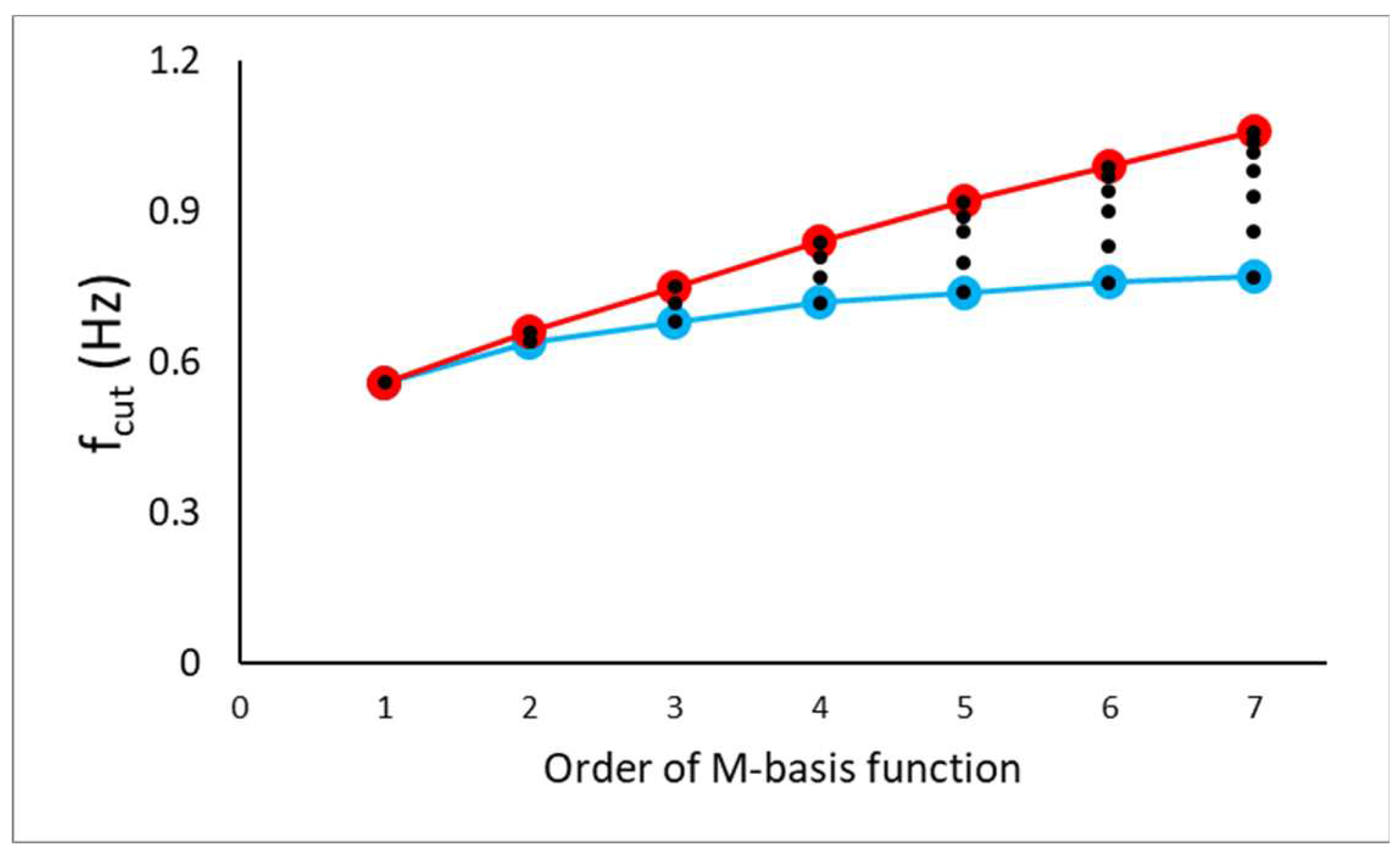
2. The frequency specification of the M-basis functions

According to the definition of the objective function, i.e., equation (1), it can be imagined that the M-basis functions are the low-frequency signals. Considering t_f = 1 sec, the Fourier transforms of the M-basis functions from the first to seventh orders are calculated. It should be added that the two M-basis functions shown in the same window in Figure 2 have the same absolute Fourier transforms. The cutoff frequencies of the M-basis functions for various orders are depicted in Figure 3.

It should be mentioned that the shorter the t_f, the higher the cutoff frequency, and vice versa. It is proportional to the length of time, so the cutoff frequency for a t_f of 0.5 sec is twice that of 1 sec. It means that for the shorter time length, the bandwidth of the M-basis functions is higher. The bandwidth of the M-basis functions, on the other hand, is lower for longer time lengths due to their low-frequency nature.

3. The applications of the M-basis function

3.1. Human movements

As shown in [1,2,3,4,5,6,7,8], one of the applications of the third-order M-basis functions is in human motor planning. Moreover, it can also be applied to humanoid robots [3,6,7].

3.2. Slow signals

With almost the same number of basis functions, the error of reconstructing a signal using the Fourier basis functions and the M-basis functions is compared. The original signal (Y) is created with a duration of 1 sec and a sampling frequency of 100 Hz. The results show that a signal with low-frequency information can be represented better by a linear combination of M-basis functions than by Fourier-based functions. Different examples are depicted in Table 1 to show the performance of M-basis functions compared to the Fourier transform. Because the signal has a time length of one second and the resolution of the Fourier basis functions is 1 Hz, the Fourier basis function produces better results for pure sinusoidal signals with integer frequency. For the non-integer frequencies, the Fourier basis functions are not efficient to reconstruct the original signal; however, the M-basis functions can reconstruct these kinds of signals with a limited number of basis functions. For signals with a wider frequency range, the order of the M-basis functions should obviously be higher to reconstruct the signal at higher frequencies, as seen in Fig. 3.

4. Discussion and conclusion

In this article, I introduced novel M-basis functions. As shown in different examples, representing a signal by M-basis functions can preserve the frequency nature of the signal, especially if the time window is short.

As the future work, the combination of the Fourier and M-basis functions can be studied. The M-basis functions can better represent the boundary of the signal than the middle of the signal, while the Fourier basis functions can better represent the middle of the signal because of the Gibbs effect. The M-basis functions can also be applied to estimate the frequency of the single frequency signals with non-integer value.