Quantum Mechanics Based on Energy Polynomials

We use a recently proposed formulation of quantum mechanics based, not on potential functions but rather, on orthogonal energy polynomials. In this context, the most important building block of a quantum mechanical system, which is the wavefunction at a given energy, is expressed as pointwise convergent series of square integrable functions in configuration space. The expansion coefficients of the series are orthogonal polynomials in the energy; they contain all physical information about the system. No reference is made at all to the usual potential function. We consider, in this new formulation, few representative problems at the level of undergraduate students who took at least two courses in quantum mechanics and are familiar with the basics of orthogonal polynomials. The objective is to demonstrate the viability of this formulation of quantum mechanics and its power in generating rich energy spectra illustrating the physical significance of these energy polynomials in the description of a quantum system. To assist students, partial solutions are given in an appendix as tables and figures.

Keywords:

Subject: Physical Sciences - Mathematical Physics

1. Introduction

According to the basic postulates of quantum mechanics, a quantum system is fully determined by its space-time wavefunction

Ψ (t, \vec{r})

and its Hamiltonian operator H. The wavefunction carries all information needed to calculate the expectation values of operators that represent physical observables. The Hamiltonian, on the other hand, generates the dynamics of the system through the famous Schrödinger equation:

i ℏ \frac{\partial}{\partial t} Ψ = H Ψ

. The Hamiltonian operator is the most vital among all observables and its eigenfunction

Φ

, defined by

H Φ = E Φ

, has a special place in quantum mechanics. Note that we designated the eigenvalue (measurement of H) as E because the physical unit of H is energy. Combining this eigenvalue equation with the Schrödinger equation gives the corresponding wavefunction for this measurement as

Ψ = e^{- i E t / ℏ} Φ

. Therefore, performing all such energy measurements on the system will give its total energy content, called the spectrum

\{E\}

. It also gives its total wavefunction as a linear sum (discrete and/or continuous) of all such energy components

{e^{- i E t / ℏ} Φ}

. Due to the extensive physical studies of the energy content of countless number of quantum mechanical systems and due to parallel extensive mathematical studies of the spectrum of Hermitian operators in Hilbert spaces, people over time understood very well the nature of the energy spectra. Generally speaking, the energy spectrum of a physical system consists of continuous and discrete parts. The continuous part is usually made up of several disconnected but continuous energy intervals called “energy bands,” which we designate here by the symbol. The discrete part, on the other hand, consists of either a finite or countably infinite set of discrete energy values

\{E_{k}\}

. These two sets do not overlap.

As such, we can represent the total space-time wavefunction

Ψ (t, \vec{r})

, which gives full information about the physical system at a given time, by writing its Fourier expansion over the entire energy spectrum as follows

Ψ (t, \vec{r}) = \int_{Ω} e^{- i E t / ℏ} ψ (\vec{r}, E) d E + \sum_{k} e^{- i E_{k} t / ℏ} ψ_{k} (\vec{r})

(1)

Therefore, the system is fully determined if we can write down its continuous and discrete Fourier components

ψ (\vec{r}, E)

and

ψ_{k} (\vec{r})

. From this point onward, we adopt the atomic units

ℏ = M = 1

and assume that the quantum mechanical system exists in a one-dimensional configuration space with coordinates

x_{-} \leq x \leq x_{+}

where

x_{\pm}

are the boundaries of the space.

In the traditional formulation of quantum mechanics, the continuous and discrete parts of the energy spectrum are determined by solving the stationary Schrödinger wave equation. The Hamiltonian operator for a single particle is defined by

H = T + V (x) = - \frac{1}{2} \frac{d^{2}}{d x^{2}} + V (x)

, where V(x) is the potential function that models the system. In this formulation the Hamiltonian expression is imported from the Hamiltonian formulation of classical mechanics in which momentum and position are promoted to operators as per first quantization rules. Hence, the concept of a potential energy is deeply rooted in the Hamiltonian formulation of classical mechanics according to which the energy of a particle can always be expressed as the sum of its kinetic energy and potential energy. Since the potential energy of a particle depends on its position, then the potential becomes a function in configuration space and, by construction, it is the only Hamiltonian component that can be related to the classical force concept. For example, the potential function of a massive particle attached to a linear massless spring of constant k is

\frac{1}{2} k x^{2}

and the spring force is

F = - \frac{d V}{d x} = - k x

. The potential function of a particle of mass M moving in the gravitational field of a point mass is

- M G / r

(G being the gravitational constant and r the radial distance to the point mass) and the gravitational force is

F = - \frac{d V (r)}{d r} =

- G M / r^{2}

, etc. More sophisticated potential functions were also proposed to describe complex systems such as the generalized Morse potential

V (x) = D (e^{- 2 μ x} - 2 α e^{- μ x})

that describes the molecular vibrations of a diatomic molecule with D, α and μ being physical parameters. This makes it clear that the concept of potential function was carried over from classical to quantum mechanics, through the construction of the system Hamiltonian, despite the fact that none of the postulates of the theory requires it. However, the Aharonov-Bohm (AB) quantum effect defied this general consensus that particles dynamics is solely due to fields at their locations [1]. In particular, AB effect has shown through a neat double slit interference experiment that the electromagnetic field can vanish everywhere where the electron moves but yet the electron motion is strongly affected by the electromagnetic interaction. In quantum theory, the AB effect can be explained without the notion of potential function. Thus, one could conclude that the potential function in quantum mechanics might be just a useful auxiliary mathematical tool that can be disposed of after all.

Concentrating on the main quantum ingredient, which is the particle wavefunction, we notice that almost all wavefunctions of systems with known exact solutions of the wave equation (e.g., the Coulomb, oscillator, Morse, Pöschl-Teller, etc.) are written in terms of classic hyper-geometric orthogonal polynomials in configurations space (such as, Hermite, Laguerre, and Jacobi polynomials). However, an alternative formulation of quantum mechanics was recently proposed with the premise that the class of analytically realizable systems is much larger than the exactly solvable class in the conventional potential function formulation [2,3]. This vision proved right and successful as demonstrated in several recent studies [4-7]. In this alternative formulation, no mention is ever made of a potential function. Consequently, the Hamiltonian operator is not written as the sum

H = T + V

. Nonetheless, the sacred Fourier expansion in the energy of the wavefunction given in (1) is still maintained. In this formulation, the continuous and discrete Fourier energy components are written as the following pointwise convergent series

ψ (x, E) = \sum_{n = 0}^{\infty} f_{n} (E) ϕ_{n} (x)

(2a)

ψ_{k} (x) = \sum_{n = 0}^{\infty} g_{n} (E_{k}) ϕ_{n} (x)

(2b)

where

{\{ϕ_{n} (x)\}}_{n = 0}^{\infty}

is a complete set of square-integrable functions and

\{f_{n}, g_{n}\}

are proper expansion coefficients. The wavefunction (2a) associated with the continuous spectrum is characterized by bounded oscillations that do not vanish all the way to the boundaries of space. However, the wavefunction (2b) associated with bound states is characterized by a finite number of oscillatory-like behavior (with a number of nodes that equals the bound state excitation level k) that vanishes rapidly at the boundaries. On the other hand, attempting to evaluate the wavefunction at an energy that does not belong to the spectrum will only result in a diverging series. That is, the result is non-stable endless oscillations that grow without bound all over space as the number of terms in the sum increases. Numerically, this is a signature of a nonphysical forbidden energy.

The action of the Hamiltonian operator on the basis set in this formulation is required to be of the following tridiagonal form

H ϕ_{n} (x) = a_{n} ϕ_{n} (x) + b_{n - 1} ϕ_{n - 1} (x) + b_{n} ϕ_{n + 1} (x)

(3)

where

a_{n}

and

b_{n}

are real constants such that

b_{n} \neq 0

for all n. Therefore, substituting (2a) and (2b) in the Schrödinger wave equation,

i \frac{\partial}{\partial t} Ψ (t, x) = H Ψ (t, x)

, gives the following algebraic equation

E f_{n} (E) = a_{n} f_{n} (E) + b_{n - 1} f_{n - 1} (E) + b_{n} f_{n + 1} (E)

(4a)

E_{k} g_{n} (E_{k}) = a_{n} g_{n} (E_{k}) + b_{n - 1} g_{n - 1} (E_{k}) + b_{n} g_{n + 1} (E_{k})

(4b)

We should note that so far, the Hamiltonian operator is not assumed to take any specific form such as

H = T + V

. Note also that the expansion coefficient,

a_{n}

and

b_{n}

, are independent of E as it is obvious from Eq. (3); they just represent the matrix elements of H in the basis set

{\{ϕ_{n} (x)\}}_{n = 0}^{\infty}

(if it happens to be an orthonormal set; see Eq. (8) below). Generally, the solution of Eq. (4) is a polynomial in E, modulo an overall multiplicative arbitrary function of E. Therefore, if we factorize this overall multiplicative function by writing

f_{n} (E) = f_{0} (E) P_{n} (E)

and

g_{n} (E_{k}) =

g_{0} (E_{k}) P_{n} (E_{k})

, then

P_{n} (E)

will be a polynomial of degree n in E with

P_{0} (E) = 1

. Equations (4a) and (4b) become collectively the following symmetric three-term recursion relation for the energy polynomials

{\{P_{n} (E)\}}_{n = 0}^{\infty}

E P_{n} (E) = a_{n} P_{n} (E) + b_{n - 1} P_{n - 1} (E) + b_{n} P_{n + 1} (E)

(5)

where E is an element of the total energy spectrum (continuous and discrete).

2. The energy polynomials

These polynomials are solutions of the three-term recursion relation (5) for

n = 0, 1, 2, ...

with the two initial seed values

P_{- 1} (E) = 0

and

P_{0} (E) = 1

. The spectral theorem of orthogonal polynomials (a.k.a. Favard theorem) [8,9] guarantees that with these initial values and the condition

b_{n} \neq 0

, they form a complete sequence of orthogonal polynomials satisfying the following general orthogonality relation [10]

\int_{Ω} ρ (E) P_{n} (E) P_{m} (E) d E + \sum_{k} ω_{k} P_{n} (E_{k}) P_{m} (E_{k}) = δ_{n, m}

(6)

where

ρ (E)

and

ω_{k}

are the continuous and discrete components of the weight function, respectively. One can show that

ρ (E) = f_{0}^{2} (E)

and

ω_{k} = g_{0}^{2} (E_{k})

[2-7]. The zeros (roots) of these polynomials play a crucial role in determining some of the most important physical properties of the system such as the allowed energy bands, density of states, bound state energies, etc. One way to find these zeros is as follows. Construct the following finite

n \times n

tridiagonal symmetric matrix

R = (\begin{matrix} a_{0} & b_{0} \\ b_{0} & a_{1} & b_{1} \\ b_{1} & a_{2} & b_{2} \\ \times & \times & \times \\ \times & \times & \times \\ b_{n - 3} & a_{n - 2} & b_{n - 2} \\ b_{n - 2} & a_{n - 1} \end{matrix})

(7)

Then the zeros of

P_{n} (E)

are the eigenvalues of R. Moreover, due to the special conditions on the recursion coefficients all these zeros are distinct, in complete agreement with the fact that the 1D Schrödinger equation has no degeneracy. Additionally, the zeros of

P_{n} (E)

interlace within those of

P_{n + 1} (E)

. Finally, what is left for determining the wavefunction in (1) and (2) is only to know the basis set

{\{ϕ_{n} (x)\}}_{n = 0}^{\infty}

. However, all physical characteristics of the system are contained in the energy polynomials whereas the basis elements are used only to facilitate realization of the system in configuration space. Moreover, the parameters in the basis elements (if any) are either derived from the physical parameters in the energy polynomials or they are non-physical and could be used to improve computations. Thus, in this formulation of quantum mechanics, a physical model is defined not by any potential function but by giving the pair

\{P_{n} (E), ϕ_{n} (x)\}

. Moreover, one may specify the set

{\{a_{n}, b_{n}\}}_{n = 0}^{\infty}

as alternative to

{\{P_{n} (E)\}}_{n = 0}^{\infty}

. Note, that if we adopt the potential picture and write

H = T + V

then for a given set

{\{a_{n}, b_{n}\}}_{n = 0}^{\infty}

, the solution of Eq. (3) for proper boundary conditions will determine the basis set

{\{ϕ_{n} (x)\}}_{n = 0}^{\infty}

. However, in this alternative formulation of quantum mechanics, Eq. (3) which is equivalent to the recursion relation (5), is considered as an algebraic definition of the Hamiltonian in place of

H = T + V

. In fact, if the basis set is orthonormal (i.e.,

〈ϕ_{n} | ϕ_{m}〉 = δ_{n, m}

) then Eq. (3) gives the following matrix representation of the Hamiltonian

H_{n, m} = 〈ϕ_{n}| H |ϕ_{m}〉 = a_{n} δ_{n, m} + b_{n - 1} δ_{n, m + 1} + b_{n} δ_{n, m - 1}

(8)

That is, the tridiagonal symmetric matrix (7) is a finite

n \times n

submatrix representation of H. In the absence of any explicit constraint on the basis functions

{\{ϕ_{n} (x)\}}_{n = 0}^{\infty}

(aside from square-integrability and completeness), we write them in a general form as

ϕ_{n} (x) = W (y) Q_{n} (y)

where

y = y (x)

is a coordinate transformation,

Q_{n} (y)

is a classic polynomial of degree n in y, and

W (y)

is a positive weight function designed to satisfy

W (y_{\pm}) = 0

, where

y_{\pm} = y (x_{\pm})

. Usually,

y (x)

takes us from the physical configuration space to the desirable finite or semi-infinite domains compatible with those of the polynomials

Q_{n} (y)

In Section 3 and Section 4, we propose several problems within this formulation of quantum mechanics. These are aimed at undergraduate students who took at least two quarters/semesters of quantum mechanics and are familiar with the basics of orthogonal polynomials. To avoid any remarkable prerequisites in advanced quantum mechanics and/or mathematical analysis, the problems were designed with emphasis on the numerical aspect rather than the analytical aspect of the solution. For example, we provide an equivalent description of the orthogonal energy polynomials by giving their three-term recursion relation vis-à-vis the recursion coefficients

\{a_{n}, b_{n}\}

. Moreover, partial solutions are given in the Appendix in the form of figures and tables. In the illustrative examples, the configuration space is either the whole real line (Section 3) or only the non-negative part of the real line (Section 4) and give a suitable square integrable basis set for each situation. Since the proposed problems are aimed at undergraduate students, then we assume general rather than specialized knowledge of orthogonal polynomials. Consequently, we just stress the importance of the structure of the recursion coefficients

\{a_{n}, b_{n}\}

in the three-term recursion relation (5). That is, we define the orthogonal energy polynomials through their recursion relation and initial values rather than through their analytic properties (e.g., weight function, generating function, Rodrigues formula, etc.). By doing so we avoid mentioning the explicit form of these energy polynomials and their associated analytical properties. Therefore, we use the three-term recursion relation and its coefficients as a defining tool for the associated energy polynomials. In particular, we want the students to get a feeling of the key role played by the recursion coefficients

\{a_{n}, b_{n}\}

and how their asymptotic behavior affects the corresponding energy spectrum. Not only that, but the same coefficients are sufficient in determining important physical properties such as the density of states, a property that describes how closely packed energy levels are in a given system, which plays a pivotal role in computing transport properties of physical systems [11].

Before we embark on computations related to specific problems, it is instructive at this point to digress on the numerical computations of the bound state energies. These are located outside the continuous energy bands and can be defined using any one of the following prescriptions:

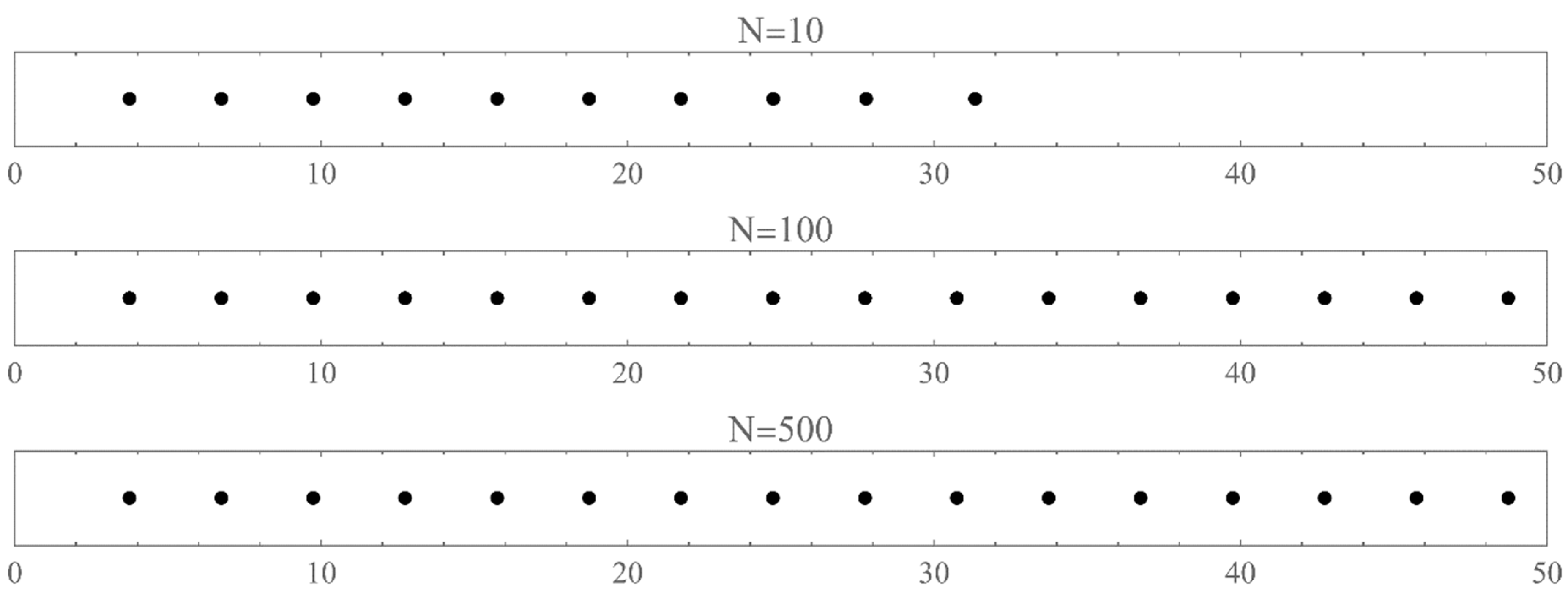
(1): The set of energies $\{E_{k}\}$ that satisfy: $\lim_{n \to \infty} P_{n} (E_{k}) = 0$ . That is, $E_{k}$ is an asymptotic zero for all energy polynomials in the limit of infinite (large enough) degrees [12].
(2): The set of eigenvalues of the tridiagonal matrix (7) that lie outside the energy bands and do not change significantly (within the desired accuracy) if we vary the size of the matrix around a large enough size $N \times N$ [13].
(3): The set of energies that make the asymptotic limit ( $n \to \infty$ ) of the polynomial $P_{n} (E)$ vanish [14]. For further understanding of this issue consider the problem stated in [14].

However, since this manuscript is mainly addressed to undergraduate students, we have opted to use mainly the simple computational scheme (2) based on matrix eigenvalues, which is a very much familiar problem to undergraduate students. Nevertheless, sometimes scheme (2) produces erroneous results. Thus, if in doubt, one needs to double check and independently verify the viability of the bound states using the asymptotic schemes (1) or (3) (see, for example, problem III and Figure 3.1).

As it is now evident from the discussion above, the energy polynomials are totally determined if the recursion coefficients

\{a_{n}, b_{n}\}

and the two initial values

\{P_{- 1} (E), P_{0} (E)\}

are given because then a unique polynomial solution of the three-term recursion relation (5) is obtained. The large n asymptotic values of

\{a_{n}, b_{n}\}

play an important role in determining the allowed energy intervals that the system can occupy (called “energy bands”). Moreover, these asymptotic values uniquely determine the boundaries of these energy bands. In fact, if this asymptotic limit is multivalued, that is

\lim_{n \to \infty} \{a_{n}, b_{n}\} = {\{A_{j}, B_{j}\}}_{j = 1}^{J}

with J being a positive integer number, then the continuous energy spectrum consists of J disconnected but continuous energy bands with

J - 1

gaps in between. Under these conditions, the infinite version of the matrix (7), which represents the Hamiltonian matrix, will have a tail consisting of identical

J \times J

tridiagonal block matrices (with A’s on the diagonal and B’s on the off-diagonal) that repeats forever. If one or more of the asymptotic values

\{A_{j}, B_{j}\}

is/are infinite, then the size of some or all of the bands is also infinite. All points within the bands correspond to energies within the continuous scattering energy states. Bound states (if they exist) have energies that correspond to discrete points located outside the energy bands (inside the gaps or beyond the bands). We refer advanced readers to reference [15] for all necessary mathematical details related to the computations of the asymptotic limits

\lim_{n \to \infty} \{a_{n}, b_{n}\} = {\{A_{j}, B_{j}\}}_{j = 1}^{J}

and how they are used to define the boundaries of the energy bands.

3. Problems in the infinite domain

For the first set of problems, the configuration space is considered to be the whole real line where

x_{\pm} = \pm \infty

. Under such circumstances we select the following suitable basis elements

ϕ_{n} (x) = \sqrt{\frac{λ / \sqrt{π}}{2^{n} n!}} e^{- λ^{2} x^{2} / 2} H_{n} (λ x); x \in] - \infty, + \infty [

(9)

where

H_{n} (λ x)

is the Hermite polynomial of degree n and is a real positive parameter of inverse length dimension which represents an extra free parameter that helps in improving the convergence of the numerical computations once judiciously chosen. These basis elements are orthonormal since

〈ϕ_{n} | ϕ_{m}〉 = \int_{- \infty}^{+ \infty} ϕ_{n} (x) ϕ_{m} (x) d x = δ_{n, m}

. In the traditional potential formulation of quantum mechanics, the functions (9) are typically associated with the eigenfunctions of the one-dimensional harmonic oscillator whose energy spectrum is discrete, infinite and bounded from below. However, in our present context, they are considered as elements of a complete basis set suitable for a wider range of analytical problems that may have discrete as well as continuous energy spectra.

3.1. Problem I

As stated above, if the coefficient of the recursion relation (5) has a single finite asymptotic limit,

\lim_{n \to \infty} a_{n} = A

and

\lim_{n \to \infty} b_{n} = B

, then it can be shown that the continuous energy spectrum of the corresponding Hamiltonian will consist of a single energy band with

Ω \in [A - 2 B, A + 2 B]

. Take, for instance,

a_{n} = 0

and

b_{n} = λ^{2} / 2

, which gives

Ω \in [- λ^{2}, + λ^{2}]

. Calculate the zeros of

P_{N} (E)

for large enough N which are just the eigenvalues of the tridiagonal matrix (7) and show that the zeros do, in fact, lie within this energy band (shown in Table 1.1). The un-normalized wavefunction at an energy E is

\tilde{ψ} (x, E) : = \sum_{n = 0}^{N} P_{n} (E) ϕ_{n} (x)

(10)

Plots of this function at the energies

E = 0

E = \pm λ^{2} / 2

and

E = \pm λ^{2}

are shown in Figure 1.2-1.5. Figure 1.1 shows the zeroes of the energy polynomial

P_{N} (E)

in units of

λ^{2}

for

N = 100

and Table 1.1 shows the edges of the allowed energy band as we increase the degree of the polynomial N. If one tries to plot the wave function at

|E| > λ^{2}

, that is outside the energy band then the wavefunction will blow up, a signature that it is a forbidden energy state of the system as shown in Figure 1.6 for

E = 3 λ^{2} / 2

. For completeness, we would like to mention that the orthogonal energy polynomial associated with these recursion coefficients is the normalized version of the Chebyshev polynomial. Moreover, the initial values

P_{- 1} (E) = 0

and

P_{0} (E) = 1

make it the Chebyshev polynomial of the second kind

U_{n} (E)

[16].

3.2. Problem II

We consider the orthogonal polynomial defined by the following recursion coefficients:

a_{n} = λ^{2} / 2

b_{2 n} = \frac{λ^{2}}{2} \sqrt{(n + \frac{1}{2}) / (n + 2)}

and

b_{2 n + 1} = λ^{2}

. In this case the continuous energy spectrum will consist of two energy bands since

\lim_{n \to \infty} b_{n} = λ^{2} \{\frac{1}{2}, 1\}

, where the limits in the parentheses are for even and odd n, respectively. The zeros of

P_{N} (E)

for large enough N and the associated four boundaries of these two bands are shown explicitly in Figure 2.1 for

N = 100

while the edges of the allowed energy bands are computed in Table 2.1 for different values of the degree of the polynomial. You will notice, however, that one of the zeros is isolated inside the energy gap between the two bands (in fact, it is located at the middle of the energy gap). This energy is associated with a bound state, let us call this energy

E

and plot

\tilde{ψ} (x, E)

as shown in Figure 2.2. This should be a remarkable observation by the students: the basis (9), which is normally associated with the harmonic oscillator whose energy spectrum consists of an infinite number of discrete bound states, is now associated with this system that has only one bound state and two continuous energy bands.

We plot

\tilde{ψ} (x, E)

for an energy from within the left band and another from the right band as shown in Figure 2.3 and 2.4, respectively. We also evaluate the wavefunction

\tilde{ψ} (x, E)

at an energy from within the forbidden gap but not equal to the bound state energy

E

as shown in Figure 2.5 which shows extremely large unbounded oscillation all over space due to the forbidden nature of the selected energy,

E = λ^{2} / 4

, within the energy gap region.

3.3. Problem III

In this problem we generalize Problem II by parametrizing the recursion coefficients

\{a_{n}, b_{n}\}

as follows

a_{2 n} = α λ^{2}, a_{2 n + 1} = (1 - α) λ^{2}

(11)

b_{2 n} = \frac{λ^{2}}{2} β \sqrt{(n + γ^{- 1}) / (n + γ)}, b_{2 n + 1} = \frac{λ^{2}}{2} γ \sqrt{(n + β) / (n + β^{- 1})}

(11b)

Problem II corresponds to

α = \frac{1}{2}

β = 1

and

γ = 2

. Note that the asymptotic limits of

a_{n}

and

b_{n}

are multi-valued. In fact,

\lim_{n \to \infty} a_{n} = λ^{2} \{α, 1 - α\}

and

\lim_{n \to \infty} b_{n} = \frac{1}{2} λ^{2} \{β, γ\}

. Therefore, as stated at the end of Section 2 above, we expect that the continuous energy spectrum to consist of two energy bands of finite size. In fact, one can show that the four boundaries of the two energy bands are:

\frac{λ^{2}}{2} [1 \pm \sqrt{{(2 α - 1)}^{2} + {(β + γ)}^{2}}], \frac{λ^{2}}{2} [1 \pm \sqrt{{(2 α - 1)}^{2} + {(β - γ)}^{2}}]

(12)

This result is verified numerically in Table 3.1 by taking N large enough. The zeros of this polynomial are shown in Figure 3.1 for

N = 100

and the wavefunction

\tilde{ψ} (x, E)

is shown in Figure 3.2 for the bound state at

E = 3 λ^{2} / 2

and for

N = 100

. The corresponding quantum mechanical system is parameterized by the four physical parameters

\{λ, α, β, γ\}

. These parameters could be adjusted to fit experimental measurements of the desired system that can be modeled by these energy polynomials.

3.4. Problem IV

Let us construct another two-energy-band system as follows:

a_{2 n} = α λ^{2}, a_{2 n + 1} = (1 - α) λ^{2}, b_{2 n} = α λ^{2} \sqrt{2 n + β}, b_{2 n + 1} = α λ^{2} \sqrt{2 n + γ}

(13)

Note that the large degree asymptotic (

n \to \infty

) limit of

b_{n}

goes to infinity as

\sqrt{n}

. Consequently, the two energy bands will have infinite sizes whereas the two boundaries of the energy gap are set at

\frac{λ^{2}}{2} (1 \pm |2 α - 1|)

, this is verified numerically in Table 4.1. The zeros of

P_{N} (E)

in units of

λ^{2}

are shown in Figure 4.1 for

α = 3

and

N = 200

which shows that the energy bands extend to infinity and the gap is located in the interval

- 2 λ^{2} < E < + 3 λ^{2}

with no bound states.

4. Problems in the semi-infinite domain

For the second set of problems, the configuration space is considered to be the non-negative part of the real line,

x_{-} = 0

and

x_{+} \to \infty

. This situation will, in particular, be suitable for the radial part of the Schrödinger equation in three dimensions with spherical symmetry. Under such circumstances we select the following orthonormal basis elements

ϕ_{n} (r) = \sqrt{\frac{2 λ Γ (n + 1)}{Γ (n + ν + 1)}} {(λ r)}^{ν + \frac{1}{2}} e^{- λ^{2} r^{2} / 2} L_{n}^{ν} (λ^{2} r^{2})

(14)

where

L_{n}^{ν} (z)

is the Laguerre polynomial and the parameters

\{ν, λ\}

are to be chosen such that

ν > - 1

. This basis forms an orthonormal set since

\int_{0}^{\infty} ϕ_{n} (r) ϕ_{m} (r) d r = δ_{n, m}

. Again, we note that in the traditional formulation of quantum mechanics and with

ν = l + \frac{1}{2}

, the functions (14) are typically associated with the eigenfunctions of the radial Schrödinger equation of a spherically symmetric harmonic oscillator (isotropic oscillator) whose energy spectrum is discrete, infinite and bounded from below. If

ν = 2 l + 1

and

λ^{2} r^{2} \mapsto λ r

then the basis (14) is associated with the Coulomb potential for the hydrogen atom whose energy spectrum consists of a combination of a single infinite continuous band with

E \geq 0

and an infinite set of discrete energies bounded from below at

E = - |E_{0}|

and from above at

E_{\infty} = 0

. However, in our present context, these eigenfunctions are taken as basis set for a wider range of analytical problems that may have discrete as well as continuous energy spectra and may be bounded or unbounded.

4.1. Problem V

We start by reproducing the results associated with the isotropic oscillator problem in this alternative formulation of quantum mechanics. For that, the recursion coefficients of the associated orthogonal energy polynomial are chosen as:

a_{n} = \frac{2 ω}{\tanh θ} (n + μ), b_{n} = - \frac{ω}{\sinh θ} \sqrt{(n + 1) (n + 2 μ)}

(15)

where

ω

is the oscillator frequency and

2 μ = l + \frac{3}{2}

. The angular parameter

θ

, being real and positive, is arbitrary but chosen to improve conversion of the calculation. We verify that the zeros are, in fact, discrete (see, Figure 5.1) and for large enough N they converge to the isotropic oscillator energy spectrum:

E_{k} = ω (2 k + l + \frac{3}{2})

(16)

Figure 5.2 shows that the difference between two consecutive states is constant and equals to

2 ω

. However, it diverges quickly due to numerical errors, but it gets more accurate as the value of θ increases. Moreover, the linear dependence of

E_{k}

on k is shown in Figure 5.3, and it exhibits the same divergence behavior. Theoretically, the proper choice for this parameter is given by

\cosh θ = \frac{ω^{2} + {(λ / 2)}^{4}}{ω^{2} - {(λ / 2)}^{4}}

with

λ < 2 \sqrt{ω}

. By the way, the orthogonal energy polynomial whose recursion coefficients are given by (15) for this problem with discrete spectrum is the Meixner polynomial

M_{n}^{μ} (z_{k}; θ)

with

z_{k} = E_{k} / 2 ω

[16].

4.2. Problem VI

For this problem, we would like to construct an energy spectrum that consists of a semi-infinite continuous band (

E \geq 0

) and a finite set of discrete negative energies

\{E_{k}\}

. To that end, we take the recursion coefficients as follows

a_{n} = λ^{2} [{(n + μ + γ)}^{2} + n (n + 2 γ - 1) - μ^{2}]

(17)

b_{n} = - λ^{2} (n + μ + γ) \sqrt{(n + 1) (n + 2 γ)}

(17b)

where

μ < 0

and

γ > - μ

. We verify for

γ = 10

μ = - 9.5

that, indeed, the energy spectrum consists of an infinite continuous positive energy band with

E \geq 0

(as shown in Figure 6.1) and a finite number of negative discrete energies (as shown in Figure 6.2). Also, the number of the discrete bound state energies is

⌊- μ⌋

, where

⌊x⌋

stands for the largest integer less than or equal to x. In the large degree N limit, we verify in Figure 6.3 that for

E < 0

, these discrete energies approach the following values:

E_{k} = - λ^{2} {(k + μ)}^{2}

(18)

where

k = 0, 1, .., ⌊- μ⌋

. Some un-normalized wavefunction

\tilde{ψ} (r, E_{k})

are shown in Figure 6.4 for different k values. These wavefunctions are physically acceptable; that is, they have k nodes and vanish rapidly at the boundaries (

r = 0

and

r \to \infty

). The un-normalized wavefunction

\tilde{ψ} (r, E)

for

E > 0

is shown in Figure 6.5 and verified to represents a continuous scattering state; that is, bounded oscillations that extends to infinity. By the way, the orthogonal energy polynomial whose recursion coefficients are given by (17) is a special case of the continuous dual Hahn polynomial

S_{n}^{μ} (E; γ, γ)

[16].

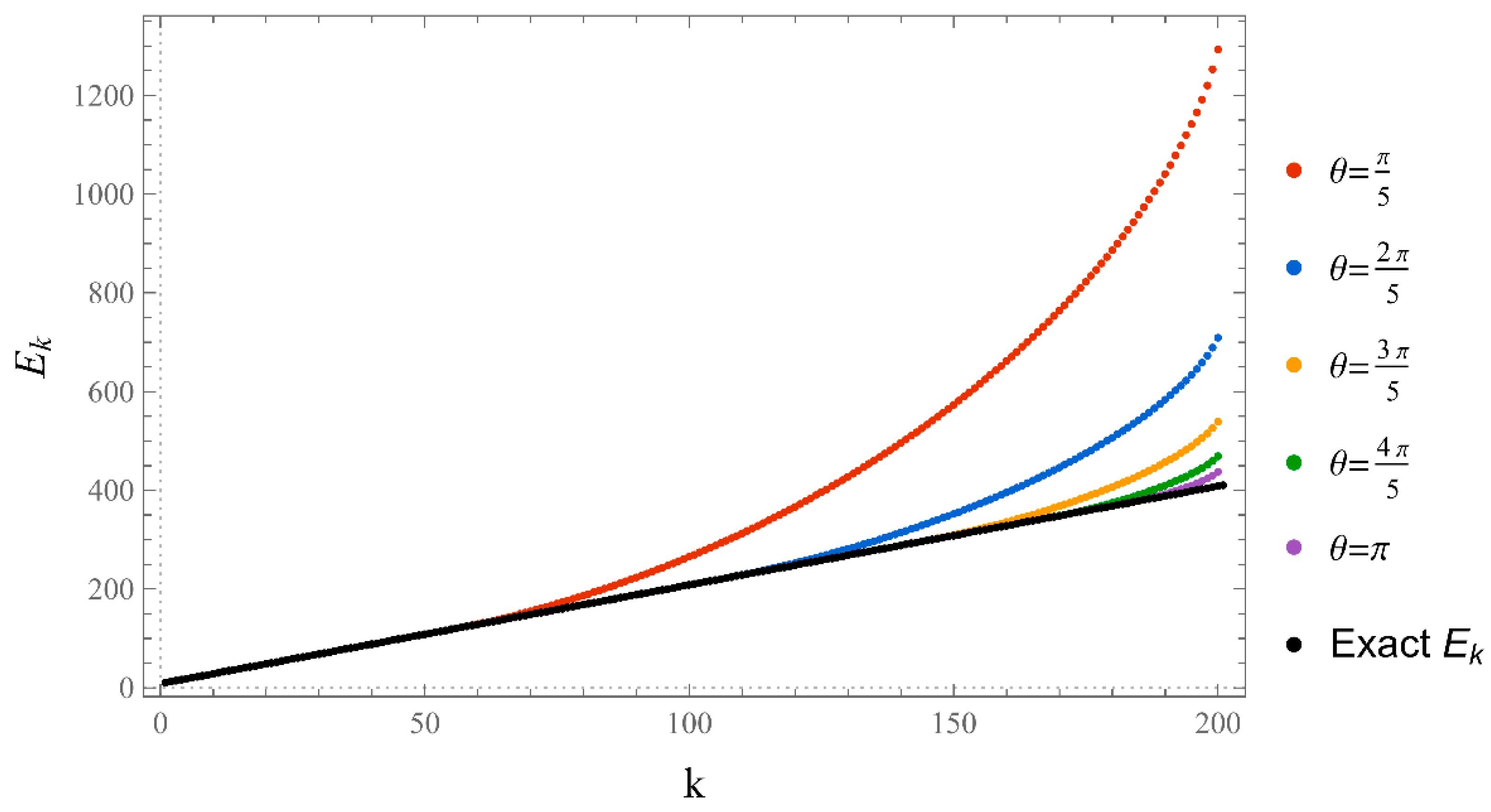
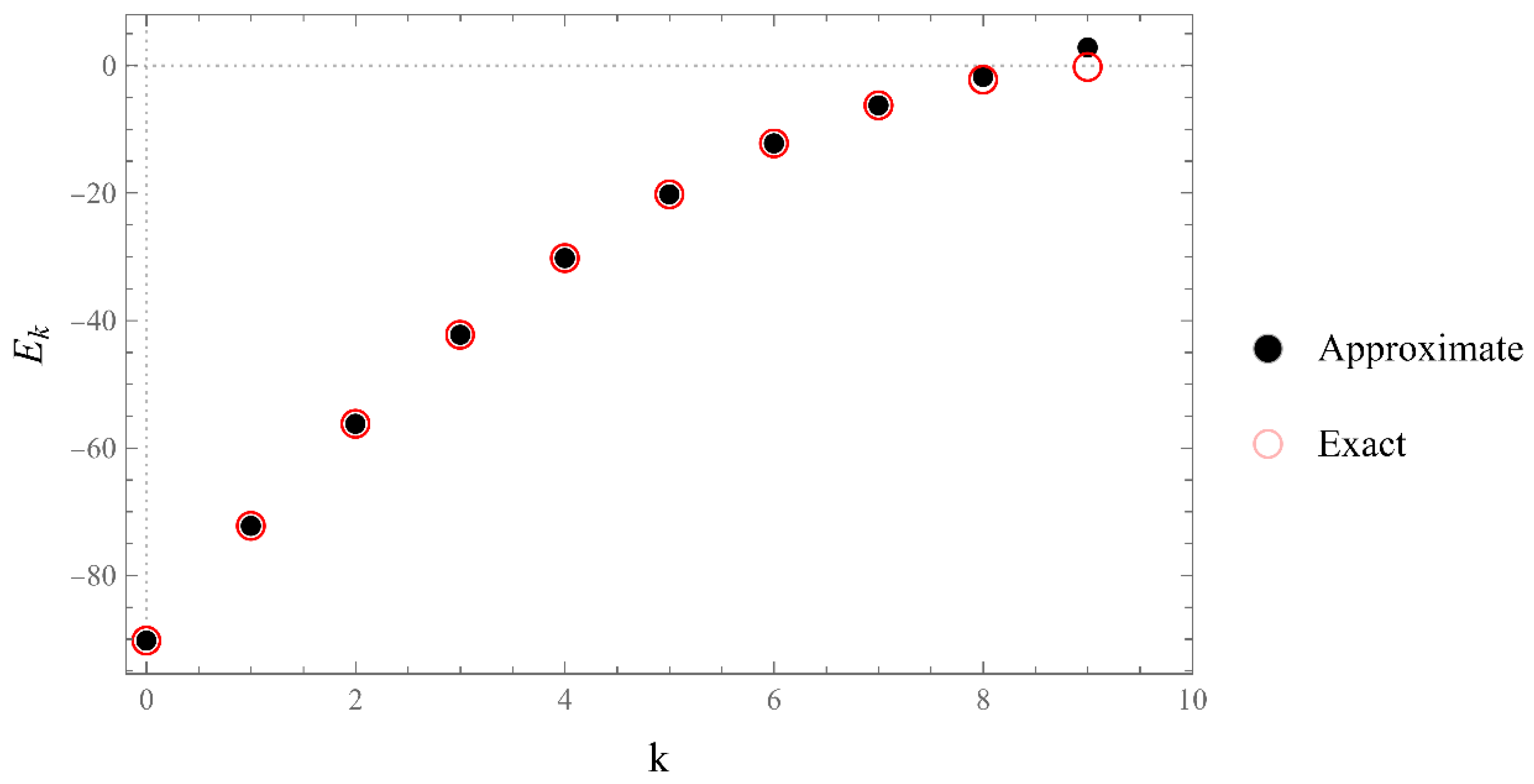
5. Conclusion

In this work we exploited the main idea behind the new formulation of quantum mechanics based, not on potential functions but rather, on orthogonal energy polynomials. We did that in a way accessible to undergraduate students who took two courses on quantum mechanics. In this approach, we express the Fourier components of the quantum mechanical wave function as a pointwise convergent series in a suitable square integrable basis set in configuration space. The expansion coefficients of the series are orthogonal polynomials in the energy domain. We considered two basis sets that are suitable for infinite and semi-infinite domains along with a variety of recursion coefficients and showed how their asymptotic behavior play a crucial role in determining the structure of the system energy spectrum.

We stressed all over the manuscript the fact that in the present formulation, no reference is made at all to the usual potential energy function. We have demonstrated the validity of this formulation of quantum mechanics and its power to generate a wide span of rich energy spectra illustrating the physical significance of these energy polynomials in the description of quantum systems. For this purpose, we have investigated few representative models that gave rise to a variety of discrete and continuous energy spectra. To keep the manuscript at the undergraduate level, all along our manuscript we have avoided talking about the analytical properties of the associated orthogonal polynomials but rather considered their equivalent representation in terms of recursion coefficients

\{a_{n}, b_{n}\}

and initial values. We also alluded to the possibility of computing the density of states which is a very fundamental quantity in condensed matter and statistical physics that controls the transport properties of physical systems.

Author Contributions

Conceptualization, Ibraheem Al-Yousef, Moayad Ekhwan, H. Bahlouli and A. Alhaidari; Formal analysis, H. Bahlouli and A. Alhaidari; Methodology, H. Bahlouli and A. Alhaidari; Project administration, H. Bahlouli; Supervision, H. Bahlouli and A. Alhaidari; Validation, Ibraheem Al-Yousef, Moayad Ekhwan and A. Alhaidari; Visualization, Ibraheem Al-Yousef, Moayad Ekhwan and A. Alhaidari; Writing – original draft, H. Bahlouli and A. Alhaidari; Writing – review & editing, Ibraheem Al-Yousef, Moayad Ekhwan, H. Bahlouli and A. Alhaidari.

Funding

This research received no funding.

Acknowledgements

We acknowledge the support of KFUPM during the progress of this research. Alhaidari acknowledges the additional support of the Saudi Center for Theoretical Physics.

Conflict of Interest

The authors declare no conflict of interest.

Appendix: Partial Solutions

Problem I:

Figure 1. 1: The zeros of

P_{N} (E)

in units of

λ^{2}

for

N = 100

Figure 1. 1: The zeros of

P_{N} (E)

in units of

λ^{2}

for

N = 100

Table 1. 1: The left and right boundaries of the energy band in units of

λ^{2}

for different values of N. The exact values are

\pm λ^{2}

Table 1. 1: The left and right boundaries of the energy band in units of

λ^{2}

for different values of N. The exact values are

\pm λ^{2}

N	Left Boundaries	Right Boundaries
10 20 50 100 200	-0.959493 -0.988831 -0.998103 -0.999516 -0.999878	0.959493 0.988831 0.998103 0.999516 0.999878

Figure 1. 2: The un-normalized wavefunction

\tilde{ψ} (x, E)

for

E = 0

at the middle of the band. The horizontal x-axis is in units of

λ^{- 1}

. We took

N = 100

Figure 1. 2: The un-normalized wavefunction

\tilde{ψ} (x, E)

for

E = 0

at the middle of the band. The horizontal x-axis is in units of

λ^{- 1}

. We took

N = 100

Figure 1. 3: The un-normalized wavefunction

\tilde{ψ} (x, E)

for

E = + λ^{2} / 2

. We took

N = 100

Figure 1. 3: The un-normalized wavefunction

\tilde{ψ} (x, E)

for

E = + λ^{2} / 2

. We took

N = 100

Figure 1. 4: The un-normalized wavefunction

\tilde{ψ} (x, E)

for

E = - λ^{2} / 2

. We took

N = 100

Figure 1. 4: The un-normalized wavefunction

\tilde{ψ} (x, E)

for

E = - λ^{2} / 2

. We took

N = 100

Figure 1. 5: The un-normalized wavefunction

\tilde{ψ} (x, E)

for

E = λ^{2}

, which is at the right edge of the energy band. We took

N = 100

Figure 1. 5: The un-normalized wavefunction

\tilde{ψ} (x, E)

for

E = λ^{2}

, which is at the right edge of the energy band. We took

N = 100

Figure 1. 6: The un-normalized wavefunction

\tilde{ψ} (x, E)

for

E = 3 λ^{2} / 2

, which is a forbidden energy outside the band. We took

N = 100

. Note the unbounded oscillations everywhere.

Figure 1. 6: The un-normalized wavefunction

\tilde{ψ} (x, E)

for

E = 3 λ^{2} / 2

, which is a forbidden energy outside the band. We took

N = 100

. Note the unbounded oscillations everywhere.

Problem II:

Figure 2. 1: The zeros of

P_{N} (E)

in units of

λ^{2}

for

N = 100

Figure 2. 1: The zeros of

P_{N} (E)

in units of

λ^{2}

for

N = 100

Table 2. 1: The boundaries of the left and right energy bands in units of

λ^{2}

for different values of N. The exact values are

- λ^{2}

, 0,

λ^{2}

, and

2 λ^{2}

Table 2. 1: The boundaries of the left and right energy bands in units of

λ^{2}

for different values of N. The exact values are

- λ^{2}

, 0,

λ^{2}

, and

2 λ^{2}

N	Left Boundaries		Right Boundaries
20 50 100 200 400	-0.926138 -0.973840 -0.988118 -0.994550 -0.997467	-0.105799 -0.034724 -0.014908 -0.006517 -0.002915	1.105799 1.034724 1.014908 1.006517 1.002915	1.926138 1.973840 1.988118 1.994550 1.997467

Figure 2. 2: The un-normalized wavefunction

\tilde{ψ} (x, E)

for the bound state in the middle of the energy gap with

E = \frac{1}{2} λ^{2}

. The horizontal x-axis is in units of

λ^{- 1}

. We took

N = 100

Figure 2. 2: The un-normalized wavefunction

\tilde{ψ} (x, E)

for the bound state in the middle of the energy gap with

E = \frac{1}{2} λ^{2}

. The horizontal x-axis is in units of

λ^{- 1}

. We took

N = 100

Figure 2. 3: The un-normalized wavefunction

\tilde{ψ} (x, E)

for

E = 3 λ^{2} / 2

in the right energy band. We took

N = 100

Figure 2. 3: The un-normalized wavefunction

\tilde{ψ} (x, E)

for

E = 3 λ^{2} / 2

in the right energy band. We took

N = 100

Figure 2. 4: The un-normalized wavefunction

\tilde{ψ} (x, E)

for

E = - λ^{2} / 2

in the left energy band. We took

N = 100

Figure 2. 4: The un-normalized wavefunction

\tilde{ψ} (x, E)

for

E = - λ^{2} / 2

in the left energy band. We took

N = 100

Figure 2. 5: The un-normalized wavefunction

\tilde{ψ} (x, E)

for

E = λ^{2} / 4

, which is a forbidden energy in the gap. We took

N = 100

. Note the unbounded oscillations everywhere.

Figure 2. 5: The un-normalized wavefunction

\tilde{ψ} (x, E)

for

E = λ^{2} / 4

, which is a forbidden energy in the gap. We took

N = 100

. Note the unbounded oscillations everywhere.

Problem III:

Figure 3. 1: The zeros of

P_{N} (E)

in units of

λ^{2}

for

N = 100

. We took

α = 1.5

β = 2.3

and

γ = 3.7

. Out of the six isolated eigenvalues (shown with red circles) only

E = 3 λ^{2} / 2

pass the asymptotic test [12] and corresponds to a bound state.

Figure 3. 1: The zeros of

P_{N} (E)

in units of

λ^{2}

for

N = 100

. We took

α = 1.5

β = 2.3

and

γ = 3.7

. Out of the six isolated eigenvalues (shown with red circles) only

E = 3 λ^{2} / 2

pass the asymptotic test [12] and corresponds to a bound state.

Table 3. 1: The left and right boundaries of the left and right energy bands in units of

λ^{2}

for different values of N. The exact values are in (12).

Table 3. 1: The left and right boundaries of the left and right energy bands in units of

λ^{2}

for different values of N. The exact values are in (12).

N	Left Boundaries		Right Boundaries
20	-2.61667	-1.02433	2.02433	3.61667
50	-2.65286	-0.81445	1.81445	3.65286
100	-2.65775	-0.760255	1.76026	3.65775
200	-2.6601	-0.737958	1.73796	3.6601
300	-2.6609	-0.731469	1.73147	3.6609
Exact	-2.66228	-0.720656	1.72066	3.66228

Figure 3. 2: The un-normalized wavefunction

\tilde{ψ} (x, E)

for the bound state inside the energy gap with

E = 3 λ^{2} / 2

. The horizontal x-axis is in units of

λ^{- 1}

. We took

N = 100

Figure 3. 2: The un-normalized wavefunction

\tilde{ψ} (x, E)

for the bound state inside the energy gap with

E = 3 λ^{2} / 2

. The horizontal x-axis is in units of

λ^{- 1}

. We took

N = 100

Problem IV:

Figure 4. 1: The zeros of

P_{N} (E)

in units of

λ^{2}

for

N = 200

. We took

α = 3

β = 2

and

γ = 1

. The energy bands extend to infinity and the gap is located in the interval

- 2 λ^{2} < E < + 3 λ^{2}

. The system has no bound states.

Figure 4. 1: The zeros of

P_{N} (E)

in units of

λ^{2}

for

N = 200

. We took

α = 3

β = 2

and

γ = 1

. The energy bands extend to infinity and the gap is located in the interval

- 2 λ^{2} < E < + 3 λ^{2}

. The system has no bound states.

Table 4. 1: The left and right boundaries energy gap in units of

λ^{2}

for different values of N. We took

α = 3

β = 2

and

γ = 1

. The exact values are

\frac{λ^{2}}{2} (1 \pm |2 α - 1|)

Table 4. 1: The left and right boundaries energy gap in units of

λ^{2}

for different values of N. We took

α = 3

β = 2

and

γ = 1

. The exact values are

\frac{λ^{2}}{2} (1 \pm |2 α - 1|)

N	Gap Boundaries
20	-2.54592	3.54592
50	-2.25155	3.25155
100	-2.13357	3.13357
200	-2.06917	3.06917
300	-2.04672	3.04672
Exact	-2.00000	3.00000

Problem V:

Figure 5. 1: The zeros of

P_{N} (E)

in units of

λ^{2}

for different values of N. We took

ω = 3 / 2

μ = 5 / 4

, and

θ = π

. The energies are found to converge to a discrete equally spaced spectrum.

Figure 5. 1: The zeros of

P_{N} (E)

in units of

λ^{2}

for different values of N. We took

ω = 3 / 2

μ = 5 / 4

, and

θ = π

. The energies are found to converge to a discrete equally spaced spectrum.

Figure 5. 2: The difference between consecutive zeros of

P_{N} (E)

for

N = 200

. We took

ω = 1

μ = 5

, for different values of θ. The difference is constant, which matches the theoretical value of

2 ω

. However, we get better convergence as θ increases.

Figure 5. 2: The difference between consecutive zeros of

P_{N} (E)

for

N = 200

. We took

ω = 1

μ = 5

, for different values of θ. The difference is constant, which matches the theoretical value of

2 ω

. However, we get better convergence as θ increases.

Figure 5. 3: The k^th zero of

P_{N} (E)

vs k for

N = 200

. We took

ω = 1

μ = 5

, for different values of θ. This shows how the plot have better convergence as θ increases.

Figure 5. 3: The k^th zero of

P_{N} (E)

vs k for

N = 200

. We took

ω = 1

μ = 5

, for different values of θ. This shows how the plot have better convergence as θ increases.

Problem VI:

Figure 6. 1: The zeros of

P_{N} (E)

in units of

λ^{2}

for

N = 200

. We took

γ = 10

and

μ = - 9.5

. The energy bands for

E \geq 0

extend to infinity.

Figure 6. 1: The zeros of

P_{N} (E)

in units of

λ^{2}

for

N = 200

. We took

γ = 10

and

μ = - 9.5

. The energy bands for

E \geq 0

extend to infinity.

Figure 6. 2: The zeros of

P_{N} (E)

in units of

λ^{2}

for different values of N. The energy bands for

E < 0

are found to converge to a discrete linearly spaced spectrum.

Figure 6. 2: The zeros of

P_{N} (E)

in units of

λ^{2}

for different values of N. The energy bands for

E < 0

are found to converge to a discrete linearly spaced spectrum.

Figure 6. 3: The k^th zero of

P_{N} (E)

vs k for

N = 500

. We took

γ = 10

and

μ = - 9.5

. When

E < 0

, the zeros of

P_{N} (E)

agrees with Eq. (18) up to

k = ⌊- μ⌋

Figure 6. 3: The k^th zero of

P_{N} (E)

vs k for

N = 500

. We took

γ = 10

and

μ = - 9.5

. When

E < 0

, the zeros of

P_{N} (E)

agrees with Eq. (18) up to

k = ⌊- μ⌋

Figure 6. 4: The un-normalized wavefunction

\tilde{ψ} (r, E_{k})

for different values of

k

. The horizontal r-axis is in units of

λ^{- 1}

. We took

μ = - 15, γ = 16

, and

ν = 1

. We can observe each wavefunction having

k

nodes, and vanishes at the boundaries.

Figure 6. 4: The un-normalized wavefunction

\tilde{ψ} (r, E_{k})

for different values of

k

. The horizontal r-axis is in units of

λ^{- 1}

. We took

μ = - 15, γ = 16

, and

ν = 1

. We can observe each wavefunction having

k

nodes, and vanishes at the boundaries.

Figure 6. 5: The un-normalized wavefunction

\tilde{ψ} (r, E)

for

N = 100

. We took

E = 150 λ^{2}

, for

μ = - 15, γ = 16

, and

ν = 2

. We can see the bounded oscillations that extends to infinity.

Figure 6. 5: The un-normalized wavefunction

\tilde{ψ} (r, E)

for

N = 100

. We took

E = 150 λ^{2}

, for

μ = - 15, γ = 16

, and

ν = 2

. We can see the bounded oscillations that extends to infinity.

References

Lev Vaidman, Role of potentials in the Aharonov-Bohm effect, Phys. Rev. A 86 (2012) 040101(R). [CrossRef]
D. Alhaidari, Formulation of quantum mechanics without potential function, Quant. Phys. Lett. 4 (2015) 51. [CrossRef]
D. Alhaidari and M. E. H. Ismail, Quantum mechanics without potential function, J. Math. Phys. 56 (2015) 072107.
D. Alhaidari and T. J. Taiwo, Wilson-Racah Quantum System, J. Math. Phys. 58 (2017) 022101.
D. Alhaidari, Reconstructing the potential function in a formulation of quantum mechanics based on orthogonal polynomials, Commun. Theor. Phys. 68 (2017) 711.
D. Alhaidari and Y.-T. Li, Quantum systems associated with the Hahn and continuous Hahn polynomials, Rep. Math. Phys. 82 (2018) 285. [CrossRef]
D. Alhaidari, Representation of the quantum mechanical wavefunction by orthogonal polynomials in the energy and physical parameters, Commun. Theor. Phys. 72 (2020) 015104.
M. E. H. Ismail, Classical and Quantum orthogonal polynomials in one variable, paperback edition (Cambridge University press, 2009).
T. S. Chihara, An Introduction to Orthogonal Polynomials (Dover, 2011).
One can write the orthogonality (6) in a compact form as $\int_{- \infty}^{+ \infty} ξ (E) P_{n} (E) P_{m} (E) d E = δ_{n, m}$ , where $ξ (E) = \sum_{j} ρ (E) θ (E, E_{j}^{\pm}) + \sum_{k} ω_{k} δ (E - E_{k})$ and $θ (E, E_{j}^{\pm}) = \{\begin{matrix} 1 & , E_{j}^{-} \leq E \leq E_{j}^{+} \\ 0 & , otherwise \end{matrix}$ .
H. Bahlouli, A. D. Alhaidari and M. S. Abdelmonem, Phys. Lett. A 367 (2007) 162; and references therein.
If for a particular value of the energy, $P_{n} (\hat{E}) = 0$ for all n (not only asymptotically) then $\hat{E}$ is not the energy of a bound state. In fact, this property makes the energy polynomials non-orthogonal. If we remove this zero by defining $P_{n} (E) = (E - \hat{E}) Q_{n - 1} (E)$ then the polynomials $\{Q_{n} (E)\}$ will form a true orthogonal sequence of energy polynomials.
It may happen that an eigenvalue $\hat{E}$ of the matrix (7), which lies isolated outside the energy bands or in an energy gap, does not correspond to a bound state. It is advisable that one evaluates the polynomial at all such eigenvalues and performs the test $\lim_{n \to \infty} P_{n} (\hat{E}) = 0$ .
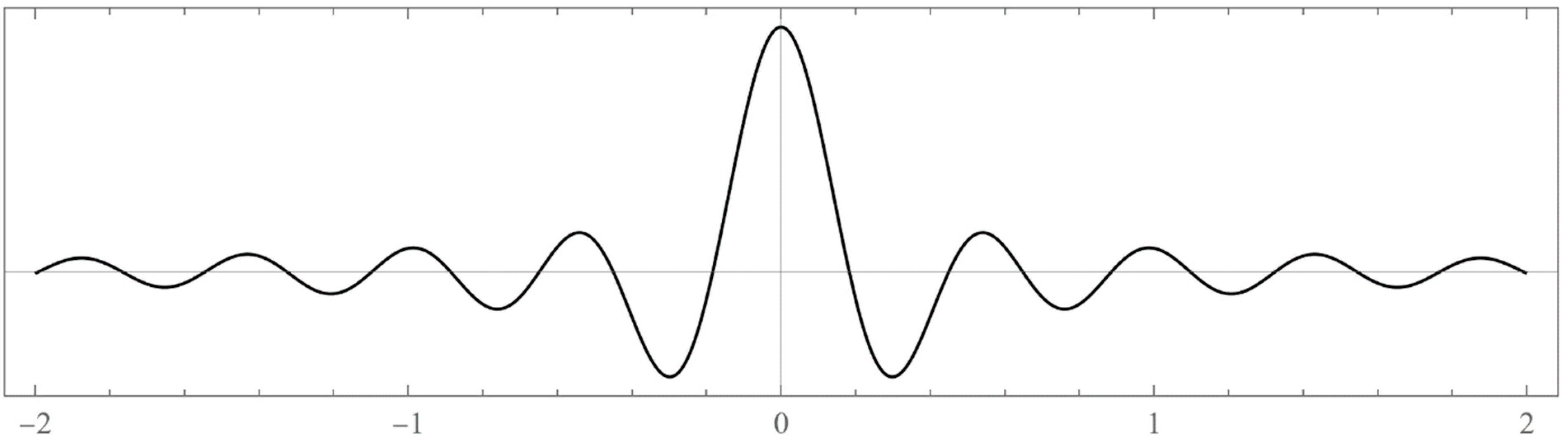
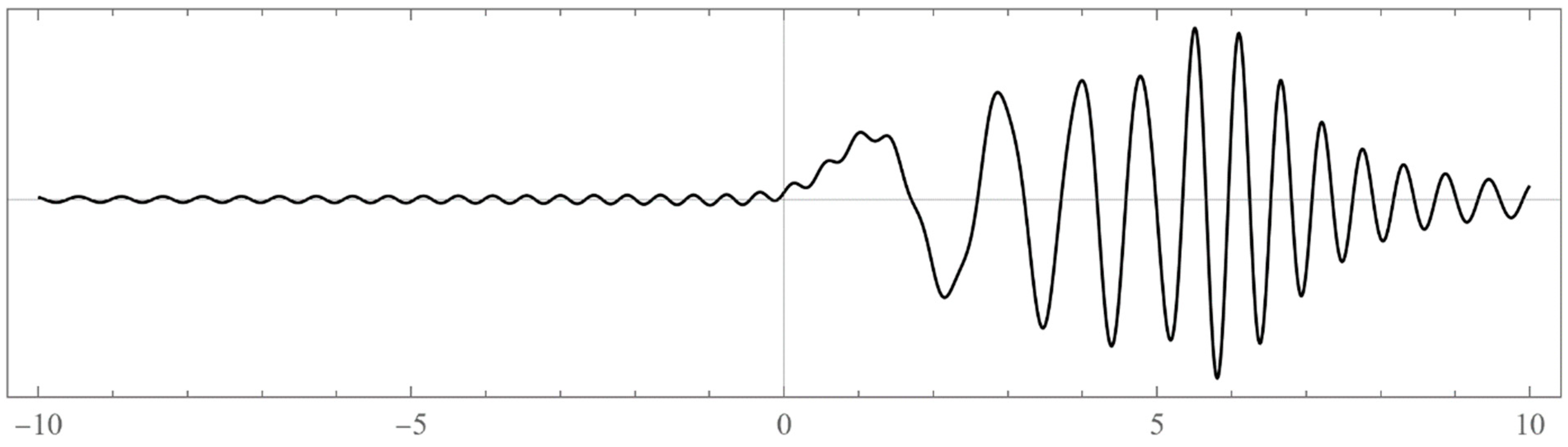
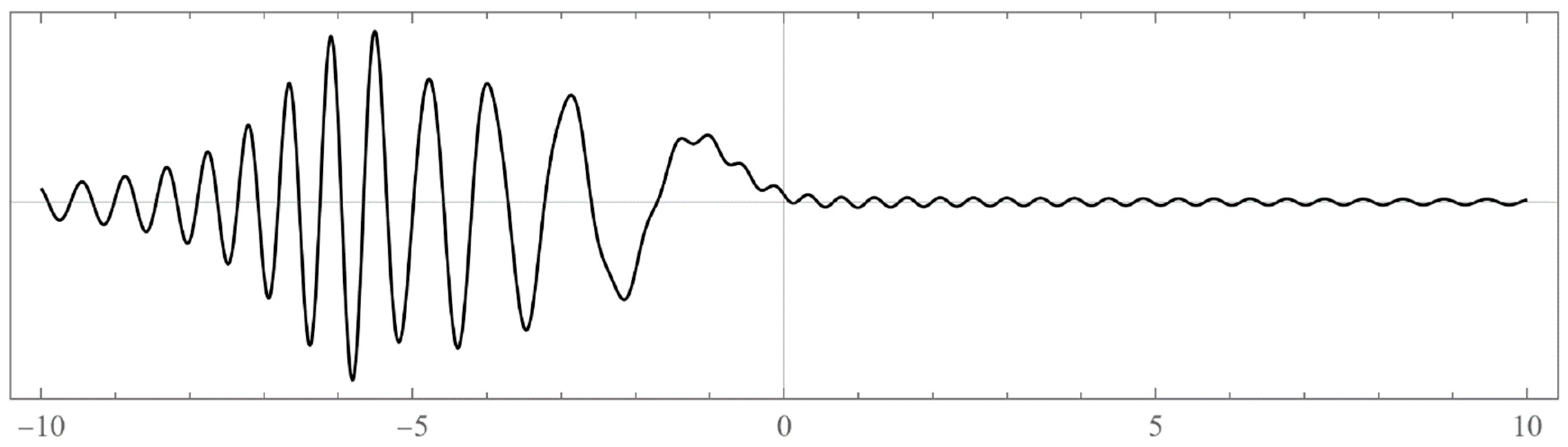
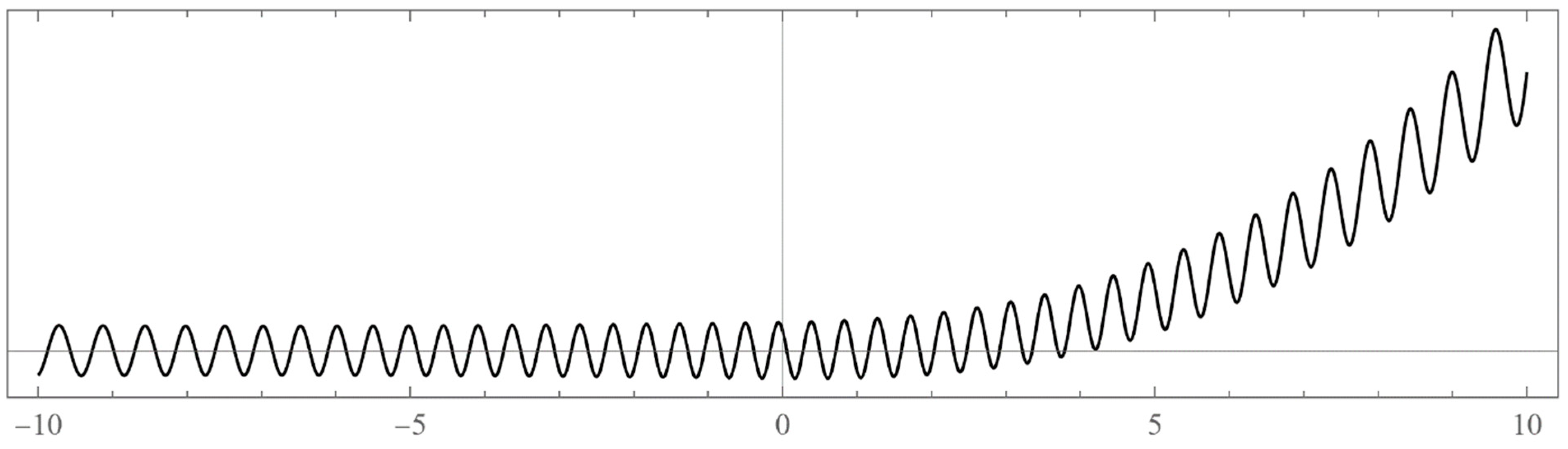
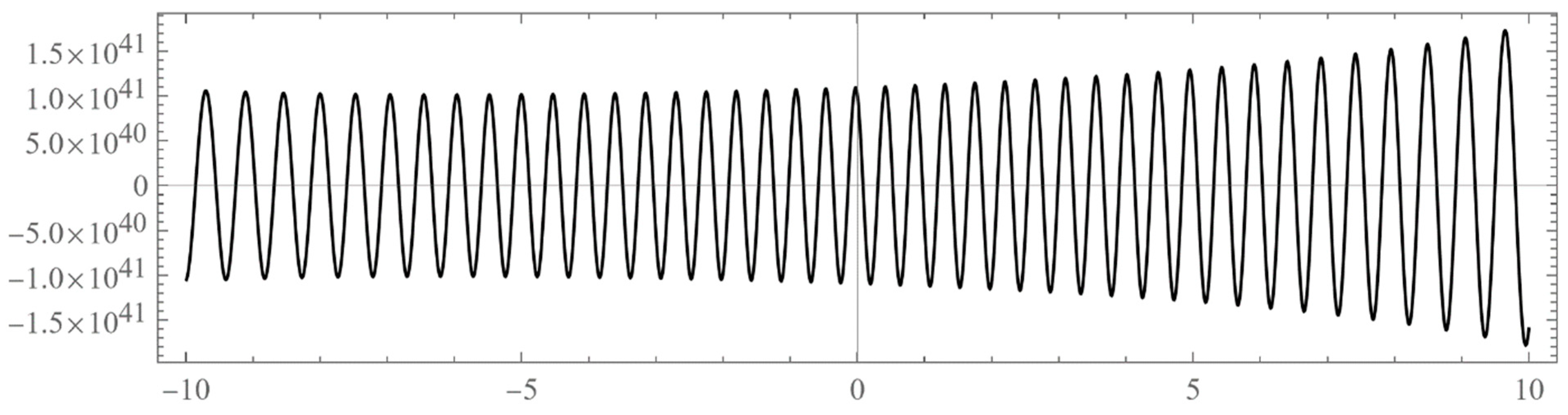
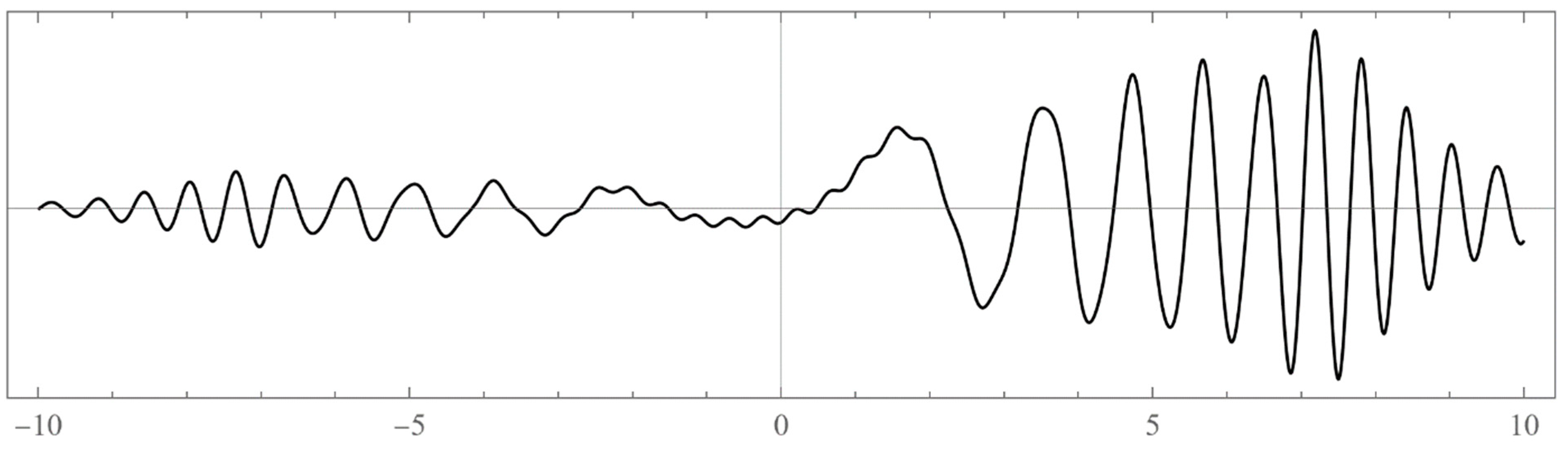
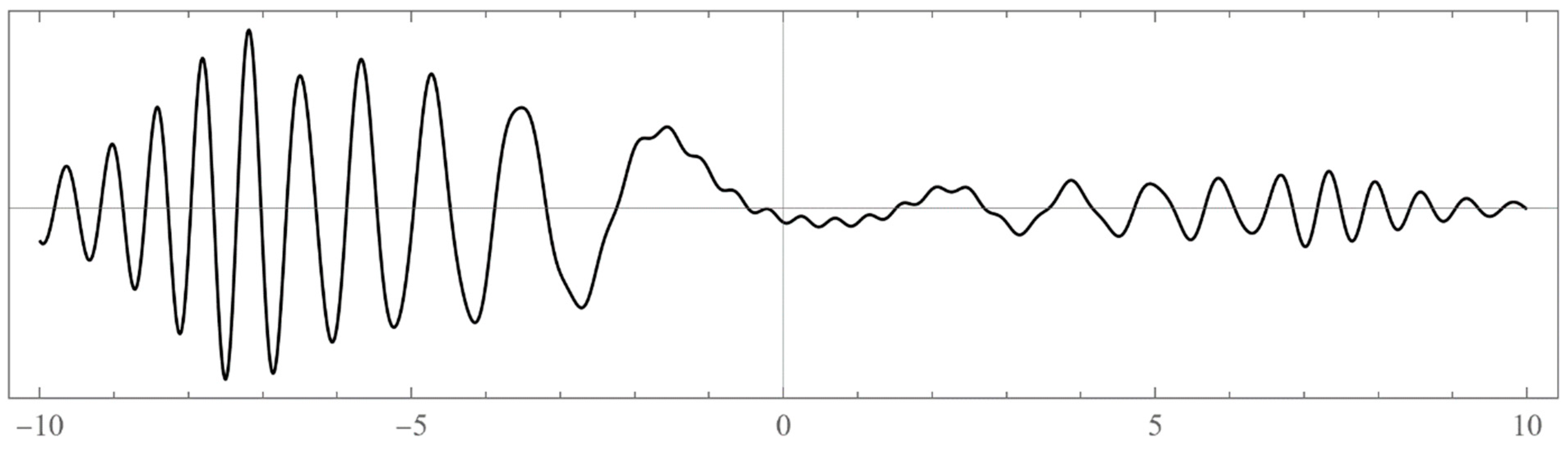
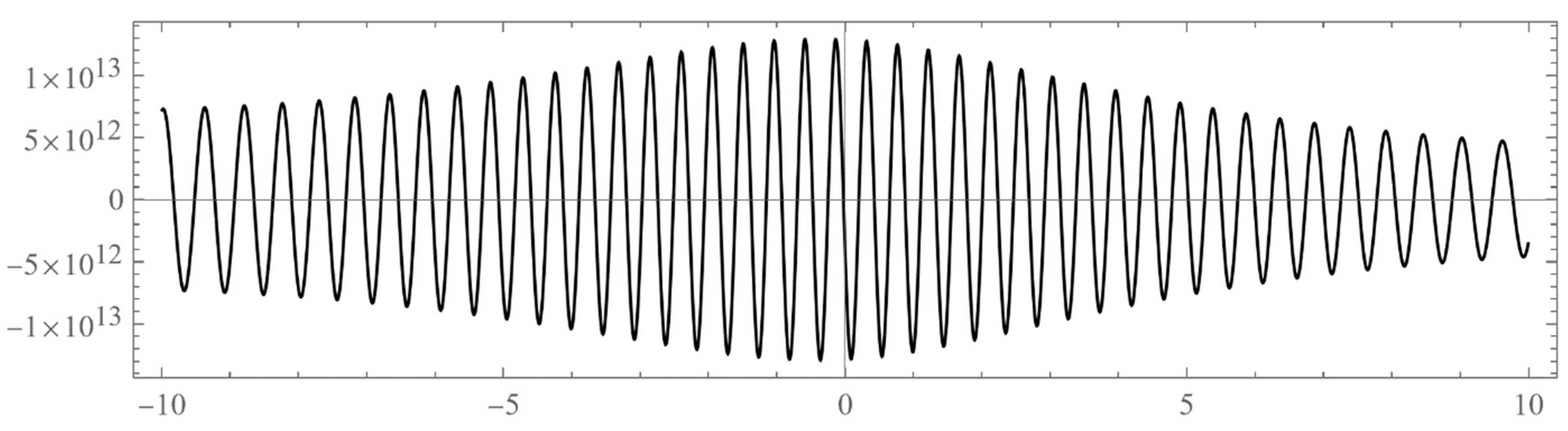
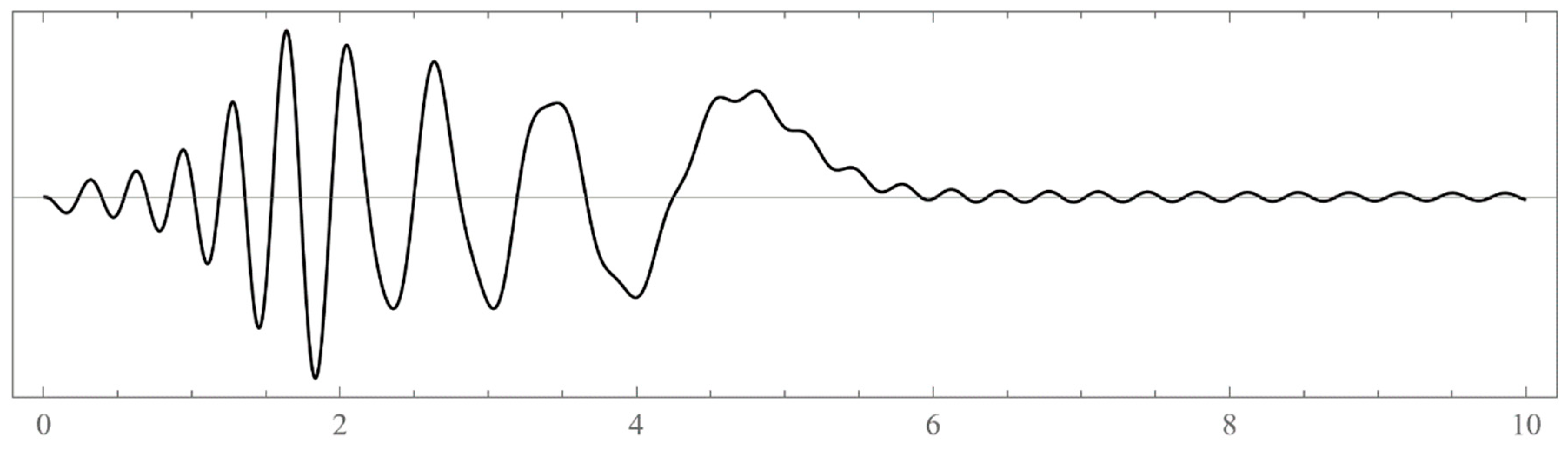
Typically, these asymptotics take the form $P_{n} (E) \to \frac{1}{n^{α} \sqrt{ρ (E)}} \cos [n^{β} φ (E) + δ (E)]$ , where and are positive real parameters, $ρ (E)$ is the weight function, $φ (E)$ is an entire function, and $δ (E)$ is the scattering phase shift. If $β \to 0$ then $n^{β} \to \ln (n)$ . As an illustration, we plot $P_{n} (E)$ as a function of n for a fixed E from within the bands in Problem II and verify the oscillatory behavior of the asymptotics (we take, for example, $E =$ $λ^{2} \{1.9, - 0.5\}$ ). We also show that the asymptotics in fact vanishes at the energy $E = λ^{2} / 2$ .
A. D. Alhaidari, Density of states engineering: normalized energy density of states band structure using the tridiagonal representation approach, Can. J. Phys. 96 (2018) 275-286.
R. Koekoek, P. A. Lesky and R. F. Swarttouw, Hypergeometric Orthogonal Polynomials and Their q-Analogues (Springer, 2010).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Quantum Mechanics Based on Energy Polynomials

Abstract

1. Introduction

2. The energy polynomials

3. Problems in the infinite domain

3.1. Problem I

3.2. Problem II

3.3. Problem III

3.4. Problem IV

4. Problems in the semi-infinite domain

4.1. Problem V

4.2. Problem VI

5. Conclusion

Author Contributions

Funding

Acknowledgements

Conflict of Interest

Appendix: Partial Solutions

References

MDPI Initiatives

Important Links

Subscribe