Prerpints.org logo
Preprint
Article

Separated Model for Stopping Point Prediction of Autoregressive Sequence

Altmetrics

Downloads

119

Views

60

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Machine and Deep Learning

Submitted:

23 January 2023

Posted:

23 January 2023

You are already at the latest version

Alerts
Abstract
While the language model using the stop sign as an independent token has been widely used to decide when the model should stop, it may lead to the growth of vocabulary dimensions and further problems. Similarly, present research on game algorithms usually estimate stopping point related problems based on the evaluation of the winning rate. However, information redundancy may also exist in such models, thus increasing the training difficulty. Above two types of tasks (and similar autoregressive tasks) show a common problem of stopping point prediction. In this paper, we describe a design of separated model, trying to separate the complexity of stopping point prediction from the main task model, so that the information used for estimating stopping point can be reduced. On this basis, in order to verify the rationality of using separated model, we propose a model-free test method. It judges the separability of transformed data based on point difference and sequence difference metrics. In this way, it can predict the credibility of the separated model inference.
Keywords: 
Subject: Computer Science and Mathematics  -   Mathematics
  • CCS Concepts: Computing methodologies • Machine learning • Machine learning approaches • Learning latent representations

1. Introduction

A common problem in autoregressive sequence prediction models is when the model should stop predicting. For example, for language models, continuous backward prediction will make the model generate meaningless repetitive text. At present, the widely used language model [1,2] generally uses the stop sign as an independent token to solve this problem, but this will lead to the growth of vocabulary dimensions, further lead to the increase of the number of model parameters, and make training more difficult. Another example, for the strategy learning of multi round gambling games, researchers can predict the state of the next moment based on the past observation sequence [3]. However, the problem is that the stop condition(stopping point) of the game may not be reflected in the observable sequence: Consider a simple game in which two players take turns drawing in the deck. Each player can choose to compare the total card value in his hand with the other player in any round. The bigger side wins. In this problem, the observable sequence of players is only the cards in their hands. We can predict the expectation of the next card value based on this information (and a priori of the deck), but this model cannot know when we should decide to compete with the opponent. At present, the research on game algorithm generally makes the model predict the winning rate to answer such questions [4,5,6,7]. However, stopping point prediction does not necessarily require all the information of the policy model. Therefore, using the same model to calculate both may also have redundancy in information, which increases the training difficulty. Therefore, for the problem of stopping point prediction in the above two types of tasks (and similar autoregressive tasks), we describe a general model to try to separate the complexity of stopping point prediction from the main task model.

2. Separated Model

Considering the autoregressive model M , at any time step n , we have:
M ( O b s 1 , … … , O b s n ) = O b s n + 1 ′
Where O b s i is the past observation value and O b s i ′ is the prediction value.
If we know the stop condition (e.g. stop at O b s i < c ), a perfect autoregressive prediction model can simultaneously calculate whether the next time step will stop. At this time, the model does not need to introduce additional complexity to calculate stopping points. However, in most cases, the stop condition depends on the sequence of past observations:
S C ( O b s 1 , … … , O b s n ) = i s S t o p n + 1   ( 1   o r   0 )
If we can determine based on prior information that M and S C calculate results based on the same information (both are based on the same hidden representation inference). Then, for the approximation of M , we can use double output:
M ′ ( O b s 1 , … … , O b s n ) = O b s n + 1 ′   ,   i s S t o p n + 1
However, for many tasks, it is easier to judge the stop condition than to predict the next value. For example, we know a priori that S C only depends on a transformation T of O b s sequence:
S C ( T ( O b s 1 , … … , O b s n ) ) = i s S t o p n + 1
At this point, we need to compare the complexity of model (3) and model (4). For example, if the number of parameters (used to approximate functions) of M ′ is far greater than the sum of S C and T . Then we have reason to think that it is better to separate S C from M ′ in estimation. Otherwise, many redundant information is used to estimate i s S t o p n + 1 , which will make training M ′ more difficult.
In this separated model, T can be regarded as a sequence encoder and S C as a classifier. At this point, the whole autoregressive prediction algorithm will become:
1.
While  S C ( T ( O b s 1 ′ , … … , O b s n ′ ) ) = 0
2.
n ← n + 1
3.
O b s n ′ ← M ( O b s 1 ′ , … … , O b s n − 1 ′ )

3. Verifying Separable

If we want to use the separated model, we need to verify whether M ′ is separable. That is, whether T ( O b s 1 , … … , O b s n ) can provide enough information to infer i s S t o p n + 1 . The sufficient condition for this proposition is that sequence T ( O b s 1 , … … , O b s n ) is autocorrelated, because the requirement for judging stopping point is weaker than prediction. Predictable sequences must be separable. The sequences we are facing may have complex patterns. To verify this sufficient condition, we need to carry out autocorrelation tests on sequences with nonlinear features. Previous work on sequence nonlinear autocorrelation test is mainly focused on testing whether the residuals of regression models are autocorrelated. "Nonlinear" describes the property of regression models. The classic Durbin-Wattson statistic only proves that residuals without autocorrelation under linear regression models present asymptotic normal distributions. It's generalization to nonlinear models may yield invalid conclusions [8], and it can only judge the first-order autocorrelation. Improvement from Barndorff [9] makes such models have faster asymptotic convergence speed. Fraser et al. [10] estimate the ancillary statistic in Barndorfff's method directly based on the data in regression models, making it easier to solve. Nguimkeu et al. [11] extend above methods to nonlinear. The third-order convergence technique of [9,10] has greatly improved its performance on small samples compared with the original Durbin-Wattson test. However, this method still only aims at first-order autocorrelated residuals. Although it is feasible to deduce for autocorrelation hypothesis tests with different lagged terms, such a case-by-case method cannot cope with various complex sequence patterns we are faced with. Besides, our purpose of verifying separability is to verify whether separation method is feasible on current data. At this time, we do not have a specific model, so we need a model-free method. Above two points mean that most of hypotheses of classical statistical tests are not applicable to this problem.
We consider the null hypothesis of the original proposition: only based on the information provided by the observed sequence, the value of the next time step cannot be classified into two categories (that is, whether it is a stopping point). This is equivalent to judging the overall prediction credibility of the separated model S C ( T ( · ) ) . The overall prediction credibility can be estimated based on multiple single prediction credibility samples. Then we need to construct statistics to measure credibility.
Obviously, if any case in positive cases is sufficiently different from the most similar case in negative cases, the training algorithm has the ability to obtain an effective classifier. Therefore, we measure credibility based on sequence difference. We firstly define point difference in sequences. Point difference calculates the difference between two sequence values:
P o i n t D i f f ( s i , s j ) = | s i − s j | − I
Where I is the difference size boundary that we expect S C ( T ( · ) ) can recognize. The larger the | s i − s j | is compared to I , the easier the difference is to be captured by the classifier. Otherwise, the difference is more difficult to be recognized.
Then, if there are sequences S 1 and S 2 :
S 1 = s 1,1 ,   … … ,   s 1 , n
S 2 = s 2,1 ,   … … ,   s 2 , n
The difference sequence is defined as:
S 1 − S 2 = P o i n t D i f f ( s 1,1 , s 2,1 ) ,   … … ,   P o i n t D i f f ( s 1 , n , s 2 , n )
Then sequence difference can be defined as:
S e q D i f f ( S 1 , S 2 ) = m a x ( S 1 − S 2 )
Taking m a x means that we consider the most recognizable difference between S 1 and S 2 . Because even if most of the values in two sequences are the same, the difference of only one value is enough for the classifier to recognize the difference between the two.
For each case in the positive cases, we can calculate a sequence difference value. These values are the samples on the credibility distribution. Based on these samples, we can obtain the characteristics of the credibility distribution and judge the original proposition. For example, compare the current data distribution with data distribution that determines can support interference. Decide whether to reject or accept the zero hypothesis according to whether there is significant difference.

4. Implementation

The next question is what kind of prototype to use to estimate S C and T . Since S C is a sequence encoder, a recurrent neural network can be used as the prototype. T classify the encoded data, which should be calculated output using sigmoid full connection layer or softmax.
It should be noted that simple neural network library (such as Keras) requires that all samples have the same shape. This means that we must define a fixed time window length (although RNN unit has the ability to encode sequences of different lengths). We suggest using the stopping time expectation of the autoregressive process as the window size. In addition, when the current observations are insufficient, the remaining positions of the time window need to be filled with values. If you want to set a token for the filling value, you need to seriously consider whether the separated model is useful for you. Because one of the reasons for using the separated model is that the introduction of stop marked tokens in the main task model will cause additional complexity. If you still use additional tokens in the separated model, you need to carefully consider the number of parameters to confirm the usefulness of the separated model. If your observation sequence is a continuous value (filling token cannot be set independently), we suggest using the value closest to white noise (such as average, mode) as the filling value.
If you can, you'd better use the neural network library that supports dynamic shape input, so that you can have a variable length time window and no longer need to fill in data.
In addition, in the training process, it should be noted that since the stopping time of most such tasks is greater than 1, most of the training samples generated will be negative (indicating that the next time step is not stopped). This is a problem of unbalanced data classification, so we should focus on recall metrics.

5. Experiment

We will illustrate the role of the separated model with a practical task. Liu et al. [12] analyzed the upper bound that an algorithm that uses only BM25 [13] as a feature may reach on reading comprehension tasks. However, to make the actual algorithm approximate this upper bound, it is necessary to accurately determine a threshold t for each (Document, Query) pair's BM25 sequence, and then discard all paragraphs whose BM25 value is less than. We can regard this process as the problem of stopping point prediction for BM25 sequence. As mentioned above, the separated model for stopping point prediction of the BM25 sequence decomposes the reading comprehension task into two steps: "calculating the BM25 value of each paragraph (sentence)" and "extracting answers based on the BM25 sequence". This makes it unnecessary to modify the BM25 algorithm itself to meet our needs.

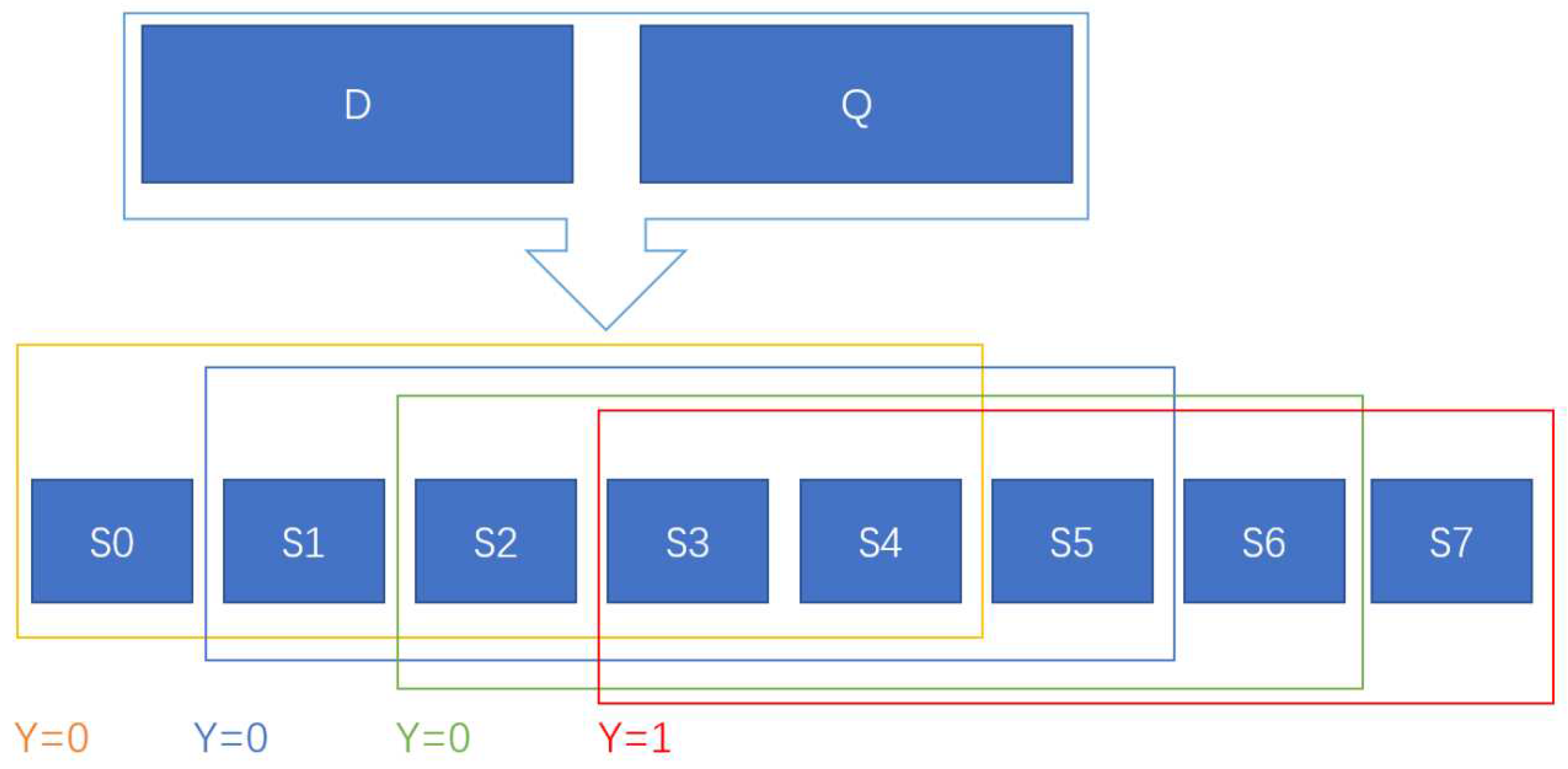
5.1. Generate Data

This experiment is based on the reading comprehension dataset of Baidu SIT [14]. The dataset mainly includes three attributes: D (document), Q (query) and A (groundtruth answer). For each D , the BM25 value of every sentence can be calculated jointly with Q after sentence segmentation. Then we can get BM25 sequences. Because the length of each BM25 sequence in this dataset is relatively uniform, we use fixed input shape. That is, use a sliding window with length w = 5 to generate l + 1 − w training data for each BM25 sequence with a length of l . If data is the last data at the end of the sequence, its corresponding y t r u e = 1 , otherwise y t r u e = 0 . Because the BM25 value of most sentences is 0, we set the empty position to 0 when l < w . The overall process is shown in Figure 1.

5.2. Verifying Separable on Data

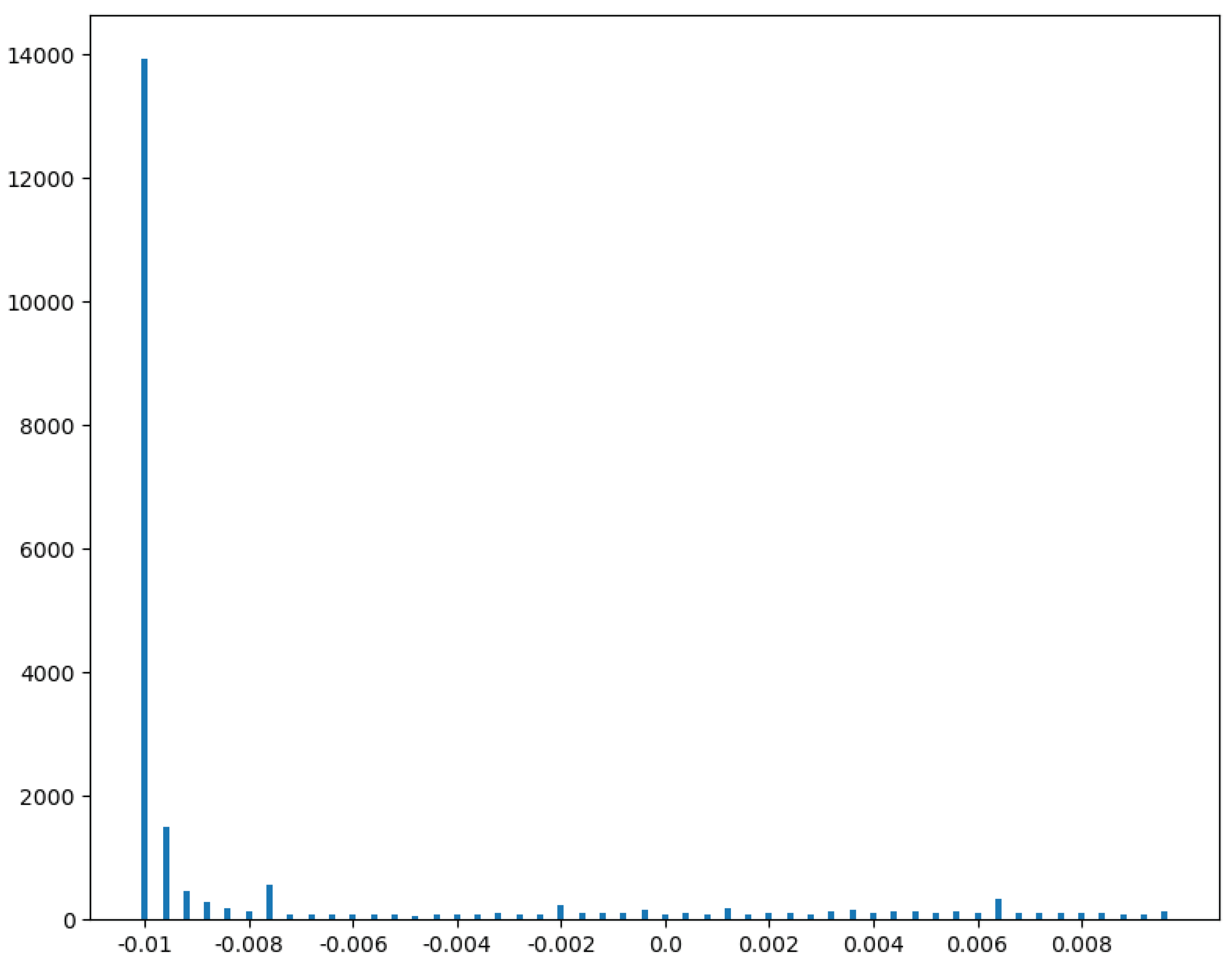
After using the method in the previous section to generate data, we use the method in Chapter 3 to conduct a separate test for the data [15]. The positive value accounts for 41.3%, and the distribution is relatively uniform; Negative values account for 58.7%, and there are sub-intervals with prominent distribution. Further, we select the range of -0.01~0.01 with more samples. The distribution of this interval is shown in Figure 2.
The range of -0.01~-0.0076 accounts for 78.1% in the range of -0.01~0.01. The sequence difference in this interval represents that the difference between the two sequences is very small, so it is difficult to classify. Value equal to -0.01 accounts for 20.9% of the total. The sequence difference is exactly equal to this value, which means that the difference between the two sequences is completely unrecognizable. This means that even if the model can distinguish the smallest difference, the recall on this data will not be higher than 79.1%.

5.3. Train

Although the separable test proves that 20.9% of the positive cases of the data cannot be separated from the negative cases, we still try to fit the data to get a preliminary observation of the training difficulty and calculation cost of the separated model. The network architecture we use is shown in Table 1.
We first trained 64 epochs with learning rate=0.007, took the checkpoint model with the highest recall value (recall=0.6 at this time), and then trained with a learning rate=1e-5. After 11 epochs, the final model was obtained: recall=0.751, accuracy=0.851.

6. Conclusion

In this paper, we describe the general idea of the separated model. On this basis, we propose a test method of verifying separable on a model-free way. We test the BM25 sequence of the STI reading comprehension dataset. In order to give preliminary observation to the training difficulty and calculation cost of the separated model, we trained a neural network model. Its recall is close to the estimated result of the separable test, which illustrates that this test method is effective. This also shows only the BM25 sequence cannot provide sufficient information for the reading comprehension task on the STI dataset, so other features need to be introduced.

References

  1. Brown T B, Mann B, Ryder N, et al. Language Models are Few-Shot Learners[C] // Proceedings of 2020 Neural Information Processing Systems. Cambridge: Harvard Press. 2020, arXiv:2005.14165.
  2. Devlin J, Chang M W, Lee K, et al. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. arXiv 2018, arXiv:1810.04805.
  3. Mealing R, Shapiro J L. Opponent Modelling by Expectation-Maximisation and Sequence Prediction in Simplified Poker. IEEE Transactions on Computational Intelligence & Ai in Games 2017, 9, 11–24. [CrossRef]
  4. Li, K. et al. (2021). MOBA Game Analysis System Based on Neural Networks[C] // Web Information Systems Engineering(WISE 2021). Lecture Notes in Computer Science, vol 13081. Springer, Cham. [CrossRef]
  5. Donghyeon Lee; Man-Je Kim; Chang Wook Ahn. Predicting combat outcomes and optimizing armies in StarCraft II by deep learning[J]. Expert Systems With Applications 2021, 185, 115592. [CrossRef]
  6. Chuang T L, Shao S H, Hsu C J, et al. Winning Prediction in WoW Strategy Game Using Evolutionary Learning[C] // International Symposium on Computer. IEEE, 2014.
  7. Lokhande R, Chawan P M. Live Cricket Score and Winning Prediction[J]. International Journal of Trend in Research and Development, 2018, Volume 5(1).
  8. White K J. The Durbin-Watson Test for Autocorrelation in Nonlinear Models. The Review of Economics and Statistics, 1992, 74.
  9. Chesher A. Modified signed log likelihood ratio. Biometrika 1991, 78, 557–563. [CrossRef]
  10. Fraser D, Reid N. Ancillaries and Third Order Significance[J]. Utilitas Mathematica, 1999, 47, 33–53.
  11. Nguimkeu P E, Rekkas M. Third-order inference for autocorrelation in nonlinear regression models. Fuel and Energy Abstracts 2011, 141, 3413–3425. [CrossRef]
  12. Liu T, Xiong Q, Zhang S. When to Use Large Language Model: Upper Bound Analysis of BM25 Algorithms in Reading Comprehension Task. Preprints 2023, 2023010219. [CrossRef]
  13. Robertson S, Zaragoza H. The Probabilistic Relevance Framework: BM25 and Beyond. Foundations & Trends in Information Retrieval 2009, 3, 333–389.
  14. Baidu AI Studio. Baidu Search Technology Innovation Challenge 2022[EB/OL]. December 6, 2022. Available online: http://sti.baidu.com/.
  15. Liu T, Xiong Q, Zhang S. STI BM25 Sequence Dataset[Dataset]. figshare. 2023. [CrossRef]
Preprints 67746 g001
Figure 1. Data Generation Process.
Figure 1. Data Generation Process.
Preprints 67746 g001
Preprints 67746 g002
Figure 2. Distribution of Interval -0.01~0.01 in Sequence Differences.
Figure 2. Distribution of Interval -0.01~0.01 in Sequence Differences.
Preprints 67746 g002
Table 1. Network Architecture.
Table 1. Network Architecture.
Layer Number of nodes Activation Note
GRU 3 Input shape=(5,1)
Dense 128 ReLU Dropout=0.8
Dense 128 tanh Dropout=0.8
Dense 128 ReLU
Dense 128 ReLU Dropout=0.8
Dense 128 tanh Dropout=0.8
Dense 1 Sigmoid
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated