WEA: A Node Importance Algorithm in Weighted Networks

1. Introduction

Network relationships exist in many complex systems, which involve all aspects of human social activities. For instance, power networks [1], social networks [2,3,4], and epidemic spread networks [5,6]. The notion of the network is widely used to depict the complex relationships between different entities [7], and the topology characteristics often play an essential role in network information mining. For a long time, researchers have focused on the research of unweighted networks, such as the node importance [7,8], the edge importance [9], and the link prediction based on it [10,11]. While, the issue of the node importance is essentially basic, and some algorithms to measure the importance of the nodes are proposed based on the network's primary topology feature. For instance, Degree Centrality is a classic, simple, and effective algorithm for unweighted networks, directly measuring the number of neighbors for each node to calculate its importance; The K-core Centrality (KC) [12] is proposed to suggest that a node’s topological location contributes more to its node importance than its first-order neighbor, and it often gets good performance in random network and scale-free network (but poor in small world network). Most of these first proposed ones are generally aimed at unweighted networks.

However, in reality, it is evident that a weighted network always carries more abundant information and is more capable of describing various complex systems [7,13]. For instance, in a traffic network, where edges represent roads and nodes represent intersections, the importance of nodes can be counted by analyzing the traffic flow as edge weight which can finally boost the traffic resource optimization [14]; On social networks, for example where weight represents the time of interactions between two nodes, adding the weighted information into account can better understand the networks’ topological functions and the evolution of a society [15,16]; Setting trade volume as weight in a large-scale economic network makes it possible to reveal the high economic potential nodes and helps the analysis of the stability and robustness of an economic system [17]; Also, the weight notion is essential in the study and application of the identification of the protein complex [18]. Many other weighted networks are being studied, like the PPI network [19], the power grid network [20,21], and the citation network [22,23]. It indicates that the direction of weighted node importance contemporarily is pretty basic.

Generally, from the perspective of complex network construction, existing methods can be classified into four categories: Neighborhood-based methods, Path-based methods, Location-based methods, and Iterative refinement-based methods, respectively. Of course, the combinatorial ones consist of two or several of these four, and those types always have high time complexity. Concisely, we primarily discuss the four basic ones. The representative earliest method based on neighborhood is Degree Centrality (DC) which performs well in studying network vulnerability on scale-free network and exponential network. However, being judged too simple since the original DC only uses a few topology information. Its weighted version then be widely used, the Node strength (Weighted Degree Centrality, WD), mainly stems from the conclusion that in the study of real networks, the degree is always correlated with Node strength [24]. Then, innumerable algorithms belonging to this category emerged, including the well-known H-index. However, H-index can hardly suit undirected weighted networks. In a recent study, Gao et al. improved H-Index and proposed another (HI) [25] that can apply to undirected networks. As for the Path-based methods, Betweenness Centrality (BT) [26] and Closeness Centrality (CL) [27] are the most classical ones, and they can well suit weighted networks. BT measures how much the shortest path goes through a node to show its hub function to control the information flow where the distribution has a power law. It performs well in scale-free networks. CL measures all the distance from the observed node to any other ones in the network to show an average propagation length of the information in the network. Still, owing to its feature, BT tends to miss the information of node importance that is not in the defined path, and some information in the defined path will be over-emphasized in computing. Location-based methods argue that the node located in the core will have much more spreading ability than the nodes in the periphery [7]. After the proposal of the unweighted K-core, many improved versions have emerged. An impressive one can be W-Core decomposition (WC) [28], which decomposes the calculation of node importance into two factors, degree strength and node strength, through a small number of adjustable parameters. Similar to WC, Marius Eidsaa et al. proposed S-Core decomposition (SC) [29], where the nearest integer to the node strength is recorded to be the importance score every time and then considered to be its core number. These two algorithms, based on KC, can well collect the edge weight contribution to the importance of its linked nodes. Nevertheless, whatever the KC, WC, or SC, they have two drawbacks: One is the careless classification mainly because usually, a considerable number of nodes belonging to the same core will be considered at the same importance score; Another, these three perform poorly in Barabasi Albert (BA) networks and tree-like networks, where the core values of all nodes are minimal and indistinguishable [7]. A very typical iterative refinement-based method is Eigenvector Centrality (EC) [30]. Algorithms in this class usually can fully consider the information of multi-order neighbors. While different from the previous ones, they reach a steady state after iterative computing and output the sorting results. Due to too much iteration, practically, it makes EC kindred algorithms inefficient.

Although many algorithms, including EC, WC, and SC, can be applied to unweighted and weighted networks, the parameters of these algorithms need to be manually assigned by pre-estimation. Furthermore, some could not reach accurate outcomes. HI aimed to solve that problem to gain better convergence and stronger robustness. Nonetheless, it becomes more time-consuming, even if it is more capable of accurately evaluating node importance. In some situations, some algorithms based on corresponding methods can ensure the sorting an excellent accuracy, such as HI, but inevitably make themselves more time-consuming.

To the best of our knowledge, until current days, few works have considered the negative weight contribution to the node importance, whereas widely exist in reality and need a framework to quantify the calculation.

Table 1. Different types of centrality Algorithms.

Classification	Representative Ones	Advantages	Disadvantages
Neighborhood-based methods	Degree Centrality	Easy to calculate	Accounting less information
	HI (improved H-Index)	Excellent accuracy	High time complexity
Path-based methods	Betweenness Centrality	Accurate in in scale-free networks	Relatively high time complexity, Only focus on the path nodes information
	Closeness Centrality	More information to support accuracy	Relatively high time complexity
Location-based methods	K-Core	Some types of networks can be well evaluated	Without weight information, poor performance in BA network and tree-like networks
	W-Core	Moderate accuracy	Need parameters, poor performance in BA network and tree-like networks
	S-Core	Moderate accuracy	Need parameters, poor performance in BA network and tree-like networks
Iterative refinement-based methods	Eigenvector Centrality	Fully consider multi-order neighbor information	Need parameters, inefficient for conducting

Table 1. Different types of centrality Algorithms.

Classification	Representative Ones	Advantages	Disadvantages
Neighborhood-based methods	Degree Centrality	Easy to calculate	Accounting less information
	HI (improved H-Index)	Excellent accuracy	High time complexity
Path-based methods	Betweenness Centrality	Accurate in in scale-free networks	Relatively high time complexity, Only focus on the path nodes information
	Closeness Centrality	More information to support accuracy	Relatively high time complexity
Location-based methods	K-Core	Some types of networks can be well evaluated	Without weight information, poor performance in BA network and tree-like networks
	W-Core	Moderate accuracy	Need parameters, poor performance in BA network and tree-like networks
	S-Core	Moderate accuracy	Need parameters, poor performance in BA network and tree-like networks
Iterative refinement-based methods	Eigenvector Centrality	Fully consider multi-order neighbor information	Need parameters, inefficient for conducting

To sum up, the mentioned above have achieved some satisfactory outcomes in some aspects, but they also have inherent limitations [31,32]. On the one hand, almost all existing algorithms do not consider whether the weights are positive or negative for the connection strength of the nodes. That means there is an absence of a unified framework to define the positive/negative contribution from the weight to the node importance (the weight issue), which over simplified the network situation in the real world [7]. On the other hand, a dilemma is that accuracy and time complexity are incompatible for most node importance algorithms. The computational complexity makes applying these algorithms a daunting task, which leads to some tasks for large-scale networks not being conducted well [7].

An instance can well illustrate the ‘weight problem’: In the global Covid-19 transmission networks, nodes always represent cities or places. If the weight represents the number of airline seats between two cities, it implies the weight is positively related to the importance of the linked nodes. In comparison, if the weight represents the airline distance between two cities, the weight is negatively connected to the nodes. Until now, few works have considered the negative weight contribution to the node importance, whereas it widely exists in reality. Regarding the second issue, one method is Dynamic programming (DP), which can significantly reduce the time complexity of computations with specific characteristics (with its development in topology). Therefore, we may appropriately solve the second issue by appealing to a design that DP optimizes.

In response to the second issue, we need a brief description of Dynamic programming mechanism. DP is often used to solve optimization problems, such as the shortest path problem and the 0-1 knapsack problem. Moreover, NP-Hard problems are usually involved in 'optimal ' issues as they often have many possible solutions and are inclined to be addressed by DP. Generally, if DP can optimize an algorithm, it should possess two main features: The optimality of substructure and the repeatability of subproblems. The optimality of the substructure means the optimal solution to the original problem can be derived from the optimal solution to its subproblems. The repeatability of subproblems means that during the process of tackling subproblems, even though the decision sequences differ, they produce repetitive states when reaching the same stage. Similar to the divide-and-conquer method, an original problem is decomposed in DP, and the subproblems are firstly solved. Then the solution to the original problem is obtained from the solution to these subproblems. In other perspectives, DP is to save every step outcome of the subproblems in each iteration and then make better use of these outcomes for the coming computing for the original problem.

Inspired by the above mentions, this paper proposed a Weighted Expectation Algorithm (WEA), which well solved the ‘weight problem’. Meanwhile, it can guarantee an accurate calculation with a low time complexity for each node importance score of the network. Experiments on connectivity and the SIR propagation model show that WEA outperforms in accuracy, and the time-consuming testing shows it possesses a high efficiency. Since adopting the idea of Dynamic programming, the time complexity of WEA is O(d_maxE_GN), where E_G is the total edge numbers, N is the total node numbers and d_max is the maximum degree of the network nodes.

2. Methodology

To better measure the node importance of weighted networks, the influence from weights always needs to be considered based on topology structure and the value [33]. For instance, WC considers both the influence of weights and degrees. We refer to the notion of possible world semantics in the uncertainty graph domain, proposing a possibility importance score factor. The information carried by the weight and its contribution to the node importance is defined as the score of the node under different degree possibilities. A node final importance score is obtained by calculating the set of all the scores in different degree possibilities.

WEA is relatively simple and efficient, which can be divided into three steps: (1). According to the node connected to strength with the weights’ meaning, the weights are pre-processed specifically; (2). The node score Pr (be elaborated in the following) to its importance score factor is calculated through Dynamic programming under all of its degree possibilities; (3). Similar to expectation calculating, a cumulative calculation of Pr scores extract the node’s final importance score.

2.1. Preliminaries

Problem definition. Given a network H(V,E,W), typically a weighted one, where V is node set, E is edge set, and the element e_ij in E represents the edge between node i and node j. The weight value is W_ij. W denotes the weight matrix where the minimum and maximum values are represented by w_min and w_max, respectively. The aim is to produce a set P ranked by the node importance scores, which contains all the nodes in the largest connected subgraph of H without any duplication.

Quantitative definition for the positive/negative weight. We set a ‘bridge’ (2.2 Equation (4)) for positive and negative contribution weight values. In absolute value, the increase in the positive contribution value to the node importance corresponds to the rise in the negative contribution value, but the sign of the contribution is the opposite.

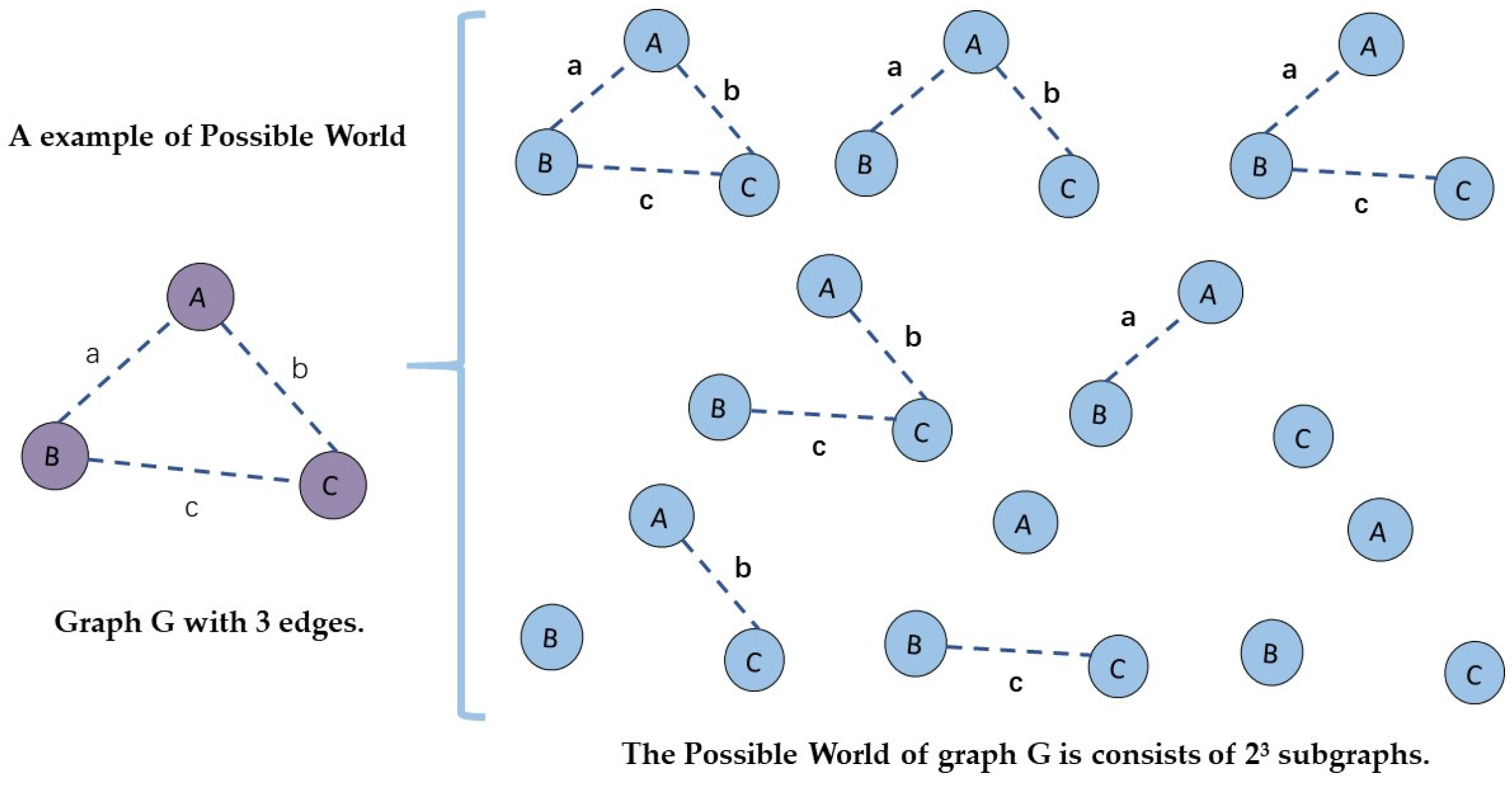
Possible World Semantics. Possible World Semantics (Pr equation) is redefining the contribution of the weighted edges in calculating node importance. Possible World Semantics interprets probability data as a set of deterministic instances called possible worlds, each associated with the probability that can be observed in the real world. Therefore, an uncertain network with t edges can be considered a set of 2^t possible deterministic networks.

Figure 1. An example of possible world: A graph with 3 edges.

Figure 1. An example of possible world: A graph with 3 edges.

Given a target graph G(V,E,W), its subgraph G′(V′,E′,W′) consists of node set V′, edge set E′ and weight set W′, where $E\prime \subseteq E$, $V\prime \subseteq V$ and $W\prime \subseteq W$. Use Pr(G′) to denote the probabilities of graph G′(V′,E′,W′), the equation is [34,35,36]:

$$\mathrm{Pr}\left(G^{\prime }\right)={\displaystyle \prod }_{ϵ\in E^{\prime }}{w}_{ij}^{\prime }{\displaystyle \prod }_{e\in E/E^{\prime }}\left(1-w_{ij}^{\prime }\right)$$

(1)

The degree of node i in graph G′ be noted as deg(i, G′), abbreviated as deg(i), and $c\in (1,2,\dots ,deg(i))$ is a corresponding factor, called possible importance score in this paper. Thus, we got the following equation [34,35,36]:

$$\mathrm{Pr}[deg(i,G″)\ge c]={\displaystyle \sum _{G_i\prime \in {G_i^{″}}^{\ge c}}\mathrm{Pr}(G_i\prime )}$$

(2)

where G_i’ represents any one of the collection of all the possible subgraphs that belong to graph G_i″ (Where i has a degree no less than the inter c). In this paper, we defined any G_i″ could only be made up of one form in this two: First, only consists of node i; Second, consist of node i and some or all of its first-order neighbor nodes [9] and the normalized weight links that between them. The ${G_i^{″}}^{\ge c}$ means $\{G_i\prime \subseteq G_i″|\mathrm{deg}(i,G\prime )\ge c\}$.

Dynamic programming (DP). DP is a method to solve certain types of sequential decision problems (if DP can solve). The original problem f₀ is its aim and a sequence F with a finite number of elements, say F=(f₁,f₂,f₃…), including all the subproblems that sever the original problem.

2.2. Pre-Processing of the Edge Weights

Below is a standard normalized W:

$$w_{ij}^{\prime }=\frac{w_{ij}-w_{min}}{w_{max}-w_{min}}$$

(3)

Note that the value of $w_{ij}^{\prime }$ falls in [0, 1] rather than (0, 1). To avoid the $w_{ij}^{\prime }$ value sitting on the boundary (the value of 0 or 1 caused by $w_{ij}=w_{min}$ or $w_{ij}=w_{max}$), we modify Equation (3) by adding an adaptive parameter l to ensure that $w_{ij}^{\prime }\in (0,1)$. In addition, it is worth noticing that the edge weight could positively or negatively contribute to a node’s importance when given different networks. Therefore, we designed the following normalization equation:

$$\left\{\begin{array}{l}{w}_{ij}^{\prime }=\frac{w_{ij}-(w_{\min }-l)}{(w_{\max }+l)-(w_{\min }-l)}=\frac{w_{ij}-w_{\min }+l}{w_{\max }-w_{\min }+2l},\hspace{1em}\hspace{1em}{w}_{ij\sim C_i}\hfill \\ w_{ij}^{\prime }=\frac{w_{ij}-(w_{\min }-l)}{(w_{\max }+l)-(w_{\min }-l)}=1-\frac{w_{ij}-w_{\min }+l}{w_{\max }-w_{\min }+2l},\hspace{1em}\hspace{1em}{w}_{ij}\sim 1/C_i\hfill \end{array}\right.$$

(4)

Where $w_{ij}^{\prime }$ is the weight of the observed edge. $w_{max}$ and $w_{min}$ are the maximum and minimum values of edge weight in the weighted network H respectively; Set l as an adaptive constant which makes no influence on the result as it is a normalization tool, and for concision, we set it as the average value of edge weights $l=\frac{{\displaystyle \sum _l^{N_G}w}}{E_G}$, where E_G is the total number of edges of the target network H. $N_G^i$ is the number of the node i’s neighbors; C_i is the importance score of node i; The ~ represents a positive correlation.

Thus, after normalization is accomplished by Equation (4), the larger the weight is, the closer to 1 it is, and vice versa, but it will never touch the boundary.

2.3. Dynamic Programming for the Node Importance Calculation

Theoretically, the results of Equation (4) will be used in Equations (1) and (2) for calculating $\mathrm{Pr}[deg(i,G″)\ge c]$. Accounting for this process is highly time-consuming, especially in large-scale network computing. It is now handled with the help of the DP by a combination process of Equations (5)–(8) [34,35]:

$$X(p,q)=w_{ij}X(p-1,q-1)+(1-w_{ij})X(p-1,q)$$

(5)

Let p and q be two integers, where $p\in (0,1,2,\dots ,deg(i))$,$q\in (0,1,2,\dots ,p)$, and p≥q; E(i)={e₁,e₂,e₃,…,e_deg(i)} is a set of consisting all the edges that connected to node i; notably, the operation between set A and set B: A\B represents taking complement of set B in set A. And let E’(i) be a subset of E(i), where $E^{\prime }(i)\subseteq E(i)$; deg(i|E’(i)) is the defined degree of node i in subset G’(V,E\(E(i)\E’(i))). Equation X(p,q)=Pr[deg(|{e₁,e₂,…,e_p})=q] means, given the ordered edge set $\{e_1,e_2,\dots ,e_{deg(i)}\}$, when node i’s degree equals q, the probability score of node i is Pr[deg(i)]=q. Under this definition, with integer q meets each $q\in [0,p]$, we can take p through each of the integer values in the natural number set [0,deg(i)], and, for any node i with a degree t in graph G_i′(has 2^t subgraphs, recorded in set G_i′’), this can realize a traversal for all the scores of the subgraphs in the possible world G_i′’ by each inside traversal on all of its corresponding linked degrees for all of the linked degrees’ possibilities. This traversal process can be seen as the nested ‘for‘ loops in coding.

Function X is a definition for DP in case it meets the boundary conditions, which is also indispensable for the calculation [34,35]:

$$\left\{\begin{array}{l}X(0,0)=1\hfill \\ X(p,-1)=0,\hspace{1em}\forall p\in [0,\hspace{1em}deg(i)];\hfill \\ X(p,q)=0,\hspace{1em}\forall p\in [0,\hspace{1em}deg(i)],\hspace{1em}q\in [p+1,c];\hfill \end{array}\right.$$

(6)

Once let $\mathrm{Pr}(deg(i)=c)={\displaystyle \sum _{q=0}^{\mathrm{deg}(i)}X(deg(i),q)}$ we have[34,35]:

$$\mathrm{Pr}(deg(i)\ge c)={\displaystyle \sum _{m=c}^{deg(i)}\mathrm{Pr}[deg(i)=m}]=1-{\displaystyle \sum _{m=0}^{c-1}\mathrm{Pr}(deg(i)=m})$$

(7)

Where the inter m is a degree flag that used during the traversal computing. And then we have [34,35]:

$$\mathrm{Pr}[deg(i)\ge m+1]=\mathrm{Pr}[deg(i)>m]-\mathrm{Pr}[deg(i)=m]$$

(8)

As can be seen, the original problem f₀ is to compute the Pr[deg(i,G’’≥c)], and the subproblems is to compute each $G_i^{\prime }$ score in the set $G_i^{″}$. That means, started by the situation of c=0, every Pr[deg(i)≥c)] can be find through the Pr[deg(i)=c)] as the integer c increasing by 1 each time.

It can be inferred that the time complexity of the above DP is O(d_maxE_G).

2.4. Rank Nodes According to Importance

After implementing the DP (described in 2.2), for any node i in G, we obtained the deg(i) probability distribution of the possible world scenarios ($c_i\in \{1,2,\dots ,deg(i)\}$), which correspond to the deg(i) importance scores c. Notably, the final importance score corresponding to node i is defined as:

$$C_i={\displaystyle \sum _{c=1}^{deg(i)}c\mathrm{Pr}(deg(i)\ge c)}$$

(9)

Before the execution of WEA, P is set to be a backup subset to the node-set V. Set V is traversed when the above-described steps are performed, and all nodes in G are ordinally sorted in P according to the node scores granted by WEA. X is a structure to record nodes and their corresponding importance. The following is a pseudocode description of WEA:

Algorithm: Weighted Expectation Method (WEA)

Input: A Weighted Network H(V,E,W)

Output: Importance Ranking of All Vertices in Target G(V,E,W’)

1: $W\prime \leftarrow \varnothing$;

2: for each $e\in E$ do:

3:  calculate $w_{ij}$ by using formula (2);

4:  $W\leftarrow W\prime \cup w_{ij}$;   5: end for

6: $P\leftarrow$Initialize an empty Priority queue;

7: for each $i\in G(V,E,W\prime )$ do:

8:  compute $\mathrm{Pr}(\mathrm{deg}(i)\ge c)$ by using formula (5)-(8);

9:  compute $C_i$ by using formula (9);

10:    $\mathit{X}\leftarrow \varnothing$ Initial an empty structure;

11:    X.NodeImportance$\leftarrow [i,C_i]$;

12:    $\mathit{P}\mathbf{.}$push(X);

13:    end for

15: return P;

End

Where $[i,C_i]$ can be seen as a Structure kindred thing in the C language, H is the original network, and G is the target graph extracted from H by taking four pre-operations: (1). Deleting the self-loop edges; (2). Taking the maximum connected subgraph; (3). Determine whether it is a directed network (if directed, combine the directed edges between the linked nodes as a whole and to be its new weight); (4). Normalizing the edge weights.

It can be seen that WEA is also suitable for computing tasks in unweighted networks.

Table 2. Time complexity comparison table for the node importance sorting algorithms in multiple weighted networks.

BT	EC	CL	WC	SC	HI	WEA
$O(n^3)$	$O(n^3)$	$O(max(e,nlogn))$	$O(n^3)$	$O(n^3)$	$O(n^3)$	$O(d_{\max }{E}_{G}N)$

Table 2. Time complexity comparison table for the node importance sorting algorithms in multiple weighted networks.

BT	EC	CL	WC	SC	HI	WEA
$O(n^3)$	$O(n^3)$	$O(max(e,nlogn))$	$O(n^3)$	$O(n^3)$	$O(n^3)$	$O(d_{\max }{E}_{G}N)$

It is cited why the network edge numbers and the max degree can be used to represent the time complexity is: There are two traversals in WEA, it needs to traverse each nodes of the dataset, and for each node, it needs to traverse each edge of it (if it has).

3. Experiments

Two typical tests, named by Connectivity and SIR propagation model, have been used to verify this proposed WEA.

3.1. Connectivity Test

The connectivity verification [36] is a classic way to verify accuracy for sorting algorithms in the field of node importance [7] (and edge importance [9]), which is mainly reflected by the size changing of the current largest connected subgraph during the deleting nodes (or edges) process. During this, if the drop rate of the site is fast, the graph structure collapses rapidly, proving that the more important nodes in the graph are removed. In other words, the algorithm performs efficiently in sorting important nodes. Precisely, the connectivity r always be depicted as [37,38]:

$$r=\frac{N_v^{\prime }}{N_v}$$

(10)

Where $N_v$ is the total node numbers contained in the largest connected component in the graph before the test is executed; $N_v^{\prime }$ represents the current numbers of nodes contained in the maximum connectivity component during the removal of the nodes by corresponding sorted order.

The well-known robustness metrics always be used to assess the effect of removing the nodes on the connectivity [37,38]:

$$R=\frac{1}{N^{\prime }}{\displaystyle \sum _{n=1}^{N^{\prime }}{r}_n}$$

(11)

Where $r_n$ refers to each time the current ratio $r$ during this iteratively nodes deleting; 1/N’ can be seen as a normalization factor to ensure that graphs in different sizes can be compared equally. Besides, for better evaluation, f is set to represent the ratio of the deleted nodes numbers and those in the original largest connected component.

3.2. Dynamic Spreading Test (SIR Propagation Model)

Another classical test of the node importance is the susceptible-infected-recovered model (SIR), which regarded the node importance rank as the node spreading power sorting [39,40,41]. Its’ aim is to test the correlation between the tested algorithm and the SIR sorting. The higher the correlation with Sir ranking, the better the performance of the tested algorithm. The higher the correlation value is, the better the tested algorithm performs. During the SIR propagation, each node in the target graph G is taken in turns as the seed node for infection, and then observe the influence of the epidemic disease spreads out. 500 independent SIR propagation simulations are conducted for each node in this experiment. Then the average number of recovery nodes in the network for this 500 SIR propagation simulation’s end is recorded as the node importance score. Eventually, all the nodes in G are sorted according to their importance scores. The most usual correlation analysis is to find the value of Kendall’s tau-b between each tested algorithm and SIR sorting.

It is needed to introduce Kendall’s tau-b correlation coefficients [42,43]: The sets $X(x_1,x_2,x_3,\dots ,x_N)$ and $Y(y_{1,}{y}_{2,}{y}_{3,},\dots ,y_N)$ are the sequence of the orderly sorting nodes that derived from the tested algorithm and the SIR propagation simulation, respectively. Then the corresponding $x_s$ and $x_t$ in sequence $X$ along with $y_s$ and $y_t$ in sequence $Y$ are taken arbitrarily to form two tuples, $(x_s,y_s)$ and $(x_t,y_t)$ respectively, where for integer variables s and t suit $s\ne t$, $s\le N$, and $t\le N$. If $x_s<x_t,y_s<y_t$ or $x_s>x_t,y_s>y_t$ they are concordant; If $x_s<x_t,y_s>y_t$ or $x_s>x_t,y_s<y_t$, they are discordant; Else they are neither concordant nor discordant. Thus, Kendall’s tau-b is defined as:

$${\tau }_b(X,Y)=\frac{2(n_c-n_d)}{N(N-1)}$$

(12)

Where $n_c$ and $n_d$ are the number of concordant and discordant, respectively.

Notably, according to the heterogeneous mean-field theory, the epidemic threshold in unweighted SIR is approximate to:

$${\beta }_C\approx \frac{<k_{avg}>}{<k_{avg}^2>-<k_{avg}>}$$

(13)

The $<k_{avg}>$ and the $<k_{avg}^2>$ denote the mean degree and mean square of degree, respectively. The heterogeneous mean field theory ensures the expectations of each node infecting neighbor nodes are regular, considered as $Exp(i)=\frac{{\displaystyle \sum K_{avg}{p}_i}}{N}$. $p_i$ is the probability of infection in the average case (broadly, $p_i$ is a constant in unweighted SIR). Considering WEA is suitable for weighted networks, and in order to make the experimental results more objective, we selected the weighted SIR (WSIR) type for verification, which takes advantage of the threshold that differs from the original one [44]:

$${\beta }_C^{\prime }\approx \frac{<k>}{l(<k^2>-<k>)}$$

(14)

We take l as the average edge weight value in the graph G (where l is defined in 2.2).

3.3. Datasets

In need of verifying the accuracy of sorting between WEA and the compared algorithms, the selected nine publicly-available real networks for experiments: (1) Email_dnc (Directed) [45]: Email network in the 2016 Democratic National Committee email leak; (2) Inf_USAir97 [45]: An American Airlines network; (3) Eco_everglades [45]: A eco-system of Florida Everglades; (4) Rt_bahrain [45]: Twitter social network (Undirected); (5) Windsurfers [46]: Natural disaster network; (6) Lesmis (Les Misérables) [46]: Social network of characters from Victor Hugo’s book; (7) Blocks [45]: The symmetrical power of the network from Gordon Royle, from University of Western Australia; and (8) C. elegans neural network (Caenorhabditis elegans, the undirected available on the website Koneck) [46]: The neural network of Caenorhabditis elegans. (9).Tech_caida (Directed) [45]: The relationships network of caida.

Table 3 lists some rudimentary topology characteristics of the eight real networks. D is to show whether this network is directed or not. V is the number of nodes, $E_G$ is the number of edges, $K_{avg}$ is the average degree, $W_{avg}$ is the average weight of each network, $W_{max}$ is the average weight of each network, T is the average triangle numbers formed by edges. C_c is the global clustering coefficient, and $\phi$ is the assortativity coefficient.

Since one central point of this work is to study the problem of how the weight be used to represent the link strength between two nodes, we define the different direction edge weight values as the component of the link strength between two nodes. In practice, it needs to consider the situations. For instance, it is required to consider the offset of the values when addressing a directed economic network. While, in some other situations, the values in two directed edges between two nodes typically shall be added as a whole for the edge weight computation.

Operations (1)–(4) are conducted for the above datasets. Firstly, the self-loops are removed if they exist; Secondly, the maximum connected subgraph is taken for the next computing; Thirdly, if they are directed, such as Email_dnc, the edge weight values between two nodes are added as a whole as their new weight value; Lastly, the weights for computing are pre-normalized by formula (4) and those weight values are assigned to be the weights of G.

Note that the absence of the self-loops ensures a better comparison and unified computing. Plus, if two or more nodes from one algorithm score the same, they are considered to be ranked in a tie, and their order in the node importance ranking will be randomly arranged. And then, the directed edges should be dealt with (if the network has).

4. Results

Seven algorithms were selected for conducting the comparison with WEA on those attached datasets, including the classical weighted version of the BT [26], CL [27], EC [30], WC [28], SC [29], the improved algorithm (HI) [25] developed by Lue et al. and the WD [24]. To validate the experiment, we chose two mainstream tests to measure the node importance sorting: Connectivity test and SIR test. We adopt the operations described above for each dataset (say network H). Then obtain the target graph G, and all the algorithms are conducted on it.

During the tests, if two or more nodes calculated by this algorithm score the same, their rankings are considered tied.

4.1. Figures, Tables and Schemes

The figures of connectivity verification have been attached below.

Table 4. Robustness R values for each algorithm on different datasets, of which WEA are always bold by the best.

Robustness	BT	EC	CL	WC	SC	HI	WD	WEA
Email_dnc	0.020	0.083	0.062	0.050	0.045	0.041	0.017	0.017
USAir97	0.140	0.143	0.417	0.158	0.141	0.293	0.129	0.128
Eco_everglades	0.507	0.500	0.506	0.501	0.500	0.488	0.500	0.440
Rt_bahrain	0.044	0.254	0.142	0.074	0.066	0.069	0.033	0.039
Windsurfers	0.476	0.479	0.493	0.444	0.435	0.468	0.432	0.426
Lesmis	0.164	0.177	0.232	0.269	0.173	0.152	0.157	0.151
Blocks	0.311	0.179	0.310	0.270	0.179	0.304	0.178	0.178
C.elegans_neural	0.341	0.450	0.421	0.403	0.416	0.394	0.375	0.340
Tech_caida	0.013	0.122	0.047	0.029	0.026	0.011	0.010	0.010
Average value	0.224	0.265	0.265	0.292	0.224	0.220	0.246	0.192

Table 4. Robustness R values for each algorithm on different datasets, of which WEA are always bold by the best.

Robustness	BT	EC	CL	WC	SC	HI	WD	WEA
Email_dnc	0.020	0.083	0.062	0.050	0.045	0.041	0.017	0.017
USAir97	0.140	0.143	0.417	0.158	0.141	0.293	0.129	0.128
Eco_everglades	0.507	0.500	0.506	0.501	0.500	0.488	0.500	0.440
Rt_bahrain	0.044	0.254	0.142	0.074	0.066	0.069	0.033	0.039
Windsurfers	0.476	0.479	0.493	0.444	0.435	0.468	0.432	0.426
Lesmis	0.164	0.177	0.232	0.269	0.173	0.152	0.157	0.151
Blocks	0.311	0.179	0.310	0.270	0.179	0.304	0.178	0.178
C.elegans_neural	0.341	0.450	0.421	0.403	0.416	0.394	0.375	0.340
Tech_caida	0.013	0.122	0.047	0.029	0.026	0.011	0.010	0.010
Average value	0.224	0.265	0.265	0.292	0.224	0.220	0.246	0.192

Table 5. Kendall’s tau-b correlation coefficients for each algorithm, the best-performed results are emphasized in bolds.

WSIR (tau-b)	BT	EC	CL	WC	SC	HI	WD	WEA
Email_dnc	0.372	0.657	0.531	0.536	0.628	0.715	0.519	0.557
USAir97	0.436	0.873	0.141	0.848	0.813	0.217	0.820	0.890
Eco_everglades	0.225	0.778	0.184	0.743	0.778	0.250	0.715	0.832
Rt_bahrain	0.131	0.423	0.523	0.511	0.685	0.580	0.573	0.588
Windsurfers	0.375	0.322	0.322	0.615	0.549	0.745	0.686	0.716
Lesmis	0.272	0.685	0.274	0.756	0.713	0.674	0.546	0.561
Blocks	0.071	0.944	0.055	0.647	0.668	0.113	0.843	0.920
C.elegans_neural	0.279	0.419	0.236	0.668	0.650	0.557	0.620	0.678
Tech_caida	0.161	0.238	0.263	0.310	0.415	0.306	0.259	0.357
Average value	0.258	0.593	0.281	0.626	0.655	0.462	0.620	0.678

Table 5. Kendall’s tau-b correlation coefficients for each algorithm, the best-performed results are emphasized in bolds.

WSIR (tau-b)	BT	EC	CL	WC	SC	HI	WD	WEA
Email_dnc	0.372	0.657	0.531	0.536	0.628	0.715	0.519	0.557
USAir97	0.436	0.873	0.141	0.848	0.813	0.217	0.820	0.890
Eco_everglades	0.225	0.778	0.184	0.743	0.778	0.250	0.715	0.832
Rt_bahrain	0.131	0.423	0.523	0.511	0.685	0.580	0.573	0.588
Windsurfers	0.375	0.322	0.322	0.615	0.549	0.745	0.686	0.716
Lesmis	0.272	0.685	0.274	0.756	0.713	0.674	0.546	0.561
Blocks	0.071	0.944	0.055	0.647	0.668	0.113	0.843	0.920
C.elegans_neural	0.279	0.419	0.236	0.668	0.650	0.557	0.620	0.678
Tech_caida	0.161	0.238	0.263	0.310	0.415	0.306	0.259	0.357
Average value	0.258	0.593	0.281	0.626	0.655	0.462	0.620	0.678

To compare the time-consuming of the algorithms outputting the result, the running time of different algorithms is recorded in Table 6. All the algorithms are conducted on the dataset in a Desktop computer with detailed information: Intel(R) Core (TM) i5-10400 CPU @2.90 GHz, RAM 16.0 GB, 64-bit operation system. The maximum iterate by 30000 times is set to EG for each dataset to ensure an outcome. Besides, the pretreatment of dealing with edge weights of directed datasets is not counted in the running time.

5. Discussion

In Table 6, we compared the time complexity of WEA with that of other algorithms, and as can be seen, the performance of WEAs’ is pretty well.

The figure varied for each algorithm in each dataset and presented vivid outcomes. A steeper downward curve means that the network structure collapses faster. The value R is to engrave the overall trend better. A smaller R corresponds to an entire faster network collapsing and thus, indicates the nodes deleted by the corresponding algorithm in order of its priority possess high importance.

There is no difficulty in finding WEA line with minimal robustness in eight networks. The connectivity curve of WEA tends to decline rapidly (which makes the structure collapse rapidly) in the figure of each dataset. The algorithm’s overall robustness is judged by measuring the area among the connectivity curve, x-axis, and y-axis (recorded as the value R). For example, in Figure 2 (b), according to the connectivity curve drawn by WEA, the decline in the early stage is relatively fast, and in the later stage, it is relatively gentle (the inflection point is around 0.17 of the ordinate value) which means that when about the first 17% of nodes are deleted, the network structure almost collapsed, and the number of the crucial nodes functioning in maintaining the network connection drops sharply. Furthermore, in Figure 2(g), the curves of WEA and SC almost coincide, which may be caused by the small number of nodes in the data set. In Figure 2(d), being inferior to WD, the curve of WEA performs at the second because of some inherent properties of the Dataset: As seen in Table 3, the value of Cc is too small.

As shown in Table 4, as the best performance value is boldly marked, the robustness (R) of WEA on the eight datasets is the lowest among all the algorithms. Compare the average R of each data, WEA is the lowest, at 0.192, followed by that of SC and classic BT. The results indicate that WEA sorting can always make the robustness value the lowest in deleting the nodes. This means WEA is more suitable for keeping accuracy in finding important node tasks.

Weighted SIR test can well test the algorithms’ performance in Dynamic spreading, so as to show whether the node importance rank is sound. We adopt it under the most proper ${\beta }_c^{\prime }$ to ensure the infected seed has an adequate spreading and performs well in each dataset.

Table 5 records each Kendall’s tau-b of these algorithms by its performance. As the best-performed results are emphasized in bold, Kendall’s tau-b of WEA in the WSIR test often gains the maximum values among most of the dataset, indicating that, in verifying the node importance, WEAs’ sorting is much closer to the results of the propagation simulation. Although, in the Rt_bahrain, SC obtains Kendall’s tau-b with 0.685 that higher than WEA and in the small datasets of Lesmis and Blocks, its value of WC and EG is higher than WEA’s (may be, under the SIR testing, WEA is not that superior at measuring the node spreading ability which possess the higher ratios of the node numbers to the edge numbers, calculated for 0.59 for Rt_bahrain, 0.30 for Lesmis, and 0.51 for Blocks respectively, which are dramatically high than other datasets). Nevertheless, WEA still wins those compared algorithms with the highest average Kendall’s tau-b. That is to say, the important nodes found by WEA possess a more substantial spreading capability, thereby indicating that WEA is more suitable for finding important nodes.

As seen in Table 6, each time, WEA has the second performance at the overall time-consuming of 160.67 Seconds, followed the WD with a total of 16.40 Seconds. The most time-consuming is BT at 6487.26 Seconds totally, and the second time-costing is CL which at the total of 3291.21 Seconds.

Even if the running time for WD is less than WEA, WEA can better ensure accuracy by a considerable time-consuming.

6. Conclusions and Outlooks

Aiming to address two issues: 1. The computing accuracy is always incompatible with low complexity. 2. Weight may contribute positively or negatively to the node’s importance, but there is an absence of a quantitative definition to deal with these two situations. This work proposes WEA, a new index for the node importance mining that considers the local topology information. Due to the design that takes advantage of Dynamic programming, WEA can significantly reduce time complexity but still guarantee high computing accuracy, which can well fit large-scale networks task. Meanwhile, by using a compact bridge (Equation (3)), WEA can make the types of negative/positive weight contribution networks be computed quantitatively and equally. Moreover, Equation (4) has portability that can be easily assembled with many other algorithms. Experimental verifications also showed WEA's high sorting accuracy and low time complexity. We mentioned in the dynamic spreading test that WEA is not that superior at measuring the node spreading function, maybe for the potential of the extremely high ratio (the node numbers to the edge numbers). Because WEA possesses the feature of flexible unlimited decimals, it ensures a precise importance score for each node. In general, as a new index, WEA is more precise and faster than the compared ones.

Based on this work, some further exploration can be done. Firstly, find some ultra-optimization ways to exert in large-scale network computing. Secondly, given the current hot trend of the relative node importance, it developed to be a challenging issue whether the statistical method can mine some invisible parts of the network from the topology information of the already known network parts since most networks possess prominent statistical characteristics, such as small world network.

Most algorithms choose the research object with conventional unweighted/weighted static networks. However, some networks in other forms are always ignored, such as dynamic networks [47,48] or spatiotemporal networks [49]. For example, an interesting issue can be how to quickly and accurately identify abnormal nodes in dynamic networks, criminal nodes in the blockchain, and social software, which will have great potential applications.

As for the current node importance research, there is a domain differentiation. Some algorithms may be more suitable for some specific fields or situations than others; in fact, the distinction between them is also for specific occasions. It is a good phenomenon because it is difficult to have an algorithm that can cover every different situation. However, the verification for these algorithms also has some domain differentiation. For example, BT performs poorly in SIR but very well in connectivity. Although this is the inevitable result of the algorithm’s applicability, this is a negative phenomenon. At present, many algorithms have been proposed, and some of them are rarely innovative. In the future, it is expected to summarize the application fields of existing algorithms and the testing methods [7,50].