Solve the 3x+1 Problem

Preprint

Article

Solve the 3x+1 Problem

Altmetrics

Downloads

440

Views

208

Comments

Jishe Feng^*

This version is not peer-reviewed

Submitted:

22 January 2023

Posted:

23 January 2023

Read the latest preprint version here

Alerts

Abstract

The 3x+1 problem asks the following: Suppose we start with a positive integer, and if it is odd then multiply it by 3 and add 1, and if it is even, divide it by 2. Then repeat this process as long as you can. Do you eventually reach the integer 1, no matter what you started with? Collatz conjecture (or 3n+1 problem) has been explored for about 85 years. In this article, we prove the Collatz conjecture by modifying Sharkovsky ordering of positive integers and denote the composition of the collatz function as a algebraic formula about $\frac{3^{m}}{(2^{r}}$, convert the problem to a algebraic problem, we can solve it completely.

Keywords:

Subject: Computer Science and Mathematics - Algebra and Number Theory

MSC: 11B25; 11B83; 03D20

1. Introduction

The

3 x + 1

problem is one of the unsolved problems in mathematics. It is also known as the Collatz conjecture,

3 x + 1

mapping, Ulam conjecture, Kakutani’s problem, Thwaites conjecture, Hasse’s algorithm, or Syracuse problem [1]. Paul Erdos (1913-1996) commented on the intractability of problem

3 n + 1

[2]: "Mathematics is not ready for those problems yet".

The

2 x + 1

problem is that, take any positive integer x, If x is even, divide x by 2. If x is odd, multiply x by 3 and add 1. Repeat this process continuously. The conjecture states that no matter which number you start with, you will always reach 1 eventually.

2. Terminology and notations

We will use the notations as in [4,7]. we describe a Collatz function as

T (n) = \{\begin{matrix} 3 n + 1, & if n is odd number, \\ \frac{n}{2} & if n is even number . \end{matrix}

(1)

Let N denote the set of positive integers. For

n \in N

, and

k = 0, 1, 2, 3, \dots

T^{0} (n)

and

T^{k + 1} (n)

denote n and

T (T^{k} (n)

, respectively.

The

3 x + 1

problem concerns the behavior of the iterates of the Collatz function, for any integer n, there must exist an integer r, so that

T^{r} (n) = 1 .

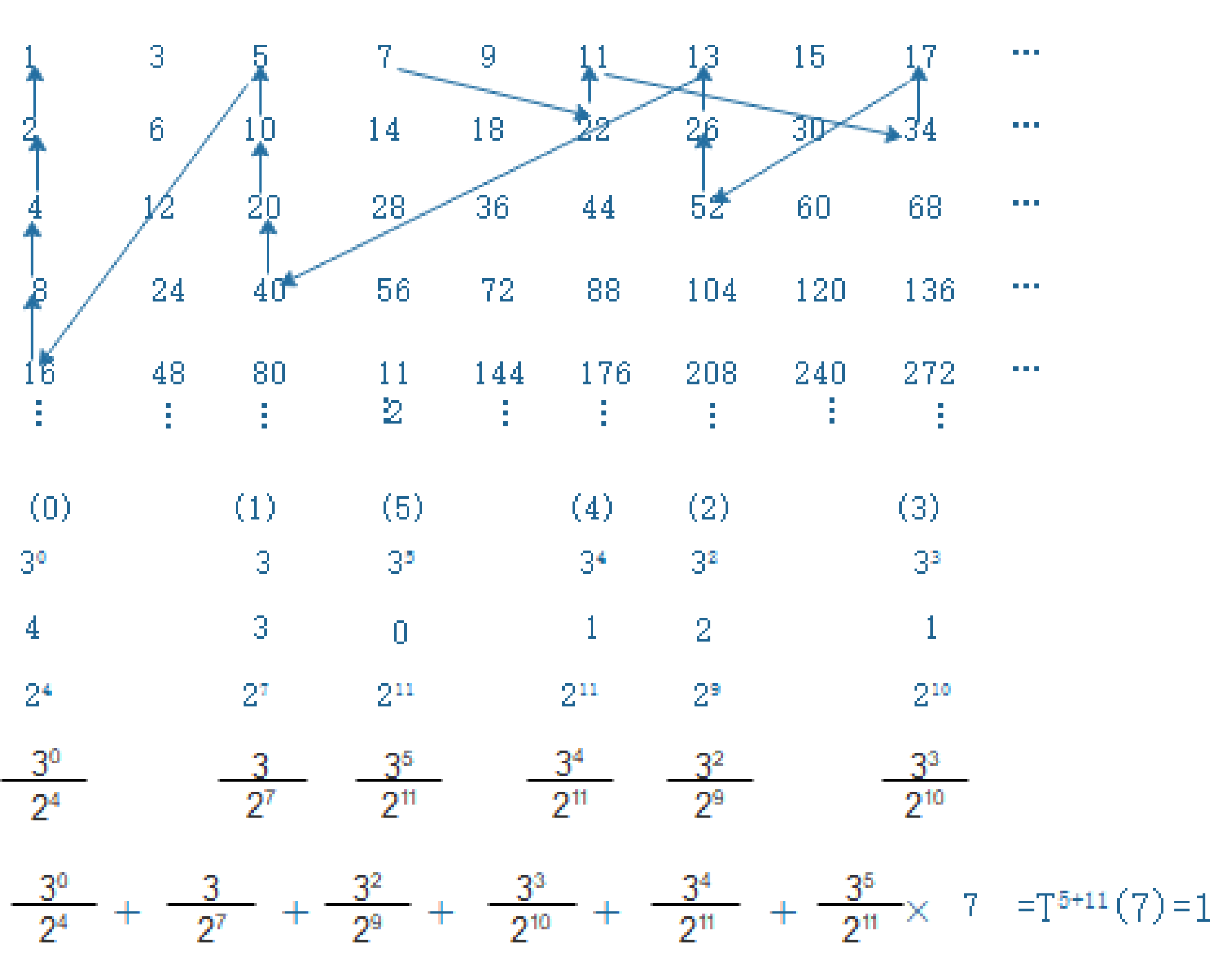
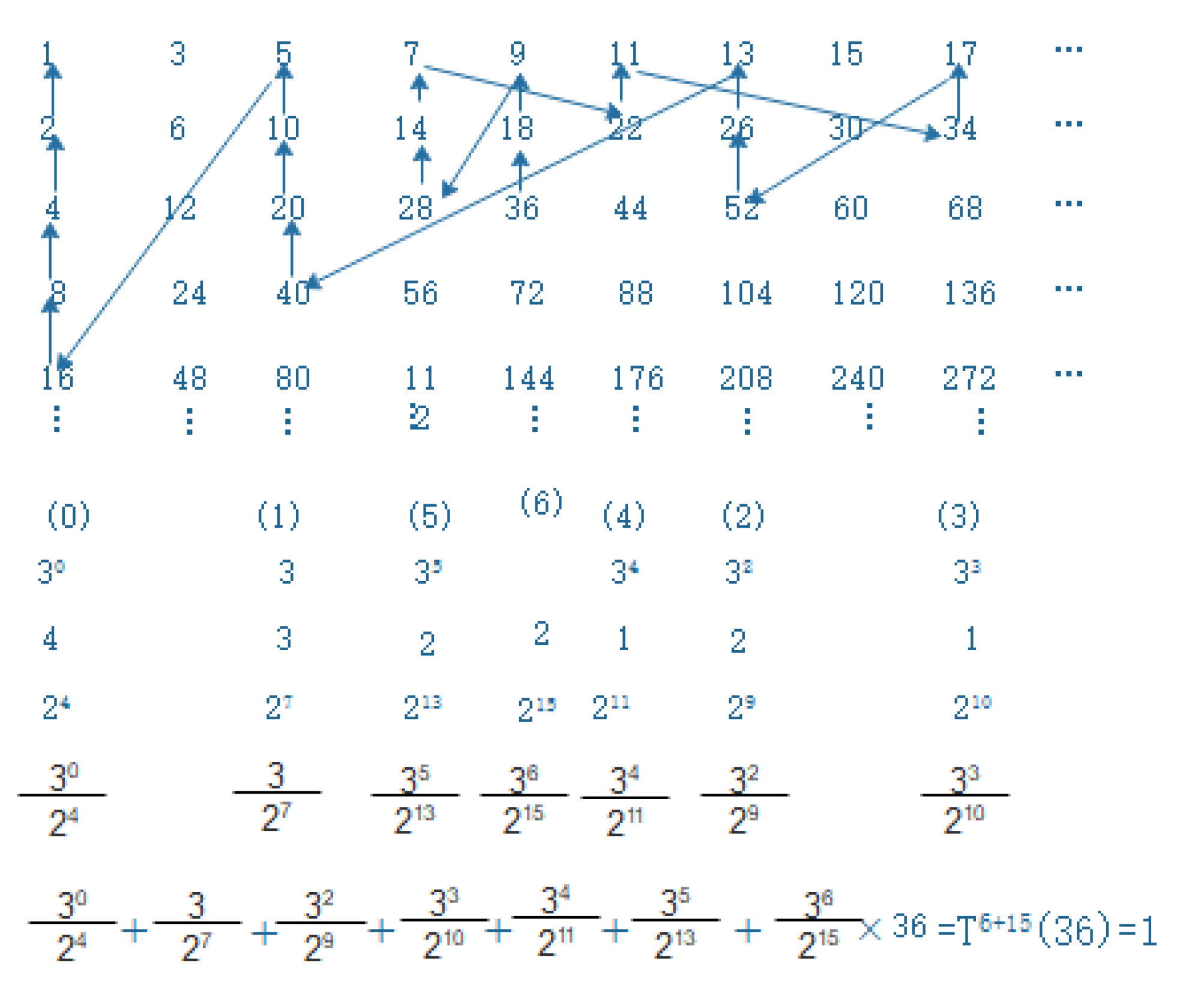
3. Proof of the Collatz Conjecture

3.1. The modified Sarkovskii ordering and integer lattice

We remove the last row number to the first column, get an integer lattice[6] of the modified Sarkovskii ordering as

\begin{matrix} 1, & 3, & 5, & 7, & 9, & 11, & 13, & 15, & 17, & 19, & \dots \\ 2, & 2 \cdot 3, & 2 \cdot 5, & 2 \cdot 7, & 2 \cdot 9, & 2 \cdot 11, & 2 \cdot 13, & 2 \cdot 15, & 2 \cdot 17, & 2 \cdot 19, & \dots \\ 2^{2}, & 2^{2} \cdot 3, & 2^{2} \cdot 5, & 2^{2} \cdot 7, & 2^{2} \cdot 9, & 2^{2} \cdot 11, & 2^{2} \cdot 13, & 2^{2} \cdot 15, & 2^{2} \cdot 17, & 2^{2} \cdot 19, & \dots \\ 2^{3}, & 2^{3} \cdot 3, & 2^{3} \cdot 5, & 2^{3} \cdot 7, & 2^{3} \cdot 9, & 2^{3} \cdot 11, & 2^{3} \cdot 13, & 2^{3} \cdot 15, & 2^{3} \cdot 17, & 2^{3} \cdot 19, & \dots \\ 2^{4}, & 2^{4} \cdot 3, & 2^{4} \cdot 5, & 2^{4} \cdot 7, & 2^{4} \cdot 9, & 2^{4} \cdot 11, & 2^{4} \cdot 13, & 2^{4} \cdot 15, & 2^{4} \cdot 17, & 2^{4} \cdot 19, & \dots \\ \dots & \dots & \dots & \dots & \dots & \dots & \dots & \dots & \dots & \dots & \dots \end{matrix}

In the first row, its are odd number from left to right, that are

1, 3, 5, 7, 9, 11, 13, \dots

, from the second row, each number is multiplying each number in its previous row by 2, and so on.

3.2. The algebraic formula and Collatz graph

If we draw a line segment of arrow between two digits in the lattice of integer in the modified Sarkovskii ordering, those are the original value x, and its value of Collatz function

T (x)

, and connect

T (x)

T^{2} (x)

, and so on

T^{2} (x)

T^{3} (x), \dots

, thus we get a graph, which can be called as Collatz graph. Using the Collatz function

T (x)

, We obtain an algebraic formula of

\frac{1}{2^{4}}, \frac{3}{2^{7}}, \frac{3^{2}}{2^{9}}, \dots, \frac{3^{m}}{2^{r}} \cdot x

. Here r is the number of perpendicular segments, m is the oblique segments in the Collatz graph,

T^{m + r} (n) = T (m, r, n) = \frac{1}{2^{4}} + \frac{3}{2^{7}} + \frac{3^{2}}{2^{9}} + \dots + \frac{3^{m}}{2^{r}} \cdot x = 1,

For example,

n = 7

, the algebraic formula is

T^{16} (7) = T (5, 11, 7) = \frac{1}{2^{4}} + \frac{3}{2^{7}} + \frac{3^{2}}{2^{9}} + \frac{3^{3}}{2^{10}} + \frac{3^{4}}{2^{11}} + \frac{3^{5}}{2^{11}} \cdot 7 = 1,

and the Collatz graph is Figure 1.

And

n = 36

, the algebraic formula is

T^{21} (36) = T (6, 15, 36) = \frac{1}{2^{4}} + \frac{3}{2^{7}} + \frac{3^{2}}{2^{9}} + \frac{3^{3}}{2^{10}} + \frac{3^{4}}{2^{11}} + \frac{3^{5}}{2^{13}} + \frac{3^{6}}{2^{15}} \cdot 36 = 1

and the Collatz graph is Figure 2.

4. Numerical example

We propose the following procedure,

T^{20} (18) = T (6, 14, 18) = \frac{1}{2^{4}} + \frac{3}{2^{7}} + \frac{3^{2}}{2^{9}} + \frac{3^{3}}{2^{10}} + \frac{3^{4}}{2^{11}} + \frac{3^{5}}{2^{13}} + \frac{3^{6}}{2^{14}} \cdot 18 = 1

T^{15} (23) = T (4, 11, 23) = \frac{1}{2^{4}} + \frac{3}{2^{9}} + \frac{3^{2}}{2^{10}} + \frac{3^{3}}{2^{11}} + \frac{3^{4}}{2^{11}} \cdot 23 = 1

T^{17} (15) = T (5, 12, 15) = \frac{1}{2^{4}} + \frac{3}{2^{9}} + \frac{3^{2}}{2^{10}} + \frac{3^{3}}{2^{11}} + \frac{3^{4}}{2^{12}} + \frac{3^{5}}{2^{12}} \cdot 15 = 1

T^{12} (17) = T (3, 9, 17) = \frac{1}{2^{4}} + \frac{3}{2^{7}} + \frac{3^{2}}{2^{9}} + \frac{3^{3}}{2^{9}} \cdot 17 = 1

T^{16} (397) = T (5, 11, 397) = \frac{1}{2^{4}} + \frac{3}{2^{7}} + \frac{3^{2}}{2^{9}} + \frac{3^{3}}{2^{10}} + \frac{3^{4}}{2^{11}} + \frac{3^{5}}{2^{17}} + \frac{3^{6}}{2^{20}} + \frac{3^{7}}{2^{20}} \cdot 397 = 1

T^{19} (61) = T (5, 14, 61) = \frac{1}{2^{4}} + \frac{3}{2^{9}} + \frac{3^{2}}{2^{10}} + \frac{3^{3}}{2^{11}} + \frac{3^{4}}{2^{14}} + \frac{3^{5}}{2^{14}} \cdot 61 = 1

We observe the three properties,

Note 1

In the algebraic formula, in numerators, it is

1, 3, 3^{2}, 3^{3}, \dots, 3^{m}

. there is not a lack. But in denominator, there are many lacks,

2, 2^{2}, 2^{3}, \dots, 2^{r} .

Note 2

For positive integers

i, j, k, l

, and

l_{k}, l_{k - 1}, \dots, l_{1}

, if

i > j

, then there is a recurrence relation

T^{i} (n) = \frac{3^{k}}{2^{l}} T^{j} (n) + \frac{3^{k - 1}}{2^{l_{k}}} + \dots + \frac{3^{2}}{2^{l_{3}}} + \frac{3}{2^{l_{2}}} + \frac{1}{2^{l_{1}}}

where

k + l = i - j

, and

l \geq l_{k} \geq l_{k - 1} \geq \dots \geq l_{1} .

Example 1.

There are

T^{3} (97) = \frac{3}{2^{2}} \cdot 97 + \frac{1}{2^{2}} = 73

T^{18} (97) = \frac{3^{7}}{2^{11}} \cdot 97 + \frac{3^{6}}{2^{11}} + \frac{3^{5}}{2^{9}} + \frac{3^{4}}{2^{7}} + \frac{3^{3}}{2^{6}} + \frac{3^{2}}{2^{5}} + \frac{3}{2^{2}} + \frac{1}{2} = 107

We can get the recurrence formula about the Collatz function

T (x)

T^{26} (97) = \frac{3^{3}}{2^{5}} \cdot T^{18} (97) + \frac{3^{2}}{2^{5}} + \frac{3}{2^{4}} + \frac{1}{2^{2}} = 91,

namely,

T^{26} (97) = \frac{3^{10}}{2^{16}} \cdot 97 + \frac{3^{9}}{2^{16}} + \frac{3^{8}}{2^{14}} + \frac{3^{7}}{2^{12}} + \frac{3^{6}}{2^{11}} + \frac{3^{5}}{2^{10}} + \frac{3^{4}}{2^{7}} + \frac{3^{3}}{2^{6}} + \frac{3^{2}}{2^{5}} + \frac{3}{2^{4}} + \frac{1}{2^{2}} = 91

T^{31} (97) = \frac{3^{2}}{2^{3}} \cdot 91 + \frac{3}{2^{3}} + \frac{1}{2^{2}} = 103

T^{40} (97) = \frac{3^{4}}{2^{5}} \cdot 103 + \frac{3^{3}}{2^{5}} + \frac{3^{2}}{2^{4}} + \frac{3}{2^{3}} + \frac{1}{2} = 263

T^{53} (97) = \frac{3^{5}}{2^{8}} \cdot 263 + \frac{3^{4}}{2^{8}} + \frac{3^{3}}{2^{7}} + \frac{3^{2}}{2^{6}} + \frac{3}{2^{4}} + \frac{1}{2} = 251

T^{53} (97) = \frac{3^{9}}{2^{13}} \cdot 103 + \frac{3^{8}}{2^{13}} + \frac{3^{7}}{2^{12}} + \frac{3^{6}}{2^{11}} + \frac{3^{5}}{2^{9}} + \frac{3^{4}}{2^{8}} + \frac{3^{3}}{2^{7}} + \frac{3^{2}}{2^{6}} + \frac{3}{2^{4}} + \frac{1}{2} = 251 = T^{53} (97)

\begin{matrix} 251 & x \\ 754 & T (x) = 3 x + 1 \\ 377 & T^{2} (x) = \frac{3}{2} x + \frac{1}{2} \\ 1132 & T^{3} (x) = \frac{3^{2}}{2} x + \frac{3}{2} + 1 \\ 566 & T^{4} (x) = \frac{3^{2}}{2^{2}} x + \frac{3}{2^{2}} + \frac{1}{2} \\ 283 & T^{5} (x) = \frac{3^{2}}{2^{3}} x + \frac{3}{2^{3}} + \frac{1}{2^{2}} \\ 850 & T^{6} (x) = \frac{3^{3}}{2^{3}} x + \frac{3^{2}}{2^{3}} + \frac{3}{2^{2}} + 1 \\ 425 & T^{7} (x) = \frac{3^{3}}{2^{4}} x + \frac{3^{2}}{2^{4}} + \frac{3}{2^{3}} + \frac{1}{2} \\ ⋮ & ⋮ \\ 958 & T^{64} (97) = \frac{3^{5}}{2^{6}} T^{53} (97) + \frac{3^{4}}{2^{6}} + \frac{3^{3}}{2^{5}} + \frac{3^{2}}{2^{3}} + \frac{3}{2^{2}} + 1 \\ 61 & T^{100} (97) = \frac{3^{7}}{2^{15}} T^{77} (97) + \frac{3^{6}}{2^{15}} + \frac{3^{5}}{2^{14}} + \frac{3^{4}}{2^{13}} + \frac{3^{3}}{2^{12}} + \frac{3^{2}}{2^{8}} + \frac{3}{2^{6}} + \frac{1}{2^{4}} \\ 1 & T^{119} (97) = T^{100} (97) \cdot \frac{3^{5}}{2^{14}} + \frac{3^{4}}{2^{14}} + \frac{3^{3}}{2^{11}} + \frac{3^{2}}{2^{10}} + \frac{3}{2^{9}} + \frac{1}{2^{4}} \end{matrix}

Note 3

We observe that

3^{5} \cdot 61 + 3^{4} + 3^{3} \cdot 2^{3} + 3^{2} \cdot 2^{4} + 3 \cdot 2^{5} + 2^{10} = 2^{14}

3^{7} \cdot 397 + 3^{6} + 3^{5} \cdot 2^{3} + 3^{4} \cdot 2^{9} + 3^{3} \cdot 2^{10} + 3^{2} + 3 \cdot 2^{13} + 2^{16} = 2^{20}

Theorem 2.

We can use the Collatz function

T (x)

, obtain that a series of

\frac{1}{2^{4}}, \frac{3}{2^{7}}, \frac{3^{2}}{2^{9}}, \dots, \frac{3^{m}}{2^{r}}

, where r is the number of perpendicular segments, m is the oblique segments in the graph. We can get a unique algebra donation about

3^{m}

in numerator and

2^{r}

in denominator, as

T (m, r, n) = 1,

So, there is

T^{m + r} (n) = T (m, r, n) = \frac{3^{m}}{2^{r}} \cdot n + \frac{3^{m - 1}}{2^{r_{m - 1}}} + \dots + \frac{3^{2}}{2^{r_{2}}} + \frac{3}{2^{r_{1}}} + \frac{1}{2^{4}} = 1

where

r \geq r_{m - 1} \geq r_{m - 2}

\geq \dots \geq r_{1} > 4 .

and there is a recurrence relation

T^{i} (n) = \frac{3^{k}}{2^{l}} T^{j} (n) + \frac{3^{k - 1}}{2^{l_{k}}} + \dots + \frac{3^{2}}{2^{l_{3}}} + \frac{3}{2^{l_{2}}} + \frac{1}{2^{l_{1}}}

where

l \geq l_{k} \geq l_{m - 2}

\geq \dots \geq l_{1} .

Theorem 3.

For positive integer, n, there must exist positive integer

m, r

and

r_{m - 1}, \dots, r_{1}

, such that

2^{r} = 3^{m} \cdot n + 3^{m - 1} \cdot 2^{m - r_{m - 1}} + \dots + 3^{2} \cdot 2^{m - r_{2}} + 3 \cdot 2^{m - r_{1}} + 2^{m - 4},

where

r \geq r_{m - 1} \geq r_{m - 2}

\geq \dots \geq r_{1} \geq 4

. This mean 3 multiply to the initial value n gradually with the digits of the abacus, must equal to

2^{r} .

Example 4

For example, for the formula

T (6, 14, 18) = \frac{1}{2^{4}} + \frac{3}{2^{7}} + \frac{3^{2}}{2^{9}} + \frac{3^{3}}{2^{10}} + \frac{3^{4}}{2^{11}} + \frac{3^{5}}{2^{13}} + \frac{3^{6}}{2^{14}} \cdot 18 = 1,

namely,

2^{10} + 3 \cdot 2^{7} + 3^{2} \cdot 2^{5} + 3^{3} \cdot 2^{4} + 3^{4} \cdot 2^{3} + 3^{5} \cdot 2 + 3^{6} \cdot 18 = 2^{14},

Proof.

We calculate

\begin{matrix} 3 & = & 2 + 1 \\ 3^{2} & = & 2^{3} + 1 \\ 3^{3} & = & 2^{4} + 2^{3} + 2 + 1 \\ 3^{4} & = & 2^{6} + 2^{4} + 1 \\ 3^{5} & = & 2^{7} + 2^{6} + 2^{5} + 2^{4} + 2 + 1 \\ 3^{6} & = & 2^{9} + 2^{7} + 2^{6} + 2^{4} + 2^{3} + 1 \\ 18 & = & 2^{4} + 2 \end{matrix}

and substitute them in the expression

\begin{matrix} 3^{6} \cdot 18 + 3^{5} \cdot 2 + 3^{4} \cdot 2^{3} + 3^{3} \cdot 2^{4} + 3^{2} \cdot 2^{5} + 3 \cdot 2^{7} + 2^{10} \\ = & (2^{9} + 2^{7} + 2^{6} + 2^{4} + 2^{3} + 1) \cdot (2^{4} + 2) + (2^{7} + 2^{6} + 2^{5} + 2^{4} + 2 + 1) \cdot 2 \\ + (2^{6} + 2^{4} + 1) \cdot 2^{3} + (2^{4} + 2^{3} + 2 + 1) \cdot 2^{4} + (2^{3} + 1) \cdot 2^{5} + (2 + 1) \cdot 2^{7} + 2^{10}, \end{matrix}

and get the value

2^{14}

. □

Remark 5.

We can say that

3 x + 1

problem is the convert statement of period three implies chaos [4].

5. Conclusion

In the integer lattice in the modifying the Sarkovskii ordering, denote the composition of the Collatz function as a algebraic formula about the

\frac{3^{m}}{2^{r}}

, we give a bridge of algebraic formula with graphs. We completely solve the

3 x + 1

problem.

References

Jeffrey, C. Lagarias. The 3x + 1 Problem and Its Generalizations. American Mathematical Monthly; Vol. 92, No. 1, pp 3-23.(1985).
Jeffrey, C. arXiv:2111.02635.
Stefan, P. A Theorem of Sarkovshii on the existence of periodic orbits of continuous endomorphisms of the real line. Commun. math. Phys. 54, 237-248(1977).
Li, T. Li, T., Yorke, J. A. Period three implies chaos. Am. Mat. Monthly 82, 985–992 (1975).
TERENCE TAO, Almost all orbits of the Collatz map attain almost bounded values. 2022, arXiv:1909.03562v51, 15.
Jishe FENG, Xiaomeng WANG, Xiaolu GAO, Zhuo PAN. The research and progress of the enumeration of lattice paths. Frontiers of Mathematics in China, 2022, 17(5): 747-766.
Alf Kimms. The structure of the 3x+1 problem, Electronic Journal of Graph Theory and Applications, 9(1)(2021),157–174.

Figure 1. The Collatz graph of

T^{16}

(7) = T(5; 11; 7) = 1 in the lattice of integers in the modified Sarkovskii ordering and the algebraic formula.

Figure 1. The Collatz graph of

T^{16}

(7) = T(5; 11; 7) = 1 in the lattice of integers in the modified Sarkovskii ordering and the algebraic formula.

Figure 2. The Collatz graph of

T^{21}

(36) = T(6; 15; 36) = 1 in the lattice of integers in the modified Sarkovskii ordering and the algebraic formula.

Figure 2. The Collatz graph of

T^{21}

(36) = T(6; 15; 36) = 1 in the lattice of integers in the modified Sarkovskii ordering and the algebraic formula.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Solve the 3x+1 Problem

Abstract

1. Introduction

2. Terminology and notations

3. Proof of the Collatz Conjecture

3.1. The modified Sarkovskii ordering and integer lattice

3.2. The algebraic formula and Collatz graph

4. Numerical example

5. Conclusion

References

MDPI Initiatives

Important Links

Subscribe