Analytical Insights Into the Spread of an Epidemic through Joint Modeling of Disease Dynamics and Attitudes towards Prophylactic Measures and Vaccines

1. Introduction

The emergence in late 2019 of the new coronavirus disease (COVID-19) caused by the pathogen SARS-CoV-2 is a devastating example of highly contagious emerging infectious diseases in response to increases in the magnitude and rate of overexploitation, habitat loss, global loss of biodiversity and climate change that many studies have warned against during the last decades [1,2,3,4]. The COVID-19 pandemic has impacted social and cultural habits, recreational and economic activities, laws and rights, among other aspects of the human civilisation. Increases in the levels of personal hygiene and social distancing from perceived sources of infection have shown significant potential to reduce the transmission of SARS-CoV-2 and thereby the spread of COVID-19. But the spread of a contagious disease in this era of mass media and connected populations is inevitably concomitant with the dissemination of antagonist information and opinions on the related pathogen, disease and prophylactic measures [5,6,7,8].

Modeling disease dynamics is the unique route to circumventing, containing, anticipating and preventing or reducing the ravages by deadly emerging or re-emerging infectious diseases. The numerous recent epidemic outbreaks (e.g. MERS, SARS, Ebola) have indeed urged the development of mathematical and statistical models for the spread dynamics of the particular diseases. Many such models include opinions regarding vaccination [9,10,11]. Indeed, vaccines’ safety and use have always and everywhere raised controversial issues [12,13,14]. For instance, controversies about COVID-19 vaccines have been widely spread once the first trials for safety and effectiveness assessment started, especially in highly connected social networks [15,16,17,18,19,20]. The opinions and the related attidudes toward vaccines have obvious consequences in the spread of diseases and their ability to cause epidemics [21]. Opinions on other prophylactic measures have however been less considered, although they can directly impact both transmission dynamics and attitudes toward vaccination. The dynamics of these other prophylactic behaviours can substantively differ from the dynamics of attitudes toward vaccination, because, for instance, they demand stronger engagement in terms of the required frequency of affirmation [22]. In the COVID-19 pandemic context in particular, hands need to be regularly washed when the environment is full of potentially contaminated areas, face masks need to be worn when using any shared public space, and minimum social distance needs to be kept in mind when interacting with fellows.

The recent development of models coupling disease, economic and opinion dynamics [23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38] provides headways towards effective joint modeling of health-related beliefs and attitudes, economic constraints, public health utility, disease dynamics, and their interactions. Most of the current models primarily rely on quite simplistic assumptions such as the SIS [24,27,39], SIR [22,23,40,41,42] and SEIV models [43] for disease dynamics. However, for highly contagious diseases such as COVID-19, the world’s reactions to outbreaks generally involved isolating some infectious individuals from the susceptible population, making the distinction of “quarantined” individuals from other infectious individuals crucial for sound modeling of this disease [44]. Moreover, the epidemiology of COVID-19 indicates even more complex disease dynamics involving presymptomatic, asymptomatic, and symptomatic infectious states [45,46,47,48,49,50,51,52]. In such situations, the use of too simplistic models can neglect crucial characteristics of target diseases, and confound some distinct disease-opinion interactions important for decision making. In addition, although vaccination is also a prophylactic measure, the attitude toward vaccination may be inconsistent with other prophylactic behaviours. For instance, an individual with a low level of prophylactic behaviour may get vaccinated in order to ignore social distancing. Likewise, an agent with initially high level of prophylactic behaviour may become overconfident after vaccination and relax personal hygiene and social distancing, lowering its level of prophylactic behaviour [53]. Once vaccination is introduced in an epidemic context, it indeed becomes crutial for a sound modeling to account for the potential interactions between opinions on both basic prophylactic measures and vaccination, including reverse effets.

To tackle this background, we build on the work of Tyson et al. [22], by introducing a disease-opinion dynamics model framework that modulates the effective contact rate in the target population based on the perceived disease prevalence generated by public health policymakers and mass media. Specifically, we propose (1) a disease-opinion dynamics model that accounts for basic prophylactic measures against emerging infectious diseases, the related beliefs and behaviours, and important disease states based on COVID-19 epidemiology, and (2) a joint model integrating attitudes toward vaccination and other prophylactic measures with disease dynamics. It is worth noticing that Arthur et al. [27] have recently proposed a discrete–time SIR model with an effective contact rate modulated by an utility function with delayed information, allowing an adaptive and optimal control of the population’s effective contact rate. In addition to the use herein of a more realistic model for COVID-19 dynamics, our proposal differs substantially from their model in regards to its construction joining two different mean field equations related to opinions and disease, and the direct insights it provides on the processes governing changes regarding opinions or disease, and their interactions. Moreover, unlike Arthur et al. [27], we do not assume that susceptible individuals rationally find an optimal contact rate by trading off how many people they want to interact with versus their risk of becoming infected. We rather consider a social influence approach [22] wherein a susceptible with a given opinion can change attitude in response to interaction with susceptibles holding a different opinion, the rate of such influences being determined by the perceived risk of becoming infected.

The objectives of this work are (i) to summarize the population dynamics (as expressed by the effective reproduction number for each introduced disease-opinion dynamics model) as a function of influence rate, rates of detection (testing policy) and isolation (“quarantining”), and vaccination rate, and (ii) to assess the impacts of the initial distribution of behaviours, nature of behavioural responses, rates of detection and isolation, initial vaccination coverage, efficacy of vaccines, vaccination rate, and distorted perception of disease prevalence on disease dynamics. The use of the proposed models is expected to make informative contributions to public policy in a context of opinion fluxes in response to perceived disease prevalence.

2. The Disease-Opinion dynamics models

We develop a generalization of the SIR–Opinion dynamics model [22] to suit the epidemiology of the pathogen SARS-CoV-2, the related coronavirus disease (COVID-19), and the availability of imperfect COVID-19 vaccines. On the one hand, we consider a disease evolution model distinguishing the infectious population into presymptomatic, asymptomatic and symptomatic individuals, and possibly the susceptible population into unvaccinated and vaccinated individuals. On the other hand, we extend the prophylactic opinion spectrum of Tyson et al. [22], introducing a prophylactic opinion field where attitudes/opinions toward both standard prophylactic measures (e.g. personal hygiene, face mask wearing and social distancing) and vaccination, and their interactions are integrated.

2.1. Disease dynamics

We describe disease evolution using a compartmental model in which the target population is basically structured into Susceptible (S), Exposed (E), Infectious (I), Quarantined (Q), and Recovered individuals (R) [54,55,56]. But the infectious population is further distinguished into presymptomatic ($I_p$), asymptomatic ($I_a$), and symptomatic infectious ($I_s$) individuals, whereas the susceptible population (S) is distinguished into unvaccinated and completely susceptible individuals (U), and vaccinated and partially immunized individuals (V). The sizes of the susceptible and the infectious compartments satisfy respectively $S\left(t\right)=U\left(t\right)+V\left(t\right)$ and $I\left(t\right)=I_p\left(t\right)+I_a\left(t\right)+I_s\left(t\right)$ at time t, and the total population size $N\left(t\right)$ is given by

$$N\left(t\right)=U\left(t\right)+V\left(t\right)+E\left(t\right)+I_p\left(t\right)+I_a\left(t\right)+I_s\left(t\right)+Q\left(t\right)+R\left(t\right).$$

(1)

In a vaccination-free context (e.g. for a new emerging disease), the size of the vaccinated population is zero ($V\left(t\right)=0$) and the susceptible population consists of only unvaccinated individuals ($S\left(t\right)=U\left(t\right)$). We have in this case a SEIQR model which is appropriate for the early phase of the COVID-19 pandemic. When vaccines become available, we have the more general UVEIQR model.

For simplicity, the susceptible population (S) is assumed homogeneous with regards to factors such as age and medical conditions. We account for natural human demography, i.e. we include a natural death rate ($\mu$) for the whole population, and assume a constant timely number of new births and net immigration ($\eta$) entering the class S of susceptibles (i.e. there is no immigration of infectives). Moreover, because isolated infectious individuals do not mix actively with other classes, we assume that they do not have adequate contacts (i.e. contacts sufficient for transmission) with susceptible individuals [57,58,59]. Under the corresponding “quarantine-adjusted incidence” mechanism [60], the force of infection ${\lambda }_o$ defined as the expected number of adequate contacts of one susceptible person with infectives per unit time (i.e. the rate at which new infections (E) are produced), is given at time t for a completely susceptible individual by

$${\lambda }_o\left(t\right)=\frac{{\beta }_p{I}_p\left(t\right)+{\beta }_a{I}_a\left(t\right)+{\beta }_s{I}_s\left(t\right)}{N\left(t\right)-Q\left(t\right)}$$

(2)

where ${\beta }_p$, ${\beta }_a$ and ${\beta }_s$ are baseline rates of effective contacts by presymptomatic, asymptomatic, and symptomatic infectious individuals, respectively. The available vaccines are considered imperfect, with an average efficacy of vaccine-induced protection $\kappa \in (0,1)$. In other words, contacts between a V individual and $I_p$, $I_a$ or $I_s$ individuals can be sufficient for transmission, but the force of infection is reduced to $(1-\kappa ){\lambda }_o\left(t\right)$. A detailed description of both the SEIQR and the UVEIQR disease dynamics models in line with the known epidemiology of COVID-19 is given in Appendix A, along with graphical representations and mathematical descriptions based on nonlinear differential equations.

2.2. The Prophylactic attitude spectrum

In a vaccination–free epidemic context, we follow Tyson et al. [22], assuming for simplicity that opinion dynamics only occur within the susceptible population S. The latter is distinguished into three groups of individuals that can be identified based on the level of prophylactic behaviour which takes values in the prophylactic attitude spectrum:

$$\mathcal{P}=\left\{-1,0,1\right\}.$$

(3)

For any opinion $i\in \mathcal{P}$, $S_i$ denotes susceptibles with attitude i: $S_{-1}$ represents individuals with the highest level of prophylactic behaviour (and thus the least susceptible to the disease), and $S_1$ corresponds to individuals with the lowest level of prophylactic behaviour (and thus the most susceptible to the disease). Individuals $S_0$ in the middle of the spectrum correspond to an intermediate level of prophylactic behaviour. Note that if the opinion $i=-1$ is opposed to $i=1$, then our model includes individuals with completely neutral position ($S_0$), unlike in the binary voter model based spectrum used by Tyson et al. [22]. However, the spectum (3) simply defines the intensity of prophylactic behaviour on an ordinal scale, and high level attitude ($i=-1$) is not necessarily opposed to low level attitude ($i=1$). The identity $S\left(t\right)={\sum }_{i\in \mathcal{P}}{S}_i\left(t\right)$ holds for the susceptible population at time t.

2.3. The source and rate of opinion dynamics

Opinion dynamics results from changes of opinions and behaviours over time, for instance, as the mass media diffuse information about disease prevalence or evolution of the pathogen, or as disease surveillance and control policies are introduced or modified. We adapt here the “influence” approach of Tyson et al. [22], opinions being updated in response to interactions between susceptibles along the prophylactic opinion spectrum (3). In this framework, opinion dynamics within the susceptible population is governed by the rates (i.e. amplitudes) and the directions of mutual opinion influences.

The rate ${\omega }_i$ at which a susceptible individual $S_i$ influences the rest of the susceptible population is referred to as “influence function”. For their SIR-Opinion dynamics model, Tyson et al. [22] introduced linear and saturating influences as functions of the proportion of the infectious population (I). We consider here influence functions ${\omega }_i$ of the form

$${\omega }_i\left(t\right)=w_i\left(\tilde{P}\left(t\right)\right),$$

(4a)

where $w_i$ are Tyson et al. [22]’s fixed-order saturating extreme influence weights, and $\tilde{P}\left(t\right)$ is the “perceived disease prevalence”. The influence weights are given for $x\in [0,1]$ by

$$w_i\left(x\right)=\left\{\begin{array}{cc}{w}_o\left[1+w_{\infty }\frac{x}{\left(\tilde{k}+x\right)}\right]& \mathrm{if}i=-1\\ w_o\left[1+\frac{\left(w_{\infty }-1\right)}{2}\frac{x}{\left(\tilde{k}+x\right)}\right]& \mathrm{if}i=0\\ w_o\left[1-\frac{x}{\left(\tilde{k}+x\right)}\right]& \mathrm{if}i=1\end{array}\right.$$

(4b)

with $w_o\in (0,1)$, the baseline influence rate for extreme opinions; $w_{\infty }\ge 1$, a skewness parameter; and $\tilde{k}>0$, a half-saturation constant (see Appendix B for a graphical overview of $w_i$). In Equation (4a), we have substituted a perceived disease prevalence to the proportion of infectious (I) used by Tyson et al. [22], because, in our SEIQR model framework, the true disease prevalence given by $P\left(t\right)=\left[I_p\left(t\right)+I_a\left(t\right)+I_s\left(t\right)+Q\left(t\right)\right]/N\left(t\right)$ is unknown to any individual in the population (only Q is observable), and estimates of P reported by the mass media are perceived as disease prevalence (see details on recovering P from epidemic and medical data in Appendix (Appendix C)). The perceived disease prevalence $\tilde{P}$ is a determinant of opinion dynamics [61,62], and indeed, a source of changes in the rates of influences on and by prophylactic opinions, as implied by Equation (4a). Clearly, the under or over estimation and reporting of disease prevalence by media or public health policymakers play a role in opinion dynamics.

In regards to the directions of influences, when an $S_i$ individual influences an $S_j$ individual the $S_j$ individual changes its attitude by moving one step towards i [22]. For instance, if the two individuals are at the opposite sides of the attitude spectrum (i.e. $i\times j<0$), then the $S_j$ individual changes its attitude by moving one step towards the other side (i.e. $S_j\to S_0$). If on the contrary the interacting individuals have the same opinion (i.e. $i\times j>0$), no change occurs. When an $S_i$ individual at a given side of the attitude spectrum ($i=\pm 1$) influences a moderate opinion holder $S_0$, then $S_0\to S_i$. Finally, when an $S_j$ individual at a side of the spectrum ($j=\pm 1$) is influenced by an $S_0$ individual, then $S_j\to S_0$. These changes of opinions in the susceptible population can be summarized by the rates ${\xi }_{(i,j)}\left(t\right)$ of outgoing flows (opinion change $i\to j$) as:

$$\begin{array}{cc}\hfill {\xi }_{(-1,0)}\left(t\right)& =\frac{{\omega }_0\left(t\right)S_0\left(t\right)+{\omega }_1\left(t\right)S_1\left(t\right)}{N\left(t\right)-Q\left(t\right)},\hfill \end{array}$$

(5a)

$$\begin{array}{cc}\hfill {\xi }_{(0,-1)}\left(t\right)& =\frac{{\omega }_{-1}\left(t\right)S_{-1}\left(t\right)}{N\left(t\right)-Q\left(t\right)},\hfill \end{array}$$

(5b)

$$\begin{array}{cc}\hfill {\xi }_{(0,1)}\left(t\right)& =\frac{{\omega }_1\left(t\right)S_1\left(t\right)}{N\left(t\right)-Q\left(t\right)},\hfill \end{array}$$

(5c)

$$\begin{array}{cc}\hfill {\xi }_{(1,0)}\left(t\right)& =\frac{{\omega }_{-1}\left(t\right)S_{-1}\left(t\right)+{\omega }_0\left(t\right)S_0\left(t\right)}{N\left(t\right)-Q\left(t\right)}.\hfill \end{array}$$

(5d)

2.4. The SEIQR-Opinion dynamics model

The proposed SEIQR-Opinion dynamics model is depicted on the flow diagram in Figure 1.

Note the use in Figure 1 of opinion-specific forces of infection (${\lambda }_i$). Indeed, since increased levels of personal hygiene or social distancing from perceived sources of infection can substantively reduce both contacts and, if any, the sufficiency of contacts for transmission, we assume that an individual’s attitude determines its susceptibility to infection in a way such that the force of infection for $S_i$ individuals has the form

$${\lambda }_i\left(t\right)=\frac{{\beta }_{ip}{I}_p\left(t\right)+{\beta }_{ia}{I}_a\left(t\right)+{\beta }_{is}{I}_s\left(t\right)}{N\left(t\right)-Q\left(t\right)}$$

(6a)

where, for $i\in \mathcal{P}$ and $j\in \left\{p,a,s\right\}$, ${\beta }_{ij}$ is the rate of contacts sufficient for transmission from an $I_j$ infectious to a $S_i$ susceptible. For simplicity, the dependence of infection rate on attitude is modeled using a single parameter [22]. It is specifically assumed that, for each infectious class $I_j$, the sufficient contact rate ${\beta }_{ij}$ is given by ${\beta }_{ij}={\varsigma }_o^{1-i}{\beta }_j$, i.e.

$${\beta }_{1j}={\beta }_j,{\beta }_{0j}={\varsigma }_o{\beta }_j,{\beta }_{-1j}={\varsigma }_o^2{\beta }_j,$$

(6b)

where ${\beta }_j$ is the baseline rate of sufficient contacts with $I_j$ infectious (this applies to $S_1$ susceptible individuals who have the lowest level of prophylactic behaviour), and ${\varsigma }_o\in (0,1)$.

From the structuring of the susceptible population S in terms of prophylactic opinions i, the overall force of infection in the whole target population is given by the weighted average ${\overline{\lambda }}_o\left(t\right)=\frac{1}{S\left(t\right)}{\sum }_{i\in \mathcal{P}}{S}_i\left(t\right){\lambda }_i\left(t\right)$. The SEIQR-Opinion dynamics model is described at time t by the following system of nonlinear differential equations:

$$\begin{array}{cc}\hfill {\dot{S}}_{-1}\left(t\right)& ={\eta }_{-1}+{\xi }_{(0,-1)}\left(t\right)S_0\left(t\right)-\left[{\psi }_{-1}\left(t\right)+\mu \right]S_{-1}\left(t\right)+{ϵ}_{-1}R\left(t\right),\hfill \end{array}$$

(7a)

$$\begin{array}{cc}\hfill {\dot{S}}_0\left(t\right)& ={\eta }_0+{\xi }_{(-1,0)}\left(t\right)S_{-1}\left(t\right)+{\xi }_{(1,0)}\left(t\right)S_1\left(t\right)-\left[{\psi }_0\left(t\right)+\mu \right]S_0\left(t\right)+{ϵ}_{0}R\left(t\right),\hfill \end{array}$$

(7b)

$$\begin{array}{cc}\hfill {\dot{S}}_1\left(t\right)& ={\eta }_1+{\xi }_{(0,1)}\left(t\right)S_0\left(t\right)-\left[{\psi }_1\left(t\right)+\mu \right]S_1\left(t\right)+{ϵ}_{1}R\left(t\right),\hfill \end{array}$$

(7c)

$$\begin{array}{cc}\hfill \dot{E}\left(t\right)& ={\lambda }_{-1}\left(t\right)S_{-1}\left(t\right)+{\lambda }_0\left(t\right)S_0\left(t\right)+{\lambda }_1\left(t\right)S_1\left(t\right)-(\theta +\mu )E\left(t\right),\hfill \end{array}$$

(7d)

$$\begin{array}{cc}\hfill {\dot{I}}_p\left(t\right)& =\theta E\left(t\right)-(\sigma +\mu )I_p\left(t\right),\hfill \end{array}$$

(7e)

$$\begin{array}{cc}\hfill {\dot{I}}_a\left(t\right)& =(1-\tau )(1-\pi )\sigma I_p\left(t\right)-({\rho }_a+{\gamma }_a+\mu )I_a\left(t\right),\hfill \end{array}$$

(7f)

$$\begin{array}{cc}\hfill {\dot{I}}_s\left(t\right)& =\tau (1-\pi )\sigma I_p\left(t\right)-({\rho }_s+{\gamma }_s+{\delta }_s+\mu )I_s\left(t\right),\hfill \end{array}$$

(7g)

$$\begin{array}{cc}\hfill \dot{Q}\left(t\right)& =\pi \sigma I_p\left(t\right)+{\rho }_a{I}_a\left(t\right)+{\rho }_s{I}_s\left(t\right)-({\gamma }_q+{\delta }_q+\mu )Q\left(t\right),\hfill \end{array}$$

(7h)

$$\begin{array}{cc}\hfill \dot{R}\left(t\right)& ={\gamma }_a{I}_a\left(t\right)+{\gamma }_s{I}_s\left(t\right)+{\gamma }_{q}Q\left(t\right)-({ϵ}_o+\mu )R\left(t\right),\hfill \end{array}$$

(7i)

with the nonnegative initial conditions $S_i\left(0\right)=S_{0i}$, $E\left(0\right)=E_0$, $I_p\left(0\right)=I_{0p}$, $I_a\left(0\right)=I_{0a}$, $I_s\left(0\right)=I_{0s}$, $Q\left(0\right)=Q_0$, and $R\left(0\right)=R_0$ where ${\left(E_0,I_{0p},I_{0a},I_{0s},Q_0,R_0\right)}^{\top }\in {[0,\infty )}^6$, and $S_{0i}\ge 0$ for $i\in \mathcal{P}$. In System (Section 2.4), the dots represent partial derivatives with respect to time (t), ${\psi }_i$ denotes the time-dependent outgoing flows rate from $S_i$ susceptibles:

$$\begin{array}{cc}\hfill {\psi }_{-1}\left(t\right)& ={\xi }_{(-1,0)}\left(t\right)+{\lambda }_{-1}\left(t\right),\hfill \end{array}$$

(8a)

$$\begin{array}{cc}\hfill {\psi }_0\left(t\right)& ={\xi }_{(0,-1)}\left(t\right)+{\xi }_{(0,1)}\left(t\right)+{\lambda }_0\left(t\right),\hfill \end{array}$$

(8b)

$$\begin{array}{cc}\hfill {\psi }_1\left(t\right)& ={\xi }_{(1,0)}\left(t\right)+{\lambda }_1\left(t\right),\hfill \end{array}$$

(8c)

${\sum }_{i\in \mathcal{P}}{\eta }_i=\eta$, ${\sum }_{i\in \mathcal{P}}{ϵ}_i={ϵ}_o$, and the constant rate parameters of the model are described in Table 1. We shall use the qualifier “disease-dependent” for any solution for which there exists a finite time $t\ge 0$ such that $E\left(t\right)+I_p\left(t\right)+I_a\left(t\right)+I_s\left(t\right)>0$.

2.5. The prophylactic attitude field

In addition to preventing infectious diseases through immunisation, vaccines have further benefits such as reduced antimicrobial resistance and herd protection to unvaccinated individuals, including the elderly with waning immune systems and those who are too young to be vaccinated, or are immunosuppressed due to particular medical conditions [63,64]. Because vaccines come with potential safety and efficacy concerns, their obvious advantages do not prevent controversies which feed a vaccine related opinion dynamics, especially in highly connected social networks [15,16,17,18,19,20]. As a result, a disease–opinion dynamics model must account for the impact of vaccination on both attitudes and disease transmissions once vaccines are introduced into an epidemic context.

The fact that the attitute towards vaccination may be inconsistent with other prophylactic behaviours advises against the use of one scale between two extreme opinions on prophylactic measures in an epidemic context involving vaccination. Hence, we consider that the prophylactic opinion spectrum in Equation (3) excludes opinions on vaccination. A spectrum of vaccination-related opinion is separately introduced into the model, resulting in a bivariate field of opinions. For simplicity, we consider only two antagonists opinions toward vaccines: favourable and unfavorable [11]. The bivariate attitude field is defined as

$$\mathcal{F}=\left\{\begin{array}{c}-1u,0u,1u\\ -1v,0v,1v\end{array}\right\}$$

(9)

where for each element $ij$, $i\in \mathcal{P}$ and $j\in \left\{u,v\right\}$, $j=u$ indexes individuals unfavourable to vaccination, and $j=v$ indexes individuals favourable to vaccination. In consequence, a class of $S_i$ susceptibles ($i\in \mathcal{P}$) is further structured into three groups: completely susceptible individuals unfavorable to vaccination ($U_{iu}$), completely susceptible individuals favorable to vaccination ($U_{iv}$), and susceptibles with active vaccine-induced immunity ($V_i$). The total susceptible population is then given by $S\left(t\right)=U\left(t\right)+V\left(t\right)$ where $U\left(t\right)=U_u\left(t\right)+U_v\left(t\right)$ denotes all completely susceptible individuals, $U_u\left(t\right)={\sum }_{i\in \mathcal{P}}{U}_{iu}\left(t\right)$ denotes completely susceptible individuals unfavorable to vaccination, $U_v\left(t\right)={\sum }_{i\in \mathcal{P}}{S}_{iv}\left(t\right)$ denotes completely susceptible individuals favorable to vaccination, and $V={\sum }_{i\in \mathcal{P}}{V}_i\left(t\right)$ denotes vaccinated individuals. The identity $S\left(t\right)={\sum }_{i\in \mathcal{P}}{S}_i\left(t\right)$ still holds for the whole susceptible population, and in addition, $S_i\left(t\right)=U_i\left(t\right)+V_i\left(t\right)$ where $U_i\left(t\right)=U_{iu}\left(t\right)+U_{iv}\left(t\right)$.

2.6. Changes in prophylactic attitudes in the presence of vaccination

We still assume that opinion dynamics only occur within the susceptible population (S), including $U_u$, $U_v$ and V individuals. Changes of opinion on prophylactic behaviours (excluding vaccination) are determined within $U_u$, $U_v$ or V individuals by an “influence” process. Assuming for simplicity that the influence rates are ceteris paribus the same within the pro-vaccine and anti-vaccine susceptible populations as well as in the vaccinated population, the rates ${\tilde{\xi }}_{(i,j)}\left(t\right)$ of outgoing flows (opinion change $i\to j$) are defined by analogy to Equations (5a)–(5d) as:

$$\begin{array}{cc}\hfill {\tilde{\xi }}_{(-1,0)}\left(t\right)& =\frac{{\tilde{\omega }}_0\left(t\right)S_0\left(t\right)+{\tilde{\omega }}_1\left(t\right)S_1\left(t\right)}{N\left(t\right)-Q\left(t\right)},\hfill \end{array}$$

(10a)

$$\begin{array}{cc}\hfill {\tilde{\xi }}_{(0,-1)}\left(t\right)& =\frac{{\tilde{\omega }}_{-1}\left(t\right)S_{-1}\left(t\right)}{N\left(t\right)-Q\left(t\right)},\hfill \end{array}$$

(10b)

$$\begin{array}{cc}\hfill {\tilde{\xi }}_{(0,1)}\left(t\right)& =\frac{{\tilde{\omega }}_1\left(t\right)S_1\left(t\right)}{N\left(t\right)-Q\left(t\right)},\hfill \end{array}$$

(10c)

$$\begin{array}{cc}\hfill {\tilde{\xi }}_{(1,0)}\left(t\right)& =\frac{{\tilde{\omega }}_{-1}\left(t\right)S_{-1}\left(t\right)+{\tilde{\omega }}_0\left(t\right)S_0\left(t\right)}{N\left(t\right)-Q\left(t\right)},\hfill \end{array}$$

(10d)

where ${\tilde{\omega }}_i$ are influence functions. As the vaccination-free influence function ${\omega }_i$ defined in Equation (4a), the influence function ${\tilde{\omega }}_i$ depends on the perceived disease prevalence $\tilde{P}$. However, in a vaccination-dependent epidemic context, vaccine coverage (i.e. the proportion $V\left(t\right)/N\left(t\right)$ of vaccinated individuals), which is widely publicised in the mass media, is also expected to impact prophylactic behaviours. It appears that when the influence of an individual with an opinion i increases with $\tilde{P}$, then it will likely decrease with vaccine coverage (see e.g. [53]) and vice-versa. Assuming independence between the relative importances of $\tilde{P}$ and V in ${\tilde{\omega }}_i$, the influence rate is given the form

$${\tilde{\omega }}_i\left(t\right)=w_o\frac{V\left(t\right)}{N\left(t\right)}+\left[1-\frac{V\left(t\right)}{N\left(t\right)}\right]w_i\left(\tilde{P}\left(t\right)\right)$$

(10e)

so that ${\tilde{\omega }}_i\left(t\right)={\omega }_i\left(t\right)$ if $V\left(t\right)=0$, i.e. Equation (10e) is reduced to Equation (4a) in a vaccination-free context, and irrespective of vaccine coverage, $w_o$ remains the initial influence rate of an extreme opinion holder when the disease is not perceived ($\tilde{P}\left(t\right)=0$, i.e. an actual disease-free context, or a failure to detect any infectious individual although $I\left(t\right)>0$). It is worth noting that the basic influence $w_i$ is a decreasing function for $i>0$ and an increasing function for $i<0$ (see graphics in Appendix B, see also Figure 1 in [22]). As a result, the influence ${\tilde{\omega }}_i$ of a high level prophylactic attitude ($i=-1$) increases with the perceived disease prevalence $\tilde{P}\left(t\right)$ but decreases with vaccine coverage. Conversely, the influence of a low level prophylactic attitude ($i=1$) decreases with $\tilde{P}\left(t\right)$ but increases with $V\left(t\right)/N\left(t\right)$. It also stems from Equation (10e) that vaccination ($V\left(t\right)>0$) reduces the slope of the influence rate for all prophylactic opinions. Specifically, when $x\%$ of the population is immunized through vaccination, the influences of prophylactic opinions become $(100-x)\%$ less responsive to changes in the perceived disease prevalence $\tilde{P}$, as compared to the response in a vaccination-free context.

2.7. Changes in attitudes towards vaccination

We consider that changes of opinion on vaccination within $U_i$ individuals ($U_{iu}$ and $U_{iv}$) are also governed by an “influence” process. Assuming that changes of attitude toward vaccines is independant of the level i of prophylactic behaviour, the rate ${\zeta }_{(v,u)}\left(t\right)$ at which $U_{iv}$ individuals lose conviction to vaccination benefits and return to the class $U_{iu}$, and the rate ${\zeta }_{(u,v)}\left(t\right)$ at which $U_{iu}$ individuals become favourable to vaccines and enter the class $U_{iv}$ are given for any opinion $i\in \mathcal{P}$ by

$$\begin{array}{cc}\hfill {\zeta }_{(v,u)}\left(t\right)& =\frac{{\tilde{\omega }}_u\left(t\right)U_u\left(t\right)}{N\left(t\right)-Q\left(t\right)},\hfill \end{array}$$

(11a)

$$\begin{array}{cc}\hfill {\zeta }_{(u,v)}\left(t\right)& =\frac{{\tilde{\omega }}_v\left(t\right)\left[U_v\left(t\right)+V\left(t\right)\right]}{N\left(t\right)-Q\left(t\right)},\hfill \end{array}$$

(11b)

where ${\tilde{\omega }}_u$ and ${\tilde{\omega }}_v$ are influence functions related to opinions on vaccination. Note that individuals with vaccine-induced immunity (V) are all assumed to be favourable to vaccines (at least until the temporary immunity vanishes). To obtain simple expressions for the influence functions ${\tilde{\omega }}_u$ and ${\tilde{\omega }}_v$, we assume that there is no change in vaccine related opinions when the disease is not perceived ($\tilde{P}\left(t\right)=0$), and the influence rates of pro-vaccine and anti-vaccine susceptibles are also constants when $V\left(t\right)=0$, i.e. there is no shift in vaccine related opinions until vaccination begins (note that this assumption is not as restrictive as it may first appear, because we have $V\left(t\right)>0$ once trials for vaccine safety and efficacy start in the population, or even when only ${\eta }_v>0$, i.e. vaccinated individuals only flow in from abroad). We also assume that an increase of either $\tilde{P}\left(t\right)$ or $V\left(t\right)/N\left(t\right)$ leads to an increase in the influence of pro-vaccine susceptibles, but to a decrease in the influence of anti-vaccine susceptibles. From these assumptions, we define the influence functions as:

$$\begin{array}{cc}\hfill {\tilde{\omega }}_u\left(t\right)& =w_o\left[1-\tilde{P}\left(t\right)\right]+\tilde{P}\left(t\right)w_1\left(\frac{V\left(t\right)}{N\left(t\right)}\right),\mathrm{and}\hfill \end{array}$$

(11c)

$$\begin{array}{cc}\hfill {\tilde{\omega }}_v\left(t\right)& =w_o\left[1-\tilde{P}\left(t\right)\right]+\tilde{P}\left(t\right)w_{-1}\left(\frac{V\left(t\right)}{N\left(t\right)}\right).\hfill \end{array}$$

(11d)

It appears from these expressions that when the perceived disease prevalence $\tilde{P}$ increases by $x\%$, the influence of any vaccination related opinion becomes $x\%$ more responsive to changes in the vaccine coverage $V\left(t\right)/N\left(t\right)$.

2.8. The UVEIQR-Opinion dynamics model

We build a Disease-Opinion dynamics model by integrating prophylactic behaviours and vaccine related opinions into the UVEIQR model. With the vaccination process, pro-vaccine susceptibles who have the prophylactic opinion i ($U_{iv}$) get vaccinated (and enter the class $V_i$) at the same rate $\upsilon$ (irrespective of i). Likewise, the vaccinated individuals in $V_i$ lose their immunity and return to the class $U_{iv}$ at the rate $\alpha$. We also assume that anti-vaccine susceptibles ($U_u$) do not get vaccinated.

The opinion-specific force of infection ${\lambda }_i$ is given by Equation (6a) for $U_i$ individuals, and is $(1-\kappa ){\lambda }_i$ for $V_i$ individuals. The overall force of infection in the whole population is then given by the weighted average

$$\overline{\lambda }\left(t\right)=\frac{1}{S\left(t\right)}\sum _{i\in \mathcal{P}}\left[U_i\left(t\right)+(1-\kappa )V_i\left(t\right)\right]{\lambda }_i\left(t\right).$$

(12)

The flow diagram of the UVEIQR-Opinion dynamics model is shown in Figure 2.

Let ${\phi }_{il}$ denote for $l\in \left\{u,uv,v\right\}$ the opinion-related incoming flows for susceptible states:

$$\begin{array}{cc}\hfill {\phi }_{-1u}\left(t\right)& ={\tilde{\xi }}_{(0,-1)}\left(t\right)U_{0u}\left(t\right)+{\zeta }_{(v,u)}\left(t\right)U_{-1v}\left(t\right),\hfill \end{array}$$

(13a)

$$\begin{array}{cc}\hfill {\phi }_{0u}\left(t\right)& ={\tilde{\xi }}_{(-1,0)}\left(t\right)U_{-1u}\left(t\right)+{\tilde{\xi }}_{(1,0)}\left(t\right)U_{1u}\left(t\right)+{\zeta }_{(v,u)}\left(t\right)U_{0v}\left(t\right),\hfill \end{array}$$

(13b)

$$\begin{array}{cc}\hfill {\phi }_{1u}\left(t\right)& ={\tilde{\xi }}_{(0,1)}\left(t\right)U_{0u}\left(t\right)+{\zeta }_{(v,u)}\left(t\right)U_{1v}\left(t\right),\hfill \end{array}$$

(13c)

$$\begin{array}{cc}\hfill {\phi }_{-1uv}\left(t\right)& ={\tilde{\xi }}_{(0,-1)}\left(t\right)U_{0v}\left(t\right)+{\zeta }_{(u,v)}\left(t\right)U_{-1u}\left(t\right)+\alpha V_{-1}\left(t\right),\hfill \end{array}$$

(13d)

$$\begin{array}{cc}\hfill {\phi }_{0uv}\left(t\right)& ={\tilde{\xi }}_{(-1,0)}\left(t\right)U_{-1v}\left(t\right)+{\tilde{\xi }}_{(1,0)}\left(t\right)U_{1v}\left(t\right)+{\zeta }_{(u,v)}\left(t\right)U_{0u}\left(t\right)+\alpha V_0\left(t\right),\hfill \end{array}$$

(13e)

$$\begin{array}{cc}\hfill {\phi }_{1uv}\left(t\right)& ={\tilde{\xi }}_{(0,1)}\left(t\right)U_{0v}\left(t\right)+{\zeta }_{(u,v)}\left(t\right)U_{1u}\left(t\right)+\alpha V_1\left(t\right),\hfill \end{array}$$

(13f)

$$\begin{array}{cc}\hfill {\phi }_{-1v}\left(t\right)& ={\tilde{\xi }}_{(0,-1)}\left(t\right)V_0\left(t\right)+\upsilon U_{-1v}\left(t\right),\hfill \end{array}$$

(13g)

$$\begin{array}{cc}\hfill {\phi }_{0v}\left(t\right)& ={\tilde{\xi }}_{(-1,0)}\left(t\right)V_{-1}\left(t\right)+{\tilde{\xi }}_{(1,0)}\left(t\right)V_1\left(t\right)+\upsilon U_{0v}\left(t\right),\hfill \end{array}$$

(13h)

$$\begin{array}{cc}\hfill {\phi }_{1v}\left(t\right)& ={\tilde{\xi }}_{(0,1)}\left(t\right)V_{0v}\left(t\right)+\upsilon U_{1v}\left(t\right),\hfill \end{array}$$

(13i)

and let ${\psi }_{il}$ denote the time-dependent outgoing flow rates:

$$\begin{array}{cc}\hfill {\psi }_{-1u}\left(t\right)& ={\tilde{\xi }}_{(-1,0)}\left(t\right)+{\zeta }_{(u,v)}\left(t\right)+{\lambda }_{-1}\left(t\right),\hfill \end{array}$$

(13j)

$$\begin{array}{cc}\hfill {\psi }_{0u}\left(t\right)& ={\tilde{\xi }}_{(0,-1)}\left(t\right)+{\tilde{\xi }}_{(0,1)}\left(t\right)+{\zeta }_{(u,v)}\left(t\right)+{\lambda }_0\left(t\right),\hfill \end{array}$$

(13k)

$$\begin{array}{cc}\hfill {\psi }_{1u}\left(t\right)& ={\tilde{\xi }}_{(1,0)}\left(t\right)+{\zeta }_{(u,v)}\left(t\right)+{\lambda }_1\left(t\right),\hfill \end{array}$$

(13l)

$$\begin{array}{cc}\hfill {\psi }_{-1uv}\left(t\right)& ={\tilde{\xi }}_{(-1,0)}\left(t\right)+{\zeta }_{(v,u)}\left(t\right)+{\lambda }_{-1}\left(t\right),\hfill \end{array}$$

(13m)

$$\begin{array}{cc}\hfill {\psi }_{0uv}\left(t\right)& ={\tilde{\xi }}_{(0,-1)}\left(t\right)+{\tilde{\xi }}_{(0,1)}\left(t\right)+{\zeta }_{(v,u)}\left(t\right)+{\lambda }_0\left(t\right),\hfill \end{array}$$

(13n)

$$\begin{array}{cc}\hfill {\psi }_{1uv}\left(t\right)& ={\tilde{\xi }}_{(1,0)}\left(t\right)+{\zeta }_{(v,u)}\left(t\right)+{\lambda }_1\left(t\right),\hfill \end{array}$$

(13o)

$$\begin{array}{cc}\hfill {\psi }_{-1v}\left(t\right)& ={\tilde{\xi }}_{(-1,0)}\left(t\right)+(1-\kappa ){\lambda }_{-1}\left(t\right),\hfill \end{array}$$

(13p)

$$\begin{array}{cc}\hfill {\psi }_{0v}\left(t\right)& ={\tilde{\xi }}_{(0,-1)}\left(t\right)+{\tilde{\xi }}_{(0,1)}\left(t\right)+(1-\kappa ){\lambda }_0\left(t\right),\hfill \end{array}$$

(13q)

$$\begin{array}{cc}\hfill {\psi }_{1v}\left(t\right)& ={\tilde{\xi }}_{(1,0)}\left(t\right)+(1-\kappa ){\lambda }_1\left(t\right).\hfill \end{array}$$

(13r)

The proposed model is described at time t by the following system of differential equations:

$$\begin{array}{cc}\hfill {\dot{U}}_{-1u}\left(t\right)& ={\eta }_{-1u}+{\phi }_{-1u}\left(t\right)-\left[{\psi }_{-1u}\left(t\right)+\mu \right]U_{-1u}\left(t\right)+{ϵ}_{-1u}R\left(t\right),\hfill \end{array}$$

(14a)

$$\begin{array}{cc}\hfill {\dot{U}}_{0u}\left(t\right)& ={\eta }_{0u}+{\phi }_{0u}\left(t\right)-\left[{\psi }_{0u}\left(t\right)+\mu \right]U_{0u}\left(t\right)+{ϵ}_{0u}R\left(t\right),\hfill \end{array}$$

(14b)

$$\begin{array}{cc}\hfill {\dot{U}}_{1u}\left(t\right)& ={\eta }_{1u}+{\phi }_{1u}\left(t\right)-\left[{\psi }_{1u}\left(t\right)+\mu \right]U_{1u}\left(t\right)+{ϵ}_{1u}R\left(t\right),\hfill \end{array}$$

(14c)

$$\begin{array}{cc}\hfill {\dot{U}}_{-1v}\left(t\right)& ={\eta }_{-1uv}+{\phi }_{-1uv}\left(t\right)-\left[{\psi }_{-1uv}\left(t\right)+\upsilon +\mu \right]U_{-1v}\left(t\right)+{ϵ}_{-1uv}R\left(t\right),\hfill \end{array}$$

(14d)

$$\begin{array}{cc}\hfill {\dot{U}}_{0v}\left(t\right)& ={\eta }_{0uv}+{\phi }_{0uv}\left(t\right)-\left[{\psi }_{0uv}\left(t\right)+\upsilon +\mu \right]U_{0v}\left(t\right)+{ϵ}_{0uv}R\left(t\right),\hfill \end{array}$$

(14e)

$$\begin{array}{cc}\hfill {\dot{U}}_{1v}\left(t\right)& ={\eta }_{1uv}+{\phi }_{1uv}\left(t\right)-\left[{\psi }_{1uv}\left(t\right)+\upsilon +\mu \right]U_{1v}\left(t\right)+{ϵ}_{1uv}R\left(t\right),\hfill \end{array}$$

(14f)

$$\begin{array}{cc}\hfill {\dot{V}}_{-1}\left(t\right)& ={\eta }_{-1v}+{\phi }_{-1v}\left(t\right)-\left[{\psi }_{-1v}\left(t\right)+{\alpha }_{}+\mu \right]V_{-1}\left(t\right),\hfill \end{array}$$

(14g)

$$\begin{array}{cc}\hfill {\dot{V}}_0\left(t\right)& ={\eta }_{0v}+{\phi }_{0v}\left(t\right)-\left[{\psi }_{0v}\left(t\right)+\alpha +\mu \right]V_0\left(t\right),\hfill \end{array}$$

(14h)

$$\begin{array}{cc}\hfill {\dot{V}}_1\left(t\right)& ={\eta }_{1v}+{\phi }_{1v}\left(t\right)-\left[{\psi }_{1v}\left(t\right)+\alpha +\mu \right]V_1\left(t\right),\hfill \end{array}$$

(14i)

$$\begin{array}{cc}\hfill \dot{E}\left(t\right)& =\overline{\lambda }\left(t\right)S\left(t\right)-(\theta +\mu )E\left(t\right),\hfill \end{array}$$

(14j)

$$\begin{array}{cc}\hfill {\dot{I}}_p\left(t\right)& =\theta E\left(t\right)-(\sigma +\mu )I_p\left(t\right),\hfill \end{array}$$

(14k)

$$\begin{array}{cc}\hfill {\dot{I}}_a\left(t\right)& =(1-\tau )(1-\pi )\sigma I_a\left(t\right)-({\rho }_a+{\gamma }_a+\mu )I_a\left(t\right),\hfill \end{array}$$

(14l)

$$\begin{array}{cc}\hfill {\dot{I}}_s\left(t\right)& =\tau (1-\pi )\sigma I_p\left(t\right)-({\rho }_s+{\gamma }_s+{\delta }_s+\mu )I_s\left(t\right),\hfill \end{array}$$

(14m)

$$\begin{array}{cc}\hfill \dot{Q}\left(t\right)& =\pi \sigma I_p\left(t\right)+{\rho }_a{I}_a\left(t\right)+{\rho }_s{I}_s\left(t\right)-({\gamma }_q+{\delta }_q+\mu )Q\left(t\right),\hfill \end{array}$$

(14n)

$$\begin{array}{cc}\hfill \dot{R}\left(t\right)& ={\gamma }_a{I}_a\left(t\right)+{\gamma }_s{I}_s\left(t\right)+{\gamma }_{q}Q\left(t\right)-({ϵ}_o+\mu )R\left(t\right),\hfill \end{array}$$

(14o)

with the nonnegative initial conditions $U_{il}\left(0\right)=U_{0il}$, $V_i\left(0\right)=V_{0i}$, $E\left(0\right)=E_0$, $I_p\left(0\right)=I_{0p}$, $I_a\left(0\right)=I_{0a}$, $I_s\left(0\right)=I_{0s}$, $Q\left(0\right)=Q_0$, and $R\left(0\right)=R_0$ where $U_{0il}\ge 0$ and $V_{0i}\ge 0$ for $i\in \mathcal{P}$ and $l\in \left\{u,uv,v\right\}$, and ${\left(E_0,I_{0p},I_{0a},I_{0s},Q_0,R_0\right)}^{\top }\in {[0,\infty )}^6$. In Equations (14a)–(14o), ${\sum }_{i\in \mathcal{P}}{\sum }_{l=u,uv,v}{\eta }_{il}=\eta$, ${\sum }_{i\in \mathcal{P}}{\sum }_{l=u,uv}{ϵ}_{il}={ϵ}_o$ (e.g. ${ϵ}_{il}={ϵ}_o/6$ for an equal repartition; or ${ϵ}_{0l}={ϵ}_o/4$ and ${ϵ}_{-1l}={ϵ}_{1l}={ϵ}_o/8$ assuming that 50% of recovered individuals have a moderate prophylactic attitude), and the constant rate parameters of the model are described in Table 1.

Note that in the special case $\upsilon =0$ and $V_{0i}={\eta }_{iv}=0$ for $i\in \mathcal{P}$, model (14) is reduced to the vaccination-free model (7) where $S_i$ susceptibles are divided into $U_{iu}$ and $U_{iv}$ with constant mutual influence rates ${\tilde{\omega }}_u\left(t\right)={\tilde{\omega }}_v\left(t\right)=w_o$ (but with no incidence on disease dynamics or basic prophylactic opinion dynamics).

3. Analytical results

The first important property of any mathematical model for a biological process is, of course, biological meaningfulness. The following result guarantees that the UVEIQR-Opinion model always has a biological interpretation.

Lemma 1

(Non-negativity and Boundedness). Under the nonnegative initial conditions $U_{iu}\left(0\right)\ge 0$, $U_{iv}\left(0\right)\ge 0$, $V_i\left(0\right)\ge 0$ for $i\in \mathcal{P}$, $E\left(0\right)\ge 0$, $I_p\left(0\right)\ge 0$, $I_a\left(0\right)\ge 0$, $I_s\left(0\right)\ge 0$, $Q\left(0\right)\ge 0$ and $R\left(0\right)\ge 0$, all solutions of Systems (14) remain nonnegative and are bounded at any time $t>0$. The total population size $N\left(t\right)$ is in particular bounded as $0\le N\left(t\right)\le \widehat{N}$ where $\widehat{N}=max\left\{N\left(0\right),N^c\right\}$ with $N^c=\eta /\mu$ the carrying capacity in disease–free conditions.

Since System (7) is a special case of System (14), Lemma 1 also assures that all solutions of the SEIQR-Opinion model (7) are biologically meaningful. In the remainder of this section, we present some important properties of disease-opinion dynamics in a population described by the introduced models. The analogous mathematical properties for the models with no differential opinion are given in Appendix A.3, and the proofs of all results are given in Appendix D. Unlike in Lemma 1, we start for clarity with the properties of the simpler model (7) without vaccination ($\upsilon =0$ and $V_{0i}={\eta }_{iv}=0$ for $i\in \mathcal{P}$) and then discuss the changes induced by the introduction of vaccines in both disease and opinion dynamics in the model (14).

3.1. Vaccination–free disease–free equilibrium and reproduction numbers

To summarize the dynamics of a population described by the SEIQR-Opinion model (7), we find the disease-free equilibrium (d.f.e.) of the model and use it to obtain the effective reproduction number by the next-generation matrix approach [65]. We further derive critical detection rates to potentially achieve disease eradication in the long run.

Proposition 1

(Vaccination–free d.f.e. & Reproduction number). The SEIQR-Opinion model (7) has a unique d.f.e. given for $w_o>0$ by

$$\begin{array}{cc}\hfill {\mathit{X}}^c& ={\left(S_{-1}^c,S_0^c,S_1^c,0,0,0,0,0,0\right)}^{\top }\mathrm{where}\hfill \end{array}$$

(15a)

$$\begin{array}{cc}\hfill S_{-1}^c& =\frac{{\eta }_{-1}}{\mu }-\frac{1}{2}\left(S_0^c-\frac{{\eta }_0}{\mu }\right),\hfill \end{array}$$

(15b)

$$\begin{array}{cc}\hfill S_0^c& =\eta \left(\frac{1}{\mu }+\frac{1}{w_o}\right)-\sqrt{\frac{4\eta {\eta }_1}{\mu w_o}+{\left(\frac{{\eta }_1-{\eta }_{-1}}{\mu }-\frac{\eta }{w_o}\right)}^2},\hfill \end{array}$$

(15c)

$$\begin{array}{cc}\hfill S_1^c& =\frac{{\eta }_1}{\mu }-\frac{1}{2}\left(S_0^c-\frac{{\eta }_0}{\mu }\right).\hfill \end{array}$$

(15d)

When $w_o=0$, we have $S_i^c=\frac{{\eta }_i}{\mu }$ for $i\in \mathcal{P}$. Moreover, for a population described by System (7), the basic reproduction number is given by

$$\begin{array}{cc}\hfill {\mathcal{R}}_0(\pi ,{\rho }_a,{\rho }_s,w_o)& =\sum _{i\in \mathcal{P}}\sum _{j=p,a,s}{\mathcal{R}}_{0ij}\mathrm{where}\hfill \\ \hfill {\mathcal{R}}_{0ij}& =\frac{\theta }{(\theta +\mu )(\sigma +\mu )}\frac{S_i^c{\varsigma }_o^{1-i}}{N^c}{\beta }_j{m}_j\hfill \end{array}$$

(16a)

is the contribution of $S_i$ susceptibles and $I_j$ infectious to ${\mathcal{R}}_0$, with $m_p=1$, $m_a=\frac{(1-\tau )(1-\pi )\sigma }{{\rho }_a+{\gamma }_a+\mu }$, and $m_s=\frac{\tau (1-\pi )\sigma }{{\rho }_s+{\gamma }_s+{\delta }_s+\mu }$. Furthermore, the basic reproduction number ${\mathcal{R}}_0$ decreases with the baseline influence rate $w_o$ (provided that the prophylaxy-induced infection rate reduction factor ${\varsigma }_o$ satisfies ${\varsigma }_o<1$). The time-varying effective reproduction number is given by

$${\mathcal{R}}_t=\frac{\theta }{(\theta +\mu )(\sigma +\mu )}\sum _{i\in \mathcal{P}}\frac{S_i\left(t\right){\varsigma }_o^{1-i}}{N\left(t\right)-Q\left(t\right)}\sum _{j=p,a,s}{\beta }_j{m}_j.$$

(16b)

Remark 1.

In the absence of opinion dynamics ($w_o=0$), each class of susceptibles $S_i$ approaches its carrying capacity ${\eta }_i/\mu$.

Remark 2.

The stationary sizes of $S_{-1}$ and $S_1$ susceptibles decrease with the baseline influence rate $w_o$ whereas $S_0$ increases with $w_o$. Indeed, the mutual influences of $S_0$ and $S_i$ individuals ($i=\pm 1$) balance and cancel each other whereas interactions between individuals on the opposite sides of the attitude spectrum all lead to positive flows into $S_0$. As a result, if for instance the recruitment rates are equal across susceptible states (${\eta }_i=\eta /3$), then more than the third of the long run population will have a moderate level of prophylactic attitute in the absence of disease. The decay of the basic reproduction number ${\mathcal{R}}_0$ as a function of the baseline influence rate $w_o$ is another consequence of this stationary dynamics.

Remark 3.

If the prophylaxy-induced infection rate reduction factor ${\varsigma }_o$ equals one (no substantive differential prophylactic attitude despite opinion changes), we would expect disease dynamics to be independent of opinion dynamics. Accordingly, $\frac{\partial {\mathcal{R}}_0}{\partial w_o}=0$ if ${\varsigma }_o=1$.

Remark 4.

The basic reproduction number ${\mathcal{R}}_0$ accounts for the implementation of a disease surveillance mechanism if any (i.e. the detection rates π, ${\rho }_a$ and ${\rho }_s$ can be positive even in a disease-free context). In an emerging disease context (e.g. right before the report in late December 2020 of the first confirmed COVID-19 case), some symptoms might be unknown, test kits might not be yet developed or available. In the special case where $\pi \approx {\rho }_a\approx {\rho }_s\approx 0$, the basic reproduction number is

$${\mathcal{R}}_o=\frac{\theta }{(\theta +\mu )(\sigma +\mu )}\left[{\beta }_p+\frac{(1-\tau )\sigma }{{\gamma }_a+\mu }{\beta }_a+\frac{\tau \sigma }{{\gamma }_s+{\delta }_s+\mu }{\beta }_s\right]\frac{\mu }{\eta }\sum _{i\in \mathcal{P}}{S}_i^c{\varsigma }_o^{1-i}$$

(17)

which satisfies ${\mathcal{R}}_o\ge {\mathcal{R}}_0(\pi ,{\rho }_a,{\rho }_s,w_o)\ge {\mathcal{R}}_0(1,{\rho }_a,{\rho }_s,w_o)$ ceteris paribus.

The first measures implemented after the epidemic outbreak of a contagious disease is the identification and isolation of infectious individuals. The detection/isolation effort (targeting and testing of most susceptible groups, contact tracing, voluntary mass testing campaign, systematic testing) is critical to the control of the propagation of the disease in the absence of vaccination. Such measures can be sufficient to contain an epidemic under some conditions detailled in the following corollary of Proposition 1.

Corollary 1

(Critical Detection Rates). Suppose that ${\mathcal{R}}_0(1,{\rho }_a,{\rho }_s,w_o)<1$.

If ${\mathcal{R}}_0(0,{\rho }_a,{\rho }_s,w_o)>1$, then the critical (minimal) early detection probability required to sufficiently lower ${\mathcal{R}}_0$ and ensure disease eradication in the long run is

$${\pi }^{*}({\rho }_a,{\rho }_s,w_o)=1-\frac{\frac{(\theta +\mu )(\sigma +\mu )\eta }{\theta \mu \left({\sum }_{i\in \mathcal{P}}{S}_i^c{\varsigma }_o^{1-i}\right)}-{\beta }_p}{\sigma \left[\frac{(1-\tau ){\beta }_a}{{\rho }_a+{\gamma }_a+\mu }+\frac{\tau {\beta }_s}{{\rho }_s+{\gamma }_s+{\delta }_s+\mu }\right]}$$

(18a)

which decreases with the baseline influence rate $w_o$, and the detection rates ${\rho }_a$ of asymptomatic infectious and ${\rho }_s$ of symptomatic infectious. If ${\mathcal{R}}_0(\pi ,1,{\rho }_s,w_o)<1<{\mathcal{R}}_0(\pi ,0,{\rho }_s,w_o)$, then the critical (minimal) detection rate of asymptomatic infectious is

$${\rho }_a^{*}(\pi ,{\rho }_s,w_o)=\left[\frac{(1-\pi )(1-\tau )\sigma {\beta }_a}{\frac{(\theta +\mu )(\sigma +\mu )\eta }{\theta \mu \left({\sum }_{i\in \mathcal{P}}{S}_i^c{\varsigma }_o^{1-i}\right)}-{\beta }_p-\frac{(1-\pi )\tau \sigma {\beta }_s}{{\rho }_s+{\gamma }_s+{\delta }_s+\mu }}\right]-{\gamma }_a-\mu$$

(18b)

which decreases with π, ${\rho }_s$, and $w_o$. Likewise, if ${\mathcal{R}}_0(\pi ,{\rho }_a,1,w_o)<1<{\mathcal{R}}_0(\pi ,{\rho }_a,0,w_o)$, then the critical (minimal) detection rate of asymptomatic infectious is

$${\rho }_s^{*}(\pi ,{\rho }_s,w_o)=\left[\frac{(1-\pi )\tau \sigma {\beta }_s}{\frac{(\theta +\mu )(\sigma +\mu )\eta }{\theta \mu \left({\sum }_{i\in \mathcal{P}}{S}_i^c{\varsigma }_o^{1-i}\right)}-{\beta }_p-\frac{(1-\pi )(1-\tau )\sigma {\beta }_a}{{\rho }_a+{\gamma }_a+\mu }}\right]-{\gamma }_s-{\delta }_s-\mu$$

(18c)

which decreases with π, ${\rho }_a$, and $w_o$.

It appears that if ${\mathcal{R}}_0<1$ under an hypothetical (and unrealistic) scenario where all infectious individuals are isolated at the presymptomatic stage, then mass testing and quanrantining can be sufficient to ensure that an epidemic is unsustainable in the target population. If ${\mathcal{R}}_0(1,{\rho }_a,{\rho }_s,w_o)>1$, then it is not possible to contain the epidemic of the target contagious disease using isolation measures only. It remains however possible to break the transmission dynamics by reducing exposition to the disease, i.e. the rate of sufficient contacts between potentially infectious and susceptible individuals (for COVID-19, this included e.g. social distancing, face mask wearing, school closing, curfew, ban of gatherings, lockdown). The introduction of vaccination is the ultimate solution to reduce transmissions while alleviating the social and economic drawbacks of the first containment measures.

3.2. Disease–free equilibrium and reproduction numbers in a vaccination context

We find the d.f.e. for a population described by the UVEIQR-Opinion model (14), and compute the related control reproduction number. We further discuss the critical vaccination rate to ensure disease eradication in the long run.

Proposition 2

(Disease–free Equilibrium & Reproduction Number). The UVEIQR-Opinion model (14) admits a unique d.f.e. given for $w_o>0$ by

$$\begin{array}{cc}\hfill {\mathit{X}}^c& ={\left({\left({\mathit{S}}^c\right)}^{\top },0,0,0,0,0,0\right)}^{\top }\hfill \end{array}$$

(19a)

where ${\mathit{S}}^c={\left(U_{-1u}^c,U_{0u}^c,U_{1u}^c,U_{-1v}^c,U_{0v}^c,U_{1v}^c,V_{-1}^c,V_0^c,V_1^c\right)}^{\top }$ is given by

$$\begin{array}{cc}\hfill {\mathit{S}}^c& ={\mathit{M}}^{-1}\mathit{\eta }\mathrm{with}\hfill \\ \hfill \mathit{\eta }& ={\left({\eta }_{-1u},{\eta }_{0u},{\eta }_{1u},{\eta }_{-1uv},{\eta }_{0uv},{\eta }_{1uv},{\eta }_{-1v},{\eta }_{0v},{\eta }_{1v}\right)}^{\top },\hfill \end{array}$$

(19b)

$$\begin{array}{cc}\hfill \mathit{M}& =\frac{w_o}{N^c}\left(\begin{array}{ccc}{\mathit{M}}_u& -U_u^c{\mathit{I}}_3& \mathbf{0}\\ -\left(U_v^c+V^c\right){\mathit{I}}_3& {\mathit{M}}_{uv}& -\frac{N^c}{w_o}\alpha {\mathit{I}}_3\\ \mathbf{0}& -\frac{N^c}{w_o}\upsilon {\mathit{I}}_3& {\mathit{M}}_v\end{array}\right)+\mu {\mathit{I}}_9,\hfill \end{array}$$

(19c)

$$\begin{array}{cc}\hfill U_u^c& =\frac{\eta {\eta }_{uu}(\alpha +\mu )}{w_o\mu ({\eta }_v+\upsilon U_v^c)+\eta \mu (\alpha +\mu )},\hfill \end{array}$$

(19d)

$$\begin{array}{cc}\hfill U_v^c& =\left\{\begin{array}{cc}\frac{w_o{C}_0}{(\alpha +\mu )\eta +w_o{\eta }_v}& \mathrm{if}\upsilon =0\\ \\ \frac{\sqrt{C_1^2+4C_0{C}_2}-C_1}{2C_2}& \mathrm{if}\upsilon \ne 0\end{array}\right.,\hfill \end{array}$$

(19e)

$$\begin{array}{cc}\hfill V^c& =\frac{{\eta }_v+\upsilon U_v^c}{\alpha +\mu },\hfill \\ \hfill {\mathit{M}}_u& ={\mathit{M}}_0+\left(U_v^c+V^c\right){\mathit{I}}_3,\hfill \\ \hfill {\mathit{M}}_{uv}& ={\mathit{M}}_0+\left(U_u^c+\frac{N^c}{w_o}\upsilon \right){\mathit{I}}_3,\hfill \\ \hfill {\mathit{M}}_v& ={\mathit{M}}_0+\frac{N^c}{w_o}\alpha {\mathit{I}}_3,\hfill \\ \hfill {\mathit{M}}_0& =\left(\begin{array}{ccc}{S}_0^c+S_1^c& -S_{-1}^c& 0\\ -(S_0^c+S_1^c)& S_{-1}^c+S_1^c& -(S_{-1}^c+S_0^c)\\ 0& -S_1^c& S_{-1}^c+S_0^c\end{array}\right),\hfill \end{array}$$

(19f)

where we have set $C_2=\upsilon \left(1+\frac{\upsilon }{\alpha +\mu }\right)$, $C_1={\eta }_u\left(\frac{\alpha +\upsilon +\mu }{w_o}-\frac{\upsilon }{\mu }\right)+{\eta }_v\left(1+\frac{\alpha +\upsilon +\mu }{w_o}+\frac{\upsilon (\mu -\alpha )}{\mu (\alpha +\mu )}\right)$ and $C_0=\eta {\eta }_{uv}\frac{\alpha +\mu }{w_o\mu }+\frac{{\eta }_v}{\mu }\left({\eta }_u+\frac{\alpha }{\alpha +\mu }{\eta }_v+\frac{\alpha }{w_o}\eta \right)$, ${\eta }_{uu}={\sum }_{i\in \mathcal{P}}{\eta }_{iu}$, ${\eta }_u={\sum }_{i\in \mathcal{P}}({\eta }_{iu}+{\eta }_{iuv})$, ${\eta }_v={\sum }_{i\in \mathcal{P}}{\eta }_{iv}$, and ${\mathit{I}}_n$ denotes the $n\times n$ identity matrix. In the absence of opinion dynamics ($w_o=0$), we have $U_{iu}^c=\frac{{\eta }_{iu}}{\mu }$, $U_{iv}^c=\frac{{\eta }_{iuv}}{\mu }$, and $V_i^c=\frac{{\eta }_{iv}}{\mu }$ for $i\in \mathcal{P}$.

Moreover, for a population described by System (Section 2.8), the control reproduction number is given by

$$\begin{array}{cc}\hfill {\mathcal{R}}_c(\upsilon ,\kappa ,\alpha ,w_o)& =\sum _{i\in \mathcal{P}}\sum _{j=p,a,s}{\mathcal{R}}_{cij}\mathrm{where}\hfill \\ \hfill {\mathcal{R}}_{cij}& =\frac{\theta }{(\theta +\mu )(\sigma +\mu )}\frac{\left[U_i^c+(1-\kappa )V_i^c\right]{\varsigma }_o^{1-i}}{N^c}{\beta }_j{m}_j\hfill \end{array}$$

(20a)

is the contribution of $S_i$ susceptibles and $I_j$ infectious to ${\mathcal{R}}_c$, with $U_i^c=U_{iu}^c+U_{iv}^c$. The control reproduction number ${\mathcal{R}}_c$ decreases with the vaccination rate υ and the baseline influence rate $w_o$, and satisfies

$$(1-\kappa ){\mathcal{R}}_0\le {\mathcal{R}}_c(\upsilon ,\kappa ,\alpha ,w_o)\le {\mathcal{R}}_0.$$

(20b)

The time-varying effective reproduction number is given by

$$\begin{array}{cc}\hfill {\mathcal{R}}_{ct}(\upsilon ,\kappa ,\alpha ,w_o)& =\sum _{i\in \mathcal{P}}\sum _{j=p,a,s}{\mathcal{R}}_{cijt}\mathrm{where}\hfill \\ \hfill {\mathcal{R}}_{cijt}& =\frac{\theta }{(\theta +\mu )(\sigma +\mu )}\frac{\left[U_i\left(t\right)+(1-\kappa )V_i\left(t\right)\right]{\varsigma }_o^{1-i}}{N\left(t\right)-Q\left(t\right)}{\beta }_j{m}_j.\hfill \end{array}$$

(20c)

Remark 5.

The expression of ${\mathit{S}}^c$ in matrix notation given by Equation (19b) is developed in Appendix E where a formula is provided for each of the nine elements of ${\mathit{S}}^c$.

It appears from Equation (20a) that, as expected, ${\mathcal{R}}_c$ decreases with both vaccination rate ($\upsilon$) and average vaccine efficacy ($\kappa$), but increases with the immunity lost rate ($\alpha$). Inequality (20b) recognizes that vaccine efficacy is an important parameter in disease control: ${\mathcal{R}}_c$ cannot fall under $(1-\kappa ){\mathcal{R}}_0$ even for a large vaccination rate $\upsilon$. On setting

$${\kappa }^{*}=\frac{{\mathcal{R}}_0-1}{{\mathcal{R}}_0}$$

(21)

for ${\mathcal{R}}_0>1$, a necessary condition for disease eradication is that the average vaccine efficacy must satisfy $\kappa >{\kappa }^{*}$ (ensuring $(1-\kappa ){\mathcal{R}}_0<1$). The following corollary gives the critical vaccination rate to eradicate the disease for a fixed average vaccine efficacy $\kappa$.

Corollary 2

(Critical Vaccination Rate). If ${\mathcal{R}}_0>1$ and $\kappa >{\kappa }^{*}$, then the critical (minimal) vaccination rate required to sufficiently lower ${\mathcal{R}}_c$ and ensure disease eradication in the long run is

$${\upsilon }^{*}(\kappa ,\alpha )=\frac{(\alpha +\mu )({\mathcal{R}}_0-1)-\kappa p_v\mu {\mathcal{R}}_0}{1-(1-\kappa ){\mathcal{R}}_0}$$

(22a)

which increases with the immunity lost rate α, decreases with κ, and satisfies

$${\upsilon }^{*}>(\alpha +\mu )({\mathcal{R}}_0-1)-p_v\mu {\mathcal{R}}_0.$$

(22b)

3.3. Stability of disease–free equilibriums and persistence of the disease

The following results establish the stability of the disease-free equilibrium (15a).

Lemma 2

(Local Asymptotic Stability of the Disease–free Equilibrium). The disease-free equilibrium ${\mathit{X}}^c$ of the SEIQR-Opinion model (7) is locally asymptotically stable if ${\mathcal{R}}_0\le 1$, and unstable if ${\mathcal{R}}_0>1$.

Proposition 3

(Global Asymptotic Stability of the Disease–free Equilibrium). The disease-free equilibrium ${\mathit{X}}^c$ of the SEIQR model (7) is globally asymptotically stable, i.e. for any solution $\mathit{X}={\left(S_{-1},S_0,S_1,E,I_p,I_a,I_s,Q,R\right)}^{\top }$, ${lim}_{t\to \infty }\mathit{X}\left(t\right)={\mathit{X}}^c$, provided that ${\mathcal{R}}_0\le 1$.

If ${\mathcal{R}}_c>1$, then the d.e.f. (19a) is not stable, and any introduction of infectious individuals has the potential to kick off and maintain an epidemic outbreak, as per the next proposition.

Proposition 4

(Disease Persistence). Let us consider the UVEIQR-Opinion model (14). If ${\mathcal{R}}_c>1$, then the disease persists uniformly, i.e. there exists a positive real constant ϱ independent of the initial data, such that for any disease-dependent solution $\mathit{X}={\left(U_{-1u},U_{0u},U_{1u},U_{-1v},U_{0v},U_{1v},V_{-1},V_0,V_1,E,I_p,I_a,I_s,Q,R\right)}^{\top }$, we have:

$$\begin{array}{cc}\hfill \underset{t\to \infty }{lim}x\left(t\right)& \ge \varrho \mathrm{for}x\in \left\{U_{-1u},U_{0u},U_{1u},U_{-1v},U_{0v},U_{1v},E,I_p,I_a,I_s,Q,R\right\},\hfill \end{array}$$

(23a)

$$\begin{array}{cc}\hfill \underset{t\to \infty }{lim}{V}_i\left(t\right)& \ge \varrho \mathrm{when}{\eta }_v>0\mathrm{or}\upsilon >0,\mathrm{and}\hfill \end{array}$$

(23b)

$$\begin{array}{cc}\hfill \underset{t\to \infty }{lim}{V}_i\left(t\right)& =0\mathrm{when}{\eta }_v=\upsilon =0.\hfill \end{array}$$

(23c)

4. Numerical results

4.1. Impacts of the initial distribution of behaviours

Responses: $\mathrm{e}=E/N$, ${\mathrm{i}}_{mix}=(I_p+I_a+I_s)/N$, $\mathrm{q}=Q/N$, $\mathrm{v}=V/N$

Responses: (true) peak time $T_p=\underset{t}{arg}max{\mathrm{i}}_{mix}\left(t\right)$, observable peak time $t_p=\underset{t}{arg}max\mathrm{q}\left(t\right)$,

Responses: (true) epidemic peak size ${\mathrm{i}}_{mix}\left(T_p\right)$, observable epidemic peak size $\mathrm{q}\left(t_p\right)$,

Responses: epidemic duration $t_f$, final (true) epidemic size, observed epidemic size

Responses: basic, control and effective reproduction numbers

4.1.1. Vaccination-free dynamics

Vary presence/absence of opinions; influence functions/parameters

Vary the initial proportion of different prophylactic opinions

4.1.2. Vaccination-dependent dynamics

Vary the initial vaccine coverage (proportion of vaccinated individuals)

Vary the initial proportion of pro-vaccine susceptibles

Vary the initial proportion of different prophylactic opinions (by vaccine-opinion)

Vary vaccination rate

4.2. Impacts of the nature of behavioural responses

The above responses

Vary influence parameters $w_o$ (relative to ${\beta }_j$), $\tilde{k}$ and $w_{max}$

(Also vary the initial proportion of different prophylactic opinions)

4.3. Impacts of detection rates and distorted perceived disease prevalence

The above responses

Vary early detection probability $\pi$ and late detection rates ${\rho }_a$ and ${\rho }_s$.

Vary the estimates of mean residential times ${\tilde{r}}_p$, ${\tilde{r}}_s$,

and ${\tilde{r}}_s$ around their true values so that the perceived disease prevalence under/over estimates the true disease prevalence.

5. Discussion and conclusion

5.1. The impact of opinions on disease dynamics

5.2. The behavioural response to vaccination

5.3. The impact of distorted perceived disease prevalence

5.4. Limits and perspectives

Because of the relatively large number of possible states given the considered disease and opinion dynamics, some simple assumptions were made in the model construction in order to reduce the number of model parameters on the one hand, and mostly to obtain a minimum of analytical closed form results on the other hand. Ahead is the use of a unique class of exposed individuals, irrespective of the vaccination status of the individuals before exposition. Although this assumption may hold for some diseases, it is not realistic in the ongoing COVID-19 pandemic context, because the effects of the currently available vaccines are beyond a mere reduction in the force of infection. Indeed, the vaccines also reduce the risk of severe forms of the disease (requiring respiratory assistance), transmission from vaccinated infected, risk of long term sequels, and disease-related mortality [66,67], so that the paths from exposition to recovery should be different for vaccinated individuals as compared to non vaccinated individuals. In addition, no age structure is included in the proposed models, although COVID-19 transmission and mortality rates, as well as vaccination scenarios are highly age dependent [68,69,70,71]. Another source of complexity we did not account for is the co-existence of many variants of SARS-CoV-2 with different transmission and mortality rates in a target human population [72,73].

Many strong assumptions were also made in regards to opinion dynamics. The strongest one is likely that opinion dynamics only occur in the susceptible population. As in Tyson et al. [22], this assumption simplifies model equations a lot. Though, all individuals in disease-dependent states, including the non-mixing population Q (which can interract with susceptibles by e.g. cell phone, social media, ...), can obviously influence the opinions of susceptibles. For instance, the prophylactic opinions of physically isolated (Q) and recovered (R) individuals can change in response to being aware of their current or past infectious states. These opinion dynamics can then contribute to the overall influence of a given opinion i holders on susceptibles who have a different opinion $j\ne i$. Clearly, as for susceptibles, disease-dependent classes should also be differentiated according to opinions, and their interactions with other classes allowed to influence, to some extent, the attitude of susceptible individuals. Another strong assumption is the consideration of only one prophylactic attitude level for each prophylactic opinion. This hypothesis supposes that all individuals with a given opinion have the same prophylactic attitude level (same degree of opinion), and thereby hides interactions between like-minded individuals. In consequence, the assumption neglects amplification of opinion, a phenomenon which can substantially impact opinion dynamics [22].

In reality, the actual attitude of a susceptible individual depends not only on its opinion, but also on the enforcement of any restriction by local and national governements. The restrictions, often referred to as non-pharmaceutical interventions (NPIs) can significanly affect effective contact rates depending on the stringency of the measures. A more realistic model should indeed account for the NPIs enforced by governements in the baseline contact rate ${\beta }_j$ by each infectious class j. Since NPIs are functions of time, so should be the contact rates. A more general model could thus consider contact rates of the form ${\beta }_{ij}\left(t\right)={\varsigma }_o^{1-i}{\beta }_j\left(t\right)$ with ${\beta }_j\left(t\right)={\beta }_{oj}exp\left({\mathit{z}}_t^{\top }{\mathit{\theta }}_j\right)$, where ${\beta }_{oj}$ is the baseline contact rate when no NPI is implemented, ${\mathit{z}}_t$ is a vector of uncorrelated indexes measuring the intensity of NPIs, and ${\mathit{\theta }}_j$ is a vector of regression parameters linking ${\mathit{z}}_t$ to ${\beta }_j$.

An additional key assumption is that all individuals have the same baseline influence rate $w_o$ in disease–free conditions, irrespective of prophylactic opinion. Instead of Equation (4b), the basic influence weights $w_i$ could have, for $x\in [0,1]$, the more general form

$$\begin{array}{c}\hfill w_i\left(x\right)=\left\{\begin{array}{cc}{w}_o\left[1+w_{\infty }\frac{x}{\left(\tilde{k}+x\right)}\right]& \mathrm{if}i=-1\\ w_o\left[\varphi +\frac{\left(w_{\infty }-\varphi \right)}{2}\frac{x}{\left(\tilde{k}+x\right)}\right]& \mathrm{if}i=0\\ w_o\left[1-\frac{x}{\left(\tilde{k}+x\right)}\right]& \mathrm{if}i=1\end{array}\right.\end{array}$$

(24a)

where $\varphi \in (0,1]$ is a baseline influence rate reduction factor for a moderate opinion. In Equation (24a), the parameter $\varphi$ allows to reduce the influence rate of moderate prophylactic opinion holders ($i=0$) relative to extreme opinion holders ($i=\pm 1$). The model presented in Section 2 corresponds to the special case $\varphi =1$. In this modified influence process based on Equations (4a) and (24a), Equation (10e) defining influence rates in a vaccination-dependent context becomes

$$\begin{array}{c}\hfill {\tilde{\omega }}_i\left(t\right)=w_o{\varphi }^{1-\left|i\right|}\frac{V\left(t\right)}{N\left(t\right)}+\left[1-\frac{V\left(t\right)}{N\left(t\right)}\right]w_i\left(\tilde{P}\left(t\right)\right).\end{array}$$

(24b)

The resulting extended SEIQR-Opinion model admits, for $w_o>0$ and $\varphi <1$, disease-free equilibriums of the form ${\mathit{X}}^c={\left(S_{-1}^c,S_0^c,S_1^c,0,0,0,0,0,0\right)}^{\top }$ where

$$\begin{array}{cc}\hfill S_{-1}^c& =\frac{{\eta }_{-1}}{\mu }-\frac{1}{2}\left[N^c+\frac{\eta }{w_o}-\sqrt{\Delta }-(1-\varphi )S_0^c\left[1+\frac{w_o({\eta }_1-{\eta }_{-1})}{\mu \left[\eta -w_o(1-\varphi )S_0^c\right]}\right]-\frac{{\eta }_0}{\mu }\right],\hfill \end{array}$$

(25a)

$$\begin{array}{cc}\hfill S_0^c& =\frac{1}{1-\varphi }\left[\frac{\eta }{w_o}-\mathrm{Proot}\left(\mathit{a}\right)\right],\hfill \end{array}$$

(25b)

$$\begin{array}{cc}\hfill S_1^c& =\frac{{\eta }_1}{\mu }-\frac{1}{2}\left[N^c+\frac{\eta }{w_o}-\sqrt{\Delta }-(1-\varphi )S_0^c\left[1-\frac{w_o({\eta }_1-{\eta }_{-1})}{\mu \left[\eta -w_o(1-\varphi )S_0^c\right]}\right]-\frac{{\eta }_0}{\mu }\right],\hfill \end{array}$$

(25c)

where $\Delta =2N^c\left(\frac{{\eta }_{-1}+{\eta }_1}{w_o}\right)+{\left[\frac{\eta }{w_o}-(1-\varphi )S_0^c\right]}^2+{\left[\frac{{\eta }_{-1}-{\eta }_1}{\mu -(1-\varphi )w_o{S}_0^c/N^c}\right]}^2$, $\mathrm{Proot}(·)$ returns the positive roots of the quartic polynomial defined for x as ${\sum }_{k=1}^5{a}_k{x}^{k-1}$, with $a_k$ the kth element of the vector $\mathit{a}$, $a_1={(1-\varphi )}^2{\left(\frac{N^c}{w_o}\right)}^2\frac{{({\eta }_1-{\eta }_{-1})}^2}{3-2\varphi }$, $a_2=0$, $a_4=\frac{2(2-\varphi )}{3-2\varphi }\left[(1-\varphi )N^c-\frac{\eta }{w_o}\right]$, $a_5=1$, and $a_3=\frac{1}{3-2\varphi }\left[{\left[(1-\varphi )N^c-\frac{\eta }{w_o}\right]}^2-2{(1-\varphi )}^2{N}^c\left(\frac{{\eta }_{-1}+{\eta }_1}{w_o}\right)\right]$. For $\varphi <1$, Remark 2 does not hold in general. Indeed, it turns out that the extended model can admit up to three DFEs, so that, as in the SIR-Opinion model of Tyson et al. [22], the basic reproduction number depends on the initial distribution of the population along the attitude spectrum. Nevertheless, in the special case ${\eta }_{-1}={\eta }_1$ (i.e. when the recruitment rates of individuals holding the two extreme opinions have the same shares in the total recruitment rate $\eta$) with opinion dynamics ($w_o>0$), the extended SEIQR-Opinion model has a unique d.f.e. where we have $S_{-1}^c=S_1^c=\frac{1}{2}\left(N^c-S_0^c\right)$ and Equation (25b) is simplified to

$$\begin{array}{cc}\hfill S_0^c& =\frac{1}{3-2\varphi }\left[(2-\varphi )N^c+\frac{\eta }{w_o}-\sqrt{D_0}\right]\hfill \end{array}$$

(25d)

with $D_0={\left[(2-\varphi )N^c+\eta /w_o\right]}^2-(3-2\varphi )N^c\left(N^c+2{\eta }_0/w_o\right)$. Here, the number $S_0^c$ of moderate opinion holders at the d.f.e. increases not only with the baseline influence rate $w_o$ (as in Remark 2), but also with the influence rate reduction factor $\varphi$, so that the basic reproduction number ${\mathcal{R}}_0$ decreases with both $w_o$ and $\varphi$. The study of the extended model could thus uncover interesting changes in opinion and disease dynamics.

Appendix A.1. The extended SEIQR model

The models considered for disease dynamics distinguish two different states during the pathogen incubation period when exposed individuals do not develop any COVID-19 symptom: the simple Exposed (E) state for non-infectious individuals, and the presymptomatic state ($I_p$) for infectious individuals. The simple exposition period lasts $1/\theta$ (up to 14 days [48], but generally short, i.e. about six days) and is followed by the presymptomatic period (which lasts $1/\sigma$) during which incubating individuals become infectious but remain without symptom [47,48,49,50,51,52]. Contacts between susceptibles and presymptomatic infectious ($I_p$) can be sufficient for transmission (see e.g. [45] and [46]). When control measures such as contact tracing and systematic tests on target groups are implemented, some presymptomatic infectious are detected with probability $\pi$ and “quarantined” (i.e. isolated) at home, hospitals or dedicated places. The remaining (undetected) presymptomatic infectious individuals evolve into two groups based on the development or not of COVID-19 symptoms: $100\tau \%$ symptomatic infectious ($I_s$) and $100(1-\tau )\%$ asymptomatic infectious ($I_a$). Some of the symptomatic infectious individuals self-isolate or are detected and enter the class Q of quarantined at the rate ${\rho }_s$. Again, contact tracing and systematic tests on target groups can lead to the detection and isolation of some asymptomatic infectious individuals at the rate ${\rho }_a$. Symptomatic infectious ($I_s$) and isolated individuals (Q) die of COVID-19 at the rates ${\delta }_s$ and ${\delta }_q$ respectively. The alive asymptomatic infectious, symptomatic infectious, and quarantined individuals finally recover from COVID-19, at the rates ${\gamma }_a$, ${\gamma }_s$ and ${\gamma }_q$ respectively, and form the class of recovered individuals (R) who acquire a temporary immunity to SARS-CoV-2. Recovered individuals lose their immunity at the rate ${ϵ}_o$ and become again susceptible to the pathogen. The flow diagram of the SEIQR model is depicted in Figure A1. The total population size $N\left(t\right)$ at time $t\ge 0$ is given by

$$N\left(t\right)=S\left(t\right)+E\left(t\right)+I_p\left(t\right)+I_a\left(t\right)+I_s\left(t\right)+Q\left(t\right)+R\left(t\right).$$

(A1)

Figure A1. Flow-chart of a SEIQR model showing the flow of humans between different compartments. The susceptible population is denoted by S, and E, $I_p$, $I_a$, $I_s$, Q and R denote respectively the exposed, the presymptomatic infectious, the asymptomatic infectious, the symptomatic infectious, the quarantined infectious, and the recovered populations. The parameters of the model are described in Table 1.

Figure A1. Flow-chart of a SEIQR model showing the flow of humans between different compartments. The susceptible population is denoted by S, and E, $I_p$, $I_a$, $I_s$, Q and R denote respectively the exposed, the presymptomatic infectious, the asymptomatic infectious, the symptomatic infectious, the quarantined infectious, and the recovered populations. The parameters of the model are described in Table 1.

The SEIQR model is described at time t by the following system of differential equations:

$$\begin{array}{cc}\hfill \dot{S}\left(t\right)& =\eta -{\lambda }_o\left(t\right)S\left(t\right)-\mu S\left(t\right)+{ϵ}_{o}R\left(t\right),\hfill \end{array}$$

(A2a)

$$\begin{array}{cc}\hfill \dot{E}\left(t\right)& ={\lambda }_o\left(t\right)S\left(t\right)-(\theta +\mu )E\left(t\right),\hfill \end{array}$$

(A2b)

$$\begin{array}{cc}\hfill {\dot{I}}_p\left(t\right)& =\theta E\left(t\right)-(\sigma +\mu )I_p\left(t\right),\hfill \end{array}$$

(A2c)

$$\begin{array}{cc}\hfill {\dot{I}}_a\left(t\right)& =(1-\tau )(1-\pi )\sigma I_p\left(t\right)-({\rho }_a+{\gamma }_a+\mu )I_a\left(t\right),\hfill \end{array}$$

(A2d)

$$\begin{array}{cc}\hfill {\dot{I}}_s\left(t\right)& =\tau (1-\pi )\sigma I_p\left(t\right)-({\rho }_s+{\gamma }_s+{\delta }_s+\mu )I_s\left(t\right),\hfill \end{array}$$

(A2e)

$$\begin{array}{cc}\hfill \dot{Q}\left(t\right)& =\pi \sigma I_p\left(t\right)+{\rho }_a{I}_a\left(t\right)+{\rho }_s{I}_s\left(t\right)-({\gamma }_q+{\delta }_q+\mu )Q\left(t\right),\hfill \end{array}$$

(A2f)

$$\begin{array}{cc}\hfill \dot{R}\left(t\right)& ={\gamma }_a{I}_a\left(t\right)+{\gamma }_s{I}_s\left(t\right)+{\gamma }_{q}Q\left(t\right)-({ϵ}_o+\mu )R\left(t\right),\hfill \end{array}$$

(A2g)

with the nonnegative initial conditions $S\left(0\right)=S_0$, $E\left(0\right)=E_0$, $I_p\left(0\right)=I_{0p}$, $I_a\left(0\right)=I_{0a}$, $I_s\left(0\right)=I_{0s}$, $Q\left(0\right)=Q_0$, and $R\left(0\right)=R_0$ where ${\left(S_0,E_0,I_{0p},I_{0a},I_{0s},Q_0,R_0\right)}^{\top }\in {[0,\infty )}^7$. In System (A2), ${\lambda }_o\left(t\right)$ is the force of infection, and the constant rate parameters of the model are described in Table 1.

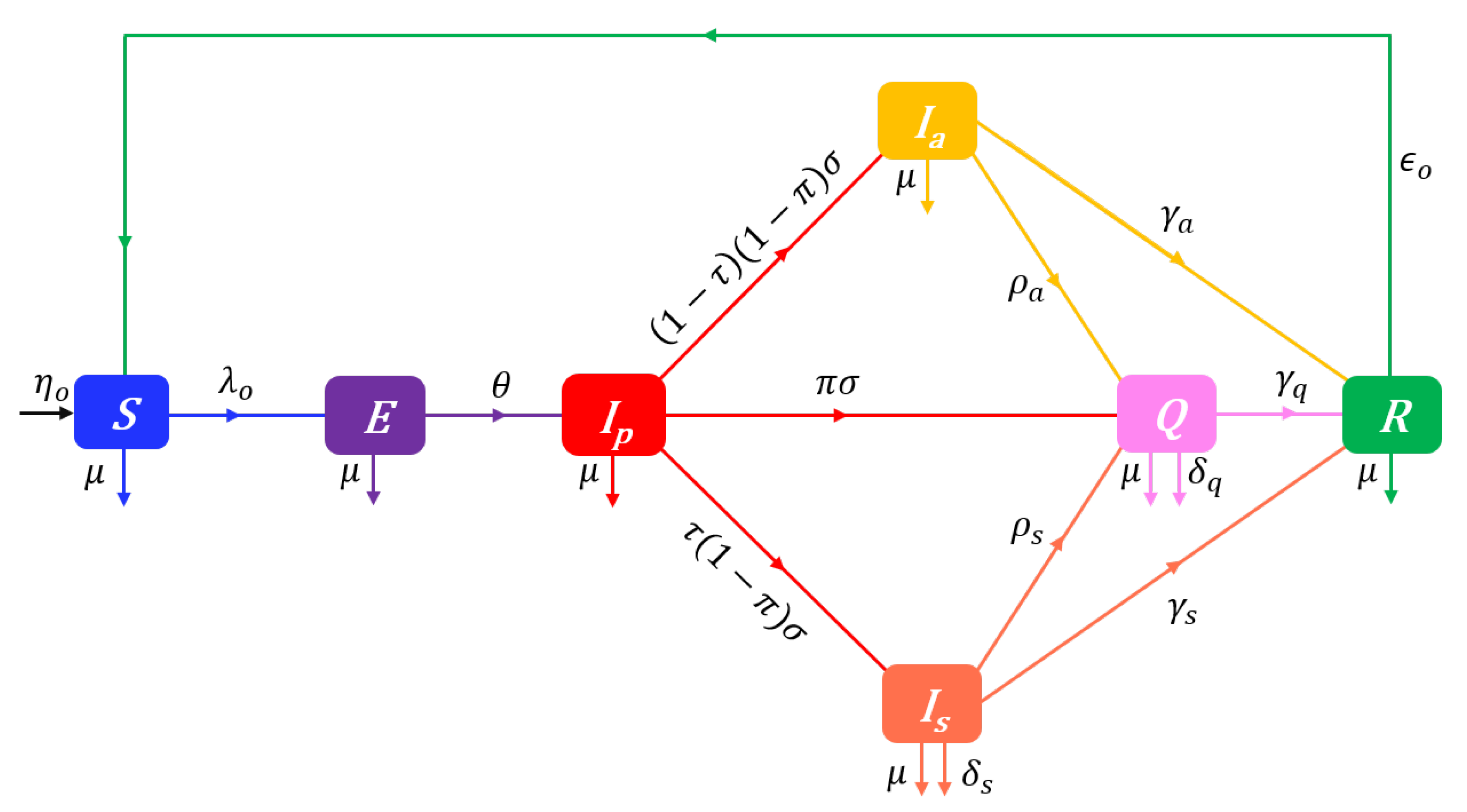
Appendix A.2. The UVEIQR model

Since many COVID-19 vaccines are currently distributed at various rates across the world, we allow the disease dynamics model to account for vaccine-induced immunity. For simplicity, we do not distinguish age groups although COVID-19 vaccination is widely implemented with different strategies and at different rates for childreen and adults [74,75,76]. Vaccines are primarily designed to prevent infectious diseases through the immunisation of vaccinated individuals [77,78], and thus increase the heterogeneity of the susceptible population S. Specifically, susceptible individuals are distinguished into an unvaccinated (and completely susceptible) population (U) which gets vaccinated at the rate $\upsilon$, and a vaccinated (with active vaccine-induced partial immunity) susceptible population (V) which loses vaccine-induced immunity at the rate $\alpha$ (the so called resusceptibility probability [79,80]). The timely number of net immigration (and new births) which enters the class of susceptibles is accordingly distinguished into unvaccinated (${\eta }_u$) and vaccinated individuals (${\eta }_v$) such that $\eta ={\eta }_u+{\eta }_v$. The flow diagram of the UVEIQR model is shown in Figure A2 and the disease dynamics is described by the following system of differential equations:

Figure A2. Flow-chart of a UVEIQR model showing the flow of humans between different compartments. U is the unvaccinated (completely susceptible) population, V is the healthy vaccinated but partially susceptible population, E, $I_p$, $I_a$, $I_s$, Q and R denote respectively the exposed, the presymptomatic infectious, the asymptomatic infectious, the symptomatic infectious, the quarantined, and the recovered populations. The parameters of the model are described in Table 1.

Figure A2. Flow-chart of a UVEIQR model showing the flow of humans between different compartments. U is the unvaccinated (completely susceptible) population, V is the healthy vaccinated but partially susceptible population, E, $I_p$, $I_a$, $I_s$, Q and R denote respectively the exposed, the presymptomatic infectious, the asymptomatic infectious, the symptomatic infectious, the quarantined, and the recovered populations. The parameters of the model are described in Table 1.

$$\begin{array}{cc}\hfill \dot{U}\left(t\right)& ={\eta }_u-\upsilon U\left(t\right)+\alpha V\left(t\right)-{\lambda }_o\left(t\right)U\left(t\right)-\mu U\left(t\right)+{ϵ}_{o}R\left(t\right),\hfill \end{array}$$

(A3a)

$$\begin{array}{cc}\hfill \dot{V}\left(t\right)& ={\eta }_v+\upsilon U\left(t\right)-\alpha V\left(t\right)-(1-\kappa ){\lambda }_o\left(t\right)V\left(t\right)-\mu V\left(t\right),\hfill \end{array}$$

(A3b)

$$\begin{array}{cc}\hfill \dot{E}\left(t\right)& ={\lambda }_o\left(t\right)U\left(t\right)+(1-\kappa ){\lambda }_o\left(t\right)V\left(t\right)-(\theta +\mu )E\left(t\right),\hfill \end{array}$$

(A3c)

$$\begin{array}{cc}\hfill {\dot{I}}_p\left(t\right)& =\theta E\left(t\right)-(\sigma +\mu )I_p\left(t\right),\hfill \end{array}$$

(A3d)

$$\begin{array}{cc}\hfill {\dot{I}}_a\left(t\right)& =(1-\tau )(1-\pi )\sigma I_p\left(t\right)-({\rho }_a+{\gamma }_a+\mu )I_a\left(t\right),\hfill \end{array}$$

(A3e)

$$\begin{array}{cc}\hfill {\dot{I}}_s\left(t\right)& =\tau (1-\pi )\sigma I_p\left(t\right)-({\rho }_s+{\gamma }_s+{\delta }_s+\mu )I_s\left(t\right),\hfill \end{array}$$

(A3f)

$$\begin{array}{cc}\hfill \dot{Q}\left(t\right)& =\pi \sigma I_p\left(t\right)+{\rho }_a{I}_a\left(t\right)+{\rho }_s{I}_s\left(t\right)-({\gamma }_q+{\delta }_q+\mu )Q\left(t\right),\hfill \end{array}$$

(A3g)

$$\begin{array}{cc}\hfill \dot{R}\left(t\right)& ={\gamma }_a{I}_a\left(t\right)+{\gamma }_s{I}_s\left(t\right)+{\gamma }_{q}Q\left(t\right)-({ϵ}_o+\mu )R\left(t\right),\hfill \end{array}$$

(A3h)

with the nonnegative initial conditions $U\left(0\right)=U_0$, $V\left(0\right)=V_0$, $E\left(0\right)=E_0$, $I_j\left(0\right)=I_{0j}$, $Q\left(0\right)=Q_0$, and $R\left(0\right)=R_0$ where ${\left(U_0,V_0,E_0,Q_0,R_0\right)}^{\top }\in {[0,\infty )}^5$ and $I_{0j}\ge 0$ for any $j\in \left\{p,a,s\right\}$. In System (A3), ${\lambda }_o\left(t\right)$ is the force of infection in the completely susceptible population as given by Equation (2), ${\eta }_u+{\eta }_v=\eta$, and the constant rate parameters are as described in Table 1. The total population size $N\left(t\right)$ is given at time t by

$$N\left(t\right)=U\left(t\right)+V\left(t\right)+E\left(t\right)+I_p\left(t\right)+I_a\left(t\right)+I_s\left(t\right)+Q\left(t\right)+R\left(t\right).$$

Note that the UVEIQR model (A3) includes the SEIQR model (A2) as a special case when $V_0=\upsilon ={\eta }_v=0$ so that $V\left(t\right)=0$ and $S\left(t\right)=U\left(t\right)$ for any $t\ge 0$. Also note that for the general UVEIQR model, the force of infection is reduced by a factor $(1-\kappa )$ in the vaccinated population.

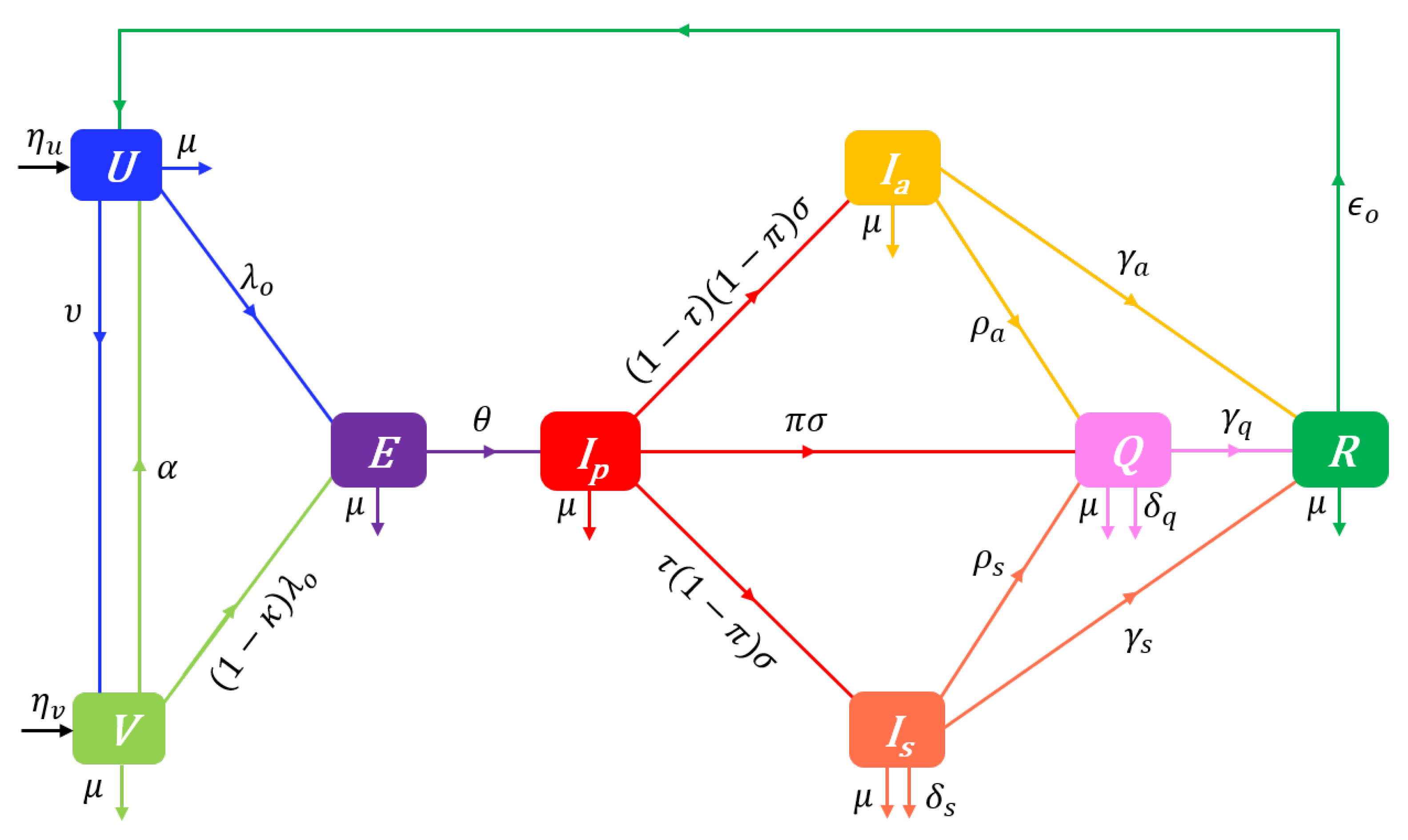
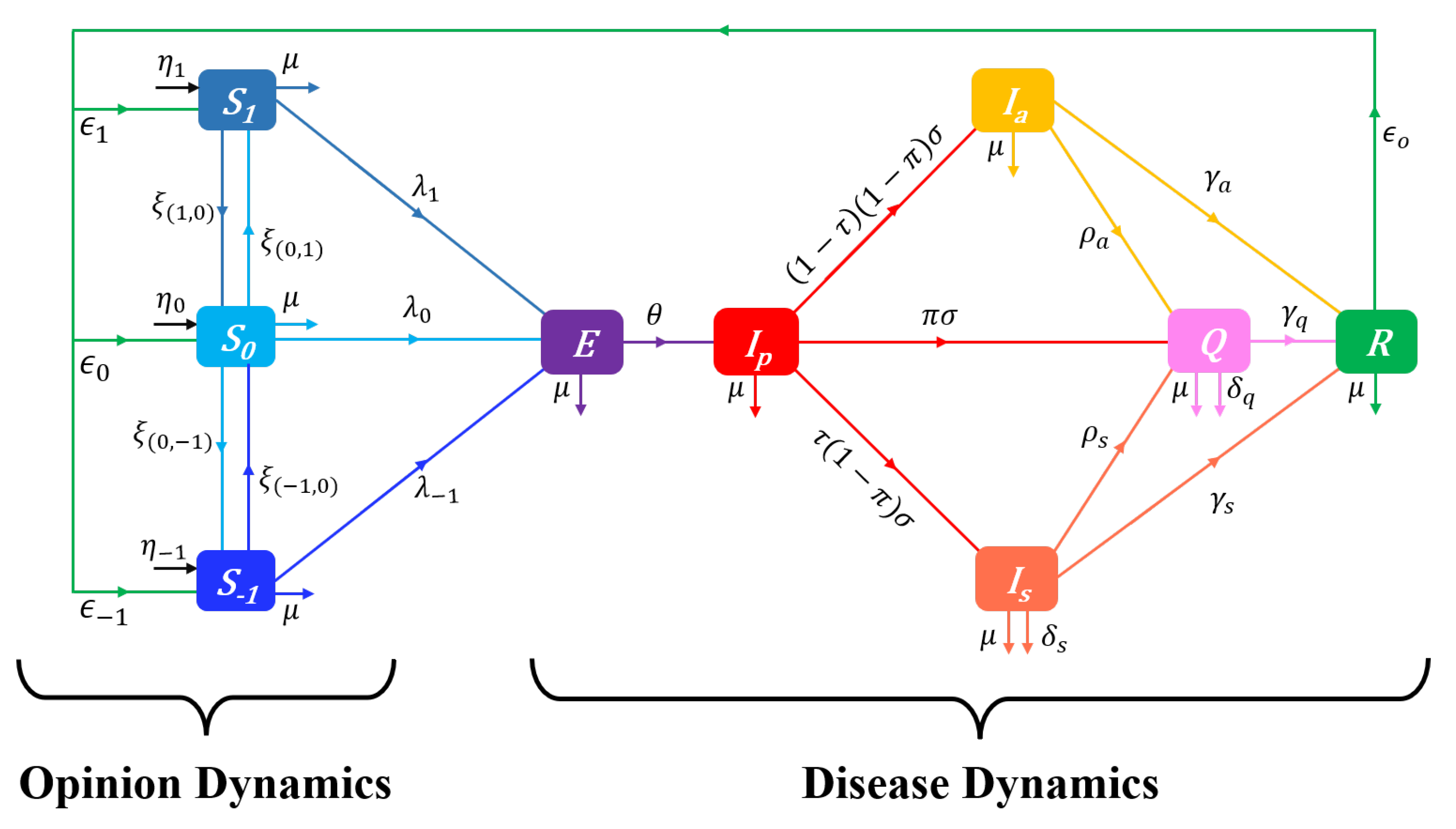
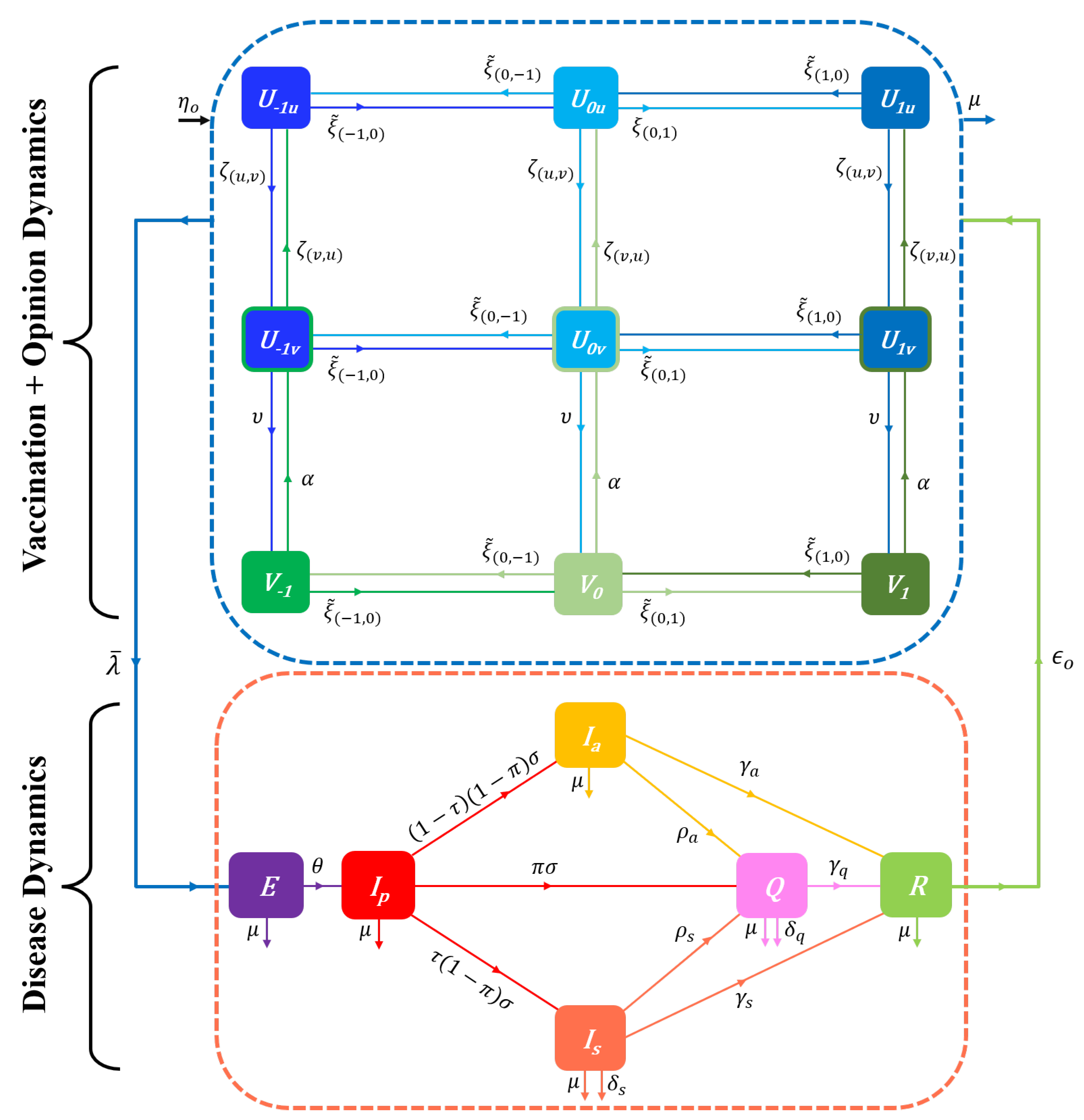
Appendix A.3. Mathematical properties

Since the SEIQR model (Appendix A.1) is nested into the UVEIQR model (Appendix A.2), we restrict attention to the latter, and then discuss the results in the special case $V_0=\upsilon ={\eta }_v=0$. The proofs of the results are given in Appendix D.1.

• Non-negativity and boundedness

Lemma A1

(Non-negativity and Boundedness). Under the nonnegative initial conditions $U\left(0\right)\ge 0$, $V\left(0\right)\ge 0$, $E\left(0\right)\ge 0$, $I_p\left(0\right)\ge 0$, $I_a\left(0\right)\ge 0$, $I_s\left(0\right)\ge 0$, $Q\left(0\right)\ge 0$ and $R\left(0\right)\ge 0$, all solutions of System (A3) remain nonnegative and are bounded for all $t>0$.

• Disease-Free Equilibrium and Reproduction Number

Proposition A1

(Disease-Free Equilibrium & Reproduction Number).

Set $p_v={\eta }_v/\eta$. The UVEIQR model (A3) admits the unique disease-free equilibrium

$$\begin{array}{cc}\hfill {\mathit{X}}^c& ={\left(U^c,V^c,0,0,0,0,0,0\right)}^{\top }\mathrm{where}\hfill \end{array}$$

(A4a)

$$\begin{array}{cc}\hfill U^c& =\frac{\eta \alpha +{\eta }_u\mu }{\mu (\alpha +\upsilon +\mu )}\mathrm{and}{V}^c=\frac{\eta \upsilon +{\eta }_v\mu }{\mu (\alpha +\upsilon +\mu )},\hfill \end{array}$$

(A4b)

with the total population size at the carrying capacity $N^c=U^c+V^c=\eta /\mu$.

Moreover, for a population described by System (A3), the basic reproduction number in a vaccination-free context (i.e. $V_0={\eta }_v=\upsilon =0$) is given by

$${\mathcal{R}}_0=\frac{\theta }{(\theta +\mu )(\sigma +\mu )}\left[{\beta }_p+\frac{(1-\tau )(1-\pi )\sigma }{{\rho }_a+{\gamma }_a+\mu }{\beta }_a+\frac{\tau (1-\pi )\sigma }{{\rho }_s+{\gamma }_s+{\delta }_s+\mu }{\beta }_s\right],$$

(A5a)

and once vaccination is introduced, the control reproduction number is given by

$${\mathcal{R}}_c(\upsilon ,\kappa ,\alpha )={\mathcal{R}}_0\left[1-\frac{\kappa (\upsilon +p_v\mu )}{\alpha +\upsilon +\mu }\right]$$

(A5b)

and satisfies

$$(1-\kappa ){\mathcal{R}}_0\le {\mathcal{R}}_c(\upsilon ,\kappa ,\alpha )\le {\mathcal{R}}_0.$$

(A5c)

The time-varying effective reproduction number is given by

$$\mathcal{R}(t,\upsilon ,\kappa ,\alpha )={\mathcal{R}}_0\left[\frac{U\left(t\right)+(1-\kappa )V\left(t\right)}{N\left(t\right)-Q\left(t\right)}\right].$$

(A5d)

It appears from Equation (A5b) that, as expected, ${\mathcal{R}}_c$ decreases with both vaccination rate ($\upsilon$) and average vaccine efficacy ($\kappa$), but increases with the immunity lost rate ($\alpha$). The inequality (A5c) recognizes that vaccine efficacy is an important parameter in disease control: ${\mathcal{R}}_c$ cannot fall under $(1-\kappa ){\mathcal{R}}_0$ even for a large vaccination rate $\upsilon$. On setting

$${\kappa }^{*}=\frac{{\mathcal{R}}_0-1}{{\mathcal{R}}_0}$$

(A6)

for ${\mathcal{R}}_0>1$, a necessary condition for disease eradication is that the average vaccine efficacy must satisfy $\kappa >{\kappa }^{*}$ (ensuring $(1-\kappa ){\mathcal{R}}_0<1$). The following corollary gives the critical vaccination rate to eradicate the disease for a fixed average vaccine efficacy $\kappa$.

Corollary A1

(Critical Vaccination Rate). If ${\mathcal{R}}_0>1$ and $\kappa >{\kappa }^{*}$, then the critical (minimal) vaccination rate required to sufficiently lower ${\mathcal{R}}_c$ and ensure disease eradication in the long run is

$${\upsilon }^{*}(\kappa ,\alpha )=\frac{(\alpha +\mu )({\mathcal{R}}_0-1)-\kappa p_v\mu {\mathcal{R}}_0}{1-(1-\kappa ){\mathcal{R}}_0}$$

(A7a)

which increases with the immunity lost rate α, decreases with κ, and satisfies

$${\upsilon }^{*}>(\alpha +\mu )({\mathcal{R}}_0-1)-p_v\mu {\mathcal{R}}_0.$$

(A7b)

Note that ${\upsilon }^{*}$ also decreases with $p_v$, so that a positive net immigration of vaccinated individuals lowers the minimal required vaccination rate. The following lemma establishes local asymptotic stability conditions for the disease-free equilibrium point, and is further used to find global asymptotic stability conditions for the disease-free steady-state.

Lemma A2

(Local Asymptotic Stability of the Disease-Free Equilibrium). The disease-free equilibrium ${\mathit{X}}^c$ of the UVEIQR model (A3) is locally asymptotically stable if ${\mathcal{R}}_c\le 1$, and unstable if ${\mathcal{R}}_c>1$.

Proposition A2

(Global Asymptotic Stability of the Disease-Free Equilibrium). The disease-free equilibrium ${\mathit{X}}^c$ of the UVEIQR model (A3) is globally asymptotically stable, i.e. ${lim}_{t\to \infty }\mathit{X}\left(t\right)={\mathit{X}}^c$ for any solution $\mathit{X}={\left(U,V,E,I_p,I_a,I_s,Q,R\right)}^{\top }$, provided that ${\mathcal{R}}_c\le 1$.

By Proposition A2, ensuring ${\mathcal{R}}_c<1$ by for instance reducing contacts, susceptibility and transmissibility, or vaccinating a large part of the population, garrantees that the disease will die out shortly. If however ${\mathcal{R}}_c>1$, then any introduction of infectious individuals has the potential to kick off and maintain an epidemic outbreak, as per the next lemma.

•Persistence of the Disease and Endemic Equilibrium

Lemma A3

(Persistence of the Disease). Let us consider the UVEIQR model (A3) Let $\underline{U}={\eta }_u/(\upsilon +\mu +max\left\{{\beta }_p,{\beta }_a,{\beta }_s\right\})$. If ${\mathcal{R}}_c>1$, then the disease persists uniformly, i.e. there exists a positive real constant $\varrho \in \left(0,\underline{U}\right)$ independent of the initial data, such that any disease-dependent solution $\mathit{X}={\left(U,V,E,I_p,I_a,I_s,Q,R\right)}^{\top }$ satisfies:

$$\begin{array}{cc}\hfill \underset{t\to \infty }{lim}x\left(t\right)& \ge \varrho \mathrm{for}x\in \left\{U,E,I_p,I_a,I_s,Q,R\right\},\hfill \end{array}$$

(A8a)

$$\begin{array}{cc}\hfill \underset{t\to \infty }{lim}V\left(t\right)& \ge \varrho \mathrm{when}{\eta }_v>0\mathrm{or}\upsilon >0,\mathrm{and}\hfill \end{array}$$

(A8b)

$$\begin{array}{cc}\hfill \underset{t\to \infty }{lim}V\left(t\right)& =0\mathrm{when}{\eta }_v=\upsilon =0.\hfill \end{array}$$

(A8c)

From Equation (A8a), it appears that in both vaccination-free (i.e. ${\eta }_v=\upsilon =0$) and vaccination-dependent contexts, the susceptible population size $S\left(t\right)=U\left(t\right)+V\left(t\right)$ satisfies ${lim}_{t\to \infty }S\left(t\right)\ge \varrho$ for any ${\mathcal{R}}_c>0$ (since $\underline{U}<N^c$). This is ensured by the positive rates of net recruitement (${\eta }_u>0$), recovery (${\gamma }_a,{\gamma }_s,{\gamma }_q>0$), and immunity lost ($\alpha ,{ϵ}_o>0$). The persistence the of disease when ${\mathcal{R}}_c>1$ implies positive disease endemism whose equilibrium is next characterized.

Proposition A3

(Endemic Equilibrium). If ${\mathcal{R}}_c\le 1$, then the UVEIQR model (A3) has no endemic equilibrium. When ${\mathcal{R}}_c>1$, the model admits the unique endemic equilibrium

$$\begin{array}{cc}\hfill {\mathit{X}}^{★}& ={\left(U^{★},V^{★},E^{★},I_p^{★},I_a^{★},I_s^{★},Q^{★},R^{★}\right)}^{\top }\mathrm{with}\hfill \end{array}$$

(A9a)

$$\begin{array}{cc}\hfill U^{★}& =\frac{\left[\alpha +\mu +(1-\kappa ){\lambda }_o^{★}\right]\left({\eta }_u+{ϵ}_o\theta d_p\sigma d_r{E}^{★}\right)+\alpha {\eta }_v}{\left[\alpha +\mu +(1-\kappa ){\lambda }_o^{★}\right]\left(\upsilon +\mu +{\lambda }_o^{★}\right)-\alpha \upsilon },\hfill \end{array}$$

(A9b)

$$\begin{array}{cc}\hfill V^{★}& =\frac{{\eta }_v+\upsilon U^{★}}{\alpha +\mu +(1-\kappa ){\lambda }_o^{★}},\hfill \end{array}$$

(A9c)

$$\begin{array}{cc}\hfill E^{★}& =\frac{{\overline{S}}^c{N}^c}{{\mathcal{R}}_c(\theta +\mu )+{\overline{S}}^c\theta d_m{\lambda }_o^{★}}{\lambda }_o^{★},\hfill \end{array}$$

(A9d)

$$\begin{array}{cc}\hfill I_p^{★}& =\theta d_p{E}^{★},\hfill \end{array}$$

(A9e)

$$\begin{array}{cc}\hfill I_a^{★}& =\theta d_p\sigma d_a{E}^{★},\hfill \end{array}$$

(A9f)

$$\begin{array}{cc}\hfill I_s^{★}& =\theta d_p\sigma d_s{E}^{★},\hfill \end{array}$$

(A9g)

$$\begin{array}{cc}\hfill Q^{★}& =\theta d_p\sigma d_q{E}^{★},\hfill \end{array}$$

(A9h)

$$\begin{array}{cc}\hfill R^{★}& =\theta d_p\sigma d_r{E}^{★},\hfill \end{array}$$

(A9i)

where we have set $d_p=\frac{1}{\sigma +\mu }$, $d_a=\frac{(1-\tau )(1-\pi )}{{\rho }_a+{\gamma }_a+\mu }$, $d_s=\frac{\tau (1-\pi )}{{\rho }_s+{\gamma }_s+{\delta }_s+\mu }$, $d_q=\frac{\pi +d_a{\rho }_a+d_s{\rho }_s}{{\gamma }_q+{\delta }_q+\mu }$, $d_r=\frac{d_a{\gamma }_a+d_s{\gamma }_s+d_q{\gamma }_q}{{ϵ}_o+\mu }$, $d_m=d_n+d_p\sigma d_q$, $d_n=\frac{d_p\sigma }{\mu }(d_s{\delta }_s+d_q{\delta }_q)$, and ${\overline{S}}^c=1-\frac{\kappa (\upsilon +p_v\mu )}{\alpha +\upsilon +\mu }$; the endemic force of infection ${\lambda }_o^{★}$ is given by

$$\begin{array}{cc}\hfill {\lambda }_o^{★}& =\frac{1}{2}\left(\sqrt{K_1^2+4K_0}-K_1\right)\mathrm{where}\hfill \\ \hfill K_0& =\frac{\mu \left(\alpha +\upsilon +\mu \right)(\theta +\mu )\left({\mathcal{R}}_c-1\right)}{(1-\kappa )\left[(\theta +\mu )-\theta \left(d_m\mu +d_p\sigma d_r{ϵ}_o\right)\right]},\mathrm{and}\hfill \\ \hfill K_1& =\frac{(\theta +\mu )\left[g_{uv}+(1-\kappa )\mu \right]-\theta \left(d_m\mu +d_p\sigma d_r{ϵ}_o\right)g_{uv}-(1-\kappa )\theta d_p\mu {\beta }_{\sigma }+\kappa p_v\theta d_m{\mu }^2}{(1-\kappa )\left[(\theta +\mu )-\theta \left(d_m\mu +d_p\sigma d_r{ϵ}_o\right)\right]}\hfill \end{array}$$

(A9j)

with $g_{uv}=\alpha +(1-\kappa )\upsilon +\mu$, and ${\beta }_{\sigma }={\beta }_p+\sigma d_a{\beta }_a+\sigma d_s{\beta }_s$; and the total population size is

$$\begin{array}{c}\hfill N^{★}=N^c-\theta d_n{E}^{★}.\end{array}$$

(A9k)

The following results establish stability for the endemic equilibrium ${\mathit{X}}^{★}$.

Lemma A4

(Local Asymptotic Stability of the Endemic Equilibrium). When it exists (${\mathcal{R}}_c>1$), the endemic equilibrium ${\mathit{X}}^{★}$ of the UVEIQR model (A3) is locally asymptotically stable.

Proposition A4

(Global Asymptotic Stability of the Endemic Equilibrium). When it exists, the endemic equilibrium ${\mathit{X}}^{★}$ of the UVEIQR model (A3) is globally asymptotically stable, i.e. ${lim}_{t\to \infty }\mathit{X}\left(t\right)={\mathit{X}}^{★}$ for any disease-dependent solution $\mathit{X}={\left(U,V,E,I_p,I_a,I_s,Q,R\right)}^{\top }$.

Note from Proposition A4 and Equation (A9k) that the persistence of disease (${\mathcal{R}}_c>1$) and the positive disease related death rates (${\delta }_s,{\delta }_q>0$) reduce the long run population size below the carrying capacity $N^c$.

Appendix B.1. Vaccination–free influence functions

Plot the 3 influences for $w_{\infty }=1,2,3$.

Appendix B.2. Influence functions accounting for vaccination

Build 3D plots of influences in terms of $\tilde{P}$ and V to support the claims.

Appendix C.1. Inferring Disease Prevalence from Medical Data

A variety of approaches have been used to estimate disease prevalence (see e.g. [81,82,83,84,85]). In this work, we assume that the perceived disease prevalence $\tilde{P}$ is equal to a consistent estimate of the true disease prevalence P, based on some consistent estimates of $I_p\left(t\right)$, $I_a\left(t\right)$, and $I_s\left(t\right)$. From our disease dynamics models (see Appendix A), the total number of timely new confirmed (positive) cases is

$$\dot{C}\left(t\right)=\pi \sigma I_p\left(t\right)+{\rho }_a{I}_a\left(t\right)+{\rho }_s{I}_s\left(t\right),$$

(A10)

where $1/\sigma$ is the mean residential time of infectious individuals in the class $I_p$, $\pi$ is the early detection probability (during the presymptomatic incubation period), and ${\rho }_a$ and ${\rho }_s$ are late detection rates from the asymptomatic and symptomatic classes, respectively. We assume that the additive elements of $\dot{C}\left(t\right)$ are available based on medical surveys of newly identified cases, i.e. we have the presymptomatic new confirmed cases ${\dot{C}}_p\left(t\right)$, the asymptomatic new confirmed cases ${\dot{C}}_a\left(t\right)$, and the symptomatic new confirmed cases ${\dot{C}}_s\left(t\right)$, such that $\dot{C}\left(t\right)={\dot{C}}_p\left(t\right)+{\dot{C}}_a\left(t\right)+{\dot{C}}_s\left(t\right)$. Likewise, we assume that medical surveys and observational data are available to compute some consistent estimates ${\tilde{r}}_p$ of the mean residential time of identified presymptomatic infectious in the class $I_p$ of presymptomatic infectives (i.e. $1/\left(\pi \sigma \right)$), ${\tilde{r}}_a$ of the mean residential time of identified asymptomatic infectious in the class $I_a$ of asymptomatic infectives (i.e. $1/{\rho }_a$), and ${\tilde{r}}_s$ of the mean residential time of identified symptomatic infectious in the class $I_s$ of symptomatic infectives (i.e. $1/{\rho }_s$). Then, $I_p\left(t\right)$, $I_a\left(t\right)$, and $I_s\left(t\right)$ can be consistently estimated as

$${\tilde{I}}_p\left(t\right)={\tilde{r}}_p{\dot{C}}_p\left(t\right),{\tilde{I}}_a\left(t\right)={\tilde{r}}_a{\dot{C}}_a\left(t\right),\mathrm{and}{\tilde{I}}_a\left(t\right)={\tilde{r}}_s{\dot{C}}_s\left(t\right),$$

(A11a)

and $\tilde{P}\left(t\right)$ is given for $t\ge 0$ by

$$\tilde{P}\left(t\right)=\frac{{\tilde{I}}_p\left(t\right)+{\tilde{I}}_a\left(t\right)+{\tilde{I}}_s\left(t\right)+Q\left(t\right)-\dot{C}\left(t\right)}{N\left(t\right)}.$$

(A11b)

where $Q\left(t\right)-\dot{C}\left(t\right)=Q(t-1)$ has been substituted for $Q\left(t\right)$ to avoid doubly accounting for $\dot{C}\left(t\right)$ (since observations are always discrete although the UVEIQR model (Appendix A.2) is continuous).

Appendix C.2. Common measures of perceived disease prevalence

The daily number of positive new cases $\dot{C}$ is a common measure of disease perceived disease risk . Other common measures include but $C\left(t\right)={\int }_0^t\dot{C}\left(s\right)ds$ , $aQ\left(t\right)$, $a\approx 10$ [85],

Appendix D.1. Proofs of lemmas and propositions related to disease dynamics Only

Proof of Lemma A1.

From Equation (A3a), we have $\dot{U}\left(t\right)\ge -(\upsilon +\tilde{\beta }+\mu )U\left(t\right)$ where $\tilde{\beta }=max\left\{{\beta }_p,{\beta }_a,{\beta }_s\right\}$ (note from Equation (2) that $\tilde{\beta }$ is a majorant of ${\lambda }_o\left(t\right)$). This leads to:

$$U\left(t\right)\ge U_0{e}^{-(\upsilon +\tilde{\beta }+\mu )t}\ge 0.$$

The same argument gives $V\left(t\right)\ge 0$, $E\left(t\right)\ge 0$, $I_p\left(t\right)\ge 0$, $I_a\left(t\right)\ge 0$, $I_s\left(t\right)\ge 0$, $Q\left(t\right)\ge 0$ and $R\left(t\right)\ge 0$ and proves nonnegativity. Next, let $N_0=N\left(0\right)$. Then, by the nonnegative initial conditions and $N_0=U_0+V_0+E_0+I_{0p}+I_{0a}+I_{0s}+Q_0+R_0$, we have $N_0\ge 0$. From Equation (1) and the System (Appendix A.2), we have

$$\dot{N}\left(t\right)=\eta -\mu N\left(t\right)-{\delta }_s{I}_s\left(t\right)-{\delta }_{q}Q\left(t\right).$$

The last equation implies that $\dot{N}\left(t\right)\le \eta -\mu N\left(t\right)$. Integrating the later yields

$$N\left(t\right)\le N^c+\left(N_0-N^c\right)e^{-\mu t}$$

with $N^c=\eta /\mu$. It appears that as t increases, the upper bound of $N\left(t\right)$ increases (when $N_0\le N^c$) or decreases (when $N_0>N^c$) to eventually approach the carrying capacity $N^c$ as $t\to \infty$. Thus $N\left(t\right)\le max\{N_0,N^c\}$. Hence we overall have

$$0\le N\left(t\right)\le max\{N_0,N^c\}.$$

The nonnegativity of $U\left(t\right)$, $V\left(t\right)$, $E\left(t\right)$, $I_p\left(t\right)$, $I_a\left(t\right)$, $I_s\left(t\right)$, $Q\left(t\right)$ and $R\left(t\right)$ then implies that these quantities are all bounded, since their sum $N\left(t\right)$ is bounded. □

Proof of Proposition A1.

Adding the disease-free restriction $E=I_p=I_a=I_s=Q=0$ to System (A3) implies that ${\lambda }_o\left(t\right)=0$. Setting all the derivatives to zero then gives $E^c=I_p^c=I_a^c=I_s^c=Q^c=R^c=0$ and we are left with the system

$$\left\{\begin{array}{cccccc}{\eta }_u& -& (\upsilon +\mu )U^c& +& \alpha V^c& =0\\ {\eta }_v& +& \upsilon U^c& -& (\alpha +\mu )V^c& =0\end{array}\right.$$

which is solved for $U^c$ and $V^c$ through substitution, and the disease-free equilibrium (d.f.e.) in Equation (A4a) is obtained using $\eta ={\eta }_u+{\eta }_v$. Next, let $\mathit{I}$ the vector of the compartments involved in the production of new infections or receiving new infections: $\mathit{I}=\left(E,I_p,I_a,I_s\right)$. The corresponding subset of System (A3) has the form $\dot{\mathit{I}}=\mathbb{F}\left(\mathit{I}\right)-\mathbb{W}\left(\mathit{I}\right)$ where

$$\mathbb{F}\left(\mathit{I}\right)=\overline{S}\left(\begin{array}{c}{\beta }_p{I}_p+{\beta }_a{I}_a+{\beta }_s{I}_s\\ 0\\ 0\\ 0\end{array}\right)\mathrm{and}\mathbb{W}\left(\mathit{I}\right)=\left(\begin{array}{c}(\theta +\mu )E\\ -\theta E+(\sigma +\mu )I_p\\ -(1-\tau )(1-\pi )\sigma I_p+({\rho }_a+{\gamma }_a+\mu )I_a\\ -\tau (1-\pi )\sigma I_p+({\rho }_s+{\gamma }_s+{\delta }_s+\mu )I_s\end{array}\right)$$

on setting $\overline{S}=\frac{U+(1-\kappa )V}{N-Q}$. Then, letting $g_e=\theta +\mu$, $g_p=\sigma +\mu$, $g_a={\rho }_a+{\gamma }_a+\mu$, $g_s={\rho }_s+{\gamma }_s+{\delta }_s+\mu$, $f_a=(1-\tau )(1-\pi )\sigma$, and $f_s=\tau (1-\pi )\sigma$, the Jacobian matrices of $\mathbb{F}$ and $\mathbb{W}$ evaluated at the d.f.e. are respectively given by

$${\mathit{F}}^c={\overline{S}}^c\left(\begin{array}{cccc}0& {\beta }_p& {\beta }_a& {\beta }_s\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right)\mathrm{and}\mathit{W}=\left(\begin{array}{cccc}{g}_e& 0& 0& 0\\ -\theta & g_p& 0& 0\\ 0& -f_a& g_a& 0\\ 0& -f_s& 0& g_s\end{array}\right)\mathrm{with}{\overline{S}}^c=\frac{U^c+(1-\kappa )V^c}{N^c-Q^c}.$$

Following [65], the basic reproduction number is defined as the spectral radius ${\mathit{s}}_{\rho }$ (largest eigenvalue) of the next-generation matrix ${\mathit{F}}^c{\mathit{W}}^{-1}$, and we find

$${\mathit{s}}_{\rho }\left({\mathit{F}}^c{\mathit{W}}^{-1}\right)=\frac{\theta }{g_e{g}_p}\left[{\beta }_p+\frac{f_a}{g_a}{\beta }_a+\frac{f_s}{g_s}{\beta }_s\right]{\overline{S}}^c.$$

Under the restriction $V_0={\eta }_v=\upsilon =0$, we have $V^c=0$ and $U^c=N^c$. We thus have in this case ${\overline{S}}^c=1$ (since $Q^c=0$), and Equation (A5a) follows. Using the Equations (A4b) gives ${\overline{S}}^c=\frac{\eta \alpha +{\eta }_u\mu +(1-\kappa )(\eta \upsilon +{\eta }_v\mu )}{\eta (\alpha +\upsilon +\mu )}$ and Equation (A5b) follows. The expression (A5c) results from noting that ${\mathcal{R}}_c(\upsilon ,\kappa ,\alpha )$ decreases with $\kappa$ and evaluating the limit ${\mathcal{R}}_c(\upsilon ,0,\alpha )$ to get an upper bound, and noting that ${\mathcal{R}}_c$ also decreases with $\upsilon$ since $\frac{\partial {\mathcal{R}}_c\left(\upsilon ,\kappa ,\alpha \right)}{\partial \upsilon }=-{\mathcal{R}}_0\frac{\kappa \left(\alpha +\mu (1-p_v)\right)}{\alpha +\upsilon +\mu }<0$, and evaluating the limit ${\mathcal{R}}_c(\infty ,\kappa ,\alpha )$ to obtain a lower bound. Finally, evaluating the Jacobian matrices of $\mathbb{F}$ and $\mathbb{W}$ at general values of U, V, Q, and N instead of the d.f.e. (i.e. replacing ${\overline{S}}^c$ by $\overline{S}$), results in Equation (A5d). □

Proof of Corollary A1.

We obtain ${\upsilon }^{*}(\kappa ,\alpha )$ by setting the expression (A5b) of ${\mathcal{R}}_c$ to one, and solving for $\upsilon$. It is obvious that ${\upsilon }^{*}$ increases with $\alpha$. From Equation (A7a), we get

$$\frac{\partial {\upsilon }^{*}(\kappa ,\alpha )}{\partial \kappa }=-\frac{\left[\alpha +\mu (1-p_v)\right]({\mathcal{R}}_0-1){\mathcal{R}}_0}{{\left[1-(1-\kappa ){\mathcal{R}}_0\right]}^2}<0,$$

hence ${\upsilon }^{*}(\kappa ,\alpha )$ decreases with $\kappa \in (0,1)$, and is lower bounded by ${\upsilon }^{*}(1,\alpha )$. □

Proof of Lemma A2.

lma:DFEquiStab0proof:lmaDFEquiStab0 A necessary and sufficient condition for an equilibrium to have local asymptotic stability (l.a.s.) is that all eigenvalues of the Jacobian matrix have negative real parts [86]. The Jacobian matrix of model (A3) at the d.f.e. has the block structure

$${\mathit{J}}^c=\left(\begin{array}{ccc}{\mathit{J}}_S& {\mathit{J}}_{SI}^c& {\mathit{J}}_{SQ}\\ \mathbf{0}& {\mathit{J}}_I^c& \mathbf{0}\\ \mathbf{0}& {\mathit{J}}_{QI}& {\mathit{J}}_Q\end{array}\right)\mathrm{where}{\mathit{J}}_S=\left(\begin{array}{cc}-(\upsilon +\mu )& \alpha \\ \upsilon & -(\alpha +\mu )\end{array}\right),$$

${\mathit{J}}_{SI}^c=\frac{-1}{N^c}\left(\begin{array}{cccc}0& {\beta }_p{U}^c& {\beta }_a{U}^c& {\beta }_s{U}^c\\ 0& (1-\kappa ){\beta }_p{V}^c& (1-\kappa ){\beta }_a{V}^c& (1-\kappa ){\beta }_s{V}^c\end{array}\right)$, ${\mathit{J}}_{SQ}=\left(\begin{array}{cc}0& {ϵ}_o\\ 0& 0\end{array}\right)$, ${\mathit{J}}_I^c={\mathit{F}}^c-\mathit{W}$, ${\mathit{J}}_{QI}^c=\left(\begin{array}{cccc}0& \pi \sigma & {\rho }_a& {\rho }_s\\ 0& 0& {\gamma }_a& {\gamma }_s\end{array}\right)$, and ${\mathit{J}}_Q=\left(\begin{array}{cc}-({\gamma }_q+{\delta }_q+\mu )& 0\\ {\gamma }_q& -({ϵ}_o+\mu )\end{array}\right)$. From this structure, the eigenvalues of ${\mathit{J}}^c$ are those of ${\mathit{J}}_S$, ${\mathit{J}}_I^c$ and ${\mathit{J}}_Q$ (using Schur complements). We get the eigenvalues $d_1=-\mu$ and $d_2=-(\upsilon +\alpha +\mu )$ from ${\mathit{J}}_S$, and $d_3=-({\gamma }_q+{\delta }_q+\mu )$ and $d_4=-({ϵ}_o+\mu )$ from ${\mathit{J}}_Q$. Since $d_k<0$ for $k=1,2,3,4$, we can next restrict attention to ${\mathit{J}}_I^c$ whose four eigenvalues must have negative real parts to ensure l.a.s.:

$${\mathit{J}}_I^c=\left(\begin{array}{cccc}-g_e& {\overline{S}}^c{\beta }_p& {\overline{S}}^c{\beta }_a& {\overline{S}}^c{\beta }_s\\ \theta & -g_p& 0& 0\\ 0& f_a& -g_a& 0\\ 0& f_s& 0& -g_s\end{array}\right).$$

The characteristic polynomial $P_c$ of ${\mathit{J}}_I^c$ is

$$P_c\left(d\right)=d^4+K_3{d}^3+K_2{d}^2+K_{1}d+g_e{g}_p{g}_a{g}_s\left(1-{\mathcal{R}}_c\right),$$

where $K_3=g_e+g_p+g_a+g_s$, $K_2=g_e(g_p+g_a+g_s)+g_p(g_a+g_s)+g_a{g}_s-\theta {\overline{S}}^c{\beta }_p$, and $K_1=g_e{g}_p(g_a+g_s)+g_a{g}_s(g_e+g_p)-\theta {\overline{S}}^c\left[(g_a+g_s){\beta }_p+f_a{\beta }_a+f_s{\beta }_s\right]$. The Routh-Hurwitz stability conditions (see Equation (A.22) in May [87]) corresponding to this polynomial are:

$$K_3>0,K_1>0,\mathrm{and}{K}_c\ge 0,$$

where $K_c=g_e{g}_p{g}_a{g}_s\left(1-{\mathcal{R}}_c\right)$. Since $g_j>0$ for any $j\in \left\{e,p,a,s\right\}$, we have (i): $K_3>0$ by definition (for any value of ${\mathcal{R}}_c$). If ${\mathcal{R}}_c>1$, then $K_c<0$. It follows that at least one eigenvalue of ${\mathit{J}}_I^c$ has a positive real part when ${\mathcal{R}}_c>1$, and unstability is established. When ${\mathcal{R}}_c\le 1$ on the contrary, we have (ii): $K_c\ge 0$. Next, notice that ${\mathcal{R}}_c\le 1$ is equivalent to $1\ge \frac{\theta {\overline{S}}^c}{g_e{g}_p}\left({\beta }_p+\frac{f_a}{g_a}{\beta }_a+\frac{f_s}{g_s}{\beta }_s\right)$. This implies that $1>\frac{\theta {\overline{S}}^c}{g_e{g}_p}\left({\beta }_p+\frac{f_a}{g_a+g_s}{\beta }_a+\frac{f_s}{g_a+g_s}{\beta }_s\right)$ since $g_a>0$ and $g_s>0$. Writing $K_1$ as

$$K_1=g_e{g}_p(g_a+g_s)\left[1-\frac{\theta {\overline{S}}^c}{g_e{g}_p}\left({\beta }_p+\frac{f_a}{g_a+g_s}{\beta }_a+\frac{f_s}{g_a+g_s}{\beta }_s\right)\right]+g_a{g}_s(g_e+g_p),$$

then shows that (iii): $K_1>0$ if ${\mathcal{R}}_c\le 1$. The statements (i), (ii) and (iii) ensure that all the four eigenvalues of ${\mathit{J}}_I^c$ have negative real parts when ${\mathcal{R}}_c\le 1$ and l.a.s. is established. □

Proof of Proposition A2.

The proof uses a global stability result derived by Castillo-Chavez et al. [88]. Let $\mathit{Y}={\left(U,V,R\right)}^{\top }$ and $\mathit{I}={\left(E,I_p,I_a,I_s,Q\right)}^{\top }$ be the vectors of uninfected and infected classes, respectively, and set $\mathit{G}(\mathit{Y},\mathit{I})=\frac{\partial \mathit{I}\left(t\right)}{\partial t}$ and ${\mathit{Y}}^c={\left(U^c,V^c,0\right)}^{\top }$. To establish global asymptotic stability (g.a.s.), we first show that the following conditions hold for the UVEIQR model (A3):

$$\begin{array}{cc}\hfill \left(H_1\right):& \underset{t\to \infty }{lim}\mathit{Y}\left(t\right)={\mathit{Y}}^c(\mathrm{i}.\mathrm{e}.{\mathit{Y}}^c\mathrm{is}\mathrm{globally}\mathrm{asymptotically}\mathrm{stable})\mathrm{when}\mathit{I}=\mathbf{0},\hfill \\ \hfill \left(H_2\right):& \mathit{G}(\mathit{Y},\mathit{I})={\mathit{A}}^c\mathit{I}-\widehat{\mathit{G}}(\mathit{Y},\mathit{I}),\widehat{\mathit{G}}(\mathit{Y},\mathit{I})\ge \mathbf{0}(\mathrm{i}.\mathrm{e}.\mathrm{all}\mathrm{entries}\mathrm{of}\widehat{\mathit{G}}\mathrm{are}\mathrm{nonnegative}),\hfill \end{array}$$

where ${\mathit{A}}^c=\partial \mathit{G}({\mathit{Y}}^c,\mathbf{0})/\partial {\mathit{I}}^{\top }$ is a Metzeler matrix (all off diagonal elements are nonnegative). To check $\left(H_1\right)$, we set $\mathit{I}=\mathbf{0}$ in System (A3) and get the reduced system

$$\begin{array}{cc}\hfill \dot{U}& ={\eta }_u-(\upsilon +\mu )U+\alpha V+{ϵ}_{o}R,\hfill \\ \hfill \dot{V}& ={\eta }_v+\upsilon U-(\alpha +\mu )V,\hfill \\ \hfill \dot{R}& =-({ϵ}_o+\mu )R.\hfill \end{array}$$

It comes that $R\left(t\right)=R_0{\mathrm{e}}^{-({ϵ}_o+\mu )t}$, and $N\left(t\right)=N^c+\left(N_0-N^c\right){\mathrm{e}}^{-\mu t}$. Replacing the expression $U\left(t\right)=N\left(t\right)-R\left(t\right)-V\left(t\right)$ in $\dot{V}\left(t\right)$ and integrating the result leads to

$$\begin{array}{cc}\hfill V\left(t\right)=& V_0{\mathrm{e}}^{-(\alpha +\upsilon +\mu )t}+\frac{{\eta }_v+\upsilon N^c}{\alpha +\upsilon +\mu }\left[1-{\mathrm{e}}^{-(\alpha +\upsilon +\mu )t}\right]+\frac{\upsilon (N_0-N^c)}{\alpha +\upsilon }\left[1-{\mathrm{e}}^{-(\alpha +\upsilon )t}\right]{\mathrm{e}}^{-\mu t}\hfill \\ \hfill & -\upsilon R_0·t·{\mathrm{e}}^{-(\alpha +\upsilon +\mu )t}\mathrm{if}\alpha +\upsilon ={ϵ}_o,\mathrm{and}\hfill \\ \hfill V\left(t\right)=& V_0{\mathrm{e}}^{-(\alpha +\upsilon +\mu )t}+\frac{{\eta }_v+\upsilon N^c}{\alpha +\upsilon +\mu }\left[1-{\mathrm{e}}^{-(\alpha +\upsilon +\mu )t}\right]+\frac{\upsilon (N_0-N^c)}{\alpha +\upsilon }\left[1-{\mathrm{e}}^{-(\alpha +\upsilon )t}\right]{\mathrm{e}}^{-\mu t}\hfill \\ \hfill & -\frac{\upsilon R_0}{\alpha +\upsilon -{ϵ}_o}\left[{\mathrm{e}}^{-{ϵ}_{o}t}-{\mathrm{e}}^{-(\alpha +\upsilon )t}\right]{\mathrm{e}}^{-\mu t}\mathrm{if}\alpha +\upsilon \ne {ϵ}_o.\hfill \end{array}$$

It appears that ${lim}_{t\to \infty }R\left(t\right)=0=R^c$ and ${lim}_{t\to \infty }V\left(t\right)=\frac{{\eta }_v+\upsilon N^c}{\alpha +\upsilon +\mu }=V^c$, both when $\alpha +\upsilon ={ϵ}_o$ (since $\alpha +\upsilon +\mu >0$) and when $\alpha +\upsilon \ne {ϵ}_o$. Then, $U\left(t\right)=N\left(t\right)-R\left(t\right)-V\left(t\right)$ leads to ${lim}_{t\to \infty }U\left(t\right)=N^c-V^c-R^c=U^c$, hence $\left(H_1\right)$ holds. Next, using System (A3) and $\widehat{\mathit{G}}(\mathit{Y},\mathit{I})={\mathit{A}}^c\mathit{I}-\mathit{G}(\mathit{Y},\mathit{I})$, and setting $g_q={\gamma }_q+{\delta }_q+\mu$, we get

$${\mathit{A}}^c=\left(\begin{array}{ccccc}-g_e& {\overline{S}}^c{\beta }_p& {\overline{S}}^c{\beta }_a& {\overline{S}}^c{\beta }_s& 0\\ \theta & -g_p& 0& 0& 0\\ 0& f_a& -g_a& 0& 0\\ 0& f_s& 0& -g_s& 0\\ 0& \pi \sigma & {\rho }_a& {\rho }_s& -g_q\end{array}\right)\mathrm{and}\widehat{\mathit{G}}(\mathit{Y},\mathit{I})=({\overline{S}}^c-\overline{S})\left(\begin{array}{c}{\beta }_p{I}_p+{\beta }_a{I}_a+{\beta }_s{I}_s\\ 0\\ 0\\ 0\\ 0\end{array}\right).$$

The matrix ${\mathit{A}}^c$ is obviously Metzeler. Moreover, the whole population is in the susceptible class S at the d.f.e., hence the maximal value of the average effective susceptibility in the mixing population $\overline{S}=\frac{U+(1-\kappa )V}{N-Q}$, is ${\overline{S}}^c=\frac{U^c+(1-\kappa )V^c}{N^c}$. We thus have $\overline{S}\le {\overline{S}}^c$ and $\widehat{\mathit{G}}(\mathit{Y},\mathit{I})\ge 0$ so that $\left(H_2\right)$ holds. Then, by the Theorem in [88], the validity of the two conditions ($\left(H_1\right)$ and $\left(H_2\right)$) ensures that the d.f.e. ${\mathit{X}}^c$ is g.a.s. provided that ${\mathit{X}}^c$ is l.a.s., i.e. ${\mathcal{R}}_c\le 1$ (by Lemma A2). □

Proof of Lemma A3.

The proof is an adaptation of the proof of Theorem 3.3 in [89], originally built for dissipative dynamical systems. The primary aim is to find a positive sub-solution of the UVEIQR model (A3). Let $\mathit{I}={\left(E,I_p,I_a,I_s\right)}^{\top }$ and set $\mathit{G}(t,\mathit{I})=\frac{\partial \mathit{I}\left(t\right)}{\partial t}$. Note that the subset of System (A3) corresponding to $\mathit{I}$ (i.e. Equations (A3c)–(A3f)) can be compactly expressed as $\dot{\mathit{I}}=\mathit{G}(t,\mathit{I})$. We first show the existence of a pair of positive principal eigenvalue and eigenvector of this subset when ${\mathcal{R}}_c>1$. Linearizing the target subset of the system around the d.f.e. ${\mathit{X}}^c$ gives $\dot{\mathit{I}}={\mathit{A}}^c\mathit{I}$, where ${\mathit{A}}^c=\partial \mathit{G}(t,\mathbf{0})/\partial {\mathit{I}}^{\top }$, i.e.

$${\mathit{A}}^c=\left(\begin{array}{cccc}-g_e& {\overline{S}}^c{\beta }_p& {\overline{S}}^c{\beta }_a& {\overline{S}}^c{\beta }_s\\ \theta & -g_p& 0& 0\\ 0& f_a& -g_a& 0\\ 0& f_s& 0& -g_s\end{array}\right).$$

Substituting a solution of the form $\mathit{I}\left(t\right)=\mathsf{\Phi }{\mathrm{e}}^{d\times t}$ with $d\in \mathbb{R}$, we get $d\mathsf{\Phi }={\mathit{A}}^c\mathsf{\Phi }$. Note that ${\mathit{A}}^c$ is a Metzeler matrix (i.e. ${\left({\mathit{A}}^c\right)}_{ij}\ge 0$ for $i\ne j$). Therefore, ${\mathit{A}}^c$ is irreducible if and only if the matrix ${\mathit{A}}_{{}_{+}}={\mathit{A}}^c+c{\mathit{I}}_6$ (with c any large real such that ${\left({\mathit{A}}_{{}_{+}}\right)}_{ij}\ge 0$ for $1\le i,j,\le 4$) is irreducible [90]. We pick $c=\nu +max\left\{g_e,g_p,g_a,g_s,g_q,g_r\right\}$ with $\nu$ a positive real, and let ${\overline{g}}_j=c+g_j\ge \nu >0$ for $j\in \left\{e,p,a,s,q,r\right\}$. Then,

$${\mathit{A}}_{{}_{+}}=\left(\begin{array}{cccc}{\overline{g}}_e& {\overline{S}}^c{\beta }_p& {\overline{S}}^c{\beta }_a& {\overline{S}}^c{\beta }_s\\ \theta & {\overline{g}}_p& 0& 0\\ 0& f_a& {\overline{g}}_a& 0\\ 0& f_s& 0& {\overline{g}}_s\end{array}\right),\mathrm{and}$$

$${\mathit{A}}_{{}_{+}}^2=\left(\begin{array}{cccc}{\overline{g}}_e^2+\theta {\overline{S}}^c{\beta }_p& {\overline{S}}^c{\overline{g}}_e{\beta }_p+{\overline{g}}_p{\beta }_p+f_a{\beta }_a+f_s{\beta }_s& {\overline{S}}^c{\beta }_a({\overline{g}}_e+{\overline{g}}_a)& {\overline{S}}^c{\beta }_s({\overline{g}}_e+{\overline{g}}_s)\\ \theta ({\overline{g}}_e+{\overline{g}}_p)& {\overline{g}}_p^2+\theta {\overline{S}}^c{\beta }_p& \theta {\overline{S}}^c{\beta }_a& \theta {\overline{S}}^c{\beta }_s\\ \theta f_a& f_a({\overline{g}}_p+{\overline{g}}_a)& {\overline{g}}_a^2& 0\\ \theta f_s& f_s({\overline{g}}_p+{\overline{g}}_s)& 0& {\overline{g}}_s^2\end{array}\right).$$

We observe that ${\left({\mathit{A}}_{{}_{+}}^2\right)}_{34}={\left({\mathit{A}}_{{}_{+}}^2\right)}_{43}=0$. However, it appears that the corresponding elements in ${\mathit{A}}_{{}_{+}}^3$ are positive, and therefore ${\mathit{A}}_{{}_{+}}^3\gg 0$ (all elements are positive), so that ${\mathit{A}}_{{}_{+}}$ is irreducible. It follows that ${\mathit{A}}^c$ is irreducible, and by Corollary 4.3.2 in [90], there exists a real eigenvalue $\tilde{d}$ of ${\mathit{A}}^c$ and a corresponding eigenvector $\tilde{\mathsf{\Phi }}={\left(\tilde{E},{\tilde{I}}_p,{\tilde{I}}_a,{\tilde{I}}_s\right)}^{\top }$ satisfying $\tilde{\mathsf{\Phi }}\gg 0$. Since ${\mathcal{R}}_c>1$, the principal eigenvalue $\tilde{d}$ of ${\mathit{A}}^c$ is positive (by Lemma A2).

To find a sub-solution of System (A3), notice that by Lemma A2, any solution of the system satisfies ${lim}_{t\to \infty }\mathit{X}\ne {\mathit{X}}^c$ (since ${\mathcal{R}}_c>1$). Along with the irreducibility of ${\mathit{A}}^c$, this implies that, in the presence of the disease, for a small constant $\nu >0$, there exists a large time T such that $\nu \le E\left(t\right),I_p\left(t\right),I_a\left(t\right),I_s\left(t\right)\le max\{N_0,N^c\}$ for $t\ge T$. On setting $\tilde{\mu }=\mu +max\left\{{\beta }_p,{\beta }_a,{\beta }_s\right\}$ and ${\tilde{g}}_u=\upsilon +\tilde{\mu }$, the solution of the Cauchy problem

$$\left\{\begin{array}{cccc}\frac{\partial U_b\left(t\right)}{\partial t}=& {\eta }_u& -& {\tilde{g}}_u{U}_b\left(t\right),t\ge T,\\ U_b\left(T\right)=& U\left(T\right),\end{array}\right.$$

is a sub-solution of Equation (A3a). We find $U_b\left(t\right)=\underline{U}+\left[U\left(T\right)-\underline{U}\right]{\mathrm{e}}^{-{\tilde{g}}_u(t-T)}$ with $\underline{U}={\eta }_u/{\tilde{g}}_u>0$, hence ${lim}_{t\to \infty }{U}_b\left(t\right)=\underline{U}$. Similarly, on setting ${\tilde{\eta }}_v={\eta }_v+\upsilon \underline{\tilde{U}}$ with $\underline{\tilde{U}}=min\left\{\underline{U},U\left(T\right)\right\}$, and ${\tilde{g}}_v=\alpha +\tilde{\mu }$, a sub-solution of Equation (A3b) is given by the solution of the Cauchy problem,

$$\left\{\begin{array}{cccccc}\frac{\partial V_b\left(t\right)}{\partial t}& =& {\tilde{\eta }}_v& -& {\tilde{g}}_v{V}_b\left(t\right),& t\ge T,\\ V_b\left(T\right)& =& V\left(T\right).\end{array}\right.$$

We find ${lim}_{t\to \infty }{V}_b\left(t\right)=\underline{V}$ with $\underline{V}={\tilde{\eta }}_v/{\tilde{g}}_v\ge 0$. Next, let $\tilde{\mathit{I}}\left(t\right)=\tilde{\nu }\tilde{\mathsf{\Phi }}$ for $t\ge T$ and $\tilde{\nu }>0$ a small constant. Substituting $\tilde{\mathit{I}}\left(t\right)$ into Equations (A3c)–(A3f), exploiting the positivity of $\tilde{d}$ and $\tilde{\mathsf{\Phi }}={\left(\tilde{E},{\tilde{I}}_p,{\tilde{I}}_a,{\tilde{I}}_s\right)}^{\top }$, and setting $\tilde{a}=\tilde{E}+{\tilde{I}}_p+{\tilde{I}}_a+{\tilde{I}}_s+R$ result in:

$$\begin{array}{cc}\hfill \dot{E}\left(t\right)-\frac{\partial \left(\tilde{\nu }\tilde{E}\right)}{\partial t}& =\tilde{\nu }({\beta }_p{\tilde{I}}_p+{\beta }_a{\tilde{I}}_a+{\beta }_s{\tilde{I}}_s)\frac{U+(1-\kappa )V}{U+V+\tilde{\nu }(\tilde{E}+{\tilde{I}}_p+{\tilde{I}}_a+{\tilde{I}}_s+R)}-\tilde{\nu }{g}_e\tilde{E},\hfill \\ \hfill & =\tilde{\nu }({\beta }_p{\tilde{I}}_p+{\beta }_a{\tilde{I}}_a+{\beta }_s{\tilde{I}}_s)\frac{U+(1-\kappa )V}{U+V+\tilde{\nu }\tilde{a}}-\tilde{\nu }{g}_e\tilde{E}\hfill \\ \hfill & +\tilde{\nu }\left({\beta }_p{\tilde{I}}_p-{\beta }_p{\tilde{I}}_p+{\beta }_a{\tilde{I}}_a-{\beta }_a{\tilde{I}}_a+{\beta }_s{\tilde{I}}_s-{\beta }_s{\tilde{I}}_s\right){\overline{S}}^c,\hfill \\ \hfill & =\tilde{\nu }\left[({\beta }_p{\tilde{I}}_p+{\beta }_a{\tilde{I}}_a+{\beta }_s{\tilde{I}}_s){\overline{S}}^c-g_e\tilde{E}\right]\hfill \\ \hfill & +\tilde{\nu }({\beta }_p{\tilde{I}}_p+{\beta }_a{\tilde{I}}_a+{\beta }_s{\tilde{I}}_s)\left[\frac{U+(1-\kappa )V}{U+V+\tilde{\nu }\tilde{a}}-{\overline{S}}^c\right],\hfill \\ \hfill & =\tilde{\nu }\tilde{d}\tilde{E}+\tilde{\nu }({\beta }_p{\tilde{I}}_p+{\beta }_a{\tilde{I}}_a+{\beta }_s{\tilde{I}}_s)\left(\frac{U}{U+V+\tilde{\nu }\tilde{a}}-\frac{{\overline{U}}^c}{{\overline{U}}^c+{\overline{V}}^c}\right)\hfill \\ \hfill & +\tilde{\nu }(1-\kappa )({\beta }_p{\tilde{I}}_p+{\beta }_a{\tilde{I}}_a+{\beta }_s{\tilde{I}}_s)\left(\frac{V}{U+V+\tilde{\nu }\tilde{a}}-\frac{{\overline{V}}^c}{{\overline{U}}^c+{\overline{V}}^c}\right)\hfill \\ \hfill & >0\mathrm{for}\mathrm{a}\mathrm{sufficiently}\mathrm{small}\tilde{\nu }>0,\hfill \\ \hfill {\dot{I}}_p\left(t\right)-\frac{\partial \left(\tilde{\nu }{\tilde{I}}_p\right)}{\partial t}& =\theta \tilde{\nu }\tilde{E}-g_p\tilde{\nu }{\tilde{I}}_p=\tilde{\nu }\tilde{d}{\tilde{I}}_p>0,\hfill \\ \hfill {\dot{I}}_a\left(t\right)-\frac{\partial \left(\tilde{\nu }{\tilde{I}}_a\right)}{\partial t}& =f_a\tilde{\nu }{\tilde{I}}_p-g_a\tilde{\nu }{\tilde{I}}_a=\tilde{\nu }\tilde{d}{\tilde{I}}_a>0,\hfill \\ \hfill {\dot{I}}_s\left(t\right)-\frac{\partial \left(\tilde{\nu }{\tilde{I}}_s\right)}{\partial t}& =f_s\tilde{\nu }{\tilde{I}}_p-g_s\tilde{\nu }{\tilde{I}}_s=\tilde{\nu }\tilde{d}{\tilde{I}}_s>0.\hfill \end{array}$$

It appears that $\tilde{\mathit{I}}\left(t\right)=\tilde{\nu }\tilde{\mathsf{\Phi }}$ is a sub-solution of $\dot{\mathit{I}}=\mathit{G}(t,\mathit{I})$. Next, we consider the Cauchy problem,

$$\left\{\begin{array}{ccccc}\frac{\partial Q_b\left(t\right)}{\partial t}& =& \tilde{\nu }\left(\pi \sigma {\tilde{I}}_p+{\rho }_a{\tilde{I}}_a+{\rho }_s{\tilde{I}}_s\right)& -& g_q{Q}_b\left(t\right),t\ge T,\\ Q_b\left(T\right)& =& Q\left(T\right),\end{array}\right.$$

whose solution is a sub-solution of Equation (A3g). We find ${lim}_{t\to \infty }{Q}_b\left(t\right)=\underline{Q}$ with $\underline{Q}=\tilde{\nu }\left(\pi \sigma {\tilde{I}}_p+{\rho }_a{\tilde{I}}_a+{\rho }_s{\tilde{I}}_s\right)/g_q>0$. Likewise, we set $\underline{\tilde{Q}}=min\left\{\underline{Q},Q\left(T\right)\right\}$ and consider the Cauchy problem,

$$\left\{\begin{array}{ccccc}\frac{\partial R_b\left(t\right)}{\partial t}& =& \tilde{\nu }\left({\gamma }_a{\tilde{I}}_a+{\gamma }_s{\tilde{I}}_s+{\gamma }_q\underline{\tilde{Q}}\right)& -& g_r{R}_b,t\ge T,\\ R_b\left(T\right)& =& R\left(T\right),\end{array}\right.$$

whose solution is a sub-solution of Equation (A3h). We find ${lim}_{t\to \infty }{R}_b\left(t\right)=\underline{R}$ with $\underline{R}=\tilde{\nu }\left({\gamma }_a{\tilde{I}}_a+{\gamma }_s{\tilde{I}}_s+{\gamma }_q\underline{\tilde{Q}}\right)/g_r>0$. In a vaccination-dependent situation where ${\eta }_v>0$ or $\upsilon >0$, we have ${\tilde{\eta }}_v={\eta }_v+\upsilon \underline{\tilde{U}}>0$, and thus $\underline{V}>0$. This allows to pick a $\varrho$ value satisfying

$$0<\varrho <min\left\{\underline{U},\underline{V},\tilde{\nu }\tilde{E},\tilde{\nu }{\tilde{I}}_p,\tilde{\nu }{\tilde{I}}_a,\tilde{\nu }{\tilde{I}}_s,\underline{Q},\underline{R}\right\},$$

so as to obtain ${lim}_{t\to \infty }U\left(t\right)\ge \varrho$, ${lim}_{t\to \infty }V\left(t\right)\ge \varrho$, ${lim}_{t\to \infty }E\left(t\right)\ge \varrho$, ${lim}_{t\to \infty }{I}_p\left(t\right)\ge \varrho$, ${lim}_{t\to \infty }{I}_a\left(t\right)\ge \varrho$, ${lim}_{t\to \infty }{I}_s\left(t\right)\ge \varrho$, ${lim}_{t\to \infty }Q\left(t\right)\ge \varrho$, and ${lim}_{t\to \infty }R\left(t\right)\ge \varrho$. When ${\eta }_v=0$ and $\upsilon =0$, Equation (A3b) gives $\dot{V}\left(t\right)=-\left[\alpha +(1-\kappa ){\lambda }_o\left(t\right)+\mu \right]V\left(t\right)\le -(\alpha +\mu )V\left(t\right)$. Any positive solution to $\dot{v}\left(t\right)=-(\alpha +\mu )v\left(t\right)$, i.e. $v\left(t\right)=V_0{\mathrm{e}}^{-(\alpha +\mu )t}$, is thus a super-solution to Equation (A3b). We here pick a $\varrho$ value satisfying

$$0<\varrho <min\left\{\underline{U},\tilde{\nu }\tilde{E},\tilde{\nu }{\tilde{I}}_p,\tilde{\nu }{\tilde{I}}_a,\tilde{\nu }{\tilde{I}}_s,\underline{Q},\underline{R}\right\},$$

as a lower bound for the limits of the state variables, except ${lim}_{t\to \infty }V\left(t\right)=0$. □

Proof of Proposition A3.

The equilibrium point (A9a) follows from setting all the derivatives in System (A3) to zero. Given ${\lambda }_o$ and $E^{★}$, we first solve the system for all other state variables. Indeed, we get Equations (A9e)-(A9i) by solving Equations (A3d)-(A3h) for $I_p$, $I_a$, $I_s$, Q and R. We then solve (A3b) for V to obtain Equation (A9c), i.e. $V^{★}=\frac{{\eta }_v+\upsilon U^{★}}{g_v+(1-\kappa ){\lambda }_o}$ where $g_v=\alpha +\mu$. Substituting $V^{★}$ for V and the expression (A9i) for R into Equation (A3a), and solving for U leads to Equation (A9b), i.e.

$$\begin{array}{cc}\hfill U^{★}& =\frac{\left[g_v+(1-\kappa ){\lambda }_o\right]\left({\eta }_u+{ϵ}_o{e}_r{E}^{★}\right)+\alpha {\eta }_v}{\left[g_v+(1-\kappa ){\lambda }_o\right]\left(g_u+{\lambda }_o\right)-\alpha \upsilon },\mathrm{and}\hfill \\ \hfill V^{★}& =\frac{\left(g_u+{\lambda }_o\right){\eta }_v+\upsilon \left({\eta }_u+{ϵ}_o{e}_r{E}^{★}\right)}{\left[g_v+(1-\kappa ){\lambda }_o\right]\left(g_u+{\lambda }_o\right)-\alpha \upsilon },\hfill \end{array}$$

where $g_u=\upsilon +\mu$ and $e_r=\theta d_p\sigma d_r$. The next step consists in solving Equation (A3c), i.e.

$$\left[U^{★}+(1-\kappa )V^{★}\right]{\lambda }_o-g_e{E}^{★}=0,$$

where $g_e=\theta +\mu$, for ${\lambda }_o$. To this end, we compute:

$$\begin{array}{ccc}\hfill U^{★}+(1-\kappa )V^{★}& =\hfill & \hfill \frac{\left[g_v+(1-\kappa )(\upsilon +{\lambda }_o)\right]\left({\eta }_u+{ϵ}_o{e}_r{E}^{★}\right)+\left[\alpha +(1-\kappa )(g_u+{\lambda }_o)\right]{\eta }_v}{\left[g_v+(1-\kappa ){\lambda }_o\right]\left(g_u+{\lambda }_o\right)-\alpha \upsilon }.\end{array}$$

From the definition of ${\lambda }_o$ in Equation (2), we have ${\lambda }_o=\frac{\theta d_p\left[{\beta }_p+\sigma d_a{\beta }_a+\sigma d_s{\beta }_s\right]E^{★}}{N^{★}-Q^{★}}$ which reads ${\lambda }_o=\frac{{\mathcal{R}}_c{g}_e}{{\overline{S}}^c}\frac{E^{★}}{N^{★}-Q^{★}}$ from using ${\mathcal{R}}_c=\frac{\theta d_p}{g_e}\left[{\beta }_p+\sigma d_a{\beta }_a+\sigma d_s{\beta }_s\right]{\overline{S}}^c$, ${\overline{S}}^c=\frac{U^c+(1-\kappa )V^c}{N^c}$. Summing all the derivatives in System (A3) gives $\dot{N}=\eta -\mu N^{★}-{\delta }_s{I}_s^{★}-{\delta }_q{Q}^{★}=0$ from which we obtain

$$N^{★}=N^c-\frac{1}{\mu }\left({\delta }_s{I}_s^{★}+{\delta }_q{Q}^{★}\right),$$

giving Equation (A9k). We thus have $N^{★}-Q^{★}=N^c-\theta d_m{E}^{★}$, so that ${\lambda }_o=\frac{{\mathcal{R}}_c{g}_e}{{\overline{S}}^c}\frac{E^{★}}{N^c-\theta d_m{E}^{★}}$. It follows that

$$E^{★}=\frac{{\overline{S}}^c{N}^c}{{\mathcal{R}}_c{g}_e+{\overline{S}}^c\theta d_m{\lambda }_o}{\lambda }_o,$$

resulting in Equation (A9d). Equation (A3c) then reads

$$\left[U^{★}+(1-\kappa )V^{★}\right]{\lambda }_o-\frac{{\overline{S}}^c{N}^c{g}_e}{{\mathcal{R}}_c{g}_e+{\overline{S}}^c\theta d_m{\lambda }_o}{\lambda }_o=0.$$

The obvious solution ${\lambda }_o=0$ corresponds to the d.f.e., and we here consider ${\lambda }_o>0$ as implied by the presence of disease. Hence we have

$$\frac{\left[g_v+(1-\kappa )(\upsilon +{\lambda }_o)\right]\left({\eta }_u+{ϵ}_o{e}_r{E}^{★}\right)+\left[\alpha +(1-\kappa )(g_u+{\lambda }_o)\right]{\eta }_v}{\left[g_v+(1-\kappa ){\lambda }_o\right]\left(g_u+{\lambda }_o\right)-\alpha \upsilon }-\frac{{\overline{S}}^c{N}^c{g}_e}{{\mathcal{R}}_c{g}_e+{\overline{S}}^c\theta d_m{\lambda }_o}=0.$$

Using the identity ${\eta }_u\left[g_v+(1-\kappa )\upsilon \right]+{\eta }_v\left[\alpha +(1-\kappa )g_u\right]={\overline{S}}^c{N}^c\left(g_u{g}_v-\alpha \upsilon \right)$ and setting $L_1={\overline{S}}^c{N}^c\left[\theta \left[d_m\mu +d_p\sigma d_r{ϵ}_o\right]g_{uv}-\kappa p_v\theta d_m{\mu }^2+(1-\kappa )\theta d_p\mu {\beta }_{\sigma }-(\theta +\mu )\left[g_{uv}+(1-\kappa )\mu \right]\right]$, and $L_2=(1-\kappa ){\overline{S}}^c{N}^c\left[\theta (d_m\mu +d_p\sigma d_r{ϵ}_o)-(\theta +\mu )\right]$ with $g_{uv}=\alpha +(1-\kappa )\upsilon +\mu$, and ${\beta }_{\sigma }={\beta }_p+\sigma d_a{\beta }_a+\sigma d_s{\beta }_s$, we get the quadratic equation

$$L_2{\lambda }_o^2+L_1{\lambda }_o+{\overline{S}}^c{N}^c{g}_e\left(g_u{g}_v-\alpha \upsilon \right)\left({\mathcal{R}}_c-1\right)=0.$$

Note that the definitions of $d_p$, $d_m$, and $d_r$ imply that:

$$\begin{array}{cc}\hfill d_m\mu +d_p\sigma d_r{ϵ}_o& =d_p\sigma \left[d_a{\gamma }_a\frac{{ϵ}_o}{{ϵ}_o+\mu }+d_s\left({\delta }_s+{\gamma }_s\frac{{ϵ}_o}{{ϵ}_o+\mu }\right)+d_q\left(\mu +{\delta }_q+{\gamma }_q\frac{{ϵ}_o}{{ϵ}_o+\mu }\right)\right],\hfill \\ \hfill & <d_p\sigma \left[d_a{\gamma }_a+d_s\left({\delta }_s+{\gamma }_s\right)+d_q\left(\mu +{\delta }_q+{\gamma }_q\right)\right],\hfill \\ \hfill & <d_p\sigma \left[d_a({\gamma }_a+{\rho }_a)+d_s\left({\delta }_s+{\gamma }_s+{\rho }_s\right)+\pi \right],\hfill \\ \hfill & <d_p\sigma \left[(1-\tau )(1-\pi )+\tau (1-\pi )+\pi \right],\hfill \\ \hfill & <d_p\sigma ,\hfill \\ \hfill & <1.\hfill \end{array}$$

It follows that $L_2<0$. For ${\mathcal{R}}_c\le 1$, on using ${\overline{S}}^c\ge 1-\kappa$, we have $(1-\kappa )\theta d_p{\beta }_{\sigma }\le g_e$ which implies that $L_1\le 0$, and since $\left(g_u{g}_v-\alpha \upsilon \right)=\mu (\alpha +\upsilon +\mu )>0$, the constant term $L_0={\overline{S}}^c{N}^c{g}_e\left(g_u{g}_v-\alpha \upsilon \right)\left({\mathcal{R}}_c-1\right)$ also satisfies $L_0\le 0$. Therefore, the above quadratic equation in ${\lambda }_o$ has no positive solution when ${\mathcal{R}}_c\le 1$. As a result, a positive endemic equilibrium exists only if ${\mathcal{R}}_c>1$. Since $L_0>0$ when ${\mathcal{R}}_c>1$, the quadratic then has a unique positive root ${\lambda }_o^{★}$ given by

$${\lambda }_o^{★}=\frac{1}{2}\left(-K_1+\sqrt{K_1^2+4K_0}\right)$$

where $K_0=-L_0/L_2$ and $K_1=L_1/L_2$. □

Proof of Lemma A4.

Let ${\overline{U}}^{★}=\frac{U^{★}}{N^{★}-Q^{★}}$, ${\overline{V}}^{★}=\frac{V^{★}}{N^{★}-Q^{★}}$, ${\overline{V}}_{\kappa }^{★}=(1-\kappa ){\overline{V}}^{★}$, ${\overline{S}}^{★}={\overline{U}}^{★}+{\overline{V}}_{\kappa }^{★}$, ${\upsilon }^{★}=\upsilon +{\overline{V}}_{\kappa }^{★}{\lambda }_o^{★}$, ${\alpha }^{★}=\alpha +{\overline{U}}^{★}{\lambda }_o^{★}$, ${ϵ}_o^{★}={ϵ}_o+{\overline{U}}^{★}{\lambda }_o^{★}$, $h_u^{★}=1-{\overline{S}}^{★}$, $h_v^{★}=1-\kappa -{\overline{S}}^{★}$, $g_u^{★}=\upsilon +\mu +(1-{\overline{U}}^{★}){\lambda }_o^{★}$, $g_v^{★}=\alpha +\mu +(1-\kappa )(1-\overline{V}){\lambda }_o^{★}$, $g_e^{★}=\theta +\mu +{\overline{S}}^{★}{\lambda }_o^{★}$, and $g_r={ϵ}_o+\mu$. Then, the Jacobian matrix ${\mathit{J}}^{★}$ of the UVEIQR model (A3) evaluated at the endemic equilibrium (e.e.) point ${\mathit{X}}^{★}$ has the block structure

$$\begin{array}{cc}\hfill {\mathit{J}}^{★}& =\left(\begin{array}{cc}{\mathit{J}}_{11}^{★}& {\mathit{J}}_{12}^{★}\\ {\mathit{J}}_{21}^{★}& {\mathit{J}}_{22}^{★}\end{array}\right),{\mathit{J}}_{11}^{★}=\left(\begin{array}{ccc}-g_u^{★}& {\alpha }^{★}& {\overline{U}}^{★}{\lambda }_o^{★}\\ {\upsilon }^{★}& -g_v^{★}& {\overline{V}}_{\kappa }^{★}{\lambda }_o^{★}\\ h_u^{★}{\lambda }_o^{★}& h_v^{★}{\lambda }_o^{★}& -g_e^{★}\end{array}\right),{\mathit{J}}_{22}^{★}=\left(\begin{array}{ccccc}-g_p& 0& 0& 0& 0\\ f_a& -g_a& 0& 0& 0\\ f_s& 0& -g_s& 0& 0\\ \pi \sigma & {\rho }_a& {\rho }_s& -g_q& 0\\ 0& {\gamma }_a& {\gamma }_s& {\gamma }_q& -g_r\end{array}\right),\hfill \\ \hfill {\mathit{J}}_{21}^{★}& =\left(\begin{array}{ccc}0& 0& \theta \\ 0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right)\mathrm{and}{\mathit{J}}_{12}^{★}=\left(\begin{array}{ccccc}{\overline{U}}^{★}({\lambda }_o^{★}-{\beta }_p)& {\overline{U}}^{★}({\lambda }_o^{★}-{\beta }_a)& {\overline{U}}^{★}({\lambda }_o^{★}-{\beta }_s)& 0& {ϵ}_o^{★}\\ {\overline{V}}_{\kappa }^{★}({\lambda }_o^{★}-{\beta }_p)& {\overline{V}}_{\kappa }^{★}({\lambda }_o^{★}-{\beta }_a)& {\overline{V}}_{\kappa }^{★}({\lambda }_o^{★}-{\beta }_s)& 0& {\overline{V}}_{\kappa }^{★}{\lambda }_o^{★}\\ {\overline{S}}^{★}({\beta }_p-{\lambda }_o^{★})& {\overline{S}}^{★}({\beta }_a-{\lambda }_o^{★})& {\overline{S}}^{★}({\beta }_s-{\lambda }_o^{★})& 0& -{\overline{S}}^{★}{\lambda }_o^{★}\end{array}\right).\hfill \end{array}$$

Let k be an arbitrary complex number and $\mathit{Z}={\left(z_1,\cdots ,z_8\right)}^{\top }$ be a nonzero complex vector. To establish l.a.s. for the e.e. point ${\mathit{X}}^{★}$, we use Krasnoselskii [91]’s sublinearity trick, a technique described for stability analysis in Hethcote and Thieme [92], to show that any solution of the form ${\mathit{Z}}_0=\mathit{Z}{\mathrm{e}}^{kt}$ for System (A3) linearized around ${\mathit{X}}^{★}$ (i.e. $\dot{\mathit{X}}={\mathit{J}}^{★}\mathit{X}$) satisfies $Re\left(k\right)<0$. Substituting ${\mathit{Z}}_0$ into the linear system results in $k\mathit{Z}={\mathit{J}}^{★}\mathit{Z}$. Following Hethcote and Thieme [92], we use contradiction to show that $Re\left(k\right)<0$ for any $\mathit{Z}$ solution of $k\mathit{Z}={\mathit{J}}^{★}\mathit{Z}$.

First assume that $k=0$. Then ${\mathit{J}}^{★}\mathit{Z}=\mathbf{0}$ and the system has a nonzero solution $\mathit{Z}$ only if $det\left({\mathit{J}}^{★}\right)=0$. From the block structure of ${\mathit{J}}^{★}$, we have $det\left({\mathit{J}}^{★}\right)=det\left({\mathit{J}}_{22}\right)\times det\left({\mathit{C}}_{★}\right)$ where ${\mathit{C}}_{★}$ is the Schur complement of ${\mathit{J}}_{22}^{★}$ in ${\mathit{J}}^{★}$: ${\mathit{C}}_{★}={\mathit{J}}_{11}^{★}-{\mathit{J}}_{12}^{★}{\left[{\mathit{J}}_{22}^{★}\right]}^{-1}{\mathit{J}}_{21}^{★}$. We obtain $det\left({\mathit{J}}_{22}\right)=-g_p{g}_a{g}_s{g}_q{g}_r$ and

$$\begin{array}{cc}\hfill {\mathit{C}}_{★}& =\left(\begin{array}{ccc}-g_u^{★}& {\alpha }^{★}& {\overline{U}}^{★}{\lambda }_o^{★}-g_p^{-1}\theta \left({\overline{U}}^{★}{y}_0^{★}+f_r\left(0\right)g_r^{-1}{ϵ}_o\right)\\ {\upsilon }^{★}& -g_v^{★}& {\overline{V}}_{\kappa }^{★}{\lambda }_o^{★}-g_p^{-1}\theta {\overline{V}}_{\kappa }^{★}{y}_0^{★}\\ h_u^{★}{\lambda }_o^{★}& h_v^{★}{\lambda }_o^{★}& -g_e^{★}+g_p^{-1}\theta {\overline{S}}^{★}{y}_0^{★}\end{array}\right)\hfill \end{array}$$

where we have set $y_0^{★}={\lambda }_o^{★}\left(1+f_a{g}_a^{-1}+f_s{g}_s^{-1}+f_r\left(0\right)g_r^{-1}\right)-\left({\beta }_p+f_a{g}_a^{-1}{\beta }_a+f_s{g}_s^{-1}{\beta }_s\right)$, and $f_r\left(k\right)=\frac{\pi \sigma }{k+g_q}{\gamma }_q+\frac{f_a}{k+g_a}\left({\gamma }_a+\frac{{\rho }_a{\gamma }_q}{k+g_q}\right)+\frac{f_s}{k+g_s}\left({\gamma }_s+\frac{{\rho }_s{\gamma }_q}{k+g_q}\right)$. It turns out that

$$\begin{array}{cc}\hfill det\left({\mathit{C}}_{★}\right)& =\left(g_u^{★}{g}_v^{★}-{\alpha }^{★}{\upsilon }^{★}\right)\left(g_p^{-1}\theta {\overline{S}}^{★}{y}_0^{★}-g_e^{★}\right)-\theta g_p^{-1}{f}_r\left(0\right)g_r^{-1}{\lambda }_o^{★}\left(h_v^{★}{\upsilon }^{★}+h_u^{★}{g}_v^{★}\right){ϵ}_o\hfill \\ \hfill & +\left[\left(h_v^{★}{\upsilon }^{★}+h_u^{★}{g}_v^{★}\right){\overline{U}}^{★}+\left(h_u^{★}{\alpha }^{★}+h_v^{★}{g}_u^{★}\right){\overline{V}}_{\kappa }^{★}\right]{\lambda }_o^{★}\left({\lambda }_o^{★}-\theta g_p^{-1}{y}_0^{★}\right),\hfill \end{array}$$

hence $det\left({\mathit{C}}_{★}\right)<0$ and $det\left({\mathit{J}}^{★}\right)>0$. Therefore $k\ne 0$. Next, assume that $Re\left(k\right)>0$. The eigen equation $k\mathit{Z}={\mathit{J}}^{★}\mathit{Z}$ reads

$$\begin{array}{cc}\hfill k{z}_1& =-g_u^{★}{z}_1+{\alpha }^{★}{z}_2+{\overline{U}}^{★}{\lambda }_o^{★}{z}_3+{\overline{U}}^{★}({\lambda }_o^{★}-{\beta }_p)z_4+{\overline{U}}^{★}({\lambda }_o^{★}-{\beta }_a)z_5+{\overline{U}}^{★}({\lambda }_o^{★}-{\beta }_s)z_6+{ϵ}_o^{★}{z}_8,\hfill \\ \hfill k{z}_2& ={\upsilon }^{★}{z}_1-g_v^{★}{z}_2+{\overline{V}}_{\kappa }^{★}{\lambda }_o^{★}{z}_3+{\overline{V}}_{\kappa }^{★}({\lambda }_o^{★}-{\beta }_p)z_4+{\overline{V}}_{\kappa }^{★}({\lambda }_o^{★}-{\beta }_a)z_5+{\overline{V}}_{\kappa }^{★}({\lambda }_o^{★}-{\beta }_s)z_6+{\overline{V}}_{\kappa }^{★}{\lambda }_o^{★}{z}_8,\hfill \\ \hfill k{z}_3& =h_u^{★}{\lambda }_o^{★}{z}_1+h_v^{★}{\lambda }_o^{★}{z}_2-g_e^{★}{z}_3+{\overline{S}}^{★}({\beta }_p-{\lambda }_o^{★})z_4+{\overline{S}}^{★}({\beta }_a-{\lambda }_o^{★})z_5+{\overline{S}}^{★}({\beta }_s-{\lambda }_o^{★})z_6-{\overline{S}}^{★}{\lambda }_o^{★}{z}_8,\hfill \\ \hfill k{z}_4& =\theta z_3-g_p{z}_4,\hfill \\ \hfill k{z}_5& =f_a{z}_4-g_a{z}_5,\hfill \\ \hfill k{z}_6& =f_s{z}_4-g_s{z}_6,\hfill \\ \hfill k{z}_7& =\pi \sigma z_4+{\rho }_a{z}_5+{\rho }_s{z}_6-g_q{z}_7,\hfill \\ \hfill k{z}_8& ={\gamma }_a{z}_5+{\gamma }_s{z}_6+{\gamma }_q{z}_7-g_r{z}_8.\hfill \end{array}$$

Subsequently solving the last five equations of the previous system for $z_j$ ($j=4,\cdots ,8$) leads to $z_8=\theta {\left(k+g_p\right)}^{-1}{f}_r\left(k\right){\left(k+g_r\right)}^{-1}{z}_3$. Then, setting $z_m=z_8+{\sum }_{j=1}^6{z}_j$, and rearranging the first three equations yield:

$$\begin{array}{cc}\hfill (k+g_u+{\lambda }_o^{★})z_1& =\alpha z_2+{\overline{U}}^{★}{\lambda }_o^{★}{z}_m-{\overline{U}}^{★}\left({\beta }_p{z}_4+{\beta }_a{z}_5+{\beta }_s{z}_6\right)+{ϵ}_o{z}_8,\hfill \end{array}$$

(A14)

$$\begin{array}{cc}\hfill \left[k+g_v+(1-\kappa ){\lambda }_o^{★}\right]z_2& =\upsilon z_1+{\overline{V}}_{\kappa }^{★}{\lambda }_o^{★}{z}_m-{\overline{V}}_{\kappa }^{★}\left({\beta }_p{z}_4+{\beta }_a{z}_5+{\beta }_s{z}_6\right),\hfill \end{array}$$

(A15)

$$\begin{array}{cc}\hfill (k+g_e)z_3& ={\lambda }_o^{★}\left[z_1+(1-\kappa )z_2\right]-{\overline{S}}^{★}{\lambda }_o^{★}{z}_m+{\overline{S}}^{★}\left({\beta }_p{z}_4+{\beta }_a{z}_5+{\beta }_s{z}_6\right).\hfill \end{array}$$

(A16)

Summing Equations (A14)-(A16) leads after some additional algebra to

$$\begin{array}{cc}\hfill \left(k+\mu \right)(z_1+z_2)& =-\left(k+\mu +\theta \right)z_3+{ϵ}_o{\left(k+g_p\right)}^{-1}{f}_r\left(k\right){\left(k+g_r\right)}^{-1}\theta z_3,\hfill \\ \hfill z_m& ={\left(k+g_p\right)}^{-1}\left(1+\frac{f_a}{k+g_a}+\frac{f_s}{k+g_s}+\frac{f_r\left(k\right)}{k+g_r}\right)\theta z_3\hfill \\ \hfill & -{\left(k+\mu \right)}^{-1}\left[1-\frac{{ϵ}_o{f}_r\left(k\right)}{\left(k+g_p\right)\left(k+g_r\right)}\right]\theta z_3,\mathrm{and}\hfill \\ \hfill \left[z_1+(1-\kappa )z_2\right]& ={\overline{S}}^{★}{z}_m+\frac{\kappa (1-\kappa ){\overline{V}}^{★}}{k+g_{uv}^{★}}\left({\beta }_p{z}_4+{\beta }_a{z}_5+{\beta }_s{z}_6\right)-\left(1-\frac{\kappa \upsilon }{k+g_{uv}^{★}}\right)z_3\hfill \\ \hfill & -\left[1-\frac{{ϵ}_o{f}_r\left(k\right)}{\left(k+g_p\right)\left(k+g_r\right)}\right]\left[1-\frac{\kappa \left[\upsilon +(1-\kappa ){\overline{V}}^{★}\right]}{k+g_{uv}^{★}}-{\overline{S}}^{★}\right]\frac{\theta }{k+\mu }{z}_3\hfill \\ \hfill & -{\overline{S}}^{★}\left(1+\frac{f_a}{k+g_a}+\frac{f_s}{k+g_s}+\frac{f_r\left(k\right)}{k+g_r}\right)\frac{\theta }{k+g_p}{z}_3,\hfill \end{array}$$

where $g_{uv}^{★}=\alpha +\upsilon +\mu +(1-\kappa ){\lambda }_o^{★}$. Equation (A16) then becomes:

$$\begin{array}{cc}\hfill \left[g_e+k+a_3\left(k\right)\right]z_3& =\left[{\overline{S}}^{★}+\frac{\kappa {\overline{V}}^{★}(1-\kappa ){\lambda }_o^{★}}{k+g_{uv}^{★}}\right]\left({\beta }_p{z}_4+{\beta }_a{z}_5+{\beta }_{s}z6\right)\mathrm{where}\hfill \\ \hfill a_3\left(k\right)& =\left[1-\frac{{ϵ}_o{f}_r\left(k\right)}{\left(k+g_p\right)\left(k+g_r\right)}\right]\left[1-\frac{\kappa \left[\upsilon +(1-\kappa ){\overline{V}}^{★}\right]}{k+g_{uv}^{★}}-{\overline{S}}^{★}\right]\frac{{\lambda }_o^{★}\theta }{k+\mu }\hfill \\ \hfill & +\left(1+\frac{f_a}{k+g_a}+\frac{f_s}{k+g_s}+\frac{f_r\left(k\right)}{k+g_r}\right)\frac{{\overline{S}}^{★}{\lambda }_o^{★}\theta }{k+g_p}+\left(1-\frac{\kappa \upsilon }{k+g_{uv}^{★}}\right){\lambda }_o^{★}.\hfill \end{array}$$

On defining $\overline{\mathit{Z}}={\left(z_3,\cdots ,z_8\right)}^{\top }$, $b_3={\overline{S}}^{★}{\left[{\overline{S}}^{★}+\frac{\kappa {\overline{V}}^{★}(1-\kappa ){\lambda }_o^{★}}{k+g_{uv}^{★}}\right]}^{-1}$, $b_j=1$ for $j=4,\cdots ,8$, $F_3\left(k\right)=g_e^{-1}{b}_3\left[k+a_3\left(k\right)\right]$, $F_4\left(k\right)=g_p^{-1}k$, $F_5\left(k\right)=g_a^{-1}k$, $F_6\left(k\right)=g_s^{-1}k$, $F_7\left(k\right)=g_q^{-1}k$, and $F_8\left(k\right)=g_r^{-1}k$, we obtain the system

$$\begin{array}{cc}\hfill \left[b_j+F_j\left(k\right)\right]{\left(\overline{\mathit{Z}}\right)}_{j-2}& ={\left(\mathit{H}\overline{\mathit{Z}}\right)}_{j-2}\mathrm{for}j=3,4,\cdots ,8;\mathrm{with}\hfill \end{array}$$

$$\mathit{H}=\left(\begin{array}{cccccc}0& g_e^{-1}{\overline{S}}^{★}{\beta }_p& g_e^{-1}{\overline{S}}^{★}{\beta }_a& g_e^{-1}{\overline{S}}^{★}{\beta }_s& 0& 0\\ g_p^{-1}\theta & 0& 0& 0& 0& 0\\ 0& g_a^{-1}{f}_a& 0& 0& 0& 0\\ 0& g_s^{-1}{f}_s& 0& 0& 0& 0\\ 0& g_q^{-1}\pi \sigma & g_q^{-1}{\rho }_a& g_q^{-1}{\rho }_s& 0& 0\\ 0& 0& g_r^{-1}{\gamma }_a& g_r^{-1}{\gamma }_s& g_r^{-1}{\gamma }_q& 0\end{array}\right).$$

Note that the matrix $\mathit{H}$ is nonnegative and satisfies $\mathit{H}{\mathit{E}}^{★}={\mathit{E}}^{★}$ where ${\mathit{E}}^{★}$ contains the endemic sizes of infected classes, i.e. ${\mathit{E}}^{★}={\left(E^{★},I_p^{★},I_a^{★},I_s^{★},Q^{★},R^{★}\right)}^{\top }$. Taking norms elementwise and setting $F\left(k\right)=inf\left\{Re\left(F_j\left(k\right)\right),j=3,\cdots ,8\right\}$ and $b_0=Re\left(b_3\right)$, we get

$$\begin{array}{cc}\hfill \left[b_0+F\left(k\right)\right]\left|\overline{\mathit{Z}}\right|& \le \mathit{H}|\overline{\mathit{Z}}|\hfill \end{array}$$

(A17)

where $|\overline{\mathit{Z}}|={\left(|z_3|,\cdots ,|z_8|\right)}^{\top }$. It appears that $Re\left(a_3\left(k\right)\right)>0$ and $b_0\in (0,1]$ for $Re\left(k\right)>0$. Therefore, $Re\left(F_j\left(k\right)\right)>0$ for all $j=3,\cdots ,8$, hence $F\left(k\right)>0$. Let $r_0$ denote the minimum number such that $|\overline{\mathit{Z}}|\le r_0{b}_0{\mathit{E}}^{★}$. The positivity of $b_0{\mathit{E}}^{★}$ ensures that $r_0$ is positive and finite, and $r=r_0{b}_0$ is the minimum number such that $|\overline{\mathit{Z}}|\le r{\mathit{E}}^{★}$. The inequality (A12) then implies that $\left[b_0+F\left(k\right)\right]|\overline{\mathit{Z}}|\le \mathit{H}|\overline{\mathit{Z}}|\le r\mathit{H}{\mathit{E}}^{★}=r_0{b}_0{\mathit{E}}^{★}$ which leads to $|\overline{\mathit{Z}}|\le \frac{r_0{b}_0}{b_0+F\left(k\right)}{\mathit{E}}^{★}$. From $b_0>0$ and $F\left(k\right)>0$, we have $\frac{b_0}{b_0+F\left(k\right)}<b_0$, hence $|\overline{\mathit{Z}}|\le \frac{r_0{b}_0}{b_0+F\left(k\right)}{\mathit{E}}^{★}<r{\mathit{E}}^{★}$ contradicts the minimality of r. Therefore, $Re\left(k\right)<0$ (i.e. all eigenvalues of ${\mathit{J}}^{★}$ have negative real parts) and l.a.s. is established for ${\mathit{X}}^{★}$. □

Proof of Proposition A4.

Let $\mathit{X}={\left(U,V,E,I_p,I_a,I_s,Q,R\right)}^{\top }$ be the vector of the states of the model (A3). For simplicity, we relabel the state variables $x_j$ ($j=1,2,\cdots ,8$) such that $\mathit{X}={\left(x_1,x_2,\cdots ,x_8\right)}^{\top }$. Let us define the function L given for $t\ge 0$ by

$$L\left(t\right)=\sum _{j=1}^8\left(x_j-x_j^{★}log{x}_j\right).$$

We claim that L is a strict Lyapunov function [93] as we next show. It first appears that L is continuous everywhere and has first order partial derivatives with respect to $\mathit{X}$ (i.e. system (A3)). Thus, we are only required to show that the first derivative $\dot{L}$ of L with respect to time satisfies $\dot{L}\left(t\right)\le 0$ for any solution $\mathit{X}$ as $t\to \infty$. To this end, we have

$$\dot{L}\left(t\right)=\sum _{j=1}^8\left(x_j-x_j^{★}\right)\frac{{\dot{x}}_j}{x_j}.$$

Note that $\dot{L}\left(t\right)=0$ for $\mathit{X}={\mathit{X}}^{★}$. By Lemma (A3), each $x_j$ is bounded and there exists $\underline{x}=min{x}_j$ such that $\underline{x}>0$ as $t\to \infty$ (in the vaccination-free context where ${\eta }_v=\upsilon =0$, the same argument holds by ignoring the state V which satisfies $V\left(t\right)\to V^{★}=0$ as $t\to \infty$). This implies that

$$\dot{L}\left(t\right)\le {\underline{x}}^{-1}\sum _{j=1}^8\left(x_j-x_j^{★}\right){\dot{x}}_j.$$

Since the derivatives ${\dot{x}}_j$ in system (A3) are additive functions of constant parameters and bounded variables $x_j$, it also follows that each ${\dot{x}}_j$ is bounded so that there exists $\overline{x}>0$ such that ${\dot{x}}_j<\overline{x}$ for $j=1,2,\cdots ,8$. This impslies that

$$\dot{L}\left(t\right)<\overline{x}{\underline{x}}^{-1}\sum _{j=1}^8\left(x_j-x_j^{★}\right)\mathrm{for}\mathit{X}\ne {\mathit{X}}^{★}.$$

Since N is bounded, it follows from Barbalat’s lemma [94] that $\dot{N}\left(t\right)\to 0$ as $t\to \infty$, so that we have from $\dot{N}\left(t\right)=\eta -\mu N\left(t\right)-{\delta }_s{I}_s\left(t\right)-{\delta }_{q}Q\left(t\right)$:

$$\begin{array}{cc}\hfill \underset{t\to \infty }{lim}N\left(t\right)& =N^c-\frac{1}{\mu }\underset{t\to \infty }{lim}\left[{\delta }_s{I}_s\left(t\right)+{\delta }_{q}Q\left(t\right)\right].\hfill \end{array}$$

We also have ${lim}_{t\to \infty }{\dot{I}}_s\left(t\right)={lim}_{t\to \infty }\dot{Q}\left(t\right)=0$ by Barbalat’s lemma and the boundedness of $I_s\left(t\right)$ and $Q\left(t\right)$, so that ${lim}_{t\to \infty }{I}_s\left(t\right)$ and ${lim}_{t\to \infty }Q\left(t\right)$ are stationary points for Equations (A3f) and (A3g). Since these limits are nonzero when ${\mathcal{R}}_c>1$ (by Lemma (A3)), the d.f.e. ($I_s^c=0$ and $Q^c=0$) is excluded, and ${lim}_{t\to \infty }{I}_s\left(t\right)=I_s^{★}$ and ${lim}_{t\to \infty }Q\left(t\right)=Q^{★}$ (the unique e.e. alternative). It follows, by Equation (A9k), that ${lim}_{t\to \infty }N\left(t\right)=N^{★}$, so that ${lim}_{t\to \infty }{\sum }_{j=1}^8\left(x_j-x_j^{★}\right)={lim}_{t\to \infty }N\left(t\right)-N^{★}=0$. As a result, $\dot{L}\left(t\right)<0$ for $\mathit{X}\ne {\mathit{X}}^{★}$ as $t\to \infty$, hence L is a strict Lyapunov function, and by Proposition (A3), ${\mathit{X}}^{★}$ is its unique stationary point: ${\mathit{X}}^{★}$ is a global minimum and therefore g.a.s. when ${\mathcal{R}}_c>1$. □

Appendix D.2. Proofs of lemmas and propositions related to Disease-Opinion dynamics

Proof of Lemma 1 .

A proof of Lemma 1 is straightforward following the argument detailled in the proof of Lemma A1 (see Appendix D.1). Each compartment size $x_j\left(t\right)$ satisfies $\frac{\partial x_j\left(t\right)}{\partial t}\ge -z_{0j}{x}_j\left(t\right)$ where $z_{0j}$ is a positive real constant. This gives $x_j\left(t\right)\ge x_{0j}{e}^{-z_{0j}t}$, which establishes nonnegativity from $x_{0j}\ge 0$. This implies that the total population size $N\left(t\right)={\sum }_j{x}_j\left(t\right)$ satisfies $N\left(t\right)\ge 0$. Then, $\frac{\partial N\left(t\right)}{\partial t}\le \eta -\mu N\left(t\right)$ leads to $0\le N\left(t\right)\le max\{N_0,N^c\}$ where $N^c=\eta /\mu$ is the carrying capacity of the biological system. This finally results in $0\le x_j\left(t\right)\le max\{N_0,N^c\}$. □

Proof of Proposition 1.

Adding the disease-free restriction $E=I_p=I_a=I_s=Q=0$ to System (7) implies that ${\lambda }_i\left(t\right)=0$. Setting all the derivatives to zero then gives $E^c=I_p^c=I_a^c=I_s^c=Q^c=R^c=0$. Since $w_o>0$, we are left with the system

$$\begin{array}{cc}\hfill {\overline{\eta }}_1& -S_{-1}^c{S}_1^c-\overline{\mu }{S}_1^c=0,\hfill \\ \hfill {\overline{\eta }}_0& +2S_{-1}^c{S}_1^c-\overline{\mu }{S}_0^c=0,\hfill \\ \hfill {\overline{\eta }}_{-1}& -S_1^c{S}_{-1}^c-\overline{\mu }{S}_{-1}^c=0,\hfill \end{array}$$

where ${\overline{\eta }}_i={\eta }_i\frac{N^c}{w_o}$, $\overline{\mu }=\mu \frac{N^c}{w_o}$ with $N^c=S_{-1}^c+S_0^c+S_1^c$. Summing the three equations gives $\eta -\mu N^c=0$, i.e. $N^c=\eta /\mu$. Solving the third equation for $S_{-1}^c$ gives $S_{-1}^c=\frac{{\overline{\eta }}_{-1}}{S_1^c+\overline{\mu }}$, and inserting this in the first equation yields the quadratic $\overline{\mu }{\left(S_1^c\right)}^2-\left({\overline{\eta }}_1-{\overline{\eta }}_{-1}-{\overline{\mu }}^2\right)S_1^c-{\overline{\eta }}_1\overline{\mu }$ which has the unique positive solution

$$\begin{array}{cc}\hfill S_1^c& =\frac{1}{2\overline{\mu }}\left[\sqrt{{\left({\overline{\eta }}_1-{\overline{\eta }}_{-1}-{\overline{\mu }}^2\right)}^2+4{\overline{\eta }}_1{\overline{\mu }}^2}+{\overline{\eta }}_1-{\overline{\eta }}_{-1}-{\overline{\mu }}^2\right].\hfill \end{array}$$

Further simplifications result in Equations (15b)-(15d). The computations of the reproduction numbers (16a) and (16b) follow the steps in the proof of Proposition A1 (see Appendix D.1), except that $\mathbb{F}\left(\mathit{I}\right)$ and ${\mathit{F}}^c$ are here defined as

$$\mathbb{F}\left(\mathit{I}\right)=\frac{1}{N-Q}\sum _{i\in \mathcal{P}}{S}_i\left(\begin{array}{c}\sum _{j=p,a,s}{\beta }_{ij}{I}_j\\ 0\\ 0\\ 0\end{array}\right)\mathrm{and}{\mathit{F}}^c=\frac{1}{N^c}\sum _{i=-1}^1{S}_i^c\left(\begin{array}{cccc}0& {\beta }_{ip}& {\beta }_{ia}& {\beta }_{is}\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right).$$

To obtain the direction of variation of the basic reproduction number ${\mathcal{R}}_0$ (16a) as a function of the baseline influence rate $w_o$, we find its derivative with respect to $w_o$. To this end, notice that, by Equations (15d)-(15b), the derivatives of $S_{-1}^c$ and $S_1^c$ with respect to $w_o$ are the same $\left(\frac{\partial S_{-1}^c}{\partial w_o}=\frac{\partial S_1^c}{\partial w_o}\right)$, and $\frac{\partial S_0^c}{\partial w_o}=-2\frac{\partial S_1^c}{\partial w_o}$. Hence $\frac{\partial {\mathcal{R}}_0}{\partial w_o}={\mathcal{R}}_{00}\left({\varsigma }_o^2-2{\varsigma }_o+1\right)\frac{\partial S_1^c}{\partial w_o}$ with ${\mathcal{R}}_{00}=\frac{\theta }{(\theta +\mu )(\sigma +\mu )}\frac{\mu }{\eta }{\sum }_{j=p,a,s}{\beta }_j{m}_j$. Setting ${\Delta }_1=\frac{\eta {\eta }_1}{\mu w_o}+{\left(\frac{{\eta }_1-{\eta }_{-1}}{2\mu }-\frac{\eta }{2w_o}\right)}^2$, we obtain after basic algebra $\frac{\partial S_1^c}{\partial w_o}=\frac{\eta }{2w_o}\left[1-\frac{(\mu +w_o)\eta -w_o{\eta }_0}{2w_o\mu \sqrt{{\Delta }_1}}\right]<0$. Hence $\frac{\partial {\mathcal{R}}_0}{\partial w_o}={\left(1-{\varsigma }_o\right)}^2{\mathcal{R}}_{00}\frac{\partial S_1^c}{\partial w_o}<0$. □

Proof of Proposition 2.

Adding the disease-free restriction $E=I_p=I_a=I_s=Q=0$ to System (Section 2.8) implies that ${\lambda }_i\left(t\right)=0$ for $i\in \mathcal{P}$. Setting all the derivatives to zero then gives $E^c=I_p^c=I_a^c=I_s^c=Q^c=R^c=0$, and we are left with the system

$$\begin{array}{c}\hfill \mathit{M}{\mathit{S}}^c=\mathit{\eta }\end{array}$$

where ${\mathit{S}}^c$, $\mathit{M}$, and $\mathit{\eta }$ are as defined in Equation (19b). Summing the partial derivatives for all $S_i$ individuals gives ${\dot{U}}_{iu}+{\dot{U}}_{iv}+{\dot{V}}_i={\dot{S}}_i$, i.e. the susceptible states in the SEIQR-Opinion model (7). It follows that $S_1^c$, $S_{-1}^c$, and $S_0^c$ are given by Equations (15b)-(15d). Likewise, summing the first three equations, the fourth to sixth equations, and the seventh to last equations results in the system

$$\begin{array}{cccccccccccccccccccccc}\hfill {\overline{\eta }}_{uu}& \hfill & \hfill +& \hfill & \hfill U_u^c{U}_v^c& \hfill & \hfill -& \hfill & \hfill (U_v^c+V^c)U_u^c& \hfill & & & & & & & & & -& & \overline{\mu }{U}_u^c& =0\left(a\right),\\ \hfill {\overline{\eta }}_{uv}& \hfill & \hfill -& \hfill & \hfill U_u^c{U}_v^c& \hfill & \hfill +& \hfill & \hfill (U_v^c+V^c)U_u^c& \hfill & +& & \overline{\alpha }{V}^c& & -& & \overline{\upsilon }{U}_v& & -& & \overline{\mu }{U}_v^c& =0\left(b\right),\\ \hfill {\overline{\eta }}_v& \hfill & & \hfill & & \hfill & & \hfill & & \hfill & -& & \overline{\alpha }{V}^c& & +& & \overline{\upsilon }{U}_v& & -& & \overline{\mu }{V}^c& =0\left(c\right),\end{array}$$

where ${\overline{\eta }}_{uu}={\sum }_{i\in \mathcal{P}}{\overline{\eta }}_{iu}$, ${\overline{\eta }}_{uv}={\sum }_{i\in \mathcal{P}}{\overline{\eta }}_{iuv}$, ${\overline{\eta }}_v={\sum }_{i\in \mathcal{P}}{\overline{\eta }}_{iv}$, ${\overline{\eta }}_{il}={\eta }_{il}\frac{N^c}{w_o}$, $\overline{\mu }=\mu \frac{N^c}{w_o}$, $\overline{\alpha }=\alpha \frac{N^c}{w_o}$, $\overline{\upsilon }=\upsilon \frac{N^c}{w_o}$, $U_u^c={\sum }_{i\in \mathcal{P}}{U}_{iu}^c$, $U_v^c={\sum }_{i\in \mathcal{P}}{U}_{iv}^c$, and $V^c={\sum }_{i\in \mathcal{P}}{V}_i^c$. From (c), we have $V^c=\frac{{\overline{\eta }}_v^c+\overline{\upsilon }{U}_v}{\overline{\alpha }+\overline{\mu }}$, and we get $U_u^c=\frac{{\overline{\eta }}_{uu}}{V^c+\overline{\mu }}=\frac{{\overline{\eta }}_{uu}(\overline{\alpha }+\overline{\mu })}{{\overline{\eta }}_v+\overline{\mu }(\overline{\alpha }+\overline{\mu })+\overline{\upsilon }{U}_v^c}$ from (a). Inserting these results in (b) leads to $C_2{\left(U_v^c\right)}^2+C_1{U}_v^c-C_0=0$ where $C_2=\upsilon \left(1+\frac{\upsilon }{\alpha +\mu }\right)$, $C_1={\eta }_u\left(\frac{\alpha +\upsilon +\mu }{w_o}-\frac{\upsilon }{\mu }\right)+{\eta }_v\left[1+\frac{\alpha +\upsilon +\mu }{w_o}+\frac{\upsilon (\mu -\alpha )}{\mu (\alpha +\mu )}\right]$, $C_0=\eta {\eta }_{uv}\frac{\alpha +\mu }{w_o\mu }+\frac{{\eta }_v}{\mu }\left({\eta }_u+\frac{\alpha {\eta }_v}{\alpha +\mu }+\frac{\alpha \eta }{w_o}\right)$. When $\upsilon =0$, we have $C_2=0$, $C_1>0$ and $C_0\ge 0$; hence $U_v^c=C_0/C_1$. For $\upsilon >0$, we have $C_2,C_1>0$. If ${\eta }_{uu}<\eta$ (i.e. ${\eta }_{uv}\ne 0$ or ${\eta }_v\ne 0$), then $C_0>0$ and we have only one sign change in the coefficient of the quadratic which, therefore, has the unique nonnegative solution $U_v^c=\left(\sqrt{C_1^2+4C_0{C}_2}-C_1\right)/\left(2C_2\right)$. If ${\eta }_{uu}=\eta$ (i.e. ${\eta }_{uv}={\eta }_v=0$), then $C_0=0$ and the quadratic has the unique nonnegative solution $U_v^c=0$, which is consistent with $U_v^c$ when ${\eta }_{uu}<\eta$. Equations (19d)-(19f) then follow. We thus have the constants $U_u^c$, $U_v^c$ and $V^c$, and in consequence, the matrix $\mathit{M}$ is available prior to the computation of the sizes of the nine susceptible states. It follows that $\mathit{M}{\mathit{S}}^c=\mathit{\eta }$ is a linear system in ${\mathit{S}}^c$. The step-wise resolution of the system $\mathit{M}{\mathit{S}}^c=\mathit{\eta }$ in Appendix E shows that the matrix $\mathit{M}$ is always non-singular, and Equation (19b) follows. The computations of the reproduction numbers (20a) and (20c) follow the steps in the proof of Proposition A1 (see Appendix D.1), except that $\mathbb{F}\left(\mathit{I}\right)$ and ${\mathit{F}}^c$ are here defined with ${\overline{S}}_i=\frac{U_i+(1-\kappa )V_i}{N-Q}$ and ${\overline{S}}_i^c=\frac{U_i^c+(1-\kappa )V_i^c}{N^c}$ as

$$\mathbb{F}\left(\mathit{I}\right)=\sum _{i\in \mathcal{P}}{\overline{S}}_i\left(\begin{array}{c}\sum _{j=p,a,s}{\beta }_{ij}{I}_j\\ 0\\ 0\\ 0\end{array}\right)\mathrm{and}{\mathit{F}}^c=\sum _{i\in \mathcal{P}}{\overline{S}}_i^c\left(\begin{array}{cccc}0& {\beta }_{ip}& {\beta }_{ia}& {\beta }_{is}\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right).$$

The derivatives of $f_i\left(\mathit{M}\right)=U_i^c+(1-\kappa )V_i^c$ with respect to $\upsilon$ is, by the Chain rule, given by $\frac{\partial g_i\left(\mathit{M}\right)}{\partial \upsilon }=trace\left\{{\left(\frac{\partial g_i\left(\mathit{M}\right)}{\partial \mathit{M}}\right)}^{\top }\frac{\partial \mathit{M}}{\partial \upsilon }\right\}$. Note that $f_i\left(\mathit{M}\right)={\mathit{E}}_i^{\top }{\mathit{S}}^c$, where ${\mathit{E}}_i={\mathit{E}}_{iu}+(1-\kappa ){\mathit{E}}_{iv}$, ${\mathit{E}}_{iu}^{\top }=\left({\mathit{e}}_{3,i+2}^{\top },{\mathit{e}}_{3,i+2}^{\top },{\mathbf{0}}_3^{\top }\right)$ and ${\mathit{E}}_{iv}^{\top }=\left({\mathbf{0}}_6^{\top },{\mathit{e}}_{3,i+2}^{\top }\right)$, and ${\mathit{e}}_{m,k}$ is the single-entry m-vector with one at the position k and zeros elsewhere. Writing $f_i\left(\mathit{M}\right)={\mathit{E}}_i^{\top }{\mathit{M}}^{-1}\mathit{\eta }$, it follows that $\frac{\partial g_i\left(\mathit{M}\right)}{\partial \mathit{M}}=-{\left({\mathit{M}}^{-1}\right)}^{\top }{\mathit{E}}_i{\mathit{\eta }}^{\top }{\left({\mathit{M}}^{-1}\right)}^{\top }$, thus ${\left(\frac{\partial g_i\left(\mathit{M}\right)}{\partial \mathit{M}}\right)}^{\top }=-{\mathit{S}}^c{\mathit{E}}_i^{\top }{\mathit{M}}^{-1}$. It then remains to find the derivative $\frac{\partial \mathit{M}}{\partial \upsilon }$. □

Proof of Lemma 2.

A proof of Lemma 2 follows the steps in of Lemma A2. Indeed, the Jacobian matrix of model (7) at the d.f.e. also has the block structure

$${\mathit{J}}^c=\left(\begin{array}{ccc}{\mathit{J}}_S^c& {\mathit{J}}_{SI}^c& {\mathit{J}}_{SQ}\\ \mathbf{0}& {\mathit{J}}_I^c& \mathbf{0}\\ \mathbf{0}& {\mathit{J}}_{QI}& {\mathit{J}}_Q\end{array}\right).$$

From this structure, the eigenvalues of ${\mathit{J}}^c$ are those of ${\mathit{J}}_S$, ${\mathit{J}}_I^c$ and ${\mathit{J}}_Q$. The blocks ${\mathit{J}}_I^c$ and ${\mathit{J}}_Q$ are as defined in the proof of Lemma A2, but ${\mathit{J}}_S^c$ is here given as

$$\begin{array}{cc}\hfill {\mathit{J}}_S& =w_o\left(\begin{array}{ccc}-\frac{S_1}{N^c}\left(1-\frac{S_{-1}}{N^c}\right)-\mu & \frac{S_{-1}}{N^c}\frac{S_1}{N^c}& -\frac{S_{-1}}{N^c}\left(1-\frac{S_1}{N^c}\right)\\ -2\frac{S_{-1}}{N^c}\frac{S_1}{N^c}& -2\frac{S_{-1}}{N^c}\frac{S_1}{N^c}-\mu & -2\frac{S_{-1}}{N^c}\frac{S_1}{N^c}\\ -\frac{S_1}{N^c}\left(1-\frac{S_{-1}}{N^c}\right)& \frac{S_{-1}}{N^c}\frac{S_1}{N^c}& -\frac{S_{-1}}{N^c}\left(1-\frac{S_1}{N^c}\right)-\mu \end{array}\right).\hfill \end{array}$$

From Lemma A2, we know that the eigenvalues of ${\mathit{J}}_Q$ are all negative, and ${\mathit{J}}_I^c$ has one or more positive eigenvalues only if ${\mathcal{R}}_c>1$. We thus restrict attention to ${\mathit{J}}_S$ whose three eigenvalues must have negative real parts to ensure l.a.s. when ${\mathcal{R}}_c\le 1$. We find $d_0=-\mu$,

$$\begin{array}{cc}\hfill d_1& =-\left[\frac{1}{2}\left(a+b+\sqrt{(a+b)(a+b-8ab)}\right)+\mu \right]\mathrm{and}\hfill \\ \hfill d_2& =-\left[\frac{1}{2}\left(a+b-\sqrt{(a+b)(a+b-8ab)}\right)+\mu \right]\hfill \end{array}$$

where $a=$

... □

Proof of Proposition 4.

scdgfhgjhkjk □