Preprint

Article

The Dirac Fermion of a Monopole Pair (MP) Model

Altmetrics

Downloads

801

Views

223

Comments

Samuel Yuguru^*

This version is not peer-reviewed

Abstract

The electron of spin −1/2 is a Dirac fermion of a complex four-component spinor field. Though it is effectively addressed by relativistic quantum field theory, an intuitive form of the fermion still remains lacking and it is often described by the so-called Dirac belt trick. In this novel undertaking, the fermion is examined within the boundary posed by a recently proposed MP model of a hydrogen atom into 4D space-time. Its physicality and transformation to Dirac fermion of four-component spinor is unveiled consistent with Dirac belt trick. The outcomes are compatible with Dirac field theory and other associated features like, space-time dynamics, non-relativistic wave function and Feynman diagram inclusive of symmetry breaking. The model though speculative, it could become important towards defining the fundamental state of matter and its quantum field theory.

Keywords:

Submitted:

26 January 2024

Posted:

29 January 2024

Read the latest preprint version here

Alerts

Abstract

Keywords:

Subject: Physical Sciences - Quantum Science and Technology

1. Introduction

At the fundamental level of matter, particles are described by wave-particle duality, charges and their spin property. These properties are revealed from light interactions and are pursued by the application of relativistic quantum field theory (QFT) [1,2]. The theory of special relativity defines lightspeed, c to be constant in a vacuum and the rest mass of particles to be,

m = E / c^{2}

with E as energy. The particle-like property of light waves consists of massless photons possessing spin 1 of neutral charge. Any differences to its spin, charge and mass-energy equivalence provide the inherent properties of particles for the matter at the fundamental level and this is termed causality [3,4]. Based on QFT, particles appear as excitation of fields permeating space at less than lightspeed. There is a level of indetermination towards unveiling of the charge and spin property, whereas the wave-particle duality is depended on the instrumental set-up [5,6]. The probability of locating the electron within the atom is defined by non-relativistic Schrödinger’s electron field,

ψ

, and it is not compatible to the excitation of the electromagnetic field for particle manifestation [7]. In other words, it is difficult to imagine wavy form of particles freely permeating space without interactions and this somehow collapses to a point at observation [8].

At the atomic state, the energy is radiated in discrete energy forms in infinitesimal steps of Planck radiation, ±h. The interpretation is consistent with observations except for the resistive nature of proton decay [9]. The preferred quest for particle observation at the atomic level is to make non-relativistic equations become relativistic due to the shared properties of both matter and light at the fundamental level as mentioned above.

Beginning with Klein-Gordon equation [10], the energy and momentum operators of Schrödinger equation,

\hat{E} = i ℏ \frac{\partial}{\partial t}, \hat{p} = - i ℏ \nabla,

(1)

are adapted in the expression,

(ℏ^{2} \frac{\partial^{2}}{\partial t^{2}} - c^{2} ℏ^{2} \nabla^{2} + m^{2} c^{4}) ψ (t, \bar{x}) = 0.

(2)

Equation 2 incorporates special relativity,

E^{2} = p^{2} c^{2} + m^{2} c^{4}

for mass-energy equivalence,

\nabla

is the del operator in 3D space, ℏ is reduced Planck constant and

i

is an imaginary number,

i = \sqrt{- 1}

. Only one component is considered in Equation 2 and it does not take into account the negative energy contribution from antimatter. In contrast, the Hamiltonian operator,

\hat{H}

of Dirac equation [11] for a free particle is,

\hat{H} ψ = (- i \nabla . a + m β) ψ .

(3)

The

ψ

has four-components of fields,

i

with vectors of momentum,

\nabla

and gamma matrices, α, β represent Pauli matrices and unitarity. The concept is akin to, e⁺ e^– ⟶ 2 𝛾, where the electron annihilates with its antimatter to produce two gamma rays. Antimatter existence is observed in Stern-Gerlach experiment and positron from cosmic rays. While the relativistic rest mass is easy to grasp, how fermions acquire mass other than Higgs field remains yet to be solved at a satisfactory level [12]. But perhaps, the most intriguing dilemma is offered by the magnetic spin ±1/2 of the electron and how this translates to a Dirac fermion of four-component spinor field. Such a case remains a very complex topic, whose intuitiveness in terms of a proper physical entity remains lacking and it is often described either by Dirac belt trick [13] or Balinese cup trick [14]. Others relatable descriptions include Klein bottle [15] and Dirac scissors problem [16]. Suppose the atom is conserved, how the electron is physically transformed into Dirac fermion is examined within a proposed a monopole pair (MP) model. Such a process is compatible with Dirac belt trick, its field theory and other associated features like space-time dynamics, non-relativistic wave function and Feynman diagram with charge conjugation, parity and time reversal (CPT) symmetry breaking. The model though speculative, it could become important towards defining the fundamental state of matter and its QFT.

2. Limitations of quantum field theory

In relativistic QFT, the atom is expected to be eventually reduced to fundamental particles like fermions and bosons based on the 2^nd law of thermodynamics. These would permeate space and any excitations from light interactions should permit their observations. Such a notion is adapted into Yukawa’s relativistic range of interaction, R = ℏ/mc with the incorporation of the uncertainty principle [17] and this forms the underlying non-abelian Yang-Mills theory of the Standard Model (SM). The relativistic mass, m = 0 sustains unitarity and gauge invariance [18]. The SM accounts quite well for the propagation of electromagnetic field in space, quark confinement and the property of asymptotic freedom and the observable particles but at the expense of infinite, R [19]. Similarly, m ≠ 0 draws divergent terms to the Fourier Transform integral,

\int d^{4} k

with k equal to 4^th dimensional variable [20]. Renormalization of particle self-interaction by Feynman diagrams to account for any exponential increase with exchanges of virtual photons adapts Dirac fermion of four-component spinor as its base [1,2]. The corrective measures are employed by the SM lagrangian for infinite high-order terms for energy conservation, while the transition from m = 0 to m > 0 is attributed to dynamic chiral symmetry breaking like the Higgs mechanism to confer a particle’s mass. The theory has seen tremendous success, whereby it ably accounts quite well for all observations made so far into the electroweak force interactions. However, for strong nuclear interactions of proton-proton collisions, the absence of supersymmetric partners offers an enigma [21,22] to the actual nature of the atom. In this study, how Dirac fermion of a hydrogen atom could be interpreted within the geometry of a MP model is examined with its implications to the application of QFT.

3. Unveiling Dirac belt trick

The electron’s orbit of time reversal in discrete continuum form of sinusoidal is defined by Planck radiation, h and is linked to Bohr orbits (BOs) into n-dimensions of energy levels. In forward time, the orbit is transformed into an elliptical shape of a monopole pair (MP) field that undergoes clockwise precession (Figure 1a,b). The torque or right- handedness shifts the electron from positions 0 to 3 to assumed 360° rotation. Maximum twist is attained at the point-boundary or vertex of the MP field at the starting position due to time reversal orbit against clockwise precession. The electron flips to spin down at position 4 to assume an isospin in violation of spherical lightspeed and begins the unfolding process. Another 360° rotation from positions 5 to 8 restores the electron to its original state. These intuitions relate well to Dirac belt trick at 720° rotation assumed at minimal energy of spherical lightspeed in wave-diffraction form. The electron-positron transition at the point-boundary of position 0 promotes radiation of the type,

E = n h v

from twisting and unfolding process and this somehow sustains the principle axis of the MP field akin to arrow of time in asymmetry. Radiation of Hilbert space at the point-boundary translates to Hamiltonian by clockwise precession at spherical lightspeed. In this way, local realism and entanglement are sustained in accordance with Pauli exclusion principle. The conditions for the inertia frame of reference (Figure 1a) are given as,

λ_{\pm}^{2} = λ_{\pm} Tr λ_{\pm} = 2 λ_{+} + λ_{-} = 1

(4)

where the trace function, Tr is the sum of all elements associated with the Dirac spinor. The point-boundary is orthonormal to any external interactions and is the base of Hilbert space for the MP field. In multielectron atoms, multiple MP fields are assumed for the electrons distribution. How the dynamics of the model aligns with Dirac field theory and other associated themes are explored in the subsequent section.

4. Dirac field theory and its associated features

The descriptions of Dirac fermion based on the MP model can further the Dirac field theory. In this section certain components of the field theory and its related features [1,2,10,11] are explored in bullet points for their relevance to this undertaking.

⇒: Discrete symmetries. The electron of a body spinning about an axis (isospin) offers chiral symmetry to the model. Its transformation to Dirac fermion field, $ψ$ and its vector gauge invariance exhibit chiral symmetry by the relationships,

$ψ_{L} \to e^{i θ L} ψ_{L}$

(5a)

ψ_{R} \to e^{i θ L} ψ_{R}

(5b)

The exponential factor, iθ provides the position, i of a complex number and the associated angular momenta, θ. The unitary rotations of right-handedness (R) or positive helicity and left-handedness (L) or negative helicity are applicable to the electron transformation to Dirac fermion (Figure 2a). The process is confined to a hemisphere and this equates to spin 1/2 property of a complex spinor (Figure 2b). Two successive rotations of the electron in orbit at more than clockwise precession of the MP field is identified by

i ℏ

. The chirality or vector axial current at the point-boundary is assigned to polarization, ±1 of the model. The helical symmetry from projections operators (isospin) acting on the spinors based on Figure 2b is,

P_{L} = \frac{1}{2} (1 - γ_{5})

(6a)

and

P_{R} = \frac{1}{2} (1 - γ_{5}) .

(6b)

Dirac matrices of eigenstates,

γ_{5}

for the spinor field is assumed at fixed momentum at an energy level. The usual properties of projection operators are: L + R = 1; RL = LR = 0; L² = L and R² = R. The boundary conditions are provided in Equation (4).

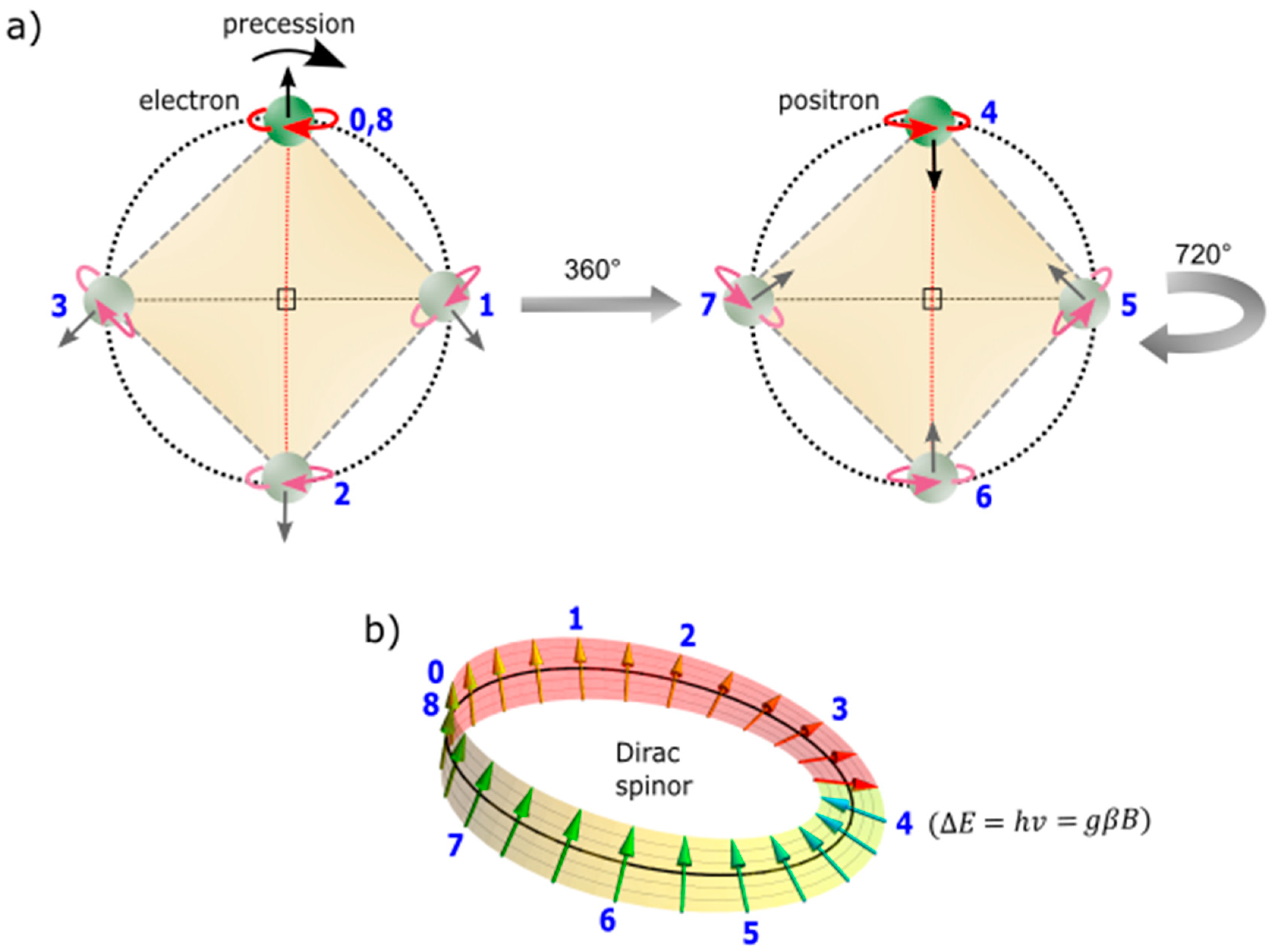
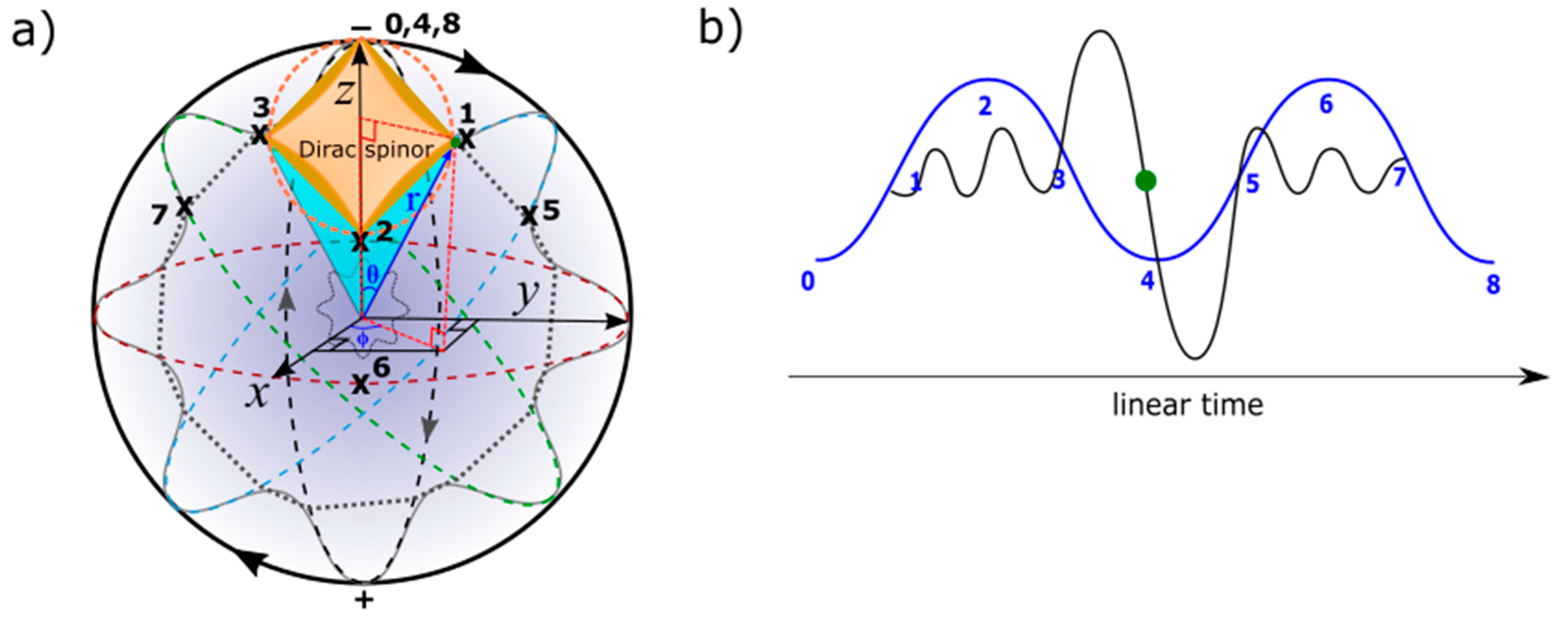
⇒: Space-time dynamics. Dirac fermion or spinor is denoted ψ(x) in 3D Euclidean space and it is superimposed onto the MP model of Minkowski space-time, ψ(x,t) by clockwise precession of the MP field (Figure 3a). Space itself is devoid of any reference points and thus, the Dirac four-component spinor, $ψ = (\begin{matrix} ψ_{0} \\ ψ_{1} \\ ψ_{2} \\ ψ_{3} \end{matrix})$ is attributed to a 3D object (electron) in orbit, $ψ_{1} \to ψ_{3}$ and it sustains the arrow of time as the principle axis of the MP field in asymmetry, $ψ_{0}$ at the point-boundary. Positions 0 to 3 are hermitian conjugates of positions 4 to 7 and the electron is restored at position 8. Their translation to linear time of Fourier transform is offered in Figure 3b.

The area defined by Dirac spinor when superimposed on the surface of Poincaré sphere can relate to both positive and negative curvatures of non-Euclidean space (Figure 3a). The latter is attributed to the electron orbit of time reversal and this is normalized by the former of geodesic motion from spherical rotation. Convergence of positions 1 and 3 at either position 0 or 2 is consistent with Equation (4) and is relevant to the equivalence principle of general relativity. The straight paths of the Dirac spinor define Euclidean space (Figure 2a). Any light paths tangential to the point-boundary is expected to transform Dirac spinor into linear time comparable to Fourier transform and thus, induce wave function collapse (Figure 3b). The probabilistic outcome of the spin is given by Born’s rule,

{|ψ|}^{2}

, with only one outcome permitted. The past or future events of the electron path from positions 0 to 8 are not accounted for in the observation of particle property. The shift in positions is Hermitian, P(0→8) =

\int_{τ} ψ^{*} \hat{H} ψ d τ

in Hamiltonian space with

τ

equal to clockwise precession. Continuity of the electron orbit against precession reflects Euler’s formula,

e^{i π}

+ 1 = 0.

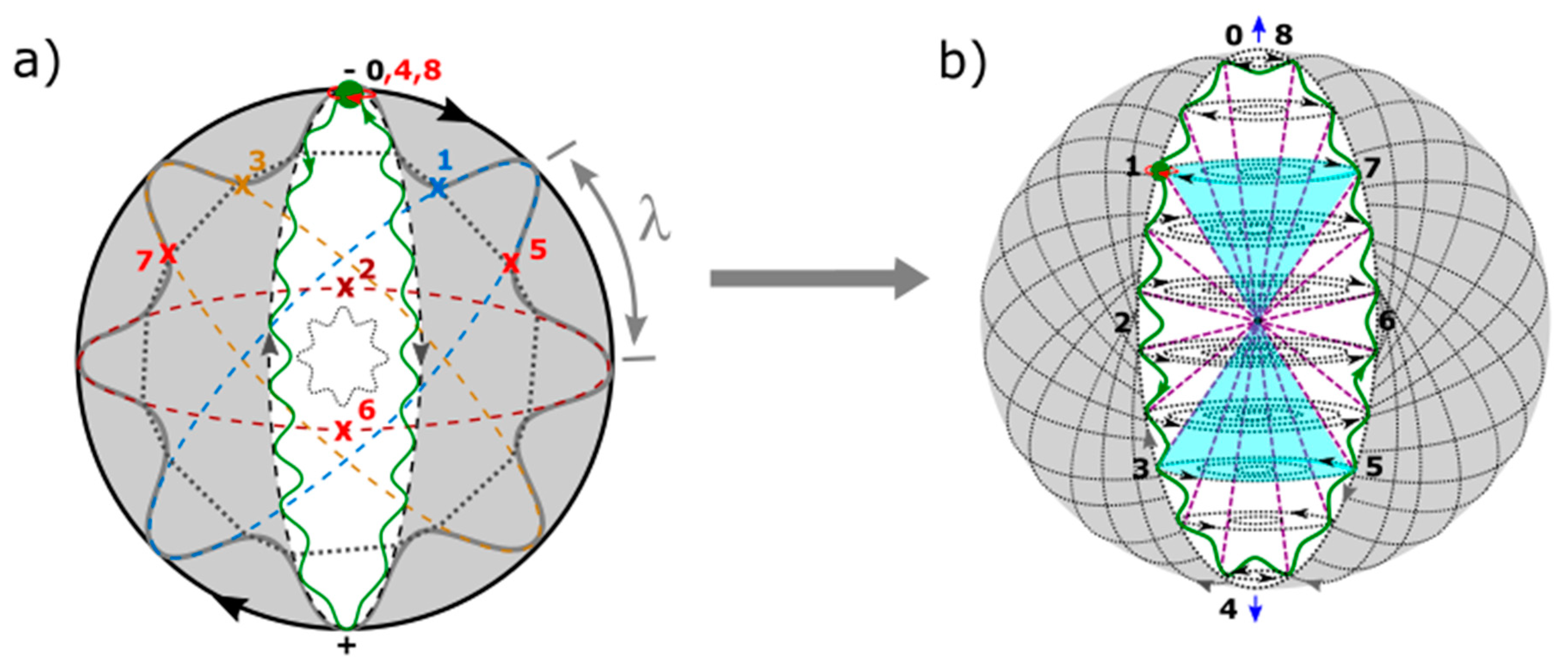
⇒: Non-relativistic wave function. The point-boundary at singularity identifies with Planck length. Observation by light-matter interaction allows for the emergence of the model from the point-boundary and this generates complex fermions, ±1/2, ±3/2, ±5/2 and so forth at the energy shells of BOs (Figure 4a). Their orbitals of 3D are defined by total angular momentum, $\vec{J} = \vec{l} + \vec{s}$ and this incorporates both orbital angular momentum, l and spin, s. From a hemisphere, the model is transformed to a classical oscillator. By clockwise precession, a holographic oscillator from the other hemisphere of the MP field remains hidden. One oscillator levitates about the other (Figure 4b) and both are not simultaneously accessible to observation due to constraints placed by the electron as a physical entity and the influence of its orbit from clockwise precession. The n-levels or shells for the fermions can be pursued for Fermi-Dirac statistics with the point-boundary assigned to zero-point energy (ZPE). Likewise, $\pm \vec{J}$ splitting (Figure 4a) can apply to Landé interval rule due to the electron isospin and this can accommodate lamb shift and thus, hyperfine structure constant. Such scenario is comparable to how vibrational spectra of a harmonic oscillator for diatoms like hydrogen molecule incorporates rotational energy levels. The quantum nature of the classical oscillator is also relevant to the spherical coordinates for the interpretation of Schrödinger wave equation (Figure 4a).

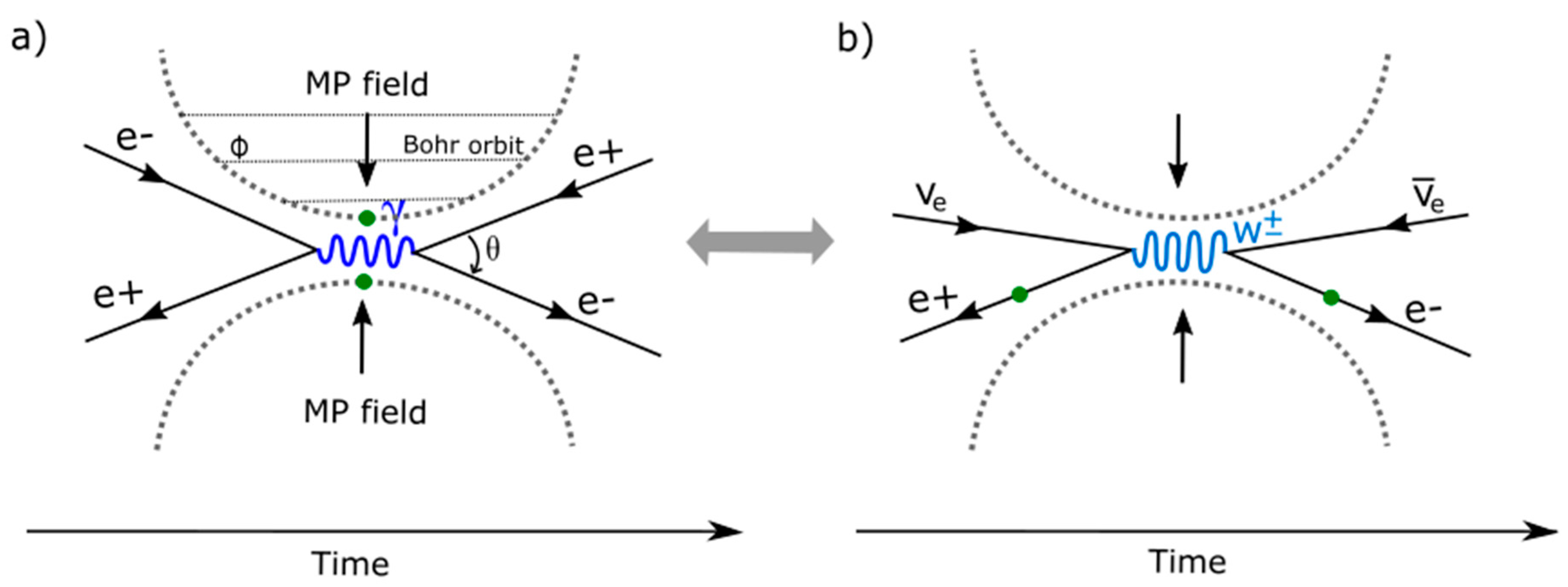
⇒: Feynman diagram and CPT symmetry breaking. Feynman diagrams of path integrals incorporate both matter and antimatter coupling and annihilation processes. These can demonstrate the paths of m = 0 at unitarity to m > 0 for symmetry breaking. When two electrons from a pair of MP models (ionized hydrogen molecules or atoms) approach each other, both attraction and repulsion can occur due to electron-positron transition at the point-boundary. Secondary photons mimicking the electron-positron pair can acquire mass with unitarity sustained (Figure 5a). Ejection of an electron (or positron) by beta decay, $β^{\pm}$ would insinuate particle-hole of isospin mimicking up and down quarks (Figure 5b). These interpretations are consistent with the transformation of the electron of isospin to Dirac fermion (Figure 2a). Particle-hole coupling can lead to W^± bosons and neutrinos and antineutrinos of helical property mimicking the electron-positron pair without requiring change of color charges by exchange of gluons from up and down quarks. In this case, the vertices of the MP models assume center of mass and ejection of the electron/positron may constitute violation of charge conjugation, parity and time reversal symmetry. The suggestion is also made for the bosons of neutral charge and whole integer spin would amass at ZPE of the point-boundary of a classical oscillator (Figure 4a). The difference in mass of the bosons by mass-energy equivalence such as for W^± can be attributed to constriction and relaxation of the model into n-dimensions or energy shells. Any scatterings at the n-dimensions (Figure 4a) can accommodate the fine-structure constant, $a = \frac{e^{2}}{ℏ c} = \frac{e^{2}}{4 π} \approx \frac{1}{137}$ and it is applicable to high energy at $c = ℏ = 1$ .

⇒: Dirac field. The fermion field is defined by the famous Dirac equation of the generic form,

$i ℏ γ^{u} \partial_{u} ψ (x) - m c ψ (x) = 0,$

(7)

where $γ^{u}$ are the gamma matrices related to the shifts in the electron’s position by clockwise precession acting on its orbit. The exponentials of the matrices, $\{γ^{o} γ^{1} γ^{2} γ^{3}\}$ are assumed by the electron of 3D object. $γ^{o}$ is assigned to the vertex of the MP field due to radiation from the electron-positron transition at position 0 and somewhat sustains arrow of time in asymmetry. The $γ^{1} γ^{2} γ^{3}$ variables are of Dirac matrices and these are applicable to the electron of 3D object and shift in its position. The orthogonal projections of the space-time variables, $\frac{1}{2} (1 \pm i γ^{0} γ^{1} γ^{2} γ^{3})$ within a hemisphere are assigned to a light cone (Figure 4a). These are all incorporated into the famous Dirac equation,

$(i γ^{0} \frac{\partial}{\partial t} + c A \frac{\partial}{\partial x} + c B \frac{\partial}{\partial y} + c C \frac{\partial}{\partial z} - \frac{m c^{2}}{ℏ}) ψ (t, \vec{x}),$

(8)

where c acts on the coefficients A, B and C and transforms them to $γ^{1}, γ^{2}$ and $γ^{3}$ . Alternatively, the exponentials of $γ$ are denoted i, where $γ^{i}$ is off-diagonal Pauli matrices assigned to a pair of light cones in Minkowski space-time (Figure 1b and Figure 4b). It is defined by,

$γ^{i} = (\begin{matrix} 0 & σ^{i} \\ - σ^{i} & 0 \end{matrix}),$

(9a)

and zero exponential, $γ^{o}$ as,

$γ^{0} = (\begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix}) .$

(9b)

$σ^{i}$ is relevant to oscillations assumed at the BOs at the intersections of the light cones (Figure 4a) and incorporate anticommutation relationship, $e^{+} (ψ) \neq e^{-} (\bar{ψ})$ (Figure 4b). The matrices, 0 and 1 are applicable to polarization of the model towards the point-boundary at position 0 (Figure 3a).

⇒: Weyl spinor. The light cone from the point-boundary within a hemisphere accommodates both matter and antimatter by parity transformation to generate Dirac spinor (Figure 4b). It is described in the form,

$ψ = (\begin{matrix} ψ_{0} \\ ψ_{1} \\ ψ_{2} \\ ψ_{3} \end{matrix}),$

(10)

and it correspond to spin up fermion, a spin down fermion, a spin up antifermion and aspin down antifermion. The electron’s shift in positions from 0 to 3 and 4 to 7 are conjugates before its restoration at the point-boundary as the base of Hilbert space for the MP field. By assuming its own antimatter within a light cone of a hemisphere, the Dirac fermion somewhat resembles Majorana fermions. It is difficult to observe them due to shift in the electron position by clockwise precession. Non-relativistic Weyl spinor of a pair of light cones relevant to Schrödinger wave equation are of holographic type (Figure 4a,b). These are defined by the reduction of Equation (10) to bispinor of the type,

$ψ = (\begin{matrix} u_{+} \\ u_{-} \end{matrix}),$

(11)

where $u_{\pm}$ are Weyl spinors of chiral form attributed to the electron of a physical entity. Hence, its parity operation x → x’ = (t, ‒ x) generates qubit 1 and −1 at the vertices of the MP field (Figure 1a and Figure 3a). Depending on the reference point-boundary, the exchanges of left- and right-handed Weyl spinor are of the process,

$(\begin{matrix} ψ_{L}^{'} \\ ψ_{R}^{'} \end{matrix}) = (\begin{matrix} ψ_{R} (x) \\ ψ_{L} (x) \end{matrix}) \Rightarrow \begin{matrix} ψ^{'} (x^{'}) = γ^{0} ψ (x) \\ {\bar{ψ}}^{'} (x^{'}) = \bar{ψ} (x) γ^{0} . \end{matrix}$

(12)

Conversion of Weyl spinors to Dirac bispinor, $ξ^{1}$ $ξ^{2}$ are assumed diagonally at positions 1 and 3 (Figure 4a). Comparably, the two-component spinor, $ξ^{1}$ $ξ^{2}$ = 1 are normalized at the point-boundaries of the MP model and ensues the orthogonal relationship, $(\begin{matrix} 1 \\ 0 \end{matrix})$ and $(\begin{matrix} 0 \\ 1 \end{matrix})$ .

⇒: Lorentz transformation. The Hermitian pair, $ψ^{†} ψ$ of Dirac fermion transiting at positions, 0, 1, 2 and 3 of BOs is not Lorentz invariant in 1D space (e.g., Figure 2b) due to radiation from electron-positron transition at the point-boundary. The same applies to Weyl spinor at spherical lightspeed due to the existence of the electron of chirality (Figure 4a). Thus, Lorentz transformation of Weyl spinor depicts the relationship,

$u^{†} u = (ξ^{†} \sqrt{p . σ,} ξ \sqrt{p . \bar{σ}} . (\begin{matrix} \sqrt{p . σ} ξ \\ \sqrt{p . \bar{σ}} ξ \end{matrix}), {= 2 E}_{P} ξ^{†} ξ .$

(13)

Equation 13 relates to Minkowski space-time by clockwise precession of the model (Figure 1b). The corresponding Lorentz scalar applicable to scattering at the BOs (Figure 4a,b) is,

\bar{u} (p) = u^{†} (p) γ^{0},

(14)

and is referenced to time axis of the MP field of a dipole moment in asymmetry (Figure 2a). By identical calculation to Equation (13), the Weyl spinor becomes,

\bar{u} u = 2 m ξ^{†} ξ,

(15)

for the complete classical rotation of the model. Though observations may not distinguish Weyl spinor and Majorana fermion from Dirac spinor, the explanations offered in this section for the MP model provide some intuitive forms to their possible existence.

Quantized Hamiltonian. Clockwise precession of the MP field is quantized at the point-boundary for the emergence of Dirac spinor and this preserves unitarity (Figure 2a). Two ansatzes adapted from Equation (7) are given as follows,

ψ = u (p) e^{- i p . x},

(16a)

ψ = v (p) e^{i p . x} .

(16b)

These are hermitian plane wave solutions and they form the basis for Fourier components in 3D space (e.g., Figure 3b). By decomposition, quantized Hamiltonian assumes the relationships,

ψ (x) = \frac{1}{{(2 π)}^{3 / 2}} \int \frac{d^{3}}{2 E_{p}} \sum_{s} (a_{P}^{s} u^{s} (p) e^{- i p . x} + b_{P}^{s †} v^{s} (p) e^{i p . x}),

(17a)

\bar{ψ} (x) = \frac{1}{{(2 π)}^{3 / 2}} \int \frac{d^{3}}{2 E_{p}} \sum_{s} (a_{P}^{s †} {\bar{u}}^{s} (p) e^{i p . x} + b_{P}^{s} {\bar{v}}^{s} (p) e^{- i p . x}) .

(17b)

The coefficients

a_{P}^{s}

and

a_{P}^{s †}

are ladder operators for u-type spinor and

b_{P}^{s}

and

b_{P}^{s †}

for v-type spinor. These are applicable to Dirac spinors of two spin states, ±1/2 and

{\bar{v}}^{s}

and

{\bar{u}}^{s}

are the antiparticles. The operators can somehow relate BOs into n-dimensions for the production of complex fermions, ±1/2, ±3/2, ±5/2 and so forth for the observable oscillator (Figure 4a). By parity transformation, the observable and holographic oscillators are canonically conjugates (Figure 4b) and its momentum is given by,

π = \frac{\partial L}{\partial ψ} - \bar{ψ} i γ^{0} = i ψ^{†} .

(18)

In 3D space, the generated oscillations of lagrangian mechanics and its Hamiltonian becomes,

H = \int d^{3} x ψ^{†} (x) [- i γ^{0} γ . \nabla + m γ^{0}] ψ (x) .

(19)

The quantity in the bracket is the Dirac Hamiltonian of one-particle quantum mechanics relevant to the MP model for hydrogen atom type (see also Equation (3)). With z-axis of MP field assigned to time axis in asymmetry of (Figure 3a), the V-A currents from the vertices are projected in either x or y directions in 3D space by the relationships,

[ψ_{α} (x, t), ψ_{β} (y, t)] = [ψ_{α}^{†} (x, t), ψ_{β}^{†} (y, t)] = 0,

(20a)

[ψ_{α} (x, t), ψ_{β}^{†} (y, t)] = δ_{α β} δ^{3} (x - y),

(20b)

where α and β denote the spinor components of the

ψ

. Equations (20a) refers to the unitarity of the model and Equation (20b) is assumed by the electron-positron transition that temporarily insinuate radiation (Figure 2b). The

ψ

independent of time in 3D space obeys the uncertainty principle with respect to the electron’s position, p and momentum, q, as conjugate operators. These are described by the polar coordinates, (r, θ, Φ) with respect to the electron position (Figure 3a). The commutation relationship of p and q obeys the relationship,

\{a_{P}^{r}, a_{q}^{s †}\} = \{b_{p}^{r}, b_{q}^{s †}\} = {(2 π)}^{3} δ^{r s} δ^{3} (p - q) .

(21)

Equation (21) incorporates both matter and antimatter and their translation to linear time (Figure 3b). The electron as a physical entity and its transition into space allows for a positive-frequency such as,

\begin{array}{l} 〈 0 | ψ (x) \bar{ψ} (y) | 0 〉 = & 〈 0 | \int \frac{d^{3} p}{{(2 π)}^{3}} \frac{1}{\sqrt{2 E_{p}}} \sum_{r} a_{p}^{r} u^{r} (p) e^{- i p x} \\ \times \int \frac{d^{3} q}{{(2 π)}^{3}} \frac{1}{\sqrt{2 E_{q}}} \sum_{s} a_{q}^{s †} {\bar{u}}^{s} (q) e^{i q y} | 0 〉 . \end{array}

(22)

Equation (22) may explain the dominance of matter (electron) over antimatter if the latter is accorded to the conceptualization process of Dirac fermion (Figure 2a,b).

⇒: Further undertakings. The themes provided above with respect to Dirac field theory and its related features can be further pursued into depth with the model serving as an approximate intuitive guide. The list could extend to include others such as energy-momentum tensor of Dirac field, Fermi-Dirac statistics, Bose-Einstein statistics, causality, Feynman propagator, charge conjugate-parity-time symmetry and so forth.

5. Conclusion

The dynamics of the MP model of 4D space-time offered in this study allows for the transformation of the electron of hydrogen atom type to Dirac fermion of a complex four-component spinor. These demonstrations are compatible with Dirac belt trick, its field theory and other related themes like space-time dynamics, non-relativistic wave function and Feynman diagram. In here, only teasers of otherwise complex themes are provided and these can be pursued into more depth within the boundary posed by the model. Such an intuitive tool can justify the removal of infinite terms during renormalization process and it can be also explored for fermions and bosons of strong and weak nuclear forces. Though the model still remains somewhat speculative, such an undertaking can become important towards defining the fundamental state of matter and its field theory.

Data availability statement

The modeling data attempted for the current study are available from the corresponding author upon reasonable request.

Competing financial interests

The author declares no competing financial interests.

References

Peskin, M. E. & Schroeder, D. V. An introduction to quantum field theory. Addison-Wesley, Massachusetts, USA (1995). pp 13–25, 40–62.
Alvarez-Gaumé, L. & Vazquez-Mozo, M. A. Introductory lectures on quantum field theory. arXiv preprint hep-th/0510040 (2005).
Pawłowski, M. et al. Information causality as a physical principle. Nature 461(7267), 1101-1104 (2009). [CrossRef]
Henson, J. Comparing causality principles. Stud. Hist. Philos M. P, 36(3), 519-543 (2005). [CrossRef]
Li, Z. Y. Elementary analysis of interferometers for wave—particle duality test and the prospect of going beyond the complementarity principle. Chin. Phys. B 23(11), 110309 (2014). [CrossRef]
Rabinowitz, M. Examination of wave-particle duality via two-slit interference. Mod. Phys. Lett. B 9(13), 763-789 (1995). [CrossRef]
Nelson, E. Derivation of the Schrödinger equation from Newtonian mechanics. Phys. Rev. 150(4), 1079 (1966). [CrossRef]
Rovelli, C. Space is blue and birds fly through it. Philos. Trans. Royal Soc. Proc. Math. Phys. Eng. 376(2123), 20170312 (2018). [CrossRef]
Perkins, D. H. Proton decay experiments. Ann. Rev. Nucl. Part. Sci. 34(1), 1-50 (1984). [CrossRef]
Sun, H. Solutions of nonrelativistic Schrödinger equation from relativistic Klein–Gordon equation. Phys. Lett. A 374(2), 116-122 (2009). [CrossRef]
Oshima, S., Kanemaki, S. & Fujita, T. Problems of Real Scalar Klein-Gordon Field. arXiv preprint hep-th/0512156 (2005).
Bass, S. D., De Roeck, A. & Kado, M. The Higgs boson implications and prospects for future discoveries. Nat. Rev. Phys. 3(9), 608-624 (2021). [CrossRef]
Weiss, L. S. et al. Controlled creation of a singular spinor vortex by circumventing the Dirac belt trick. Nat. Commun. 10(1), 1-8 (2019). [CrossRef]
Silagadze, Z. K. Mirror objects in the solar system?. arXiv preprint astro-ph/0110161 (2001).
Franzoni, G. The klein bottle: Variations on a theme. Notices of the Am. Math. Soc. 59(8), 1094-1099 (2012). [CrossRef]
Rieflin, E. Some mechanisms related to Dirac’s strings. Am. J. Phys. 47(4), 379-380 (1979).
Almasi, A. et al. New limits on anomalous spin-spin interactions. Phys. Rev. Lett. 125(20), 201802 (2020). [CrossRef]
Yang, C. N. & Mills, R. Conservation of isotopic spin and isotopic gauge invariance. Phys. Rev. 96, 191 (1954). [CrossRef]
Gross, D. J. Nobel lecture: The discovery of asymptotic freedom and the emergence of QCD. Rev. Mod. Phys.77(3), 837 (2005). [CrossRef]
Gell-Mann, M. & Low, F. E. Quantum electrodynamics at small distances. Phys. Rev. 95(5), 1300 (1954). [CrossRef]
Arkani-Hamed, N. et al. Solving the hierarchy problem with exponentially large dimensions. Phys. Rev. D 62(10), 105002 (2000). [CrossRef]
Craig, N. Naturalness hits a snag with Higgs. Physics 13, 174 (2020). [CrossRef]
Yuguru, S. P. Unconventional reconciliation path for quantum mechanics and general relativity. IET Quant. Comm. 3(2), 99–111 (2022). [CrossRef]
https://en.wikipedia.org/wiki/Spinor Retrieved 15 December 2022.

Figure 1. The MP model [23]. (a) In flat space, a spinning electron (green dot) in orbit of sinusoidal form (green curve) is of time reversal. It is normalized to an elliptical MP field (white area) of a magnetic field, B by clockwise precession (black arrows), and this generates a circular electric field, E of inertia frame, λ. The shift in the electron’s position from positions 0 to 4 at 360° rotation against clockwise precession generates maximum twist. At position 4, the electron flips to a positron to begin the unfolding process from positions 5 to 8 for another 360° rotation to restore the electron to its original state. By 720° rotations, a dipole moment (±) is generated for the MP field within a classical spherical rotation of 360° at lightspeed analogous to Dirac belt trick. (b) The BOs are defined by the numbered pairs, 1,5 and 3,7 and these translate to angular momentum (purple dotted lines) of spin ±1/2 depicted by a pair of light cones (navy colored) in Minkowski space-time. These are assumed in degeneracy and are projected toward singularity at the center.

Figure 2. Dirac fermion of chirality. (a) The electron at the point-boundary is assumed at the base of Hilbert space for the MP field. By rotation, the positive helicity of spin up or right-handedness correlates with outward clockwise precession of the MP field. At position 4 of 360° rotation, maximum twist is attained from the torque of the Bohr orbits (BOs) due to the electron orbit of time reversal against clockwise precession. The electron spin flips to a positron of negative helicity or left-handedness. The unfolding process towards 720° rotation from shift in positions 5 to 8 restores the electron to its original state. (b) The electron path of vector transport precesses at Lamour frequency, where at the point of electron-positron transition, Planck radiation is emitted. Polarization of the model generates qubits 0 and ±1 at positions, 0, 4 and 8 (see also Figure 1a). Image adapted from ref. [24].

Figure 3. Dirac spinor. (a) The spinor is superimposed on Poincaré sphere and consists of both Euclidean (straight paths) and non-Euclidean (negative curves) spaces. Clockwise precession by geodesic motion induces a circle at 360° rotation to the negative curves at positions 0 to 3. The polar coordinates (r, θ, Φ) with respect to the particle’s shift in position is linked to a light cone (navy colored). (b) Fourier transform. It incorporates both radial (blue wavy curve) and angular (black wavy curve) wave functions in linear time with the electron-positron entangled state assumed at the point-boundary. The process somewhat mimics wave function collapse.

Figure 4. Light-MP model coupling. (a) To an external observer, the topological point-boundary provides the origin for the emergence of the oscillator,

J_{z} = S + L

(maroon light cones). Increase into n-dimensions, k to l offers asymptotic boundary to the energy shells and subshells. The Bohr orbits (BOs) in degeneracy, Φ_i at the n-levels of the observable oscillator can accommodate Fermi-Dirac statistics (green wavy curve) and Fock space for non-relativistic many-particle systems. The observable oscillator is partitioned at the infinite boundary or classical limit of the holographic oscillator at the center of the MP field. The blue light cone is from the perspective of the observer at the center. (b) Quantized magnetic moment,

\pm J_{z} = m_{j} ℏ

from the point-boundary (maroon light cones) levitates about the internal frame of the model (blue light cones). Parity transformation for the conjugate pairs is confined to a hemisphere. Scatterings (green wavy curves) are applicable to light-MP model interactions.

Figure 4. Light-MP model coupling. (a) To an external observer, the topological point-boundary provides the origin for the emergence of the oscillator,

J_{z} = S + L

\pm J_{z} = m_{j} ℏ

Figure 5. Feynman diagrams for MP models coupling. a) Two electrons, each at a vertex of a MP model undergo either repulsion or attraction when approaching each other due to electron-positron transition at the point-boundary. Symmetry is sustained when secondary photons mimic the electron-positron pair with center of mass assumed at the point-boundary. b) Actual ejection of the electron/positron would induce particle-hole of isospin. Particle-hole interactions at ZPE can generate boson types including neutrinos and antineutrinos of helical property mimicking the electron/positron. These are relevant to both positive beta (+) and negative beta (-) decays without requiring change in color charges of up and down quarks. The emergence of particle-hole may break CPT symmetry if it does not mimic shift in charges at the point-boundary of an entangled state comparable to the electron-positron transition.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

The Dirac Fermion of a Monopole Pair (MP) Model

Abstract

Abstract

1. Introduction

2. Limitations of quantum field theory

3. Unveiling Dirac belt trick

4. Dirac field theory and its associated features

5. Conclusion

Data availability statement

Competing financial interests

References

MDPI Initiatives

Important Links

Subscribe