An Ontology of Dirac Fermion of a Monopole Pair (MP) Model of 4D Quantum Space‐Time and Its Multifaceted Dynamics

1. Introduction

In this section, the rationale for why it is necessary to consider the ontology of Dirac fermion within a boundary of 4D space-time is explored by first outlining the transition of the electron defined by a wave function and its incorporation into both QM and QFT. In section II, the transformation of the valence electron to Dirac fermion by the process of Dirac belt trick (DBT) on a geometry basis is demonstrated within a MP model of hydrogen atom type. Center of mass (COM) reference frame relevant to Newtonian gravity is assigned to a spherical point-boundary of the model and this offers an intricate dynamic tool compatible with basic aspects of both QM and QFT. Some of these are demonstrated for both QM and QFT respectively in Sections III and IV with respect to non-relativistic wave function and its collapse, quantized Hamiltonian, Dirac spinors, Weyl spinors, Majorana fermions and Lorentz transformation. In Section V, the ontology of the MP model to general relativity is plotted beginning with space-time fabric to internal structures by Lie group representation. This is ensued by space-time curvature and gravitational horizon. In Section VI, some concluding remarks are offered.

1.1. Non-Relativistic to Relativistic Quantum Field Theory

The electron of a point-particle of mass is attributed to $i\hslash$ with $i$ a complex number assigned to a point of a rotating sphere and $\hslash$ to Planck constant of infinitesimal radiation in quantized form [1,2]. The first order space-time derivative of the particle in motion is attributed to non-relativistic Schrödinger equation, $i\hslash \partial /\partial t$ and it is a fundamental concept of particles in QM that cannot be derived by QFT [3]. For light-matter coupling, the energy and momentum operators of Schrödinger equation,

$$\widehat{E}=i\hslash {\displaystyle \frac{\partial }{\partial t}}, \widehat{p}=-i\hslash \nabla ,$$

(1)

are adapted into QFT beginning with Klein-Gordon equation [4] by second derivation of space-time given in the expression,

$$\left({i^2\hslash }^2{\displaystyle \frac{{\partial }^2}{\partial t^2}}-c^2{\hslash }^2{\nabla }^2+m^2{c}^4\right)\psi \left(t,\overline{x}\right)=0.$$

(2)

Equation (2) is a relativistic form of Equation (1) and it incorporates special relativity, $E^2=p^2{c}^2+m^2{c}^4$ with the first term representing momentum and second term to mass-energy equivalence, $E={mc}^2$. The del operator, $\nabla$ presents 3D space for a particle in motion in space-time. Only one component is considered in Equation (2) and is relevant to describe bosons of whole integer spin and their charges. However, it does not take into account fermions of spin 1/2 and negative energy contribution from antimatter. These are accommodated into the famous Dirac equation [3] of the generic form,

$$i\hslash {\gamma }^u{\partial }_u\psi \left(x\right)-mc\psi \left(x\right)=0.$$

(3)

The symbol, ${\gamma }^u$ is a set of 4 x 4 gamma matrices, i.e., ${\gamma }^u$ = ${\gamma }^0$, ${\gamma }^1$, ${\gamma }^2$, ${\gamma }^3$ and this combines with partial derivative of space-time, ${\partial }_u=$ $x_0$, $x_1$, $x_2$, $x_3$ to give a scalar quantity which is invariant under Lorentz transformation. The imaginary unit, $i$ unifies space and time according to special relativity and distinguishes 1D time from 3D space by orthonormal relationship. The complex four-component spinor, $\psi$ from Equation (3) is represented in the form,

$$\psi =\left(\begin{array}{c}\begin{array}{c}{\psi }_0\\ {\psi }_1\\ {\psi }_2\end{array}\\ {\psi }_3\end{array}\right),$$

(4)

where ${\psi }_0$ and ${\psi }_1$ are spin-up and spin-down components of positive energy with ${\psi }_2$ and ${\psi }_3$ as corresponding antimatter for spin-up and spin-down of negative energy. In order to include space-time-energy matrices of the particles, standard Pauli matrix convention is applied such as [5,6],

$$\begin{gathered} { { \sigma }_0=\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right), \sigma }_1=\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right), \\ {\sigma }_2=\left(\begin{array}{cc}0& -i\\ i& 0\end{array}\right), {\sigma }_3=\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right). \end{gathered}$$

(5)

These are a set of 2 x 2 dimensions of complex traceless, Hermitian matrices that are equivalent of involutry matrices and are identified as unitary matrices. The matrices relate to angular momentum operator of observable spin 1/2 particle respectively in three spatial directions, ${\sigma }_1$, ${\sigma }_2$ and ${\sigma }_3$ with ${\sigma }_0$ equal to identity matrix, $\mathrm{I}$ . Any 2 x 2 Hermitian matrices have determinant and traceless values respectively of $-1$ and 0. Their matrix product are given by [7],

$${\sigma }_i{\sigma }_j={\delta }_{ij}I+{iϵ}_{ijk}{\sigma }_k,$$

(6)

where ${ϵ}_{ijk}$ is the Levi-Civita symbol and is applicable to the relations of both commutation by cyclic permutation, i.e., $\left[{\sigma }_i,{\sigma }_j\right]={\sigma }_i{\sigma }_I-{\sigma }_j{\sigma }_i={iϵ}_{ijk}{\sigma }_k$ and anticommutation by combination $\left[{\sigma }_i,{\sigma }_j\right]={\sigma }_i{\sigma }_I+{\sigma }_j{\sigma }_i={2\delta }_{ij}I$ with $ijk=\mathrm{1,2},3$. The orthonormal basis of vector space of 2 x 2 Hermitian matrices over the real numbers, under addition for ${\sigma }_{13}$ and ${\sigma }_0$ is the matrix ${\sigma }_2$ by isomorphism [6],

$$\left(\begin{array}{cc}a& -ib\\ ib& a\end{array}\right)={a\sigma }_0+{b\sigma }_{13} ⟷a+ib.$$

(7)

Equation (7) considers real numbers $a$ → ${\psi }_0$ and $b$ → ${\psi }_1$ respectively as real and imaginary parts of ${\sigma }_2$. The orthonormal basis for vector space is relevant to Clifford group and Clifford algebra, $\mathbb{C}\cong C\left(\mathrm{0,1}\right)$. The four matrices in $\mathbb{C}\left(4\right)$ generate the vector space $C\left(\mathrm{3,1}\right)$ or $C\left(\mathrm{1,3}\right)$ and by isomorphism is denoted ${\gamma }^i$ with respect to Dirac matrices inclusive of a fifth related matrix [6],

$${\gamma }^0=\left(\begin{array}{cc}I& 0\\ 0& -I\end{array}\right), {\gamma }^i=\left(\begin{array}{cc}0& {\sigma }_i\\ {-\sigma }_i& 0\end{array}\right)⟹ {\gamma }_5=\left(\begin{array}{cc}0& I\\ I& 0\end{array}\right).$$

(8)

The matrix, ${\gamma }_5={i\gamma }^u$ couples the spinor field, i defined by modes of oscillation, stress-energy tensor and momentum to space-time structure. There is no space-time boundary to the quantum state defined by $\psi$. Its ontology by QM is deterministic in the generic form of Schrödinger’s equation,

$$i\hslash {\displaystyle \frac{d\psi (x,t)}{dt}}={\displaystyle \frac{{-\hslash }^2}{2m}}{\displaystyle \frac{d^2\psi (x,t)}{{dx}^2}}+V\left(x\right)\psi \left(x,t\right).$$

(9)

To the left of Equation (9), the evolution of the electron of a point-particle into space is time dependent. This is equated to time independent component by 2nd derivative of space to account for $\psi$ of probabilistic interpretation of finding a particle at a point in space. Variations in time are not accounted for as this will violate unitarity [8]. Discrete times in QFT is attributed to creation and annihilation of virtual particles, ${\psi }_2$ and ${\psi }_3$ in a vacuum before the emergence of real particles, ${\psi }_0$ and ${\psi }_1$ in superposition states such as the electron and positron. However, unitary theory of QM forbids the creation and destruction of particles even as excitation of fields [8]. Conversely, how $\psi$ collapses to a point at observation without interactions remains unclear in field theory [9]. The four-component momenta or Dirac spinor as local hidden variables are relevant in Bohmian mechanics based on De Broglie wave-particle duality [10]. But these are completely ruled out by experiments affirming violation of Bell’s inequality tests from observed values. This is evident in experiments conducted for correlated photon pairs measured either at small distances of 10 km apart [11] or independently from distant astronomical sources [12]. Such experiments are constrained to distinguish locality from non-locality of $\psi$ or ascertain the boundary between classical and QM. In this case, neither the realist nor instrumentalist views offer satisfactory explanations for decoding of $\psi$ [13]. This requires a realistic ontological representation of $\psi$ in QFT application as presented next.

1.2. Evolution of Dirac Fermion into Space-Time

In relativistic QFT, ${\gamma }^u$ is broken up into four-position coordinates, four-momentum and four-vector for the force in the form [14],

$$\overrightarrow{R}=\left(\begin{array}{c}\begin{array}{c}ct\\ x\\ y\end{array}\\ z\end{array}\right), \overrightarrow{P}=\left(\begin{array}{c}\begin{array}{c}E\\ p_{x}c\\ p_{y}c\end{array}\\ p_{z}c\end{array}\right), {\chi }^{\mu }=\left(\begin{array}{c}\begin{array}{c}{x}^0\\ x^1\\ x^2\end{array}\\ x^3\end{array}\right).$$

(10)

The components of Equation (10) relate to how $\psi$ permeates space and is transformed contravariantly by continuity of rotation, translation and inversion. Contraction from the 4-gradient covariant term, ${\partial }_u=\partial /\partial t,\stackrel{⃑}{\nabla }$, shown in Equation (3) is applied to comply with unitary at a point in space. The dominance of positive matter over antimatter for the four-component spinor as in electroweak baryogenesis [15] is represented in forward time. Antimatter requires time reversal, where discrete times are integrated to space coordinates to demonstrate violation of charge, parity or their combination in the renormalization process using Feynman diagrams [16]. Antimatter existence by violation of charge conjugation parity is readily observed in both Stern-Gerlach experiment and cosmic rays. In field theory, its intuitive form,$\pm \hslash$ is represented by Dirac’s string trick or belt trick [17], where the electron is converted to a positron at 360° rotation and is restored at 720° rotation. The same is applicable to other related descriptions like Balinese cup trick [18] or Dirac scissors problem [19]. To account for conservation of energy into forward time, the creation and annihilation of virtual particles is employed for Hamiltonian operators of Hilbert space towards the emergence of real particles like electron and positron [20]. This is pursued mainly in massless quantum electrodynamics [5]. However, how discrete times are added up for exponential rise of Hilbert space for multiparticle systems into classical time remains vague. Microscopic arrow of time is generally investigated for decay of neutral kaons [21] but not for a typical hydrogen atom of diameter about 0.1 to 0.5 nanometers. Instead, current leading theories attempt to quantize space-time and thus, matter field in the pursuit of quantum gravity.

String theory and its likes consider particles to be made up of strings of different vibrational modes and are contained within multidimensional space-time [22]. This is yet to be proven in the absence of supersymmetry noted in experiments conducted in high energy particle physics. Conversely, in both twister approach [23] and loop quantum gravity [24], the notion is based on non-commutative spin network of dynamical triangulations to simulate quantum space-time tetrahedra. This has been successfully trailed in experiments using nuclear magnetic resonance simulator from four ${}_{13}C$ nuclei to generate spinfoam vertex amplitudes mimicking angular momenta of space-time tetrahedral [25]. The outcome looks promising for quantum computation to accommodate exponential rise in non-perturbative regimes of vectors in Hilbert space which cannot be easily done by classical computers. Perhaps, the most perplexing quest for such novel undertaking and its similar kinds [26,27] in the future would be to translate all these to simulate commutative spin network in a Block sphere of an atom or in an array of atoms. This is because there is lack of data offering new insights into the generation of either microscale black holes from collective bombardment of hadrons from protonized hydrogen molecules [28] or from observations of cosmic black holes to decipher their relationship to space-time singularities [29], where the tenets of entanglement and gravity are intertwined. Hence, an atom appears to be an ideal place to begin the process of unveiling a proper ontology of $\psi$ in order to facilitate its realistic adaption in both QM and QFT interpretations.

1.3. Motivation of this Study

In this study, how Rutherford’s atomic model of an electron in an elliptical orbit of a MP field is animated into 3D space by clockwise precession of 1D time to generate 4D quantum space-time of a spherical model is explored. The model appears compatible with both Schrödinger electron cloud and Bohr models of the hydrogen atom. The transformation of the valence electron of a point-particle to a composite Dirac fermion or monopole is assumed by the process of DBT for the generation of superposition states of ±1/2 spin and their antimatter. Such an atom prototype encompasses both Euclidean and Minkowski quantum space-times on a geometry basis. The COM reference frame relevant to the electron-positron transition is assigned to the vertex of the MP field. All these measures offer a multifaceted dynamical model and it is able to consolidate many basic aspects of both QM and QFT into a proper perspective. Whether such a tool can become vital towards the investigations of the quantum realm of both matter field and space-time fabric on an axiomatic basis appears appealing and it is worth further considerations.

2. Ontology of Dirac fermion of a MP model

Additional details on the conceptualization path of the model from electron wave-diffraction is offered elsewhere [30]. In this section, the transformation of an electron of hydrogen atom type to a fermion by Dirac process within a spherical MP model of 4D space-time is unveiled. First, the enigma of atomic space-time is described and how its ontology can be described on a geometry basis is unveiled from a geometry perspective of the MP model of hydrogen atom type. This is ensued by outlining the COM reference frame assigned to the spherical boundary of the model and its intricate dynamics.

2.1. An Enigma of Atomic Space-Time

The widely accepted model of the atom is the electron cloud model described by Schrödinger’s $\psi$. The probability of finding the electron at a time is relegated to orbitals of quantum waves. These are standing waves permeating certain regions of the atom and possess both kinetic and potential energies as demonstrated in Equation (9). However, how these collapse to a definite state at observation remains a mystery and this cannot be ably explained neither by realist or instrumentalist viewpoint [13]. The electron in 3D space requires 1D time to account for its shift in position from the first principle as shown in Equation (1). Because the electron is in a superposition state prior to observation, how it evolves with time related to entanglement [31] or entropy [32] or both [33] remains oblivious. Moreover, at the Planck scale, quantum gravity is expected to be a dominant force [34] and at the moment it is difficult to differentiate this from the electromagnetic Coulomb force between either electron-positron or electron-proton pairs. A review of quantum gravity suggests that it lacks a proper ontology in 2⁺ 1 dimensions and it is generally a mathematical quest at the moment to reconcile general relativity and QM [35]. Neither can the ontology of atomic space-time be related to the pursuit of atomic clock [36] which is a collective measure of resonate frequencies of atoms at different energy levels. Thus, in this undertaking, how the electron of a point-particle is converted to a composite Dirac fermion of quantum space-time is examined from the geometry perspective of an atom. It is a novel quest and to make it compatible with physics, basic knowledge in both QM and QFT are applied and investigated within the realm of the proposed model.

2.2. Unveiling of Dirac Belt Trick Within the MP Model

The ontology of the proposed MP model and some of its main features are presented in Figure 1a–d. The electron orbit in discrete sinusoidal wave form is considered to be of time reversal defined by Planck constant, h. In forward time, the orbit is transformed into an elliptical shape of a MP field mimicking Dirac’s string of a small magnet (Figure 1a). The electron at the vertex mimics a Dirac monopole as quantized state of the MP field of a dipole moment by the process of DBT. Clockwise precession generates flat Euclidean space-time for the atomic state. Perturbations such as nonlinearity of differential gravitation, acceleration between two body-masses, eccentricity of the reference orbit and its oblateness including relative motion of one-body mass in motion against the other body-mass are evident in classical planetary orbit [37] and these are considered negligible for the atomic state. Similarly, frictional force is constrained for the quantum state, while centrifugal force is not applicable to a free electron undergoing DBT. How all these apply to a MP model akin to Bohr model is explored in this subsection. Clockwise precession of the

MP field institutes the process of DBT, where the torque or right-handedness exerted on the vertex shifts the electron of spin up from positions 0 to 4 for 360° rotation. At position 4, maximum twist is attained owed to time reversal orbit against clockwise precession. The electron then flips to spin down mimicking a positron to begin the unfolding process and emits infinitesimal radiation by, $E=nhv$. The positron is short-lived from possible repulsion of the proton and by another 360° rotation from positions 5 to 8, it is converted to the electron and restored to its original state. The transition of electron-positron is restricted to a hemisphere of the MP field resembling Gaussian soliton (GS) and is interchangeable with the other hemisphere. There is a time lap for the electron transition to positron between the GS pair and this adheres to both Born’s rule of square modulus of the wave function, ${\left|\psi \right|}^2$ and Pauli exclusion principle. These intuitions are relevant to DBT with Dirac four-component spinor, ${\psi }_0, {\psi }_1,{\psi }_2, {\psi }_3$ given in Equation (4) assigned respectively to positions 0, 1, 2, 3 for the emergence of real particles from continuous shift in the electron’s position in orbit. The z-axis of quantum time at COM for electron-positron transition point aligns with ${\psi }_0$ and the interchangeable GS pair can relate to both positive and negative energies of spin-up and spin-down in accordance with Born’s rule. By clockwise precession, ${\gamma }^u$ and the components, $\overrightarrow{R}$, $\overrightarrow{P}$ and ${\chi }^{\mu }$ are contained within the spherical MP model of 2D Euclidean space-time geometry (Figure 1a). Any perturbations from the electron-positron transition is balanced out by clockwise precession in accordance with Newton’s first law. An inertia reference frame, λ is generated for COM under the conditions,

$${\lambda }_{\pm }^2={\lambda }_{\pm }, Tr{\lambda }_{\pm }=2, {\lambda }_{+}+{\lambda }_{-}=1,$$

(11)

where the trace function, Tr is the sum of all elements within the model. Classically, the COM is subjected to Newton’s second law of motion and its dynamics are explored next.

2.3. COM Reference Frame and Its Intricate Dynamics

The positioning of COM at the interface of the classical and atomic states has a number of important implications. Some of them are succinctly described in here.

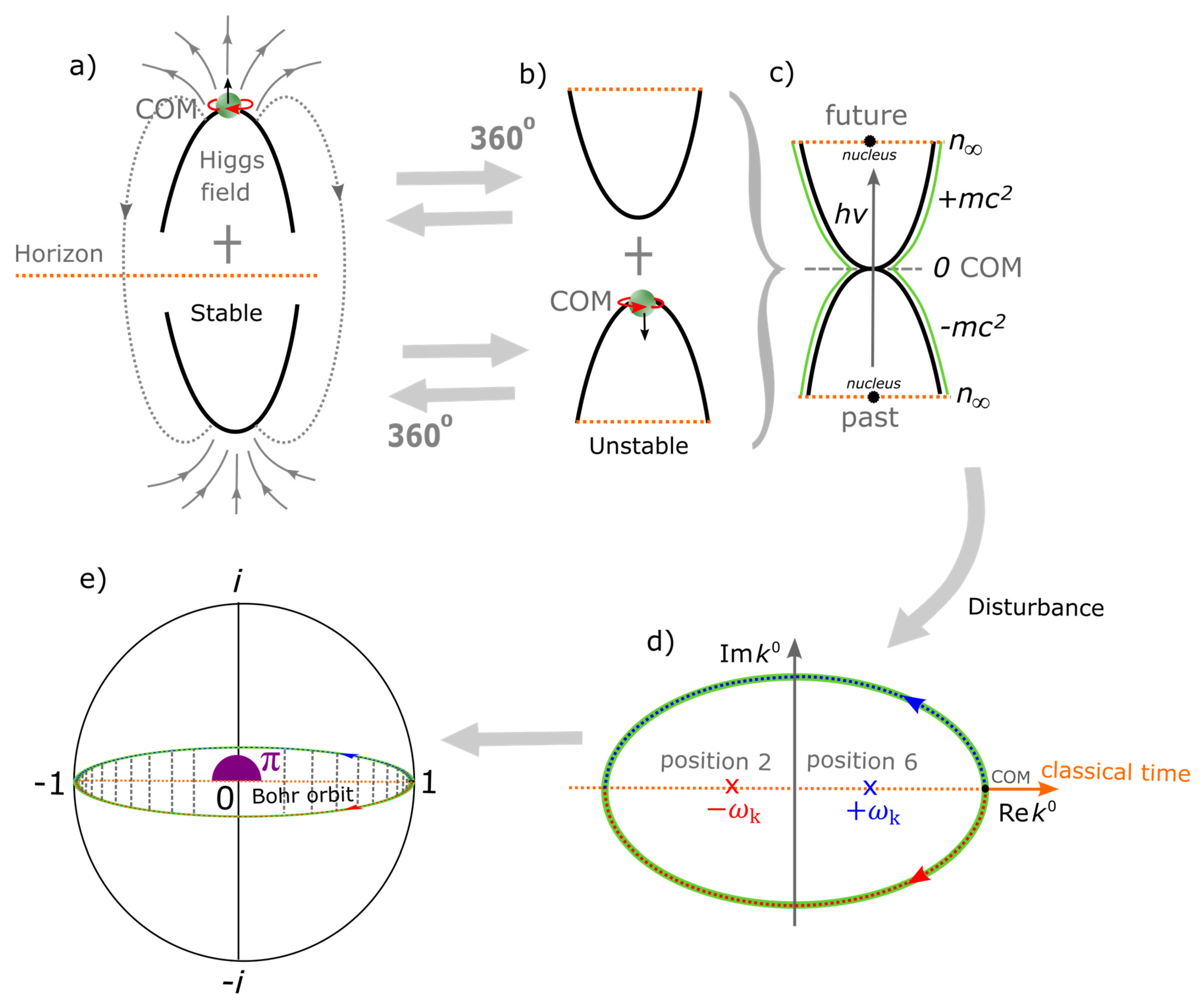
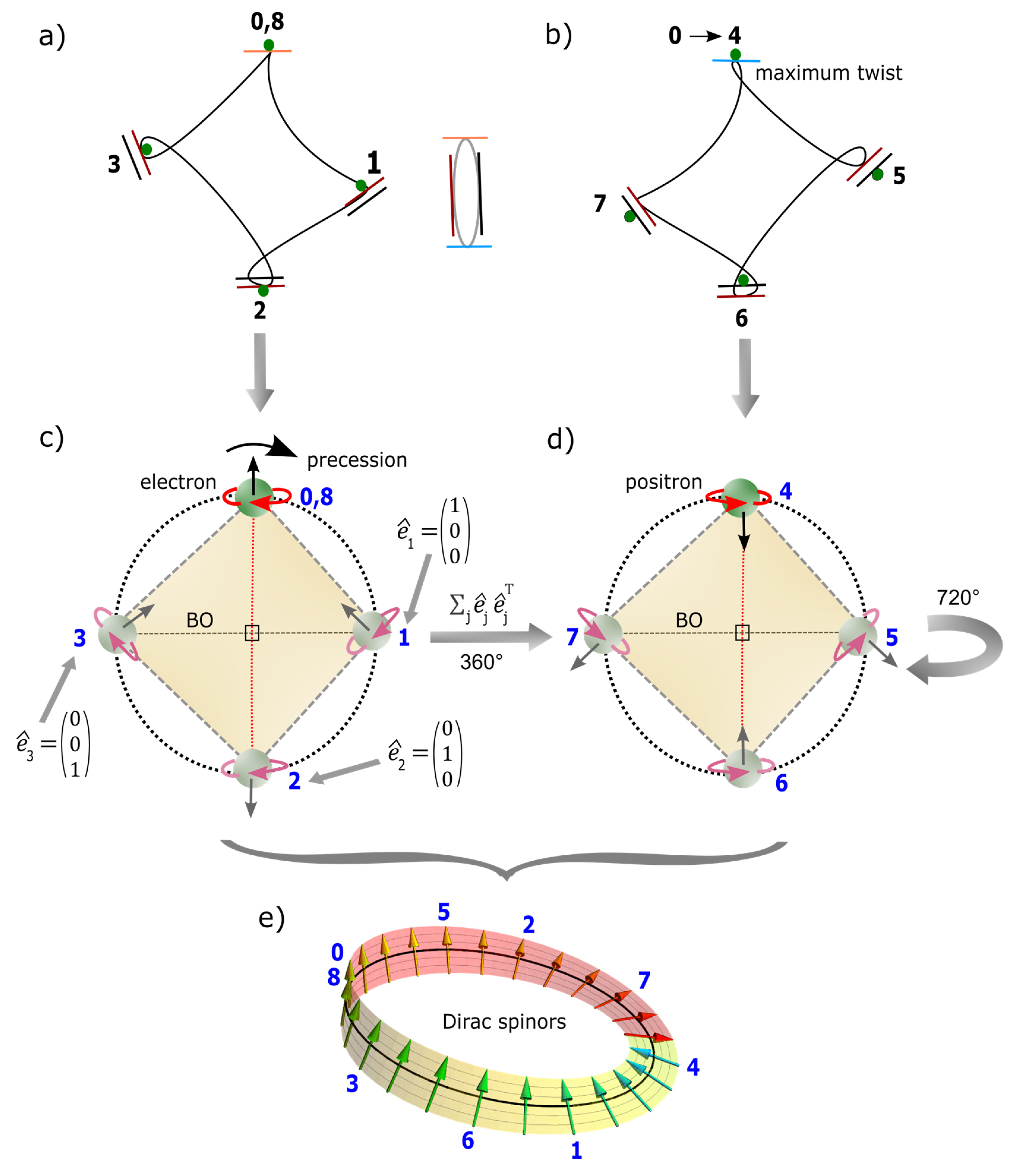
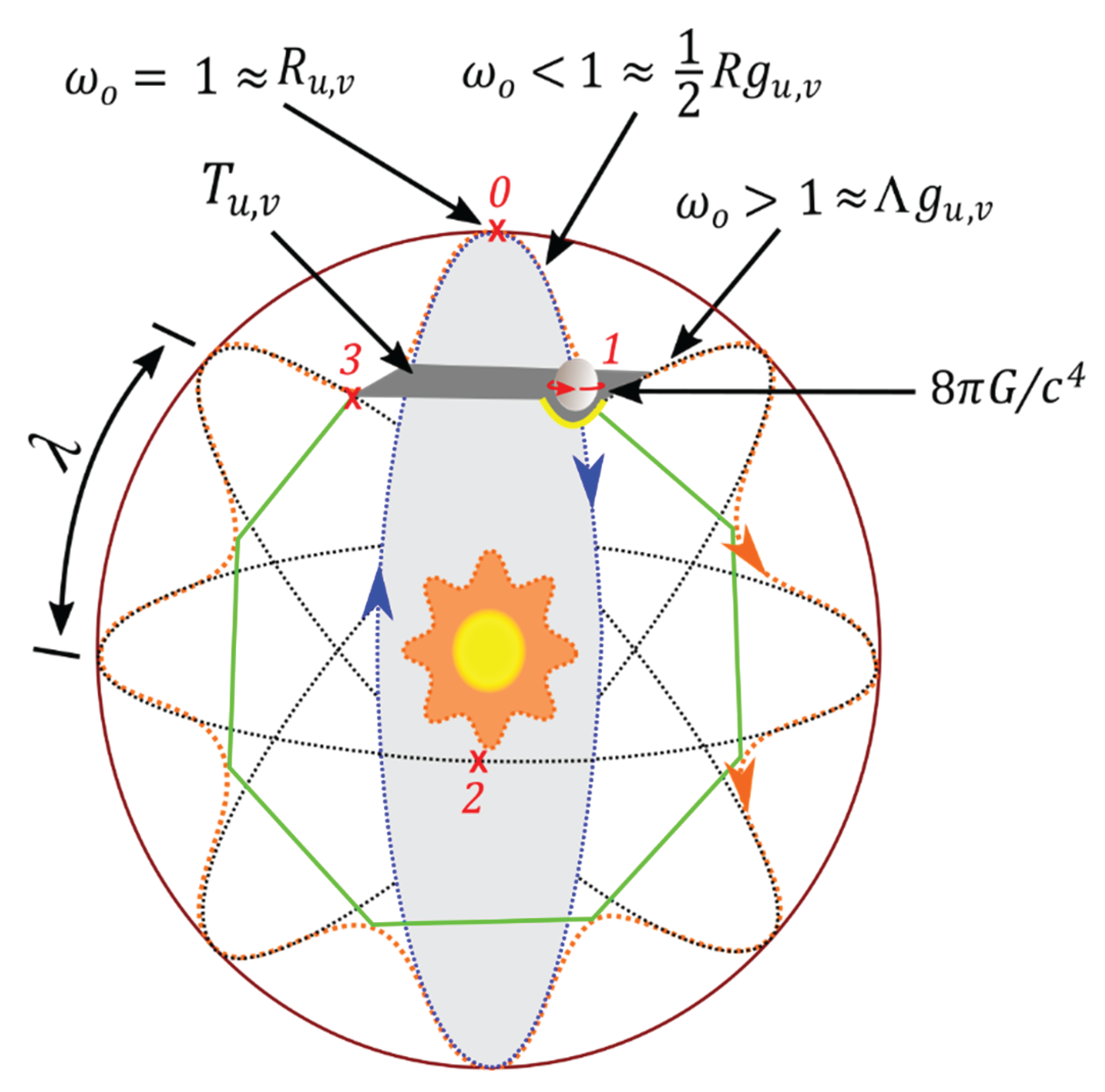
• The COM reference frame is assigned to the point of electron-positron transition by DBT at the vertex of the MP field of Dirac’s string. It resembles Dirac monopole or Higgs boson at Planck length (Figure 2a). By ionization from ejection of the electron, a particle-hole symmetry of protonized form is induced for an irreducible spinor of the MP field. At 360° shift in the monopole’s position from 0 → 4 by DBT, the combined GS pair of a two Higgs doublet field becomes unstable and oscillates (Figure 2b). The COM then assumes the point of singularity and breaks electroweak symmetry by radiation from electron-positron transition. Particles acquire mass by, $m=E/c^2$ with $E=nhv$ for promotion of BO into n-dimensions (Figure 2c). Another 360° rotation and the electron is restored at the vertex. Such intuition allows for the development of quark flavor and color confinement by assuming that disturbance from either light-matter coupling or protonized MP models coupling will transit from the weak oscillation mode to elongated Hadron-jet like mode (Figure 2d). The shift of COM from the center towards the boundary is linked to the classical time under the natural setting, $n_{\infty }=$ ${\epsilon }_0=c=\hslash =1$ and somehow coincides with the correspondence principle.
• Observations are constrained to light-matter interactions at COM and this partitions elongation or the stretching out of MP field into the intervals, x + dx by DBT under confinement. The accompanied extension of envelop solitons and integration of positions 2 and 6 can become massive akin to Nambu-Goldstone boson types at higher dimensions of compacted BOs. Somehow, these are reduced to COM of Higgs boson type at 125 GeV with r = 0 at the boundary (Figure 2d). In this case, the Higgs is applicable from low and high energies, where in the latter, the property of asymptotic freedom [38] is enforced and quarks and gluons are free to interact weakly with each other. Thus, the strong coupling strength, ${\alpha }_5$ from oscillations vanishes from stretching out of the MP field. At the potential wells of short distance (e.g., Figure 2c), fermions and bosons interact but weakly over long distance.
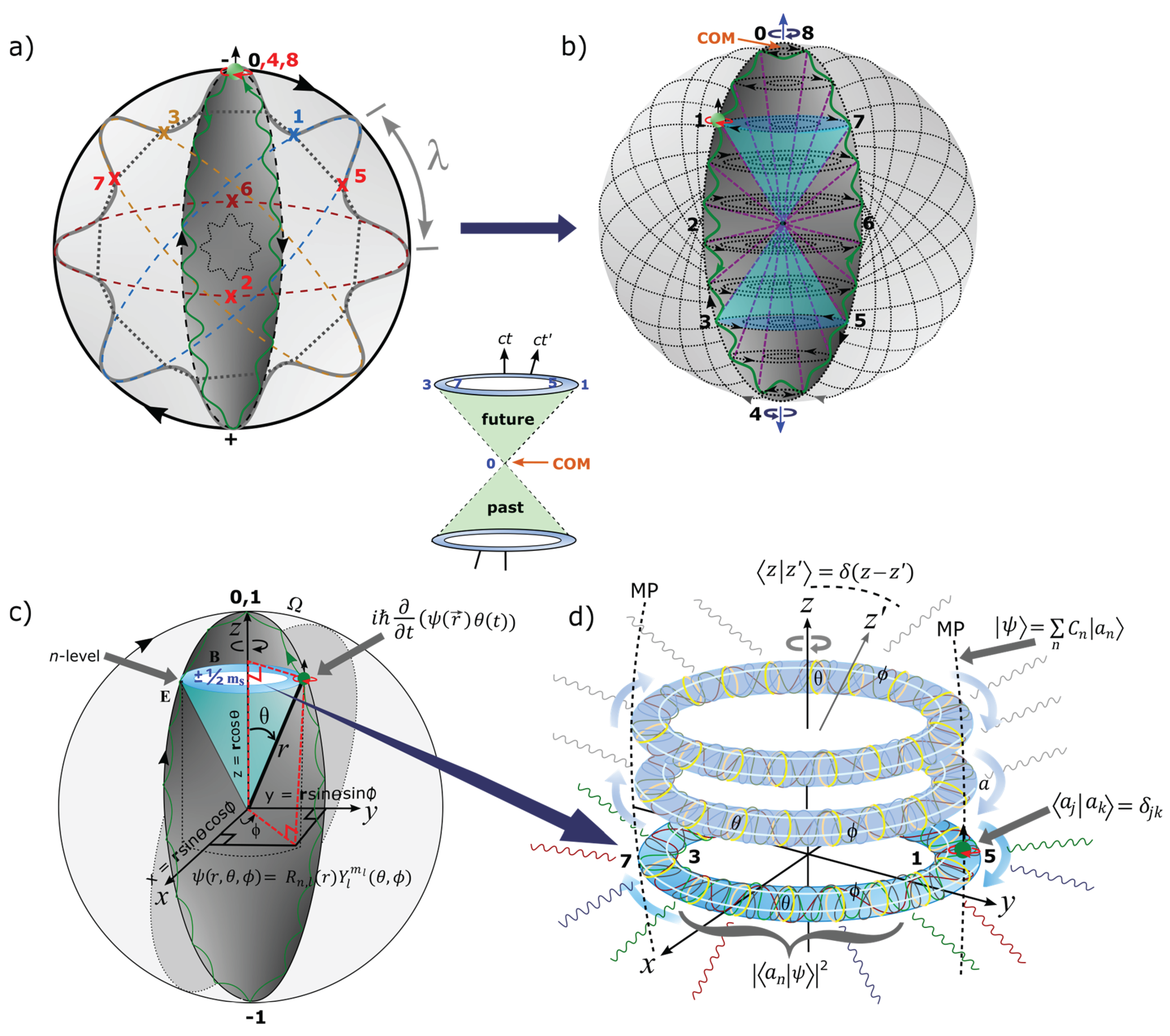
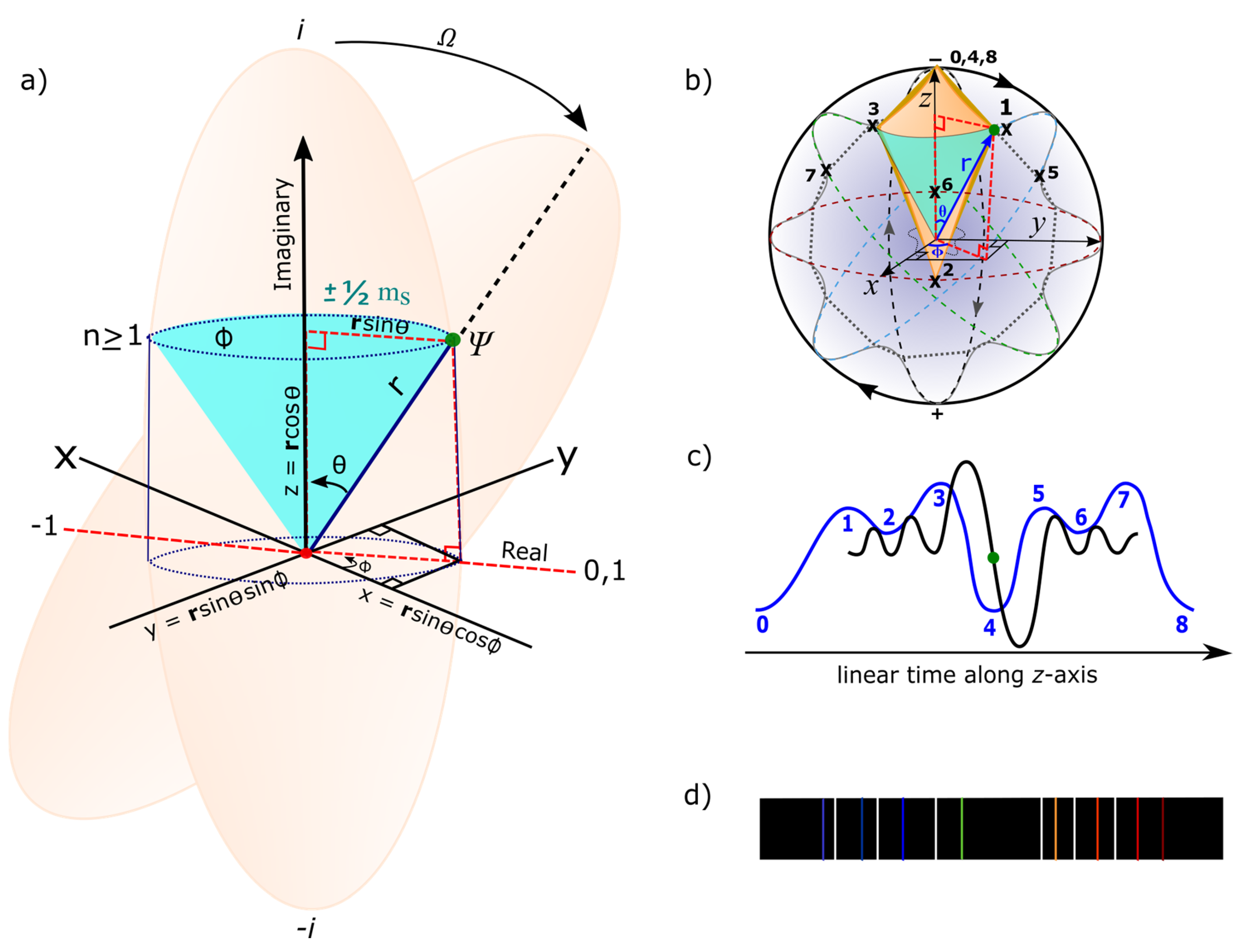
• With respect to rotating z-axis of the MP field, the complex plane of x-y axes can relate to combined scattering matrix from both the decreasing length of BO into n-dimensions of Hamiltonian mode. Non-linearity for shift in COM by DBT at 720° allows for both vertical and horizontal polarization in the production of qubits, 0, 1. The determinant –1 from the positron emergence at position 4 is physical and preserves unitary but it is absorbed by the overall DBT. The polarization states are relevant to both Euler’s identity, $e^{i\pi }$ + 1 = 0 and Pauli matrices in a Bloch sphere of the atom. Comparably, these offer the limit of local entanglement for the electron of a hydrogen atom. The continuity of 4D space-time from 2D space by clockwise precession offer gravitational horizon to COM assigned at the vertex and this is relevant to the holographic principle. Its intercept by linear light paths coupled tangential to the MP model can become relevant to quantum tunneling, von Neumann and Shannon entropies and these are worth further considerations.
• Low energy physics is applicable for the increase in the length of BO of quantized states, $E_n=\left(n+{\displaystyle \frac{1}{2}}\right)\hslash \omega$ towards infinite n-dimensions at the interface of quantum and classical levels defined by the correspondence principle (Figure 2c). The COM then assumes ZPE of 13.6 eV at $E_n={\displaystyle \frac{1}{2}}\hslash \omega$ for the hydrogen atom and how it could accommodate energy shells and lamb shift is expounded later in the text. Radioactive decay is not described for the MP model of one-electron hydrogen type.
• The ontology of a probable reconciliation path for all four forces of electromagnetism, gravity, weak and strong nuclear forces is presented in Figure 2a–e. The tendency of the monopole at the top vertex of Dirac’s string to transit to the bottom vertex by DBT breaks the electroweak symmetry. The shift in COM of Higgs boson type from the vertex to the center and vice versa identifies with gravity of Coulomb force, $F_e=k_e{q}_1{q}_2/r^2$, with $k_e$ equal to the dipole moment of the MP field and $q_1{q}_2$ to electron-positron pair. Nuclear interaction is not required to sustain the valence electron in orbit undergoing DBT. The COM at the point of singularity is coupled to any outgoing radiation for both linear and non-linearity where particles acquire mass (Figure 2c). Orthonormal translation of z-axis from the point-boundary towards COM identifies with quantum arrow of time and it is intercepted by classical time (Figure 2d). Infinitesimal radiation of Planck constant, $\pm h$ by DBT are accommodated by the horizontal shift in COM towards the boundary.
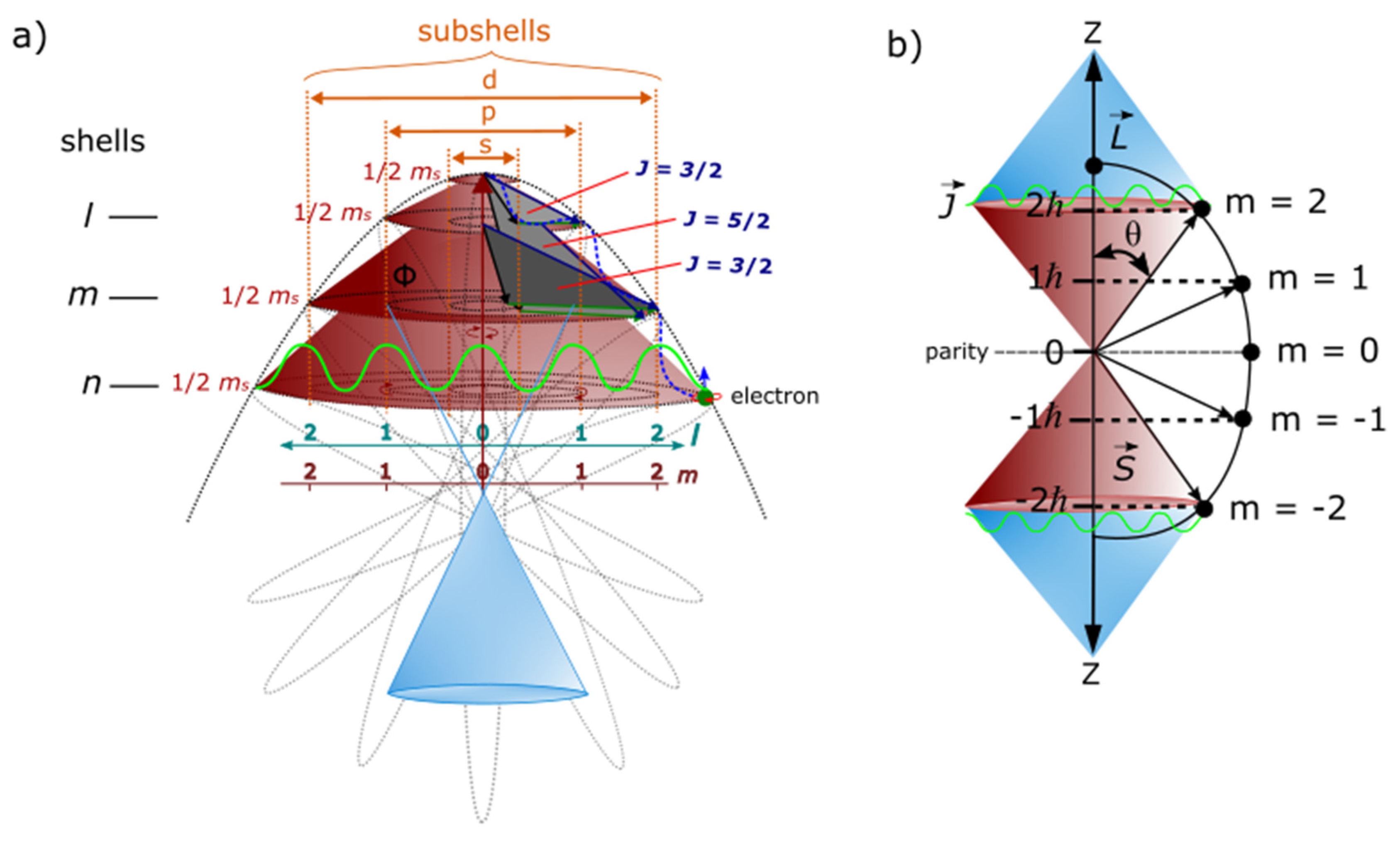
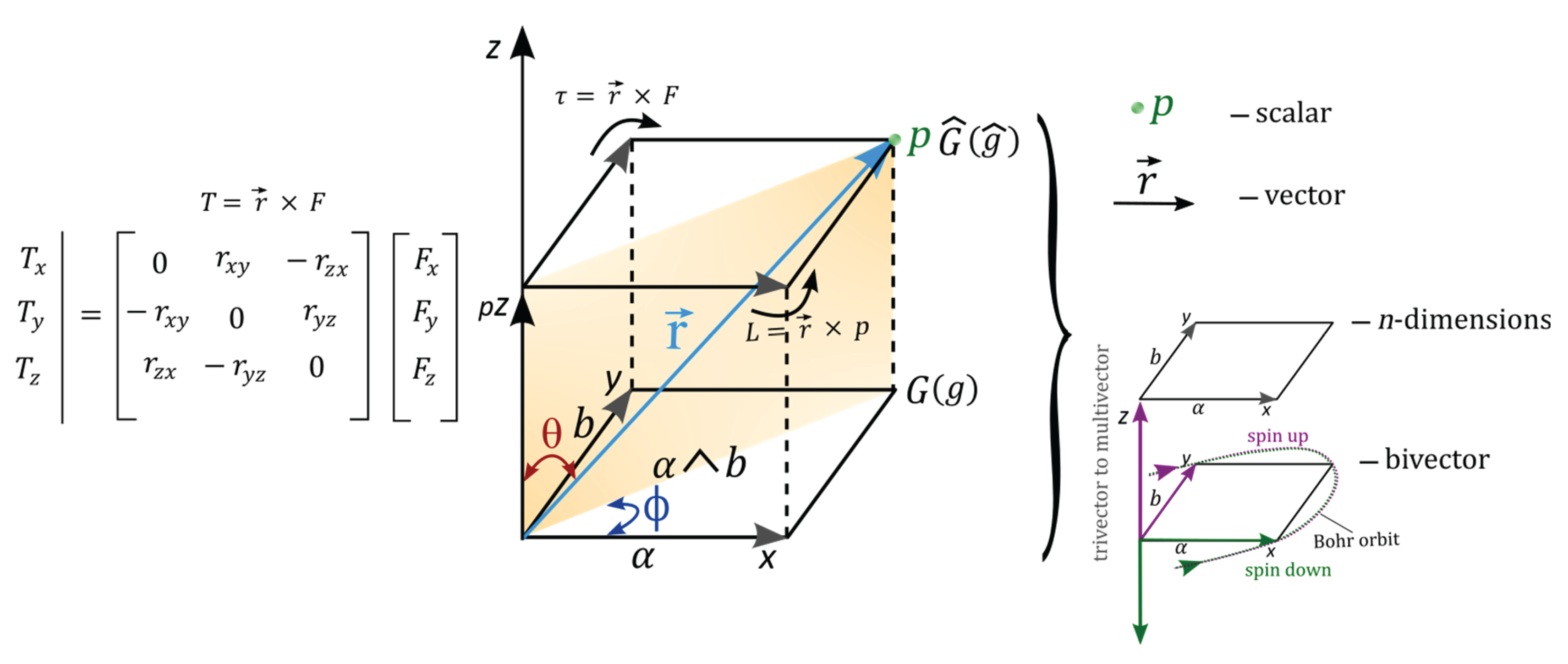
• The position of the electron undergoing clockwise precession with respect to z-axis is relatable to first derivation of space-time, $i\hslash {\displaystyle \frac{\partial }{\partial t}}\left(\psi \left(\overrightarrow{r}\right)\theta \left(t\right)\right)$ (Figure 1c). This is a fundamental equation of QM and forms the basis vectors, $\overrightarrow{r}$ and $\theta$ for BO along x-y plane and orthonormal to z-axis. The particle’s position in orbit can be split into both radial and angular wave components, $\psi \left(r,\theta ,\varphi \right)=R_{n,l}\left(r\right)Y_l^{m_l}\left(\theta ,\varphi \right)$. The radial component,$R_{n,l}$ is attributed to the principal quantum number, n associated with BO and its angular momentum, l to a light-cone at a distance, r from the nucleus. The angular part, $Y_l^{m_l}$ of degenerate states, ${\pm m}_l$ is assigned to the BO defined by both $\theta$ and $\varphi$ of topological torus (e.g., Figure 1d). Its inner product, ${⟨\psi |\varphi ⟩}^{*}=⟨\psi |\varphi ⟩$ from GS pair can translate to second derivative of space, ${\displaystyle \frac{{-\hslash }^2}{2m}}{\displaystyle \frac{d^2\psi \left(x,t\right)}{{dx}^2}}$by observation. Dirac fermion is linked to shift in the electron’s position of ${\psi }_0, {\psi }_1,{\psi }_2 \mathrm{and} {\psi }_3$. The vacant GS becomes the antimatter and its corresponding GS occupied by either the electron or positron to positive matter.
• Shift in COM coupled to linear light paths tangential to the model is subjected to mixing. The output signal from a point-spread Green function at COM (Figure 2e) is applicable to Fourier transform [39] of electromagnetism. The generated electric field, $\nabla . E\left(\psi \right)=-\partial B/\partial t\left(\psi \right)=m_j\hslash \left(\psi \right)$ is assumed at the ground state, with the electron resembling a Dirac monopole, $\nabla . B\left(\psi \right)=0$ (Figure 2a). By DBT, the solenoid loops of instantons are polarized, $\nabla . E \left(\psi \right)=\rho /{\epsilon }_0\left(\psi \right)$ with $\rho$ attributed to BO of n-dimensions and ${\epsilon }_0$ to dipole moment of the MP field. The solenoid path for the vortex electron is essential to the application of Ampere-Maxwell circuit law, $\nabla . H=J+\partial D/\partial t$. Propagators from signal processing provide integral kernels of Greens function like the wave operator, $\psi =A{e}^{+ikx}+B{e}^{-ikx}$ with respect to the electron’s position. Klein-Gordon operator, ${\partial }^{\mu }{\partial }_{\mu }\varphi =0$ is applicable to BO of hyperbolic surface for the light-cones (see Figure 1b–d). Mixing and output at COM for Klein-Gordon Greens function is, ${\partial }^{\mu }{\partial }_{\mu }\varphi G\left(x-y\right)={\delta }^4(x-y)$ and this can apply to massless scalar Higgs field of second-order space-time. The Dirac delta function, ${\delta }^4$ integrates the scattering matrix towards COM. These are of sine wave function consist of both homogeneous and inhomogeneous waves. The former by spherical boundary of GS pair and the latter to the electron’s position at the light-cones. Other relatable Fourier transforms are also applicable to the model include invariance commutation, propagators of casual and retarded Feynman path integral. Comparably, spectral function for hydrogen spectrum is valid for BO of n-dimensions for light paths coupled to the x-y plane.
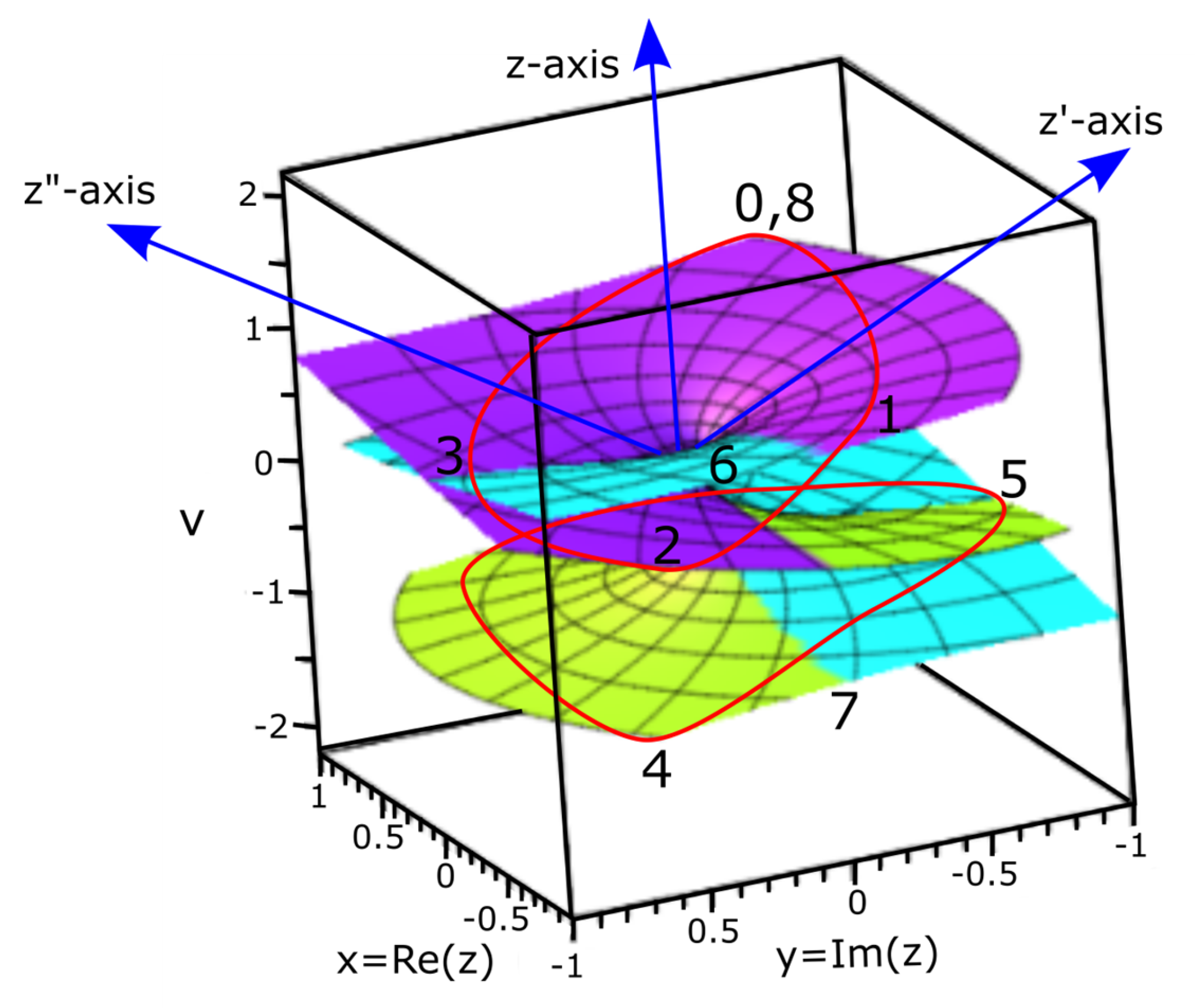
• CPT symmetry for the electron at position 0 appears invariant for both multidimensional Euclidean (Figure 1a) and 4D Minkowski (Figure 1b) space-times with z-axis equal to quantum time. At 360° rotation, electroweak symmetry breaking for combined charge conjugation and parity inversion at COM of the hyperbolic GS pair coincides with vacuum expectation value of Higgs boson (Figure 2c). Thus, the charges, $H^{-}$,$H^0$ and $H^{+}$ can coincide with the electron-positron transition at the vertex of the MP field. Because the GS pair are interchangeable, the occupied one of chirality with respect to the electron shift in position, ${\psi }_{0⟶3}$ can relate to either the electron or positron and the unoccupied GS to either an antielectron or an antipositron as previously mentioned. Time reversal for the electron orbit when subjected to DBT remains invariant under Lorentz transformation. The light-cones of geometrical hyperbola [40], $z-z^{\prime }\equiv ct-c{t}^{\prime }={tan}^{-1}v/c=\alpha$ is normalized to time-like circle by clockwise precession.
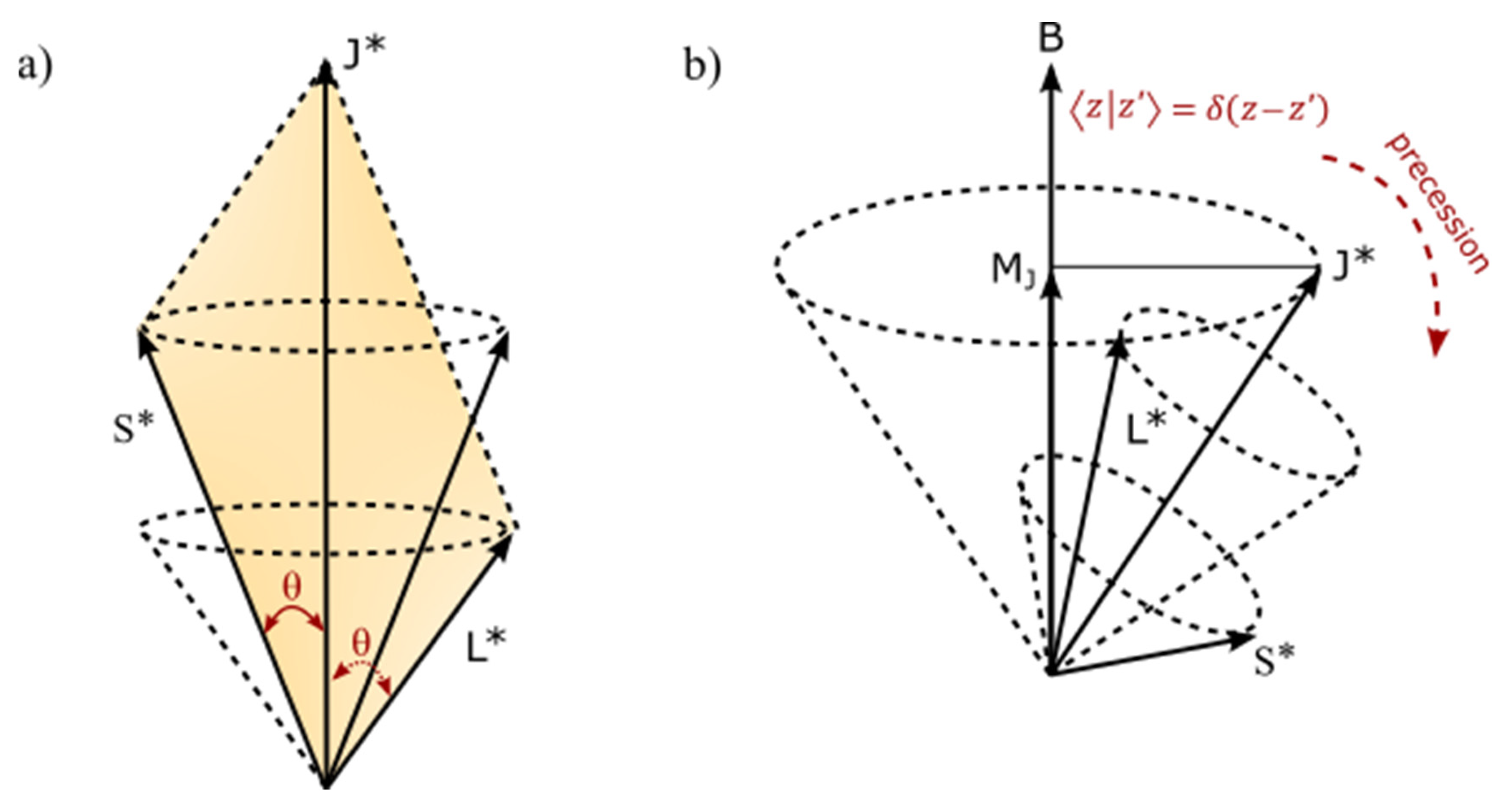
• The COM is the point of singularity of Hilbert space into Minkowski space-time and it initiates the magnetic dipole moment,$u$. The spaces of inner product to vector to metric to topology of n-dimensions are formed. These are confined to moduli of vertices by continuity of precession and this generates infinite Hamiltonian spaces for virtual particles, i.e., P(0→8) = ${\int }_{\tau }{\psi }^{*}\widehat{H}\psi d\tau$ with time equal to $\tau$. The Hermitian is represented by GS with electron in orbit and non-Hermitian to GS devoid of the electron. The former is ascribed to either electron or positron and the latter to their respective antimatter. Combining both Planck theory and Einstein mass-energy equivalence (Figure 2c), ${\gamma }^{\theta }$ relationship, $\lambda =h/mv$ of wave-particle duality is formed with ±h linked to DBT. The electron in constant motion acquires $J_z$ at positions 1 and 3 and exhibits centrifugal force, $F_c=m{v}^2/r$. It acts as a free electron with nuclear attractive force, $F_e=Z{e}^2/4\pi {\epsilon }_0{r}^2$ accorded to DBT at COM.
• Commutation for electron-electron pair at 720° offers an inertia reference frame, whereas anticommutation is at 360° can relate to the form [41], $⟨a_j|a_k⟩=\int dx{\psi }_{a_j}^{*}\left(x\right){\psi }_{a_k}\left(x\right)={\delta }_{jk}$. The sum of expansion coefficients, $C_n$, by continuity of precession renders the expectant value, $\left|\psi \right.⟩=\sum _n{C}_n/a_n⟩$ and its probability as ${⟨a_n|\psi ⟩}^2$. Spherical light path tangential to the model is polarized along both vertical and horizontal axes and is transformed linearly towards the COM (Figure 2e) in the form [42], $x^{\prime }=\gamma (x-vt/c^2)$. The corresponding 1D time is, $t^{\prime }=\gamma (t-vx/c^2)$ with Lorentz factor, $\gamma =1/\left(\sqrt{1-v^2/c^2}\right)$ at $y^{\prime }=y$ and $z^{\prime }=z$. The GS pair is Lorentz invariance under rotation, inversion and translation into space-time for $x=\gamma (x\prime -vt\prime /c^2)$ and $t=\gamma (t\prime -vx\prime /c^2)$.

The themes speculated above are teasers of otherwise much complex topics. Based on the ontology of the model, some of them are combined into specific headings and explored further in the text. These are plotted from an alternative perspective that could be applicable to conventional methods for further pursuits.

3. Ontology of MP Model to Quantum Mechanics

The attributes of MP model with respect to QM are explored into three parts. First, the non-relativistic aspect of $\psi$ is presented ensued by its collapse at observation. Third, some perspectives on quantized Hamiltonian is presented with reference to the ontology of the model.

3.1. Non-Relativistic Wave Function

From a theoretical perspective, the difference of classical oscillator to quantum oscillator is given by the application of Schrödinger’s wave equation and this forms the basis for QM. Nevertheless, QM cannot fully explain the combination of orbital angular momenta, spin angular momenta and magnetic moments of valence electrons observed in atomic spectra [43]. Similarly, how both integers to half-integers spins are accommodated by relativistic transformation of $\psi$ in QFT remains oblivious. How the translation can be attained from a geometry perspective is demonstrated in Figure 2a–e. Its model is given in Figure 1a–e. How all these can be aligned to the energy shells of BOs at n-levels is explored in this subsection.

In Figure 3a, the levitation of BO into n-dimensions for complex fermions of ±1/2, ±3/2, ±5/2 and so forth is demonstrated. It extends towards the boundary of the hyperbolic surface for the GS pair dissecting the nucleus (Figure 2c). Perturbation by oscillation is quantized and the emergent light-cones are of superposition states (Figure 3b). The spin angular momentum can be calculated based on both Russell-Saunders orbital-spin (L-S) coupling and Clebsch-Gordon series. The eigenvalue of total angular momentum is, $\overrightarrow{J}=\overrightarrow{l}+\overrightarrow{s}$ for orbitals in 3D and this combines eigenvalues of both orbital angular momentum, l and spin angular momentum, s (Figure 4a). The magnitude of l takes the form,

$$\left|\mathbf{L}\right|=\sqrt{{\mathbf{L}}_{\mathrm{n}}\left({\mathbf{L}}_{\mathrm{n}}+1\right)}\mathrm{\hslash },$$

(12a)

where ${\mathbf{L}}_{\mathrm{n}}$ is attributed to the electron’s position along BO of n-dimension. It is linked to degenerate states of subshells. The GS pair of 2π accommodates the electron-positron transition, ±h as mentioned earlier in the preceding section. The resultant orbital angular momentum L is a combination of $\sum l_i$ in a complete loop of BO, with the values of 0, $\sqrt{2}\hslash$ and $\sqrt{6}\hslash$ respectively generated at n = 0, n =1 and n = 2 (Figure 3b). Their projection about z-axis for an irreducible spinor of the MP field becomes,

$$\left|{\mathbf{L}}_{\mathit{Z}}\right|=M_L\hslash ,$$

(12b)

where $M_L$is the magnitude of the BO. For BO in vector space applicable to the hyperbolic surface of a light-cone of Minkowski space-time, $L_z$ is translated to $J_Z$ by,

$$J_Z=m_l\hslash ,$$

(12c)

where $m_l$ can take the values, 2l + 1 from the subshells or degenerate states of BO as eigenfunciton of $M_L$. Further distinctions between these parameters are provided in Figure 4a, where $J^{*}$ is not aligned to z-axis given that $\left|m\right|<\sqrt{j (j+1)}$ (Figure 4b). These are necessary for quantization of infinitesimal space with quantum time aligned to z-axis. Based on these demonstrations, Lamb shift can be explained in the following manner.

At n = 2, l = 1, this is split into s and p orbitals, each one accommodating ±1/2 spin from the electron-positron transition by DBT. The total angular momentum, $\overrightarrow{J}=l\pm {\displaystyle \frac{1}{2}}$, will then equate to ${\displaystyle \frac{3}{2}}$ and ${\displaystyle \frac{1}{2}}$ . If applied to Figure 3a, the summation of spin, 1/2 + 1/2 + 1/2 is made from combined s and $p_{x,y}$ subshells at $n_2$ + $n_1$ = ${\displaystyle \frac{3}{2}}$ for l = 1 and l = 0. The $p_z$ subshell is indistinguishable from s subshell for the vector axis aligned to z-axis. In this case, both orbital and spin angular momenta are in the same direction and it is at low energy. The resultant spin angular momentum, S of a light-cone assumes COM at singularity (e.g., Figure 2c). If the orbital and spin are not aligned at low energy, then $n_2-$ $n_1$ = ${\displaystyle \frac{1}{2}}$ and it is given by, 1/2 +1/2 −1/2 (Figure 3b). The combined $p_z$ and s subshells for spin down of z-axis are subtracted from $p_{x,y}$ subshells. Thus, the Lamb shift spacing of 0.035cm^-1 between ${}_2{S}_{1/2}$ and ${}_2{P}_{1/2}$ is applicable to ZPE fluctuations at COM from DBT accommodating $\pm i\hslash$ with respect to position and momentum (e.g., Figure 2c). The point of electron-positron transition can further accommodate the fundamental fine-structure constant of hydrogen spectral lines, $\alpha =e^2/4\pi$ $\approx 1/137$. Fine-tuning of $\alpha$ is required to minimize the effects of DBT at 720° rotation and this is pertinent to the anomalous magnetic moment, $a_e=a/2\pi$. Similarly, the acquired $J_z$ by rotation of MP field space at positions 1 and 3 is relevant to the calculation of the gyromagnetic ratio or $g$-factor, $\gamma =u/\left|J_z\right|$ or ${\gamma =2a}_e+2$. Any exponential increase in quantum perturbation from moduli of vertices and $\pm \overrightarrow{J}$ splitting for Landé interval rule from on-shell momentum are mixed with output by Fourier transform assumed at COM (Figure 2e). Such explanations might perhaps shed some useful insights into Zeeman effect of odd spin types and the refinement of Rydberg constant [44], $R_{\infty }={a^{2}m}_{e}c/2h$ for the hydrogen atom in terms of proton radius puzzle. Similarly, the envelop solitons of hyperbolic surface at positions 2 and 6 (Figure 2c) may restrict accessibility to the nucleus and this can become important in the quest of constraining quantum critical point [45] for Rydberg atom arrays of ferromagnetism.

3.2. Wave Function Collapse

Dirac fermion of a four-component spinor is denoted ψ(x) in 3D Euclidean space. Quantum time is trivial, $\left(z-z^{\prime }\right)=⟨z|z\prime ⟩$ in flat space (Figure 1a) and is absorbed into classical time, $ct-c{t}^{\prime }$ at COM (Figure 2d). The distance between any two events is always positive like position 2 and 6 in space as given in the form [46],

$${ds}^2={dx}^2+{dy}^2+{dz}^2={(x_2-x_1)}^2+{(y_2-y_1)}^2+{(z_2-z_1)}^2.$$

(13)

Once the electron gains spin angular momentum by DBT, Euclidean space-time is transformed into 4D Minkowski space-time, ψ(x,t) (Figure 1b). The hyperbolic space of the light-cone for both the inertia reference frame and accelerated reference frame is subject to Lorentz transformation of time invariance [46],

$${ds}^2={dx}^2+{dy}^2+{dz}^2-{ct}^2.$$

(14)

Both Equations (13) and (14) appear independent of a stationary observer with respect to the electron probability distribution as demonstrated in Figure 2a–e. The orthonormal shift identifies with both vertical and horizontal polarization. The emergence of the pair of light-cones coincides with Minkowski space-time and these are dissected by z-axis of quantum time in asymmetry. In non-Euclidean space, both positive and negative curvatures from the electron-positron transition are normalized to straight paths of Euclidean space (Figure 5a). Convergence of quantum space-time at COM is relevant to the equivalence principle for Euclidean space superimposed on the surface of the spherical MP model mimicking a Bloch sphere (Figure 5b). In such a case, the quantum aspect of de Sitter space by geodetic clockwise precession is balanced out by anti-de Sitter form of the electron transition in its orbit of time reversal to allow for the development of an inertia frame. Perturbation of the model is initiated and completed at COM of orthonormal relationship (Figure 2d). These are expected to translate by Fourier transform when quantum time coincides with classical time (Figure 2e). Comparably, the collapse of $\psi$ towards a point-spread Green function is reduced to $i\hslash$ (Figure 5c) for the outcome of a determinate value. The same applies to scattering matrix of wave amplitudes from the migration of COM intercepting BO into n-dimensions. Its Fourier transform is expected to mimic hydrogen emission spectrum (Figure 5d). Constraining the electron’s position towards COM presents the uncertainty principle from on-shell momentum of BO in degeneracy and levitation between the GS pair.

3.3. Quantized Hamiltonian

Two ansatzes adapted from Equation (3) are given by,

$$\psi =u\left(\mathbf{p}\right)e^{-ip.x},$$

(15a)

and

$$\psi =v\left(\mathbf{p}\right)e^{ip.x},$$

(15b)

where outward projection of electron spin is of $v$ type and inward projection to $u$ type. Equations 15(a) and 15(b) can relate to oscillations between GS pair from the electron-positron transition (e.g., Figure 2c). Linear transformation for quantum time merging into classical time can accommodate Hermitian plane wave solutions and this forms the basis for Fourier components in 3D space as earlier suggested (e.g., Figure 2d and Figure 5c). Decomposition of quantized Hamiltonian becomes [47],

$$\psi \left(x\right)={\displaystyle \frac{1}{{\left(2\pi \right)}^{3/2}}}\int {\displaystyle \frac{d^3}{2E_{\mathbf{p}}}}\sum _s\left(a_{\mathbf{P}}^s{u}^s\left(p\right)e^{-ip.x}+b_{\mathbf{P}}^{s†}{v}^s\left(p\right)e^{ip.x}\right),$$

(16a)

where the constant, ${\displaystyle \frac{1}{{\left(2\pi \right)}^{3/2}}}$ is attributed to GS pair accommodating Lamb shift at minimal energy as described in subsection IIIa. Its conjugate is,

$$\overline{\psi }\left(x\right)={\displaystyle \frac{1}{{\left(2\pi \right)}^{3/2}}}\int {\displaystyle \frac{d^3}{2E_{\mathbf{p}}}}\sum _s\left(a_{\mathbf{P}}^{s†}{\overline{u}}^s\left(p\right)e^{ip.x}+{b_{\mathbf{P}}^s\overline{v}}^s\left(p\right)e^{-ip.x}\right).$$

(16b)

The coefficients $a_{\mathbf{P}}^s$ and $a_{\mathbf{P}}^{s†}$ are ladder operators for u-type spinor and $b_{\mathbf{P}}^s$ and $b_{\mathbf{P}}^{s†}$ for v-type spinor. The operators are applicable to BOs of topological torus into n-dimensions intersected by moduli of vertices mimicking COM. The spinors of two spin states, ±1/2 are accompanied by their respective antiparticles, ${\overline{v}}^s$ and ${\overline{u}}^s$. These can relate to the electron-positron transition within the GS pair, where the devoid component assumes the antimatter role. In this case, Dirac Hamiltonian of one-particle hydrogen atom is [48],

$$H=\int d^{3}x{\psi }^{†}\left(x\right)\left[-i\nabla .\mathsf{\alpha }+m\beta \right]\psi \left(x\right),$$

(17)

where the electron, i acquires vectors of momentum, $\nabla$ by shift in its position and gamma matrices are given by the standard Pauli matrices, $\alpha$, $\beta$ (Figure 2e). The associated momentum is then given by,

$$\pi ={\displaystyle \frac{\partial \mathcal{L}}{\partial \psi }}-\overline{\psi }i{\gamma }^0=i{\psi }^{†}.$$

(18)

Parity transformation by levitation of GS pair can account for both observable and holographic oscillators of canonical conjugates (see also Figure 2c and Figure 3b). Projection of the electric currents in the x-y directions is analogous to Fourier transform (e.g., Figure 2d). This renders the following relationship [49],

$$\left[{\psi }_{\alpha }\left(\mathbf{x}, t\right),{\psi }_{\beta }\left(\mathbf{y}, t\right) \right]=\left[{\psi }_{\alpha }^{†}\left(\mathbf{x}, t\right),{\psi }_{\beta }^{†}\left(\mathbf{y}, t\right) \right]=0.$$

(19a)

Equation (19a) by unitary is assumed at COM (Figure 2e). Because the electron is a physical entity of non-abelian, the matrix form for anticommutation becomes,

$$\left[{\psi }_{\alpha }\left(\mathbf{x}, t\right),{\psi }_{\beta }^{†}\left(\mathbf{y}, t\right) \right]={\delta }_{\alpha \beta }{\delta }^3\left(\mathbf{x}-\mathbf{y}\right),$$

(19b)

where α and β denote the spinor components of $\psi$. In 3D space independent of time, the electron’s position, p and momentum, q, of conjugate operators commute in the form,

$$\left\{a_{\mathbf{P}}^r,a_{\mathbf{q}}^{s†} \right\}=\left\{b_{\mathbf{p}}^r,b_{\mathbf{q}}^{s†} \right\}={\left(2\pi \right)}^3{\delta }^{rs}{\delta }^3\left(\mathbf{p}-\mathbf{q}\right).$$

(20)

Equation (20) can relate to the electron popping in and out of existence with observations of real particles assumed at COM. The GS devoid of the electron is interchangeable with its counterpart so that only positive-frequency is generated into classical time such as [50],

$$\begin{gathered} ⟨0|\psi \left(x\right)\overline{\psi }\left(y\right)|0⟩=⟨0│\int {\displaystyle \frac{d^{3}p}{{\left(2\pi \right)}^3}}{\displaystyle \frac{1}{\sqrt{{2E}_{\mathrm{p}}}}} \sum _r{a}_{\mathrm{p}}^r{u}^r\left(p\right)e^{-ipx} \\ \times \int {\displaystyle \frac{d^{3}q}{{\left(2\pi \right)}^3}}{\displaystyle \frac{1}{\sqrt{{2E}_{\mathrm{q}}}}} \sum _s{a}_{\mathrm{q}}^{s†}{\overline{u}}^s\left(q\right)e^{iqy}│0⟩. \end{gathered}$$

(21)

Equation (21) implies to the dominance of matter over antimatter for the spinor attributed to the electron shift in positions, ${\psi }_{0⟶3}$ in repetition. Observations are assumed into classical time (e.g., Figure 2e).

4. Ontology of MP Model to Quantum Field Theory

This section explores the ontology of the MP model to QFT with respect to Dirac spinor and how this is also relevant to string theory of multidimensional space-time structure and loop quantum gravity of non-commutative spin tetrahedra. This is followed by brief explanations of Weyl spinors, Majorana fermions and Lorentz transformation. All these are plotted based on ref. [3, 6, 49 and 50] in order to pave the path for further examinations the conventional way.

4.1. Dirac Spinors, String Theory and Loop Quantum Gravity

The elliptical MP field is a closed form of a string. The electron of a point-particle becomes the excitation of the field. The vertices of ZPE mimic virtual particles in a vacuum. The emergence of real particle coincides with the electron-positron transition at COM during orbit. Twisting and unfolding process by DBT instigates the helical spin property (Figure 6a,b). The branes formed from the electron path from position 0 → 3 or 4 → 8 of continuity mimics multidimensional space-time structure as the particle is looped to different vibrational modes away from the vertices of ZPE at COM. When the electron’s orbit is against clockwise precession, negative helicity or left-handedness is assumed (Figure 6c) and vice versa for positive helicity or right-handedness (Figure 6d). In the process, non-commutative spin network of dynamical triangulations for quantum space-time tetrahedral is generated and this is a fundamental aspect of loop quantum gravity. The electron-positron transition satisfies the relations [6] $\sum _j{\widehat{e}}_j{\widehat{e}}_j^T=\left[e_i{e}_j\right]=c_{ij}^k{e}_k$ in flat Euclidean space. The coupling of angular momenta at positions 1, 3 is transposed to positions 5, 7 and the resultant tensor component as expansion coefficients, $c_{ij}^k$ are multiplied to the basis vector, $e_k$ of topological torus (see also Figure 2d). Outgoing signal at angular frequency, ${\omega }^2=k/m$ with the unit matrices, ${\widehat{e}}_k$ into extra dimensions from COM allows for the emanation of Planck radiation from an irreducible spinor (Figure 6e). The nucleus is confined to the center and its replication by COM from perturbations of Minkowski space-time allows for the emergence of Higgs boson type (e.g., Figure 2c), where there is no distinction between helicity and chirality. In this case, discreet symmetry breaking of charge conjugation and parity inversion or their combination is assumed by separation of chirality and helicity. Quantum time is invariant for the MP model undergoing DBT and this can be differentiated from classical time (e.g., Figure 2d). At 720° rotation, combined CPT symmetry is restored. The translation of 2D Euclidean space to 4D Minkowski space-time by rotation with COM at gravitational horizon towards the spherical point-boundary is relevant to the holographic principle. It provides the boundary between the quantum state and classical level and further incorporates Euler’s formula for both hyperbolic and parabolic complex numbers inclusive of Pauli matrices, $i, 0, -1, 1$. The matrices are traceless, Hermitian and of unitary with determinant –1. All these become realistic when applied to the MP model, where the GS accommodating either the electron or positron during transition can relate to actual particle and its counterpart to corresponding antiparticle as earlier mentioned. The GS pair of superposition state is devoid of observation when observation is limited to light-matter coupling. In this case, the model can still accommodate the generic Dirac equation in the extended form,

$$\left(i{\gamma }^0{\displaystyle \frac{\partial }{\partial t}}+cA{\displaystyle \frac{\partial }{\partial x}}+cB{\displaystyle \frac{\partial }{\partial y}}+cC{\displaystyle \frac{\partial }{\partial z}}-{\displaystyle \frac{{mc}^2}{\hslash }}\right)\psi \left(t,\overrightarrow{x}\right),$$

(22)

where c acts on the coefficients A, B and C and transforms them to ${\gamma }^1{, \gamma }^2$and ${\gamma }^3$ with respect to the electron shift in position, ${\psi }_{0\to 3}$ of continuity. The exponentials of $\gamma$ are denoted i for off-diagonal Pauli matrix for the light-cone of irreducible spinor and ${\gamma }^0$ to 0, 1 polarization states. Determinant –1 at position 4 from time reversal preserves the volume and orientation of BO into n-dimensional MP field space. The unitary matrices, ${\sigma }^i$ relate to oscillations from on-shell momentum of BO with anticommutative relationship, $e^{+}\left(\psi \right)\ne e^{-}\left(\overline{\psi }\right)$ from the electron-positron pair. The associated vector gauge invariance exhibits the following relationships,

$${\psi }_L\to e^{i\theta L}{\psi }_L$$

(23a)

and

$${\psi }_R\to e^{i\theta L}{\psi }_R$$

(23b)

The exponential factor, iθ is given by the shift in the electron’s position at an angle with respect to z-axis (Figure 5a). The unitary rotations of right-handedness (R) or positive helicity and left-handedness (L) or negative helicity are restored in the interchangeable GS pair. The helical symmetry from projections operators acting on the spinors are of the form,

$${ P}_L={\displaystyle \frac{1}{2}} \left(1-{\gamma }_5\right)$$

(24a)

and

$${ P}_R={\displaystyle \frac{1}{2}} \left(1-{\gamma }_5\right),$$

(24b)

where ${\gamma }_5$ relates to I matrices (Equation (8)) relatable to the electron shift in positions 0 $\to$ 3 in repetition. The usual properties of projection operators like: L + R = 1; RL = LR = 0; L² = L and R² = R can identify with the GS pair accommodating the shift in the electron’s position by DBT.

4.2. Weyl Spinors and Majorana Fermions

Dirac fermion is convertible to Weyl spinor and possibly to Majorana fermion of a natural neutrino type. In condensed matter physics, these are pursued for an array of atoms in lattice structure for it is difficult to examine them for individual atoms. Suppose a spherical atom is a replicate of multielectron atoms, it is also possible to consider both Weyl and Majorana fermions within the realm of the MP model of hydrogen atom type. In this case, the four-component spinor, ${\psi }_{0⟶3}$ is reduced to two-component bispinor of the form,

$$\psi =\left(\begin{array}{c}\begin{array}{c}{\psi }_0\\ {\psi }_1\\ {\psi }_2\end{array}\\ {\psi }_3\end{array}\right)=\left(\begin{array}{c}{u}_{+}\\ u_{-}\end{array}\right),$$

(25)

where $u_{\pm }$ are Weyl spinors of chirality with respect to the electron’s position. Because only spin up and spin down fermions are observed in experiments from a occupied GS of squared amplitude (i.e., ${\psi }_0$, ${\psi }_1$), the antifermions of both spin up and spin down (${\psi }_2$ and ${\psi }_3$) are attributed to the unoccupied GS as previously mentioned. For the Lamb shift ascribed to the COM of the MP model (see subsection IIIa), the creation and annihilation of virtual particles are attributed to the vertices of the MP field contained within the GS pair. The emergence of real particle is assumed at COM of position 0 (Figure 2d). The exchange of left- and right-handed Weyl spinor for the GS pair is given by the process,

$$\left(\begin{array}{c}{\psi }_L^{\prime }\\ {\psi }_R^{\prime }\end{array}\right)=\left(\begin{array}{c}{\psi }_R\left(x\right)\\ {\psi }_L\left(x\right)\end{array}\right)\Rightarrow \begin{array}{c}{\psi }^{\prime }\left(x^{\prime }\right)={\gamma }^0\psi \left(x\right)\\ {\overline{\psi }}^{\prime }\left(x^{\prime }\right)=\overline{\psi }\left(x\right){\gamma }^0.\end{array}$$

(26)

Equation (26) conserves local symmetry and corresponding global symmetry of Minkowski space-time by clockwise precession. In a similar manner, Dirac fermion can also relate to Majorana fermions. In this case, the toroidal moments of BO of topological torus by linearization towards COM will also generate Majorana types (Figure 2e) with the moduli of vertices assigned to creation and annihilation operators $\gamma \left(E\right), {\gamma }^{†}\left(E\right)$. At the Fermi level $\gamma \left(0\right)\equiv \gamma ={\gamma }^{†}$, the fermion is promoted to the conductance band of higher n-dimensions. Comparable to Greens function (see subsection IIc), the anticommutation relation for the Majorana is given by [52],

$${\gamma }_n{\gamma }_m+{\gamma }_m{\gamma }_n={2\delta }_{nm}.$$

(27)

The product of Equation (27), ${\gamma }_n^2=1$ is assumed at a potential well of oscillators (e.g., Figure 2c) for bosonic field like the Higgs. Similarly, for the Majorana fermion of neutrino type at the COM of Newtonian gravity, there is no barrier to the passage of neutrinos along x-y plane.

4.3. Lorentz Transformation

The Hermitian pair, ${\psi }^{†}\psi$ for the electron-positron transition undergo Lorentz boost in the form,

$$\begin{gathered} u^{†}u=({\xi }^{†}\sqrt{p.\sigma ,} \xi \sqrt{p.\overline{\sigma }} . \left(\begin{array}{c}\sqrt{p. \sigma }\xi \\ \sqrt{p.\overline{\sigma }}\xi \end{array}\right), \\ =2{\mathrm{E}}_{\mathrm{P}}{\mathsf{\xi }}^{†}\mathsf{\xi } . \end{gathered}$$

(28)

The conversion of Weyl spinors to two component Dirac bispinor, ${\xi }^1$ ${\xi }^2=1$ of transposition state is normalized to COM (Figure 2d). The corresponding Lorentz scalar for scattering from on-shell momentum of BO is,

$$\overline{u}\left(p\right)=u^{†}\left(p\right){\gamma }^0.$$

(29)

Equation (29) is applicable to merging of z-axis linearly to classical time to induce Fourier transform. In the process, the BO of n-levels are contracted (Figure 2e). By identical calculation to Equation (28), the Weyl spinors of chirality due to the electron’s position is given by,

$$\overline{u}u=2m{\xi }^{†}\xi .$$

(30)

The acquisition of mass at COM from low energy towards linear transformation at high energy is relevant to Higgs boson (e.g., Figure 2c,d) and a plethora of particle types can be envisioned. For the overarching GS pair of the MP field, this makes it difficult to distinguish Dirac spinors from either Weyl or Majorana types.

5. Ontology of MP Model to General Relativity

General relativity portrays framework of space-time fabric in 3D flat Euclidean space. It is bend by the gravitational force exerted between two bodies at a distance, one heavier than the other. The force becomes weaker when the distance is increased and is inversely proportional to the square of the distance that separates the centers of two bodies. From these intuitions, the field equations describing both space-time and matter fields breaks down towards singularity and requires renormalization process for long distances. By assigning COM to the spherical point-boundary and its transition to the center by perturbation from DBT, this can cater for gravity without inferring to smaller infinitesimal forms (see subsection IIc). How this is applicable to a multiverse of the MP models at a hierarchy of scales is examined in this section. First, an irreducible space-time fabric of an elliptical orbit mimicking MP field is plotted. Second, its relevance to Lie group is unveiled for 2D manifolds, 3D space and 4D space-time. Third, a brief outlook of how a body-mass in orbit curves space-time and its path dictated by clockwise precession of the MP field are described. Such demonstrations are expected to offer an alternative version of general relativity and forge possible links between high energy physics and condensed matter physics on a geometry basis.

5.1. Space-Time Fabric of an Elliptical Orbit

The framework of space-time fabric in an elliptical orbit is warped and unwarped for a GS pair subjected to DBT. The Cartesian coordinates of space-time, t, x, y, z are assumed by spherical polar coordinates is, $\delta \left(z-z^{\prime }\right)=ct$, $r, \theta ,$ ϕ and this demonstrates the transition of Euclidean space-time to Minkowski space-time (e.g., Figure 1a,b). In the former, the clock face background is projected in flat space of n-dimensions $\ge 1$ akin to Bohr model of hydrogen atom with distance between any two points being positive. In the latter, space-time is dynamic and a body-mass at a distance, r of n-dimension acquires angular momentum, $\theta$ with respect to z-axis as quantum time. The associated rotation of BO in degeneracy is attributed to ϕ. The basis vector, r and $\theta$ for time-distance relationship are projected to x-y plane (Figure 1c). The resultant plane wave solution, $e^{r\theta }=cos\theta +rsin\theta$ is accessed at COM by coupling of linear light paths tangential to the model (e.g., Figure 2e). Any access to singularity at the nucleus is constrained from moduli of vertices from the MP field undergoing clockwise precession. The vortex electron’s path of helical solenoid is of the form,

$$B=\mu \left({\gamma }^u{\partial }_v\right)\epsilon L,$$

(31)

where $\mu$ is permeability of space, ${\gamma }^u{\partial }_{v=\theta ,\varphi }$ depicts BO into n-dimensions, $\epsilon$ is electric current and L is length equal to z-axis. By DBT, the path somewhat curves the pair of light-cones to resemble Riemann surface (Figure 7). Its component of Ricci tensor is attributed to the hypersurface of the manifolds of BO into n-dimensions resembling Riemannian manifolds (see also Figure 1d). The curvature of the manifolds from COM at singularity for combined GS pair is defined by Ricci tensor curvature, $R_{\alpha \beta }=0$ (Figure 2c). The emergence of positive curvature, $R_{\alpha \beta }>0$ and negative curvature, $R_{\alpha \beta }<0$ for GS pair of oscillation mode is related to Minkowski space-time. The time-like region is referenced to the z-axis of a pair of light-cones and space-like region to BO of hyperbola geometry. The expansion of Ricci-type tensors along z- axis is of the form [53],

$$R_{\alpha \beta }\equiv {R^{\gamma }}_{\alpha \gamma \beta , } R_{\mu ,\omega }\equiv {R_{\alpha \beta }\mu }^{\alpha }{\omega }^{\beta }.$$

(32)

In Equation (32), the Riemann tensor sign convention consists of four indices and these are very complicated and are not explored in this section. However, these could apply to the vortex electron’s path for the Riemann surface comprised of manifolds of BO into n-dimensions (Figure 7). Contraction along z-axis towards the COM sustains the relationship,

$$R\equiv g^{\alpha \beta }{R}_{\alpha \beta },$$

(33)

where $g$ is subset of space applicable to the metric tensor field and R is Ricci scalar. Examples of covariant and contravariant components of the inner products of $g$ are such as,

$$g_{ij}=\left(\begin{array}{cc}1& 0\\ 0& {sin}^2\theta \end{array}\right), { g}^{ij}=\left(\begin{array}{cc}1& 0\\ 0& {\displaystyle \frac{1}{{sin}^2\theta }}\end{array}\right).$$

(34a)

Its Levi-Civita connection has non-zero Christoffel symbols of the form,

$${\mathsf{\Gamma }}_{\varphi \theta }^{\varphi }={\displaystyle \frac{cos\theta }{sin\theta }}, {\mathsf{\Gamma }}_{\varphi \varphi }^{\theta }=-cos\theta sin\theta .$$

(34b)

Equation (34b) is applicable to the basis vector, $\overrightarrow{e}\theta$ and$\overrightarrow{e}r$ by continuity into space-time within a sphere. The combined metric for the two space-time spheres of Euclidean and Minkowski, S² at radius, α is given by,

$${ ds}^2=a^2{(d\theta }^2+{sin}^2\theta d{\varphi }^2 ).$$

(35)

Equation (35) is relevant to linear Fourier transform at COM on a 2D sphere (e.g., Figure 2e). How all the above are incorporated into Lie group ladder operators,$G\left(g\right)$ and $\widehat{G}\left(\widehat{g}\right)$ for 2D manifolds, 3D space and 4D space-time are examined next within the confinement of the MP model.

5.2. Internal Structures by Lie Group Representation

The rotation matrices of the type, ${Rr}_{yz}\left(\theta \right)$ and $R_{zx}\left(\theta \right)$ are attributed to clockwise precession of the MP field. Precession stages with respect to z-axis at position 0 is such that, $⟨z|z\prime ⟩=\delta (z-z^{\prime })$ and these are transformed to linear time as plane wave solutions. The rotation matrix, $R_{xy}\left(\theta \right)$ intersects the BO defined by $\varphi$ into n-dimension. These matrices are relevant to describe both integer and half-integer spins like, 0, 1/2 and 1 for complete rotation towards COM. How all these are interpreted within the Lie group are explored based on refs. [53,55]. On a geometry basis, the accompanied intuitive guide for the gauge symmetry is provided in Figure 2e. The basis for vectors, matrices, tensors and Fourier transform are given in Figure 8. The electron of chirality is non-abelian. Only when positioned at COM, it is abelian and offers a symmetric MP field. Away from the vertices, the particle’s position is described by,

$$g\in G,$$

(36)

where $g$ is subset of space tangential to the manifolds of BOs and G represents the Lie group.

For the conjugate positions of, 1, 3 or 5, 7 of the BO (Figure 1d), contravariant of space expansion by rotation, ${\gamma }^{\mu }$ at spherical lightspeed is balanced out by covariant measure, ${\partial }_v$ of the coordinates $\left\{\theta ,\varphi \right\}$ to induce a hyperbolic geometry. In this case, Equation (36) validates the operations,

$$g_{\mathrm{1,5}}+g_{\mathrm{3,7}}\in G$$

(37a)

and

$$g+\left(-g\right)=i,$$

(37b)

where $i$ is spin matrix for spin ±1/2 mimicking the electron path within the GS pair. Anticommutation, $g_1+g_3\ne g_5+g_7$ from electron-positron transition (±$g$) is transient for positions 0, 4 and is overridden by the commutation of electron-electron, $g_1+g_3=g_3+g_1$ upon completion of DBT for positions, 0, 8 to allow for superposition state (e.g., Figure 2a). The hyperbolic surfaces of the light-cones are compacted orthonormal to isomorphic BOs (Figure 2e). Non-linear to linear sum of expansion coefficients to the particle position is, $\left|\psi \right.⟩=\sum _n{C}_n/a_n⟩$. The inner product of r is a scalar and at any two points by precession forms vectors such as,

$${\overrightarrow{r}}_1 {. \overrightarrow{r}}_2=\left|{\overrightarrow{r}}_1 \right|\left|{ \overrightarrow{r}}_2\right|cos\theta ,$$

(38)

where the lengths and relative angles are preserved in a sphere (e.g., Figure 1c). By assigning rotation matrix, R to Equation (38), the transposition becomes,

$${\left(R{r}_1\right)}^T\left(R{r}_2\right)=r_1^T{r}_{2}I,$$

(39)

where the identity matrix, $I=R^T\times R$ by compaction of vector bundles is assumed in homogenous spaces of BO. The shift in both $\theta$ and $\mathsf{\Phi }$ provides double cover of SU(2) for vector to multivectors. Inhomogeneity is expected from the electron’s position linked to the pair of light-cones. In a cube, $\overrightarrow{r}$ is a four 3-fold axis in 3D and its matrices are defined by the Cartesian coordinates, x, y and z (Figure 8). The bivector field resonates with $z/pz$ of integers modulo p of prime along the z-axis. Translation of isomorphic cubes about z-axis are compacted linearly into classical time (e.g., Figure 2d). The process coincides with vertical to horizontal polarization or vice versa. The Levi-Civita connection, ${\widehat{e}}_{\theta }={\widehat{e}}_r$ offers the basis factors for any changes of square infinitesimals, $d\theta =dr$ for rotational matrix of the tensors.

The ladder operators for SU(2) of BO become irreducible of the type, $\left(\begin{array}{c}SU\left(2\right)\\ n\times n\end{array}\right)\ne \left(\begin{array}{c}SU\left(2\right)\\ l\times l\end{array}\right)⨁\left(\begin{array}{c}SU\left(2\right)\\ m\times m\end{array}\right)$. Translation of SU(2) by $\left(\begin{array}{c}SU\left(2\right)\\ 2\times 2\end{array}\right)⨁\left(\begin{array}{c}SU\left(2\right)\\ 2\times 2\end{array}\right)$ to SO(4) somehow resembles the emergence of Dirac spinor within the MP model. The particle’s position, when y = 0, z = x is a real number with the imaginary number at x = 0, $z=y$ (e.g., Figure 2e). Similarly, the SO(2) group of BO in 2D is of the form [6],

$$\left(\begin{array}{cc}cos\theta & sin\theta \\ -sin\theta & cos\theta \end{array}\right)\cong \left(\begin{array}{cc}1& \theta \\ -\theta & 1\end{array}\right)=I+\theta \left(\begin{array}{cc}0& 1\\ -1& 0\end{array}\right),$$

(40)

where, $\theta \in \left[\mathrm{0,2}\pi \right]$ of complex phases accommodating the electron-positron transition by DBT. The orthogonal relationship of BO aligned to classical time suggests, $R\in \mathrm{S}\mathrm{O}\left(3\right)$ (e.g., Figure 2e). The SO(3) group rotation for integer spin 0 or 1 in 3D space can then be expanded into a series like,

$${\mathsf{\Pi }}_{\mu }\left(g_{\varphi }\right)={\mathsf{\Pi }}_{\mu }\left[\left(\begin{array}{ccc}cos\varphi & -sin\varphi & 0\\ sin\varphi & cos\varphi & 0\\ 0& 0& 1\end{array}\right)\right]=\pm \left(\begin{array}{cc}{e}^{i{\displaystyle \frac{\varphi }{2}}}& 0\\ 0& e^{-i{\displaystyle \frac{\varphi }{2}}}\end{array}\right)=R_{xy}\left(\varphi \right)$$

(41a)

and

$${\mathsf{\Pi }}_{\mu }\left(g_{\theta }\right)={\mathsf{\Pi }}_{\mu }\left[\left(\begin{array}{ccc}1& 0& 0\\ 0& cos\theta & -sin\theta \\ 0& sin\theta & cos\theta \end{array}\right)\right]=\pm \left(\begin{array}{cc}cos{\displaystyle \frac{\theta }{2}}& isin{\displaystyle \frac{\theta }{2}}\\ isin{\displaystyle \frac{\theta }{2}}& cos{\displaystyle \frac{\theta }{2}}\end{array}\right)=R_{yz}\left(\theta \right).$$

(41b)

Similar to Equation (41a), when rotating as 2 x 2 Pauli vector for SU(2) group, Equation (41b) is reduced to the form,

$$\pm \left(\begin{array}{cc}cos{\displaystyle \frac{\theta }{2}}& isin{\displaystyle \frac{\theta }{2}}\\ isin{\displaystyle \frac{\theta }{2}}& cos{\displaystyle \frac{\theta }{2}}\end{array}\right)=\left(\begin{array}{cc}z& x-y_i\\ x+y_i& -z\end{array}\right)=\left|\begin{array}{c}{\mathsf{\xi }}_1\\ {\mathsf{\xi }}_2\end{array}\right|\left|\begin{array}{cc}-{\mathsf{\xi }}_2& {\mathsf{\xi }}_1\end{array}\right|,$$

(41c)

where ${\mathsf{\xi }}_1$ and ${\mathsf{\xi }}_2$ are Pauli spinors of rank 1 to rank 1/2 tensor relevant for Dirac matrices (see also Equation (28)). Equation (41c) considers out of phase for the electron (–) against clockwise rotation and in phase for positron (+) towards the generation of the helical property (Figure 6c,d). The relationship, $R_{xy}\left(\varphi \right)=e^{\theta }$from Equation (41a) identifies with polarization states of 0, 1 and the associated matrix is,

$$e^{\theta }\left[\begin{array}{ccc}0& -1& 0\\ 1& 0& 0\\ 0& 0& 0\end{array}\right]=\left[\begin{array}{ccc}cos\theta & -sin\theta & 0\\ sin\theta & cos\theta & 0\\ 0& 0& 1\end{array}\right].$$

(42)

Equation (42) is applicable to Fourier transforms of z-axis orthonormal to classical time (Figure 2d). The resultant shift of COM is accorded to the form,

$${\mathsf{\Pi }}_{\nu }\left(g_{\psi }\right)={\mathsf{\Pi }}_{\nu }\left[\begin{array}{ccc}cos\psi & 0& sin\psi \\ 0& 1& 0\\ -sin\psi & 0& cos\psi \end{array}\right]=R_{zx}\left(\psi \right).$$

(43)

For the irreducible spinor representation, $\mathsf{\Pi }$, the algebraic relationship is,

$$\rho \left(g\right)=\left[\mathsf{\Pi }\left(\widehat{g}\right)\right],$$

(44)

where $\rho$ is composed of algebraic structure ($pz$, $+p$ and $\mathrm{x}p$) for vectorization, V into p-dimensional space defined by $\alpha \wedge b$ of BO space (Figure 8). The two operators, $T_a$ and $S_a$ acting on V are of the form,

$$\left(T_{a}f\right)\left(b\right)=f\left(b-a\right)$$

(45a)

and

$$\left(S_{a}f\right)\left(b\right)=e^{2\pi iab}f\left(b\right),$$

(45b)

where T is identified by the rotational matrices, $T=\overrightarrow{r}\times F$ and $S_a$ is the shift in frequency in space by outsourcing at COM. In this case, the following relationship can be forged between I of quantum mechanics and metric tensor of general relativity such as [6],

$$g_{r\theta }=\left[\begin{array}{cc}1& 0\\ 0& r^2\end{array}\right]\equiv \mathrm{I}=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right],$$

(46)

where $g_{r\theta }= g_{\overrightarrow{v}.\overrightarrow{\omega }}$ is for speed, v by rotation and $\omega =2\pi /\tau$ for angular frequency. The discrete Christoffel symbols, ${\mathsf{\Gamma }}_{r\theta }^r$ or ${\mathsf{\Gamma }}_{\theta r}^{\theta }$ and their variations by, $g_{r\theta }$ are applicable to a body-mass in an elliptical orbit of both 2D and 3D. By precession, both the metric and stress-energy tensors appear symmetric so that $g_{\mu v}=g_{v\mu }$ and $T_{\mu v}=T_{v\mu }$. Each one of them requires 10 independent components from 4 x 4 matrices and these can be applied to MP model of 4D quantum space-time. The relationship between the two in a rest frame is given by [56],

$${ g}_{v\mu }=k{T}_{v\mu }={\eta }_{\alpha \beta }$$

(47)

where $k=8\pi G/C^4$ is Einstein constant and ${\eta }_{\alpha \beta }$ is Minkowski space-time (Figure 1b). The space-time metric, $g_{v\mu }$ within two space-time spheres is comparable to Equation (35) in the form,

$${ ds}^2={g_{\mu v}dx}^{\mu }{dx}^{\nu } ,$$

(48)

where $\mu \nu =\mathrm{0,1},\mathrm{2,3}$. The relevance of the indices for the electron path suggests that $T_{v\mu }$ is the result of the presence of a body-mass in an elliptical orbit. Its matrices are of the generalized form,

$${ T}_{\mu \nu }=\left(\begin{array}{c}\begin{array}{cc}{T}_{tt}& T_{tx}\\ T_{xt}& T_{xx}\end{array} \begin{array}{cc}{T}_{ty}& T_{tz}\\ T_{xy}& T_{xz}\end{array}\\ \begin{array}{cc}{T}_{yt}& T_{yx}\\ T_{zt}& T_{zx}\end{array} \begin{array}{cc}{T}_{yy}& T_{yz}\\ T_{zy}& T_{zz}\end{array}\end{array}\right).$$

(49)

Equation (49) can be dissected as follows [57]. Energy density, $T_{tt}$ is attributed to twisting and unfolding process of the electron-positron at COM by DBT. The momentum density, $T_{xt} T_{yt} T_{zt}$ or $T_{tx} T_{ty} T_{tz}$ for the plane wave solutions is referenced to orthonormal combination of quantum time to classical time for quantized Hamiltonian (e.g., Figure 2d). Shear stress like the rate of change in x-momentum in the y-direction is given by $T_{xy}$ and for y-momentum in the z-direction by, $T_{yz}$ and so forth. These identify with diagonal invariant rotation of the x-y plane (Figure 8). The plane is part of the four 3-fold rotational axes for a body-mass at a lattice point of a cube. There are also three 4-fold rotational axes on the faces and six 2-fold rotational axes at the edges. The negative pressure force, $T_{xx}$ $T_{yy}$ $T_{zz}$ directions are balanced out between the GS pair. Similarly, the matrix for ${\eta }_{\alpha \beta }$ such as,

$${ \eta }_{\alpha \beta }=\left[\begin{array}{c}\begin{array}{cc}1& 0\\ 0& -1\end{array} \begin{array}{cc}0& 0\\ 0& 0\end{array}\\ \begin{array}{cc} 0 & 0\\ 0& 0\end{array} \begin{array}{cc}-1& 0\\ 0& -1\end{array}\end{array}\right],$$

(50)

can be equated to Equation (49) to forged the relationship, ${\eta }^{\alpha \beta }=T^{\mu \nu }$. This can be relevant towards merging of both Euclidean and Minkowski space-times within the MP model. And a body-mass of superposition state by homomorphism is separated into two points of oscillation mode in general agreement with gravity (e.g., Figure 2c). How all these are applicable to a planet in orbit of the sun in a multiverse of the MP models at a hierarchy of scales is explored next.

5.3. Space-Time Curvature and Gravitational Horizon

Based on the descriptions of geometry offered for the MP model, an alternative interpretation of Einstein field equation described in ref. [30] is reproduced in Figure 9 for the planetary model in a multiverse. How this can accommodate perturbations from nonlinearity of differential gravitation acceleration, eccentricity of the reference orbit and its oblatenes in addition to the relative motion of the planet against the sun’s gravity appears to be more complex phenomena [37]. These are not covered in here. However, by assigning gravity to COM, some of these perturbations can relate to the process of DBT assumed at a higher hierarchy of scales in a multiverse of the MP models. In this case, the curvature of space-time does not require framework of space-time fabric into smaller infinitesimal forms. Instead, the relative position of the observer towards gravitational horizon comes into the foreplay [58] when viewing planets at the vertices of the MP fields. This imply that multielectron atom of MP fields is comparable to the solar system accommodating multiple planets but are distinct in chemical compositions and of different time frames. The Earth’s orbit at the vertex forms an aphelion with respect to the sun. At positions 2 and 6, the planet is perihelion to the sun. The COM integrates both Coulomb force and Newton’s law of gravity, $F=G{\displaystyle \frac{q_1{q}_2}{r^2}}$ , with $G={\displaystyle \frac{1}{4\pi {\epsilon }_0}}$ applicable to the dipole moment by DBT. Whether this could be linked to the vertical electric dipole from layered surface of Earth or sea [59] remains a possibility as gravity alone cannot adequately account [60] for the anomalous advances in Mercury’s perihelion precession. When applied to the MP model, first the process of DBT at COM will constantly variate the position of vertices of the MP field undergoing clockwise precession to accommodate any outgoing radiation. Second, for a body-mass confined to a hemisphere of GS, there will be overlap to the cycles of elliptical loops to generate a sphere. Both of them are observed for Mercury’s orbit, so the notion of matter curves space-time and space-time tells matter how to move is applicable to the model. Such suggestion mimics well studies [61] into the damping of the torque from electromagnetic coupling of core-mantle towards tidal dissipation in order to allow for free precession of Mercury’s orbit. In a multiverse, the exertion of torque at COM into Hilbert space is of the form [30],

$${8\pi GT}_{\mu ,\nu }\equiv {i\hslash }_{\mu ,\nu }.$$

(51)

For observations limited to light-matter coupling, the Dirac’s string of the MP field can be stretched out or relaxed without partitioning akin to the magnetic dipole moment. Any infinitesimal spatial and temporal changes by precession becomes,

$$8\pi G{\int }_{-\infty }^{\infty }{\left(dRdTdg\right)}_{u,v}\equiv i{\int }_{-\infty }^{\infty }{\left(d\Omega d\varphi d\theta \right)}_{u,v}.$$

(52)

Equation (52) offers an alternative version of Einstein’s field equation with, $1/2{\mathrm{R}\mathrm{g}}_{\mu \nu }^{\lambda }-{\mathsf{\Lambda }\mathrm{g}}_{\mu \nu }^{\lambda }=R_{\mu v}$ assumed at positions 1 and 3 at the vertices of the cube (Figure 8) akin to ZPE of COM for the MP field at axial position. In this case, space-time singularities from dense matter with respect to quantum gravity is evaded and both negative and positive curvatures are generated from the lattice points by diagonal rotations to induce helical solenoid of Riemann surface (e.g., Figure 7). These alternative interpretations of general relativity are worth noting supposing that no new insights are forthcoming from the black holes.

6. Conclusions

The electron defined by $\psi$ and its hidden variables relevant to a composite Dirac fermion is vigorously pursued in both QM and QFT but its realistic ontology remains vague and this cannot be satisfactorily unveiled in experiments conducted in both low to high energy physics. How it could be interpreted within a MP model of 4D quantum space-time of hydrogen atom type on a geometry basis is explored in this study. The model is able to account for the transformation of the electron by DBT to Dirac fermion and is compatible with many aspects of both QM and QFT. The COM reference frame relevant to Newtonian gravity is assigned to the spherical point-boundary of ZPE at the interface of atomic and classical scales. Similar scenario is assumed in a multiverse of the models at a hierarchy of scale such as for a planet in orbit of the sun. Perhaps, Coulomb attractive force in addition to gravity of respective body-masses are expected to stabilize the multiverse by polarization. How this can apply to account for Mercury’s anomalous perihelion precession has been inferred in this study and the ontology of the MP model as an approximate intuitive tool to guide fundamental physics in general is worth further considerations.