Prerpints.org logo
Preprint
Article

This version is not peer-reviewed.

Dirac Fermion of a Monopole Pair (MP) Model of 4D Quantum Space-Time and Its Multifaceted Dynamics

Submitted:

27 February 2025

Posted:

28 February 2025

Read the latest preprint version here

Abstract
In quantum mechanics (QM), the electron of spin-charge, ±1/2 in probabilistic distribution about the nucleus of an atom is described by non-relativistic Schrödinger wave equation. Its transformation to Dirac fermion of a complex four-component spinor is incorporated into relativistic quantum field theory (QFT). The link between QM and QFT on the basis of space-time structure remains lacking without the development of a complete theory of quantum gravity. In this study, how a proposed MP model of 4D quantum space-time of hydrogen atom type is able to combine both QM and QFT into a proper perspective is explored. The electron of a point-particle and its transformation to Dirac fermion appears consistent with Dirac belt trick for the generation of superposition states of spin-charge. Center of mass reference frame relevant to Newtonian gravity is assigned to the point-boundary of the spherical model. Such a tool, though metaphysical, its multifaceted dynamics appear compatible with some basic aspects of both QM and QFT such as non-relativistic wave function and its collapse, quantized Hamiltonian, Dirac spinors, Weyl spinors, Majorana fermions and Lorentz transformation. How it could further relate to space-time geometry for a body-mass in an elliptical orbit is plotted for general relativity and a multiverse of the MP models at a hierarchy of scales is proposed for further investigations.
Keywords: 
Dirac fermion
;  
Quantum mechanics
;  
Quantum field theory
;  
Dirac belt-trick
;  
4D space-time
Subject: 
Physical Sciences  -   Theoretical Physics
Preprints 150724 i001

I. Introduction

In this section, the rationale for why it is necessary to consider an electron within a boundary of 4D space-time is explored by first outlining the transition from QM to QFT and then describing the transformation of the electron to composite Dirac fermion of four-component spinor. The MP model of 4D space-time resembling a hydrogen atom type is explored in Section II. Physical intuition on a geometry basis is applied to explain the transformation of the valence electron to a Dirac fermion by the process of Dirac belt trick (DBT) to attain superposition states of spin-charge into quantum space-time. Center of mass (COM) reference frame is assigned to a point-boundary of the spherical model and this offers an intricate dynamic tool. The model’s compatible to both QM and QFT are respectively explored in Sections III and IV by considering some of their features relevant to the discussions. In Section V, space-time geometry of the model is examined with respect to its framework of fabric and internal structure relevant to Lie group representation. In addition, how classical space-time curvature can be incorporated in a multiverse of the MP models at a hierarchy of scales is plotted. In Section VI, some concluding remarks for future prospects are presented.
A. Non-relativistic to relativistic theory and space-time enigma
The electron of a point-particle of mass is attributed to i ℏ with i a complex number assigned to a point of a rotating sphere and ℏ to Planck constant of infinitesimal radiation in quantized form [1,2]. The first order space-time derivative of the particle in motion is attributed to non-relativistic Schrödinger equation, i ℏ ∂ / ∂ t and it is a fundamental concept of particles in QM that cannot be derived by QFT [3]. For light-matter coupling, the energy and momentum operators of Schrödinger equation,
    E ^ = i ℏ ∂ ∂ t ,                   p ^ = − i ℏ ∇ ,
are adapted into QFT beginning with Klein-Gordon equation [4] by second derivation of space-time given in the expression,
i 2 ℏ 2 ∂ 2 ∂ t 2 − c 2 ℏ 2 ∇ 2 + m 2 c 4 ψ t , x ¯ = 0 .  
Equation (2) is a relativistic form of Equation (1) and it incorporates special relativity, E 2 = p 2 c 2 + m 2 c 4 with the first term representing momentum and second term to mass-energy equivalence, E = m c 2 . The del operator, ∇ presents 3D space for a particle in motion in space-time. Only one component is considered in Equation (2) and is relevant to describe bosons of whole integer spin and their charges. However, it does not take into account fermions of spin 1/2 and negative energy contribution from antimatter. These are accommodated into the famous Dirac equation [3] of the generic form,
i ℏ γ u ∂ u ψ x − m c ψ x = 0 .    
The symbol, γ u is a set of 4 x 4 gamma matrices, i.e., γ u = γ 0 , γ 1 , γ 2 , γ 3 and this combines with partial derivative of space-time, ∂ u =   x 0 , x 1 , x 2 , x 3 to give a scalar quantity which is invariant under Lorentz transformation. The imaginary unit, i unifies space and time according to special relativity and distinguishes 1D time from 3D space by orthonormal relationship. The complex four-component spinor, ψ from Equation (3) is represented in the form,
ψ = ψ 0 ψ 1 ψ 2 ψ 3 ,    
where ψ 0 and ψ 1 are spin-up and spin-down components of positive energy with ψ 2 and ψ 3 as corresponding antimatter for spin-up and spin-down of negative energy. Negative energy is associated with the creation and annihilation of virtual particles in a vacuum towards the emergence of real particles, ψ 0 and ψ 1 of superposition states like the electron of spin-charge, ±1/2 in probabilistic distributions [3]. In order to include space-time-energy matrices of the particles, standard Pauli matrix convention is applied such as [5,6],
                                                    σ 0 = 1 0 0 1 ,                             σ 1 = 0 1 1 0 ,
σ 2 = 0 − i i 0 ,                         σ 3 = 1 0 0 − 1 .
These are a set of 2 x 2 dimensions of complex traceless, Hermitian matrices that are equivalent of involutry matrices and are identified as unitary matrices. The matrices relate to angular momentum operator of observable spin 1/2 particle respectively in three spatial directions, σ 1 , σ 2 and σ 3 with σ 0 equal to identity matrix, I . Any 2 x 2 Hermitian matrices have determinant and traceless values respectively of − 1 and 0. Their matrix product are given by [7],
  σ i σ j = δ i j I + i ϵ i j k σ k ,  
where ϵ i j k is the Levi-Civita symbol and is applicable to the relations of both commutation by cyclic permutation, i.e., σ i , σ j = σ i σ I − σ j σ i = i ϵ i j k σ k and anticommutation by combination σ i , σ j = σ i σ I + σ j σ i = 2 δ i j I with i j k = 1,2 , 3 . The orthonormal basis of vector space of 2 x 2 Hermitian matrices over the real numbers, under addition for σ 13 and σ 0 is the matrix σ 2 by isomorphism [6],
  a − i b i b a = a σ 0 + b σ 13   ⟷ a + i b .    
Equation (7) considers real numbers a → ψ 0 and b → ψ 1 respectively as real and imaginary parts of σ 2 . The orthonormal basis for vector space is relevant to Clifford group and Clifford algebra, C ≅ C ( 0,1 ) . The four matrices in C ( 4 ) generate the vector space C ( 3,1 ) or C ( 1,3 ) and by isomorphism is denoted γ i with respect to Dirac matrices inclusive of a fifth related matrix [6],
γ 0 = I 0 0 − I ,     γ i = 0 σ i − σ i 0 ⟹     γ 5 = 0 I I 0 .  
The matrix, γ 5 = i γ u couples the spinor field, i defined by modes of oscillation, stress-energy tensor and momentum to space-time structure. There is no space-time boundary to the quantum state defined by relativistic QFT with observation limited to a point in space-time. Similarly, both QFT and QM cannot be integrated by 1st derivative of space-time shown in Equation (1). Instead, 2nd derivative of Schrödinger relationship in the generic form,
i ℏ d ψ ( x , t ) d t = − ℏ 2 2 m d 2 ψ ( x , t ) d x 2 + V x ψ x , t ,    
is applied and integrated into Equation (2) for relativistic transformation. The ontology of 1st derivative of space-time remains unclear, whereas both QM and QFT consider wave behavior of electron permeating space and it consists of both kinetic and potential energies. How it collapses without interactions to a point at observation still offers an enigma of space-time yet to be properly resolved in field theory [8]. Similarly, how concentrated matter in a vanishing small volume is able to curve space-time towards singularity is not yet evident either by observation of a black hole or empirical data garnered from high energy experiments [9].
B. Rationale for 4D quantum space-time in field theory
In relativistic QFT, γ u is broken up into four-position coordinates, four-momentum and four-vector for the force respectively given as [10],
R → = c t x y z ,       P → = E p x c p y c p z c ,       χ μ = x 0 x 1 x 2 x 3 .
The components of Equation (10) are transformed contravariantly by continuity of rotation, translation and inversion into space. These are combined with 4-gradient covariant term, ∂ u = ∂ / ∂ t , ∇ ⃑ shown in Equation (3) to agree with measurements. However, the evolution of the electron field into space-time by 2nd law of thermodynamics and its collapse towards superposition states of matter-antimatter coexistence remains unclear. The dominance of electron for matter over antimatter like electroweak baryogenesis [11] is represented in forward time. Antimatter requires time reversal in order to demonstrate violation of charge, parity or their combination like for CPT symmetry in the renormalization process using Feynman diagrams [12]. Antimatter existence is readily observed in both Stern-Gerlach experiment [13] and cosmic rays [14]. At the quantum state, the conservation of combined charge conjugation, parity inversion and time reversal symmetry with exponential rise of Hilbert space linearly requires a proper demonstration of space-time. In the former, charge conjugation parity is associated with Dirac’s string trick or belt trick [15], which describes the electron conversion to a positron at 360° rotation and its restoration at 720° rotation. The same extends to other related descriptions like Balinese cup trick [16] or Dirac scissors problem [17]. In the latter, quantum space-time remains elusive, where creation and annihilation of virtual particles is employed to comply with the dominance of classical thermodynamic arrow of time such as in massless quantum electrodynamics [5,18]. Theoretical approach to quantum space-time is necessary for an apparent reason. The microscopic arrow of time assigned to decay of neutral kaons [19] is difficult to investigate for the electron of a typical hydrogen atom of diameter about 0.1 to 0.5 nanometers. For example, the electron of a point-particle into 3D space and its shift in position of 1D time about the nucleus implies to quantum space-time. Its motion by derivation of space-time from a ground state is demonstrated in Equation (1) for QM and under Lorentz boost, the electron of probability distribution, ψ 2 is transformed to a composite Dirac fermion.
Leading theoretical approaches to address quantum space-time is to quantize both matter field and space-time like in both twister approach [20] and in loop quantum gravity [21]. The notion in both instances is based on non-commutative spin network of dynamical triangulations to simulate quantum space-time tetrahedra. By using four C 13 nuclei in nuclear magnetic resonance simulator, spinfoam vertex amplitude mimicking angular momenta is generated for space-time tetrahedral as predicted by loop quantum gravity [22]. The outcome looks promising for quantum computation of exponential rise in non-perturbative regimes of vectors in Hilbert space leading to classical arrow of time that cannot be easily done by classical computers. Nonetheless, the key ingredient for such novel undertaking and its similar kinds [23,24] is how to integrate both quantum gravity and quantum fluctuations of matter field into a Block sphere replicating an atom. Technically, this appears unfeasible to unveil by both ontology and methodology on how to constrain time link to either entanglement [25] or entropy [26] or both [27] at Planck scale, where quantum gravity is expected to be a dominant force [28]. Observables into multidimensional quantum space-time is predicted by string theory and these are yet to be established due to lack of supersymmetry or decay of composite Higgs boson observed in experiments conducted in high energy particle physics [29]. Similarly, there is lack of data offering new insights into the relationship of space-time singularities and black holes, where the principles of QM are intertwined with gravity [30].
C. Motivation of this study
In this study, how Rutherford’s atomic model of an electron in an elliptical orbit of a MP field is animated into 3D space by clockwise precession of 1D time to generate 4D quantum space-time of a spherical model is investigated. The model appears compatible with both Schrödinger electron cloud and Bohr models of the hydrogen atom. The transformation of the electron of a point-particle to a composite Dirac fermion or monopole is assumed by the process of DBT, for the generation of superposition states of ±1/2 spin. Such a prototype model includes both Euclidean and Minkowski quantum space-times on a geometry basis. The COM reference frame for the electron-positron transition is assigned to the vertex of the elliptical orbit. All these measures offer a multifaceted dynamic model and it is able to consolidate basic aspects of both QM and QFT into a proper perspective. If considered, it can become critical to push physics forward into a whole new direction by assuming a multiverse of the models at hierarchy of scales for a body-mass in an elliptical orbit and this warrants further investigations.

II. Dirac fermion of a MP model of hydrogen atom type

Additional details on the conceptualization path of the model from electron wave-diffraction is offered elsewhere [31]. In this section, the transformation of an electron of hydrogen atom type to a fermion by Dirac process within a spherical MP model of 4D space-time is unveiled. First, a brief overview of the atomic models is provided on how it is not able to accommodate the electron spin, ± 1/2 superposition states. Then how this can be incorporated into the model by DBT into quantum space-time is demonstrated. This is ensued by outlining COM reference frame assigned to the spherical boundary and its intricate dynamics before exploring the compatibility of the model to both QM and QFT on a geometry basis.
A. A brief overview of existing atomic models
In this subsection, the history of the atomic model is not pursued and there many texts available in both chemistry and physics for the reader to explore this further. Rather only a brief anecdote of the concept of modern atom and its limitations are offered and how these can be addressed in this undertaking. The widely accepted model of the atom is the electron cloud model described by Schrödinger’s ψ . The probability of finding the electron at a time is relegated to orbitals of quantum waves. These are standing waves permeating particular regions of the atom and possess both kinetic and potential energies as demonstrated in Equation (9). However, it cannot explain how these collapse to a definite state at observation. Similarly, Bohr model depicts electron to occupy certain orbits of quantized energy about the nucleus. Its promotion to higher energy levels from the ground state requires external energy inputs like for light-matter coupling as observed in the hydrogen spectrum. The model was developed to explain how an electron in orbit around the nucleus of Rutherford’s atomic model does not lose energy by radiation and collapse into the center. The major limitations to such model inclusive of Schrödinger’s model is that, they cannot account for the electron’s magnetic spin, ±1/2 in superposition states and its transition in orbit of indeterminacy. How all these could be attained within the proposed MP model by the process of DBT is plotted and it includes elucidation of both Euclidean and Minkowski quantum space-times. Such an approach appears metaphysical to an extent, so to make it compatible to physics in general, basic knowledge in both QM and QFT are applied and investigated within the realm of the model on a geometry basis.
B. Unveiling of Dirac belt trick
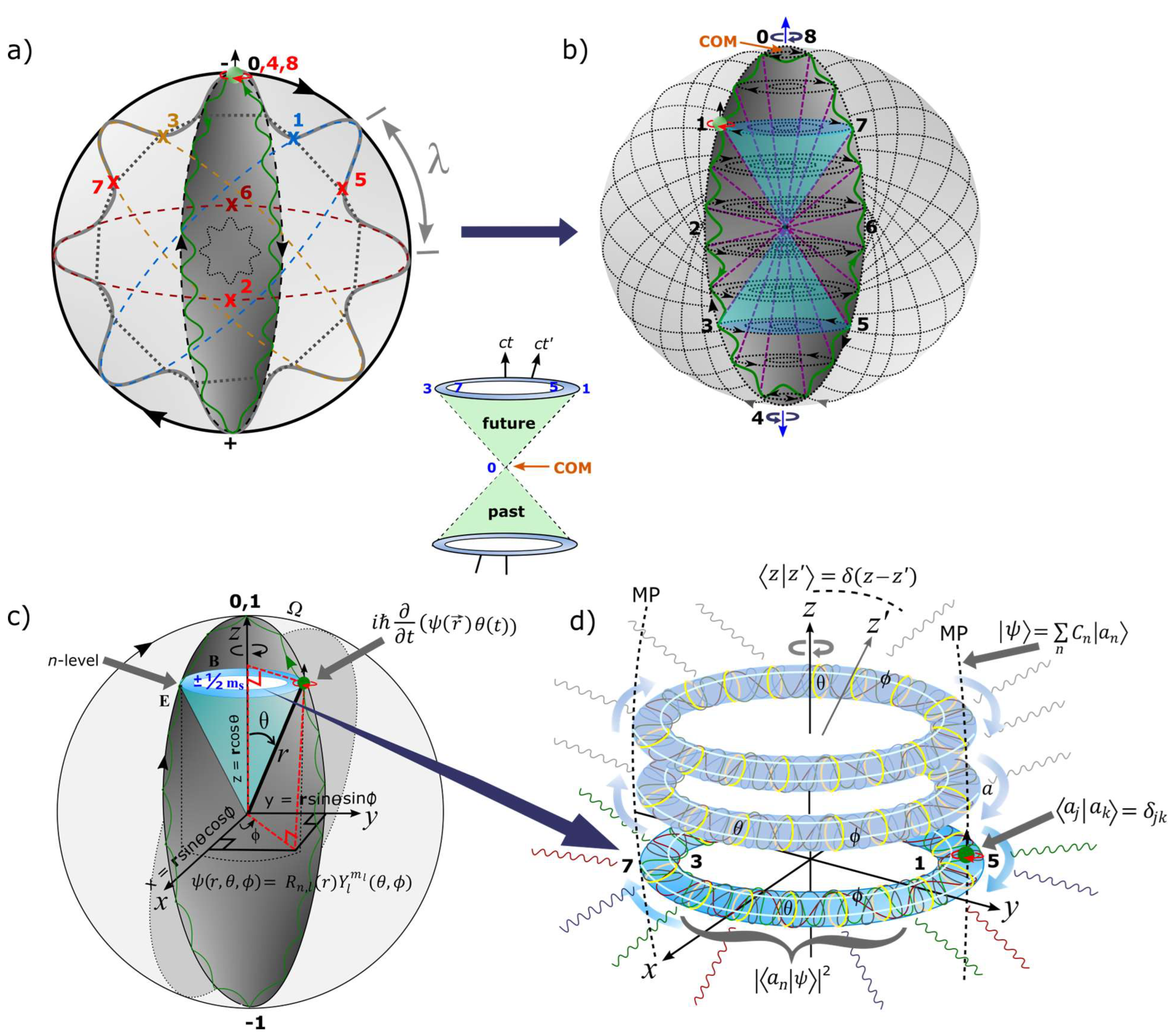
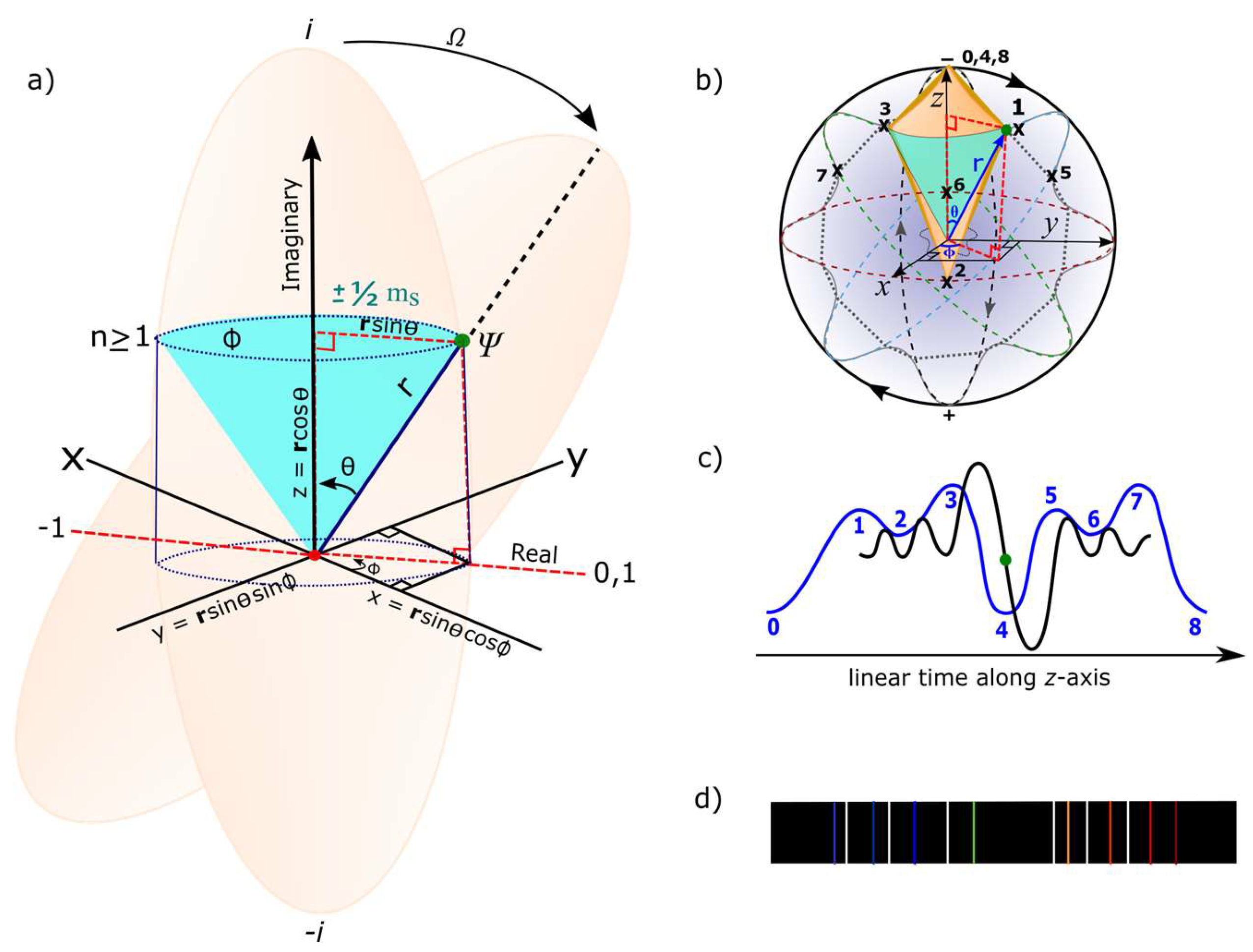
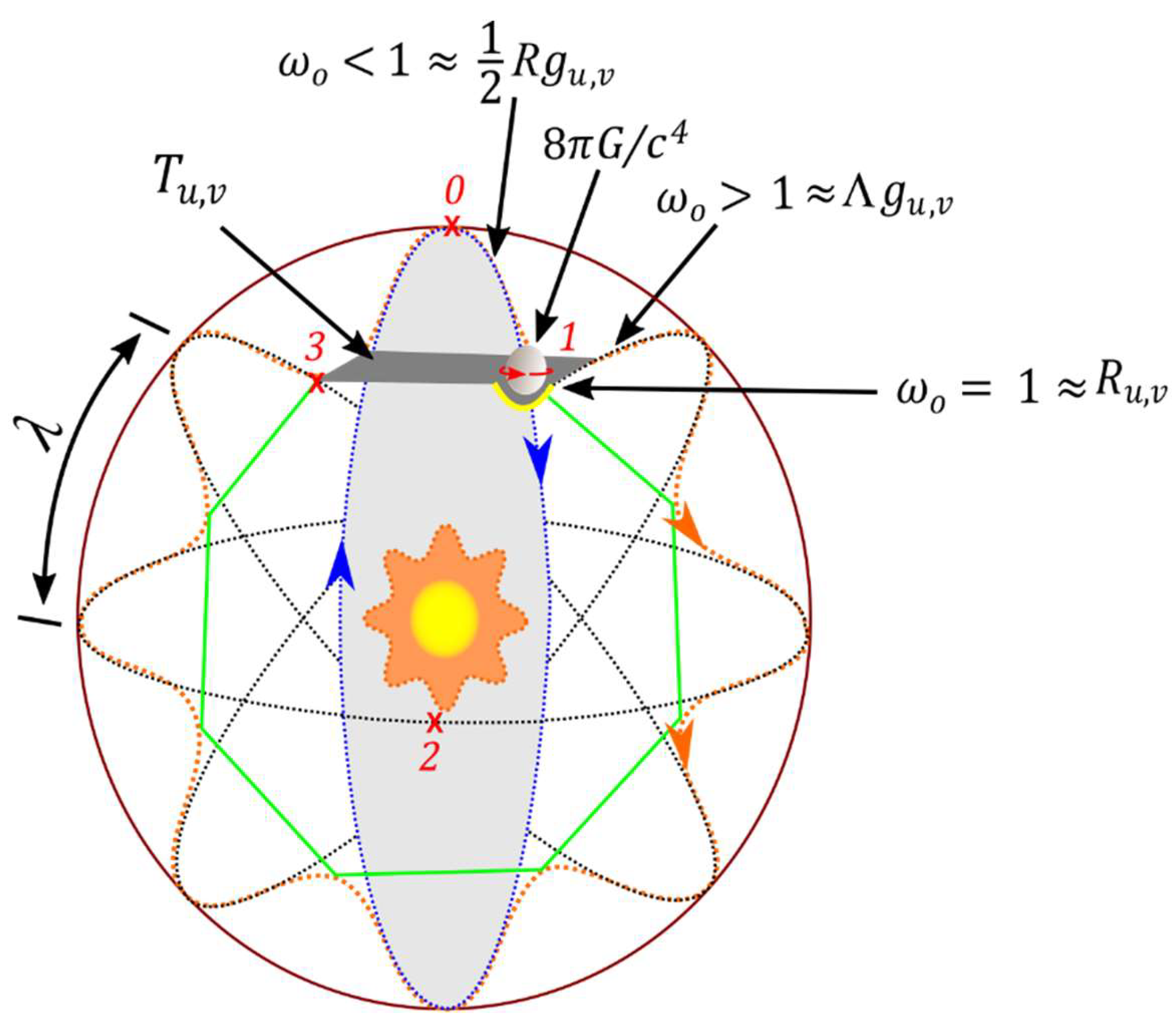
The proposed MP model and some of its main features are presented in Figure 1a–d. The electron orbit is considered of time reversal of discrete sinusoidal wave form defined by Planck constant, h. In forward time, the orbit is transformed into an elliptical shape of a MP field mimicking Dirac’s string of a small magnet (Figure 1a). The electron at the vertex mimics a Dirac monopole as quantized state of the MP field of a dipole moment by the process of DBT. Clockwise precession generates flat Euclidean space-time for the atomic state. Perturbations such as nonlinearity of differential gravitation, acceleration between two body-masses, eccentricity of the reference orbit and its oblateness, and relative motion of one-body mass in motion against the other body-mass are evident in classical planetary orbit [32] and these are considered negligible for the atomic state. Frictional force is negligible for the quantum state, while centrifugal force is not applicable to a free electron undergoing DBT. How all these apply to a MP model akin to Bohr model is explored in this subsection.
Clockwise precession of the MP field institutes the process of DBT, where the torque or right-handedness exerted on the vertex shifts the electron of spin up from positions 0 to 4 for
360° rotation. At position 4, maximum twist is attained owed to time reversal orbit against clockwise precession. The electron then flips to spin down mimicking a positron to begin the unfolding process and emits infinitesimal radiation by, E = n h v . The positron is short-lived from possible repulsion of the proton and by another 360° rotation from positions 5 to 8, it is converted to the electron and restored to its original state. The transition of electron-positron is restricted to a hemisphere of the MP field resembling Gaussian soliton (GS) and is interchangeable with the other hemisphere. There is a time lap for the electron transition to positron between the GS pair and this adheres to both Born’s rule of square modulus of the wave function, ψ 2 and Pauli exclusion principle for the ground state, n = 1. These intuitions are relevant to DBT with Dirac four-component spinor, ψ 0 ,   ψ 1 , ψ 2 ,   ψ 3 given in Equation (4) assigned respectively to positions 0, 1, 2, 3 for the emergence of real particles from continuous shift in the electron’s position in orbit. The z-axis of quantum time at COM for electron-positron transition point aligns with ψ 0 and the interchangeable GS pair can relate to both positive and negative energies of spin-up and spin-down in accordance with Born’s rule. By clockwise precession, γ u is transformed to γ θ and the components, R → , P → and χ μ are contained within the spherical MP model of 2D Euclidean space-time geometry. By relativistic transformation of time axis, z − z ' ≡ c t − c t ' , the COM assumes the point of singularity of Hilbert space into Minkowski space-time (see centered image of Figure 1a–d). The moduli of vertices by continuity of precession generates infinite Hamiltonian spaces for virtual particles, i.e., P(0→8) = ∫ τ ψ * H ^ ψ d τ with time equal to τ . These are confined to both Hermitian (GS with electron in orbit) and non-Hermitian (GS devoid of the electron) of oscillation mode into Minkowski space-time when coupled to linear light paths and is consistent with Pauli matrices. Balancing out charges at positions, 1, 3 and the conjugate positions 5,7 somehow transforms the hyperbolic surfaces of the pair of light-cones to form compact topological torus of Bohr orbit (BO). The presence of the electron of chirality offers angular momentum of a quantized state, m v r = n h / 2 π for the BO and it levitates into n-dimensions or n-energy levels between the GS pair. At COM, the magnetic dipole moment,   u is initiated into Hilbert space by DBT, where the spaces of inner product to vector to metric and topological spaces into n-dimensions are formed. The acquired angular momentum, J z of BO by rotation of space at positions 1 and 3 is relevant for the calculation of the gyromagnetic ratio or g -factor, γ = u / J z . The anomalous magnetic moment, a e = γ − 2 / 2 is forged at COM by electron-positron transition undergoing DBT. One loop correction, a e = a / 2 π is assumed at 720° rotation for the restoration of the electron to its original state. Any perturbations from the electron orbit and its transition to positron at COM is balanced out by clockwise precession in accordance with Newton’s first law. An inertia reference frame, λ is generated for COM under the conditions,
λ ± 2 = λ ± , T r λ ± = 2 ,   λ + + λ − = 1 ,
where the trace function, Tr is the sum of all elements within the model. Classically, the COM is subjected to Newton’s second law of motion, whereas its dynamics is attributed to DBT of quantum space-time and these are explored next.
C. COM reference frame and its intricate dynamics
In this subsection, the complex dynamics of COM at the spherical point-boundary of the MP model of 4D quantum space-time are unveiled from a geometry perspective.
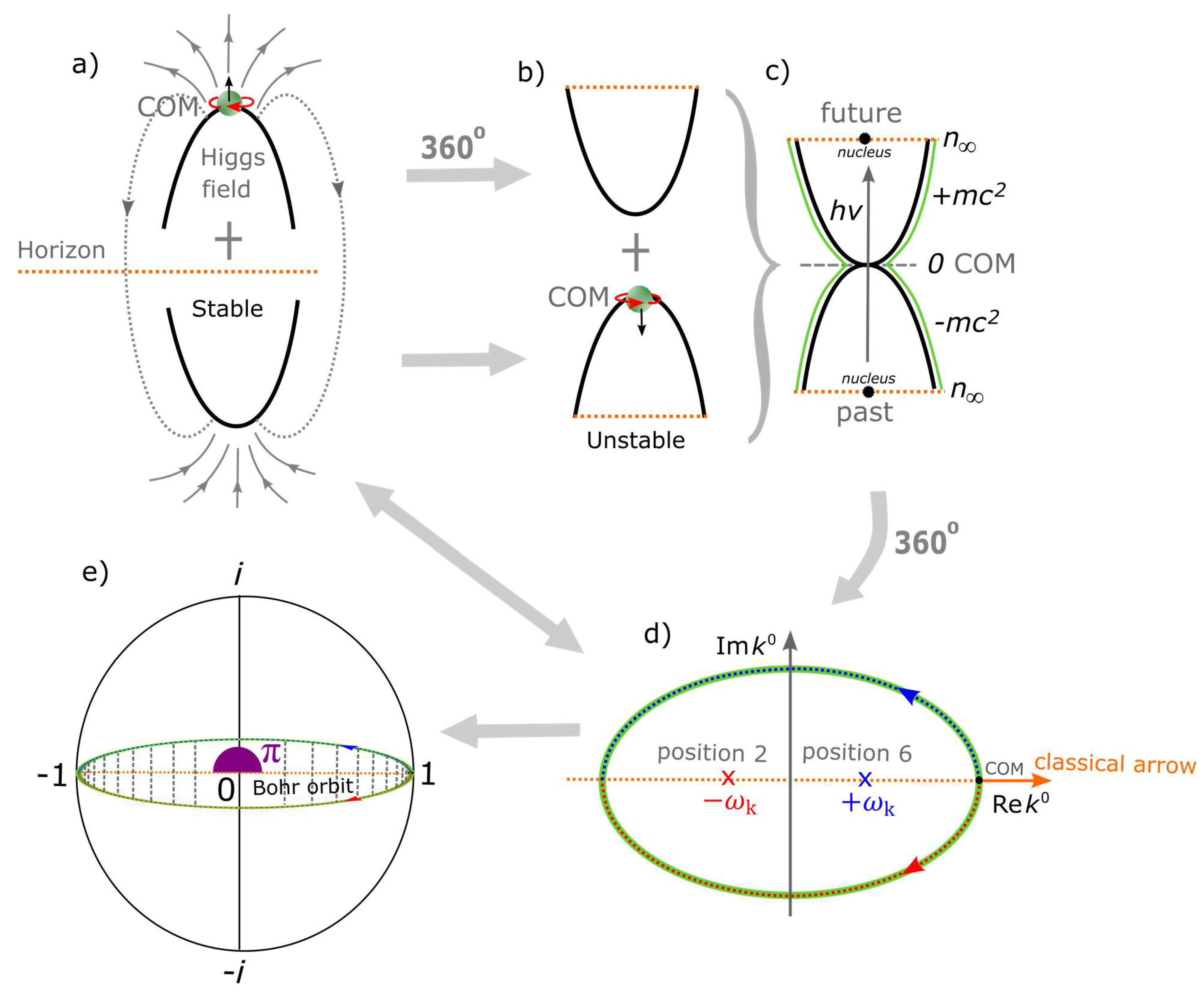
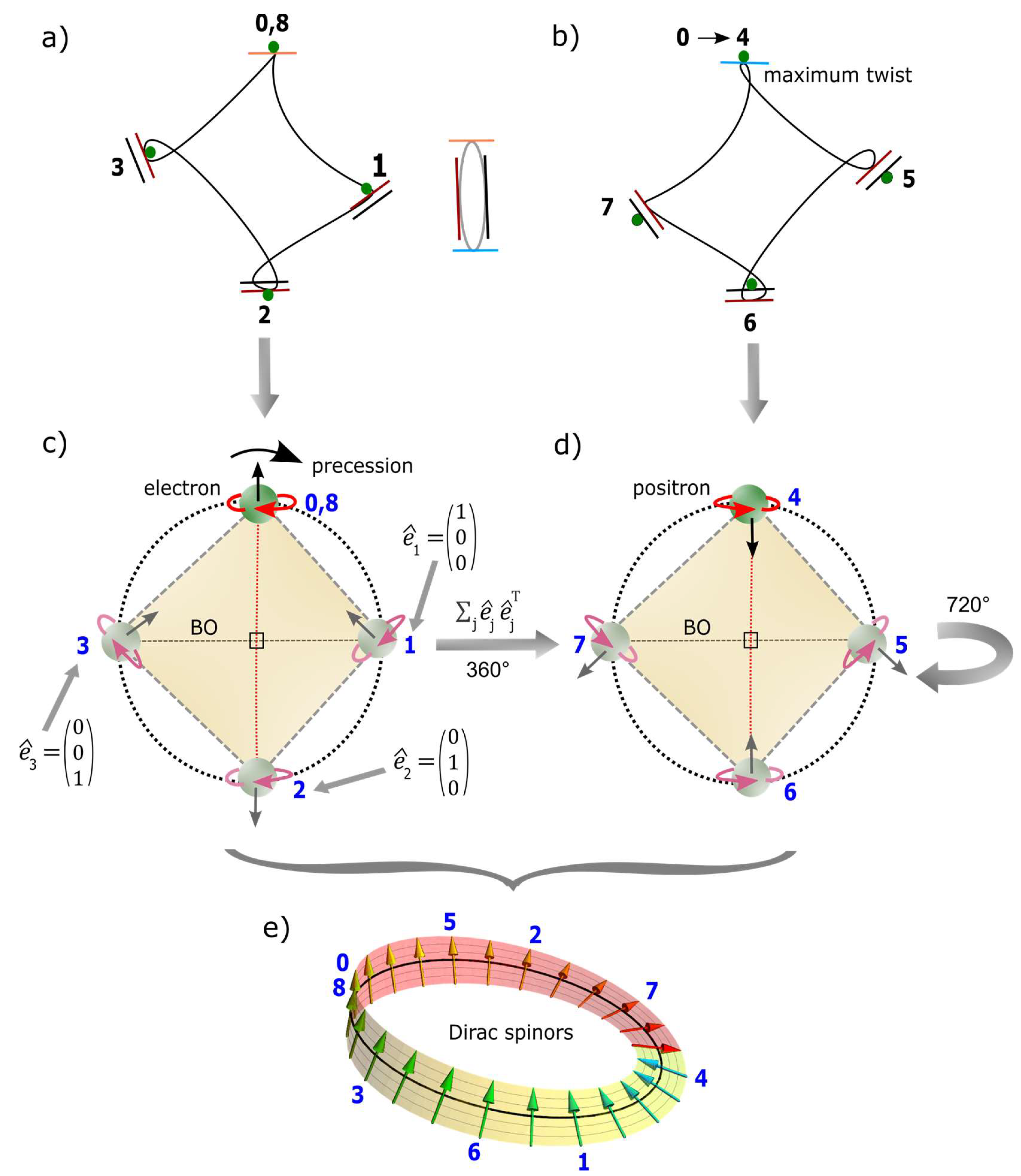
  • The COM reference frame is assigned to the vertex at the point of electron-positron transition by DBT. It also comparable to Dirac monopole or Higgs boson at Planck length, where ionization by ejection of the electron induces particle-hole symmetry of protonized form for an irreducible spinor equal to the MP field (Figure 2a). At 360° shift in the monopole’s position from positions 0 → 3 by DBT, the combined GS pair of a two Higgs doublet field becomes unstable and oscillates (Figure 2b). The COM assumes point of singularity and breaks electroweak symmetry, where particles acquire mass by, m = E / c 2 with E = n h v (Figure 2c). Another 360° rotation towards restoration of COM at the top vertex by DBT allows for the development of quark flavor and color confinement, where electron-positron transition at positions 2 and 6 (see also Figure 1a) snaps the elongated MP field of Hadron-jet like to resemble particle-hole MP model of hydrogen atom type (Figure 2d). Similarly, envelop solitons of massive Nambu-Goldstone boson types from positions 2 and 6 can relate to emergence of real particles from electron-positron transition. Combined with scattering matrix from BO into n-dimensions along the horizontal axis for linear light paths coupled tangential to the model, these are absorbed by Higgs boson at COM of singularity, r = 0 and this intercepts classical arrow of time. The overriding process of DBT at 720° allows for vertical and horizontal polarization and the produced qubits, 0, 1 and hypercharge –1 appear consistent with Euler’s identity, e i π  + 1 = 0 of a Bloch sphere (Figure 2e) (see also Figure 1c). Access to the nucleus under the natural setting, n ∞ =   ε 0 = c = ℏ = 1 becomes asymptotically weaker at increasing energy and decreasing length of BO into n-dimensions aligned horizontally to a complex plane linked to COM (Figure 2d) and this identifies with the property of asymptotic freedom. The strong coupling strength, α 5 from oscillation vanishes and quarks and gluons become free and weakly interact with each other [33]. In low energy physics, there is increase in the length of BO and this is quantized, E n = n + 1 2 ℏ ω towards infinite n-dimensions of hyperbolic surface at the interface of quantum and classical levels defined by the correspondence principle. The COM then assumes ZPE at E n = 1 2 ℏ ω for the hydrogen atom and this can become relevant to the pursuit of both Bose-Einstein and Fermi-Dirac statistics. Such interpretations appear consistent with the use of low-energy radio waves in nuclear magnetic resonance to probe quantum spin of atomic nuclei. In here, radioactive decay is not described for the MP model resembling one-electron atom of hydrogen.
  • A probable unification path for all four forces of electromagnetism, gravity, weak and strong nuclear forces is presented in Figure 2a–e. The tendency of Dirac monopole at the top vertex of Dirac’s string to transit to the bottom vertex by DBT of quantum space-time somehow breaks the electroweak symmetry. The accompanied shift in COM of Higgs boson type towards point of singularity identifies with gravity associated with Coulomb interaction, F e = k e q 1 q 2 / r 2 , with k e equal to the dipole moment of the MP field and q 1 q 2 to electron-positron transition. Nuclear interaction is not required to sustain the electron in orbit undergoing DBT with the conservation of the MP model assumed. The COM at point of singularity is coupled to any outgoing radiation, where particles acquire mass (Figure 2c). The z-axis of Planck length is equal to nuclear isospin or quantum arrow of time and it accommodates infinitesimal radiation of Planck constant, ± h with the nucleus subjected to the property asymptotic freedom described above. Local entanglement by von Neumann entropy for the polarization states of qubits, 0, 1 and hypercharge –1 (for z-axis mimicking nuclear isospin) are assigned to COM at the spherical boundary (Figure 2d) and its continuity is somewhat analogous to the holographic principle. Information output quantum tunneling along z-axis and its translation to classical linear time along horizontal axis of a complex plane at COM can become relevant to Shannon entropy for light paths coupling tangential to the MP model.
  • The first derivation of space-time for non-relativistic Schrödinger equation, i ℏ ∂ ∂ t ( ψ r → θ t ) is attributed to the position of the electron undergoing clockwise precession with respect to z-axis and the center of the model (Figure 1c). It is a fundamental equation of QM and forms the basis vectors, r → and θ for BO along x-axis and orthonormal to z-axis. The particle’s position in orbit of quantum space-time can be split into both radial and angular wave components, ψ r , θ , ϕ = R n , l ( r ) Y l m l ( θ , ϕ ) . The radial component, R n , l is attributed to the principal quantum number, n associated with BO and its angular momentum, l to a light-cone at a distance, r from the nucleus. The angular part, Y l m l of degenerate states, ± m l is assigned to the BO in degeneracy defined by both θ and ϕ of topological torus (e.g., Figure 1d). Its inner product, ψ ϕ * = ψ ϕ sustains unitary for the electron of weak isospin.
  • Linear light paths tangential to the model undergo mixing at COM as a point-spread function (Figure 2e) and this can relate to Fourier transform of both electromagnetism and Green function for signal processing [34]. In the former, the generation of electric field, ∇ . E ψ = − ∂ B / ∂ t ( ψ ) = m j ℏ ψ is assumed at the spherical point-boundary of a classical magnet, where the electron resembles a Dirac monopole, ∇ . B ψ = 0 (Figure 2a). By DBT, the solenoid loops of instantons is polarized, ∇ . E ψ = ρ / ε 0 ( ψ ) with ρ attributed to BO of n-dimensions and ε 0 to the dipole moment of the MP field. The solenoid path for the vortex electron is essential to the application of Ampere-Maxwell circuit law, ∇ . H = J + ∂ D / ∂ t . In the latter, propagators from signal processing are integral kernels of Greens function such as the wave operator, ψ = A e + i k x + B e − i k x with respect to the electron’s position and Klein-Gordon operator, ∂ μ ∂ μ ϕ = 0 in terms of BO of hyperbolic surface of the pair of light-cones (see Figure 1b–d). Mixing and output at COM can identify well with Klein-Gordon Greens function, ∂ μ ∂ μ ϕ G x − y = δ 4 ( x − y ) for massless scalar Higgs field of second-order space-time. Dirac delta function, δ 4 can relate to integration of scattering matrix of BO into n-dimensions towards COM as the point of electron-positron transition. These are sine wave function consisting of both homogeneous and inhomogeneous waves. The former by spherical boundary of GS pair and the latter to the pair of light-cones accommodating BOs. Other applicable Fourier transforms include both invariance commutation and propagators of casual, retarded, Feynman path integral and so forth along horizontal axis of a complex plane towards classical time (Figure 2d). Similarly, spectral function for hydrogen spectrum is applicable to BO of n-dimensions that is orthonormal to linear light paths.
  • CPT symmetry for the electron of a point-particle appears invariant for both multidimensional Euclidean (Figure 1a) and 4D Minkowski (Figure 1b) space-times with z-axis equal to nuclear isospin. Electroweak symmetry breaking for combined charge conjugation and parity inversion at COM for the hyperbolic GS pair coincides with vacuum expectation value of Higgs boson (Figure 2c). Hence, the charges, H − , H 0 and H + coincide with the electron-positron transition. Because the GS pair are interchangeable, the occupied one of chirality with respect to the electron shift in position, ψ 0 ⟶ 3 can relate to either the electron or position and the unoccupied GS to either an antielectron or an antipositron. Time reversal for the electron orbit when subjected to DBT remains invariant under Lorentz transformation and this can identify with the fundamental fine-structure constant of hydrogen spectral lines in the manner [35], z − z ' ≡ c t − c t ' = t a n − 1 v / c = α . Similarly, α = e 2 / 4 π   ≈ 1 / 137 is applicable to the electron-positron transition within the GS pair. Fine-tuning of α at COM can then account for the anomalous magnetic moment, a e = a / 2 π and thus, Lamb shift. Any exponential increase in quantum perturbation from both moduli of vertices and scattering matrix all coalescing at COM for mixing and output as mentioned above (Figure 2e). Such intuition might perhaps also shed some useful insights in the refinement of Rydberg constant, R ∞ = a 2 m e c / 2 h for the hydrogen atom and thus, proton radius puzzle [36]. Similarly, the envelop solitons from positions 2 and 6 of hyperbolic surface (Figure 2c) may restrict accessibility to the nucleus and this can become important to the quest of constraining quantum critical point for Rydberg atom arrays of ferromagnets [37].
  • The electron at constant motion, mv acquires J z during its transition at positions 1 and 3 and exhibits centrifugal force, F c = m v 2 / r . It acts as a free electron with nuclear attractive force, F e = Z e 2 / 4 π ε 0 r 2 accorded to DBT at COM of position 0 and nuclear isospin to z-axis. Combining both Planck theory and Einstein mass-energy equivalence (Figure 2c) presents Broglie relationship, λ = h / m v of wave-particle duality. The sinusoidal orbit of the electron is linked to ±h and is subjected to DBT by clockwise precession. Commutation at 720° for electron-electron pair offers an inertia reference frame and this incorporates anticommutation at 360° in the form [38], a j a k = ∫ d x ψ a j * x ψ a k x = δ j k . The sum of expansion coefficients, C n , by continuity of precession gives the expectant value, ψ = ∑ n C n / a n and its probability as a n ψ 2 . Spherical light path tangential to the model is polarized along both vertical and horizontal axes (Figure 2e) and is transformed linearly in the form [39], x ' = γ ( x − v t / c 2 ) . The corresponding 1D time is, t ' = γ ( t − v x / c 2 ) with Lorentz factor, γ = 1 / 1 − v 2 / c 2 at y ' = y and z ' = z . The GS pair is Lorentz invariance under rotation, inversion and translation into space-time for x = γ ( x ' − v t ' / c 2 ) and t = γ ( t ' − v x ' / c 2 ) .
The themes described above are teasers of otherwise much complex themes. These can be further pursued by applying the model as an approximate intuitive guide. How all these align with some basic aspects of both QM and QFT on a geometry basis are explored next in order to pave the path for further investigations using conventional methods.

III. Relevance of quantum mechanics on the MP model

The attributes of QM related to the MP model is dissected into three parts. First, its non-relativistic aspect is presented ensued by its translation at observations with respect to wave function collapse and quantized Hamiltonian. These are relevant towards demonstrating the transition of non-relativistic MP model described by the electron towards relativistic QFT related to the translation of the electron to a fermion by DBT.
A. Non-relativistic wave function
From a theoretical perspective, the difference of classical oscillator to the quantum oscillator is given by both the application of Schrödinger wave equation and this forms the basis for QM. However, QM cannot further explain properly the combination of orbital angular momenta, spin angular momenta and magnetic moments of valence electrons observed in atomic spectra [40]. Similarly, how both integers to half-integers spins are accommodated by relativistic transformation of the electron remains oblivious in QFT interpretations. How the distinction could be made from a geometry perspective including the translation from QM to QFT are demonstrated in Figure 2a–e. How this can be modelled to align with the energy shells of BOs at the n-levels is explored in this subsection on a geometry basis. 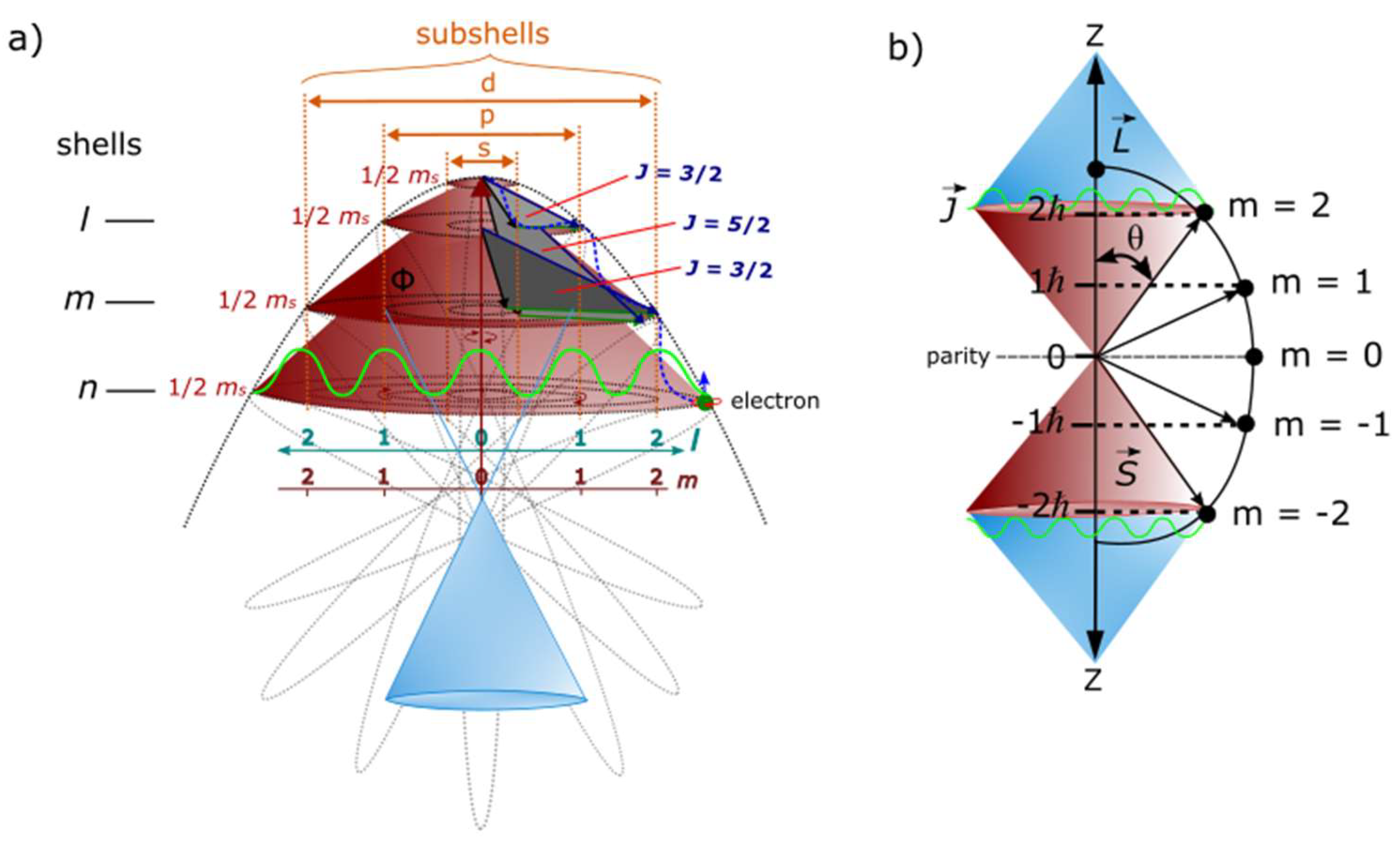In Figure 3a, the levitation of BO into n-dimensions for complex fermions of ±1/2, ±3/2, ±5/2 and so forth is demonstrated. This
extends towards the boundary of the hyperbolic surface for the GS pair dissecting the nucleus (Figure 2c). Perturbation by oscillation is quantized and the emergent light-cones are of superposition states (Figure 3b). The spin angular momentum can be calculated based on both Russell-Saunders orbital-spin (L-S) coupling and Clebsch-Gordon series. The eigenvalue of total angular momentum is, J → = l → + s → for orbitals in 3D combines eigenvalues of both orbital angular momentum, l and spin angular momentum, s (Figure 4a). The magnitude of l then takes the form,
  L = L n L n + 1 ℏ ,
where n-dimension is linked to the subshells and ℏ to GS pair of 2π and the electron orbit defined by h as mentioned earlier in the preceding section. The resultant orbital angular momentum L is by combination of ∑ l i in a complete loop of BO and it includes the degenerate states, where the values such as 0, 2 ℏ and 6 ℏ are respectively generated at n = 0, n =1 and n = 2 (Figure 3b). Their projection about z-axis for an irreducible spinor of the MP field of Dirac’s string becomes,
L Z = M L ℏ .    
Equation (12c) is applicable to the hyperbolic surface of a light-cone of Minkowski space-time. In vector space with z-axis equal to quantum time, L z is translated to J Z of the form,
J Z = m l ℏ ,  
where m l can take (2l + 1) values as eigenfunciton of M L (Figure 4b). So for n = 2, l = 1,
this is split into s and p orbitals and each one accommodating ±1/2 spin from the electron-positron transition by DBT. The total angular momentum, J → = l ± 1 2 , equates to 3 2 and 1 2 . If applied to Figure 3a, the summation of spin, 1/2 + 1/2 + 1/2 from combined s and p subshells of n 2 + n 1 = 3 2 . In this case, both orbital and spin angular momenta are aligned in the same direction and it provides the resultant spin angular momentum, S of a light-cone with singularity towards COM. When orbital and spin are not aligned at low energy, then n 2 −   n 1 = 1 2 is of the form, 1/2 +1/2 −1/2 (Figure 3b). This is assigned to p orbital by cancelling out 1s orbital with the orientation of orbital types attributed to precession. The physical distinctions between the above parameters are provided in Figure 4a and Figure 4b and these are necessary for quantization of infinitesimal space for quantum time assumed by clockwise precession. If these are considered, the geometry of the MP model can shed some useful insights into both Zeeman effect of odd spin types and lamb shift perhaps including quantum gravity. Similarly, ± J → splitting for Landé interval rule for on-shell momentum of weak isospin is relevant to scattering matrix of BO into n-levels (e.g., Figure 2e) by continuity of clockwise precession.
B. Wave function collapse
Dirac fermion of a four-component spinor is denoted ψ(x) in 3D Euclidean space. Quantum time is trivial, z − z ' = z z ' in flat space and hidden among any of the axis applied as vertical axis such as for z-axis of the MP field (Figure 1a). The distance between two events is always positive like position 1 and 3 in space as given in the form [41],
d s 2 = d x 2 + d y 2 + d z 2 = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 + ( z 2 − z 1 ) 2 .
Once the electron gains spin angular momentum by DBT, Euclidean space-time is transformed into 4D Minkowski space-time, ψ(x,t) (Figure 1b). The hyperbolic space of the light-cone for both the inertia reference frame and accelerated reference frame is subject to Lorentz transformation of time invariance [41],
d s 2 = d x 2 + d y 2 + d z 2 − c t 2 .
Both Equations (14) and (15) appear independent of a stationary observer with respect to the electron probability distribution. The emergence of the pair of light-cones coincides with Minkowski space-time and these are dissected by z-axis of quantum time in asymmetry. Both positive and negative curvatures of non-Euclidean space are normalized to straight paths of Euclidean space (Figure 5a). The electron’s position is non-abelian and its transition to a positron by DBT generates four-component spinor and induces a dipole moment. Convergence of quantum space-time at COM is relevant to the equivalence principle for Euclidean space superimposed on the surface of the spherical MP model mimicking Bloch sphere (Figure 5b). In such a case, the quantum aspect of de Sitter space by geodetic clockwise precession is balanced out by anti-de Sitter form of the electron transition in its orbit of time reversal to allow for the development of an inertia frame. Perturbation of the model by coupling to light is initiated at COM towards the BO of hyperbolic surface into n-dimensions (Figure 2c). These are expected to translate by Fourier transform along z-axis of quantum time by wave function collapse towards COM (Figure 5c) as point-spread Green function of matter-antimatter into classical time (e.g., Figure 2d). This can accommodate scattering matrix of wave amplitudes of Fourier transform inclusive of hydrogen emission spectrum of classical time (Figure 5d). Constraining the electron’s position towards COM presents the uncertainty principle for on-shell momentum of BO into n-dimensions by levitation between the GS pair.
C. Quantized Hamiltonian
Two ansatzes adapted from Equation (3) are given by,
ψ = u p e − i p . x ,
and
ψ = v p e i p . x ,
where outward projection of electron spin is v and inward projection is u . Equations 16(a) and 16(b) relates to oscillations between GS pair from the electron-positron transition (e.g., Figure 2c). Linear transformation along z-axis of quantum time into classical time can accommodate the Hermitian plane wave solutions and this forms the basis for Fourier components in 3D space (e.g., Figure 2d and Figure 5c). Decomposition for quantized Hamiltonian is [42],
ψ x = 1 2 π 3 / 2 ∫ d 3 2 E p ∑ s a P s u s p e − i p . x + b P s † v s p e i p . x ,
where the constant, 1 2 π 3 / 2 is attributed to dissection of BOs along z-axis by linear light paths. Its conjugate is,
ψ ¯ x = 1 2 π 3 / 2 ∫ d 3 2 E p ∑ s a P s † u ¯ s p e i p . x + b P s v ¯ s p e − i p . x .
The coefficients a P s and a P s † are ladder operators for u-type spinor and b P s and b P s † for v-type spinor. These are attributed to BOs of n-dimensions of topological torus within the GS pair. The Dirac spinors of two spin states, ±1/2 with v ¯ s and u ¯ s as their antiparticles is reflected levitation of GS pair and moduli vertices mimicking COM. Dirac Hamiltonian of one-particle like in the hydrogen atom is [43],
H = ∫ d 3 x ψ † x − i ∇ . α + m β ψ x ,
where the electron, i acquires vectors of momentum, ∇ with shift in its position and gamma matrices represented by the standard Pauli matrices, α , β . Parity transformation by levitation of GS pair can provide for both observable and holographic oscillators of canonical conjugates (see also Figure 2c and Figure 3b). The associated momentum is,
π = ∂ L ∂ ψ − ψ ¯ i γ 0 = i ψ † .
For the quantum time axis assumed by z-axis of the MP field towards COM, the electric currents are projected in the x-y directions into classical time analogous to Fourier transform (e.g., Figure 2d). The projections are of the relationship [44],
ψ α x , t , ψ β y , t = ψ α † x , t , ψ β † y , t = 0 .
Equation (20a) by unitary is assumed at COM at the point-boundary. Because the electron of a physical entity is non-abelian, the matrix form for anticommutation becomes,
ψ α x , t , ψ β † y , t = δ α β δ 3 x − y ,
where α and β denote the spinor components of ψ . In 3D space independent of time, electron’s position, p and momentum, q, of conjugate operators commute by,
a P r , a q s † = b p r , b q s † = 2 π 3 δ r s δ 3 p − q .
Equation (21) relates the uncertainty principle to the MP model, where the electron pops in and out of existence within the space of GS pair with observations of real particles applicable to positions 1 and 3. The GS type devoid of the electron is interchangeable with its counterpart so that only positive-frequency is generated into classical time such as [45],
0 ψ ( x ) ψ ¯ ( y ) 0 = 0 │ ∫ d 3 p 2 π 3 1 2 E p ∑ r a p r u r p e − i p x
× ∫ d 3 q 2 π 3 1 2 E q ∑ s a q s † u ¯ s q e i q y │ 0 .
Equation (21) implies to the dominance of matter over antimatter for the spinor attributed to the electron shift in positions, ψ 0 ⟶ 3 . Whether this can accommodate electroweak baryogenesis for the MP model acting as microcanonical ensemble remains an open question with its compatibility to Higgs mechanism demonstrated earlier (see subsection IIc).

IV. Relevance of quantum field theory on the MP model

Extending from the preceding section on QM, this section explores the relevance of QFT on space-time geometry of the MP model by exemplifying some of its components like Dirac spinors, Weyl spinors and Majorana fermions including Lorentz transformation. These are succinctly explored based on ref. [3, 6, 44 and 45] in order to pave the path for future researches by having the model as an approximate intuitive guide.
A. Dirac spinors
The emergence of the spinor field from DBT for the electron-positron transition of a physical entity has been demonstrated in Section II with respect to Figure 1a–d. In here, the process is further elucidated by pictorial demonstrations. The helical spin property of the electron is assumed by DBT, where the MP field of Dirac’s string is warped and unwarped from twisting and unfolding processes (Figure 6a and Figure 6b). The particle provides chirality for the GS pair and when the electron orbit is against clockwise precession, negative helicity or left-handedness is assumed (Figure 6c). When the orbit is aligned to precession, positive helicity or right-handedness is generated (Figure 6d). At COM of Higgs boson type, both helicity and chirality are combined and there is no distinction between them (e.g., Figure 2c). The process of DBT is attained within the GS pair of an irreducible spinor of spherical geometry (Figure 6e) and it incorporates Euler’s formula for both hyperbolic and parabolic complex numbers with respect to the electron’s position in orbit (see also Figure 2e). Components of Pauli matrices, i ,   0 ,   − 1 ,   1   for the sphere are distinguishable to Dirac matrices related to the electron shift in position, ψ 0 → 3 by DBT. 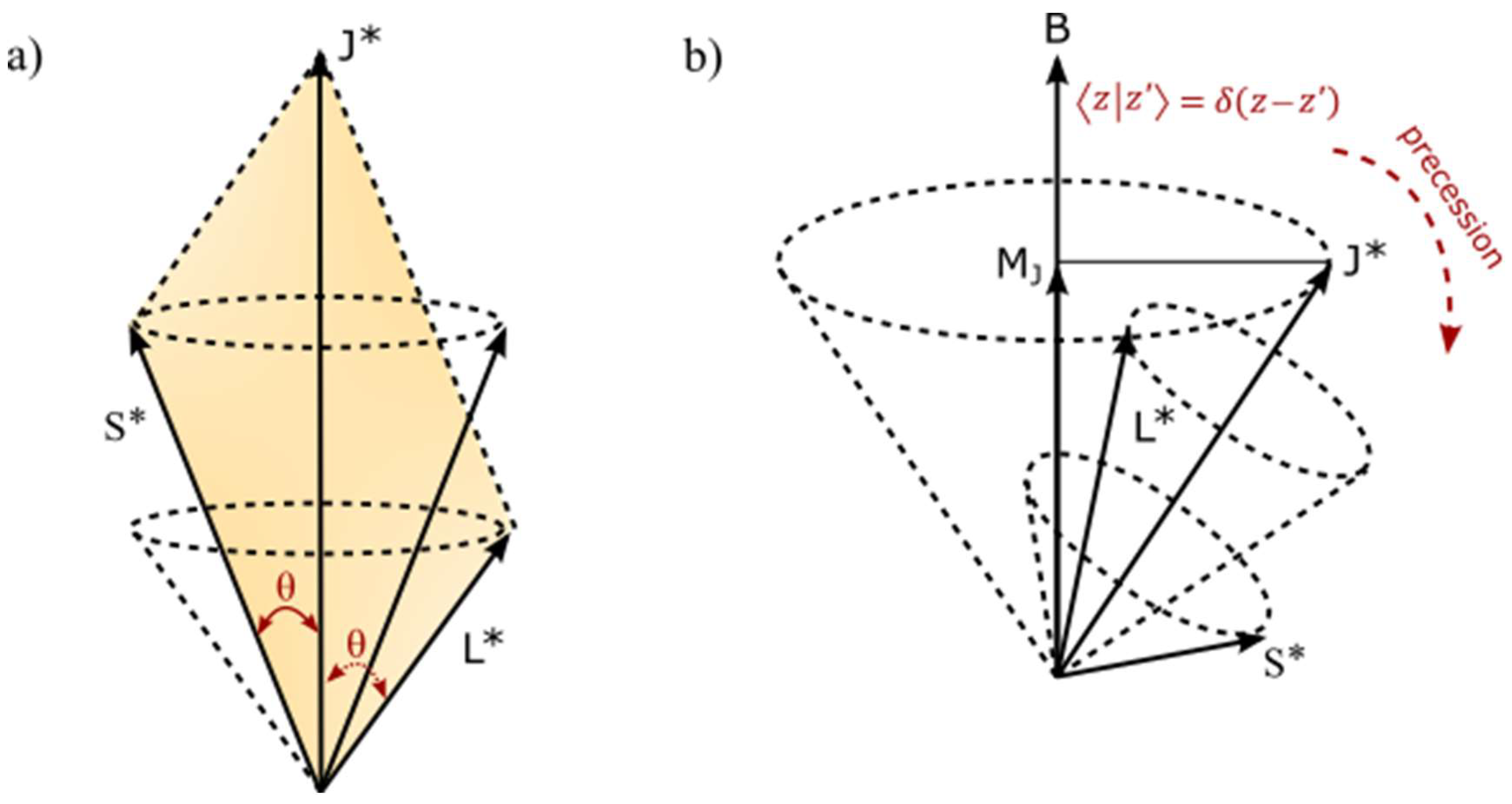In the former, the matrices are traceless [6], Hermitian and of unitary with determinant –1 and satisfy the relations ∑ j e ^ j e ^ j T = e i e j = c i j k e k for Euclidean space. This describes the transposition of spin angular momentum, j to a superposition state of electron-positron pair, i at COM. The outgoing signal at angular frequency, ω 2 = k / m has expansion coefficients, c i j k and unit matrices, e ^ k (see also Figure 2d). Discreet symmetry breaking of C, P, T or a combination of any of its pair is assumed by separation of both chirality and helicity from COM at 360° rotation by DBT (e.g., Figure 2c). At 720° rotation, the model is restored and this sustains combined CPT symmetry. Thus, the GS accommodating either the electron or positron during transition can
relate to actual particle and its counterpart to either an antielectron or an antipositron. These intuitions are incorporated into Dirac equation in the extended form,
i γ 0 ∂ ∂ t + c A ∂ ∂ x + c B ∂ ∂ y + c C ∂ ∂ z − m c 2 ℏ ψ t , x → ,
where c acts on the coefficients A, B and C and transforms them to γ 1 ,     γ 2   and γ 3 with respect to the electron shift in position, ψ 0 → 3 . The exponentials of γ are denoted i for off-diagonal Pauli matrix for the light-cone of irreducible spinor and γ 0 to 0, 1 polarization states. Hypercharge, –1 is expected at position 4 along z-axis as nuclear isospin and σ i can relate to oscillations from on-shell momentum of BOs of topological torus into n-dimensions (e.g., Figure 1a with anticommutation relationship, e + ( ψ ) ≠ e − ψ ¯ from electron-positron transition. The associated vector gauge invariance exhibits the following relationships,
ψ L → e i θ L ψ L
and
ψ R → e i θ L ψ R
The exponential factor, iθ refers to the position, i of the electron of a complex number and θ, is its angular momentum (Figure 5a). The unitary rotations of right-handedness (R) or positive helicity and left-handedness (L) or negative helicity are applicable to the electron transformation to Dirac fermion (Figure 6c and Figure 6d). The helical symmetry from projections operators acting on the spinors are of the form,
P L = 1 2 1 − γ 5
and
P R = 1 2 1 − γ 5 ,
where γ 5 relates to I matrices (Equation (8)) based on the electron shift in positions 0 → 3 in repetition. The usual properties of projection operators like: L + R = 1; RL = LR = 0; L2 = L and R2 = R are relatable to the interchangeable GS pair accommodating the electron shift in its position and these can be further explored from a geometry perspective of a spherical atomic model.
B. Weyl spinors and Majorana fermions
Dirac fermion can be converted to Weyl spinor and possibly to Majorana fermion of a natural neutrino type. In condensed matter physics, these are pursued for an array of atoms in lattice structure for it is difficult to examine for individual atoms. Theoretically, how this is applicable to Dirac fermion incorporated by the MP model of hydrogen atom type has been demonstrated on a geometry basis in section II and are explained in here. The electron shifts in position and acquired angular momentum is related to a pair of light-cones of Minkowski space-time (Figure 1b). In this case, the four-component spinor, ψ 0 ⟶ 3 is reduced to two-component bispinor of the form,
ψ = ψ 0 ψ 1 ψ 2 ψ 3 = u + u − ,
where u ± are Weyl spinors of chirality with respect to the electron’s position. Because only spin up and spin down fermions are observed in experiments from occupied GS by squared amplitude (i.e., ψ 0 , ψ 1 ), the antifermions of both spin up and spin down ( ψ 2 and ψ 3 ) are attributed to the unoccupied GS as previously mentioned. In this case, creation and annihilation of virtual particles are attributed to the vertices of the MP field by clockwise precession with emergence of real particles at COM assigned to position 0. The exchange of left- and right-handed Weyl spinor for the GS pair is assumed by the process,
ψ L ' ψ R ' = ψ R ( x ) ψ L ( x ) ⇒ ψ ' x ' = γ 0 ψ ( x ) ψ ¯ ' x ' = ψ ¯ x γ 0 .
Equation (27) conserves local symmetry and corresponding global symmetry of Minkowski space-time by clockwise precession. So apart from Weyl spinor, Dirac fermion can further relate to Majorana fermions. In this case, the toroidal moments of BO of topological torus by linearization towards COM can translate to Majorana types (Figure 1d and Figure 2e) with moduli of vertices to creation and annihilation operators γ E ,   γ † ( E ) . At Fermi level γ 0 ≡ γ = γ † assigned to COM, the ejected fermion is promoted to the conductance band higher n-dimension. Comparable to Greens function (see subsection IIc), the anticommutation relation for the Majorana is of the form [47],
γ n γ m + γ m γ n = 2 δ n m .
The product of Equation (28), γ n 2 = 1 is assumed at a potential well assigned to COM (e.g., Figure 2c) and the value can equate to a bosonic field of qubits, 0 1 such as for the Higgs field. Thus, if Majorana fermion naturally resemble neutrino, the COM exerts gravitational force and there is no barrier to the passage of neutrinos along z-axis as quantum time towards the classical scale.
C. Lorentz transformation
The Hermitian pair, ψ † ψ for the electron-positron transition undergo Lorentz boost in the form,
u † u = ( ξ † p . σ , ξ p . σ ¯ . p . σ ξ p . σ ¯ ξ ,
= 2 E P ξ † ξ   .
The conversion of Weyl spinors to two component Dirac bispinor, ξ 1   ξ 2 = 1 of transposition state is normalized to COM. The corresponding Lorentz scalar for scattering from on-shell momentum of BOs is,
u ¯ p = u † p γ 0 .
Equation (30) is related to combination of z-axis to classical arrow of time and is relevant to Fourier transform into linear time. By identical calculation to Equation (29), the Weyl spinors of chirality due to the electron’s position are of the form,
u ¯ u = 2 m ξ † ξ .
The acquisition of mass at COM is applicable to Higgs boson (e.g., Figure 2c) and the GS pair makes it difficult to distinguish Dirac spinors from both Weyl and Majorana types. All these demonstrations relate to the multifaceted dynamics of the MP model and this can also be applied to pursue other related aspects of QFT.

V. Space-time geometry of the MP model

General relativity portrays framework of space-time fabric in 3D flat Euclidean space. It is bend by the gravitational force exerted between two bodies at a distance, one heavier than the other. The force becomes weaker when the distance is increased and is inversely proportional to the square of the distance that separates the centers of two bodies. From these intuitions, the field equations describing both space-time and matter fields breaks down at singularity and requires renormalization process for long distances. By assigning COM to the spherical point-boundary and its transition to the center by perturbation from DBT, this can cater for gravity without inferring to smaller infinitesimal forms (see subsection IIc). How this is applicable to a multiverse of the MP models at a hierarchy of scales is examined in this section. First, an irreducible space-time fabric of an elliptical orbit mimicking MP field is plotted. Second, its relevance to Lie group is unveiled ensued by descriptions of 2D manifolds into 4D space-time. Third, a brief outlook of how a body-mass in orbit curves space-time and its path dictated by clockwise precession of the MP field are described. Such demonstrations are expected to offer an alternative version to general relativity and forge possible links between high energy physics and condensed matter physics on a geometry basis.
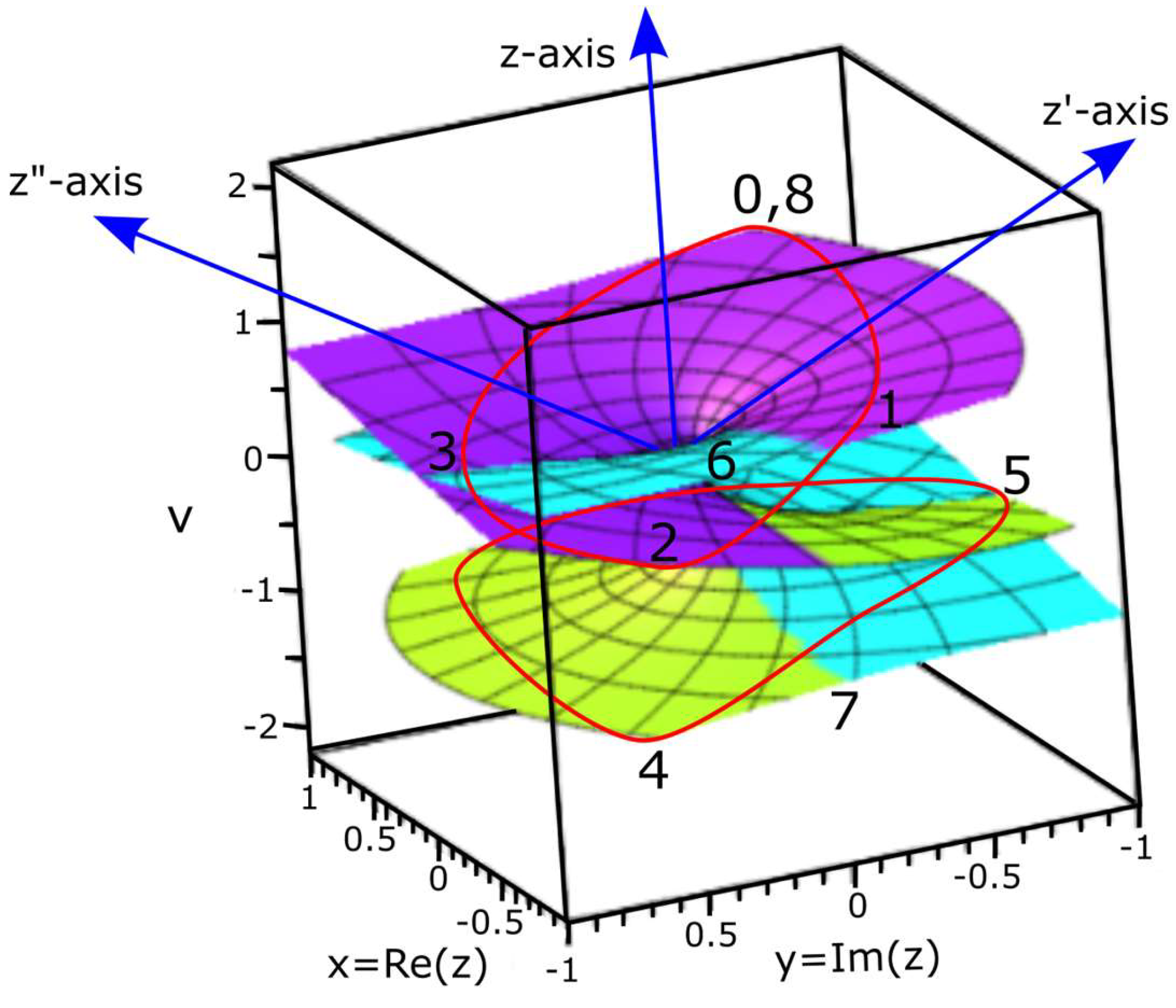
A. Space-time fabric of an elliptical orbit
The framework of space-time fabric in an elliptical orbit is warped and unwarped for a GS pair subjected to DBT. A body-mass like a vortex electron on helical solenoid path between a pair of light-cones can resemble Riemann surface (Figure 7). The Cartesian coordinates of space-time, t, x,
y, z are assumed by spherical polar coordinates is, δ z − z ' = c t , r ,   θ , ϕ and this demonstrates the transition of Euclidean space-time to Minkowski space-time (e.g., Figure 1a and Figure 1b). In the former, the clock face background is projected in flat space of n-dimensions ≥ 1 akin to Bohr model of hydrogen atom with distance between any two points being positive. In the latter, space-time is dynamic and a body-mass at a distance, r of n-dimension acquires angular momentum, θ with respect to z-axis as quantum time. The associated rotation of degenerate BO is attributed to ϕ. The basis vector, r and θ for time-distance relationship are projected to x-y plane (Figure 8). The plane wave solution, e r θ = c o s θ + r s i n θ is attributed to the spherical boundary (e.g., Figure 2e). Access to singularity at the nucleus is constrained by infinite hyperbolic surface of the GS pair of a complex plane. The generated Riemann surface incorporates both Ricci scalar and Ricci tensor. Its associated magnetic field of helical solenoid becomes,
B = μ ( γ θ ∂ ϕ ) ε L ,
where μ is permeability of space, γ θ ∂ ϕ depicts BOs of n-dimensions, ε is electric current linked to the electron path and L is length of extension between the vertices or poles of the MP field. Under the natural setting, n ∞ =   ε 0 = c = ℏ = 1 , then R μ ν = 0 . From singularity at COM, the emergence of positive curvature, R μ ν > 0 and negative curvature, R μ ν < 0 are linked to the GS pair of oscillation mode (e.g., Figure 2c). Contraction by Pauli matrix from the vortex electron of a helical solenoid is given by [49],
R α β ≡ R γ α γ β , R μ , ω ≡ R α β μ α ω β ,
where the electron emergence at positions 1, 3 tangential to BO is defined by μ α ω β and coupling to light becomes traceless,   R α β = 1 unless it is derived from the COM. Vertical extension along z-axis towards the point-boundary sustains the relationship,
R ≡ g α β R α β ,
where g is subset of space applicable to the metric tensor field and R is Ricci scalar. The combined metric of the two space-time spheres of Euclidean and Minkowski, S2 is,
d s 2 = d θ 2 + s i n 2 θ d ϕ 2 .
Another rotation of COM about the spherical boundary dictates both space-times (e.g., Figure 2e). Comparable to Pauli matrices, the coordinates θ , ϕ are ordered into the forms,
g i j = 1 0 0 s i n 2 θ , g i j = 1 0 0 1 s i n 2 θ .
Equation (36a) has discreet non-zero Christoffel symbols such as,
Γ ϕ θ ϕ = c o s θ s i n θ , Γ ϕ ϕ θ = − c o s θ s i n θ .
Equation (36b) is for the basis vector, e → θ and e → r of continuity in space-time within a sphere and this is subjected to Fourier transform at COM for outgoing radiation (e.g., Figure 2d). These brief illustrations unveil the basic aspects of general relativity applicable to the model. Such a scenario is applicable to a body-mass in an elliptical orbit and this is explored later towards the end of this section. But first, the relevance of the Lie group ladder operators,   G ( g ) and G ^ ( g ^ ) of both 3D space and 4D space-time for the quantum model are examined.
B. Internal structure by Lie group representation
The rotation matrices of the type, R r y z ( θ ) and R z x ( θ ) for the spherical MP model (e.g., Figure 1c) are attributed to clockwise precession of the MP field. The precession stage is referenced to the original z-axis at position 0 such as, z z ' = δ ( z − z ' ) and this translates to linear time as plane wave solutions. The rotation matrix, R x y ( θ ) intersects BO defined by ϕ into n-dimension. These matrices are relevant to describe both integer and half-integer spins like, 0, 1/2 and 1 towards complete rotation at COM of the spherical point-boundary. How all these are applicable to the Lie group by Lorentz transformation are explored based on refs. [49,50] with respect to gauge symmetry representation (e.g., Figure 2e).
The chirality of the electron of non-abelian in a symmetrical MP field is described by,
g ∈ G ,
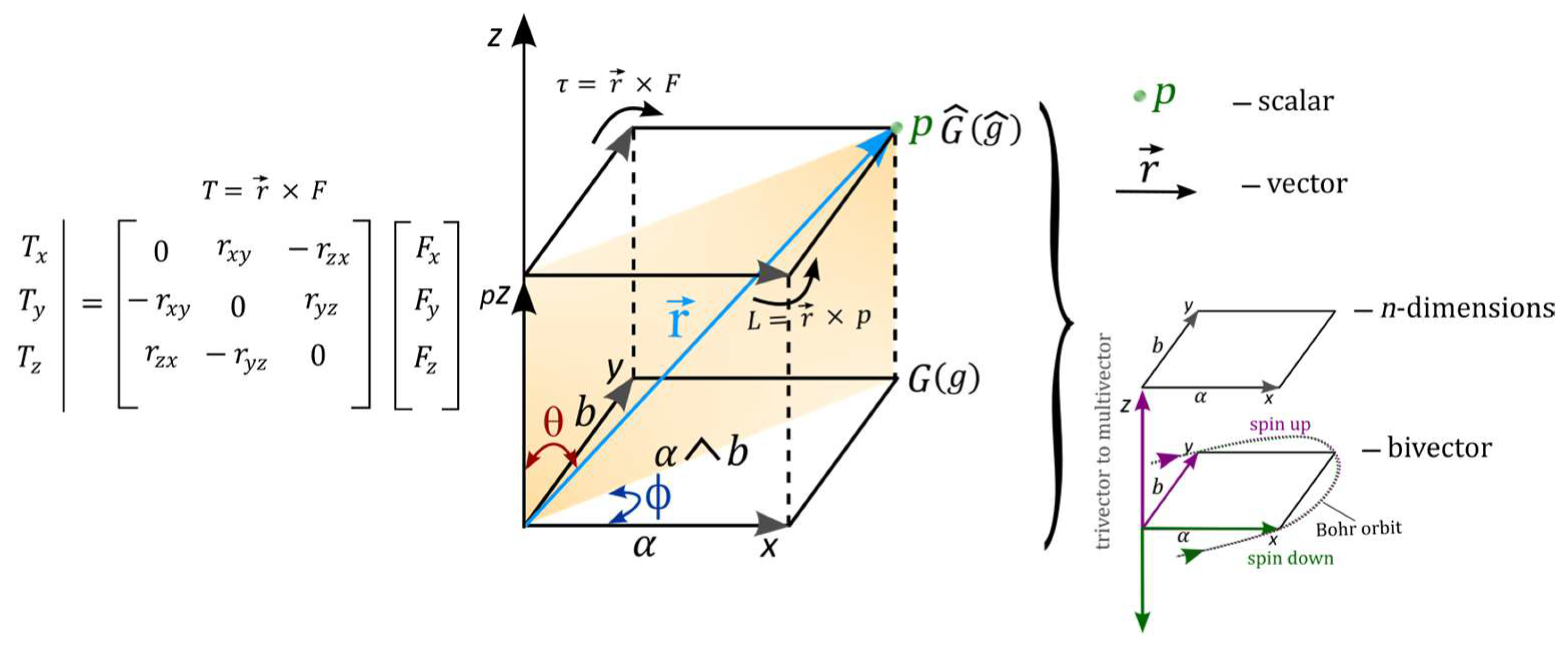
where g is electron’s position at subset of space tangential to the manifolds of BOs and G represents the Lie group (Figure 8). For the conjugate positions pairs, 1, 3 and 5, 7 of BO (Figure 1d), contravariant of space expansion by rotation, γ θ at spherical lightspeed is balanced out by covariant measure, ∂ ϕ to induce a hyperbolic geometry so Equation (37) validates the operations,
g 1,5 + g 3,7 ∈ G
and
g + − g = i
where i is spin matrix for both spin ±1/2 mimicking the electron path between the GS pair. Anticommutation, g 1 + g 3 ≠   g 5 + g 7 from electron-positron (±   g ) transition is transient and is linked to radiation loss, E = n h v tangential to the manifolds of BO. It is overridden by commutation of electron-electron assuming its original state at the completion of DBT. For linear transformation along z-axis in 1D space, the hyperbolic surface of the light-cones are compacted to isomorphic BOs with respect to the particle position, ψ = ∑ n C n / a n (e.g., Figure 5c and Figure 8).
By intermittent precession, the inner product of r is a scalar and relates to COM at the boundary of the MP field in the form,
r → 1 . r → 2 = r → 1 r → 2 c o s θ
where rotation of both vectors preserve the lengths and relative angles (e.g., Figure 1c). By assigning rotation matrix, R to Equation (39), its transposition becomes,
R r 1 T R r 2 = r 1 T r 2 I ,
where the identity matrix, I = R T × R by reduction and compaction of vector bundles is assumed in homogenous spaces (Figure 8). Any form of inhomogeneity is expected from the electron position linked to a pair of light-cones. The rotation by r → is a four 3-fold axis in 3D and its matrices are defined by the Cartesian coordinates, x, y and z. These are linked to the shift in both θ and Φ as double cover of SU(2) for vector to multivectors and are assigned to BOs of n-dimensions. The bivector field resonates with z / p z of integers modulo p of prime and this can relate to the vertices of the MP field at clockwise precession. The isomorphic cubes undergo Fourier transforms along z-axis and these are combined to classical time at COM (e.g., Figure 2d). The process coincides with vertical and horizontal polarization of the spherical model. In this case, both forward and backward transforms can be performed on the rotational matrix of the tensors for Levi-Civita connection, e ^ θ = e ^ r as basis factors for any changes of square infinitesimals, d θ = d r .
For the ladder operators of BO into n-dimension along z-axis such as the topological torus (Figure 1d), SU(2) becomes irreducible with shift in both θ and ϕ of the type, S U ( 2 ) n × n ≠ S U ( 2 ) l × l ⨁ S U ( 2 ) m × m . Translation of SU(2) by S U ( 2 ) 2 × 2 ⨁ S U ( 2 ) 2 × 2 to SO(4) somehow resembles the emergence of Dirac spinor within the MP model. The particle’s position, when y = 0, z = x is a real number with the imaginary number at x = 0, z = y (see also Figure 2e and Figure 5a). The BO for SO(2) group in 2D is of the form [6],
c o s θ s i n θ − s i n θ c o s θ ≅ 1 θ − θ 1 = I + θ 0 1 − 1 0 ,
where, θ ∈ [ 0,2 π ] is related to the GS pair accommodating electron-positron transition by DBT. Similarly, the orthogonal relationship of BO aligned to classical time suggests, R ∈ S O ( 3 ) . The SO(3) group rotation for integer spin 0 or 1 in 3D space can be expanded into a series such as,
Π μ g ϕ = Π μ c o s ϕ − s i n ϕ 0 s i n ϕ c o s ϕ 0 0 0 1 = ± e i ϕ 2 0 0 e − i ϕ 2 = R x y ϕ
and
Π μ g θ = Π μ 1 0 0 0 c o s θ − s i n θ 0 s i n θ c o s θ = ± c o s θ 2 i s i n θ 2 i s i n θ 2 c o s θ 2 = R y z θ .
Similar to Equation (42a), when rotating as 2 x 2 Pauli vector for SU(2) symmetry, Equation (42b) is reduced to the form,
± c o s θ 2 i s i n θ 2 i s i n θ 2 c o s θ 2 = z x − y i x + y i − z = ξ 1 ξ 2 − ξ 2 ξ 1 ,
where ξ 1 and ξ 2 are Pauli spinors of rank 1 to rank 1/2 tensor relevant for Dirac matrices (see also Equation (29)). Equation (42c) considers the electron orbit of time reversal against clockwise rotation (–) and in phase for positron (+) towards the generation of the helical property (Figure 6c and Figure 6d). The relationship, R x y ( ϕ ) = e θ   from Equation (42a) relates to the polarization states, 0, 1 at COM by continuum of clockwise precession (e.g., Figure 2e). The related matrix is,
e θ 0 − 1 0 1 0 0 0 0 0 = c o s θ − s i n θ 0 s i n θ c o s θ 0 0 0 1 .
Equation (43) is applicable to Fourier transforms of z-axis orthonormal to classical time. The resultant shift in the position of the electron is accorded to the form,
Π ν g ψ = Π ν c o s ψ 0 s i n ψ 0 1 0 − s i n ψ 0 c o s ψ = R z x ψ .
For the irreducible representation, Π , the algebraic relationship is,
ρ g = Π g ^ ,
where ρ is composed of algebraic structure ( p z , + p and x p ) for vectorization, V into p-dimensional space defined by α ∧ b of BO space (Figure 8). The two operators, T a and S a acting on V are of the forms,
T a f b = f b − a
and
S a f b = e 2 π i a b f b ,
where T is identified by the rotational matrices, T = r → × F (Figure 8) and S a is the shift in frequency in space by outsourcing from COM (e.g., Figure 2d). In this case, the following relationship can be forged between the identity matrix I of quantum mechanics and metric tensor of general relativity such as [6],
g r θ = 1 0 0 r 2 ≡   I = 1 0 0 1 ,  
where g r θ =   g v → . ω → is for speed, v by rotation and ω = 2 π / τ for angular frequency. The discrete Christoffel symbols, Γ r θ r or Γ θ r θ and their variations by, g r θ are applicable to a body-mass in an elliptical orbit of 2D and 3D with respect to BO. By precession, both the metric and stress-energy tensors appear symmetric so that g μ v = g v μ and T μ v = T v μ . Each one of them requires 10 independent components from 4 x 4 matrices and these can be applied to MP model of quantum space-time. The relationship between the two in a rest frame is given by [51],
g v μ = k T v μ = η α β
where k = 8 π G / C 4 is Einstein constant and η α β is Minkowski space-time (Figure 1b). The space-time metric, g v μ is incorporated into the two space-time spheres comparable to Equation (35) in the form,
d s 2 = g μ v d x μ d x ν ,
where μ ν = 0,1 , 2,3 . The relevance of the indices for the electron path suggests that T v μ is the result of the presence of a body-mass in an elliptical orbit. Its matrices are of the generalized form,
T μ ν = T t t T t x T x t T x x         T t y T t z T x y T x z T y t T y x T z t T z x         T y y T y z T z y T z z .
Equation (50) can be dissected as follows [52]. Energy density, T t t is attributed to twisting and unfolding process of the electron-positron at COM by DBT The momentum density, T x t   T y t   T z t or T t x   T t y   T t z for the plane wave solutions is referenced to orthonormal combination of quantum time to classical time for quantized Hamiltonian (e.g., Figure 2d). Shear stress like the rate of change in x-momentum in the y-direction is given by T x y and for y-momentum in the z-direction by, T y z and so forth. These identify with diagonal invariant rotation of the x-y plane (Figure 8). The plane is part of the four 3-fold rotational axes for a body-mass at a lattice point of a cube defined by x, y, z coordinates. In a cube, there are also three 4-fold rotational axes on the faces and six 2-fold rotational axes at the edges. The negative pressure force, T x x   T y y   T z z directions are balanced out between the GS pair. Similarly, the matrix for η α β is,
η α β = 1 0 0 − 1               0 0 0 0 0 0 0 0       − 1 0 0 − 1 .
By combining both Euclidean and Minkowski space-times, the relationship, η α β = T μ ν is forged within the spherical MP model for the rest mass assumed at COM (see also Figure 2e). So a body-mass of superposition state by homomorphism is separated to two points of oscillation mode in general agreement with gravity (e.g., Figure 2c). How all these become relevant to a multiverse of the MP models at a hierarchy of scales is explored next for a planet in orbit of the solar system.
C. Space-time curvature
Based on the descriptions of geometry offered for the MP model, an alternative interpretation of Einstein field equation described in ref. [31] is reproduced in Figure 9 for the planetary model in a multiverse. How this can accommodate perturbations from nonlinearity of differential gravitation
acceleration, eccentricity of the reference orbit and its oblatenes in addition to the relative motion of the planet against the sun’s gravity appears to be more complex phenomena [32]. These are not covered in here. However, by assigning gravity to COM, some of these perturbations can relate to the process of DBT assumed at a higher hierarchy of scales in a multiverse of the MP models. This is demonstrated later to explain the anomalous Mercury’s perihelion precession. In an elliptical orbit subjected to clockwise precession, its curvature of space-time does not require framework of space-time fabric into smaller infinitesimal forms. Instead the time reversal orbit of Earth, ψ is balanced out by clockwise precession of the elliptical orbit to generate an inertia frame at the spherical boundary. The Earth’s orbit towards the vertex of the MP field of COM, it forms an aphelion with respect to the sun. At positions 2 and 6, the planet will appear perihelion to the sun. The COM is applicable to Newton’s law of gravity, F = G m 1 m 2 r 2 . The planet of a scalar quantity resembles Higgs boson at COM without requiring attractive force of the sun (e.g., Figure 2c). In this case, the relationship between gravitational constant and the dipole moment, G = 1 4 π ε 0 can be applied to polarization of the spherical model of GS pair by DBT. This considers the body-masses to be distinctive in chemical compositions and are of different time frames for the planet and atom. By the same token, a multielectron atom inhibiting multiple MP fields is equivalent of a solar system accommodating multiple planets. Any infinitesimal spatial and temporal changes by precession becomes,
8 π G ∫ − ∞ ∞ d R d T d g u , v ≡ i ∫ − ∞ ∞ d Ω d ϕ d θ u , v .
Equation (52) is an alternative version of Einstein’s field equation with 1 / 2 R g μ ν λ − Λ g μ ν λ = R μ v assumed at positions 1 and 3 at the vertices of the cube (Figure 8). At the lattice points, both negative and positive curvatures are generated as demonstrated for the helical solenoid of Riemann surface (e.g., Figure 7). The reduction of Equation (52) offers approximate correspondence of the MP models in a multiverse and this is given as [31],
8 π G T μ , ν ≡ i ℏ μ , ν ,
where both T μ , ν and ℏ μ , ν   are initiated by exertion of torque at COM into Hilbert space but confined to an electromagnetic field of Dirac’s string (e.g., Figure 2a). It is important to note the string can be stretched out or contracted, whereas the monopole at COM can be of distinct mass-bodies. So in a space-time of a clock face, a body-mass dictates how precession of the MP field should progress by subjecting it to the initiation of DBT at COM. In turn, clockwise precession determines how the body-mass will progress by the process of DBT. If considered, this alternative interpretation of general relativity can possibly explain the anomalous advances observed in Mercury’s perihelion precession, which cannot be ably accounted by both Newtonian gravity and general relativity due to discrepancies observed in measurements [53]. The process of DBT at COM from matter-antimatter transition will constantly variate the continuity of how the MP field undergoes clockwise precession. Stability between the universes can be attributed to Coulomb attraction between polarized poles akin to a hydrogen molecule. In this case, the model’s applicability to counterclockwise precession such as of Uranus [54] is not addressed in here.

VI. Conclusions

The multifaceted dynamics of the MP model of 4D quantum space-time of hydrogen atom type is theoretically able to incorporate non-relativistic form of the electron described by QM to its transformation by DBT to a composite Dirac fermion pursued in QFT. The COM reference frame relevant to Newtonian gravity is assigned to the spherical point-boundary of ZPE at the vertex of an elliptical MP field of Dirac’s string undergoing clockwise precession. Similar scenario is assumed in a multiverse of the models at a hierarchy of scale such as for a planet in orbit of the sun. Perhaps, Coulomb attractive force is expected to stabilize the multiverse by polarization with the extent of the observable universe limited to an elliptical cosmic microwave background resembling a MP field. How this can accommodate black hole, cosmic inflation, cosmological principle, dipole anisotropy, dark matter, dark energy and so forth has been previously inferred [31]. Similarly, entanglement appears to be an intrinsic property for linear light paths coupling tangential to a body-mass undergoing the process of DBT in a MP model. Although the model may seem metaphysical to a certain extent to account for intricate details of actual observations for multielectron atoms, in this study, the pursuit of a representative hydrogen atom type appears consistent with basic interpretations of both QM and QFT. If considered, such a tool can guide researches into the quantum realm of both matter field and space-time fabric on a geometric basis and this warrants further investigations.

Data Availability Statement

The modeling data attempted for the current study are available from the corresponding author upon reasonable request.

Conflicts of Interest

The author declares no competing financial interests.

References

  1. Lanciani, P. A model of the electron in a 6-dimensional spacetime. Found. Phys. 29(2), 251-265 (1999). [CrossRef]
  2. Nahin, P. Dr. Euler’s fabulous formula: cures many mathematical ills (Vol. 52). Princeton University Press (2011).
  3. Thaller, B. The Dirac Equation. Springer Science & Business Media (2013).
  4. Sun, H. Solutions of nonrelativistic Schrödinger equation from relativistic Klein–Gordon equation. Phys. Lett. A 374(2), 116-122 (2009). [CrossRef]
  5. Grandpeix, J. Y. and Lurçat, F. Particle Description of Zero-Energy Vacuum I: Virtual Particles. Found. Phys. 32(1), 109-131 (2002). [CrossRef]
  6. Nicol, M. Mathematics for physics: an illustrated handbook (2018).
  7. Blinder, S. M. Pauli Spin Matrices. Wolfram Demonstrations Project (2011).
  8. Rovelli, C. Space is blue and birds fly through it. Philos. Trans. Royal Soc. Proc. Math. Phys. Eng. 376(2123), 20170312 (2018). [CrossRef]
  9. Joshi, P. S. Spacetime singularities. Springer Handbook of Spacetime, 409-436 (2014).
  10. Chanyal, B. C. A relativistic quantum theory of dyons wave propagation. Can. J. Phys. 95(12), 1200-1207 (2017). [CrossRef]
  11. Trodden, M. Electroweak baryogenesis. Rev. Mod. Phys. 71(5), 1463 (1999).
  12. S. Santos, T. R. and Sobreiro, R. F. Remarks on the renormalization properties of Lorentz-and CPT-violating quantum electrodynamics. Braz. J. Phys. 46, 437-452 (2016).
  13. Meshkov, I. N. Experimental studies of antihydrogen and positronium physics: problems and possibilities. Phys. Part. Nucl. 28(2), 198 (1997). [CrossRef]
  14. Blasi, P. Origin of the positron excess in cosmic rays. Phys. Rev. Lett. 103(5), 051104 (2009). [CrossRef]
  15. Schiller, C. A conjecture on deducing general relativity and the standard model with its fundamental constants from rational tangles of strands. Phys. Part. Nucl. Lett. 50, 259-299 (2019). [CrossRef]
  16. Silagadze, Z. K. Mirror objects in the solar system?. arXiv preprint astro-ph/0110161 (2001).
  17. Rieflin, E. Some mechanisms related to Dirac’s strings. Am. J. Phys. 47(4), 379-380 (1979).
  18. Fox, T. Haunted by the spectre of virtual particles: a philosophical reconsideration. J. Gen. Philos. Sci. 39, 35-51 (2008). [CrossRef]
  19. Atkinson, D. Does quantum electrodynamics have an arrow of time?. Stud. Hist. Philos. Mod. Phys. 37(3), 528-541 (2006). [CrossRef]
  20. Penrose, R. and MacCallum, M. A. Twistor theory: an approach to the quantisation of fields and space-time. Phys. Rep. 6(4), 241-315 (1973). [CrossRef]
  21. Smolin, L. How far are we from the quantum theory of gravity?. arXiv preprint hep-th/0303185 (2003).
  22. Li, K. et al. Quantum spacetime on a quantum simulator. Commun. Phys. 2(1), 122 (2019).
  23. Cohen, L. et al. Efficient simulation of loop quantum gravity: A scalable linear-optical approach. Phys. Rev. Lett. 126(2), 020501 (2021). [CrossRef]
  24. van der Meer, R. et al. Experimental simulation of loop quantum gravity on a photonic chip. Npj Quantum Inf. 9(1), 32 (2023).
  25. Wootters, W. K. “Time” replaced by quantum correlations. Int. J. Theor. Phys. 23, 701-711 (1984).
  26. Page, D. N. Clock time and entropy. arXiv preprint gr-qc/9303020 (1993).
  27. Calabrese, P. and Cardy, J. Evolution of entanglement entropy in one-dimensional systems. J. Stat. Mech. Theor. Exp. 2005(04), P04010 (2005). [CrossRef]
  28. Callender, C. and Huggett, N. (Eds.). Physics meets philosophy at the Planck scale: Contemporary theories in quantum gravity. Cambridge University Press (2001).
  29. Draper, P. and Rzehak, H. A review of Higgs mass calculations in supersymmetric models. Phys. Rep. 619, 1-24 (2016). [CrossRef]
  30. Curiel, E. Singularities and black hole. Stanford Encyclopedia of Philosophy (2019).
  31. Yuguru, S. P. Unconventional reconciliation path for quantum mechanics and general relativity. IET Quant. Comm. 3(2), 99–111 (2022). [CrossRef]
  32. Jiang, F. et al. Study on relative orbit geometry of spacecraft formations in elliptical reference orbits. J. Guid. Control Dyn. 31(1), 123-134 (2008). [CrossRef]
  33. Bethke, S. Experimental tests of asymptotic freedom. Prog. Part. Nucl. Phys. 58(2), 351-386 (2007). [CrossRef]
  34. Sheppard, C. J., Kou, S. S. and Lin, J. The Green-function transform and wave propagation. Front. Phys. 2, 67 (2014). [CrossRef]
  35. Recami, E., Zamboni-Rached, M. and Licata, I. On a Time–Space Operator (and other Non-Self-Adjoint Operators) for Observables in QM and QFT. In Beyond peaceful coexistence: The Emergence of Space, Time and Quantum (pp. 371-417) (2016).
  36. Bernauer, J. C. The proton radius puzzle–9 years later. In EPJ Web of Conferences (Vol. 234, p. 01001). EDP Sciences (2020).
  37. Samajdar, R. et al. Complex density wave orders and quantum phase transitions in a model of square-lattice Rydberg atom arrays. Phys. Rev. Lett. 124(10), 103601 (2020). [CrossRef]
  38. Jaffe. R. L. Supplementary notes on Dirac notation, quantum states, etc. https://web.mit.edu/8.05/handouts/jaffe1.pdf (September, 2007).
  39. Recami, E., Zamboni-Rached, M. and Licata, I. On a Time–Space Operator (and other Non-Self-Adjoint Operators) for Observables in QM and QFT. In Beyond peaceful coexistence: The Emergence of Space, Time and Quantum (pp. 371-417) (2016).
  40. Singh, R. B. Introduction to modern physics. New Age International (2008).
  41. Machotka, R. Euclidean model of space and time. J. Mod. Phys. 9(06), 1215 (2018).
  42. Burdman, G. Quantum field theory I_Lectures. http://fma.if.usp.br/~burdman (October, 2023).
  43. Oshima, S., Kanemaki, S. and Fujita, T. Problems of Real Scalar Klein-Gordon Field. arXiv preprint hep-th/0512156 (2005).
  44. Peskin, M. E. and Schroeder, D. V. An introduction to quantum field theory. Addison-Wesley, Massachusetts, USA (1995).
  45. Alvarez-Gaumé, L. and Vazquez-Mozo, M. A. Introductory lectures on quantum field theory. arXiv preprint hep-th/0510040 (2005).
  46. https://en.wikipedia.org/wiki/Spinor (updated February 2024).
  47. Beenakker, C. W. J. Search for Majorana fermions in superconductors. Annu. Rev. Condens. Matter Phys. 4(1), 113-136 (2013). [CrossRef]
  48. Jeffrey, D. J. Branch cuts and Riemann surfaces. arXiv preprint arXiv:2302.13188 (2023).
  49. Callahan, J. J. The geometry of spacetime: an introduction to special and general relativity. Springer Science and Business Media (2013).
  50. Freed, D. S. et al. Topological quantum field theories from compact Lie groups. arXiv preprint arXiv:0905.0731 (2009).
  51. Monteiro, R., Nicholson, I. and O’Connell, D. (2019). Spinor-helicity and the algebraic classification of higher-dimensional spacetimes. Class. Quantum Gravity 36(6), 065006 (2019). [CrossRef]
  52. Markley, L. C. and Lindner, J. F. Artificial gravity field. Results Phys. 3, 24-29 (2013). [CrossRef]
  53. Vankov, A. A. General Relativity Problem of Mercury’s Perihelion Advance Revisited. arXiv preprint arXiv:1008.1811 (2010).
  54. Karkoschka, E. Uranus’ southern circulation revealed by Voyager 2: unique characteristics. Icarus, 250, 294-307 (2015). [CrossRef]
Preprints 150724 g001
Figure 1. The MP model of 4D quantum space-time [31]. (a) In flat Euclidean space-time, quantum time axis or arrow of time in asymmetry is aligned with the principal axis or z-axis of the MP of a clock face. A spinning electron (green dot) in orbit of sinusoidal form (green curve) assumes time reversal and it is normalized to an elliptical MP field (black area) of Dirac’s string. Clockwise precession of the MP field (black arrows) against time reversal generates an inertia frame, λ. The electron at position 0 is assigned center of mass and is subjected to Newton’s first law of motion, F = m a . By DBT, the shift in the electron’s position from positions 0 to 4 at 360° rotation offers maximum twist and the electron is converted to a positron. The unfolding process from positions 5 to 8 for another 360° rotation restores the electron to its original state at position 0. The transition at the point-boundary relates to zero-point energy (ZPE). A dipole moment (±) of an electric field, E is induced at 720° rotation between two interchangeable hemispheres of Gaussian-shaped soliton for the MP. (b) Twisting and unfolding process for the electron-positron transition generates hyperbolic solenoid of spin angular momentum, ±1/2 (navy colored pair of light-cones) into Minkowski space-time. This levitates into n-dimensions (purple dotted diagonal lines) within the hemispheres of Gaussian soliton type and are linked to smooth manifolds of Bohr orbit (BO) as quantized states and perpendicular to the light-cones. The undisturbed helical solenoid of a magnetic field, B by unitary is referenced to the hypersurface of the MP field. (c) In a Bloch sphere, the precession stages, Ω , is polarized by electron-positron transition with qubits, 0 and 1 assumed at positions, 0, 8 and hypercharge -1 at position 4 at the vertices of the MP field (see also notes in Figure 2a–e for further explanations). The polar coordinates (r, θ, Φ) with respect to the electron’s position in space are applicable to Schrödinger wave function. (d) Hyperbolic surface of the light-cone by orthonormal integration of ϕ (white loops) and θ (yellow circles) forms compact topological torus of BO of n-dimension and this is holonomically constrained within a hemisphere of GS. At n-1 of ZPE, the BO offers hypersurface of Euclidean space with clockwise precession. Balancing out charges at homomorphic positions 1, 3 and 5, 7 becomes isomorphic to BO. Relativistic transformation of COM reference frame at the point-boundary (b) to point of singularity of the light-cones (insert image) is accommodated by clockwise transition in z-axis of quantum time, z − z ' ≡ c t − c t ' . Other embedded terms and equations are described in the text.
Figure 1. The MP model of 4D quantum space-time [31]. (a) In flat Euclidean space-time, quantum time axis or arrow of time in asymmetry is aligned with the principal axis or z-axis of the MP of a clock face. A spinning electron (green dot) in orbit of sinusoidal form (green curve) assumes time reversal and it is normalized to an elliptical MP field (black area) of Dirac’s string. Clockwise precession of the MP field (black arrows) against time reversal generates an inertia frame, λ. The electron at position 0 is assigned center of mass and is subjected to Newton’s first law of motion, F = m a . By DBT, the shift in the electron’s position from positions 0 to 4 at 360° rotation offers maximum twist and the electron is converted to a positron. The unfolding process from positions 5 to 8 for another 360° rotation restores the electron to its original state at position 0. The transition at the point-boundary relates to zero-point energy (ZPE). A dipole moment (±) of an electric field, E is induced at 720° rotation between two interchangeable hemispheres of Gaussian-shaped soliton for the MP. (b) Twisting and unfolding process for the electron-positron transition generates hyperbolic solenoid of spin angular momentum, ±1/2 (navy colored pair of light-cones) into Minkowski space-time. This levitates into n-dimensions (purple dotted diagonal lines) within the hemispheres of Gaussian soliton type and are linked to smooth manifolds of Bohr orbit (BO) as quantized states and perpendicular to the light-cones. The undisturbed helical solenoid of a magnetic field, B by unitary is referenced to the hypersurface of the MP field. (c) In a Bloch sphere, the precession stages, Ω , is polarized by electron-positron transition with qubits, 0 and 1 assumed at positions, 0, 8 and hypercharge -1 at position 4 at the vertices of the MP field (see also notes in Figure 2a–e for further explanations). The polar coordinates (r, θ, Φ) with respect to the electron’s position in space are applicable to Schrödinger wave function. (d) Hyperbolic surface of the light-cone by orthonormal integration of ϕ (white loops) and θ (yellow circles) forms compact topological torus of BO of n-dimension and this is holonomically constrained within a hemisphere of GS. At n-1 of ZPE, the BO offers hypersurface of Euclidean space with clockwise precession. Balancing out charges at homomorphic positions 1, 3 and 5, 7 becomes isomorphic to BO. Relativistic transformation of COM reference frame at the point-boundary (b) to point of singularity of the light-cones (insert image) is accommodated by clockwise transition in z-axis of quantum time, z − z ' ≡ c t − c t ' . Other embedded terms and equations are described in the text.
Preprints 150724 g001
Preprints 150724 g002
Figure 2. Dirac monopole at COM reference frame. (a) Under clockwise precession of the elliptical MP field of Dirac’s string, the monopole or electron at the top vertex is compelled towards the unoccupied bottom vertex by the process of DBT to induce a dipole moment akin to a classical small magnet. The process is attained at 360° rotation confined to a GS type and it is interchangeable with its adjoining GS by levitation and fulfils Born’s rule of squared wave function (see also Figure 1a). (b) The monopole at COM is likened to Higgs boson and the GS pair to a two Higgs doublet amplitude or field. Transient instability of combined GS pair of hyperbolic geometry assumes an oscillation mode. (c) The COM is translated to point of singularity and it accommodates the unfolding process by DBT to instigate electroweak symmetry breaking, where either a positive or negative scalar field potential is generated and this coincides with the electron-positron transition. Extension of BO into n-dimensions is quantized, E = n h v and is stretched out towards hyperbolic surface by levitation akin to a classical oscillator. (d) Another 360° rotation and the levitated GS pair and monopole are restored to the original state. In the process, linear light path long horizontal axis intercepts BO of n-dimension and generates scattering matrix along z-axis of quantum time towards COM into classical arrow of time. (e) Under the natural setting, n ∞ =   ε 0 = c = ℏ = 1   ( C O M ) , interactions between fermions and bosons become asymptotically weaker towards n ∞ with reduction of BO at n-dimensions. Polarization of the model either horizontally or vertically by the electron-positron pair, ±i generates the qubits 0, 1 with hypercharge, –1 equal to time reversal of the electron’s orbit. This appears consistent with Euler’s identity and the MP model (e.g., Figure 1a).
Figure 2. Dirac monopole at COM reference frame. (a) Under clockwise precession of the elliptical MP field of Dirac’s string, the monopole or electron at the top vertex is compelled towards the unoccupied bottom vertex by the process of DBT to induce a dipole moment akin to a classical small magnet. The process is attained at 360° rotation confined to a GS type and it is interchangeable with its adjoining GS by levitation and fulfils Born’s rule of squared wave function (see also Figure 1a). (b) The monopole at COM is likened to Higgs boson and the GS pair to a two Higgs doublet amplitude or field. Transient instability of combined GS pair of hyperbolic geometry assumes an oscillation mode. (c) The COM is translated to point of singularity and it accommodates the unfolding process by DBT to instigate electroweak symmetry breaking, where either a positive or negative scalar field potential is generated and this coincides with the electron-positron transition. Extension of BO into n-dimensions is quantized, E = n h v and is stretched out towards hyperbolic surface by levitation akin to a classical oscillator. (d) Another 360° rotation and the levitated GS pair and monopole are restored to the original state. In the process, linear light path long horizontal axis intercepts BO of n-dimension and generates scattering matrix along z-axis of quantum time towards COM into classical arrow of time. (e) Under the natural setting, n ∞ =   ε 0 = c = ℏ = 1   ( C O M ) , interactions between fermions and bosons become asymptotically weaker towards n ∞ with reduction of BO at n-dimensions. Polarization of the model either horizontally or vertically by the electron-positron pair, ±i generates the qubits 0, 1 with hypercharge, –1 equal to time reversal of the electron’s orbit. This appears consistent with Euler’s identity and the MP model (e.g., Figure 1a).
Preprints 150724 g002
Preprints 150724 g003
Figure 3. Quantum oscillation of GS pair. (a) The COM of topological point-boundary provides the origin of the emergence of quantum oscillators (maroon light-cones) (see also Figure 2c). Total angular momentum, J z = S + L is minimal with S and L in opposite directions. Extension of BOs into n-dimensions from k to n∞ for the GS pair towards the classical scale is defined by the correspondence principle. It is partitioned in accordance with Born’s rule for squared wave function. The BOs in degeneracy, Φi of n-dimensions are assigned spectroscopic notations, s, p, d and so forth. These can relate to Fermi-Dirac statistics (green wavy curve) and possibly Fock space for non-relativistic many-particle systems if multielectron are assigned to multiple MP fields. At completion of DBT, the blue light-cone emerges and is pertinent to non-relativistic Schrödinger wave function (e.g., Figure 1c). (b) Superposition states, ± J z = m j ℏ is applicable to the GS pair by DBT at 360° rotation with charge conjugation and parity violation assumed at COM. Another 360° rotation, CPT symmetry is restored, where accessibility to the nucleus is constrained for the GS pair of irreducible spinor field (e.g., Figure 2d)).
Figure 3. Quantum oscillation of GS pair. (a) The COM of topological point-boundary provides the origin of the emergence of quantum oscillators (maroon light-cones) (see also Figure 2c). Total angular momentum, J z = S + L is minimal with S and L in opposite directions. Extension of BOs into n-dimensions from k to n∞ for the GS pair towards the classical scale is defined by the correspondence principle. It is partitioned in accordance with Born’s rule for squared wave function. The BOs in degeneracy, Φi of n-dimensions are assigned spectroscopic notations, s, p, d and so forth. These can relate to Fermi-Dirac statistics (green wavy curve) and possibly Fock space for non-relativistic many-particle systems if multielectron are assigned to multiple MP fields. At completion of DBT, the blue light-cone emerges and is pertinent to non-relativistic Schrödinger wave function (e.g., Figure 1c). (b) Superposition states, ± J z = m j ℏ is applicable to the GS pair by DBT at 360° rotation with charge conjugation and parity violation assumed at COM. Another 360° rotation, CPT symmetry is restored, where accessibility to the nucleus is constrained for the GS pair of irreducible spinor field (e.g., Figure 2d)).
Preprints 150724 g003
Preprints 150724 g004
Figure 4. Vectors of angular momentum. (a) J results from precession of vectors L and S. The shaded area of bivector is extended to COM at the point-boundary of the spherical model (see also Figure 3a). (b) Precession of J of hyperbolic surface in Minkowski space-time can coincides with applied external magnetic field B. Both images are adapted from ref. [40].
Figure 4. Vectors of angular momentum. (a) J results from precession of vectors L and S. The shaded area of bivector is extended to COM at the point-boundary of the spherical model (see also Figure 3a). (b) Precession of J of hyperbolic surface in Minkowski space-time can coincides with applied external magnetic field B. Both images are adapted from ref. [40].
Preprints 150724 g004
Preprints 150724 g005
Figure 5. A wave function collapse scenario. (a) At clockwise precession, the irreducible MP field of Dirac’s string incorporates the electron shift in position by DBT. The particle at a diagonal line, r is assigned the polar coordinates (r, θ, Φ) and is linked to a light-cone (navy colored). This is applicable to Euler’s formula, e i π = c o s π + i s i n π with θ = π (see also Figure 2e). The real part, cosπ is aligned to x-y plane and the imaginary part, isinπ to z-axis. Unitary, ψ 2 = x 2 + y 2 = 1   is sustained, where qubits, 0, 1 is assumed at COM and hypercharge -1 by time reversal. (b) Vector space of Dirac spinor (shaded yellow) is superimposed on a Bloch sphere. It consists of both Euclidean (straight paths) and non-Euclidean (negative and positive curves) spaces. (c) On-shell momentum of BO accommodating the electron path and tangential to the MP field is applicable to Fourier transform (blue wavy curve) from vertical to horizontal polarization towards classical time. Constraining the particle’s position presents the Heisenberg uncertainty principle (black wavy curve) and its momentum to blue wavy curve. These can translate to (d) a typical hydrogen emission spectrum by light-MP model coupling in real-time from excitation towards infinite n-dimension towards the delegated ground state such as from Humphery to Lynman series (see subsection IIc). .
Figure 5. A wave function collapse scenario. (a) At clockwise precession, the irreducible MP field of Dirac’s string incorporates the electron shift in position by DBT. The particle at a diagonal line, r is assigned the polar coordinates (r, θ, Φ) and is linked to a light-cone (navy colored). This is applicable to Euler’s formula, e i π = c o s π + i s i n π with θ = π (see also Figure 2e). The real part, cosπ is aligned to x-y plane and the imaginary part, isinπ to z-axis. Unitary, ψ 2 = x 2 + y 2 = 1   is sustained, where qubits, 0, 1 is assumed at COM and hypercharge -1 by time reversal. (b) Vector space of Dirac spinor (shaded yellow) is superimposed on a Bloch sphere. It consists of both Euclidean (straight paths) and non-Euclidean (negative and positive curves) spaces. (c) On-shell momentum of BO accommodating the electron path and tangential to the MP field is applicable to Fourier transform (blue wavy curve) from vertical to horizontal polarization towards classical time. Constraining the particle’s position presents the Heisenberg uncertainty principle (black wavy curve) and its momentum to blue wavy curve. These can translate to (d) a typical hydrogen emission spectrum by light-MP model coupling in real-time from excitation towards infinite n-dimension towards the delegated ground state such as from Humphery to Lynman series (see subsection IIc). .
Preprints 150724 g005
Preprints 150724 g006
Figure 6. Dirac spinor. (a) The electron’s (green dot) shift in position of time reversal is balanced out by clockwise precession of the MP model and this allows twisting and unfolding by DBT. The position of the particle on a straight path (colored lines) is referenced to the elliptical MP field (centered image). (b) Maximum twist is attained at position 4 and the unfolding process as detectable energy is assumed at another 360° rotation for a total of 720° rotation to restore the electron to its original state at position 8 or 0. (c) Precession normalizes the loop to generate an electron of negative helicity or left-handedness. Spin up vector subjected to DBT generally differs from the direction of precession. (d) At position 4, the electron flips to a positron of positive helicity or right-handedness. The spin down vector correlates to the direction of precession to begin the unfolding process. By transposition, the electron is converted to a positron and vice versa, i.e., ∑ j e ^ j e ^ j T = e i e j = c i j k e k . (e) The GS pair combines to form an irreducible spinor field. Cancelation of charges at conjugate positions, 1, 3 and 5, 7 from on-shell momentum offers close loops of BOs into 3D of discrete form. This stabilizes the electron to only generate either spin up or spin down states respectively at position 0 and 4. The slight tilt at position 4 compared to position 0 is attributed to energy loss from the electron-positron transition in the form, E = h v = g β B . Image adapted from ref. [46].
Figure 6. Dirac spinor. (a) The electron’s (green dot) shift in position of time reversal is balanced out by clockwise precession of the MP model and this allows twisting and unfolding by DBT. The position of the particle on a straight path (colored lines) is referenced to the elliptical MP field (centered image). (b) Maximum twist is attained at position 4 and the unfolding process as detectable energy is assumed at another 360° rotation for a total of 720° rotation to restore the electron to its original state at position 8 or 0. (c) Precession normalizes the loop to generate an electron of negative helicity or left-handedness. Spin up vector subjected to DBT generally differs from the direction of precession. (d) At position 4, the electron flips to a positron of positive helicity or right-handedness. The spin down vector correlates to the direction of precession to begin the unfolding process. By transposition, the electron is converted to a positron and vice versa, i.e., ∑ j e ^ j e ^ j T = e i e j = c i j k e k . (e) The GS pair combines to form an irreducible spinor field. Cancelation of charges at conjugate positions, 1, 3 and 5, 7 from on-shell momentum offers close loops of BOs into 3D of discrete form. This stabilizes the electron to only generate either spin up or spin down states respectively at position 0 and 4. The slight tilt at position 4 compared to position 0 is attributed to energy loss from the electron-positron transition in the form, E = h v = g β B . Image adapted from ref. [46].
Preprints 150724 g006
Preprints 150724 g007
Figure 7. A periodic Riemann surface for the cube-root function of 4D. This is integrated within the GS pair. The 3D warping and unwarping by DBT (red loops) for the electron-positron transition is numbered. The top GS (purple colored) combines with the hyperbolic surface of BO of a pair of light-cones (turquoise colored) and the same applies to bottom GS (greenish yellow colored) to provide a complex spinor field. Clockwise precession of quantum time is translated from z to z’ and then to z”. Both real and imaginary potentials are applicable to the spinor (see also Figure 5a). Image modified after ref. [48] and interpreted according to Dirac spinor of the MP model of quantum space-time.
Figure 7. A periodic Riemann surface for the cube-root function of 4D. This is integrated within the GS pair. The 3D warping and unwarping by DBT (red loops) for the electron-positron transition is numbered. The top GS (purple colored) combines with the hyperbolic surface of BO of a pair of light-cones (turquoise colored) and the same applies to bottom GS (greenish yellow colored) to provide a complex spinor field. Clockwise precession of quantum time is translated from z to z’ and then to z”. Both real and imaginary potentials are applicable to the spinor (see also Figure 5a). Image modified after ref. [48] and interpreted according to Dirac spinor of the MP model of quantum space-time.
Preprints 150724 g007
Preprints 150724 g008
Figure 8. The basis of vectors to multivectors, matrices, tensors and Fourier transform for the electron’s position (P) assigned to a unit cell within the MP model (see also Figure 1c). The z-axis of quantum time is orthonormal to distances projected in the x-y directions. Fourier transform of tensor matrices is by commutation, p Z to Z . The electron of a resultant vector, r → of four 3-fold rotational axes (shaded orange plane) in 3D of a cube can relate to the vector space, J → = L → + S → offered in Figure 4a and Figure 4b. These are ascribed to 4-gradient Dirac operator, ∇ for vectors to multivector into n-dimensions by the cube translation along z-axis. Stress-energy tensor of BO mimicking rotation into forward time, τ = r → × F by the emergence of spin up is balanced out by spin down of time reversal, L = r → × p . The spin rotation matrices applicable to Clifford algebra are shown to the left. The half-integer spins of SU(2) group provide double cover (bivector) with shift in both θ and ϕ for BOs of topological torus. These are relevant to the Lie group ladder operators, G ( g ) and G ^ ( g ^ ) . Some key features of the dimensional cube are expounded to the right.
Figure 8. The basis of vectors to multivectors, matrices, tensors and Fourier transform for the electron’s position (P) assigned to a unit cell within the MP model (see also Figure 1c). The z-axis of quantum time is orthonormal to distances projected in the x-y directions. Fourier transform of tensor matrices is by commutation, p Z to Z . The electron of a resultant vector, r → of four 3-fold rotational axes (shaded orange plane) in 3D of a cube can relate to the vector space, J → = L → + S → offered in Figure 4a and Figure 4b. These are ascribed to 4-gradient Dirac operator, ∇ for vectors to multivector into n-dimensions by the cube translation along z-axis. Stress-energy tensor of BO mimicking rotation into forward time, τ = r → × F by the emergence of spin up is balanced out by spin down of time reversal, L = r → × p . The spin rotation matrices applicable to Clifford algebra are shown to the left. The half-integer spins of SU(2) group provide double cover (bivector) with shift in both θ and ϕ for BOs of topological torus. These are relevant to the Lie group ladder operators, G ( g ) and G ^ ( g ^ ) . Some key features of the dimensional cube are expounded to the right.
Preprints 150724 g008
Preprints 150724 g009
Figure 9. The components of Einstein field equation when applied to the MP model of 4D space-time for a planet in orbit of the solar system at a higher hierarchy of scales. Space-time is warped and unwarped by shift in the body-mass, ψ from positions 0 → 3 undergoing DBT. The emergence of angular momentum,   J → at position 1 and 3 mimics stress-energy tensor, T μ , ν with ω = 1 resembling precession stages of the MP field. Space expansion by rotation, ω > 1 ≅ γ θ   is balanced out by contraction, ω < 1   ≅ ∂ ϕ for clockwise precession. Hamiltonian of moduli space (green outline) of hypersurface generates Riemann curvature (yellow curve), R μ , ν = 1 / 2 R g μ ν λ − Λ g μ ν λ at the lattice points, 1 and 3 of a cube (e.g., Figure 8). This can be woven into space network of fine fabric (Figure 7). Image adapted from ref. [31] and slightly modified.
Figure 9. The components of Einstein field equation when applied to the MP model of 4D space-time for a planet in orbit of the solar system at a higher hierarchy of scales. Space-time is warped and unwarped by shift in the body-mass, ψ from positions 0 → 3 undergoing DBT. The emergence of angular momentum,   J → at position 1 and 3 mimics stress-energy tensor, T μ , ν with ω = 1 resembling precession stages of the MP field. Space expansion by rotation, ω > 1 ≅ γ θ   is balanced out by contraction, ω < 1   ≅ ∂ ϕ for clockwise precession. Hamiltonian of moduli space (green outline) of hypersurface generates Riemann curvature (yellow curve), R μ , ν = 1 / 2 R g μ ν λ − Λ g μ ν λ at the lattice points, 1 and 3 of a cube (e.g., Figure 8). This can be woven into space network of fine fabric (Figure 7). Image adapted from ref. [31] and slightly modified.
Preprints 150724 g009
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
bsky
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

Privacy Settings

© 2026 MDPI (Basel, Switzerland) unless otherwise stated