Submitted:
13 December 2024
Posted:
13 December 2024
Read the latest preprint version here
Abstract
In quantum mechanics (QM), the electron of spin-charge, ±1/2 in probabilistic distribution about a nucleus of an atom is described by non-relativistic Schrödinger wave equation. Its transformation to Dirac fermion of a complex four-component spinor is incorporated into relativistic quantum field theory (QFT) based on Dirac theory. The link between QM and QFT on the basis of space-time structure remains lacking without the development of a proper, complete theory of quantum gravity. In this study, how a proposed MP model of 4D space-time mimicking hydrogen atom type is able to combine both QM and QFT into a proper perspective is explored. The electron of a point-particle and its transformation to Dirac fermion appears consistent with Dirac belt trick while sustaining unitarity of spin-charge and wave-particle duality with center of mass reference frame relevant to Newtonian gravity assigned to the point-boundary of the spherical model. Such a tool appears dynamic and is compatible with basic aspects of both QM and QFT such as non-relativistic wave function and its collapse, quantized Hamiltonian, Dirac theory, Weyl spinor, Marjorana fermions and Lorentz transformation. How all these relate to space-time curvature for an elliptical orbit without invoking a framework of space-time fabric is plotted for general relativity and a multiverse of the MP models at a hierarchy of scales is proposed for further investigations.
Keywords:
Contents

I. Introduction
A. Non-Relativistic Theory to Relativistic Field Theory
B. Relevance of Quantum Space-Time in Dirac Theory
II. Dirac Fermion of a MP Model of Hydrogen Atom Type
A. Unveiling of Dirac Belt Trick and CPT Symmetry
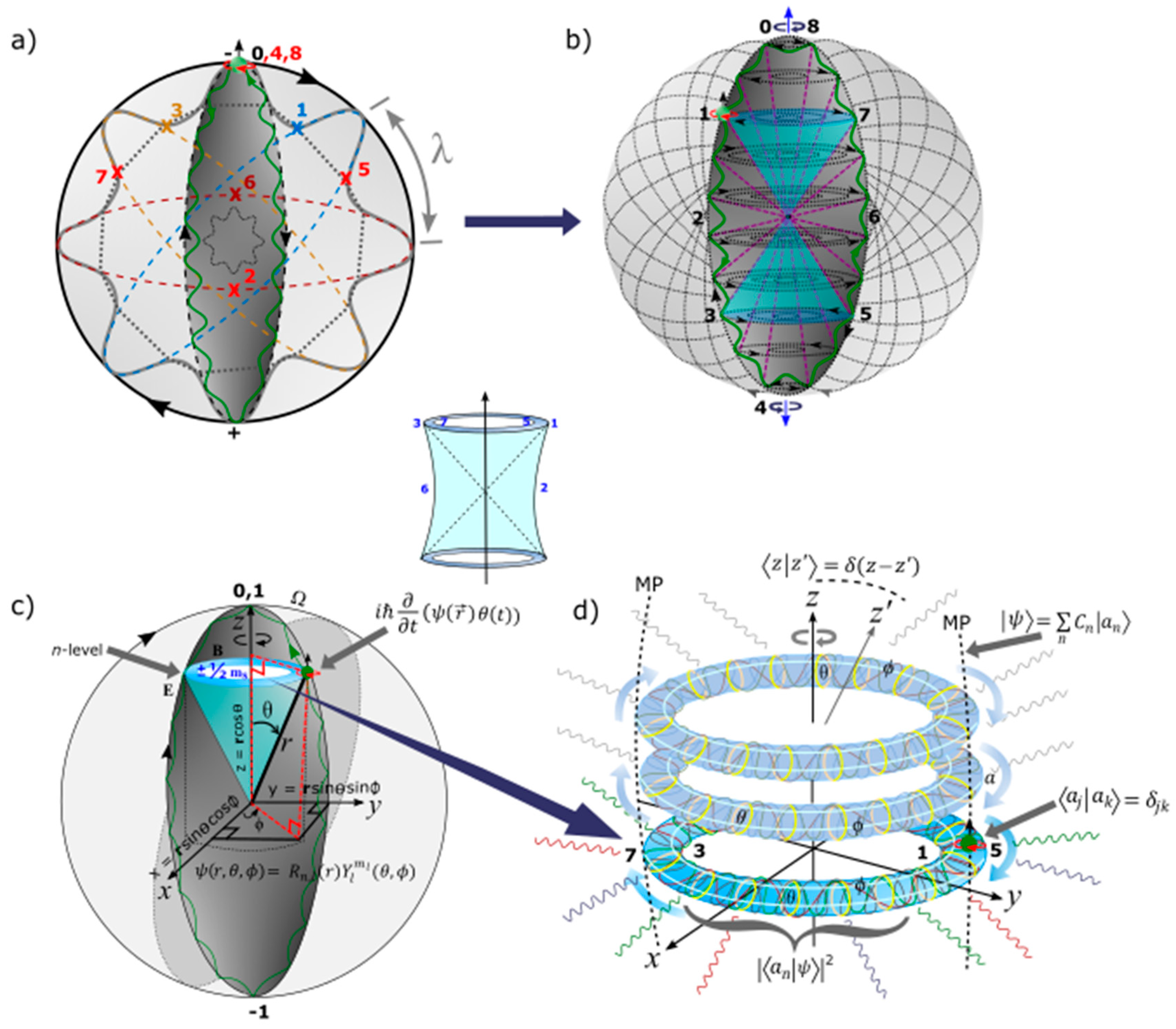
B. Dynamics of Space-Time Geometry in an Atom
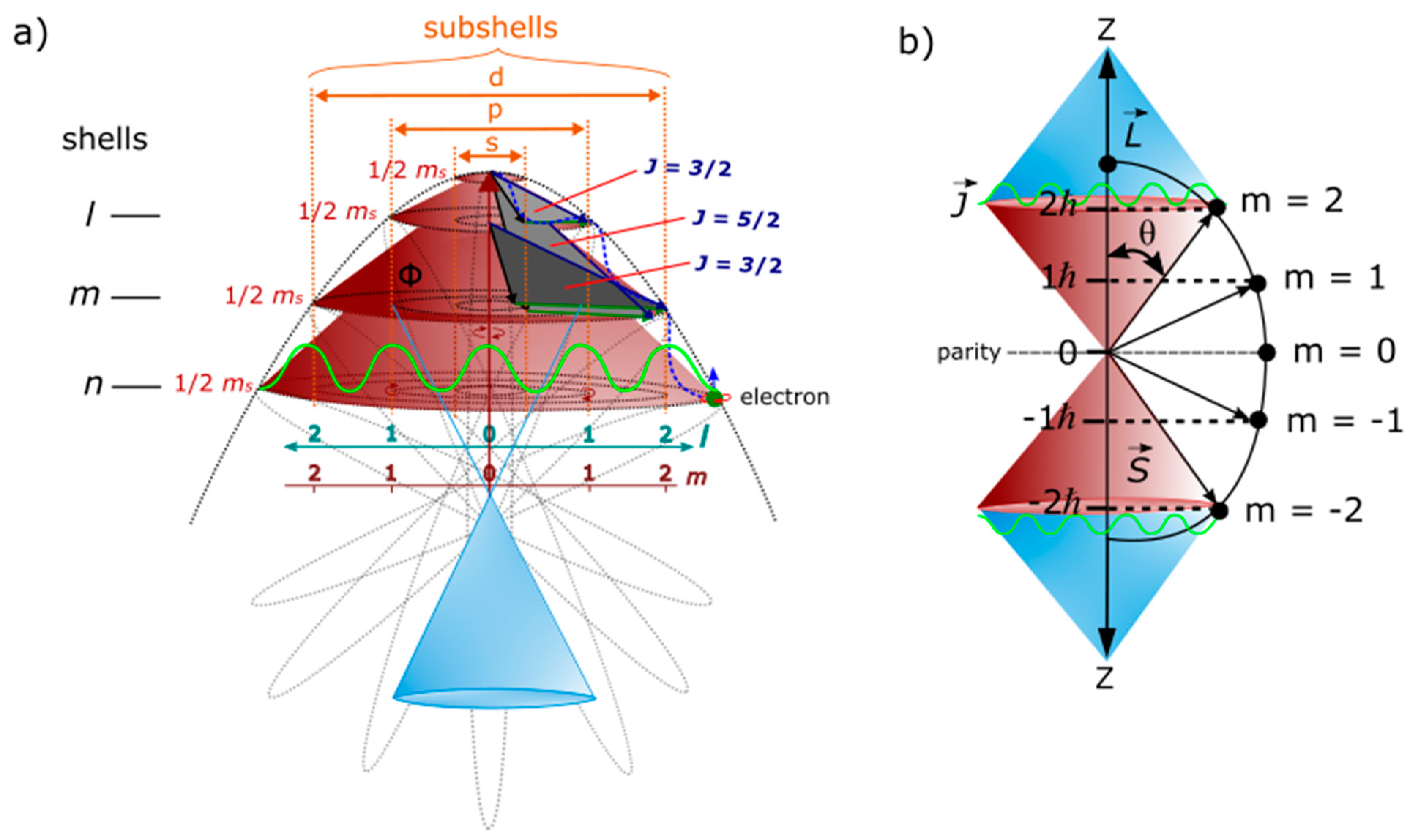
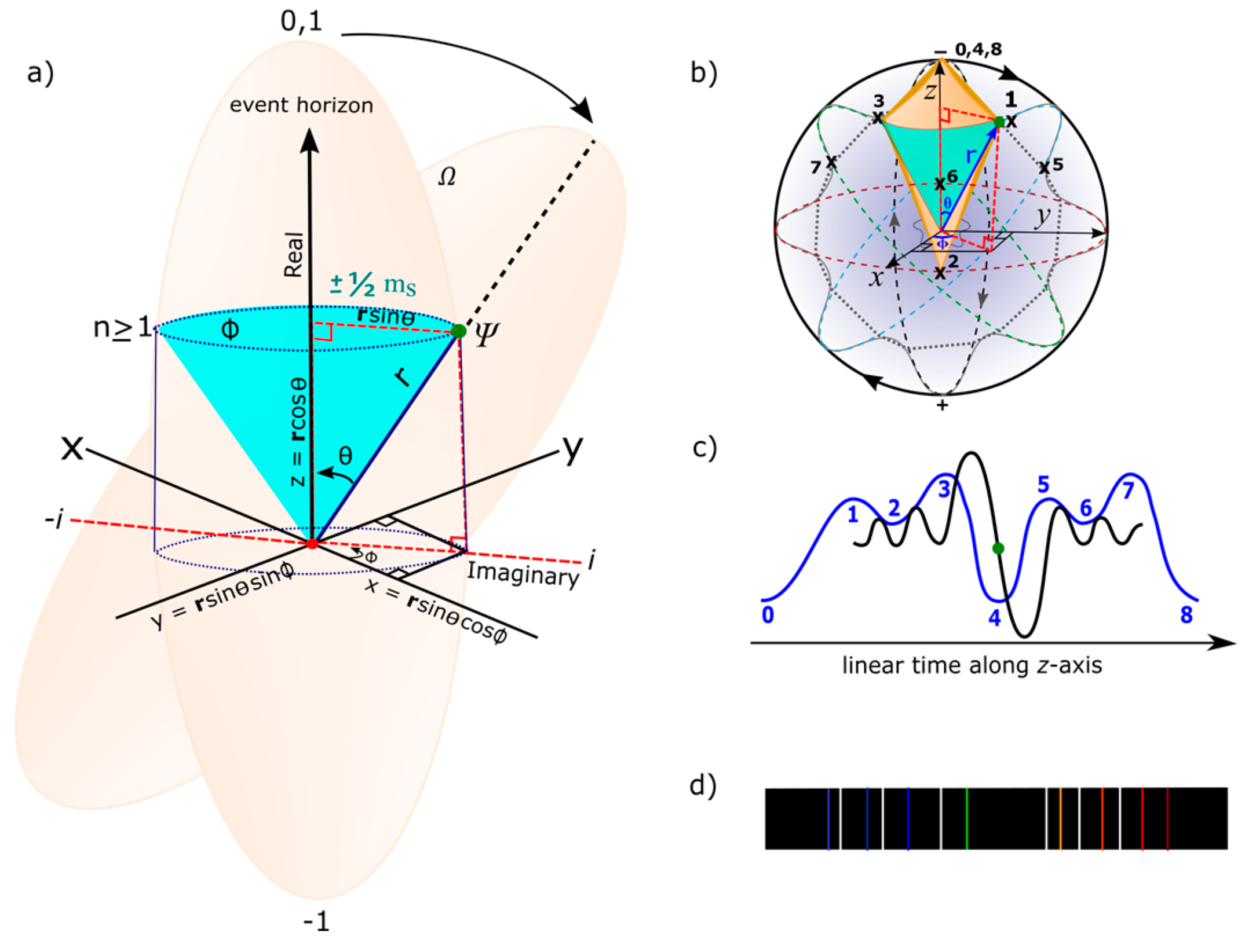
- The MP model is limited to light-matter coupling at observation with the matter property attributed to the electron’s position of a point-particle. The vertices of the elliptical MP field by clockwise precession at positions, 0, 4 and 8 at a point-boundary offer moduli spaces of Hermitian forms by the electron-positron transition. The positions respectively accommodate polarization states, 0, 1 and hypercharge –1 for the two hemispheres of ±1/2 with respect to the electron shift in positions 0 → 8 in accordance with Pauli exclusion principle. Unitarity by Euler’s formula, + 1 = 0 in real space is sustained.
- Polarization of other moduli spaces of vertices devoid of the electron by clockwise precession mimics creation and annihilation of virtual particles in a vacuum. Real particle emergence with spin angular momentum is assumed at positions 1, 3 or its conjugates positions, 5 and 7 (Figure 1b) with the electron popping in and out of existence by the process of DBT. The Hamiltonian, P(0→8) = is sustained for the electron shift in position and its transition to a positron with the time taken equal to .
- The electron at the vertex of the MP field at position 0 mimics monopole instanton (MI). It offers the base point for transmission of vortex electron through a helical solenoid which intersects topological torus of BO at n-dimensions by levitation between two hemispheres of the MP field. The base point presents COM reference frame from the electron-positron transition with time reversal orbit of the electron balanced out by clockwise precession in accordance with Newton’s second law of motion. The COM is about Planck length ~ 1.62 x 10-35 meters) is aligned to the principal axis or z-axis of the MP field as nuclear isospin (about 1.1 angstroms for the hydrogen atom) and it depicts arrow of time in asymmetry. Infinitesimal radiation of Planck constant, is assumed from twisting and unfolding process of the electron-positron transition by DBT at COM. It can also cater for ZPE of the hydrogen atom at ultraviolet range in a potential well of a harmonic oscillator, at a value of -13.60 electronvolts.
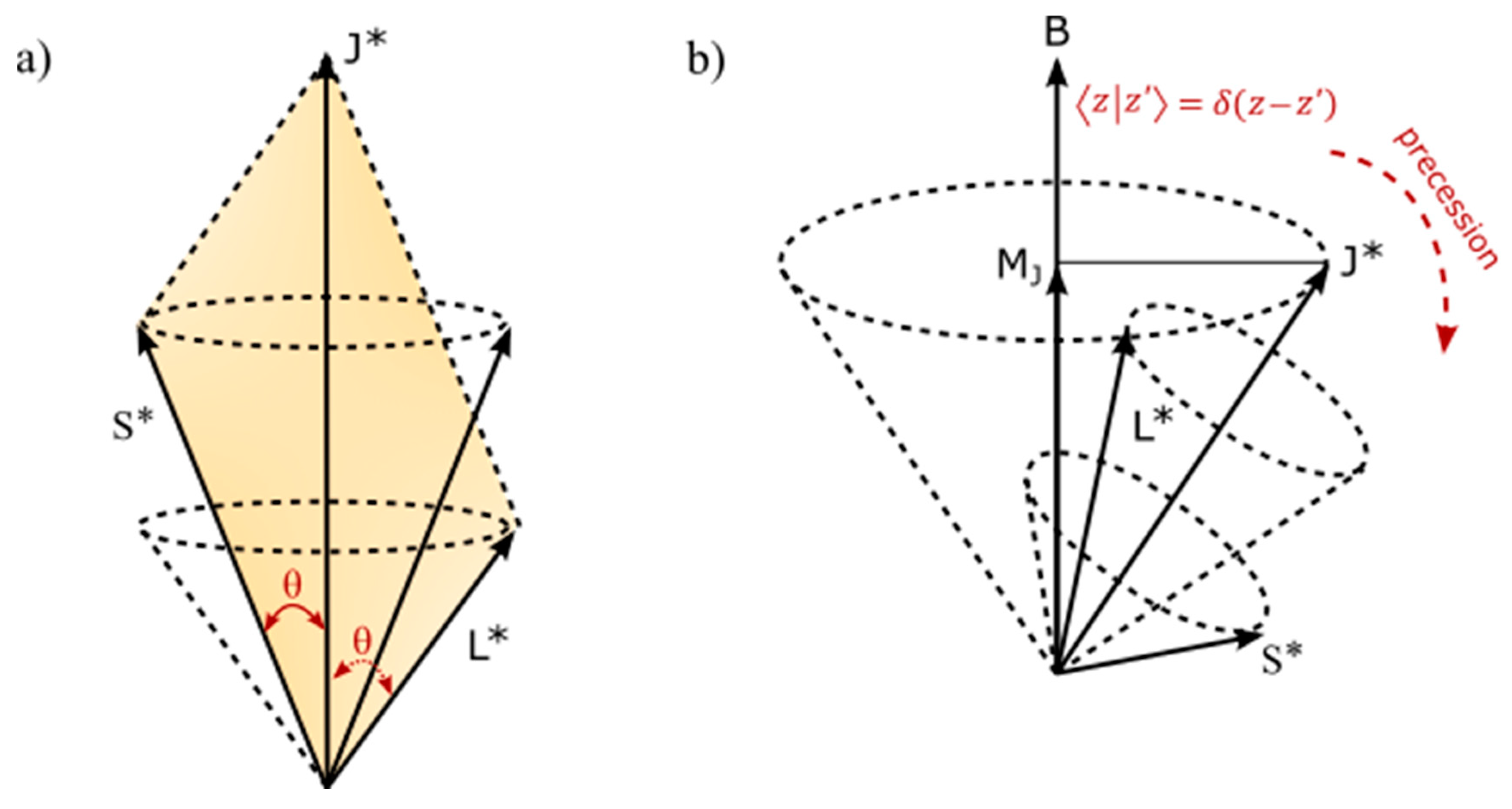
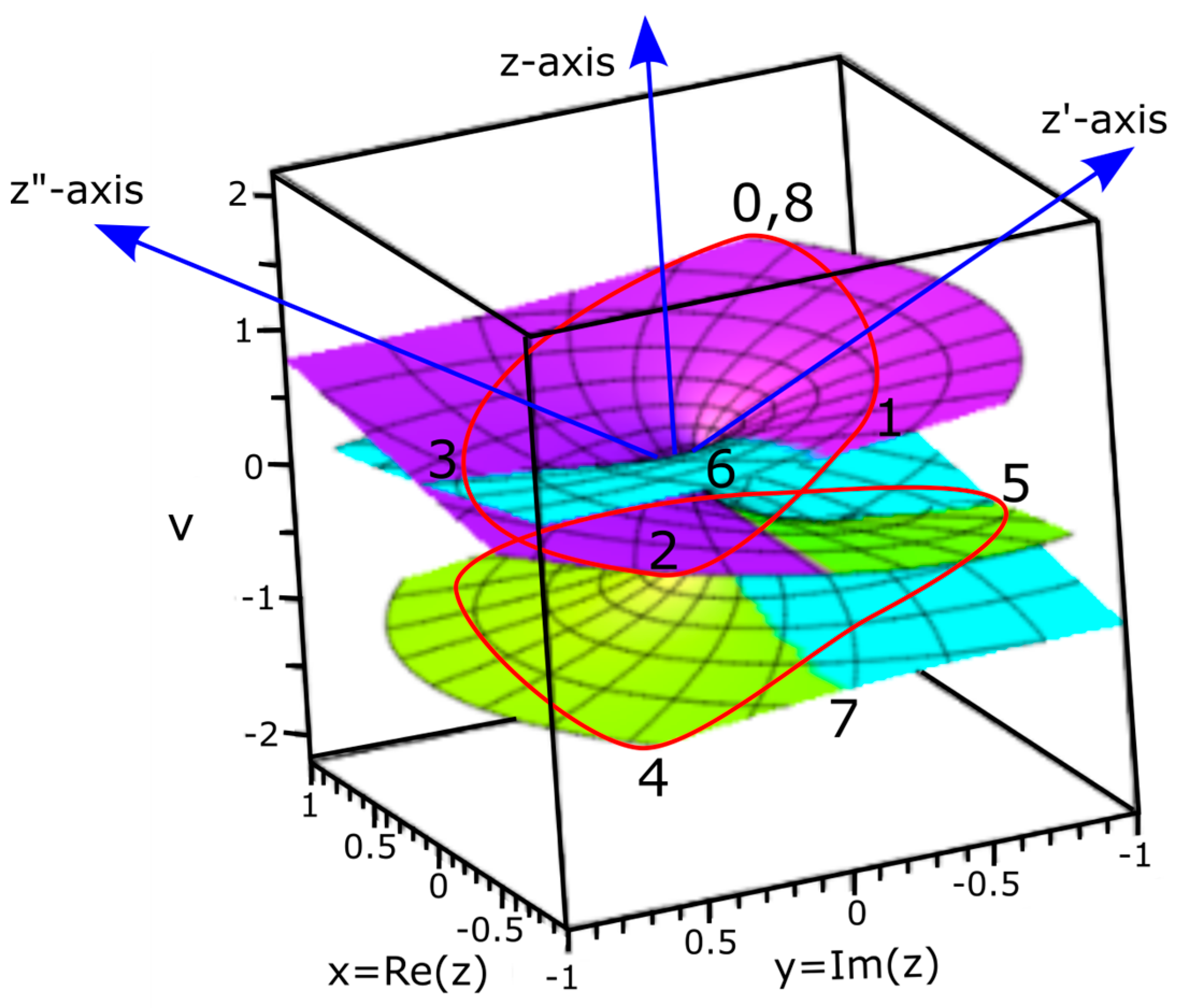
- In flat Euclidean space-time of inertia frame (Figure 1a), any deviation from z-axis of the MP field by precession is trivial, (Figure 1d) and time remains absolute from a background of clock face with distances between any two points being positive and COM is assigned to point-boundary at position 0 as mentioned above. The electron position in space within the model is defined by the Cartesian coordinates, x, y, z. At positions 1 and 3 or 5 and 7, electron-positron transition of superposition states obey Born’s rule, and acquires spin angular momentum to mimic Weyl spinor of Minkowski space-time (Figure 1b). Hyperbolic surface of the light-cone of holonomic is contained within hypersurface of the MP field of Euclidean space towards position 0 of ZPE at N-1. Balancing out of charges at homomorphic positions 1, 3 and 5, 7 is isomorphic to compact topological torus of BO. By clockwise precession, time is relative, i.e., with (Figure 1c). By Lorentz transformation in 1D for accelerated reference frame, the volume or dipole moment of the MP field remains constant so, and with Lorentz factor, and and . Its invariance, and sustains the unitarity of the model. Observation by light-MP model coupling is confined to the electron and its motion and this can relate to Lorentz transformation with any outgoing radiation being of linear time. In this way, 4D Minkowski space-time (Figure 1b) is applicable to multidimension of Euclidean space-time (Figure 1a) with COM by Newtonian gravity assigned to position 0 as mentioned above. Cancellation of charges for the conjugate positions, 1, 3 and 5, 7 transforms the hyperbolic surface of light-cone to compact topological torus (Figure 1c) and these levitates between the hemispheres of the MP field into extra dimensions.
- Singularity towards the nucleus is constrained by the dipole moment of the MP field of an irreducible spinor generated by the electron-positron transition at positions 0 to 3 in repetition. Stochastic behavior from the emergence of envelop solitons at positons 2 and 6 insinuates a chaotic system. Combined with the quantum critical region of the light-cones at positions 1 and 3, the quest towards quantum critical point at the baseline of the hemisphere remains elusive by quantum chaos of butterfly effect for the hydrogen atom (e.g., Figure 1a). Such intuition is important in the pursuit of quantum critical point in condensed matter physics for an array of atoms in one-dimensional line.
- The electron is a point-particle at constant motion, mv and this offers wave-particle duality for the overall spherical reference frame, in accordance with de Broglie relationship. In this case, ±h is assigned to the electron-positron transition of a sinusoidal orbital. The electron is defined by the wave function, and its orbit of time reversal by time derivative is accorded to Schrödinger equation, . It is a fundamental equation with the basis vector, and assumed into Minkowski space-time (Figure 1c) against z-axis as time axis and x-axis equal to distance.
- The electron’s spin-charge of superposition states is linked to BO of topological torus defined by and this is projected in the x-y plane (Figure 1c). Its inner product, sustains unitarity for the electron of weak isospin into n-dimensions of topological torus by disturbance (Figure 1d). The electron’s position can be split into both radial and angular wave functions, . The radial part, is attributed to the principal quantum number, n and angular momentum, l of a light-cone with respect to r (Figure 1c). The angular part, of degenerate states, is assigned to the BO defined by both and (Figure 1d).
- The BO of a constant structure, ɑ is orthogonal to z-axis by linearization (Figure 1d). Its tangential link to electron-positron pair of anticommutation is, for continuous derivation of MP field due to clockwise precession. Linear translation of n-dimensions or n-levels by Fourier transform is by the generalized state, and this is standardized to the z-axis. By continuity, the sum of expansion coefficients, , from the electron’s position offers the expectant value, with its probability given as, .
III. Relevance of Quantum Mechanics on the MP Model
A. Non-Relativistic Wave Function
B. Wave Function Collapse
C. Quantized Hamiltonian
IV. Relevance of Quantum Field Theory on the MP Model
A. Dirac Theory
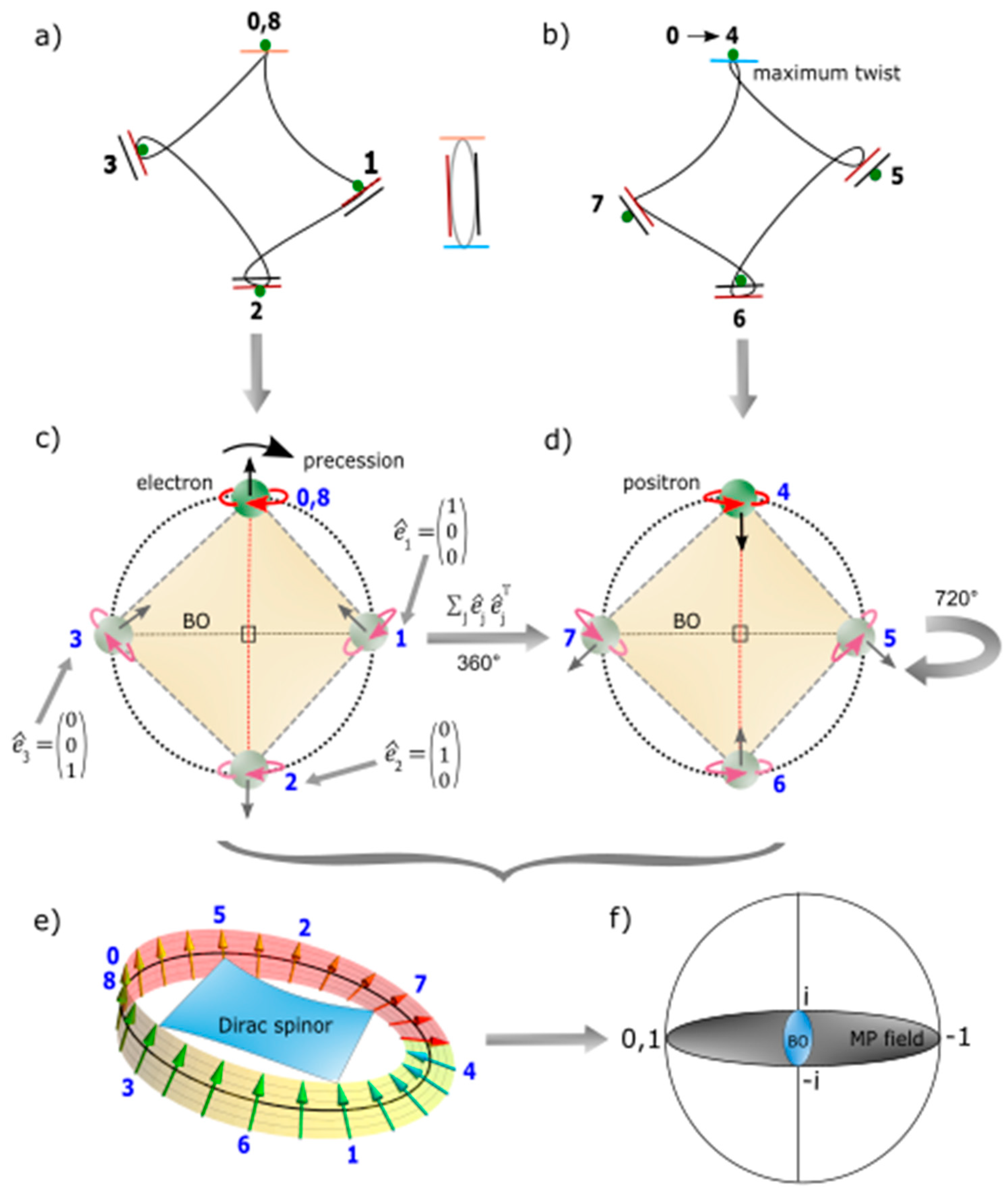
B. Weyl Spinor and Majorana Fermions
C. Lorentz Transformation
V. Space-Time Geometry of the MP Model
A. Space-Time Fabric of an Elliptical Orbit
B. Internal Structure by Lie Group Representation
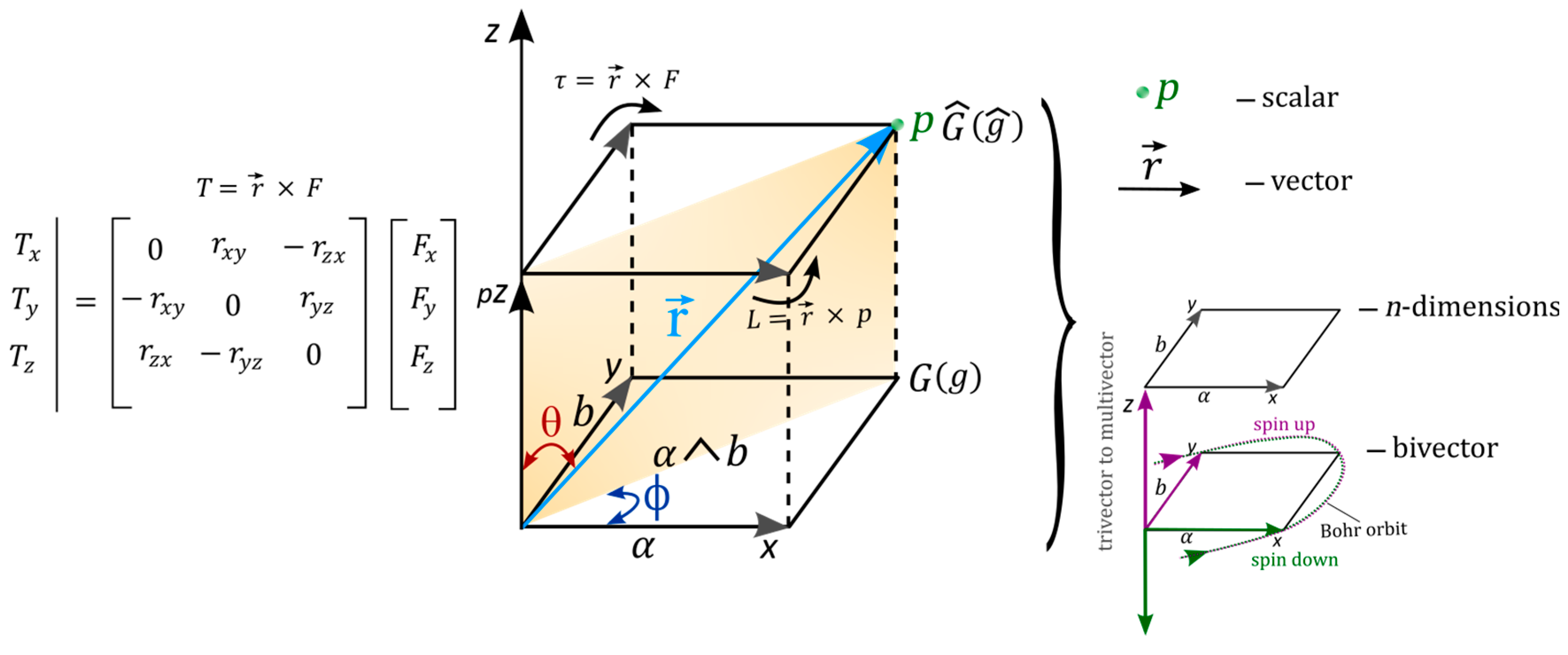
C. Visualization of 2D Manifolds into 4D Space-Time
D. Space-Time Curvature
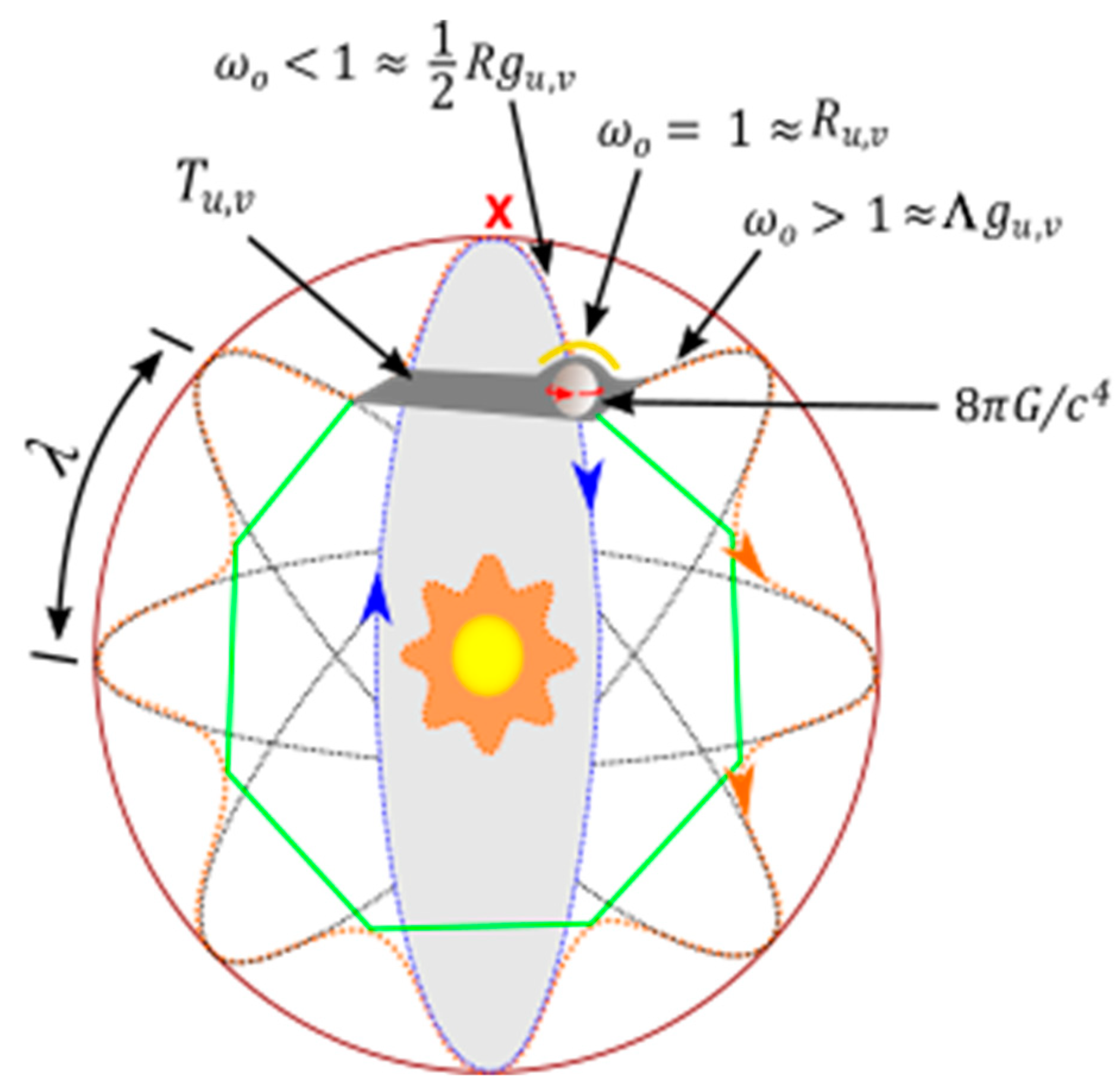
VI. Conclusion
Data availability statement
Competing financial interests
References
- Lanciani, P. A model of the electron in a 6-dimensional spacetime. Found. Phys. 29(2), 251-265 (1999). [CrossRef]
- Nahin, P. Dr. Euler's fabulous formula: cures many mathematical ills (Vol. 52). Princeton University Press (2011).
- Thaller, B. The Dirac Equation. Springer Science & Business Media (2013).
- Sun, H. Solutions of nonrelativistic Schrödinger equation from relativistic Klein–Gordon equation. Phys. Lett. A 374(2), 116-122 (2009). [CrossRef]
- Grandpeix, J. Y. and Lurçat, F. Particle Description of Zero-Energy Vacuum I: Virtual Particles. Found. Phys. 32(1), 109-131 (2002). [CrossRef]
- Nicol, M. Mathematics for physics: an illustrated handbook (2018). [CrossRef]
- Chanyal, B. C. A relativistic quantum theory of dyons wave propagation. Can. J. Phys. 95(12), 1200-1207 (2017). [CrossRef]
- Okun, L. B. C, P, T are Broken. Why Not CPT?. arXiv preprint hep-ph/0210052 (2002).
- Lehnert, R. CPT symmetry and its violation. Symmetry 8(11), 114 (2016). [CrossRef]
- Weiss, L. S. et al. Controlled creation of a singular spinor vortex by circumventing the Dirac belt trick. Nat. Commun. 10(1), 1-8 (2019). [CrossRef]
- Fox, T. Haunted by the spectre of virtual particles: a philosophical reconsideration. J. Gen. Philos. Sci. 39, 35-51 (2008). [CrossRef]
- Silagadze, Z. K. Mirror objects in the solar system?. arXiv preprint astro-ph/0110161 (2001).
- Rieflin, E. Some mechanisms related to Dirac’s strings. Am. J. Phys. 47(4), 379-380 (1979).
- Yuguru, S. P. Unconventional reconciliation path for quantum mechanics and general relativity. IET Quant. Comm. 3(2), 99–111 (2022). [CrossRef]
- Jaffe. R. L. Supplementary notes on Dirac notation, quantum states, etc. https://web.mit.edu/8.05/handouts/jaffe1.pdf (September, 2007).
- Recami, E., Zamboni-Rached, M. and Licata, I. On a Time–Space Operator (and other Non-Self-Adjoint Operators) for Observables in QM and QFT. In BEYOND PEACEFUL COEXISTENCE: The Emergence of Space, Time and Quantum (pp. 371-417) (2016).
- Singh, R. B. Introduction to modern physics. New Age International (2008).
- Machotka, R. Euclidean model of space and time. J. Mod. Phys. 9(06), 1215 (2018). [CrossRef]
- Burdman, G. Quantum field theory I_Lectures. http://fma.if.usp.br/~burdman (October, 2023).
- Oshima, S., Kanemaki, S. and Fujita, T. Problems of Real Scalar Klein-Gordon Field. arXiv preprint hep-th/0512156 (2005).
- Peskin, M. E. and Schroeder, D. V. An introduction to quantum field theory. Addison-Wesley, Massachusetts, USA (1995). [CrossRef]
- Alvarez-Gaumé, L. and Vazquez-Mozo, M. A. Introductory lectures on quantum field theory. arXiv preprint hep-th/0510040 (2005).
- https://en.wikipedia.org/wiki/Spinor (updated February 2024).
- Beenakker, C. W. J. Search for Majorana fermions in superconductors. Annu. Rev. Condens. Matter Phys. 4(1), 113-136 (2013). [CrossRef]
- Jeffrey, D. J. Branch cuts and Riemann surfaces. arXiv preprint arXiv:2302.13188 (2023). arXiv:2302.13188.
- Callahan, J. J. The geometry of spacetime: an introduction to special and general relativity. Springer Science and Business Media (2013).
- Zhelobenko, D. P. Compact Lie groups and their representations. J. Amer. Math. Soc. 40, 26-49 (1973).
- Freed, D. S., Hopkins, M. J., Lurie, J. and Teleman, C. Topological quantum field theories from compact Lie groups. arXiv preprint arXiv:0905.0731 (2009). arXiv:0905.0731.
- Monteiro, R., Nicholson, I. and O’Connell, D. (2019). Spinor-helicity and the algebraic classification of higher-dimensional spacetimes. Class. Quantum Gravity 36(6), 065006 (2019). [CrossRef]
- Naber, G. L. The geometry of Minkowski spacetime. Springer (2012).
- Markley, L. C. and Lindner, J. F. Artificial gravity field. Results Phys. 3, 24-29 (2013). [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




