preprints.org > medicine and pharmacology > pharmacology and toxicology > doi: 10.20944/preprints202208.0171.v1

Preprint Article Version 1 Preserved in Portico This version is not peer-reviewed

Version 1 : Received: 6 August 2022 / Approved: 9 August 2022 / Online: 9 August 2022 (04:19:53 CEST)
Version 2 : Received: 13 September 2022 / Approved: 13 September 2022 / Online: 13 September 2022 (07:53:32 CEST)

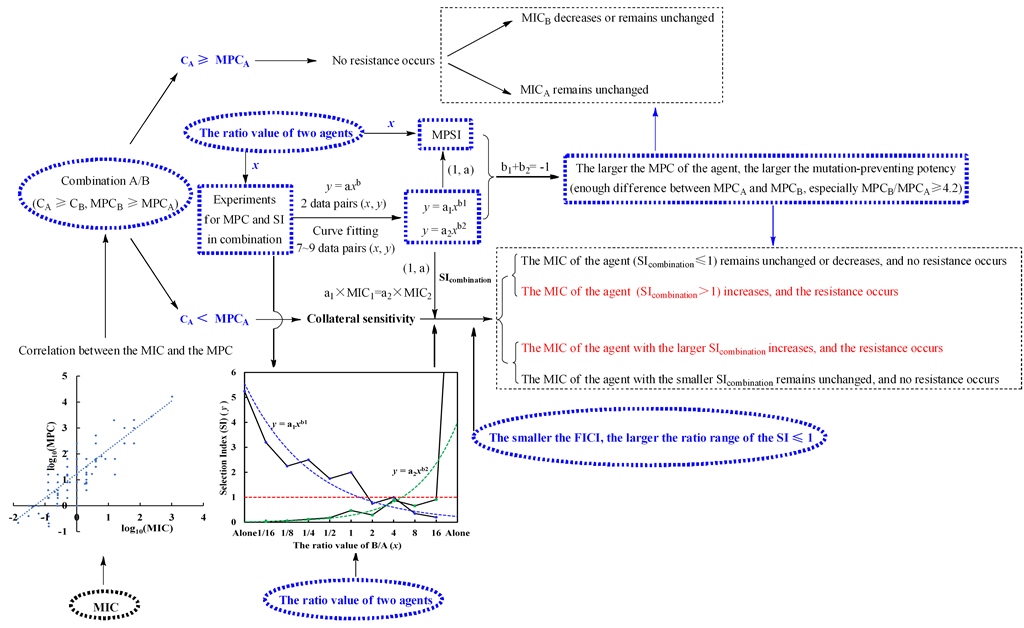
Antimicrobial resistance (AMR) has been a serious threat to human health, and combination therapy is proved to be an economic and effective strategy to fight the resistance. However, the abuse of drug combinations would conversely accelerate the spread of AMR. To guide the practice, some regularity conclusions had been drawn in our previous work. Based on those experimental data, here the power function (y=ax^b, a>0) correlation between the mutant selection index (SI) (y) of one agent and the ratio value (x) of two agents in a drug combination was established, and two rules a₁ × MIC₁ = a₂ × MIC₂ and b₁ + b₂ = -1 were discovered from both equations of y=a₁x^b1 and y=a₂x^b2 for two agents in drug combinations. Simultaneously, it was found that one agent with larger MPC alone for drug combinations would present a larger |b| and show greater potency for narrowing itself MSW and preventing the resistance. Another, a new concept as mutation-preventing selection index (MPSI) was proposed and used for evaluating the mutation-preventing potency difference of two agents in drug combinations, and the positive correlation between the MPSI and the mutant prevention concentration (MPC) or minimal inhibitory concentration (MIC) was subsequently established. Inspired by this, the significantly positive correlation, contrary to previous reports, between the MIC and the corresponding MPC of antimicrobial agents against pathogenic bacteria was established using one hundred and eighty-one of data pairs reported. These above together indicate that the MPCs in alone and combination are very important indexes for drug combinations to predict the mutation-preventing effects and the trajectories of collateral sensitivity, and the MPC of an agent can be roughly calculated from its corresponding MIC. Subsequently, this was further verified and improved by the antibiotic exposure to forty-three groups designed as different drug concentrations and various proportions. Based on these, the diagram of the mutation-preventing effects and the resistant trajectories of drug combinations with different concentrations and ratio of two agents was presented, and the C/MPC for the agent with larger proportion in drug combinations is the key to judge whether the resistance and the collateral sensitivity occur to two agents. Furthermore, the stress factors 1/MPC alone of two agents, together with their SI in combination, are the key to predict the mutation-preventing effects, and control the trajectories of collateral sensitivity. Combined the discussion and analyses for the above results and previous work, a preliminary scheme for antimicrobial combinations preventing the AMR was further proposed for subsequent improvement research and clinic popularization. Moreover, some other proposals and regularity conclusions related to preventing the AMR, involving fractional inhibitory concentration index (FICI), mutant selection index (SI), and pharmacokinetic parameters (t_1/2, AUC₂₄/MPC, C_max/MPC, and f %T > MPC, etc.), were analyzed and discussed, and finally some similar conclusions were speculated for triple or multiple drug combinations.

combination; antimicrobial resistance; selection index; collateral sensitivity; mutant prevention concentration; minimal inhibitory concentration; fractional inhibitory concentration index; stress factor

Medicine and Pharmacology, Pharmacology and Toxicology

* All users must log in before leaving a comment