1. Introduction
Bell, of course, just like Einstein, believed that quantum mechanics implies “Spooky action at a distance.” But contrary to a widespread opinion, we argue that an unbiased reading of Bell’s work shows that he did not claim his inequality proves it. Through a chronological perspective of Bell’s work, we show that the usual argument upholding the nonlocal character of quantum mechanics based on the Bell theorem is inappropriately posed and does not entirely agree with Bell’s ideas.
Consequently, we obtain a polemic formulation that spawns the extreme opposite position taken by the quantum localists, sometimes leading to heated debates [
2,
3,
4,
5]. The localists’ stance reflects in expressions such as:
The terms “non-locality” or “quantum non-locality” are buzzwords in foundations of quantum mechanics and quantum information. Most of scientists treat these terms as a more handy expression equivalent to the clumsy “violation of Bell’s inequalities”. Unfortunately, some treat them seriously.
Expressions like the above represent a common opinion among quantum localists. It would be justified only if quantum nonlocality is assumed to be proved by violations of Bell’s inequalities. Claiming that quantum nonlocality is a consequence of the Bell inequality violation is unconvincing, and most importantly, as his writings show, John Bell avoided interpreting his inequality in that way.
In
Section 2 and
Section 3, we respectively analyze Bell’s 1964 formulation and his papers on nonlocality after 1964. We shall see that, although in some papers he left the issue ambiguous, in a few others, he uncontroversially interpreted his inequality as a no-local-hidden variables theorem instead of a quantum nonlocality theorem.
Then, in
Section 4, we analyze Bell’s actual quantum nonlocality argument. We propose a slight argumentation change that puts on a more formal basis the reasons why quantum mechanics is not locally causal.
Of course, since we are dealing with quantum mechanics interpretation, we also have counterarguments in favor of quantum locality. We briefly review some of those arguments in
Section 5. Finally, we present our conclusions in
Section 6 and
Section 7.
2. The 1964 Bell Theorem
We propose a different reading of Bell’s 1964 theorem [
7] from the usual one. We claim our proposal is more according to what Bell intended in 1964 and clarifies the origin of the conflicts between localists and non-localists. The difference is subtle but crucial.
A usual and widespread interpretation asserts that Bell formulated his inequality to prove that quantum mechanics is not a local theory, presenting the Bell theorem as a quantum nonlocality theorem. But an attentive reading of his 1964 arguments reveals two solid proofs of the contrary:
- a)
Bell already considered quantum mechanics as nonlocal from the beginning, i.e., before formulating his inequality. Indeed, in the third line of the introduction, he wrote: “These additional variables were to restore to the theory causality and locality.” That is, the inclusion of hidden variables into the theory was supposed to modify it and recover locality instead of proving its nonlocality.
- b)
Bell starts the conclusion section by saying: “In a theory in which parameters are added to quantum mechanics....”; so, clearly, he was not inferring properties of quantum mechanics, but only of a modified theory in which parameters are added.
Bell took the argument where EPR [
8] has left it, namely, if local, quantum mechanics must be incomplete. Since the orthodox interpretation asserts quantum mechanics is complete, then, according to EPR, it must be nonlocal. The previous inference was implicit in his expression a) asserting that additional variables were necessary to restore locality. Then, following an EPR-like reasoning, Bell derived determinism and proved through his inequality that a local completion is untenable. Therefore, the impossibility of a local completion only proves that we cannot modify orthodox quantum mechanics to make it local.
Thus, if we accept the EPR reasoning, as Bell did, the inequality is unnecessary to prove quantum nonlocality, so claiming that Bell’s inequality proves it (which Bell did not) would only be circular reasoning.
On the other hand, Bell’s theorem is a mere mathematical theorem that should be free of any polemic if we strictly follow Bell’s rationale, namely, that a local completion is untenable. Richard Feynman put that clearly when he said that Bell’s theorem
It is not an important theorem. It is simply a statement of something we know is true – a mathematical proof of it.
However, we disagree with Feynman about the unimportance of the Bell theorem since it was a significant advancement in the Bohr-Einstein debate that remained stagnant for almost thirty years.
3. Bell’s Theorem after 1964
Bell’s arguments evolved over the years. In later works, he abandoned the polemic EPR reasoning dissipating the fog around it. However, a persistent view remains that dispenses with Bell’s later arguments and insists on a polemic reading of Bell’s 1964 reasoning advertising the Bell theorem as a quantum nonlocality theorem. We call this view “radical non-localist”.
According to the radical non-localist stance, the EPR argument is unassailable. They even consider it an “analytic concept”, i.e., we cannot coherently deny it [
2]. However, as we observed in the previous section, be it analytic or not, when we accept the EPR reasoning, we do not need the inequality to prove quantum nonlocality. Also, Bell’s 1964 paper shows that, unless we dismiss the unambiguous expressions we highlighted in a) and b) of
Section 2, Bell did not invoke his inequality to prove quantum nonlocality in 1964 when he instead used the EPR reasoning.
We do not claim the EPR argument is incorrect. We consider it polemic and point out that Bell, except on the occasions where there is ambiguity, clearly separated his arguments of quantum nonlocality from his inequality, which he used to prove the impossibility of a local completion. Above, ambiguous means he neither claimed his inequality proved quantum nonlocality nor said otherwise. In support of our previous assertion, next, we chronologically review some of Bell’s papers discussing nonlocality after 1964.
3.1. Introduction to the Hidden Variable Problem
In 1971 he wrote the paper “Introduction to the hidden-variable question” [
10]. Here Bell did not mention quantum nonlocality but investigated the de Broglie-Bohm hidden variables theory and highlights its explicit nonlocal character as “the difficulty”.
Without discussing whether the de Broglie-Bohm model proves quantum nonlocality, what concerns us here is what Bell concluded after formulating his inequality and proving that quantum mechanics violates it. He wrote:
Thus the quantum-mechanical result cannot be reproduced by a hidden-variable theory which is local in the way described.
Once more, he did not conclude “quantum-mechanics is not a local theory”. So, those who interpret the previous expression as proof of quantum nonlocality should accept such an interpretation as theirs but not Bell’s.
3.2. The Theory of Local Beables
This article appeared in 1975.
1 Here Bell abandoned the EPR reasoning and introduced the concept of local causality. He argued that quantum mechanics violates this form of locality in
Section 3 without mentioning any inequality. He starts that section by asserting:
1Bell’s work is reproduced in [11].
Ordinary quantum mechanics, even the relativistic quantum field theory, is not locally causal in the sense of (2).
(2) above refers to local causality. Then he develops his quantum nonlocality argument. It is similar to the one given by Einstein in 1927.
2 In the same section, immediately after establishing the nonlocal character of quantum mechanics, Bell explored the problem of adding hidden variables. Then in
Section 4, “Locality inequality”, he derived a stochastic Bell-CHSH inequality. Finally, in
Section 5, he established the impossibility of a local completion by proving that quantum mechanics violates his inequality, concluding:
2Einstein’s argument is reproduced by Laudisa in [12] and also by Harrigan and Spekkens in [13].
So quantum mechanics is not embeddable in a locally causal theory as formulated above.
That is different from concluding, “So quantum mechanics is not a local theory”. Otherwise, why would he bother to prove quantum mechanics violates local causality two sections before without using any inequality or hidden variables? Because he was well aware of the logical loophole of concluding quantum nonlocality from his inequality. As Stapp once clearly explained [
14]:
Thus whatever is proved is not a feature of quantum mechanics, but is a property of a theory that tries to combine quantum theory with quasi-classical features that go beyond what is entailed by quantum theory itself. One cannot logically prove properties of a system by establishing, instead, properties of a system modified by adding properties alien to the original system.
Above, “properties alien to the original system” rigorously mean variables that do not legitimately pertain to quantum mechanics. Although some have observed that the hidden variables can include the quantum state [
1,
15,
16], the problem persists with the other “additional variables”. As we observe in Appendix 8, the Bell inequality cannot be formulated without additional variables foreign to quantum mechanics, notwithstanding that one of those variables may include the quantum state.
3.3. Bertlmann’s socks
In 1981 Bell wrote his celebrated paper “Bertlmann’s socks and the nature of reality” [
17]. On this occasion, Bell did not explicitly prove quantum nonlocality before formulating the inequality. He based his arguments on EPR. But he also uses common causes to explain local correlations.
This is one of the papers where he left ambiguous whether his inequality violation should be interpreted as proof of quantum nonlocality. Can we assume that Bell changed his mind about the meaning of his inequality? We do not think so because, in his last paper (cf.
Section 3.4), he returned to his previous formulations, i.e., either accepting (1964) or proving (1975) quantum nonlocality without introducing hidden variables or mentioning any inequality.
In [
17], Bell chose intuition and ease of interpretation over logical rigor. In Bell’s own words, this paper was one of those that:
...are nontechnical introductions to the subject. They are meant to be intelligible to nonphysicists.
That is why he spent great effort explaining the difference between quantum and classical entanglement through naive analogies, such as those of Mr. Bertlmann’s socks.
3.4. La nouvelle cuisine
This is Bell’s last paper which appeared in 1990 [
19]. Here again, Bell’s view of his inequality and quantum nonlocality is crystal clear. This time Bell mentions EPR in the two sections that concern us here. In
Section 8, when proving that “Ordinary quantum mechanics is not locally causal” without mentioning any inequality and without actually using an EPR argument. Then, in Section 10, when explicitly introducing hidden variables as local common causes, for proving, through his inequality, that:
Quantum mechanics cannot be embedded in a locally causal theory
Again the order in which he presents his argument, first establishing quantum nonlocality without using any inequality and then proving the impossibility of a local completion, is unambiguous and uncontroversial. Thus, those who interpret the expression “Quantum mechanics cannot be embedded in a locally causal theory” as proof of quantum nonlocality should not ascribe their interpretation to John Bell.
4. Bell’s Proof of Quantum Nonlocality
In this section, we closely analyze Bell’s arguments about the nonlocal character of quantum mechanics. In his 1975 paper, “The theory of local beables” [
11], Bell gave an explicit argument for quantum nonlocality for the first time. This paper has four outstanding characteristics that were missing in 1964:
A rigorous definition of locality he called local causality (LC).
A proof that quantum mechanics violates LC, therefore, is nonlocal.
A physical justification for assuming what later became known as the statistical independence (SI) hypothesis. In 1964, SI was an ad hoc implicit assumption.
An absence of any reference to the EPR paper.
Next, we briefly address each of these characteristics.
4.1. Local Causality3
3An excellent and didactic exposition of the concept can be found in [1].
Bell’s definition of LC is a formalization of the idea that, according to relativity theory, interactions can happen only at a finite speed. It means that causes cannot have an instantaneous effect on distant events. He formulated LC so that it can be applied to not deterministic theories like quantum mechanics. It is a locality argument that avoids a purportedly classical EPR-like reasoning. A concept directly applicable to orthodox quantum mechanics without distorting its nature.
For the particular case that concerns us, i.e., the singlet state correlations in a Bell-type experiment, LC takes the following form. Let
be the probability of a joint measurement giving the results
conditional on the respective measurements directions
. The laws of probabilities require
So far, it is just about probabilities. Let us now add some physics and assume that both observers, Alice and Bob, choose their measurement directions at the last moment so that both measurements are spacelike separated events. Then LC requires that neither the results
nor the measurement settings
made on one side can affect the state of affairs on the other side. However, we cannot exclude the existence of correlations. In the r.h.s of (
1), we can have that
notwithstanding that events
A and
a are spacelike separated from
B and
b. However, relativistic causality requires the correlations implied by (
2) and (
3) to be explained by local common causes
. They are local because they are supposed to lie at the intersection of the backward light cones of the measurement events. Once the common causes
are specified, the inclusion of spacelike separated parameters in the l.h.s of (
2) and (
3) become redundant
Including
in (
1)
Replacing (
4) and (
5) in (
6)
The last equation is also known as the screening-off condition. It is the formal expression of the intuitive idea behind relativistic locality and is Bell’s definition of LC for the case at hand.
The common cause is usually called “hidden variables”; however, it is somewhat misleading to believe the variables are necessarily unknown parameters. The only condition they need to comply with is lying at the intersection of the backward light cones of the measuring events to constitute a local explanation of the correlations. It is also utterly misleading to think they are EPR elements of physical reality; on the contrary, their role is to eliminate any EPR-like argument. Furthermore, local causality is independent of the stochastic properties of the common causes. More concretely, they are independent of the statistical independence hypothesis.
Although Bell did not mention Reichenbach, his
variables are according to Reichenbach’s common cause principle [
20]. The last point is relevant because, as we shall see later, one possibility to block the argument in favor of quantum nonlocality is to reject Reichenbach’s principle of common causes [
21].
4.2. Quantum Nonlocality
After defining local causality, Bell gave an argument explaining why, when considered complete, quantum mechanics violates it. Bell’s argument is similar to the one given by Einstein in 1927.
4
4Einstein’s argument is reproduced by Laudisa in [12] and also by Harrigan and Spekkens in [13].
We can recast Bell’s and Einstein’s arguments in more formal terms through the mathematical formulation of local causality. The crucial point is that (
7) avoids the polemic around an EPR-like classical argument. If quantum mechanics is complete and local, the locally causal explanation of its correlations must lie within the quantum state. In our case
Thus, if locally causal, ordinary quantum mechanics must satisfy (
7) when
However, choosing
,
, and
, an elementary quantum mechanical calculation gives
Given that (
10) is not widely known as a non-classical argument for quantum nonlocality, and some find (
9) puzzling or inappropriate, appendix 8 contains a detailed explanation.
Since in (
10)
, ordinary quantum mechanics lacks a locally causal explanation of its correlations, i.e.,
the quantum state alone cannot screen-off events on one side from spacelike separated events on the other far away side. Hence, it conspicuously fails the LC locality criterion.
Note that (
10) is not an EPR-like argument. It relies exclusively on quantum mechanical objective predictions. It is independent of the wave function interpretation and wave function collapse. In particular, it is independent of the ontic or epistemic nature of the quantum state, depending only on the quantum formalism irrespective of any interpretation. It is an argument in line with the Copenhagen approach, an operational definition that does not rely on metaphysical assumptions.
Formally, that is the counterargument against claims asserting the singlet correlations find a local common cause explanation in their preparation with the same generating event [
22]. There is no doubt they find an explanation in their preparation. Unfortunately, that explanation is not locally causal because all we know from its preparation is its quantum state, and as (
10) proves, it does not contain a common cause explanation. Nor does the magic of superposition justify those correlations, at least in a locally causal way [
23].
As we explained in
Section 3.2, Bell introduced his inequality only after proving that quantum mechanics is not a locally causal theory. The controversial approach of using a “classical inequality” to derive properties of quantum theory is not ascribable to John Bell. Unfortunately, often the same does not apply either to localists or non-localists [
1,
2,
3,
6,
15,
16,
23,
24,
25].
4.3. Statistical Independence
As we mentioned above, in Bell’s 1964 paper, he implicitly assumed the hidden variables distribution function
5 was not conditional on the experimental settings
a and
b.
We can justify (
11) by requiring the experimental settings to be independent of the same common factors
affecting the results
According to Bayes theorem we have
Then from (
12) and (
13) we get (
11). The ansatz (
12) seems to be a reasonable assumption justifying (
11).
5Note that the distribution function of the common causes is irrelevant for the definition of local causality. is necessary only to derive the Bell inequality.
Thus, (
12) and (
11) are equivalent and are known as
statistical independence,
measurement independence,
freedom, or
no-conspiracy. We shall come back to SI in
Section 5.3.
4.4. The EPR Paper
Although Bell conceived his 1964 paper as a continuation of the EPR argument, one of the virtues of his 1975 formulation is not referencing the EPR paper. Besides presumably being a classical-like argument, the EPR reasoning contains an unnecessary construction that has been the source of much superfluous metaphysical speculation, namely, the elements of physical reality.
The reality criterion has a highly metaphysical burden because it assumes the existence of physical magnitudes from the mere possibility of predicting their values, notwithstanding that we do not indeed measure them. They are unnecessary because they are employed neither to prove quantum nonlocality (
10) nor to derive the Bell inequality [
26].
Bohr attacked the reality criterion [
27]. Einstein did not write the EPR paper, and he did not like how it came out. In a letter to Schrödinger he wrote
But still it has not come out as well as I really wanted; on the contrary, the main point was, so to speak, buried by erudition [
28]
Einstein based his argument for incompleteness in his separation principle and avoided any reference to the reality criterion. Thus, it is worth noticing that Einstein and Bell distanced themselves from the original EPR elements of physical reality criterion. Even in 1964, when Bell referenced the EPR article, he never mentioned the elements of physical reality.
5. Quantum Locality
We briefly mention three counterarguments that may justify considering quantum mechanics as a local theory. Only the third one contemplates the use of the Bell theorem and is related to the Bell inequality. We mention them only for completeness as possible logically admissible counterarguments.
These arguments are, of course, well-known and not new. There are also others we do not mention, such as the many-worlds interpretation and QBism, that also claim to preserve quantum locality.
5.1. Rejecting Local Causality
Jarrett [
29] helped clarify the nature of local causality by decomposing it into the conjunction of two different conditions, which Shimony respectively called parameter independence (PI) and outcome independence (OI)
6Shimony also proposed the more picturesque expressions controllable and uncontrollable nonlocality, respectively. We refer the non-specialist to Ref. [
30] for a detailed explanation of these concepts.
6Jarrett used the terms “locality” and “completeness”, implying that PI alone is locality. Shimony terminology is better because it is more neutral.
Jarret proved that a theory complying with PI is no-signaling. He also showed quantum mechanics respects PI, hence is no-signaling. However, quantum mechanics violates OI, thus violating LC.
We can effectively block the argument in favor of quantum nonlocality by adopting parameter independence as the appropriate concept for locality and rejecting outcome independence as a necessary condition.
In summary, by accepting no-signaling (parameter independence) as a sufficient criterion for locality, we reject the more stringent condition of local causality, recovering quantum mechanics locality. Of course, those who claim quantum mechanics is not local will not accept the definition [
31].
However, more rational discussions are possible by explicitly acknowledging the different criteria. It is fair to note that even some who can be considered radical nonlocalists accept that quantum nonlocality is not right out “action at a distance” [
32].
5.2. Rejecting Realism
Realism has been justly criticized as an obscure concept [
4,
15,
33,
34]. However, there is a concrete meaning we can ascribe to realism for rejecting quantum nonlocality, namely, causal explanation.
Please note that this rational meaning of realism has nothing with the usual metaphysical significance related to the term realism in the common expression “local realism”, which is purportedly ruled out by the Bell inequality violation [
35].
Causation in physics has been criticized by Bertrand Russell in 1912 [
36] and was proposed to solve the quantum nonlocality problem by Van Fraassen in 1982 [
37]. There is no action at a distance simply because there is no need for a causal explanation.
Whether we like it or not, when we interpret realism as a causal explanation, its rejection constitutes a logically correct option to solve the quantum nonlocality problem.
5.3. Completing Quantum Mechanics
This approach is different from the former two because it implies going beyond orthodox quantum mechanics. If we are willing to accept local causality as the correct locality concept and recover a causal explanation, we must consider quantum mechanics as an emergent theory.
We can complete quantum mechanics with local hidden variables if we reject statistical independence. The 1975 version of the Bell theorem is
Thus, we can retain local causality in a hidden variables theory by rejecting statistical independence. Indeed, well-known local hidden variables models exist reproducing the singlet correlations violating statistical independence [
38,
39].
Whether statistical independence is a necessary physical condition is a contentious issue. According to some physicists, its rejection is a rational position [
40,
41,
42]. Others, including John Bell [
17], sustain its rejection as inadmissible since it purportedly compromises the experimental freedom implying unreasonable conspiracies.
6. Conclusions
Accepting Bell’s interpretation of his inequality requires a modification in a widespread view allowing a more rational approach to the current controversy around the not local character of quantum mechanics.
A stance we dub as radical non-localist interprets the Bell inequality violations as definitive proofs of quantum nonlocality [
1,
2,
15,
16,
25,
43,
44]. That interpretation, however, is controversial and does not fairly reflect Bell’s clear line of reasoning. It spawns a radical localist stance asserting no solid arguments exist for sustaining the nonlocal character of quantum mechanics [
3,
6,
22,
23]. Radical localists base their assertions on plain statements such as:
Thus the usual derivations of CHSH and other Bell inequalities employ classical physics to discuss quantum systems, so it is not surprising when these inequalities fail to agree with quantum predictions, or the experiments that confirm these predictions.
In fact, since all derivations (either deterministic or stochastic) of Bell-type inequalities are not based on quantum formalism, the former claim is arguably well justified.
The current impasse arises from the incorrect mixing of two different issues, the arguments for quantum nonlocality on the one hand and quantum completion on the other. We propose a clear separation of those arguments that imply changing the usual interpretation of the Bell theorem as a quantum nonlocality theorem. Our proposed reinterpretation, however, is far from being original. It is already there, explicit and well-documented, in the writings that John Bell has left us.
In 1964, Bell assumed nonlocality from the beginning, and only afterward he derived his inequality to prove that a rational local completion is untenable. Then, in 1975 [
11] and again in 1990 [
19], he proved that quantum mechanics is not locally causal before setting out his inequality.
7 In all cases, the conclusion he drew from his line of reasoning, i.e., the thesis of his theorem, was:
7Unfortunately, Bell did not make this point explicitly clear in one of his most celebrated papers, as we explained is sect. Section 3.3.
Quantum mechanics cannot be embedded in a locally causal theory.
Because the alleged locally causal theory is a hidden variables theory, it is questionable to argue that quantum nonlocality should follow from the Bell theorem. That explains why Bell was so reticent to conclude from his inequality that quantum mechanics is not local.
We call for the scientific community to vindicate John Bell and not to distort his clear line of reasoning as he laid it out from 1975 onwards. The allegedly not local character of orthodox quantum mechanics arises because it violates local causality (or, equivalently, the common cause principle), not because it violates Bell-type inequalities.
Admittedly, it could be confusing that since local causality is a hypothesis of the Bell inequality in (
15), wouldn’t its violation by quantum mechanics implies that the last violates local causality? The answer is negative because the target of the inequality is “classical theories”, i.e., theories containing parameters that are not present in orthodox quantum mechanics (cf. discussion after (32)).
Thus, quantum mechanics’ violation of local causality requires independent proof, such as in (
10) or done by Bell in [
19,
45]. Hence, Bell did not intend his inequality to prove quantum nonlocality. As an unbiased reading of his papers reveals, there is no evidence to claim otherwise. A coherent formulation requires that the Bell theorem be a no-local-hidden-variables theorem, not a quantum nonlocality theorem.
7. Final Remarks
Simultaneity and nonlocality are closely related concepts. Both lack direct and clear-cut physical determination. Admitting a certain degree of convention is necessary if we want to maintain a coherent level of discourse. Although the locality problem will remain controversial, it is essential to recognize its contentious nature for the correct motives instead of incorrect or obscure reasonings.
The quantum nonlocality problem cannot be summarily dismissed by looking for trivial conceptual or logical issues within the Bell-type inequalities and Bell’s arguments [
22,
46,
47,
48] or through superfluous metaphysical ideas [
35]. Quantum mechanics may require a revision of our notion of causality, just as relativity prompted us to revise our concept of simultaneity. The other possibility is that quantum mechanics is emergent and, because of Bell’s theorem, that would require the acceptance of superdeterminism.
8 These options are still valid open questions, and pretending they are closed or inexistent is not the best scientific attitude.
8By superdeterminism we mean the violation of the mathematical condition (11) without implying any particular interpretation.
8. Appendix
Some researchers find it perplexing that the quantum state
can be considered a common cause in the definition of local causality. That is owed to the incorrect metaphysical meaning usually attached to the
variables as preexisting EPR elements of physical reality [
49] or a necessarily classical concept.
Sustaining that
is by necessity an element foreign to quantum mechanics amounts to forbidding the application of the local causality concept to quantum mechanics. It is particularly convenient for summarily dismissing its annoying nonlocal character decreeing it local by construction [
3]. But the physical meaning of
is not limited to classical or metaphysical concepts other than representing local common causes. Bell also explained that the hidden variables may include the quantum state:
It is notable that in this argument nothing is said about the locality, or even localizability, of the variable . These variables could well include, for example, quantum mechanical state vectors, which have no particular localization in ordinary space-time.
Unfortunately, researchers often grossly overlook Bell’s explanation of the meaning of the
variables. They generally identify
with metaphysical entities such as preexisting values [
49] or believe they must necessarily be unknown parameters.
The particular case is necessary to formalize Bell’s (and Einstein’s) qualitative arguments of quantum nonlocality according to the rigorous definition of local causality. This step is in complete agreement with viewing the quantum state as already containing the local common cause capable of explaining the quantum correlations. At least if quantum mechanics, as some people claim, is locally causal. Thus, there is no valid argument against submitting quantum mechanics, within its own rules, to the local causality test.
To see whether ordinary quantum mechanics complies with the local causality criterion, all we have to do is set
in (
7) with
given by (
8), where
and
denote the spin eigenstates in the
z-direction. We assume that motion takes place in
y direction with setting angles
a and
b lying the
plane measured with respect to the
z axis. If
and
are the spin eigenstates in the
a direction
Analogously for the particle measured at the other laboratory, we have
The joint probability according the quantum formalism is
Letting
,
according to (
8), (
16) and (
19)
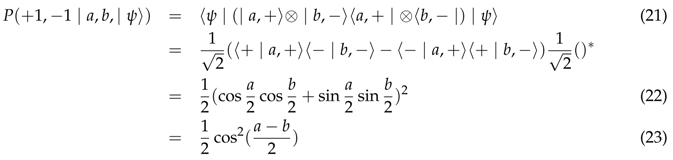
Where
represents the complex conjugate of the first factor in parenthesis. If we further assume
, (23) gives
When we perform a measurement only in Alice’s laboratory, the quantum formalism prescribes
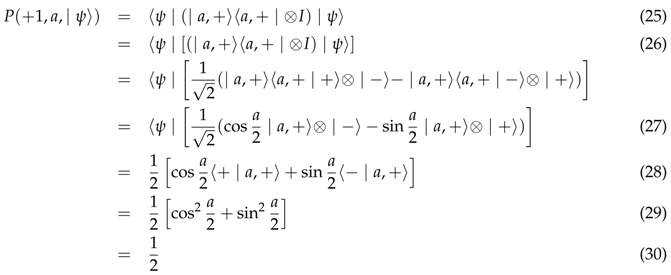
Where
is the identity operator in the one particle two-dimensional Hilbert-space. In a similar way, performing a measurement only on Bob’s laboratory we find
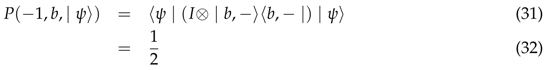
From (
24), (30), and (32), we obtain (
10) formally proving that ordinary quantum mechanics lacks a local common cause explanation for its correlations.
As we explain in the main text and contrary to widespread beliefs, Bell inequality violation does not tell us that quantum mechanics is not local. Nonlocality follows from quantum formalism itself. John Bell (and Einstein) did not claim otherwise. What is puzzling about the Bell theorem is that we cannot complete quantum mechanics with additional parameters under reasonable assumptions, proving that the experimentally tested quantum predictions seem to be hopelessly nonlocal. Probably that would have disappointed Einstein.
The violation of local causality by quantum mechanics through the singlet state is well known and was observed by other authors [
1,
16]. However, most non-localists give it only a superficial importance. They prefer to use the Bell inequality as their main argument. On the other hand, localists conveniently overlook it.
For instance, in Ref. [
1], Norsen ultimately presents the CHSH inequality as a quantum nonlocality proof when, after taking for granted statistical independence, he declares:
...the empirically violated Clauser-Horne-Shimony-Holt inequality can be derived from Bell’s concept of local causality alone, without the need for further assumptions involving determinism, hidden variables, “realism,” or anything of that sort.
In our opinion, that move is unwarranted and justifies the opposite stance held by localists. Indeed, the CHSH inequality cannot be formulated without hidden variables or common causes not present in quantum mechanics precisely because quantum mechanics violates (
7), as proved by (
10). Certainly, proving Bell-type inequalities require writing joint probabilities as
which is impossible without going beyond quantum mechanics. Admittedly, it is a trivial logical loophole. However, an endemic loophole that is frequently exploited by localists to debunk even the most lucid quantum nonlocality presentations like the one by Brunner et al. [
43] where again (
7) is correctly explained but finally (
33) is highlighted as the “locality constraint”, declaring
This is the content of Bell’s theorem, establishing the nonlocal character of quantum theory and of any model reproducing its predictions.
Quantum localists respond by saying that since the inequality based on (
33) is not about quantum mechanics, it signals the nonlocality of something else. That is why the Bell theorem concerns the impossibility of a local completion of quantum mechanics. Most importantly, It is unfounded and unfair to claim that John Bell interpreted otherwise.
References
- Travis Norsen. John S. Bell’s concept of local causality. American Journal of Physics 2011, 79, 1261–1275. [CrossRef]
- Tim Maudlin. What Bell did. J. Phys. A 2014, 47, 424010. [CrossRef]
- R. F. Werner. Comment on “What Bell did”. J. Phys. A 2014, 47, 424011. [CrossRef]
- Tim Maudlin. Reply to comment on What Bell did. J. Phys. A 2014, 47, 424012. [CrossRef]
- R. F. Werner. What Maudlin replied to, 2014.
- M. Zukowski and C. Brukner. Quantum non-locality it ain’t necessarily so. Phys. A: Math. Theor. 2014, 47, 424009. [CrossRef]
- J. S. Bell. On the Einstein-Podolsky-Rosen paradox. Physics 1964, 1, 195–200. [CrossRef]
- A. Einstein, B. Podolsky, and N. Rosen. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 1935, 47, 777–780. [CrossRef]
- Andrew Whitaker. RICHARD FEYNMAN AND BELL’S THEOREM. American Journal of Physics 2016, 84, 493–494. [CrossRef]
- J. S. Bell. Speakable and Unspeakable in Quantum Mechanics, chapter Introduction to the hidden variable question, pages 36–37. Cambridge University Press, Cambridge, 2004.
- J.S. Bell, A. Shimony, M.A. Horne, and J.F. Clauser. An exchange on local beables. Dialectica 1985, 39, 85–110.
- F. Laudisa. Counterfactual Reasoning, Realism and Quantum Mechanics: Much Ado About Nothing? Erkenn 2019, 84, 1103–1118. [CrossRef]
- Nicholas Harrigan and Robert W. Spekkens. Einstein, Incompleteness, and the Epistemic View of Quantum States. Foundations of Physics 2010, 40, 125–157. [CrossRef]
- Henry P. Stapp. Quantum Locality? Foundations of Physics 2012, 42, 647–655. [CrossRef]
- Nicolas Gisin. Non-realism: Deep Thought or a Soft Option? Foundations of Physics 2012, 42, 80–85. [CrossRef]
- F. Laudisa. Stop making sense of Bell’s theorem and nonlocality? European Journal for Philosophy of Science 2018, 8, 293–306. [CrossRef]
- J. S. Bell. Bertlmann’s socks and the nature of reality. Journal of Physque 1981, 42, 41–61.
- J. S. Bell and Alain Aspect. Preface to the first edition, pages 11–13. Cambridge University Press, Cambridge, 2 edition, 2004.
- J. S. Bell. La nouvelle cuisine, pages 216–234. WORLD SCIENTIFIC, Farrer Road, Singapore 912805, 2001.
- Christopher Hitchcock and Miklós Rédei. Reichenbach’s Common Cause Principle. In Edward N. Zalta, editor, The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University, spring 2020 edition, 2020.
- Eric G Cavalcanti and Raymond Lal. On modifications of Reichenbach’s principle of common cause in light of Bell’s theorem. Journal of Physics A: Mathematical and Theoretical 2014, 47, 424018. [CrossRef]
- Robert Griffiths. Nonlocality claims are inconsistent with Hilbert-space quantum mechanics. Physical Review A 2020, 101, 022117. [CrossRef]
- S. Boughn. Making sense of Bell’s theorem and quantum nonlocality. Found. of Phys. 2017, 47, 640–657. [CrossRef]
- Robert B. Griffiths. Reply to “Comment on ‘Nonlocality claims are inconsistent with Hilbert-space quantum mechanics’ ”. Phys. Rev. A 2021, 104, 066202. [CrossRef]
- S. Goldstein, T. Norsen, D. Tausk, and N. Zanghi. Bell’s theorem. Scholarpedia 2011, 6, 8378.
- J. P. Lambare and R. Franco. A Note on Bell’s Theorem Logical Consistency. Found Phys. 2021, 51.
- Niels Bohr. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 1935, 48, 696–702. [CrossRef]
- Don Howard. Einstein on locality and separability. Studies in History and Philosophy of Science Part A 1985, 16, 171–201. [CrossRef]
- Jon P. Jarrett. On the Physical Significance of the Locality Conditions in the Bell Arguments. Noûs 1984, 18, 569–589. [CrossRef]
- Abner Shimony. Controllable and uncontrollable non-locality, volume 2, pages 130–139. Cambridge University Press, Cambrige, 1993.
- Travis Norsen. Local Causality and Completeness: Bell vs. Jarrett. Found. Phys. 2009, 39, 273–294. [CrossRef]
- Nicolas Gisin. Quantum non-locality: from denigration to the Nobel prize, via quantum cryptography. Europhysics News 2023, 54, 20–23. [CrossRef]
- T. Norsen. Against “realism”. Found. Phys. 2007, 37, 311–454.
- F. Laudisa. The Uninvited Guest: “Local Realism” and the Bell Theorem. In de Regt H., Hartmann S., and Okasha S., editors, The European Philosophy of Science Association Proceedings, vol 1. Springer, Dordrecht, 2012.
- Justo Pastor Lambare. On the Meaning of Local Realism. Found Phys 2022, 52.
- Bertrand Russell. On the notion of cause. Proceedings of the Aristotelian Society 1913, 13, 1–26. [CrossRef]
- B. C. Van Fraassen. The Charybdis of realism: epistemological implications of Bell’s inequality. Synthese 1982, 52, 25–38. [CrossRef]
- Michel Feldmann. New loophole for the Einstein-Podolsky-Rosen paradox. Foundations of Physics Letters 1995, 8, 41–53. [CrossRef]
- Julien Degorre, Sophie Laplante, and Jérémie Roland. Simulating quantum correlations as a distributed sampling problem. Phys. Rev. A 2005, 72, 062314. [CrossRef]
- Michael J. W. Hall. The Significance of Measurement Independence for Bell Inequalities and Locality, pages 189–204. Springer International Publishing, Cham, 2016.
- Sabine Hossenfelder and Tim Palmer. Rethinking superdeterminism. Frontiers in Physics 2020, 8, 139. [CrossRef]
- Gerard ’t Hooft. Fast Vacuum Fluctuations and the Emergence of Quantum Mechanics. Foundations of Physics 2021, 51.
- Nicolas Brunner, Daniel Cavalcanti, Stefano Pironio, Valerio Scarani, and Stephanie Wehner. Bell nonlocality. Rev. Mod. Phys. 2014, 86, 419–478.
- Tumulka and Roderich. Quantum Nonlocality and Reality: 50 Years of Bell’s Theorem, chapter The Assumptions of Bell’s Proof, pages 79–90. Cambridge University Press, Cambridge CB2 8BS, United Kingdom, 2016.
- J. S. Bell. Locality in quantum mechanics: reply to critics. Epistemological Letters 1975, 2–6.
- Andrei Khrennikov. Epr-Bohm Experiment and Bell’s Inequality: Quantum Physics Meets Probability Theory. Theoretical and Mathematical Physics 2008, 157, 1448–1460. [CrossRef]
- Th. M. Nieuwenhuizen. Is the contextuality loophole fatal for the derivation of Bell inequalities? Found. Phys. 2011, 41, 580–591. [CrossRef]
- M. Kupczynski. Is the Moon There If Nobody Looks: Bell Inequalities and Physical Reality. Frontiers in Physics 2020, 8, 273. [CrossRef]
- Giuseppe Nisticò. Non Locality Proofs in Quantum Mechanics Analyzed by Ordinary Mathematical Logic. Int J Theor Phys 2014, 53, 3475–3487. [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
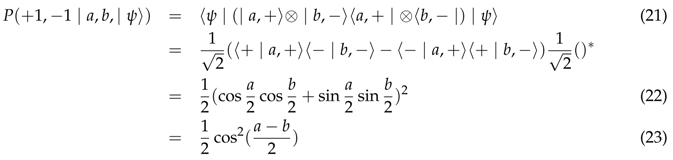 Where represents the complex conjugate of the first factor in parenthesis. If we further assume , (23) gives
Where represents the complex conjugate of the first factor in parenthesis. If we further assume , (23) gives
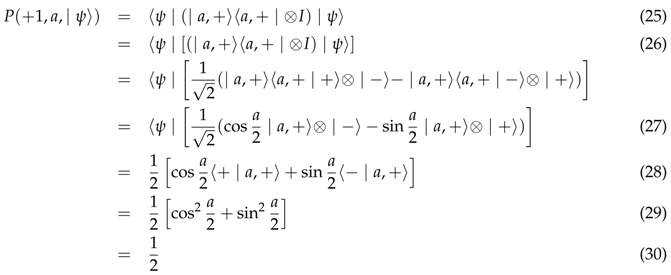 Where is the identity operator in the one particle two-dimensional Hilbert-space. In a similar way, performing a measurement only on Bob’s laboratory we find
Where is the identity operator in the one particle two-dimensional Hilbert-space. In a similar way, performing a measurement only on Bob’s laboratory we find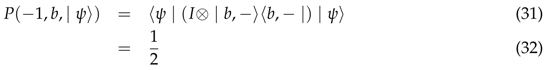 From (24), (30), and (32), we obtain (10) formally proving that ordinary quantum mechanics lacks a local common cause explanation for its correlations.
From (24), (30), and (32), we obtain (10) formally proving that ordinary quantum mechanics lacks a local common cause explanation for its correlations.



