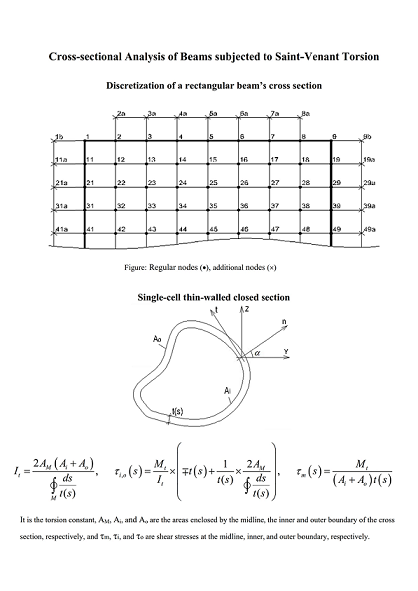
This paper presents an approach to the elastic analysis of beams subjected to Saint-Venant torsion using Green’s theorem and the finite difference method (FDM). The Saint-Venant torsion of beams, also called free torsion or unrestrained torsion, is characterized by the absence of axial stresses due to torsion; only shear stresses are developed. A solution to this torsion problem consists of finding a stress function that satisfies the governing equation and the boundary conditions. The FDM is an approximate method for solving problems described with differential equations; it does not involve solving differential equations, equations are formulated with values at selected nodes of the structure. In this paper, the beam’s cross-section was discretized using a two-dimensional grid and additional nodes were introduced on the boundaries. The introduction of additional nodes allowed us to apply the governing equations at boundary nodes and satisfy the boundary conditions. Beams with solid sections as well as multiply connected cross-sections were analyzed using this model; shear stresses and localized stresses at reentrant corners, torsion constant, and warping displacements were determined. Furthermore, beams with thin-walled closed sections, single-cell or multiple-cell, were analyzed using the Prandtl stress function whereby a linear distribution of the shear stresses over the thickness was considered; closed-form solutions for shear stresses and torsion constant were derived. The results obtained in this study showed good agreement with the exact results for rectangular cross-sections, and the accuracy was increased through a grid refinement. For thin-walled closed sections, the shear stresses obtained at the centerline using the closed-form solutions were in agreement with the values using Bredt’s analysis but the maximal values in the cross-section, which did not necessarily occur at the position with the smallest thickness, were higher; in addition, the results using the closed-form solutions were in good agreement with those using FDM.