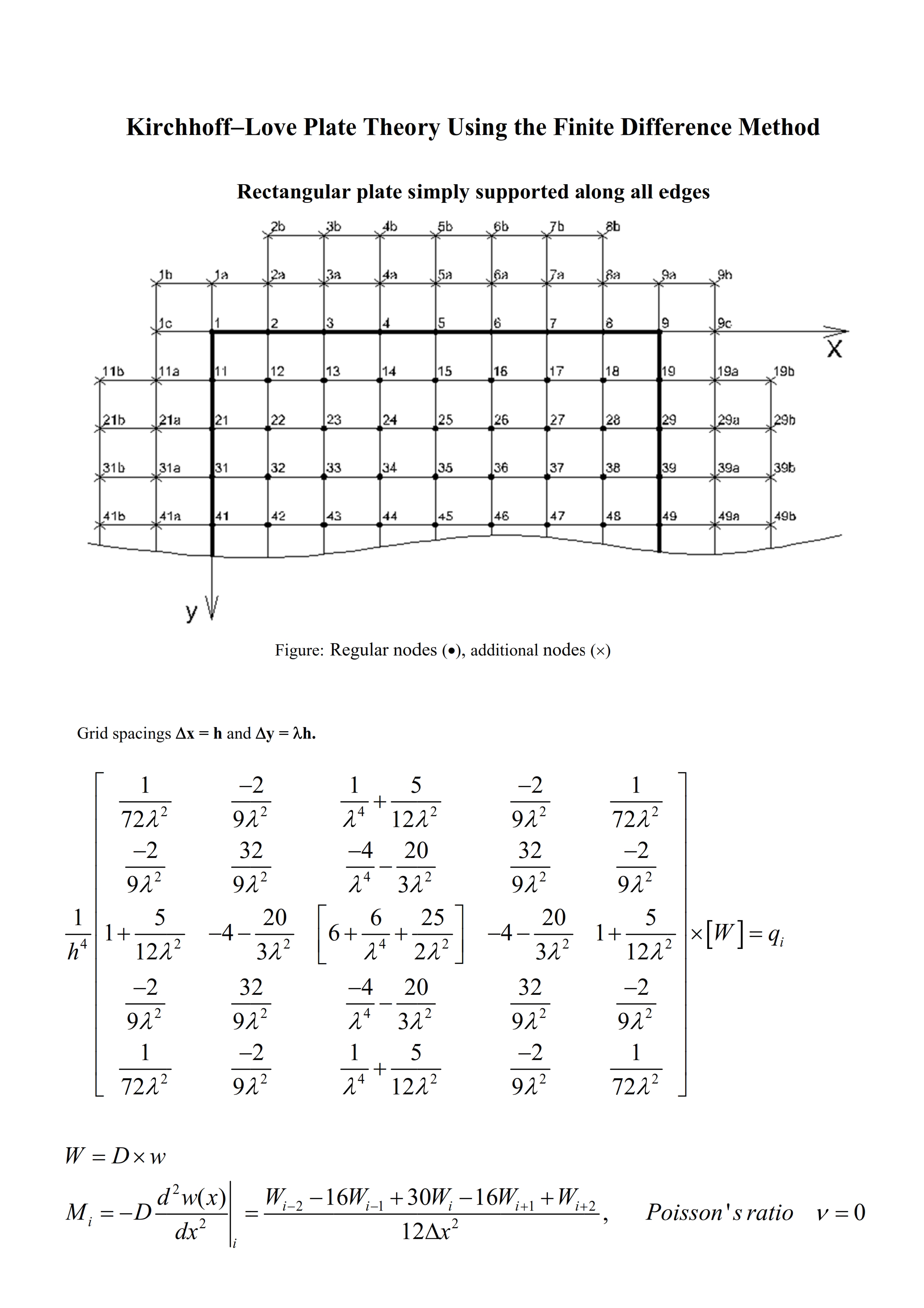
This paper presents an approach to the Kirchhoff-Love plate theory (KLPT) using the finite difference method (FDM). The KLPT covers the case of small deflections, and shear deformations are not considered. The FDM is an approximate method for solving problems described with differential equations. The FDM does not involve solving differential equations; equations are formulated with values at selected points of the structure. Generally in the case of KLPT, the finite difference approximations are derived based on the fourth-order polynomial hypothesis (FOPH) and second-order polynomial hypothesis (SOPH) for the deflection surface. The FOPH is made for the fourth and third derivative of the deflection surface while the SOPH is made for its second and first derivative; this leads to a 13-point stencil for the governing equation. In addition, the boundary conditions and not the governing equations are applied at the plate edges. In this paper, the FOPH was made for all of the derivatives of the deflection surface; this led to a 25-point stencil for the governing equation. Furthermore, additional nodes were introduced at plate edges and at positions of discontinuity (continuous supports/hinges, incorporated beams, stiffeners, brutal change of stiffness, etc.), the number of additional nodes corresponding to the number of boundary conditions at the node of interest. The introduction of additional nodes allowed us to apply the governing equations at the plate edges and to satisfy the boundary and continuity conditions. First-order analysis, second-order analysis, buckling analysis, and vibration analysis of plates were conducted with this model. Moreover, plates of varying thickness and plates with stiffeners were analyzed. Finally, a direct time integration method (DTIM) was presented. The FDM-based DTIM enabled the analysis of forced vibration of structures, with damping taken into account. In first-order, second-order, buckling, and vibration analyses of rectangular plates, the results obtained in this paper were in good agreement with those of well-established methods, and the accuracy was increased through a grid refinement.