On the Indian Tradition of Mathematical Names: A Scientific Analysis

1. Introduction: What’s in a Name?

“What’s in a name? That which we call a rose, by any other name would smell as sweet.” – the famous quote from William Shakespeare’s play Romeo and Juliet (lines 43-44, Act-II, Scene-II) qualifies how the true worth of things outweighs the names per se by which the society may choose to call them. Inconsequential as it may appear on a cursory examination, the names which we use to refer to things, however, possess many covert, imperceptible, and hitherto unexplored implications. For instance, there is ample evidence to show that names can sometimes be given in accordance with the value and significance associated with things across all the cultures of the world. It is thus quite likely that the very premise of “name-giving” and the connotations behind names may possibly have an altogether substantial basis, beyond intangibility and insignificance.

To begin with the most obvious, getting a name can be verily regarded as the inception of a person’s biography, not just a symbol of the beginning of human existence but the onset of a life program. The naming of a child in this context is very much akin to legitimizing a new being by gifting him/her an identity, a means through which the world addresses him, and which in some measure, influences his life script to some degree. A name is a marker of a person’s individuality, and generally shapes one’s conceptions of oneself as well as the impressions others carry of them, during or before the first encounter. An individual, after he has become enough cognizant and conscious of the existence around him, repeats his own name several times to others, sometimes trying to explain its meaning for gaining better acceptability or simply by helping them pronounce it appropriately especially in a foreign land. It is also not uncommon for people to identify closely with people having similar names, and a unique camaraderie oftentimes stems from the shared glory of an identical name or names with similar meanings. In a group or a community setting, a sub-conscious comparison is inevitably drawn between people who share an identical name, signifying a tenuous credulity behind the association of name and assumed merit. More so, if the name of an individual resembles a past name of a stalwart, the society indiscreetly tends to gauge the person’s credentials at par with the personality of distinction, and the person may struggle to live up to the exalted expectations which his name has fortuitously brought upon him. In many of these scenarios, the individuals concerned grow with an increasing awareness of their names and the weight it carries. Hurlock (1985) discusses the consequences of a particular name on a child’s social development. She suggested that as the children expand their social circle and begin to venture outside their homes, it dawns upon them that their peers and adults treat their names as identity symbols, and thus their names can be a measure of their personal appeal or its lack thereof. She presented a comprehensive list of names that can produce negative psychological consequences. These names are typically so familiar and nondescript that their bearers are divested of any uniqueness, or so abstruse that a person becomes highly conspicuous, names that rob the gender identity, names so long that others are compelled to use shortened versions or diminutives which are unpleasant and demeaning. Similarly, prior research has shown that foreign-sounding names and symbolic names are also burdensome (James and Jongeward 1971).

Beyond psychological implications, the process of giving a name to a child can also be examined from other perspectives such as social, regional, cultural, and religious. A perfunctory examination may reveal that the parents tend to choose a child’s name in accordance with the passing fashion, their ephemeral infatuations or fascination with a character from cinema or theatre, or someone whom they bear admiration for. They may even choose names that are more trendy and fashionable and may not endorse names that are rooted in traditions. However, there are others who, although may consider most of the traditions as passe in their daily chores, still attach a lot of solemnity to the family traditions, especially when it comes to ceremonies such as marriage, the birth of a child or even naming of a child, particularly in the Hindu tradition. Thus, family traditions have a paramount role in the selection of a name for a child, and it is thus, not a mere coincidence that religions across the world give this event a sound consideration. According to James and Jongeward (1971), many children are given symbolic names from literature, family genealogy, or history and it is anticipated that the child may stand up to the desired qualities and character. This preliminary analysis here may suffice to show that names have a noteworthy psychological bearing upon the individuals as well as the society, and hence the science and the art behind the naming of children, with a focus on the family and the society of child’s birth, is a topic worthy of research and analysis. The current manuscript focuses on one such aspect of name-giving – of what we label as ‘mathematical names’, something that we discover to be a pervasive feature of the current Indian Hindu society.

2. Importance of Name-Giving with Reference to the Indian Tradition

While selecting the first name of a newly-born child, the parents want it to sound nice, unique, and authentic whereas the second name is usually the same as the family name. Jagieła and Gębuś (2015) report that interviews of students conducted by them revealed a clear interrelationship between the names and different facets of life script. A similar opinion had been expressed by Eric Berne (1972) when he asserts that given names, short names, and nicknames, or whatever that is bestowed on an innocent baby, is a clear marker of where his parents want him to go. Much before a name can evoke any meaningful fervor from a grown-up child when he begins to identify with his labeled identity, the names are, in good measure, a reflection of the parents’ aspirations, beliefs, intentions, and even social position (Doroszkiewicz 2005). Prior research establishes the fact that parents bestow a name to their children after careful consideration and expectations, for which they assume responsibility, but which can also impose certain restraints and anticipations upon them regarding their future course (Jagieła and Gębuś 2015). In any case, the complex and peculiar repercussions of a name on its carrier is abundantly clear from the prior research. According to Christenfield and Larsen (2008), ‘‘Names seem far more than arbitrary labels useful for telling one’s children apart, or alerting friends to falling safes and other imminent dangers. They seem instead to capture and shape the individuals’’. Be that as it may, the name-givers of a child are their gene-givers as well, and their value systems have an indispensable role not only in the naming of a child but also in his upbringing and the value systems he imbibes during such a phase. Thus, the impact of names on individuals can’t be singularly extricated and explored, since names are not randomly assigned labels, but are intricately related to the consciousness and belief systems of the parents. However, research does indicate that the names matter sufficiently to captivate a sufficient amount of care and attention from the parents (Christenfield and Larsen 2008).

Loferska (2011) asserts that this observance is not a unique moment in the life of a child alone but the entire family as well. It is a moment for the entire family to reflect on the unique identity they want to bestow on the child - a singularly important thing that the child has to invariably carry throughout life. This special moment engages the entire family since there often exists differing opinions on this vital issue of names – the superiors clinging to the names they have cherished in their fond memories, whereas the youngsters proposing funky, and even outrageous alternatives. Overall, the names chosen are those that epitomize anticipations and aspirations of the parents – what they want the child to become, to whom and what they are connected, and also what they want to preserve for posterity (Jagieła and Gębuś 2015). It is not surprising then, that the name-giving event for a newborn comes with a ceremonial commemoration since it represents a special moment in time at the onset of a child’s life.

The Hindu name-giving ceremony of a child, also referred to as ‘Naamkaran’ (Sanskrit Naam = ‘Name’; karan = ‘Create’) is considered to be one of the most important of the sixteen ceremonies in the passage of one’s life. Ideally, the ceremony is performed eleven days after the birth of the child, although sometimes variations are possible based on the advice of the family priest or an astrologer. The traditional function is held at home or a temple, with worship and a fire sacrifice wherein auspicious hymns are recited and prayers are offered for the well-being of the child and his good health, long and prosperous life in the future. In a typical Hindu rite, rice grains are strewn on a bronze dish and the father writes the chosen name using a gold stick while chanting God’s name. This is followed by whispering the selected name into the child’s right ear, repeating it four times along with a prayer. This is followed by incantations are recitations headed by the priest, as a marker of formal acceptance of the child’s name. Hindu belief holds that the name of the child has a profound bearing on the character and the destiny of the newborn, and thus the name has to be in accordance with the principles of Vedic astrology, for it to have an auspicious effect. According to the Hindu tradition, the initial letter of a child’s name is extremely important is chosen based on the nakshatra, or the star under which the child is born, the moon sign, the planetary positions at the moment of child’s birth, the child’s zodiac sign or the Deity who presides over the month of birth. Having selected an initial letter, few propitious names are suggested by the priest or astrologer, which is deliberated upon by the family members, and a suitable name is selected. Although minor variations in these traditions are not surprising in a highly heterogeneous Hindu society, two common principles can be delineated as it relates to their tradition of name-giving: first, the consciousness of the parents, family, and the larger society does have an instrumental role in this process. Second, the name-giving per se is hardly a random event ever, but a well-structured and organized one, where an individual or a group or individuals reflect inward, groping for deeper identities of the child or their own selves and at times even confer sound astrological principles, to arrive at the suitable name of a child.

In the already set-up context of the naming of Hindu children in India, however, there is an intriguing observation that can be made. Our research indicates that there is a significant number of names that are directly derived from mathematical concepts and terminologies. These names broadly termed here as ‘mathematical names’ stem from different branches of mathematics such as geometry, trigonometry, algebra, arithmetic, number system, probability, statistics, etc. Apart from the names corresponding to different mathematical concepts, people are also named as per the terminologies pertaining to the development of mathematics in the Vedic/Indian tradition, the names of the mathematicians, or after the names of their compendiums. However, to fully understand this phenomenon, it is important first to take a stock of such names that belong to different areas of mathematics, try to understand its genesis and mathematical roots, and examine the reasons behind such a phenomenon, particularly with reference to the prior literature on name-giving and its psychological and sociological perspectives. To fully understand the genealogy of such names and the possible underlying reasons behind it, it is worth taking a brief look at the mathematical traditions of India, so as to assess its impact on the overall consciousness of the populace.

3. A Glimpse into the Rich Mathematical Traditions of India

India has a glorious history of mathematical traditions from the early Vedic period itself and the developments in the areas of numbers, arithmetic, algebra, geometry, trigonometry, probability, prosody, astronomy, etc. can be easily gauged from the early mathematical texts available, archaeological evidence such as the bricks from Harappan findings and other exemplars of early Indian mathematics such as the Bakhshali manuscript. The pervasiveness of the mathematical principles in the commonplace of Indian social fabric, and its recognition can be ascertained from an appreciation of mathematics, as penned down by Mahavira (850 CE), one of the celebrated mathematicians of his time:

“In all transactions which relate to worldly, Vedic or other similar religious affairs, calculation is of use. In the science of love, in the science of wealth, in music and in drama, in the art of cooking, medicine, in architecture, in prosody, in poetics and poetry, in logic and grammar and such other things, and in relation to all that constitutes the peculiar value of the arts, the science of calculation (gaṇita) is held in high esteem.

In relation to the movements of the sun and other heavenly bodies, in connection with eclipses and conjunction of planets, and in connection with the tripraśna (direction, position, and time) and the course of the moon – indeed in all these it is utilized.

The number, the diameter, and the perimeter of islands, oceans, and mountains; the extensive dimension of the rows of habitations of the world, of the interspace between the worlds, of the world of light, of the world of gods and of the dwellers in hell, and other miscellaneous measurements of all sorts – all these are made out by the help of gaṇita.

The configuration of living beings therein, the length of their lives, their eight attributes, and other similar things; their progress and other such things, their staying together, etc. – all these are dependent upon gaṇita (for their due comprehension). What is the good of saying much? Whatever there is in all the three worlds, which are possessed of moving and non-moving beings, cannot exist as apart from gaṇita (measurement and calculation).” (Rangacharya 1912)

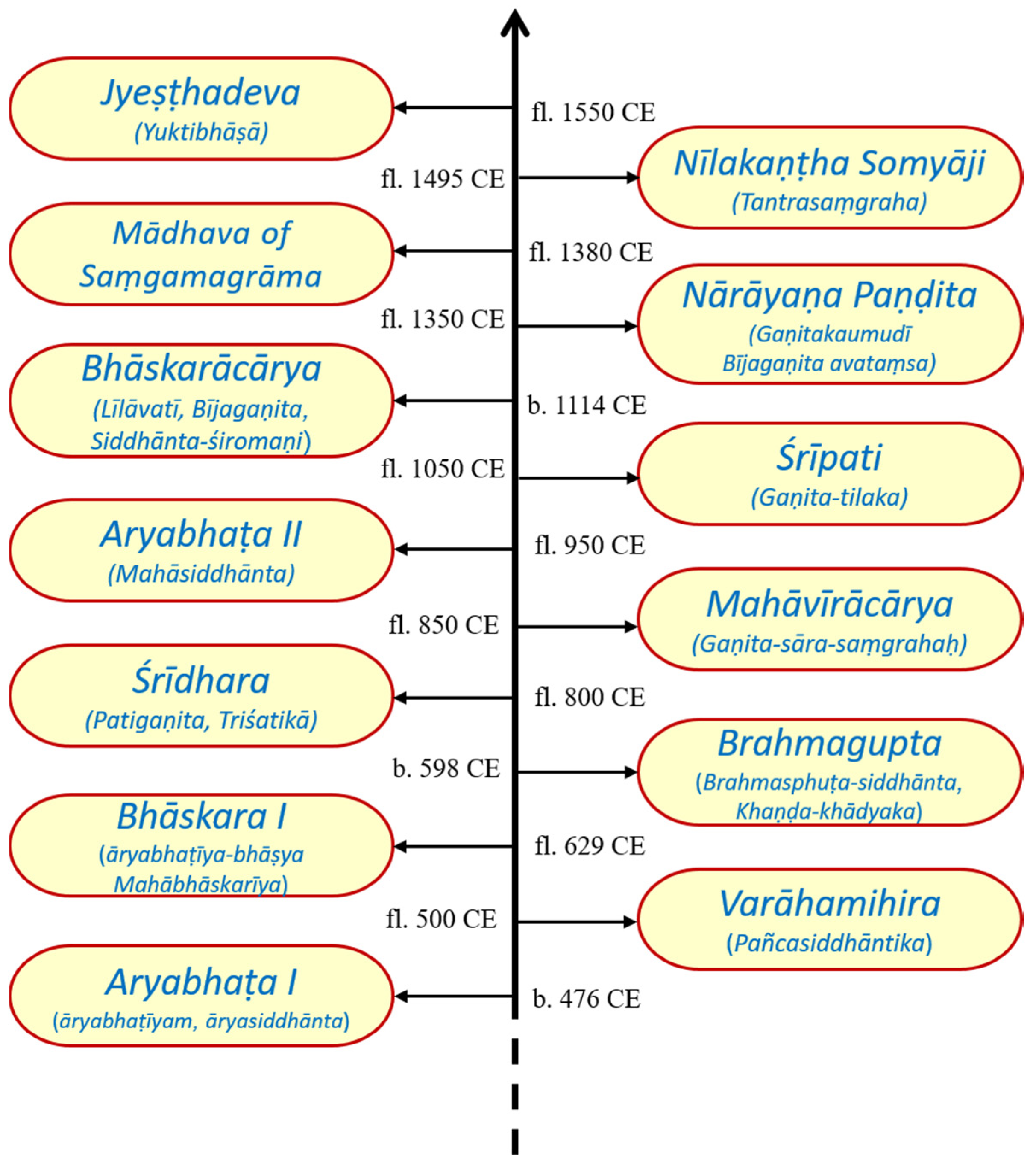
The dissemination of mathematics in the social psyche and recognition of its importance was carried out by the works and treatises of many stalwart mathematicians and astronomers who made notable contributions to the field of mathematics, astronomy, and many other related branches of knowledge. Figure 1 shows a chronological depiction of several mathematician-astronomers from India along with their treatises. Put simply, some of the notable contributions of these mathematicians include the expression of very large numbers by indices of ten, the use of fractions, the concept of nine numerals, and the decimal place-value with the introduction of zero, which was a significant contribution to the development of arithmetic. An efficient and direct methodology of fundamental mathematical operations such as addition, subtraction, multiplication, division, square, cube, square roots, cube roots, etc., and the rule of three (trairaśika) method of calculation also owes its genesis to the Indian soil. A detailed exposition on the properties of zero and infinity, as well as accurate results for surds, have been given by Indian mathematicians. As regards algebra, particular details on symbols of operation, equations, linear and quadratic equations, indeterminate equations of the first and second degree, progressive series, permutation and combination, and the binomial theorem (Bag 1979).

The intricate knowledge of ancient Indians pertaining to altar constructions has been described in the śulbasūtra by Baudhāyana and Apastamba. In this age of śulba geometry (~600 B.C.) a statement on the so-called Pythagoras theorem appears, determination of the value of √2 by the geometrical method has been described along with the classification of geometrical figures on the basis of angles and sides. Brahmagupta’s lemmas and his methods for the construction of a cyclic quadrilateral or diagonals of a cyclic quadrilateral are some remarkable achievements of geometry. Aryabhata, a mathematician, and an astronomer made several important contributions including the calculation of the area of a triangle, as early as 476 AD. Combinatorics formed an integral part of Indian mathematics and the tradition commenced with the formal theory of Sanskrit prosody as propounded by Piṅgala in 2nd century BC (Shah 1991). Halāyudha, a mathematician and commentator on chandaśāstra of Piṅgala presents a comprehensive interpretation of meru-prastāra scheme, which has also been proposed as Pascal’s triangle in the European world. The knowledge of trigonometry in India can be gauged from the trigonometrical formulae, sine tables, value of ℼ, and the fact that the trigonometrical series such as ℼ, sine, cosine, and tan was first outlined more than a century before Newton (1664 AD) and Leibniz (1676 AD). Similarly, advances in infinitesimal (integral) calculus were reported in Yuktibhāṣā in connection with the summation of infinite series, a century before Newton and Leibniz. Bhaskara II (1150 AD) from the Kerala school of mathematics, reported the concepts of both differential and integral calculus (Bag 1979).

Given this rich tradition, the question we ask is as follows: How did this rich mathematical tradition and lineage impact the society at large? How did the non-mathematical society at large view these mathematical developments and imbibe them? According to Datta and Singh (1935, p. 150), since the knowledge of higher mathematics could not be turned to material gain, there are very few who seriously undertook its study, although the religious practices of the Hindus necessitated a certain knowledge of mathematics and astronomy, It is clear that in the Indian context, mathematicians and their contributions were venerated and the society readily imbibed all that it could, from them – be it their concepts and terminologies, their names or the names of their compendiums. All these got absorbed into the social consciousness. The extant remains of such a deep veneration for a scientific and mathematical (not necessarily empirical) culture can be gauged to date, by a subtle examination of the concurrent names of the Hindu Indian society. Needless to say, many of these names can even be found in other neighboring countries such as Indonesia, Malaysia, Nepal, Sri Lanka, Korea, Bangladesh, and Japan.

4. Research Methodology

To explore the existence of the mathematical names in present India, three directories of names were utilized. The first directory was created by compiling names of enrolled students from higher educational institutions (HEI database) in India for the last eight years (2013-2020), amounting to a total of more than 28,650 names. It is worth pointing out that the names database was deliberately created from recent years, so that the names collected could be a reflection of the ethos of the current populace of the Indian society. In addition to the HEI database, Facebook (FB) and LinkedIn (LI) databases were also utilized. Our research can be distinctly categorized into qualitative and quantitative categories.

4.1. The Qualitative Approach to Analysis

Towards the qualitative analysis, a detailed study of several Indian texts in all aspects of mathematics (categorized into geometry, trigonometry, numeration, arithmetic, algebra, and mathematics in the Vedic tradition (beginning with the śulbasūtras) is conducted including not only the ancient and medieval texts in mathematics but also the modern mathematics textbooks prescribed in the existing school curriculum. The concepts and terminologies discovered from the extensive mathematical research are then juxtaposed and searched for, in the directories of names and one typical example is chosen for illustration for both genders. Facebook users directory (FB database) which consists of approximately two billion users in its database, as of 2021, is referred to search and substantiate the existence of such mathematical names in India. Further, to avoid dubious names, only factual names with surnames are manually selected and with the help of the location as a marker, only the names corresponding to the Indian subcontinent are filtered out, since the current paper focuses on the extant mathematical names primarily in this geographical region. To ensure verifiability of the data presented in this manuscript, we present some representative textual pieces of evidence behind the mathematical names as well as sample names that any reader can easily verify by any available search engine on the web, or directly by Facebook directory search. For the sake of brevity, textual evidence is kept to a bare minimum in this manuscript.

4.2. A Description of the Quantitative Approach of Data Extraction and Processing

In order to quantify the occurrences of such mathematical names, a more formal database of professionals such as LinkedIn (LI database) is utilized. However, to reduce the time requirements as well as to minimize the manual errors, the process of quantification of the recurrence of names is automated. Selenium web scrapper is employed to extract the list of names from LinkedIn. A step-by-step process of the extraction algorithm is described as follows: A spreadsheet of the list of mathematical terms (names) is created and pandas library is used to read the data in Python. Chrome web driver is used to route to the specific LinkedIn page, where HTML tags for the input fields are located and the credentials are entered for sign-in. Upon successful login, the homepage of LinkedIn is navigated and HTML tags for the search input are located, the names are input, and the ‘People’ option is selected to narrow down the results. Finally, the text string containing the number of people is extracted corresponding to each term. Pandas is then utilized to store the numeric result corresponding to each term. Overall, the data extraction process with Selenium was found to be a very time-efficient one. Moreover, thorough testing of the efficacy and accuracy of this algorithm is carried out and the above-described computational process yielded repeatable results for all the terminologies tested. To ensure the correctness of the collected data, an alternative manual procedure was utilized on the FB database and the proximity of the obtained results from both the databases validates the data recorded.

Thereafter, a systematic investigation and analysis of the data from both the HEI dataset and LI dataset is taken up, using MATLAB software. A MATLAB script is applied to the HEI dataset to extract forty-eight (mathematical or non-mathematical) names occurring with the highest frequency. Again, extraction using Selenium provided for an estimate of the numbers corresponding to the most frequent names in India. An average of these forty-eight numbers provides for a number that can be used for normalization of the number of occurrences of mathematical names to yield a ‘Name recurrence factor’. Name recurrence factor $\left(\widehat{n}\right)$ is a normalized quantity that indicates the relative occurrence of the mathematical names vis-à-vis the “most ubiquitous” name in a particular dataset and thus helps us to evaluate the effective prevalence of these names. This factor in combination with the absolute number counts corresponding to each name provides for a sound basis for comparison amongst these mathematical names. Finally, a survey has been conducted of persons who possess these mathematical names and their detailed responses have been solicited. Apart from the general prevalence of such names, we also intend to explore how the bearers of mathematical names feel about their names (at least when they are made aware of it), what led to their mathematical naming, any possible interlinks between such mathematical names and the tradition and great regard of mathematics in their families, or even the impact that such a name had on their own aptitude towards mathematics in general.

4.3. The Average Frequency of the “Most Ubiquitous” Indian Name

Admittedly, the task of estimating the average frequency of the most ubiquitous Indian name is a convoluted one, compounded by the dearth of readily available census data as of 2020. While even identifying such a “most ubiquitous” name in a multicultural and multilingual Indian society would be an onerous task, much less be said of the difficulties that beset its quantification. In fact, India has had a multilingual culture since ancient times and marked variations in both spoken and written languages have existed (Joseph 2010). Things are further muddled by the interrelationships between these cultural, linguistic, and religious aspects – and by the fact that owing to such cross-interactions, identical words, cognates or similar-sounding syllables appear in different languages, sometimes with a common root from Sanskrit or Persian. However, these difficulties can somewhat be reconciled if some commonly available databases could be utilized to gain some insight.

In our study, we circumvent these difficulties by a two-step process before we arrive at any conclusive estimate. First, a considerably large HEI dataset is utilized to deduce a list of the forty-eight most common names of students enrolled in India’s higher educational institutions. In the next step, LinkedIn database of users is employed to get the occurrence frequency of the names in this list. This is followed by an averaging of the five largest entries in the list to yield the highest frequency name.While this may not appear most scientific to arrive at an “exact” count, it is not inappropriate to use it as a normalizing factor against the count corresponding to the names derived from the same LI dataset. In such a scenario, $\widehat{n}$just denotes the relative occurrence of a mathematical name, vis-à-vis one of the “most ubiquitous” names in the LI dataset. It is not wrong, however, to talk of $\widehat{n}$ values greater than unity, unlike the efficiency measurements in engineering calculations. It is indeed possible that a “mathematical name” may have $\widehat{n}$ values greater than unity. Moreover, there is a caution that needs to be exercised before one interprets these $\widehat{n}$values. The underlying assumption here is that our HEI dataset and LI dataset provide a true representation of the existing names in India. However, there is no concrete evidence to posit this assumption. On the contrary, it is expected that both our HEI and LI datasets are a more accurate reflection of the urban India and not the rural. It is more likely then, that rural India, which expectedly carries a stronger impression of the cultural and religious foothold, essentially transmitted a greater amount of these mathematical names in the social consciousness through the course of time. This difference is further underscored by the fact that English being a foreign language in India, carries with it the dialectical impressions of different regional languages of India when regional names deriving from the Sanskrit root are transliterated into it. For instance, the name “mandal” which connotes a circle, becomes ‘mondal’ or ‘mondol’ in Bengal and Bengali-speaking regions. Under the given circumstances, it is implicit that the $\widehat{n}$ values presented here merely denotes the lower bound of the actual recurrence of these names.

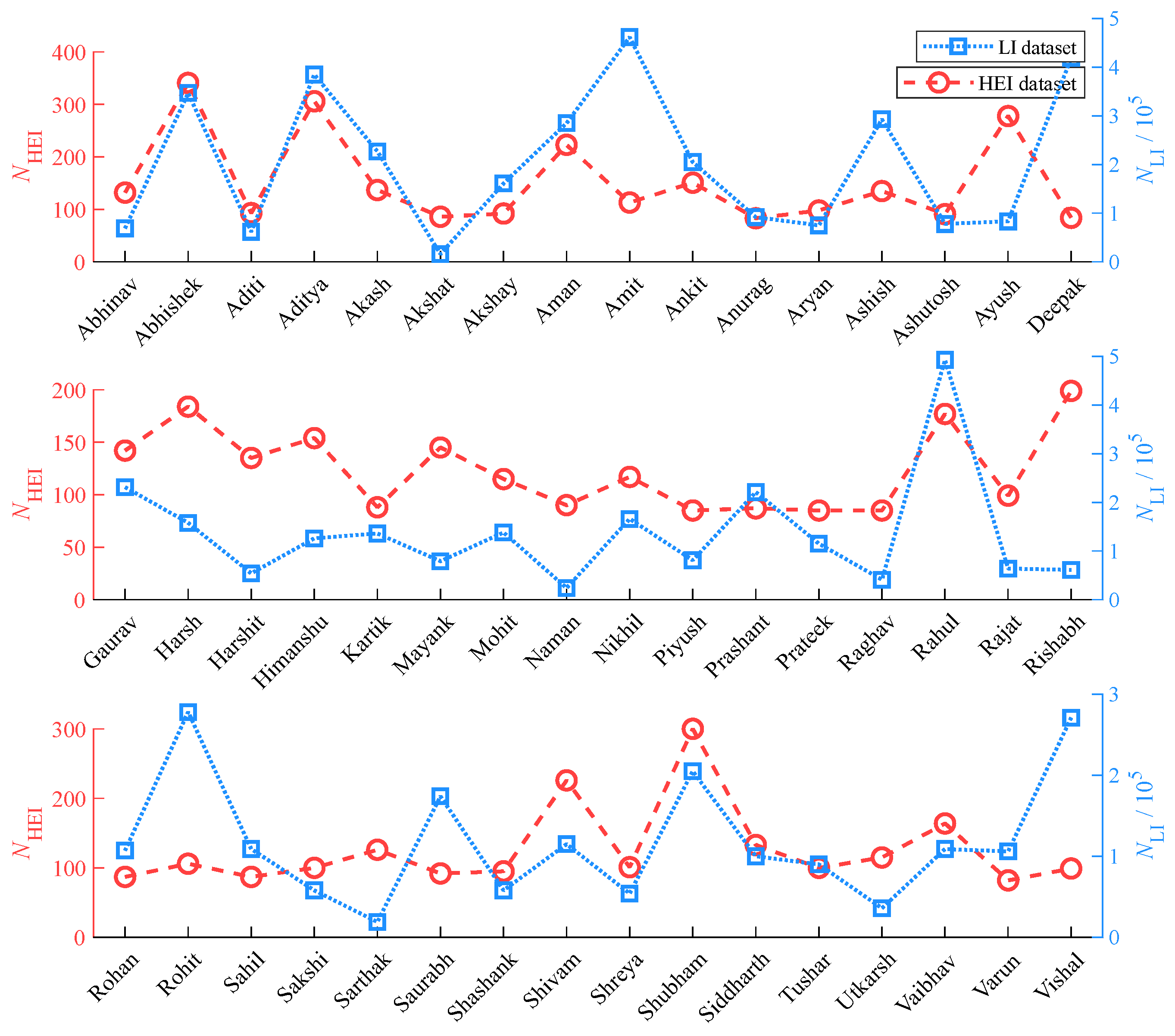
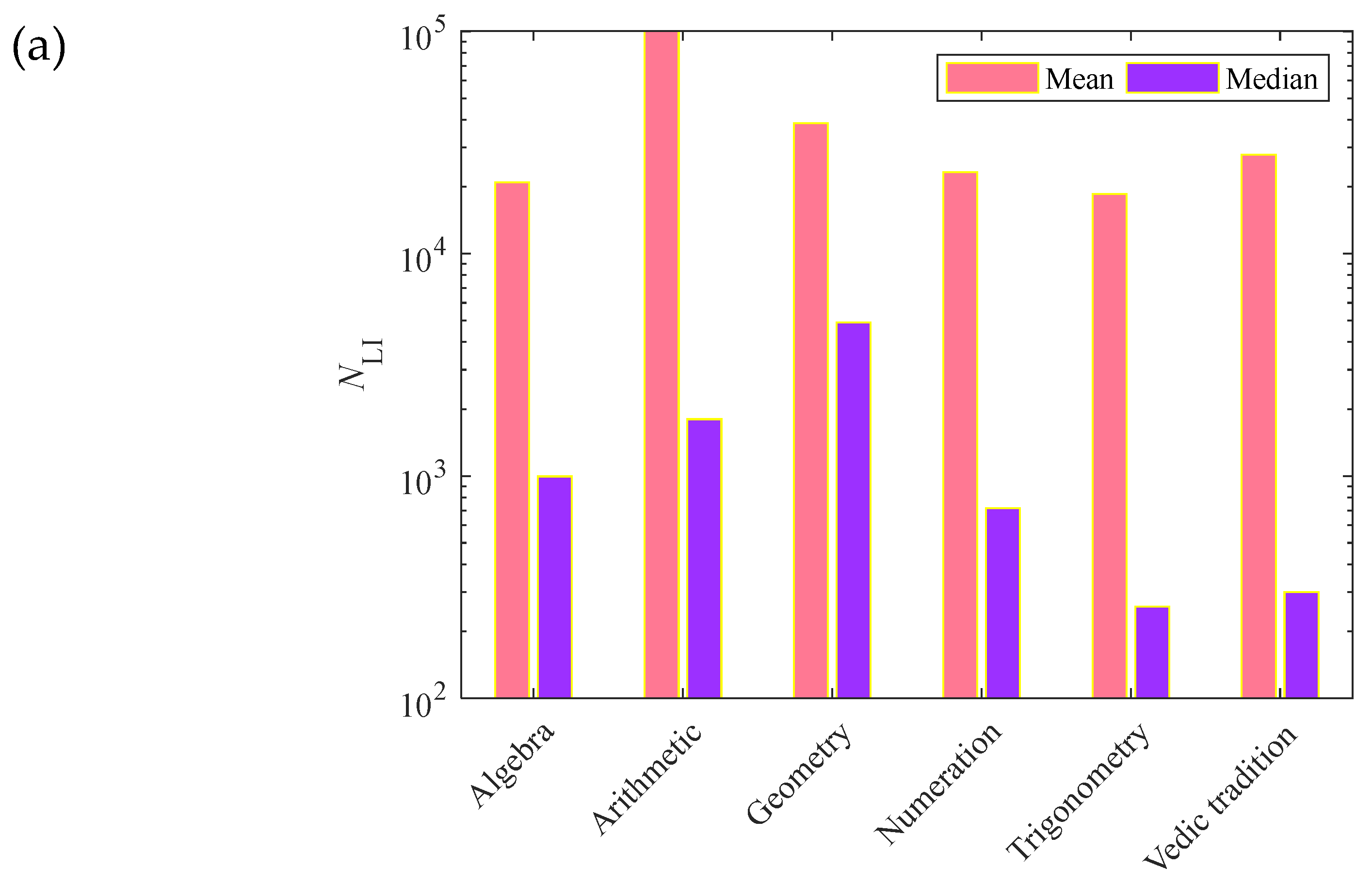
Figure 2 presents an exact count of the most ubiquitous names from the HEI dataset in alphabetical order. Out of the 28658 names in the HEI dataset, automated extraction of the forty-eight highest frequency names are done and it can be observed that the frequency varies between 82 and 341, or a recurrence fraction of 0.00286 to 0.0118. The name with the highest occurrence frequency is ‘Abhishek’ followed by ‘Aditya’, ‘Shubham’, ‘Ayush’ and ‘Shivam’, with a corresponding count of 306, 300, 278, and 226 respectively. These names are indeed one of the most common names around, as is also shown by the corresponding numbers of the LI dataset (N_LI). Interestingly, the LI dataset and HEI dataset show the exact same trend of number count for some of the high-frequency names, which include these five. The trends for other names between the two datasets are not coterminous. As shown in the figure, N_LI/10⁵ values for these names are 4.93, 4.62, 4.19, 3.85, and 3.47 respectively yielding an average value of 4.212. Hence, for the sake of computation of $\widehat{n}$, the average frequency of the most ubiquitous name in the LI dataset is taken to be 421200.

5. The Genealogy and Prevalence of the Mathematical Names in India: A Qualitative and Quantitative Analysis

In order to better understand the genealogy and the prevalence of ‘mathematical names’ in India, six distinct categories have been created, namely Geometry, Trigonometry, Number system, Arithmetic, Algebra, and Mathematics in the Vedic/Indian tradition and their name recurrence factors are designated by ${\widehat{n}}_{ge},$ ${\widehat{n}}_{tr},$ ${\widehat{n}}_{nu},$ ${\widehat{n}}_{ar}$, ${\widehat{n}}_{al}$and ${\widehat{n}}_{ve},$ respectively. Of these, the last category is in fact a miscellany of not just the evolution of mathematics in the Vedic period, but also some unique terms that got introduced and absorbed in the Indian tradition of mathematics. In the sections that follow, we produce a running text on these distinct sub-categories as it pertains to mathematics in the Indian tradition, with the underpinning ‘mathematical terms’ being underlined, when every term appears for the first time in the text. Later, all these names are collated in a tabular format with an example of a name corresponding to both genders, and a quantitative analysis then follows.

5.1. Geometry

The description on the geometry may begin with emptiness (rikt) and next a point (bindu), which, in Euclidean geometry is an exclusively primitive concept upon which the foundation of geometry is built, and which has been treated only by axioms (Gerla 1995). When two such “invisible points” are concerned, as per the second postulate of Birkhoff’s metric geometry, there exists one and only one such unique line that connects them (Birkhoff 1932). In the Indian tradition of geometry, a line has been referred to as ‘rekha’, which connects two fixed points and thus has a finite length (vistara). However, if one of the points i.e., the vertex (sheersh) is fixed, whereas the other can hypothetically lie at infinity, a ray (‘kiran’) results, possibly bearing an allusion to the rays of the sun that extend infinitely into deep space. It is possible that the two rays can touch at a common endpoint and in such a case, an angle (‘kon’) results. These angles could be of different magnitudes. It could be a straight angle (riju), acute angle, right angle or an obtuse angle (adhik kona). The word angle owes its genesis to its Latin equivalent angulus meaning “corner” (equivalent to Sanskrit “kon”) and its linguistic cognates such as ankylos in Greek, meaning “curved” and the English word “ankle”. Both the Greek and English cognates are linked to the Proto-Indo-European root “ank”, meaning a “bow” (Slocum 2007). Interestingly, the Sanskrit equivalent for a bow is “dhanu” or “chaap”, which is used to refer to an arc in Hindu geometry. The measure of the ratio of the length of a circular arc to its radius is the estimate of an angle, which is described to a considerable level of accuracy in Hindu geometry. For instance, Surya-siddhanta (Gangooly and Burgess 1997) gives the angle measurements in text 128 as –

विकलानां कलाषष्ट्याः तत् षष्ट्या भाग उच्यते |

तत्-त्रिशतां भवेद् राशिः भगणो द्वादशैव ते ||

vikalānāṃ  kalāṣaṣṭyāḥ  tat  ṣaṣṭyā  bhāga ucyate |

tat-triśatāṃbhaved rāśiḥ  bhagaṇo dvādaśaiva te ||

Sixty vikalas make up a kalaaand sixty kalaas comprise a bhaag. Thirty of such bhaag constitute a rashi, and a spherical revolution, bhagana consists of twelve such rashis.

It is worth noting that the current system of measurement of angles is precisely similar to that mentioned in Surya-Siddhanta, where a minute consists of sixty seconds, a degree consists of sixty minutes, and 30 x 12 = 360 such degrees make up a revolution. A degree in Hindu geometry is sometime also referred to as ansh. Moreover, in his Siddhanta-Shiromani, while computing the instantaneous motion of a planet, Bhaskaracharya notes that the timespan between consecutive positions of the planet is no greater than a truti, or 1/33,750 of a second, and he gives the measures of the velocity in terms of this small unit of time (Joseph 2010).

After discussing basic shapes such as a line and a ray and the angles between them, construction (Rachna) of a curve (Vakra) is of cardinal interest in geometry. However, these may sometimes be a closed curve (Aakriti), and in such a scenario, the boundary (Seema) and its length, or the perimeter (Parimap) and area (Kshetra) are quantities of natural interest. Kshetra primarily refers to a closed figure, but can also denote the area of a figure (Amma 1999). Thus, different kinds of closed geometrical shapes, also called polygons may be looked into, beginning from a triangle (Tribhuj), quadrilateral (Chaturbhuj), square (Varg/ Kriti/ Karani), rectangle (Ayat), pentagon (Panchakarn), octagon (Ashtbhuj) to any n-sided polygons (Bahubhuj), etc. The sides of polygons have been mentioned as rashmi. Of the geometrical shapes possible, the triangles, quadrilaterals, and circles can be examined in some greater detail, owing to their simplicity and thus pervasiveness in all kinds of practical applications.

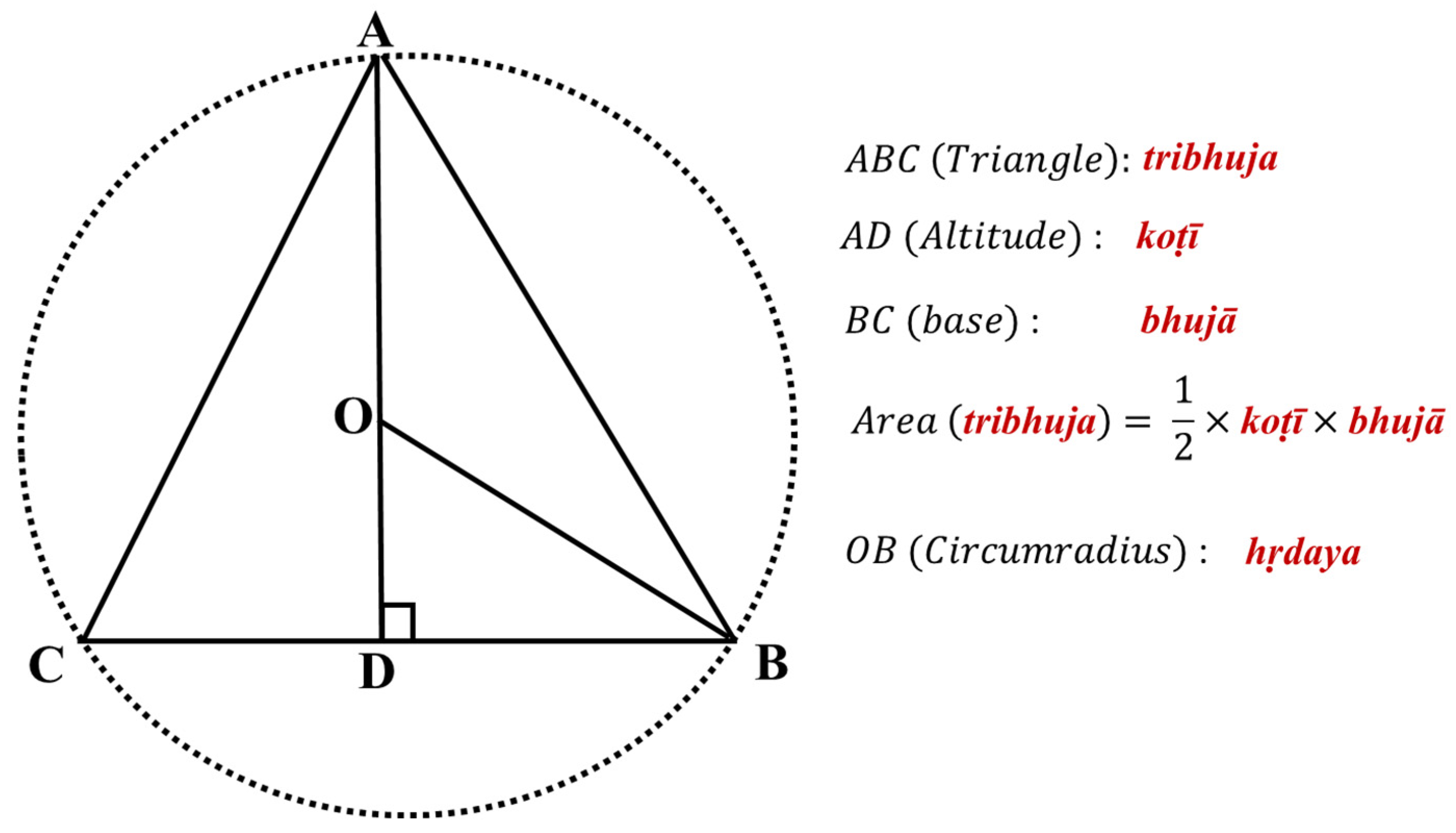
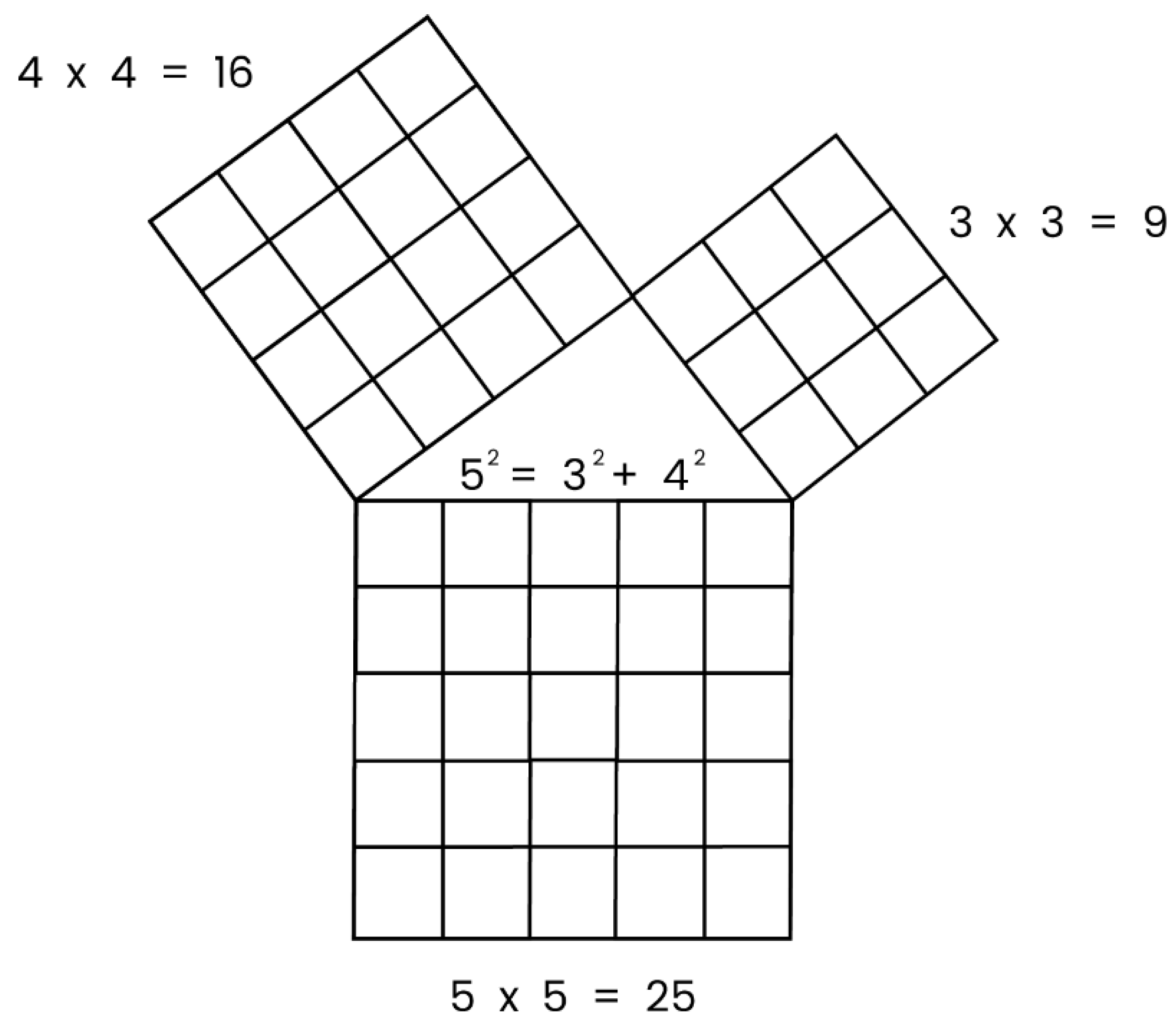
In his Aryabhata Ganitapda 6, Aryabhata discusses the calculation of area of a triangle in these words –

त्रिभुजस्य फलशरीरं सम-दल-कोटी भुजार्ध-संवर्गः |

tribhujasya phalaśarīraṃ  sama-dala-koṭī  bhujārdha-saṃvargaḥ|

The result of the perpendicular (from opposite vertex) and its product with half the length of the side is its area. As illustrated in Figure 3, here, Aryabhata refers to the base of the triangle as the bhuja, whereas the perpendicular from the base (dal) is referred to as koti. This altitude of a triangle has also been referred to as isuby Katyayana (Amma 1999), although conventionally isu (meaning arrow) has been used to denote height of an arc, which is denoted by chaapor dhanu. Bhaskaracharya describes this in his Leelavati (Text 141)

इष्टो बाहुर्यः स्यात् तत्स्पर्धिन्यां दिशीतरो बाहुः |

त्र्यस्त्रे चतुरस्त्रे वा सा कोटिः कीर्तिताः तज्ज्ञैः ||

iṣṭo bāhuryaḥ  syāt tatspardhinyāṃdiśītaro bāhuḥ|

tryastre caturastre vā sā koṭiḥ  kīrtitāḥ  tajjñaiḥ||

In a right-angled triangle, one of the sides is called the base (bhujaor bahu), and the side perpendicular to it is called the altitude, koti (Patwardhan et al. 2006).

Next, a quadrilateral is referred to as chaturbhuja (or Chaturasra) and can be a parallelogram, rhombus, rectangle (Ayat), or a square (Vargaor Kriti). The Shulbasutras provide a clear understanding between lengths and areas. Apastamba (Ap. Sl. III. 6-7) says –

द्वाभ्यां चत्वारि, त्रिभिर्नव | यावत्-प्रमाणा रज्जुस्तावतस्तावतो वर्गान् करोति |

dvābhyāṃcatvāri, tribhirnava | yāvat-pramāṇārajjustāvatastāvato vargān karoti |

“With two four, with three nine. As many units as there are in a cord, so many squares are produced by it” (Srinivasachar and Narasimhachar, 1931).

भुज्युत्यर्धचतुष्कात् भुजहीनात् घातितात् पदं सूक्ष्मम् |

अथवा मुखतलयुति दलमवलम्बकगुणं न विषमचतुरश्रे |

bhujyutyardhacatuṣkāt bhujahīnāt ghātitāt padaṃsūkṣmam |

athavā mukhatalayuti dalamavalambakaguṇaṃna viṣamacaturaśre |

The square root from four sets of half the sum of the sides respectively diminished by the sides and multiplied together is the exact area. Or, half the sum of the base and the face multiplied by the altitude, but not in a vishama quadrilateral. This is ample evidence that Mahavira knew that the expression

$$A=\sqrt{(s-a)(s-b)(s-c)(s-d)}$$

holds good for isosceles trapezium, although he does not state this to apply to scalene trapezium too. Brahmagupta in his Brahma-sphuta-Siddhanta highlights some other properties of trapezium, although he does not comment upon its area.

अविषम-चतुरश्र-भुज्प्रतिभुजवधयोर्युतेः पदं कर्णः |

कर्ण-कृति-भूर्मुखयुतिदलवर्गोना पदं लम्बः ||

aviṣama-caturaśra-bhujpratibhujavadhayoryuteḥ  padaṃkarṇaḥ|

karṇa-kṛti-bhūrmukhayutidalavargonā  padaṃ  lambaḥ||

In quadrilaterals other than the vishama, the square root of the sum of the products of the opposite sides is the diagonal. The square of the diagonal less the square of half the sum of the base and the face is the altitude (Sharma et al. 1966). Rectangles are addressed differently, sometimes as visama chaturasra or Ayat as well, as shown in the text below:

गणितविदौ मस्करी-पूरण-पूतनादयः सर्वेषां क्षेत्राणां फलम् आयतचतुरश्रक्षेत्रे प्रत्याययन्ति |

gaṇitavidau maskarī-pūraṇa-pūtanādayaḥ  sarveṣāṃ  kṣetrāṇāṃphalam  āyatacaturaśrakṣetre pratyāyayanti |

Mathematicians like Maskari, Purana, and Putana show the rationale of the areas of all figures in rectangular figures.

The diagonal of a square or a rectangle is denoted by karna, karanam, vikarnaor shruti, all referring to ear, although the semantic basis for this usage is not exactly clear (Amma 1999). The Sanskrit word karani means “producer” or “that which makes”, and gradually it came to represent the sides of a rectilinear geometrical figure of any shape, and later, more specifically, the side of a square. Katyayana Shulbasutra (II. 15-18) describes –

तृतीयकरणी एतेन व्याख्याता, प्रमाणविभागस्तु नवधा | करणीतृतीयं नवभागः नवभागास्त्रयस्तृतीयकरणी

tṛtīyakaraṇīetena vyākhyātā, pramāṇavibhāgastu navadhā| karaṇītṛtīyaṃnavabhāgaḥ  navabhāgāstrayastṛtīyakaraṇī

“The one-third maker is expounded by this. The division of the measure (of the area) is into nine parts. One-third of the karanii.e., the side of the square makes one-ninth (of the area). Three ninth parts have one-third as its karani or maker”(Amma 1999). Further, Katyayana also discusses the construction and properties of pentalaterals or panchakarna(Datta 1932).

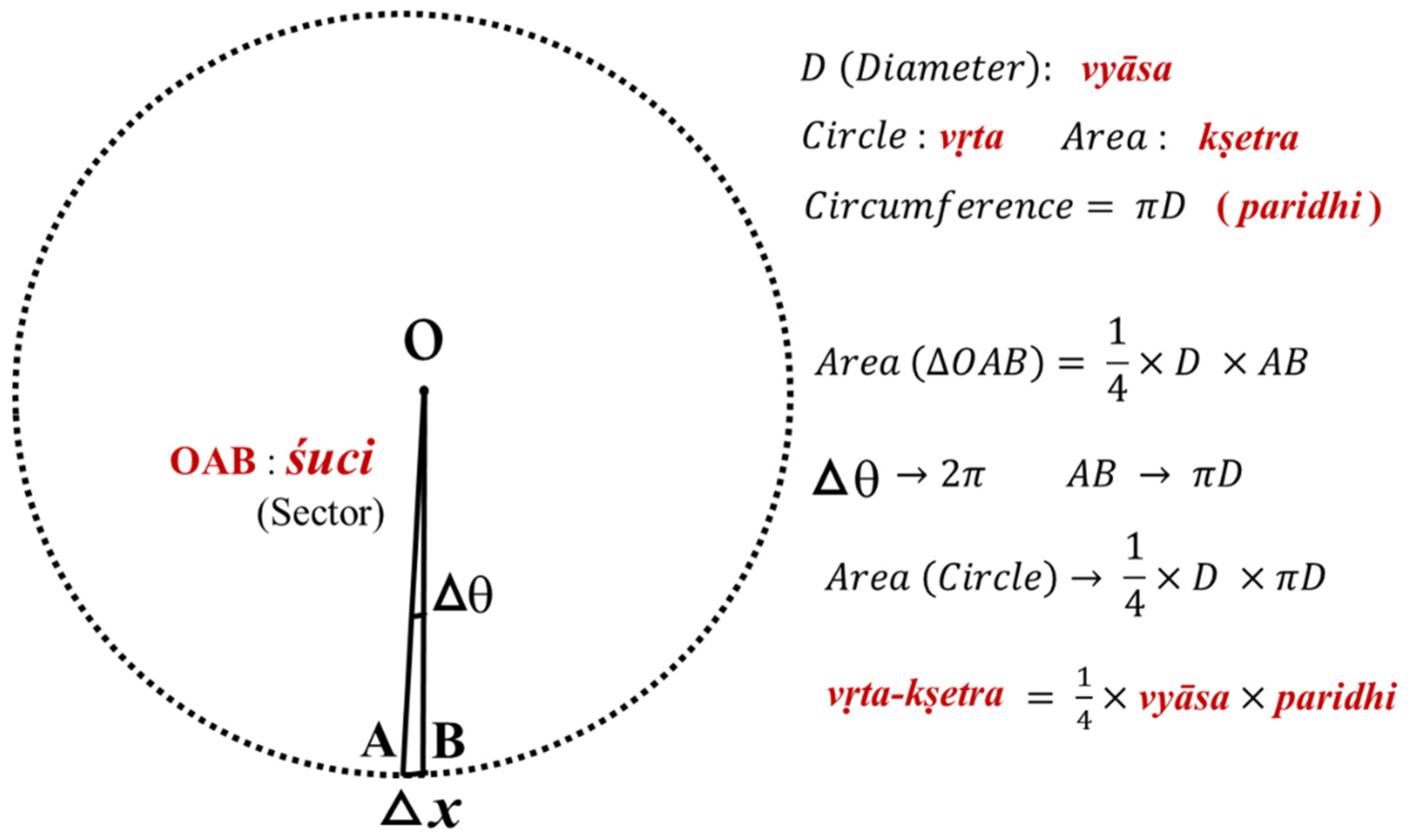
MandalaorParimandaladenotes a circle, and Parinahastands for circumference, although it is less commonly used. The other word for the circumference is paridhi, as can also be seen in the Lilavati text 201 by Bhaskaracharya –

वृत्तक्षेत्रे परिधिगुणित-व्यास-पादः फलं यत्क्षुण्णं वेदैरूपरि परितः कन्दुकस्येव जालम् |

गोलस्यैवं तदपि च फलं पृष्ठजं व्यासनिघ्नम् षड्भिर्भक्तं भवति नियतं गोलगर्भे घनाख्यम् ||

vṛttakṣetre paridhiguṇita-vyāsa-pādaḥphalaṃyatkṣuṇṇaṃ

vedairūpari paritaḥkandukasyeva jālam |

golasyaivaṃtadapi ca phalaṃpṛṣṭhajaṃvyāsanighnam

ṣaḍbhirbhaktaṃbhavati niyataṃgolagarbhe ghanākhyam ||

“In a circle, the circumference multiplied by one-fourth the diameter is the area, which multiplied by four, is its surface area going round it like a net round a ball. This (surface area) multiplied by the diameter and divided by six is the volume inside the sphere (Amma 1999).” Indeed, as illustrated in Figure 4, the area of a circle ($\pi d^2/4$) is identical to circumference ($\pi d)\times d/4.$ So, does the surface area of a sphere ($\pi d^2)$ correspond to the area of the great circle ($\pi d^2/4)\times 4.$ Finally, the surface area ($\pi d^2\times d/6$ is equivalent to ($4\pi r^3/3)$, the volume of a sphere. At this point, it may also be important to notice the usage of parinaha for circumference by Aryabhata in Aryabhata Ganitpada in a text, which also gives an approximate value of $\pi .$

चतुर्-अधिकं शतम् अष्टगुणं द्विषष्चटिस्था सहस्राणाम् |

अयुतद्वय-विष्कम्भस्य आसन्नो वृत्तपरिणाहः ||

catur-adhikaṃ śatam aṣṭaguṇaṃdviṣaṣcaṭisthāsahasrāṇām |

ayutadvaya-viṣkambhasyaāsanno vṛttapariṇāhaḥ||

“Four more (of) hundred, times eight, likewise (more) of sixty-two thousand, nears the circumference of a circle of diameter 20000.” In other words, the approximate value of $\pi$, as suggested by Aryabhata is $\left\{\left(4+100\right)\times 8+62000\right\}/20000$, or 3.1416. The radius and diameter of a circle are represented by trijyaand vyas(or viskambha) respectively. Shuchi refers to the sector of a circle, and jeev to its chord. Hridaya refers to the circumradius and jya refers to the sine in trigonometry.

Moreover, Indian mathematicians have extensively elaborated on three-dimensional surfaces as well, and some relevant terminologies worth indicating are the allusion to a three-dimensional surface by falak, the reference to a sphere by gola, annulus by nirgama, part of an annulus by nemi,and a cone by a shanku. The list of extant names of people from geometry in the Indian context is practically endless, although some more examples are presented in a later section on names specific to the practice of mathematics in the Vedic tradition. It is worth mentioning that the mathematical pretext provided above is not to provide an exhaustive account of the developments of geometry in India, which would be a cumbersome task. Rather, the goal is to merely point out a sample of terminologies pertaining to geometry which pervasively appear as names of individuals in India. Table 1 enlists all the terminologies introduced above, with examples of the verifiable names of the individuals in the Indian subcontinent currently. As the table presents, names based on geometry exist in all the sub-categories of fundamental geometrical concepts, arc and angle measurements, curves and its characteristics, triangles, quadrilaterals, polygons, circles, and three-dimensional surfaces. Further, for all the suggested terms in geometry, names can be found to exist in both genders, barring a few exceptions, when only feminine names have been found. That such an observation could be made in the Indian society may not just seem counter-intuitive, but may even come as a surprise to those who have subscribed to the usual tirade of deprivation meted out to women in terms of basic education, much less, a subject such as geometry. However, if so were to be the case that women in India were not taught a subject such as geometry, it is highly unlikely that their names would be associated with it, when they had to be supposedly kept away from it. At any rate, such names would not be at par, or greater than the male names. Needless to say at this point that such naming among the females isn’t a recent phenomenon brought about by the westernization in education and society.

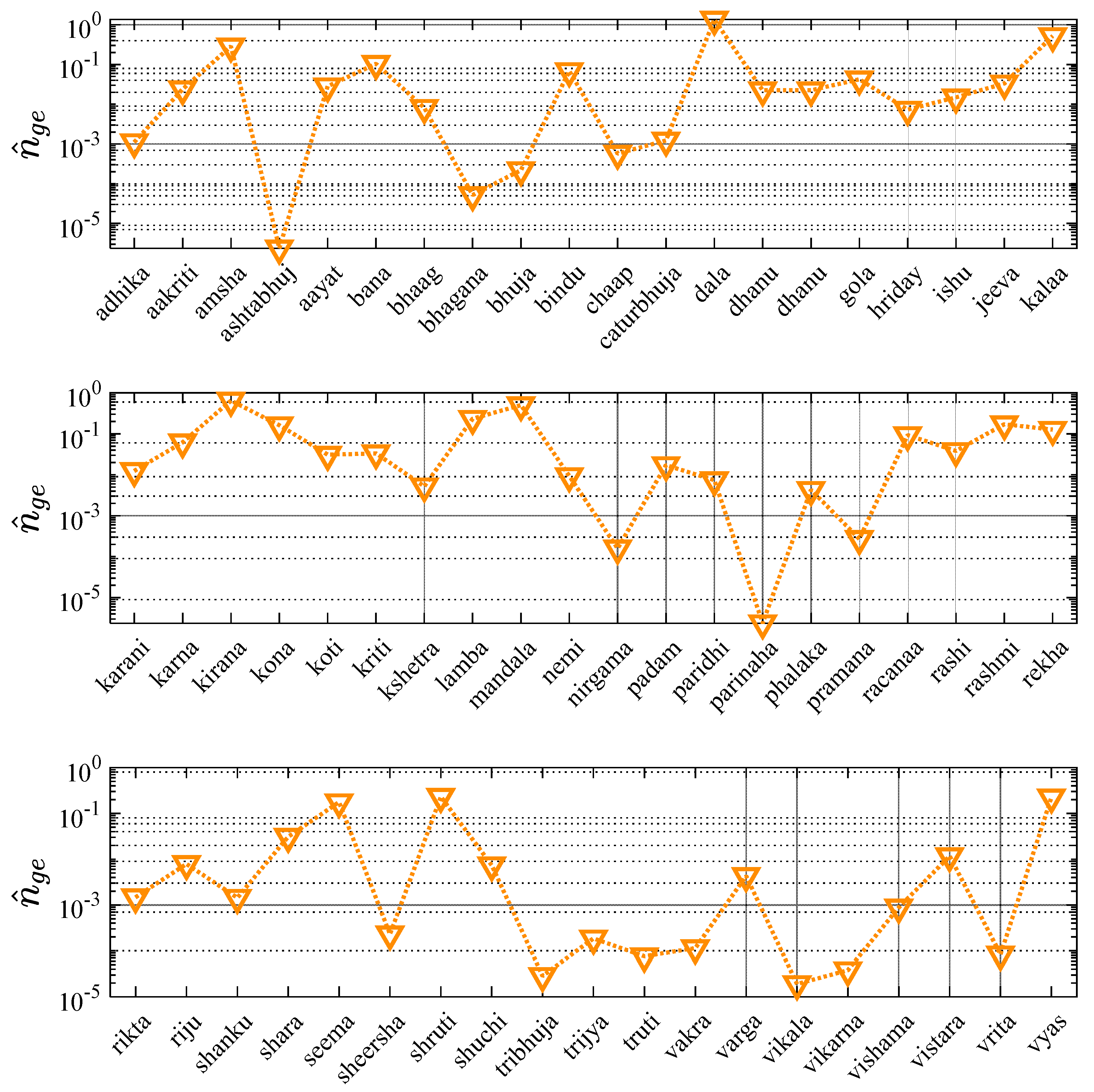
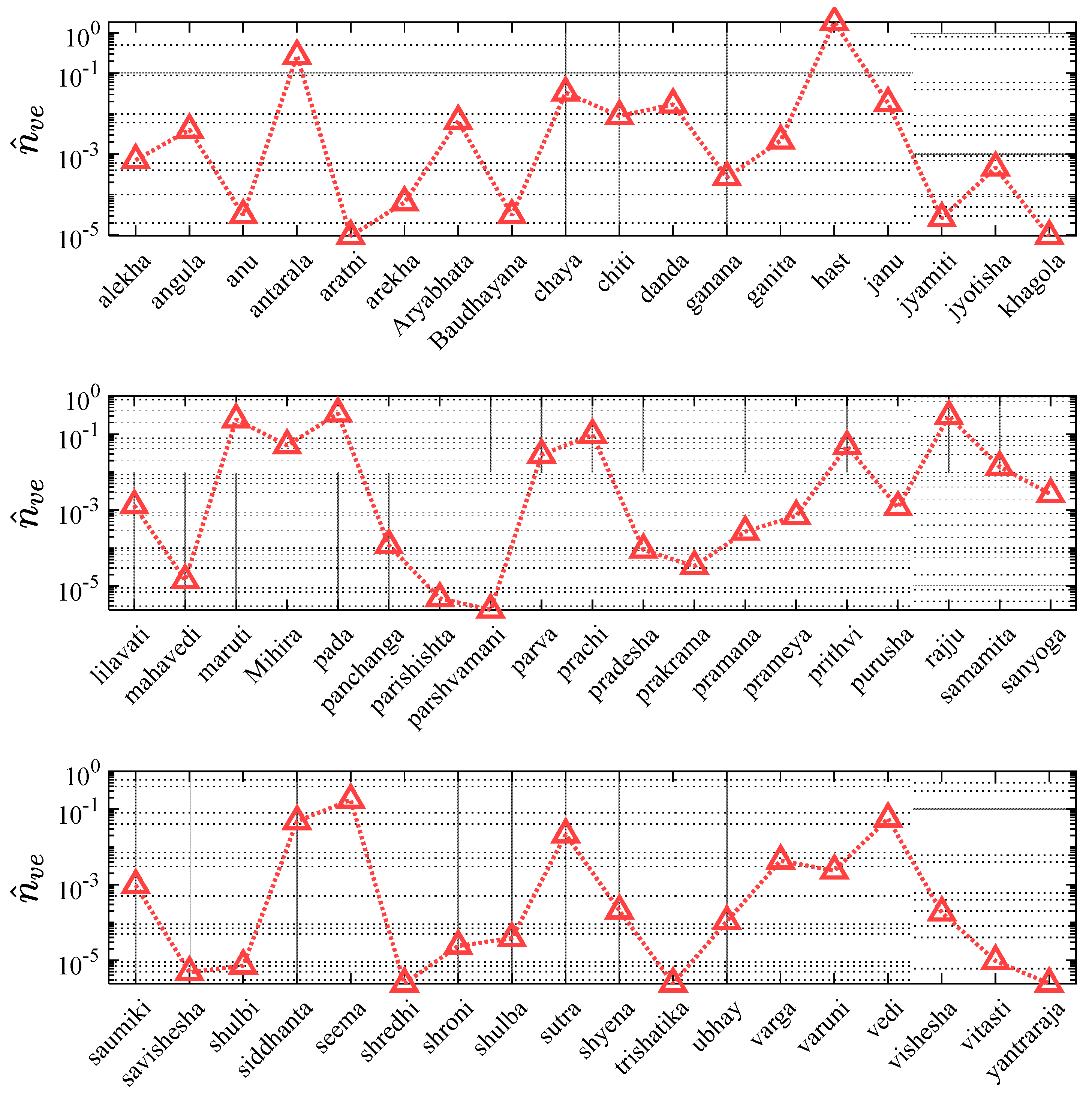
Figure 5 furnishes the quantitative evidence of the recurrence of the names based on geometry as presented in Table 1, from the LI dataset. It presents the specific name recurrence fraction for sixty-three names based on geometry, ${\widehat{n}}_{ge}$ in an alphabetical fashion. As the figure shows, the left axis denotes name recurrence factor in the LI dataset, which multiplied by a hundred yields ‘recurrence percentage’. This figure demonstrates that ${\widehat{n}}_{ge}$ varies between 2.37x10^-6 to 1.36, or in other words, between 0.0002 % to 136%. It is not surprising to find a percentage value corresponding to the term ‘dala’ attain a value greater than cent percent, since ‘dala’ is a name in multiple cultures apart from Indian. Thus, the LI dataset yields a greater count for ‘dala’ than the normalizing “most ubiquitous Indian name” say, ‘Rahul’ which is a name mostly in India and southern Asia. Further, some of the terms with highest ${\widehat{n}}_{ge}$ are ‘dala’, ‘kirana’, ‘kala’, ‘mandala’ and ‘amsha’ with ${\widehat{n}}_{ge}$corresponding to 1.36, 0.64. 0.52, 0.50 and 0.28 respectively. On the other hand, terms like parinaha, astabhuja, vikala, tribhuj and vikarna fare very low on the ${\widehat{n}}_{ge}$ value. Other terms which occur in the high frequency range are sruti, vyas, seema, rashmi, kona, rekha, bana, rachna, rashi etc. – names that can be very commonly heard in the Indian setting.

5.2. Trigonometry

The original Hindu name for the science of trigonometry is jyotpatti, which is a compound term made of ‘jya’ (implying ‘Sine’) and ‘utpatti’ (meaning construction) and thus it connotes ‘The science of the construction of the Sines’ (Dutta and Singh 1983). This term can very easily be traced back to as early as Brahma-sphuta-siddhanta of Brahmagupta (628 CE), although the science per se can be dated to be much older. In fact, the reference to this science as trikonamiti is of much recent origin, after the literal translation of its Grecian counterpart. 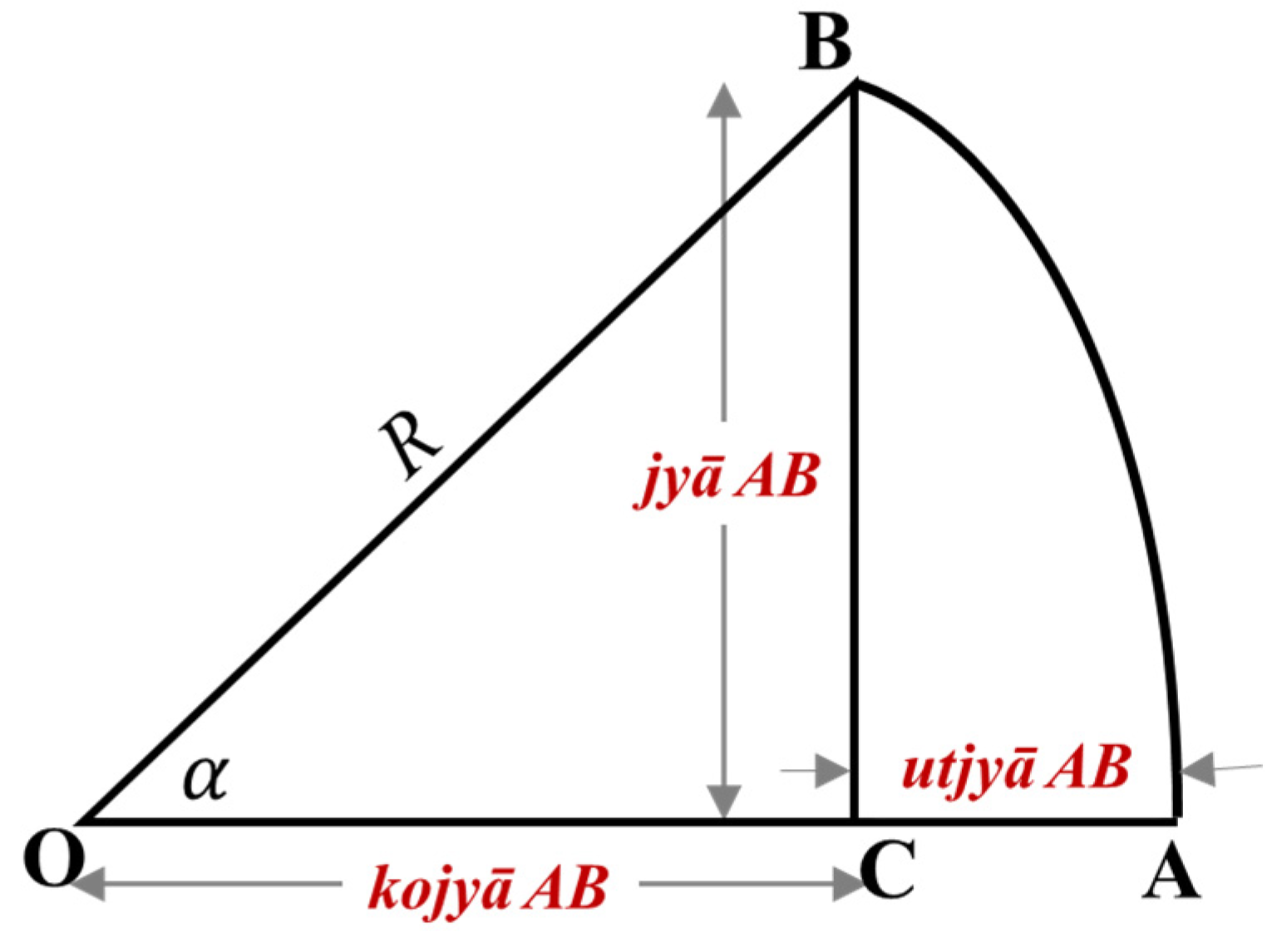As per the earliest extant records available in the Surya-siddhanta, the Hindus typically utilized three trigonometrical functions (‘phalan’) of an arc of a circle: jyā, koti-jyā and utkrama-jyā as presented in Figure 6. From Figure 6, it is clearly evident that if AB be an arc of a circle centered at O, then BC, OC and AC are denoted by jyā AB, koti-jyā AB (abbreviated as kojyā) and utkrama-jyā AB (shortened as utjyā), respectively. Further, when normalized by the radius of the arc (trijya) R, these yield sin α, cos α and versin α (= 1 - cos α), respectively where α is the angle subtended by the arc at the centre O.

An etymological account of the metamorphosis of the modern ‘sine’ is an interesting tale in itself. Incidentally, the modern sine derives from the Hindu term for chord jyā or jīvā, which was transliterated as jībā in Arabic, and abbreviated as “jb” since Arabic is not written with short vowels. Later in the 12th century, during the translation of these Arabic texts into Latin, “jb” was interpreted as “jaib” implying chest, so the Latin equivalent for ‘bosom’ was employed and the term “sinus” was suggested. Thus, the modern sine was introduced in the 1590s. Moreover, since jyā evolved into sine, naturally kojyāgot transformed into kosine, or the cosine. Similar degeneration and alteration of the term kramajyā occurred upon its translation into Arabic, where it appears as karaja or kardaja and later as kardaga, karkaya, gardaga etc. in Latin (Dutta and Singh 1983).

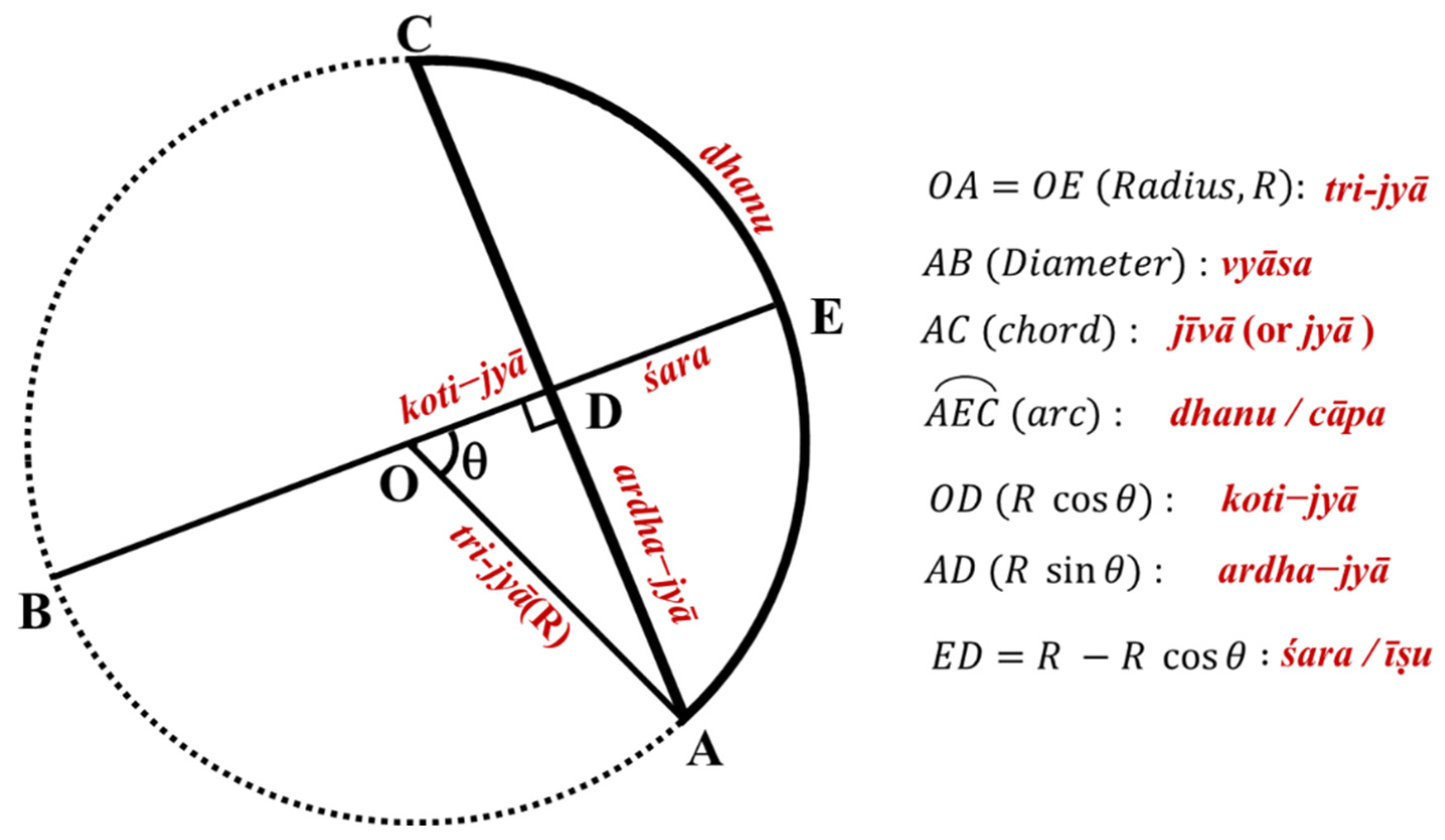
In an attempt to understand the various terminologies pertaining to trigonometry, an analogy of a bow first must be grasped. Figure 7 further explicates these terminologies using modern trigonometric notations. The arc of a circle (AEC), because of its sheer resemblance to a bow is often called chapa or dhanu.The sanskrit word jyā meaning “the string of a bow” literally represents the chord of an arc (AC) formed by connecting the extremities of an arc (A and C). This “full-chord” is termed as samasta-jyā, maurvī, siñjinī or jīvā. Half of this length is called a “half-chord” (AD) and half of the arc AEC (i.e., arc AE) is called the bow of the half chord AD. This half-chord or ardha-jyā, for brevity, is simply referred to as jyā by mathematicians. To distinguish it from the full chord, it is also sometimes stated as krama-jyā, meaning ‘direct Sine’ or ‘direct half-chord’, i.e., R$\sin \theta$. Next, koti denotes the complement of an arc to 90^o, and hence koti-jyā (kojyā) represents ‘the jyā of the complementary arc’, or agra, as stated in the Vateshvara-Siddhanta (Shukla 1986). Put differently, agra connotes the jyā of the poorak kona (complementary angle) and accordingly, kojyā (OD) is identical to the modern R$\cos \theta$. Finally, utkrama-jyā (utjyā or by Sanskrit liaison, ujjyā) literally means “reversed sine” and is computed as $ED=R[1-\sin \left(\pi /2-\theta \right)]$, or simply put, the difference between tri-jyā (R) and kojyā (R$\cos \theta$). It is also referred to as ‘viloma-jyā ‘ or ‘vyasta-jyā’ and owing to its similarity to an arrow placed over a bow, it is alternatively called as ‘śara’, ‘īṣu’ or ‘bāṇa’. In Hindu trigonometry, although tangent and secant functions were utilized in astronomical calculations, no express recognition was given to these functions. Needless to say, these geometrical functions can easily be represented in terms of jyā and kojyā.

In Hindu trigonometry, a circle is divided into four equal parts by two perpendicular lines intersecting at the centre, usually the east-to-west (prācī) and the north-to-south (udīchī). The resulting four quadrants (vrit-pada) are categorized into odd (ayugma) and even (yugma). According to Bhaskaracharya, proceeding from the east-point (prachi), the quadrants should be labeled as odd and even successively (Dutta and Singh 1983). It is worth noting that the Hindu system of quadrants is identically alike to the modern system. Further, one can get a fair idea of how much the developments in modern trigonometry owe their genesis to the Hindu mathematicians by even a cursory study of the treatises of Aryabhata, Lallacharya, Bhaskara I, Bhaskaracharya, Varahamihira, Madhava, Sripati, Manjula, Kamalakara, Brahmagupta, Paramesvara, Balabhadra, Munisvara among others. Table 2 presents a comparison between the trigonometry identities as proposed by Hindu mathematicians when these are juxtaposed with their modern trigonometric counterparts. It should suffice to say that some of these salient examples should patently establish to any reader of their cardinal contributions to trigonometry, be it the basic relation between functions such as sine and cosine (#1), functions of a complement (#2), change of sign of a function in different quadrants (#3), functions of multiple and submultiple angles (#4-7), addition and subtraction rules for sines and cosines (#8-9), values of functions for particular angles, the law of Sines ordinarily used in the solution of triangles (#10), trigonometrical tables in astronomy, technique of interpolation for getting function of any arc, various approximation of functions (#11), infinite series of sine (#12), cosine (#13) and spherical trigonometry.

Some typical references may be produced here for the sake of illustration of the usage of these terminologies in the Indian texts. Although possible, for the sake of brevity, a text corresponding to every term is not being produced, rather a few are being cited. For instance, the approximation of the value of the arc in terms of the chord given by the Aryabhata school is attributed to Nilkantha Somyaji in Aryabhata Ganitapada -

सत्त्वयंशादिषुवर्गाज्ज्यावर्गाढ्यात् पदं धनुः प्रायः |

sattvayaṃśādiṣuvargājjyāvargāḍhyāt padaṃdhanuḥprāyaḥ

Or, the square root of the sum of one and one-third the square of the arrow and the square of the (sine) chord is nearly equal to arc.

A commentary on Tantrasamgraha explains:

ज्ययोः परस्परं घातः त्रिज्याप्तो लम्ब इष्यते |

jyayoḥparasparaṃghātaḥtrijyāpto lamba iṣyate |

“The mutual product of the sine chords divided by the radius is regarded as the altitude” (Amma 1999).

Bhaskaracharya in his Jyotpatti, which occurs in an appendix to the Siddhanta-Siromani-Goladhyay provides an exact value of Sine of 18 degrees, as follows:

त्रिज्याकृतीषुघातान्मूलं त्रिजयोनितं चतुर्भक्तम् |

अष्टादशभागानां जीवा स्पष्टा भवत्येवम् ||

trijyākṛtīṣughātānmūlaṃ trijayonitaṃ caturbhaktam |

aṣṭādaśabhāgānāṃ jīvā spaṣṭā bhavatyevam ||

“Subtract the radius from the square root of the product of the radius-square and five, and divide by four; that becomes the true Sine of the eighteen degrees”. In other words,

$$R\mathit{sin}{18}^o=\left(\sqrt{5R^2}-R\right)/4$$

Or, $\mathit{sin}{18}^o=\left(\sqrt{5}-1\right)/4$

Table 3 enlists all the terminologies in trigonometry introduced above, with examples of the verifiable names of the individuals in the Indian subcontinent currently. As the table presents, names based on trigonometry span across arc, chord, sine, cosine, versin, quadrants, etc. Further, as before, for all the suggested terms in geometry, names can be found to exist in both genders, barring a few exceptions, when only feminine names have been found. That such an observation could be made in the Indian society may not just seem counter-intuitive, but may even come as a surprise to those who have subscribed to the usual tirade of deprivation meted out to women in terms of basic education, much less, a subject such as trigonometry. However, if so were to be the case that women in India were not taught a subject such as trigonometry, it is highly unlikely that their names would be associated with it, when they had to be supposedly kept away from it. At any rate, such names would not be at par, or greater than the male names. Needless to say at this point that such naming among the females isn’t a recent phenomenon brought about by the westernization in education and society.

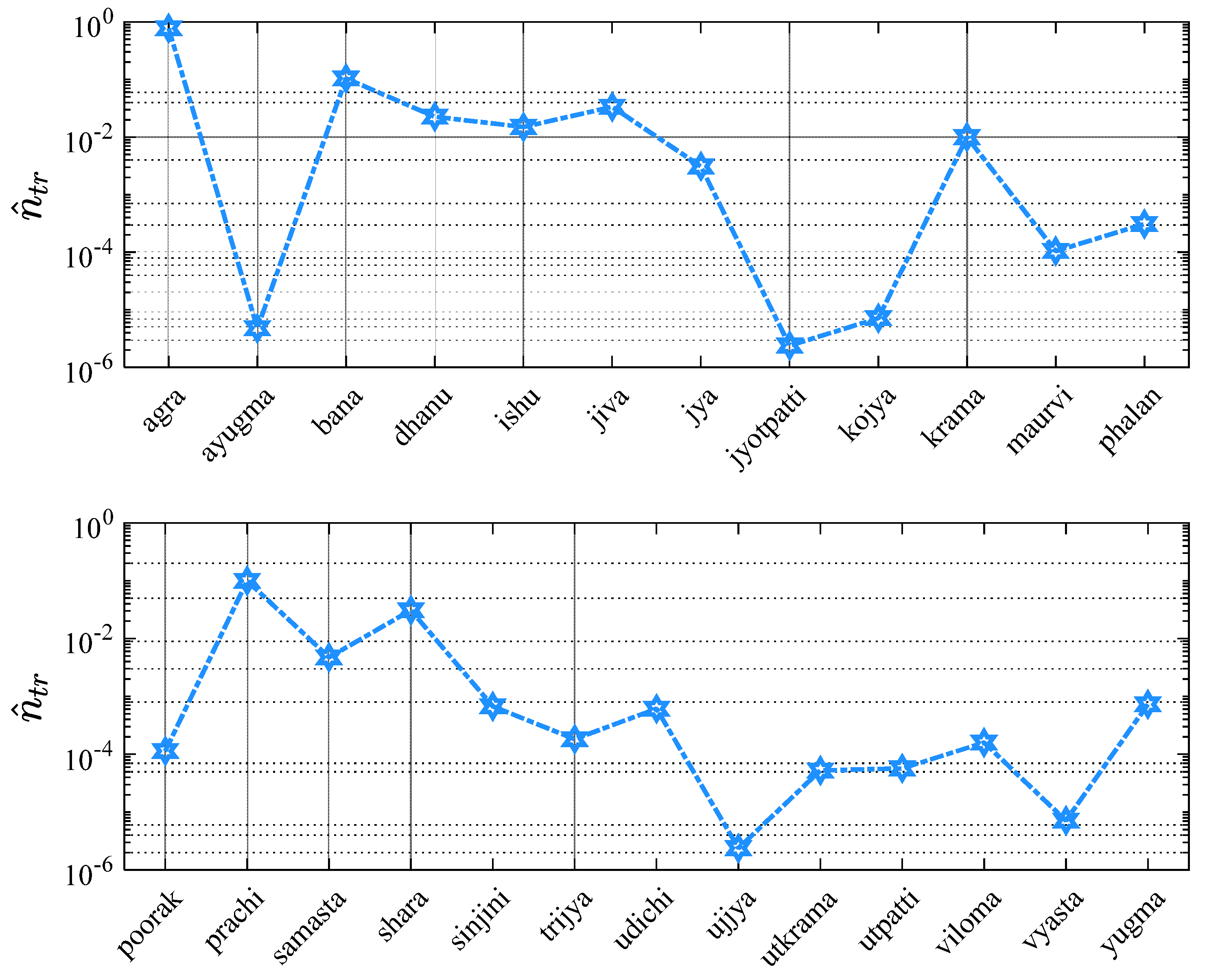
Figure 8 provides the quantitative evidence of the recurrence of the names based on trigonometry as presented in Table 3, from the LI dataset. It presents the specific name recurrence fraction for twenty-four names based on trigonometry, ${\widehat{n}}_{tr}$ in an alphabetical fashion. As the figure shows, the left axis denotes the name recurrence factor in the LI dataset, which multiplied by a hundred yields ‘recurrence percentage’. This figure demonstrates that ${\widehat{n}}_{tr}$ varies between 2.37x10^-6 to 0.77, or in other words, between 0.0002 % to 77.4%. Further, some of the terrms with highest${\widehat{n}}_{tr}$ are ‘agra’, ‘bana’, ‘prachi’, ‘jiva’ and ‘shara’ with ${\widehat{n}}_{tr}$corresponding to 0.77, 0.10, 0.099, 0.033 and 0.03, respectively. On the other hand, terms like ujjya, ayugma, vyasta, kojya and utkrama fare very low on the ${\widehat{n}}_{tr}$ value. In general, names under this division are somewhat uncommon to be heard, particularly in the North Indian setting. For instance, names like yugma, sinjini, udichi, phalan, trijya, maurvi and utpatti fall under this category. However, there is a point worth taking into account – any conclusion regarding the mathematical traditions of India can’t be just gauged and summarized from a limited perspective of a particular region, be it Kerala, Bihar, Ujjain, Bengal or Gujarat. Rather, the influence of mathematics upon the entire Indian kaleidoscope has to be observed. Thus, terms such as sinjini and udichi may not appear a befitting name of an individual in north and west regions of India such as Punjab, Rajasthan, or Delhi – but appears as a name in West Bengal. This observation further underscores the need for a comprehensive study such as this.

5.3. Numeration

The description of the number system and its standing tradition in India may befittingly begin with the description of the invention of zero, also called shunya. The earliest description of zero can be found in Gayatri Chanda by Pingala Acharya in at least 300 BCE:

गायत्रे षड्संख्यामर्धेऽपनीते द्वयङ्के अवशिष्टस्त्रयस्तेषु रूपमपनीय द्वयङ्काधः शून्यं स्थाप्यम् ||

gāyatreṣaḍsaṃkhyāmardhe'panīte dvayaṅke avaśiṣṭastrayasteṣu rūpamapanīya dvayaṅkādhaḥ śūnyaṃsthāpyam

“In Gayatri-chanda, one pada has six letters. When that is made into half, it becomes three. Remove one from it and make it half to get one. Remove one from it and put a zero (Shunyam).” However, it was Brahmagupta, who in his Brahma-Sphuta-Siddhanta, written in 628 CE, introduced the seminal concept of zero as a number in its own right, a conceptual leap from what had been done before him. The Sanskrit equivalent for one is pratham or ekam, both of which figure out commonly as Indian names in various forms. The Sanskrit root for two is dvi, which can be heard most commonly in the surname dwivedi, which literally means ‘the knower of the two vedas’. Along the same lines, of the four vedas, Rgveda, Samveda, Yajurveda and Atharvaveda, one who knows only one may be termed vedi, or presumably in its colloquial form as bedi. Similarly, the knower of the three vedas are called trivedi and the knower of all the four Vedas are chaturvedi. Colloquially, the word for two is ‘dwitiya’. The sense of ‘two’ is also captured in the words advaita and dvaita, i.e., non-dual and dual, most certainly due to the existence of these schools of spiritual tradition as enunciated and taught by Adi Shankaracharya and Madhvacharya, respectively. Other names representing three such as trayee or tritiya also exist as feminine names. Chatur which is a root meaning four occur as names in its root form, or in other forms described earlier such as chaturth, chaturthi, chturbhuja and chaturvedi. In the same way, panch also occurs in its root form, as well as another colloquial form panchama or panchami. Names pertaining to six to ten appear frequently, in the names of shad, sapt, ashta, nava and dash, respectively or in a feminine sense shashthi, saptami, ashtami, navami and dashmi. The names eleven to fourteen such as Ekadashi, dvadashi, trayodashi, chaturdashi etc. correspond to the eleventh, twelvth, thirteenth, and fourteenth day from the new/full moon and appear in both genders, most probably due to the repeated reinforcement caused in the collective Indian social consciousness by the existing lunar calendar. A similar is the case with shodashi, which typically connotes a sixteen-syllable incantation (mantra). Next, the numeric names can only be found in multiples of ten, such as twenty (Vinshti), thirty (trinsh), sixty (shashtih), seventy (saptati), eighty (ashiti), ninty (navati), and hundred (shata). It may also be pointed out that hundred and thousand are frequently used to denote large quantities in mundane and ordinary transactions, and thus it is not surprising to find many other derivatives of these units such as Shatakshi (meaning one with hundred eyes) and Sahasrabudhe (One with a thousand-fold intelligence). Post hundred, the names can be found in the exponents of ten – and some variations can be found in how different powers of ten are described in Jaina tradition, by Hindu mathematicians such as Aryabhata and in ancient texts such as Valmiki Ramayana. However, the focus of the current paper is not to dwell on the correctness, exactitude, origin, or even pre-eminence of any system of numeration, but solely to focus on the terminologies which are extant as names in modern India, irrespective of the mathematical tradition from which it is derived.

In the decimal place-value system of numerals in India, which is a remarkable scientific gift to the civilized mankind, ten has been the base for counting since Vedic times. Ranging from hundred (10³), and thousand (10³), the higher exponents such as ayuta (10⁴), niyuta (10⁵) and prayuta (10⁶) referring to a million are also common. Another frequent alternative to niyuta is laksha. In fact, several non-decimal scales of numeration were current in India for practical enumeration up to very large numbers, and one of such schemes as presented in the Valmiki Ramayana describes the laksha-scale numeration system in these twelve lines (Gupta 2008):

शतं शतसहस्राणां कोटिमाहुर्मनीषिणः| शतं कोटिसहस्राणां शङ्कुः इत्यभिधीयते | शतं शङ्कुसहस्राणां महाशङ्कुः इति स्मृतः | महाशङ्कु-सहस्राणां शतं वृन्दम् इहोच्यते | शतं वृन्दसहस्राणां महावृन्दम् इति स्मृतम् | महावृन्द-सहस्राणां शतं पद्मम् इहोच्यते | शतं पद्म-सहस्राणां महापद्मम् इति स्मृतम् | महापद्म-सहस्राणां शतं खर्वम् इहोच्यते | शतं खर्व-सहस्राणां महाखर्वम् इति स्मृतम् | महाखर्व-सहस्राणां समुद्रम् अभिधीयते | शतं समुद्र-सहस्रम् ओघ इत्यभिधीयते | शतम् ओघ-सहस्राणां महौघ इति विश्रुतः |

śataṃ śatasahasrāṇāṃ koṭimāhurmanīṣiṇaḥ| śataṃ koṭisahasrāṇāṃ śaṅkuḥ ityabhidhīyate | śataṃ śaṅkusahasrāṇāṃ mahāśaṅkuḥ iti smṛtaḥ | mahāśaṅku-sahasrāṇāṃ śataṃ vṛndam ihocyate | śataṃ vṛndasahasrāṇāṃ mahāvṛndam iti smṛtam | mahāvṛnda-sahasrāṇāṃ śataṃ padmam ihocyate | śataṃ padma-sahasrāṇāṃ mahāpadmam iti smṛtam | mahāpadma-sahasrāṇāṃ śataṃ kharvam ihocyate | śataṃ kharva-sahasrāṇāṃ mahākharvam iti smṛtam | mahākharva-sahasrāṇāṃ samudram abhidhīyate | śataṃ samudra-sahasram ogha ityabhidhīyate | śatam ogha-sahasrāṇāṃ mahaugha iti viśrutaḥ |

“A hundred of hundred thousand is said to be koti by the learned, a hunderd of thousand koti is termed shanku, a hundred of thousand shanku is known as mahashanku, a hundred of thousand mahashanku is called vrinda, a hundred of thousand vrinda is known as mahavrinda, a hundred of thousand mahavrinda is called padma, a hundred of thousand padma is known as mahapadma, a hundred of thousand mahapadma is called kharva, a hundred of thousand kharva is known as mahakharva, thousand mahakharva is termed samudra, a hundred of thousand samudra is termed ogha, a hundred of thousand ogha is heard to be mahaugha.”

To sum it up, 10⁷ is referred to as koti, 10⁸ as dashkoti and 10⁹ (a billion) as shatakoti. Billion and trillion (10¹²) are also referred to as arbuda and shanku, respectively. Shankha and Vrinda denote 10¹⁷ and 10²² respectively and Padma denotes a quadrillion (10³²). Extremely large quantities such as 10⁴², 10⁵⁰ and 10⁵⁵ have been represented by kharva, samudra and ogha and finally poorna connotes unlimitedly large numbers, whereas ananta symbolizes infinity. In fact, zero, infinity, and finite but extremely large numbers owe their genesis to Hinduism, Buddhism and Jainism because of their rich metaphysical traditions (Aczel 2015). The concept of infinity has fascinated many Hindu mathematicians and Bhaskaracharya refers to it as khahara (Zero divisor) and while commenting upon its invariability, likens it to God Visnu. The invocation mantra of īśopaniṣad refers to this inifinite whole as poorna and states that when poorna is subtracted from poorna, what remains is still poorna.

ॐ पूर्णम् अदः पूर्णम् इदम् पूर्णात् पूर्णम् उदच्यते |

पूर्णस्य पूर्णम् आदाय पूर्णम् एव अवशिष्यते ||

- ईशोपनिषद्

oṃ pūrṇam adaḥ pūrṇam idam pūrṇāt pūrṇam udacyate |

pūrṇasya pūrṇam ādāya pūrṇam eva avaśiṣyate ||

- īśopaniṣad

It is worth noting that there are varying nomenclatures for numeration in India (particularly of large numbers), and here we only focus on the terms existing in mathematics that are extant in societal parlance through the usage of mathematical names. It is interesting to note, however, that there was no concept of denoting such large numbers in the contemporary works of other nations: the Greeks managed a maximum up to 10⁴ (myriad), whereas the Roman terminology ended with 10³(mile).

Table 4 enlists all the terminologies in the numeration introduced above, with examples of the verifiable names of the individuals in the Indian subcontinent currently. As the table presents, names based on numeration spans the entire range of the number line from zero to infinity. Further, as before, for all the numbers, be it zero, a single-digit number, a double-digit number, or greater exponents of ten, names can be found to exist in both genders, barring a few exceptions, when only feminine names have been found. That such an observation could be made in the Indian society may not just seem counter-intuitive, but may even come as a surprise to those who have subscribed to the usual tirade of deprivation meted out to women in terms of basic education, much less, a subject such as the study of numbers. However, if so were to be the case that women in India were not taught a subject such as numeration or number theory, it is highly unlikely that their names would be associated with it, when they had to be supposedly kept away from it. At any rate, such names would not be at par, or greater than the male names. Again, we wish to reiterate that such naming among the females isn’t a recent phenomenon brought about by the westernization in education and society.

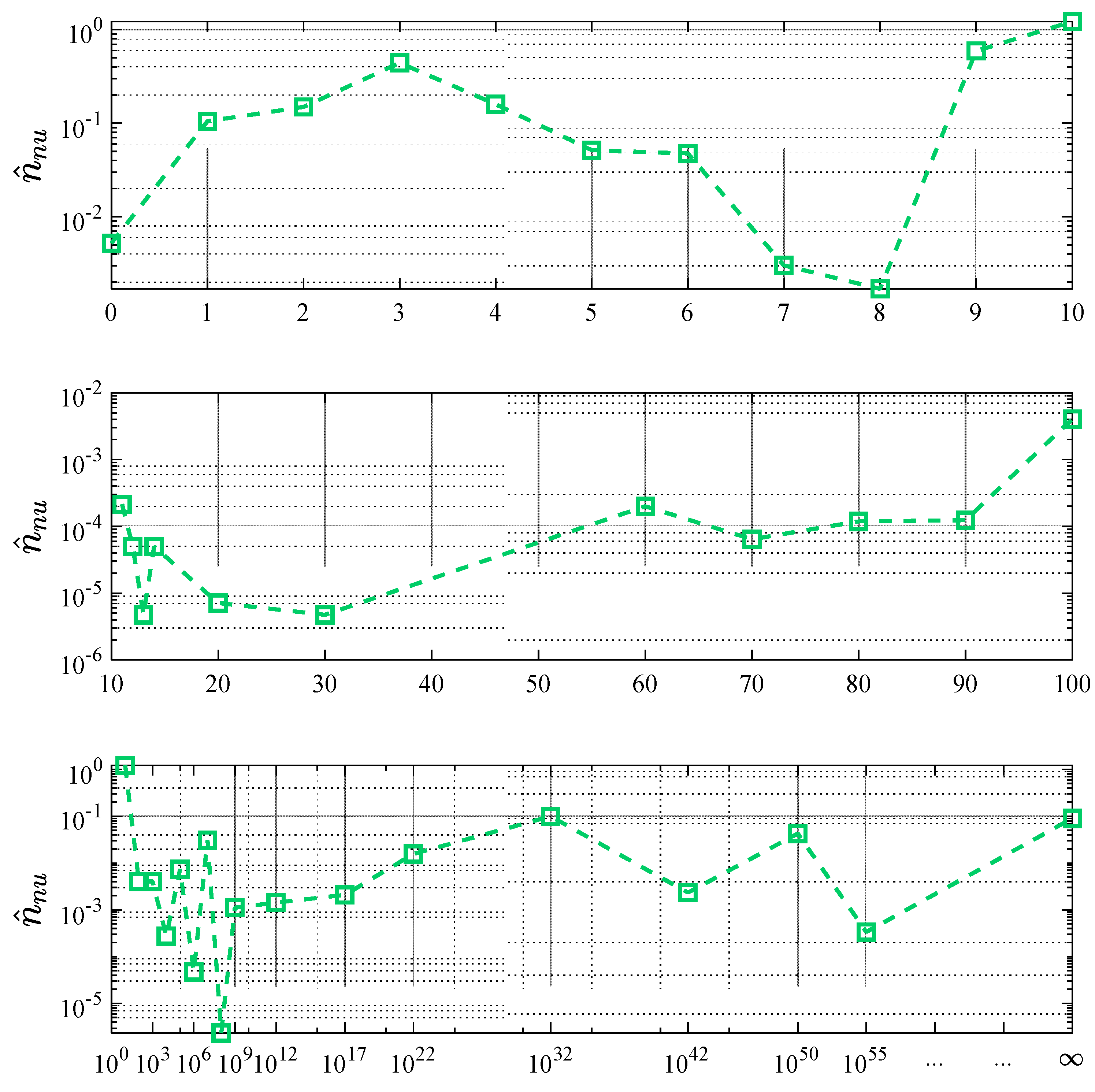
Figure 9 demonstrates the quantitative evidence of the recurrence of the names based on numeration as presented in Table 4, from the LI dataset. It presents the specific name recurrence fraction for forty-six names based on numeration, ${\widehat{n}}_{nu}$. As the figure shows, the left axis denotes the name recurrence factor in the LI dataset, which multiplied by a hundred yields ‘name recurrence percentage’. In presenting this figure, however, a different methodology has been followed as compared to before. All the terms corresponding to a particular number have been grouped together and their numeric values have been summed up. For instance, for the number 2, all the terms such as dvi, dvitiya, dvaita, advaita etc. have been clubbed together. This figure demonstrates that ${\widehat{n}}_{nu}$ varies between 2.37x10^-6 to 1.2, or in other words, between 0.0002 % to 122%. It is not surprising to find a percentage value corresponding to the term ‘dash’ attain a value greater than cent percent, since ‘dash’ is a name in multiple cultures apart from Indian. Thus, the LI dataset yields a greater count for ‘dash’ than the normalizing “most ubiquitous Indian name” say, ‘Rahul’ which is a name mostly in India and southern Asia. Further, some of the terrms with highest ${\widehat{n}}_{nu}$are ‘dash’, ‘nava’, ‘dvi’ (e.g., dvivedi), ‘tri’ (e.g., trivedi) and ‘padma’ with ${\widehat{n}}_{nu}$corresponding to 1.22, 0.59. 0.14, 0.14 and 0.1 respectively. On the other hand, terms like dashkoti, khahara, trinsha, trayodashi, vimshati etc. fare very low on the ${\widehat{n}}_{nu}$ value. Other terms which occur in the high frequency range are eka, ananta, shad, prathama, samudra, pancha, purna, etc. – names that can be very commonly heard in the Indian setting.

Moreover, a system existed and was perfected in India of expressing numbers by words arranged as in place-value notation, called the bhūtasaṃkhyā system, or the “word-numeral” system as referred to by Datta and Singh (1935). In this scheme, the numerals are denoted by names of objects, beings, or concepts which naturally in accordance with the scriptural understanding, connote numbers. Some associations are universal (for instance, ‘eyes’ and ‘ears’ for two) while others are deeply rooted in aspects of Indian culture, traditions, cosmology, and cosmogony (Yano 2006). For instance, zero could be represented by words that mean void, sky, etc. ‘One’ could be denoted by something that is truly unique such as the moon or the earth, and its synonyms (Datta and Singh, 1935 p. 55). ‘Two’ could be denoted by eyes, arms, hands, ears, thighs, ashvini or yamala; ‘Three’ could be represente by guna, loka etc.’ ‘Four’ by the Vedas, shruti etc.; ‘Five’ by the senses (indriya), mahabhuta (five gross material elements) or Pandava; ‘Six’ by rasa, rtu (season); ‘Seven’ by parvata, shaila etc.; ‘Eight’ by vasu; ‘Nine’ by dvara, nidhi, Durga etc.; ‘Ten’ by dik, disha etc.; ‘Eleven’ by Rudra; ‘Twelve’ by Aditya, ‘Fourteen’ by Manu, vidya, ‘Fifteen’ by tithi, dina, paksha, etc. and so on. However, if these names were included, the actual list of ‘mathematical names’ would be truly sizable. It is indeed possible that many of these names (such as indu, triguna etc.) may have been reinforced in the societal cognizance on account of veneration for mathematics, it would be very difficult to extricate the fraction of such naming that occurred because of it owing to the simultaneous existence of what we could call as “involutory mathematical names”. The import of the “involutory mathematical names” can be understood by a two-fold process: first, when the pervasive natural names evolved and got absorbed into the mathematical semantics, and the later process of involution in which these names were again codified in the society, possibly with a tinge of mathematical symbolism. At any rate, this bhūtasaṃkhyā system led Yano (2006) to concede that the existence of such a system indicates that the ancient Indians were extremely number-conscious.

5.4. Arithmetic

In fact, arithmetic in Hindu mathematics is called ‘rashi-vidya’ (Datta and Singh, 1935, p.4), since rashi refers to a sum or a number for a mathematical operation. The fundamental quantity is a digit (anka) ranging from zero, one, two etc. to nine, any of which can combine to form a number (sankhya). Hindu mathematicians have dealt extensively with real numbers (Vaastavik sankhya), which can be categorized into rational (Parimeya) and irrational numbers. Irrational numbers such as $\sqrt{2}$ and $\pi$ were known to the ancient Indians about three millennia ago and more exact approximations to them have been proposed by several mathematicians over the centuries, although it is a matter of conjecture as to whether the concept of irrationality was known to the ancient Indians (Kannan 2014). However, a lot has been reported on the concept and characteristics of rational numbers. Rational numbers can be classified as integers or fractions (bhinna sankhya). Integers can be negative (ṛṇa sankhya), zero (shunya) or positive (dhana sankhya), these terminologies of seeing negative numbers as ‘debt’ and positive numbers as ‘property’, enunciated by Brahmagupta. The set of positive integers ranging from one to infinity can be termed as natural numbers (prākṛta sankhya) and its assortment with zero are the whole numbers (poorna sankhya). Further, the whole numbers can be classified as either odd (viṣama) or even (sama) – depending upon whether it yields a whole number upon division by two. Similarly, natural numbers could also be classified as prime or composite (sanyukta) numbers. Composite numbers have more than two factors, whereas prime numbers do not. Apart from integers, fractions (bhinnaor kalā) could also form a part of rational number. Fraction typically refers to the number of parts in a whole – it is denoted by the number of parts selected or, numerator (ansh) and total number of parts in a whole, denominator (hara) separated by a line. Fractions could be of multiple types: such as a simple (saral), mixed (miśra), equivalent (tulya) or composite (sanyukta). One could even refer to a combination of fractions asprabhāga. Moreover, one can also talk about other kinds of numbers such as a perfect number (saṃpūrṇa saṃkhyā) which in number theory refers to a positive integer that equals the addition of its positive divisors, apart from the number itself. Any finite quantity may be referred to as parimit sankhya. In the Hindu mathematics, many times, the numbers are arranged in a row (pankti) for a mathematical operation, and the numbers may need to be placed in the increasing (ārohana) or decreasing order (avarohana).

Arithmetic usually involves four basic operations: addition, subtraction, multiplication, and division although Hindu mathematicians such as Brahmagupta and Bhaskara II have discussed the squares/cubes and square and cube roots in the same vein (Patwardhan et al. 2006). The process of adding two numbers is denoted by yoga, which means the union, and which follows the additive identity (tat-samaka) as well as closure property (sanvrit). On the other hand, the process of subtracting two numbers is referred to as viyogaor kanitaand the difference is called antara. In a typical multiplication (sanvarga) operation of $a\times b=c$, a and b are called multiplicands (gunakara) whereas c is known as the product (gunaja). When both the multiplicands are identical, the resulting product is a square (varg), and in the case of three identical multiplicands, the product is a cube (ghana). To put the same thing conversely, a and b are factors (karak) of c ; and c is a multiple (bahuguna) of a and b. Similarly, a division operation (bhaag) of m/n yields a quotient, q (labdhior labdha) and a remainder, r (śeṣa) where m is called dividend (hārya or bhājya) and n is known as the divisor (bhājakaor hara). Abhyāsadenotes an addition or a multiplication operation and the square root of a number (maybe a surd) is called karani. Moreover, arithmetic usually forms the backbone of day-to-day ordinary transactions of profit (laabh) and loss.

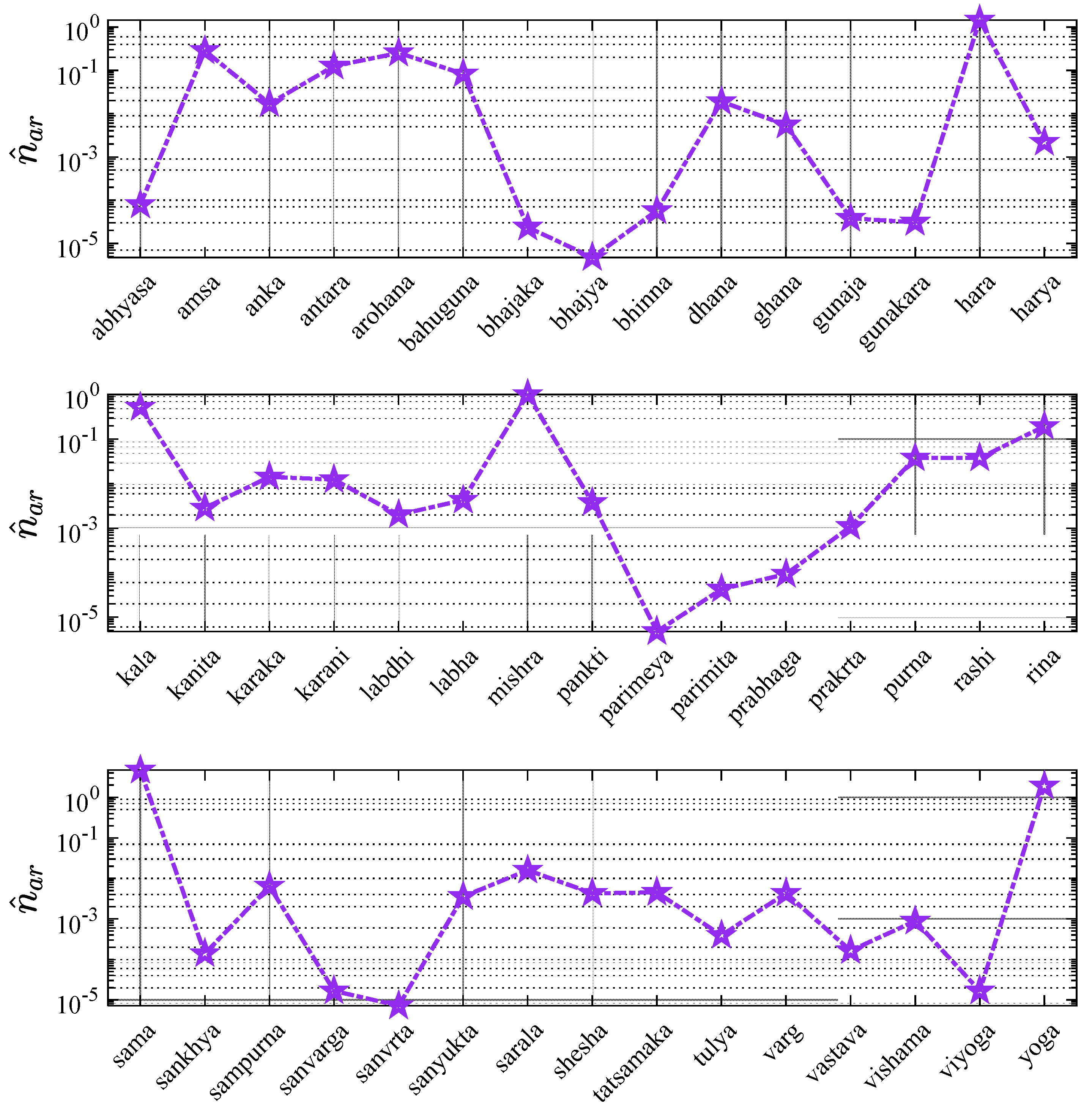
Figure 10 shows that the quantitative evidence of the recurrence of the names based on arithmetic as presented in Table 5, from the LI dataset. It presents the specific name recurrence fraction for forty-six names based on arithmetic, ${\widehat{n}}_{ar}$ in an alphabetical fashion. As the figure shows, the left axis denotes the name recurrence factor in the LI dataset, which multiplied by a hundred yields ‘recurrence percentage’. This figure evidently demonstrates that ${\widehat{n}}_{ar}$ varies between 2.37x10^-6 to 4.7. It is not surprising to find a fractional value corresponding to the term ‘dash’ larger than unity, since ‘dash’ is a name in multiple cultures apart from Indian. Thus, the LI dataset yields a greater count for ‘dash’ than the normalizing “most ubiquitous Indian name” say, ‘Rahul’ which is a name mostly in India and southern Asia. Further, some of the terms with highest ${\widehat{n}}_{ar}$ are ‘sama’, ‘yoga’, ‘hara’, ‘mishra’ and ‘kalaa’ with ${\widehat{n}}_{ar}$corresponding to 4.70, 1.89. 1.44, 1.01 and 0.52 respectively. On the other hand, terms like parimeya, bhajya, samvrita, viyoga and samvarga fare very low on the ${\widehat{n}}_{ar}$ value. Other terms which occur in the high frequency range are amsha, arohana, rina, antara, bahuguna, purna, rashi etc. – names that can be very commonly heard in the Indian setting.

5.5. Algebra

Unlike Arithmetic which is the most basic branch of mathematics, that deals with the basic counting of numbers with operations like addition, subtraction, multiplication, and division, algebra, on the other hand, deals with similar operations but with variables and numbers. Algebra has been referred to as ‘Bijaganita’ by Hindu mathematicians, literally alluding to “mathematics by the means of seeds (bija)”. Bijaganita is so called since it employs algebraic equations (samee, saamyaor samika) and analysis, which, similar to seeds (bija) of plants have the potential to generate solutions to mathematical problems (Hayashi 2013). Since it deals with unknown quantities expressed in symbols (varna / cara), it is also called avyakta-ganita, or “mathematics of unknown quantities”. In such problems, a sami-karana (equation) is laid out to find the solution (hala), i.e., value (maana) of a desired quantity (called kamika or vancha). Usually, such algebraic relations are expressed with polynomials (bahupad) on the two sides (paksha) of the equality (samtaa), or inequality (when such quantities are called atulya) and the ratio of two variables is called anupat. In bijaganita, the unknown numers are represented by symbols which are the initial syllables of the word यावत् – तावत् (yāvat-tāvat) or the color names such as kālaka (black), nīlaka (blue) and pīta (yellow) as per Aryabhata’s gulikā. A combination of the initials of terms such as varga (square), ghana (cube), and ghāta (product) is used to denote the powers of the unknown numbers and their coefficients are placed to the right of the symbol, with the both sides of the equation being placed one above the other. Negative coefficients are written with a dot above the numbers and the absolute terms in an equation are denoted by the initial of rūpa, which means an integer (also called as dṛśya). Joseph (2013) noted that Indian mathematicians were the first to use symbols to denote unknown quantities. For instance, in Prthudakaswami’s commentary on Brahma Sphuta-siddhanta, an illustration of yavat-tavat representation is given. As per his illustration, an equation such as $8x^5+9x^4-7x^3+x=6x^2-1$ would be expressed as:

यावघघा ८ यावव ९ याघ ७याव ० या १ रू ०,

यावघघा ० यावव ० याघ याव ६ या ० रू १,

yāvaghaghā 8 yāvava 9 yāgha 7 yāva 0 yā 1 rū 0

yāvaghaghā 0 yāvava 0 yāgha 0 yāva 6 yā 0 rū 1

,

The product of two different unknowns is known as bhāvita(produced) and denoted by its initial letter as in yākābhā 5 for 5xy (Hayashi 2013). Bhaskaracharya, however, did not use the yavat-tavat system for solving equations, although it was well developed during his time. For instance, in his book, Leelavati, he gives many methods for solving equations, such as the method of transition (Sankramana) in text 61 -

योगो-अन्तरेणोनयुतो-अर्धितस्तौ राशी स्मृतौ-संक्रमणाख्यम्-एतत् |

yogo-antareṇonayuto-ardhitastau rāśīsmṛtau-saṃkramaṇākhyam-etat |

This text states the Sankramana method, by which one can obtain two unknown numbers whose sum and differences are known – by adding and subtracting the numbers and dividing them by two. Similarly, the rule of concurrence is known as sankrama.

Aryabhata used gulikāas a term for unknown numbers in his rule for solving linear equations of the type mx + c = px + q in his Aryabhatiya (499 CE). Brahmagupta, on the other hand, suggested many theorems for the indeterminate equations of the second degree, also called varga-prakriti(literally meaning ‘square nature’) by Hindu mathematicians, later called (incorrectly) as the Pell’s equation: Nx² + z = y² (where N, z are integers). The coefficient N is called gunaka (multiplier) and z is called ksepa(additive). Brahmagupta’s bhāvanā (lemma) combines two solutions (x₁, y₁, z₁) and (x₂, y₂, z₂) of the varg-prakriti Nx² + z = y² to produce a third solution (x₃, y₃, z₃) which are given as x₃ = x₁ y₂ + x₂ y₁, y₃ = N x₁ x₂ + y₁ y_{2 ,} z₃ = z₁ z₂. In general, bhāvanā was used by ancient Indian algebraists to refer to a principle of “composition” introduced by Brahmagupta, by which two mathematical objects of a certain type can be combined to yield a third object of the same type (Dutta 2017). For instance, the Samasa-bhavana (additive composition) provides infinitely many integral solutions to the equation Nx² + 1 = y² from a given non-trivial integral solution. Brahmagupta’s novel concepts also led to the discovery of the cakravala(cyclic) algorithm, which is a perfect error-free method for obtaining minimum positive integral solutions to Nx² + 1 = y² for any N (Dutta 2002).

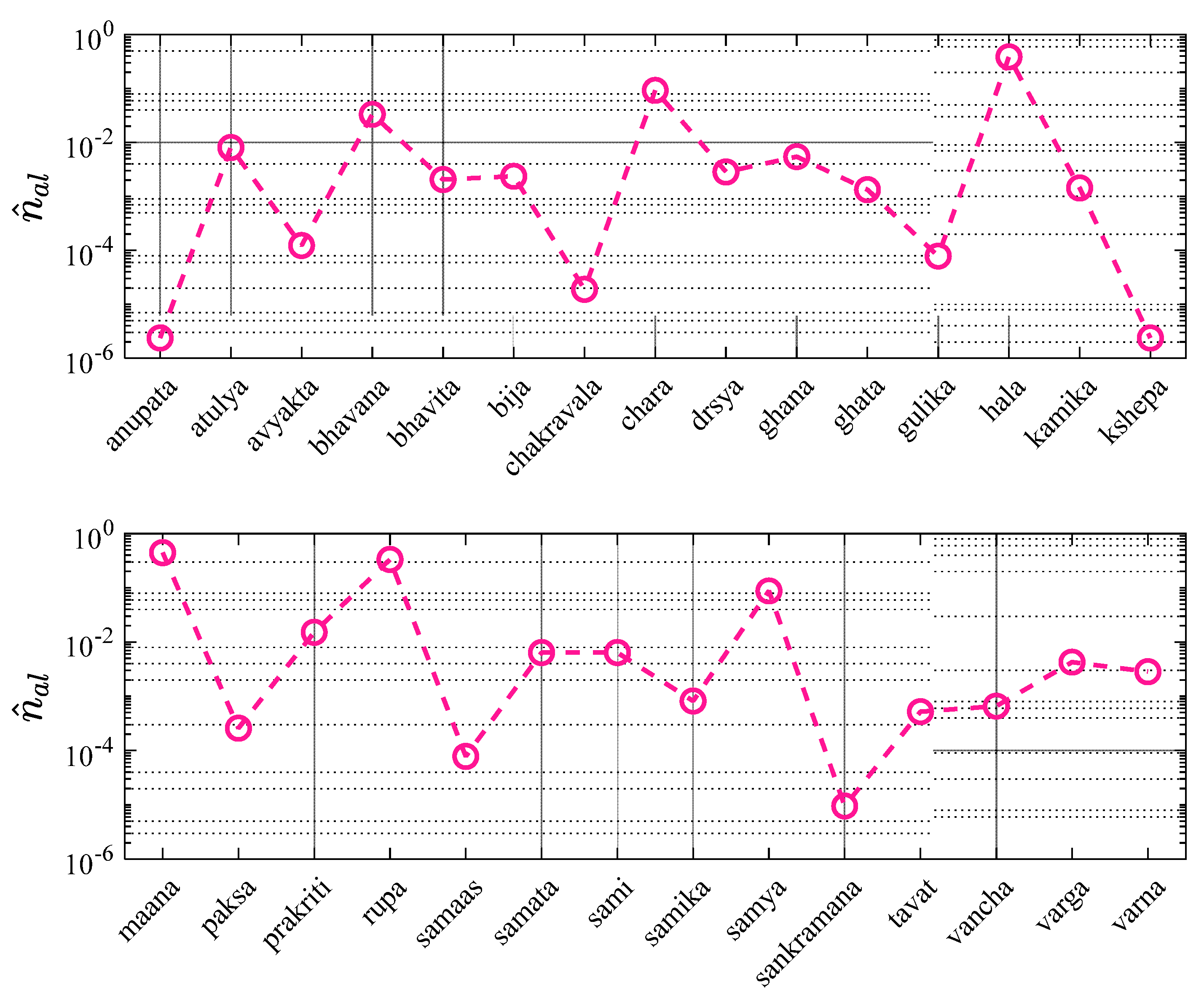
Figure 11 shows that the quantitative evidence of the recurrence of the names based on algebra as presented in Table 6, from the LI dataset. It presents the specific name recurrence fraction for thirty names based on algebra, ${\widehat{n}}_{al}$ in an alphabetical fashion. As the figure shows, the left axis denotes the name recurrence factor in the LI dataset, which multiplied by a hundred yields ‘recurrence percentage’. This figure evidently demonstrates that ${\widehat{n}}_{al}$ varies between 2.37x10^-6 to 0.44. It is worth noting that the upper bound on ${\widehat{n}}_{al}$ is by far the least, as observed for names based on algebra, although it must be incumbent on the classification of terms between algebra and arithmetic as well. Further, some of the terms with the highest ${\widehat{n}}_{al}$ are ‘mana’, ‘hala’, ‘rupa’, ‘chara’ and ‘samya’ with ${\widehat{n}}_{al}$corresponding to 0.44, 0.38. 0.33, 0.09 and 0.08 respectively. On the other hand, terms like kshepa, anupata, sankramana, chakravala and samaas fare very low on the ${\widehat{n}}_{al}$ value. Other terms which occur in the high-frequency range are bhavana, prakriti, atulya, samataa, sami, ghana, varga etc. – names that can be commonly heard in the Indian setting.

5.6. Mathematics and Mathematicians in the Vedic/Indian Tradition

The incipient stages of mathematics (ganita) and its development witnessed two imbricated schools – that of geometry as well as that of arithmetic and algebra. Incidentally, both of these schools of mathematics were greatly cultivated and nurtured in India. In fact, A Seidenberg, a pre-eminent historian of mathematics traced the origin of advanced mathematics to the Rig-vedic rituals (Seidenberg 1978; Seidenberg 1983). Truly, one of the most primeval texts in mathematics are the shulba-sutras, which are compendiums or handbooks that illustrate the methodology of altar construction for the sacrifices of the Vedic Hindus. At present, only seven shulba-sutras are known: Vadhula shulba, of Baudhayana, Apastamba, Varaha, Manava, Maitrayana from Krsna-Yajur Veda and Katyayana Shulba sutra from Shukla yajur Veda. In ancient India, the construction of fire altars of proper sizes and shapes had to be done with great accuracy for the purpose of sacrifices, and thus arose the problems of geometry, algebra, and arithmetic. This is akin to how the study of astronomy (khagola) in India originated from the need to conduct such Vedic sacrifices at the proper time (Dutta 1932). The pervasiveness of the science of astrology (jyotisha) in India and the preparation of astrological charts (panchanga) by such sound principles, may also be understood in the same context.

In the title ‘shulba-sutra’, ‘sutra’ just refers to an aphorism or a ‘pithy rule’ and is indicative only of the style of the composition, and not the actual content. In fact, Katyayana’s second part of the work titled shulba parishishta (‘Appendix to the Shulba’) and shulbi-kriya (‘The practice of the Shulba’) definitively establishes that the true name of this science of geometry is shulba. Geometry was also oftentimes referred to as ‘Rajju’, meaning a rope or a cord. Etymologically, shulba means ‘to measure’ or an act of measurement, and in the shulbas, the measuring tape is called rajju. One of the connotations of the word Shulba is a line (or a surface) which is the result obtained by measuring, and thus is a later work on Shilpa-shashtras, the surveyor is alluded to as as a sutra-dhara ("rope-holder") or as an expert in alignment (rekha-jna) or one who knows the line (Datta 1932). Not surprisingly, geometry is commonly also referred to as ‘Rekha-ganita’ or jyamiti.

The sulbasutras enunciated a scheme of linear measurement units, based on the magnitudes and proportions of the human body, which later evolved into traditional units that became popular across India. For instance,

14 anus (millet grain size) → 1 angula

3 angulas → 1 parva

12 angulas → 1 pradesha (/vitasti)

15 angulas → 1 pada

24 angulas → 1 aratni (/hasta)

30 angulas → 1 prakrama

96 angulas → 1 danda

120 angulas → 1 purusa

An angula in Sanskrit refers to a finger or a finger’s breadth which is typically identical to fourteen millet grains (anu) or eight barleycorns. Three angulas form a parva, four such parvas constitute a pradeshaor vitasti, i.e., a span and fifteen angulas make a pada. Twice the vitasti is also called an aratnior hastai.e., a cubit. Further, a prakramacomprises of thirty angulas, a danda of ninty-six angulas and one hundred twenty angulas make up a purusa, which is identical to the height of a man. The ancient Indian unit of length, ‘danda’ has been identified equivalent to the modern ‘metre’ (Dongre 1994).

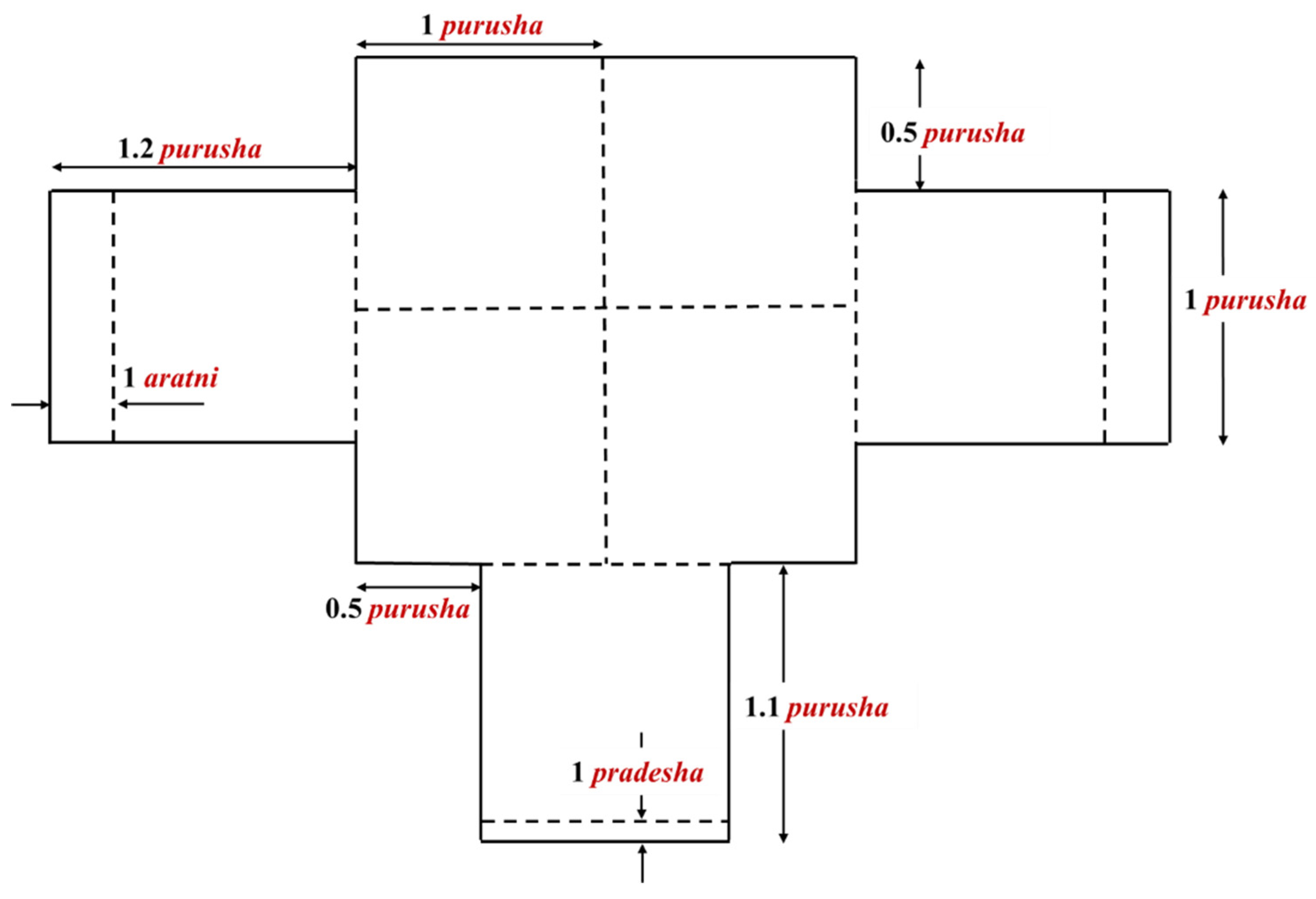
In Vedic India, the accurate construction of the fire altars (vedior chiti) for sacrifices required geometrical operations of very complex nature. Among fire altars, the most ancient and primitive one is the shyena-cit (or the altar of the form of the falcon) having 16 corners (shroni) which is shown in Figure 12. The body of this altar consists of four squares of one square purusaeach, whereas its wings are rectangles of one purusa by one purusa and one aratni (i.e., 1.2 purusa). Its tail comprises of a rectangle of one purusa by one purusa and one pradesha (i.e., 1.1 purusa). This altar is often known as सप्तविधा-सारत्नि-प्रदेश-चतुरश्र-श्येनचित् since it is made up of square bricks and its symmetrical (samamit) shape resembles that of a falcon with an area of 7.5 square purusas (Datta 1932). Saumiki-vedi or Mahavedi is an isosceles trapezium with face length 24 padas (or prakramas), base 30 padas and altitude 36 padas. The Sautramani vedi and Paitriki vedi are similar in shape to a Mahavedi, but with an area equaling one third and one-twenty seventh of the Mahavedi, respectively (Datta 1932). Januis yet another unit of measurement, used frequently in the Vedic tradition, as are Varuniand Marutivedis different kinds of sacrificial altars.

The understanding of the east-west line (Prachi) is crucial to the construction of all the altars and fireplaces in the Vedic literature, and this is very a fundamental concept discussed by Katyayana, unlike Baudhayana and Apastamba. Katyayana describes the Prachi thus:

समे शङ्कुं निखाय शङ्कुसम्मितया रज्ज्वा मण्डलं परिलिख्य यत्र लेखयोः शङ्कु-अग्रछाया निपतति तत्र शङ्कु निहन्ति सा प्राची |

same śaṅkuṃnikhāyaśaṅkusammitayārajjvāmaṇḍalaṃparilikhya yatra lekhayoḥ śaṅku-agrachāyānipatati tatraśaṅku nihanti sāprācī|

Fixing a pin (or gnomon) on level ground and drawing a circle with a cord measured by the gnomon, he fixes pins at points on the line (of the circumference) where the shadow (chhaya) of the tip of the gnomon falls. That is the prachi (Amma 1999). Aryabhata in his Ganitapada (Text 16) discusses further on chhaya:

छायागणितं छायाग्रविवरमूनेन भाजिता कोटी | शङ्कुगुणा कोटी सा छायाभक्ता भुजा भवति ||

chāyāgaṇitaṃ  chāyāgravivaramūnena bhājitā  koṭī|śaṅkuguṇā  koṭī  sā  chāyābhaktā  bhujā  bhavati ||

The distance between the tips of the shadows multiplied by the length of the shadow and divided by the difference between the two shadows is the koti. This koti multiplied by the length of the gnomon and divided by the length of the shadow gives the length of the bhuja (Amma 1999).

The terms visesa and savisesa appear frequently in the vedic mathematical tradition and deserves mention here. A reference to Vishesha can be seen in the Apastamba Shulbasutra II.2 in these words (Srinivasachar and Narasimhachar 1931):

पृष्ठयान्तयोर्मध्ये च शङ्कुं निहत्यार्धे तद्-विशेषमम्यस्य लक्षणं कृत्वा अर्धमागमयेत् | अन्तयोः पाशौ कृत्वा सविशेषं प्रतिमुच्य ...

pṛṣṭhayāntayormadhye caśaṅkuṃnihatyārdhe tad-viśeṣamamyasya lakṣaṇaṃkṛtvāardhamāgamayet | antayoḥpāśau kṛtvāsaviśeṣaṃpratimucya ...

Fixing pins at the ends and middle of the prsthya one should add to a cord of half the length its visesa, make a mark there and then add half the side again. Making nooses at the ends, and fixing the side with the visesa to the middle pin. It is worth noting that in the Shulba-sutras, $\left(\sqrt{2}-1\right)$ of any length is called its visesa. Another similar term savishesha appears in both the Baudhayana Shulbasutra (I.61-62) and Apastamba Shulbasutras (I.5):

प्रमाणं तृतीयेन वर्धयेत् तच्चतुर्थेन आत्मचतुस्त्रिंशोनेन सविशेषः |

pramāṇaṃtṛtīyena vardhayet taccaturthenaātmacatustriṃśonena saviśeṣaḥ|

The measure of the side of a square (pramaan) is to be increased by the third and this third again by its own fourth, followed by reduction with its thirty-fourth part; this is (the value of) the diagonal of a square (Kannan 2014). This is tantamount to saying that

$$\sqrt{2}a\left(savisheshaofa\right)=a+{\displaystyle \frac{a}{3}}+\left({\displaystyle \frac{a}{3\times 4}}\right)-\left({\displaystyle \frac{a}{3\times 4\times 34}}\right)+\dots$$

$$\left(\sqrt{2}-1\right)a\left(vishesha\right)={\displaystyle \frac{a}{3}}+\left({\displaystyle \frac{a}{3\times 4}}\right)-\left({\displaystyle \frac{a}{3\times 4\times 34}}\right)+\dots$$

In the Shulba, the calculated value of the diagonal of a square is technaically called the savishesha of its side. Datta (1932) has extensively discussed the terminologies visehesha and savishesha in light of the commentaries by prior historians of mathematics and his own analysis and concludes that it is that measure by which the diagonal (dvi-karani) exceeds the measure of one side of the square. It may quickly be added here that pramaan also conventionally signifies proof of a theorem (prameya or siddhanta).

The mainstay of the Plane geometry rests on two important factors: first, the relationship between base, height, and hypotenuse of a right triangle (erroneously known as the Pythagoras theorem), and second, the properties of similar figures (Dutta 2002). However, before we take a look at the shulba sutra statement of the so-called ‘Pythagoras theorem’, some terminologies need some mention. In the shulba, rajju has been used to refer to a line. For instance, Aksnya rajju refers to a diagonal line, tiryakmani refers to the transverse measure and parshvamanito the side measure, respectively. Figure 13 produces a visual demonstration of the shulbasutra theorem of the diagonal, which reads thus -

दीर्घचतुरसस्याक्ष्णया रज्जुः पार्श्वमानी तिर्यक्मानी च यत्पृथग्भूते कुरुतस्तद् उभयं करोति ||

dīrghacaturasasyākṣṇayā  rajjuḥ  pārśvamānī tiryakmānī ca yatpṛthagbhūte kurutastad ubhayaṃ  karoti

“The area of the square formed by the diagonal line equals the sum of the areas of squares produced by both the transverse and the side measure.”

Finally, it must be pointed out that the names of the stalwart proponents of mathematics in ancient India have registered in the Indian social psyche, which surfaces as the modern Indian names, albeit less frequently as compared to the concepts enunciated by them. The Indians have held such great exponents of mathematics in high regard. This overwhelming veneration naturally reflected in Indians naming their children based on their names, names of their treatises, or even their students sometimes, who were equally gifted and blessed by their knowledge of mathematics. For instance, modern India to date revers the name of Aryabhata, Brahmagupta, Baudhayana, Varaha-Mihira, Bhaskara as well as their treatises such as Trishatika(by Sridhara) and Leelavati(by Bhaskara II) . Among many acharyas of India, the names of these mathematicians are clearly unique, and upon finding someone of a similar name, it would not be an exaggeration to trace back its source. Such has been their impact and their contribution that their indelible impressions on the Indian society continues to remain, and possibly grow. A growing resurgence in such an awakening can be seen in the way India’s first earth satellite was named Aryabhata, and a subsequent satellite was named Bhaskara-II by ISRO, or for that matter, the Leelavati award being instituted by the International Mathematical Union. Truly, no account of Indian mathematicians would ever be complete without the mention of the author of Leelavati, Bhaskaracharya. Bhaskara II, as he is frequently called, will be forever regarded in the history of Indian mathematical tradition, for his compendiums including Siddhānta-Śiromaṇī and Karaṇa-kutūhala. And, of the various masterpieces of mathematics that he penned down, Līlāvatī deserves a special mention. Bhaskaracharya’s Leelavati is an exquisite compendium of not just mathematics, but also of an amazing pedagogy in mathematics education that continues to inspire mathematicians and teachers alike. His contribution in making mathematics interesting and available to the common man has been exemplary and has survived generations. And of the entire Līlāvatī, the last text is right to the point, as regards the current manuscript in question. The text reads thus:

येषां सुजाति-गुण-वर्ग-भूषिताङ्गी शुद्धाखिल-व्यवहृतिः खलु कण्ठसक्ता |

लीलावतीह सरसोक्तिम् उदाहरन्ती तेषां सदैव सुखसंपद् उपैति वृद्धिम् ||

- लीलावती २२८

yeṣāṃsujāti-guṇa-varga-bhūṣitāṅgī śuddhākhila-vyavahṛtiḥkhalu kaṇṭhasaktā |

līlāvatīha sarasoktim udāharantī teṣāṃsadaiva sukhasaṃpad upaiti vṛddhim ||

“This Līlāvatī clearly explains fractions, simple fractions, multiplication etc. It also beautifully describes problems in day-to-day transactions. Rules are transparent and examples are beautifully worded. Those who master this Līlāvatī will be happy and prosperous.”

Is that all? What makes this this text so special? Here is what: this text is actualy a double-entendre. The allusion to Līlāvatī in this text obviouly refers to the book Līlāvatī composed by Acharya Bhaskara. But, it also refers to the person Līlāvatī as well – the daughter of Acharya Bhaskara. Here is an alternative meaning to the same text:

“Girl Līlāvatī is born in a respectable family, stands out in any group of enlightened persons and has mastered idioms and proverbs. Whomsoever she embraces (marries) will be happy and prosperous.”

This suffices to establish that Leelavati today is a common name in modern India, despite it not being a short and pithy one. It can truly be argued extensively whether Leelvati in the current setting is a mathematical name, or it is an instance of involution phenomenon, since Bhaskara II named his text upon his daughter’s name. Be that as it may, the impact of the text Leelavati on the collective Indian social consciousness has been tremendous over centuries, and to suggest that the text itself may have inspired the names of individuals is a possibility that can be asserted with some certitude.

This is not all. While the current manuscript focuses on such instances of ‘mathematical names’ within the ambits of geometry, numeration, arithmetic, algebra, and the Vedic tradition, etc., a careful student of mathematics of the Indian tradition can very well extricate such names from virtually every aspect of mathematics such as statistics (viz. varg/antaraal: an interval; seema: upper/lower limit of an interval), probability (sanyog: probability), astronomy or astrology (prithvi: earth, yantraraj: astrolabes used for measuring astronomical measurements such as altitudes of celestial bodies and for calculation of latitudes in navigation), etc.

Figure 14 shows the quantitative evidence of the recurrence of the names based on mathematics in the Vedic/Indian tradition, as presented in Table 7, from the LI dataset. It presents the specific name recurrence fraction for fifty-one names based on terms from Vedic/Indian tradition, ${\widehat{n}}_{ve}$ in an alphabetical fashion. As the figure shows, the left axis denotes the name recurrence factor in the LI dataset, which multiplied by a hundred yields ‘recurrence percentage’. This figure evidently demonstrates that ${\widehat{n}}_{ve}$ varies between 2.37x10^-6 to 0.34. Further, some of the terms with the highest ${\widehat{n}}_{ve}$ are ‘pada’, ‘rajju’, ‘maruti’, ‘seema’ and ‘prachi’ with ${\widehat{n}}_{ve}$corresponding to 0.34, 0.29. 0.24, 0.17 and 0.09 respectively. On the other hand, terms like yantraraja, shredhi, savishesha, parshvamani, parishishta, and shulbi fare very low on the ${\widehat{n}}_{ve}$ value. Other terms which occur in the high-frequency range are vedi, mihira, prithvi, siddhanta, chaya, sutra, janu, etc. – names that can be very commonly heard in the Indian setting.

5.7. General Comments on All Six Categories

Considering the broad nature of these sub-categories, which are at times imbricated, it is difficult to provide an exact estimate of the mean and median occurrences for them. However, some general comparisons could be made based on the terms introduced in this paper. Figure 15a presents a comparison of the mean and median of the counts in each of these sub-categories. As the figure shows, the mean counts are maximum for arithmetic, with a value of 100370, followed by geometry (38526), mathematics in the Vedic tradition (27818), numeration (23203), algebra (20959), and trigonometry (18547). The median counts for algebra, arithmetic, geometry, numeration, trigonometry, and Vedic tradition are 995, 1800, 4900, 716, 258, and 301, respectively. Clearly, there is a slight difference in the median counts, with the values peaking for geometry. Although the mean counts for arithmetic exceed that of geometry because of a few names having large counts because of cross-cultural occurrence of names, but the considerably greater median count for geometry indicates that there exist more names that have a larger number of counts. Some more comparative insights could be gleaned from Figure 15b. The figure presents a cumulative frequency plot with ‘percentage in the LI dataset’ on the abscissa. It denotes what fraction (or percentage) of the total names within a sub-category are less than the percentage value on any point on the abscissa. For instance, the first point on the horizontal axis, at 0.01% represents the fraction of the number of names that are less than 0.01% in the LI dataset. It is obvious that around 12% of all the names in the ‘geometry’ category appear less than 0.01% in the LI dataset, whereas 30% of all the names in the ‘Vedic tradition’ division appear less than 0.01%. Another similar observation could be made at an x-axis value of 4%. In such a scenario, approximately 72% of the geometrical names appear less than 4% in the LI dataset, while for trigonometry based names, this number is as high as 92%. This observation also substantiates the greater prevalence of the names on geometrical concepts.

Finally, some more understanding can be gleaned from the responses collected from the bearers of such ‘mathematical names’. Interviews conducted with several students from higher educational institutions confirmed either explicit or implicit links between names and various life scripts especially mathematical consciousness and awareness; either of their own, their parents or whosoever named them. A significant population strongly feel and believe that the meaning and attributes attached to a name by virtue of the field of its origin (mathematics in this case) have an imprint on the person’s behavioral inclination because a majority of the names in Indian culture have deeper meanings are not merely ‘proper nouns’ with no meaning attached to it. A child is consciously made aware of his/her name right from childhood either by asking his/her name and by letting them know their meaning afterward. Subconsciously, this practice kept the mathematical consciousness alive over centuries which is evident from some of the responses like, ‘Now that I know that my name is mathematical/scientific, it feels so exciting’. It was interesting to note that in some cases, a person was named by his/her elder sibling who later happened to excel better in maths than the named person though the named person also has an inkling of interest and veneration for mathematics. An analysis of the survey results indicated that more than half of the participants (53%) thought that the name influenced their lives and shaped their life trajectories in subtle ways. Since it is relatively uncommon to possess a mathematical name, and much less with complete cognizance of it, such names are a significant element behind increasing self-confidence, as many interviewees remarked ‘‘It is amazing to know that I have such a rare and beautiful name,’’. Many others affirm to be aware of the mathematical overtones that permeate their name, and they feel unique about their name. More than 90% of the interviewees contend that they are happy with their names, and would not exchange it for something else, for instance on social media platforms. For almost the same percentage of people, such mathematical names serve as a tenuous link between them and the Indian culture they have not known much about. In about 60% of the participants who have such mathematical names, a discussion on their names brings about cultural reminiscences of their region and religion within their families or their own very selves, establishing that such mathematical names are indeed intrinsically grounded in Indian culture and are not mere chance events. Although most of the participants agree that in trying to name a ‘child’, they would choose a name that is pleasant and has positive connotations – and mathematical names provide them with a ‘positive explanation’ behind the rationale of their names. However, for some, life did not always pan out as intended at the moment of their naming, for instance, in cases where mothers and fathers were negotiating issues of difference and belonging in bringing up the children (Edwards and Caballero 2008). Thus, this study suggests the need for further empirical research into the life script formation in the context of such mathematical names. It would be worthwhile quantitatively exploring the extent of the impact a mathematical name has towards his or her general appreciation and aptitude in mathematics. Equally important is the investigation of how the attitude of individuals towards his or her name is a repercussion of the mathematical interest in individuals. Further research could reveal reflective, formative, and mutual relationships among names, life scripts, and particular behavior and aptitude in mathematics.

6. Conclusions

The detailed qualitative and quantitative analysis presented in this manuscript, along with the textual references and the survey of individuals with such names provide the underpinnings behind the suggested inter-relationship between mathematics and its impact on common culture and society in the form of names. Under the six categories of geometry, trigonometry, numeration, arithmetic, algebra, and mathematics in the Vedic/Indian tradition, a host of mathematical terms have been presented, which have been absorbed as names in the Indian society. Further, quantitative analysis for the six categories showed that under each of them, there are a few names under each category with significantly high name recurrence factors. The mean-median calculations and the cumulative frequency curves show that there are a relatively larger fraction of names based on geometry in India as compared to other categories. In addition, the abundance of feminine mathematical names rooted strongly in Indian culture, even more than the masculine names insinuates the association of mathematical education to the women in India. Moreover, it is worth noting that the concept of mathematical names as introduced in this research becomes obvious only when a comprehensive picture of the Indian mathematical tradition spanning the entire geographical boundaries of India is considered. When done so, as in this manuscript, such an interlink becomes patently obvious. Yet, some missing dots still need to be connected for a deeper understanding of this socio-mathematical phenomenon.

6.1. Are Mathematical Names in the Indian Tradition Semantic Chance Events?

It may be tempting to some to suggest that such ‘mathematical names’ may simply be a product of semantic chance or a mere resemblance to similar more prevalent terms in society and culture. Let’s take a brief look at the proposition of ‘semantic chance’. In fact, there has been limited research on the psychology behind the naming of children, particularly in the context of Indian culture. However, a subtle question warrants being asked here: can ‘unconscious factors’ simply be relegated to a blind ‘semantic chance’? There is clearly, little evidence to underpin this unsubstantiated hypothesis. On the other hand, one particular study with regard to the naming of children by Bell (2009), argues that unconscious factors have a significant role in many events that seem unpremeditated and may appear ‘blind chance’, but such unconscious factors bear a great impact upon the final result. Further, he even suggested that day-to-day observations indicate that within the sphere of mental life, hardly anything happens by chance. Extrapolating this understanding within the realm of the naming of children, he asserts that it is impossible for parents to choose a random name and it will invariably turn out to be significant for some reason (Bell 2009). There is no reason to deny that such an event is but a manifestation of the names lying in the undercurrents of the collective social consciousness. There have been multiple instances in other cultures of the world where such an observation can be made. Say, in the process of restoring names as exemplified by the solemn ceremony of reading out the names of Polish officers massacred in 1940 by the Soviet secret police in the Katyn Forest in Russia. Another example could be the case or when the names of the victims of Stalin’s crimes were read out during the day of political prisoners in the USSR in front of the Solovetsky Stone in Lubyanka Square in Moscow (Jagieła and Gębuś 2015). In fact, earlier in section 2, in the context of the Hindu ceremony of naming children, we have shown the consciousness of the parents, family and the larger society does have an instrumental role in this process. Further, the name-giving per se is hardly a random event ever in Hindu society, but a well-structured and organized, where an individual or group or individuals reflect inward, groping for deeper identities of the child or their own selves and even confer sound astrological principles, to arrive at the suitable name of a child.

Next, the possibility of a sheer resemblance with other terms in society and culture can be addressed. It is certainly true that some of the ‘mathematical names’ as proposed in the current manuscript can also be found in other components of Indian culture or can have a linguistically different meaning altogether, for instance, ‘vyas’ could denote ‘Sage Vedvyas’ and not the diameter of a circle. A similar observation was made in the context of differentiating a ‘mathematical name’ with an ‘involutory mathematical name’ as described in a prior section. However, a more careful examination is warranted in this regard. The current manuscript has selected different categories of mathematics and extricated mathematical names from a wide variety of the concepts within such divisions. For example, within the realm of arithmetic, all four basic operations, square and cube roots and the associated terms contributed a number of such names. So is true within the realm of geometry – where mathematical names emerged from the fundamental geometrical concepts such as a line, ray, dot or angles, arc, triangles, quadrilaterals, polygons, circles, three-dimensional surfaces, etc. Within the domain of numbers, the entire range of number line from zero to infinity were covered, sometimes even including multiple terms for the same number. On a similar vein, algebraic terms such as variables, equations and the algorithms, trigonometrical functions viz. sine and the cosine and the fire altars and their descriptions, measurement units etc. from the texts of shulbasutra all find an assimilation into the names of the Individual society. Notwithstanding that some ‘mathematical names’ may possess alternative meaning in common culture, the fraction of names with solely a mathematical connotation far exceeds them.While this may be self-evident for a majority of names, a deeper consideration is required for others. Consider, for instance, the name ‘viloma’ or ‘vyasta’. While an onlooker uninformed of Indian mathematics may surmise that such names signify the word ‘opposite’ and ‘busy’, respectively, it is doubtful that the children can be named after terms that are so obscure and uncomplimentary. A person conversant of the Indian trigonometry, however, can reveal that both these terms correspond to the versed sine. In view of this analysis presented, as well as the span of such terms within the realm of mathematics, this moot conjecture can be easily put to rest.

A closer scrutiny sheds light on another profound facet behind bestowing such mathematical names upon children. One often wonders why the new ones in a family would be named after inanimate mathematical objects such as a cone or a triangle if a value worth life is not associated with these terms themselves. Evidently, it makes little sense to address life with reference to the lifeless. Rather, an exactly antithetical observation can be frequently observed in the form of personification in the literary writings, whereby inanimate objects are portrayed with human emotions and characteristics. We are then left to conclude that the culture of mathematics in an Indian setting has been an extremely dynamic, lively, and vibrant one, even to the brink of touching spiritual truths. These names reflect impressions of the rich mathematical legacy of Indian stalwarts and thus attract a reverence in the Indian society, one that equals the reverence given to life itself.

6.2. Are Mathematical Names Unique to the Indian Tradition? A Deeper Insight

At this point, a question may be worth asking: are such mathematical names, or at least, the pervasiveness of it, unique to the Indian tradition? Or, is it something that may equally be found with other traditions such as Grecian, Islamic, or Chinese? While there is no reason to presuppose the exclusivity of Indian tradition in this regard, to the best of our knowledge, there are hardly any such reports that we have come across from other cultures. One probable reason is that it is unlikely to hear of names such as ‘John Circumference’ or ‘ Samuel Perimeter’ or the like. Such names are of course, not so common. However, what is more common, is a somewhat related phenomenon of ‘names in mathematics’, a trend perhaps set up by the European mathematicians post-renaissance period. Few examples would make things clearer in this regard. One could consider different equations, laws, or parameters in mathematics/physics, and one finds an effusively large number of such cases of ‘names in mathematics’. Consider, for instance, Jacobian or Hamiltonian, Bernoulli differential equation or Cauchy’s integral equation, Eulerian or Lagrangian perspectives, Newton’s laws of motion, Gauss-Seidel method, Newton-Fourier method, Weber’s equation, Poisson’s equation, Gregory series, Taylor’s series, Leibniz’s rule, Reynolds number, Prandtl number, etc. This list in the history of mathematics and science will probably be one of the longest one, and rightly so, beyond the scope of this paper.

This tendency of intromission of names in mathematics, however, had an obsessive fervor, when this was done despite a glaring antecedent. For instance, Brahmagupta gave an iterative algorithm to compute the square root of a number, which becomes later known as ‘Newton-Raphson iterative formula’; the expansion for ℼ given by Madhava of Sangamagrama and enunciated by Neelkantha Somyaji becomes known as the ‘Gregory series’; Series expansions for trigonometric functions given by Nilkantha Somyaji in his Tantrasangraha appears later as Taylor’s series, the mean-value theorem given by Bhaskaracharya afterwards becomes known as the Rolle’s theorem, finite difference interpolation given by Brahmagupta in his Khand-khadyaka is later christened as Newton-stirling approximation to second order differences, a rule for second-order interpolation proposed by Govindswamin in 800-850 CE resurfaces as Newton-Gauss interpolation formula, indeterminate quadratic equations such as 61x² + 1 = y² , whose solution and its algorithm was given by Brahmagupta, Jayadeva and Bhaskaracharya becomes known as the Pell’s equation and was popular as Fermat’s challenge problem. Similar is the case with how the sequence of numbers proposed by Virahanka in 700CE, based on Matra Meru of Pingala was introduced to the western world by Fibonacci and remains popular by his name to date, inscrutably similar in a way how the ‘shulbasutra’ theorem giving the relationship between squares of sides and diagonals is famously (but erroneously) popular as the Pythagoras theorem. In fact, the whole edifice of western mathematics as a secret weapon of cultural imperialism, that de-recognized contributions of other cultures including India, misappropriated credit to several mathematical discoveries and imposed its own version of western mathematics with a zealous Eurocentric spirit, has begin to surface with the modern evidence, of late (Bishop 1990, Joseph 2010).

Probably, this was a legitimate way of taking credit for one’s supposed contribution to mathematical advancements. Possibly, this was also a way of immortalizing one’s name in the annals of the history of mathematics/science. All this seems very plausible, at least, in the current context. But then, why was this tendency of naming mathematical concepts by one’s name to claim the ‘just credit’ for one’s achievements, not current in the Indian tradition? Well, this is not entirely correct. A large fraction of the Indian mathematical texts are in fact, well known by the mathematicians who authored them, and we even hear of Aryabhateeyam, Mahabhaskariya, Laghubhaskariya, or Leelavati. These texts are all named after a person. This was of course needed, to claim responsibility for authorship, as well as to clarify the disciplic succession of mathematicians to which the texts belonged – e.g., the Kerala school, Aryabhata school, or the Ujjyain school. But, going beyond that – inserting one’s name in every single concept, series, sequence, algorithm, or technique was not considered warranted. Rather, it seemed more logical to name things by their characteristics. For instance, the indeterminate quadratic equation such as Nx² + z = y², was classified as ‘Varg-Prakriti’, meaning an equation of the nature of square (i.e., a quadratic equation). Similarly, iterative solutions to such indeterminate equations were called chakravala, insinuating the cyclic algorithm. Or, for that matter, even a text on the rationale in mathematics was named as ‘Ganita Yukti Dipika’ meaning ‘a discourse on rationale in mathematics’ (Raju 2007). There was another subtle reason - Indian mathematicians differed profoundly from their European (or specifically, Grecian) counterparts since knowledge for its own sake was not valued so much by them. In the Indian context, every field of study (including mathematics) must have a purpose. And self-realization and the resulting deliverance from birth and death has been understood to be the legitimate purpose of life. Subsequently, those branches of knowledge that facilitated this ultimate end were pursued most meticulously. Hence, the science of astronomy was most actively researched and studied to help determine the exact auspicious date and time for the performance of sacrifices, and thus all those aspects of mathematics that aligned with this necessity (not the only one, though) got a strong boost (Amma 1999). To these Indian mathematicians, who had a clear grasp over the ephemeral nature of the manifest world and the eternality of the soul, the spirit of ‘taking credit’ was not of much significance. Although innovation was valued, identifying oneself as the innovator was not as important, as has been manifestly observed through the examples of Newton and Leibniz, who haggled nastily to take priority over calculus, although none of them actually deserved it in the first place since Bhaskaracharya’s work on calculus itself predated both of them by over half a millenium (Seal 1915, Sarkar 1918, Raju 2007). The spirit of argumentation and debate in scholarly circles is indeed a fairly old one, but the ambition of establishing one’s innovativeness to posteriority was unimaginable, as evinced by Newton threatening Hooke to withhold publication for securing a priority (Arnol’d 1990). How remote a possibility then it must have been, for mathematicians in the Indian tradition to insert one’s name into every nook and corner of their field of study? And what were the repercussions of their not doing so? All the laws of science or mathematics were available as common knowledge of the society, not wedded to each of these understandings was the name of an innovator who somehow ‘owned’ these. This open-ended non-ownership-based model of scientific development meant anyone educated in such fields of study could learn, comment and disseminate such knowledge to the qualified lot. It is this open-ended model of science that has led to the permeation of such mathematical names in the common Indian social psyche, observable to date.

To sum it up, in spite of a plethora of ‘names in mathematics’ in the western sphere, there is no such published account of the ‘mathematical names’. Although, one does hear sporadic names such as Mathilda, Mathilde and Mathea and less frequently after Newton, Taylor, Descartes, Euler, Pascal, Galileo, Euclid etc., detailed accounts are not available on Western, Chinese and Islamic mathematical names in the English language. Thus, to get a full picture of this socio-mathematical topic, a cross-cultural investigation is much warranted. However, some poised comments can be made on the Indian tradition of mathematics. As already stated, in the Indian tradition the roots of mathematics lie in facilitating a practical end of meeting the religious requirements. The geometry of the sulbasutras arises out of a need to ensure strict compliance of the orientation, shape, and area of the altars to the Vedic scriptural prescriptions since it was deemed absolutely essential for the performance of the sacrifices. Similarly, for Jains, the study of mathematics form one of their anuyogas or auxiliary science which was necessary for the attainment of the salvation of the soul (Rangacharya 1912). So, the study of mathematics and spirituality are invariably interlinked in the Indian tradition, and as a society of people driven by a spiritual purpose of life, the deep veneration towards spirituality has tacitly passed down in the form of a comparable reverence for mathematics. It is not surprising then, that India, with its profound roots in spirituality, the science of the soul, and also mathematics, carries these deep cultural impressions in the form of the names of its people.

6.3. Mathematics as an Instrument of Religion? A Cross-Cultural Comparison

Some passing comments need to be made on mathematics and its association with religion in India and Europe. Of course, many may even find it difficult to put mathematics and religion together, which according to them are exactly antithetical, being somewhat synonymous with ‘scientific’ and ‘primitive’, respectively. Such a perception is certainly not new but has been bolstered over centuries by various groups of Eurocentric scholars. For instance, early researchers on the Sulbasutras, most notably Thibaut (1875), who painstakingly buttressed the stereotypical view of an Indian society dominated by priests, overwhelmed by rituals and scientifically retrogressive ideas, and thus in dire dearth of mathematical and scientific genius (Joseph 2010). Thibaut proceeds with an unceremonious supposition that any true science must not have a practical bent, and thus he deems the science of the shulba to be ‘primitive’, since it is directed towards a practical purpose (Thibaut 1875). In his fervid endeavour of what can be rightly described as dogmatism compounded with error, he accentuates the religious element of these texts, conveniently ignoring the secular aspects of it. Since it is no exemplary scientific integrity to accept the ‘convenient’ and reject the ‘inconvenient’, a cautious examination of the mathematico-religious association across different cultures is required, to not be swayed by the usual diatribe that insidiously attempts to nullify the rich heritage of scientific and mathematical ingenuity, using religion as a convenient scapegoat.

In the European context, the ‘Elements’ can justly be regarded as a mathematical classic, ascribed to ‘Euclid’. The arrangement of its theorems is aligned with Proclus’ idea of mathematics meaning ‘by derivation’ or ‘the science of learning’, or more generically, ‘learning on the basis of what has been previously learned’. Such an idea was promulgated right from the time of Socrates. Socrates, in his famous ‘slave boy experiment’, had put a series of questions to a slave boy, ignorant of geometry, and showed that he has capable of learning a convoluted geometrical problem. Since all Socrates did was ask questions and did not ‘teach’ him anything – he posited all learning to be a reminiscence of the knowledge the ‘soul’ had acquired in previous lives and hence his postulate that the soul is immortal (Bluck 1961). Similarly, Plato conceived that the study of geometry is uplifting to the soul and thus students in Plato’s Republic were required to study geometry. Plato’s belief was that geometry is the knowledge of the eternally existent, and thus it impels one to look within and contemplate the totality of existence. As a spiritual exercise that turns one away from the empirical considerations to the certain truths, Plato’s firm conviction in this role of mathematics is reflected in his statement – “if it (geometry) only forces the changeful and perishing upon our notice, it does not concern us”. In line with Socrates and Plato, Proclus too believed in the eternality of the soul and that the soul was stirred by the eternal mathematical truths, which pertain to the eternal cosmos (Raju 2007). Proclus’ philosophy of mathematics and its interrelationship with religious beliefs were in stark contrast with the Augustinian doctrines of resurrection, creation, and apocalypse. Proclus considered mathematics as an instrument of religion and used geometry as a tool to advocate political equity. Proclus too, held that mathematics is not valuable so much for its practical applications, but because it leads to knowledge of the soul. In other words, for Proclus, mathematics was a technique to make a person more meditative, and help him go inward. In fact, a similar interlink between association between mathematics and religion proposed by Proclus prevailed in the consequent rational theology of the Islamic tradition, aql-i-kalam (Raju 2006).

In comparison to the European and Islamic tradition, where mathematics was used as an instrument of religion and was associated with religious beliefs, Indian mathematics although, aligned with the spiritual and religious needs, was invariably directed to a practical end and not an end into itself. This is indeed such a stark difference that this reiterates our earlier statement that in India, knowledge for the sake of it was not valued so much. So, geometry in the sulbasutra wasn’t targetted towards a spiritual end, but to prepare a brick structure as per the Vedic directions (Raju 2007). Similarly, contrary to the Plato-Procluvian tradition, calculations were valued and taught for their use in commercial transactions (e.g., Leelavati), mensuration, and for practical applications in navigation with astronomy and timekeeping. Even in the matter of proofs, unlike the Grecian counterparts, the Indian mathematicians did not attempt to build an edifice of geometry on self-evident axioms, but simply to convince an intelligent learner of the validity of the theorem and hence visual illustration was considered an acceptable form of proof (Amma 1991). Similarly, infinite series expansions for sine, cosine, and arctan functions were developed in the pursuit of determining the length of the arc, since Indian geometry was cord or rope-based. Since Indians used a flexible rope (and not a rigid ruler) for measurement, the length of the arc did not pose a conceptual problem, whereas even a champion of metric geometry in Europe such as Descartes, wrote in his La Geometrie, that measuring the length of a curved line was ‘beyond the capacity of the human mind’ (Raju 2007).

An average Indian learner of the modern era seems to have a sheer rough grasp over the rich antecedent or even the extant legacy of mathematics of this land, but rather laments (if at all he is informed enough) of India’s disjunction with her “past glory” since one can’t trace many clear markers of it. We have however provided an insight into the extant remains of the immensely rich and diverse mathematical heritage of India that can yet be perceived indirectly through the medium of the names of its people. It is a sincere hope that the current study establishes the interconnection between the present names of Indians with its collective social psyche, formed by a rich precedent of the mathematical legacy of centuries. It is expected that the current study should provide some substantial food for thought to the students of ‘mathematics and culture’, who explore the roots of mathematics across different civilizations of the world. It would be truly interesting to see similar studies from different cultures of the world, as we inch along for a more complete outlook. However, till then, as one exercises his/her liberty to take perspectives on matters pertaining to the history of mathematics or civilizations in general, it would be amiss to be oblivious to the obvious regarding the mathematical names in the Indian society. At the very least, when seen from this perspective, a decorous response to the classical Shakespearean question ‘What’s in a name?’ seems an emphatic and befitting – ‘There is indeed a lot in the names’.