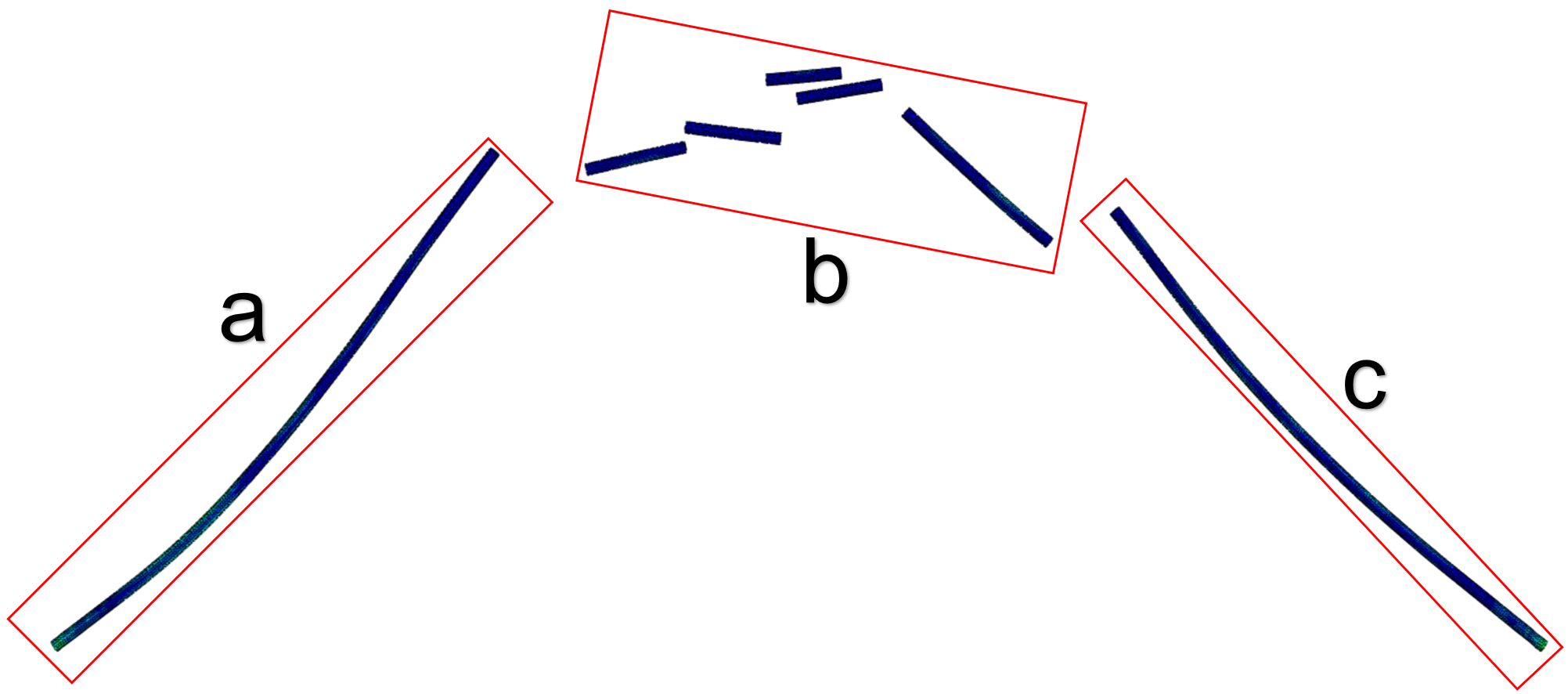
Why are pieces of spaghetti generally broken into three to ten segments instead of two as one thinks? How can one obtain the desired number of fracture segments? For these problems, in this paper a strand of spaghetti is considered an elastic rod, and the finite-element software ABAQUS is used to simulate the detailed fracture dynamics of the elastic rod. By changing the size (length and diameter) of the rod, the relevant data on the fracture limit curvature and the number of fractured segments of the elastic rod are obtained. The ABAQUS simulation results confirm the scientific judgment of B. Audoly and S. Neukirch (Fragmentation of rods by cascading cracks: Why spaghetti does not break in half. Phys Rev Lett 95: 095505). Using dimensional analysis to fit the finite-element data, two relations of the elastic rod fracture dynamics are obtained: (1) the relationship between the fracture limit curvature and the diameter, and (2) the relationship between the number of fracture segments and the diameter-length ratio. Results reveal that when the length is constant, the larger the diameter (the smaller the diameter-length ratio D/L), the smaller the limit curvature; and the larger the diameter-length ratio D/L, the fewer the number of fractured segments. The relevant formulations can be used to obtain the desired number of broken segments of spaghetti by changing the diameter-to-length ratio.