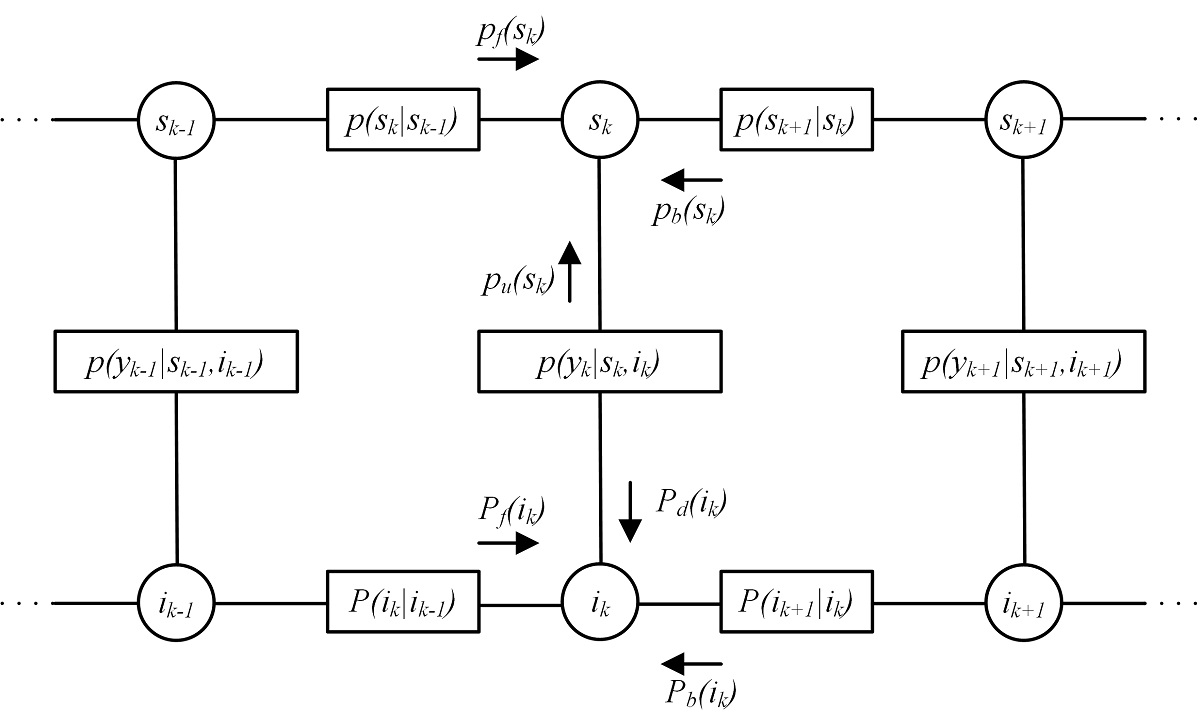
Impulsive noise is the main limiting factor for transmission over channels affected by electromagnetic interference. We study the estimation of (correlated) Gaussian signals in an impulsive noise scenarios. In this work, we analyze some of the existing as well as some novel estimation algorithms. Their performance is compared, for the first time, for different channel conditions, including the Markov-Middleton scenario, where the impulsive noise switches between different noise states. Following a modern approach in digital communications, the receiver design is based on a factor graph model and implements a message passing algorithm. The correlation among signal samples as well as among noise states brings about a loopy factor graph, where an iterative message passing scheme should be employed. As it is well known, approximate variational inference techniques are necessary in these cases. We propose and analyze different algorithms and provide a complete performance comparison among them, showing that both Expectation Propagation, Transparent Propagation, and the Parallel Iterative Schedule approaches reach a performance close to the optimal, at different channel conditions.