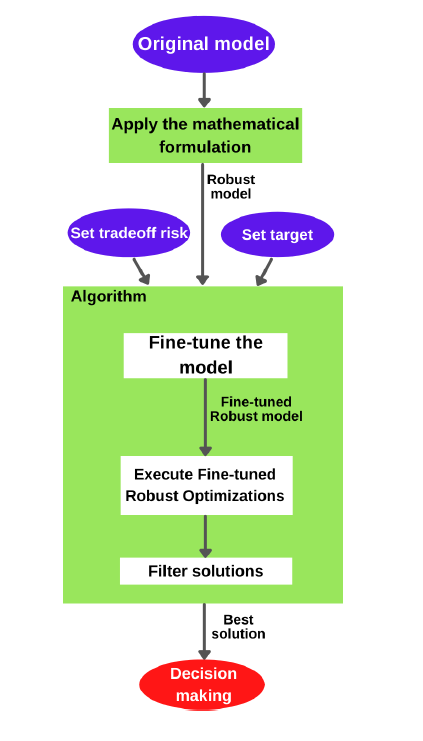
A Robust Optimization framework with original concepts and fundamentals also admitting a fusion of ideals from relative regret models and static robust optimization, containing conservatism concepts is disclosed. The algorithm uses a fine-tune strategy to tune the model so the robustness and a target ideality can be mutually achieved with a specified risk. The framework comprises original concepts, a mathematical approach and an algorithm. The statistical treatment of the data with the original concepts from the framework make it able to make short, middle or long-term decision-making setting. The framework has high tractability since the algorithm forces the creation of a setting that makes a robust optimization with the specified risk. The framework can be applied in linear and nonlinear mathematical models since that the objective function is monotonic in the domain of the active convex region. Several examples are solved to best understand the framework and all results demonstrated high tractability and performance. There is a wide range of applications. Along all the text, there is a profound discussion about its philosophy, objective, original concepts, fields of application, statistical and probabilistic fundamentals.