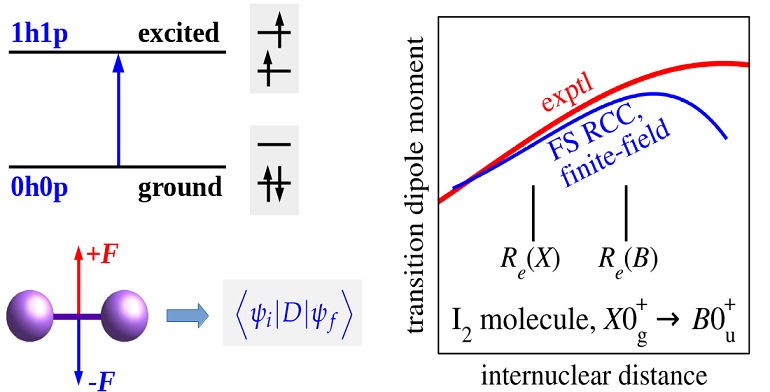
Reliable information on transition matrix elements of various property operators between molecular electronic states is of crucial importance for predicting spectroscopic, electric, magnetic and radiative properties of molecules. The finite-field technique is a simple and rather accurate tool for evaluating transition matrix elements of first-order properties in the frames of the Fock space relativistic coupled cluster approach. We formulate and discuss the extension of this technique to the case of transitions between the electronic states associated with different sectors of the Fock space. Pilot applications to the evaluation of transition dipole moments between the closed-shell-like states (vacuum sector) and those dominated by single excitations of the Fermi vacuum (the $1h1p$ sector) in heavy atoms (Xe, Hg) and simple molecules of heavy element compounds (I${}_2$, TlF) are reported.